Конустық
бет
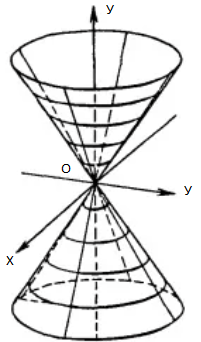
Берілген В сызығын қиып өткен
және белгілі бір Р нүктеден өтетін түзуден тұратын бетті конустық
бет дейді. Берілген В түзуін конустық беттік бағыттауышы, ал Р
нүктені оның төбесі, ал бетті құрайтын түзулерді оның жасаушылары
дейді.
+
-
=0
(1)
болады.Бұл беттің төбесі
координатадағы схемасының симметрия осіне
ұқсас.
- + =0;
- + + =0
(2)
Конус төбесінің координаталар
сақинасының бас нүктесінде симметрия ға сәйкес және
о
осьтері
болады.
25
=0 конусы у=2
жазықтығымен қалай қиылысады?
Шешуі: Конустың теңдеуіндегі
у-тың орнына у=2 жазықтығының теңдеуін
қойсақ
=0
немесе 
-
=1 теңдеуі
алынады.
Бұл теңдеу у=2 теңдеуімен
алынған жазықтығында жататын гипербола түзеді. Бұл гиперболаның
нақты осі Р осына параллель , ал жартылай осі ох осіне параллель
болып табылады.
Демек,
=0 конусы у=2
жазықтығымен жартылай бойынша қиылысады.
26
№2. Конустың бағыттаушы
теңдеуі, элементтің теңдеуімен 
+
=1,
=3 анықталады және
төбесі В (0;0,1) нүктесінде орналасқан конустың бетінің теңдеуін
табыңыздар.
Шешуі: Конустың АВ
құраушысының координаталарынтабайық. Мұнда В (0;0,1) және А (х,
у, 
нүктесіндегі өлшемінің
нүктелері болады. СондықтанАВ жасауышының
теңдеуі
=
Сондай-ақ А нүктесі эллипсте
жататындықтан, оның координаталарының осі эллипстің теңдеуін
қанағаттандырады, яғни
+
0
27
Конустық осьтің төбесі
координаталары сақинасының осьтерінде және жазықтығында
болады.
(1)
Осьінің сақиналарымен
бағытталған. Конустық беттін теңдеуін
құрыңдар.
Шешуі: Конустық беттің
жасаушысының 0(0,0,0) нүктесінен өтетін және (х,
у, арасынан өтетін
бағыттауышының теңдеуі
-
(2)
болады. Енді (1), (2)
теңдеуден х пен у – ті тапсақ, онда
х
у
Осы табылған х пен у-ті (1)-ге
қоссақ,
+
*
немесе 
*
Демек, алынған теңдеу екінші
ретті конустық бетті анықтайды. 29
№5 Конустың беттерінің
координаталарының сферасы жанама болады және координаталар
системасында бас нүктесінен өтеді. Осы конустық беттің теңдеуін
табыңыздар.
Шешуі: Конустық беттің
жасаушысы
*
теңдеулерімен анықталады.
Мұнда m мен n параметрлері жасаушылары мен сферасының жанамалығын
анықтау қажет. Бұл шарт, жасаушы мен сфералары-ның теңдеулерін
қосып шыққан кезде, квадрат теңдеуге алып келеді,
яғни
(
-
+(
+
+ 2 
(
+1) -2(
Сонда осы теңдеудің
дискриминантты
D
(
-
-16( +1)
Нольге тең болуы тиіс. Соңғы
шарттардан және m мен n параметрлерінің
теңдеулерінен, конустық беттің (у-
-10
=0 теңдеуі
алынады.
Демек,
(х- +(у+ +
=16 сферасына жанама
болатын коррдинаталар сақинасының бас нүктесінен өтетін жанама
теңдеу (у- -10 =0 болады.
30
Төбедегі координаталар
сақинасының бас нүктесінде және бағыттауышында
; 
=с болатын конустың
теңдеуін табыңыздар.
Шешуі: Конустық беттің
жасаушысы 0(0,0,0) нүктесінде және нүктесінен өтетін бағыттауышысі
(х, у, нүктесінен өтетін
теңдеу
(1)
түрінде жазылады. Бұл
теңдеуден
;
немесе
х
,
у
Табылған мәндерді (1)-ге
қоссақ, онда
+
немесе 
- .
Демек, конустың
теңдеуі - болады.
31
Енді
Х0,
У0,
0
нүктелері эллипсте
жатқандықтан,
,
, 
теңдеулерінде келтірілген
теңдіктерді қанағаттандырады.Сондықтан
-
Демек, конустың
теңдеуі - түрінде
жазылады.
х2+у2-2 2 теңдеуімен берілген
конус, у
жазықтықпен қандай бет
бойында қиылысады?
Шешуі: Берілген
х2+у2-2 2
у теңдеулерден
х2+у2 немесе 
=1
теңдеуі алынады. Сондықтан,
у жазықтығында жатқан
нақты осі О осіне параллель және
ижорымал осі ОХ осіне параллель болатын гиперболаны
анықтайды.
Демек, үйлесімді қиылысу
сызығы, у жазықтығында жататын
гипербола болады.
16 Қырқүйек 2024
161
0 рет жүктелген
