Тахиржанова Гавхор Адхамовна
"Күрделі тригонометриялық теңсіздіктерді шешу әдістері"
Аннотация
Мақалада теориялық және дидактикалық мазмұндағы мәселелер, «Күрделі тригонометриялық теңсіздіктер»тақырыбын оқыту әдістемесі қарастырылған.Оқытудың тиімділігі мен қолданбалы бағытын арттыру үшін көптеген маңызды факторлар ескерілген,атап айтқанда,осы тақырып бойынша бірқатар практикалық тапсырмалар ұсынылған.
Summary
This article is devoted to questions of theoretical and didactic content, methods ofteaching the topic. To improve the efficiency and appliedorientation of training a number of important factors taken into account,in particular,itoffersanumberofpracticalproblemsonthistopic.
Тригонметриялық теңсіздіктерді шешу - сандық теңсіздіктерді шешу, сандық теңсіздіктер жүйесін шешу сияқты маңызды тақырыптармен сәйкес келеді.
Бірлік шеңбер арқылы тригононметриялық теңсіздіктерді шешу теңсіздікті көрнекі түрде шығарып жауабын жазып алуда өте ыңғайлы.
Есептеудің алгоритмі:
-
Бірлік шеңбер сызамыз;
-
х-тың берілген теңсіздікті қанағаттандыратын мәндеріне а-дан үлкен немесе тең, кіші немесе оған тең болады;
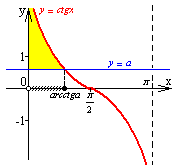
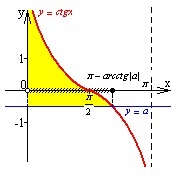
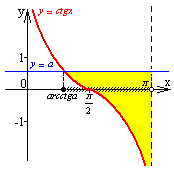
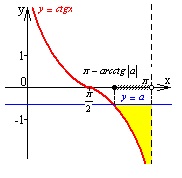
-
Берілген мәнді шеңберге енгізіп, пайда болған доғаға байланысты сағат тіліне қарама-қарсы бағытта қозғалысын анықтаймыз;
-
Пайда болған аралықта теңсіздіктің шешімін табамыз;
-
Сәйкес кері тригонометриялық функцияның мәнін ескеріп, бас аралықтың шеткі нүктелерінің абсциссаларының мәнін табу;
-
Тригонометриялық функцияның периодтылық қасиетін пайдаланып, теңсіздіктің жалпы шешімін жазу.
Теңсіздіктерді тез, әрі жылдам шешу үшін мына шеңберді пайдаланған ыңғайлы:
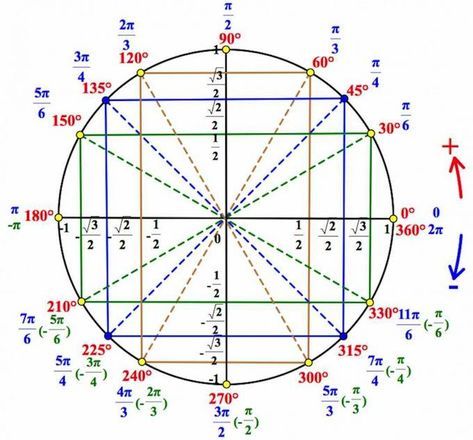
Білім алушылар уақыттарын жоғалтпастан нақты дұрыс жауап ала алады.
1 есеп.  теңсіздігін шеш.
теңсіздігін шеш.
Шешуі: 1.  түріне келтірген
соң
түріне келтірген
соң
2. y =
sinx синусоидасы мен  түзуінің графиктерін бір координаталық жазықтыққа саламыз.
Синусойданың түзуден жоғары орналасқан координаталар басына ең
жақын (не координата басы арқылы өтетін сары түспен ерекшеленген)
аралықты табамыз.
түзуінің графиктерін бір координаталық жазықтыққа саламыз.
Синусойданың түзуден жоғары орналасқан координаталар басына ең
жақын (не координата басы арқылы өтетін сары түспен ерекшеленген)
аралықты табамыз.
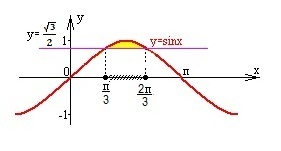

Бас аралық  , y = sinx функциясы периодты
болғандықтан ұзындығы бас аралыққа тең шексіз көп аралықтар бар,
демек, берілген теңсіздіктің шешімі:
, y = sinx функциясы периодты
болғандықтан ұзындығы бас аралыққа тең шексіз көп аралықтар бар,
демек, берілген теңсіздіктің шешімі:  болады,
болады,  -ге мүшелеп
-ге мүшелеп
көбейтіп х-ті табамыз.
Жауабы: 
2 есеп.  теңсіздігін шеш.
теңсіздігін шеш.
Шешуі: 1.
 және
және  графиктерін саламыз.
графиктерін саламыз.
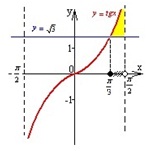

Бас аралық: 
2.Қос теңсіздік:
 .5-ке мүшелеп
көбейтсек,
.5-ке мүшелеп
көбейтсек,
 болады.
болады.
Жауабы: 
 3 есеп.
3 есеп.  теңдеуін шеш.
теңдеуін шеш.
Шешуі: 1.  түріне
келтіреміз
түріне
келтіреміз
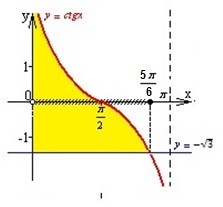
2. График : y=ctgx пен
y= графиктерін бір
жазықтыққа саламыз.
графиктерін бір
жазықтыққа саламыз.
Бас аралық : 
3.Қос
теңсіздік:  ,
,  -ке мүшелеп көбейтеміз.
Сонда
-ке мүшелеп көбейтеміз.
Сонда
 болады.
болады.
Жауабы: 
4 есеп.  теңдеуін шеш.
теңдеуін шеш.
Шешуі: 1. 
2. y=cosx , y= функцияларының графиктерін бір
жазықтыққа саламыз.
функцияларының графиктерін бір
жазықтыққа саламыз.
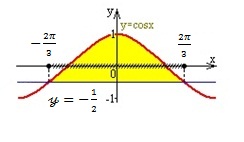

Бас аралық: 
3.Қос теңсіздік:

 +
+ 

 ;
;
 / .
/ . 

Жауабы: 
Қарапайым тригонометриялық теңсіздіктерді шешу кестелері
|
№ |
Теңсіздік |
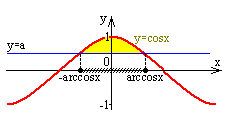
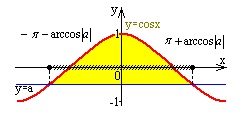
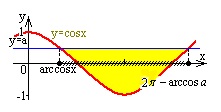
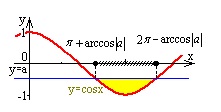
а |
графиктер |
шешімдер |
|
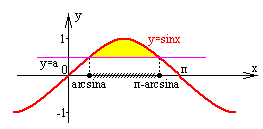
1 |
синусойда жоғары |
0<a<1 |
|
|
|
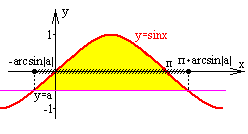
2 |
синусойда жоғары |
-1<а<0 |
|
|
|
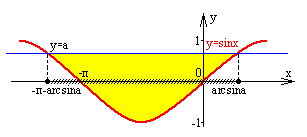
3 |
синусойда төмен |
0<a<1 |
|
|
|
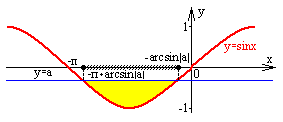
4 |
синусойда төмен |
-1<a<0 |
|
|
|
5 |
косинусойда жоғары |
0<a<1 |
|
|
|
6 |
косинусойда жоғары |
-1<a<0 |
|
|
|
7 |
косинусойда төмен |
0<a<1 |
|
|
|
8 |
косинусойда төмен |
-1<a<0 |
|
|
|
9 |
тангенсойда жоғары |
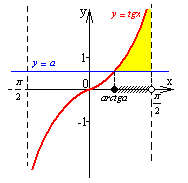
a>0 |
|
|
|
10 |
тангенсойда жоғары |
a<0 |
|
|
|
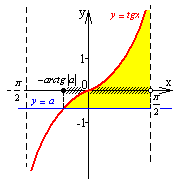
11 |
тангенсойда төмен |
a>0 |
|
|
|
12 |
тангенсойда төмен |
a<0 |
|
|
|
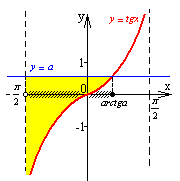
13 |
котангенсойда жоғары |
a>0 |
|
|
|
14 |
котангенсойда жоғары |
a<0 |
|
|
|
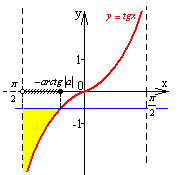
15 |
котангенсойда төмен |
a>0 |
|
|
|
16 |
котангенсойда төмен |
a<0 |
|
|

Пайдаланылған әдебиеттер:
А.Е.Абылкасымова, З.А.Жумагулова "МЕКТЕП"-2019
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Күрделі тригонометриялық теңсіздіктерді шешу әдістері
Күрделі тригонометриялық теңсіздіктерді шешу әдістері
Тахиржанова Гавхор Адхамовна
"Күрделі тригонометриялық теңсіздіктерді шешу әдістері"
Аннотация
Мақалада теориялық және дидактикалық мазмұндағы мәселелер, «Күрделі тригонометриялық теңсіздіктер»тақырыбын оқыту әдістемесі қарастырылған.Оқытудың тиімділігі мен қолданбалы бағытын арттыру үшін көптеген маңызды факторлар ескерілген,атап айтқанда,осы тақырып бойынша бірқатар практикалық тапсырмалар ұсынылған.
Summary
This article is devoted to questions of theoretical and didactic content, methods ofteaching the topic. To improve the efficiency and appliedorientation of training a number of important factors taken into account,in particular,itoffersanumberofpracticalproblemsonthistopic.
Тригонметриялық теңсіздіктерді шешу - сандық теңсіздіктерді шешу, сандық теңсіздіктер жүйесін шешу сияқты маңызды тақырыптармен сәйкес келеді.
Бірлік шеңбер арқылы тригононметриялық теңсіздіктерді шешу теңсіздікті көрнекі түрде шығарып жауабын жазып алуда өте ыңғайлы.
Есептеудің алгоритмі:
-
Бірлік шеңбер сызамыз;
-
х-тың берілген теңсіздікті қанағаттандыратын мәндеріне а-дан үлкен немесе тең, кіші немесе оған тең болады;
-
Берілген мәнді шеңберге енгізіп, пайда болған доғаға байланысты сағат тіліне қарама-қарсы бағытта қозғалысын анықтаймыз;
-
Пайда болған аралықта теңсіздіктің шешімін табамыз;
-
Сәйкес кері тригонометриялық функцияның мәнін ескеріп, бас аралықтың шеткі нүктелерінің абсциссаларының мәнін табу;
-
Тригонометриялық функцияның периодтылық қасиетін пайдаланып, теңсіздіктің жалпы шешімін жазу.
Теңсіздіктерді тез, әрі жылдам шешу үшін мына шеңберді пайдаланған ыңғайлы:

Білім алушылар уақыттарын жоғалтпастан нақты дұрыс жауап ала алады.
1 есеп.  теңсіздігін шеш.
теңсіздігін шеш.
Шешуі: 1.  түріне келтірген
соң
түріне келтірген
соң
2. y =
sinx синусоидасы мен  түзуінің графиктерін бір координаталық жазықтыққа саламыз.
Синусойданың түзуден жоғары орналасқан координаталар басына ең
жақын (не координата басы арқылы өтетін сары түспен ерекшеленген)
аралықты табамыз.
түзуінің графиктерін бір координаталық жазықтыққа саламыз.
Синусойданың түзуден жоғары орналасқан координаталар басына ең
жақын (не координата басы арқылы өтетін сары түспен ерекшеленген)
аралықты табамыз.


Бас аралық  , y = sinx функциясы периодты
болғандықтан ұзындығы бас аралыққа тең шексіз көп аралықтар бар,
демек, берілген теңсіздіктің шешімі:
, y = sinx функциясы периодты
болғандықтан ұзындығы бас аралыққа тең шексіз көп аралықтар бар,
демек, берілген теңсіздіктің шешімі:  болады,
болады,  -ге мүшелеп
-ге мүшелеп
көбейтіп х-ті табамыз.
Жауабы: 
2 есеп.  теңсіздігін шеш.
теңсіздігін шеш.
Шешуі: 1.
 және
және  графиктерін саламыз.
графиктерін саламыз.


Бас аралық: 
2.Қос теңсіздік:
 .5-ке мүшелеп
көбейтсек,
.5-ке мүшелеп
көбейтсек,
 болады.
болады.
Жауабы: 

 3 есеп.
3 есеп.  теңдеуін шеш.
теңдеуін шеш.
Шешуі: 1.  түріне
келтіреміз
түріне
келтіреміз
2. График : y=ctgx пен
y= графиктерін бір
жазықтыққа саламыз.
графиктерін бір
жазықтыққа саламыз.
Бас аралық : 
3.Қос
теңсіздік:  ,
,  -ке мүшелеп көбейтеміз.
Сонда
-ке мүшелеп көбейтеміз.
Сонда
 болады.
болады.
Жауабы: 
4 есеп.  теңдеуін шеш.
теңдеуін шеш.
Шешуі: 1. 
2. y=cosx , y= функцияларының графиктерін бір
жазықтыққа саламыз.
функцияларының графиктерін бір
жазықтыққа саламыз.


Бас аралық: 
3.Қос теңсіздік:

 +
+ 

 ;
;
 / .
/ . 

Жауабы: 
Қарапайым тригонометриялық теңсіздіктерді шешу кестелері
|
№ |
Теңсіздік |
а |
графиктер |
шешімдер |
|
1 |
синусойда жоғары |
0<a<1 |
|
|
|
2 |
синусойда жоғары |
-1<а<0 |
|
|
|
3 |
синусойда төмен |
0<a<1 |
|
|
|
4 |
синусойда төмен |
-1<a<0 |
|
|
|
5 |
косинусойда жоғары |
0<a<1 |
|
|
|
6 |
косинусойда жоғары |
-1<a<0 |
|
|
|
7 |
косинусойда төмен |
0<a<1 |
|
|
|
8 |
косинусойда төмен |
-1<a<0 |
|
|
|
9 |
тангенсойда жоғары |
a>0 |
|
|
|
10 |
тангенсойда жоғары |
a<0 |
|
|
|
11 |
тангенсойда төмен |
a>0 |
|
|
|
12 |
тангенсойда төмен |
a<0 |
|
|
|
13 |
котангенсойда жоғары |
a>0 |
|
|
|
14 |
котангенсойда жоғары |
a<0 |
|
|
|
15 |
котангенсойда төмен |
a>0 |
|
|
|
16 |
котангенсойда төмен |
a<0 |
|
|

Пайдаланылған әдебиеттер:
А.Е.Абылкасымова, З.А.Жумагулова "МЕКТЕП"-2019

шағым қалдыра аласыз