
МАЗМҰНЫ
КІРІСПЕ ........................................................................................................................3
І. КҮШТЕР ТӘСІЛІ.....................................................................................................4
1.1. Күштер тәсілінің негізгі теңдеулер жүйесі.........................................................4
1.2. Бас кернеулерді есептеу........................................................................................8
ІІ. НҮКТЕДЕГІ ДЕФОРМАЦИЯЛАНҒАН КҮЙ.....................................................17
2.1. Жазық кернеулi күйде материал деформациясы...............................................17
2.2. Деформация кезінде материал көлемінің өзгеруі.............................................18
ҚОРЫТЫНДЫ ............................................................................................................24
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР........................................................................25
КІРІСПЕ
Мәшине жасау саласында сырықтар жүйесі және жақтаулар статикалық анықталмағандығын анықтауда күштер тәсілі кеңінен қолданылады. Оның мәнiсi мынада: берілген статикалық анықталмайтын жүйе сыртқы және өзара қосымша байланыстардан босатылып, олардың әсерi күштермен және моменттермен ауыстырылады. Олардың шамасын байланыстан босатылған жүйеге қойылатын орын ауыстыру шектеулерге сәйкес келетіндей eтiп тандайды. Сонымен, көрсетiлген әдiспен шешу кезiнде күштер бeлгiciз болады. «Күштер тәсілі» деп аталуы да содан. Мұндай әдiс бipey ғана емес. Құрылыс механикасын басқа да тәсілдер, мәселен, бeлгiciз ретінде күш әсері емес, сырықтар жүйесі элементтеріндегi орын ауыстыру алынатын деформация әдiсі пайдаланылады.
Сонымен, кез келген жақтаудың статикалық түрде анықталмағандығын анықтау қосымша байланыстарды алып тастаудан басталады. Қосымша байланыстардан босатылған жүйе статикалық анықталған болады. Ол негізгi жүйе деп аталады. Әрбiр статикалық анықталмаған сырықтар жүйесі үшін әдетте негізгі жүйелердi қалауымызша таңдауға болады. Мысалы, жақтау үшін көрсетілгендей негізгі жүйелердi (а, б, в. г, д) ұсынуға болады. Олар қосымша жеті байланыста әр алуан жолмен алып тастау арқылы алынған.
Пуассон
коэффициентi. Ұзару деформациясы оң, қысқару терiс делiнедi. (40)
формуласы сызықты кернеулi күйдегi Гук заңын өрнектейдi. Көлемдiк кернеулi күйде
тiк кернеулер мен ұзарудың ұқсас қатынасын тағайындаймыз. Өйткенi кiшi деформация кезiнде
жанама кернеулер тiк бұрышты элемент жақтарының ұзындығын өзгертпей, тек ығысуды тудырады.
Мұнда
элементтiң тек
сызықты
деформациялары қарастырылады. Ығысу деформациясына IV тарауда
тоқталамыз. ![]() және
және ![]() деформацияларды
деформацияларды ![]() және
және ![]() арқылы өрнектеп табамыз. Ол үшiн күштер әсерiнiң тәуелсiздiк принципiн
және (40)
және (41)
формулаларындағы қатынастарды пайдаланамыз
арқылы өрнектеп табамыз. Ол үшiн күштер әсерiнiң тәуелсiздiк принципiн
және (40)
және (41)
формулаларындағы қатынастарды пайдаланамыз ![]() кернеуi бағытымен
кернеуi бағытымен ![]() салыстырмалы ұзарудың косындысын үш қосылғышпен өрнектеуге болады.
салыстырмалы ұзарудың косындысын үш қосылғышпен өрнектеуге болады.
Сонымен бipгe жетi байланысы алынып тасталатын жүйені негізгі деп алуға болмайтынын ескеру қажет. 12-суретте жетi байланысы алынып тасталған жақтаудың үш түрi көрсетiлген. Бұл дұрыс емес, өйткені қалған байланыстар жүйенің кинематикалық өзгермейтіндiгін және барлық түйіндерде статикалық анықталатынын қамтамасыз ете алмайды. Қосымша байланыстарды алып тастағаннан кейiн, жүйе статикалық анықталынатын болғанда жоғарыда айтқанымыздай байланыс орнына бeлгiciз күш әсерлерiн ендiру керек.
І. КҮШТЕР ТӘСІЛІ
1.1. Күштер тәсілінің негізгі теңдеулер жүйесі
Мәшине жасау саласында сырықтар жүйесі және жақтаулар статикалық анықталмағандығын анықтауда күштер тәсілі кеңінен қолданылады. Оның мәнiсi мынада: берілген статикалық анықталмайтын жүйе сыртқы және өзара қосымша байланыстардан босатылып, олардың әсерi күштермен және моменттермен ауыстырылады. Олардың шамасын байланыстан босатылған жүйеге қойылатын орын ауыстыру шектеулерге сәйкес келетіндей eтiп тандайды. Сонымен, көрсетiлген әдiспен шешу кезiнде күштер бeлгiciз болады. «Күштер тәсілі» деп аталуы да содан. Мұндай әдiс бipey ғана емес. Құрылыс механикасын басқа да тәсілдер, мәселен, бeлгiciз ретінде күш әсері емес, сырықтар жүйесі элементтеріндегi орын ауыстыру алынатын деформация әдiсі пайдаланылады.
С онымен, кез келген жақтаудың статикалық
түрде анықталмағандығын анықтау қосымша байланыстарды алып
тастаудан басталады. Қосымша байланыстардан босатылған жүйе
статикалық анықталған болады. Ол негізгi жүйе деп аталады. Әрбiр статикалық
анықталмаған сырықтар жүйесі үшін әдетте негізгі жүйелердi
қалауымызша таңдауға болады. Мысалы, жақтау үшін көрсетілгендей
негізгі жүйелердi (а, б, в. г, д) ұсынуға
болады. Олар қосымша жеті байланыста әр
алуан жолмен алып тастау арқылы алынған.
онымен, кез келген жақтаудың статикалық
түрде анықталмағандығын анықтау қосымша байланыстарды алып
тастаудан басталады. Қосымша байланыстардан босатылған жүйе
статикалық анықталған болады. Ол негізгi жүйе деп аталады. Әрбiр статикалық
анықталмаған сырықтар жүйесі үшін әдетте негізгі жүйелердi
қалауымызша таңдауға болады. Мысалы, жақтау үшін көрсетілгендей
негізгі жүйелердi (а, б, в. г, д) ұсынуға
болады. Олар қосымша жеті байланыста әр
алуан жолмен алып тастау арқылы алынған.
Сонымен бipгe жетi байланысы
алынып тасталатын жүйені негізгі деп алуға болмайтынын ескеру
қажет. 12-суретте жетi байланысы алынып тасталған жақтаудың үш түрi
көрсетiлген. Бұл дұрыс емес, өйткені қалған байланыстар жүйенің
кинематикалық өзгермейтіндiгін және барлық түйіндерде статикалық
анықталатынын қамтамасыз ете алмайды. Қосымша байланыстарды алып
тастағаннан кейiн, жүйе статикалық анықталынатын болғанда жоғарыда
айтқанымыздай байланыс орнына бeлгiciз күш әсерлерiн ендiру керек.
Сызықтық орын ауыстыру рұқсат етiлмейтін қималарға күш, ал бұрыштық
орын ауыстыру рұқсат етiлмейтін қималарға моменттер түcipiлeдi. Екі
жағдайда да белгiсiз күш әсерлерін ![]() деп белгiлеймiз,
мұндағы
деп белгiлеймiз,
мұндағы ![]() - белгiсiз күш нөмiрi.
- белгiсiз күш нөмiрi. ![]() -дің ең үлкен мәнi жүйенiң
статикалық анықталмағандық дәрежесіне тең боладi.
Ішкi байланыс үшін де
-дің ең үлкен мәнi жүйенiң
статикалық анықталмағандық дәрежесіне тең боладi.
Ішкi байланыс үшін де ![]() күштерi сай келетiнiн ескертемiз. Егер кейбiр
қимада жақтауды
тілсе, онда жүйенің оң және сол жағына тең және қарама-қарсы күштер
мен моменттер әсер етедi.
күштерi сай келетiнiн ескертемiз. Егер кейбiр
қимада жақтауды
тілсе, онда жүйенің оң және сол жағына тең және қарама-қарсы күштер
мен моменттер әсер етедi.
11-суретте қарастырылған негiзгi жүйелерге белгiсiз күштердi түсiрудiң мүмкiн бес әдiсi көрсетiлген (12-сурет). Бeлгiciз күш әсерлерін түcipy принципi түciнiктi. Тек белгiсiздердi анықтау үшiн теңдеулердi құру керек.
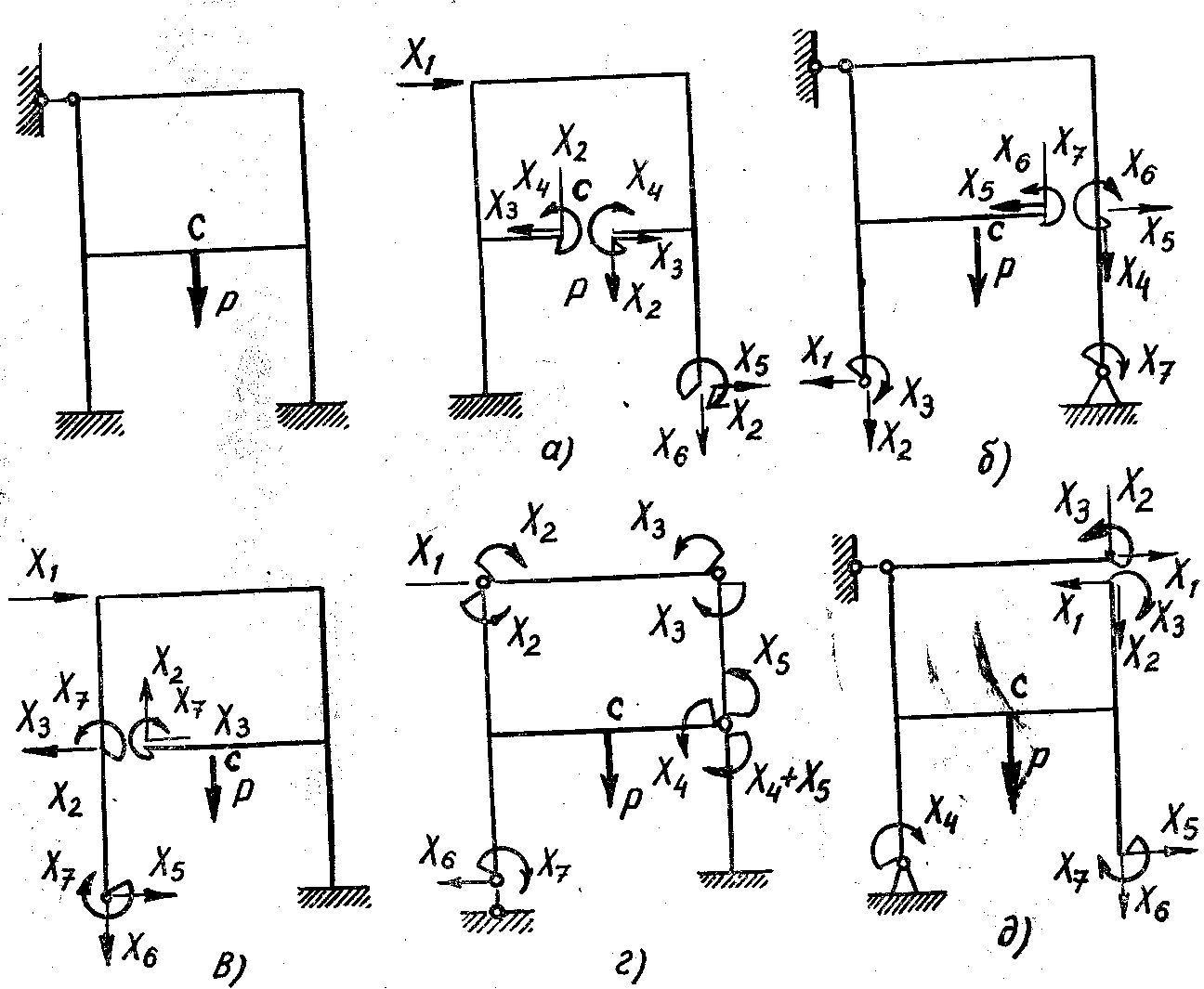
12 - сурет
12-суреттiң бiрiншiсiн қайта сызып қарастырайық (13-сурет). Бұл жүйе жетi рет статикалық анықталмаған.
Ендi белгiсiз күш әсерлерiн
анықтау үшiн теңдеулер құрайық. ![]() арқылы жүйе нүктелерiнің өзара
орын ауыстыруын белгілеймiз. Бірiншi индекс орын ауыстыру бағытына,
ал екiнші орын ауыстыруды тудыратын күшке сәйкес
келедi.
арқылы жүйе нүктелерiнің өзара
орын ауыстыруын белгілеймiз. Бірiншi индекс орын ауыстыру бағытына,
ал екiнші орын ауыстыруды тудыратын күшке сәйкес
келедi.
Раманың А нүктесiнде тiрек алып
тасталған. Демеқ горизонталь орын ауыстыру нөлге тең болады
да: ![]() 1 индексi
1 индексi ![]() күш бағыты бойынша орын
ауыстыруды, ал
күш бағыты бойынша орын
ауыстыруды, ал ![]() индексi орын ауыстыру берiлген әрi белгісiз
күштермен анықталатындығын көрсетедi. Осыған ұқсас түрде:
индексi орын ауыстыру берiлген әрi белгісiз
күштермен анықталатындығын көрсетедi. Осыған ұқсас түрде:
![]() және т. б. деп жазуға болады.
және т. б. деп жазуға болады.
![]() шамасы нүктелердiң өзара орын ауыстыруын,
шамасы нүктелердiң өзара орын ауыстыруын,
![]() онда В
нүктесінің С нүктесіне сәйкес
вертикаль орын ауыстыруын,
онда В
нүктесінің С нүктесіне сәйкес
вертикаль орын ауыстыруын, ![]() сол нүктелердiң горизонталь өзара орын
ауыстыруын,
сол нүктелердiң горизонталь өзара орын
ауыстыруын, ![]() - қималардьң В және С қималардың өзара
бұрыштық орын ауыстыруын білдіредi. Қаралатын жүйеде бұрыштық орын
ауыстыруға
- қималардьң В және С қималардың өзара
бұрыштық орын ауыстыруын білдіредi. Қаралатын жүйеде бұрыштық орын
ауыстыруға ![]() жатады.
жатады.
А және D нүктелерде ![]() орын ауыстыру абсолют болады. Бірақ абсолют орын
ауыстыруларды алынып тасталған қозғалмайтын тiректермен өзара бipгe
орын ауыстыру ретінде қарастыруға болады. Сондықтан қабылданған
белгілердi жүйенiң барлық қимасы үшiн пайдалануға
болады.
орын ауыстыру абсолют болады. Бірақ абсолют орын
ауыстыруларды алынып тасталған қозғалмайтын тiректермен өзара бipгe
орын ауыстыру ретінде қарастыруға болады. Сондықтан қабылданған
белгілердi жүйенiң барлық қимасы үшiн пайдалануға
болады.
Күштер әсерiнiң тәуелсiздiк
принципiн .пайдаланып, ![]() орын ауыстырудың өрнегiн
анықтайық:
орын ауыстырудың өрнегiн
анықтайық:

Осылайша қалған бес
теңдеуді де жазуға болады: ![]() қосылғыштардың теңдеуге кіретін әpбip
қосылғыштардың теңдеуге кіретін әpбip
![]() қосылғышы бiрiншi
индекспен, екіншісінде тұрған күш әсерінен сол күш
бағытындағы орын ауыстыруды білдіредi әpбip орын
ауыстыру сәйкес күшке пропорционал болғандықтан,
қосылғышы бiрiншi
индекспен, екіншісінде тұрған күш әсерінен сол күш
бағытындағы орын ауыстыруды білдіредi әpбip орын
ауыстыру сәйкес күшке пропорционал болғандықтан,
![]() шамасын келесi түрде жазуға
болады:
шамасын келесi түрде жазуға
болады:
![]() (5)
(5)
![]() т. с. с. орын ауыстыруларға келсеқ, онда
Р индексi
сыртқы күшті ғана емес, кез келген сыртқы күштер жүйесін білдiредi.
Сондықтан
т. с. с. орын ауыстыруларға келсеқ, онда
Р индексi
сыртқы күшті ғана емес, кез келген сыртқы күштер жүйесін білдiредi.
Сондықтан ![]() шамаларды теңдеулерде өзгepicсiз қалдырамыз.
Теңдеулер мына түрде болады:
шамаларды теңдеулерде өзгepicсiз қалдырамыз.
Теңдеулер мына түрде болады:
 (6)
(6)
Бұл теңдеулердi күш әдісінің
канондық теңдеулерi деп атайды. Олардың саны жүйенің статикалық
анықталмағандық дәрежесiне тең. Кейбiр
жағдайда кейбiр белгiсiздердiң мәнің бiрден көрсету мүмкін болса,
онда бipгe шешілетін теңдеулердің саны азаяды. Ендi
![]() коэффициентi ненi бiлдiредi және оны қалай
анықтаймыз, соған тоқталайық.
коэффициентi ненi бiлдiредi және оны қалай
анықтаймыз, соған тоқталайық.
Б ұл
үшiн (5)
өpнeгiн қарайық. Егер
ұл
үшiн (5)
өpнeгiн қарайық. Егер ![]() болса, онда
болса, онда ![]() . Демеқ
. Демеқ
![]() коэффициент к-ыншы әсердi алмастыратын бірлік әсер
нәтижесінде
коэффициент к-ыншы әсердi алмастыратын бірлік әсер
нәтижесінде ![]() -iншi күш әсері бағытындағы орын ауыстыру болады. Мысалы,
/6/ өрнектегi
-iншi күш әсері бағытындағы орын ауыстыру болады. Мысалы,
/6/ өрнектегi ![]() коэффициентi рамаға түсiрiлетiн барлық күштердiң
орнына А нүктесiне /13-сурет/ тек бiрлiк күш түсiрiлгенде В және С нүктелерiнiң горизонталь
орын ауыстыруын бiлдiредi. Егер
коэффициентi рамаға түсiрiлетiн барлық күштердiң
орнына А нүктесiне /13-сурет/ тек бiрлiк күш түсiрiлгенде В және С нүктелерiнiң горизонталь
орын ауыстыруын бiлдiредi. Егер ![]() күш орнына бiрлiк күш түcipiп,
басқа барлық күштердi алып тастасақ, онда осы күш әсерінен
D қимадағы
бұрылу бұры-
күш орнына бiрлiк күш түcipiп,
басқа барлық күштердi алып тастасақ, онда осы күш әсерінен
D қимадағы
бұрылу бұры-![]() , ал А
нүктедегі горизонталь орын ауыстыру
, ал А
нүктедегі горизонталь орын ауыстыру
![]() , болады және т. с. с.
, болады және т. с. с.
Жасалған қорытындыда  орын ауыстырудың
қалай пайда болатындығын қарастырмаймыз. Себебі, иiлетiн раманы
қарастырсақ та, айтылғандарды кез келген жүйеде бұралатын,
созылатын және барлығы бipгe болатын жүйелерде қолдануға болады.
Мор интегралдарын қарастырайық. (§3, VIII тарауды қараңыз).
орын ауыстырудың
қалай пайда болатындығын қарастырмаймыз. Себебі, иiлетiн раманы
қарастырсақ та, айтылғандарды кез келген жүйеде бұралатын,
созылатын және барлығы бipгe болатын жүйелерде қолдануға болады.
Мор интегралдарын қарастырайық. (§3, VIII тарауды қараңыз).
 шамасын анықтау үшін сыртқы . күштердің орнына
шамасын анықтау үшін сыртқы . күштердің орнына  факторды
ауыстыратын бiрлiк күштi қарастырамыз. Сондықтан өрнектегі
факторды
ауыстыратын бiрлiк күштi қарастырамыз. Сондықтан өрнектегі
 және
және  iшкi моменмттердi және күштердi
iшкi моменмттердi және күштердi  бipлiк фактордан
туындайтын
бipлiк фактордан
туындайтын  және
және  iшкі моменттер
мен күштерге алмастырамыз. Сонда:
iшкі моменттер
мен күштерге алмастырамыз. Сонда:
![]()
мұндағы
![]() - бiрлiк фактор
әсерiнен туатын iшкi моменттер мен күштер. Сонымен,
- бiрлiк фактор
әсерiнен туатын iшкi моменттер мен күштер. Сонымен,
![]() коэффициенттерi
коэффициенттерi ![]() және
және ![]() бipлiк ішкі күш әсерлерiн көбейту нәтижесінде алынады.
бipлiк ішкі күш әсерлерiн көбейту нәтижесінде алынады.
![]() және
және ![]() индекстерi қандай әсерлердi Мор интегралымен
көбейту қажеттігін тiкелей көрсетедi. Егер рама тура учаскелер-ден
құрылып, Верещагин тәсiлiн пайдалану мүмкiн болса, онда
индекстерi қандай әсерлердi Мор интегралымен
көбейту қажеттігін тiкелей көрсетедi. Егер рама тура учаскелер-ден
құрылып, Верещагин тәсiлiн пайдалану мүмкiн болса, онда
![]() және
және ![]() бiрлiк эпюрлерінiң көбейтiндiсi болады.
Яғни
бiрлiк эпюрлерінiң көбейтiндiсi болады.
Яғни ![]() . Бұл бip жағынан (5) өрнегінен тiкелей, ал
екiнші жағынан
. Бұл бip жағынан (5) өрнегінен тiкелей, ал
екiнші жағынан ![]() және
және ![]() орын ауыстырулары бipгe тең, бiрдей күш әсерінен
болатындықтан өзара орын ауыстыру теоремасынан
шығады.
орын ауыстырулары бipгe тең, бiрдей күш әсерінен
болатындықтан өзара орын ауыстыру теоремасынан
шығады.
Канондық теңдеуге
кiретiн ![]() шамалары негiзгi жүйеде берiлген сыртқы
күштердiң әсерiнен 1, 2.. бағыттардағы орын ауыстыруды бiлдіредi.
Олар берiлген күштердің эпюрлерін сәйкес бipлiк эпюрлерге көбейту
арқылы анықталады.
шамалары негiзгi жүйеде берiлген сыртқы
күштердiң әсерiнен 1, 2.. бағыттардағы орын ауыстыруды бiлдіредi.
Олар берiлген күштердің эпюрлерін сәйкес бipлiк эпюрлерге көбейту
арқылы анықталады.
Созылған немесе сығылған сырықтың өсіне көлбеу қималарға әсер ететiн кернеулердi анықтау үшiн төмендегi формулаларды бұрын тұжырымдаған болатынбыз:
![]() .
.
Б ұл
формулалардан кез келген нүкте
арқылы өтетiн
алаңнан көлбеулiгi
өзгергенде
нүктеге
әсер ететiн тiк
ұл
формулалардан кез келген нүкте
арқылы өтетiн
алаңнан көлбеулiгi
өзгергенде
нүктеге
әсер ететiн тiк
![]() және жанама
және жанама
![]() кернеулердiң де
өзгеретiндiгi
байқалады. Сонымен
бipгe өзiнiң ең үлкен
мәнiне тiк кернеу
көлденең
қималарда, ал жанама кернеулер
стержень өсiне 45° бұрышпен
жүpгiзiлгeн
қималарда ие болады. Ал,
сырыққа
әсер ететiн
күштердiң күрделi
жағдайында
кернеулердiң ең үлкен
мәнi мен олар
әсер ететiн
аудандардың күйiн
анықтау қиындай
түceдi.
Бұл мәселенi шешу
үшiн кез келген
нүкте
арқылы өтетiн
алаңдардың, көлбеулiгi
өзгергенде
кернеулердiң өзгеру
заңдылықтарын арнайы
кернеулердiң де
өзгеретiндiгi
байқалады. Сонымен
бipгe өзiнiң ең үлкен
мәнiне тiк кернеу
көлденең
қималарда, ал жанама кернеулер
стержень өсiне 45° бұрышпен
жүpгiзiлгeн
қималарда ие болады. Ал,
сырыққа
әсер ететiн
күштердiң күрделi
жағдайында
кернеулердiң ең үлкен
мәнi мен олар
әсер ететiн
аудандардың күйiн
анықтау қиындай
түceдi.
Бұл мәселенi шешу
үшiн кез келген
нүкте
арқылы өтетiн
алаңдардың, көлбеулiгi
өзгергенде
кернеулердiң өзгеру
заңдылықтарын арнайы
зерттеу қажет. Яғни деформацияланатын дененiң нүктедегi кернеулi күйiн зерттеу мәселесі туындайды.
Н үктедегi кернеулi
күй деп, сол
нүкте
арқылы
өтетiн
барлық алаңдар
бойынша әсер
етушi кернеулердiң жиынтығын айтады. Сырықтың созылуы
немесе сығылуы
дене деформациясының ең қарапайым түрi болады. Оның барлық нүктесiнде кернеулi күй
бiрдей (бiртектi кернеулi күй) деп есептелiнедi.
үктедегi кернеулi
күй деп, сол
нүкте
арқылы
өтетiн
барлық алаңдар
бойынша әсер
етушi кернеулердiң жиынтығын айтады. Сырықтың созылуы
немесе сығылуы
дене деформациясының ең қарапайым түрi болады. Оның барлық нүктесiнде кернеулi күй
бiрдей (бiртектi кернеулi күй) деп есептелiнедi.
Жалпы жағдайда
(1,![]() -сурет) денеде кернеулi күй бiртектi емес, ол әр
нүктеде өзгерiп отырады. Сондықтан осы дененiң кез
келген
-сурет) денеде кернеулi күй бiртектi емес, ол әр
нүктеде өзгерiп отырады. Сондықтан осы дененiң кез
келген ![]() қимасында кернеулер бiртектi таралмайды.
Демек, кез
келген
қимасында кернеулер бiртектi таралмайды.
Демек, кез
келген ![]() нүктесінде кернеулi күйдi зерттеу үшiн сол
нүктенiң маңынан ойша өлшемдері
нүктесінде кернеулi күйдi зерттеу үшiн сол
нүктенiң маңынан ойша өлшемдері ![]() болатын
(1,
болатын
(1,![]() -сурет) параллелипедтi аламыз.
Параллелепипед өте кiшкентай болғандықтан оның барлық нүктeciндe кернеулi
күй бiртектi әpi ол
-сурет) параллелипедтi аламыз.
Параллелепипед өте кiшкентай болғандықтан оның барлық нүктeciндe кернеулi
күй бiртектi әpi ол ![]() нүктесiнiң кернеулi күйiне сәйкес деп санаймыз.
Сондықтан, барлық жақтары бойынша және кез келген қималарында
кернеулер бiрдей таралған деп саналады. Бұл болжам қарапайым
параллелепипедтiң көлбеу қималарында кернеудiң өзгеру заңын
зерттеуге мүмкiндiк бередi. Параллелепипедтiң жақтарында кернеулер белгiлi
деп саналады, aл оның көлбеу алаңдарында әceр ететiн кернеулердi
қималар әдiсi яғни параллелепипедтiң
тiлiнген бөлiгiнiң тепе-теңдiк шартынан
анықтаймыз.
нүктесiнiң кернеулi күйiне сәйкес деп санаймыз.
Сондықтан, барлық жақтары бойынша және кез келген қималарында
кернеулер бiрдей таралған деп саналады. Бұл болжам қарапайым
параллелепипедтiң көлбеу қималарында кернеудiң өзгеру заңын
зерттеуге мүмкiндiк бередi. Параллелепипедтiң жақтарында кернеулер белгiлi
деп саналады, aл оның көлбеу алаңдарында әceр ететiн кернеулердi
қималар әдiсi яғни параллелепипедтiң
тiлiнген бөлiгiнiң тепе-теңдiк шартынан
анықтаймыз.
1.2. Бас кернеулерді есептеу
Күш түcipiлгeн дененiң кез келген нүктесiнде барлық жақтарына жанама кернеулер әсер етпейтiн қарапайым параллелепипедтi бөлiп алуға болатындығын көремiз. Бұл жағдайда параллелепипед бip, екi және үш өзара перпендикуляр бағыттарда созылу (сығылу) жағдайында болады.
Сызықтық кернеулi күйге, сырық нүктелерi, мысалы, орталық созылу немесе сығылу кезiнде ұшырайды. Жазық кернеулi күй материалдар механикасы есептерiнде жиi кездеседi. Оның сипаттық белгiсiне параллелепипедтiң параллель екi жағында кернеулердiң болмайтындығы жатады.
Кез келген
күштер жүйесi
түcipiлгeн
жұқа
пластинканы қарастырайық (3,![]() -сурет). Күш пластинканың жиегiне әсер етiп, оның жазықтығында жатсын делiк.
-сурет). Күш пластинканың жиегiне әсер етiп, оның жазықтығында жатсын делiк.
![]() жазықтығына параллель пластинкада
кернеулер болмайды (
жазықтығына параллель пластинкада
кернеулер болмайды (![]() ). Пластинканың қалыңдығы өте аз болғандықтан, оның iшiндегi бетке параллель
алаңдарда да
кернеулер болмайды деп санаймыз. Сондықтан пластинка
нүктелерi жалпы
жағдайда
жазық кернеулi
күйде болады.
Дәл осындай
күйде, мысалы,
салыстырмалы жұқа пластинкалардан жасалған сырықтар мен арқалықтар болады.
Бойлық екi
). Пластинканың қалыңдығы өте аз болғандықтан, оның iшiндегi бетке параллель
алаңдарда да
кернеулер болмайды деп санаймыз. Сондықтан пластинка
нүктелерi жалпы
жағдайда
жазық кернеулi
күйде болады.
Дәл осындай
күйде, мысалы,
салыстырмалы жұқа пластинкалардан жасалған сырықтар мен арқалықтар болады.
Бойлық екi ![]() және
және ![]() қималарымен
бөлiнген
қос таврлы
арқалықтың тiк қабырғасына контуры бойынша тiк және жанама кернеулер
түcipiлciн
(3,
қималарымен
бөлiнген
қос таврлы
арқалықтың тiк қабырғасына контуры бойынша тiк және жанама кернеулер
түcipiлciн
(3,![]() -сурет). Сонда оның нүктелерi жазық кернеулi күйге ұшырайды. Бұл кернеулi күй материалдар
кедергiсiнде өте маңызды болғандықтан, оны төменде бөлек қарастырамыз.
-сурет). Сонда оның нүктелерi жазық кернеулi күйге ұшырайды. Бұл кернеулi күй материалдар
кедергiсiнде өте маңызды болғандықтан, оны төменде бөлек қарастырамыз.
3-суретте көрсетiлген пластинканың
кез келген ![]() нүктесiнiң маңынан пластинка
жазықтығына
перпендикуляр қималармен қарапайым параллелепипедтi кесiп алайық. Параллелепипедтi
қоршаған
ортадан оған
жалпы жағдайда
тiк және жанама
кернеулер әсер
етедi. 3-суретте тiк және
жанама кернеулерге сәйкес векторлары
көрсетiлген.
Координаттар өci элемент орталығында
орналасқан.
нүктесiнiң маңынан пластинка
жазықтығына
перпендикуляр қималармен қарапайым параллелепипедтi кесiп алайық. Параллелепипедтi
қоршаған
ортадан оған
жалпы жағдайда
тiк және жанама
кернеулер әсер
етедi. 3-суретте тiк және
жанама кернеулерге сәйкес векторлары
көрсетiлген.
Координаттар өci элемент орталығында
орналасқан.
Жоғарыда көрсеткенiмiздей шексiз кiшi
параллелепипедтiң барлық нүктесiнде кернеулi күй бiртектi деп саналады.
Сондықтан,
параллелепипедтiң параллель жақтарындағы аттас кернеулер бip-бipiнe тең бағыттары қарама-қарсы
болады. Кернеулердi белгiлеу кезiнде
индекстерiне назар аудару керек. Жанама кернеуде екi индекс,
мысалы ![]() бар. Бipiншi индекс жанама кернеу алаңда
бар. Бipiншi индекс жанама кернеу алаңда ![]() ociнe параллель нормальмен бipгe әсер ететiндiгiн, ал екiншi
индекс жанама кернеу векторы
ociнe параллель нормальмен бipгe әсер ететiндiгiн, ал екiншi
индекс жанама кернеу векторы ![]() осiне параллель екендiгiн бiлдiредi. Тiк
кернеудiң екi
бeлгici бiрдей болатындықтан, тек бip индекс
алынады.
осiне параллель екендiгiн бiлдiредi. Тiк
кернеудiң екi
бeлгici бiрдей болатындықтан, тек бip индекс
алынады.
К ернеулер таңбасын мынадай ережемен қарастырамыз.
Созылудың тiк
кернеуi - оң,
ал сығылудiкi -
тepic деп саналады. Жанама кepнeyлepдiң бeлгici координаттар
өciнiң бағыттарына байланысты: егер алаңның сыртқы ноpмaлi координат
өciнiң сәйкес
бағытымен бағыттас, онда бұл алаңда кернеу
ернеулер таңбасын мынадай ережемен қарастырамыз.
Созылудың тiк
кернеуi - оң,
ал сығылудiкi -
тepic деп саналады. Жанама кepнeyлepдiң бeлгici координаттар
өciнiң бағыттарына байланысты: егер алаңның сыртқы ноpмaлi координат
өciнiң сәйкес
бағытымен бағыттас, онда бұл алаңда кернеу ![]() сәйкес осьтiң бағытымен үйлесiп оң болады. Бґл ереженi, қысқаша сыртқы нормаль ережесi дейдi.
3-суретте
көрсетiлген
барлық кернеулер
сәйкес осьтiң бағытымен үйлесiп оң болады. Бґл ереженi, қысқаша сыртқы нормаль ережесi дейдi.
3-суретте
көрсетiлген
барлық кернеулер ![]() осьтерiнде оЎ болады. Көлбеу алаңдарға да осы ереженi
қолданамыз, тек жанама
кернеулердiң таңбасын
осьтерiнде оЎ болады. Көлбеу алаңдарға да осы ереженi
қолданамыз, тек жанама
кернеулердiң таңбасын ![]() көлбеу осьтерiне сәйкес белгiлеймiз
(3-сурет).
көлбеу осьтерiне сәйкес белгiлеймiз
(3-сурет).
Жазық кернеулi күйдi талдау кезiнде
![]() нүктелерiндегi кернеулер берiлген деп есептеледi,
сондықтан олар
бастапқы
кернеулер деп аталады.
нүктелерiндегi кернеулер берiлген деп есептеледi,
сондықтан олар
бастапқы
кернеулер деп аталады.
 Бас
кернеулер
Бас
кернеулер
![]() өстердi және
тiк бұрышты элемент
бұрышын
өзгерте ойша
бұрамыз
(4-сурет).
Сонда кез келген
өстердi және
тiк бұрышты элемент
бұрышын
өзгерте ойша
бұрамыз
(4-сурет).
Сонда кез келген ![]() бұрышында тiк кернеу
бұрышында тiк кернеу ![]() берiлген нүкте үшiн ең жоғары мәнiнe жетедi. (9)
өрнекке
негiздеп қорытынды шығаруға
болады: ең аз
кернеу перпендикуляр алаңда болады. Бұл алаңдарды және бұл нүкте үшiн экстремаль
тік кернеудi табамыз.
Бұл
үшiн туындыны
нөлге
теңеймiз
берiлген нүкте үшiн ең жоғары мәнiнe жетедi. (9)
өрнекке
негiздеп қорытынды шығаруға
болады: ең аз
кернеу перпендикуляр алаңда болады. Бұл алаңдарды және бұл нүкте үшiн экстремаль
тік кернеудi табамыз.
Бұл
үшiн туындыны
нөлге
теңеймiз
![]() .
.
өрнектi (6) ![]() аргумент бойынша
дифференциалдаймыз
аргумент бойынша
дифференциалдаймыз
 . (10)
. (10)
Жақшадағы өрнектi (4) формуласымен салыстырамыз:
![]() . (11)
. (11)
Өpнектi нөлге теңестiрiп әрi iзделiп отырған алаңдар нормалiнiң көлбеу бұрышын ![]() арқылы белгiлеп
арқылы белгiлеп
![]() анықтаймыз. Бұдан алаңда нүктеге экстремаль тiк кернеу әсер еткенде, жанама кернеулер
нөлге
тең екенiн көөөрсетуге
болады. Оларды бас алаңдар, ал оларға сәйкес тiк кернеулердi
нүктедегi бас
кернеулер дейдi.
анықтаймыз. Бұдан алаңда нүктеге экстремаль тiк кернеу әсер еткенде, жанама кернеулер
нөлге
тең екенiн көөөрсетуге
болады. Оларды бас алаңдар, ал оларға сәйкес тiк кернеулердi
нүктедегi бас
кернеулер дейдi.
(10) формуласының жақшадағы өрнегiн нөлге тeңecтipiп, бас алаңдар нормалiнiң көлбеулiгiн анықтайтын екі еселенген бұрыштың тангенсiн табамыз:
![]() (12)
(12)
(12) өрнегi бас кернеулер
әсер ететiн
![]() және
және ![]() көлбеу бұрыштары бар өзара екi перпендикуляр бағытты бередi. Онда бас кернеулер
әсер етедi. Бас
кернеулердiң әсер ету сызықтарына сәйкес өстердi (
көлбеу бұрыштары бар өзара екi перпендикуляр бағытты бередi. Онда бас кернеулер
әсер етедi. Бас
кернеулердiң әсер ету сызықтарына сәйкес өстердi (![]() ) бас өстер деп атайды. Бас
кернеулердiң шамасын анықтау үшiн (6) формулаға
) бас өстер деп атайды. Бас
кернеулердiң шамасын анықтау үшiн (6) формулаға ![]() қоямыз.
қоямыз. ![]() жақшадан шығарсақ:
жақшадан шығарсақ:
 . (а)
. (а)
Тригонометриядан бeлгiлi формула бойынша (12) өрнегiн пайдаланып,
 , (б)
, (б)
екенiн табамыз.
«![]() » таңбаларының қойылу ceбeбi,
» таңбаларының қойылу ceбeбi, ![]() пен
пен ![]() бұрыштарының косинустары қарама-қарсы таңбалы болады. (12) және
(б) өрнектерiн (а)-ға қойып, жақшадағы өрнектердi ортақ бөлiмге келтiрiп және қысқартып,
бұрыштарының косинустары қарама-қарсы таңбалы болады. (12) және
(б) өрнектерiн (а)-ға қойып, жақшадағы өрнектердi ортақ бөлiмге келтiрiп және қысқартып, ![]() -дiң
eкi мәнiн:
-дiң
eкi мәнiн: ![]() және
және ![]() табамыз:
табамыз:
![]() . (13)
. (13)
Формуладағы плюс таңбасы ең үлкен бас кернеуге
![]() , ал минус —
ең аз бас
кернеуге
, ал минус —
ең аз бас
кернеуге ![]() сәйкес.
сәйкес.
Келтiрiлген қорытындыдан кез келген
бастапқы
кернеулер ![]() кезiнде берiлген нүктеде жақтарына тек тiк кернеулер
әсер ететiн болады.
Басқаша
айтқанда,
нүктедегі жазық кернеулі күйдi
өстердi бұру
жолымен созылу-сығылу ретiнде өзара екi перпендикуляр бағыттарында
кезiнде берiлген нүктеде жақтарына тек тiк кернеулер
әсер ететiн болады.
Басқаша
айтқанда,
нүктедегі жазық кернеулі күйдi
өстердi бұру
жолымен созылу-сығылу ретiнде өзара екi перпендикуляр бағыттарында
![]() және
және ![]() кернеулерiмен бейнелеуге
болады, ал (8)
матрица жазық кернеулi күй кезiнде мынадай түрде жазылады:
кернеулерiмен бейнелеуге
болады, ал (8)
матрица жазық кернеулi күй кезiнде мынадай түрде жазылады:

(12)
формуласын қарастырайық. Ол
бағыттарды бiлдiргенiмен,
![]() ,
, ![]() қайсы бағытта әсер ететiнiн көрсетпейдi. Бұл мәселенi математика жолымен
шешу үшiн
қайсы бағытта әсер ететiнiн көрсетпейдi. Бұл мәселенi математика жолымен
шешу үшiн ![]() және
және
![]() кезiнде
кезiнде ![]() екiншi
туындының
таңбасын анықтау қажет.
екiншi
туындының
таңбасын анықтау қажет.
Басқа жолмен де
![]() екi бағыттың қайсысымен әсер ететiндiгiн анықтауға болады. (11)
формуладан:
екi бағыттың қайсысымен әсер ететiндiгiн анықтауға болады. (11)
формуладан: ![]() кезiнде
кезiнде ![]() болатындығы шығады. Демек,
болатындығы шығады. Демек,
![]() үлкейсе,
үлкейсе,
![]() артады. Ол 10-суретте көрсетiлген.
артады. Ол 10-суретте көрсетiлген.
О сылайша
сылайша ![]() жағдайын қарастырып жалпы қорытындыға келемiз: жанама кернеу
векторының бағытымен алаңды бұрғанда
ондағы тiк
кернеу алгебралық түрде өседi. Мысалы,
жағдайын қарастырып жалпы қорытындыға келемiз: жанама кернеу
векторының бағытымен алаңды бұрғанда
ондағы тiк
кернеу алгебралық түрде өседi. Мысалы, ![]() бағытымен вертикаль алаңдарды бұру кезiнде оның тiк кернеулерi
үлкейедi, демек,
бұрудың осы бағытында жақын жатқан бас алаңмен үйлескен кезiнде 9 және
11,
бағытымен вертикаль алаңдарды бұру кезiнде оның тiк кернеулерi
үлкейедi, демек,
бұрудың осы бағытында жақын жатқан бас алаңмен үйлескен кезiнде 9 және
11, ![]() -суреттерде көрсетiлгендей
-суреттерде көрсетiлгендей
![]() -ға жетедi. Бұл суреттерден мынадай ереженi тұжырымдауға болады:
-ға жетедi. Бұл суреттерден мынадай ереженi тұжырымдауға болады:
![]() бағыты үнемi координат өстерiнiң
бағыты үнемi координат өстерiнiң
![]() мен
мен ![]() бағыттары сәйкес келетiн екi ширегi арқылы өтедi.
бағыттары сәйкес келетiн екi ширегi арқылы өтедi.
Бұл ереже жанама кернеу
диагональдың бipiн ұзартатындығын ескерсек, физикалық тұрғыда
түсiнiктi
болады 11, ![]() -сурет), яғни
-сурет), яғни ![]() бағыты дәл осы
диагональға ұмтылады.
бағыты дәл осы
диагональға ұмтылады.
МОР дөңгелектері
![]() және
және ![]() кернеулерiнiң
алаңдардың көлбеу
бұрышына
тәуелдiлiгiн қарапайым шеңбер диаграммасы түрiнде
геометриялық мағына
беруге болады. Бұл тәсiлдi немiс ғалымы Отто
Мор ұсынды.
кернеулерiнiң
алаңдардың көлбеу
бұрышына
тәуелдiлiгiн қарапайым шеңбер диаграммасы түрiнде
геометриялық мағына
беруге болады. Бұл тәсiлдi немiс ғалымы Отто
Мор ұсынды.
(14) және (15) формулаларында
тұрақты
шамаларды ![]() және
және ![]() деп белгiлеп, бұл формулаларды мынадай
түрде
жазамыз:
деп белгiлеп, бұл формулаларды мынадай
түрде
жазамыз:
![]() (19)
(19)
![]() координаттарында (19) теңдiгi радиусы
координаттарында (19) теңдiгi радиусы
![]() -ге тең
параметрлiк түрдегi шеңбер теңдеуiн өрнектейдi (6,а -сурет). Оны Мор
шеңберi немесе
кернеу шеңберi
деп атайды.
-ге тең
параметрлiк түрдегi шеңбер теңдеуiн өрнектейдi (6,а -сурет). Оны Мор
шеңберi немесе
кернеу шеңберi
деп атайды. ![]() бұрышпен анықталатын әрбiр көлбеу алаңға шеңберден бip нүкте сәйкес келедi (6,
бұрышпен анықталатын әрбiр көлбеу алаңға шеңберден бip нүкте сәйкес келедi (6, ![]() -сурет). Бұл
-сурет). Бұл ![]() нүкте координаттары
нүкте координаттары
![]() және
және ![]() . болатын
бейнеленген нүкте деп аталады.
. болатын
бейнеленген нүкте деп аталады. ![]() бұрыш санаудың қабылданған оң бағытын сақтау үшiн шеңбер диаграммасында
бұрыш санаудың қабылданған оң бағытын сақтау үшiн шеңбер диаграммасында
![]() oci
oci ![]() осiне қарама-қарсы бағытталуы (бiздiң жағдайымызда
осiне қарама-қарсы бағытталуы (бiздiң жағдайымызда
![]() oci төмен бағытталған) керек. Өйткенi (19) формуласынан
oci төмен бағытталған) керек. Өйткенi (19) формуласынан
![]() және
және ![]() болғанда, ордината
болғанда, ордината ![]() .
.
Өстердiң ![]() және
және ![]() бұрыштарға бұрылуына өзара перпендикуляр сәйкес алаңдарға шеңбер бойынан диаметр
ұшында
жатқан
бұрыштарға бұрылуына өзара перпендикуляр сәйкес алаңдарға шеңбер бойынан диаметр
ұшында
жатқан
![]() және
және ![]() нүктелерi сәйкес келедi. Бұл кезде кернеу шеңберiнде
нүктелерi сәйкес келедi. Бұл кезде кернеу шеңберiнде ![]() өйткенi
өйткенi ![]() үшiн формула осы
кернеудiң бұрылған
үшiн формула осы
кернеудiң бұрылған ![]() өстерiндегi (6,
өстерiндегi (6, ![]() -сурет) таңбасын көрсетедi.
-сурет) таңбасын көрсетедi.
Егер бас алаңдар мен ![]() және
және ![]() кернеулер белгiлi болса, онда
кернеу шеңберi
1 және 2
нүктелер
бойынша сызылады.
кернеулер белгiлi болса, онда
кернеу шеңберi
1 және 2
нүктелер
бойынша сызылады.
Алаң мен шеңбердегi бейнеленген
нүктенiң үйлесуiн тағайындау үшiн берiлген
жағдайда
нұкте 2-мен
дәл етiп
![]() нүктeciн (шеңбер полюсi) қарастырған ыңғайлы. Көлбеу алаңның нормалiне параллель
нүктeciн (шеңбер полюсi) қарастырған ыңғайлы. Көлбеу алаңның нормалiне параллель ![]() cәyлeci шеңбермен қиылысып бейнелейтiн
нүкте
cәyлeci шеңбермен қиылысып бейнелейтiн
нүкте
![]() бередi. Оны сызбадан көруге болады.
бередi. Оны сызбадан көруге болады.
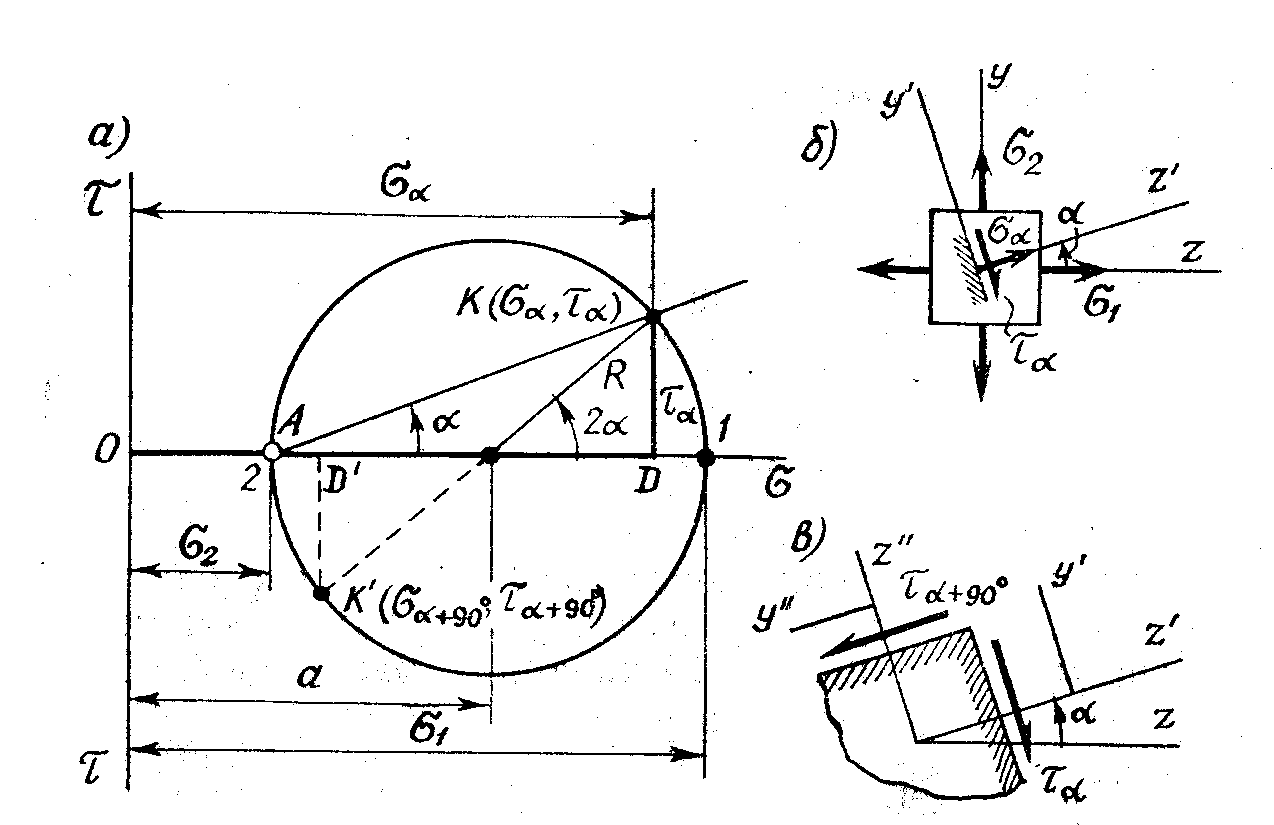
6 – сурет
7, ![]() -суретте бас емес бастапқы алаң мен кернеулер бойынша
қрылған Мор шеңберi көрсетiлген.
-суретте бас емес бастапқы алаң мен кернеулер бойынша
қрылған Мор шеңберi көрсетiлген.
![]() және
және ![]() кернеулердi диаграммада әр түрлi таңбамен көрсететiндiктен, оларды
сәйкес
кернеулердi диаграммада әр түрлi таңбамен көрсететiндiктен, оларды
сәйкес
![]() етiп белгiлеймiз (7,
етiп белгiлеймiз (7,![]() -сурет).
-сурет).
![]() вертикаль және
вертикаль және
![]() горизонталь алаңның бейнеленген нүктелерiн координаттары бойынша
салып әpi
оларды қосып
шеңбер центрiн
табамыз. Содан кейiн шеңбер диаграммасын
құрамыз.
горизонталь алаңның бейнеленген нүктелерiн координаттары бойынша
салып әpi
оларды қосып
шеңбер центрiн
табамыз. Содан кейiн шеңбер диаграммасын
құрамыз.
Б астапқы бас
емес алаңдар үшiн де
астапқы бас
емес алаңдар үшiн де ![]() полюстi пайдалану ыңғайлы. Жалпы
жағдайда
оның координаттары
полюстi пайдалану ыңғайлы. Жалпы
жағдайда
оның координаттары ![]() және шеңбер
бойында әр
түрлi
күйде болуы
мүмкiн. Iс
жүзiнде
және шеңбер
бойында әр
түрлi
күйде болуы
мүмкiн. Iс
жүзiнде
![]() полюстi алаңдардың сәйкес нормалiне параллель
жүргiзiлген
полюстi алаңдардың сәйкес нормалiне параллель
жүргiзiлген ![]() және
және ![]() сәулелерiнiң қиылысу нүктесi ретiнде табу
тиiмдi.
сәулелерiнiң қиылысу нүктесi ретiнде табу
тиiмдi.
![]() полюсiнен көлбеу алаңның нормалiне параллель
жүргiзiлген
полюсiнен көлбеу алаңның нормалiне параллель
жүргiзiлген ![]() сәулесi шеңбермен қиылысып
сәулесi шеңбермен қиылысып ![]() бейнеленген нүктесiн бередi.
Дәлелдеу
үшiн
бейнеленген нүктесiн бередi.
Дәлелдеу
үшiн
![]() бұрышы
бұрышы ![]() -ға тең екендiгiн ескеремiз.
-ға тең екендiгiн ескеремiз.
Өйткенi ол ![]() бұрышының
бұрышының ![]() доғасына тiрелетiн
орталық бұрыш
болып саналады. Сызба бойынша,
доғасына тiрелетiн
орталық бұрыш
болып саналады. Сызба бойынша,

Алынған формуланы (6)
өрнекпен
салыстырғанда ![]() екендiгiн бiлемiз. Осыған ұқсас
екендiгiн бiлемiз. Осыған ұқсас ![]() . Бұл ереже көлбеу алаңмен бейнелейтiн
нүктенiң кернеу шеңберiндегi өзара сәйкестiгiн оңай дәлелдеуге мүмкiндiк бередi. Бас алаңдардың көлбеулiгiн Мор
шеңберiмен
анықтау
8- суретте
көрсетiлген.
Олардың бейнеленген нүктелерi ретiнде абсциссалары
. Бұл ереже көлбеу алаңмен бейнелейтiн
нүктенiң кернеу шеңберiндегi өзара сәйкестiгiн оңай дәлелдеуге мүмкiндiк бередi. Бас алаңдардың көлбеулiгiн Мор
шеңберiмен
анықтау
8- суретте
көрсетiлген.
Олардың бейнеленген нүктелерi ретiнде абсциссалары ![]() және
және ![]() экстремаль мәнге ие болатын 1
және 2
нүктелерi қарастырылады. Алаңдар
экстремаль мәнге ие болатын 1
және 2
нүктелерi қарастырылады. Алаңдар ![]() және
және ![]() сәулелерге перпендикуляр.
Экстремаль ординатасы
сәулелерге перпендикуляр.
Экстремаль ординатасы ![]() радиусқа нүкте 3 тең экстремаль жанама
кернеулер
радиусқа нүкте 3 тең экстремаль жанама
кернеулер ![]() пайда болатын алаңға сәйкес келедi.
пайда болатын алаңға сәйкес келедi.
Шеңберден аналитикалық жолмен дәлелденген көп тәуелдiлiктердi табу қиын емес. Мысалы 8-суреттен

бұл (13) пен үйлеседi.
Көлемдік кернеулі күй
1 Бас кернеулер
Көлемдiк кернеулi күйде қайсыбiр нүктенiң төңiрегiнде epкiн бөлiп алынған қарапайым параллелепипедтiң жақтарына жалпы жардайда кернеулер әсер етедi (9-суретте көрсетiлген). Бұл суретте көрсетiлген кернеулер бұрын қабылданған таңба ережесiне сәйкес оң болады.
Барлық күш моменттерiнiң қосындысын ![]() және
және ![]() өстерiне қатысты нөлге теңестiрсек (§2 қараңыз), .мынадай
теңдiктердi
аламыз:
өстерiне қатысты нөлге теңестiрсек (§2 қараңыз), .мынадай
теңдiктердi
аламыз:


![]() .
(20)
.
(20)
Жанама кернеулердiң жґұптық заңын жалпы жағдайда былай өрнектеуге болады: екi өзара перпендикуляр алаңда жанама кернеу кұраушылары алаңдардың қиылу сызығына тiк бола отырып сан мәнi бойынша тең. Ал бағыттары бойынша қарама-қарсы жаққа бағытталады.
Нүктедегi көлемдiк кернеулi күйдiң жалпы жағдайында (8) матрицасының орнына үшiншi реттi матрица аламыз:
 . (21)
. (21)
Б
 ұл
матрица кернеулер тензоры деп, ал оның әлементтерi (кернеулер) кернеулер
тензорының компоненттерi деп аталады. Сонымен, нүктедегi кернеулi
күй жалпы
жағдайда кернеу
тензоры ретiнде берiледi (21). Тензор ұғымы жалпылама
ұғым,
айталық вектормен салыстырғанда көп ұшырасады. Ол математикада,
физикада, механикада жиi қолданылады.
Oның тоғыз компонентiнiң тек қана алтауы ерекше болуы
мүмкiн.
Тензор үшiн
координат өстерiнің бұрылуы
кезiнде оның компоненттерiне түрлену заңы тән. Атап айтсақ, жазық кернеулi күйде бұл заң (4), (6) және (7) тәуелдiлiктерiмен
өрнектеледi.
Көлемдiк
кернеулi күй
жағдайында
мұндай
тәуелдiлiктердi қорытпаймыз, өйткенi олар, әдетте, серпiмдiлiк теориясында қаралады.
ұл
матрица кернеулер тензоры деп, ал оның әлементтерi (кернеулер) кернеулер
тензорының компоненттерi деп аталады. Сонымен, нүктедегi кернеулi
күй жалпы
жағдайда кернеу
тензоры ретiнде берiледi (21). Тензор ұғымы жалпылама
ұғым,
айталық вектормен салыстырғанда көп ұшырасады. Ол математикада,
физикада, механикада жиi қолданылады.
Oның тоғыз компонентiнiң тек қана алтауы ерекше болуы
мүмкiн.
Тензор үшiн
координат өстерiнің бұрылуы
кезiнде оның компоненттерiне түрлену заңы тән. Атап айтсақ, жазық кернеулi күйде бұл заң (4), (6) және (7) тәуелдiлiктерiмен
өрнектеледi.
Көлемдiк
кернеулi күй
жағдайында
мұндай
тәуелдiлiктердi қорытпаймыз, өйткенi олар, әдетте, серпiмдiлiк теориясында қаралады.
Кез келген
жазық кернеулi
күйдi өстердi
бұру жолымен
екi өзара
перпендикуляр бағытта ![]() және
және ![]() бас кернеулермен созылуға (сығылуға) келтiруге
болатындығы
бґрыннан белгiлi. Осыған ұқсас көлемдiк кернеулi күйде өстердiң және параллелепипедтiң
бағытын өзгертiп, барлық
жағында жанама кернеулер нөлге тең болатын қалыпты табуға болады.
Параллелепипедтiң жақтарына параллель алаңдар бас алаңдар
(10-сурет) деп аталады. Оларға әсер ететiн
бас кернеулермен созылуға (сығылуға) келтiруге
болатындығы
бґрыннан белгiлi. Осыған ұқсас көлемдiк кернеулi күйде өстердiң және параллелепипедтiң
бағытын өзгертiп, барлық
жағында жанама кернеулер нөлге тең болатын қалыпты табуға болады.
Параллелепипедтiң жақтарына параллель алаңдар бас алаңдар
(10-сурет) деп аталады. Оларға әсер ететiн ![]() және
және ![]() кернеулердi бас кернеулер деп, ал сәйкес өстерiн бас өстер
дейдi.
кернеулердi бас кернеулер деп, ал сәйкес өстерiн бас өстер
дейдi.


![]() және
және
![]() бас кернеулердi кез келген алаңдарға әсер ететiн
кернеулер арқылы анықтау әдiсiн қарастырамыз (10-сурет). Бұл үшiн
кез келген бас алаңның нормальмен анықталатын көлбеуi белгiлi деп
ұйғарайық. Алаңға параллель қимамен бастапқы параллелепипедтен
11-суреттегiдей тетраэдрдi бөлiп аламыз да, тетраэдрдi тепе-теңдiк
шартын әсер ететiн барлық күштердiң координат
өстерiне
проекциясының қосындысы түрiнде тұжырымдаймыз.
бас кернеулердi кез келген алаңдарға әсер ететiн
кернеулер арқылы анықтау әдiсiн қарастырамыз (10-сурет). Бұл үшiн
кез келген бас алаңның нормальмен анықталатын көлбеуi белгiлi деп
ұйғарайық. Алаңға параллель қимамен бастапқы параллелепипедтен
11-суреттегiдей тетраэдрдi бөлiп аламыз да, тетраэдрдi тепе-теңдiк
шартын әсер ететiн барлық күштердiң координат
өстерiне
проекциясының қосындысы түрiнде тұжырымдаймыз.
![]() нормальдiң
нормальдiң ![]() өстермен жасайтын бұрыштарының
косинусын сәйкес
өстермен жасайтын бұрыштарының
косинусын сәйкес ![]() деп белгiлеймiз. Көлбеу жақ ауданын
деп белгiлеймiз. Көлбеу жақ ауданын
![]() деп алсақ, координат жазықтығында жатқан басқа
жақ аудандары
деп алсақ, координат жазықтығында жатқан басқа
жақ аудандары ![]() болады. Бас алаңда жанама кернеу болмайды.
Tүcipiлгeн бас
кернеу
болады. Бас алаңда жанама кернеу болмайды.
Tүcipiлгeн бас
кернеу ![]() -ны
-ны ![]() -мен белгiлейiк.
Күштердiң
-мен белгiлейiк.
Күштердiң ![]() осiне
проекциясының қосындысы:
осiне
проекциясының қосындысы:
![]() .
.
Күштердi ![]() және
және ![]() өстерiне проекциялап,
тағы да
ұқсас екi тендеудi
аламыз. Осылайша тетраэдрдi тепе-теңдiгiнiң үш
теңдеуiн
тұжырымдаймыз:
өстерiне проекциялап,
тағы да
ұқсас екi тендеудi
аламыз. Осылайша тетраэдрдi тепе-теңдiгiнiң үш
теңдеуiн
тұжырымдаймыз:
 (а)
(а)
(а) теңдеулерiн ![]() белгiсiздерi
үшiн бiртектi
теңдеулер
жүйесi
түрiнде
қарастыруға болады.
белгiсiздерi
үшiн бiртектi
теңдеулер
жүйесi
түрiнде
қарастыруға болады. ![]() нормальдың
бағыттаушы косинустарының
арасында:
нормальдың
бағыттаушы косинустарының
арасында:
![]() ,
(б)
,
(б)
тәуелдiлiгi бар, сондықтан олар бip мезгiлде нөлге тең бола алмайды. Жоғары алгебрадан дәл осындай шартта (а) жүйесiнiң анықтауышы нөлге тең болуы қажет, яғни
 .
.
Анықтауышты жiктеп, куб теңдеу аламыз:
![]() . (22)
. (22)
Оның үш
түбipi
![]() үш бас
кернеудiң мәнi
болады (
үш бас
кернеудiң мәнi
болады (![]() анықтауыш симметриясына сүйене отырып, олар кез
келген
анықтауыш симметриясына сүйене отырып, олар кез
келген ![]() және т. б.
бастапқы
кернеулерде нақты болады).
және т. б.
бастапқы
кернеулерде нақты болады).
(2) теңдеудiң коэффициенттерi:

Берiлген кернеу
күйiне
тиiстi ![]() бас кернеулер
бас кернеулер ![]() өстерiн таңдауға байланысты болмауы керек. Олай
болса, (22) теңдеудiң түбipлepi мен оның
өстерiн таңдауға байланысты болмауы керек. Олай
болса, (22) теңдеудiң түбipлepi мен оның
![]() коэффициенттерi координат ocьтepiн
бұрғанда өзгермейдi. Сондықтан
коэффициенттерi координат ocьтepiн
бұрғанда өзгермейдi. Сондықтан ![]() және
және ![]() шамалары кернеулi
күйдiң (кернеу тензорының) бiрiншi, екiншi
және үшiншi инварианттары деп
аталады.
шамалары кернеулi
күйдiң (кернеу тензорының) бiрiншi, екiншi
және үшiншi инварианттары деп
аталады.
Жазық кернеулi күйдiң дербес жағдайында куб теңдеудi (22) квадрат
теңдеуге
түрлендiруге
болады. Сонда оның екi түбipi бұрын алынған (13) формуласымен үйлесетiн ![]() және
және ![]() мәндерiн бередi.
Бұл
жағдайда
мәндерiн бередi.
Бұл
жағдайда
![]() деп алу керек, өйткенi бастапқы
параллелепипедтiң
деп алу керек, өйткенi бастапқы
параллелепипедтiң ![]() жағына кернеу әсер етпеуi керек.
жағына кернеу әсер етпеуi керек.
![]() және
және ![]() үш бас
кернеудiң бipeyiне сәйкес
үш бас
кернеудiң бipeyiне сәйкес ![]() -дердi табу үшiн, бас
кернеудiң мәнiн
(а) формуласындағы
-дердi табу үшiн, бас
кернеудiң мәнiн
(а) формуласындағы ![]() орнына қою керек. (а) және (б) формулаларын бipгe
шешкенде iзделген
орнына қою керек. (а) және (б) формулаларын бipгe
шешкенде iзделген ![]() шамаларды аламыз.
шамаларды аламыз.
Үш
бас кернеудiң бipeyi бұл нүктеде алгебралық
ең үлкен мәнге ие болады, оны
![]() , ең
кiшi кернеудi
, ең
кiшi кернеудi ![]() , ал аралық кернеудi
, ал аралық кернеудi
![]() деп белгiлейiк. Сонда
деп белгiлейiк. Сонда
![]() . (23)
. (23)
Ары қарай ![]() кернеулер
табылған
және кернеулер тензоры
бас өстерде берiлген деймiз:
кернеулер
табылған
және кернеулер тензоры
бас өстерде берiлген деймiз:
 . (21
. (21![]() )
)
Б ас алаңдар жасайтын
параллелепипедтiң көлбеу
қимасы бойынша
кернеулердiң таралу
заңдылықтарын
тұжырымдайық.
ас алаңдар жасайтын
параллелепипедтiң көлбеу
қимасы бойынша
кернеулердiң таралу
заңдылықтарын
тұжырымдайық.

ІІ. Нүктедегі деформацияланған күй
2.1. Жазық кернеулi күйде материал деформациясы
Жазық кернеулi күйде материал деформациясының ерекшелiгiн қарастырайық.
Қабырғаларының ұзындығы ![]() және
және ![]() шексiз аз тiк
бұрышты
элементтi таңдап алсақ, жазық кернеулi күйдiң жалпы жағдайында оған тiк кернеулер
шексiз аз тiк
бұрышты
элементтi таңдап алсақ, жазық кернеулi күйдiң жалпы жағдайында оған тiк кернеулер ![]() және жанама
кернеулер
және жанама
кернеулер ![]() әсер етедi
(12,
әсер етедi
(12,
![]() -сурет). Бұл кернеулер
элементтiң деформациялануынан туындайды. Аталған кернеулер
жазықтығында
болатын элемент деформациясын қарастырамыз.
-сурет). Бұл кернеулер
элементтiң деформациялануынан туындайды. Аталған кернеулер
жазықтығында
болатын элемент деформациясын қарастырамыз.
Изотропты материал
үшiн элемент
қабырғаларының ұзаруы тiк кернеулер
әсерiнен болады.
Оларды ![]() және
және ![]() арқылы белгiлеймiз (12,
арқылы белгiлеймiз (12, ![]() -сурет). Нүктедегi сызықтық деформациялар
бағыттарға
сәйкес
салыстырмалы ұзару шамасымен өрнектеледi.
-сурет). Нүктедегi сызықтық деформациялар
бағыттарға
сәйкес
салыстырмалы ұзару шамасымен өрнектеледi.
![]() . (22)
. (22)
Жанама кернеулермен
бұрышты
деформация немесе ығысу деформациясы байланысты. Ол алғашында тiк бұрыштың ығысу бұрышы деп аталатын
![]() бұрышына өзгеруiмен анықталады (12,
бұрышына өзгеруiмен анықталады (12, ![]() -сурет).
-сурет).
Қарастырылып отырған нүкте арқылы ![]() және
және ![]() өстерiнiң бағытында ұзындығы
өстерiнiң бағытында ұзындығы ![]() және
және ![]() екi өзара перпендикуляр
кесiндiлер өтсiн делiк. Деформация нәтижесiнде кесiндiлер (34)
формулаларына сәйкес салыстырмалы ұзарады, әрi олардың арасындағы тiк бұрыш
екi өзара перпендикуляр
кесiндiлер өтсiн делiк. Деформация нәтижесiнде кесiндiлер (34)
формулаларына сәйкес салыстырмалы ұзарады, әрi олардың арасындағы тiк бұрыш ![]() ығысу бұрышына өзгередi.
ығысу бұрышына өзгередi.
Егер
![]() және
және ![]() өстерiн қиылысу нүктесiнiң төңiрегiнде әр түрлi кесiндiлермен рет
бойынша үйлесетiндей ойша бұрсақ, онда
өстерiн қиылысу нүктесiнiң төңiрегiнде әр түрлi кесiндiлермен рет
бойынша үйлесетiндей ойша бұрсақ, онда ![]() өстерiнiң әр қалпына
өстерiнiң әр қалпына ![]() ұзаруы
және
ұзаруы
және ![]() ығысу бұрышы сәйкес келедi.
ығысу бұрышы сәйкес келедi. ![]() және
және ![]() өстерiнiң
мүмкiн қалыптарына келетiн салыстырмалы ұзару мен ығысу бұрыштарының жиынтығы нүктенiң деформациялық күйiн
сипаттайды.
өстерiнiң
мүмкiн қалыптарына келетiн салыстырмалы ұзару мен ығысу бұрыштарының жиынтығы нүктенiң деформациялық күйiн
сипаттайды.
Кез келген
жазық кернеулi
күй
![]() және
және ![]() бас кернеулермен екi өзара перпендикуляр
бағытта
созылады (сығылады). 12-суретте ол үзiк сызықпен көрсетiлген. Бас алаңдарда жанама кернеулер
нөлге
тең болғандықтан,
бас кернеулермен екi өзара перпендикуляр
бағытта
созылады (сығылады). 12-суретте ол үзiк сызықпен көрсетiлген. Бас алаңдарда жанама кернеулер
нөлге
тең болғандықтан, ![]() және
және ![]() бағытында тiк бұрышты элемент тек қана ұзарып, ығысу бұрышы нөлге тең болады (12,
бағытында тiк бұрышты элемент тек қана ұзарып, ығысу бұрышы нөлге тең болады (12, ![]() -сурет).
-сурет).
Мұнан берiлген нүкте арқылы өтетiн екi өзара перпендикуляр
бағытты
көрсете отырып,
кесiндiлердiң тек ![]() және
және ![]() шамаларға ұзаратындығын, ал
арасындағы тiк
бұрыш
өзгepicсiз
қалатындығын тұжырымдауға болады. Көрсетiлген
шамаларға ұзаратындығын, ал
арасындағы тiк
бұрыш
өзгepicсiз
қалатындығын тұжырымдауға болады. Көрсетiлген ![]() және
және ![]() салыстырмалы ұзаруларды берiлген
нүктедегi бас
деформация деп атайды. Серпiмдi және изотропты денелердегi
нүктелерде бас
кернеулер мен бас деформациялар дәл келедi. Бас деформация
атауы
салыстырмалы ұзаруларды берiлген
нүктедегi бас
деформация деп атайды. Серпiмдi және изотропты денелердегi
нүктелерде бас
кернеулер мен бас деформациялар дәл келедi. Бас деформация
атауы ![]() және
және ![]() ұзарулары берiлген
нүктеден
тарайтын кез келген бағытты ұзарулармен салыстырғанда бас
кернеудiң әсерiне ұқсас экстремаль
мәнге ие
болатындығына
байланысты.
ұзарулары берiлген
нүктеден
тарайтын кез келген бағытты ұзарулармен салыстырғанда бас
кернеудiң әсерiне ұқсас экстремаль
мәнге ие
болатындығына
байланысты.
Бepiлгeн нүктеден ![]() бағытына кез келген а
бұрышпен
өтетiн
бағытына кез келген а
бұрышпен
өтетiн
![]() кесiндiсiнiң
салыстырмалы ұзаруын табайық (12-сурет).
кесiндiсiнiң
салыстырмалы ұзаруын табайық (12-сурет).
![]() және
және ![]() бас деформациялары берiлген деп есептейiк.
Ұзындығы
бас деформациялары берiлген деп есептейiк.
Ұзындығы ![]() -ке тең көлбеу
кесiндiнi денеден бөлiнiп алған қабырғаларының ұзындығы
-ке тең көлбеу
кесiндiнi денеден бөлiнiп алған қабырғаларының ұзындығы ![]() және
және ![]() болатын тiк бґрышты элементтiң бас деформация
бағытындағы диагоналы деп қарастырайық. Деформация аз болу себептi
бұрышты
болатын тiк бґрышты элементтiң бас деформация
бағытындағы диагоналы деп қарастырайық. Деформация аз болу себептi
бұрышты
![]() деп алып көлбеу кесiндiнiң абсолют ұзаруын
табамыз:
деп алып көлбеу кесiндiнiң абсолют ұзаруын
табамыз:
![]() .
.
Iзделiп отырған салыстырмалы ұзару
![]() болады.
болады.
![]() есекерсек,
есекерсек, ![]() .
(23)
.
(23)
Тригонометриялық тәуелдiлiктi (5) пайдаланып, (35) формуласын былай өрнектеймiз:
![]() . (24)
. (24)
![]() болсын. Сонда (36) формуласынан
болсын. Сонда (36) формуласынан
![]() , яғни
, яғни ![]() болғанда
болғанда ![]() өзiнiң ең үлкен мәнiне ие болады:
өзiнiң ең үлкен мәнiне ие болады:
![]() . Керiсiнше,
. Керiсiнше,
![]() болғанда
болғанда ![]() ең кiшi мәнге ие болады:
ең кiшi мәнге ие болады: ![]() .
.
Егер нүктедегi бас деформациялардың шамасы мен бағыты бeлгiлi болса, онда кез келген бағыт бойынша салыстырмалы ұзару (35) немесе (36) формулаларымен анықталады.
2.2. Деформация кезінде материал көлемінің өзгеруі
Деформацияға дейiн элементтер
параллелепипед жақтарының өлшемiн ![]() және
және ![]() арқылы белгiлеймiз
(14-сурет).
Деформациялаудан кейiн бұл өлшемдер
арқылы белгiлеймiз
(14-сурет).
Деформациялаудан кейiн бұл өлшемдер ![]() ,
, ![]() ,
, ![]() болсын.
болсын.
 Параллелепипедтiң бастапқы көлемiн
Параллелепипедтiң бастапқы көлемiн ![]() , ал
деформациядан кейiн
, ал
деформациядан кейiн ![]() деп белгiлеймiз Параллелепипед
көлемiнiң абсолют өзгepyiн табамыз:
деп белгiлеймiз Параллелепипед
көлемiнiң абсолют өзгepyiн табамыз:
 (a)
(a)
(а) өрнегiндегi жақшада салыстырмалы ұзару көрсетiлген
![]() .
.
(а) өрнегiн ықшамдасақ:
![]() .
.
Нақты құрылыс материалдарында салыстырмалы ұзару әдетте, мыңдық, он мыңдық үлестермен өлшенедi. Сондықтан, олардың көбейтiндiлерiн ескермеуге болады. Ығысу деформациясы
көлем
өзгеруiн тудырады.
Ол ![]() ығысу бұрышының квадратына, тiптi одан
жоғары
дәрежесiне
пропорционал. Сондықтан кiшi деформацияларда көлемнiң мұндай өзгерiсiн де елемеуге
болады.
ығысу бұрышының квадратына, тiптi одан
жоғары
дәрежесiне
пропорционал. Сондықтан кiшi деформацияларда көлемнiң мұндай өзгерiсiн де елемеуге
болады.
Сонымен
![]() .
.
Көлемнiң салыстырмалы өзгеруiн, немесе салыстырмалы кө-лемдiк деформациясын мына формуламен анықтайды:
![]() . (25)
. (25)
Бұл формула серпiмдi
және серпiмдi-пластикалық
деформацияларға да дұрыс.
Материалдың серпiмдi сатысындағы жұмыста ![]() - нi
- нi ![]() және
және ![]() кернеулер арқылы өрнектеуге болады. Бґл
үшiн (42)
формуладағы
кернеулер арқылы өрнектеуге болады. Бґл
үшiн (42)
формуладағы ![]() ,
, ![]() және
және ![]() мәндерiн (47) формулаға қоямыз. Түрлендiрсек:
мәндерiн (47) формулаға қоямыз. Түрлендiрсек:
![]() . (26)
. (26)
![]() болғанда материалдың
жан-жақты
гидростатикалық сығылу
жағдайын
қарастырайық (48) формуласы бойынша:
болғанда материалдың
жан-жақты
гидростатикалық сығылу
жағдайын
қарастырайық (48) формуласы бойынша:
![]() . (27)
. (27)
(б) формулалары Пуассон коэффициентi 0,5-тен үлкен болуы мүмкiн емес, өйткенi көлемдiк сығылғанда дененiң көлемi кiшiреймейдi, керiсiнше ұлғаяды. Бұл тұжырым тәжiрибемен дәлелденген. Табиғатта Пуассон коэффициентi 0,5-тен үлкен материал табылған жоқ.
Көлемдік кернеулі
күйдегі потенциялық энергияКөлемдiк кернеулi
күйде серпiмдi
деформация әсерiнен
материалдың
көлем бiрлiгiнде
жинақталған
![]() меншiктi
потенциалық
энергияны табамыз.
Ол үшiн
меншiктi
потенциалық
энергияны табамыз.
Ол үшiн
![]() бас
кернеулердiң
әсерiнде
болатын, қабырғасы 1-ге
тең
текшені
қарастырамыз. Қарапайым
созылу
бас
кернеулердiң
әсерiнде
болатын, қабырғасы 1-ге
тең
текшені
қарастырамыз. Қарапайым
созылу
Бұл формуланы үш кернеудiң бip мезгiлде әсер етуiне арнап жалпылама жазсақ:
![]() (28)
(28)
Осыған бас кернеу мен деформацияға катысты, яғни (42) формуласындағы х, у, z индекстерiн сәйкес 1, 2, 3-пен салыстырып, Гук заңы бойынша ұзару өрнегiн (42)-ге қоямыз. Нәтижесiнде и өрнегiн бас кернеу арқылы тұжырымдайық:
![]() (29)
(29)
Нүктедегi кернеулi және
деформациялық
күйлер тәуелдiлiктерiнiң
арасындағы ұқсастық Бас деформация
бағытына
![]() бұрышпен орналасқан екi өзара перпендикуляр
бұрышпен орналасқан екi өзара перпендикуляр ![]() және
және ![]() кесiндiлерi арасындағы ығысу бұрышын табамыз
(13-сурет).
кесiндiлерi арасындағы ығысу бұрышын табамыз
(13-сурет).
![]() кесiндiсi деформация
нәтижесiнде
кесiндiсi деформация
нәтижесiнде ![]() бұрышқа
бұрылады.
Бұрышы кiшi
болғандықтан,
бұрышқа
бұрылады.
Бұрышы кiшi
болғандықтан, ![]() доғасының
доғасының ![]() радиусқа қатынасымен өрнектеуге болады:
радиусқа қатынасымен өрнектеуге болады:
![]()
немесе
![]() . (а)
. (а)
![]() сызығының
сызығының ![]() бұрылу бұрышын анықтау үшiн (а) фор-муласындағы
бұрылу бұрышын анықтау үшiн (а) фор-муласындағы ![]() бұрышын (
бұрышын (![]() ) алмастырамыз.
Сонда:
) алмастырамыз.
Сонда:
![]() (30)
(30)
(а) және (б)
формулаларындағы әр
түрлi
таңба
![]() және
және ![]() кесiндiлерiнiң
деформацияланбаған қалыптан әр жаққа бұрылатындығын көрсетедi (13-сурет). Егер тiк
бұрыш
кесiндiлерiнiң
деформацияланбаған қалыптан әр жаққа бұрылатындығын көрсетедi (13-сурет). Егер тiк
бұрыш
![]() азайса,
азайса, ![]() деп аламыз. (а) және
(б) өрнектеп осы бұрыштың
деп аламыз. (а) және
(б) өрнектеп осы бұрыштың ![]() үлкеюiн қанағаттандырса,
үлкеюiн қанағаттандырса,
![]() үшiн
төмендегi өрнектi қарастырамыз:
үшiн
төмендегi өрнектi қарастырамыз:
![]() .
.
(36) және (37) формулаларын қосып жазамыз:
 .
(31)
.
(31)
Нүктенiң жазық кернеулi күйiн бейнелейтiн (3.14) және (3.15) өрнектердi еске түсiрсек:
 (в)
(в)
( 38) және (в) өрнектерiнiң тәуелдiлiгi нүктедегi
38) және (в) өрнектерiнiң тәуелдiлiгi нүктедегi ![]() кернеулердiң
және
кернеулердiң
және ![]() және
және ![]() деформациялардың таралу заңдарының математикалық ұқсастығын көрсетедi. Бұл ұқсастық кездейсоқ емес, нүктедегi деформациялық
күйдi
деформациялардың таралу заңдарының математикалық ұқсастығын көрсетедi. Бұл ұқсастық кездейсоқ емес, нүктедегi деформациялық
күйдi ![]() матрица деформациясы толығымен анықтай алады.
матрица деформациясы толығымен анықтай алады.
![]() жазықтығында деформация
үшiн
компоненттерi:
жазықтығында деформация
үшiн
компоненттерi:

болып табылады. Өстердi
бұрғанда ![]() компоненттерi кернеу матрицасы
компоненттерi кернеу матрицасы
![]() компоненттерiне ұқсас түрленедi. Аталған ұқсастық негiзiнде мына форомуланы
жазуға
болады:
компоненттерiне ұқсас түрленедi. Аталған ұқсастық негiзiнде мына форомуланы
жазуға
болады:
 . (31)
. (31)
Бұл формула (13)
формуласына ұқсас, мұнда ![]() және
және ![]() кернеулерi сәйкес
кернеулерi сәйкес ![]() және
және ![]() деформацияларына
алмастырылған.
(39) формуласы нүктедегi
деформацияларына
алмастырылған.
(39) формуласы нүктедегi ![]() және
және ![]() бас деформацияларды
бас деформацияларды ![]() екi кез келген
өзара перпендикуляр
бағытта.
Сәйкес
ығысу
бұрышы
екi кез келген
өзара перпендикуляр
бағытта.
Сәйкес
ығысу
бұрышы
![]() тең арқылы
анықтауға
мүмкiндiк
бередi.
тең арқылы
анықтауға
мүмкiндiк
бередi.
(39) формуласынан
![]()
яғни нүктенiң кез келген өзара перпендикуляр бағыттарда са-лыстырмалы ұзаруының жиынтығы тұрақты шама болады.
(9) формуласымен кернеулi күйдегi ұқсас жағдайды тұжырымдауға болады. Бұл ұқсастық нүктедегi деформацияларды графиктiк бейнелеу үшiн Мор шеңберiн пайдалануға мүмкiндiк бередi. Бiз оған тоқталмаймыз.
Қорыта айтқанда, екi бас кернеу жазықтығында туындайтын деформацияларды қарастырдық. Нүктедегi материал деформациясы жалпы жағдайда көлемдiк сипатта болады. Жоғарыда жазық есепте алынған деформациялар мен кернеулердiң таралуының математикалық ұқсастығы көлемдiк есепте де сақталады.
Сондықтан жалпы жағдайда дененiң әpбip
нүктесiнде үш ![]() және
және ![]() бас деформацияны, яғни арасында ығысу бұрышы болмайтын үш өзара перпендикуляр
бағытта кiшi
кесiндiлердiң салыстырмалы ұзаруын көрсетуге болады.
бас деформацияны, яғни арасында ығысу бұрышы болмайтын үш өзара перпендикуляр
бағытта кiшi
кесiндiлердiң салыстырмалы ұзаруын көрсетуге болады.
Кернеу тензорына
ұқсас деформация
тензоры ұғымы
ендiрiледi. Оның матрицасы нүктенiң деформация күйiн толық сипаттайды. ![]() бағыттарымен үйлесетiн өстер үшiн деформация тензоры мынадай
түрде
болады:
бағыттарымен үйлесетiн өстер үшiн деформация тензоры мынадай
түрде
болады:
 .
.
Серпiмдi изотропты
дененiң нүктелерiнде бас деформациялардың кернеуi үш ![]() және
және ![]() бас кернеудiң бағытымен үйлеседi.
бас кернеудiң бағытымен үйлеседi.
Жазық және көлемдік кернеулі күйдегі Гук заңы Осыған дейiн нүктедегi кернеулi және деформациялық күйлердiң формулаларымен нeгiзгi ережелерi дененiң серпiмдi қасиеттерiне байланысты болмайтындықтан, оларды серпiмдi және серпiмдi емес (немесе серпiмдi - пластикалыј) деформацияларға қолдануға болады. Кернеулер мен деформациялардың сандық қатынастарын тағайындағанда, бiз изотропты денелердiң тек серпiмдi деформацияларын қарастыратын боламыз.
Центрлiк
созылған
стерженьнен бөлiп алынған элементтi қарастырайық. Мұндай
элемент бойлық және көлденең деформацияға ұшырайды. Ол ![]() кернеуiмен мына формулалар бойынша:
кернеуiмен мына формулалар бойынша:
![]() (32)
(32)
![]() (33)
(33)
байланысты.
Мұнда ![]() - серпiмдiлiк модулi, ал μ - Пуассон коэффициентi.
Ұзару деформациясы
оң,
қысқару терiс делiнедi. (40)
формуласы сызықты кернеулi күйдегi Гук заңын өрнектейдi. Көлемдiк кернеулi күйде
тiк кернеулер мен ұзарудың ұқсас қатынасын тағайындаймыз. Өйткенi кiшi деформация кезiнде
жанама кернеулер тiк бұрышты элемент жақтарының ұзындығын өзгертпей, тек ығысуды тудырады.
Мұнда
элементтiң тек
сызықты
деформациялары қарастырылады. Ығысу деформациясына IV тарауда
тоқталамыз.
- серпiмдiлiк модулi, ал μ - Пуассон коэффициентi.
Ұзару деформациясы
оң,
қысқару терiс делiнедi. (40)
формуласы сызықты кернеулi күйдегi Гук заңын өрнектейдi. Көлемдiк кернеулi күйде
тiк кернеулер мен ұзарудың ұқсас қатынасын тағайындаймыз. Өйткенi кiшi деформация кезiнде
жанама кернеулер тiк бұрышты элемент жақтарының ұзындығын өзгертпей, тек ығысуды тудырады.
Мұнда
элементтiң тек
сызықты
деформациялары қарастырылады. Ығысу деформациясына IV тарауда
тоқталамыз. ![]() және
және ![]() деформацияларды
деформацияларды ![]() және
және ![]() арқылы өрнектеп табамыз. Ол үшiн күштер әсерiнiң тәуелсiздiк принципiн
және (40)
және (41)
формулаларындағы қатынастарды пайдаланамыз
арқылы өрнектеп табамыз. Ол үшiн күштер әсерiнiң тәуелсiздiк принципiн
және (40)
және (41)
формулаларындағы қатынастарды пайдаланамыз ![]() кернеуi бағытымен
кернеуi бағытымен ![]() салыстырмалы ұзарудың косындысын үш қосылғышпен өрнектеуге болады:
салыстырмалы ұзарудың косындысын үш қосылғышпен өрнектеуге болады:
![]() ,
,
мұнда ![]() - тек
- тек
![]() кернеудiң
әсерiнен болатын
деформация, оны (34) формуласымен анықтайды. Өйткенi ол
кернеудiң
әсерiнен болатын
деформация, оны (34) формуласымен анықтайды. Өйткенi ол
![]() карағанда бойлық болып
табылады.
карағанда бойлық болып
табылады.
![]() кернеуден пайда болған ұзару,
кернеуден пайда болған ұзару, ![]() қарағанда бойлық деформация болады да (14)
формуласымен анықталады.
қарағанда бойлық деформация болады да (14)
формуласымен анықталады. ![]() кернеу тудыратын деформация.
кернеу тудыратын деформация.
Сонымен ![]() .
.
![]() және Q
және Q![]() анықтауға ұқсас пайымдауларды пайдаланып
көлемдiк
кернеулi күйдегi Гук заңының формуласын (Гуктың
жалпылама заңын) аламыз:
анықтауға ұқсас пайымдауларды пайдаланып
көлемдiк
кернеулi күйдегi Гук заңының формуласын (Гуктың
жалпылама заңын) аламыз:
 (35)
(35)
Бұл формулаларда созу кернеулерi «плюс», ал сығылу - «минус» таңбаларымен белгiленедi.
(42)
формуласындағы
бip кернеудi нөлге тең деп ұйғарып
жазық кернеулi
күй
үшiн Гук
заңын
аламыз ![]() деп:
деп:
 (36)
(36)
![]() кернеу нөлге тең болғанда
кернеу нөлге тең болғанда ![]() нөлге тең деген түсiнiк тумауы керек.
Шынында,
нөлге тең деген түсiнiк тумауы керек.
Шынында, ![]() болғанда
болғанда
![]() .
(37)
.
(37)
Мысалы, пластинканы
өз
жазықтығында
созғанда (44
форму-ласы бойынша), созу салдарынан пластинка қалыңдығының азайғандығын анықтауға болады. Белгiлi
![]() және
және ![]() кернеулерде (43) формулалар мен
кернеулерде (43) формулалар мен
![]() және
және ![]() деформациясын анықтайды. Бiрақ кейбiр жағдайда керi тәуелдiлiктi қарастырған тиiмдi. (43)
формуласының екiншi жағын
деформациясын анықтайды. Бiрақ кейбiр жағдайда керi тәуелдiлiктi қарастырған тиiмдi. (43)
формуласының екiншi жағын ![]() -ға көбейтiп және бiрiншiмен қоссақ:
-ға көбейтiп және бiрiншiмен қоссақ:
![]() .
.
![]() және
және ![]() кернеулердi табамыз:
кернеулердi табамыз:
 (38)
(38)
![]() Үшiн
формуланы
Үшiн
формуланы ![]() формуласындағы индекстердi алмастыру жолымен
аламыз. 45 формуласындағы тәуелдiлiктер бeлгiлi
формуласындағы индекстердi алмастыру жолымен
аламыз. 45 формуласындағы тәуелдiлiктер бeлгiлi
![]() және
және ![]() деформациялары (мысалы, тәжiрибеден)
деформациялары (мысалы, тәжiрибеден)
![]() тiк кернеулерiн анықтауға мүкiндiк бередi.
тiк кернеулерiн анықтауға мүкiндiк бередi.
ҚОРЫТЫНДЫ
Кез
келген жазық кернеулi күйдi өстердi бұру жолымен екi өзара перпендикуляр
бағытта
![]() және
және ![]() бас кернеулермен созылуға (сығылуға) келтiруге
болатындығы
бґрыннан белгiлi. Осыған ұқсас көлемдiк кернеулi күйде өстердiң және параллелепипедтiң
бағытын өзгертiп, барлық
жағында жанама кернеулер нөлге тең болатын қалыпты табуға болады.
Параллелепипедтiң жақтарына параллель алаңдар бас алаңдар
деп аталады. Оларға әсер ететiн
бас кернеулермен созылуға (сығылуға) келтiруге
болатындығы
бґрыннан белгiлi. Осыған ұқсас көлемдiк кернеулi күйде өстердiң және параллелепипедтiң
бағытын өзгертiп, барлық
жағында жанама кернеулер нөлге тең болатын қалыпты табуға болады.
Параллелепипедтiң жақтарына параллель алаңдар бас алаңдар
деп аталады. Оларға әсер ететiн ![]() және
және ![]() кернеулердi бас кернеулер деп, ал сәйкес өстерiн бас өстер
дейдi.
кернеулердi бас кернеулер деп, ал сәйкес өстерiн бас өстер
дейдi.
![]() және
және ![]() бас кернеулердi кез келген алаңдарға әсер ететiн
кернеулер арқылы анықтау әдiсiн қарастырамыз.
бас кернеулердi кез келген алаңдарға әсер ететiн
кернеулер арқылы анықтау әдiсiн қарастырамыз.
Бұл үшiн кез келген бас алаңның нормальмен анықталатын көлбеуi белгiлi деп ұйғарайық. Алаңға параллель қимамен бастапқы параллелепипедтен 11-суреттегiдей тетраэдрдi бөлiп аламыз да, тетраэдрдi тепе-теңдiк шартын әсер ететiн барлық күштердiң координат өстерiне проекциясының қосындысы түрiнде тұжырымдаймыз.
Мәшине жасау саласында сырықтар жүйесі және жақтаулар статикалық анықталмағандығын анықтауда күштер тәсілі кеңінен қолданылады. Оның мәнiсi мынада: берілген статикалық анықталмайтын жүйе сыртқы және өзара қосымша байланыстардан босатылып, олардың әсерi күштермен және моменттермен ауыстырылады. Олардың шамасын байланыстан босатылған жүйеге қойылатын орын ауыстыру шектеулерге сәйкес келетіндей eтiп тандайды. Сонымен, көрсетiлген әдiспен шешу кезiнде күштер бeлгiciз болады. «Күштер тәсілі» деп аталуы да содан. Мұндай әдiс бipey ғана емес. Құрылыс механикасын басқа да тәсілдер, мәселен, бeлгiciз ретінде күш әсері емес, сырықтар жүйесі элементтеріндегi орын ауыстыру алынатын деформация әдiсі пайдаланылады.
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР
-
Н.Қожаспаев, С.Кешуов, И.Мухитов Электротехника /оқу құралы/ - Алматы. Республикалық баспа кабинеті, 1996 ж., 300 бет
-
Электротехника /Под ред- проф. В. Г. Герасимова.— М.: Высшая школа. 1935.
-
Волынский Б. А., Зейн Е. Н..Шатерников В. Е.Электротехника.— Москва.:Эпергоатомиздат, 1987.
-
Борисов Ю.М., Липатов Д.Н., Зорин Ю.Н., Электротехника —Москва.:Эпергоатомиздат, 1985.
-
Касаткин А. С., Немцов М. В..Электротехника.— М.: Энерогоатомиздат. 1983.
-
Иванов И. И., Равдоник С. С. Электротехника.— М.: Высшее школа, 1984.
-
Электротехника. Программированное учебное пособие /Под ред. проф. В. Г. Герасимова.— М.: Высшая школа, 1983.
-
Основы промышленной электроники. /Под ред. проф. А Г. Герасимова.— М.:Высшая школа, 1986.
30
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
КҮШТЕР ТӘСІЛІ
КҮШТЕР ТӘСІЛІ
МАЗМҰНЫ
КІРІСПЕ ........................................................................................................................3
І. КҮШТЕР ТӘСІЛІ.....................................................................................................4
1.1. Күштер тәсілінің негізгі теңдеулер жүйесі.........................................................4
1.2. Бас кернеулерді есептеу........................................................................................8
ІІ. НҮКТЕДЕГІ ДЕФОРМАЦИЯЛАНҒАН КҮЙ.....................................................17
2.1. Жазық кернеулi күйде материал деформациясы...............................................17
2.2. Деформация кезінде материал көлемінің өзгеруі.............................................18
ҚОРЫТЫНДЫ ............................................................................................................24
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР........................................................................25
КІРІСПЕ
Мәшине жасау саласында сырықтар жүйесі және жақтаулар статикалық анықталмағандығын анықтауда күштер тәсілі кеңінен қолданылады. Оның мәнiсi мынада: берілген статикалық анықталмайтын жүйе сыртқы және өзара қосымша байланыстардан босатылып, олардың әсерi күштермен және моменттермен ауыстырылады. Олардың шамасын байланыстан босатылған жүйеге қойылатын орын ауыстыру шектеулерге сәйкес келетіндей eтiп тандайды. Сонымен, көрсетiлген әдiспен шешу кезiнде күштер бeлгiciз болады. «Күштер тәсілі» деп аталуы да содан. Мұндай әдiс бipey ғана емес. Құрылыс механикасын басқа да тәсілдер, мәселен, бeлгiciз ретінде күш әсері емес, сырықтар жүйесі элементтеріндегi орын ауыстыру алынатын деформация әдiсі пайдаланылады.
Сонымен, кез келген жақтаудың статикалық түрде анықталмағандығын анықтау қосымша байланыстарды алып тастаудан басталады. Қосымша байланыстардан босатылған жүйе статикалық анықталған болады. Ол негізгi жүйе деп аталады. Әрбiр статикалық анықталмаған сырықтар жүйесі үшін әдетте негізгі жүйелердi қалауымызша таңдауға болады. Мысалы, жақтау үшін көрсетілгендей негізгі жүйелердi (а, б, в. г, д) ұсынуға болады. Олар қосымша жеті байланыста әр алуан жолмен алып тастау арқылы алынған.
Пуассон
коэффициентi. Ұзару деформациясы оң, қысқару терiс делiнедi. (40)
формуласы сызықты кернеулi күйдегi Гук заңын өрнектейдi. Көлемдiк кернеулi күйде
тiк кернеулер мен ұзарудың ұқсас қатынасын тағайындаймыз. Өйткенi кiшi деформация кезiнде
жанама кернеулер тiк бұрышты элемент жақтарының ұзындығын өзгертпей, тек ығысуды тудырады.
Мұнда
элементтiң тек
сызықты
деформациялары қарастырылады. Ығысу деформациясына IV тарауда
тоқталамыз. ![]() және
және ![]() деформацияларды
деформацияларды ![]() және
және ![]() арқылы өрнектеп табамыз. Ол үшiн күштер әсерiнiң тәуелсiздiк принципiн
және (40)
және (41)
формулаларындағы қатынастарды пайдаланамыз
арқылы өрнектеп табамыз. Ол үшiн күштер әсерiнiң тәуелсiздiк принципiн
және (40)
және (41)
формулаларындағы қатынастарды пайдаланамыз ![]() кернеуi бағытымен
кернеуi бағытымен ![]() салыстырмалы ұзарудың косындысын үш қосылғышпен өрнектеуге болады.
салыстырмалы ұзарудың косындысын үш қосылғышпен өрнектеуге болады.
Сонымен бipгe жетi байланысы алынып тасталатын жүйені негізгі деп алуға болмайтынын ескеру қажет. 12-суретте жетi байланысы алынып тасталған жақтаудың үш түрi көрсетiлген. Бұл дұрыс емес, өйткені қалған байланыстар жүйенің кинематикалық өзгермейтіндiгін және барлық түйіндерде статикалық анықталатынын қамтамасыз ете алмайды. Қосымша байланыстарды алып тастағаннан кейiн, жүйе статикалық анықталынатын болғанда жоғарыда айтқанымыздай байланыс орнына бeлгiciз күш әсерлерiн ендiру керек.
І. КҮШТЕР ТӘСІЛІ
1.1. Күштер тәсілінің негізгі теңдеулер жүйесі
Мәшине жасау саласында сырықтар жүйесі және жақтаулар статикалық анықталмағандығын анықтауда күштер тәсілі кеңінен қолданылады. Оның мәнiсi мынада: берілген статикалық анықталмайтын жүйе сыртқы және өзара қосымша байланыстардан босатылып, олардың әсерi күштермен және моменттермен ауыстырылады. Олардың шамасын байланыстан босатылған жүйеге қойылатын орын ауыстыру шектеулерге сәйкес келетіндей eтiп тандайды. Сонымен, көрсетiлген әдiспен шешу кезiнде күштер бeлгiciз болады. «Күштер тәсілі» деп аталуы да содан. Мұндай әдiс бipey ғана емес. Құрылыс механикасын басқа да тәсілдер, мәселен, бeлгiciз ретінде күш әсері емес, сырықтар жүйесі элементтеріндегi орын ауыстыру алынатын деформация әдiсі пайдаланылады.
С онымен, кез келген жақтаудың статикалық
түрде анықталмағандығын анықтау қосымша байланыстарды алып
тастаудан басталады. Қосымша байланыстардан босатылған жүйе
статикалық анықталған болады. Ол негізгi жүйе деп аталады. Әрбiр статикалық
анықталмаған сырықтар жүйесі үшін әдетте негізгі жүйелердi
қалауымызша таңдауға болады. Мысалы, жақтау үшін көрсетілгендей
негізгі жүйелердi (а, б, в. г, д) ұсынуға
болады. Олар қосымша жеті байланыста әр
алуан жолмен алып тастау арқылы алынған.
онымен, кез келген жақтаудың статикалық
түрде анықталмағандығын анықтау қосымша байланыстарды алып
тастаудан басталады. Қосымша байланыстардан босатылған жүйе
статикалық анықталған болады. Ол негізгi жүйе деп аталады. Әрбiр статикалық
анықталмаған сырықтар жүйесі үшін әдетте негізгі жүйелердi
қалауымызша таңдауға болады. Мысалы, жақтау үшін көрсетілгендей
негізгі жүйелердi (а, б, в. г, д) ұсынуға
болады. Олар қосымша жеті байланыста әр
алуан жолмен алып тастау арқылы алынған.
Сонымен бipгe жетi байланысы
алынып тасталатын жүйені негізгі деп алуға болмайтынын ескеру
қажет. 12-суретте жетi байланысы алынып тасталған жақтаудың үш түрi
көрсетiлген. Бұл дұрыс емес, өйткені қалған байланыстар жүйенің
кинематикалық өзгермейтіндiгін және барлық түйіндерде статикалық
анықталатынын қамтамасыз ете алмайды. Қосымша байланыстарды алып
тастағаннан кейiн, жүйе статикалық анықталынатын болғанда жоғарыда
айтқанымыздай байланыс орнына бeлгiciз күш әсерлерiн ендiру керек.
Сызықтық орын ауыстыру рұқсат етiлмейтін қималарға күш, ал бұрыштық
орын ауыстыру рұқсат етiлмейтін қималарға моменттер түcipiлeдi. Екі
жағдайда да белгiсiз күш әсерлерін ![]() деп белгiлеймiз,
мұндағы
деп белгiлеймiз,
мұндағы ![]() - белгiсiз күш нөмiрi.
- белгiсiз күш нөмiрi. ![]() -дің ең үлкен мәнi жүйенiң
статикалық анықталмағандық дәрежесіне тең боладi.
Ішкi байланыс үшін де
-дің ең үлкен мәнi жүйенiң
статикалық анықталмағандық дәрежесіне тең боладi.
Ішкi байланыс үшін де ![]() күштерi сай келетiнiн ескертемiз. Егер кейбiр
қимада жақтауды
тілсе, онда жүйенің оң және сол жағына тең және қарама-қарсы күштер
мен моменттер әсер етедi.
күштерi сай келетiнiн ескертемiз. Егер кейбiр
қимада жақтауды
тілсе, онда жүйенің оң және сол жағына тең және қарама-қарсы күштер
мен моменттер әсер етедi.
11-суретте қарастырылған негiзгi жүйелерге белгiсiз күштердi түсiрудiң мүмкiн бес әдiсi көрсетiлген (12-сурет). Бeлгiciз күш әсерлерін түcipy принципi түciнiктi. Тек белгiсiздердi анықтау үшiн теңдеулердi құру керек.

12 - сурет
12-суреттiң бiрiншiсiн қайта сызып қарастырайық (13-сурет). Бұл жүйе жетi рет статикалық анықталмаған.
Ендi белгiсiз күш әсерлерiн
анықтау үшiн теңдеулер құрайық. ![]() арқылы жүйе нүктелерiнің өзара
орын ауыстыруын белгілеймiз. Бірiншi индекс орын ауыстыру бағытына,
ал екiнші орын ауыстыруды тудыратын күшке сәйкес
келедi.
арқылы жүйе нүктелерiнің өзара
орын ауыстыруын белгілеймiз. Бірiншi индекс орын ауыстыру бағытына,
ал екiнші орын ауыстыруды тудыратын күшке сәйкес
келедi.
Раманың А нүктесiнде тiрек алып
тасталған. Демеқ горизонталь орын ауыстыру нөлге тең болады
да: ![]() 1 индексi
1 индексi ![]() күш бағыты бойынша орын
ауыстыруды, ал
күш бағыты бойынша орын
ауыстыруды, ал ![]() индексi орын ауыстыру берiлген әрi белгісiз
күштермен анықталатындығын көрсетедi. Осыған ұқсас түрде:
индексi орын ауыстыру берiлген әрi белгісiз
күштермен анықталатындығын көрсетедi. Осыған ұқсас түрде:
![]() және т. б. деп жазуға болады.
және т. б. деп жазуға болады.
![]() шамасы нүктелердiң өзара орын ауыстыруын,
шамасы нүктелердiң өзара орын ауыстыруын,
![]() онда В
нүктесінің С нүктесіне сәйкес
вертикаль орын ауыстыруын,
онда В
нүктесінің С нүктесіне сәйкес
вертикаль орын ауыстыруын, ![]() сол нүктелердiң горизонталь өзара орын
ауыстыруын,
сол нүктелердiң горизонталь өзара орын
ауыстыруын, ![]() - қималардьң В және С қималардың өзара
бұрыштық орын ауыстыруын білдіредi. Қаралатын жүйеде бұрыштық орын
ауыстыруға
- қималардьң В және С қималардың өзара
бұрыштық орын ауыстыруын білдіредi. Қаралатын жүйеде бұрыштық орын
ауыстыруға ![]() жатады.
жатады.
А және D нүктелерде ![]() орын ауыстыру абсолют болады. Бірақ абсолют орын
ауыстыруларды алынып тасталған қозғалмайтын тiректермен өзара бipгe
орын ауыстыру ретінде қарастыруға болады. Сондықтан қабылданған
белгілердi жүйенiң барлық қимасы үшiн пайдалануға
болады.
орын ауыстыру абсолют болады. Бірақ абсолют орын
ауыстыруларды алынып тасталған қозғалмайтын тiректермен өзара бipгe
орын ауыстыру ретінде қарастыруға болады. Сондықтан қабылданған
белгілердi жүйенiң барлық қимасы үшiн пайдалануға
болады.
Күштер әсерiнiң тәуелсiздiк
принципiн .пайдаланып, ![]() орын ауыстырудың өрнегiн
анықтайық:
орын ауыстырудың өрнегiн
анықтайық:

Осылайша қалған бес
теңдеуді де жазуға болады: ![]() қосылғыштардың теңдеуге кіретін әpбip
қосылғыштардың теңдеуге кіретін әpбip
![]() қосылғышы бiрiншi
индекспен, екіншісінде тұрған күш әсерінен сол күш
бағытындағы орын ауыстыруды білдіредi әpбip орын
ауыстыру сәйкес күшке пропорционал болғандықтан,
қосылғышы бiрiншi
индекспен, екіншісінде тұрған күш әсерінен сол күш
бағытындағы орын ауыстыруды білдіредi әpбip орын
ауыстыру сәйкес күшке пропорционал болғандықтан,
![]() шамасын келесi түрде жазуға
болады:
шамасын келесi түрде жазуға
болады:
![]() (5)
(5)
![]() т. с. с. орын ауыстыруларға келсеқ, онда
Р индексi
сыртқы күшті ғана емес, кез келген сыртқы күштер жүйесін білдiредi.
Сондықтан
т. с. с. орын ауыстыруларға келсеқ, онда
Р индексi
сыртқы күшті ғана емес, кез келген сыртқы күштер жүйесін білдiредi.
Сондықтан ![]() шамаларды теңдеулерде өзгepicсiз қалдырамыз.
Теңдеулер мына түрде болады:
шамаларды теңдеулерде өзгepicсiз қалдырамыз.
Теңдеулер мына түрде болады:
 (6)
(6)
Бұл теңдеулердi күш әдісінің
канондық теңдеулерi деп атайды. Олардың саны жүйенің статикалық
анықталмағандық дәрежесiне тең. Кейбiр
жағдайда кейбiр белгiсiздердiң мәнің бiрден көрсету мүмкін болса,
онда бipгe шешілетін теңдеулердің саны азаяды. Ендi
![]() коэффициентi ненi бiлдiредi және оны қалай
анықтаймыз, соған тоқталайық.
коэффициентi ненi бiлдiредi және оны қалай
анықтаймыз, соған тоқталайық.
Б ұл
үшiн (5)
өpнeгiн қарайық. Егер
ұл
үшiн (5)
өpнeгiн қарайық. Егер ![]() болса, онда
болса, онда ![]() . Демеқ
. Демеқ
![]() коэффициент к-ыншы әсердi алмастыратын бірлік әсер
нәтижесінде
коэффициент к-ыншы әсердi алмастыратын бірлік әсер
нәтижесінде ![]() -iншi күш әсері бағытындағы орын ауыстыру болады. Мысалы,
/6/ өрнектегi
-iншi күш әсері бағытындағы орын ауыстыру болады. Мысалы,
/6/ өрнектегi ![]() коэффициентi рамаға түсiрiлетiн барлық күштердiң
орнына А нүктесiне /13-сурет/ тек бiрлiк күш түсiрiлгенде В және С нүктелерiнiң горизонталь
орын ауыстыруын бiлдiредi. Егер
коэффициентi рамаға түсiрiлетiн барлық күштердiң
орнына А нүктесiне /13-сурет/ тек бiрлiк күш түсiрiлгенде В және С нүктелерiнiң горизонталь
орын ауыстыруын бiлдiредi. Егер ![]() күш орнына бiрлiк күш түcipiп,
басқа барлық күштердi алып тастасақ, онда осы күш әсерінен
D қимадағы
бұрылу бұры-
күш орнына бiрлiк күш түcipiп,
басқа барлық күштердi алып тастасақ, онда осы күш әсерінен
D қимадағы
бұрылу бұры-![]() , ал А
нүктедегі горизонталь орын ауыстыру
, ал А
нүктедегі горизонталь орын ауыстыру
![]() , болады және т. с. с.
, болады және т. с. с.
Жасалған қорытындыда  орын ауыстырудың
қалай пайда болатындығын қарастырмаймыз. Себебі, иiлетiн раманы
қарастырсақ та, айтылғандарды кез келген жүйеде бұралатын,
созылатын және барлығы бipгe болатын жүйелерде қолдануға болады.
Мор интегралдарын қарастырайық. (§3, VIII тарауды қараңыз).
орын ауыстырудың
қалай пайда болатындығын қарастырмаймыз. Себебі, иiлетiн раманы
қарастырсақ та, айтылғандарды кез келген жүйеде бұралатын,
созылатын және барлығы бipгe болатын жүйелерде қолдануға болады.
Мор интегралдарын қарастырайық. (§3, VIII тарауды қараңыз).
 шамасын анықтау үшін сыртқы . күштердің орнына
шамасын анықтау үшін сыртқы . күштердің орнына  факторды
ауыстыратын бiрлiк күштi қарастырамыз. Сондықтан өрнектегі
факторды
ауыстыратын бiрлiк күштi қарастырамыз. Сондықтан өрнектегі
 және
және  iшкi моменмттердi және күштердi
iшкi моменмттердi және күштердi  бipлiк фактордан
туындайтын
бipлiк фактордан
туындайтын  және
және  iшкі моменттер
мен күштерге алмастырамыз. Сонда:
iшкі моменттер
мен күштерге алмастырамыз. Сонда:
![]()
мұндағы
![]() - бiрлiк фактор
әсерiнен туатын iшкi моменттер мен күштер. Сонымен,
- бiрлiк фактор
әсерiнен туатын iшкi моменттер мен күштер. Сонымен,
![]() коэффициенттерi
коэффициенттерi ![]() және
және ![]() бipлiк ішкі күш әсерлерiн көбейту нәтижесінде алынады.
бipлiк ішкі күш әсерлерiн көбейту нәтижесінде алынады.
![]() және
және ![]() индекстерi қандай әсерлердi Мор интегралымен
көбейту қажеттігін тiкелей көрсетедi. Егер рама тура учаскелер-ден
құрылып, Верещагин тәсiлiн пайдалану мүмкiн болса, онда
индекстерi қандай әсерлердi Мор интегралымен
көбейту қажеттігін тiкелей көрсетедi. Егер рама тура учаскелер-ден
құрылып, Верещагин тәсiлiн пайдалану мүмкiн болса, онда
![]() және
және ![]() бiрлiк эпюрлерінiң көбейтiндiсi болады.
Яғни
бiрлiк эпюрлерінiң көбейтiндiсi болады.
Яғни ![]() . Бұл бip жағынан (5) өрнегінен тiкелей, ал
екiнші жағынан
. Бұл бip жағынан (5) өрнегінен тiкелей, ал
екiнші жағынан ![]() және
және ![]() орын ауыстырулары бipгe тең, бiрдей күш әсерінен
болатындықтан өзара орын ауыстыру теоремасынан
шығады.
орын ауыстырулары бipгe тең, бiрдей күш әсерінен
болатындықтан өзара орын ауыстыру теоремасынан
шығады.
Канондық теңдеуге
кiретiн ![]() шамалары негiзгi жүйеде берiлген сыртқы
күштердiң әсерiнен 1, 2.. бағыттардағы орын ауыстыруды бiлдіредi.
Олар берiлген күштердің эпюрлерін сәйкес бipлiк эпюрлерге көбейту
арқылы анықталады.
шамалары негiзгi жүйеде берiлген сыртқы
күштердiң әсерiнен 1, 2.. бағыттардағы орын ауыстыруды бiлдіредi.
Олар берiлген күштердің эпюрлерін сәйкес бipлiк эпюрлерге көбейту
арқылы анықталады.
Созылған немесе сығылған сырықтың өсіне көлбеу қималарға әсер ететiн кернеулердi анықтау үшiн төмендегi формулаларды бұрын тұжырымдаған болатынбыз:
![]() .
.
Б ұл
формулалардан кез келген нүкте
арқылы өтетiн
алаңнан көлбеулiгi
өзгергенде
нүктеге
әсер ететiн тiк
ұл
формулалардан кез келген нүкте
арқылы өтетiн
алаңнан көлбеулiгi
өзгергенде
нүктеге
әсер ететiн тiк
![]() және жанама
және жанама
![]() кернеулердiң де
өзгеретiндiгi
байқалады. Сонымен
бipгe өзiнiң ең үлкен
мәнiне тiк кернеу
көлденең
қималарда, ал жанама кернеулер
стержень өсiне 45° бұрышпен
жүpгiзiлгeн
қималарда ие болады. Ал,
сырыққа
әсер ететiн
күштердiң күрделi
жағдайында
кернеулердiң ең үлкен
мәнi мен олар
әсер ететiн
аудандардың күйiн
анықтау қиындай
түceдi.
Бұл мәселенi шешу
үшiн кез келген
нүкте
арқылы өтетiн
алаңдардың, көлбеулiгi
өзгергенде
кернеулердiң өзгеру
заңдылықтарын арнайы
кернеулердiң де
өзгеретiндiгi
байқалады. Сонымен
бipгe өзiнiң ең үлкен
мәнiне тiк кернеу
көлденең
қималарда, ал жанама кернеулер
стержень өсiне 45° бұрышпен
жүpгiзiлгeн
қималарда ие болады. Ал,
сырыққа
әсер ететiн
күштердiң күрделi
жағдайында
кернеулердiң ең үлкен
мәнi мен олар
әсер ететiн
аудандардың күйiн
анықтау қиындай
түceдi.
Бұл мәселенi шешу
үшiн кез келген
нүкте
арқылы өтетiн
алаңдардың, көлбеулiгi
өзгергенде
кернеулердiң өзгеру
заңдылықтарын арнайы
зерттеу қажет. Яғни деформацияланатын дененiң нүктедегi кернеулi күйiн зерттеу мәселесі туындайды.
Н үктедегi кернеулi
күй деп, сол
нүкте
арқылы
өтетiн
барлық алаңдар
бойынша әсер
етушi кернеулердiң жиынтығын айтады. Сырықтың созылуы
немесе сығылуы
дене деформациясының ең қарапайым түрi болады. Оның барлық нүктесiнде кернеулi күй
бiрдей (бiртектi кернеулi күй) деп есептелiнедi.
үктедегi кернеулi
күй деп, сол
нүкте
арқылы
өтетiн
барлық алаңдар
бойынша әсер
етушi кернеулердiң жиынтығын айтады. Сырықтың созылуы
немесе сығылуы
дене деформациясының ең қарапайым түрi болады. Оның барлық нүктесiнде кернеулi күй
бiрдей (бiртектi кернеулi күй) деп есептелiнедi.
Жалпы жағдайда
(1,![]() -сурет) денеде кернеулi күй бiртектi емес, ол әр
нүктеде өзгерiп отырады. Сондықтан осы дененiң кез
келген
-сурет) денеде кернеулi күй бiртектi емес, ол әр
нүктеде өзгерiп отырады. Сондықтан осы дененiң кез
келген ![]() қимасында кернеулер бiртектi таралмайды.
Демек, кез
келген
қимасында кернеулер бiртектi таралмайды.
Демек, кез
келген ![]() нүктесінде кернеулi күйдi зерттеу үшiн сол
нүктенiң маңынан ойша өлшемдері
нүктесінде кернеулi күйдi зерттеу үшiн сол
нүктенiң маңынан ойша өлшемдері ![]() болатын
(1,
болатын
(1,![]() -сурет) параллелипедтi аламыз.
Параллелепипед өте кiшкентай болғандықтан оның барлық нүктeciндe кернеулi
күй бiртектi әpi ол
-сурет) параллелипедтi аламыз.
Параллелепипед өте кiшкентай болғандықтан оның барлық нүктeciндe кернеулi
күй бiртектi әpi ол ![]() нүктесiнiң кернеулi күйiне сәйкес деп санаймыз.
Сондықтан, барлық жақтары бойынша және кез келген қималарында
кернеулер бiрдей таралған деп саналады. Бұл болжам қарапайым
параллелепипедтiң көлбеу қималарында кернеудiң өзгеру заңын
зерттеуге мүмкiндiк бередi. Параллелепипедтiң жақтарында кернеулер белгiлi
деп саналады, aл оның көлбеу алаңдарында әceр ететiн кернеулердi
қималар әдiсi яғни параллелепипедтiң
тiлiнген бөлiгiнiң тепе-теңдiк шартынан
анықтаймыз.
нүктесiнiң кернеулi күйiне сәйкес деп санаймыз.
Сондықтан, барлық жақтары бойынша және кез келген қималарында
кернеулер бiрдей таралған деп саналады. Бұл болжам қарапайым
параллелепипедтiң көлбеу қималарында кернеудiң өзгеру заңын
зерттеуге мүмкiндiк бередi. Параллелепипедтiң жақтарында кернеулер белгiлi
деп саналады, aл оның көлбеу алаңдарында әceр ететiн кернеулердi
қималар әдiсi яғни параллелепипедтiң
тiлiнген бөлiгiнiң тепе-теңдiк шартынан
анықтаймыз.
1.2. Бас кернеулерді есептеу
Күш түcipiлгeн дененiң кез келген нүктесiнде барлық жақтарына жанама кернеулер әсер етпейтiн қарапайым параллелепипедтi бөлiп алуға болатындығын көремiз. Бұл жағдайда параллелепипед бip, екi және үш өзара перпендикуляр бағыттарда созылу (сығылу) жағдайында болады.
Сызықтық кернеулi күйге, сырық нүктелерi, мысалы, орталық созылу немесе сығылу кезiнде ұшырайды. Жазық кернеулi күй материалдар механикасы есептерiнде жиi кездеседi. Оның сипаттық белгiсiне параллелепипедтiң параллель екi жағында кернеулердiң болмайтындығы жатады.
Кез келген
күштер жүйесi
түcipiлгeн
жұқа
пластинканы қарастырайық (3,![]() -сурет). Күш пластинканың жиегiне әсер етiп, оның жазықтығында жатсын делiк.
-сурет). Күш пластинканың жиегiне әсер етiп, оның жазықтығында жатсын делiк.
![]() жазықтығына параллель пластинкада
кернеулер болмайды (
жазықтығына параллель пластинкада
кернеулер болмайды (![]() ). Пластинканың қалыңдығы өте аз болғандықтан, оның iшiндегi бетке параллель
алаңдарда да
кернеулер болмайды деп санаймыз. Сондықтан пластинка
нүктелерi жалпы
жағдайда
жазық кернеулi
күйде болады.
Дәл осындай
күйде, мысалы,
салыстырмалы жұқа пластинкалардан жасалған сырықтар мен арқалықтар болады.
Бойлық екi
). Пластинканың қалыңдығы өте аз болғандықтан, оның iшiндегi бетке параллель
алаңдарда да
кернеулер болмайды деп санаймыз. Сондықтан пластинка
нүктелерi жалпы
жағдайда
жазық кернеулi
күйде болады.
Дәл осындай
күйде, мысалы,
салыстырмалы жұқа пластинкалардан жасалған сырықтар мен арқалықтар болады.
Бойлық екi ![]() және
және ![]() қималарымен
бөлiнген
қос таврлы
арқалықтың тiк қабырғасына контуры бойынша тiк және жанама кернеулер
түcipiлciн
(3,
қималарымен
бөлiнген
қос таврлы
арқалықтың тiк қабырғасына контуры бойынша тiк және жанама кернеулер
түcipiлciн
(3,![]() -сурет). Сонда оның нүктелерi жазық кернеулi күйге ұшырайды. Бұл кернеулi күй материалдар
кедергiсiнде өте маңызды болғандықтан, оны төменде бөлек қарастырамыз.
-сурет). Сонда оның нүктелерi жазық кернеулi күйге ұшырайды. Бұл кернеулi күй материалдар
кедергiсiнде өте маңызды болғандықтан, оны төменде бөлек қарастырамыз.
3-суретте көрсетiлген пластинканың
кез келген ![]() нүктесiнiң маңынан пластинка
жазықтығына
перпендикуляр қималармен қарапайым параллелепипедтi кесiп алайық. Параллелепипедтi
қоршаған
ортадан оған
жалпы жағдайда
тiк және жанама
кернеулер әсер
етедi. 3-суретте тiк және
жанама кернеулерге сәйкес векторлары
көрсетiлген.
Координаттар өci элемент орталығында
орналасқан.
нүктесiнiң маңынан пластинка
жазықтығына
перпендикуляр қималармен қарапайым параллелепипедтi кесiп алайық. Параллелепипедтi
қоршаған
ортадан оған
жалпы жағдайда
тiк және жанама
кернеулер әсер
етедi. 3-суретте тiк және
жанама кернеулерге сәйкес векторлары
көрсетiлген.
Координаттар өci элемент орталығында
орналасқан.
Жоғарыда көрсеткенiмiздей шексiз кiшi
параллелепипедтiң барлық нүктесiнде кернеулi күй бiртектi деп саналады.
Сондықтан,
параллелепипедтiң параллель жақтарындағы аттас кернеулер бip-бipiнe тең бағыттары қарама-қарсы
болады. Кернеулердi белгiлеу кезiнде
индекстерiне назар аудару керек. Жанама кернеуде екi индекс,
мысалы ![]() бар. Бipiншi индекс жанама кернеу алаңда
бар. Бipiншi индекс жанама кернеу алаңда ![]() ociнe параллель нормальмен бipгe әсер ететiндiгiн, ал екiншi
индекс жанама кернеу векторы
ociнe параллель нормальмен бipгe әсер ететiндiгiн, ал екiншi
индекс жанама кернеу векторы ![]() осiне параллель екендiгiн бiлдiредi. Тiк
кернеудiң екi
бeлгici бiрдей болатындықтан, тек бip индекс
алынады.
осiне параллель екендiгiн бiлдiредi. Тiк
кернеудiң екi
бeлгici бiрдей болатындықтан, тек бip индекс
алынады.
К ернеулер таңбасын мынадай ережемен қарастырамыз.
Созылудың тiк
кернеуi - оң,
ал сығылудiкi -
тepic деп саналады. Жанама кepнeyлepдiң бeлгici координаттар
өciнiң бағыттарына байланысты: егер алаңның сыртқы ноpмaлi координат
өciнiң сәйкес
бағытымен бағыттас, онда бұл алаңда кернеу
ернеулер таңбасын мынадай ережемен қарастырамыз.
Созылудың тiк
кернеуi - оң,
ал сығылудiкi -
тepic деп саналады. Жанама кepнeyлepдiң бeлгici координаттар
өciнiң бағыттарына байланысты: егер алаңның сыртқы ноpмaлi координат
өciнiң сәйкес
бағытымен бағыттас, онда бұл алаңда кернеу ![]() сәйкес осьтiң бағытымен үйлесiп оң болады. Бґл ереженi, қысқаша сыртқы нормаль ережесi дейдi.
3-суретте
көрсетiлген
барлық кернеулер
сәйкес осьтiң бағытымен үйлесiп оң болады. Бґл ереженi, қысқаша сыртқы нормаль ережесi дейдi.
3-суретте
көрсетiлген
барлық кернеулер ![]() осьтерiнде оЎ болады. Көлбеу алаңдарға да осы ереженi
қолданамыз, тек жанама
кернеулердiң таңбасын
осьтерiнде оЎ болады. Көлбеу алаңдарға да осы ереженi
қолданамыз, тек жанама
кернеулердiң таңбасын ![]() көлбеу осьтерiне сәйкес белгiлеймiз
(3-сурет).
көлбеу осьтерiне сәйкес белгiлеймiз
(3-сурет).
Жазық кернеулi күйдi талдау кезiнде
![]() нүктелерiндегi кернеулер берiлген деп есептеледi,
сондықтан олар
бастапқы
кернеулер деп аталады.
нүктелерiндегi кернеулер берiлген деп есептеледi,
сондықтан олар
бастапқы
кернеулер деп аталады.
 Бас
кернеулер
Бас
кернеулер
![]() өстердi және
тiк бұрышты элемент
бұрышын
өзгерте ойша
бұрамыз
(4-сурет).
Сонда кез келген
өстердi және
тiк бұрышты элемент
бұрышын
өзгерте ойша
бұрамыз
(4-сурет).
Сонда кез келген ![]() бұрышында тiк кернеу
бұрышында тiк кернеу ![]() берiлген нүкте үшiн ең жоғары мәнiнe жетедi. (9)
өрнекке
негiздеп қорытынды шығаруға
болады: ең аз
кернеу перпендикуляр алаңда болады. Бұл алаңдарды және бұл нүкте үшiн экстремаль
тік кернеудi табамыз.
Бұл
үшiн туындыны
нөлге
теңеймiз
берiлген нүкте үшiн ең жоғары мәнiнe жетедi. (9)
өрнекке
негiздеп қорытынды шығаруға
болады: ең аз
кернеу перпендикуляр алаңда болады. Бұл алаңдарды және бұл нүкте үшiн экстремаль
тік кернеудi табамыз.
Бұл
үшiн туындыны
нөлге
теңеймiз
![]() .
.
өрнектi (6) ![]() аргумент бойынша
дифференциалдаймыз
аргумент бойынша
дифференциалдаймыз
 . (10)
. (10)
Жақшадағы өрнектi (4) формуласымен салыстырамыз:
![]() . (11)
. (11)
Өpнектi нөлге теңестiрiп әрi iзделiп отырған алаңдар нормалiнiң көлбеу бұрышын ![]() арқылы белгiлеп
арқылы белгiлеп
![]() анықтаймыз. Бұдан алаңда нүктеге экстремаль тiк кернеу әсер еткенде, жанама кернеулер
нөлге
тең екенiн көөөрсетуге
болады. Оларды бас алаңдар, ал оларға сәйкес тiк кернеулердi
нүктедегi бас
кернеулер дейдi.
анықтаймыз. Бұдан алаңда нүктеге экстремаль тiк кернеу әсер еткенде, жанама кернеулер
нөлге
тең екенiн көөөрсетуге
болады. Оларды бас алаңдар, ал оларға сәйкес тiк кернеулердi
нүктедегi бас
кернеулер дейдi.
(10) формуласының жақшадағы өрнегiн нөлге тeңecтipiп, бас алаңдар нормалiнiң көлбеулiгiн анықтайтын екі еселенген бұрыштың тангенсiн табамыз:
![]() (12)
(12)
(12) өрнегi бас кернеулер
әсер ететiн
![]() және
және ![]() көлбеу бұрыштары бар өзара екi перпендикуляр бағытты бередi. Онда бас кернеулер
әсер етедi. Бас
кернеулердiң әсер ету сызықтарына сәйкес өстердi (
көлбеу бұрыштары бар өзара екi перпендикуляр бағытты бередi. Онда бас кернеулер
әсер етедi. Бас
кернеулердiң әсер ету сызықтарына сәйкес өстердi (![]() ) бас өстер деп атайды. Бас
кернеулердiң шамасын анықтау үшiн (6) формулаға
) бас өстер деп атайды. Бас
кернеулердiң шамасын анықтау үшiн (6) формулаға ![]() қоямыз.
қоямыз. ![]() жақшадан шығарсақ:
жақшадан шығарсақ:
 . (а)
. (а)
Тригонометриядан бeлгiлi формула бойынша (12) өрнегiн пайдаланып,
 , (б)
, (б)
екенiн табамыз.
«![]() » таңбаларының қойылу ceбeбi,
» таңбаларының қойылу ceбeбi, ![]() пен
пен ![]() бұрыштарының косинустары қарама-қарсы таңбалы болады. (12) және
(б) өрнектерiн (а)-ға қойып, жақшадағы өрнектердi ортақ бөлiмге келтiрiп және қысқартып,
бұрыштарының косинустары қарама-қарсы таңбалы болады. (12) және
(б) өрнектерiн (а)-ға қойып, жақшадағы өрнектердi ортақ бөлiмге келтiрiп және қысқартып, ![]() -дiң
eкi мәнiн:
-дiң
eкi мәнiн: ![]() және
және ![]() табамыз:
табамыз:
![]() . (13)
. (13)
Формуладағы плюс таңбасы ең үлкен бас кернеуге
![]() , ал минус —
ең аз бас
кернеуге
, ал минус —
ең аз бас
кернеуге ![]() сәйкес.
сәйкес.
Келтiрiлген қорытындыдан кез келген
бастапқы
кернеулер ![]() кезiнде берiлген нүктеде жақтарына тек тiк кернеулер
әсер ететiн болады.
Басқаша
айтқанда,
нүктедегі жазық кернеулі күйдi
өстердi бұру
жолымен созылу-сығылу ретiнде өзара екi перпендикуляр бағыттарында
кезiнде берiлген нүктеде жақтарына тек тiк кернеулер
әсер ететiн болады.
Басқаша
айтқанда,
нүктедегі жазық кернеулі күйдi
өстердi бұру
жолымен созылу-сығылу ретiнде өзара екi перпендикуляр бағыттарында
![]() және
және ![]() кернеулерiмен бейнелеуге
болады, ал (8)
матрица жазық кернеулi күй кезiнде мынадай түрде жазылады:
кернеулерiмен бейнелеуге
болады, ал (8)
матрица жазық кернеулi күй кезiнде мынадай түрде жазылады:

(12)
формуласын қарастырайық. Ол
бағыттарды бiлдiргенiмен,
![]() ,
, ![]() қайсы бағытта әсер ететiнiн көрсетпейдi. Бұл мәселенi математика жолымен
шешу үшiн
қайсы бағытта әсер ететiнiн көрсетпейдi. Бұл мәселенi математика жолымен
шешу үшiн ![]() және
және
![]() кезiнде
кезiнде ![]() екiншi
туындының
таңбасын анықтау қажет.
екiншi
туындының
таңбасын анықтау қажет.
Басқа жолмен де
![]() екi бағыттың қайсысымен әсер ететiндiгiн анықтауға болады. (11)
формуладан:
екi бағыттың қайсысымен әсер ететiндiгiн анықтауға болады. (11)
формуладан: ![]() кезiнде
кезiнде ![]() болатындығы шығады. Демек,
болатындығы шығады. Демек,
![]() үлкейсе,
үлкейсе,
![]() артады. Ол 10-суретте көрсетiлген.
артады. Ол 10-суретте көрсетiлген.
О сылайша
сылайша ![]() жағдайын қарастырып жалпы қорытындыға келемiз: жанама кернеу
векторының бағытымен алаңды бұрғанда
ондағы тiк
кернеу алгебралық түрде өседi. Мысалы,
жағдайын қарастырып жалпы қорытындыға келемiз: жанама кернеу
векторының бағытымен алаңды бұрғанда
ондағы тiк
кернеу алгебралық түрде өседi. Мысалы, ![]() бағытымен вертикаль алаңдарды бұру кезiнде оның тiк кернеулерi
үлкейедi, демек,
бұрудың осы бағытында жақын жатқан бас алаңмен үйлескен кезiнде 9 және
11,
бағытымен вертикаль алаңдарды бұру кезiнде оның тiк кернеулерi
үлкейедi, демек,
бұрудың осы бағытында жақын жатқан бас алаңмен үйлескен кезiнде 9 және
11, ![]() -суреттерде көрсетiлгендей
-суреттерде көрсетiлгендей
![]() -ға жетедi. Бұл суреттерден мынадай ереженi тұжырымдауға болады:
-ға жетедi. Бұл суреттерден мынадай ереженi тұжырымдауға болады:
![]() бағыты үнемi координат өстерiнiң
бағыты үнемi координат өстерiнiң
![]() мен
мен ![]() бағыттары сәйкес келетiн екi ширегi арқылы өтедi.
бағыттары сәйкес келетiн екi ширегi арқылы өтедi.
Бұл ереже жанама кернеу
диагональдың бipiн ұзартатындығын ескерсек, физикалық тұрғыда
түсiнiктi
болады 11, ![]() -сурет), яғни
-сурет), яғни ![]() бағыты дәл осы
диагональға ұмтылады.
бағыты дәл осы
диагональға ұмтылады.
МОР дөңгелектері
![]() және
және ![]() кернеулерiнiң
алаңдардың көлбеу
бұрышына
тәуелдiлiгiн қарапайым шеңбер диаграммасы түрiнде
геометриялық мағына
беруге болады. Бұл тәсiлдi немiс ғалымы Отто
Мор ұсынды.
кернеулерiнiң
алаңдардың көлбеу
бұрышына
тәуелдiлiгiн қарапайым шеңбер диаграммасы түрiнде
геометриялық мағына
беруге болады. Бұл тәсiлдi немiс ғалымы Отто
Мор ұсынды.
(14) және (15) формулаларында
тұрақты
шамаларды ![]() және
және ![]() деп белгiлеп, бұл формулаларды мынадай
түрде
жазамыз:
деп белгiлеп, бұл формулаларды мынадай
түрде
жазамыз:
![]() (19)
(19)
![]() координаттарында (19) теңдiгi радиусы
координаттарында (19) теңдiгi радиусы
![]() -ге тең
параметрлiк түрдегi шеңбер теңдеуiн өрнектейдi (6,а -сурет). Оны Мор
шеңберi немесе
кернеу шеңберi
деп атайды.
-ге тең
параметрлiк түрдегi шеңбер теңдеуiн өрнектейдi (6,а -сурет). Оны Мор
шеңберi немесе
кернеу шеңберi
деп атайды. ![]() бұрышпен анықталатын әрбiр көлбеу алаңға шеңберден бip нүкте сәйкес келедi (6,
бұрышпен анықталатын әрбiр көлбеу алаңға шеңберден бip нүкте сәйкес келедi (6, ![]() -сурет). Бұл
-сурет). Бұл ![]() нүкте координаттары
нүкте координаттары
![]() және
және ![]() . болатын
бейнеленген нүкте деп аталады.
. болатын
бейнеленген нүкте деп аталады. ![]() бұрыш санаудың қабылданған оң бағытын сақтау үшiн шеңбер диаграммасында
бұрыш санаудың қабылданған оң бағытын сақтау үшiн шеңбер диаграммасында
![]() oci
oci ![]() осiне қарама-қарсы бағытталуы (бiздiң жағдайымызда
осiне қарама-қарсы бағытталуы (бiздiң жағдайымызда
![]() oci төмен бағытталған) керек. Өйткенi (19) формуласынан
oci төмен бағытталған) керек. Өйткенi (19) формуласынан
![]() және
және ![]() болғанда, ордината
болғанда, ордината ![]() .
.
Өстердiң ![]() және
және ![]() бұрыштарға бұрылуына өзара перпендикуляр сәйкес алаңдарға шеңбер бойынан диаметр
ұшында
жатқан
бұрыштарға бұрылуына өзара перпендикуляр сәйкес алаңдарға шеңбер бойынан диаметр
ұшында
жатқан
![]() және
және ![]() нүктелерi сәйкес келедi. Бұл кезде кернеу шеңберiнде
нүктелерi сәйкес келедi. Бұл кезде кернеу шеңберiнде ![]() өйткенi
өйткенi ![]() үшiн формула осы
кернеудiң бұрылған
үшiн формула осы
кернеудiң бұрылған ![]() өстерiндегi (6,
өстерiндегi (6, ![]() -сурет) таңбасын көрсетедi.
-сурет) таңбасын көрсетедi.
Егер бас алаңдар мен ![]() және
және ![]() кернеулер белгiлi болса, онда
кернеу шеңберi
1 және 2
нүктелер
бойынша сызылады.
кернеулер белгiлi болса, онда
кернеу шеңберi
1 және 2
нүктелер
бойынша сызылады.
Алаң мен шеңбердегi бейнеленген
нүктенiң үйлесуiн тағайындау үшiн берiлген
жағдайда
нұкте 2-мен
дәл етiп
![]() нүктeciн (шеңбер полюсi) қарастырған ыңғайлы. Көлбеу алаңның нормалiне параллель
нүктeciн (шеңбер полюсi) қарастырған ыңғайлы. Көлбеу алаңның нормалiне параллель ![]() cәyлeci шеңбермен қиылысып бейнелейтiн
нүкте
cәyлeci шеңбермен қиылысып бейнелейтiн
нүкте
![]() бередi. Оны сызбадан көруге болады.
бередi. Оны сызбадан көруге болады.

6 – сурет
7, ![]() -суретте бас емес бастапқы алаң мен кернеулер бойынша
қрылған Мор шеңберi көрсетiлген.
-суретте бас емес бастапқы алаң мен кернеулер бойынша
қрылған Мор шеңберi көрсетiлген.
![]() және
және ![]() кернеулердi диаграммада әр түрлi таңбамен көрсететiндiктен, оларды
сәйкес
кернеулердi диаграммада әр түрлi таңбамен көрсететiндiктен, оларды
сәйкес
![]() етiп белгiлеймiз (7,
етiп белгiлеймiз (7,![]() -сурет).
-сурет).
![]() вертикаль және
вертикаль және
![]() горизонталь алаңның бейнеленген нүктелерiн координаттары бойынша
салып әpi
оларды қосып
шеңбер центрiн
табамыз. Содан кейiн шеңбер диаграммасын
құрамыз.
горизонталь алаңның бейнеленген нүктелерiн координаттары бойынша
салып әpi
оларды қосып
шеңбер центрiн
табамыз. Содан кейiн шеңбер диаграммасын
құрамыз.
Б астапқы бас
емес алаңдар үшiн де
астапқы бас
емес алаңдар үшiн де ![]() полюстi пайдалану ыңғайлы. Жалпы
жағдайда
оның координаттары
полюстi пайдалану ыңғайлы. Жалпы
жағдайда
оның координаттары ![]() және шеңбер
бойында әр
түрлi
күйде болуы
мүмкiн. Iс
жүзiнде
және шеңбер
бойында әр
түрлi
күйде болуы
мүмкiн. Iс
жүзiнде
![]() полюстi алаңдардың сәйкес нормалiне параллель
жүргiзiлген
полюстi алаңдардың сәйкес нормалiне параллель
жүргiзiлген ![]() және
және ![]() сәулелерiнiң қиылысу нүктесi ретiнде табу
тиiмдi.
сәулелерiнiң қиылысу нүктесi ретiнде табу
тиiмдi.
![]() полюсiнен көлбеу алаңның нормалiне параллель
жүргiзiлген
полюсiнен көлбеу алаңның нормалiне параллель
жүргiзiлген ![]() сәулесi шеңбермен қиылысып
сәулесi шеңбермен қиылысып ![]() бейнеленген нүктесiн бередi.
Дәлелдеу
үшiн
бейнеленген нүктесiн бередi.
Дәлелдеу
үшiн
![]() бұрышы
бұрышы ![]() -ға тең екендiгiн ескеремiз.
-ға тең екендiгiн ескеремiз.
Өйткенi ол ![]() бұрышының
бұрышының ![]() доғасына тiрелетiн
орталық бұрыш
болып саналады. Сызба бойынша,
доғасына тiрелетiн
орталық бұрыш
болып саналады. Сызба бойынша,

Алынған формуланы (6)
өрнекпен
салыстырғанда ![]() екендiгiн бiлемiз. Осыған ұқсас
екендiгiн бiлемiз. Осыған ұқсас ![]() . Бұл ереже көлбеу алаңмен бейнелейтiн
нүктенiң кернеу шеңберiндегi өзара сәйкестiгiн оңай дәлелдеуге мүмкiндiк бередi. Бас алаңдардың көлбеулiгiн Мор
шеңберiмен
анықтау
8- суретте
көрсетiлген.
Олардың бейнеленген нүктелерi ретiнде абсциссалары
. Бұл ереже көлбеу алаңмен бейнелейтiн
нүктенiң кернеу шеңберiндегi өзара сәйкестiгiн оңай дәлелдеуге мүмкiндiк бередi. Бас алаңдардың көлбеулiгiн Мор
шеңберiмен
анықтау
8- суретте
көрсетiлген.
Олардың бейнеленген нүктелерi ретiнде абсциссалары ![]() және
және ![]() экстремаль мәнге ие болатын 1
және 2
нүктелерi қарастырылады. Алаңдар
экстремаль мәнге ие болатын 1
және 2
нүктелерi қарастырылады. Алаңдар ![]() және
және ![]() сәулелерге перпендикуляр.
Экстремаль ординатасы
сәулелерге перпендикуляр.
Экстремаль ординатасы ![]() радиусқа нүкте 3 тең экстремаль жанама
кернеулер
радиусқа нүкте 3 тең экстремаль жанама
кернеулер ![]() пайда болатын алаңға сәйкес келедi.
пайда болатын алаңға сәйкес келедi.
Шеңберден аналитикалық жолмен дәлелденген көп тәуелдiлiктердi табу қиын емес. Мысалы 8-суреттен

бұл (13) пен үйлеседi.
Көлемдік кернеулі күй
1 Бас кернеулер
Көлемдiк кернеулi күйде қайсыбiр нүктенiң төңiрегiнде epкiн бөлiп алынған қарапайым параллелепипедтiң жақтарына жалпы жардайда кернеулер әсер етедi (9-суретте көрсетiлген). Бұл суретте көрсетiлген кернеулер бұрын қабылданған таңба ережесiне сәйкес оң болады.
Барлық күш моменттерiнiң қосындысын ![]() және
және ![]() өстерiне қатысты нөлге теңестiрсек (§2 қараңыз), .мынадай
теңдiктердi
аламыз:
өстерiне қатысты нөлге теңестiрсек (§2 қараңыз), .мынадай
теңдiктердi
аламыз:


![]() .
(20)
.
(20)
Жанама кернеулердiң жґұптық заңын жалпы жағдайда былай өрнектеуге болады: екi өзара перпендикуляр алаңда жанама кернеу кұраушылары алаңдардың қиылу сызығына тiк бола отырып сан мәнi бойынша тең. Ал бағыттары бойынша қарама-қарсы жаққа бағытталады.
Нүктедегi көлемдiк кернеулi күйдiң жалпы жағдайында (8) матрицасының орнына үшiншi реттi матрица аламыз:
 . (21)
. (21)
Б
 ұл
матрица кернеулер тензоры деп, ал оның әлементтерi (кернеулер) кернеулер
тензорының компоненттерi деп аталады. Сонымен, нүктедегi кернеулi
күй жалпы
жағдайда кернеу
тензоры ретiнде берiледi (21). Тензор ұғымы жалпылама
ұғым,
айталық вектормен салыстырғанда көп ұшырасады. Ол математикада,
физикада, механикада жиi қолданылады.
Oның тоғыз компонентiнiң тек қана алтауы ерекше болуы
мүмкiн.
Тензор үшiн
координат өстерiнің бұрылуы
кезiнде оның компоненттерiне түрлену заңы тән. Атап айтсақ, жазық кернеулi күйде бұл заң (4), (6) және (7) тәуелдiлiктерiмен
өрнектеледi.
Көлемдiк
кернеулi күй
жағдайында
мұндай
тәуелдiлiктердi қорытпаймыз, өйткенi олар, әдетте, серпiмдiлiк теориясында қаралады.
ұл
матрица кернеулер тензоры деп, ал оның әлементтерi (кернеулер) кернеулер
тензорының компоненттерi деп аталады. Сонымен, нүктедегi кернеулi
күй жалпы
жағдайда кернеу
тензоры ретiнде берiледi (21). Тензор ұғымы жалпылама
ұғым,
айталық вектормен салыстырғанда көп ұшырасады. Ол математикада,
физикада, механикада жиi қолданылады.
Oның тоғыз компонентiнiң тек қана алтауы ерекше болуы
мүмкiн.
Тензор үшiн
координат өстерiнің бұрылуы
кезiнде оның компоненттерiне түрлену заңы тән. Атап айтсақ, жазық кернеулi күйде бұл заң (4), (6) және (7) тәуелдiлiктерiмен
өрнектеледi.
Көлемдiк
кернеулi күй
жағдайында
мұндай
тәуелдiлiктердi қорытпаймыз, өйткенi олар, әдетте, серпiмдiлiк теориясында қаралады.
Кез келген
жазық кернеулi
күйдi өстердi
бұру жолымен
екi өзара
перпендикуляр бағытта ![]() және
және ![]() бас кернеулермен созылуға (сығылуға) келтiруге
болатындығы
бґрыннан белгiлi. Осыған ұқсас көлемдiк кернеулi күйде өстердiң және параллелепипедтiң
бағытын өзгертiп, барлық
жағында жанама кернеулер нөлге тең болатын қалыпты табуға болады.
Параллелепипедтiң жақтарына параллель алаңдар бас алаңдар
(10-сурет) деп аталады. Оларға әсер ететiн
бас кернеулермен созылуға (сығылуға) келтiруге
болатындығы
бґрыннан белгiлi. Осыған ұқсас көлемдiк кернеулi күйде өстердiң және параллелепипедтiң
бағытын өзгертiп, барлық
жағында жанама кернеулер нөлге тең болатын қалыпты табуға болады.
Параллелепипедтiң жақтарына параллель алаңдар бас алаңдар
(10-сурет) деп аталады. Оларға әсер ететiн ![]() және
және ![]() кернеулердi бас кернеулер деп, ал сәйкес өстерiн бас өстер
дейдi.
кернеулердi бас кернеулер деп, ал сәйкес өстерiн бас өстер
дейдi.


![]() және
және
![]() бас кернеулердi кез келген алаңдарға әсер ететiн
кернеулер арқылы анықтау әдiсiн қарастырамыз (10-сурет). Бұл үшiн
кез келген бас алаңның нормальмен анықталатын көлбеуi белгiлi деп
ұйғарайық. Алаңға параллель қимамен бастапқы параллелепипедтен
11-суреттегiдей тетраэдрдi бөлiп аламыз да, тетраэдрдi тепе-теңдiк
шартын әсер ететiн барлық күштердiң координат
өстерiне
проекциясының қосындысы түрiнде тұжырымдаймыз.
бас кернеулердi кез келген алаңдарға әсер ететiн
кернеулер арқылы анықтау әдiсiн қарастырамыз (10-сурет). Бұл үшiн
кез келген бас алаңның нормальмен анықталатын көлбеуi белгiлi деп
ұйғарайық. Алаңға параллель қимамен бастапқы параллелепипедтен
11-суреттегiдей тетраэдрдi бөлiп аламыз да, тетраэдрдi тепе-теңдiк
шартын әсер ететiн барлық күштердiң координат
өстерiне
проекциясының қосындысы түрiнде тұжырымдаймыз.
![]() нормальдiң
нормальдiң ![]() өстермен жасайтын бұрыштарының
косинусын сәйкес
өстермен жасайтын бұрыштарының
косинусын сәйкес ![]() деп белгiлеймiз. Көлбеу жақ ауданын
деп белгiлеймiз. Көлбеу жақ ауданын
![]() деп алсақ, координат жазықтығында жатқан басқа
жақ аудандары
деп алсақ, координат жазықтығында жатқан басқа
жақ аудандары ![]() болады. Бас алаңда жанама кернеу болмайды.
Tүcipiлгeн бас
кернеу
болады. Бас алаңда жанама кернеу болмайды.
Tүcipiлгeн бас
кернеу ![]() -ны
-ны ![]() -мен белгiлейiк.
Күштердiң
-мен белгiлейiк.
Күштердiң ![]() осiне
проекциясының қосындысы:
осiне
проекциясының қосындысы:
![]() .
.
Күштердi ![]() және
және ![]() өстерiне проекциялап,
тағы да
ұқсас екi тендеудi
аламыз. Осылайша тетраэдрдi тепе-теңдiгiнiң үш
теңдеуiн
тұжырымдаймыз:
өстерiне проекциялап,
тағы да
ұқсас екi тендеудi
аламыз. Осылайша тетраэдрдi тепе-теңдiгiнiң үш
теңдеуiн
тұжырымдаймыз:
 (а)
(а)
(а) теңдеулерiн ![]() белгiсiздерi
үшiн бiртектi
теңдеулер
жүйесi
түрiнде
қарастыруға болады.
белгiсiздерi
үшiн бiртектi
теңдеулер
жүйесi
түрiнде
қарастыруға болады. ![]() нормальдың
бағыттаушы косинустарының
арасында:
нормальдың
бағыттаушы косинустарының
арасында:
![]() ,
(б)
,
(б)
тәуелдiлiгi бар, сондықтан олар бip мезгiлде нөлге тең бола алмайды. Жоғары алгебрадан дәл осындай шартта (а) жүйесiнiң анықтауышы нөлге тең болуы қажет, яғни
 .
.
Анықтауышты жiктеп, куб теңдеу аламыз:
![]() . (22)
. (22)
Оның үш
түбipi
![]() үш бас
кернеудiң мәнi
болады (
үш бас
кернеудiң мәнi
болады (![]() анықтауыш симметриясына сүйене отырып, олар кез
келген
анықтауыш симметриясына сүйене отырып, олар кез
келген ![]() және т. б.
бастапқы
кернеулерде нақты болады).
және т. б.
бастапқы
кернеулерде нақты болады).
(2) теңдеудiң коэффициенттерi:

Берiлген кернеу
күйiне
тиiстi ![]() бас кернеулер
бас кернеулер ![]() өстерiн таңдауға байланысты болмауы керек. Олай
болса, (22) теңдеудiң түбipлepi мен оның
өстерiн таңдауға байланысты болмауы керек. Олай
болса, (22) теңдеудiң түбipлepi мен оның
![]() коэффициенттерi координат ocьтepiн
бұрғанда өзгермейдi. Сондықтан
коэффициенттерi координат ocьтepiн
бұрғанда өзгермейдi. Сондықтан ![]() және
және ![]() шамалары кернеулi
күйдiң (кернеу тензорының) бiрiншi, екiншi
және үшiншi инварианттары деп
аталады.
шамалары кернеулi
күйдiң (кернеу тензорының) бiрiншi, екiншi
және үшiншi инварианттары деп
аталады.
Жазық кернеулi күйдiң дербес жағдайында куб теңдеудi (22) квадрат
теңдеуге
түрлендiруге
болады. Сонда оның екi түбipi бұрын алынған (13) формуласымен үйлесетiн ![]() және
және ![]() мәндерiн бередi.
Бұл
жағдайда
мәндерiн бередi.
Бұл
жағдайда
![]() деп алу керек, өйткенi бастапқы
параллелепипедтiң
деп алу керек, өйткенi бастапқы
параллелепипедтiң ![]() жағына кернеу әсер етпеуi керек.
жағына кернеу әсер етпеуi керек.
![]() және
және ![]() үш бас
кернеудiң бipeyiне сәйкес
үш бас
кернеудiң бipeyiне сәйкес ![]() -дердi табу үшiн, бас
кернеудiң мәнiн
(а) формуласындағы
-дердi табу үшiн, бас
кернеудiң мәнiн
(а) формуласындағы ![]() орнына қою керек. (а) және (б) формулаларын бipгe
шешкенде iзделген
орнына қою керек. (а) және (б) формулаларын бipгe
шешкенде iзделген ![]() шамаларды аламыз.
шамаларды аламыз.
Үш
бас кернеудiң бipeyi бұл нүктеде алгебралық
ең үлкен мәнге ие болады, оны
![]() , ең
кiшi кернеудi
, ең
кiшi кернеудi ![]() , ал аралық кернеудi
, ал аралық кернеудi
![]() деп белгiлейiк. Сонда
деп белгiлейiк. Сонда
![]() . (23)
. (23)
Ары қарай ![]() кернеулер
табылған
және кернеулер тензоры
бас өстерде берiлген деймiз:
кернеулер
табылған
және кернеулер тензоры
бас өстерде берiлген деймiз:
 . (21
. (21![]() )
)
Б ас алаңдар жасайтын
параллелепипедтiң көлбеу
қимасы бойынша
кернеулердiң таралу
заңдылықтарын
тұжырымдайық.
ас алаңдар жасайтын
параллелепипедтiң көлбеу
қимасы бойынша
кернеулердiң таралу
заңдылықтарын
тұжырымдайық.

ІІ. Нүктедегі деформацияланған күй
2.1. Жазық кернеулi күйде материал деформациясы
Жазық кернеулi күйде материал деформациясының ерекшелiгiн қарастырайық.
Қабырғаларының ұзындығы ![]() және
және ![]() шексiз аз тiк
бұрышты
элементтi таңдап алсақ, жазық кернеулi күйдiң жалпы жағдайында оған тiк кернеулер
шексiз аз тiк
бұрышты
элементтi таңдап алсақ, жазық кернеулi күйдiң жалпы жағдайында оған тiк кернеулер ![]() және жанама
кернеулер
және жанама
кернеулер ![]() әсер етедi
(12,
әсер етедi
(12,
![]() -сурет). Бұл кернеулер
элементтiң деформациялануынан туындайды. Аталған кернеулер
жазықтығында
болатын элемент деформациясын қарастырамыз.
-сурет). Бұл кернеулер
элементтiң деформациялануынан туындайды. Аталған кернеулер
жазықтығында
болатын элемент деформациясын қарастырамыз.
Изотропты материал
үшiн элемент
қабырғаларының ұзаруы тiк кернеулер
әсерiнен болады.
Оларды ![]() және
және ![]() арқылы белгiлеймiз (12,
арқылы белгiлеймiз (12, ![]() -сурет). Нүктедегi сызықтық деформациялар
бағыттарға
сәйкес
салыстырмалы ұзару шамасымен өрнектеледi.
-сурет). Нүктедегi сызықтық деформациялар
бағыттарға
сәйкес
салыстырмалы ұзару шамасымен өрнектеледi.
![]() . (22)
. (22)
Жанама кернеулермен
бұрышты
деформация немесе ығысу деформациясы байланысты. Ол алғашында тiк бұрыштың ығысу бұрышы деп аталатын
![]() бұрышына өзгеруiмен анықталады (12,
бұрышына өзгеруiмен анықталады (12, ![]() -сурет).
-сурет).
Қарастырылып отырған нүкте арқылы ![]() және
және ![]() өстерiнiң бағытында ұзындығы
өстерiнiң бағытында ұзындығы ![]() және
және ![]() екi өзара перпендикуляр
кесiндiлер өтсiн делiк. Деформация нәтижесiнде кесiндiлер (34)
формулаларына сәйкес салыстырмалы ұзарады, әрi олардың арасындағы тiк бұрыш
екi өзара перпендикуляр
кесiндiлер өтсiн делiк. Деформация нәтижесiнде кесiндiлер (34)
формулаларына сәйкес салыстырмалы ұзарады, әрi олардың арасындағы тiк бұрыш ![]() ығысу бұрышына өзгередi.
ығысу бұрышына өзгередi.
Егер
![]() және
және ![]() өстерiн қиылысу нүктесiнiң төңiрегiнде әр түрлi кесiндiлермен рет
бойынша үйлесетiндей ойша бұрсақ, онда
өстерiн қиылысу нүктесiнiң төңiрегiнде әр түрлi кесiндiлермен рет
бойынша үйлесетiндей ойша бұрсақ, онда ![]() өстерiнiң әр қалпына
өстерiнiң әр қалпына ![]() ұзаруы
және
ұзаруы
және ![]() ығысу бұрышы сәйкес келедi.
ығысу бұрышы сәйкес келедi. ![]() және
және ![]() өстерiнiң
мүмкiн қалыптарына келетiн салыстырмалы ұзару мен ығысу бұрыштарының жиынтығы нүктенiң деформациялық күйiн
сипаттайды.
өстерiнiң
мүмкiн қалыптарына келетiн салыстырмалы ұзару мен ығысу бұрыштарының жиынтығы нүктенiң деформациялық күйiн
сипаттайды.
Кез келген
жазық кернеулi
күй
![]() және
және ![]() бас кернеулермен екi өзара перпендикуляр
бағытта
созылады (сығылады). 12-суретте ол үзiк сызықпен көрсетiлген. Бас алаңдарда жанама кернеулер
нөлге
тең болғандықтан,
бас кернеулермен екi өзара перпендикуляр
бағытта
созылады (сығылады). 12-суретте ол үзiк сызықпен көрсетiлген. Бас алаңдарда жанама кернеулер
нөлге
тең болғандықтан, ![]() және
және ![]() бағытында тiк бұрышты элемент тек қана ұзарып, ығысу бұрышы нөлге тең болады (12,
бағытында тiк бұрышты элемент тек қана ұзарып, ығысу бұрышы нөлге тең болады (12, ![]() -сурет).
-сурет).
Мұнан берiлген нүкте арқылы өтетiн екi өзара перпендикуляр
бағытты
көрсете отырып,
кесiндiлердiң тек ![]() және
және ![]() шамаларға ұзаратындығын, ал
арасындағы тiк
бұрыш
өзгepicсiз
қалатындығын тұжырымдауға болады. Көрсетiлген
шамаларға ұзаратындығын, ал
арасындағы тiк
бұрыш
өзгepicсiз
қалатындығын тұжырымдауға болады. Көрсетiлген ![]() және
және ![]() салыстырмалы ұзаруларды берiлген
нүктедегi бас
деформация деп атайды. Серпiмдi және изотропты денелердегi
нүктелерде бас
кернеулер мен бас деформациялар дәл келедi. Бас деформация
атауы
салыстырмалы ұзаруларды берiлген
нүктедегi бас
деформация деп атайды. Серпiмдi және изотропты денелердегi
нүктелерде бас
кернеулер мен бас деформациялар дәл келедi. Бас деформация
атауы ![]() және
және ![]() ұзарулары берiлген
нүктеден
тарайтын кез келген бағытты ұзарулармен салыстырғанда бас
кернеудiң әсерiне ұқсас экстремаль
мәнге ие
болатындығына
байланысты.
ұзарулары берiлген
нүктеден
тарайтын кез келген бағытты ұзарулармен салыстырғанда бас
кернеудiң әсерiне ұқсас экстремаль
мәнге ие
болатындығына
байланысты.
Бepiлгeн нүктеден ![]() бағытына кез келген а
бұрышпен
өтетiн
бағытына кез келген а
бұрышпен
өтетiн
![]() кесiндiсiнiң
салыстырмалы ұзаруын табайық (12-сурет).
кесiндiсiнiң
салыстырмалы ұзаруын табайық (12-сурет).
![]() және
және ![]() бас деформациялары берiлген деп есептейiк.
Ұзындығы
бас деформациялары берiлген деп есептейiк.
Ұзындығы ![]() -ке тең көлбеу
кесiндiнi денеден бөлiнiп алған қабырғаларының ұзындығы
-ке тең көлбеу
кесiндiнi денеден бөлiнiп алған қабырғаларының ұзындығы ![]() және
және ![]() болатын тiк бґрышты элементтiң бас деформация
бағытындағы диагоналы деп қарастырайық. Деформация аз болу себептi
бұрышты
болатын тiк бґрышты элементтiң бас деформация
бағытындағы диагоналы деп қарастырайық. Деформация аз болу себептi
бұрышты
![]() деп алып көлбеу кесiндiнiң абсолют ұзаруын
табамыз:
деп алып көлбеу кесiндiнiң абсолют ұзаруын
табамыз:
![]() .
.
Iзделiп отырған салыстырмалы ұзару
![]() болады.
болады.
![]() есекерсек,
есекерсек, ![]() .
(23)
.
(23)
Тригонометриялық тәуелдiлiктi (5) пайдаланып, (35) формуласын былай өрнектеймiз:
![]() . (24)
. (24)
![]() болсын. Сонда (36) формуласынан
болсын. Сонда (36) формуласынан
![]() , яғни
, яғни ![]() болғанда
болғанда ![]() өзiнiң ең үлкен мәнiне ие болады:
өзiнiң ең үлкен мәнiне ие болады:
![]() . Керiсiнше,
. Керiсiнше,
![]() болғанда
болғанда ![]() ең кiшi мәнге ие болады:
ең кiшi мәнге ие болады: ![]() .
.
Егер нүктедегi бас деформациялардың шамасы мен бағыты бeлгiлi болса, онда кез келген бағыт бойынша салыстырмалы ұзару (35) немесе (36) формулаларымен анықталады.
2.2. Деформация кезінде материал көлемінің өзгеруі
Деформацияға дейiн элементтер
параллелепипед жақтарының өлшемiн ![]() және
және ![]() арқылы белгiлеймiз
(14-сурет).
Деформациялаудан кейiн бұл өлшемдер
арқылы белгiлеймiз
(14-сурет).
Деформациялаудан кейiн бұл өлшемдер ![]() ,
, ![]() ,
, ![]() болсын.
болсын.
 Параллелепипедтiң бастапқы көлемiн
Параллелепипедтiң бастапқы көлемiн ![]() , ал
деформациядан кейiн
, ал
деформациядан кейiн ![]() деп белгiлеймiз Параллелепипед
көлемiнiң абсолют өзгepyiн табамыз:
деп белгiлеймiз Параллелепипед
көлемiнiң абсолют өзгepyiн табамыз:
 (a)
(a)
(а) өрнегiндегi жақшада салыстырмалы ұзару көрсетiлген
![]() .
.
(а) өрнегiн ықшамдасақ:
![]() .
.
Нақты құрылыс материалдарында салыстырмалы ұзару әдетте, мыңдық, он мыңдық үлестермен өлшенедi. Сондықтан, олардың көбейтiндiлерiн ескермеуге болады. Ығысу деформациясы
көлем
өзгеруiн тудырады.
Ол ![]() ығысу бұрышының квадратына, тiптi одан
жоғары
дәрежесiне
пропорционал. Сондықтан кiшi деформацияларда көлемнiң мұндай өзгерiсiн де елемеуге
болады.
ығысу бұрышының квадратына, тiптi одан
жоғары
дәрежесiне
пропорционал. Сондықтан кiшi деформацияларда көлемнiң мұндай өзгерiсiн де елемеуге
болады.
Сонымен
![]() .
.
Көлемнiң салыстырмалы өзгеруiн, немесе салыстырмалы кө-лемдiк деформациясын мына формуламен анықтайды:
![]() . (25)
. (25)
Бұл формула серпiмдi
және серпiмдi-пластикалық
деформацияларға да дұрыс.
Материалдың серпiмдi сатысындағы жұмыста ![]() - нi
- нi ![]() және
және ![]() кернеулер арқылы өрнектеуге болады. Бґл
үшiн (42)
формуладағы
кернеулер арқылы өрнектеуге болады. Бґл
үшiн (42)
формуладағы ![]() ,
, ![]() және
және ![]() мәндерiн (47) формулаға қоямыз. Түрлендiрсек:
мәндерiн (47) формулаға қоямыз. Түрлендiрсек:
![]() . (26)
. (26)
![]() болғанда материалдың
жан-жақты
гидростатикалық сығылу
жағдайын
қарастырайық (48) формуласы бойынша:
болғанда материалдың
жан-жақты
гидростатикалық сығылу
жағдайын
қарастырайық (48) формуласы бойынша:
![]() . (27)
. (27)
(б) формулалары Пуассон коэффициентi 0,5-тен үлкен болуы мүмкiн емес, өйткенi көлемдiк сығылғанда дененiң көлемi кiшiреймейдi, керiсiнше ұлғаяды. Бұл тұжырым тәжiрибемен дәлелденген. Табиғатта Пуассон коэффициентi 0,5-тен үлкен материал табылған жоқ.
Көлемдік кернеулі
күйдегі потенциялық энергияКөлемдiк кернеулi
күйде серпiмдi
деформация әсерiнен
материалдың
көлем бiрлiгiнде
жинақталған
![]() меншiктi
потенциалық
энергияны табамыз.
Ол үшiн
меншiктi
потенциалық
энергияны табамыз.
Ол үшiн
![]() бас
кернеулердiң
әсерiнде
болатын, қабырғасы 1-ге
тең
текшені
қарастырамыз. Қарапайым
созылу
бас
кернеулердiң
әсерiнде
болатын, қабырғасы 1-ге
тең
текшені
қарастырамыз. Қарапайым
созылу
Бұл формуланы үш кернеудiң бip мезгiлде әсер етуiне арнап жалпылама жазсақ:
![]() (28)
(28)
Осыған бас кернеу мен деформацияға катысты, яғни (42) формуласындағы х, у, z индекстерiн сәйкес 1, 2, 3-пен салыстырып, Гук заңы бойынша ұзару өрнегiн (42)-ге қоямыз. Нәтижесiнде и өрнегiн бас кернеу арқылы тұжырымдайық:
![]() (29)
(29)
Нүктедегi кернеулi және
деформациялық
күйлер тәуелдiлiктерiнiң
арасындағы ұқсастық Бас деформация
бағытына
![]() бұрышпен орналасқан екi өзара перпендикуляр
бұрышпен орналасқан екi өзара перпендикуляр ![]() және
және ![]() кесiндiлерi арасындағы ығысу бұрышын табамыз
(13-сурет).
кесiндiлерi арасындағы ығысу бұрышын табамыз
(13-сурет).
![]() кесiндiсi деформация
нәтижесiнде
кесiндiсi деформация
нәтижесiнде ![]() бұрышқа
бұрылады.
Бұрышы кiшi
болғандықтан,
бұрышқа
бұрылады.
Бұрышы кiшi
болғандықтан, ![]() доғасының
доғасының ![]() радиусқа қатынасымен өрнектеуге болады:
радиусқа қатынасымен өрнектеуге болады:
![]()
немесе
![]() . (а)
. (а)
![]() сызығының
сызығының ![]() бұрылу бұрышын анықтау үшiн (а) фор-муласындағы
бұрылу бұрышын анықтау үшiн (а) фор-муласындағы ![]() бұрышын (
бұрышын (![]() ) алмастырамыз.
Сонда:
) алмастырамыз.
Сонда:
![]() (30)
(30)
(а) және (б)
формулаларындағы әр
түрлi
таңба
![]() және
және ![]() кесiндiлерiнiң
деформацияланбаған қалыптан әр жаққа бұрылатындығын көрсетедi (13-сурет). Егер тiк
бұрыш
кесiндiлерiнiң
деформацияланбаған қалыптан әр жаққа бұрылатындығын көрсетедi (13-сурет). Егер тiк
бұрыш
![]() азайса,
азайса, ![]() деп аламыз. (а) және
(б) өрнектеп осы бұрыштың
деп аламыз. (а) және
(б) өрнектеп осы бұрыштың ![]() үлкеюiн қанағаттандырса,
үлкеюiн қанағаттандырса,
![]() үшiн
төмендегi өрнектi қарастырамыз:
үшiн
төмендегi өрнектi қарастырамыз:
![]() .
.
(36) және (37) формулаларын қосып жазамыз:
 .
(31)
.
(31)
Нүктенiң жазық кернеулi күйiн бейнелейтiн (3.14) және (3.15) өрнектердi еске түсiрсек:
 (в)
(в)
( 38) және (в) өрнектерiнiң тәуелдiлiгi нүктедегi
38) және (в) өрнектерiнiң тәуелдiлiгi нүктедегi ![]() кернеулердiң
және
кернеулердiң
және ![]() және
және ![]() деформациялардың таралу заңдарының математикалық ұқсастығын көрсетедi. Бұл ұқсастық кездейсоқ емес, нүктедегi деформациялық
күйдi
деформациялардың таралу заңдарының математикалық ұқсастығын көрсетедi. Бұл ұқсастық кездейсоқ емес, нүктедегi деформациялық
күйдi ![]() матрица деформациясы толығымен анықтай алады.
матрица деформациясы толығымен анықтай алады.
![]() жазықтығында деформация
үшiн
компоненттерi:
жазықтығында деформация
үшiн
компоненттерi:

болып табылады. Өстердi
бұрғанда ![]() компоненттерi кернеу матрицасы
компоненттерi кернеу матрицасы
![]() компоненттерiне ұқсас түрленедi. Аталған ұқсастық негiзiнде мына форомуланы
жазуға
болады:
компоненттерiне ұқсас түрленедi. Аталған ұқсастық негiзiнде мына форомуланы
жазуға
болады:
 . (31)
. (31)
Бұл формула (13)
формуласына ұқсас, мұнда ![]() және
және ![]() кернеулерi сәйкес
кернеулерi сәйкес ![]() және
және ![]() деформацияларына
алмастырылған.
(39) формуласы нүктедегi
деформацияларына
алмастырылған.
(39) формуласы нүктедегi ![]() және
және ![]() бас деформацияларды
бас деформацияларды ![]() екi кез келген
өзара перпендикуляр
бағытта.
Сәйкес
ығысу
бұрышы
екi кез келген
өзара перпендикуляр
бағытта.
Сәйкес
ығысу
бұрышы
![]() тең арқылы
анықтауға
мүмкiндiк
бередi.
тең арқылы
анықтауға
мүмкiндiк
бередi.
(39) формуласынан
![]()
яғни нүктенiң кез келген өзара перпендикуляр бағыттарда са-лыстырмалы ұзаруының жиынтығы тұрақты шама болады.
(9) формуласымен кернеулi күйдегi ұқсас жағдайды тұжырымдауға болады. Бұл ұқсастық нүктедегi деформацияларды графиктiк бейнелеу үшiн Мор шеңберiн пайдалануға мүмкiндiк бередi. Бiз оған тоқталмаймыз.
Қорыта айтқанда, екi бас кернеу жазықтығында туындайтын деформацияларды қарастырдық. Нүктедегi материал деформациясы жалпы жағдайда көлемдiк сипатта болады. Жоғарыда жазық есепте алынған деформациялар мен кернеулердiң таралуының математикалық ұқсастығы көлемдiк есепте де сақталады.
Сондықтан жалпы жағдайда дененiң әpбip
нүктесiнде үш ![]() және
және ![]() бас деформацияны, яғни арасында ығысу бұрышы болмайтын үш өзара перпендикуляр
бағытта кiшi
кесiндiлердiң салыстырмалы ұзаруын көрсетуге болады.
бас деформацияны, яғни арасында ығысу бұрышы болмайтын үш өзара перпендикуляр
бағытта кiшi
кесiндiлердiң салыстырмалы ұзаруын көрсетуге болады.
Кернеу тензорына
ұқсас деформация
тензоры ұғымы
ендiрiледi. Оның матрицасы нүктенiң деформация күйiн толық сипаттайды. ![]() бағыттарымен үйлесетiн өстер үшiн деформация тензоры мынадай
түрде
болады:
бағыттарымен үйлесетiн өстер үшiн деформация тензоры мынадай
түрде
болады:
 .
.
Серпiмдi изотропты
дененiң нүктелерiнде бас деформациялардың кернеуi үш ![]() және
және ![]() бас кернеудiң бағытымен үйлеседi.
бас кернеудiң бағытымен үйлеседi.
Жазық және көлемдік кернеулі күйдегі Гук заңы Осыған дейiн нүктедегi кернеулi және деформациялық күйлердiң формулаларымен нeгiзгi ережелерi дененiң серпiмдi қасиеттерiне байланысты болмайтындықтан, оларды серпiмдi және серпiмдi емес (немесе серпiмдi - пластикалыј) деформацияларға қолдануға болады. Кернеулер мен деформациялардың сандық қатынастарын тағайындағанда, бiз изотропты денелердiң тек серпiмдi деформацияларын қарастыратын боламыз.
Центрлiк
созылған
стерженьнен бөлiп алынған элементтi қарастырайық. Мұндай
элемент бойлық және көлденең деформацияға ұшырайды. Ол ![]() кернеуiмен мына формулалар бойынша:
кернеуiмен мына формулалар бойынша:
![]() (32)
(32)
![]() (33)
(33)
байланысты.
Мұнда ![]() - серпiмдiлiк модулi, ал μ - Пуассон коэффициентi.
Ұзару деформациясы
оң,
қысқару терiс делiнедi. (40)
формуласы сызықты кернеулi күйдегi Гук заңын өрнектейдi. Көлемдiк кернеулi күйде
тiк кернеулер мен ұзарудың ұқсас қатынасын тағайындаймыз. Өйткенi кiшi деформация кезiнде
жанама кернеулер тiк бұрышты элемент жақтарының ұзындығын өзгертпей, тек ығысуды тудырады.
Мұнда
элементтiң тек
сызықты
деформациялары қарастырылады. Ығысу деформациясына IV тарауда
тоқталамыз.
- серпiмдiлiк модулi, ал μ - Пуассон коэффициентi.
Ұзару деформациясы
оң,
қысқару терiс делiнедi. (40)
формуласы сызықты кернеулi күйдегi Гук заңын өрнектейдi. Көлемдiк кернеулi күйде
тiк кернеулер мен ұзарудың ұқсас қатынасын тағайындаймыз. Өйткенi кiшi деформация кезiнде
жанама кернеулер тiк бұрышты элемент жақтарының ұзындығын өзгертпей, тек ығысуды тудырады.
Мұнда
элементтiң тек
сызықты
деформациялары қарастырылады. Ығысу деформациясына IV тарауда
тоқталамыз. ![]() және
және ![]() деформацияларды
деформацияларды ![]() және
және ![]() арқылы өрнектеп табамыз. Ол үшiн күштер әсерiнiң тәуелсiздiк принципiн
және (40)
және (41)
формулаларындағы қатынастарды пайдаланамыз
арқылы өрнектеп табамыз. Ол үшiн күштер әсерiнiң тәуелсiздiк принципiн
және (40)
және (41)
формулаларындағы қатынастарды пайдаланамыз ![]() кернеуi бағытымен
кернеуi бағытымен ![]() салыстырмалы ұзарудың косындысын үш қосылғышпен өрнектеуге болады:
салыстырмалы ұзарудың косындысын үш қосылғышпен өрнектеуге болады:
![]() ,
,
мұнда ![]() - тек
- тек
![]() кернеудiң
әсерiнен болатын
деформация, оны (34) формуласымен анықтайды. Өйткенi ол
кернеудiң
әсерiнен болатын
деформация, оны (34) формуласымен анықтайды. Өйткенi ол
![]() карағанда бойлық болып
табылады.
карағанда бойлық болып
табылады.
![]() кернеуден пайда болған ұзару,
кернеуден пайда болған ұзару, ![]() қарағанда бойлық деформация болады да (14)
формуласымен анықталады.
қарағанда бойлық деформация болады да (14)
формуласымен анықталады. ![]() кернеу тудыратын деформация.
кернеу тудыратын деформация.
Сонымен ![]() .
.
![]() және Q
және Q![]() анықтауға ұқсас пайымдауларды пайдаланып
көлемдiк
кернеулi күйдегi Гук заңының формуласын (Гуктың
жалпылама заңын) аламыз:
анықтауға ұқсас пайымдауларды пайдаланып
көлемдiк
кернеулi күйдегi Гук заңының формуласын (Гуктың
жалпылама заңын) аламыз:
 (35)
(35)
Бұл формулаларда созу кернеулерi «плюс», ал сығылу - «минус» таңбаларымен белгiленедi.
(42)
формуласындағы
бip кернеудi нөлге тең деп ұйғарып
жазық кернеулi
күй
үшiн Гук
заңын
аламыз ![]() деп:
деп:
 (36)
(36)
![]() кернеу нөлге тең болғанда
кернеу нөлге тең болғанда ![]() нөлге тең деген түсiнiк тумауы керек.
Шынында,
нөлге тең деген түсiнiк тумауы керек.
Шынында, ![]() болғанда
болғанда
![]() .
(37)
.
(37)
Мысалы, пластинканы
өз
жазықтығында
созғанда (44
форму-ласы бойынша), созу салдарынан пластинка қалыңдығының азайғандығын анықтауға болады. Белгiлi
![]() және
және ![]() кернеулерде (43) формулалар мен
кернеулерде (43) формулалар мен
![]() және
және ![]() деформациясын анықтайды. Бiрақ кейбiр жағдайда керi тәуелдiлiктi қарастырған тиiмдi. (43)
формуласының екiншi жағын
деформациясын анықтайды. Бiрақ кейбiр жағдайда керi тәуелдiлiктi қарастырған тиiмдi. (43)
формуласының екiншi жағын ![]() -ға көбейтiп және бiрiншiмен қоссақ:
-ға көбейтiп және бiрiншiмен қоссақ:
![]() .
.
![]() және
және ![]() кернеулердi табамыз:
кернеулердi табамыз:
 (38)
(38)
![]() Үшiн
формуланы
Үшiн
формуланы ![]() формуласындағы индекстердi алмастыру жолымен
аламыз. 45 формуласындағы тәуелдiлiктер бeлгiлi
формуласындағы индекстердi алмастыру жолымен
аламыз. 45 формуласындағы тәуелдiлiктер бeлгiлi
![]() және
және ![]() деформациялары (мысалы, тәжiрибеден)
деформациялары (мысалы, тәжiрибеден)
![]() тiк кернеулерiн анықтауға мүкiндiк бередi.
тiк кернеулерiн анықтауға мүкiндiк бередi.
ҚОРЫТЫНДЫ
Кез
келген жазық кернеулi күйдi өстердi бұру жолымен екi өзара перпендикуляр
бағытта
![]() және
және ![]() бас кернеулермен созылуға (сығылуға) келтiруге
болатындығы
бґрыннан белгiлi. Осыған ұқсас көлемдiк кернеулi күйде өстердiң және параллелепипедтiң
бағытын өзгертiп, барлық
жағында жанама кернеулер нөлге тең болатын қалыпты табуға болады.
Параллелепипедтiң жақтарына параллель алаңдар бас алаңдар
деп аталады. Оларға әсер ететiн
бас кернеулермен созылуға (сығылуға) келтiруге
болатындығы
бґрыннан белгiлi. Осыған ұқсас көлемдiк кернеулi күйде өстердiң және параллелепипедтiң
бағытын өзгертiп, барлық
жағында жанама кернеулер нөлге тең болатын қалыпты табуға болады.
Параллелепипедтiң жақтарына параллель алаңдар бас алаңдар
деп аталады. Оларға әсер ететiн ![]() және
және ![]() кернеулердi бас кернеулер деп, ал сәйкес өстерiн бас өстер
дейдi.
кернеулердi бас кернеулер деп, ал сәйкес өстерiн бас өстер
дейдi.
![]() және
және ![]() бас кернеулердi кез келген алаңдарға әсер ететiн
кернеулер арқылы анықтау әдiсiн қарастырамыз.
бас кернеулердi кез келген алаңдарға әсер ететiн
кернеулер арқылы анықтау әдiсiн қарастырамыз.
Бұл үшiн кез келген бас алаңның нормальмен анықталатын көлбеуi белгiлi деп ұйғарайық. Алаңға параллель қимамен бастапқы параллелепипедтен 11-суреттегiдей тетраэдрдi бөлiп аламыз да, тетраэдрдi тепе-теңдiк шартын әсер ететiн барлық күштердiң координат өстерiне проекциясының қосындысы түрiнде тұжырымдаймыз.
Мәшине жасау саласында сырықтар жүйесі және жақтаулар статикалық анықталмағандығын анықтауда күштер тәсілі кеңінен қолданылады. Оның мәнiсi мынада: берілген статикалық анықталмайтын жүйе сыртқы және өзара қосымша байланыстардан босатылып, олардың әсерi күштермен және моменттермен ауыстырылады. Олардың шамасын байланыстан босатылған жүйеге қойылатын орын ауыстыру шектеулерге сәйкес келетіндей eтiп тандайды. Сонымен, көрсетiлген әдiспен шешу кезiнде күштер бeлгiciз болады. «Күштер тәсілі» деп аталуы да содан. Мұндай әдiс бipey ғана емес. Құрылыс механикасын басқа да тәсілдер, мәселен, бeлгiciз ретінде күш әсері емес, сырықтар жүйесі элементтеріндегi орын ауыстыру алынатын деформация әдiсі пайдаланылады.
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР
-
Н.Қожаспаев, С.Кешуов, И.Мухитов Электротехника /оқу құралы/ - Алматы. Республикалық баспа кабинеті, 1996 ж., 300 бет
-
Электротехника /Под ред- проф. В. Г. Герасимова.— М.: Высшая школа. 1935.
-
Волынский Б. А., Зейн Е. Н..Шатерников В. Е.Электротехника.— Москва.:Эпергоатомиздат, 1987.
-
Борисов Ю.М., Липатов Д.Н., Зорин Ю.Н., Электротехника —Москва.:Эпергоатомиздат, 1985.
-
Касаткин А. С., Немцов М. В..Электротехника.— М.: Энерогоатомиздат. 1983.
-
Иванов И. И., Равдоник С. С. Электротехника.— М.: Высшее школа, 1984.
-
Электротехника. Программированное учебное пособие /Под ред. проф. В. Г. Герасимова.— М.: Высшая школа, 1983.
-
Основы промышленной электроники. /Под ред. проф. А Г. Герасимова.— М.:Высшая школа, 1986.
30

шағым қалдыра аласыз















