Квадрат теңдеу түбірлерінің фррмулаларына есептер шығару

Алгебра 8 «А» сынып
Сабақтың тақырыбы	Квадрат теңдеу түбірлерінің формулалары. Дискриминант
Мақсаты	Квадрат теңдеулер туралы алған білімдерін жинақтап, тиянақтау
Сабақтың әдісі	Интербелсенді тақта, бағалау
Мұғалім үшін оқу нәтижелері	Сабақтың ғылымилығы, нәтижеге жету үшін ұйымдастырылған жұмыстардың толық орындалуы. Оқушылардың тақырыпты жеткілікті меңгеруі.
Сабақта туындаған негізгі идеялар	Оқушылардың өз бетінше жұмыстарын ұйымдастыруда уақытты дұрыс бөлу, тексеруді ұйымдастыру формасын ойластыру. Тапсырмаларды топпен орындау дағдысын жетілдіру.
Тапсырмалар	Пікірлесу,есептерді шығару және талдау,нәтижені салыстыру, сұрақ- жауап
Жұмыс түрлері	Сыныппен жұмыс	Топтық жұмыс	Сөзжұмбақ шешу	Бірін-бірі бағалау

Психологиялық ахуал /2 мин/ «Шаттық шеңбері». (Окушылар ортаға шығып, шеңбер құрайды. Бір-бірлеріне,шарикті беретін оқушыға сол оқушының бойындағы жақсы қасиетін айтып, өз тілегін қысқаша айтады. Болған соң шарикті жарып, ішінде жазылған топ бойынша екіге бөлінеді).

Топ басшысын сайланады. Екі топқа бағалау парағы таратылады.

Үй жұмысын тексеру. № 133 (2;5,6).

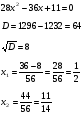
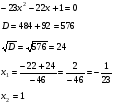
Жауабы: -1; -7/3 Жауабы: ½; 11/14 Жауабы; -1/23; 1

Анаграмманы шешу.

Таиимдкисрнн (дискриминант), детуең (теңдеу), тваракд (квадрат), ірітңрбліүне (түбірлерінің), ррыллафаома (формулалары)

- Әріптерді дұрыс жинап, тақырыпты айтыңдар (Квадрат теңдеу түбірлерінің формулалары. Дискриминант)
- Иә, біз бүгін квадрат теңдеулермен танысуды жалғастырамыз, өткен сабақтарда алған білімдерді еске түсіріп, жалпылаймыз.

Қайталау – білім анасы. Кір жаю әдісі (балалар теорияны айтып, қағазға формуланы жазып, жіпке қыстырғышпен іледі)

1) Қандай теңдеуді квадрат теңдеу деп атайды? Мұндағы а,в,сдегеніміз нелер? Мысал келтіріңдер.

2) Квадрат теңдеудің қандай түрлері бар? Әрқайсысына анықтама беріңдер.

3) Келтірілген квадрат теңдеу дегеніміз не?

4) Квадрат теңдеудің түбірлерін қалай табамыз?

5) Дискриминанттың неше жайы бар. Оларды ата.

1. Кім жылдам? Ойыны:

№

Теңдеулер

1

5х²+2х-4=0

2

х²-7х+8=0

3

6х²+х=0

4

Зх²-9=0

5

2х²-4х=1

6

х²+10х-15=0

7

1,3х²-х+4,5=0

8

4х²=0

9

-x+12x²=0

10

17+9x=0

2. Кварат теңдеудің коэффициенттерін анықтаңдар:

а)14у² – 5у – 1 = 0 а)16х² – 8х + 1 = 0

a = 14, b = − 5, c = −1. a = 16, b = − 8, c = 1.

б) 1 − 18у + 81у² = 0 б)18 + 3у² – у = 0

а = 81, b = − 18, c = 1. a = 3, b = − 1, c = 18.

Қателеспес үшін, алдымен теңдеуді

81у² −18у + 1 = 0 3у² − у + 18 = 0

Осы түрге келтіріп аламыз.

3. Дискриминант. Квадрат теңдеудің түбірлерін табу

а) 2х² + 3х + 1 = 0 а) 9х² + 6х + 1 = 0

D = b² − 4ac D = b² − 4ac

D = 3² − 4∙2∙1 = 9 − 8 = 1. D = 6² − 4∙9∙1 = 36 − 36 = 0.

D = 1, D > 0 екі түбірі бар D = 0, бір ғана түбірі бар

 

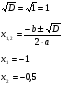
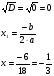
Жауабы: -1: -0,5 Жауабы. -1/3

3) 2х² + х + 2 = 0 4) х² + 5х − 6 = 0

D = b² − 4ac D = b² − 4ac

D = 1² − 4∙2∙2 = 1 − 16 = −15. D = 5² − 4∙1∙(−6) = 25 +24 = 49.

D = −15, D < 0, теңдеудің шешімі жоқ. D = 49, D > 0, екі түбірі бар.

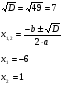
Жауабы: -6; 1

5. 2у² – 9у + 10 = 0.

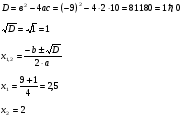_{Жауабы: 2,5; 2}

6. у² – 11у – 152 = 0

_{Жауабы: 19; -8}

7. 2р² + 7р – 30 = 0

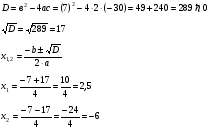_{Жауабы: 2,5; -6}

8)

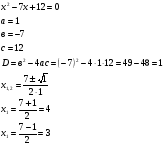
Жауабы: 4; 3

4. Қорытынды. Сөзжұмбақ шешу

д

т

п

 

и

е

б

а

 

с

ң

і

р

 

К

В

А

Д

Р

А

Т

р

л

е

б

о

и

т

у

о

л

м

ы

л

ы

и

а

ы

н

д

а

ы

н

 

т

 

1.   өрнегін квадрат теңдеудің ....... деп атайды?

2. Квадрат теңдеудің екінші коэффиценті  қандай әріппен белгіленеді?

3. х²+6х+10=0  мұндағы в-ны тап

4. Құрамында мәнін табу керек болатын әрпі бар теңдік

5. Д=0 болса теңдеудің неше шешімі бар

6. Квадрат функцияның графигі

7. Квадрат теңдеудің түрі.

5. Рефлексия:

Не білдім

сабаққа дейін?

Не білдім

сабақта?

Не білгім келеді келешекте?

6. Үй тапсырмасы. №135 (2;4); 136 (2;4). 53- бет.

7. Бағалау:

Оқушылардың

аты-жөні

Үй

жұмысы

Теорияны қайталау

1 тапсырма

2

тапсырма

3

тапсырма

4

тапсырма

Қорытынды баға

Ануарбекова

Мөлдір

Жаксылыкова Еркежан

Зиядаев

Ерасыл

Казбекова

Риза

Мұқатай

Садуақас

Нуртаев

Ерасыл

Салимбаева

Атлана

Өте тамаша! Жарайсын! “5”. Тарауды толық меңгеріп, сабаққа сараптама жасай отырып, логикалық ойлау қабілеті дамыған, өзіндік ойы бар оқушы.

Жақсы! Алға! “4”. Тарауды жақсы меңгерген. Есеп шығара алатын оқушы.
Ойлану керек! Қалма! “3”. Әлі де дайындалуды қажет ететін оқушы.

6. Тапсырма. Сыйлық.
Мына жәшіктің ішінде не жатқанын табу керек. Бұл затқа үш анықтама беремін.
- сөздің өзгермейтін бөлігі;
- теңдеудегі орнына қойғанда оны тура теңдікке айналдыратын сан;
- өсімдіктің негізгі органдарының бірі? (түбір) Раушан гүлінің түбірі

Балалар жәшіктің ішінде раушан гүлінің түбірі жатыр екен. Ол туралы халық былай дейді: «Періштедей гүл, ал бірақ тырнағы өткір».Мынадай аңыз бар: Анакреонның айтуынша, раушан гүлі теңізден шығып келе жатқан Афродитаның денесін жапқан аппақ көбіктен туған екен. Алғашқыда раушан ақ түсті болған, сонан соң тікенек қадалған періштенің қанына боялып, қызыл түске айналған дейді.

Оқушыларға раушан гүлі таратылады. Олар сабақ соңында келген қонақтарға табыс етеді.

Дискриминант (латынша – бөлуші, ажыратушы) – ax2+bx+c – екі дәрежелі үш мүшенің дискриминанты b2-4ac – болса, x2+px+q үш мүшенің дискриминанты (p/2)2 – q – ға тең. X3+px+q – үш мүшенің дискриминанты. D=-4P3-27Q2. Үш мүшенің нақты түбірлерінің саны дискриминантын таңбасына тәуелді анықталады.”Дискриминант” ғылыми атауын ағылшын математигі Джеймс Сильвестр (1814 – 1897) енгізген.

{\displaystyle p(x)=a_{0}+a_{1}x+...+a_{n}x^{n}} көпмүшесінің Дискримина́нты

{\displaystyle D(p)=a_{n}^{2n-2}\prod _{i<j}(\alpha _{i}-\alpha _{j})^{2}} өргнегінің туындысы, бұл жерде {\displaystyle \alpha _{1},\alpha _{2},...,\alpha _{n}} — барлық түбірлер.

Негізгі қасиеттері[өңдеу]

• Дискриминант түбірлері еселік болған жайғдайда ғана нөлге тең болады.

• Дискриминант көпмүшенің түбірлеріне қатысты симметриялы көпмүше болып табылады.

• {\displaystyle D(p)={\frac {(-1)^{n(n-1)/2}}{a_{n}}}R(p,p')}, мұнда {\displaystyle R(p,p')} — {\displaystyle p(x)} көпмүшесінің және оның {\displaystyle p'(x)} туындысының нәтижесі.

  • сонымен қатар, көпмүше дискриминанты

{\displaystyle p(x)=x^{n}+a_{n-1}x^{n-1}+\ldots +a_{1}x+a_{0}}

көпмүшесінің дискриминанты келесі {\displaystyle (2n-1)\times (2n-1)}-матрицасының анықтауышына тең:

1	{\displaystyle a_{n-1}}	{\displaystyle a_{n-2}}	.	.	.	{\displaystyle a_{0}}	0	.	.	.	0
0	1	{\displaystyle a_{n-1}}	{\displaystyle a_{n-2}}	.	.	.	{\displaystyle a_{0}}	0	.	.	0
0	0	1	{\displaystyle a_{n-1}}	{\displaystyle a_{n-2}}	.	.	.	{\displaystyle a_{0}}	0	.	0
.	.	.	.	.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.	.	.	.	.
0	0	0	0	0	1	{\displaystyle a_{n-1}}	{\displaystyle a_{n-2}}	.	.	.	{\displaystyle a_{0}}
{\displaystyle n}	{\displaystyle (n-1)a_{n-1}}	{\displaystyle (n-2)a_{n-2}}	.	.	{\displaystyle a_{1}}	0	0	.	.	.	0
0	{\displaystyle n}	{\displaystyle (n-1)a_{n-1}}	{\displaystyle (n-2)a_{n-2}}	.	.	{\displaystyle a_{1}}	0	0	.	.	0
0	0	{\displaystyle n}	{\displaystyle (n-1)a_{n-1}}	{\displaystyle (n-2)a_{n-2}}	.	.	{\displaystyle a_{1}}	0	0	.	0
.	.	.	.	.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.	.	.	.	.
0	0	0	0	0	{\displaystyle n}	{\displaystyle (n-1)a_{n-1}}	{\displaystyle (n-2)a_{n-2}}	.	.	{\displaystyle a_{1}}	0
0	0	0	0	0	0	{\displaystyle n}	{\displaystyle (n-1)a_{n-1}}	{\displaystyle (n-2)a_{n-2}}	.	.	{\displaystyle a_{1}}

Мысалдар[өңдеу]

• {\displaystyle ax^{2}+bx+c} квадраттық үшмүшелігінің дискриминанты {\displaystyle b^{2}-4ac} тең. Егер {\displaystyle D>0} болса, теңдеудің екі түбірі болады. Ол түбірлерді

{\displaystyle x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}};}       (1)

формуласымен есептейді.

• ал {\displaystyle D=0} болған жағдайда, теңдеудің жалғыз түбірі болады және ол

{\displaystyle x={\frac {-b}{2a}};}

формуласымен есептеледі.

• егер {\displaystyle D<0} болса, теңдеудің шешімі болмайды. (1) формуламен немесе

{\displaystyle x_{1,2}={\frac {-b\pm i{\sqrt {4ac-b^{2}}}}{2a}}.}

формуласымен өрнектелетін екі кешенді түбір бар.

• {\displaystyle a_{3}x^{3}+a_{2}x^{2}+a_{1}x+a_{0}} көпмүшесінің дискриминанты

{\displaystyle -4a_{1}^{3}a_{3}+a_{1}^{2}a_{2}^{2}-4a_{0}a_{2}^{3}+18a_{0}a_{1}a_{2}a_{3}-27a_{0}^{2}a_{3}^{2}.} тең.

• Сонымен қатар {\displaystyle x^{3}+px+q} көпмүшесінің (түберлері Кардано формуласымен есептелетін) дискриминанты {\displaystyle -27q^{2}-4p^{3}} тең.

Дереккөздер[өңдеу]

2-дәрежелі көпмүше немесе квадраттық теңдеу, квадраттық үшмүшелік деп

{\displaystyle ax^{2}+bx+c=0,\,\!}

түріндегі көпмүшелі теңдеуді айтамыз. Мұндағы a≠0 (Егер a = 0 болса, теңдеу ). Квадрат теңдеудің графигі - парабола (яғни квадрат функция).Квадрат теңдеу – 2-дәрежелі алгебралық теңдеу. Оның жалпы түрі мынадай: ax2+bx+c=0, a≠0. Квадрат үшмүше комплекс сандар жиынында {\displaystyle ~(C)} сызықтық көбейткіштерге жіктеледі: {\displaystyle ~ax^{2}+bx+c=a\left(x-x_{1}\right)\left(x-x_{2}\right)},мұндағы{\displaystyle ~x_{1},x_{2}-ax^{2}+bx+c=0} квадрат тендеудің түбірлері; {\displaystyle ~x_{1},x_{2}} — сандарыквадрат үшмүшенің түбірлері деп те, сонымен қатар бұлар {\displaystyle ~y=f\left(x\right)=ax^{2}+bx+c}квадрат функциясының нөлдері деп те аталады. Квадрат үшмүшені мына түрде де жазуға болады:

• {\displaystyle ~ax^{2}+bx+c=a\left(x+{\dfrac {b}{2a}}\right)^{2}-{\dfrac {b^{2}-4ac}{4a}}}

Осы өрнек нақты айнымалының квадрат функциясының графигін салу кезінде функцияның ең үлкен ({\displaystyle ~a>0} болғанда) немесе ең кіші ({\displaystyle ~a<0} болғанда) мәндерін анықтау үшін пайдаланылады.{\displaystyle ~ax^{2}+bx+c} квадрат функциясының графигі парабола болады, оның {\displaystyle ~\left(-{\dfrac {b}{2a}},{\dfrac {b^{2}-4ac}{4a}}\right)} нүктесінде орналасқан.

{\displaystyle ~x=-{\dfrac {b}{2a}}} -— түзуі параболаның симметрия осі болып табылады. {\displaystyle ~a>0}болғанда параболаның тармақтары жоғары карай, {\displaystyle ~a<0} болғанда — төмен қарай бағытталады.{\displaystyle ~a<0} болғанда {\displaystyle ~x=-{\dfrac {b}{2a}}} нүктесінде максимумға кетерілсе, ал {\displaystyle ~a>0}болғанда {\displaystyle ~y=-{\dfrac {b^{2}-4ac}{4a}}} нүктесінде минимумға төмендейді.

Парабола ордината осін ({\displaystyle ~0,b}) нүктелерінде қиып өтеді. Егер квадрат үшмүшенің нақтытүбірлері {\displaystyle ~x_{1}\neq x_{2}} болса, онда парабола абсцисса осін {\displaystyle ~(x_{1},0)} және {\displaystyle ~(x_{2},0)} нүктелерінде қиып өтеді, {\displaystyle ~x=x_{2}} болса, парабола абсцисса осімен {\displaystyle ~(x_{1},0)} нүктесінде жанасады.^[1]

a, b, және c әріптері - коэффиценттер деп аталады: a квадраттық коэффиценті - x²-тың коэффиценті, b коэффиценті - x-тің коэффиценті, ал c - тұрақты коэффицент немесе тұрақты мүше

ax² + bx + c - ның графиктері (Әр коэффицентінің мәнін өзгерткенде)

Мазмұны

  [жасыру] 

• 1Квадрат формуласы

• 2Дискриминант

  • 2.1Виет формуласы

• 3Мысалдар

Квадрат формуласы

Квадрат теңдеудің коэффиценттері нақты болса, оның екі шешімі немесе түбірі болады. Оларды квадрат формуласы сипаттайды:

{\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}} ,

яғни:

{\displaystyle x_{+}={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}}

және

{\displaystyle x_{-}={\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}}

Дискриминант

Дискриминант мәндеріне байланысты түбірлер
■ <0: x²+¹⁄₂
■ =0: −⁴⁄₃x²+⁴⁄₃x−¹⁄₃
■ >0: ³⁄₂x²+¹⁄₂x−⁴⁄₃

Төмендегі формула квадрат түбірлерді табуға қажет:

{\displaystyle D=b^{2}-4ac,\,\!}

Бұл дискриминант деп аталады.

Квадрат функцияның коэффиценттері нақты сан болса (комплекс сан емес) онда оның бір әлде екі нақты немесе екі комплекс түбірлері бар. Осыған байланысты дискриминант түбірлердің түрі мен санын анықтайды. Дискриминант мәніне байланысты үш жағдай болуы мүмкін:

• Егер дискриминант оң сан болса теңдеудің 2 түбірі бар және олар нақты:

{\displaystyle {\begin{aligned}x_{1}&={\frac {-b+{\sqrt {D}}}{2a}}\\x_{2}&={\frac {-b-{\sqrt {D}}}{2a}}\\\end{aligned}}}

• Егер дискриминант нөлге тең болса, теңдеудің бір нақты түбірі бар:

{\displaystyle x=-{\frac {b}{2a}}.\,\!}

• Егер дискриминант теріс сан болса теңдеудің нақты түбірлері жоқ. Керісінше, теңдеудің екі комплекс түбірі бар:

{\displaystyle {\begin{aligned}x_{1}&={\frac {-b}{2a}}+i{\frac {\sqrt {|D|}}{2a}}\end{aligned}}} мұнда {\displaystyle {\begin{aligned}|D|\end{aligned}}} - абсолют мәні(+ve) және {\displaystyle {\begin{aligned}i\end{aligned}}} = {\displaystyle {\begin{aligned}{\sqrt {-1}}\end{aligned}}}

{\displaystyle {\begin{aligned}x_{2}&={\frac {-b}{2a}}-i{\frac {\sqrt {|D|}}{2a}}\end{aligned}}}

Виет формуласы

x2+px+q=0 түріндегі келтірілген квадрат теңдеудің шешімі төмендегіше өрнектеледі: x1,2=. Квадрат теңдеудің түбірлері мен коэффициенттері бір-бірімен мынадай қатынастар арқылы байланысқан: x1+x2=, x1x2= .

Мысалдар

• {\displaystyle 7x+15-2x^{2}=0} теңдеуінде дискриминант оң: {\displaystyle \Delta =169} және екі нақты шешімі (түбірлері) бар:

{\displaystyle x_{1}={\frac {-7-{\sqrt {169}}}{2\cdot (-2)}}=5}

{\displaystyle x_{2}={\frac {-7+{\sqrt {169}}}{2\cdot (-2)}}=-{\frac {3}{2}}.}

• {\displaystyle x^{2}-2x+1=0} теңдеуінің дискриминанты нөлге тең: {\displaystyle \Delta }=0 яғни, теңдеудің бір шешімі бар:

{\displaystyle x=-{\frac {-2}{2}}=1}

• {\displaystyle x^{2}+3x+3=0} теңдеуінің нақты сандар арасында шешімі жоқ, өйткені: {\displaystyle \Delta =-3<0}. Бірақ екі комплекс түбірлері бар:

{\displaystyle x_{1}={\frac {-3-{\sqrt {3}}i}{2}}}

{\displaystyle x_{2}={\frac {-3+{\sqrt {3}}i}{2}}.}

Квадрат теңдеудің сол жақ бөлігін (x–x2)=0a(x–x1) түрінде көрсетуге болады. ге келтірілетін есептерді шешу мәселесі ежелгі дәуір математиктеріне де белгілі болған. Квадрат теңдеу терминін неміс философы әрі математигі Х.Вольф (1679 – 1754) енгізген (1710).

1. Жоғарыға көтеріліңіз↑ "Математикалық ойашар", "Қазақ энциклопедиясы" Алматы, 2009 ISBN

Т ақырыбы: Квадрат теңдеудің түбірлерінің формулалары.

Сабақтың мақсаты:

а) Оқушылардың квадрат теңдеулерді және оған келтіретін теңдеулерді шешу дағдыларын жетілдіру;

ә) Оқушыларды ұйымшылдыққа, ұқыптылыққа, дәлдікке тәрбиелеу;

б) Оқушылардың ойын жеткізе білуін және ой өрісін дамыту.

Әдісі: Деңгейлеп, саралап оқыту.

Түрі: Біліктілік пен дағдыны игеру және қалыптастыру сабағы.

Көрнекілігі: слайдта жазылған есептер, карточкалар, кестелер.

Сабақтың құрылымы: Сабақ 4 – деңгейлік құрылымынан тұрады:

1. Танымдық деңгей (ауызша)

2. Алгоритмдік деңгей (карточкамен жеке жұмыс) «Зерде» ойыны;

3. Эвристикалық деңгей (математикалық лото);

4. Шығармашылық деңгей (деңгейлік есептер).

Әр сатыда берілетін есептер өз бетімен деңгейлеп оқытуға негізделген жүйеде шешіледі. Оқушылар білімдеріне қарай деңгейлерді өздері таңдайды.

- күрделі - орташа - жеңіл

І. Танымдық деңгей: (репетитивті деңгей 11%)(слайдка қарап оқушылар жауап береді) 1-слайд.

1. Қандай жағдайда ах² + вх + с = 0 теңдеуі квадрат теңдеу деп аталады? (а≠0, а, в, с-сандар, х-айнымалы шама)

2. 1) в=0, с=0 2) в=0, с≠0 3) в≠0, с=0 теңдеудің түрі қандай болады? ( 1) ах²=0, 2) ах² + с = 0, 3) ах² + вх = 0)

ах² + вх + с = 0

І₁

в=0, с=0

түбірі

І₂

в=0, с≠0

І₃

в≠0, с=0

2 түбірі

D>0

D=0

D<0

І₄

а=1, в≠0, с≠0

түбір формуласы

1-слайд

3. ах²=0, ах² + с = 0, ах² + вх = 0 теңдеудің түрі қандай болады? Неше түбірі бар?

4. а=1, в≠0, с≠0 түріндегі теңдеу қандай теңдеу деп аталады? (х²+ вх + с = 0)

5. Квадрат теңдеулердің түбірлерінің формуласын жазыңдар.

(D=в² – 4ас, D>0, х₁= ; х₂= ;

D=в² – 4ас, D=0, х₁= ;

D=в² – 4ас, D<0, теңдеудің түбірі болмайды.

ІІ. «Зерде» ойыны: (карточка). Мақалдардың жалғасын тап.

1. Жеті рет өлшеп, (бір рет кес)

х² – 8х + 7 = 0

Шешуі: D=(-8²) – 4*1*7=64 – 28 = 36 > 0

х₁= = =1; х₂= = =7

Жауабы: х₁=1, х₂=7

2. Бір тал кессең, (он тал ек)

х² – 11х + 10 = 0

Шешуі: D=(-11)² – 4*1*10 = 121 – 40 = 81 > 0

х₁= = =1; х₂= = =10

Жауабы: х₁=1, х₂=10

3. Жігіт бір сырлы, (сегіз қырлы)

х² – 9х + 8 = 0

Шешуі: D=(-9)² – 4*1*8 = 81 – 32 = 49 > 0

х₁= = =1; х₂= = =8

Жауабы: х₁=1, х₂=8

4. Ұлға 30 үйден, (қызға 40 үйден) тыю

х² – 70х + 1200 = 0

Шешуі: D=(-70)² – 4*1*1200 = 4900 – 4800 = 100 > 0

х₁= = =30; х₂= = =40

Жауабы: х₁=30, х₂=40

ІІІ. Эвристикалық деңгей: Математикалық лото.

Квадрат теңдеулер

Дұрыс шешімі

Түбірлер

х² – 2х – 35 = 0

х₁=1, х₂=7

х² + 4х + 3 = 0

х₁=-5, х₂=3

х² – 8х + 7 = 0

х₁=-1, х₂=-3

х² + 10х – 11 = 0

х₁=-5, х₂=7

х² + 2х – 15 = 0

х₁=11, х₂=1

ІV. Шығармашылық деңгей: (таратпа карточкалар)

• күрделі

1. 2х(5х – 7) = 2х² – 5

2. (х + 4)² = 4х² + 5

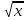3. х² + ( )² – 6 = 0

- орташа

1. 5х² + 4х – 1 = 0

2. -23х² – 22х + 1 = 0

3. 28х² – 36х + 11 = 0

• жеңіл

1. 3х² + 5х – 2 = 0, а, в, с = ?

2. 9х² – 6х + 1 = 0, а, в, с = ?

3. 5х² – 14х + 8 = 0, а, в, с = ?

V. Қорытындылау:

Рефлексия.

1. Біз тақырыптың барлық сұрақтарын талқыладық па?

2. Сәттілік баспалдағы.

Сендердің алдарыңдағы парақтарда баспалдақ салынған. Баспалдақтың төменгі жағында «түсінген жоқпын», бірінші баспалдақта «азғантай түсіндім», екінші баспалдақта «түсіндім», үшінші баспалдақта «жақсы түсіндім», төртінші баспалдақта «өте жақсы түсіндім» сөздері жазылған. Осы баспалдақтардың біреуінің қасына, өтілген материалды түсіну деңгейін көрсететін кез келген белгіні қойыңдар.

өте жақсы түсіндім

жақсы түсіндім

түсіндім

азғантай түсіндім

түсінген жоқпын

VІ. Үйге тапсырма: № 133, №134 оқулықтан 49-бет.

 

 

Краткое описание документа:

Тақырыбы: Квадрат теңдеудің түбірлерінің формулалары.

Сабақтың мақсаты:

а) Оқушылардың квадрат теңдеулерді және оған келтіретін теңдеулерді шешу дағдыларын жетілдіру;

ә) Оқушыларды ұйымшылдыққа, ұқыптылыққа, дәлдікке тәрбиелеу;

б) Оқушылардың ойын жеткізе білуін және ой өрісін дамыту.

Әдісі: Деңгейлеп, саралап оқыту.

Түрі: Біліктілік пен дағдыны игеру және қалыптастыру сабағы.

Көрнекілігі: слайдта жазылған есептер, карточкалар, кестелер.

Сабақтың құрылымы: Сабақ 4 – деңгейлік құрылымынан тұрады:

1.     Танымдық деңгей (ауызша)

2.     Алгоритмдік деңгей (карточкамен жеке жұмыс) «Зерде» ойыны;

3.     Эвристикалық деңгей (математикалық лото);

4.     Шығармашылық деңгей (деңгейлік есептер).

Әр сатыда берілетін есептер өз бетімен деңгейлеп оқытуға негізделген жүйеде шешіледі. Оқушылар білімдеріне қарай деңгейлерді өздері таңдайды.

 

 

           - күрделі                       - орташа                     - жеңіл

Кестені толтыр! Кестені толтыр!

Үлгерімі төмен оқушымен жұмыс Үлгерімі төмен оқушымен жұмыс

Оқушының аты-жөні: Оқушының аты-жөні:

Квадраттық теңдеу	а	b	c	Квадраттық теңдеу	а	b	c
-3x2+x-2=0				-5x2+x-3=0
4x2 +3x=0				6x2 +x=0
2x2+3x-5=0				3x2+7x-5=0
5x2=0				7x2=0
2x2+7=0				4x2+7=0
Кестені толтыр! Кестені толтыр! Үлгерімі төмен оқушымен жұмыс Үлгерімі төмен оқушымен жұмыс Оқушының аты-жөні: Оқушының аты-жөні:
Квадраттық теңдеу	а	b	c	Квадраттық теңдеу	а	b	c
x2+6x+8=0				5x2+8x+3=0
3x2 -8x=0				5x2 +4x=0
x2+5x-14=0				x2+7x+18=0
8x2=0				3x2=0
2X2+4=0				12x2-8x=0

Кестені толтыр! Кестені толтыр! Үлгерімі төмен оқушымен жұмыс Үлгерімі төмен оқушымен жұмыс Оқушының аты-жөні: Оқушының аты-жөні:
Квадраттық теңдеу	а	b	c	Квадраттық теңдеу	а	b	c
9x2+6x+1=0				2x2-9x+2=0
x2 -3x=0				5x2 +2x=0
7x2+5x-1=0				6x2+3x+2=0
3x2=0				10x2=0
4х2+5=0				3x2-5x=0

Квадрат теңдеу

ax²+bx+c=0

а- бірінші коэффициент, b- екінші коэффициент, c- бос мүше.

а 0, х – айнымалы.

Келтірілген квадрат теңдеу

x² +px+q=0

(a=1) , p және q – нөлден өзгеше кез келген сан.

Кері байланыс

Кері байланыс

І ширек-Өте жақсы түсіндім

ІІ ширек-Кейбір есептер қиындық тудырды

ІІІ ширек-Түсінгендей болдым

IV ширек-Мүлдем түсінбедім