
«КВАДРАТ ТЕҢДЕУЛЕРДІ ШЕШУДІҢ 10 ТӘСІЛІ»
2023-2024 оқу жылы
Кіріспе
Білім өркениеттіліктің әрі өлшемі, әрі тетігі болып табылатындықтан кез келген мемлекеттің рухани және әлеуметтік дәрежесі білім деңгейіне байланысты бағаланады.
Жан-жақты
үйлесімді, өркениетті елдің ұрпағын тәрбиелеп шығу бүгінгі
мектептің алдына қойылған мақсаттардың бірі.
Бұл мақсат әрбір орта мектеп
мұғалімінен бүгінгі заман талабына сай оқыту әдістемесін күннен
күнге жетілдіре түсуін талап етеді. Осы талаптың орындалуы орта
мектеп бағдарламасындағы әрбір пәннің әр тарауының әр тақырыбын
оқушы санасына жететіндей етіп оқытқанда ғана орындалады. Олай
болса, оқушыларды жеке тұлға етіп тәрбиелеуде математика пәнінің де
алатын орны, салмағы зор.
Бұл мақала алгебра курсында
қарастырылатын квадрат теңдеулерге және оларды шешу жолдарының әр
түрлі әдістеріне негізделініп отыр.
«Квадрат
теңдеулер» мектептегі алгебра курсының маңызды тақырыптарының
бірі. Көптеген
табиғи үдірістер мен құбылыстар, с.с. мазмұнды есептердің шығарылуы
квадрат теңдеулерді шешуге келіп тіреледі. Теңсіздіктерді шешу,
функцияларды зерттеу (функцияның нөлдерін, экстремум нүктелерін,
өсу және кему аралықтарын табу), ең үлкен және ең кіші мәндерді
табу есептерін шығару және т.б. жағдайларда квадрат теңдеулерді
шеше білу қажеттігі туындайды. Сондай-ақ тригонометриялық,
көрсеткіштік және логарифмдік теңдеулерді, физикада және техникада,
геометрия курсының есептерін алмастыру тәсілімен шешкенде квадрат
теңдеулерге келтіріледі.
Зерттеу барысында мектеп
оқушыларына «квадрат теңдеулерді» шешу жолдарының тоғыз түрлі
әдісімен таныстыруға мүмкіндік бар екендігін анықтадық. Атап
айтқанда, олар төмендегідей болып табылады: Зерттеу барысында «квадрат теңдеулерді» шешу жолдарының 10
түрлі әдісімен таныстым. Ол тәсілдерге алда жеке – жеке
тоқталамын.
Квадрат теңдеудің даму тарихы
2-ші дәрежелі теңдеулерді
шешуді б.э.д II мыңжылдықта Ежелгі Вавилонда шығара
білген.Ежелгі Греция математиктері квадрат теңдеулерді
геометриялық тәсілмен шешкен; мысалы, Евклид –кесіндіні орта
және шеткі қатынастарға бөлу арқылы шешкен.
Квадрат
теңдеудің түбірлерінің формуласы бірнеше рет «қайтадан ашылған».
Бізге жеткен деректер бойынша ең бірінші бұл формулаларды үнді
математигі Брахмагупте ашқан(жуықтап 598
ж.).
Ортаазия ғалымы
ал-Хорезми (IX.ғ) өзінің «Китаб аль-джебр валь-мукабала»
трактатында бұл формуланы екімүшенің толық квадратын
геометриялық интерпретация арқылы айырып алу жолымен
шешкен.
Ертедегі Диофанттың есебі
Есеп. Екі санның квадраттарының қосындысына тең санды басқа екі санның квадраттарының қосындысына тең болатындай жаз.
Диофант теңдеулердің оң бүтін және бөлшек шешулерін табуға баса назар аударады. Шешуі теріс сан болатындай теңдеуді ол мағынасыз теңдеу деп санап, бүтіндей қарастырмайды. Тек бір оң түбір табумен қанағаттанады.
Алдыңғы есепке оралайық. Бұл проблеманы шешуі мынадай есеппен түсіндіреді: Берілген сан 13 болсын, ол 2 мен 3-тің квадраттарының қосындысына тең. Бір квадраттың қабырғасының ұзындығы х+2 болсын, ал екінші квадрат қабырғасының ұзындығы 2х-тен 3-і кем, яғни 2х-3. Сонда бірінші квадраттың ауданы (х+2)² =x² +4x+4, екіншісінікі (2х-3)² =4х² -12х+9.
Екеуінің ауданың қоссақ (х² +4х+4) + (4х² -12х+9)=5х²-8х+13. Есептің шарты бойынша бұл 13-ке тең болуы керек:
5х² -8х+13=13
5х² -8х=0
х(5х-8)=0 5x-8=0
5x=8
x=![]()
Сонымен
бірінші квадраттың қабырғасы х+2=![]() + 2=
+ 2=![]() ,
екіншісінікі 2х-3=2*
,
екіншісінікі 2х-3=2*![]() -3=
-3=![]() -3=
-3=![]() .
.
Квадраттың аудандары: (![]() )²
=
)²
=![]()
(![]() )² =
)² =![]()
Бұл
сандардың қосындысы ![]()
![]() +
+![]() =
=![]() =13 болады, яғни есепті
қанағаттандырады.
=13 болады, яғни есепті
қанағаттандырады.
Квадрат теңдеудің әл-Харезмде дамуы
Кітаптың
өзінде пайдаланылған әдебиеттер көрсетілмегендіктен, әл-Хорезми
қандай кітаптарды қолданылғаны белгісіз. Кітапта кез келген квадрат
теңдеуді алты негізгі түрдің біріне келтіріп, сол негізгі түрлерді
шешудің алгебралық және геометриялық тәсілдері келтірілген. Қазіргі
кезде қолданылатын абстрактылы шартты белгілер кітапта атымен жоқ
болғандықтан, «әл-Хорезмидің алгебрасы толығымен сөзбен сипаттау
арқылы баяндалған. Гректің «Арифметикасында» немесе Браһмагуптаның
еңбектерінде қолданылатын синкопациялар мүлдем қолданылмаған. Тіпті
сандар арнайы таңбамен бейнеленген емес, толығымен сөздер ретінде
жазылған!»Сондықтан теңдеулер сөзбен «шаршы» деп (яғни бүгіндері
“x2” деп), «түбір» деп
(бүгін оны “x” деп) және «сандар» деп (мысалы, «қырық екі», «жеті»
деп толығымен жазып отырды) деп белгіленіп отырды. Бүгінгі күннің
шартты белгілерін қолданса, теңдеудің негізгі алты түрі
мыналар:
1) квадраттар тең
түбірге тең (ax2 =
bx)
2) квадраттар санға тең
(ax2 =
c)
3) түбірлер санға тең (bx =
c)
4) квадраттар мен түбірлер санға тең
(ax2 + bx =
c)
5) квадраттар мен сандар түбірге тең
(ax2 + c =
bx)
6) түбірлер мен сандар квадраттарға тең (bx +
c = ax2)
Әл-жәбр (араб жазуымен: ‘الجبر’) («толықтыру») амалы:
теріс шаманы теңдеудің бір жағынан екінші жағына жіберіп, оң шама
етіп өзгерту.
Әл-Хорезмидің
мысалында (қазіргі белгілерді қолданса)
“x2 = 40x –
4x2” теңдеуі «әл-жәбр»
амалын қолдану арқылы мынаған өзгертіледі:
“5x2 = 40x” Осы ережені
қайталап қолдану арқылы есептеулерді пайда болатын теріс сандардан
құтылуға болады.
Әл-мұқабала
(араб жазуымен ‘المقابله’) («теңдестіру»)
дегеніміз – теңдеудің екі жағынан да бірдей оң шаманы алып тастау,
сонда мына теңдеу: “x2 + 5 = 40x + 4x2” мына түрге келеді: “5 =
40x + 3x2“. Осы ережені қайталап
қолдану арқылы әр түрлі шамалардың (квадрат, түбір, сан сияқты)
теңдеудің бір жағында тек бір рет қана кездесетіндей етіп
түрлендіруге болады.
Кітаптың
келесі бөлігінде жоғарыда айтылған ережелерді іс жүзінде қолданудың
практикалық мысалдары келтірілген. Одан кейінгі бөлігінде аудан мен
көлемді есептеудің жолдары қарастырылған.
1-әдіс. Теңдеудің сол жақ бөлігін көбейткіштерге жіктеу
х2 + 10х - 24 = 0 теңдеуді жіктейміз .
Теңдеудің сол жақ бөлігін көбейткіштерге жіктейміз:
х2 + 10х - 24 = х2 + 12х - 2х - 24 = х(х + 12) - 2(х + 12) = (х + 12)(х - 2).
Демек, теңдеуді былай жазуға болады:
(х + 12)(х - 2) = 0
Көбейтінді нөлге тең болғандықтан, ең болмағанда көбейткіштердің біреуі нөлге тең болуы керек. Сондықтан теңдеулердің сол жақ бөлігіндегі х = 2 және х = - 12 сандары х2 + 10х - 24 = 0 теңдеуінің түбірлері болып табылады.
2-әдіс. Толық квадратқа келтіру әдісі
Мысал: х2 + 6х - 7 = 0=0 теңдеуін шешейік.
Сол жақ бөлігін толық квадратқа келтіреміз. Ол үшін х2 + 6х өрнегін төмендегідей жазып аламыз:
х2 + 6х = х2 + 2• х • 3.
Алынған өрнектің бірінші қосындысы х-тың квадраты, ал екінші қосындысы х пен 3-тің екі еселенгені. Толық квадрат алу үшін 32-ын қосу керек. Сонда
х2 + 2• х • 3 + 32 = (х + 3)2.
Енді теңдеудің сол жағын түрлендіреміз. Берілген теңдеуге 32 -ын қосып, алып тастаймыз. Сонда шығатыны:
х2 + 6х - 7 = х2 + 2• х • 3 + 32 - 32 - 7 = (х + 3)2 - 9 - 7 = (х + 3)2 - 16.
Сонымен, берілген теңдеуді былайша жазуға болады:
(х + 3)2 - 16 =0, (х + 3)2 = 16.
Бұдан , х + 3 - 4 = 0, х1 = 1, немесе х + 3 = -4, х2 = -7.
3-әдіс. Квадраттық теңдеулерді формула арқылы шешу
ах2 + bх + с = 0, а ≠ 0
теңдеудің екі жағын да 4а-ға көбейтеміз де, төмендегі өрнекті аламыз:
4а2х2 + 4аbх + 4ас = 0,
((2ах)2 + 2ах • b + b2) - b2 + 4ac = 0,
(2ax + b)2 = b2 - 4ac,
2ax + b = ± √ b2 - 4ac,
2ax = - b ± √ b2 - 4ac,
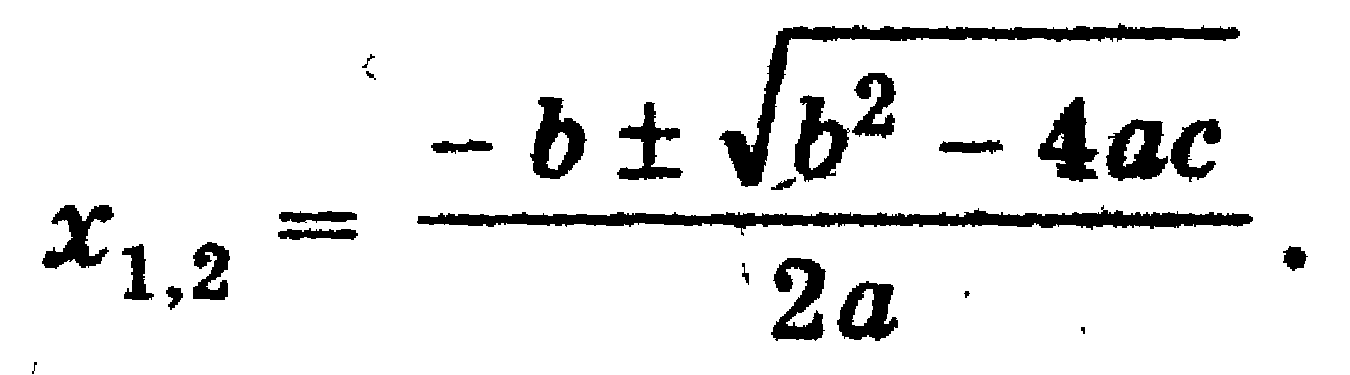
Оған келесідегідей мысалдар келтіруге болады: 4х2 + 7х + 3 = 0.
а = 4, b = 7, с = 3, D = b2 - 4ac = 72 - 4 • 4 • 3 = 49 - 48 = 1,
Д>0 болғандықтан, екі әр
түрлі түбір болады:![]()
![]()
Сонымен, дискриминант оң болғанда, яғни в2-4ас>0, ах2+вх+с=0 теңдеуінің екі түрлі түбірі болады.
б) 4х2 - 4х + 1 = 0, теңдеуін шешейік.
а = 4, b = - 4, с = 1, D = b2 - 4ac = (-4)2 - 4 • 4 • 1= 16 - 16 = 0,
D = 0, болғандықтан, бір ғана түбір бар болады
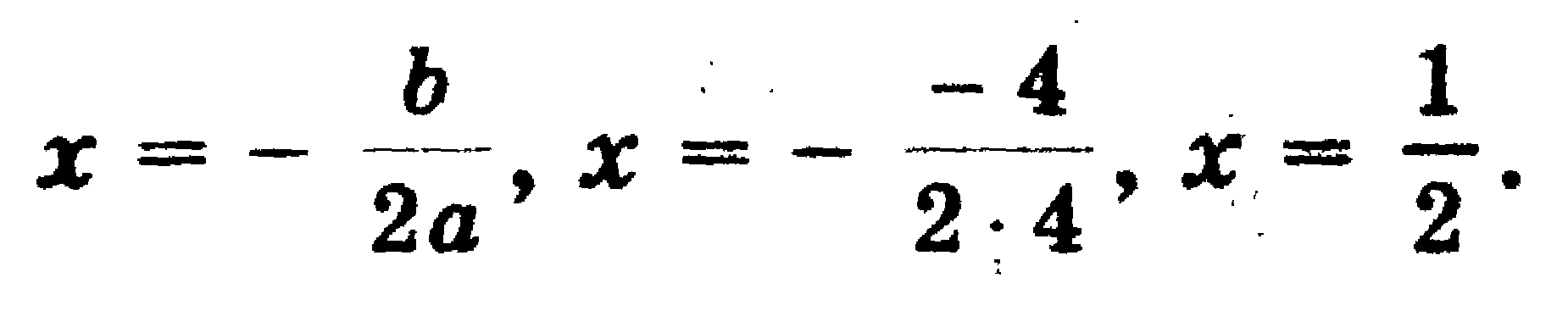
Сонымен, егер дискриминант нөлге тең болса, b2 - 4ac = 0, то уравнение
а![]() х2
+ bх + с = 0 теңдеуінің жалғыз түбірі бар болады
х2
+ bх + с = 0 теңдеуінің жалғыз түбірі бар болады
в) 2х2 + 3х + 4 = 0, теңдеуін шешейік.
а = 2, b = 3, с = 4, D = b2 - 4ac = 32 - 4 • 2 • 4 = 9 - 32 = - 13 , D < 0.
Д<0 болғандықтан, теңдеудің нақты сандар өрісінде түбірі болмайды..
Д<0 болғандықтан, теңдеудің нақты сандар өрісінде түбірі болмайды. b2 - 4ac < 0 онда ах2 + bх + с = 0 теңдеуінің түбірі болмайды
4-әдіс. Виет теоремасын пайдаланып теңдеулерді шешуКелтірілген түбірлері Виет теоремасын қанағаттандырады.
Ол былай беріледі: х2 + px + c = 0. (1)
а=1 болғанда,
x1 x2 = q,
x1 + x2 = - p
Бұдан келесі тұжырымдарды шығаруға болады:
а) Егер q (1) теңдеудің бос мүшесі оң болса (q0) онда теңдеудің екі бірдей таңбалы түбірі болады. Егер р>0, онда екі түбірі де теріс болады, егер р<0, онда түбірлері оң болады.
Мысал,x2 – 3x + 2 = 0; x1 = 2 және x2 = 1, мұнда q = 2 > 0 , p = - 3 < 0;
x2 + 8x + 7 = 0; x1 = - 7 және x2 = - 1, мұнда q = 7 > 0 , p= 8 > 0.
б) Егер q (1) теңдеудің бос мүшесі теріс болса (q <0), онда теңдеудің екі түрлі, таңбалы екі түбірі болады, түбірдің модулі бойынша үлкені оң болады, егер р <0 болса, теріс болады, егер р >0.
Мысал:
x2 + 4x – 5 = 0; x1 = - 5 , x2 = 1, мұнда q= - 5 < 0 , p = 4 > 0;
x2 – 8x – 9 = 0; x1 = 9 и x2 = - 1, мұнда q = - 9 < 0 , p = - 8 < 0.
5-әдіс. Теңдеуді «асыра лақтыру» әдісімен шешу
ах2 + bх + с = 0, а ≠ 0.
квадрат теңдеуін қарастырамыз. Теңдеудің екі жағын да а-ға көбейтіп, мынаны аламыз:
а2х2 + аbх + ас = 0.
. ах = у деп белгілесек, х = у/а
Олай болса
у2 + by + ас = 0,
теңдеуіне келеміз. Бұл бастапқы теңдеумен тең. Теңдеудің түбірлерін у1, у2 –ні Виет теоремасы арқылы табамыз.
Соңында х1 = у1/а , х1 = у2/а -ны аламыз. Бұл жағдайда а коэффициентін бос мүшеге көбейтеді. Сондықтан да бұл әдісті «асыра лақтыру» әдісі деп атайды . Бұл әдісті көбінесе Виет теоремасын пайдаланып түбірді оңай табуда және дискриминант дәл квадрат болғанда қолданады.
мысалы, 2х2 – 11х + 15 = 0 теңдеуін шешейік.
Шешуі: 2 коэффициенті теңдеудің бос мүшесіне асыра лақтырамыз, нәтижесінде:
у2 – 11у + 30 = 0.
Виет теоремасы бойынша
![]()
![]()
![]()
![]() у1 = 5 х1
= 5/2 x1
= 2,5
у1 = 5 х1
= 5/2 x1
= 2,5
![]() у2 = 6 x2 = 6/2 x2 = 3.
у2 = 6 x2 = 6/2 x2 = 3.
Жауабы: 2,5; 3.
6-әдіс. Квадрат теңдеулердің коэффициенттерінің қасиеттерін қолдану.
ах2 + bх + с = 0, , а ≠ 0 квадрат теңдеуі берілген.
1) Егер, а+ b + с = 0 (яғни коэффициенттер қосындысы 0-ге тең) болса, онда х1 = 1,
х2 = с/а.
Дәлелдеу: а ≠ 0, келесідей квадрат теңдеуге келеміз.
x2 + b/a • x + c/a = 0.
![]() Виет
теоремасы арқылы
Виет
теоремасы арқылы
x1 + x2 = - b/a,
x1x2 = 1• c/a.
![]() а
– b + с = 0 шарты бойынша, b = а + с аламыз. Олай
болса,
а
– b + с = 0 шарты бойынша, b = а + с аламыз. Олай
болса,
x1 + x2 = - а + b/a= -1 – c/a,
x1x2 = - 1• ( - c/a),
х1 = -1 , х2 = c/a болатынын дәлелдндік.
-
Мысал: 345х2 – 137х – 208 = 0 теңдеуін шешейік.
Шешуі. а + b + с = 0 (345 – 137 – 208 = 0),
онда
х1 = 1, х2 = c/a = -208/345.
Жауабы: 1; -208/345.
2) 132х2 – 247х + 115 = 0 теңдеуін шешейік.
Шешуі. а + b + с = 0 (132 – 247 + 115 = 0),
онда
х1 = 1, х2 = c/a = 115/132.
Жауабы: 1; 115/132.
7-әдіс Квадрат теңдеуді шешудің графиктік
түрі
![]() теңдеуінен екінші, үшінші мүшелерін оң жағына
шығарсақ,
теңдеуінен екінші, үшінші мүшелерін оң жағына
шығарсақ, ![]() аламыз.
аламыз.
![]() функциялардыңграфиктерін
тұрғызамыз.
функциялардыңграфиктерін
тұрғызамыз.
Б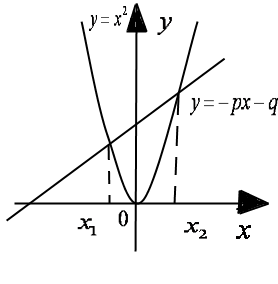 ірінші функцияның
графигі – координат басынан өтетін парабола, екінші функцияның
графигі – түзу (1-сурет). Енді келесі жағдайлар болуы
мүмкін:
ірінші функцияның
графигі – координат басынан өтетін парабола, екінші функцияның
графигі – түзу (1-сурет). Енді келесі жағдайлар болуы
мүмкін:
-түзу және парабола екі нүктеде
қиылысуы мүмкін, қиылысу нүктесінің абциссасы квадрат теңдеудің
түбірі болады.
- түзу және парабола жанасуы
мүмкін (бір ғана ортақ нүктеде), яғни теңдеудің бір ғана шешімі
болады.
-парабола және түзудің ортақ
нүктелері жоқ, яғни теңдеудің түбірі жоқ.
Мысал:
1)![]()
![]() теңдеуін графиктік тәсілмен
шешеміз.
теңдеуін графиктік тәсілмен
шешеміз.
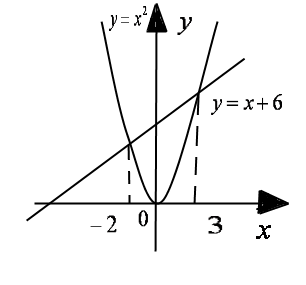
Шешуі: ![]() түрінде жазамыз.
түрінде жазамыз. ![]() параболасын және
параболасын және ![]() түзуін тұрғызайық.
түзуін тұрғызайық. ![]() түзуін мына М(0,6) және N(3,9) нүктелері
арқылы тұрғызуға болады. Түзу және парабола А,В нүктелері
абсциссалары
түзуін мына М(0,6) және N(3,9) нүктелері
арқылы тұрғызуға болады. Түзу және парабола А,В нүктелері
абсциссалары ![]() -пен қиылысады.
-пен қиылысады.
Жауабы:![]()
2)![]() теңдеуін графиктік тәсілмен
шешеміз
теңдеуін графиктік тәсілмен
шешеміз
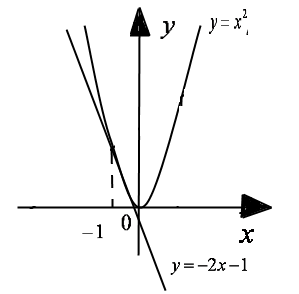
Шешуі:![]() түрінде жазамыз. y=х2 параболасын және у=-2х-1 түзуін тұрғызайық.
у=-2х-1 түзуін М(0;-1) және N(
түрінде жазамыз. y=х2 параболасын және у=-2х-1 түзуін тұрғызайық.
у=-2х-1 түзуін М(0;-1) және N(![]() ) нүктелері арқылы жүргіземіз. Парабола мен
түзу А нүктесінде қиылысады, абциссасы х=-1 тең.
) нүктелері арқылы жүргіземіз. Парабола мен
түзу А нүктесінде қиылысады, абциссасы х=-1 тең.
Жауабы:х=-1
8-әдіс. Квадрат теңдеуді
циркуль және сызғыш көмегімен шешу. 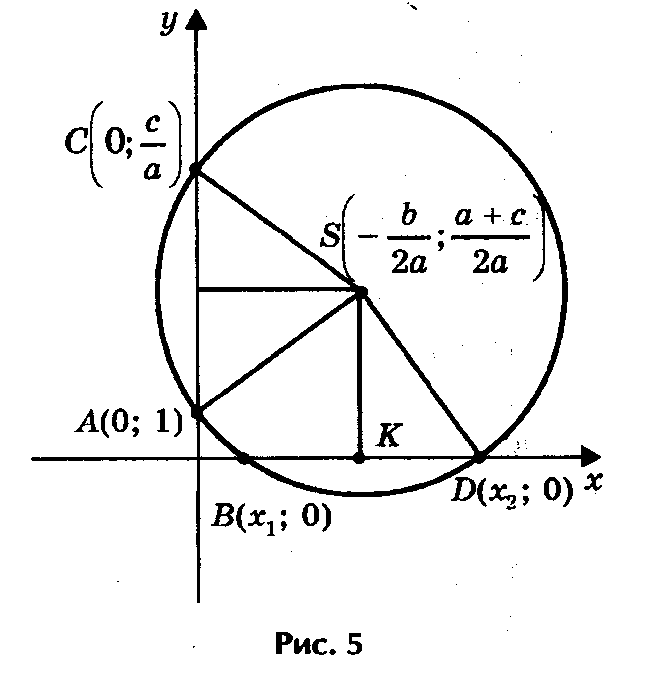 ах2 +вх+с=0 квадраттық теңдеуін циркуль және сызғыш көмегімен
шешу әдісін ұсынамыз (5-сурет). Ізделінді шеңбер абцисса өсінде
В(х1 ;0) және Д (х2;0) нүктелерінде қиылыссын
делік. Мұндағы х1, х2 -
ах2 + вх + с=0 теңдеуінің түбірлері және ординат осінен А(0;1)
және С(0; а с ) нүктелері арқылы өтеді делік. Олай болса, қима
туралы теорема бойынша мынаны аламыз: OB • OD = OA • OC,
келесі OC = OB •
OD/ OA=
х1х2/
1 = c/a.
ах2 +вх+с=0 квадраттық теңдеуін циркуль және сызғыш көмегімен
шешу әдісін ұсынамыз (5-сурет). Ізделінді шеңбер абцисса өсінде
В(х1 ;0) және Д (х2;0) нүктелерінде қиылыссын
делік. Мұндағы х1, х2 -
ах2 + вх + с=0 теңдеуінің түбірлері және ординат осінен А(0;1)
және С(0; а с ) нүктелері арқылы өтеді делік. Олай болса, қима
туралы теорема бойынша мынаны аламыз: OB • OD = OA • OC,
келесі OC = OB •
OD/ OA=
х1х2/
1 = c/a.
Шеңбер центрі АС және ВД хорда ортасында орналасқан перпендикуляр SF пен SК-ның қиылысу нүктелері болып табылады, сондықтан SК= а а в в х х 2 2 2 1 2 ; SF = а а с а с у у 2 2 1 2 1 2 Сонымен, 1) S а а с а в 2 , 2 (шеңбер центрі) және А (0;1) нүктелерін тұрғызамыз; 2) SА радиусты шеңбер жүргіземіз; 3) Осы шеңбердің Ох осі арқылы өтетін қиылысу нүктелері бастапқы квадрат теңдеудің түбірі болады. Сонымен үш түрлі жағд
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
"Квадрат теңдеуді шешудің 10 тәсілі"
"Квадрат теңдеуді шешудің 10 тәсілі"
«КВАДРАТ ТЕҢДЕУЛЕРДІ ШЕШУДІҢ 10 ТӘСІЛІ»
2023-2024 оқу жылы
Кіріспе
Білім өркениеттіліктің әрі өлшемі, әрі тетігі болып табылатындықтан кез келген мемлекеттің рухани және әлеуметтік дәрежесі білім деңгейіне байланысты бағаланады.
Жан-жақты
үйлесімді, өркениетті елдің ұрпағын тәрбиелеп шығу бүгінгі
мектептің алдына қойылған мақсаттардың бірі.
Бұл мақсат әрбір орта мектеп
мұғалімінен бүгінгі заман талабына сай оқыту әдістемесін күннен
күнге жетілдіре түсуін талап етеді. Осы талаптың орындалуы орта
мектеп бағдарламасындағы әрбір пәннің әр тарауының әр тақырыбын
оқушы санасына жететіндей етіп оқытқанда ғана орындалады. Олай
болса, оқушыларды жеке тұлға етіп тәрбиелеуде математика пәнінің де
алатын орны, салмағы зор.
Бұл мақала алгебра курсында
қарастырылатын квадрат теңдеулерге және оларды шешу жолдарының әр
түрлі әдістеріне негізделініп отыр.
«Квадрат
теңдеулер» мектептегі алгебра курсының маңызды тақырыптарының
бірі. Көптеген
табиғи үдірістер мен құбылыстар, с.с. мазмұнды есептердің шығарылуы
квадрат теңдеулерді шешуге келіп тіреледі. Теңсіздіктерді шешу,
функцияларды зерттеу (функцияның нөлдерін, экстремум нүктелерін,
өсу және кему аралықтарын табу), ең үлкен және ең кіші мәндерді
табу есептерін шығару және т.б. жағдайларда квадрат теңдеулерді
шеше білу қажеттігі туындайды. Сондай-ақ тригонометриялық,
көрсеткіштік және логарифмдік теңдеулерді, физикада және техникада,
геометрия курсының есептерін алмастыру тәсілімен шешкенде квадрат
теңдеулерге келтіріледі.
Зерттеу барысында мектеп
оқушыларына «квадрат теңдеулерді» шешу жолдарының тоғыз түрлі
әдісімен таныстыруға мүмкіндік бар екендігін анықтадық. Атап
айтқанда, олар төмендегідей болып табылады: Зерттеу барысында «квадрат теңдеулерді» шешу жолдарының 10
түрлі әдісімен таныстым. Ол тәсілдерге алда жеке – жеке
тоқталамын.
Квадрат теңдеудің даму тарихы
2-ші дәрежелі теңдеулерді
шешуді б.э.д II мыңжылдықта Ежелгі Вавилонда шығара
білген.Ежелгі Греция математиктері квадрат теңдеулерді
геометриялық тәсілмен шешкен; мысалы, Евклид –кесіндіні орта
және шеткі қатынастарға бөлу арқылы шешкен.
Квадрат
теңдеудің түбірлерінің формуласы бірнеше рет «қайтадан ашылған».
Бізге жеткен деректер бойынша ең бірінші бұл формулаларды үнді
математигі Брахмагупте ашқан(жуықтап 598
ж.).
Ортаазия ғалымы
ал-Хорезми (IX.ғ) өзінің «Китаб аль-джебр валь-мукабала»
трактатында бұл формуланы екімүшенің толық квадратын
геометриялық интерпретация арқылы айырып алу жолымен
шешкен.
Ертедегі Диофанттың есебі
Есеп. Екі санның квадраттарының қосындысына тең санды басқа екі санның квадраттарының қосындысына тең болатындай жаз.
Диофант теңдеулердің оң бүтін және бөлшек шешулерін табуға баса назар аударады. Шешуі теріс сан болатындай теңдеуді ол мағынасыз теңдеу деп санап, бүтіндей қарастырмайды. Тек бір оң түбір табумен қанағаттанады.
Алдыңғы есепке оралайық. Бұл проблеманы шешуі мынадай есеппен түсіндіреді: Берілген сан 13 болсын, ол 2 мен 3-тің квадраттарының қосындысына тең. Бір квадраттың қабырғасының ұзындығы х+2 болсын, ал екінші квадрат қабырғасының ұзындығы 2х-тен 3-і кем, яғни 2х-3. Сонда бірінші квадраттың ауданы (х+2)² =x² +4x+4, екіншісінікі (2х-3)² =4х² -12х+9.
Екеуінің ауданың қоссақ (х² +4х+4) + (4х² -12х+9)=5х²-8х+13. Есептің шарты бойынша бұл 13-ке тең болуы керек:
5х² -8х+13=13
5х² -8х=0
х(5х-8)=0 5x-8=0
5x=8
x=![]()
Сонымен
бірінші квадраттың қабырғасы х+2=![]() + 2=
+ 2=![]() ,
екіншісінікі 2х-3=2*
,
екіншісінікі 2х-3=2*![]() -3=
-3=![]() -3=
-3=![]() .
.
Квадраттың аудандары: (![]() )²
=
)²
=![]()
(![]() )² =
)² =![]()
Бұл
сандардың қосындысы ![]()
![]() +
+![]() =
=![]() =13 болады, яғни есепті
қанағаттандырады.
=13 болады, яғни есепті
қанағаттандырады.
Квадрат теңдеудің әл-Харезмде дамуы
Кітаптың
өзінде пайдаланылған әдебиеттер көрсетілмегендіктен, әл-Хорезми
қандай кітаптарды қолданылғаны белгісіз. Кітапта кез келген квадрат
теңдеуді алты негізгі түрдің біріне келтіріп, сол негізгі түрлерді
шешудің алгебралық және геометриялық тәсілдері келтірілген. Қазіргі
кезде қолданылатын абстрактылы шартты белгілер кітапта атымен жоқ
болғандықтан, «әл-Хорезмидің алгебрасы толығымен сөзбен сипаттау
арқылы баяндалған. Гректің «Арифметикасында» немесе Браһмагуптаның
еңбектерінде қолданылатын синкопациялар мүлдем қолданылмаған. Тіпті
сандар арнайы таңбамен бейнеленген емес, толығымен сөздер ретінде
жазылған!»Сондықтан теңдеулер сөзбен «шаршы» деп (яғни бүгіндері
“x2” деп), «түбір» деп
(бүгін оны “x” деп) және «сандар» деп (мысалы, «қырық екі», «жеті»
деп толығымен жазып отырды) деп белгіленіп отырды. Бүгінгі күннің
шартты белгілерін қолданса, теңдеудің негізгі алты түрі
мыналар:
1) квадраттар тең
түбірге тең (ax2 =
bx)
2) квадраттар санға тең
(ax2 =
c)
3) түбірлер санға тең (bx =
c)
4) квадраттар мен түбірлер санға тең
(ax2 + bx =
c)
5) квадраттар мен сандар түбірге тең
(ax2 + c =
bx)
6) түбірлер мен сандар квадраттарға тең (bx +
c = ax2)
Әл-жәбр (араб жазуымен: ‘الجبر’) («толықтыру») амалы:
теріс шаманы теңдеудің бір жағынан екінші жағына жіберіп, оң шама
етіп өзгерту.
Әл-Хорезмидің
мысалында (қазіргі белгілерді қолданса)
“x2 = 40x –
4x2” теңдеуі «әл-жәбр»
амалын қолдану арқылы мынаған өзгертіледі:
“5x2 = 40x” Осы ережені
қайталап қолдану арқылы есептеулерді пайда болатын теріс сандардан
құтылуға болады.
Әл-мұқабала
(араб жазуымен ‘المقابله’) («теңдестіру»)
дегеніміз – теңдеудің екі жағынан да бірдей оң шаманы алып тастау,
сонда мына теңдеу: “x2 + 5 = 40x + 4x2” мына түрге келеді: “5 =
40x + 3x2“. Осы ережені қайталап
қолдану арқылы әр түрлі шамалардың (квадрат, түбір, сан сияқты)
теңдеудің бір жағында тек бір рет қана кездесетіндей етіп
түрлендіруге болады.
Кітаптың
келесі бөлігінде жоғарыда айтылған ережелерді іс жүзінде қолданудың
практикалық мысалдары келтірілген. Одан кейінгі бөлігінде аудан мен
көлемді есептеудің жолдары қарастырылған.
1-әдіс. Теңдеудің сол жақ бөлігін көбейткіштерге жіктеу
х2 + 10х - 24 = 0 теңдеуді жіктейміз .
Теңдеудің сол жақ бөлігін көбейткіштерге жіктейміз:
х2 + 10х - 24 = х2 + 12х - 2х - 24 = х(х + 12) - 2(х + 12) = (х + 12)(х - 2).
Демек, теңдеуді былай жазуға болады:
(х + 12)(х - 2) = 0
Көбейтінді нөлге тең болғандықтан, ең болмағанда көбейткіштердің біреуі нөлге тең болуы керек. Сондықтан теңдеулердің сол жақ бөлігіндегі х = 2 және х = - 12 сандары х2 + 10х - 24 = 0 теңдеуінің түбірлері болып табылады.
2-әдіс. Толық квадратқа келтіру әдісі
Мысал: х2 + 6х - 7 = 0=0 теңдеуін шешейік.
Сол жақ бөлігін толық квадратқа келтіреміз. Ол үшін х2 + 6х өрнегін төмендегідей жазып аламыз:
х2 + 6х = х2 + 2• х • 3.
Алынған өрнектің бірінші қосындысы х-тың квадраты, ал екінші қосындысы х пен 3-тің екі еселенгені. Толық квадрат алу үшін 32-ын қосу керек. Сонда
х2 + 2• х • 3 + 32 = (х + 3)2.
Енді теңдеудің сол жағын түрлендіреміз. Берілген теңдеуге 32 -ын қосып, алып тастаймыз. Сонда шығатыны:
х2 + 6х - 7 = х2 + 2• х • 3 + 32 - 32 - 7 = (х + 3)2 - 9 - 7 = (х + 3)2 - 16.
Сонымен, берілген теңдеуді былайша жазуға болады:
(х + 3)2 - 16 =0, (х + 3)2 = 16.
Бұдан , х + 3 - 4 = 0, х1 = 1, немесе х + 3 = -4, х2 = -7.
3-әдіс. Квадраттық теңдеулерді формула арқылы шешу
ах2 + bх + с = 0, а ≠ 0
теңдеудің екі жағын да 4а-ға көбейтеміз де, төмендегі өрнекті аламыз:
4а2х2 + 4аbх + 4ас = 0,
((2ах)2 + 2ах • b + b2) - b2 + 4ac = 0,
(2ax + b)2 = b2 - 4ac,
2ax + b = ± √ b2 - 4ac,
2ax = - b ± √ b2 - 4ac,
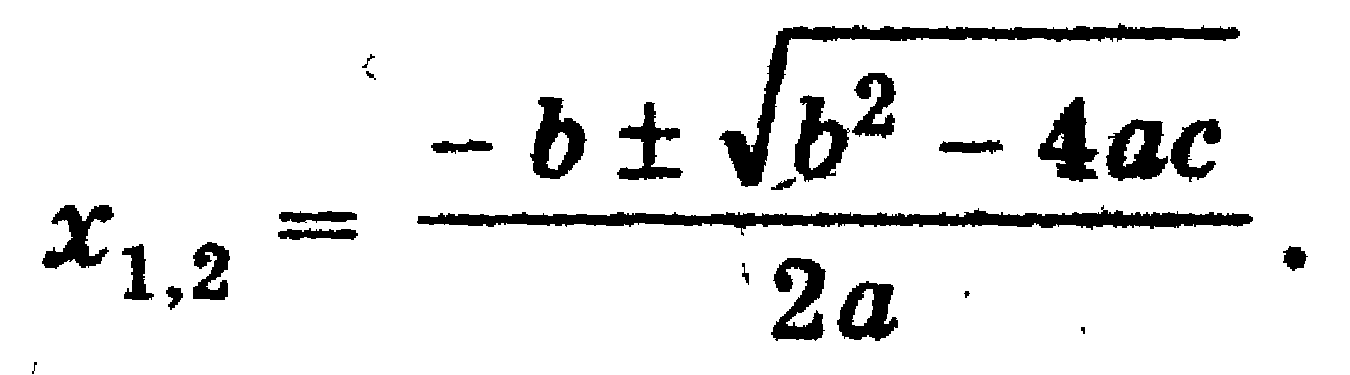
Оған келесідегідей мысалдар келтіруге болады: 4х2 + 7х + 3 = 0.
а = 4, b = 7, с = 3, D = b2 - 4ac = 72 - 4 • 4 • 3 = 49 - 48 = 1,
Д>0 болғандықтан, екі әр
түрлі түбір болады:![]()
![]()
Сонымен, дискриминант оң болғанда, яғни в2-4ас>0, ах2+вх+с=0 теңдеуінің екі түрлі түбірі болады.
б) 4х2 - 4х + 1 = 0, теңдеуін шешейік.
а = 4, b = - 4, с = 1, D = b2 - 4ac = (-4)2 - 4 • 4 • 1= 16 - 16 = 0,
D = 0, болғандықтан, бір ғана түбір бар болады
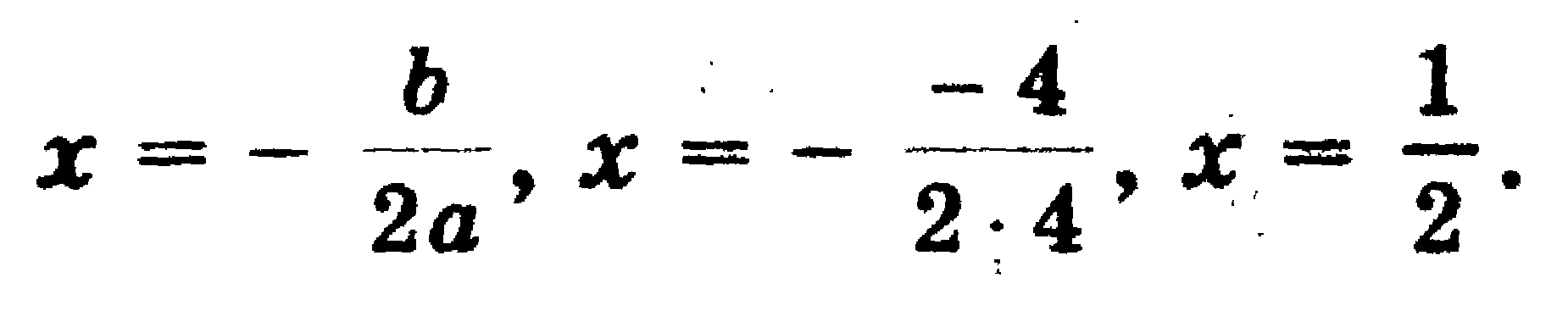
Сонымен, егер дискриминант нөлге тең болса, b2 - 4ac = 0, то уравнение
а![]() х2
+ bх + с = 0 теңдеуінің жалғыз түбірі бар болады
х2
+ bх + с = 0 теңдеуінің жалғыз түбірі бар болады
в) 2х2 + 3х + 4 = 0, теңдеуін шешейік.
а = 2, b = 3, с = 4, D = b2 - 4ac = 32 - 4 • 2 • 4 = 9 - 32 = - 13 , D < 0.
Д<0 болғандықтан, теңдеудің нақты сандар өрісінде түбірі болмайды..
Д<0 болғандықтан, теңдеудің нақты сандар өрісінде түбірі болмайды. b2 - 4ac < 0 онда ах2 + bх + с = 0 теңдеуінің түбірі болмайды
4-әдіс. Виет теоремасын пайдаланып теңдеулерді шешуКелтірілген түбірлері Виет теоремасын қанағаттандырады.
Ол былай беріледі: х2 + px + c = 0. (1)
а=1 болғанда,
x1 x2 = q,
x1 + x2 = - p
Бұдан келесі тұжырымдарды шығаруға болады:
а) Егер q (1) теңдеудің бос мүшесі оң болса (q0) онда теңдеудің екі бірдей таңбалы түбірі болады. Егер р>0, онда екі түбірі де теріс болады, егер р<0, онда түбірлері оң болады.
Мысал,x2 – 3x + 2 = 0; x1 = 2 және x2 = 1, мұнда q = 2 > 0 , p = - 3 < 0;
x2 + 8x + 7 = 0; x1 = - 7 және x2 = - 1, мұнда q = 7 > 0 , p= 8 > 0.
б) Егер q (1) теңдеудің бос мүшесі теріс болса (q <0), онда теңдеудің екі түрлі, таңбалы екі түбірі болады, түбірдің модулі бойынша үлкені оң болады, егер р <0 болса, теріс болады, егер р >0.
Мысал:
x2 + 4x – 5 = 0; x1 = - 5 , x2 = 1, мұнда q= - 5 < 0 , p = 4 > 0;
x2 – 8x – 9 = 0; x1 = 9 и x2 = - 1, мұнда q = - 9 < 0 , p = - 8 < 0.
5-әдіс. Теңдеуді «асыра лақтыру» әдісімен шешу
ах2 + bх + с = 0, а ≠ 0.
квадрат теңдеуін қарастырамыз. Теңдеудің екі жағын да а-ға көбейтіп, мынаны аламыз:
а2х2 + аbх + ас = 0.
. ах = у деп белгілесек, х = у/а
Олай болса
у2 + by + ас = 0,
теңдеуіне келеміз. Бұл бастапқы теңдеумен тең. Теңдеудің түбірлерін у1, у2 –ні Виет теоремасы арқылы табамыз.
Соңында х1 = у1/а , х1 = у2/а -ны аламыз. Бұл жағдайда а коэффициентін бос мүшеге көбейтеді. Сондықтан да бұл әдісті «асыра лақтыру» әдісі деп атайды . Бұл әдісті көбінесе Виет теоремасын пайдаланып түбірді оңай табуда және дискриминант дәл квадрат болғанда қолданады.
мысалы, 2х2 – 11х + 15 = 0 теңдеуін шешейік.
Шешуі: 2 коэффициенті теңдеудің бос мүшесіне асыра лақтырамыз, нәтижесінде:
у2 – 11у + 30 = 0.
Виет теоремасы бойынша
![]()
![]()
![]()
![]() у1 = 5 х1
= 5/2 x1
= 2,5
у1 = 5 х1
= 5/2 x1
= 2,5
![]() у2 = 6 x2 = 6/2 x2 = 3.
у2 = 6 x2 = 6/2 x2 = 3.
Жауабы: 2,5; 3.
6-әдіс. Квадрат теңдеулердің коэффициенттерінің қасиеттерін қолдану.
ах2 + bх + с = 0, , а ≠ 0 квадрат теңдеуі берілген.
1) Егер, а+ b + с = 0 (яғни коэффициенттер қосындысы 0-ге тең) болса, онда х1 = 1,
х2 = с/а.
Дәлелдеу: а ≠ 0, келесідей квадрат теңдеуге келеміз.
x2 + b/a • x + c/a = 0.
![]() Виет
теоремасы арқылы
Виет
теоремасы арқылы
x1 + x2 = - b/a,
x1x2 = 1• c/a.
![]() а
– b + с = 0 шарты бойынша, b = а + с аламыз. Олай
болса,
а
– b + с = 0 шарты бойынша, b = а + с аламыз. Олай
болса,
x1 + x2 = - а + b/a= -1 – c/a,
x1x2 = - 1• ( - c/a),
х1 = -1 , х2 = c/a болатынын дәлелдндік.
-
Мысал: 345х2 – 137х – 208 = 0 теңдеуін шешейік.
Шешуі. а + b + с = 0 (345 – 137 – 208 = 0),
онда
х1 = 1, х2 = c/a = -208/345.
Жауабы: 1; -208/345.
2) 132х2 – 247х + 115 = 0 теңдеуін шешейік.
Шешуі. а + b + с = 0 (132 – 247 + 115 = 0),
онда
х1 = 1, х2 = c/a = 115/132.
Жауабы: 1; 115/132.
7-әдіс Квадрат теңдеуді шешудің графиктік
түрі
![]() теңдеуінен екінші, үшінші мүшелерін оң жағына
шығарсақ,
теңдеуінен екінші, үшінші мүшелерін оң жағына
шығарсақ, ![]() аламыз.
аламыз.
![]() функциялардыңграфиктерін
тұрғызамыз.
функциялардыңграфиктерін
тұрғызамыз.
Б ірінші функцияның
графигі – координат басынан өтетін парабола, екінші функцияның
графигі – түзу (1-сурет). Енді келесі жағдайлар болуы
мүмкін:
ірінші функцияның
графигі – координат басынан өтетін парабола, екінші функцияның
графигі – түзу (1-сурет). Енді келесі жағдайлар болуы
мүмкін:
-түзу және парабола екі нүктеде
қиылысуы мүмкін, қиылысу нүктесінің абциссасы квадрат теңдеудің
түбірі болады.
- түзу және парабола жанасуы
мүмкін (бір ғана ортақ нүктеде), яғни теңдеудің бір ғана шешімі
болады.
-парабола және түзудің ортақ
нүктелері жоқ, яғни теңдеудің түбірі жоқ.
Мысал:
1)![]()
![]() теңдеуін графиктік тәсілмен
шешеміз.
теңдеуін графиктік тәсілмен
шешеміз.
Шешуі: ![]() түрінде жазамыз.
түрінде жазамыз. ![]() параболасын және
параболасын және ![]() түзуін тұрғызайық.
түзуін тұрғызайық. ![]() түзуін мына М(0,6) және N(3,9) нүктелері
арқылы тұрғызуға болады. Түзу және парабола А,В нүктелері
абсциссалары
түзуін мына М(0,6) және N(3,9) нүктелері
арқылы тұрғызуға болады. Түзу және парабола А,В нүктелері
абсциссалары ![]() -пен қиылысады.
-пен қиылысады.
Жауабы:![]()


2)![]() теңдеуін графиктік тәсілмен
шешеміз
теңдеуін графиктік тәсілмен
шешеміз
Шешуі:![]() түрінде жазамыз. y=х2 параболасын және у=-2х-1 түзуін тұрғызайық.
у=-2х-1 түзуін М(0;-1) және N(
түрінде жазамыз. y=х2 параболасын және у=-2х-1 түзуін тұрғызайық.
у=-2х-1 түзуін М(0;-1) және N(![]() ) нүктелері арқылы жүргіземіз. Парабола мен
түзу А нүктесінде қиылысады, абциссасы х=-1 тең.
) нүктелері арқылы жүргіземіз. Парабола мен
түзу А нүктесінде қиылысады, абциссасы х=-1 тең.
Жауабы:х=-1
8-әдіс. Квадрат теңдеуді
циркуль және сызғыш көмегімен шешу.  ах2 +вх+с=0 квадраттық теңдеуін циркуль және сызғыш көмегімен
шешу әдісін ұсынамыз (5-сурет). Ізделінді шеңбер абцисса өсінде
В(х1 ;0) және Д (х2;0) нүктелерінде қиылыссын
делік. Мұндағы х1, х2 -
ах2 + вх + с=0 теңдеуінің түбірлері және ординат осінен А(0;1)
және С(0; а с ) нүктелері арқылы өтеді делік. Олай болса, қима
туралы теорема бойынша мынаны аламыз: OB • OD = OA • OC,
келесі OC = OB •
OD/ OA=
х1х2/
1 = c/a.
ах2 +вх+с=0 квадраттық теңдеуін циркуль және сызғыш көмегімен
шешу әдісін ұсынамыз (5-сурет). Ізделінді шеңбер абцисса өсінде
В(х1 ;0) және Д (х2;0) нүктелерінде қиылыссын
делік. Мұндағы х1, х2 -
ах2 + вх + с=0 теңдеуінің түбірлері және ординат осінен А(0;1)
және С(0; а с ) нүктелері арқылы өтеді делік. Олай болса, қима
туралы теорема бойынша мынаны аламыз: OB • OD = OA • OC,
келесі OC = OB •
OD/ OA=
х1х2/
1 = c/a.
Шеңбер центрі АС және ВД хорда ортасында орналасқан перпендикуляр SF пен SК-ның қиылысу нүктелері болып табылады, сондықтан SК= а а в в х х 2 2 2 1 2 ; SF = а а с а с у у 2 2 1 2 1 2 Сонымен, 1) S а а с а в 2 , 2 (шеңбер центрі) және А (0;1) нүктелерін тұрғызамыз; 2) SА радиусты шеңбер жүргіземіз; 3) Осы шеңбердің Ох осі арқылы өтетін қиылысу нүктелері бастапқы квадрат теңдеудің түбірі болады. Сонымен үш түрлі жағд

шағым қалдыра аласыз















