
1-2 Қысқа мерзімді жоспар
|
Ұзақ мерзімді жоспар бөлімі: 8.4А Квадрат теңсіздіктер |
Мектеп: №26 Жамбыл атындағы мектеп-гимназиясы |
|||
|
Күні: |
Мұғалімнің аты-жөні: |
|||
|
Сынып: 8 |
Қатысқандар саны: |
Қатыспағандар саны: |
||
|
Сабақ тақырыбы |
Квадрат теңсіздіктерді шешу |
|||
|
Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасына сілтеме) |
8.2.2.8 квадрат теңсіздіктерді шешеді |
|||
|
Сабақ мақсаттары |
Оқушы:
|
|||
|
Бағалау критерийлері |
Оқушы:
|
|||
|
Тілдік мақсаттар |
Пәнге тән лексика мен терминология: - сан осі - сан осіндегі нүктенің координатасы - теңсіздік - inequality теңсіздіктердің қасиеті квадрат үшмүшені көбейткіштерге жіктеу қысқаша көбейту формулалары - квадрат үшмүше; - квадрат үшмүшенің түбірі; - квадрат теңдеу; - квадрат теңсіздік; - екінші дәрежелі теңдеу; - екінші дәрежелі теңсіздік; - толық және толымсыз квадрат теңдеулер; - келтірілген квадрат теңдеу; - бірінші немесе басты коэффициент, екінші коэффициент немесе х-тің коэффициенті, бос мүше; - дискриминант; - екімүшенің квадратын бөліп алу; Диалог пен жазу үшін пайдалы сөздер мен тіркестер: - теңдеудің сол жақ бөлігін екімүшенің квадраты түріне келтірейік; -... квадрат теңдеудің дискриминанты деп аталады; - берілген квадрат теңдеудің... (түбірлер саны) түбірі бар, өйткені ... квадрат теңдеу - квадратное уравнение - quadratic equation квадрат теңсіздік - квадратное неравенство - quadratic inequality теңдеудің түбірі - корень уравнения - root of equation коэффициент - коэффициент - coefficient |
|||
|
Құндылықтарды дарыту
|
Сабақтарда терминдерді дұрыс қолдана білу арқылы математикалық сауаттылықты дамыту, орындалатын жаттығуларды сөзбе-сөз айтылымдау. Жұппен жұмыста және өзара бағалау әрекеті арқылы жүргізілген ынтымақтастық. |
|||
|
Негізгі дағдылары |
АКТ қолдану дағдылары: Интерактивті тақта мүмкіндіктерін қолдану, интернет ресурстар Ойлау дағдылары: Практикалық жұмыс орындай отыра ойлау қабілеттерін дамыту. |
|||
|
Пәнаралық байланыстар |
Физика, информатика |
|||
|
Бастапқы білім
|
Квадрат түбір және арифметикалық квадрат түбір анықтамаларын білу, квадрат түбірлерді таба алу, иррационал өрнектердің мәнін есептеу, бүтін және иррационал өрнектерді ықшамдау дағдылары. |
|||
|
Сабақ барысы |
||||
|
Сабақтың жоспарланған кезеңдері |
Сабақтағы жоспарланған іс-әрекет |
Ресурстар |
||
|
Сабақтың басы 1-5 мин |
Мұғалім оқушылармен сәлімдесіп, олардың сабаққа дайындығын тексереді. Мұғалім сабақтың тақырыбы мен оқу мақсаттарын оқушылармен бірге талқылайды. Бағалау критерийлерін оқушылар өздері құрастырады, мұғалім қажет жағдайда толықтырады |
|
||
|
Сабақтың ортасы 6-20 мин 21-35 мин |
мұнда
Бір айнымалысы бар екінші дәрежелі (квадрат) теңсіздікті шешу алгоритмі 1. Теңсіздікті ax2+bx+c>0 (ax2+bx+c<0) түріне келтіру 2. y=ax2+bx+c функциясын қарастырамыз 3. Парабола тармақтарының бағытын анықтау 4. Параболаның ох осін қиятын нүктелерін анықтау (ax2+bx+c=0 теңдеуін шешіп; х1 және х2 табамыз 5. y=ax2+bx+c схемалық графигін саламыз 6. y>0 (y<0) болатындай параболаның бөлігін көрсетеміз 7. Абсцисса осінен y>0 (y<0) болатындай х-тің мәнін көрсетеміз Есеп №1.
1.5х2+9х-2<0 2.y=5х2+9х-2 функциясын қарастырамыз 3. Тармағы жоғары бағытталған парабола.
4
х1=-2; х2=
Квадрат теңсіздікті шешу
барысында сәйкес Үш жағдай болуы мүмкін: 1) D=0, квадрат теңдеудің тек бір түбірі бар; 2) D>0 квадрат теңдеудің екі түбірі бар; 3) D<0 квадрат теңдеудің түбірлері жоқ.
Алынған түбірлерге
және
Егер
Егер Егер квадрат теңсіздік қатаң емес болса, онда түбірлер сандық аралыққа енеді, ал егер – қатаң болса, онда енбейді. Бірінші әдіс Квадрат теңсіздікті осылай шешу әдісі графиктік деп аталады.
Мысал. х²-4х+7≤0 теңсіздігін шешіңіз. Шешуі. Есепті графиктік тәсілмен шешейік. Бір оқушы тақтада х²-4х+7≤0 теңсіздігін талдап шешеді.
1) у=
х²-4х+7
Бұл функцияның графигі -
төбесінің координатасы
х-тің кез келген
мәнінде
2-ші тәсіл: х²-4х+7=0 D=
16-28=-12<0. Түбірі жоқ. Өйткені есептің шарты
бойынша у = х2 – х – 6 функциясын қарастырайық. Оқушыларға нұсқау айта отырып, өздіктерінен орындауға мүмкіндік беру: Теңсіздікті шеш. №2. х2 – х – 6 > 0 Ж №3. х Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз 1-2 Қысқа мерзімді
жоспар
Ұзақ мерзімді жоспар
бөлімі: 8.4А Квадрат
теңсіздіктер
Мектеп: №26 Жамбыл атындағы
мектеп-гимназиясы
Күні:
Мұғалімнің
аты-жөні:
Сынып:
8
Қатысқандар
саны:
Қатыспағандар
саны:
Сабақ
тақырыбы Квадрат теңсіздіктерді шешу Осы сабақта қол жеткізілетін оқу мақсаттары (оқу
бағдарламасына сілтеме)
8.2.2.8 квадрат
теңсіздіктерді шешеді
Сабақ мақсаттары Оқушы: Квадрат теңсіздікті графиктік тәсілмен шешу дағдысын
үйренеді және есептерді
шешеді
Бағалау критерийлері Оқушы: -квадрат
теңсіздік ұғымын біледі -шешу
тәсілдерін біледі және есептер шығаруда
қолданады
Тілдік
мақсаттар
Пәнге тән лексика мен
терминология:
- сан
осі
- сан осіндегі
нүктенің координатасы
- теңсіздік
- inequality
теңсіздіктердің
қасиеті
квадрат
үшмүшені көбейткіштерге жіктеу
қысқаша көбейту
формулалары
- квадрат
үшмүше;
- квадрат үшмүшенің
түбірі;
- квадрат
теңдеу;
- квадрат
теңсіздік;
- екінші дәрежелі
теңдеу;
- екінші дәрежелі
теңсіздік;
- толық және толымсыз квадрат
теңдеулер;
- келтірілген квадрат
теңдеу;
- бірінші немесе басты
коэффициент, екінші коэффициент немесе
х-тің коэффициенті, бос
мүше;
-
дискриминант;
- екімүшенің квадратын бөліп
алу;
Диалог пен жазу үшін
пайдалы сөздер мен
тіркестер:
- теңдеудің сол жақ бөлігін
екімүшенің квадраты түріне
келтірейік;
-... квадрат теңдеудің
дискриминанты деп аталады;
- берілген квадрат
теңдеудің... (түбірлер саны) түбірі бар, өйткені
...
квадрат теңдеу - квадратное
уравнение - quadratic
equation
квадрат теңсіздік - квадратное
неравенство - quadratic inequality
теңдеудің түбірі - корень уравнения
- root of
equation
коэффициент - коэффициент
- coefficient
Құндылықтарды
дарыту
Сабақтарда терминдерді дұрыс
қолдана білу арқылы математикалық сауаттылықты дамыту, орындалатын
жаттығуларды сөзбе-сөз айтылымдау.
Жұппен жұмыста және өзара
бағалау әрекеті арқылы жүргізілген
ынтымақтастық.
Негізгі дағдылары
АКТ
қолдану дағдылары: Интерактивті тақта
мүмкіндіктерін қолдану, интернет
ресурстар
Ойлау
дағдылары: Практикалық жұмыс
орындай отыра ойлау қабілеттерін дамыту.
Пәнаралық
байланыстар
Физика,
информатика
Бастапқы
білім
Квадрат түбір және
арифметикалық квадрат түбір анықтамаларын білу, квадрат түбірлерді
таба алу, иррационал өрнектердің мәнін есептеу, бүтін және
иррационал өрнектерді ықшамдау
дағдылары.
Сабақ барысы Сабақтың жоспарланған
кезеңдері Сабақтағы жоспарланған
іс-әрекет Ресурстар Сабақтың басы 1-5
мин Ұйымдастыру кезеңі.
Сабақ мақсатын қою.
Мұғалім оқушылармен сәлімдесіп, олардың
сабаққа дайындығын тексереді. Мұғалім сабақтың тақырыбы мен оқу
мақсаттарын оқушылармен бірге талқылайды. Бағалау критерийлерін
оқушылар өздері құрастырады, мұғалім қажет жағдайда
толықтырады
Сабақтың
ортасы 6-20
мин 21-35
мин
мұнда
Бір айнымалысы бар екінші
дәрежелі (квадрат)
теңсіздікті шешу
алгоритмі
1.
Теңсіздікті ax2+bx+c>0
(ax2+bx+c<0) түріне
келтіру
2.
y=ax2+bx+c функциясын
қарастырамыз
3. Парабола тармақтарының
бағытын анықтау
4. Параболаның ох осін қиятын
нүктелерін анықтау (ax2+bx+c=0 теңдеуін шешіп;
х1 және
х2 табамыз
5.
y=ax2+bx+c схемалық графигін
саламыз
6. y>0 (y<0) болатындай
параболаның бөлігін көрсетеміз
7. Абсцисса осінен y>0
(y<0) болатындай х-тің мәнін
көрсетеміз
Есеп
№1.
1.5х2+9х-2<0
2.y=5х2+9х-2 функциясын
қарастырамыз
3.
Тармағы жоғары бағытталған парабола.
4
х1=-2; х2=
Квадрат теңсіздікті шешу
барысында сәйкес
Үш жағдай болуы
мүмкін:
1) D=0, квадрат теңдеудің тек бір
түбірі бар;
2) D>0 квадрат теңдеудің екі
түбірі бар;
3) D<0 квадрат теңдеудің
түбірлері жоқ.
Алынған түбірлерге
және
Егер
Егер
Егер квадрат теңсіздік қатаң
емес болса, онда түбірлер сандық аралыққа енеді, ал егер – қатаң
болса, онда енбейді.
Бірінші
әдіс
Квадрат теңсіздікті осылай
шешу әдісі графиктік деп
аталады.
Мысал. х²-4х+7≤0 теңсіздігін
шешіңіз.
Шешуі. Есепті графиктік
тәсілмен шешейік.
Бір оқушы тақтада х²-4х+7≤0
теңсіздігін талдап шешеді.
1) у=
х²-4х+7
Бұл функцияның графигі -
төбесінің координатасы
х-тің кез келген
мәнінде
2-ші тәсіл: х²-4х+7=0 D=
16-28=-12<0. Түбірі жоқ. Өйткені есептің шарты
бойынша у =
х2
– х –
6 функциясын
қарастырайық. Оқушыларға нұсқау айта
отырып, өздіктерінен орындауға мүмкіндік
беру: Теңсіздікті
шеш. №2. х2
– х – 6 >
0 Ж №3. х | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||








 . 5х2+9х-2=0
. 5х2+9х-2=0



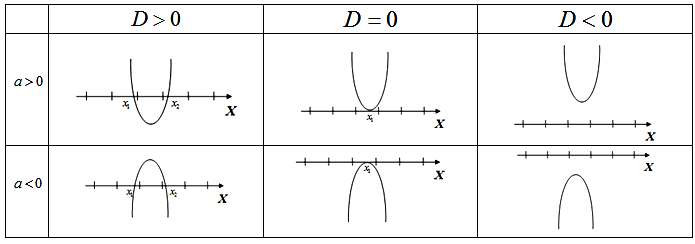







 ауабы:
ауабы:













