
ЛАПЛАС ТҮРЛЕНДІРУІ АРҚЫЛЫ КОЭФФИЦИЕНТТЕРІ ТҰРАҚТЫ СЫЗЫҚТЫ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕРДІ ШЕШУ
Молшылықова А.Ө., «Математика мұғалімдерін даярлау» мамандығының 4 курс студенті, М.Х.Дулати атындағы Тараз университеті «Жаратылыстану ғылымдары» факультеті Тараз қ., molshylykovaaaaa@mail.ru
Чанбаева А.И., М.Х.Дулати атындағы Тараз университеті, PhD доктор, Тараз қ., ai.chanbayeva@dulaty.kz
Аннотация: Бұл мақалада Лаплас түрлендіруі әдісі арқылы коэффициенттері тұрақты сызықты дифференциалдық теңдеулерді шешу тәсілдері қарастырылады. Лаплас түрлендіруі — дифференциалдық теңдеулерді алгебралық теңдеулерге түрлендіріп, оларды шешуді жеңілдететін тиімді аналитикалық әдіс. Мақалада алдымен Лаплас түрлендіруінің негізгі теориялық негіздері мен қасиеттері сипатталып, одан кейін оның көмегімен бірінші және екінші ретті сызықты дифференциалдық теңдеулерді шешу мысалдары келтіріледі. Сондай-ақ бастапқы шарттарды ескере отырып есептер шығару жолдары түсіндіріледі.
Кілт сөздер: Лаплас түрлендіруі, дифференциалдық теңдеу, тұрақты коэффициент, сызықты теңдеу, аналитикалық әдіс, бастапқы шарттар, математикалық модельдеу.
Лаплас түрлендіруі арқылы коэффициенттері тұрақты сызықты дифференциалдық теңдеулерді шешу
n-ші ретті тұрақты коэффициенттері бар сызықты дифференциалдық теңдеуді қарастырайық:

Бұл теңдеудің  болғандағы
шешімін табу керек.
болғандағы
шешімін табу керек.
Айталық,  функциясы мен
оның барлық туындыларын n – мен қоса алғанда
функциясы мен
оның барлық туындыларын n – мен қоса алғанда  ,
сондай‑ақ,
,
сондай‑ақ,  –түпнұсқа болып табылады.
–түпнұсқа болып табылады.
 – түпнұсқалар.
– түпнұсқалар.
Дифференциалдық теңдеуге
оның шешімін  шешімімен
алмастыра отырып, тепе‑теңдікті аламыз. Осы тепе‑теңдіктің кескінін
табамыз, яғни тепе‑теңдіктің оң және сол бөлігінің кескінін
табамыз.
шешімімен
алмастыра отырып, тепе‑теңдікті аламыз. Осы тепе‑теңдіктің кескінін
табамыз, яғни тепе‑теңдіктің оң және сол бөлігінің кескінін
табамыз.
Теорема бойынша, егер түпнұсқалар бірдей тең болса, онда олардың кескіндері де тең болады (бұл кескіннің анықтамасынан тікелей шығады). Демек, сәйкестіктің сол жағындағы кескін оның оң жағындағы кескінге тең болады.
Осы дифференциалдық теңдеудің кескініне көшейік, яғни оның оң және сол бөлігінің кескінін табайық:

Сызықтық қасиеті бойынша түпнұсқалардың сызықты комбинациясының кескіні осы түпнұсқалардың бірдей сызықтық кескін комбинациясына тең. Сондықтан төмендегі теңдікті аламыз:

Дифференциалдық теңдеудің
шешімінің кескінін  арқылы
белгілеп, яғни
арқылы
белгілеп, яғни  ,
немесе
,
немесе
![]()
 функциясының
кескіні, яғни, дифференциалдық теңдеудің оң жағын
функциясының
кескіні, яғни, дифференциалдық теңдеудің оң жағын  арқылы
белгілейміз:
арқылы
белгілейміз:
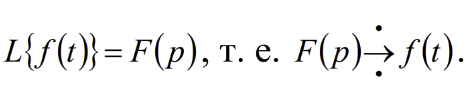
Коши есебінің шешімін табайық, яғни берілген бастапқы шарттарды қанағаттандыратын осы дифференциалдық теңдеудің нақты шешімін іздейміз:

мұндағы  ‑
сандар.
‑
сандар.
Алдымен нөлдік бастапқы
шарттардың жағдайын қарастырайық, яғни,  .
.
Сонда
 x(t) яғни
x(t) яғни 
 яғни
яғни

 яғни
яғни

………………. …………………...
 яғни
яғни

Бұдан төмендегідей теңдікті аламыз:

немесе

 деп
белгілейміз.
деп
белгілейміз.
Сонда, мына теңдікті
аламыз: 
Осы жерден нөлдік бастапқы
шарттармен  , яғни, нөлдік бастапқы шарттарды
қанағаттандыратын дифференциалдық теңдеудің шешімінің кескінін
таптық.
, яғни, нөлдік бастапқы шарттарды
қанағаттандыратын дифференциалдық теңдеудің шешімінің кескінін
таптық.
Кескіннен түпнұсқаға ауыса отырып, төмендегі шешімді аламыз:

Енді бастапқы шарттар нөлге
тең болмасын (яғни жалпы жағдайды қарастырайық). Дифференциалдық
теңдеудің коэффициенттерін  функциясы мен
оның туындыларының кескіндеріне көбейтейік:
функциясы мен
оның туындыларының кескіндеріне көбейтейік:
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
…………………………………………………………………………..
 ,
,
 ,
,
 ,
,
 .
.
Алынған өрнектерді (3.1.3) теңдеуіне ауыстырайық,
Белгілеу енгізейік :


Нөлдік бастапқы
шарттарда  екенін ескереміз.
екенін ескереміз.
Сонда енгізілген белгілерді ескере отырып, төмендегі теңдікті аламыз:

Алынған теңдеу берілген дифференциалдық теңдеу үшін көмекші теңдеу деп аталады (немесе бейнедегі теңдеу).
Бұл теңдеу кескіннің теңдеуі деп те аталады. Осылайша, кескінге ауыса отырып, дифференциалдық теңдеудің орнына қарапайым алгебралық теңдеуді аламыз. Оны шешкен кезде іздеген шешімнің кескінін табамыз.

Бұдан

Алынған формула кескіндердегі теңдеудің операторлық шешімі деп аталады. Кескін бойынша оған сәйкес түпнұсқаны тауып, керек шешімді аламыз:
![]()
Сол сияқты тұрақты коэффициенттері бар сызықтық дифференциалдық теңдеулер жүйесі де шешіледі. Бұл жағдайда кескіндерге өтіп, алгебралық теңдеулер жүйесін аламыз. Осындай алгебралық жүйені шеше отырып, дифференциалдық теңдеулер жүйесінің шешімдерінің кескінін табамыз, содан кейін түпнұсқаларға және осы шешімдерге көшеміз.
Мысал – 1.1.1
 теңдеуімен берілген
теңдеуімен берілген  ;
;
 ;
;
 бастапқы
шарттарын қанағаттандыратын дифференциалдық теңдеудің нақты шешімін
табу керек.
бастапқы
шарттарын қанағаттандыратын дифференциалдық теңдеудің нақты шешімін
табу керек.
Кескінді теңдеуге көшірейік

 яғни,
яғни,
 кескіннің
сызықтылығы нәтижесінде
кескіннің
сызықтылығы нәтижесінде  кез-келген
түпнұсқа
кез-келген
түпнұсқа  үшін және оның кескіндері
үшін және оның кескіндері  немесе кескін
анықтамасынан
немесе кескін
анықтамасынан  табамыз.
табамыз.
Бұдан

Мұндағы
 – сипаттамалық
көпмүше.
– сипаттамалық
көпмүше.

 - көмекші
теңдеу.
- көмекші
теңдеу.
 ,
,
 яғни,
яғни,

Бөлшектің бөлімінің комплекс түбірлері бар болғандықтан, толық квадратын бөліп аламыз.
 .
.
Осылайшы, есептің жауабы:  .
.
Шешімнің кескінін және осы кескінге сәйкес келетін түпнұсқаны таптық. Бұл түпнұсқа және ізделетін шешім болады.
Мысал – 1.1.2
 теңдеуімен берілген
теңдеуімен берілген  ;
;
 бастапқы
шарттарын қанағаттандыратын дифференциалдық теңдеуін, яғни, Коши
есебін туындының бастапқы шарттарымен шешімін табайық.
бастапқы
шарттарын қанағаттандыратын дифференциалдық теңдеуін, яғни, Коши
есебін туындының бастапқы шарттарымен шешімін табайық.
Кескіннің теңдеуіне көшейік,


 .
.

 .
.


Сонымен, Коши есебінің шешімі табылды:

 және
және
 шамаларын
белгілеу енгізу арқылы
шамаларын
белгілеу енгізу арқылы  ,
,
 түрде
бастапқы дифференциалдық теңдеудің жалпы шешімін алуға
болады.
түрде
бастапқы дифференциалдық теңдеудің жалпы шешімін алуға
болады.
Жауабы:  .
.
Мысал – 1.1.3
 теңдеуімен берілген
теңдеуімен берілген  шарттарымен
берілген дифференциалдық теңдеуін шешейік,
шарттарымен
берілген дифференциалдық теңдеуін шешейік,
Дифференциалдық теңдеуді шешу үшін кескінге көшейік,

немесе, 
Рационал бөлшекті қарапайым бөлшектерге бөліп жазамыз,


 деп
алып,
деп
алып,  деген мәнді аламыз, яғни,
деген мәнді аламыз, яғни,  ;
;
 болғанда,
болғанда,  деген мәнді
аламыз, яғни,
деген мәнді
аламыз, яғни,  тең
болады.
тең
болады.  болғандағы коэффиценттерін салыстыра отырып, мына
мәнді аламыз
болғандағы коэффиценттерін салыстыра отырып, мына
мәнді аламыз  яғни,
яғни, тең
болады.
тең
болады.

Бұдан төмендегідей жауап шығады:

Мысал‑1.1.4
 берілген
теңдеуді
берілген
теңдеуді  бастапқы шарттарын қанағаттандыратын
дифференциалдық теңдеуін шешу керек.
бастапқы шарттарын қанағаттандыратын
дифференциалдық теңдеуін шешу керек.
Шешуі:Бірінші қадамда
түпнұсқадан тиісті кескінге көшейік. Біз түпнұсқалар мен кескіннің
кестесінің сол жағын қолданамыз. Алдымен бастапқы теңдеудің сол
жағын түрлендіреміз. Лапласты түрлендіруі үшін функцияның сызықты
болуы шарт, сондықтан біз барлық тұрақтыларды елемейміз және
 функциямен және оның туындыларымен бөлек жұмыс
жасаймыз.
функциямен және оның туындыларымен бөлек жұмыс
жасаймыз.
Кестедегі  мәнге сәйкес
функцияны
мәнге сәйкес
функцияны  түрлендіреміз. Кестедегі
түрлендіреміз. Кестедегі  мәнге сәйкес
түрлендіру
мәнге сәйкес
түрлендіру  жасаймыз. Бастапқы шарттарды ескере
отырып,
жасаймыз. Бастапқы шарттарды ескере
отырып,  туындыны түрлендіреміз:
туындыны түрлендіреміз:
 . Кестедегі 3 –
мәнге сәйкес
. Кестедегі 3 –
мәнге сәйкес
 , бастапқы
шарттарды
, бастапқы
шарттарды 
ескере отырып, екінші туындыны түрлендіреміз:

Енді теңдеудің оң жағындағы
көпмүшелікпен  жұмыс жасаймыз.
Лаплас түрлендіруінің сызықтылығы ережесіне байланысты біз әр
қосылғышпен бөлек жұмыс жасаймыз. Бірінші қосылғышты қарастырайық:
бұл тұрақтыға көбейтілген тәуелсіз
жұмыс жасаймыз.
Лаплас түрлендіруінің сызықтылығы ережесіне байланысты біз әр
қосылғышпен бөлек жұмыс жасаймыз. Бірінші қосылғышты қарастырайық:
бұл тұрақтыға көбейтілген тәуелсіз  айнымалысы. Біз
тұрақтыны елемейміз және кестедегі 4 – мәнін қолдана отырып,
түрлендіруді орындаймыз:
айнымалысы. Біз
тұрақтыны елемейміз және кестедегі 4 – мәнін қолдана отырып,
түрлендіруді орындаймыз:

Екінші қосылғышты
қарастырайық: -5. Бір ғана тұрақтыны келесідей жазуға болады
 ,
түсінікті болу үшін осы түрлендіруді бірлікке
қолданамыз:
,
түсінікті болу үшін осы түрлендіруді бірлікке
қолданамыз:

Осылайша, кестенің көмегімен дифференциалдық теңдеудің
 барлық
элементтері (түпнұсқалары) үшін сәйкес кескіндер
табылды:
барлық
элементтері (түпнұсқалары) үшін сәйкес кескіндер
табылды:





Табылған кескіндерді
берілген теңдеуге  апарып
қоямыз,
апарып
қоямыз, 
Әрі қарай операторлық
шешімді  арқылы, атап айтқанда бір бөлшек арқылы жазамыз.
Бұл жағдайда келесі әрекеттерді жасаймыз:
арқылы, атап айтқанда бір бөлшек арқылы жазамыз.
Бұл жағдайда келесі әрекеттерді жасаймыз:
Ең алдымен теңдіктің сол жағын ашамыз:

Сол жақ бөліктегі ұқсас мүшелерді біріктіреміз. Бұл жағдайда –2 мен
–3 сандарын қосамыз.

 айнымалысы бар мүшелерді сол жақта қалдырамыз,
қалған мүшелерді таңбасын өзгертіп, оң жаққа өткіземіз:
айнымалысы бар мүшелерді сол жақта қалдырамыз,
қалған мүшелерді таңбасын өзгертіп, оң жаққа өткіземіз:

Сол жақ бөлікте
 операторлық шешімді жақша сыртына шығарамыз, ал
оң жақ бөлікте өрнекті ортақ бөлімге келтіреміз:
операторлық шешімді жақша сыртына шығарамыз, ал
оң жақ бөлікте өрнекті ортақ бөлімге келтіреміз:

Сол жақтағы көпмүшені көбейткіштерге жіктеу керек. Квадрат теңдеуді шешеміз.





Осылайша,


теңдіктің оң жағына бөлу ретінде өткіземіз,

Мақсат орындалды
– операторлық шешім бір ғана бөлшек түрінде
өрнектелді.
операторлық шешім бір ғана бөлшек түрінде
өрнектелді.
Екінші әрекет. Белгісіз коэффициенттер әдісін қолданып, теңдеудің операторлық шешімін қарапайым бөлшектердің қосындысы түрінде жіктеу қажет.



Сәйкес дәрежелердің алдындағы коэффициенттерді теңестіріп, шыққан теңдеулер жүйесін шешеміз:

Сонымен,  коэффициенттер
табылды және операторлық шешім бөлшектерге жіктелген түрде
алынды.
коэффициенттер
табылды және операторлық шешім бөлшектерге жіктелген түрде
алынды.

Есептің соңғы кезеңі — Лаплас түрлендіруінің кері түрін қолданып, кескіннен бастапқы функцияларға (түпнұсқаларға) өту. Ол үшін түпнұсқалар мен кескіндер кестесінің оң жақ бағанын пайдаланамыз.
Кескінге сәйкес бастапқы функцияларға (түпнұсқаға) өтейік.




Берілген теңдеу

Шыққан теңдеуіміз

Жауабы: дербес шешім

жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
ЛАПЛАС ТҮРЛЕНДІРУІ АРҚЫЛЫ КОЭФФИЦИЕНТТЕРІ ТҰРАҚТЫ СЫЗЫҚТЫ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕРДІ ШЕШУ
ЛАПЛАС ТҮРЛЕНДІРУІ АРҚЫЛЫ КОЭФФИЦИЕНТТЕРІ ТҰРАҚТЫ СЫЗЫҚТЫ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕРДІ ШЕШУ
ЛАПЛАС ТҮРЛЕНДІРУІ АРҚЫЛЫ КОЭФФИЦИЕНТТЕРІ ТҰРАҚТЫ СЫЗЫҚТЫ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕРДІ ШЕШУ
Молшылықова А.Ө., «Математика мұғалімдерін даярлау» мамандығының 4 курс студенті, М.Х.Дулати атындағы Тараз университеті «Жаратылыстану ғылымдары» факультеті Тараз қ., molshylykovaaaaa@mail.ru
Чанбаева А.И., М.Х.Дулати атындағы Тараз университеті, PhD доктор, Тараз қ., ai.chanbayeva@dulaty.kz
Аннотация: Бұл мақалада Лаплас түрлендіруі әдісі арқылы коэффициенттері тұрақты сызықты дифференциалдық теңдеулерді шешу тәсілдері қарастырылады. Лаплас түрлендіруі — дифференциалдық теңдеулерді алгебралық теңдеулерге түрлендіріп, оларды шешуді жеңілдететін тиімді аналитикалық әдіс. Мақалада алдымен Лаплас түрлендіруінің негізгі теориялық негіздері мен қасиеттері сипатталып, одан кейін оның көмегімен бірінші және екінші ретті сызықты дифференциалдық теңдеулерді шешу мысалдары келтіріледі. Сондай-ақ бастапқы шарттарды ескере отырып есептер шығару жолдары түсіндіріледі.
Кілт сөздер: Лаплас түрлендіруі, дифференциалдық теңдеу, тұрақты коэффициент, сызықты теңдеу, аналитикалық әдіс, бастапқы шарттар, математикалық модельдеу.
Лаплас түрлендіруі арқылы коэффициенттері тұрақты сызықты дифференциалдық теңдеулерді шешу
n-ші ретті тұрақты коэффициенттері бар сызықты дифференциалдық теңдеуді қарастырайық:

Бұл теңдеудің  болғандағы
шешімін табу керек.
болғандағы
шешімін табу керек.
Айталық,  функциясы мен
оның барлық туындыларын n – мен қоса алғанда
функциясы мен
оның барлық туындыларын n – мен қоса алғанда  ,
сондай‑ақ,
,
сондай‑ақ,  –түпнұсқа болып табылады.
–түпнұсқа болып табылады.
 – түпнұсқалар.
– түпнұсқалар.
Дифференциалдық теңдеуге
оның шешімін  шешімімен
алмастыра отырып, тепе‑теңдікті аламыз. Осы тепе‑теңдіктің кескінін
табамыз, яғни тепе‑теңдіктің оң және сол бөлігінің кескінін
табамыз.
шешімімен
алмастыра отырып, тепе‑теңдікті аламыз. Осы тепе‑теңдіктің кескінін
табамыз, яғни тепе‑теңдіктің оң және сол бөлігінің кескінін
табамыз.
Теорема бойынша, егер түпнұсқалар бірдей тең болса, онда олардың кескіндері де тең болады (бұл кескіннің анықтамасынан тікелей шығады). Демек, сәйкестіктің сол жағындағы кескін оның оң жағындағы кескінге тең болады.
Осы дифференциалдық теңдеудің кескініне көшейік, яғни оның оң және сол бөлігінің кескінін табайық:

Сызықтық қасиеті бойынша түпнұсқалардың сызықты комбинациясының кескіні осы түпнұсқалардың бірдей сызықтық кескін комбинациясына тең. Сондықтан төмендегі теңдікті аламыз:

Дифференциалдық теңдеудің
шешімінің кескінін  арқылы
белгілеп, яғни
арқылы
белгілеп, яғни  ,
немесе
,
немесе
![]()
 функциясының
кескіні, яғни, дифференциалдық теңдеудің оң жағын
функциясының
кескіні, яғни, дифференциалдық теңдеудің оң жағын  арқылы
белгілейміз:
арқылы
белгілейміз:
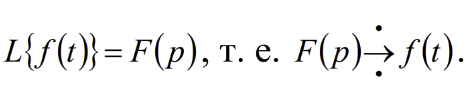
Коши есебінің шешімін табайық, яғни берілген бастапқы шарттарды қанағаттандыратын осы дифференциалдық теңдеудің нақты шешімін іздейміз:

мұндағы  ‑
сандар.
‑
сандар.
Алдымен нөлдік бастапқы
шарттардың жағдайын қарастырайық, яғни,  .
.
Сонда
 x(t) яғни
x(t) яғни 
 яғни
яғни

 яғни
яғни

………………. …………………...
 яғни
яғни

Бұдан төмендегідей теңдікті аламыз:

немесе

 деп
белгілейміз.
деп
белгілейміз.
Сонда, мына теңдікті
аламыз: 
Осы жерден нөлдік бастапқы
шарттармен  , яғни, нөлдік бастапқы шарттарды
қанағаттандыратын дифференциалдық теңдеудің шешімінің кескінін
таптық.
, яғни, нөлдік бастапқы шарттарды
қанағаттандыратын дифференциалдық теңдеудің шешімінің кескінін
таптық.
Кескіннен түпнұсқаға ауыса отырып, төмендегі шешімді аламыз:

Енді бастапқы шарттар нөлге
тең болмасын (яғни жалпы жағдайды қарастырайық). Дифференциалдық
теңдеудің коэффициенттерін  функциясы мен
оның туындыларының кескіндеріне көбейтейік:
функциясы мен
оның туындыларының кескіндеріне көбейтейік:
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
…………………………………………………………………………..
 ,
,
 ,
,
 ,
,
 .
.
Алынған өрнектерді (3.1.3) теңдеуіне ауыстырайық,
Белгілеу енгізейік :


Нөлдік бастапқы
шарттарда  екенін ескереміз.
екенін ескереміз.
Сонда енгізілген белгілерді ескере отырып, төмендегі теңдікті аламыз:

Алынған теңдеу берілген дифференциалдық теңдеу үшін көмекші теңдеу деп аталады (немесе бейнедегі теңдеу).
Бұл теңдеу кескіннің теңдеуі деп те аталады. Осылайша, кескінге ауыса отырып, дифференциалдық теңдеудің орнына қарапайым алгебралық теңдеуді аламыз. Оны шешкен кезде іздеген шешімнің кескінін табамыз.

Бұдан

Алынған формула кескіндердегі теңдеудің операторлық шешімі деп аталады. Кескін бойынша оған сәйкес түпнұсқаны тауып, керек шешімді аламыз:
![]()
Сол сияқты тұрақты коэффициенттері бар сызықтық дифференциалдық теңдеулер жүйесі де шешіледі. Бұл жағдайда кескіндерге өтіп, алгебралық теңдеулер жүйесін аламыз. Осындай алгебралық жүйені шеше отырып, дифференциалдық теңдеулер жүйесінің шешімдерінің кескінін табамыз, содан кейін түпнұсқаларға және осы шешімдерге көшеміз.
Мысал – 1.1.1
 теңдеуімен берілген
теңдеуімен берілген  ;
;
 ;
;
 бастапқы
шарттарын қанағаттандыратын дифференциалдық теңдеудің нақты шешімін
табу керек.
бастапқы
шарттарын қанағаттандыратын дифференциалдық теңдеудің нақты шешімін
табу керек.
Кескінді теңдеуге көшірейік

 яғни,
яғни,
 кескіннің
сызықтылығы нәтижесінде
кескіннің
сызықтылығы нәтижесінде  кез-келген
түпнұсқа
кез-келген
түпнұсқа  үшін және оның кескіндері
үшін және оның кескіндері  немесе кескін
анықтамасынан
немесе кескін
анықтамасынан  табамыз.
табамыз.
Бұдан

Мұндағы
 – сипаттамалық
көпмүше.
– сипаттамалық
көпмүше.

 - көмекші
теңдеу.
- көмекші
теңдеу.
 ,
,
 яғни,
яғни,

Бөлшектің бөлімінің комплекс түбірлері бар болғандықтан, толық квадратын бөліп аламыз.
 .
.
Осылайшы, есептің жауабы:  .
.
Шешімнің кескінін және осы кескінге сәйкес келетін түпнұсқаны таптық. Бұл түпнұсқа және ізделетін шешім болады.
Мысал – 1.1.2
 теңдеуімен берілген
теңдеуімен берілген  ;
;
 бастапқы
шарттарын қанағаттандыратын дифференциалдық теңдеуін, яғни, Коши
есебін туындының бастапқы шарттарымен шешімін табайық.
бастапқы
шарттарын қанағаттандыратын дифференциалдық теңдеуін, яғни, Коши
есебін туындының бастапқы шарттарымен шешімін табайық.
Кескіннің теңдеуіне көшейік,


 .
.

 .
.


Сонымен, Коши есебінің шешімі табылды:

 және
және
 шамаларын
белгілеу енгізу арқылы
шамаларын
белгілеу енгізу арқылы  ,
,
 түрде
бастапқы дифференциалдық теңдеудің жалпы шешімін алуға
болады.
түрде
бастапқы дифференциалдық теңдеудің жалпы шешімін алуға
болады.
Жауабы:  .
.
Мысал – 1.1.3
 теңдеуімен берілген
теңдеуімен берілген  шарттарымен
берілген дифференциалдық теңдеуін шешейік,
шарттарымен
берілген дифференциалдық теңдеуін шешейік,
Дифференциалдық теңдеуді шешу үшін кескінге көшейік,

немесе, 
Рационал бөлшекті қарапайым бөлшектерге бөліп жазамыз,


 деп
алып,
деп
алып,  деген мәнді аламыз, яғни,
деген мәнді аламыз, яғни,  ;
;
 болғанда,
болғанда,  деген мәнді
аламыз, яғни,
деген мәнді
аламыз, яғни,  тең
болады.
тең
болады.  болғандағы коэффиценттерін салыстыра отырып, мына
мәнді аламыз
болғандағы коэффиценттерін салыстыра отырып, мына
мәнді аламыз  яғни,
яғни, тең
болады.
тең
болады.

Бұдан төмендегідей жауап шығады:

Мысал‑1.1.4
 берілген
теңдеуді
берілген
теңдеуді  бастапқы шарттарын қанағаттандыратын
дифференциалдық теңдеуін шешу керек.
бастапқы шарттарын қанағаттандыратын
дифференциалдық теңдеуін шешу керек.
Шешуі:Бірінші қадамда
түпнұсқадан тиісті кескінге көшейік. Біз түпнұсқалар мен кескіннің
кестесінің сол жағын қолданамыз. Алдымен бастапқы теңдеудің сол
жағын түрлендіреміз. Лапласты түрлендіруі үшін функцияның сызықты
болуы шарт, сондықтан біз барлық тұрақтыларды елемейміз және
 функциямен және оның туындыларымен бөлек жұмыс
жасаймыз.
функциямен және оның туындыларымен бөлек жұмыс
жасаймыз.
Кестедегі  мәнге сәйкес
функцияны
мәнге сәйкес
функцияны  түрлендіреміз. Кестедегі
түрлендіреміз. Кестедегі  мәнге сәйкес
түрлендіру
мәнге сәйкес
түрлендіру  жасаймыз. Бастапқы шарттарды ескере
отырып,
жасаймыз. Бастапқы шарттарды ескере
отырып,  туындыны түрлендіреміз:
туындыны түрлендіреміз:
 . Кестедегі 3 –
мәнге сәйкес
. Кестедегі 3 –
мәнге сәйкес
 , бастапқы
шарттарды
, бастапқы
шарттарды 
ескере отырып, екінші туындыны түрлендіреміз:

Енді теңдеудің оң жағындағы
көпмүшелікпен  жұмыс жасаймыз.
Лаплас түрлендіруінің сызықтылығы ережесіне байланысты біз әр
қосылғышпен бөлек жұмыс жасаймыз. Бірінші қосылғышты қарастырайық:
бұл тұрақтыға көбейтілген тәуелсіз
жұмыс жасаймыз.
Лаплас түрлендіруінің сызықтылығы ережесіне байланысты біз әр
қосылғышпен бөлек жұмыс жасаймыз. Бірінші қосылғышты қарастырайық:
бұл тұрақтыға көбейтілген тәуелсіз  айнымалысы. Біз
тұрақтыны елемейміз және кестедегі 4 – мәнін қолдана отырып,
түрлендіруді орындаймыз:
айнымалысы. Біз
тұрақтыны елемейміз және кестедегі 4 – мәнін қолдана отырып,
түрлендіруді орындаймыз:

Екінші қосылғышты
қарастырайық: -5. Бір ғана тұрақтыны келесідей жазуға болады
 ,
түсінікті болу үшін осы түрлендіруді бірлікке
қолданамыз:
,
түсінікті болу үшін осы түрлендіруді бірлікке
қолданамыз:

Осылайша, кестенің көмегімен дифференциалдық теңдеудің
 барлық
элементтері (түпнұсқалары) үшін сәйкес кескіндер
табылды:
барлық
элементтері (түпнұсқалары) үшін сәйкес кескіндер
табылды:





Табылған кескіндерді
берілген теңдеуге  апарып
қоямыз,
апарып
қоямыз, 
Әрі қарай операторлық
шешімді  арқылы, атап айтқанда бір бөлшек арқылы жазамыз.
Бұл жағдайда келесі әрекеттерді жасаймыз:
арқылы, атап айтқанда бір бөлшек арқылы жазамыз.
Бұл жағдайда келесі әрекеттерді жасаймыз:
Ең алдымен теңдіктің сол жағын ашамыз:

Сол жақ бөліктегі ұқсас мүшелерді біріктіреміз. Бұл жағдайда –2 мен
–3 сандарын қосамыз.

 айнымалысы бар мүшелерді сол жақта қалдырамыз,
қалған мүшелерді таңбасын өзгертіп, оң жаққа өткіземіз:
айнымалысы бар мүшелерді сол жақта қалдырамыз,
қалған мүшелерді таңбасын өзгертіп, оң жаққа өткіземіз:

Сол жақ бөлікте
 операторлық шешімді жақша сыртына шығарамыз, ал
оң жақ бөлікте өрнекті ортақ бөлімге келтіреміз:
операторлық шешімді жақша сыртына шығарамыз, ал
оң жақ бөлікте өрнекті ортақ бөлімге келтіреміз:

Сол жақтағы көпмүшені көбейткіштерге жіктеу керек. Квадрат теңдеуді шешеміз.





Осылайша,


теңдіктің оң жағына бөлу ретінде өткіземіз,

Мақсат орындалды
– операторлық шешім бір ғана бөлшек түрінде
өрнектелді.
операторлық шешім бір ғана бөлшек түрінде
өрнектелді.
Екінші әрекет. Белгісіз коэффициенттер әдісін қолданып, теңдеудің операторлық шешімін қарапайым бөлшектердің қосындысы түрінде жіктеу қажет.



Сәйкес дәрежелердің алдындағы коэффициенттерді теңестіріп, шыққан теңдеулер жүйесін шешеміз:

Сонымен,  коэффициенттер
табылды және операторлық шешім бөлшектерге жіктелген түрде
алынды.
коэффициенттер
табылды және операторлық шешім бөлшектерге жіктелген түрде
алынды.

Есептің соңғы кезеңі — Лаплас түрлендіруінің кері түрін қолданып, кескіннен бастапқы функцияларға (түпнұсқаларға) өту. Ол үшін түпнұсқалар мен кескіндер кестесінің оң жақ бағанын пайдаланамыз.
Кескінге сәйкес бастапқы функцияларға (түпнұсқаға) өтейік.




Берілген теңдеу

Шыққан теңдеуіміз

Жауабы: дербес шешім


шағым қалдыра аласыз















