
На данном уроке мы рассмотрим уравнение с двумя переменными, дадим его определение и построим график.
Мы познакомились с понятиями координатной оси и координатной плоскости. Мы знаем, что каждая точка плоскости однозначно задает пару чисел (х; у), причем первое число есть абсцисса точки, а второе – ордината.
Мы будем очень часто встречаться с линейным уравнением с двумя переменными, решением которого и есть пара чисел, которую можно представить на координатной плоскости.
Уравнение вида:
![]() , где a, b, с – числа,
причем
, где a, b, с – числа,
причем ![]()
Называется линейным уравнением с двумя переменными х и у. Решением такого уравнения будет любая такая пара чисел х и у, подставив которую в уравнение мы получим верное числовое равенство.
Пара чисел будет изображаться на координатной плоскости в виде точки.
У таких уравнений мы увидим много решений, то есть много пар чисел, и все соответствующие точки будут лежать на одной прямой.
Изучение алгоритма построения графика уравнения на примере
Рассмотрим пример:
Пример 1:
![]()
![]() ;
; ![]() ;
; ![]() ;
;
Чтобы найти решения данного уравнения нужно подобрать соответствующие пары чисел х и у:
Пусть ![]() , тогда исходное уравнение превращается в
уравнение с одной неизвестной:
, тогда исходное уравнение превращается в
уравнение с одной неизвестной:
![]() ,
, ![]()
То есть, первая пара чисел, являющаяся решением заданного уравнения (0; 3). Получили точку А(0; 3)
Пусть ![]() . Получим исходное уравнение с одной
переменной:
. Получим исходное уравнение с одной
переменной: ![]() , отсюда
, отсюда ![]() , получили точку В(3; 0)
, получили точку В(3; 0)
Занесем пары чисел в таблицу:
|
х |
0 |
3 |
|
у |
3 |
0 |
Построим на графике точки и проведем прямую:
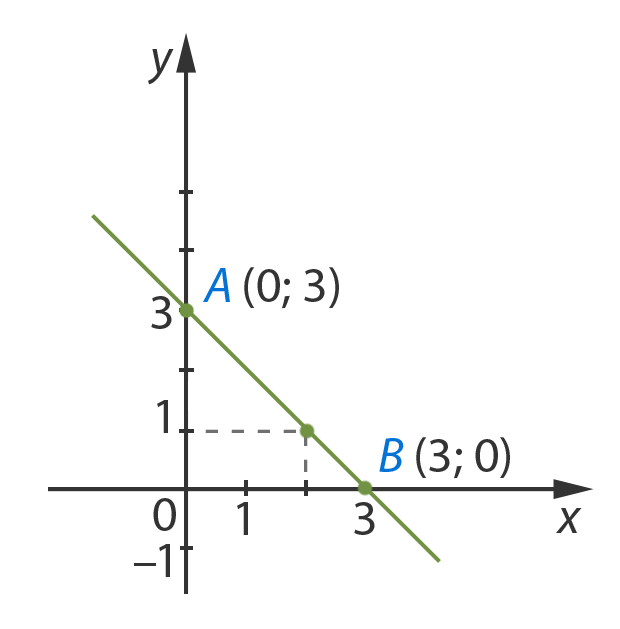
Отметим, что любая точка на данной прямой
будет решением заданного уравнения. Проверим – возьмем точку с
координатой ![]() и по графику найдем ее вторую координату.
Очевидно, что в этой точке
и по графику найдем ее вторую координату.
Очевидно, что в этой точке ![]() . Подставим данную пару чисел в уравнение.
Получим 0=0 – верное числовое равенство, значит точка, лежащая на
прямой, является решением.
. Подставим данную пару чисел в уравнение.
Получим 0=0 – верное числовое равенство, значит точка, лежащая на
прямой, является решением.
Пока доказать, что любая точка, лежащая на построенной прямой является решением уравнения, мы не можем, поэтому принимаем это за правду и докажем позже.
Пример 2 – построить график уравнения:
![]()
Составим таблицу, нам достаточно для построения прямой двух точек, но возьмем третью для контроля:
|
х |
0 |
-2 |
2 |
|
у |
3 |
0 |
6 |
В первой колонке мы взяли
удобный ![]() , найдем у:
, найдем у:
![]() ,
, ![]() ,
, ![]()
Во втором столбике мы взяли
удобный ![]() , найдем х:
, найдем х:
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Возьмем для
проверки ![]() и найдем у:
и найдем у:
![]() ,
, ![]() ,
, ![]()
Построим график:
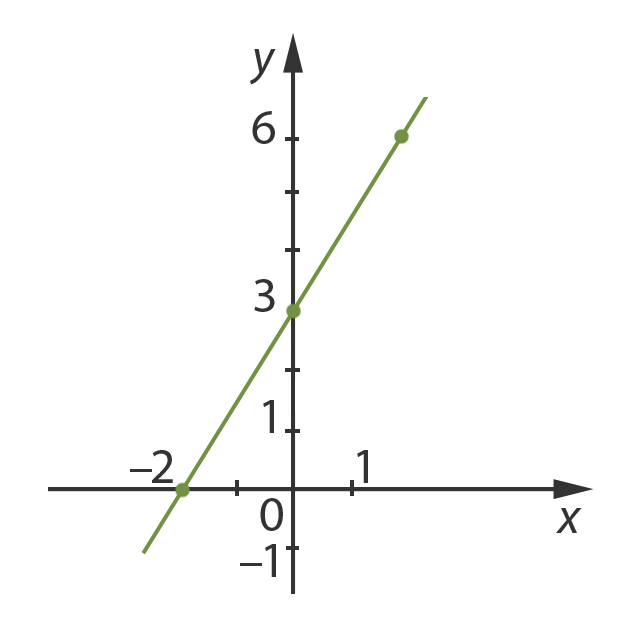
Умножим заданное уравнение на два:
![]()
От такого преобразования множество решений не изменится и график останется таким же самым.
Вывод: мы научились решать уравнения с двумя переменными и строить их графики, узнали, что графиком подобного уравнения есть прямая и что любая точка этой прямой является решением уравнения
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Линейные уравнения с двумя переменными
Линейные уравнения с двумя переменными
На данном уроке мы рассмотрим уравнение с двумя переменными, дадим его определение и построим график.
Мы познакомились с понятиями координатной оси и координатной плоскости. Мы знаем, что каждая точка плоскости однозначно задает пару чисел (х; у), причем первое число есть абсцисса точки, а второе – ордината.
Мы будем очень часто встречаться с линейным уравнением с двумя переменными, решением которого и есть пара чисел, которую можно представить на координатной плоскости.
Уравнение вида:
![]() , где a, b, с – числа,
причем
, где a, b, с – числа,
причем ![]()
Называется линейным уравнением с двумя переменными х и у. Решением такого уравнения будет любая такая пара чисел х и у, подставив которую в уравнение мы получим верное числовое равенство.
Пара чисел будет изображаться на координатной плоскости в виде точки.
У таких уравнений мы увидим много решений, то есть много пар чисел, и все соответствующие точки будут лежать на одной прямой.
Изучение алгоритма построения графика уравнения на примере
Рассмотрим пример:
Пример 1:
![]()
![]() ;
; ![]() ;
; ![]() ;
;
Чтобы найти решения данного уравнения нужно подобрать соответствующие пары чисел х и у:
Пусть ![]() , тогда исходное уравнение превращается в
уравнение с одной неизвестной:
, тогда исходное уравнение превращается в
уравнение с одной неизвестной:
![]() ,
, ![]()
То есть, первая пара чисел, являющаяся решением заданного уравнения (0; 3). Получили точку А(0; 3)
Пусть ![]() . Получим исходное уравнение с одной
переменной:
. Получим исходное уравнение с одной
переменной: ![]() , отсюда
, отсюда ![]() , получили точку В(3; 0)
, получили точку В(3; 0)
Занесем пары чисел в таблицу:
|
х |
0 |
3 |
|
у |
3 |
0 |
Построим на графике точки и проведем прямую:

Отметим, что любая точка на данной прямой
будет решением заданного уравнения. Проверим – возьмем точку с
координатой ![]() и по графику найдем ее вторую координату.
Очевидно, что в этой точке
и по графику найдем ее вторую координату.
Очевидно, что в этой точке ![]() . Подставим данную пару чисел в уравнение.
Получим 0=0 – верное числовое равенство, значит точка, лежащая на
прямой, является решением.
. Подставим данную пару чисел в уравнение.
Получим 0=0 – верное числовое равенство, значит точка, лежащая на
прямой, является решением.
Пока доказать, что любая точка, лежащая на построенной прямой является решением уравнения, мы не можем, поэтому принимаем это за правду и докажем позже.
Пример 2 – построить график уравнения:
![]()
Составим таблицу, нам достаточно для построения прямой двух точек, но возьмем третью для контроля:
|
х |
0 |
-2 |
2 |
|
у |
3 |
0 |
6 |
В первой колонке мы взяли
удобный ![]() , найдем у:
, найдем у:
![]() ,
, ![]() ,
, ![]()
Во втором столбике мы взяли
удобный ![]() , найдем х:
, найдем х:
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Возьмем для
проверки ![]() и найдем у:
и найдем у:
![]() ,
, ![]() ,
, ![]()
Построим график:

Умножим заданное уравнение на два:
![]()
От такого преобразования множество решений не изменится и график останется таким же самым.
Вывод: мы научились решать уравнения с двумя переменными и строить их графики, узнали, что графиком подобного уравнения есть прямая и что любая точка этой прямой является решением уравнения

шағым қалдыра аласыз















