
Математика — тек формула емес, ойлау мәдениеті.
Қазіргі білім беру жүйесіндегі
басты міндеттердің бірі – оқушылардың функционалдық сауаттылығын
қалыптастыру. Функционалдық сауаттылық дегеніміз – алған
білімін өмірлік жағдаяттарда тиімді қолдана алу, логикалық ойлау,
талдау, дәлелдеу және шешім қабылдау қабілеттерінің жиынтығы.
Әсіресе 9-сынып – оқушының абстрактілі ойлауы қалыптасып,
математиканы саналы түрде түсіне бастайтын маңызды
кезең.
Математика сабағында функционалдық сауаттылықты дамытуда стандартты емес, логикалық, өмірмен байланысты есептердің рөлі ерекше.
-
Логикалық парадокстар арқылы ойлауды дамыту
Парадокс немесе өмір
Кейбір парадокстар тек сырттай ғана парадокс тәрізді көрінеді, ал шын мәнінде оларда ешқандай қайшылық жоқ. Соның біріне қатысты мынадай аңыз бар.
Ертеде бір философ өлім жазасына кесіледі. Ол түрмеде үкімнің орындалуын күтеді. Бір жексенбі күні түрме басшысы келіп, жазаның екі шартын хабарлайды: біріншіден, өлім жазасы келесі аптаның бір күнінде, дәл түсте жүзеге асады; екіншіден, бұл күн тұтқын үшін алдын ала белгісіз болуы тиіс.
Ф илософ
логикалық талдау жүргізе бастайды. Оның пайымдауынша, жаза жексенбі
күні орындала алмайды. Себебі, егер ол сенбіге дейін тірі қалса,
жексенбі жалғыз мүмкін күн болып қалады да, өлім күні беймәлім
болмай шығады. Бұл екінші шартқа қайшы. Демек, жексенбі тізімнен
шығады.
илософ
логикалық талдау жүргізе бастайды. Оның пайымдауынша, жаза жексенбі
күні орындала алмайды. Себебі, егер ол сенбіге дейін тірі қалса,
жексенбі жалғыз мүмкін күн болып қалады да, өлім күні беймәлім
болмай шығады. Бұл екінші шартқа қайшы. Демек, жексенбі тізімнен
шығады.
Осы ой желісін жалғастыра отырып, философ сенбіні де жоққа шығарады: егер дүйсенбі мен жұма аралығында жаза қолданылмаса, сенбі күні өлім болатыны анық болып қалады. Бұл да кенеттен болмайды. Сол сияқты, ол біртіндеп жұма, бейсенбі және аптаның қалған күндерін де логикалық тұрғыдан мүмкін емес деп есептейді.
А қырында
философ келесі аптада оны ешбір күні өлім жазасына кесу мүмкін емес
деген қорытындыға келеді. Өз шешіміне марқайып отырған сәтінде,
сейсенбі күні кенеттен жендеттер келіп, үкімді
орындайды.
қырында
философ келесі аптада оны ешбір күні өлім жазасына кесу мүмкін емес
деген қорытындыға келеді. Өз шешіміне марқайып отырған сәтінде,
сейсенбі күні кенеттен жендеттер келіп, үкімді
орындайды.
Мәселе түрме басшысының философиялық парадокстарға мән бермеуінде емес. Негізгі түйін — тұтқын аптаның әр күнін логикалық жолмен жоққа шығара отырып, шын мәнінде олардың барлығын өзі үшін беймәлім күнге айналдырды. Демек, парадокстармен жұмыс істегенде аса мұқият болу қажет.
Философтың өлім жазасына қатысты «күтпеген күн» парадоксы оқушылардың:
-
логикалық пайымдау жасауына;
-
өз тұжырымын тексеруге;
-
шарттарды дұрыс түсінуге үйретеді.
Бұл есепте оқушы:
-
әр күнді логикалық тұрғыдан жоққа шығара отырып,
-
соңында сол күндердің бәрі «беймәлім» бола алатынын түсінеді.
-
Функционалдық нәтиже:
Оқушы формальды логика мен нақты өмір арасындағы айырмашылықты сезінеді, парадокс ұғымын түсінеді және асығыс қорытындыдан сақтануды үйренеді.
-
Геометриялық мазмұндағы өмірлік есептер
Есеп-1. Ұзындығы 5 м баспалдақ үй қабырғасына сүйеліп тұр. Баспалдақтың жерге түсірілген көлеңкесінің ұзындығы қабырға мен баспалдақтың төменгі ұшының арасындағы қашықтықтан 1 м-ге қысқа. Баспалдақтың жердегі проекциясының ұзындығын табыңыз.
Ұзындығы 5 м болатын баспалдақ туралы есеп — геометрияны өмірмен байланыстыратын классикалық мысал.

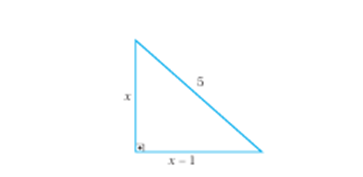
3-сурет.
Шешуі: Айталық, х-жерден баспалдыққа дейінгі ара қашықтық болса, онда проекциясының ұзындығы х-1 м. Суретте көрсетілгендей баспалдақтың орналасуынан тік бұрышты үшбұрышты көруге болады. Пифагор теоремасын қолдану арқылы есептейміз:
![]()
![]()
![]()
![]()
(x+3)(x-4)=0
Жауабы:
Баспалдақтың проекциясының ұзындығы — 3 м.
Бұл есеп арқылы оқушы:
-
физикалық жағдайды сызбаға айналдыруды;
-
тікбұрышты үшбұрыш моделін құруды;
-
Пифагор теоремасын практикада қолдануды
үйренеді.
Функционалдық
нәтиже:
Оқушы формуланы жаттау емес, оны жағдайға сәйкес қолдану
дағдысын қалыптастырады.
Дирихле
-
Дирихле қағидасы және жіктеу дағдысы
Бұл принципін алғаш болып Лежен Дирихле (1805-1859) деген неміс математигі тұжырымдаған еді.
Бұл есеп конструктивті емес әдіспен шешіледі, яғни тордың бар болуы анықталғанымен, оның нақты координаталық орналасуы белгісіз күйінде қалады.
Дирихле принципінің негізгі ерекшілігі осы еді.
N тор көзде m қоян отыр, n>? болса, ең құрығында бір төр көз бос табылады, ал конструктивті шешімін табу қиындықтар туғызуы әбден мүмкін.
Логикалық әдістер көптеген есептерді шешуде қолданылады және Дирихле принципі арқылы қалай шешілетінді қарастырамыз және бұл принцип өте қарапайым, өте қуатты идея екенің айтқымыз келеді.
Бұл принцип математиканың көптеген салаларында, мысалы, анализде, геометрияда, жиындар теориясында және т.б., қолданылады.
Дирихле принципі сандар теориясында өзінің ойып тұрып алған орны бар.
Қарапайым әрі түсінікті болғанына қарамастан, Дирихле қағидасы көптеген теоремаларды дәлелдеуде және алғашында шешімі жоқ сияқты көрінетін есептерді шығаруда кеңінен қолданылады.
Бұл қағиданы түсіндіру үшін әлемдік математикада дәстүрлі түрде «көжектер мен қораптар» үлгісі қолданылады (ал ағылшын тілінде ол «көгершіндер мен ұяшықтар» деп аталады). Біз де осы кең тараған тәсілді негізге алайық. Айта кету керек, бұл қағиданың ғылымда орнығуы неміс математигі Петер Густав Лежён Дирихле есімімен тығыз байланысты.
 Айталық, белгілі бір мөлшерде
көжектер m және қораптар n бар болсын. Егер көжектер саны қораптар
санынан артық болса (m >
n) барлық көжектерді қораптарға
орналастырғанда, кем дегенде бір қорапта бір көжектен артық
орналасуы міндетті түрде орын
алады.
Айталық, белгілі бір мөлшерде
көжектер m және қораптар n бар болсын. Егер көжектер саны қораптар
санынан артық болса (m >
n) барлық көжектерді қораптарға
орналастырғанда, кем дегенде бір қорапта бір көжектен артық
орналасуы міндетті түрде орын
алады.
Ойланып көріп, шешім шығарамыз: алдымен қораптарға n көжектерді
салып шығамыз. Қалған көжектер саны m-n -ге тең болады. Тапсырма
шарты бойынша, барлық көжектер қорап ішінде болуы тиіс. Сәйкесінше,
n-m көжектерді біз бос емес қораптарға сала бастаймыз. Сондықтан да
ішінде бірден көп көжектері бар қораптар да болады. Біз қарапайым
ойлау жүргіздік, бұдан қиынырақ мысалдарды математикалық индукция
әдісін пайдалану арқылы өз еріктеріңізбен ойластыруды ұсынамыз.
Дирихле әдісін пайдаланудың басты қиыншылығы анықтаманың
ауырлығында: не «көжек», ал не
«қорап».
«Көжектер мен қораптар» мысалы арқылы түсіндірілетін Дирихле қағидасы оқушыларды:
-
объектілерді топтастыруға;
-
міндетті нәтиже мен ықтимал нәтижені ажыратуға;
-
дәлелдеуге негізделген ойлауға
баулиды.
Функционалдық
нәтиже:
Оқушы күнделікті өмірдегі «міндетті түрде болады» деген ұғымды
математикалық тұрғыда дәлелдеуді меңгереді.
Қорытынды
Жоғарыда қарастырылған есептер:
-
оқушылардың логикалық ойлауын;
-
математикалық тілде сөйлеуін;
-
өмірлік жағдаяттарды модельдеу қабілетін
қалыптастырады.
Функционалдық сауаттылықты дамыту — тек есеп шығарумен шектелмейді, ол оқушыны ойлауға, дәлелдеуге және шешім қабылдауға үйретеді. Сондықтан 9-сыныпта осындай мазмұнды, ойландыратын есептерді жүйелі қолдану — заманауи математиканың басты талаптарының бірі.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Математика — тек формула емес, ойлау мәдениеті.
Математика — тек формула емес, ойлау мәдениеті.
Математика — тек формула емес, ойлау мәдениеті.
Қазіргі білім беру жүйесіндегі
басты міндеттердің бірі – оқушылардың функционалдық сауаттылығын
қалыптастыру. Функционалдық сауаттылық дегеніміз – алған
білімін өмірлік жағдаяттарда тиімді қолдана алу, логикалық ойлау,
талдау, дәлелдеу және шешім қабылдау қабілеттерінің жиынтығы.
Әсіресе 9-сынып – оқушының абстрактілі ойлауы қалыптасып,
математиканы саналы түрде түсіне бастайтын маңызды
кезең.
Математика сабағында функционалдық сауаттылықты дамытуда стандартты емес, логикалық, өмірмен байланысты есептердің рөлі ерекше.
-
Логикалық парадокстар арқылы ойлауды дамыту
Парадокс немесе өмір
Кейбір парадокстар тек сырттай ғана парадокс тәрізді көрінеді, ал шын мәнінде оларда ешқандай қайшылық жоқ. Соның біріне қатысты мынадай аңыз бар.
Ертеде бір философ өлім жазасына кесіледі. Ол түрмеде үкімнің орындалуын күтеді. Бір жексенбі күні түрме басшысы келіп, жазаның екі шартын хабарлайды: біріншіден, өлім жазасы келесі аптаның бір күнінде, дәл түсте жүзеге асады; екіншіден, бұл күн тұтқын үшін алдын ала белгісіз болуы тиіс.
Ф илософ
логикалық талдау жүргізе бастайды. Оның пайымдауынша, жаза жексенбі
күні орындала алмайды. Себебі, егер ол сенбіге дейін тірі қалса,
жексенбі жалғыз мүмкін күн болып қалады да, өлім күні беймәлім
болмай шығады. Бұл екінші шартқа қайшы. Демек, жексенбі тізімнен
шығады.
илософ
логикалық талдау жүргізе бастайды. Оның пайымдауынша, жаза жексенбі
күні орындала алмайды. Себебі, егер ол сенбіге дейін тірі қалса,
жексенбі жалғыз мүмкін күн болып қалады да, өлім күні беймәлім
болмай шығады. Бұл екінші шартқа қайшы. Демек, жексенбі тізімнен
шығады.
Осы ой желісін жалғастыра отырып, философ сенбіні де жоққа шығарады: егер дүйсенбі мен жұма аралығында жаза қолданылмаса, сенбі күні өлім болатыны анық болып қалады. Бұл да кенеттен болмайды. Сол сияқты, ол біртіндеп жұма, бейсенбі және аптаның қалған күндерін де логикалық тұрғыдан мүмкін емес деп есептейді.
А қырында
философ келесі аптада оны ешбір күні өлім жазасына кесу мүмкін емес
деген қорытындыға келеді. Өз шешіміне марқайып отырған сәтінде,
сейсенбі күні кенеттен жендеттер келіп, үкімді
орындайды.
қырында
философ келесі аптада оны ешбір күні өлім жазасына кесу мүмкін емес
деген қорытындыға келеді. Өз шешіміне марқайып отырған сәтінде,
сейсенбі күні кенеттен жендеттер келіп, үкімді
орындайды.
Мәселе түрме басшысының философиялық парадокстарға мән бермеуінде емес. Негізгі түйін — тұтқын аптаның әр күнін логикалық жолмен жоққа шығара отырып, шын мәнінде олардың барлығын өзі үшін беймәлім күнге айналдырды. Демек, парадокстармен жұмыс істегенде аса мұқият болу қажет.
Философтың өлім жазасына қатысты «күтпеген күн» парадоксы оқушылардың:
-
логикалық пайымдау жасауына;
-
өз тұжырымын тексеруге;
-
шарттарды дұрыс түсінуге үйретеді.
Бұл есепте оқушы:
-
әр күнді логикалық тұрғыдан жоққа шығара отырып,
-
соңында сол күндердің бәрі «беймәлім» бола алатынын түсінеді.
-
Функционалдық нәтиже:
Оқушы формальды логика мен нақты өмір арасындағы айырмашылықты сезінеді, парадокс ұғымын түсінеді және асығыс қорытындыдан сақтануды үйренеді.
-
Геометриялық мазмұндағы өмірлік есептер
Есеп-1. Ұзындығы 5 м баспалдақ үй қабырғасына сүйеліп тұр. Баспалдақтың жерге түсірілген көлеңкесінің ұзындығы қабырға мен баспалдақтың төменгі ұшының арасындағы қашықтықтан 1 м-ге қысқа. Баспалдақтың жердегі проекциясының ұзындығын табыңыз.
Ұзындығы 5 м болатын баспалдақ туралы есеп — геометрияны өмірмен байланыстыратын классикалық мысал.


3-сурет.
Шешуі: Айталық, х-жерден баспалдыққа дейінгі ара қашықтық болса, онда проекциясының ұзындығы х-1 м. Суретте көрсетілгендей баспалдақтың орналасуынан тік бұрышты үшбұрышты көруге болады. Пифагор теоремасын қолдану арқылы есептейміз:
![]()
![]()
![]()
![]()
(x+3)(x-4)=0
Жауабы:
Баспалдақтың проекциясының ұзындығы — 3 м.
Бұл есеп арқылы оқушы:
-
физикалық жағдайды сызбаға айналдыруды;
-
тікбұрышты үшбұрыш моделін құруды;
-
Пифагор теоремасын практикада қолдануды
үйренеді.
Функционалдық
нәтиже:
Оқушы формуланы жаттау емес, оны жағдайға сәйкес қолдану
дағдысын қалыптастырады.
Дирихле
-
Дирихле қағидасы және жіктеу дағдысы
Бұл принципін алғаш болып Лежен Дирихле (1805-1859) деген неміс математигі тұжырымдаған еді.
Бұл есеп конструктивті емес әдіспен шешіледі, яғни тордың бар болуы анықталғанымен, оның нақты координаталық орналасуы белгісіз күйінде қалады.
Дирихле принципінің негізгі ерекшілігі осы еді.
N тор көзде m қоян отыр, n>? болса, ең құрығында бір төр көз бос табылады, ал конструктивті шешімін табу қиындықтар туғызуы әбден мүмкін.
Логикалық әдістер көптеген есептерді шешуде қолданылады және Дирихле принципі арқылы қалай шешілетінді қарастырамыз және бұл принцип өте қарапайым, өте қуатты идея екенің айтқымыз келеді.
Бұл принцип математиканың көптеген салаларында, мысалы, анализде, геометрияда, жиындар теориясында және т.б., қолданылады.
Дирихле принципі сандар теориясында өзінің ойып тұрып алған орны бар.
Қарапайым әрі түсінікті болғанына қарамастан, Дирихле қағидасы көптеген теоремаларды дәлелдеуде және алғашында шешімі жоқ сияқты көрінетін есептерді шығаруда кеңінен қолданылады.
Бұл қағиданы түсіндіру үшін әлемдік математикада дәстүрлі түрде «көжектер мен қораптар» үлгісі қолданылады (ал ағылшын тілінде ол «көгершіндер мен ұяшықтар» деп аталады). Біз де осы кең тараған тәсілді негізге алайық. Айта кету керек, бұл қағиданың ғылымда орнығуы неміс математигі Петер Густав Лежён Дирихле есімімен тығыз байланысты.
 Айталық, белгілі бір мөлшерде
көжектер m және қораптар n бар болсын. Егер көжектер саны қораптар
санынан артық болса (m >
n) барлық көжектерді қораптарға
орналастырғанда, кем дегенде бір қорапта бір көжектен артық
орналасуы міндетті түрде орын
алады.
Айталық, белгілі бір мөлшерде
көжектер m және қораптар n бар болсын. Егер көжектер саны қораптар
санынан артық болса (m >
n) барлық көжектерді қораптарға
орналастырғанда, кем дегенде бір қорапта бір көжектен артық
орналасуы міндетті түрде орын
алады.
Ойланып көріп, шешім шығарамыз: алдымен қораптарға n көжектерді
салып шығамыз. Қалған көжектер саны m-n -ге тең болады. Тапсырма
шарты бойынша, барлық көжектер қорап ішінде болуы тиіс. Сәйкесінше,
n-m көжектерді біз бос емес қораптарға сала бастаймыз. Сондықтан да
ішінде бірден көп көжектері бар қораптар да болады. Біз қарапайым
ойлау жүргіздік, бұдан қиынырақ мысалдарды математикалық индукция
әдісін пайдалану арқылы өз еріктеріңізбен ойластыруды ұсынамыз.
Дирихле әдісін пайдаланудың басты қиыншылығы анықтаманың
ауырлығында: не «көжек», ал не
«қорап».
«Көжектер мен қораптар» мысалы арқылы түсіндірілетін Дирихле қағидасы оқушыларды:
-
объектілерді топтастыруға;
-
міндетті нәтиже мен ықтимал нәтижені ажыратуға;
-
дәлелдеуге негізделген ойлауға
баулиды.
Функционалдық
нәтиже:
Оқушы күнделікті өмірдегі «міндетті түрде болады» деген ұғымды
математикалық тұрғыда дәлелдеуді меңгереді.
Қорытынды
Жоғарыда қарастырылған есептер:
-
оқушылардың логикалық ойлауын;
-
математикалық тілде сөйлеуін;
-
өмірлік жағдаяттарды модельдеу қабілетін
қалыптастырады.
Функционалдық сауаттылықты дамыту — тек есеп шығарумен шектелмейді, ол оқушыны ойлауға, дәлелдеуге және шешім қабылдауға үйретеді. Сондықтан 9-сыныпта осындай мазмұнды, ойландыратын есептерді жүйелі қолдану — заманауи математиканың басты талаптарының бірі.

шағым қалдыра аласыз















