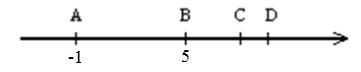Математика
Бөлім бойынша жиынтық бағалау тапсырмалары орындауға арналған дәптері
6сынып оқушысы
ІІ нұсқа
.........................................................
|
№ |
Тапсырма 2-нұсқа |
Балл |
|
1 |
24 :8 = 4,8:1,6 берілген
пропорциядағы сандарды пайдаланып, басқа неше пропорция құрастыруға
болады және оларды жазыңыз. |
2 |
|
2 |
Автоматты станок сағатына 58 бөлшек дайындап, берілген уақытта 348 бөлшек дайындады. Егер осы автоматты станок сағатына 75 бөлшек дайындайтын болса, берілген уақытта неше бөлшек дайындайды?
|
3 |
|
3 |
Арба дөңгелегінің радиусы 0,3м болса, осы дөңгелек 10 рет айналғанда неше метр жол жүреді? Мұндағы π ≈ 3,14.
|
3 |
|
4 |
Жер бетіндегі 68 км арақашықтық картада 3,4 см-ге сәйкес келеді. Осы картадағы 0,62 дм кесіндіге жер бетіндегі неше километр арақашықтық сәйкес келеді? Масштабты табыңыз
|
4 |
|
|
Жалпы балл |
12 |
|
2 |
||
|
4 |
Екі таңбалы санның бірлігі ондығынан 2-ге артық. Осы санды оның цифрларының қосындысына көбейтсек 144-ке тең болады. Берілген санды табыңыз.
|
|
|
|
Жалпы балл |
15 |
15
«Екі айнымалысы бар сызықтық теңдеулер және олардың жүйелері» бөлімі БЖБ№10
|
№ |
Тапсырма 2-нұсқа |
балл |
|
1 |
Берілген (2; 1), (0; –3), (12; 5), (10; 4,2) нүктелерінің қайсысы -2х + 5у -1= 0 теңдеуінің шешімі болады?
|
3 |
|
2 |
Теңдеулер жүйесін қосу тәсілімен шешіңіз:
|
4
|
|
3 |
Теңдеулер жүйесін алмастыру тәсілімен шешіңіз:
|
4
|
14
|
№ |
Тапсырма 2-нұсқа |
балл |
|
1 |
-16;
−
Q
Z 
N |
3 |
|
2 |
С нүктесі – АВ кесіндісінің ортасы. Егер С(–5), B(3) болса, А нүктесінің координаталарын салыңыз.
|
2 |
|
3 |
Есептеңіз: 1) 3,7 + (–1,3)= 2) – 5,9 − (–3,21) = 3) –13,2 + | – 0,2 |= |
3 |
|
4 |
A, В, С, D нүктелері координаталық түзуде тізбектеле орналасқан. A және В нүктелерінің координаталары берілген. Егер |??| = 1,5|??|, |??| = 2|??| болса, AD ұзындығын табыңыз
|
4 |
|
|
Жалпы балл |
12 |
3
«Рационал сандарға амалдар қолдану» бөлімі БЖБ №3
|
№ |
Тапсырма 2-нұсқа |
балл |
|
1 |
Есептеңіз:
|
2 |
|
2 |
Өрнектің мәнін
табыңыз:
|
4 |
|
3 |
(? + ?) ∙ ? = ?? + ?? көбейтудің үлестірімділік қасиетінің орындалатынын ? = 0,4; ? = −0,2; ? = −5 сандары арқылы тексеріңіз.
|
4 |
|
4 |
Мағжан бір сан ойлады. Осы санға -1,5-ті қосып,қосындының мәнін 1,6-ға көбейткенде 4,8 саны шықса, Мағжан бастапқыда қандай сан ойлаған еді.
|
4
|
|
|
Жалпы балл |
14 |
|
4 |
|
|
|
4 |
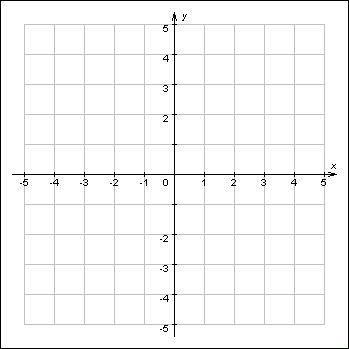
В(3; –4) нүктесінен өтетін және тура пропорционалды болатын графикті салыңыз. Суретті пайдаланып, графиктің формуласын жазыңыз. |
3 |
|
|
Жалпы балл |
12 |
13
«Шамалар арасындағы тәуелділіктер» бөлімі БЖБ №9
12
|
№ |
Тапсырма 2-нұсқа |
балл |
|
1 |
Төмендегі берілген шамалар арасындағы тәуелділіктерді формула арқылы жазыңыз:
a) Ауданы
72 b) 75 тетікті жасау станогының өнімділігі мен уақыт; c) Шаршының периметрі мен оның ұзындығы; d) 30 км арақашықтықтағы жылдамдықтық пен уақыт. Тура пропорционалдығы бар формуланы тауып, олардың пропорционалдық коэффицентін жазыңыз.
|
5 |
|
|
Баланың велосипедпен қозғалысының графигін пайдаланып, сұрақтарға жауап беріңіз: a) Графикте бала қанша уақыт жолда болған? b) Бала қанша уақыт орнында тұрған? c) Баланың ең үлкен жылдамдығы қандай болған? d) 20-шы секундтан 50-ші секундқа дейін бала қанша жол жүрген?
|
4 |
|
4 |
Катер 4 сағат ағыспен және 5 сағат ағысқа қарсы жүзді. Егер катердің меншікті жылдамдығы v км/сағ, ал өзен жылдамдығы х км/сағ болса: a) катердің ағыспен жүрген жолын; b) катердің ағысқа қарсы жүрген жолын; c) барлық жолды; d) ағыспен жүрген жолдың ағысқа қарсы жүрген жолға қарағанда қаншаға көп екенін математикалық модель түрінде көрсетіңіз
|
5 |
|
|
Жалпы балл |
15 |
5
|
№ |
Тапсырма 2-нұсқа |
балл |
|
1 |
x=−6
болса,
|
3 |
|
2 |
Өрнектерді ықшамдаңыз:
|
3 |
|
3 |
Алгебралық өрнекпен берілген тепе-теңдікті дәлелдеңіз: (4х + 28)∙1,2 +1,3∙(х + 3) + (– 1,7 – 6,1х)=35,8
|
4 |
БЖБ №4
6
«Статистика. Комбинаторика» бөлімі БЖБ №8
|
№ |
Тапсырма 2-нұсқа |
балл |
|
1 |
3, 11, 7, ___, 17, 18, 26 қатары берілген. Төмендегі ақпараттарды пайдаланып, қатардағы жетіспейтін натурал санды табыңыз: а) арифметикалық ортасы 14-ке тең; b) өзгеріс ауқымы 23-ге тең; с) қатар модасы 17-ға тең.
|
5
|
|
2 |
Серікте әртүрлі түсті екі
жейде, төрт футболка және екі шалбар бар. Егер ол жейде, футболка
және шалбар кисе, Берік қанша түрлі киіне алады? Жауабыңызды
нұсқалар талын құрып көрсетіңіз. |
3 |
|
3 |
Поезд жолдың 160
км-ін 40 км/сағ жылдамдықпен, екінші бөлігін 120 км-ді 60 км/сағ
жылдамдықпен, үшінші бөлігін 40 км-ді 20 км/сағ жылдамдықпен жүріп
өтті. Жолдың барлық бөлігіндегі поездің орташа жылдамдығы
қанша? |
4 |
|
|
Жалпы балл |
12 |
11
|
4 |
M(-5; 3), N(–2; -3) және Р(-1; 5) нүктелері берілген. МNР үшбұрышын салыңыз. а)МNР үшбұрышына абсцисса осіне карағанда симметриялы; b)МNР үшбұрышына ордината осіне карағанда симметриялы; с) МNР үшбұрышына координаталар басына карағанда симметриялы болатындай үшбұрыштар салыңыз.
|
6 |
|
|
Жалпы балл |
13 |
10
«Бір айнымалысы бар сызықтық теңдеу» бөлімі БЖБ№5
|
№ |
Тапсырма 2-нұсқа |
балл |
|
1 |
b–ның қандай мәнінде 2х+18=36
және 3х-5b=7 теңдеулері мәндес болады?
|
3 |
|
2 |
Теңдеуді шешіңіз: 6,8х–1,7х+3,6=8,6+4,1х.
|
3 |
|
3 |
Теңдеуді шешіңіз: a) 3 |х – 2| = 9 b) 5|3х – 5|
= –20. |
4 |
|
4 |
Теңдеу құру арқылы шығарыңыз. Екі пунктен бір-біріне
қарама-қарсы бір уақытта екі автобус жолға шықты. Бірінші
автобустың жылдамдығы 35 км/сағ, ал екіншісінікі 62 км/сағ. Екеуі
кездескенде бірінші автобус екінші автобусқа қарағанда 125 км аз
жүрген болса, онда екінші автобус қанша жол
жүрді? |
3 |
|
|
Жалпы балл |
13 |
«Бір айнымалысы бар сызықтық теңсіздіктер» бөлім бойынша жиынтық бағалау БЖБ№6
|
№ |
Тапсырма 2-нұсқа |
балл |
|
1 |
Тіктөртбұрыш қабырғалары 11,2 ≤ a ≤ 12,4 , 2,1≤ b ≤ 4,5 аралығында болса, онда осы төртбұрыштың ауданы мен периметрін бағалаңыз.
|
4 |
|
2 |
Берілген сан аралықтарының сан түзуінде кескіндеп, қиылысуы мен бірігуін жазыңыз: (−∞; −3] және (−6; +∞)
|
3 |
|
3 |
Төмендегі сан аралықтарды теңсіздік түрінде жазыңыз: a) [–3; 6); b) [3,5; +∞)
|
2 |
|
4 |
Теңсіздіктер
жүйесінің бүтін шешімдерінің санын
табыңыз:
|
5 |
|
|
Жалпы балл |
14 |
|
№ |
Тапсырма 2-нұсқа |
балл |
|
1 |
Төмендегі шарттарға байланысты мысалдар келтіріңіз. Егер фигуралар: a)центрлік симметриясы бар, бірақ осьтік симметриясы жоқ; b) осьтік симметриясы бар, бірақ центрлік симметриясы жоқ; c) центрлік және осьтік симметриясы бар.
|
3 |
|
2 |
Координаталық жазықтықта ABCD төртбұрыш төбелері сәйкесінше (–2;2), (5;3), (5;–5), (–1;–7) нүктелерінде жатыр. a) ВС қабырғасы абсцисса осімен; b) АВ қабырғасы ордината осімен; c)АС кесіндісінің ордината осімен; қай нүктеде қиылысатынын жазыңыз.
|
4 |
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
МАТЕМАТИКА БЖБ 6-сынып толық нұсқа
МАТЕМАТИКА БЖБ 6-сынып толық нұсқа
Математика
Бөлім бойынша жиынтық бағалау тапсырмалары орындауға арналған дәптері
6сынып оқушысы
ІІ нұсқа
.........................................................
|
№ |
Тапсырма 2-нұсқа |
Балл |
|
1 |
24 :8 = 4,8:1,6 берілген
пропорциядағы сандарды пайдаланып, басқа неше пропорция құрастыруға
болады және оларды жазыңыз. |
2 |
|
2 |
Автоматты станок сағатына 58 бөлшек дайындап, берілген уақытта 348 бөлшек дайындады. Егер осы автоматты станок сағатына 75 бөлшек дайындайтын болса, берілген уақытта неше бөлшек дайындайды?
|
3 |
|
3 |
Арба дөңгелегінің радиусы 0,3м болса, осы дөңгелек 10 рет айналғанда неше метр жол жүреді? Мұндағы π ≈ 3,14.
|
3 |
|
4 |
Жер бетіндегі 68 км арақашықтық картада 3,4 см-ге сәйкес келеді. Осы картадағы 0,62 дм кесіндіге жер бетіндегі неше километр арақашықтық сәйкес келеді? Масштабты табыңыз
|
4 |
|
|
Жалпы балл |
12 |
|
2 |
||
|
4 |
Екі таңбалы санның бірлігі ондығынан 2-ге артық. Осы санды оның цифрларының қосындысына көбейтсек 144-ке тең болады. Берілген санды табыңыз.
|
|
|
|
Жалпы балл |
15 |
15
«Екі айнымалысы бар сызықтық теңдеулер және олардың жүйелері» бөлімі БЖБ№10
|
№ |
Тапсырма 2-нұсқа |
балл |
|
1 |
Берілген (2; 1), (0; –3), (12; 5), (10; 4,2) нүктелерінің қайсысы -2х + 5у -1= 0 теңдеуінің шешімі болады?
|
3 |
|
2 |
Теңдеулер жүйесін қосу тәсілімен шешіңіз:
|
4
|
|
3 |
Теңдеулер жүйесін алмастыру тәсілімен шешіңіз:
|
4
|
14
|
№ |
Тапсырма 2-нұсқа |
балл |
|
1 |
-16;
−
Q
Z 
N |
3 |
|
2 |
С нүктесі – АВ кесіндісінің ортасы. Егер С(–5), B(3) болса, А нүктесінің координаталарын салыңыз.
|
2 |
|
3 |
Есептеңіз: 1) 3,7 + (–1,3)= 2) – 5,9 − (–3,21) = 3) –13,2 + | – 0,2 |= |
3 |
|
4 |
A, В, С, D нүктелері координаталық түзуде тізбектеле орналасқан. A және В нүктелерінің координаталары берілген. Егер |??| = 1,5|??|, |??| = 2|??| болса, AD ұзындығын табыңыз
|
4 |
|
|
Жалпы балл |
12 |
3
«Рационал сандарға амалдар қолдану» бөлімі БЖБ №3
|
№ |
Тапсырма 2-нұсқа |
балл |
|
1 |
Есептеңіз:
|
2 |
|
2 |
Өрнектің мәнін
табыңыз:
|
4 |
|
3 |
(? + ?) ∙ ? = ?? + ?? көбейтудің үлестірімділік қасиетінің орындалатынын ? = 0,4; ? = −0,2; ? = −5 сандары арқылы тексеріңіз.
|
4 |
|
4 |
Мағжан бір сан ойлады. Осы санға -1,5-ті қосып,қосындының мәнін 1,6-ға көбейткенде 4,8 саны шықса, Мағжан бастапқыда қандай сан ойлаған еді.
|
4
|
|
|
Жалпы балл |
14 |
|
4 |
|
|
|
4 |
В(3; –4) нүктесінен өтетін және тура пропорционалды болатын графикті салыңыз. Суретті пайдаланып, графиктің формуласын жазыңыз. |
3 |
|
|
Жалпы балл |
12 |
13
«Шамалар арасындағы тәуелділіктер» бөлімі БЖБ №9
12
|
№ |
Тапсырма 2-нұсқа |
балл |
|
1 |
Төмендегі берілген шамалар арасындағы тәуелділіктерді формула арқылы жазыңыз:
a) Ауданы
72 b) 75 тетікті жасау станогының өнімділігі мен уақыт; c) Шаршының периметрі мен оның ұзындығы; d) 30 км арақашықтықтағы жылдамдықтық пен уақыт. Тура пропорционалдығы бар формуланы тауып, олардың пропорционалдық коэффицентін жазыңыз.
|
5 |
|
|
Баланың велосипедпен қозғалысының графигін пайдаланып, сұрақтарға жауап беріңіз: a) Графикте бала қанша уақыт жолда болған? b) Бала қанша уақыт орнында тұрған? c) Баланың ең үлкен жылдамдығы қандай болған? d) 20-шы секундтан 50-ші секундқа дейін бала қанша жол жүрген?
|
4 |
|
4 |
Катер 4 сағат ағыспен және 5 сағат ағысқа қарсы жүзді. Егер катердің меншікті жылдамдығы v км/сағ, ал өзен жылдамдығы х км/сағ болса: a) катердің ағыспен жүрген жолын; b) катердің ағысқа қарсы жүрген жолын; c) барлық жолды; d) ағыспен жүрген жолдың ағысқа қарсы жүрген жолға қарағанда қаншаға көп екенін математикалық модель түрінде көрсетіңіз
|
5 |
|
|
Жалпы балл |
15 |
5
|
№ |
Тапсырма 2-нұсқа |
балл |
|
1 |
x=−6
болса,
|
3 |
|
2 |
Өрнектерді ықшамдаңыз:
|
3 |
|
3 |
Алгебралық өрнекпен берілген тепе-теңдікті дәлелдеңіз: (4х + 28)∙1,2 +1,3∙(х + 3) + (– 1,7 – 6,1х)=35,8
|
4 |
БЖБ №4
6
«Статистика. Комбинаторика» бөлімі БЖБ №8
|
№ |
Тапсырма 2-нұсқа |
балл |
|
1 |
3, 11, 7, ___, 17, 18, 26 қатары берілген. Төмендегі ақпараттарды пайдаланып, қатардағы жетіспейтін натурал санды табыңыз: а) арифметикалық ортасы 14-ке тең; b) өзгеріс ауқымы 23-ге тең; с) қатар модасы 17-ға тең.
|
5
|
|
2 |
Серікте әртүрлі түсті екі
жейде, төрт футболка және екі шалбар бар. Егер ол жейде, футболка
және шалбар кисе, Берік қанша түрлі киіне алады? Жауабыңызды
нұсқалар талын құрып көрсетіңіз. |
3 |
|
3 |
Поезд жолдың 160
км-ін 40 км/сағ жылдамдықпен, екінші бөлігін 120 км-ді 60 км/сағ
жылдамдықпен, үшінші бөлігін 40 км-ді 20 км/сағ жылдамдықпен жүріп
өтті. Жолдың барлық бөлігіндегі поездің орташа жылдамдығы
қанша? |
4 |
|
|
Жалпы балл |
12 |
11
|
4 |
M(-5; 3), N(–2; -3) және Р(-1; 5) нүктелері берілген. МNР үшбұрышын салыңыз. а)МNР үшбұрышына абсцисса осіне карағанда симметриялы; b)МNР үшбұрышына ордината осіне карағанда симметриялы; с) МNР үшбұрышына координаталар басына карағанда симметриялы болатындай үшбұрыштар салыңыз.
|
6 |
|
|
Жалпы балл |
13 |
10
«Бір айнымалысы бар сызықтық теңдеу» бөлімі БЖБ№5
|
№ |
Тапсырма 2-нұсқа |
балл |
|
1 |
b–ның қандай мәнінде 2х+18=36
және 3х-5b=7 теңдеулері мәндес болады?
|
3 |
|
2 |
Теңдеуді шешіңіз: 6,8х–1,7х+3,6=8,6+4,1х.
|
3 |
|
3 |
Теңдеуді шешіңіз: a) 3 |х – 2| = 9 b) 5|3х – 5|
= –20. |
4 |
|
4 |
Теңдеу құру арқылы шығарыңыз. Екі пунктен бір-біріне
қарама-қарсы бір уақытта екі автобус жолға шықты. Бірінші
автобустың жылдамдығы 35 км/сағ, ал екіншісінікі 62 км/сағ. Екеуі
кездескенде бірінші автобус екінші автобусқа қарағанда 125 км аз
жүрген болса, онда екінші автобус қанша жол
жүрді? |
3 |
|
|
Жалпы балл |
13 |
«Бір айнымалысы бар сызықтық теңсіздіктер» бөлім бойынша жиынтық бағалау БЖБ№6
|
№ |
Тапсырма 2-нұсқа |
балл |
|
1 |
Тіктөртбұрыш қабырғалары 11,2 ≤ a ≤ 12,4 , 2,1≤ b ≤ 4,5 аралығында болса, онда осы төртбұрыштың ауданы мен периметрін бағалаңыз.
|
4 |
|
2 |
Берілген сан аралықтарының сан түзуінде кескіндеп, қиылысуы мен бірігуін жазыңыз: (−∞; −3] және (−6; +∞)
|
3 |
|
3 |
Төмендегі сан аралықтарды теңсіздік түрінде жазыңыз: a) [–3; 6); b) [3,5; +∞)
|
2 |
|
4 |
Теңсіздіктер
жүйесінің бүтін шешімдерінің санын
табыңыз:
|
5 |
|
|
Жалпы балл |
14 |
|
№ |
Тапсырма 2-нұсқа |
балл |
|
1 |
Төмендегі шарттарға байланысты мысалдар келтіріңіз. Егер фигуралар: a)центрлік симметриясы бар, бірақ осьтік симметриясы жоқ; b) осьтік симметриясы бар, бірақ центрлік симметриясы жоқ; c) центрлік және осьтік симметриясы бар.
|
3 |
|
2 |
Координаталық жазықтықта ABCD төртбұрыш төбелері сәйкесінше (–2;2), (5;3), (5;–5), (–1;–7) нүктелерінде жатыр. a) ВС қабырғасы абсцисса осімен; b) АВ қабырғасы ордината осімен; c)АС кесіндісінің ордината осімен; қай нүктеде қиылысатынын жазыңыз.
|
4 |

шағым қалдыра аласыз