
Математика пәнін кәсіптік бағыт негізінде оқыту
Г. А. Хамитова
Қарағанды көлік –технологиялық колледжі КММ
Бұл мақалада математиканы оқыту барысында кәсіптік бағыттағы есептерді шығару, математикалық білімді еңбекпен байланысты іс-әрекеттерге қолдана білуге қөмектесетіндігі, математиканың қажеттілігіне қөз жеткізу пәнді оқытуда студенттердің қызығушылығын арттыратындығы айтылған.
В этой статье говорится о том, какие умения и навыки приобретают студенты в процессе обучения математики: решение задач на профессианальном уровне, приобретение навыков делового качества в ходе трудовой деятельности, развитие интересов студентов в деле изучения математики.
Қазіргі кезде математиканың рөлі ғылым мен техниканың дамуымен күрт өзгеріп отыр. Сондықтанда заман талабына сай, бәсекеге қабілетті, жан – жақты жетілген кәсіби мамандар даярлауда математиканың алатын орны ерекше. Бұл әрбір келешек маманның математикалық даярлықтар деңгейін көтеруді талап етеді.
Студенттер болашақ кәсіптік мамандығында математика пәнінің нақтылы практикалық қолданысымен таныспайтындықтары математиканы өмірден аулақ ғылым деп есептеуге негіз болып отыр. Оқыту процесінде шығарылатын есептердің үйретушілік сипаты бар екеніне назар аударылмайды, сондықтан практикалық қолдануды талап ететін күнделікті түрлі мәселелерге қолдана алмайды. Олар тек қабылдағанды қайта жаңғыртуды қайталау деңгейіндегі есептерді шығаруды ғана біледі.
Математика пәні оқытушыларының алдында тұрған мақсат, студенттерді қызықтықтыру, олардың болашақта өз өмірлерінде, жұмыстарында математиканың қажеттілігіне көз жеткізе отырып, математикалық білім беруді шығармашылықпен іске асыру.
Математиканы оқыту барысында студенттің өзі таңдаған кәсіптік бағытындағы мазмұнды есептерді шығару - математикалық білімді өмірмен ұштастыруға, алған білімдерін еңбекпен байланысты іс-әрекеттерге қолдана білуге көмектесер еді. Осы мақсатқа жету үшін кәсіптік мазмұнды математикалық есептерді қарастыру, оларды шығарудың әдіс-тәсілдерін үйрету, есеп шығару дағдыларын қалыптастыру қажет. Есеп шығару барысында кәсіптік ұғымдардың мағынасы ашылып, нақтыланады, оның ескерілмей жатқан жаңа бір қырлары байқалады. Математикалық теория мен практиканы ұштастыруда есептердің атқаратын рөлі зор. Сабақта шығарылатын есептердің әрбірі өтілген тақырып мазмұнын аша алуы, ол тақырыпты қайталауға, оны кәсіптік қолдануға мүмкіндік беруі керек.
Кәсіптік оқу орындарында математика пәні мұғалімдері үшін нақты бір мамандыққа бағытталған әдістемелік құрал – жабдықтар, дидактикалық материалдар жоқтың қасы.
Егер математиканы кәсіптік бағдар бағытында оқытудың әдістемелік жүйесін жасап, оларды оқыту үдерісіне қолдансақ, онда математиканы оқытудың тиімділігі артып, ойлау қабілетін қалыптастыруға мол мүмкіндіктер туар еді және студенттердің математикалық білім деңгейі көтерілер еді.
Бұл тығырықтан шығу үшін кәсіптік пән бағдарламаларымен таныса отырып, тақырыптарды сай іріктеп, есептер құрастырдық. Әрбір мамандық бойынша қандай тақырыптарға ерекше көңіл бөлу керектігін айқындалдық.
Іріктеу барысында мына талаптарды ескеруіміз қажет:
-
Танымдық мақсатына;
-
Есептің шартындағы сандық көрсеткіштердің дұрыс берілуіне;
-
Сұрақтың қойылуына және табылған шешімнің ақиқаттығына.
Есептің сұрағының шындыққа жанасуына және практикалық мазмұны дұрыс құрастырылуына мән бере отырып, есептерді жинақтағанда, оларды ой елегінен өткізіп мұқият болу керек.
Кәсіптік бағыттағы тапсырмалар әр түрлі әдістермен құрылуы мүмкін. Мысалы, оқулықтағы есептің мәтіні кәсіптік мағына беретіндей өзгертіліп берілуі немесе сурет, сызба, бойынша құрастырылуы мүмкін. Сондай – ақ кәсіптік бағыттағы ауызша тапсырмаларды да сабақтың барлық кезеңінде қолданауға болады.
Бізді айнала қоршаған әлемнің бәрінде геометриялық объектілер толып жатыр. Былайша айтқанда, адам әрқашанда геометриялық әлемнің қоршауында. Әсіресе, салынып жатқан құрылыстар геометриялық бейнелер арқылы танылады. Сондықтан стереометрия курсын оқыту барысында көпжақтар, айналу денелері, стереометрия аксиомалары, кеңістіктегі параллельдік, кеңістіктегі перпендикулярлық тақырыптарын «Кәсіптік білім беру (салалар бойынша)» мамандығында қалай оқытқаныма тоқталайын.
Жаңа түсініктің анықтамасын студенттің өзі беретіндей нәтижеге жеткізу үшін жаңа түсінікті қалыптастыру кезеңінде қолданған тиімді. Егер ол тапсырмалар студенттердің қызығушылығын, белсенділігін арттыратындай кәсіптік сұрақтарға байланысты болса, проблемалық жағдаяттардың туындауына әкеледі.
Мысалы, қабылдаған аксиомаларға нақты өмірден мысалдар келтіріп олардың қолданысын практикаға қайшылықсыз екендігін көрсету қажет.
Стереометрия курсындағы стереометрия аксиомаларын өту барысында студенттерге мынадай сұрақ қоюға болады. «Үш аяқты орындық орнықты ма, әлде төрт аяқты орнықты ма?» Өмірде төрт аяқты орындықтарды жиі кездестіргендіктен ойланбастан төрт аяқты дейді. Сонда мына тапсырманы беру керек. «Құрылыс алаңында пайдаланылатын геодезиялық құрылғы теодолит, нивелир неге үш аяқты қондырғыға орналастырған?»
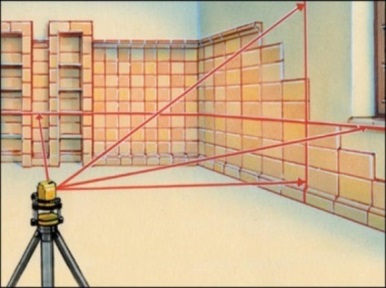

Талдау барысында «Берілген түзуде жатпайтын үш нүкте арқылы бір жазықтық жүргізуге болады және ол жалғыз ғана» деген аксиомадан шығатын салдардың көмегімен «Үш аяқты орындық әрқашан орнықты тұрады»,- деген тұжырымдамаға келдік. (Үш нүкте әрқашанда бір жазықтықта жатады)
Студенттер екіжақты бұрыш және сызықтық бұрыш ұғымдарын үлкен қызығушылықпен қабылдайды. Егер алдын – ала мына сұрақты беретін болсақ: «Бөлме қабырғасы мен еден бұрыш жасайды. Бұл бұрышты қалай өлшеуге болады?» Талдау барысында қабырға мен еденнің ортақ нүктесі арқылы перпендикуляр түзулер жүргізіп, пайда болған бұрышты өлшеу керек екендігін айтады. Нәтижесінде екіжақты бұрыш пен оның сызықтық бұрышына анықтама беріп, екі жақты бұрыштың шамасы өзінің сызықтық бұрышымен өлшенетіні нақтыланады.
Геометриялық денелердің көлемдерін, беттерінің аудандарын есептеу ұғымдарын қалыптастыруда кәсіптік мазмұнды есептерді көптеп қарастыруға болады.
1. Есеп. Ұзындығы 6 м, ені 4 м, биіктігі 3 м, ал
есік пен әйнектің ауданы барлық кабырғаның ауданының
 құрайтын бөлмеге түсқағаз
жапсыру керек. Егер түсқағаздың бір орамының ұзындығы 10 м, ал ені
50 см болса, онда бөлмеге қанша түсқағаз орамы қажет.
құрайтын бөлмеге түсқағаз
жапсыру керек. Егер түсқағаздың бір орамының ұзындығы 10 м, ал ені
50 см болса, онда бөлмеге қанша түсқағаз орамы қажет.

Алдымен берілген бөлме бетінің ауданын мына
формулалардың а)  ,
, 
 қайсысын пайдаланып
табуға болады деген сұрақ беріледі:
қайсысын пайдаланып
табуға болады деген сұрақ беріледі:
ә) формуласын қолданған дұрыс деп
ойлайсың? деген сияқты проблема қоя отырып есептің шешімін
табамыз.
формуласын қолданған дұрыс деп
ойлайсың? деген сияқты проблема қоя отырып есептің шешімін
табамыз.
Шешуі:
-
 3=60
3=60
-

-

-

-
 Жауабы: 10
Жауабы: 10
Сонымен
қатар, тағы мынандай есеп те шығартуға болады. Бөлменің қабырғасын
бояу үшін  - на 0,2 кг
бояу жұмсалсын және есік – терезе бөлме бетінің 12% -н құрайтын
болса, суреттегі берілген өлшемдер бойынша қанша колер жұмсалатынын
есепте.
- на 0,2 кг
бояу жұмсалсын және есік – терезе бөлме бетінің 12% -н құрайтын
болса, суреттегі берілген өлшемдер бойынша қанша колер жұмсалатынын
есепте.
Түзу мен жазықтықтың параллельдігі, перпендикулярлығы тақырыптарын бекіту кезеңінде мынадай тапсырманы студенттер қызығушылықпен орындайды.
Төрт еңісті шатырлы үйдің схемалық үлгісі бойынша «||», «⊥», «⋂» белгілер арқылы мына кестені толтыр.

|
Жазықтық Түзу |
ABCD |
|
|
|
|
MK |
|
|
|
|
|
BC |
|
|
|
|
|
MP |
|
|
|
|
|
AB |
|
|
|
|
«Темір жол көлігінде қозғалысты басқару және тасымалды ұйымдастыру» тобында да «Көпжақтар» мен «Айналу денелеріне» көп есептер қарастыруға болады. Суреттен көргендегідей жүк тасымалдау вагондары геометриялық фигуралар үлгісінде берілген. Жүк вагондары: жабық вагон, ашық вагон, жайдақ вагон (үсті ашық вагон), цистерна, хоппер-дозатор деп бөлінеді.

«Цилиндрдің, конустың көлемдерін» бекіту кезеңінде кәсіптік мағынасы ашылатындай мынандай тапсырма орындалды.


Сурет арқылы «Өндірістік көліктер» курсынан танысқан шахталық вагонетканың құрылысы, не үшін қолданылатынын пысықтап алғаннан кейін вагонетканың сыйымдылығын, яғни көлемін табуға тапсырма бердім. Алдымен вагонетканың геометриялық формасын анықтап алдық. Яғни жарты цилиндр мен тік бұрышты параллелепипедтің бірігуі деп қарастырып, көлемді есептеуге қажетті формулаларды анықтап алдық.



 берілген өлшемдер
берілген өлшемдер
 ,
, 
 арқылы
вагонетканың көлемін есептедік.
арқылы
вагонетканың көлемін есептедік.
Жабық вагон- әртүрлі жүктерді тасымалдауға, өзара сақтауға және ауа-райының әсерінен қорғауға арналған.
Оның: Жүк көтерімділігі - 66 т, сыйымдылық көлемі -
156 
ұзындығы - 17,6 м
ені - 2,7 м
биіктігі - 3,3 м. Осы жабық вагонның берілген өлшемдері арқылы есептер құрастыртып шығартуға болады.
«Көліктегі қозғалысты басқару мен тасымалдауды ұйымдастыру» мамандығында оқитын студенттермен «Функция» тақырыбына мынандай есеп құрастыруға болады.
Есеп. Таксиге отыру бағасы 250 тг, ал есептегішті қосқанда әр минутына 12 тг қосылып отырады.
а) у – тің х –ке тәуелдігін анықтайтын функцияның формуласын жаз.
ә) Осы формуламен берілген функция қандай функция?
б) Осы функцияның анықталу облысын тап.
Математиканың маңызды ұғымдарының бірі – интеграл. Анықталған интеграл арқылы жазық фигуралардың ауданы, дененің көлемі мен беті табылатындығын айтумен қатар, анықталған интегралды кәсіптік мазмұнды математикалық есептер шығарғанда қолдануға болатындығын айтып кеткен жөн.
1. Күндік жұмыс уақытының а-дан b- ға дейінгі уақыт аралығындағы жұмысшының өндірген өнімі мына формуламен есептеледі.
у= (1)
(1)
2. а-дан b -ға дейінгі уақыт аралығындағы қоймаға әкелінген тауар саны
да (1) формуламен есептеледі. Мұндағы  -бірлік уақыт ішінде қоймаға әкелінген
тауардың орташа есебі.
-бірлік уақыт ішінде қоймаға әкелінген
тауардың орташа есебі.
Мысалы:
Машина жасау өнеркәсібі бірінші жылы 31000 станок шығарды, одан кейін шығаруды жылына 55 данаға ұлғайтты. Амортизация шамасы 10% болғандағы 10 жыл ішіндегі амортизация аударымдылық құнын анықта.
Есептің шарты бойынша станоктардың шығарылуы у = 31000х + 55, мұндағы х – жылдар саны. Онда 10 жыл ішіндегі өнімді шығару көлемін мына интеграл арқылы беруге болады.
V =  , ал амортизация шамасы
, ал амортизация шамасы
 -ді құрайды.
-ді құрайды.
Туынды ұғымында да осындай мысалдарды көптеп келтіруге болады. Мысалы, сындық нүктелерді табуда мынандай мысал қарастыруға болады.
Жанармайдың шығыны тұрақты болатын әрбір автокөлік үшін бір жылдамдық бар. Ол қандай жылдамдық деп алдын- ала студенттерге сұрақ қоюға болады.
Мысалы: ГАЗ-69 автокөлігінің жанармай жұмсалысы оның қозғалыс жылдамдығына тәуелді және мына формуламен анықталатындығы тәжірибеде айқындалған.
 ,
,  ,
,
Мұндағы х
- жылдамдық, км/сағ;  - жолдың 100 км- дегі жанармай шығыны,
литрмен.
- жолдың 100 км- дегі жанармай шығыны,
литрмен.
Автокөліктің 100, 75, 40 км/сағ. жылдамдықтағы отынның жану жылдамдығын анықта.
 - функциясының туындысын
табамыз.
- функциясының туындысын
табамыз.
 = - 0,3+
0,006х
= - 0,3+
0,006х
Жанармайдың шығыны тұрақты болатын әрбір автокөлік үшін бір
жылдамдық бар. Ол жылдамдықты «сындық» деп атаймыз. Сындық
жылдамдықты анықтау үшін  = 0 табамыз. – 0,3 +
0,006х =
0,
= 0 табамыз. – 0,3 +
0,006х =
0,
х = 50 км/сағ.
Бұдан, қозғалыс жылдамдығы 50 км/сағ.- қа дейін болса отын шығыны азаяды, ал одан кейін көбейеді.
 = 0,3;
= 0,3;  = 0,15;
= 0,15;  = - 0,06.
= - 0,06.
«-» таңбасы жанармай шығынының жылдамдығы азайып бара жатқандығын көрсетеді.
Тексеретін болсақ:


Көріп тұрғандай шығын 0,297 л. – ге азайды.
х - жылдамдықтың өзгерісі жанармайдың шығынына әртүрлі әсер етеді. Бұдан байқағанымыз жанармайдың шығыны аз жылдамдықта азаяды, ал үлкен жылдамдықта көбейеді.
Біз математика бағдарламасында көбіне абстрактілі мазмұнды есептер шығарамыз. Тәжірибелік есептер көптеп кездеспейді, сондықтан есептердің мазмұнын өзгертіп есепті жаңа мағынада беруімізге тура келеді. Яғни оның дерексіз түрін тәжірибелік түрге айналдырып кәсіптік бағытқа икемдейміз.
Мысалы геометрия оқулығындағы есепті екі мамандыққа икемдеп мазмұнын мына түрге келтіріп өзгерттім. «Кәсіптік білім беру (салалар бойынша)» мамандығында.
Есеп. Көп кабатты тұрғын үйлер салу үшін 94
м құм әкелу керек. Құм
биіктігі 2 м, жасаушысы 4 м болатын конус пішіндес үймелерге тең
бөлінген. Қанша үйме
құм әкелу керек. Құм
биіктігі 2 м, жасаушысы 4 м болатын конус пішіндес үймелерге тең
бөлінген. Қанша үйме
құм әкелу керек?

Немесе осы есепті «Теміржол көлігінде қозғалысты басқару және тасымалдауды ұйымдастыру» мамандығына

Көмір биіктігі 2 м, жасаушысы 4 м болатын конус
пішіндес үймелерге тең бөлінген. Көлемі 94 м болатын көмір тасымалдайтын ашық
вагонға қанша үйме көмір салуға болады?
болатын көмір тасымалдайтын ашық
вагонға қанша үйме көмір салуға болады?
Сонымен қатар студенттердің өздеріне де өтіліп отырған тақырыптың өмірдегі қолданыстары, мамандыққа байланысы бар ма деген қосымша тапсырмаларға дайындалып келулеріне тапсырма беріп отырамын.
Және мынадай тақырыптарда қосымша баяндамалар мен жобалар жазуға тапсырмалар бердім. «Геодезия және математика» «Неліктен көптеген құрылыс материалдары мен объектілер тікбұрышты параллелепипед түрінде болады?», «Айналу денелері үлгісіндегі құрылыс материалдары мен құралдары» «Көпжақтар үлгісіндегі құрылыс материалдары мен құралдары»
Қорыта айтқанда, оқыту процесінде математиканы кәсіппен байланыстыру абстрактілі математикалық теорияларды тереңірек ұғудың қажетті шарты болып табылады. Олай болса математиканы өмір тәжірибесіне сүйене оқыту студенттердің математикаға қызығушылығын және дайындық сапасын сөзсіз арттырады. Кәсіптік мазмұндағы бағдарламадағы тақырыптарға сай құрастырған есептер арқылы студенттер математиканың пайдасы мен қажеттілігін түсінеді.
Қолданылған әдебиеттер
1. В.М. Монохов, В.Ф. Любичева Т.В.Малкова Преподавание математики и экономическая подготовка учащихся профтехучилищ. Москва «Высшая школа» 1989
2. Н.Н. Михайлова Профессиональная направленность обучения на уроках математики. Москва «Высшая школа» 1989
3. Г.Х. Заббарова Профессиональная ориентация на уроках математики Қазақстан кәсіпкері. Профессионал Казақстана 2008, №9
4. А.Н. Колмогоров, А. М. Абрамов және басқалар. Алгебра және анализ бастамалары. Жалпы білім беретін мектептің 10-11 сыныптарына арналған оқулық. «Просвещение-Казакстан» Алматы, 2002
5. Ж.Қайдасов, В. Гусев, Ә. Қағазбаева Геометрия. Жалпы білім беретін мектептің жаратылыстану – математика бағытындағы 10 сыныбына арналған оқулық. Алматы, «Мектеп» 2006
6. А.П. Погорелов Геометрия Орта мектептің 7 -11 сыныбына арналған оқулық М.; Просвещение, 2002
7. Ж.Бердікеев. І.Есенғабылов. Орта мектепте математиканы оқыту мәселелері.Математика және физика 2009, №1
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Математика пәнін кәсіптік бағыт негізінде оқыту
Математика пәнін кәсіптік бағыт негізінде оқыту
Математика пәнін кәсіптік бағыт негізінде оқыту
Г. А. Хамитова
Қарағанды көлік –технологиялық колледжі КММ
Бұл мақалада математиканы оқыту барысында кәсіптік бағыттағы есептерді шығару, математикалық білімді еңбекпен байланысты іс-әрекеттерге қолдана білуге қөмектесетіндігі, математиканың қажеттілігіне қөз жеткізу пәнді оқытуда студенттердің қызығушылығын арттыратындығы айтылған.
В этой статье говорится о том, какие умения и навыки приобретают студенты в процессе обучения математики: решение задач на профессианальном уровне, приобретение навыков делового качества в ходе трудовой деятельности, развитие интересов студентов в деле изучения математики.
Қазіргі кезде математиканың рөлі ғылым мен техниканың дамуымен күрт өзгеріп отыр. Сондықтанда заман талабына сай, бәсекеге қабілетті, жан – жақты жетілген кәсіби мамандар даярлауда математиканың алатын орны ерекше. Бұл әрбір келешек маманның математикалық даярлықтар деңгейін көтеруді талап етеді.
Студенттер болашақ кәсіптік мамандығында математика пәнінің нақтылы практикалық қолданысымен таныспайтындықтары математиканы өмірден аулақ ғылым деп есептеуге негіз болып отыр. Оқыту процесінде шығарылатын есептердің үйретушілік сипаты бар екеніне назар аударылмайды, сондықтан практикалық қолдануды талап ететін күнделікті түрлі мәселелерге қолдана алмайды. Олар тек қабылдағанды қайта жаңғыртуды қайталау деңгейіндегі есептерді шығаруды ғана біледі.
Математика пәні оқытушыларының алдында тұрған мақсат, студенттерді қызықтықтыру, олардың болашақта өз өмірлерінде, жұмыстарында математиканың қажеттілігіне көз жеткізе отырып, математикалық білім беруді шығармашылықпен іске асыру.
Математиканы оқыту барысында студенттің өзі таңдаған кәсіптік бағытындағы мазмұнды есептерді шығару - математикалық білімді өмірмен ұштастыруға, алған білімдерін еңбекпен байланысты іс-әрекеттерге қолдана білуге көмектесер еді. Осы мақсатқа жету үшін кәсіптік мазмұнды математикалық есептерді қарастыру, оларды шығарудың әдіс-тәсілдерін үйрету, есеп шығару дағдыларын қалыптастыру қажет. Есеп шығару барысында кәсіптік ұғымдардың мағынасы ашылып, нақтыланады, оның ескерілмей жатқан жаңа бір қырлары байқалады. Математикалық теория мен практиканы ұштастыруда есептердің атқаратын рөлі зор. Сабақта шығарылатын есептердің әрбірі өтілген тақырып мазмұнын аша алуы, ол тақырыпты қайталауға, оны кәсіптік қолдануға мүмкіндік беруі керек.
Кәсіптік оқу орындарында математика пәні мұғалімдері үшін нақты бір мамандыққа бағытталған әдістемелік құрал – жабдықтар, дидактикалық материалдар жоқтың қасы.
Егер математиканы кәсіптік бағдар бағытында оқытудың әдістемелік жүйесін жасап, оларды оқыту үдерісіне қолдансақ, онда математиканы оқытудың тиімділігі артып, ойлау қабілетін қалыптастыруға мол мүмкіндіктер туар еді және студенттердің математикалық білім деңгейі көтерілер еді.
Бұл тығырықтан шығу үшін кәсіптік пән бағдарламаларымен таныса отырып, тақырыптарды сай іріктеп, есептер құрастырдық. Әрбір мамандық бойынша қандай тақырыптарға ерекше көңіл бөлу керектігін айқындалдық.
Іріктеу барысында мына талаптарды ескеруіміз қажет:
-
Танымдық мақсатына;
-
Есептің шартындағы сандық көрсеткіштердің дұрыс берілуіне;
-
Сұрақтың қойылуына және табылған шешімнің ақиқаттығына.
Есептің сұрағының шындыққа жанасуына және практикалық мазмұны дұрыс құрастырылуына мән бере отырып, есептерді жинақтағанда, оларды ой елегінен өткізіп мұқият болу керек.
Кәсіптік бағыттағы тапсырмалар әр түрлі әдістермен құрылуы мүмкін. Мысалы, оқулықтағы есептің мәтіні кәсіптік мағына беретіндей өзгертіліп берілуі немесе сурет, сызба, бойынша құрастырылуы мүмкін. Сондай – ақ кәсіптік бағыттағы ауызша тапсырмаларды да сабақтың барлық кезеңінде қолданауға болады.
Бізді айнала қоршаған әлемнің бәрінде геометриялық объектілер толып жатыр. Былайша айтқанда, адам әрқашанда геометриялық әлемнің қоршауында. Әсіресе, салынып жатқан құрылыстар геометриялық бейнелер арқылы танылады. Сондықтан стереометрия курсын оқыту барысында көпжақтар, айналу денелері, стереометрия аксиомалары, кеңістіктегі параллельдік, кеңістіктегі перпендикулярлық тақырыптарын «Кәсіптік білім беру (салалар бойынша)» мамандығында қалай оқытқаныма тоқталайын.
Жаңа түсініктің анықтамасын студенттің өзі беретіндей нәтижеге жеткізу үшін жаңа түсінікті қалыптастыру кезеңінде қолданған тиімді. Егер ол тапсырмалар студенттердің қызығушылығын, белсенділігін арттыратындай кәсіптік сұрақтарға байланысты болса, проблемалық жағдаяттардың туындауына әкеледі.
Мысалы, қабылдаған аксиомаларға нақты өмірден мысалдар келтіріп олардың қолданысын практикаға қайшылықсыз екендігін көрсету қажет.
Стереометрия курсындағы стереометрия аксиомаларын өту барысында студенттерге мынадай сұрақ қоюға болады. «Үш аяқты орындық орнықты ма, әлде төрт аяқты орнықты ма?» Өмірде төрт аяқты орындықтарды жиі кездестіргендіктен ойланбастан төрт аяқты дейді. Сонда мына тапсырманы беру керек. «Құрылыс алаңында пайдаланылатын геодезиялық құрылғы теодолит, нивелир неге үш аяқты қондырғыға орналастырған?»


Талдау барысында «Берілген түзуде жатпайтын үш нүкте арқылы бір жазықтық жүргізуге болады және ол жалғыз ғана» деген аксиомадан шығатын салдардың көмегімен «Үш аяқты орындық әрқашан орнықты тұрады»,- деген тұжырымдамаға келдік. (Үш нүкте әрқашанда бір жазықтықта жатады)
Студенттер екіжақты бұрыш және сызықтық бұрыш ұғымдарын үлкен қызығушылықпен қабылдайды. Егер алдын – ала мына сұрақты беретін болсақ: «Бөлме қабырғасы мен еден бұрыш жасайды. Бұл бұрышты қалай өлшеуге болады?» Талдау барысында қабырға мен еденнің ортақ нүктесі арқылы перпендикуляр түзулер жүргізіп, пайда болған бұрышты өлшеу керек екендігін айтады. Нәтижесінде екіжақты бұрыш пен оның сызықтық бұрышына анықтама беріп, екі жақты бұрыштың шамасы өзінің сызықтық бұрышымен өлшенетіні нақтыланады.
Геометриялық денелердің көлемдерін, беттерінің аудандарын есептеу ұғымдарын қалыптастыруда кәсіптік мазмұнды есептерді көптеп қарастыруға болады.
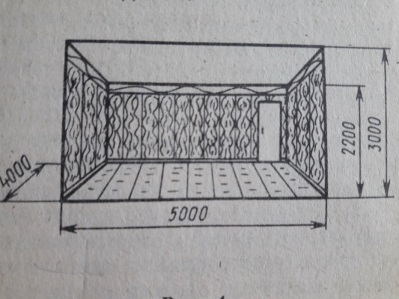
1. Есеп. Ұзындығы 6 м, ені 4 м, биіктігі 3 м, ал
есік пен әйнектің ауданы барлық кабырғаның ауданының
 құрайтын бөлмеге түсқағаз
жапсыру керек. Егер түсқағаздың бір орамының ұзындығы 10 м, ал ені
50 см болса, онда бөлмеге қанша түсқағаз орамы қажет.
құрайтын бөлмеге түсқағаз
жапсыру керек. Егер түсқағаздың бір орамының ұзындығы 10 м, ал ені
50 см болса, онда бөлмеге қанша түсқағаз орамы қажет.

Алдымен берілген бөлме бетінің ауданын мына
формулалардың а)  ,
, 
 қайсысын пайдаланып
табуға болады деген сұрақ беріледі:
қайсысын пайдаланып
табуға болады деген сұрақ беріледі:
ә) формуласын қолданған дұрыс деп
ойлайсың? деген сияқты проблема қоя отырып есептің шешімін
табамыз.
формуласын қолданған дұрыс деп
ойлайсың? деген сияқты проблема қоя отырып есептің шешімін
табамыз.
Шешуі:
-
 3=60
3=60
-

-

-

-
 Жауабы: 10
Жауабы: 10

Сонымен
қатар, тағы мынандай есеп те шығартуға болады. Бөлменің қабырғасын
бояу үшін  - на 0,2 кг
бояу жұмсалсын және есік – терезе бөлме бетінің 12% -н құрайтын
болса, суреттегі берілген өлшемдер бойынша қанша колер жұмсалатынын
есепте.
- на 0,2 кг
бояу жұмсалсын және есік – терезе бөлме бетінің 12% -н құрайтын
болса, суреттегі берілген өлшемдер бойынша қанша колер жұмсалатынын
есепте.
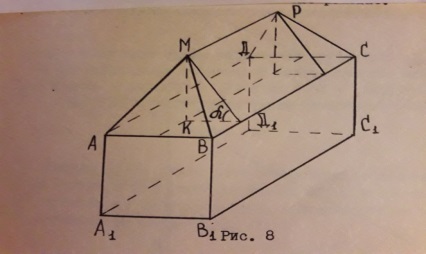
Түзу мен жазықтықтың параллельдігі, перпендикулярлығы тақырыптарын бекіту кезеңінде мынадай тапсырманы студенттер қызығушылықпен орындайды.
Төрт еңісті шатырлы үйдің схемалық үлгісі бойынша «||», «⊥», «⋂» белгілер арқылы мына кестені толтыр.


|
Жазықтық Түзу |
ABCD |
|
|
|
|
MK |
|
|
|
|
|
BC |
|
|
|
|
|
MP |
|
|
|
|
|
AB |
|
|
|
|
«Темір жол көлігінде қозғалысты басқару және тасымалды ұйымдастыру» тобында да «Көпжақтар» мен «Айналу денелеріне» көп есептер қарастыруға болады. Суреттен көргендегідей жүк тасымалдау вагондары геометриялық фигуралар үлгісінде берілген. Жүк вагондары: жабық вагон, ашық вагон, жайдақ вагон (үсті ашық вагон), цистерна, хоппер-дозатор деп бөлінеді.

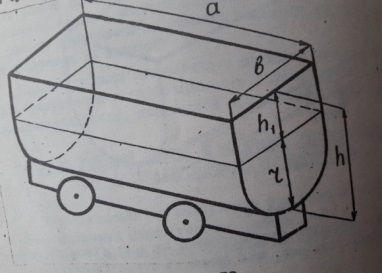
«Цилиндрдің, конустың көлемдерін» бекіту кезеңінде кәсіптік мағынасы ашылатындай мынандай тапсырма орындалды.



Сурет арқылы «Өндірістік көліктер» курсынан танысқан шахталық вагонетканың құрылысы, не үшін қолданылатынын пысықтап алғаннан кейін вагонетканың сыйымдылығын, яғни көлемін табуға тапсырма бердім. Алдымен вагонетканың геометриялық формасын анықтап алдық. Яғни жарты цилиндр мен тік бұрышты параллелепипедтің бірігуі деп қарастырып, көлемді есептеуге қажетті формулаларды анықтап алдық.



 берілген өлшемдер
берілген өлшемдер
 ,
, 
 арқылы
вагонетканың көлемін есептедік.
арқылы
вагонетканың көлемін есептедік.
Жабық вагон- әртүрлі жүктерді тасымалдауға, өзара сақтауға және ауа-райының әсерінен қорғауға арналған.
Оның: Жүк көтерімділігі - 66 т, сыйымдылық көлемі -
156 
ұзындығы - 17,6 м
ені - 2,7 м
биіктігі - 3,3 м. Осы жабық вагонның берілген өлшемдері арқылы есептер құрастыртып шығартуға болады.
«Көліктегі қозғалысты басқару мен тасымалдауды ұйымдастыру» мамандығында оқитын студенттермен «Функция» тақырыбына мынандай есеп құрастыруға болады.
Есеп. Таксиге отыру бағасы 250 тг, ал есептегішті қосқанда әр минутына 12 тг қосылып отырады.
а) у – тің х –ке тәуелдігін анықтайтын функцияның формуласын жаз.
ә) Осы формуламен берілген функция қандай функция?
б) Осы функцияның анықталу облысын тап.
Математиканың маңызды ұғымдарының бірі – интеграл. Анықталған интеграл арқылы жазық фигуралардың ауданы, дененің көлемі мен беті табылатындығын айтумен қатар, анықталған интегралды кәсіптік мазмұнды математикалық есептер шығарғанда қолдануға болатындығын айтып кеткен жөн.
1. Күндік жұмыс уақытының а-дан b- ға дейінгі уақыт аралығындағы жұмысшының өндірген өнімі мына формуламен есептеледі.
у= (1)
(1)
2. а-дан b -ға дейінгі уақыт аралығындағы қоймаға әкелінген тауар саны
да (1) формуламен есептеледі. Мұндағы  -бірлік уақыт ішінде қоймаға әкелінген
тауардың орташа есебі.
-бірлік уақыт ішінде қоймаға әкелінген
тауардың орташа есебі.
Мысалы:
Машина жасау өнеркәсібі бірінші жылы 31000 станок шығарды, одан кейін шығаруды жылына 55 данаға ұлғайтты. Амортизация шамасы 10% болғандағы 10 жыл ішіндегі амортизация аударымдылық құнын анықта.
Есептің шарты бойынша станоктардың шығарылуы у = 31000х + 55, мұндағы х – жылдар саны. Онда 10 жыл ішіндегі өнімді шығару көлемін мына интеграл арқылы беруге болады.
V =  , ал амортизация шамасы
, ал амортизация шамасы
 -ді құрайды.
-ді құрайды.
Туынды ұғымында да осындай мысалдарды көптеп келтіруге болады. Мысалы, сындық нүктелерді табуда мынандай мысал қарастыруға болады.
Жанармайдың шығыны тұрақты болатын әрбір автокөлік үшін бір жылдамдық бар. Ол қандай жылдамдық деп алдын- ала студенттерге сұрақ қоюға болады.
Мысалы: ГАЗ-69 автокөлігінің жанармай жұмсалысы оның қозғалыс жылдамдығына тәуелді және мына формуламен анықталатындығы тәжірибеде айқындалған.
 ,
,  ,
,
Мұндағы х
- жылдамдық, км/сағ;  - жолдың 100 км- дегі жанармай шығыны,
литрмен.
- жолдың 100 км- дегі жанармай шығыны,
литрмен.
Автокөліктің 100, 75, 40 км/сағ. жылдамдықтағы отынның жану жылдамдығын анықта.
 - функциясының туындысын
табамыз.
- функциясының туындысын
табамыз.
 = - 0,3+
0,006х
= - 0,3+
0,006х
Жанармайдың шығыны тұрақты болатын әрбір автокөлік үшін бір
жылдамдық бар. Ол жылдамдықты «сындық» деп атаймыз. Сындық
жылдамдықты анықтау үшін  = 0 табамыз. – 0,3 +
0,006х =
0,
= 0 табамыз. – 0,3 +
0,006х =
0,
х = 50 км/сағ.
Бұдан, қозғалыс жылдамдығы 50 км/сағ.- қа дейін болса отын шығыны азаяды, ал одан кейін көбейеді.
 = 0,3;
= 0,3;  = 0,15;
= 0,15;  = - 0,06.
= - 0,06.
«-» таңбасы жанармай шығынының жылдамдығы азайып бара жатқандығын көрсетеді.
Тексеретін болсақ:


Көріп тұрғандай шығын 0,297 л. – ге азайды.
х - жылдамдықтың өзгерісі жанармайдың шығынына әртүрлі әсер етеді. Бұдан байқағанымыз жанармайдың шығыны аз жылдамдықта азаяды, ал үлкен жылдамдықта көбейеді.
Біз математика бағдарламасында көбіне абстрактілі мазмұнды есептер шығарамыз. Тәжірибелік есептер көптеп кездеспейді, сондықтан есептердің мазмұнын өзгертіп есепті жаңа мағынада беруімізге тура келеді. Яғни оның дерексіз түрін тәжірибелік түрге айналдырып кәсіптік бағытқа икемдейміз.
Мысалы геометрия оқулығындағы есепті екі мамандыққа икемдеп мазмұнын мына түрге келтіріп өзгерттім. «Кәсіптік білім беру (салалар бойынша)» мамандығында.
Есеп. Көп кабатты тұрғын үйлер салу үшін 94
м құм әкелу керек. Құм
биіктігі 2 м, жасаушысы 4 м болатын конус пішіндес үймелерге тең
бөлінген. Қанша үйме
құм әкелу керек. Құм
биіктігі 2 м, жасаушысы 4 м болатын конус пішіндес үймелерге тең
бөлінген. Қанша үйме
құм әкелу керек?

Немесе осы есепті «Теміржол көлігінде қозғалысты басқару және тасымалдауды ұйымдастыру» мамандығына

Көмір биіктігі 2 м, жасаушысы 4 м болатын конус
пішіндес үймелерге тең бөлінген. Көлемі 94 м болатын көмір тасымалдайтын ашық
вагонға қанша үйме көмір салуға болады?
болатын көмір тасымалдайтын ашық
вагонға қанша үйме көмір салуға болады?
Сонымен қатар студенттердің өздеріне де өтіліп отырған тақырыптың өмірдегі қолданыстары, мамандыққа байланысы бар ма деген қосымша тапсырмаларға дайындалып келулеріне тапсырма беріп отырамын.
Және мынадай тақырыптарда қосымша баяндамалар мен жобалар жазуға тапсырмалар бердім. «Геодезия және математика» «Неліктен көптеген құрылыс материалдары мен объектілер тікбұрышты параллелепипед түрінде болады?», «Айналу денелері үлгісіндегі құрылыс материалдары мен құралдары» «Көпжақтар үлгісіндегі құрылыс материалдары мен құралдары»
Қорыта айтқанда, оқыту процесінде математиканы кәсіппен байланыстыру абстрактілі математикалық теорияларды тереңірек ұғудың қажетті шарты болып табылады. Олай болса математиканы өмір тәжірибесіне сүйене оқыту студенттердің математикаға қызығушылығын және дайындық сапасын сөзсіз арттырады. Кәсіптік мазмұндағы бағдарламадағы тақырыптарға сай құрастырған есептер арқылы студенттер математиканың пайдасы мен қажеттілігін түсінеді.
Қолданылған әдебиеттер
1. В.М. Монохов, В.Ф. Любичева Т.В.Малкова Преподавание математики и экономическая подготовка учащихся профтехучилищ. Москва «Высшая школа» 1989
2. Н.Н. Михайлова Профессиональная направленность обучения на уроках математики. Москва «Высшая школа» 1989
3. Г.Х. Заббарова Профессиональная ориентация на уроках математики Қазақстан кәсіпкері. Профессионал Казақстана 2008, №9
4. А.Н. Колмогоров, А. М. Абрамов және басқалар. Алгебра және анализ бастамалары. Жалпы білім беретін мектептің 10-11 сыныптарына арналған оқулық. «Просвещение-Казакстан» Алматы, 2002
5. Ж.Қайдасов, В. Гусев, Ә. Қағазбаева Геометрия. Жалпы білім беретін мектептің жаратылыстану – математика бағытындағы 10 сыныбына арналған оқулық. Алматы, «Мектеп» 2006
6. А.П. Погорелов Геометрия Орта мектептің 7 -11 сыныбына арналған оқулық М.; Просвещение, 2002
7. Ж.Бердікеев. І.Есенғабылов. Орта мектепте математиканы оқыту мәселелері.Математика және физика 2009, №1

шағым қалдыра аласыз


















