
қ Қайролла М.М
Математика пәнінен деңгейлік тапсырмалар
2-сынып
2015-2016 жыл
Кіріспе
Ұсынылып отырған әдістемелік құрал математика пәні бойынша жалпы білім беретін орта мектептің 2-кластарына арналған мемлекеттік оқу бағдарламасы негізінде жасалған.
«Қазақстан Республикасының Білім туралы» Заңына сәйкес «Әр баланың жеке қабілетіне қарай интеллектуалдық дамуын, жеке адамның дарындылығын, талантын, қабілетін дамыту» сияқты өзекті мәселе енгізіліп отырғаны белгілі. Осыған орай, оқу үрдісін оқу қызметіне сәйкестендіріп ұйымдастырса, оқушылыр өз мүмкіндіктерін одан да жоғары деңгейде жүзеге асырулары әбден мүмкін.
Әдістемелік құралда баланың ақыл – ойын, логикалық ойлау мен шығармашылық қабілеттерін дамыту, әрекет нәтижесінде белгілі тұжырым жасауға үйрететін деңгейлік тапсырмалар берілген.
Деңгейлеп оқыту барысында оқушының бірінші деңгейдегі тапсырмаларды дұрыс орындағаны есепке алынып отырылады.
Қандай оқушы болмасын, мысалы
өзінің жақсы оқитынына қарамастан, жұмысын
«оқушылық»,
«міндетті», 1-ші деңгейдің , ол үшін жеңіл болса да, тапсырмаларын
орындаудан бастайды.
Барлық оқушылар жұмысын бір мезгілде бастап: әрқайсысы, білім
игерудегі өз қабілетіне қарай, өз биігіне жетеді. Бұл барлық
оқушыларды тірек білімімен қамтамасыз етеді және Қазақстан
Республикасының Білім туралы Заңының талаптарына сай келеді.
Нақтырақ айтсақ - барлық оқушылардың оқу мақсатында 100% қол
жеткізуінің кепілі болады және оқу пәндерінің барлық тақырыбы
бойынша ең болмағанда міндетті бірінші деңгейді игеруін толық жүзеге асырады.
Деңгейлік тапсырмаларға математика пәнінен, төмендегідей талаптар қойылады.
Бірінші деңгейдегі тапсырмаларға:
1.Жаттап алуға лайықталған болуы керек
2.Алдыңғы сабақта жаңадан меңгерілген білімнің өңін өзгертпей қайталап, пысықтануына мүмкіндік беруі тиіс
3.Тапсырмалар жаңа тақырып үшін типті және өмірмен байланысты болуы керек.
Математика пәнінде мұндай талаптар жаңа тақырыпты игеру соңында шығарған есептерге ұқсас тапсырмалар құру арқылы орындалады және олар оқушының өзі шығарған ереже, анықтама, заңдарын бекітуге арналады. Мұндай тапсырмаларды құрастырған кезде олардың танымдылығы мен қызықтылық жақтарына ерекше көңіл аударған жөн.
Екінші деңгейдегі тапсырмаларға:
1.Өтіп кеткен материалдарды реттеуге және жүйелеуге берілген тапсырмалар. Бұлар өзгертілген жағдайлардағы тапсырмалар, яғни бұрынғы тапсырмаларға ұқсас, бірақ оларды орындау үшін алғашқы алған білімдерін түрлендіріп пайдалану қажет болады.
2.Математика мұндай іс-әрекетке келтіретін тапсырмалар: мәтінмен берілген кері есептер; кері байланыс функциясын атқаратын тексеру тапсырмалары т.с. с.
3.Оқушының ойлау қабылетін жетілдіруге берілетін тапсырмалар. Оларда біздің ұлттық ерекшеліктеріміз ескеріліп, танымдық және үйретімділік маңызы болуы қажет болады. Бұлар : логикалық есептер, ребустар мен сөзжұмбақтар.
Үшінші эвристикалық деңгейдегі тапсырмаларды біз төмендегінше топтастырдық:
1.Танымдық-іздену (эвристикалық) түрдегі тапсырмаларды орындау барысында оқушылар жаңа тақырып бойынша меңгерген алғашқы қарапайым білімдерін (заңдылықтар шығару, анықтамалар жаттау, т .с. с. жетілдіріп, тереңдетумен қатар, ол тағы да жаңа білімді меңгеріп, өзі үшін жаңалық ашуы тиіс.Мұндай жұмыс –анализ бен синтез және салыстыру арқылы негізгісін анықтау, қорытындылау сияқты ой жұмыстарын қажет етеді. Мұндай есептерді шешу барысын оқушылар жаңа есептерге тап болады да, проблемалық жағдай туындайды. Оны шешу үшін оқушы жаңа әдістер іздеуі керек.
2. Әртүрлі әдіс, тәсілдермен шешілетін есептер
Қорыта келе, оқытудың жаңа технологиясы , яғни «Деңгейлеп оқыту технологиясы » еліміздің көптеген мектептерінде қолданылып жүр. Деңгейлік тапсырмалар қызғылықты мазмұндалған болса, оқушыларда ынталану пайда болады. Олар өзара бәсекелесе отырып жұмбақ , сөзжұмбақ , ребустар сияқты әртүрлі тапсырмаларды шешіп , өтіп жатқан тақырыпты өзі қорытындылауға тырысады, себебі, ертең жаңа тақырып басталады. Нәтижесінде оқушылардың ынтасы артып, сонымен қатар қызығушылығы де күннен –күнге жоғарылай түседі. Демек , мұғалім берген тапсырмалар оқушылардың біліктілігі мен дағдысын қалыптастыруа отырып және бағалау деңгейі жоғарылай түседі. Сонымен қатар, тапсырмалар ауқымы да өсіп , шығармашылыққа ұласады.
Ақыл-ойды тәртіпке келтіретін математика
Мектеп оқушылары кейде: «Маған математиканың керегі жоқ, өйткені мен тіл-әдебиет мұғалімі, артист, немесе суретші боламын»— дейді. Әрине, олардың бұлай деуі дұрыс емес. Бала кезінен бастап математикамен шұғылданған адам өзінің ой өрісі мен зеректігін дамытады, мақсатына жету үшін табанды болуға ерік-жігерін тәрбиелей алады. Сондықтан да мұғалімге де, дәрігерге де, артиске де және суретшіге де математика қажет.
Ежелгі гректер заманынан бастап-ақ математикамен шұғылдану адамды дұрыс және жүйелі түрде ойлауға, өз ойын тиянақты тұжырымдап айта білуге үйрететіндігі белгілі болған. Математика бізге айнала қоршаған сандар мен фигуралардан тұратын ерекше әлемнің құпия сырын ашып береді.
Адамның бұйымдарды қажетті ретпен топтау, санау, өлшемдері мен түрін табу, олардың өзара орналасу қалпын анықтау секілді жұмыстармен түйіспейтін қызмет саласын атау қиын. Қарапайым есептеу мен өлшеу — бұл әлі математика емес! Maтематика бізді керексіз қайта-қайта санаудан құтылуға, бұрыннан белгі-жайттар арқылы бізге белгісіз жайтты таба білуге үйретеді. Мұның техника мен ғылым үшін аса зор маңызы осы қасиетінде.
Қарапайым мысал келтірейік: бір бумада 20 кітап бар, қоймадағы осындай барлық бумалардың саны 150. Математикалық тұрғыдан барлық бумаларды шешіп, олардағы кітаптарды «жеке-жеке санап жатудың керегі жоқ. Көбейту амалы қоймада барлығы 20Х 150=3000 кітап бар екенін көрсетеді.
Математика бұдан жүз жиырма жыл бұрын астрономдар француз Леверье мен ағылшын Адамсқа Уран планетасының қозғалысындағы шамалы ауытқудың себебі одан әрірек, Күннен қашықтау орналасқан белгісіз бір планетаның қозғалысы әсерінен болады деп тұжырымдауларына мүмкіндік берді. Олар бұл планетаны аспанның қай жерінен іздеу керектігін есептеп тауып, телескопты сол тұсқа бағыттап қарағанда жаңа планета көрінген. Олар бұл планетаға Нептун деп ат қойған.
Кей кездері математикаға ешбір қатысы жоқ болып көрінетін мәселенің өзі математикалық жаңалық ашуға әкеп соқтырады. Мысалы, бұдан 350 жыл бұрын өмір сүрген тамаша ғалым Кеплерді шарап саудагерлерінің формалары әр түрлі бөшкелерінің сыйымдылықтарын қалай анықтайтыны ойға қалдырған. Олар бөшкенің аузындағы тесіктен таяқ жүгіртіп, оның түбіне дейінгі аралықты өлшеген.
Кеплер саудагерлердің бөшке көлемін қалай анықтағанын көріп, формлары бөшке, алма, айва, тгпті түрік сәлдесі секілді заттардың да көлемдерін есептеуге арналған математикалық формула ойлап тапқан. Осы жайт кейіннен өзге ғалымдардың бұл күнде инженерлер мен физиктерге өте қажет жаңа математикалық ғылым — интегралдық есептеуді жасап шығаруларына көмектесті.
Орыс ғалымдары Н. Е. Жуковский мен С. А. Чаплыгин бұдан жарты ғасыр бұрын математиканың көмегімен самолеттің белгілі бір мөлшердегі жүкті көтеріп ұшуы үшін, оның қанатының формасы мен өлшемдерінің қандай болуы керектігін есептеген. Математика ауа райын алдын ала болжауға, көпірлердің және ғимараттар күмбездерінің беріктігін, спутниктер орбиталарын есептеп табуға көмектеседі...
Математика ғылым ретінде ешқашан бір орнында тапжылмай тұрып қалған емес. Өмір, практика, толассыз дамып келе жатқан техника және басқа да ғылымдар оның алдына әркез жаңа мәселелер қойып отырады. Бұларды шешу үшін, бұрыннан белгілі білім атаулы жеткіліксіз, сондықтан математик ғалымдарға жаңа әдістер табуға, жаңа теориялар жасауға тура келеді. Қазіргі кезде көптеген күрделі математикалық есептеулерді адамның орнына машиналар атқарады.
Мектеп оқушылары алатын мәліметтер мен тәсілдер әрине, математиканың тек әліппесі ғана. Құдіретті де қызғылықты математика ғылымының шалқыған дариядай, тіптен ұшы-қиыры жоқ салаларына апаратын даңғыл жол, оқушылар үшін мектеп қабырғасындағы математикалық білімдер: арифметимка, алгебра және геометрия пәндерінен басталады.
Математика (грекше: μάθημα — ғылым, білім, оқу; μαθηματικός — білуге құштарлық) — әлдебір әлемнің сандық қатынастары мен кеңістіктік формалары, оның ішінде — структуралар, өзгерістер, белгісіздік жөніндегі ғылым. Ол абстрактілендіру және логикалық қорыту, есептеу, санау, өлшеу және физикалық нәрселерді жүйелі түрде орнықтыру, бейнелеу мен өзгерістерді оқыту арқылы көрініс табады.
Математиктер жаңа тұжырымдамаларды сипаттайтын осы түсніктерді ретімен таңдалып алынған аксиомалар мен анықтамаларды пайдалана қорыта отырып зерттейді.
Математика тарихы
Көне Мысыр математикасы
Көне Мысыр әлемдегі ең байырғы мәдениет ошақтарының бірі. Ніл өзенінің екі жағалауына орналасқан бұл ел б.з.б. 3200-ші жж біртұтас мемлекет болып бірікті. Ніл өзені әр жылда тасып, жағалаудағы егістік жерлерді шайып кетіп отырған, тасу мезгілі аяқталған соң тұрғындардың жерін қайта өлшеп бөлу керек болады, ұзақ жылғы жер өлшеу тәжірибесінің арқасында геометрия ғылымы пайда болған (геометрия – грекше сөз, гео — жер, метро — өлшеу деген мағына береді).
Көне мысырлықтар ертеден ондық санау жүйесін қолдануды білген, бірақ оның әрбір орындағы сандардың жазылу ережесін білмеген, мысалға 111-ді жазу үшін, 1-ді үш рет қайталап жазбаған, керісінше әр орындағы 1-лерді әр түрлі белгілермен бейнелеген. Көне мысырлықтардың негізгі амалы қосу болған, ал көбейту қосудың қайталанып келуі ретінде есептелген. Олар бір айнымалысы бар бірінші дәрежелі теңдеулерді шеше алған, әрі арифметикалық, геометриялық прогрессиялардың қарапайым есептерін шеше алатын болған.
Ежелгі Бабыл математикасы
Көне Мысырда математиканың туумен қатар ертедегі Бабыл тұрғындары және шумерлер мен аккадтықтар өз алдына өздерінің дербес математикасын жасап шығарды. Бұл халықтар сына сияқты сызықшалардан құралатын таңбалар арқылы (19 ғ-да археологиялық қазбалар кезінде табылған) күн көзіне қойғанда тастай қатайып қалатын, балшықтан жасалған саз балшықты тақталарға (плиткаларға) білімдерін жазып қалдырған. Мұндай балшық тақталар Бабыл жерінен мыңдап табылады.
Бабылдықтардың барлық математикалық жетістіктері жинақталып жазылған (шамамен айтқанда б.з.б. 200-шы ж., яғни Бабыл мәдениеті өркендеп өзінің ең жоғарғы сатысына көтерілген кезге жатады) қырық төрт кестеден құралған бабылдықтардың математикалық энциклопедиясы табылған. Бұл энциклопедиядан бабылдықтардың сол ертедегі заманда күнделікті мұқтаждықтары алға қойған практикалық есептерді: егіншілік, жер суаруды реттеу, сауда жасаудағы есептерді шешудің бірсыдырғы тиімді тәсілдерін білгендігі көрінеді.
Бабылдықтар астрономия ғылымының негізін салған. Бір аптаны жеті күнге бөлу, шеңберді 360 градусқа, сағатты 60 минутқа, минутты 60 секундқа, секундты 60 терцияға бөлу солардан бізге мирас болып қалған. Жұлдыздарға қарап болашақты болжау, яғни астрология да солардың арасында туған.
Бабылдықтар санаудың негізіне қазіргідей 10-дық жүйе емес, көп жағдайда арифметиканың аса қиын амалы — бөлу амалын жеңілдететін 60-тық санау жүйесін қолданған. Мысалы: 1 574 640 санын алпыстық жүйеде өрнектесек: 1 603 + 57 602 + 46 60 + 40, яғни қосындысы 424000 етіп жазылады.
Әрбір өлшеуіш алдыңғысынан 60 есе артық болып келіп отыратын өлшеуіштер мен таразылар жүйесін де солар жасаған. Біздің қазіргі уақыт өлшемдеріміз — сағатты, минутты және секундты 60 бөлікке бөлуміз содан басталады.
Бабылдықтар екінші дәрежелі теңдеулерді, ал арнаулы кестелер арқылы үшінші дәрежелі теңдеулерді шеше білген.
Ежелгі Урарту математикасы
Б.з.б. екінші мыңжылдықтың орта шенінен бастап бір жағынан Бабыл патшалығына, кейіннен оның орнына келген Ассирия патшалығына, екінші жағынан Кавказ сыртына шектескен территорияда Ван патшалығы немесе Урарту патшалығы болды, бұл патшалық 8 ғ-да Кавказ сыртының оңтүстік облыстарын жаулап алды.
Урарту халықтары Бабыл математикасын меңгеріп, қазіргі позициялық ондық (тұрған орнына қарай бір цифрдің өзі әр түрлі разрядтардың белгісі болатын) нумерацияға жақын және позициялық принципті білмейтін, мысырлық ондық нумерацияға мүлде ұқсамайтын, ондық нумерацияға көшкендігі анықталған.
Урарту арифметикасы көбінесе ертедегі Армян арифметикасына ұқсас. Бұлай болса ертедегі бабылдықтардың математикасы Урарту халықтары арқылы Кавказ сыртындағы халықтардың, әсіресе армяндардың өте ерте замандағы математикалық мәдениетіне ықпалын тигізіп математиканың ауқымды дамуына зор үлесін қосқан.
-
IX-ғасырдың ортасынан XIII ғ-ға дейін араб математикасының гүлдену дәуірі деп қарауға
болады. Осы кезеңде Бағдадта, Бұхара, Қаһира және Испанияның Кордова және Толедо қалаларында көптеген ғылыми зерттеу орталықтары пайда болды, бұл дәуірдегі атақты математиктерден Батани, Әбу-Уафа, Карачи, әл-Бируни, Омар Хайям, Насыреддин Туси, Банналарды атауға болады.
-
XIV ғ-дан соң XV ғасырдағы Әмір Темірдің Самарқандтағы телескоп мен сонда зерттеумен
айналысқан әл-Кашиды айтпағанда, бүкіл араб математикасының құлдыраған кезеңі болып табылады.
Араб математикасының негізгі жетістіктерінен, арифметика жағында: ондық санау жүйесі, жазбаша есеп (бұл екеуіне Үндістанның тигізген әсері бар), дәрежеге көтеру, біріз қатарлардың қосындысын табу формуласы, т. б. Ал алгебра жағында: бірінші және екінші дәрежелі теңдеулерді шешу, үшінші дәрежелі теңдеудің геометриялық шешу әдісі, екімүшеліктің жіктелуіндегі коэфициенттері т. б; геометрия жағынан: Евклидтің «геометрияның алғашқы кітабының» аудармасы, парралелдік туралы аксиоманың тереңдей зеріттелуі, π санының мәні (әл-Каши 16-орынға дейін дұрыс есептеген) т. б; тригонометрия саласы да ертедегі грек пен үндіге қарағанда анағұрлым толық зерттелген.
12 ғ-дан бастап, араб математикасы Солтүстік Африкадағы Жерорта теңізі жағалау арқылы өтетін мәдени жолдары арқылы Испания мен Еуропаға тараған. Әсіресе ондық санау жүйесі мен жазбаша есеп, Евклидтің «Геометрия бастамалары» кітабының аударма нұсқасы т. б. бұлар бүкіл Еуропаның, тіпті дүние жүзінің математикасының дамуына орасан зор ықпал еткен.
Бірак, араб математикасының керемет туындылары латын тіліне аударылып Еуропаға тарамаған, тек 19-ғасырдан кейін араб математикасы реттеліп бір жүйеге келтіріле бастаған. Араб математикасы ертедегі гректің, Индияның, Қытайдың, Шығыс пен Батыстың математикалық жетістіктерін пайдаланып және оларды бір қалыпқа түсіріп Еуропаға таратқандықтан мәдениеттің қайта гүлденуі кезеңінде математика керемет дамыды, сондықтан да араб математикасы әлемдік математика тарихында ойып тұрып орын алады
Араб сандары
1, 2, 3, 4, 5, 6, 7, 8, 9 араб сандары деп аталады. Олар ондық санау системасы бойынша сан жазудың негізі. Араб сандарын үнділер тапқан, кейін келе ол арабтардың арасына тараған. 12 ғ-дың басында Италия ғалымы Фибоначчи (Leonardo Fibonacci, 1170-1250 жж.) латын тілінде жазылған «Есеп шот» деген кітабында үнді сандарын еуропалықтарға таныстырған. Еуропалықтар бұл сандарды арабтардан қабылдағандықтан, мұны араб сандары деп атап кеткен.
Арифме́тика (грекше: ἀριθμός «сан») — математиканың, қарапайым сандар түрлерін (натурал сандар, бүтін сандар, рационал сандар) және оларға қолданатын қарапайым арифметикалық операцияларды (қосу, алу, көбейту, бөлу) зерттейтін саласы.
Планиметрия (латынша: planum — жазықтық, көне грекше:) — екі өлшемді фигураларды, яки жазықтықта жатқан фигураларды, олардың қасиеттерін зерттейтін геометрия бөлімі.
Алгебра (арабша әл-жәбр)-Математиканың теңдеулерді шешу жөніндегі есептерге байланысты дамыған негізгі бөлімдерінің бірі. Алгебра атау және жеке ғылым саласы ретінде Әбу Абдаллаһ әл-Хорезмидің 1-ші, 2-ші дәрежелі теңдеулерге келтірілетін есептердің жалпы шешімі көрсетілген «Әл-жәбр уә-л-Мұқабала» атты еңбегінен бастау алады. Ал, Омар Хайям(1038/48-1123/24)— 3-ші дәрежелі теңдеулерді зерттеуді жүйелеп, өзінің «Алгебрасын» жазған. Орта ғасырлық шығыс ғұламалары гректер мен үнділердің математикасын түрлендіріп, қайта өңдеп Еуропаға табыс еткен. Амалдарды белгілейтін таңбалар енгізу нәтижесінде алгебра одан әрі дамыды. 17-ғасырдың ортасында қазіргі алгебрада қолданылатын таңбалар, әріптер толық орнықты. Ал 18-ші ғасырдың басында алгебра математиканың жеке бөлімі ретінде қалыптасты. 17-18—шің ғасырларда теңдеулердің жалпы теориясы (көпмүшеліктер алгебрасы, т. б) қарқындап дамыды. Оған сол кездегі ірі ғалымдар — Рене Декарт, Исаак Ньютон, Жан Даламбер мен Жозеф Лагранж үлкен үлес қосты. Неміс математигі Карл Гаусс кез-келген n дәрежелі алгебралық теңдеудің нақты не жорамал n түбірі болатындығын анықтаған (1799). 19-шы ғасырдың басында норвег математигі Нильс Абель және франсуз математигі Эварист Галуа дәрежесі 4 тен жоғары болатын теңдеулердің шешуін алгебралық амалдар көмегімен теңдеудің коэффиценті арқылы өрнектеуге болмайтындығын дәлелдеген.
1-сыныпта өткен материалдарды еске түсіруге арналған деңгейлік тапсырмалар
Кестелік қосу және азайту
І деңгей
І. 7 + 1 10 – 1 2 + 1 9 + 1
9 – 1 8 + 1 5 – 1 4 – 1
ІІ. Сандардың қатарын салыстыр:
0 1 2 3 4 5 6 7 8 9 10
10 9 8 7 6 5 4 3 2 1 0
ІІ деңгей
І. Керекті цифрларды қой:
5 + = 6 2 + = 3 8 + = 9 9 - = 8
4 + = 5 1 + = 2 7 + = 8 8 - = 7
3 + = 4 9 + = 10 10 - = 9 7 - = 6
ІІ. А) 5 7 8 2 3 4 9 1 6 1- ге арттыр
Ә) 6 1 9 4 3 2 8 7 5 1- ге кеміт
Б) 1 1
1 1 1
1 1 1 1
ІІІ. 5 – 1 – 1 – 1= 8 – 1 – 1 – 1 – 1=
6 – 1 – 1 – 1= 9 – 1 – 1 – 1 – 1=
7 – 1 – 1 – 1= 10 – 1 – 1 – 1 – 1=
ІІІ деңгей
І. 2 1 3 10 8 9 7
3 1 4 10 7 9 6
ІІ. 7 - = 5 2 - = 0
4 - = 2 5 - = 3
3 - = 1 6 - = 4
ІІІ.
|
1 2 3 4 5 6 7 8 9 10 |
1 2 3 4 5 6 7 8 9 10 |
Екі санын қосу және азайту тәсілдері
І деңгей
І.

![]()
5+2 = +2 = +2 =
7-2 = -2 = -2 =
ІІ.

ІІІ. Бір сан аттай отырып, өсу ретімен және кему ретімен жаз.
А) _______________________________
Б) _______________________________
ІІ деңгей
І.

![]()
+2 = +2 = +2 =
-2 = -2 = -2 =
ІІ. Осы кесіндіден 2 см артық және кем кесінді сыз.
![]()
ІІІ.

ІІІ деңгей
І. Ыдыста 7 жұмыртқа бар еді. Оның екеуін сен жеп қойдың. Ыдыста неше жұмыртқа қалды?
ІІ. Азайтқышы 2 болатын айырмаларды жаз және мәндерін тап.

Сонда 2-ні қосу кестесіндегі теңдіктің нешеуін пайдаландың ? _______
Кесінділердің қосындысы және айырмасы
І деңгей
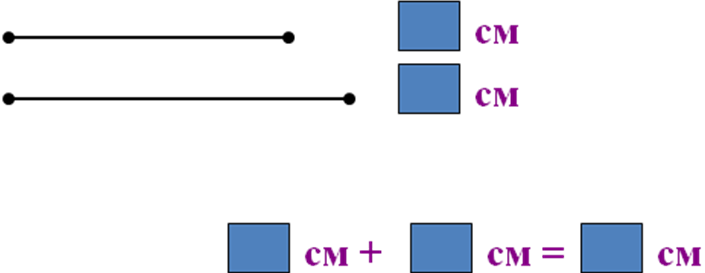
ІІ деңгей
![]() Осыдан 1 см ұзын кесінді
сыз
Осыдан 1 см ұзын кесінді
сыз
![]() Осыдан 1 см қысқа кесінді сыз
Осыдан 1 см қысқа кесінді сыз
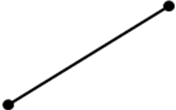
Кесінділердің айырмасына тең кесінді сыз және жаз
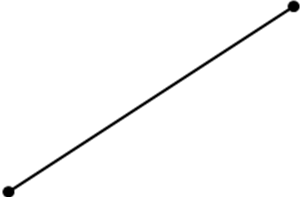
Кесінділердің қосындысына тең кесінді сыз және жаз
ІІІ деңгей
І. Мына кесінділерден үшбұрыш сыз:

ІІ. Мына кесінділерден шаршы сыз:

5 саны және цифры
І деңгей
І.Есепте
ІІ.
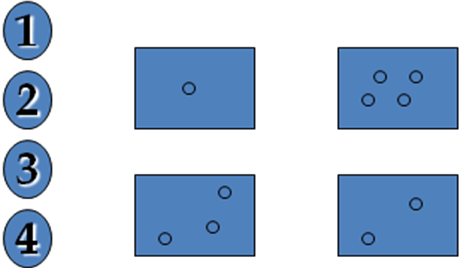
ІІІ деңгей
Әр санды сәйкес белгілермен сызық арқылы жалғастыр.
Тест жұмысы
-
Теңдіктерді ата.
а) 2 > 1 ә) 3 < 4 б) 3 = 3
-
Теңсіздіктерді ата.
а) 2 = 1 ә) 14 = 4 б) 4 = 1
3. Қосындыны тап.
а) 3 + 1 = 4 ә) 4 + 1 б) 3 – 2
4. Айырманы тап.
а) 5 – 4 = 1 ә) 4 – 2 б) 2 + 3
5. Тақ сандарды тап.
а) 1, 3, 5, 7, 9 ә) 2, 3, 4, 5, 6 б) 3, 6, 5
6.Жұп сандарды тап.
а) 3, 5, 7, 8 ә) 2, 4, 6, 8 б) 3, 4, 5, 9
7. 1 дм- де неше см бар?
а) 1 дм = 9 см ә) 1 дм = 10 см б) 1 дм = 12 см
8. Бір таңбалы сандарды тап.
а) 10, 9 ә) 0, 1, 2, 3, 4 б) 11, 2, 3, 12
9. Тура теңдікті тап.
а) 3 = 2 ә) 4 = 4 б) 5 = 6
10. Тура теңсіздікті тап.
а) 3 < 2 ә) 4 < 4 б) 6 > 9
Артығын тап.


Ә
Б
В


Доминоның қайсысы 5 санын құрайды?
А Ә Б
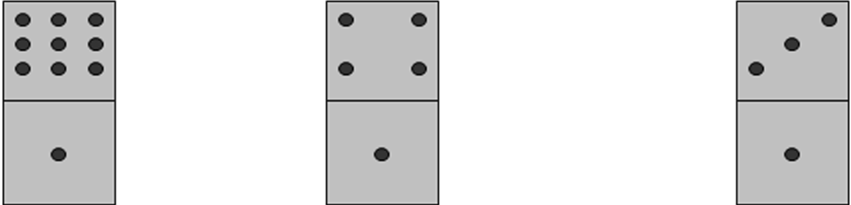
Қайсысы жылдам жүреді?

Биік - аласа
А Ә Б

Сәулені тап .

Есепте.

Фигураның жетпегенін тап және сыз.
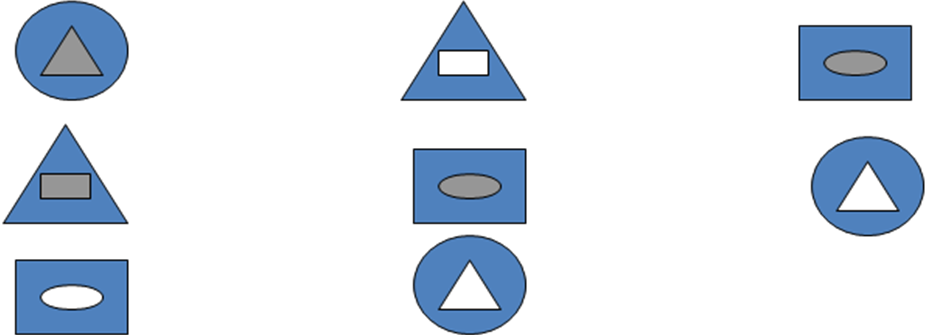
Цифрларды сәйкес суреттермен қос:

2-сыныпқа арналған дейгейлік тапсырмалар
Ондық құрам негізінде қосу және азайту
І-деңгей
8+50
86-80
27-20
74+70
60+4
83-80
40+9
72-70
95-5
ІІ-деңгей
69- (18-9)
30+(14-7)
(14-5)+50
(60+40)-30
ІІІ-деңгей
50+(20+10) * 60+(20-10)
(20+70)+7 * (60-10)+7
(50+40)-10 * (70-10)+20
90+(11-3) * 80+(10+10)
Сандарды салыстыруға арналған есептер
І-деңгей
|
Сан |
18 |
26 |
0 |
1 |
9 |
100 |
57 |
63 |
|
1ге қос |
|
|
|
|
|
|
|
|
ІІ-деңгей
|
Сан |
99 |
43 |
14 |
8 |
16 |
76 |
32 |
18 |
|
1ден азайт |
|
|
|
|
|
|
|
|
ІІІ-деңгей
96-3 ... 38-2
27+60 ... 89-3
57-3 ... 25+30
69-7 ... 60+4
90-50 ... 43-2
38-5 ... 30+3
74+20 ... 98-3
81+8 ... 83+6
1000 көлеміндегі сандардың нумерациясы
І-деңгей
700+8
800+2
905+40
806+40
540+8
200+60
ІІ-деңгей
784-4
605-5
784-700
650-50
784-80
650-600
ІІІ-деңгей
5ц 9кг – 5ц
8м 55см – 5 см
8ц 30кг – 8ц
5м 5дм 5см – 5дм
9ц 70кг – 70кг
282см – 2м
1000 көлемінде разрядтан өтпей қосу және азайту
І-деңгей
540+30
800+123
450-300
960-400
250+430
377-245
980-70
399-271
272-314
836-210
998-482
472+521
ІІ-деңгей
970-(20+40
880-(440-40)
356+140-20
600-(220-20)
(1000-800)+125
980-40+20
(900-300)+189
840-(300+30)
ІІІ-деңгей
9м 4см – 3см
4м +2дм
6м + 1дм 8см
2см + 4м 1дм
Екі таңбалы сандарды екі таңбалы сандармен разрядтан аттамай қосу
І-деңгей
53+26
34+65
27+42
31+58
ІІ-деңгей
32+(52+15)
(21+23)+45
24+(44+11)
(34+12)+23
ІІІ-деңгей
34+23+12
21+35+42
13+62+21
51+14+22
100 көлеміндегі сандарды разрядтан аттамай қосу
І-деңгей
63+14 41+5
83+16
52+5
27+12 39+21
66+2
71+24
53+6 45+43
32+7
86+3
ІІ-деңгей
85-41-14
56-11-42
67-33-21
99-50-16
49-11-25
67-24-13
87-22-32
95-12-80
ІІІ-деңгей
(36+28)-18
(47+34)-25
17+(19-12)
55+(75-69)
66-(49+50)
56+(27-18)
Екі таңбалы сандардан екі таңбалы сандардан разрядтан аттамай азайту
І-деңгей
...+14 =47
...-13 =25
79-... =56
52+...=58
52-41=
23+35=
ІІ-деңгей
34-21
34-12
45-32
45-23
53-13
53-31
65-42
65-24
ІІІ-деңгей
79-22
55=В 75=Г 57=Б
87-15
72=Ү 77=А 83=У
67-53
68=С 14=Р 46=Т
44-23
11=П 21=К 12=Л
58-34
28=И 44=Ы 24=І
63-12
51=Т 75=Д 42=М
Жақшалар. Амалдардың орындалу реті
І-деңгей
...-...+... =2
...-...+... =1
...+...+... =3
...+...-... =1
ІІ-деңгей
15+(3+2)*(15+3)+2
15+(3-2)*(15+3)-2
15-(3-2)*(15-3)-2
(15-3)+2*15-(3+2)
ІІІ-деңгей
13-1+2=10
14-4+2=12
16-3-1=14
14-6+1=10
19-5+1=13
16-5-4=15
17+3-2=18
15+4-3=16
18-8-3=13
19-3-2=14
14+6-5=15
15-3+2=10
Екі таңбалы сандарды қосу және азайт
І-деңгей
60-10 ... 60-7
30-10 ... 30-5
50-10 ... 50-8
40-10 ... 40-6
70-10 ... 70-3
80-10 ... 80-9
90-10 ... 90-4
70-10 ... 70-6
ІІ-деңгей
56 ... 4=60
40 ... 5=35
56 ... 4=52
5 ... 40=45
30 ... 5=35
70 ... 5=75
45 ... 5=40
85 ... 5=80
ІІІ-деңгей
|
Сан |
5 |
2 |
4 |
7 |
8 |
9 |
3 |
10 |
|
8ге қос |
|
|
|
|
|
|
|
|
Есептер шығару
І-деңгей
|
Сан |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
4ке қос |
|
|
|
|
|
|
|
|
|
ІІ-деңгей
40+5=
40-5=
30+5=
30-5=
20+5=
20-5=
10+5=
10-5=
ІІІ-деңгей
18+2 ... 13+7
20-13 ... 30-25
17+8 ... 14+6
38-20 ... 14+5
15+5 .. 25-5
44+6 ... 74-23
100 көлеміндегі сандарды ауызша қосу және азайту тәсілдері
І-деңгей
53+4
61+8
74+5
69-6
70-8
98-4
ІІ-деңгей
68-9
79+7
94-9
46+5
32-8
57+6
ІІІ-деңгей
Х+20 = 34+16
80-у = 12+8
Кестелік есептер
І-деңгей
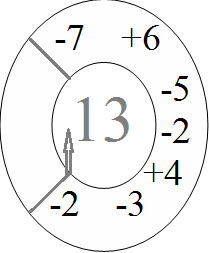
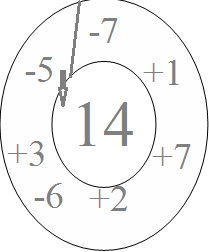
ІІ-деңгей
2+9
8+9
15-7
8+6
12-3
14-9
11-6
5+7
16-9
9+7
8+4
15-9
ІІІ-деңгей
44+6*51-1
24-4*26+4
5см +3см * 8см
9м+6дм * 840см
100 көлеміндегі сандарды ауызша қосу және азайту тәсілдері
І-деңгей
67-25 70-56
49+7
78+9
63-8
33-7
100-9 66+24
51-3
19+8
78+7
44-7
ІІ-деңгей
67+5 80-7
63+17
74+9
81-8
23+31
58+5 9+36
42+18
56-8
16-9
90-6
ІІІ-деңгей
56+26
91-22
39см + 33см
47+26
74-48
97см – 18см
38+29
67-59
28см + 47см
56-38
45+47
92см – 48см
Сандарды ондықтар мен бірліктердің құрамына жіктеу.
І-деңгей.
Цифрмен жаз және теңдікке айналдыр.
2 онд + 4 онд=
9 онд- 3 онд=
1 онд + 2 онд=
3 онд + 7 онд=
10 онд-5 онд=
3 онд+ 5 онд=
5 онд + 1 онд=
6 онд - 2 онд=
6 онд + 3 онд=
6 онд + 4 онд=
8 онд – 4 онд=
2 онд + 5 онд=
1 онд+ 8 онд=
7 онд – 3 онд=
7 онд +2 онд=
ІІ- деңгей.
Керекті сандарды жаз.
11. ( он және үш)
12. ( он және екі)
1 онд+1 бірл= ... онд. ... бірл
... онд. + ... бірл.= ... онд. ... бірл
10 + ... =...
... ... + ... = ... ...
13. ( он және үш)
14. ( он және төрт)
... онд. + ... бірл.=... онд. ... бірл
... онд. + ... бірл. = ... онд. ... бірл.
... ... + ...= ... ...
... ... + ... =...
15. ( он және бес)
16. ( он және алты)
... онд. + ... бірл. = ... онд. ... бірл
... онд. + ... бірл= ... онд. ... бірл
... ... + ... = ... ...
... ... + ... = ... ...
ІІІ- деңгей.
Бос орынға теңдік дұрыс шығатындай етіп сандар қой.
64+...= 67
57 - ... = 51
79- ...= 73
99 - ...= 90
98 - ...= 92
100+ ...=100
Салыстыр ( < ,=,>)
12 + 6 * 17
13+12 *13+14
13+ 4 * 9
29+1 * 33- 3
Екі таңбалы сандарды екі таңбалы сандармен разрядтан аттамай қосу.
1- деңгей.
Есепте. Мәндері бірдей өрнектерді сызықтармен жалға.
53+26 =
34+65 =
27+42 =
31+58 =
ІІ-деңгей.
Есепте. Мәндері бірдей өрнектерді сызықтармен жалға.
32+ (52+ 15)=
(21+23) +45=
24+ (44 + 11)=
(34+12) + 23=
ІІІ-деңгей.
Теңдіктердің қандай қасиеттер бойынша жалғанғанын анықта. Осыған ұқсас теңдік жұптарын тап және оларды үлгі бойынша жалға. Есепте.
34+23+12=
21+35+ 42
Ондық құрам негізінде қосу және азайту
І-деңгей
10+9
16-6
17-7
12-10
18-10
3+10
ІІ-деңгей
Доп – 9 дана
Секіртпе -? Дана, 4-еуі кем
ІІІ-деңгей
14-х=9
Х+8=13
Есептерді шығар. Дұрыс жауапты қорша
Көкөніс сататын дүңгіршікте 11 қарбыз болды.түске дейін 9 қарбыз сатылды. Дүңгіршікте сататын тағы неше қарбыз қалды?
А) 2
ә) 3
б)20
Кестелеп қосу және азайту
І-деңгей
6+5 7+6
14-9 13-8
9+3 7+8
16-7 15-8
ІІ-деңгей
Бумадан 9 шар алынғаннан кейін, одан тағы 6 шар қалды. Бумада бастапқыда неше шар болған?
ІІІ-деңгей
9+(40+30)
95-(50+30)
75+10-50
(90-30)+40
87-(60+20)
33-(23-3)
52+7-9
Ұзындықтың өлшем бірліктері, құрама есеп
І-деңгей
89-(54+25)
20+(62-41)
100-70+9
(63+25)-76
17+52-26
20+68-47
ІІ-деңгей
Конструктор жинағанда 17 көк және 22 қызыл бөлшек бар.
25 бөлшек қолданылды.
Неше бөлшек қалды?
ІІІ-деңгей
...см -8см*12см
7дм + 6 см * 15дм
1 жүзд + 2 онд * 120бірл
7дм + 2см * 3см +8 см
9см * 2 дм
1 сағ + 10 мин * 100 мин
48 сағ * 2 тәул
Есепті әртүрлі тәсілмен шығар
І-деңгей
47+3
90-9
52
8
70-4
24+56
100-73
91+9
60-37
ІІ-деңгей
(53+29)-19
(31+19)-12
ІІІ-деңгей
5ц 9 кг – 5ц
8ц 30 кг – 8 ц
9ц 70кг – 70кг
8м 55см – 5см
5м 5дм 5см – 5дм
282см – 2м
Есептерді қөосу және азайту
І-деңгей
47-28 70-34
56+29
75-37 62-48
59+38
ІІ-деңгей
Бақтан 70 кг алма жиналды. Алманың бір бөлігі жәшіктерге салынғанда, тағы 18 килограмм алма қалды. Жәшіктерге неше килограмм алма салынды?
Есепті шығар дәне кері амалмен екі есеп құрастыр.
ІІІ-деңгей
6 жүздік * 600 бірл
2 онд * 20 бірл,
2-жүзд * 20 онд
500 бірл * 1 жүзд
704 см = ...м ...дм ...см
620 см = ...м ...дм ...см
364 см= ...м ...дм ...см
460 см = ...м ...дм ...см
213 см = ...м ...дм ...см
301 см = ...м ...дм ...см
890 см = ...м ...дм ...см
600 см = ...м ...дм ...см
Жақшаларды қоюға арналған есептер
І-деңгей
7+(4+1) 6-(2+3)
(7+4)+1 (6-2)+3
3-1+2 5-3-2
9+(7-5) (9-7)+5
(3+7)-4 3+(7-4)
10-5+4 9+7-5
ІІ-деңгей
7+9+3+1
(7+3)+(9+1)
16+8+4+2
(16+4)+(8+2)
40+30+6+4
50+5+25-50
4+6+17+3
3+7+7+4
ІІІ-деңгей
14-9+5 = 10
19+1-6=14
17-8+4=5
13+3-10=6
15-6-1=10
12-3+8=1
19-1+2=20
20-3-2=19
16-4+2=10
11-5+1=7
18-7+1=10
10-2+3=11
27-10-2-2=15
32-20+10=2
73-30+10=33
50-40-10=0
45-5+4=44
16-8+7=1
Екі таңбалы сандарды қосу және азайту
І-деңгей
21+8 78+2
34+6 17+3
18+2 72+4
29+1 64+30
45+20 41+20
60+17 87+2
ІІ-деңгей
15+20+5+10
40+3+30+7
50+6+20+4
2+24+8+6
18+11+9+2
17+22+3+8
5+64+5+6
1+80+19
ІІІ-деңгей
Себетке Айнұр 3 алмұрт, ал Арман 2 алмұрт салды. Себеттегі барлық алмұрт нешеу?
Шарты: Себетке Айнұр 3 алмұрт, Ал Арман 2 алмұрт салды.
Сұрағы: Себеттегі барлық алмұрт нешеу?
С![]() ызба:
ызба:
3 алма 2 алма
Өрнек: 3 + 2
Шешуі: 3 + 2 = 5 алмұрт
Жауабы: Барлығы 5 алмұрт.
Жанарда 5 тиын, ал Маратта 2 тиын бар.
Сұрағы: Жанар мен Маратта барлығы неше тиын бар?
С ызба:
ызба:
?
Ж М
5 т 2 т
Өрнек: +
Шешуі: + =
Жауабы: Барлығы тиын.
Есептерді қосу және азайтуға арналған есептер
І-деңгей
72+3 30-9 23-8
65+4 21-5 37-4
76+20 47-30 65-9
53+40 62-40 82+7
32+6 82-8 61+4
52+20 54-20 93+7
13+8 93-8 31-6
43+8 18-10 37+12
9-27 17-8 43+54
12+10 16-9 65+32
32+40 15-6 28+51
47+50 14-8 71+23
26+7 13-4 54+32
12+6 12-6 86-43
ІІ-деңгей
9дм 1см – 5дм 4 см
2 дм 8 см – 3 дм 6 см
2 дм 8 см + 4 дм 6 см
7 дм 2 см – 1дм 9 см
ІІІ-деңгей
540+30
960-400
980-70
836-210
800+123
520+430
399-271
998-482
450-300
377-245
272+314
472+521
Үш таңбалы сандарды қосу және азайту
І-деңгей
507+40 362+224
809-800 602+24
909-9 890-710
860-40 649-415
604-400 960-440
531+302 520+407
ІІ-деңгей
651+123 505-103
492+104 980-450
976-651 478-107
790-650 51+708
ІІІ-деңгей
980-(40+30)
508+200-1
(800-100) -125
(1000-200)-65
909-(404-400)
200+(505-5)
458-(25+25)
28
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Математика пәнінен деңгейлік тапсырмалар
Математика пәнінен деңгейлік тапсырмалар
қ Қайролла М.М
Математика пәнінен деңгейлік тапсырмалар
2-сынып
2015-2016 жыл
Кіріспе
Ұсынылып отырған әдістемелік құрал математика пәні бойынша жалпы білім беретін орта мектептің 2-кластарына арналған мемлекеттік оқу бағдарламасы негізінде жасалған.
«Қазақстан Республикасының Білім туралы» Заңына сәйкес «Әр баланың жеке қабілетіне қарай интеллектуалдық дамуын, жеке адамның дарындылығын, талантын, қабілетін дамыту» сияқты өзекті мәселе енгізіліп отырғаны белгілі. Осыған орай, оқу үрдісін оқу қызметіне сәйкестендіріп ұйымдастырса, оқушылыр өз мүмкіндіктерін одан да жоғары деңгейде жүзеге асырулары әбден мүмкін.
Әдістемелік құралда баланың ақыл – ойын, логикалық ойлау мен шығармашылық қабілеттерін дамыту, әрекет нәтижесінде белгілі тұжырым жасауға үйрететін деңгейлік тапсырмалар берілген.
Деңгейлеп оқыту барысында оқушының бірінші деңгейдегі тапсырмаларды дұрыс орындағаны есепке алынып отырылады.
Қандай оқушы болмасын, мысалы
өзінің жақсы оқитынына қарамастан, жұмысын
«оқушылық»,
«міндетті», 1-ші деңгейдің , ол үшін жеңіл болса да, тапсырмаларын
орындаудан бастайды.
Барлық оқушылар жұмысын бір мезгілде бастап: әрқайсысы, білім
игерудегі өз қабілетіне қарай, өз биігіне жетеді. Бұл барлық
оқушыларды тірек білімімен қамтамасыз етеді және Қазақстан
Республикасының Білім туралы Заңының талаптарына сай келеді.
Нақтырақ айтсақ - барлық оқушылардың оқу мақсатында 100% қол
жеткізуінің кепілі болады және оқу пәндерінің барлық тақырыбы
бойынша ең болмағанда міндетті бірінші деңгейді игеруін толық жүзеге асырады.
Деңгейлік тапсырмаларға математика пәнінен, төмендегідей талаптар қойылады.
Бірінші деңгейдегі тапсырмаларға:
1.Жаттап алуға лайықталған болуы керек
2.Алдыңғы сабақта жаңадан меңгерілген білімнің өңін өзгертпей қайталап, пысықтануына мүмкіндік беруі тиіс
3.Тапсырмалар жаңа тақырып үшін типті және өмірмен байланысты болуы керек.
Математика пәнінде мұндай талаптар жаңа тақырыпты игеру соңында шығарған есептерге ұқсас тапсырмалар құру арқылы орындалады және олар оқушының өзі шығарған ереже, анықтама, заңдарын бекітуге арналады. Мұндай тапсырмаларды құрастырған кезде олардың танымдылығы мен қызықтылық жақтарына ерекше көңіл аударған жөн.
Екінші деңгейдегі тапсырмаларға:
1.Өтіп кеткен материалдарды реттеуге және жүйелеуге берілген тапсырмалар. Бұлар өзгертілген жағдайлардағы тапсырмалар, яғни бұрынғы тапсырмаларға ұқсас, бірақ оларды орындау үшін алғашқы алған білімдерін түрлендіріп пайдалану қажет болады.
2.Математика мұндай іс-әрекетке келтіретін тапсырмалар: мәтінмен берілген кері есептер; кері байланыс функциясын атқаратын тексеру тапсырмалары т.с. с.
3.Оқушының ойлау қабылетін жетілдіруге берілетін тапсырмалар. Оларда біздің ұлттық ерекшеліктеріміз ескеріліп, танымдық және үйретімділік маңызы болуы қажет болады. Бұлар : логикалық есептер, ребустар мен сөзжұмбақтар.
Үшінші эвристикалық деңгейдегі тапсырмаларды біз төмендегінше топтастырдық:
1.Танымдық-іздену (эвристикалық) түрдегі тапсырмаларды орындау барысында оқушылар жаңа тақырып бойынша меңгерген алғашқы қарапайым білімдерін (заңдылықтар шығару, анықтамалар жаттау, т .с. с. жетілдіріп, тереңдетумен қатар, ол тағы да жаңа білімді меңгеріп, өзі үшін жаңалық ашуы тиіс.Мұндай жұмыс –анализ бен синтез және салыстыру арқылы негізгісін анықтау, қорытындылау сияқты ой жұмыстарын қажет етеді. Мұндай есептерді шешу барысын оқушылар жаңа есептерге тап болады да, проблемалық жағдай туындайды. Оны шешу үшін оқушы жаңа әдістер іздеуі керек.
2. Әртүрлі әдіс, тәсілдермен шешілетін есептер
Қорыта келе, оқытудың жаңа технологиясы , яғни «Деңгейлеп оқыту технологиясы » еліміздің көптеген мектептерінде қолданылып жүр. Деңгейлік тапсырмалар қызғылықты мазмұндалған болса, оқушыларда ынталану пайда болады. Олар өзара бәсекелесе отырып жұмбақ , сөзжұмбақ , ребустар сияқты әртүрлі тапсырмаларды шешіп , өтіп жатқан тақырыпты өзі қорытындылауға тырысады, себебі, ертең жаңа тақырып басталады. Нәтижесінде оқушылардың ынтасы артып, сонымен қатар қызығушылығы де күннен –күнге жоғарылай түседі. Демек , мұғалім берген тапсырмалар оқушылардың біліктілігі мен дағдысын қалыптастыруа отырып және бағалау деңгейі жоғарылай түседі. Сонымен қатар, тапсырмалар ауқымы да өсіп , шығармашылыққа ұласады.
Ақыл-ойды тәртіпке келтіретін математика
Мектеп оқушылары кейде: «Маған математиканың керегі жоқ, өйткені мен тіл-әдебиет мұғалімі, артист, немесе суретші боламын»— дейді. Әрине, олардың бұлай деуі дұрыс емес. Бала кезінен бастап математикамен шұғылданған адам өзінің ой өрісі мен зеректігін дамытады, мақсатына жету үшін табанды болуға ерік-жігерін тәрбиелей алады. Сондықтан да мұғалімге де, дәрігерге де, артиске де және суретшіге де математика қажет.
Ежелгі гректер заманынан бастап-ақ математикамен шұғылдану адамды дұрыс және жүйелі түрде ойлауға, өз ойын тиянақты тұжырымдап айта білуге үйрететіндігі белгілі болған. Математика бізге айнала қоршаған сандар мен фигуралардан тұратын ерекше әлемнің құпия сырын ашып береді.
Адамның бұйымдарды қажетті ретпен топтау, санау, өлшемдері мен түрін табу, олардың өзара орналасу қалпын анықтау секілді жұмыстармен түйіспейтін қызмет саласын атау қиын. Қарапайым есептеу мен өлшеу — бұл әлі математика емес! Maтематика бізді керексіз қайта-қайта санаудан құтылуға, бұрыннан белгі-жайттар арқылы бізге белгісіз жайтты таба білуге үйретеді. Мұның техника мен ғылым үшін аса зор маңызы осы қасиетінде.
Қарапайым мысал келтірейік: бір бумада 20 кітап бар, қоймадағы осындай барлық бумалардың саны 150. Математикалық тұрғыдан барлық бумаларды шешіп, олардағы кітаптарды «жеке-жеке санап жатудың керегі жоқ. Көбейту амалы қоймада барлығы 20Х 150=3000 кітап бар екенін көрсетеді.
Математика бұдан жүз жиырма жыл бұрын астрономдар француз Леверье мен ағылшын Адамсқа Уран планетасының қозғалысындағы шамалы ауытқудың себебі одан әрірек, Күннен қашықтау орналасқан белгісіз бір планетаның қозғалысы әсерінен болады деп тұжырымдауларына мүмкіндік берді. Олар бұл планетаны аспанның қай жерінен іздеу керектігін есептеп тауып, телескопты сол тұсқа бағыттап қарағанда жаңа планета көрінген. Олар бұл планетаға Нептун деп ат қойған.
Кей кездері математикаға ешбір қатысы жоқ болып көрінетін мәселенің өзі математикалық жаңалық ашуға әкеп соқтырады. Мысалы, бұдан 350 жыл бұрын өмір сүрген тамаша ғалым Кеплерді шарап саудагерлерінің формалары әр түрлі бөшкелерінің сыйымдылықтарын қалай анықтайтыны ойға қалдырған. Олар бөшкенің аузындағы тесіктен таяқ жүгіртіп, оның түбіне дейінгі аралықты өлшеген.
Кеплер саудагерлердің бөшке көлемін қалай анықтағанын көріп, формлары бөшке, алма, айва, тгпті түрік сәлдесі секілді заттардың да көлемдерін есептеуге арналған математикалық формула ойлап тапқан. Осы жайт кейіннен өзге ғалымдардың бұл күнде инженерлер мен физиктерге өте қажет жаңа математикалық ғылым — интегралдық есептеуді жасап шығаруларына көмектесті.
Орыс ғалымдары Н. Е. Жуковский мен С. А. Чаплыгин бұдан жарты ғасыр бұрын математиканың көмегімен самолеттің белгілі бір мөлшердегі жүкті көтеріп ұшуы үшін, оның қанатының формасы мен өлшемдерінің қандай болуы керектігін есептеген. Математика ауа райын алдын ала болжауға, көпірлердің және ғимараттар күмбездерінің беріктігін, спутниктер орбиталарын есептеп табуға көмектеседі...
Математика ғылым ретінде ешқашан бір орнында тапжылмай тұрып қалған емес. Өмір, практика, толассыз дамып келе жатқан техника және басқа да ғылымдар оның алдына әркез жаңа мәселелер қойып отырады. Бұларды шешу үшін, бұрыннан белгілі білім атаулы жеткіліксіз, сондықтан математик ғалымдарға жаңа әдістер табуға, жаңа теориялар жасауға тура келеді. Қазіргі кезде көптеген күрделі математикалық есептеулерді адамның орнына машиналар атқарады.
Мектеп оқушылары алатын мәліметтер мен тәсілдер әрине, математиканың тек әліппесі ғана. Құдіретті де қызғылықты математика ғылымының шалқыған дариядай, тіптен ұшы-қиыры жоқ салаларына апаратын даңғыл жол, оқушылар үшін мектеп қабырғасындағы математикалық білімдер: арифметимка, алгебра және геометрия пәндерінен басталады.
Математика (грекше: μάθημα — ғылым, білім, оқу; μαθηματικός — білуге құштарлық) — әлдебір әлемнің сандық қатынастары мен кеңістіктік формалары, оның ішінде — структуралар, өзгерістер, белгісіздік жөніндегі ғылым. Ол абстрактілендіру және логикалық қорыту, есептеу, санау, өлшеу және физикалық нәрселерді жүйелі түрде орнықтыру, бейнелеу мен өзгерістерді оқыту арқылы көрініс табады.
Математиктер жаңа тұжырымдамаларды сипаттайтын осы түсніктерді ретімен таңдалып алынған аксиомалар мен анықтамаларды пайдалана қорыта отырып зерттейді.
Математика тарихы
Көне Мысыр математикасы
Көне Мысыр әлемдегі ең байырғы мәдениет ошақтарының бірі. Ніл өзенінің екі жағалауына орналасқан бұл ел б.з.б. 3200-ші жж біртұтас мемлекет болып бірікті. Ніл өзені әр жылда тасып, жағалаудағы егістік жерлерді шайып кетіп отырған, тасу мезгілі аяқталған соң тұрғындардың жерін қайта өлшеп бөлу керек болады, ұзақ жылғы жер өлшеу тәжірибесінің арқасында геометрия ғылымы пайда болған (геометрия – грекше сөз, гео — жер, метро — өлшеу деген мағына береді).
Көне мысырлықтар ертеден ондық санау жүйесін қолдануды білген, бірақ оның әрбір орындағы сандардың жазылу ережесін білмеген, мысалға 111-ді жазу үшін, 1-ді үш рет қайталап жазбаған, керісінше әр орындағы 1-лерді әр түрлі белгілермен бейнелеген. Көне мысырлықтардың негізгі амалы қосу болған, ал көбейту қосудың қайталанып келуі ретінде есептелген. Олар бір айнымалысы бар бірінші дәрежелі теңдеулерді шеше алған, әрі арифметикалық, геометриялық прогрессиялардың қарапайым есептерін шеше алатын болған.
Ежелгі Бабыл математикасы
Көне Мысырда математиканың туумен қатар ертедегі Бабыл тұрғындары және шумерлер мен аккадтықтар өз алдына өздерінің дербес математикасын жасап шығарды. Бұл халықтар сына сияқты сызықшалардан құралатын таңбалар арқылы (19 ғ-да археологиялық қазбалар кезінде табылған) күн көзіне қойғанда тастай қатайып қалатын, балшықтан жасалған саз балшықты тақталарға (плиткаларға) білімдерін жазып қалдырған. Мұндай балшық тақталар Бабыл жерінен мыңдап табылады.
Бабылдықтардың барлық математикалық жетістіктері жинақталып жазылған (шамамен айтқанда б.з.б. 200-шы ж., яғни Бабыл мәдениеті өркендеп өзінің ең жоғарғы сатысына көтерілген кезге жатады) қырық төрт кестеден құралған бабылдықтардың математикалық энциклопедиясы табылған. Бұл энциклопедиядан бабылдықтардың сол ертедегі заманда күнделікті мұқтаждықтары алға қойған практикалық есептерді: егіншілік, жер суаруды реттеу, сауда жасаудағы есептерді шешудің бірсыдырғы тиімді тәсілдерін білгендігі көрінеді.
Бабылдықтар астрономия ғылымының негізін салған. Бір аптаны жеті күнге бөлу, шеңберді 360 градусқа, сағатты 60 минутқа, минутты 60 секундқа, секундты 60 терцияға бөлу солардан бізге мирас болып қалған. Жұлдыздарға қарап болашақты болжау, яғни астрология да солардың арасында туған.
Бабылдықтар санаудың негізіне қазіргідей 10-дық жүйе емес, көп жағдайда арифметиканың аса қиын амалы — бөлу амалын жеңілдететін 60-тық санау жүйесін қолданған. Мысалы: 1 574 640 санын алпыстық жүйеде өрнектесек: 1 603 + 57 602 + 46 60 + 40, яғни қосындысы 424000 етіп жазылады.
Әрбір өлшеуіш алдыңғысынан 60 есе артық болып келіп отыратын өлшеуіштер мен таразылар жүйесін де солар жасаған. Біздің қазіргі уақыт өлшемдеріміз — сағатты, минутты және секундты 60 бөлікке бөлуміз содан басталады.
Бабылдықтар екінші дәрежелі теңдеулерді, ал арнаулы кестелер арқылы үшінші дәрежелі теңдеулерді шеше білген.
Ежелгі Урарту математикасы
Б.з.б. екінші мыңжылдықтың орта шенінен бастап бір жағынан Бабыл патшалығына, кейіннен оның орнына келген Ассирия патшалығына, екінші жағынан Кавказ сыртына шектескен территорияда Ван патшалығы немесе Урарту патшалығы болды, бұл патшалық 8 ғ-да Кавказ сыртының оңтүстік облыстарын жаулап алды.
Урарту халықтары Бабыл математикасын меңгеріп, қазіргі позициялық ондық (тұрған орнына қарай бір цифрдің өзі әр түрлі разрядтардың белгісі болатын) нумерацияға жақын және позициялық принципті білмейтін, мысырлық ондық нумерацияға мүлде ұқсамайтын, ондық нумерацияға көшкендігі анықталған.
Урарту арифметикасы көбінесе ертедегі Армян арифметикасына ұқсас. Бұлай болса ертедегі бабылдықтардың математикасы Урарту халықтары арқылы Кавказ сыртындағы халықтардың, әсіресе армяндардың өте ерте замандағы математикалық мәдениетіне ықпалын тигізіп математиканың ауқымды дамуына зор үлесін қосқан.
-
IX-ғасырдың ортасынан XIII ғ-ға дейін араб математикасының гүлдену дәуірі деп қарауға
болады. Осы кезеңде Бағдадта, Бұхара, Қаһира және Испанияның Кордова және Толедо қалаларында көптеген ғылыми зерттеу орталықтары пайда болды, бұл дәуірдегі атақты математиктерден Батани, Әбу-Уафа, Карачи, әл-Бируни, Омар Хайям, Насыреддин Туси, Банналарды атауға болады.
-
XIV ғ-дан соң XV ғасырдағы Әмір Темірдің Самарқандтағы телескоп мен сонда зерттеумен
айналысқан әл-Кашиды айтпағанда, бүкіл араб математикасының құлдыраған кезеңі болып табылады.
Араб математикасының негізгі жетістіктерінен, арифметика жағында: ондық санау жүйесі, жазбаша есеп (бұл екеуіне Үндістанның тигізген әсері бар), дәрежеге көтеру, біріз қатарлардың қосындысын табу формуласы, т. б. Ал алгебра жағында: бірінші және екінші дәрежелі теңдеулерді шешу, үшінші дәрежелі теңдеудің геометриялық шешу әдісі, екімүшеліктің жіктелуіндегі коэфициенттері т. б; геометрия жағынан: Евклидтің «геометрияның алғашқы кітабының» аудармасы, парралелдік туралы аксиоманың тереңдей зеріттелуі, π санының мәні (әл-Каши 16-орынға дейін дұрыс есептеген) т. б; тригонометрия саласы да ертедегі грек пен үндіге қарағанда анағұрлым толық зерттелген.
12 ғ-дан бастап, араб математикасы Солтүстік Африкадағы Жерорта теңізі жағалау арқылы өтетін мәдени жолдары арқылы Испания мен Еуропаға тараған. Әсіресе ондық санау жүйесі мен жазбаша есеп, Евклидтің «Геометрия бастамалары» кітабының аударма нұсқасы т. б. бұлар бүкіл Еуропаның, тіпті дүние жүзінің математикасының дамуына орасан зор ықпал еткен.
Бірак, араб математикасының керемет туындылары латын тіліне аударылып Еуропаға тарамаған, тек 19-ғасырдан кейін араб математикасы реттеліп бір жүйеге келтіріле бастаған. Араб математикасы ертедегі гректің, Индияның, Қытайдың, Шығыс пен Батыстың математикалық жетістіктерін пайдаланып және оларды бір қалыпқа түсіріп Еуропаға таратқандықтан мәдениеттің қайта гүлденуі кезеңінде математика керемет дамыды, сондықтан да араб математикасы әлемдік математика тарихында ойып тұрып орын алады
Араб сандары
1, 2, 3, 4, 5, 6, 7, 8, 9 араб сандары деп аталады. Олар ондық санау системасы бойынша сан жазудың негізі. Араб сандарын үнділер тапқан, кейін келе ол арабтардың арасына тараған. 12 ғ-дың басында Италия ғалымы Фибоначчи (Leonardo Fibonacci, 1170-1250 жж.) латын тілінде жазылған «Есеп шот» деген кітабында үнді сандарын еуропалықтарға таныстырған. Еуропалықтар бұл сандарды арабтардан қабылдағандықтан, мұны араб сандары деп атап кеткен.
Арифме́тика (грекше: ἀριθμός «сан») — математиканың, қарапайым сандар түрлерін (натурал сандар, бүтін сандар, рационал сандар) және оларға қолданатын қарапайым арифметикалық операцияларды (қосу, алу, көбейту, бөлу) зерттейтін саласы.
Планиметрия (латынша: planum — жазықтық, көне грекше:) — екі өлшемді фигураларды, яки жазықтықта жатқан фигураларды, олардың қасиеттерін зерттейтін геометрия бөлімі.
Алгебра (арабша әл-жәбр)-Математиканың теңдеулерді шешу жөніндегі есептерге байланысты дамыған негізгі бөлімдерінің бірі. Алгебра атау және жеке ғылым саласы ретінде Әбу Абдаллаһ әл-Хорезмидің 1-ші, 2-ші дәрежелі теңдеулерге келтірілетін есептердің жалпы шешімі көрсетілген «Әл-жәбр уә-л-Мұқабала» атты еңбегінен бастау алады. Ал, Омар Хайям(1038/48-1123/24)— 3-ші дәрежелі теңдеулерді зерттеуді жүйелеп, өзінің «Алгебрасын» жазған. Орта ғасырлық шығыс ғұламалары гректер мен үнділердің математикасын түрлендіріп, қайта өңдеп Еуропаға табыс еткен. Амалдарды белгілейтін таңбалар енгізу нәтижесінде алгебра одан әрі дамыды. 17-ғасырдың ортасында қазіргі алгебрада қолданылатын таңбалар, әріптер толық орнықты. Ал 18-ші ғасырдың басында алгебра математиканың жеке бөлімі ретінде қалыптасты. 17-18—шің ғасырларда теңдеулердің жалпы теориясы (көпмүшеліктер алгебрасы, т. б) қарқындап дамыды. Оған сол кездегі ірі ғалымдар — Рене Декарт, Исаак Ньютон, Жан Даламбер мен Жозеф Лагранж үлкен үлес қосты. Неміс математигі Карл Гаусс кез-келген n дәрежелі алгебралық теңдеудің нақты не жорамал n түбірі болатындығын анықтаған (1799). 19-шы ғасырдың басында норвег математигі Нильс Абель және франсуз математигі Эварист Галуа дәрежесі 4 тен жоғары болатын теңдеулердің шешуін алгебралық амалдар көмегімен теңдеудің коэффиценті арқылы өрнектеуге болмайтындығын дәлелдеген.
1-сыныпта өткен материалдарды еске түсіруге арналған деңгейлік тапсырмалар
Кестелік қосу және азайту
І деңгей
І. 7 + 1 10 – 1 2 + 1 9 + 1
9 – 1 8 + 1 5 – 1 4 – 1
ІІ. Сандардың қатарын салыстыр:
0 1 2 3 4 5 6 7 8 9 10
10 9 8 7 6 5 4 3 2 1 0
ІІ деңгей
І. Керекті цифрларды қой:
5 + = 6 2 + = 3 8 + = 9 9 - = 8
4 + = 5 1 + = 2 7 + = 8 8 - = 7
3 + = 4 9 + = 10 10 - = 9 7 - = 6
ІІ. А) 5 7 8 2 3 4 9 1 6 1- ге арттыр
Ә) 6 1 9 4 3 2 8 7 5 1- ге кеміт
Б) 1 1
1 1 1
1 1 1 1
ІІІ. 5 – 1 – 1 – 1= 8 – 1 – 1 – 1 – 1=
6 – 1 – 1 – 1= 9 – 1 – 1 – 1 – 1=
7 – 1 – 1 – 1= 10 – 1 – 1 – 1 – 1=
ІІІ деңгей
І. 2 1 3 10 8 9 7
3 1 4 10 7 9 6
ІІ. 7 - = 5 2 - = 0
4 - = 2 5 - = 3
3 - = 1 6 - = 4
ІІІ.
|
1 2 3 4 5 6 7 8 9 10 |
1 2 3 4 5 6 7 8 9 10 |
Екі санын қосу және азайту тәсілдері
І деңгей
І.

![]()
5+2 = +2 = +2 =
7-2 = -2 = -2 =
ІІ.

ІІІ. Бір сан аттай отырып, өсу ретімен және кему ретімен жаз.
А) _______________________________
Б) _______________________________
ІІ деңгей
І.

![]()
+2 = +2 = +2 =
-2 = -2 = -2 =
ІІ. Осы кесіндіден 2 см артық және кем кесінді сыз.
![]()
ІІІ.

ІІІ деңгей
І. Ыдыста 7 жұмыртқа бар еді. Оның екеуін сен жеп қойдың. Ыдыста неше жұмыртқа қалды?
ІІ. Азайтқышы 2 болатын айырмаларды жаз және мәндерін тап.

Сонда 2-ні қосу кестесіндегі теңдіктің нешеуін пайдаландың ? _______
Кесінділердің қосындысы және айырмасы
І деңгей

ІІ деңгей
![]() Осыдан 1 см ұзын кесінді
сыз
Осыдан 1 см ұзын кесінді
сыз
![]() Осыдан 1 см қысқа кесінді сыз
Осыдан 1 см қысқа кесінді сыз

Кесінділердің айырмасына тең кесінді сыз және жаз

Кесінділердің қосындысына тең кесінді сыз және жаз
ІІІ деңгей
І. Мына кесінділерден үшбұрыш сыз:

ІІ. Мына кесінділерден шаршы сыз:

5 саны және цифры
І деңгей
І.Есепте

ІІ.


ІІІ деңгей
Әр санды сәйкес белгілермен сызық арқылы жалғастыр.

Тест жұмысы
-
Теңдіктерді ата.
а) 2 > 1 ә) 3 < 4 б) 3 = 3
-
Теңсіздіктерді ата.
а) 2 = 1 ә) 14 = 4 б) 4 = 1
3. Қосындыны тап.
а) 3 + 1 = 4 ә) 4 + 1 б) 3 – 2
4. Айырманы тап.
а) 5 – 4 = 1 ә) 4 – 2 б) 2 + 3
5. Тақ сандарды тап.
а) 1, 3, 5, 7, 9 ә) 2, 3, 4, 5, 6 б) 3, 6, 5
6.Жұп сандарды тап.
а) 3, 5, 7, 8 ә) 2, 4, 6, 8 б) 3, 4, 5, 9
7. 1 дм- де неше см бар?
а) 1 дм = 9 см ә) 1 дм = 10 см б) 1 дм = 12 см
8. Бір таңбалы сандарды тап.
а) 10, 9 ә) 0, 1, 2, 3, 4 б) 11, 2, 3, 12
9. Тура теңдікті тап.
а) 3 = 2 ә) 4 = 4 б) 5 = 6
10. Тура теңсіздікті тап.
а) 3 < 2 ә) 4 < 4 б) 6 > 9
Артығын тап.


Ә
Б
В


Доминоның қайсысы 5 санын құрайды?
А Ә Б

Қайсысы жылдам жүреді?

Биік - аласа
А Ә Б

Сәулені тап .

Есепте.

Фигураның жетпегенін тап және сыз.

Цифрларды сәйкес суреттермен қос:

2-сыныпқа арналған дейгейлік тапсырмалар
Ондық құрам негізінде қосу және азайту
І-деңгей
8+50
86-80
27-20
74+70
60+4
83-80
40+9
72-70
95-5
ІІ-деңгей
69- (18-9)
30+(14-7)
(14-5)+50
(60+40)-30
ІІІ-деңгей
50+(20+10) * 60+(20-10)
(20+70)+7 * (60-10)+7
(50+40)-10 * (70-10)+20
90+(11-3) * 80+(10+10)
Сандарды салыстыруға арналған есептер
І-деңгей
|
Сан |
18 |
26 |
0 |
1 |
9 |
100 |
57 |
63 |
|
1ге қос |
|
|
|
|
|
|
|
|
ІІ-деңгей
|
Сан |
99 |
43 |
14 |
8 |
16 |
76 |
32 |
18 |
|
1ден азайт |
|
|
|
|
|
|
|
|
ІІІ-деңгей
96-3 ... 38-2
27+60 ... 89-3
57-3 ... 25+30
69-7 ... 60+4
90-50 ... 43-2
38-5 ... 30+3
74+20 ... 98-3
81+8 ... 83+6
1000 көлеміндегі сандардың нумерациясы
І-деңгей
700+8
800+2
905+40
806+40
540+8
200+60
ІІ-деңгей
784-4
605-5
784-700
650-50
784-80
650-600
ІІІ-деңгей
5ц 9кг – 5ц
8м 55см – 5 см
8ц 30кг – 8ц
5м 5дм 5см – 5дм
9ц 70кг – 70кг
282см – 2м
1000 көлемінде разрядтан өтпей қосу және азайту
І-деңгей
540+30
800+123
450-300
960-400
250+430
377-245
980-70
399-271
272-314
836-210
998-482
472+521
ІІ-деңгей
970-(20+40
880-(440-40)
356+140-20
600-(220-20)
(1000-800)+125
980-40+20
(900-300)+189
840-(300+30)
ІІІ-деңгей
9м 4см – 3см
4м +2дм
6м + 1дм 8см
2см + 4м 1дм
Екі таңбалы сандарды екі таңбалы сандармен разрядтан аттамай қосу
І-деңгей
53+26
34+65
27+42
31+58
ІІ-деңгей
32+(52+15)
(21+23)+45
24+(44+11)
(34+12)+23
ІІІ-деңгей
34+23+12
21+35+42
13+62+21
51+14+22
100 көлеміндегі сандарды разрядтан аттамай қосу
І-деңгей
63+14 41+5
83+16
52+5
27+12 39+21
66+2
71+24
53+6 45+43
32+7
86+3
ІІ-деңгей
85-41-14
56-11-42
67-33-21
99-50-16
49-11-25
67-24-13
87-22-32
95-12-80
ІІІ-деңгей
(36+28)-18
(47+34)-25
17+(19-12)
55+(75-69)
66-(49+50)
56+(27-18)
Екі таңбалы сандардан екі таңбалы сандардан разрядтан аттамай азайту
І-деңгей
...+14 =47
...-13 =25
79-... =56
52+...=58
52-41=
23+35=
ІІ-деңгей
34-21
34-12
45-32
45-23
53-13
53-31
65-42
65-24
ІІІ-деңгей
79-22
55=В 75=Г 57=Б
87-15
72=Ү 77=А 83=У
67-53
68=С 14=Р 46=Т
44-23
11=П 21=К 12=Л
58-34
28=И 44=Ы 24=І
63-12
51=Т 75=Д 42=М
Жақшалар. Амалдардың орындалу реті
І-деңгей
...-...+... =2
...-...+... =1
...+...+... =3
...+...-... =1
ІІ-деңгей
15+(3+2)*(15+3)+2
15+(3-2)*(15+3)-2
15-(3-2)*(15-3)-2
(15-3)+2*15-(3+2)
ІІІ-деңгей
13-1+2=10
14-4+2=12
16-3-1=14
14-6+1=10
19-5+1=13
16-5-4=15
17+3-2=18
15+4-3=16
18-8-3=13
19-3-2=14
14+6-5=15
15-3+2=10
Екі таңбалы сандарды қосу және азайт
І-деңгей
60-10 ... 60-7
30-10 ... 30-5
50-10 ... 50-8
40-10 ... 40-6
70-10 ... 70-3
80-10 ... 80-9
90-10 ... 90-4
70-10 ... 70-6
ІІ-деңгей
56 ... 4=60
40 ... 5=35
56 ... 4=52
5 ... 40=45
30 ... 5=35
70 ... 5=75
45 ... 5=40
85 ... 5=80
ІІІ-деңгей
|
Сан |
5 |
2 |
4 |
7 |
8 |
9 |
3 |
10 |
|
8ге қос |
|
|
|
|
|
|
|
|
Есептер шығару
І-деңгей
|
Сан |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
4ке қос |
|
|
|
|
|
|
|
|
|
ІІ-деңгей
40+5=
40-5=
30+5=
30-5=
20+5=
20-5=
10+5=
10-5=
ІІІ-деңгей
18+2 ... 13+7
20-13 ... 30-25
17+8 ... 14+6
38-20 ... 14+5
15+5 .. 25-5
44+6 ... 74-23
100 көлеміндегі сандарды ауызша қосу және азайту тәсілдері
І-деңгей
53+4
61+8
74+5
69-6
70-8
98-4
ІІ-деңгей
68-9
79+7
94-9
46+5
32-8
57+6
ІІІ-деңгей
Х+20 = 34+16
80-у = 12+8
Кестелік есептер
І-деңгей


ІІ-деңгей
2+9
8+9
15-7
8+6
12-3
14-9
11-6
5+7
16-9
9+7
8+4
15-9
ІІІ-деңгей
44+6*51-1
24-4*26+4
5см +3см * 8см
9м+6дм * 840см
100 көлеміндегі сандарды ауызша қосу және азайту тәсілдері
І-деңгей
67-25 70-56
49+7
78+9
63-8
33-7
100-9 66+24
51-3
19+8
78+7
44-7
ІІ-деңгей
67+5 80-7
63+17
74+9
81-8
23+31
58+5 9+36
42+18
56-8
16-9
90-6
ІІІ-деңгей
56+26
91-22
39см + 33см
47+26
74-48
97см – 18см
38+29
67-59
28см + 47см
56-38
45+47
92см – 48см
Сандарды ондықтар мен бірліктердің құрамына жіктеу.
І-деңгей.
Цифрмен жаз және теңдікке айналдыр.
2 онд + 4 онд=
9 онд- 3 онд=
1 онд + 2 онд=
3 онд + 7 онд=
10 онд-5 онд=
3 онд+ 5 онд=
5 онд + 1 онд=
6 онд - 2 онд=
6 онд + 3 онд=
6 онд + 4 онд=
8 онд – 4 онд=
2 онд + 5 онд=
1 онд+ 8 онд=
7 онд – 3 онд=
7 онд +2 онд=
ІІ- деңгей.
Керекті сандарды жаз.
11. ( он және үш)
12. ( он және екі)
1 онд+1 бірл= ... онд. ... бірл
... онд. + ... бірл.= ... онд. ... бірл
10 + ... =...
... ... + ... = ... ...
13. ( он және үш)
14. ( он және төрт)
... онд. + ... бірл.=... онд. ... бірл
... онд. + ... бірл. = ... онд. ... бірл.
... ... + ...= ... ...
... ... + ... =...
15. ( он және бес)
16. ( он және алты)
... онд. + ... бірл. = ... онд. ... бірл
... онд. + ... бірл= ... онд. ... бірл
... ... + ... = ... ...
... ... + ... = ... ...
ІІІ- деңгей.
Бос орынға теңдік дұрыс шығатындай етіп сандар қой.
64+...= 67
57 - ... = 51
79- ...= 73
99 - ...= 90
98 - ...= 92
100+ ...=100
Салыстыр ( < ,=,>)
12 + 6 * 17
13+12 *13+14
13+ 4 * 9
29+1 * 33- 3
Екі таңбалы сандарды екі таңбалы сандармен разрядтан аттамай қосу.
1- деңгей.
Есепте. Мәндері бірдей өрнектерді сызықтармен жалға.
53+26 =
34+65 =
27+42 =
31+58 =
ІІ-деңгей.
Есепте. Мәндері бірдей өрнектерді сызықтармен жалға.
32+ (52+ 15)=
(21+23) +45=
24+ (44 + 11)=
(34+12) + 23=
ІІІ-деңгей.
Теңдіктердің қандай қасиеттер бойынша жалғанғанын анықта. Осыған ұқсас теңдік жұптарын тап және оларды үлгі бойынша жалға. Есепте.
34+23+12=
21+35+ 42
Ондық құрам негізінде қосу және азайту
І-деңгей
10+9
16-6
17-7
12-10
18-10
3+10
ІІ-деңгей
Доп – 9 дана
Секіртпе -? Дана, 4-еуі кем
ІІІ-деңгей
14-х=9
Х+8=13
Есептерді шығар. Дұрыс жауапты қорша
Көкөніс сататын дүңгіршікте 11 қарбыз болды.түске дейін 9 қарбыз сатылды. Дүңгіршікте сататын тағы неше қарбыз қалды?
А) 2
ә) 3
б)20
Кестелеп қосу және азайту
І-деңгей
6+5 7+6
14-9 13-8
9+3 7+8
16-7 15-8
ІІ-деңгей
Бумадан 9 шар алынғаннан кейін, одан тағы 6 шар қалды. Бумада бастапқыда неше шар болған?
ІІІ-деңгей
9+(40+30)
95-(50+30)
75+10-50
(90-30)+40
87-(60+20)
33-(23-3)
52+7-9
Ұзындықтың өлшем бірліктері, құрама есеп
І-деңгей
89-(54+25)
20+(62-41)
100-70+9
(63+25)-76
17+52-26
20+68-47
ІІ-деңгей
Конструктор жинағанда 17 көк және 22 қызыл бөлшек бар.
25 бөлшек қолданылды.
Неше бөлшек қалды?
ІІІ-деңгей
...см -8см*12см
7дм + 6 см * 15дм
1 жүзд + 2 онд * 120бірл
7дм + 2см * 3см +8 см
9см * 2 дм
1 сағ + 10 мин * 100 мин
48 сағ * 2 тәул
Есепті әртүрлі тәсілмен шығар
І-деңгей
47+3
90-9
52
8
70-4
24+56
100-73
91+9
60-37
ІІ-деңгей
(53+29)-19
(31+19)-12
ІІІ-деңгей
5ц 9 кг – 5ц
8ц 30 кг – 8 ц
9ц 70кг – 70кг
8м 55см – 5см
5м 5дм 5см – 5дм
282см – 2м
Есептерді қөосу және азайту
І-деңгей
47-28 70-34
56+29
75-37 62-48
59+38
ІІ-деңгей
Бақтан 70 кг алма жиналды. Алманың бір бөлігі жәшіктерге салынғанда, тағы 18 килограмм алма қалды. Жәшіктерге неше килограмм алма салынды?
Есепті шығар дәне кері амалмен екі есеп құрастыр.
ІІІ-деңгей
6 жүздік * 600 бірл
2 онд * 20 бірл,
2-жүзд * 20 онд
500 бірл * 1 жүзд
704 см = ...м ...дм ...см
620 см = ...м ...дм ...см
364 см= ...м ...дм ...см
460 см = ...м ...дм ...см
213 см = ...м ...дм ...см
301 см = ...м ...дм ...см
890 см = ...м ...дм ...см
600 см = ...м ...дм ...см
Жақшаларды қоюға арналған есептер
І-деңгей
7+(4+1) 6-(2+3)
(7+4)+1 (6-2)+3
3-1+2 5-3-2
9+(7-5) (9-7)+5
(3+7)-4 3+(7-4)
10-5+4 9+7-5
ІІ-деңгей
7+9+3+1
(7+3)+(9+1)
16+8+4+2
(16+4)+(8+2)
40+30+6+4
50+5+25-50
4+6+17+3
3+7+7+4
ІІІ-деңгей
14-9+5 = 10
19+1-6=14
17-8+4=5
13+3-10=6
15-6-1=10
12-3+8=1
19-1+2=20
20-3-2=19
16-4+2=10
11-5+1=7
18-7+1=10
10-2+3=11
27-10-2-2=15
32-20+10=2
73-30+10=33
50-40-10=0
45-5+4=44
16-8+7=1
Екі таңбалы сандарды қосу және азайту
І-деңгей
21+8 78+2
34+6 17+3
18+2 72+4
29+1 64+30
45+20 41+20
60+17 87+2
ІІ-деңгей
15+20+5+10
40+3+30+7
50+6+20+4
2+24+8+6
18+11+9+2
17+22+3+8
5+64+5+6
1+80+19
ІІІ-деңгей
Себетке Айнұр 3 алмұрт, ал Арман 2 алмұрт салды. Себеттегі барлық алмұрт нешеу?
Шарты: Себетке Айнұр 3 алмұрт, Ал Арман 2 алмұрт салды.
Сұрағы: Себеттегі барлық алмұрт нешеу?
С![]() ызба:
ызба:
3 алма 2 алма
Өрнек: 3 + 2
Шешуі: 3 + 2 = 5 алмұрт
Жауабы: Барлығы 5 алмұрт.
Жанарда 5 тиын, ал Маратта 2 тиын бар.
Сұрағы: Жанар мен Маратта барлығы неше тиын бар?
С ызба:
ызба:
?
Ж М
5 т 2 т
Өрнек: +
Шешуі: + =
Жауабы: Барлығы тиын.
Есептерді қосу және азайтуға арналған есептер
І-деңгей
72+3 30-9 23-8
65+4 21-5 37-4
76+20 47-30 65-9
53+40 62-40 82+7
32+6 82-8 61+4
52+20 54-20 93+7
13+8 93-8 31-6
43+8 18-10 37+12
9-27 17-8 43+54
12+10 16-9 65+32
32+40 15-6 28+51
47+50 14-8 71+23
26+7 13-4 54+32
12+6 12-6 86-43
ІІ-деңгей
9дм 1см – 5дм 4 см
2 дм 8 см – 3 дм 6 см
2 дм 8 см + 4 дм 6 см
7 дм 2 см – 1дм 9 см
ІІІ-деңгей
540+30
960-400
980-70
836-210
800+123
520+430
399-271
998-482
450-300
377-245
272+314
472+521
Үш таңбалы сандарды қосу және азайту
І-деңгей
507+40 362+224
809-800 602+24
909-9 890-710
860-40 649-415
604-400 960-440
531+302 520+407
ІІ-деңгей
651+123 505-103
492+104 980-450
976-651 478-107
790-650 51+708
ІІІ-деңгей
980-(40+30)
508+200-1
(800-100) -125
(1000-200)-65
909-(404-400)
200+(505-5)
458-(25+25)
28

шағым қалдыра аласыз















