Математика: “Сан аралықтардың бірігуі мен қиылысуы”

Бөлім:

6.3В Бір айнымалысы бар сызықтық теңсіздіктер

Практиканттың Т.А.Ә.(болған жағдайда

Жумабаева Гулжайна Махсетқызы

Күні:

05.02.24

Пән/Сынып:

Математика, 6 В сыныбы

Қатысушылар саны:

Қатыспағандар саны:

Сабақтың тақырыбы:

Сан аралықтардың бірігуі мен қиылысуы

Оқу бағдарламасына сәйкес оқыту мақсаттары:

6.2.2.9 сан аралықтардың бірігуін және қиылысуын табу;

Сабақтың мақсаты:

• сан аралықтарын жазу үшін белгілеулерді пайдалану;

• сан аралықтарды кескіндеу.

Уақыты

Кезең дері

Педагогтің әрекеті

Оқушының әрекеті

Бағалау

Ресурстар

5 минут

Ұйым

дастыру

Сәлеметсіздерме!

Бүгін, Сан аралықтардың бірігуі мен қиылысуы тақырыбын қарастырамыз

Бүгінгі сабақта меңгеретініңіз:

-сан аралықтарын жазу үшін белгілеулерді пайдалану;

-сан аралықтарды кескіндеу.

Үй тапсырмасын тексеру. №914, №915.

"Миға шабуыл"

-Сан аралықтары дегеніміз не?

-Сан аралығының қандай түрлерін білесіңдер?

-Қатаң теңсіздіктің шешімдер жиыны координаталық түзуде қалай кескінделеді?

-Қатаң емес теңсіздіктің сан аралығын жазу үшін қандай жақша қолданылады?

-Неліктен кесіндіде координаталық түзуде көрсетілген сандар шешімдер жиынына кіреді? - деген жабық және ашық сұрақтар қоямын.

Амандасады, үй тапсырмасына жауап береді.

Сұрақтарға жауап береді

Оқулық, жұмыс дәптері

Тақта

10 мин

Жаңа сабақ

1. Сан аралықтарының қиылысуы ∩

А ∩ В қиылысу белгісі

Мысал 1. (– ∞; 3] және [– 4; +∞) сан аралықтарының қиылысу аралығын табайық. Жазылуы: (– ∞; 3] ∩ [– 4; +∞) = [– 4; 3].

Мысал 2.Сан аралықтарының қиылысуы. [-2;4] және [1;6] сан аралықтарының қиылысуы - [1;4]. Бұл олардың ортақ сан аралығы. Белгіленуі: [-2;4] [1;6]=[1;4]

Мысал 3. [– 2; 9] және [5; 12] сан аралықтарының қиылысу аралығын табайық. Жазылуы: [– 2; 5] ∩ [5; 12) = [5; 9].

Сан аралықтарының қиылыcпайтын болуы.

[-4;1] және [3;7] сан аралықтары қиылыспайды немесе оларға ортақ сан аралығы жоқ.

Белгіленуі: [-4;1] [3;7]=

Сан аралықтарының бірігуі 

[-2;6] аралығының әрбір саны [-2;3] және [1;6] аралықтарының ең болмағанда біреуіне немесе екеуіне де тиісті.

Белгіленуі: [-2;3] [1;6]=[-2;6]

Мысал 4: [– 2; 7] және [4; 11] сан аралықтарының бірігуін табайық.

Жазылуы: [– 2; 7] [4; 11] = [– 2 ; 11]

Мысал 5: [– 6; 1] және [4; 10] сан аралықтарының бірігуін табайық. Жазылуы: [– 6; 1] [4; 10]

Тақырып бойынша ресурстарды қарап, танысады

Оқулық, жұмыс дәптері

Тақта

25

минут

Бекіту тапсыр

масы

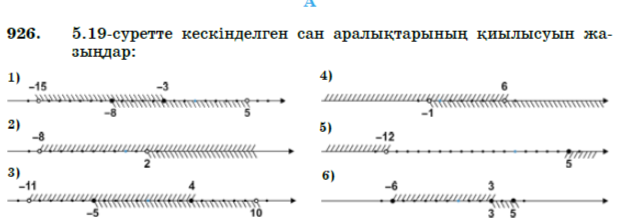
"Ойлан, жұптас, бөліс" әдісін қолданамын. Бұл әдісті қолдану арқылы оқушылар арасында қарым-қатынасы дамып, бірлесе отырып жұмыс жасауды үйренеді.

А деңгейі. №926. Оқулықтағы 5.19-суретте кескінделген сан аралықтарының қиылысуын жазыңдар.

№928.

В деңгейі. №933.

Берілген сан аралықтарын координаталық сәуледе кескіндеп,олардың бірігуін жазыңдар.

С деңгейі. №934. Координаталық түзіді пайдаланып, сан аралықтарының қиылысуын табыңдар.

1. (-7; , (-4; + және ;

2. (- ; , және ;

3. (-8; 7), (-5; 10) және ;

4. (- ; , (-4; + және

Өз бетімен жұмыс.

[-2; 5 ] және [ 1;7] сан аралықтарының қиылысуын тап және сатылай кешенді талда.

[-2; 5 ] ∩ [ 1;7 ] = [ 1; 5 ]

. [ 1; 5 ]

1 аталуы --------------
2 оқылуы --------------
3 координаталық түзуде кескінделуі --------
4 теңсіздік түрінде жазылуы -------------------
5 аралыққа тиісті бүтін сандар ----------------------
6 аралыққа тиісті ең кіші бүтін сан ------------
7 аралыққа тиісті ең үлкен бүтін сан -----------

Кестені толтырады

Оқулықтан тақырыпқа қатысты есептерді шығарады.

Дескриптор:

- берілген бір айнымалысы бар сызықтық теңсіздіктерді сан аралығының қиылысуы мен бірігуін жазады.

«Басбармақ» әдісімен бағалау алады

жүргізіледі

Интернет ресурстары

Жалпы білім беретін мектептің 6–сыныбына арналған оқулық.

Оқулық авторлары: Т.А.Алдамұратова, Қ.С.Байшоланова, Е.С.Байшоланов Алматы «Атамұра» баспасы 2018 жыл

Жеке жұмыс

Жеке орындалатын тапсырма.

№1. Мына сан аралықтарына тиісті ең үлкен бүтін санды және ең кіші бүтін санды жаз.

(-6;2 ] және (-3; 7]

( -7;7 ) және [ -2; 3]

Тапсырманы орындайды

Дескриптор:

-Сан аралықтарын кескіндейді;

-Сан аралықтарының қиылысуын табады;

-Қиылысу аралықтарынан бүтін сандарды табады.

Оқулық, жұмыс дәптері

Тақта

слайд

5 минут

Бүгінгі сабақта:

-сан аралықтарын жазу үшін белгілеулерді пайдалану;

-сан аралықтарды кескіндеу.

Кері байланыс

Үйге тапсырма.

Тақырыпты меңгергенін анықтау

Кері байланыс

Оқулық

Оқулық, жұмыс дәптері

Тақта

слайд