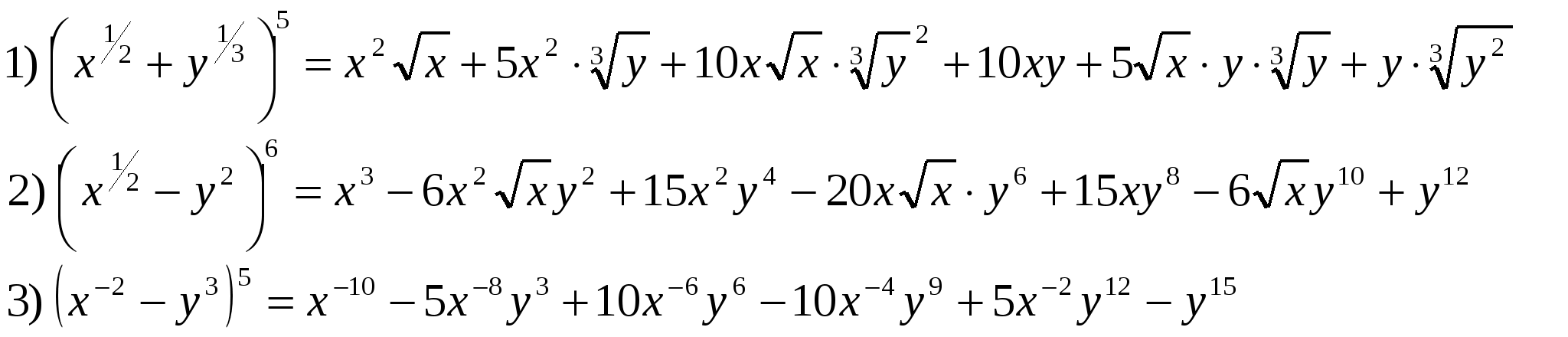Математикадан олимпиада есептерін шығару жолдары
сынып оқушыларына арналған
аптасына 1 сағат, барлығы 34 сағат
Математика пәні мұғалімі Утешова Жайна Баяновна
Пікір жазған: Абай атындағы ҚазҮПУ, Математика және математикалық модельдеу кафедрасы п.ғ.к., аға оқытушы Б.А.Қадырбаева
2025 ж
Түсінік хаты
Бұл жазбада мен сіздерге оқушыларыңызға пайдалы болуы мүмкін математикалық олимпиада есептерін шешу жолдарын шолуды ұсынғым келеді. Бұл әдістер оқушылардың аналитикалық ойлау, логикалық ойлау және математикалық есептерге есептер шығару тәсілдерін дамытуға мүмкіндік береді, бұл олимпиадаларға қатысудың маңызды бөлігі болып табылады.
1. Декомпозиция және модельдеу әдісі: Бұл әдіс күрделі есепті қарапайым құрамдас бөліктерге бөлуді қамтиды. Содан кейін әрбір компонент жеке талданады және шешіледі. Содан кейін қорытынды жауапқа жету үшін нәтижелер біріктіріледі. Бұл әдіс әсіресе әртүрлі формулалармен және теңдеулермен жұмыс істеуді қажет ететін есептерді шешуде тиімді.
2. Сынақ және қате әдісі: Бұл әдіс мәселені шешудің әртүрлі тәсілдерін жүйелі түрде сынап көруді қамтиды. Қарапайым қадамдардан бастап, оқушылар өз шешімін біртіндеп жақсарту үшін итерациялық процесті пайдалана алады. Бұл әдіс шыдамдылықты, табандылықты және ойлау икемділігін дамытуға ықпал етеді.
3. Аналогтарды қолдану әдісі: Бұл әдіс бұрыннан шешілген ұқсас есептерді табуға негізделген. Оқушылар жалпы үлгілер мен шешімдерді іздеу үшін бұрын орындалған математикалық мысалдарды немесе олимпиада есептерін пайдалана алады. Бұл әдіс аналитикалық ойлауды дамытуға және әртүрлі математикалық ұғымдар арасында байланыс орнатуға көмектеседі.
4. Графиктер мен диаграммалар әдісі: Бұл әдіс графиктер мен диаграммаларды пайдаланып мәселені визуализациялауға баса назар аударады. Оқушылар қандай деректер берілгенін және есепте не қажет екенін жақсы түсіну үшін графикалық бейнені пайдалана алады. Бұл әдіс деректерді талдау және интерпретациялау дағдыларын дамытады.
5. Математикалық индукция әдісі: Бұл әдіс есепті дәлелдеу үшін логикалық пайымдау мен математикалық индукцияны қолдануды қамтиды. Оның көмегімен оқушылар жалпы заңдылықтарды тауып, әртүрлі жағдайларға қолданылатын ережелерді белгілей алады. Бұл әдіс теориялық ойлауды дамытады және күрделі мәселелерді шешуді жеңілдетеді.
Әртүрлі тапсырмалардың бірегей сипаттамаларына байланысты бірнеше әдістердің тіркесімін немесе теңшелген тәсілді қажет ететінін есте ұстаған жөн. Математикадан олимпиада есептеріне қатысу оқушыларға математика саласында дамуға, есептерді шығару және математикалық теоремаларды дәлелдеу дағдыларын жетілдіруге, университеттік сынақтарға және болашақ ғылыми мансапқа дайындалуға мүмкіндік береді.
Мәселені шешудің әртүрлі әдістерін ескере отырып, мен сізге оқушылар осы тәсілдердің әрқайсысын тәжірибеден өткізе алатын тәжірибе сабағын өткізуді ұсынамын. Бұл олардың аналитикалық ойлау қабілеттерін дамытуға көмектеседі, сондай-ақ олимпиада тапсырмаларына қатысу кезінде сенімділігін арттырады.
Математикалық олимпиада есептерін шешудің бұл әдістері оқушыларыңызға тек математикалық ойлауды ғана емес, жалпы есептерді шығару дағдыларын дамытуға көмектеседі деп ойлаймын. Оқушыларіңіз әртүрлі есептерді шешу әдістерін үйреніп, оларды тәжірибеде қолдануды ұнататынына сенімдімін.
Өзектілігі: математикадан олимпиада есептері оқушылардан негізгі ұғымдар мен алгоритмдерді білуді ғана емес, сонымен қатар шешімдердің тривиальды емес тәсілдерін табуды және әртүрлі стратегиялар мен әдістерді қолдана білуді талап етеді. Бұл дағдылар креативті ойлауды дамытудың және әдеттен тыс есептерді шешудің кілті болып табылады, бұл математикада ғана емес, шынайы өмірде де маңызды.
Бағдарламаның мақсаты: оқушылардың күрделі математикалық есептерді талдау және шешу дағдыларын дамыту, олимпиадаларға қатысуға дайындау және математиканы оқуға қызығушылығын арттыру.
Бағдарламаның міндеттері:
1. Оқушыларды математикадан типтік олимпиада есептерімен таныстыру, оларды шешудің әртүрлі тәсілдері мен стратегияларын талдау және талдау.
2. Оқушыларды тривиальды емес шешімдерді табу әдістеріне және олимпиада есептерін шығаруда әртүрлі математикалық тәсілдерді қолдануға жаттықтыру.
3. Математикалық модельдермен жұмыс істеу, логикалық ойлау және шығармашылық ойлау дағдыларын дамыту.
4. Оқушыларды есептерді шешу жолдарын, сонымен қатар басқа олимпиада қатысушыларының шешімдерін талдауға және бағалауға үйрету.
5. Оқушыларды олимпиадалық сынақтарға дайындау және олардың жарыстардағы көрсеткіштерін арттыру.
6. Математикаға және жалпы пәнге деген қызығушылықтың дамуына ықпал ету.
Күтілетін нәтиже:
1. Оқушылардың математикалық дайындық деңгейін арттыру.
2. Логикалық ойлау қабілеттерін дамыту, шығармашылық көзқарас пен күрделі есептерді аналитикалық шешу.
3. Математикадан олимпиадаларға дайын және сәтті өнер көрсететін оқушылардың санын арттыру.
4. Оқушылардың математиканы оқуға деген сенімі мен ынтасын нығайту.
5.Оқушылардың жарыстардағы жетістіктерінің арқасында мектеп пен оқу орнының беделін арттыру.
Бағдарламаның жаңалығы:
Бағдарламаның ғылыми жаңалығы әртүрлі әдістер мен тәсілдерді қолдана отырып, олимпиада есептерін талдау мен шешудің жүйелі тәсілін ұсынуында. Сондай-ақ бағдарлама негізгі есептерден кеңейтілген мәселелерге дейінгі мәселелердің күрделілігінің әртүрлі деңгейлерін қамтиды. Бұл оқушылардың жеке ерекшеліктерін ескере отырып, есептерді шешу дағдыларын біртіндеп дамытуға мүмкіндік береді.
Тұрақтылау (мазмұндық) бөлім
-сынып
Аптасына – 1 сағат. Барлығы – 34 сағат
I – бөлім. Математикадан олимпиада есептерін секциялары бойынша шешу (10 сағат)
Бағдарламаның бірінші бөлімі бөлімдер бойынша математикадан олимпиаданың іріктеу кезеңінің есептерін шешуге арналған. Бұл бөлімнің жетекші идеясы олимпиадалық есептерді сәтті шешу математиканың әртүрлі салаларын терең түсінуді және оларды бірге қолдана білуді талап етеді. Бағдарлама оқушылардың математикалық дағдыларын дамытуға және олимпиаданың ең қиын есептерін шешуге көмектесетін стратегиялар мен есептерді шешу әдістерін ұсынады.
Бағдарламаның бірінші бөлімінің мақсаты – оқушыларды математиканың әртүрлі салаларымен таныстыру және оларды тереңдетіп оқуға көмектесу, осылайша олар алған білімдерін олимпиада есептерін шешуде сәтті қолдана алады. Бұл бөлім математиканың алгебра, геометрия, комбинаторика және сандар теориясы сияқты салаларын қамтиды. Әрбір бөлім оқушыларға олардың жұмысы мен қолданылуын толық түсінуге мүмкіндік беру үшін әртүрлі әдістер мен тәсілдер арқылы зерттеледі.
Бұл авторлық бағдарлама оқушылардың олимпиадалық математикадағы мүмкіндіктерін жүзеге асыруға және жоғары нәтижелерге жетуге көмектеседі деп сенемін. Математиканың әртүрлі салаларындағы есептерді шешуде жүйелі оқу және машықтандыру арқылы ғана адам осы күрделі де қызықты өнердің нағыз шебері бола алады.
II – бөлім. Жоғары қиындық деңгейлі есептерді шешу (10 сағат)
Біздің қолтаңба математикалық бағдарламамыздың екінші бөлімі бізді күрделіліктің жоғары деңгейіндегі есептерді шешудің қызықты және ойландыратын әлемімен таныстырады. Бұл бөлім бізге біліміміз бен дағдыларымыздың көмегімен математикалық жұмбақтардың тереңдігіне үңіліп, олардың жұмбақтарын шешуге бірегей мүмкіндік береді. Мұнда аналитикалық ойлауды, тапқырлықты және шығармашылықты қажет ететін мәселелерге тап боламыз. Әрбір тапсырма жаңа сынақты, әрбір шешім қиындықтарды жеңуді білдіреді. Бізге осы қызықты саяхатқа қосылыңыз, өйткені біз зерттеп, үйреніп, жоғары деңгейдегі міндеттерді шешуде ұлылыққа қол жеткіземіз.
III – бөлім. Ұзақ уақыт алатын есептерді шешу (5 сағат)
Мұғалімнің математикаға арналған бастапқы бағдарламасының үшінші бөлімі арнайы тақырыпқа - көп уақытты қажет ететін есептерді шешуге арналған. Бұл бөлімде біз толық шешу үшін көп уақыт пен күш жұмсауды қажет ететін тапсырмаларға тоқталамыз.
Күрделі математикалық есептерді шешу оқу процесінің маңызды бөлігі болып табылады және оқушылардың аналитикалық ойлауын, есептер шығару және алған білімдерін практикада қолдана білу дағдыларын дамытуға көмектеседі. Дегенмен, біз көптеген тапсырмаларды орындау күрделі және уақытты қажет ететінін түсінеміз.
Авторлық бағдарламаның бұл бөлімінде біздің мақсатымыз – оқушыларға ұзақ уақыт пен терең талдауды қажет ететін есептерді тиімді шешуге үйрету. Біз оқушыларға жұмыстарын ұйымдастыруға, ақпаратты құрылымдауға және шешімге жетудің ең жақсы жолдарын табуға көмектесетін әдістер мен стратегияларды ұсынамыз.
Бағдарлама күрделі математикалық есептерден бастап ұзақ мерзімді жобаларға дейінгі әртүрлі есеп түрлерін қамтиды. Біз оқушыларды көп уақытты қажет ететін есептерді шешу процесін жеңілдету үшін математикалық модельдеу, графикалық бейнелеу және есептеуіш технологияларды пайдалану сияқты әртүрлі құралдарды қолдануға шақырамыз.
Математика пәнінің мұғалімі ретінде біз оқушыларда есеп шығару дағдыларын ғана емес, сонымен қатар олардың қабілетіне деген сенімділікті дамытуға ұмтыламыз. Біз оларды проблемаларды шешуде тәуелсіздік пен ерекшелікті дамытуға көмектесу үшін зерттеу тәсілдері мен балама шешімдерінде қолдаймыз және қолдаймыз.
Бұл бөлімде ұсынылған барлық материалдар мен жаттығулар тапсырмалардың күрделілігін, оқушылар үшін орындылығын және материалды қызықты және қолжетімді түрде ұсынуды ескере отырып әзірленген. Бағдарламаның осы бөлімін меңгеру оқушыларға көп уақытты қажет ететін есептерді шешуде кездесетін қиындықтарды жеңуге көмектесетініне сенімдіміз.
IV – бөлім. Логикалық есептерді шешу (9 сағат)
Логикалық есептерді шешу математиканы оқытудың маңызды кезеңі болып табылады. Ол оқушылардың аналитикалық және сыни тұрғыдан ойлауын, сондай-ақ математикалық дағдылар мен білімдерін өмірлік жағдаяттарда қолдана білуді дамытуға бағытталған.
Біздің меншікті бағдарламамыздың төртінші бөлімінде біз логикалық есептерді зерттеуге терең еніп, оқушыларға оларды сәтті шешуге арналған құралдар жиынтығын ұсынамыз. Біз оқушыларға дерексіз ұғымдармен жұмыс істеуде сенімділік пен дағдыларды дамытуға көмектесетін әртүрлі мәселелерді шешу стратегияларын ұсынамыз.
Логикалық есептерді шешуді зерттеудің бірінші қадамы есептің шарттарын талдау болып табылады. Оқушылар белгілі бір математикалық операциялармен немесе ұғымдармен байланысты болуы мүмкін негізгі сөздер мен сөз тіркестерін анықтауды үйренеді. Бұл мәселені құрылымдауға және оны шешу үшін қажетті операцияларды анықтауға көмектеседі.
Содан кейін біз логикалық ойлау тізбегін құруға көшеміз. Оқушылар маңызды ақпаратты проблемалық мәлімдемеден оқшаулауды және қосымша деректерді шығару үшін логикалық операцияларды қолдануды үйренеді. Сондай-ақ біз оқушыларды ақпаратты жүйелеуге және шешімнің логикалық ағынын оңайырақ қадағалауға көмектесетін кестелер мен диаграммалар сияқты есептерді шешудің әртүрлі әдістерімен таныстырамыз.
Біздің бағдарламамыздың төртінші бөлімінің маңызды бөлігі - дәлелдеу және жауаптарды негіздеу дағдыларын дамыту. Оқушылар өз ойларын және дәлелдемелерін түсінікті және логикалық түрде тұжырымдауға үйренеді. Біз бұл аспектіге үлкен мән береміз, өйткені ол оқушыларға өз ойларын сенімдірек жеткізуге және логикалық ережелерге негізделген дәлелдер құруға көмектеседі.
Нормативті бөлім
|
Бөлім |
Бөлімше |
Тақырып |
Оқу мақсаты |
Барлығы (сағ) |
Теория (сағ) |
Практика (сағ) |
Білім өнімі |
|
I бөлім |
1. Математикадан олимпиада есептеріне кіріспе |
Математикадан олимпиада есептеріне кіріспе |
Олимпиадалық есептердің маңыздылығын түсіну |
1 |
1 |
0 |
Олимпиадалық есептердің ерекшеліктерін білу |
|
|
2. Алгебраны пайдаланып есептер шығару әдістері |
Алгебраны пайдаланып есептер шығару әдістері |
Алгебралық әдістерді есептер шығаруда қолдана білу |
1 |
1 |
0 |
Алгебралық әдістерді қолдану дағдысын меңгеру |
|
|
3. Математикадан олимпиада есептерін шешу |
Математикадан олимпиада есептерін шешу |
Түрлі деңгейдегі олимпиадалық есептерді шеше білу |
1 |
0 |
1 |
Олимпиадалық есептерді шешу тәсілдерін қолдана білу |
|
|
4. Бір айнымалысы бар сызықтық теңдеулерді шешу |
Бір айнымалысы бар сызықтық теңдеулерді шешу |
Бір айнымалысы бар сызықтық теңдеулерді шеше білу |
1 |
1 |
0 |
Сызықтық теңдеулерді шешудің алгоритмін меңгеру |
|
|
5. Тест тапсырмалары |
Тест тапсырмалары |
Өткен материалдарды қайталау және білімді бағалау |
1 |
0 |
1 |
Тақырыптар бойынша білімді тексеру |
|
|
6. Сызықтық теңдеулер жүйесін ауыстыру арқылы шешу |
Сызықтық теңдеулер жүйесін ауыстыру арқылы шешу |
Сызықтық теңдеулер жүйесін ауыстыру әдісімен шешуді меңгеру |
1 |
1 |
0 |
Сызықтық теңдеулер жүйесін шешудің әдістерін білу |
|
|
7. Сызықтық теңдеулер жүйесін қосу және азайту әдісімен шешу |
Сызықтық теңдеулер жүйесін қосу және азайту әдісімен шешу |
Сызықтық теңдеулер жүйесін қосу және азайту әдістерімен шешуді меңгеру |
1 |
1 |
0 |
Сызықтық теңдеулер жүйесін шешудің әдістерін қолдана білу |
|
|
8. Анықтауыш әдісі арқылы сызықтық теңдеулер жүйесін шешу |
Анықтауыш әдісі арқылы сызықтық теңдеулер жүйесін шешу |
Анықтауыш әдісі арқылы сызықтық теңдеулер жүйесін шешуді меңгеру |
1 |
1 |
0 |
Сызықтық теңдеулер жүйесін анықтауыш әдісі арқылы шеше білу |
|
|
9. Функциялар және олардың графиктері |
Функциялар және олардың графиктері |
Функция және оның графигі туралы түсінік қалыптастыру |
1 |
1 |
0 |
Функциялардың негізгі қасиеттерін білу және графиктерді салу |
|
|
10. Тест тапсырмалары |
Тест тапсырмалары |
Өткен материалдарды қайталау және білімді бағалау |
1 |
0 |
1 |
Тақырыптар бойынша білімді тексеру |
|
II бөлім |
11. Арифметикалық және геометриялық прогрессиялар |
Арифметикалық және геометриялық прогрессиялар |
Арифметикалық және геометриялық прогрессиялардың формулаларын қолдана білу |
1 |
1 |
0 |
Прогрессиялардың қасиеттерін қолдануды меңгеру |
|
|
12. Квадрат теңдеулерді шешу |
Квадрат теңдеулерді шешу |
Квадрат теңдеулерді шешудің әдістерін меңгеру |
1 |
1 |
0 |
Квадрат теңдеулерді шешу әдістерін қолдана білу |
|
|
13. Дәреже функциясы, оның қасиеттері және графигі |
Дәреже функциясы, оның қасиеттері және графигі |
Дәреже функциясының қасиеттерін білу және графигін сала білу |
1 |
1 |
0 |
Дәреже функциясының негізгі қасиеттерін қолдану |
|
|
14. Көпмүшені көбейткіштерге бөлу |
Көпмүшені көбейткіштерге бөлу |
Көпмүшені көбейткіштерге бөлудің әдістерін меңгеру |
1 |
1 |
0 |
Көпмүшені көбейткіштерге бөлуді қолдану |
|
|
15. Тест тапсырмалары |
Тест тапсырмалары |
Өткен материалдарды қайталау және білімді бағалау |
1 |
0 |
1 |
Тақырыптар бойынша білімді тексеру |
|
|
16. Рационал теңдеулер мен теңсіздіктерді шешу |
Рационал теңдеулер мен теңсіздіктерді шешу |
Рационал теңдеулер мен теңсіздіктерді шешу әдістерін білу |
1 |
1 |
0 |
Рационал теңдеулер мен теңсіздіктерді шешуді меңгеру |
|
|
17. Иррационал теңдеулер |
Иррационал теңдеулер |
Иррационал теңдеулерді шешу әдістерін меңгеру |
1 |
1 |
0 |
Иррационал теңдеулерді шешуде қасиеттерін қолдануды меңгеру |
|
|
18. Комбинаторикадан көбейту әдісі бойынша олимпиада тапсырмалары |
Комбинаторикадан көбейту әдісі бойынша олимпиада тапсырмалары |
Комбинаториканың көбейту әдісін олимпиадалық есептерде қолдана білу |
1 |
1 |
0 |
Комбинаторикалық есептерді шығарудың әдістерін меңгеру |
|
|
19. Ықтималдықтар теориясы және статистика |
Ықтималдықтар теориясы және статистика |
Ықтималдықтар теориясы мен статистиканың негізгі ұғымдарын білу |
1 |
1 |
0 |
Ықтималдықтар теориясы мен статистика элементтерін есеп шығаруда қолдана білу |
|
|
20. Тест тапсырмалары |
Тест тапсырмалары |
Өткен материалдарды қайталау және білімді бағалау |
1 |
0 |
1 |
Тақырыптар бойынша білімді тексеру |
|
III бөлім |
21. Ньютонның Биномы. Паскаль Үшбұрышы |
Ньютонның Биномы. Паскаль Үшбұрышы |
Ньютонның биномы мен Паскаль үшбұрышын қолдана білу |
1 |
1 |
0 |
Ньютон биномы мен Паскаль үшбұрышын практикада қолдану |
|
|
22. Теңдеулерді пайдаланып сөздік есептерді шығару |
Теңдеулерді пайдаланып сөздік есептерді шығару |
Теңдеулерді қолданып сөздік есептерді шығару дағдыларын дамыту |
1 |
0 |
1 |
Сөздік есептерді шешу үшін теңдеу құрастыру |
|
|
23. Логарифмдер және оның қасиеттері |
Логарифмдер және оның қасиеттері |
Логарифмдердің қасиеттерін білу және есептер шығаруда қолдана білу |
1 |
1 |
0 |
Логарифмдік өрнектерді түрлендіру және есептеу |
|
|
24. Рекурсия. Рекурсиялық есептерді шешу |
Рекурсия. Рекурсиялық есептерді шешу |
Рекурсия ұғымын меңгеру және рекурсиялық есептерді шеше білу |
1 |
1 |
0 |
Рекурсиялық есептерді шығаруды меңгеру |
|
|
25. Тест тапсырмалары |
Тест тапсырмалары |
Өткен материалдарды қайталау және білімді бағалау |
1 |
0 |
1 |
Тақырыптар бойынша білімді тексеру |
|
IV бөлім |
26. Олимпиада есептерін шешу |
Олимпиада есептерін шешу |
Түрлі деңгейдегі олимпиадалық есептерді шешу |
1 |
0 |
1 |
Олимпиадалық есептерді шешу тәсілдерін қолдана білу |
|
|
27. Олимпиада есептерін шығаруда сандар теориясын қолдану |
Олимпиада есептерін шығаруда сандар теориясын қолдану |
Олимпиадалық есептерді шешуде сандар теориясын қолдана білу |
1 |
1 |
0 |
Сандар теориясын қолдану дағдысын меңгеру |
|
|
28. Күрделі есептерді қарапайым қосалқы тапсырмаларға бөлу |
Күрделі есептерді қарапайым қосалқы тапсырмаларға бөлу |
Күрделі есептерді қарапайым қосалқы тапсырмаларға бөлу әдісін меңгеру |
1 |
1 |
0 |
Күрделі есептерді қарапайым есептерге айналдыра білу |
|
|
29. Күрделі есептерді қарапайым қосалқы тапсырмаларға бөлу бойынша практикалық жұмыс |
Күрделі есептерді қарапайым қосалқы тапсырмаларға бөлу бойынша практикалық жұмыс |
Күрделі есептерді қарапайым бөліктерге бөлуді практикада қолдана білу |
1 |
0 |
1 |
Күрделі есептерді шешуде бөлшектеу әдісін қолдану |
|
|
30. Тест тапсырмалары |
Тест тапсырмалары |
Өткен материалдарды қайталау және білімді бағалау |
1 |
0 |
1 |
Тақырыптар бойынша білімді тексеру |
|
|
31. Стандартты емес есептерді шешу |
Стандартты емес есептерді шешу |
Стандартты емес есептерді шығару дағдыларын дамыту |
1 |
0 |
1 |
Стандартты емес есептерді шешудің әдістерін қолдану |
|
|
32. Ребустар мен жұмбақ түріндегі олимпиадалық тапсырмалар |
Ребустар мен жұмбақ түріндегі олимпиадалық тапсырмалар |
Ребустар мен жұмбақ түріндегі олимпиадалық тапсырмаларды шеше білу |
1 |
0 |
1 |
Логикалық ойлауды дамыту |
|
|
33. Ойын теориясы және олимпиада есептері |
Ойын теориясы және олимпиада есептері |
Ойын теориясының негізгі ұғымдарын меңгеру және олимпиадалық есептерге қолдану |
1 |
1 |
0 |
Ойын теориясын олимпиадалық есептерді шығаруда қолдану |
|
|
34. Қайталауға арналған тест тапсырмалары |
Қайталауға арналған тест тапсырмалары |
Барлық өткен материалдарды қайталау және білімді тексеру |
1 |
0 |
1 |
Барлық тақырыптар бойынша білімді тексеру |
Ақпараттық - әдістемелік бөлім
«Математикадан олимпиада есептерін шығару жолдары» авторлық бағдарламасы бойынша сабақтардың әртүрлі формалары көрсетілген, олар оқушылардың математика пәніне деген қызығушылығын арттырып, ойлау қабілеттерін дамытуға бағытталған. Мұндай сабақтардың негізгі формалары:
Дәстүрлі сабақтар (лекциялар және практикалық сабақтар):
-
Мұнда мұғалім теориялық түсініктерді және есеп шығарудың негізгі әдістерін түсіндіреді.
-
Оқушылар топтық немесе жеке түрде есептерді шешіп, түсініктерін тереңдете алады.
-
Жазбаша жұмыстар және есептерді жинақтап шығару.
Талқылау сабақтары:
-
Оқушылар топтарға бөлініп, түрлі олимпиада есептері бойынша пікір алмасып, шешу жолдарын талқылайды.
-
Топтық жұмыс барысында шығармашылық пен сыни ойлау дағдыларын дамытуға мүмкіндік туады.
Кейс-стади әдісі:
-
Математикадағы нақты жағдайларды шешу арқылы әртүрлі олимпиада есептерінің мысалдары ұсынылады.
-
Бұл әдіс нақты өмірмен байланыстыруға және теорияны тәжірибемен байланыстыруға көмектеседі.
Ойын элементтерін қолдану:
-
Математикадан ойындар ұйымдастыру, мысалы, «математикалық викторина», «ойын түріндегі турнирлер».
-
Оқушыларға олимпиада есептерін шешудің қызықты және көңілді тәсілін ұсыну.
Семинарлар мен тренингтер:
-
Олимпиадалық есептердің түрлі категориялары мен шешу әдістері бойынша оқушыларға тереңірек білім беру.
-
Семинарда оқушылар мен мұғалімдер өзара тәжірибе алмасып, күрделі есептерді шешудің тәсілдерімен бөліседі.
Тәжірибелік сабақтар (компьютерлік қолдау):
-
Математикадан олимпиада есептерін шешуде арнайы бағдарламалық құралдарды (мысалы, геогебра, математикалық симуляторлар) қолдану.
-
Бұл тәсіл есептерді визуализациялау мен динамикалық түрде талдауға мүмкіндік береді.
Олимпиадалық сынақтар мен тесттер:
-
Оқушыларға нақты олимпиада тапсырмаларын орындау арқылы өз білімдерін сынау.
-
Бұл түрі оқушылардың дайындық деңгейін бағалауға және оларды тестілеуге көмектеседі.
Қашықтықтан оқыту:
-
Онлайн ресурстар мен платформалар арқылы олимпиадалық есептерді шешу әдістерін үйрету.
-
Бұл әдіс оқушыларға уақыт және кеңістік шектеулерінсіз оқу мүмкіндігін береді.
Әрбір сабақтың формасы оқушылардың жеке қажеттіліктеріне және деңгейіне қарай түрлендірілуі мүмкін, оларды олимпиадаға дайындауда тиімді әрі қызықты тәсілдермен қамтамасыз етуге бағытталған.
«Математикадан олимпиада есептерін шығару жолдары» авторлық бағдарламасында қолданылатын әдіс-тәсілдер оқушылардың математикалық ойлау қабілеттерін дамытуға, олардың олимпиадалық есептерді дұрыс және тиімді шешу дағдыларын қалыптастыруға бағытталған. Мынадай әдіс-тәсілдер қолданылады:
1. Проблемалық оқыту әдісі
-
Мақсаты: Оқушыларды қиыншылықтар мен мәселелерді өздігінен шешуге үйрету.
-
Қолданылуы: Математикадан олимпиада есептерін шешу барысында оқушыларға күрделі есептер ұсынылады, олар мәселенің шешімін табу үшін әртүрлі әдістерді пайдаланады. Бұл әдіс оқушылардың шығармашылық ойлау қабілетін арттырады.
2. Дедуктивті әдіс
-
Мақсаты: Жалпы қағидалар мен ережелерді негізге ала отырып, нақты жағдайларды талдау және шешімдер жасау.
-
Қолданылуы: Олимпиадалық есептерді шешу барысында оқушылар теориялық білімдерін (құралдар, теоремалар) нақты есептерді шешуге қолданады. Теоремалар мен ережелер арқылы шешімдер шығарылады.
3. Индуктивті әдіс
-
Мақсаты: Жеке мысалдар мен тәжірибелер негізінде жалпы қағидаларды тұжырымдау.
-
Қолданылуы: Мұғалім оқушыларға бірнеше жеке есептерді шешуді ұсынып, сол арқылы жалпы ережелер мен шешу тәсілдерін шығаруына көмектеседі. Бұл әдіс оқушылардың интуициясын дамытады.
4. Топтық жұмыс
-
Мақсаты: Оқушылардың бір-бірімен пікір алмасуын, топта жұмыс істей білу дағдыларын дамыту.
-
Қолданылуы: Оқушыларды топтарға бөліп, әр топқа олимпиадалық тапсырма беріледі. Топтар есептерді бірге шешіп, нәтижелерін талқылайды. Бұл әдіс математикалық ойлау мен ынтымақтастықты дамытуға ықпал етеді.
5. Қадамдық шешу әдісі (Алгоритмдік әдіс)
-
Мақсаты: Әрбір есепті бірнеше қадамға бөліп шешу, күрделі есептерді жеңілдету.
-
Қолданылуы: Оқушыларға есепті шешудің қадамдық жоспары ұсынылады. Әр қадамды орындау арқылы есептің шешіміне біртіндеп жақындайды. Бұл әдіс оқушылардың жүйелі түрде ойлау дағдыларын дамытады.
6. Қателерді талдау әдісі
-
Мақсаты: Оқушылардың бұрын жасаған қателерінен сабақ алу.
-
Қолданылуы: Оқушыларға шешімдерді қатемен орындаған жағдайда, олар өз қателіктерін анықтап, сол қателіктерді түзету жолдарын талдайды. Бұл әдіс оқушылардың мәселелерге қатысты сыни тұрғыдан ойлауын дамытады.
7. Геймификация (Ойын әдісі)
-
Мақсаты: Математикадан олимпиадалық тапсырмаларды ойын түрінде шешуге үйрету.
-
Қолданылуы: Оқушылар математикалық тапсырмаларды шешуде ойын элементтерін (мысалы, викториналар, турнирлер, командалық жарыстар) қолдана отырып қызығушылықтарын арттырады. Бұл әдіс оқушылардың мотивациясын жоғарылатады.
8. Кейс-стади әдісі
-
Мақсаты: Математикадан нақты өмірдегі мәселелерді шешу.
-
Қолданылуы: Оқушыларға нақты өмірден алынған олимпиадалық есептер мен тапсырмалар беріледі, олардың шешімі арқылы теория мен практиканың байланысы түсіндіріледі. Бұл әдіс есептердің өмірмен байланысын түсіндіреді.
9. Математикалық модельдеу
-
Мақсаты: Математикадағы теориялық білімді нақты жағдайлармен байланыстыру.
-
Қолданылуы: Оқушыларға математикалық модельдер құруға және оларды олимпиадалық есептерді шешуде қолдануға мүмкіндік беріледі. Бұл әдіс абстрактілі ойлау мен логикалық тұжырым жасау қабілеттерін дамытады.
10. Шығармашылық тапсырмалар
-
Мақсаты: Оқушыларды өз бетімен зерттеуге және жаңа шешу жолдарын табуға ынталандыру.
-
Қолданылуы: Оқушыларға шығармашылық тапсырмалар беріледі, мысалы, жаңа типтегі есептерді ойлап табу немесе есептерді түрлі тәсілдермен шешу. Бұл әдіс оқушылардың шығармашылық дағдыларын дамытады.
11. Бақылау және кері байланыс әдісі
-
Мақсаты: Оқушылардың нәтижелерін бақылап, қателерді анықтап, кері байланыс беру.
-
Қолданылуы: Мұғалім оқушылардың шешімдерін мұқият бақылап, оларға дұрыс бағыт береді, қателерін көрсетіп, оларды түзету жолдарын ұсынады. Кері байланыс оқушылардың қателіктерін жөндеуге және жаңа ақпараттарды терең меңгеруге көмектеседі.
Бұл әдіс-тәсілдер оқушылардың математика пәніне деген қызығушылығын арттырып, олардың олимпиадалық тапсырмаларды тиімді әрі нәтижелі шешуге мүмкіндік береді.
«Математикадан олимпиада есептерін шығару жолдары» авторлық бағдарламасында қолданылатын көрнекі құралдар мен ресурстар оқушылардың математикадан олимпиада есептерін шешу дағдыларын қалыптастыруға және тақырыптарды жақсы меңгеруіне көмектесетін маңызды компонент болып табылады. Мұнда әртүрлі көрнекі құралдар мен ресурстар қолданылып, оқушылардың оқу процесін тиімді және қызықты ету мақсатында түрлі тәсілдер қолданылады.
1. Көрнекі құралдар
-
Интерактивті тақталар: Сабақ барысында интерактивті тақтаны қолдану есептерді шешу процесін визуализациялауға, диаграммаларды, графиктерді көрсетуге және оқушыларды топтық жұмысқа тартуға мүмкіндік береді.
-
Графикалық материалдар: Геометриялық есептерді шешу үшін әртүрлі геометриялық фигуралар мен диаграммалар. Мысалы, көпбұрыштар, дөңгелектер, түзу сызықтар мен қиылысуларды көрсету үшін қолданылады.
-
Математикалық сызбалар мен диаграммалар: Есептерді шешуде қажет болатын сызбалар, графиктер, функциялардың көрнекі графиктері және геометриялық конструкциялар. Бұл әсіресе геометрия және функциялар тақырыптарында пайдалы.
-
Математикалық модельдер: Математикалық есептерді шешу үшін жасалған модельдер. Мысалы, 3D модельдер, геометриялық фигуралардың көлемдерін немесе ауданын есептеу үшін пайдаланылатын көрнекі құралдар.
-
Слайд-презентациялар: Теориялық бөлімдер мен есептерді түсіндіру үшін қолданылатын слайдтар. Презентациялар оқушыларға визуалды ақпаратты жеңіл қабылдауға мүмкіндік береді.
-
Флипчарттар мен постерлер: Есептерді шешудің қадамдарын көрсету үшін уақытша жазылатын немесе сурет салынатын флипчарттар. Бұл құрал оқушыларға тапсырмаларды топтық жұмыс арқылы талқылауға көмектеседі.
-
Таблица мен схемалар: Математикалық формулалар мен теоремалардың қысқаша тізімдерін, шешу әдістерін көрсете отырып, оқушыларға ақпаратты тиімді түрде ұсынуға мүмкіндік береді.
2. Ресурстар
-
Электронды оқулықтар мен әдістемелік материалдар: Онлайн платформалар мен ресурстар арқылы оқушыларға математикадан олимпиада есептерін шешуге арналған электронды оқулықтар мен әдістемелік құралдар ұсынылады. Мысалы, Khan Academy, Brilliant.org сияқты халықаралық платформаларды қолдану.
-
Математика бойынша сайттар: Математика олимпиадасына дайындық үшін ресурстар ұсынатын сайттар. Мысалы, matholymp.kz, artofproblemsolving.com және басқа да олимпиадалық есептерге арналған сайттар.
-
Видеолар мен онлайн курстар: Математикадан олимпиада есептерін шешу әдістерін түсіндіретін видеолар мен онлайн курстар. Бұл ресурстарды пайдалану оқушылардың визуалды және аудио ақпаратты қабылдау мүмкіндігін арттырады.
-
Математикалық бағдарламалар мен қосымшалар: Мысалы, GeoGebra, Wolfram Mathematica сияқты математикалық бағдарламаларды пайдалану. Бұл құралдар геометрияны, алгебраны, функцияларды зерттеу мен модельдеуге көмектеседі.
-
Олимпиадалық есептердің жинақтары мен кітаптар: Математика олимпиадаларының есептерін жинақтаған кітаптар мен жинақтар. Бұл әдебиет түрлері олимпиадалық есептердің үлгілері мен шешу әдістерін ұсынуға арналған. Мысалы, А. С. Алдабергеновтің «Математикадан олимпиада есептерін шешу жолдары» сияқты кітаптар.
-
Математикалық тренажерлар: Әртүрлі онлайн немесе офлайн тренажерлар мен есеп шешу платформалары. Олар оқушыларға тапсырмаларды шешуді жүйелі түрде жаттықтыруға мүмкіндік береді.
-
Математика бойынша журналдар мен мақалалар: Математикалық зерттеулер мен олимпиадалық есептерге қатысты мақалалар жариялайтын арнайы журналдар. Бұл ресурстар студенттердің тереңірек зерттеу жүргізуіне мүмкіндік береді.
-
Қосымша тапсырмалар мен жаттығулар: Әр тақырыпқа қатысты қосымша тапсырмалар мен жаттығулар, олимпиадалық есептер мен шешу тәсілдерін қамтитын жұмыс дәптерлері мен карточкалар.
3. Интерактивті және практикалық құралдар
-
Математика ойындары: Математикалық тапсырмаларды шешу арқылы қызықты түрде білім алуға мүмкіндік беретін ойындар мен викториналар. Бұл әдіс оқушылардың мотивациясын арттырып, пәнге деген қызығушылығын жоғарылатады.
-
Математикалық симуляторлар мен анимациялар: Геометриялық есептерді шешу кезінде қолданылатын анимациялар мен визуализация құралдары. Мысалы, геометриялық фигураларды өзара байланыстырып, олардың қасиеттерін зерттейтін құралдар.
-
Проблемалық-ситуациялық тапсырмалар: Қиын есептер мен нақты өмірден алынған тапсырмалар арқылы оқушыларды өздігінен шешімдер табуға үйрету. Бұл тапсырмалар нақты өмірдегі математикалық мәселелерді шешуге бағытталған.
4. Қосымша ақпараттық құралдар
-
Форумдар мен чаттар: Оқушылар мен мұғалімдер арасында пікір алмасуға мүмкіндік беретін онлайн платформалар, бұл жерлерде олимпиадалық есептерді талқылап, бір-біріне көмек көрсетуге болады.
-
Онлайн тесттер мен сауалнамалар: Оқушылардың білім деңгейін анықтау үшін онлайн тесттер мен сауалнамаларды пайдалану. Бұл құралдар оқушылардың дайындық деңгейін бақылауға мүмкіндік береді.
Бұл көрнекі құралдар мен ресурстар оқушылардың білімін тереңдетуге, олардың олимпиадалық есептерді шешу дағдыларын дамытуға, әрі олардың қызығушылығын арттыруға көмектеседі.
«Математикадан олимпиада есептерін шығару жолдары» авторлық бағдарламасында қолданылатын бағалау түрлері оқушылардың білімін және дағдыларын тиімді әрі жан-жақты бағалауға мүмкіндік береді. Бағалау түрлері оқушылардың жеке жетістіктерін, топтық жұмысқа қатысуын, шығармашылық қабілеттерін, ойлау дағдыларын және тапсырмаларды шешу тәсілдерін бағалауға бағытталған.
1. Қалыптастырушы бағалау
-
Мақсаты: Оқушылардың білімін үнемі бақылау арқылы оқу процесінде қажетті түзетулер енгізу.
-
Қолданылуы: Бұл бағалау түрі оқушылардың әр сабақтағы жетістіктерін бағалауға арналған. Оқушыларға есептерді шығару кезінде мұғалім үнемі кері байланыс беріп, қателіктерді түсіндіріп, дұрыс шешімдер ұсынады. Қалыптастырушы бағалау нәтижесінде оқушылар өз білімін жетілдіруге мүмкіндік алады.
-
Әдістері: Жұмыс нәтижелерін тексеру, ауызша сұрау, тапсырмалар бойынша пікір алмасу, өзара бағалау.
2. Жиынтық бағалау
-
Мақсаты: Оқушылардың белгілі бір оқу кезеңіндегі жалпы нәтижелерін бағалау.
-
Қолданылуы: Оқушылардың оқу кезеңі аяқталғаннан кейін немесе белгілі бір тақырыпты өткен соң, жиынтық бағалау жүргізіледі. Бұл бағалау түрі олимпиада есептері мен тапсырмалары бойынша оқушылардың толық дайындық деңгейін анықтауға көмектеседі.
-
Әдістері: Кешенді тестілеу, олимпиадалық есептерді шешу, жазбаша жұмыстар, жазбаша және ауызша емтихандар.
3. Өзін-өзі бағалау
-
Мақсаты: Оқушыларды өз оқу процесі мен нәтижелерін бағалауға үйрету.
-
Қолданылуы: Оқушылар өздерінің жеке жетістіктерін, қателіктерін, күшті және әлсіз тұстарын бағалайды. Бұл әдіс оқушылардың сыни ойлау қабілетін дамытуға көмектеседі.
-
Әдістері: Өзін-өзі бағалау парақшалары, рефлексиялық жазбалар, оқушының жеке жетістіктерін талқылау.
4. Топтық бағалау
-
Мақсаты: Оқушылардың топтық жұмысын бағалау, ынтымақтастықта жұмыс істеу дағдыларын анықтау.
-
Қолданылуы: Топтық жұмыс барысында оқушылар бірлесіп олимпиадалық есептерді шешеді, нәтижесінде топтың жұмысы бағаланады. Бұл бағалау түрі оқушылардың бір-бірімен өзара әрекеттесуін және топтық жұмысқа қатысуын бағалауға мүмкіндік береді.
-
Әдістері: Топтың жұмысына баға беру, нәтижелерін талқылау, ынтымақтастық деңгейін анықтау.
5. Кері байланыс
-
Мақсаты: Оқушылардың оқу барысында қандай қиындықтар туындайтынын, қандай нәтижелерге жеткенін анықтау.
-
Қолданылуы: Кері байланыс оқушылардың жұмысын бағалау және келешекте дұрыс шешімдер табуға көмектесу үшін қолданылады. Мұғалім оқушыларға өз жұмыстарын жақсарту жолдары мен қосымша тапсырмалар ұсынады.
-
Әдістері: Жазбаша немесе ауызша кері байланыс, жеке пікірлер, топтық талқылаулар.
6. Практикалық бағалау
-
Мақсаты: Оқушылардың практикалық дағдыларын, есептерді шешу қабілетін нақты тапсырмалар арқылы бағалау.
-
Қолданылуы: Бұл бағалау түрі оқушылардың олимпиадалық есептерді шешу кезінде қолданатын техникалық және аналитикалық дағдыларын тексереді.
-
Әдістері: Практикалық тапсырмалар, есептерді шешудің қадамдық процесін бақылау, шешімдер ұсынысы.
7. Қатысу бағасы
-
Мақсаты: Оқушылардың сабаққа қатысуын, белсенділігін және оқу процесіне қатысуын бағалау.
-
Қолданылуы: Сабақтар барысында оқушылардың белсенділігі, сұрақтарға жауап беруі, өз ойларын білдіруі және тапсырмаларды орындау деңгейі бағаланады. Бұл әдіс оқушылардың пәнге деген қызығушылығын анықтауға көмектеседі.
-
Әдістері: Сабаққа қатысу, талқылауға қосылу, сыныптық жұмыстар мен дебаттардағы белсенділік.
8. Шығармашылық және зерттеу бағасы
-
Мақсаты: Оқушылардың шығармашылық ойлауын, математикалық зерттеу дағдыларын бағалау.
-
Қолданылуы: Оқушыларға шығармашылық тапсырмалар мен зерттеу жобалары беріледі, олар өздерінің шешімдер мен ұсыныстарын ұсынады. Бұл бағалау түрі оқушылардың тәуелсіз ойлау қабілетін және математикалық зерттеулерге деген ынтасын бағалауға мүмкіндік береді.
-
Әдістері: Шығармашылық жобалар, зерттеу жұмыстарын қорғау, есептерді шешуде жаңашылдық пен креативтілікті бағалау.
9. Мотивациялық бағалау
-
Мақсаты: Оқушылардың оқу процесіне деген мотивациясын анықтау.
-
Қолданылуы: Оқушылардың тапсырмаларды орындауға деген ынтасы мен қызығушылығын бағалау. Бұл бағалау түрі оқушылардың пәнге деген жалпы қарым-қатынасын және оқуға деген ынтасын өлшеуге бағытталған.
-
Әдістері: Сабаққа қатысу, тапсырмаларды орындау белсенділігі, өз бетімен іздену.
Бұл бағалау түрлері оқушылардың білімін және қабілеттерін жан-жақты және әділ бағалауға мүмкіндік береді. Әр бағалау түрі оқушылардың түрлі дағдыларын, шығармашылық қабілеттерін және пәнге деген ынтасын дамытуға ықпал етеді.
«Математикадан олимпиада есептерін шығару жолдары» авторлық бағдарламасы – оқушылардың математикалық ойлау қабілетін дамытуға, оларды олимпиадалық есептерді шешуге дайындауға бағытталған маңызды оқу құралы. Бұл бағдарламаның маңызы бірнеше аспектілерде көрінеді:
1. Оқушылардың математикалық дағдыларын дамыту
-
Күрделі мәселелерді шешу қабілетін арттыру: Олимпиадалық есептер әдеттегі мектеп бағдарламасынан тыс, ерекше ойлау мен талдау дағдыларын талап етеді. Бұл бағдарламаны оқу оқушылардың күрделі математикалық мәселелерді шешу қабілетін арттырады, сыни ойлау мен аналитикалық дағдыларын дамытады.
-
Шығармашылық ойлауды дамыту: Олимпиада есептерін шешу кезінде стандартты әдістерден тыс тәсілдер қолдануға тура келеді. Бұл оқушыларды шығармашылық тұрғыдан ойлауға, жаңа шешу жолдарын табуға ынталандырады.
2. Теория мен практиканың байланысын нығайту
-
Теориялық білімді практикада қолдану: Бағдарлама оқушыларға математикалық теорияны нақты есептерді шешу кезінде қолдануды үйретеді. Бұл оларға математикалық концепцияларды тереңірек түсінуге көмектеседі.
-
Тәжірибелік дағдыларды қалыптастыру: Оқушылар тек теорияны оқып қоймай, оны әртүрлі олимпиадалық есептерді шешу арқылы қолдану тәжірибесін алады. Бұл олардың білімін тереңдетіп, дағдыларын шыңдайды.
3. Оқушылардың мотивациясын арттыру
-
Математикаға деген қызығушылықты ояту: Олимпиадалық есептерді шешу барысында оқушылардың математикаға деген қызығушылығы мен ынтасы артады. Қиын тапсырмаларды жеңу оқушыларға қанағаттанарлық сезім сыйлап, математиканы жақсы меңгеруге деген құштарлықтарын күшейтеді.
-
Жеке жетістіктерге қол жеткізу: Олимпиадалық жеңістер оқушыларға жеке жетістік сезімін береді. Бұл оларды әрі қарайғы зерттеулер мен білім алуға ынталандырады.
4. Математикалық қабілеттерді бағалау
-
Әртүрлі деңгейдегі тапсырмалар: Бағдарламада олимпиадалық тапсырмалар әртүрлі қиындық деңгейінде ұсынылған, бұл оқушылардың жеке деңгейіне қарай тапсырмаларды орындауға мүмкіндік береді. Бұл дағдыларды объективті бағалауға және жетістіктерді бақылауға мүмкіндік береді.
-
Оқушылардың дайындық деңгейін анықтау: Олимпиадалық есептер оқушылардың тек математикалық білімі ғана емес, сонымен қатар олардың проблемаларды шешу тәсілдерін бағалауға мүмкіндік береді.
5. Оқушылардың ойлау қабілетін кеңейту
-
Логикалық ойлауды дамыту: Олимпиадалық есептер көбінесе логикалық және аналитикалық ойлауды қажет етеді. Бағдарлама оқушылардың ойлау қабілетін кеңейтіп, математикалық логика мен дәлелдеу дағдыларын нығайтады.
-
Стратегиялық ойлауды қалыптастыру: Математикалық есептерді шешу оқушылардың жоспарлау және стратегия құру дағдыларын дамытуға ықпал етеді. Бұл дағдылар олардың тек математикада ғана емес, өмірде де пайдалы болады.
6. Ғылыми зерттеу дағдыларын дамыту
-
Зерттеу дағдыларын қалыптастыру: Олимпиадалық тапсырмаларды шешу барысында оқушылар өз бетімен зерттеу жүргізіп, мәселелерді шешу үшін жаңа идеялар мен тәсілдер ұсынады. Бұл ғылыми зерттеу мен жаңалық ашуға деген қызығушылығын арттырады.
-
Құрылымдық ойлау және дәлелдеу дағдыларын жетілдіру: Олимпиада есептерін шешу көбінесе дәлелдемелер мен шешімдерге негізделеді, бұл оқушыларды математикалық дәлдікке үйретеді.
7. Табиғи дарынды оқушыларды анықтау және дамыту
-
Математикадан талантты оқушыларды таңдау: Бағдарлама олимпиадалық есептер арқылы математикалық дарынды оқушыларды анықтауға көмектеседі. Мұндай оқушыларға арнайы бағдарламалар мен қосымша дайындықтар ұсыну арқылы олардың қабілеттерін одан әрі дамытуға мүмкіндік беріледі.
-
Дарынды балаларға арналған ресурстарды ұсыну: Математикадан дарынды оқушылар үшін арнайы тапсырмалар мен ресурстарды ұсыну олардың білімін тереңдетіп, болашақта жоғары деңгейдегі математик болуына жол ашады.
8. Оқушылардың әлеуметтік дағдыларын дамыту
-
Топтық жұмыс дағдыларын дамыту: Бағдарлама бойынша топтық жұмыстар жүргізу оқушылардың бір-бірімен қарым-қатынас жасау, пікір алмасу және ынтымақтастықта жұмыс істеу дағдыларын қалыптастырады.
-
Жауапкершілік пен көшбасшылық: Олимпиадалық тапсырмаларды шешу кезінде оқушылар бір-біріне көмектесіп, көшбасшылық қасиеттерін көрсету мүмкіндігіне ие болады.
9. Болашаққа дайындық
-
Жоғары оқу орындарына дайындық: Олимпиадалық бағдарламалар жоғары оқу орындарына түсу үшін жақсы дайындық көзі болып табылады. Математикадан олимпиада есептерін шешу университет деңгейінде қажет болатын дағдыларды дамытуға көмектеседі.
-
Халықаралық олимпиадаларға дайындық: Бағдарлама оқушыларды халықаралық олимпиадалар мен конкурстарға дайындалуға ынталандырады, бұл олардың халықаралық аренада жетістіктерге жету мүмкіндігін арттырады.
«Математикадан олимпиада есептерін шығару жолдары» авторлық бағдарламасы оқушылардың математикалық білімдерін тереңдетіп, оларды шығармашылық, аналитикалық және логикалық тұрғыдан дамытады. Бағдарламаның маңызы тек оқушылардың математикалық дағдыларын арттыруда ғана емес, олардың жеке тұлғалық дамуына, сыни ойлау қабілетін қалыптастыруға және болашақтағы ғылыми және кәсіби жетістіктеріне ықпал етуінде жатыр.
Оқу - әдістемелік нұсқаулығы
Қысқа мерзімді жоспары
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Математикадан олимпиада есептеріне кіріспе |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Математикадан олимпиада есептерінің негізгі түрлерімен және оларды шешу стратегияларымен танысу. Математикалық есептерді шешу кезінде логикалық және сыни ойлау қабілеттерін дамыту. Шешімдер мен стратегияларды талқылау кезінде топтық жұмыс пен коммуникация дағдыларын жетілдіріңіз. Ұлы математиктер және олардың ғылымның дамуына қосқан үлесі туралы білімдеріңізді кеңейтіңіз. |
|
|
Сабақтың мақсаты |
Оқушыларды математикалық олимпиадаларға табысты қатысуға дайындау, логикалық және шығармашылық ойлауын дамыту, математикаға ғылым ретінде қызығушылықтарын арттыру. |
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
Ұйымдастыру кезеңі «Қолдағы хат». |
Оқушылар ойын ойнайды
|
Формативті бағалау үнемі жүргізіліп отырады.
Жұлдыздар суреттерін тарату арқылы бағалау жүргізіледі |
Оқулықтар суреттер, слайдтар Кестелер беріледі. |
|
Жаңа білім 15 мин 2 мин Бекіту 15 мин |
Арифметика математиканың, ал математика ғылымдардың патшасы. Карл Фридрих Гаусс Фридрих Гаусстың ұлағатты сөзіне назар аударыңыздар, қалай ойлайсыздар, Фридрих не айтқысы келді?
2 - тапсырма «Постер» әдісімен орындалады.
Математика сөзіне сипаттама
бер
- Мұғалім математикалық олимпиада есептері стандартты емес жағдайларда математикалық білімді қолдана білуді талап ететін күрделі және қызықты тапсырмалар екенін түсіндіреді. - Мұғалім математикалық олимпиадаларға қатысудың артықшылықтары: логикалық ойлауды, шығармашылық әлеуетті дамыту және жоғары оқу орындарына түсуге дайындалу мүмкіндігі туралы айтады. - Мұғалім бастапқы кезеңде оқушыларды олимпиадада кездесетін мәселелердің негізгі түрлерімен танысуға шақырады. 2. Практикалық бөлім: - Мұғалім қолданылған әдістер мен шешу жолдарын түсіндіре отырып, оқушыларға бірнеше мысал есептерді шығаруды ұсынады. Ондықтары бірдей сандарды дөңгелектеңіз: 67, 86, 46, 61, 16, 68, 76, 64 Бірліктері бірдей сандарды дөңгелектеңіз: 84, 48, 74, 47, 58, 85, 64, 46 - Оқушылар алған білімдерін дәлелдеп, қолдана отырып, өз мүмкіндіктері деңгейінде есептерді шешеді. Сандардың ондық құрамын жаз: 5 ұпай (37) (41) (52) (76) (70) - Мұғалім қажет болған жағдайда көмек пен кеңес береді, оқушыларды дұрыс шешім қабылдауға бағыттайды, шығармашылық ойлауды ынталандырады. 3. Рефлексия: - Мұғалім барлық мектеп оқушыларының қатысуымен есептерді шешу жолдарын талқылайды, әдіс-тәсілдері мен шешу жолдарын сұрайды, материалды түсінгенін тексеру үшін сұрақтар қояды. - Мұғалім оқушылардың үлгерімі туралы қорытынды жасайды, дұрыс шешімдерді атап өтеді және сабақты қорытындылайды. |
Оқушылар презентацияны көреді.
Оқушылар құлақ салып тыңдайды
Оқушылар постерді толтырады
|
Дескриптор: Математикадан олимпидалық есептерге кіріспе жасайды ҚБ: Баспалдақ Дескриптор: Оқушылар негізгі терминдерді түсінеді ҚБ: Баспалдақ Оқушылар постерді өз ойларымен толтыра алады ҚБ: Мадақтау |
Оқулықтар суреттер Кестелер Сызғыш қарындаштар Қайшы Қағаздар, плакаттар, графиктер
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: «Математика олимпиадасының маңыздылығы» тақырыбына презентация дайындау. |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Алгебраны пайдаланып есептер шығару әдістері |
|
|
мҰ |
Алгебра арқылы есептерді шешудің негізгі әдістерін үйреніңіз. Осы әдістерді тәжірибеде қолдана білуге үйрету. Логикалық ойлау, талдау қабілеттерін дамыту. |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
І.Ұйымдастыру Оқушылармен сәлемдесу, түгелдеу, сынып бөлмесінің тазалығына көңіл бөлу, оқушылардың сабаққа дайындығын тексеру, оқушылардың назарын сабаққа аудару. Үй жұмысын
сұрау: |
Оқушылар амандасып, сабаққа дайындалады |
Формативті бағалау үнемі жүргізіліп отырады. |
Оқулықтар суреттер Кестелер Слайдтар |
|
Жаңа білім Бекіту |
Математика – барлық ғылымдардың тұңғышы және оларға пайдалы да, қажет те. Роджэр Бэкон
Роджэр Бэконның ұлағатты сөзі бойынша талдау жасаңыздар, Роджэр не айтқысы келді? - Сабақтың мақсатын және оның математикалық әдістерді түсіну және қолдану үшін маңыздылығын түсіндіру. - Оқушылардың есептерді шешу әдістері мен алгебра түсінігі бойынша алдын ала білімдерін тексеру үшін сұрақтар қою. - алмастыру әдісі, теңдеулер әдісі және коэффициенттер әдісі сияқты алгебра көмегімен есептерді шешудің әртүрлі әдістерін түсіндіру. - Әрбір әдісті қолдануға болатын есептерге мысалдар келтіріңіз. - Әр әдістің артықшылықтары мен шектеулерін талқылаңыз. - Әртүрлі әдістерді қолдану арқылы шешілетін күрделілік деңгейі әртүрлі бірнеше есептерді ұсыну. - Есептерді шешуге мысалдар арқылы әр әдісті суреттеңіз. - Сұрақтар қойып, оқушылардан есептерді шешудегі қадамдары мен дәлелдерін түсіндіруді сұраңыз. 1. x-ті басқа айнымалы арқылы өрнектеңіз. 2x = 7 - 3 2x = 4 x = 4/2 x = 2 2. Алынған х мәнін бастапқы теңдеуге ауыстырыңыз және тексеріңіз: 2*2 + 3 = 7 4 + 3 = 7 7 = 7 Сонымен 2x + 3 = 7 теңдеуінің шешімі х = 2 болады. Теңдеулер жүйесін теңдеу әдісімен шешуге мысал: Теңдеулер жүйесін шешейік: 2x + y = 5 x - y = 1 1. x үшін екінші теңдеуді шешейік: x = 1 + y 2. Бірінші теңдеудегі х өрнекті ауыстырыңыз: 2(1 + у) + у = 5 2 + 2ж + у = 5 3ж = 5 - 2 3ж = 3 y = 1 3. Алынған у-ның мәнін х үшін өрнекке ауыстырыңыз: x = 1 + 1 x = 2 Сонымен, 2х + у = 5 және х - у = 1 теңдеулер жүйесінің шешімі х = 2, у = 1 болады. Коэффиценттік әдісті қолданып есепті шешуге мысал: Тапсырма: Әлихан мен Данияр бірге 60 алма жинады. Әлихан Даниярдан 2 есе көп алма жинады. Олардың әрқайсысы неше алма жинады? 1. Данияр жинаған алма саны х болсын. Содан кейін Вася 2 рет алма жинады. 2. Қосындысы 60 болатын теңдеу құрайық: x + 2x = 60 3x = 60 x = 60/3 x = 20 3. Әлиханның өрнекке х мәнін қойыңыз: 2x = 2 * 20 2x = 40 Осылайша Данияр 20 алма, Әлихан 40 алма жинады. - Мектеп оқушыларын 3-4 адамнан топтарға бөлу. - Әр топқа есептер жинағын беру, олар оларды шешуде үйренген әдіс-тәсілдерін қолдана алады. - Топпен жұмыс істеу ережелерін түсіндіріп, тапсырмаларды орындау уақытын белгілеңіз. - Әр топтың үлгерімін бақылап, қажет болған жағдайда көмектесу. - Әр топтың жұмысын жинақтап, есептерді шешу әдістерін қолдануды бағалау. - Дұрыс жауаптар мен тәсілдерді талқылаңыз, сондай-ақ ықтимал қателер мен оларды түзету жолдарын табыңыз. - Оқушылардың материалды қаншалықты меңгергенін және оны тәжірибеде қолдана алатынын түсіну үшін талқылау үшін сұрақтар қойыңыз. |
Оқушылар топқа бөлініп, өздеріне берілген атауларға байланысты ақпаратты сіңіріп талдайды
Оқушылар РАФТ стратегиясы арқылы тапсырма орындайды
|
Дескриптор: ҚБ: Баспалдақ Дескриптор: Оқушы берілген нысанға байланысты өз пікірін жаза алады ҚБ: Смайлик |
Оқулықтар суреттер Кестелер Сызғыш қарындаштар Қайшы Қағаздар, плакаттар, графиктер
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: «есептер шығару әдістері» тақырыбына шағын эссе жазу. |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Математикадан олимпиада есептерін шешу |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Математикадан олимпиада есептерінің әр түрін зерттеу. Логикалық ойлау қабілеттерін дамыту және стандартты емес есептер шығару. Тапсырмаларды талқылау кезінде топтық жұмыс пен тиімді қарым-қатынасқа тәрбиелеу. Ұлы математиктер және олардың жетістіктері туралы білімдерін кеңейту. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру |
І. Ұйымдастыру
кезеңі. Психологиялық сәт. ІІ. Үй тапсырмасын сұрау. |
Қойылған сұрақтарға жауап береді. |
Оқушының жауабын толықтыру немесе тиімді кері байланыс жасау. |
Интерактивті тақта, оқулық. |
|
Жаңа білім Бекіту 15 мин |
1. Сабаққа кірісу Ақыл - ойды тәртіпке келтіретін математика. Михаил Ломоносов
Төбедегі айтылған ұлағат сөз жайлы не ойлайсыздар? Өз пікірлеріңмен бөлісіңдер. 2. Проблеманы баяндау - Мұғалім олимпиадалық есепті ұсынады және барлық оқушылардың есеп шарттарын түсінгеніне көз жеткізе отырып, оны дауыстап оқиды. - Мұғалім оқушыларды сыни тұрғыдан ойлауға, талдауға итермелейтін сұрақтар қою арқылы ойлауға жетелейді. 3. Жеке шешім - Мұғалім әр оқушыға жеткілікті уақыт пен ресурстар бере отырып, мәселені өз бетінше шешуге тырысуға шақырады. - Мұғалім әр оқушының жеке кеңестер мен кеңестер беріп, шешім қабылдау процесіне мән береді. 4. Топтық талқылау - Мұғалім оқушыларды өз шешімдерімен бөлісуге және мәселені шешу әдістерін түсіндіруге шақырады. - Мұғалім шешудің әртүрлі тәсілдерін талқылайды, олардың артықшылықтары мен кемшіліктерін бағалайды. -Мұғалім мәселені шешудің әртүрлі тәсілдерінің тиімділігіне салыстырмалы талдау жүргізеді. 1.Лесовичпен бірге Ракон серуендеп, гүл шоқтарын жинауға шешім қабылдады. Ракон 9 түсті жұлып алды. Бұл орманшының жұлып алғанынан 3 есе көп. Лесовичка букетінен гөрі Ракон букетінде қанша гүл бар? 2 Театр гастрольде тура 3 апта болды. Театрдың гастрольдік сапары неше күнге созылды?
3.Ән құстары байқауында Бұлбұл 12 ән шырқады, түрлі-түсті қарақұйрық сонша ән айтты. Робин бірнеше ән айтты. Барлығы 31 ән айтылды. Робин қанша ән айтты? А) 12 Б) 11 В) 9 Г) 7 4. Сымға 9 шам ілулі. Бірінші және соңғы фонарь арасындағы қашықтық қандай, егер олардың барлығы бір-бірінен бірдей қашықтықта болса және көршілес екі фонарь арасындағы қашықтық 1 м болса?
Есептің аяқталуы - Мұғалім есепті шығара алмаған белгілі бір оқушыларды оны аяқтауға тырысуға шақырады. - Мұғалім оқушыларға мәселені шешудің жаңа идеялары мен әдістерін береді. |
Оқушылар құлақ салып тыңдайды
Оқушылар топқа бөлініп өз арасында жұмыс өткізеді
- шешімдерді жетілдіру туралы айту
|
Дескриптор: Оқушылар лерін біледі ҚБ: Баспалдақ Дескриптор: Ұлағат сөзге талдау - шешімдерді жетілдіру туралы айту ҚБ: Баспалдақ ҚБ: Мадақтау |
интербелсенді тақта, оқулық
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: «Олимпиадағы математикалық есептер» тақырында презентация жасап кел «көлемі 3-4 слайд) |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Бір айнымалысы бар сызықтық теңдеулерді шешу. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Бір айнымалысы бар сызықтық теңдеу түсінігін үйреніңіз және оны анықтауды үйреніңіз. Сызықтық теңдеулердің негізгі қасиеттерін түсіну және қолдануды үйрену. Бір айнымалысы бар сызықтық теңдеулерді әртүрлі әдістер арқылы шешуге үйрету. Сызықтық теңдеуді шешудің дұрыстығын тексеруге үйрету. Сызықтық теңдеулерді шешуге дейінгі есептерді шешу. |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Психологиялық ахуал қалыптастыру. Оқушылардың көңілін сабаққа
аудару Үй жұмысын сұрау. |
Оқушылар бір-бірімен амандасады. |
Формативті бағалау үнемі жүргізіліп отырады |
|
|
Сабақтың ортасы |
Әлем математика тілімен бейнеленген. Галилео Галилей. Төбедегі айтылған ұлағат сөз жайлы не ойлайсыздар? Өз пікірлеріңмен бөлісіңдер. 1 – тапсырма
Fishbone техникасы, оның көмегімен проблемалар мен оларды шешу жолдарын анықтауға, себеп-салдар байланысын анықтауға болады. Сонымен, сіз бен біз сабақта сәтті жұмыс істеу үшін ережелерді қайталауымыз керек: 1) мономиалды көпмүшеге көбейту ережесі Жақшаны ашу ережелері. 3) теңдеуді шешу нені білдіреді? 4) теңдеудің түбірі дегеніміз не? Біз ережелерді қайталаймыз. Мұғалім оқушылардың бірінен ережелерді дауыстап айтуды сұрайды. - Енді өзіңізді бағалаңыз.(ең жоғары балл-3б) Енді біз қаламдарды қойып, ауызша жұмыс жасаймыз.(Слайд) Өрнекті жеңілдетіңіз а) 3 (x-1)=3x-3 б) -5 (2-у)=-10+5у в) 3х*х2=6х3 г) 5х2+3х-6х2=3х-х2 Теңдеуді шешіңіз: а) 5х=-10; б) - 3х+2 = 17 - Балалар, біз теңдеулерді бұрын шешкенбіз. Менде тақтада теңдеулер жазылған. Оларды кім шеше алады? а) 3х+2 (х-3)= - 5х+3 б) 8-5х(х-7)=1-5х2 -Балалар, сендер теңдеулерді шешуді жақсы орындадыңдар, енді жұппен жұмыс істеуге көшеміз, онда сендер қайтадан теңдеулерді шешуге жаттығасыңдар, не істей алмайтыныңды табыңдар. - Жұмысыңызды тексере аласыз. Егер бәрі ойдағыдай болса, сізге жауаптар ұсынылады. Егер сізде қандай да бір қиындықтар болса, кеңес картасын пайдалануға болады. Егер сіз өз жұмысыңызды бәрінен бұрын аяқтаған болсаңыз, картаны қосымша тапсырмамен пайдалана аласыз, сонымен қатар өзіңізді сынай аласыз. Жұппен жұмыс жасау барысында мұғалім жұмыс барысын бақылап, қиындық көрген жұпқа көмек көрсетеді. -Жұптық жұмысты аяқтадық. Егер сіз бәрін дұрыс орындаған болсаңыз, онда сіз өзіңізді бағалау картасына 5 ұпай бересіз. Егер сіз қосымша тапсырманы орындай алсаңыз, «Қосымша тапсырма» бөлімінде өзіңізге ұпай беріңіз: бірінші тапсырма үшін - 3 ұпай, екінші тапсырма үшін - 4 ұпай. -Барлығын дұрыс жасаған оқушылар бар ма? Қолыңызды көтеріңіз. -Енді нұсқалармен өзіңіз жұмыс жасай аласыз. I нұсқа: 3x-5(2x)=54 2) 7(2у-2)-2(3у-3,5)=9 3) 5x(12x-7)-4x(15x-11)=30+29x II нұсқа: 1) 7х-3(4х)=48 2) 5(3ж-1)-4(6ж-0,5)=15 3) 24x-6x(13x-9)= -13-13(6x-1) - Өзіндік жұмысты аяқтады. Тексереміз (слайд). Егер сіз бәрін дұрыс орындасаңыз, біз өзімізге 5 ұпай береміз. Екі мысал – 4 ұпай, бір мысал – 3 ұпай. -Ендеше, балалар, сабақты қорытындылайық. Сіз бүкіл сабақты өзіңізді бағалаумен өткіздіңіз. Енді ұпайларды бағалау парағындағы бағаға айналдырайық (слайд 8). Өзін-өзі бағалау картасы арқылы біз қанша ұпай бар екенін санаймыз. Біз өзімізді бағалаймыз. Бағаға қанағаттансаңыз және оны журналға салғанымды қаласаңыз, оны дөңгелектеп алыңыз. Сабақта мақсатымызға жеттік пе? Сіз біліміңізге жаңа нәрсе қостыңыз ба? |
Болжамдар жасау
Пікірталас
Тапсырманы өз бетінше орындау
Жұппен жұмыс |
ҚБ: Формативті бағалау
Формативті бағалау
Формативті бағалау
|
Оқулық, Бірнеше тар |
|
Қорытынды |
|
|
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Тест тапсырмалары. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушылардың алған білімдерін тексеру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
І. Ұйымдастыру
кезеңі. Психологиялық сәт.
|
|
|
Интерактивті тақта, оқулық. |
|
Жаңа білім 15 мин 2 мин Бекіту 15 мин |
1 – нұсқа 1. Математикадан олимпиадалық есептерді шешу үшін төменде келтірілген әдістердің қайсысын қолдануға болады? а) ауыстыру әдісі б) толық шамадан тыс әдіс в) істерді талдау әдісі 2. Алгебралық есептерді шешуде қандай ұғым қолданылады? а) туынды б) Интеграл в) Коэффициент 3. Бір айнымалы сызықтық теңдеулерді шешу үшін қандай алгоритм қолданылады? а) Гаусс әдісі б) дихотомия әдісі в) Ньютон әдісі 4. Теңдеулердің қайсысы сызықтық? а) x^2 + 2x = 5 б ) 3x + 2 = 7 в) sin (x) + 2 = 3 5. Төмендегі өрнектердің қайсысы сызықтық? а) x^3 + 2x^2 + 3x + 4 б) 3x + 2 в) log (x) + 2x 6. Формулалардың қайсысы тіктөртбұрыштың ауданын табуға мүмкіндік береді? а) S = πr^2 б) S = a * b в) S = 1/2 * a * h 7. Геометриялық прогрессия дегеніміз не? а) әрқайсысы алдыңғы санды прогрессия бөлгіші деп аталатын тұрақты санға көбейту арқылы алынған сандар тізбегі б) әрқайсысы прогрессия қадамы деп аталатын тұрақты санның алдыңғы санына қосу арқылы алынған сандар тізбегі в) сандар тізбегі, олардың әрқайсысы алдыңғы санды прогрессия бөлгіші деп аталатын тұрақты санға бөлу арқылы алынады 8. Теңдеулердің қайсысы квадрат? а) x^3 + 2x = 5 б ) 3x + 2 = 7 в) x^2-3x = 10 9. Төмендегі өрнектердің қайсысы квадрат? а) x^3 + 2x^2 + 3x + 4 б) 3x + 2 в) x^2 + 3x-4 10. Квадрат теңдеудің түбірлерін қалай табуға болады? а) кемсітушілік формуласын қолдану б) Гаусс әдісін қолдану в) Ньютон әдісін қолдану 2 – нұсқа 1. Сұрақ: Төмендегі есептердің қайсысы математикалық олимпиадаға жатады? а) қабырғалары берілген тіктөртбұрыштың ауданын табу; ә) Белгілі қабырғаларды пайдаланып үшбұрыштың периметрін есептеңіз; в) Емтиханнан өткен талапкерлердің санын, егер өту пайызы және топтағы талапкерлердің жалпы саны белгілі болса, анықтаңыз. 2-сұрақ: Функция графиктерін талдауға байланысты олимпиадалық есепті шешу үшін қандай әдісті қолдануға болады? а) Қосу және азайту амалдары; б) Графикалық шешу әдісі; в) Құнды ауыстыру әдісі. 3-сұрақ: Ауданды есептеуге байланысты есептерді шешу үшін қандай алгебралық әдістерді қолдануға болады? а) Факторизация әдісі; б) Толық ыдырау әдісі; в) Көбейту және бөлу әдісі. 4-сұрақ: Төмендегілердің қайсысы математикалық олимпиада есептері болып табылады? а) 3х + 7 = 22 теңдеуін шеш; ә) Екі санның арифметикалық ортасын есептеу; в) cos(x) функциясының туындысын табыңыз. 5-сұрақ: Белгісіз мәнді анықтауға байланысты олимпиадалық есепті шешу үшін қандай әдісті қолдану ұсынылады? а) Құнды ауыстыру әдісі; б) Графикалық шешу әдісі; в) Ортақ көбейткішке бөлу әдісі. 6-сұрақ: Төмендегілердің қайсысы математикалық олимпиада есептері болып табылады? а) Теңдеулер жүйесін шешу; б) Екі санның пайыздық қатынасын анықтау; в) Параллелепипедтің көлемін есептеңдер. 7-сұрақ: Көпмүшелік теңдеулердің түбірін табуға байланысты есептерді қандай алгебралық әдіспен шешуге болады? а) Құнды ауыстыру әдісі; б) Терминдерді жою әдісі; в) Қалдықпен бөлу әдісі. 8-сұрақ: Төмендегі есептердің қайсысы математикалық олимпиадаға жатады? а) Арифметикалық прогрессияның алғашқы N мүшесінің қосындысын табыңыз; б) Берілген радиус негізінде шеңбердің ауданын анықтау; в) Санның бөлгіштерінің санын санау. 9-сұрақ: Геометриялық дизайнға байланысты олимпиадалық есепті шешу үшін қандай әдісті қолдану ұсынылады? а) Мәндерді салыстыру әдісі; б) Терминдерді ауыстыру әдісі; в) Пифагор теоремасын қолдану әдісі. 10-сұрақ: Шексіз кемімелі геометриялық прогрессияның қосындысын есептеуге байланысты есептерді қандай алгебралық әдіспен шешуге болады? а) Күрделі бөлшек әдісі; б) Бөлшектерді ортақ бөлімге келтіру әдісі; в) Шексіз геометриялық прогрессияның қосындысы әдісі. |
|
|
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: Өткен тақырыптарды қайталау |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Сызықтық теңдеулер жүйесін ауыстыру арқылы шешу. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Сызықтық теңдеулер жүйесін шешудің негізгі әдістерінің бірі ретінде алмастыру әдісімен танысыңыз. Сызықтық теңдеулер жүйесін алмастыру арқылы шешу дағдыларын дамыту. Тәжірибелік есептерді шешуде алмастыру әдісін қолдануға үйрету. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
Психологиялық ахуал қалыптастыру.
2.Жағымды көңіл-күйге келу. Тыныс алуға зейін қою. |
Қойылған сұрақтарға жауап береді. |
Оқушының жауабын толықтыру немесе тиімді кері байланыс жасау. |
Интерактивті тақта, оқулық. |
|
Жаңа білім 15 мин 2 мин Бекіту 15 мин |
Математика - ақиқат дүниесінің сандық қатынастары мен кеңістік формалары жайлы ғылым. Фридрих Энгельс. Фридрих Энгельс кім? Фридрихтың ұлағатты сөзін талдаңыздар
Сабақтың тақырыбын тұжырымдау, сабақтың дидактикалық мақсатын қабылдау Сіз үйде жаңа материалмен таныстыңыз. Сонымен, сіз сабақтың тақырыбын өзіңіз атай аласыз: "сызықтық теңдеулер жүйесін алмастыру әдісімен шешу" Бұл сабаққа қандай мақсаттар қоямыз деп ойлайсыз? (Үйде алынған ақпаратты өзіміз жүйелейміз, оны қолдануды үйренеміз) Ақыл-ой әрекетін белсендіру 1. Ұсынылған теңдеулерден Екі айнымалысы бар сызықтық теңдеулерді таңдаңыз: а) 3х + 3у – 1 = 0 г) 1/х +1/у = 3 б) 3х2 + ж = 5 д) х + ж = 3 в) 5х + 5 = 6х е) 1/2х + у-5/6 = 0 Екі айнымалы сызықтық теңдеулер жүйесі дегеніміз не? Сызықтық теңдеулер жүйесін шешу нені білдіреді? Сызықтық теңдеулер жүйесін шешу деп не аталады? Теңдеуден х-ны білдіріңіз: 5х-10у=20; 12х + 3у= 1,2 Өрнек ж теңдеуден: ж+5х=0; 4х-3у=5 Сіз құрастырған алгоритмді атаңыз. Зерттелген нәрсені түсінуді тексеру Опциялар бойынша жұпта жұмыс істеу 1 нұсқа Теңдеулер жүйесін ауыстыру арқылы шешіңіз: а)
б)
в) 2 нұсқа Теңдеулер жүйесін ауыстыру арқылы шешіңіз: а) б) в) Реакция тексеру. Біз реакцияны тексереміз. Астарлы әңгіме ұсынылады: бірде Үнді раджасы өз субъектілері үшін жарыс ұйымдастырды: кім қабырғаға жүгіріп өтіп, басына су құйып, бір тамшы төгілмеді. Қабырғаның астында көптеген адамдар тұрды, олардың әрқайсысы айқайлап, құбырларды үрлеп, барабандарды ұрды. Тек бір адам құмыраны су төгілместен жеткізе алды. Раджа мұны қалай істегенін сұрағанда, ол ештеңе естімегенін айтты, өйткені ол суды алып жүрді. Мұғалім сөздерді атайды (демалыс, емтихан, шешім, рождество, жүйе, Астана, ауыстыру, боран, Токио, теңдеу, мереке, Мәскеу, үстел, Вашингтон, Париж) ал оқушылар естуі керек: 1) математикалық терминдер, 2) Мемлекет астаналары. |
|
|
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: Қазақстанның басқа да көне мәдениеттері туралы білімдерін кеңейту және таңдалған мәдениет туралы шағын презентация дайындау. |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Сызықтық теңдеулер жүйесін қосу және азайту әдісімен шешу. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушыларды сызықтық теңдеулер жүйесін шешу тәсілдерінің бірі ретінде қосу және азайту амалдарымен таныстыру. Оқушыларды сызықтық теңдеулер жүйесін шешуде қосу және азайту амалдарын қолдануға үйрету. Оқу материалдарымен және тапсырмалармен өз бетінше жұмыс істеу дағдыларын дамыту. |
|
|
Сабақтың мақсаты |
Оқушылардың қосу және азайту әдістерін қолдана отырып, сызықтық теңдеулер жүйесін шешу дағдыларын дамыту, логикалық және аналитикалық ойлауын дамыту, сонымен қатар қолданбалы есептердегі математикалық білімдерді қолданудың практикалық дағдыларын дамыту. |
|
|
Сабақ барысы |
Оқытушының іс- әрекеті |
Оқушының іс- әрекеті |
Бағалау |
ресурстар |
|
Сабақтың басы
|
І. Ұйымдастыру кезеңі.
Психологиялық
сәт. ІІ. Үй тапсырмасын сұрау. |
Қойылған сұрақтарға жауап береді.
|
Оқушының жауабын толықтыру немесе тиімді кері байланыс жасау. |
Интерактивті тақта, оқулық. |
|
Сабақтың ортасы 20 минут |
Алгебра біреу. Ол ұлтқа, дінге, мәдениетке, елге, жерге бөлінбейді. «Төрткен төртқараның» айырмашылығы неде? Тек қазақша атауында ғана. Асқар Жұмаділдаев атамыздың ұлағатты сөзі жайлы не ойлайсыздар? Пікірлеріңмен бөлісіңдер
Фронтальды шолу. Екі айнымалысы бар екі сызықтық теңдеулер жүйесі қалай аталады? Екі айнымалысы бар екі сызықтық теңдеулер жүйесінің шешімі қандай? Екі айнымалысы бар теңдеулер жүйесін шешу нені білдіреді? (1;1) сандар жұбы теңдеулер жүйесінің шешімі болып табылады
Екі айнымалысы бар теңдеулер жүйесін шешудің қандай әдістерін білесіз? Теңдеулер жүйесін шешуде не қолданасыз? Ауыстыру әдісі және графикалық әдіс дегеніміз не? (Ережені құрастыру).
Фронтальды зерттеу: Бір айнымалыны екіншісі арқылы өрнектеуге ыңғайлы теңдеуді таңдайық. Бұл жағдайда бұрын зерттелген әдістер бізге сәйкес келмейді. Бұл жағдайдан шығудың жолы қандай? Бірінші жүйені шешкеннен кейін жеткен қорытындыға назар аударыңыз. Бір айнымалысы бар сызықтық теңдеуді алғаннан кейін ғана жүйені шешу мүмкін болды. Теңдеулер жүйесін қараңыз және берілген екі теңдеуден бір айнымалысы бар бір теңдеуді қалай алуға болатынын ойлаңыз. Теңдеулерді қосыңыз. Теңдеулерді қосу деген нені білдіреді? Теңдеулердің сол жақтарының қосындысын, оң жақтарының қосындысын бөлек құрастырып, алынған қосындыларды теңестір. Сабақтың тақырыбы мен мақсатын тұжырымдау Сабақтың тақырыбын жазу Қосу әдісі арқылы сызықтық теңдеулер жүйесін шешу 13x+17y+14x-7y=43+11 27x+0=54 27x=54 ; x=54:27; x=2 |
Оқушылар жаңа сабақты меңгереді Теңдеулерді қосу деген нені білдіретінін біледі |
Теңдеулер жүйесін шешуді үйренеді ҚБ: Гулдер Оқушылар ауыстыру әдісін біледі ҚБ: От шашу |
Слайд, оқулық, Интерактивті тақта, оқулық, фигуралары және тақтасы.
|
|
Сабақтың соңы |
Үйге тапсырма: Сызықтық теңдеулер жүйесін қосу және азайту арқылы шешу жайлы презентация дайындап кел |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Анықтауыш әдісі арқылы сызықтық теңдеулер жүйесін шешу |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Сызықтық теңдеулер жүйесін шешу әдістерінің бірі ретінде анықтауыштар әдісімен оқушыларды таныстыру. Оқушыларға сызықтық теңдеулер жүйесін шешу үшін осы әдісті қолдануға үйрету. Оқу материалымен өз бетінше жұмыс істеу дағдыларын дамыту. Пәннің өмірмен және практикалық іс-әрекетімен байланысын көрсете отырып, математикаға деген қызығушылықтарын арттыру. |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Психологиялық ахуал қалыптастыру. Оқушылардың көңілін сабаққа
аудару |
Оқушылар бір-бірімен амандасады. |
Формативті бағалау үнемі жүргізіліп отырады |
Оқулықтар |
|
Сабақтың ортасы |
Кітапқа енген кез келген формула оны сатып алушылардың санын екі есеге азайтады. Стивен Хокинг. Стивенг Хокингтың ұлағатты сөзі жайлы не
ойлайсыздар? - Мұғалім бүгінгі сабақта сызықтық теңдеулер жүйесін шешу әдісі - анықтауыштар әдісімен танысамыз деп түсіндіреді. - Мұғалім оқушыларға сызықтық теңдеулер жүйесі туралы түсінікті еске салады және мұндай жүйенің бір, шексіз көп немесе шешімдері жоқ болуы мүмкін екенін есіне түсіреді. - Мұғалім анықтауыштар әдісі матрицалардың анықтауыштарын қолдануға негізделгенін түсіндіреді. - Мұғалім оқушыларға матрицаның анықтауышы және оның қасиеттері туралы еске салады. - Мұғалім сызықтық теңдеулер жүйесін бейнелейтін матрицаны қалай құру керектігін түсіндіреді. - Мұғалім сызықтық теңдеулер жүйесін шешу үшін матрицаның анықтауышын қалай қолдану керектігін түсіндіреді. Анықтама 1. Матрица –
сандардан тұратын төртбұрышты кесте. Белгілер: А-матрица, аіj-матрица элементі, i-берілген элемент тұрған жол нөмірі, j-тиісті баған нөмірі; m – матрица жолдарының саны, n – оның бағандарының саны. Анықтама 2. m және n сандары матрицаның өлшемдері деп аталады. Анықтама 3. Егер m = n болса, матрица квадрат деп аталады. Бұл жағдайда n саны шаршы матрицаның реті деп аталады. Әрбір шаршы матрицаны
матрицаның барлық элементтерін пайдаланып бірегей түрде анықталатын
санмен байланыстыруға болады. Бұл сан анықтауыш деп
аталады Крамер әдісі. (Габриэль Крамер (1704-1752) швейцариялық математик) Бұл әдіс айнымалылар саны теңдеулер санымен сәйкес келетін сызықтық теңдеулер жүйесінде ғана қолданылады. Сонымен қатар, жүйе коэффициенттеріне шектеулер енгізу қажет. Барлық теңдеулер сызықтық тәуелсіз болуы қажет, яғни. ешбір теңдеу басқаларының сызықтық комбинациясы болмайды. Ол үшін жүйелік матрицаның анықтауышы 0-ге тең болмауы керек. Шынында да, жүйенің кез келген теңдеуі басқаларының сызықтық комбинациясы болса, онда сызықтық түрлендірулерді пайдалана отырып, бір жолдың элементтеріне басқа жолдың элементтерін кейбір санға көбейтетін қоссаңыз, нөлдік жолды алуға болады. Бұл жағдайда анықтауыш нөлге тең болады. Теорема (Крамер Ережесі). N
белгісіз n теңдеулер жүйесі |
Оқушылар Анықтауыш әдісін талқылайды.
Оқушылар осы материал бойынша өз бетінше жұмыс істейді |
Дескриптор: Оқушылар шын/жалған ойына бойынша ойынға кірісе алады |
|
|
Қорытынды |
Үйге тапсырма беру: Функциялар және графиктер жайлы ақпарат жинап келіңдер |
|
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Функциялар және олардың графиктері |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Функция ұғымын меңгеру, функцияның негізгі элементтерін анықтауды үйрену (аргумент, функция мәні, анықтау облысы және мәндер жиыны). Функциялардың негізгі түрлерін (сызықтық, квадраттық, дәрежелік және т.б.) оқып, оларды ажырата білуге үйрету. Функцияны көрсетудің әртүрлі тәсілдерімен (аналитикалық, графикалық, кестелік) танысыңыз және бір әдістен екіншісіне өтуді үйреніңіз. Әртүрлі функциялардың графиктерін құруды және олардың қасиеттерін талдауды үйрену. Функциялар мен олардың графиктеріне байланысты есептер шығару дағдыларын дамыту. |
|
|
Сабақтың мақсаты |
Функциялардың әртүрлі түрлері, олардың графиктері туралы білімді меңгеру, сонымен қатар ғылым мен техниканың әртүрлі салаларындағы қолданбалы есептерді шешу үшін әртүрлі координаталар жүйесіндегі функциялардың графиктерін оқу, тұрғызу және талдау дағдыларын дамыту. |
|
|
Сабақ барысы |
Оқытушының іс- әрекеті |
Оқушының іс- әрекеті |
Бағалау |
ресурстар |
|
Сабақтың басы 10 минут |
Ұйымдастыру кезеңі «Денелік өзара әрекеттесу» жаттығуы. |
Оқушыларды сабаққа дайындау. Оқушылар ойын ойнау арқылы серпіліп қалады. Оқушылар қойылған сұраққа жауап береді |
Формативті бағалау үнемі жүргізіліп отырады. Гүлдердің суреттерін тарату арқылы бағалау жүргізіледі
|
Оқулықтар суреттер, |
|
Сабақтың ортасы
|
Фрэнсис Бэконның ұлағатты сөзі жайлы не ойлайсыздар? Әкімдік тұрғындарға әрқайсысының ауданы 6 акр (600 м2) болатын саяжай үшін төртбұрышты жер телімін бөлді. Егер ауданның өлшемдерінің бірі х болса, онда оның екінші y өлшемін қалай табуға болады? Анықтама. Х айнымалысының әрбір мәні тәуелді y айнымалысының бір мәнімен байланысты болатын үлгіні функция немесе функционалдық тәуелділік деп атайды. Немесе х айнымалысының әрбір мәні у айнымалысының бір ғана мәніне сәйкес келеді. Талқылау «Графиктерді қай жерде кездестіреміз?» Мысалдар Температураның тәулік уақытына қатысты графигі. 1. График арқылы сағат 4-те ауа температурасы қандай болғанын анықтаңыз? Сағат 12-де? сағат 24-те? Ең жоғары температура қашан болды? Тәуелді айнымалыны атаңыз? Тәуелді айнымалыны атаңыз? Қозғалыс кестесі Тәуелді айнымалыны атаңыз? Тәуелді айнымалыны атаңыз? Функцияның графигін қалай саламыз? Функция мына формуламен берілсін: y = x(4 – x), мұндағы -1 ≤ x ≤ 5 Осы функция үшін мәндер кестесін
құрайық: 3. Кесте деректерін пайдалана отырып, біз координаталық жазықтықта нүктелерді саламыз (презентацияда қалам мен таңдауды қолданамыз және нүктелерді координаталық жазықтыққа орнатамыз) 4. Осы нүктелерді тегіс сызықпен қосамыз, алынған қисық y = x(4 – x) функциясының графигі болады. 5.Бекіту Функция у = 2x – 3 формуласымен берілген, мұндағы -2 ≤ x ≤ 2 К Құрылған графикті тексеру. |
Оқушылар сұрақтарға жауап береді Оқушылар дәрісті мұқият тыңдайды |
Дескриптор: Оқушылар график жайлы біледі. Гүлдердің суреттерін тарату арқылы бағалау жүргізіледі
ҚБ: Бес бармақ
|
Оқулықтар суреттер, слайдтар Кестелер, Интерактивті тақта, оқулық, |
|
Үйге тапсырма беру |
Кері
байланыс: Үйге тапсырма: «Функция және график» тақырыбында ребус жасап кел |
Күнделікке үй тапсырмасын жазады. |
|
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Тест тапсырмалары. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушылардың алған білімдерін тексеру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
І. Ұйымдастыру кезеңі. Сәлемдесу, түгелдеу
|
|
|
Интерактивті тақта, оқулық. |
|
Жаңа білім 15 мин 2 мин Бекіту 15 мин |
1 – нұсқа 1. Функцияның визуализациясы қалай аталады? а) Кесте б) Туынды в) интегралдық 2. Сызықтық теңдеулер жүйесін анықтауыштардың көмегімен шешу үшін қандай әдіс қолданылады? а) Гаусс әдісі б) Крамер әдісі в) Иордан әдісі 3. Сызықтық теңдеулер жүйесін шешудің қандай әдісі теңдеулерді қосу және азайтуға негізделген? а) Иордан әдісі б) Крамер әдісі в) Гаусс әдісі 4. Бір теңдеу екіншісімен ауыстырылатын сызықтық теңдеулер жүйесін шешу әдісі қалай аталады? а) Иордан әдісі б) Крамер әдісі в) Айнымалы ауыстыру әдісі 5. Функцияның координаталық жазықтықта көрінісін бейнелейтін график қалай аталады? а) Сызықтық график б) Көрсеткіштік график в) Функционалдық диаграмма 6. Анықтауыш әдісін қолданғанда сызықтық теңдеулер жүйесінің бірегей шешімі болуы үшін қандай шарт орындалуы керек? а) Жүйе матрицасының анықтауышы нөлге тең болуы керек б) Жүйе матрицасының анықтауышы нөлге тең болмауы керек в) Жүйе матрицасы симметриялы болуы керек 7. Қосу және азайту арқылы шешкенде жүйе қанша теңдеуден тұрады? а) Дәл бір теңдеу б) Екі теңдеу в) Үш теңдеу 8. Математикадағы қандай әдіс теңдеуді шешпей-ақ функциялардың жуық мәндерін табуға мүмкіндік береді? а) жуықтау әдісі б) Ауыстыру әдісі в) Гаусс әдісі 9. Функцияның негізгі сипаттамаларын анықтауға мүмкіндік беретін функцияның сипаттама графигі қалай аталады? а) Функцияның графигі б) Теңдік графигі в) Аналитикалық график 10. Функцияның графигін зерттеу арқылы ол туралы қандай ақпаратты алуға болады? а) Функцияның белгілі бір нүктедегі мәні б) Функцияның туындысының мәні в) Функция облысы 2 – нұсқа 1. Функция дегеніміз не? а) Математикалық өрнек б) Екі шама арасындағы байланыс в) Белгілі бір операцияларды орындағаннан кейін алынған сан 2. Қандай график у = х^2 функциясын көрсетеді? а) (Параболаны көрсететін график) б) (Түзу сызықты бейнелейтін график) в) (Синустық толқынды көрсететін график) 3. Төмендегі теңдеулердің қайсысы функция болып табылады? а) х + у = 5 б) у = 3 в) х^2 + у^2 = 9 Тақырыбы: Анықтауыш әдісі арқылы сызықтық теңдеулер жүйесін шешу 4. Анықтауыш әдісі арқылы сызықтық теңдеулер жүйесінің шешімін қалай табуға болады? а) матрицаның анықтауышын есептеп, оның мәндерін формулаға қойыңыз б) Теңдеулердің коэффициенттерінің қосындысын есептеп, алынған теңдеуді шеш в) Теңдеулердің графиктерінің қиылысу нүктесінің координаталарын табыңдар 5. Сызықтық теңдеулер жүйесінің матрицасының анықтауышы нөлге тең болса, бұл нені білдіреді? а) Жүйенің шешімі жоқ б) Жүйенің шешімдерінің шексіз саны бар в) Жүйенің бірегей шешімі бар 6. Анықтауыш әдісі арқылы сызықтық теңдеулер жүйесінің табылған шешімінің дұрыстығын қалай тексеруге болады? а) Табылған мәндерді жүйенің барлық теңдеулеріне ауыстырыңыз және олардың дұрыстығын тексеріңіз б) Теңдеулер жүйесін басқа түрге айналдырып, алынған нәтижені салыстыру в) Теңдеулердің барлық коэффициенттерін анықтауышқа көбейтіп, қосымша есептеулер жүргізіңдер Тақырыбы: Қосу және азайту әдісі арқылы сызықтық теңдеулер жүйесін шешу 7.Сызықтық теңдеулер жүйесін қосу және азайту әдісі арқылы қалай шешуге болады? а) Екі теңдеуді де белгілі бір санға көбейтіп, оларды қосу/азайту ә) Бір теңдеудегі бір айнымалыны екінші айнымалымен өрнектеп, оны басқа теңдеумен алмастыру в) Берілген жүйеге тән белгілі бір формулалар мен шешу әдістерін қолдану 8.Сызықтық теңдеулер жүйесінің табылған шешімінің дұрыстығын қосу және азайту әдісі арқылы қалай тексеруге болады? а) Табылған мәндерді шешілмеген теңдеулердің орнына қойып, олардың дұрыстығын тексеріңіз б) Теңдеулер жүйесін басқа түрге айналдырып, алынған нәтижені салыстыру в) Ауыстыру әдісін қолданыңыз және алынған шешім жүйенің басқа теңдеулерін де қанағаттандыратынын тексеріңіз Тақырыбы: Сызықтық теңдеулер жүйесін алмастыру әдісі арқылы шешу 9. Сызықтық теңдеулер жүйесін алмастыру әдісі арқылы қалай шешеді? а) Дискриминантты есептеп, оның мәнін теңдеулердің түбірін табу үшін пайдаланыңыз ә) Бір теңдеуді екінші теңдеуге ауыстырып, алынған теңдеуді шеш в) Бір теңдеудегі бір айнымалыны екіншісімен өрнектеп, оны басқа теңдеуге ауыстыр 10. Сызықтық теңдеулер жүйесінің табылған шешімінің дұрыстығын ауыстыру әдісі арқылы қалай тексеруге болады? а) Табылған мәндерді жүйенің барлық теңдеулеріне ауыстырыңыз және олардың дұрыстығын тексеріңіз б) Жүйенің шешілген теңдеулерін пайдаланып қосымша теңдеу құрып, дұрыстығын тексеру в) Теңдеулердің барлық коэффициенттерін белгілі бір санға көбейтіп, қосымша есептеулер жүргізу |
|
|
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: Өткен тақырыптарды қайталау |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Арифметикалық және геометриялық прогрессиялар |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушыларды арифметикалық және геометриялық прогрессия ұғымдарымен және олардың зерттелу тарихымен таныстыру. Оқушыларға прогрессияның n-ші мүшесі және алғашқы n мүшесінің қосындысы формулаларын пайдаланып есептер шығаруға үйрету. Алған білімдерін талдау және жалпылау, әртүрлі күрделіліктегі есептерді шешуде қолдану қабілеттерін дамыту. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
Ұйымдастыру кезеңі:
|
Қойылған сұрақтарға жауап береді. |
Оқушының жауабын толықтыру немесе тиімді кері байланыс жасау. |
Интерактивті тақта, оқулық. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Жаңа білім 15 мин 2 мин Бекіту 15 мин |
Шынайы өмірге қатысы бар
математика заңдылықтары сенімді емес, ал сенімді математика
заңдылықтарының шынайы өмірге түк қатысы
жоқ. Альберт
Эйнштейн. Альберт Энштейн не айтқысы
келді? Ежелгі дәуірдегі арифметикалық прогрессиялар (Тарихи есептер). Вавилондықтардың сына жазу кестелерінде, Египет пирамидаларында (б.з.д. 2 ғ.) арифметикалық прогрессиялардың мысалдары бар. Мысырлық ахмес папирусынан алынған тапсырманың мысалы: "Сізге айтсын: арпаның 10 шарасын 10 адамға бөліңіз, әр адам мен оның көршісі арасындағы айырмашылық шараның 1/8 бөлігіне тең.» Міне, мысырлықтар қолданған формула:
Ежелгі заманнан бізге жеткен прогрессивтік мәселелер шаруашылық өмірінің талаптарымен байланысты болды: өнімді бөлу, мұраны бөлу және т.б. Прогрессияларға қатысты кейбір формулалар қытай және үнді ғалымдарына белгілі болды. Арьябхатта (5 ғасыр) арифмдердің жалпы сандары мен қосындылары үшін формулаларды пайдаланды. Прогрессия. Бірақ ерікті арифмнің мүшелерінің қосындысын табу ережесі. прогрессия алғаш рет 1202 жылы Пизалық Леонардоның «Абак кітабы» еңбегінде кездеседі.
Мәселені шешейік – біздің дәуір басындағы аңыз.
Үнді патшасы Шерам шахмат ойынының өнертапқышы Сетуды тапқыр ойлап тапқаны үшін марапаттау үшін шақырып, оны жомарттықпен марапаттауға уәде берді. Өнертапқыш Сет шахмат тақтасының бірінші шаршысына бір дән, екіншісіне 2, үшіншісіне 4, т.б. беруді сұрады. Қуанған патша осындай «қарапайымды сый» беруді бұйырады. Алайда король өнертапқыш Сетаның тілегін орындай алмағаны белгілі болды, өйткені... астық саны өте көп болды. Есеп шығарайық. (Драмалық қойылым) Берілгені:
Шешілім: Репродуктивті сипаттағы мәселелерді шешу. Өзара бақылауды ұйымдастыру. Енді заманауи мәселелерді шешуге көшейік. Сабақтың күні мен тақырыбын дәптерлеріңе жазып алыңдар. Тапсырмалар жазылған карточкаларды таратып, 2 адамды тақтаға шақырамын, қалған сынып дәптерлеріне жазады. 1) *(сn) реті сn =n/2 -4 формуласымен берілген. c1, c8, c300, ck+1 табыңыз. 2) Арифметикалық прогрессияның әріппен жазылған мүшелерін табыңыз: a1, a2, 15, a4, a5, 33, a7, . . . 3) (– 2,6) тең арифметикалық прогрессияның (xn) мүшесінің санын табыңыз, егер x1 = 8,2 және d = -0,3 болса. 4) Арифметикалық прогрессия берілген -3,6; -3, 3; -3; ...Қай саннан бастап оның мүшелері оң болады? 5) х-1 болатын х мәндерін табыңыз; 4x-3 және x2+1 арифметикалық прогрессияны құрайды ма? 6) a5=6, a12=27 болса, арифметикалық прогрессияның алғашқы жиырма мүшесінің қосындысын табыңыз. 7) Сол жағында жазылған қосындыдағы мүшелер 56+50+44+ …+x=280 арифметикалық прогрессиясын құрайтын теңдеуді шешіңіз.
Енді геометриялық прогрессияны қайталайық. 9) *Геометриялық прогрессияның (bn) бөлімін табыңыз, егер b4 =4, b6 =8 болса. 10)162 саны 2/9 геометриялық прогрессияның мүшесі; 2/3; 2;... Осы мүшенің санын табыңыз. 11) q=3/4, S4 =350 болатын геометриялық прогрессияның b1-ін табыңыз. 12) Геометриялық прогрессияда b1=7, bn =567, Sn =847. q және n табыңыз. 13) Геометриялық прогрессияның бесінші және үшінші мүшелерінің айырмасы 240, ал төртінші мен екінші мүшелерінің айырмасы 60. Осы прогрессияның алғашқы алты мүшесінің қосындысын табыңыз. 14) Оң мүшелері S2=8, S3=26 болатын геометриялық прогрессияда. S5 табыңыз. 15) Кесте бойынша өзіндік жұмыс (жауапты экранда көрсетемін, өзара тексеру жүргізіледі, нәтиже көршінің жеке картасына енгізіледі)
|
Оқушыар жаңа сабақты меңгереді
Оқушылар құлақ салып тыңдайды
|
ҚБ: Оқушылар ортаңғы кезеңнің қыр-сыры мен маңыздылығын ұғады ҚБ: Мадақтау
|
Оқулықтар суреттер Кестелер Сызғыш қарындаштар Қайшы Қағаздар, плакаттар, графиктер
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: «Идеал тапсырма» старегиясы.
(Шығармашылық ізденіс тапсырмасы) – Арифметикалық және геометриялық прогрессиялар жайлы презентация дайындап кел |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Квадрат теңдеулерді шешу. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушыларды квадрат теңдеу ұғымымен және оның негізгі түрлерімен таныстыру. Квадрат теңдеудің түбірін табу формулаларын үйреніңіз. Оқушыларды квадрат теңдеулердің әртүрлі түрлерін шешу үшін осы формулаларды қолдануға үйрету. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақ барысы |
Оқытушының іс- әрекеті |
Оқушының іс- әрекеті |
Бағалау |
ресурстар |
|
Сабақтың басы 10 минут |
Ұйымдастыру кезеңі
Есте қалған қызықты
оқиға |
Оқушылар қимыл іс әркетін орындайды |
Формативті бағалау үнемі жүргізіліп отырады. |
Оқулықтар суреттер, слайдтар Кестелер |
|
Сабақтың ортасы 20 минут |
Үлкен пирамидалы храмдардың архитектурасын мылқау математика десе де болады. Освальд Шпенглер.
Келесі сұрақтарға жауап беріңіз: Сұрақтарға жауап бер: 1. Қай теңдеу квадрат деп аталады? 2. Теңдеуді шешу деген нені білдіреді? 3. Қандай квадрат теңдеулер толық емес, қайсысы толық деп аталады? 4. Толымсыз квадрат теңдеулердің түрлерін көрсетіңіз 5. Толық шаршы урандардың түрлерін атаңыз 6. Толық квадрат теңдеудің қанша түбірі болуы мүмкін? Анықтамалық диаграмманы пайдалана отырып, мәселені талдап, шешеміз. 1 тапсырма. Арман Маратұлы дүкенге өзінің төртбұрышты учаскесіне қоршау алу үшін келгенімен оның өлшемдерін ұмытып кеткен. Арман Маратұлының есінде тек жер учаскесінің ауданы 750 м2 болса, ал жер учаскесінің ұзындығы енінен 5 метр үлкен болса, қанша уақытқа қоршау сатып алуы керек? Шешімі: Ауданның ені х болсын. Көбінесе беймәлім шамалардың кішісі деп х-ті қабылдаған ыңғайлы. Сонда кесіндінің ұзындығы x + 5 болады. Тіктөртбұрыштың ауданы S = x • (x + 5) x • (x + 5) = 750, x² + 5x - 750 = 0. Осы теңдеудің дискриминантын және оның түбірлерін табайық. a = 1, b = 5, c = -750 D = b² - 4ac D = 5² - 4 • 1 • (-750) = 25 + 3000 = 3025 = 552 x₁, ₂ = (-5 ± √3025)/(2 • 1), x1 = (-5 - 55)/2 немесе x2 = (-5 + 55)/2. x₁ = -30 немесе x₂ = 25 Табылған түбірлердің біріншісі мәселенің мағынасында бөгде болып табылады, яғни қиманың ені 25 м-ге тең болады.Демек, ұзындығы 25 + 5 = 30 м-ге тең болады. Енді Арман Маратұлы өз сайтының периметрін есептей алады. P = 2 • (25 + 30) = 110 м Сізге 110 м қоршау сатып алу керек. Әр топқа таблеткалар
дайындалды. Әр топ Kahoot арқылы есептің шешімін
тексереді. Жеке тапсырмалар. Экранда квадрат теңдеулерді көрсетемін: 1. x2 -49=0 2. 64x+4x2 = 0 3. 2x(x+3)=6x-x2 4. 5x2 + 9x –14 = 0; 5. 5x2 + x – 6 = 0; 6. 3х2 – 5х + 2 = 0 7. 2x2 + 5x + 2=0, Мен жеке тапсырмаларды Kahoot порталы арқылы планшеттер арқылы тексеремін. Топтық тапсырма: Бұған дейін сіз екеуміз Арман Маратұлына өз меншігіндегі қоршау үшін қанша материал қажет екенін есептеуге көмектестік, жақсы жұмыс жасағаныңыз үшін Арман Маратұлы бізге жаңа өтінішпен жүгінді. Оған үй салуға, құрылыс материалдарының логистикасына және т.б. көмектесуге тура келеді. Тақтадағы тапсырмаларды тізімдеймін: Арман Маратұлының үйінің құрылысын бастап жатырмыз 1 топ. Үй төртбұрышты пішінді. Бір жағы екіншісінен 4 метрге кіші. Алып жатқан жер аумағы 396 м². Үйдің периметрін табыңыз және бір стандартты панельдің ұзындығы 4 метр болса, үй салу үшін қанша бетон панелі қажет болатынын табыңыз. Шешімі: Үйдің ені х болсын. Сонда үйдің ұзындығы х + 4 болады. Тіктөртбұрыштың ауданы S = x • (x + 4) x • (x + 4) = 396, x² + 4x -396 = 0. Осы теңдеудің дискриминантын және оның түбірлерін табайық. a = 1, b = 4, c=-396 D = b² - 4ac D = 4² - 4 • 1 • (-396) = 16 + 1584 = 1600 x₁, ₂ = (-4 ± √1600)/(2 • 1), x1 = (-4 - 40)/2 немесе x2 = (-4 + 40)/2. x₁ = -22 немесе x₂ = 18 Табылған түбірлердің біріншісі мәселенің мағынасында бөгде, яғни үйдің ені 18 м-ге тең болады.Демек, ұзындығы 18 + 4 = 22 м-ге тең болады. Енді Арман Маратұлы өз сайтының периметрін есептей алады. P = 2 • (18+ 22) = 80 м 80/4=20 дана панельдер Жауап: сізге 20 дана бетон панельдері қажет 2-топ. Құрылыс материалдарына қайда бару керек? Үйден солтүстікке қарай В зауыты, ал шығысында А зауыты орналасқан. Зауыттардың арасы үйден А зауытына дейін 3 км, ал В зауытына қарағанда 6 км артық. Сізге қанша қашықтық қажет. А зауытында блоктарды сатып алу үшін саяхаттаңыз ба? Шешуі: х км – зауыттар арасындағы қашықтық. (x-3) км – А дейін қашықтық (x-6) км – В дейінгі қашықтық Пифагор теоремасы бойынша (x-6)²+(x-3)²=x² x²-12x+36+ x²-6x+9- x²=0 x²-18x+45=0 (x-9)²-81+45=0 (x-9)²=36 x-9=6 x-9=-6 x=15 x=3 3-6 А қондырғысына 15-3=12 км жол жүру керек. Жауабы: А зауытына дейін 12 км 3-топ. Алаңды көгалдандыру Гүлзарға жер учаскесін дайындау керек. Мұны істеу үшін, егер үй иесі тікбұрышты үшбұрыш түрінде гүлзар жасауды шешсе, оның жақтарын табу керек. Оң жақ бұрышқа қарама-қарсы жатқан жағы 5 м. қалған екі жақтың бірі 1 м аз. Гүлзардың белгісіз жақтарын табыңыз. Шешім: Пифагор теоремасы бойынша шешеміз. 1 аяғы=x 2 аяғы=x-1 X2 +(x-1) 2 = 52 X2+x2-2x+1=25 2Х2-2х-24=0 (/2) X2-x-12=0 X1=4, x2=-3 X2 сәйкес келмейді, осы себепті x=4 1 аяғы=4 м, 2 аяғы=5 м Жауап: 4м, 5м. |
Оқушылар жаңа сабақты меңгереді Оқушылар квадратты теңдеулерді шеше алады Оқушылар топта жұмыс жасай алады |
Оқушылар өз болжауын айтады Мадақтау Оқушылар берілген материалды дәптеріне жазады Қолшапалақтау
Дескриптор: Оқушылар ойынның жапырақшалық ойыны арқылы жаңа тақырыпты тиімді меңгереді алады Басбармақ
|
Слайд, оқулық, интерактивті тақта, графиктер, сызбалар, |
|
Сабақтың соңы 10 минут |
Кері байланыс:
Үйге тапсырма: Дәреже функциясы, оның қасиеттері және графигі жайлы сабаққа дайындалып кел |
Оқушылар мұғаліммен кері байланыс жасайды |
|
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Дәреже функциясы, оның қасиеттері және графигі |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Қазақстан жеріндегі алғашқы тайпалардың қалыптасу тарихын зерттеу. Географиялық орнының тайпалардың қалыптасуына әсерін талдау. Тайпалардың мәдени және діни ерекшеліктерін зерттеу. |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 5 мин |
Ынтымақтастық атмосферасын қалыптастыру Сәлемдесу, түгелдеу. Өткен тақырыпқа шолу: -Өткен тақырыпты мазмұндаңдар. -Өткен тақырыптарға байланысты бір-біріңе сұрақ қойып, жауап алыңдар |
Өткен тақырыпқа қатысты сұрақтарға жауап береді. Тақырыпты табады |
Оқушының жауабын толықтыру немесе тиімді кері байланыс жасау. |
Интербел-сенді тақта |
|
Жаңа білім 15 мин 2 мин Бекіту 18 мин |
Тарих дегеніміз — математикаға қатысы жоқ дегеннің бəрінің жиынтығы. Освальд Шпенглер. Ұсынылған ұлағатты сөзге пікір қалдырыңыздар
1. Қуат функциясы. Осы функциялардың барлығында қандай ортақ нәрсе бар? Бұл функциялардың барлығы қуат функциясының ерекше жағдайлары болып табылады. Дәрежелік функцияның анықтамасын берейік. y = xp, мұндағы p – берілген нақты сан. Дәрежелік функцияның қасиеттері мен графигі нақты көрсеткіші бар дәреженің қасиеттеріне, атап айтқанда, xp күші мағынасы бар x және p мәндеріне байланысты. Енді сіздердің әрқайсысыңыз «Қуат функциясы» тақырыбына тірек жазба жасайсыз. Бұл жазбаны аяқтағаннан кейін оны сабаққа дайындалу үшін пайдалану сізге ыңғайлы болады. Қолдау контурында графиктердің эскиздері бар. Сіздің тапсырмаңыз: функциялардың қасиеттерін тұжырымдап, жазбаларыңызға ескертулер жасаңыз. Сыныппен фронтальды жұмыс. Функциялардың қасиеттерін төмендегі жоспар бойынша тізімдейміз. 1. Анықтау аясы. 2. Мәндер ауқымы (мәндер жиыны). 3. Жұп, тақ функция. Жұп, тақ функцияның графикалық иллюстрациясы. Жұп және тақ қасиеттердің аналитикалық белгіленуі. 4. Функцияның өсу және кему аралықтарын жазыңыз. Фронтальды жұмыс кезінде жауаптарды бос орындар немесе теңсіздіктер түрінде жазудың мүмкін нұсқаларына назар аударамын. Слайдтарда р көрсеткіші өзгерген кезде графиктің сыртқы түрі қалай өзгеретінін көрсетемін. 2. Көрсеткіштік функция. Көрсеткіштік функцияның қасиеттерін негіздеу үшін дәрежелердің қасиеттері туралы материалды білу қажет. Сондықтан бұл қасиеттерді қайталауды келесі жаттығуларды ауызша орындау кезінде жасауға болады: 1-жаттығу: 1.
2.
3.
4.
5. 6. 7. 8.
2-тапсырма: Функцияның графигінен оның қасиеттерін анықтауды оқушылармен бірге қайталау тиімді. Осы мақсатта 13-суретте мыналарды табуға болады: 1) функция мәні нөлге тең болатын аргумент мәндері; 2) графтың ордината осімен қиылысу нүктесінің координаталары; 3) функция оң (теріс) мәндерді қабылдайтын аргумент мәндері; 4) функцияның өсу (кему) интервалдары.
Бүгін біз дәреже ұғымын кеңейтуге тырысамыз. Рационал сандармен қатар иррационал сандар да бар екенін білесіздер. Санды иррационал дәрежеге көтеруге бола ма? Кейбір тұрақты a>0 санын бекітейік және рационал сандар жиынындағы әрбір \frac{m}{n} санын a^\frac{m}{n} санымен байланыстырайық. Осылайша, f(x)\ =a^x функциясы туралы айтуға болады. Осы функциямен және оның қасиеттерімен танысу үшін мұғалім оқушыларға нұсқалар бойынша жұмысты ұсынады. Бірінші нұсқа a=2 жағдайын қарастырады. Екінші нұсқа – a=\frac{1}{2}. Оқушылар сәйкес функциялардың графигін салып, олардың қасиеттерін қарастыруы керек. 1. y=2^x функциялары
y=2^x функциясының қасиеттері:
3) жұп та, тақ та емес; 4) өседі; 5) жоғарыдан шектелмеген, төменнен шектелген; 6) ең үлкен немесе ең кіші мәндері жоқ; 7) үздіксіз; 8) дөңес төмен.
3) жұп та, тақ та емес; 4) азаяды; 5) жоғарыдан шектелмеген, төменнен шектелген; 6) ең үлкен немесе ең кіші мәндері жоқ; 7) үздіксіз; 8) дөңес төмен.
Бұл тапсырмаға 10-12 минут беріледі. Төменгі жол: экспоненциалды функцияны анықтау және негізгі қасиеттері. Анықтамасы: |
Қойылған сөздерге ассоцияция жасайды.
Өз пікірлерін білдіреді.
|
Дескриптор: Оқушылардың ассоцияциялау қабілеті жақсы ҚБ:мадақтау Дескриптор: ҚБ:шарлар - Оқушылар топта жұмыс жасай алады. ҚБ:мадақтау |
Оқулық, Карточкалар, Қайшы Қағаздар,
|
|
Қорытынды 5 мин |
Кері
байланысты Оқу тапсырмасы: Дәреже функциясының формуларын қайталау |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Көпмүшені көбейткіштерге бөлу |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушыларды көпмүшелерді көбейткіштерге бөлудің негізгі әдістерімен таныстыру. Алгебралық өрнектерді жеңілдету және теңдеулерді шешу үшін алған білімдерін қолдана білуге үйрету. Оқушылардың логикалық және аналитикалық ойлауын дамыту. |
|
|
Сабақтың мақсаты |
Оқушылардың көпмүшені сызықтық көбейткіштерге жіктеу және осы әдісті өрнектерді жеңілдету, теңдеулер мен теңсіздіктерді шешу үшін қолдану дағдыларын дамыту. |
|
|
Сабақ барысы |
Оқытушының іс- әрекеті |
Оқушының іс- әрекеті |
Бағалау |
ресурстар |
||
|
Сабақтың басы 10 минут |
Ұйымдастыру кезеңі «Денелік өзара әрекеттесу» жаттығуы. |
Оқушыларды сабаққа дайындау. Оқушылар ойын ойнау арқылы серпіліп қалады. Оқушылар қойылған сұраққа жауап береді |
Формативті бағалау үнемі жүргізіліп отырады. Гүлдердің суреттерін тарату арқылы бағалау жүргізіледі
|
Оқулықтар суреттер, слайдтар Кестелер,
|
||
|
Сабақтың ортасы 20 минут |
Математика да —
өнер: оның өз стильдері мен стильді кезеңдері
бар. Освальд Шпенглер. Освальд бізге не айтқысы
келді? Теңдеулерді шешіңіз:
Көпмүшені көбейткіштерге бөлу қажеттілігін ынталандыру.
Теңдеуді шешіңіз: x2 +3x +6 +2x =0
Проблемалық жағдай туады: мәселе бір қарағанда таныс, бірақ оны шешу мүмкін емес. Оң жағы 0 болатын теңдеуді сол жағын көбейткіштерге бөлу арқылы шешу ыңғайлы екенін білеміз.
- Барлық терминдердің ортақ факторы бар ма?
- Демек, бұл факторизация әдісі қолайлы емес.
Оқу тапсырмасының тұжырымы: көпмүшені басқа тәсілмен көбейтуді үйрену.
Жаңа материалды зерттеу:
Жұптық жұмыс: білу үшін көпмүшені қалай көбейтуге болады, егер барлық терминдердің ортақ факторлары болмаса. Мен сізге жұппен жұмыс істеуді және біраз зерттеу жүргізуді ұсынамын.
Шағын зерттеудің дұрыстығын тексеру:
3x +3y +m x +my көпмүшесін қарастырайық.
- Барлық терминдерде ортақ фактор бар ма?
Біз "мұқият қарау әдісін"қолданамыз. Сіз не көрдіңіз?
- Оларды топтарға біріктірейік. - Біз қандай қосу Заңын қолданамыз? ( 3x +3y ) +(m x +my) - Әр топтағы ортақ мультипликатормен не істеуге болады?
- Көбейтудің қандай Заңын қолданамыз?
3(x +y) +m (x +y)
- Қазір қанша термин шықты?
- Алынған өрнекте не қызықты болды? - Біз оны жақшадан шығарамыз. (x +y) (3 +m) - Біз не алдық? - Демек, көпмүшелік өнім түрінде ұсынылған. Қандай жолмен?
- Бұл ыдырау әдісі қалай аталады?
Топтарға бөлу: бірінші партада отырған оқушылар екінші партада отырған оқушыларға қосылады. Үшінші партаның оқушылары төртінші партаның оқушыларына қосылады және әр қатарда.
Топтық жұмыс: көпмүшенің көбейткіштерге ыдырау алгоритмін жасаңыз. Алгоритмдердің құрастырылған нұсқалары тыңдалады. Содан кейін олар түзетіледі. Осылайша, алгоритм моделі, оны талдау, нақтылау жасалады.
Соңғы нұсқа: а) ортақ мультипликаторы бар терминдерді топтастыруды орындау; |
Оқушылар өз пікірлерін білдіреді
Өз тұжырымын айтады
ҚБ: Бес бармақ
Оқушылар топтық жұмыс жасайды
ҚБ: Бес бармақ
Оқушылар сұраққа жауап береді
|
ҚБ: Шарлар
Әр сұрақ – 1 балл
Мадақтау |
Слайд, оқулық, интерактивті тақта, графиктер, сызбалар, |
||
|
Үйге тапсырма беру |
Кері
байланыс: Үйге тапсырма: Өткенді қайталап тестке дайындалып кел |
Күнделікке үй тапсырмасын жазады. |
|
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Тест тапсырмалары. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушылардың алған білімдерін тексеру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
І. Ұйымдастыру
кезеңі. Психологиялық сәт.
|
|
|
Интерактивті тақта, оқулық. |
|
Жаңа білім 15 мин 2 мин Бекіту 15 мин |
1 – нұсқа 1. Көпмүшені көбейткіштерге бөлу процесі қалай аталады? а) факторизация б) интеграция в) дифференциация 2. Төмендегі функциялардың қайсысы қуат функциясы болып табылады? а) f(x) = 2x + 3 б) f(x) = x^2 + 1 c) f(x) = sin(x) 3. Оң көрсеткішті дәрежелік функцияның графигі қандай болады? а) ұлғайту б) төмендеу в) түзу 4. Қай теңдеу квадрат болып табылады? а) 2х + 3 = 0 б) x^2 + 4x + 4 = 0 в) 3x - 1 = 5 5. Екі түрлі нақты түбір болса, квадрат теңдеудің дискриминанты неге тең болады? а) теріс б) нөл в) оң 6. Арифметикалық прогрессия дегеніміз не? а) әрбір элемент алдыңғысынан бірдей санға артық болатын тізбек б) әрбір элемент алдыңғысынан берілген санға артық болатын реттілік в) әрбір элемент алдыңғы екі элементтің қосындысы болатын тізбек 7. 2, 6, 18, ... геометриялық прогрессиясында келесі сан қандай болады? а) 24 б) 54 в) 36 8. Қандай формула арифметикалық прогрессияның алғашқы n мүшесінің қосындысын табуға мүмкіндік береді? а) Sn = n(a1 + an) / 2 б) Sn = 2n + 5 c) Sn = n(a1 + d) 9. Квадрат теңдеудің түбірлерін табу процесі қалай аталады? а) рационалды кеңейту б) қайталау әдісі в) шешім 10. Квадрат теңдеудің қанша түбірі болуы мүмкін? а) 1 б) 2 3-те 2 – нұсқа Тақырыбы: Көпмүшені көбейткіштерге бөлу 1. Көпмүшені көбейткішке бөлгенде қалдықтың дәрежесі қандай болады? а) Көбейткіштің дәрежесінен кем немесе оған тең б) Көбейткіштің қуатынан артық в) Көбейткіштің дәрежесіне тең 2. Көпмүшені көбейткішке бөлудің нәтижесі қандай болады? а) Қалдық + бөлім ә) Қалдық – бөлінді в) Қалдық * факторы Тақырыбы: Дәреже функциясы, оның қасиеттері және графигі 3. График (1, 2) нүктесі арқылы өтетін болса, дәреже функциясының дәрежесі қандай? а) 1 б) 2 в) 3 4. Дәрежесі өскен сайын дәреже функциясының графигі қалай өзгереді? а) Оңға қарай жылжиды б) Солға жылжиды в) өзгермейді Тақырыбы: Квадрат теңдеулерді шешу 5. Квадрат теңдеудегі дискриминант дегеніміз не? а) х^2 коэффициенті b) x кезіндегі коэффициент в) Түбір санын анықтайтын коэффициент 6. Квадрат теңдеудің түбірін табу формуласы қандай? a) x = (-b ± √(b^2 - 4ac)) / (2a) b) x = (-b ± √(b^2 + 4ac)) / (2a) c) x = (-b ± √(b^2 - ac)) / (2a) Тақырыбы: Арифметикалық және геометриялық прогрессиялар 7. Қандай қадам арифметикалық прогрессияның сипаттамасы болып табылады? а) Элементтер арасындағы айырмашылық б) Барлық элементтердің қосындысы в) Барлық элементтердің туындысы 8. Геометриялық прогрессияның n элементінің қосындысын табу формуласы неге ұқсайды? a) S_n = a * r^n ә) S_n = a * (1 - r^n) / (1 - r) в) S_n = a + (n - 1) * d 9. Геометриялық прогрессия өзінің соңғы шегіне қашан жиналады? a) Тек 0 < r < 1 үшін b) Тек r > 1 үшін c) кез келген r мәндері үшін 10. Геометриялық прогрессияның тізбекті мүшелері арасында қандай байланыс бар? а) a_n = a_1 + (n - 1) * d б) a_n = a_1 * r^(n-1) c) a_n = a_1 * n^(n-1) |
|
|
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: Өткен тақырыптарды қайталау |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Рационал теңдеулер мен теңсіздіктерді шешу. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушыларға рационал теңдеулер мен теңсіздіктерді шешудің негізгі әдістерін үйрету; Оқушыларда алгебралық және бөлшек-рационал өрнектерді бірдей түрлендіру дағдыларын қалыптастыру; Оқушыларда қолданбалы есептерді шығаруда алған білімдерін қолдана білу дағдыларын дамыту; Оқушылардың логикалық және аналитикалық ойлауын, сонымен қатар математикалық мәтінмен жұмыс істеу қабілетін дамыту; |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың барысы |
Мұғалімнің іс- әрекеті |
Оқушының іс-әрекеті |
бағалау |
ресурстар |
|
Сабақтың басы
|
І. Ұйымдастыру кезеңі. Психологиялық ахуал. Сәлемдесу, түгелдеу.
|
Психологиялық ахуалға берілген психогиялық жаттығуларды орындау арқылы жаңа сабаққа назар аудару. |
|
Оқулықтар суреттер, кестелер, |
|
Сабақтың ортасы
|
Сұрақтарға жауап беру: 1. Қандай теңдік теңдеу деп аталады? 2. Қай теңдеу квадрат деп аталады? 3. Теңдеуді шешу деген нені білдіреді? 4. Дискриминантты табу формуласы? 5. Қандай теңдеулер толық емес деп аталады? 6. Қандай жағдайда квадрат теңдеудің екі түбірі болады? 7. Қандай жағдайда квадрат теңдеудің бір түбірі болады? 8. Қандай жағдайда квадрат теңдеудің түбірі болмайды? 3. Ауызша санау (тапсырманы экранда көрсету) 3.1. Теңдік дұрыс жазылған ба? Х*18=34 14х=56 2:(х-3)=4
3.2. Теңдеуді шешіңіз: 0*x=0 5x=0 2x-4=2x
3.3. Теңсіздіктерді шеш: X - 2 > 0 X+4 <0 2x<4 X - 5 ≥ 0 X+4≤0 Ауызша есептің соңында сызықтық теңдеулердің бір түбірі, түбірі жоқ немесе олардың шексіз саны болуы мүмкін екеніне назар аударыңыз. Квадрат теңдеулердің екі түрлі түбірі, екі бірдей түбірі болуы немесе түбірі болмауы мүмкін. 3.4. Формула бойынша белгісізді өрнектеңіз: V=? егер S=V*t I=? егер P= I^2*K R=? егер Q=F^2*R*t R_6 =? егер F_1*5 +q*\frac{6}{2} - R_6=0 N_2=? егер N_2*sin30°-C_1=0 t =? егер a=\frac{V-V_0}{t} A=? егер N= \frac{A}{t} V=? егер E= \frac{mV^2}{2}
Топтық жұмыс Топпен жұмыс істеу үшін оқушылардың көпшілігі орындай алмаған тақтадағы тапсырманы орындауға болады. 4. рационал теңдеулер емес
X(x+1) ≠ 0 X+1=0 X ≠ -1 2x+5-2x-2-3 -
3 3-3 -3
|
Оқушылар жаңа сабақты меңгереді
Өз топтарының атынан пікірлерін айтады ҚБ: Екі жұлдыз, бір тілек
Топтық жұмыс жасайды
ҚБ: Шарлар
|
Оқушылар теңдікпен жұмыс жасайды
Теңсіздіктерді шеше алады
|
Интербелсенді тақта, тар, оқулық, жұмыс дәптерлері
|
|
Соңы 10 минут
|
Кері байланыс
Үйге тапсырма беру: келесі есептерді шешіп кел а)4 б) в) г) a) 5(x – 1)+7≤1 – 3(x+2) б)4(a+8) – 7(a – 1)<12 в) (x -2)(x – 5)(x – 12)>0 г) |
Оқушылар мұғаліммен кері байланыс жасайды |
|
Кері байланыс тақтай шасы. |
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Иррационал теңдеулер |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Иррационал теңдеу түсінігін зерттеп, оны шешудің әртүрлі жолдарын қарастырыңыз. Иррационал өрнектерді талдау және түрлендіру қабілеттерін дамыту. Түрлі түрдегі иррационал теңдеулерді шешу дағдыларын дамыту. Математикалық ой-өрісіңізді кеңейтіп, оқытылатын материалға деген қызығушылықты арттырыңыз. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың барысы |
Мұғалімнің іс- әрекеті |
Оқушының іс-әрекеті |
бағалау |
ресурстар |
|
Сабақтың басы 10 минут
|
І. Ұйымдастыру кезеңі. Психологиялық ахуал. Сәлемдесу, түгелдеу.
Өткен сабаққа шолу |
Психологиялық ахуалға берілген психогиялық жаттығуларды орындау арқылы жаңа сабаққа назар аудару. |
Әр дұрыс жауапқа 1 балл
|
Оқулықтар суреттер, кестелер, |
|
Сабақтың ортасы 20 минут
|
Қалыптасқан нәтижелер мен сабақтың мақсаттарын қою. Оқушылардың оқу әрекетіне мотивация - Экранда сіз теңдеулерді көресіз. Мұқият қарап, қандай теңдеулерді шешуді білетініңізді және қайсысы қиын екенін анықтаңыз?
-Өздеріңізге таныс теңдеу түрлерін атаңыздар? Жауабы: квадраттық, сызықтық, бөлшек рационал. Қорытынды: Сіз әлі шеше алмайтын теңдеулер бар. – Бұл теңдеулердің жазылуы біз атаған теңдеулерден несімен ерекшеленеді? Жауабы: белгісіз түбір белгісінің астында. - Дұрыс! Түбір белгісінің астында айнымалысы болатын мұндай теңдеулер иррационал теңдеулер деп аталады. Иррационалдық (латын тілінен Irrationalis – ақылға қонымсыз, бейсаналық) – логикаға қайшы, парасаттылық шегінен тыс нәрсе. Әдетте ұтымдыға парасатты, орынды, негізделген ретінде қарама-қарсы қойылады. Олай болса, сабағымыздың тақырыбы «Иррационал теңдеулер». - Бүгін біз иррационал теңдеудің анықтамасымен танысамыз және иррационал теңдеулерді шешудің әртүрлі әдістерін қарастырамыз. Жаңа материалды меңгеру - «Иррационал теңдеулер» сабағының тақырыбын дәптерлеріңе жазып алыңдар. Анықтамасы: Айнымалысы түбір (радикал) белгісінің астында болатын теңдеулер иррационал деп аталады.
Экранда иррационал теңдеулердің мысалдарын көресіз:
- Экранда сіз үш теңдеуді көресіз «ШЕШУГЕ ОҚЫТАЙЫҚ», оларды шешіңіз. Содан кейін шешімдеріңізді менімен бірге тексеріңіз, ол келесі слайдта болады «ӨЗІҢІЗДІ ТЕКСЕР».
Бекіту: Төмендегі теңдеулерді өзіңіз шешіңіз.
- Енді интерактивті тақтадағы шешімдермен өз шешімдеріңізді тексеріңіз.
|
Оқушылар жаңа сабақты меңгереді
Шілікті және Бесшатыр қорғандарының ортақ белгілерін ашады • Шілікті және Бесшатыр қорғандарының ерекшеліктерін анықтайды
археологиялық олжалардың айрықша белгілерін анықтайды.
Топтық тапсырмаларды орындайды. Оқушылар алған білімдерін практикалық тұрғыда көрсетеді |
Оқушылар концептуалды ойлау мен тың байланысын біледі Мадақтау
«патша қорғандарының» салыну себептеріне дәлел келтіріңіз
Салыстыру сызықтарын анықтай алады
Шілікті және Бесшатыр қорғандарын салыстыра отырып, олардың ұқсастықтары мен айырмашылықтарын табады ҚБ: сэндвич
|
Оқулықтар суреттер, слайд Кестелер Сызғыш қарындаштар Қайшы Қағаздар, плакаттар, , интербелсенді тақта
|
|
Соңы |
|
Оқушылар мұғаліммен кері байланыс жасайды |
|
Кері байланыс тақтай шасы. |
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Комбинаторикадан көбейту әдісі бойынша олимпиада тапсырмалары |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Комбинаторика бойынша олимпиада тапсырмаларын шешу әдістерін меңгеру. Оқушылардың логикалық және сыни ойлауын дамыту. Оқушылардың математиканы оқуға деген қызығушылығын арттыру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақ барысы |
Оқытушының іс- әрекеті |
Оқушының іс- әрекеті |
Бағалау |
ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Сәлемдесу, түгелдеу |
Оқушылар ойын ойнайды
|
Формативті бағалау үнемі жүргізіліп отырады. |
Оқулықтар суреттер, слайдтар кестелер |
|
Сабақтың ортасы 20 минут |
Аксиома – дәлелі аз ақиқат. В. Хмурый Хмурыйдың аксиома жайлы қанатты сөзіне назар аударыңыздар, бұнымен Хмурый не айтқысы келді? «Ребус» мотивациялық кезең - Сабақтың тақырыбын түсіну
үшін жұмбақ шешіңіз: Логика ең түсініксіз математикалық есептерді шешуге көмектеседі! -Бүгін сабақта комбинаторика есептерін көбейту әдісі арқылы шығаруды үйренеміз. - Комбинаторика – берілген ережелер бойынша құрастырылған бастапқы жиыннан элементтерді таңдау және оларды белгілі бір комбинацияда орналастыру есептері зерттелетін және шешілетін математика саласы. - Мұғалім сабақтың мақсатын түсіндіреді және «Олимпиада есептерін шығарудың комбинациялық әдістері» тақырыбын жариялайды. - Мұғалім комбинаторлық әдістерді өмірде қолдану туралы сұрақтар қою арқылы оқушылардың алдыңғы білімдерін белсендіреді. - Мұғалім негізгі комбинаторлық әдістермен таныстырады: ауыстыру, комбинация, орналастыру. - Мұғалім әрбір әдіске мысал келтіріп, олимпиада есептерін шығаруда қолдануды түсіндіреді. - Мұғалім комбинаторлық
әдістерді қолдану арқылы шығарылатын қарапайым есептерді
көрсетеді. Мен комбинаторикадағы бірінші мәселені шешуді ұсынамын: 1-міндет. Әр түрлі сандармен жазылған Үш таңбалы сандар 6, 7, 8 сандарынан қанша тұрады? Мәселені шешуді талдау 1: - Үш санның кез келгені жүздеген санатта тұра ала ма? (үш сан болуы мүмкін) - Қалған екі санның кез келгені ондаған санатта болуы мүмкін? (екі сан болуы мүмкін) - Бірлік санатында қалған бір ғана сан болуы мүмкін? (иә, бір) - Демек, үш сан жүздеген болуы мүмкін; ондықтар санатындағы екі сан және бір Сан санатындағы бір Сан. - Нұсқалардың санын қандай әрекетпен санауға болады? (көбейту арқылы) - Үш таңбалы сандардың мүмкін болатын санын қалай санауға болады? (3 x 2 x 1). - 6, 7, 8 сандарынан әртүрлі сандармен жазылған неше үш таңбалы сандарды жасауға болады? - Барлығы 6 Үш таңбалы сан алынады. - Нақты өмірде қажет комбинаторикаға 2 мәселені шешуге тырысайық: Тапсырма 2. Сәрсенбі күні 3 «М» сыныбында бес сабақта бес түрлі пән бар. Сынып жетекшісі 3 «М» сыныбының сәрсенбі күнінің кестесін неше түрлі жолмен құруы мүмкін? 2 есептің шешімін талдау: - Бірінші сабақ бес пәннің кез келгені болуы мүмкін бе? - Қалған төрт пәннің кез келгені екінші сабақта бола ала ма? - Қалған үш пәннің кез келгені үшінші сабақта бола ала ма? - Төртінші сабақта - қалған екі пәннің қайсысы? - Бесінші сабақта қалған бесінші пән оқытылады. - Опциялардың санын қалай санауға болады? (көбейту арқылы) – Сондықтан сәрсенбінің кестесін 120 тәсілмен жасауға болады. (5x4x3x2x1) - Үшінші комбинаторика есебін мектеп өмірінен көбейту әдісі арқылы шығарамыз: 3-тапсырма.Ағылшын тілі сабағына алты бала келді. Олар қос партаға неше түрлі жолмен жұптасып отыра алады? 3 есептің шешімін талдау: - Сол жақтағы бірінші партаға неше түрлі бала отыруға болады? (алты түрлі бала) -Оң жақтағы бірінші партаға қалған балалардан неше түрлі бала отыра алады? (бес түрлі бала) -Қалған балалардың сол жағындағы екінші партаға неше түрлі бала отыруға болады? (төртеуі отыра алады) -Қалған балалардың оң жағындағы екінші партаға неше түрлі бала отыруға болады? (үшеуі отыра алады) - Қалған балалардың сол жағындағы үшінші партаға неше түрлі бала отыруға болады? (екеуі отыра алады) - Қалған балалардың оң жағындағы үшінші партаға неше түрлі бала отыруға болады? (жалғыз отыруға болады) - Опциялардың санын қалай санауға болады? (көбейту арқылы) - Бұл есепті шешу үшін қандай өрнек қолдануға болады? (6x5x4x3x2x1) - Сабақта алты баланы отырғызудың неше түрі болуы мүмкін? (720) «Жалпы әдісті модельдеу» -Бүгін біз қандай мәселелерді шештік? - Математиканың бұл бөлімі қалай аталады? (комбинаторика) - Бұл тапсырмалардағы нұсқалардың санын қалай санауға болады? (көбейту арқылы) -Егер n есептердегі варианттардың (элементтердің) саны болса, онда комбинаторлық есептерді көбейту әдісімен шешу формуласы қандай болуы керек? n x (n-1) x (n-2) x (n-3) x ..., соңғы көбейткіш бірге тең болғанша көбейтіңіз. - Жарайсың! |
Оқушылар жаңа сабақты меңгереді Оқушылар комбинаторка не екенін меңгереді |
Әр дұрыс жауап 1 балл Мадақтау Қол шапалақтау
|
Слайд, оқулық |
|
Сабақтың соңы |
Үйге тапсырма: Ықтималдық теориясының формулаларын жаттап кел |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Ықтималдықтар теориясы және статистика |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Ықтималдықтар теориясының негізгі ұғымдары мен формулаларын оқып үйрену. Олимпиада есептерін шешу үшін ықтималдықтар теориясын қолдануды үйреніңіз. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақ барысы |
Оқытушының іс- әрекеті |
Оқушының іс- әрекеті |
Бағалау |
ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 5 мин |
Психологиялық ахуал қалыптастыру.
2.Жағымды көңіл-күйге келу. Тыныс алуға зейін қою. |
Психологиялық ахуалға берілген тақпақтарды дауыстап айтып, тілді жаттықтыру және жаңа сабаққа назар аудару. Оқушылар жұмысты берілген түріне қарай орындайды |
Қол шапалақтау арқылы бір бірін бағалайды |
Оқулықтар суреттер Кестелер
|
|
Сабақтың ортасы 20 минут |
Рух пен материя арасында
математика бар. Хуго Штейнхаус. Хуго Штейнхаустың қанатты сөзі
жайлы не ойлайсыздар? Жақында бір журналдан мынадай мәселені оқыдым: «Әйел мен балық ұғымдарының арасындағы арифметикалық ортаны табыңыз?» Қандай жауап бересіз? (Су перісі)
Арифметикалық орта сияқты сипаттамаларды математиканың қай саласы зерттейді? (Статистика) Сабақтан кейін мектептен шығып бара жатқаныңызды елестетіп көріңіз және клуб бақшасында терек бұтағында отырған су перісін көрдіңіз. Мен қандай оқиғаға мысал келтірдім? (мүмкін емес) Осы немесе басқа оқиғаның болуын математиканың қай саласы зерттейді? (ықтималдық теориясы) Қалай ойлайсыңдар, сабағымыздың тақырыбы қандай, егер келесіде есептер шығарудың мысалын қолдана отырып, статистикалық сипаттамалар мен кездейсоқ оқиғалардың пайда болу ықтималдығының қалай табылатынын көрсетуді сұрасам? (Тақырып бойынша жалпы сабақ: Ықтималдық және математикалық статистика) Келесі сабақта осы тақырып бойынша тест болады. Бүгін өзіңізге қандай мақсаттар мен міндеттер қоясыз? (Оқылған материалды қайталау, бекіту және жүйелеу) Негізгі білімді жаңарту. 1) Ассоциацияны қабылдау, түйінді сөз үшін ұсынылған ұғымдарды сипаттайтын сөздерді, формулаларды, фактілерді таңдаңыз. Сыныпты топқа бөлу, тақтада жұмыс жасау. Негізгі сөздер: Статистика, ықтималдық теориясы. 2) Енді оқиғалардың жіктелуін қаншалықты түсінетініңізді тексерейік. Викторина түрінде қозғалмалы үзіліс өткізейік. Түпнұсқа мобильді викторина: Оқиғалардың орын алу мүмкіндігін келесі әрекеттер арқылы бағалаңыз: «сенімді оқиға» (барлығы отырады және тұрмайды), «кездейсоқ оқиға» (қолыңызды көтеріңіз), «мүмкін емес оқиға» (тұруы керек). 1. «Ертең ауа-райы жақсы болады». (кездейсоқ) 2. «Қаңтар айында Климковкада қар жауады». (сенімді) 3. «Сағат 12-де Белая Холуницада жаңбыр жауады, ал 24 сағаттан кейін күн жарқырайды». (кездейсоқ) 4. «Туған күніңізге сөйлейтін қолтырауын аласыз». (мүмкін емес) 5. «Суға лақтырылған тас суға батады». (сенімді) 6. «Сіз ұтыс-жеңіс лотереясына қатысу арқылы ұтпайсыз». (мүмкін емес) IV.Білімді жалпылау және жүйелеу. Есептер шығару (Жұппен жұмыс) тақтада жауап береді. 1-тапсырма: Тоғызыншы сынып оқушылары математикадан тест бойынша келесі ұпайларды алды: 10, 9, 12, 6, 9, 15, 14, 14, 12, 15, 13, 13, 9, 10, 14, 14. Осы нәтижелер бойынша тестілеуден өткен оқушылардың жартысы одан әрі конкурстық тестілеуге іріктелді. Алынған сандар қатарының арифметикалық ортасын (11,81), модасын (14), медианасын (12,5) және диапазонын (9) табыңыз. Жарысқа одан әрі қатысу үшін өту балы қандай болды? (12.5) Табылған сипаттамалардың қайсысы сұраққа нақты жауап береді? «Пирамида» сөзі карточкалардан жасалған. Қай әріптік картаны салу ықтималдығы жоғары? Қандай оқиғалар бірдей ықтимал? (Барлығы 8 әріп бар. “i” әрпі 2 рет кездеседі – P = 2/8 = 1/4; “a” әрпі 2 рет кездеседі – P = 2/8 = 1/4; қалғаны 1 рет – P = 1/8 .) 3-тапсырма. Қосымша. Кездейсоқ экспериментте симметриялы монета үш рет лақтырылады. Бастардың бір рет болса да келмеу ықтималдығын табыңыз.(1/8) Ықтималдықтарды қосу және көбейту А және В екі үйлесімсіз оқиғалардың кем дегенде біреуінің пайда болу ықтималдығы Р(С) олардың ықтималдықтарының қосындысына тең. P(C) = P(A + B) = P(A) + P(B) Қарама-қарсы оқиғаның ықтималдығы: P(A) = 1 - P(A). Екі тәуелсіз А және В оқиғаларының бірігіп пайда болу ықтималдығы Р(С) А және В оқиғаларының ықтималдықтарының көбейтіндісіне тең. P(C) = P(A) P(B) Өзін-өзі бақылау. Өздік жұмыс. ҰБТ-да Ықтималдықтар теориясы бойынша тапсырмалар бар екенін білесіздер, енді мен емтиханға дайындығыңызды тексеріп, осы тақырып бойынша есептер шығару дағдыларыңызды шыңдауды ұсынамын. Мен сізге quar кодын сканерлеп, сынақтан өтуді ұсынамын. Оқиға ықтималдығының классикалық анықтамасын таңдаңыз: Оқиғаның ықтималдығы - … а) бұл оқиғаға қолайлы сынақ нәтижелері санының барлық бірдей ықтимал нәтижелер санына қатынасы. б) бұл оқиға үшін қолайсыз сынақ нәтижелерінің санының барлық бірдей ықтимал нәтижелер санына қатынасы. в) бұл барлық сынақ нәтижелерінің санының оқиғаға қолайлы нәтижелер санына қатынасы. г) бұл барлық сынақ нәтижелерінің санының оқиғаға қолайсыз нәтижелер санына қатынасы 2. Қалтадан еденге тиын түсті. "Елтаңбаның" түсу ықтималдығын табыңыз: а) 0,1 б) 0,2; в) 0,5; г) 1; |
Оқушылар жаңа сабақты меңгереді Түсіндіре отырып, сұрақтарға ауызша жауап беру. |
Мадақтау Қолшапалақтау
мадақтау |
Слайд, оқулық, |
|
Қорытынды |
Кері
байланысты Оқу тапсырмасы: Өткенді қайталап тестке дайындал |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Тест тапсырмалары. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушылардың алған білімдерін тексеру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
І. Ұйымдастыру
кезеңі. Психологиялық сәт. Қайырлы күн болсын! Сәрсенбінің күні Сәттілікке толсын! Біздің алар бағамыз Кілең бестік болсын!
|
|
|
Интерактивті тақта, оқулық. |
|
Жаңа білім 15 мин 2 мин Бекіту 15 мин |
1 – нұсқа 1. Төмендегі формулалардың қайсысы А оқиғасының ықтималдығын сипаттайды? a) P(A) = n(A)/n(S) б) P(A) = n(S)/n(A) c) P(A) = n(A) + n(S) 2. Қайталанатын цифрлары жоқ неше төрт таңбалы сан бар? а) 524 б) 3024 в) 9 3. Төмендегі теңдеулердің қайсысы иррационал болып табылады? а) x^2 = 9 б) x^2 + 4 = 0 в) √x = 5 4. 2х^2 - 3х + 1 = 0 теңдеуінің түбірі қандай? а) х = -1/2, 1/2 б) x = -1, 1 в) x = -1,1/2 5. Төмендегі теңсіздіктердің қайсысы нақты сандар жиынындағы барлық х үшін орындалады? a) x^2 + 3 > 0 б) x^2 - 5 < 0 в) x^2 + 1 < 0 6. Монетада сандардың түсу ықтималдығы қандай? а) 1/2 б) 1 в) 0 7. «ШАР» сөзінің әріптерінен неше түрлі үш әріпті сөз жасауға болады? а) 6 б) 15 в) 24 8. Төмендегі теңдеулердің қайсысы иррационал болып табылады? а) 3х - 5 = 0 б) x^2 = 16 в) x = 2 9. x^2 - 9 = 0 теңдеуінің түбірі неге тең? а) x = -3, 3 б) x = -3,9 в) x = -3,6 10. Төмендегі теңсіздіктердің қайсысы барлық x < -3 үшін орындалады? a) x^2 - 4 > 0 б) x^2 + 5 < 0 c) x^2 + 1 > 0 2 – нұсқа 1. Оқиғаның ықтималдығы 0,8. Қарама-қарсы оқиғаның болу ықтималдығы қандай? (а) 0,2 (b) 0,5 (c) 0,8 2. 10 емтихан нәтижесінің орташа арифметикалық мәні 4,5-ке тең. Тағы 5 нәтиже қосқаннан кейін арифметикалық орта 3,5 болды. Қосылған нәтижелердің көлемі қандай? (а) 10 (b) 15 (c) 25 3. «КОМБИНАТОРИКА» сөзінің әріптерінен неше түрлі сөз жасауға болады? (а) 120 (b) 240 (c) 360 4. 10 адамнан тұратын топта сіз президентті, вице-президентті және хатшыны таңдауыңыз керек. Мұны қанша жолмен жасауға болады? (а) 720 (b) 900 (c) 1120 5. √(x - 3) = 5 теңдеуін шешіңіз: (а) x = 8 (b) x = 28 (c) x = 38 6. √(x + 2) - √(x - 5) = 1 теңдеуінің түбірін табыңыз: (а) x = 1 (b) x = 6 (c) x = 11 7. Теңдеуді шешіңіз: (3х - 5)/(4х + 7) = 5/9 (а) x = 1/4 (b) x = -1/4 (c) x = 1 8. Теңсіздікті шешіңіз: x^2 - 5x + 6 >= 0 (a) (-∞; 2] U [3; ∞) (b) [-2; 3] (c) (2; 3) 9. Төмендегі теңдеулердің қайсысының [0, π] интервалында екі шешімі бар? a) sin(x) = 0 б) sin(x) = 1 c) sin(x) = -1 10. Төмендегі теңдеулердің қайсысының жалғыз бүтін шешімі бар? а) (х - 1) / 2 = 3 б) (x + 2) / 5 = 4 в) (x + 3) / 7 = 2 |
|
|
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: Ньютон Биномы жайлы ақпарат жинап кел |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Ньютонның Биномы. Паскаль Үшбұрышы |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Ньютон биномымен және оның әртүрлі есептерді шығаруда қолданылуымен танысады. Формулалар мен теңдеулермен жұмыс істеу дағдыларын дамыту. Олимпиада есептерін шығару үшін Ньютон биномдық жүйесін қолдануды үйреніңіз. Ньютон биномы мен Паскаль үшбұрышын зерттеу. Логикалық және аналитикалық ойлауды дамыту. Математикалық есептерді шешу үшін алынған білімді қолдану. Жалпы математика мен ғылымдарды оқуға деген қызығушылықты арттыру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақ барысы |
Оқытушының іс- әрекеті |
Оқушының іс- әрекеті |
Бағалау |
ресурстар |
|
Сабақтың басы 5 минут |
Ұйымдастыру кезеңі Ұйымдастыру кезеңі
|
Оқушыларды сабаққа дайындау. Топқа бөлініп отырады Оқушылар ойын ойнау арқылы серпіліп қалады. |
Формативті бағалау үнемі жүргізіліп отырады. Гүлдердің суреттерін тарату арқылы бағалау жүргізіледі
|
Оқулықтар суреттер, слайдтар Кестелер,
|
|
Сабақтың ортасы 20 минут |
Біздің сабағымыздың тақырыбы " Бином Ньютон. Паскаль Үшбұрышы". Бүгін сабақта біз өткен материалды қорытындылап, қайталауымыз керек. Биномдық формулаларды қолдануда алынған білім мен дағдыларды математикалық есептерді шешуге бекітеміз. Сабақ барысында біз топтарда жұмыс істейміз, содан кейін сабақты қорытындылаймыз және сіз үй тапсырмасын аласыз. 1. Кроссвордты шешіңіз. 1. Мономиалды көпмүшеге
көбейту кезінде қолданылатын көбейту қасиеті. 2. Көпмүшені
көбейткіштерге бөлу тәсілі. 3. Теңдеу дұрыс теңдікке айналатын
айнымалының мәні. 4.Айнымалылардың кез-келген мәндеріне сәйкес
келетін теңдік. 5. Мономиалдардың қосындысы болып табылатын өрнек.
6. Бір әріптік бөлігі бар терминдер. 7. Сандық мультипликатор ж o
мономиалдар. Жауаптары: Тарату Топтар Түбір Жеке басын куәландыратын Көпмүшелік Ұқсас Коэффицент Көбейтіндіні көпмүшемен ауыстырыңыз,
нәтижесінде алынған сәйкестік теңсіздік
болады
- Бұл тапсырмада қандай формулаларды қолдандың? Олардың атын атап, тұжырымдап көрейік. 1. Екі өрнектің қосындысы мен айырмасының квадратының формулалары 2. Шаршы айырымының формуласы 3. Кубтардың қосындысы мен айырмасының формулалары 4. Дәреженің қасиеті. Жаңа материалды түсіндіру Қысқартылған көбейту формулалары Ньютон биномының ерекше жағдайы болып табылады. Бүгін сабақта біз алған білімімізді жинақтап, осы формулалармен танысамыз. Ньютон биномының формуласы. Екі терминнің қосындысын N дәрежесіне қалай көтеруге болады? Исаак Ньютон өз заманының нағыз ұлы физигі, мүмкін барлық уақыттар мен халықтардың ең ұлы физигі болған. Бірақ біз оны бағаламаймыз. Алайда, Ньютонның да керемет математик болғанын атап өткен жөн. Айтпақшы, Ньютонның Бином формуласы сол кездегі қазіргі заманның ең үлкен ашылуы ретінде оның қабірінің құлпытасына ойып жазылған! Ньютонның Бином формуласынан басқа, мектеп орындығынан Ньютон-Лейбниц формуласы бәріне белгілі. Осылайша, ұлы Ньютон Лейбницпен бірге дифференциалдық және интегралдық есептеулердің негізін қалады. Шектер теориясының негіздері және математикалық талдаудағы қатаң көзқарас Августин Коши, Георг Кантор, Карл Вейерштрасс сияқты данышпандардың еңбектерінде басталды және дамыды. Әрине, Леонард Эйлердің есімін айналып өту мүмкін емес. Бірақ біз мұнда негізгі ойлау сызығынан алшақтадық. Өйткені, Ньютон биномының формуласы алгебраға, сондай-ақ комбинаторика деп аталатын математика саласына қатысты!
Мысалы - бұл мағына көпмүше Ал екі мүшенің қосындысы Бин деп
аталады! Яғни Ньютон екі мүшенің қосындысын 2-ге тең
көрсеткішпен ғана емес, кез келген көрсеткішпен дәрежеге көтеруге
мүмкіндік беретін формуланы ойлап тапты! Ньютон биномының
формуласының мәнін асыра бағалау мүмкін
емес функциялардың шектерін
шешу. Сондықтан,
дұрыс,
бұл жерде қарастырылып отырған формула биномның дәрежесі үшін Ньютон формуласы деп аталады.
Біз бұл формуланы бірден жалпы түрде жазбаймыз,
алдымен мектеп алгебрасына жүгінеміз!
Бұл қосынды квадратының формуласы немесе биномның квадратының формуласы немесе биномның екінші дәрежесінің формуласы! Ал енді екі мүшенің қосындысын үшінші дәрежеге көтереміз немесе үшінші дәрежелі биномды ашамыз. Жақшаларды алгебраның үлестірімділік немесе үлестірімділік заңын әдеттегідей қолданатындай етіп кеңейтеміз:
Мұнда бізде қазірдің өзінде алты термин бар, дәлірек айтсақ, алты емес, 8 = 23 қосылғыштардың, өйткені екі қосылғыштың коэффициенттері 2-ге тең.
Біз
текшелердің қосындысының формуласын дәлелдедік. Ол сізге мектептегі
алгебра курсынан жақсы таныс болуы керек.
Бұл
жерде біз жақшалардың егжей-тегжейлі кеңейтімдерін жасауды
бастамадық, бірақ кеңейту нәтижесін бірден жазып алдық, өйткені
есептеулер мұны екі рет жасағанымызға ұқсас.
Яғни, биномның төртінші дәрежесінің орнына біз оның бұрын есептелген өрнегін алмастырамыз және жақшаларды қайтадан ашамыз, егжей-тегжейлі есептеулерді қалдырамыз, өйткені олар биномның үшінші және екінші дәрежелерін есептеу кезінде жоғарыда бірнеше рет орындалған.
Сіз сұрайсыз: биномды тұрғызу дәрежесінің ретін осылай көбейтуді қаншаға жалғастыра беруге болады? Жауап: шексіздікке дейін мүмкін! Сол сияқты, мысалы, n=100 болғанда, нәтижені көбейтеміз бойынша 99 дәрежесіне көтеру x+y, сонда біз 100-ге дәрежелеудің нәтижесін аламыз.
Бірақ біз бұл өрнектің барлығын боямаймыз,
өйткені мұндай терминдерді келтіргеннен кейін оның 101 термині
болады және бір жолға сыймайды, ал он жолға оқу өте қиын
болады!
Мұнда біз қарапайым және тапқыр қорытынды жасаймыз: формуласын алу үшін n, үшін осы формуланы білу қажет (n-1). Формуласын білу үшін (n-1) оны алу керек (n-1) біз 2,3,4 және 5-ші дәрежелер үшін жасағандай рет, яғни дәреже үшін бұрыннан белгілі нәтижені берілген дәрежеден кіші бірлікке бірлікке тең дәрежеге көбейттік! Ал енді екінші данышпан қорытынды өзін көрсетеді! Ал егер n-1 дәрежесінің биномдық формуласына әкелетін осы әрекеттердің барлығын бір сәтте жазуға болатын болса ше?! Сонда қайта жазбауға болады (n-1) бір рет іс жүзінде бірдей есептеулер үшін 2, 3, 4, 5, 6,..., биномның n-1 дәрежесі, және оларды бір формуламен жазып, осы формуланы биномның бірінші дәрежесіне тағы бір рет көбейтіп, қажетті формуланы толығымен дәлелдеңдер! Міне, сізде Ньютонның пайымдау алгоритмі бар! Мұнда біз соңғы сөйлемдерді қарамен жаздық, өйткені олар Ньютон биномының формуласын дәлелдеуге негіз болып табылады және біздің барлық пайымдауларымыздағы ең маңызды және күрделі қадам болып табылады. Айтпақшы, бұл қадам индуктивті, ал индуктивті қадамға негізделген әдіс математикалық индукция әдісі деп аталады. Осылайша, біз мұнда математиканың ең іргелі және маңызды әдістерінің бірімен таныстық. Бірақ енді келесі қиындық туындайды: биномның n-1-ге тең дәрежесінің жалпы формуласын қалай жазуға болады? Бұған биномның 3,4 және 5-ке тең дәрежелерінің дәлелденген формулалары көмектеседі.
Биномды дәрежеге көтеру кезінде коэффициенттерді комбинациялар арқылы есептеу өте көп еңбекті қажет ететіндігімен келісіңіз. Бұл есептеулерді жеңілдету үшін мыналарды пайдаланыңыз:
Паскаль үшбұрышы 0 1 1 1 1 2 1 2 1 3 1 3 3 1 4 1 4 6 4 1 5 1 5 10 10 5 1 6 1 6 15 20 15 6 1 … … № Паскаль үшбұрышы 0
1
2
3
4
5
6
Паскаль үшбұрышын құрайтын сандар биномдық коэффициенттер болғандықтан, Паскаль үшбұрышын басқа түрде қайта жазуға болады: 4 Бастапқы бекіту Ньютон биномы мен Паскаль үшбұрышын пайдаланып формуланы жалғастырыңыз.
1/27a³+1/3a²∙2/5b+a∙4/25b²+8/125b³ Жауап: 1/27a³+2a²b/15+4ab²/25+8b³/125
0,8a∙0,027b³+0,0081b4 Жауабы: 0,0016а4-0,0096а³b+0,0216a²b²-0,0216ab³+0,0081b4 3. (1/2a-3/4b)³=(1/2a)³-3(1/2a)²∙3/4b+3(1/2a)(3/4b)²-(3/4b)³= =a³/8-3/8a²∙3/4b+3/2a∙9/16b²-27/64b³= a³/8-9a²b/32+27ab²/32-27b³/64 Жауап: a³/8-9a²b/32+27ab²/32-27b³/64 Оқытушы оқушылардың көмегімен тақтада шешеді. |
Жаңа сабақты меңгереді елдің және хронологиялық шеңберді анықтайды; - контурлық картада Ғұн мемлекетінің бастапқы аумағын көрсетеді; - сұрақтарды дұрыс құрастырады; - өз пікірін білдіре отырып, сұрақтарға жауап береді; |
Гүлдердің тарату арқылы
бағалау жүргізіледі |
Слайд, оқулық, Оқулықтар суреттер, Кестелер, |
|
Соңы
|
Кері байланыс
|
Оқушылар мұғаліммен кері байланыс жасайды |
|
Кері байланыс тақтай шасы. |
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Теңдеулерді пайдаланып сөздік есептерді шығару |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Теңдеулерді қолданып сөздік есептерді шығаруға үйрету. Математикалық ойлау қабілеттерін дамыту. Негізгі математикалық ұғымдар туралы түсінігіңізді арттырыңыз. Есептерді шығару нәтижелерін талдауға және түсіндіруге үйрету. Математикаға ғылым ретінде қызығушылықты арттыру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақ барысы |
Оқытушының іс- әрекеті |
Оқушының іс- әрекеті |
Бағалау |
ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Психологиялық ахуал қалыптастыру.
|
Оқушыларды сабаққа дайындау.оқушылар қимыл қозғалысын жасап көңілдерін көтереді |
Формативті бағалау үнемі жүргізіліп отырады. |
Оқулықтар суреттер, слайдтар Кестелер, |
|
Сабақтың ортасы 20 минут |
Ол ақын болып кетті, математик
болу үшін фантазиясы жетпей қалды. Давид Гильберт. Давидтың қанатты сөзіне
назар аударыңыздар. Давид не айтқысы келді?
Сызықтық теңдеулерді қолданып сөздік есептерді шығаруда негізгі білім мен дағдыларды пайдалана отырып, сабақтың тақырыбын ашады. Біз осындай мәселелерді шешуде осы кезеңдердің барлығын көрсетеміз. 1. Есепте сипатталған жағдайдың математикалық моделін құрастыру 2. Математикалық модельмен жұмыс 3. Негізгі сұраққа жауап Сабақтың тақырыбын түсіну үшін келесі тапсырманы қарастырыңыз: Тапсырма. Бір қорапта екіншісінен 3 есе көп алма болды. Бірінші жәшіктен екіншісіне 4 килограмм алманы ауыстырғанда екі жәшіктегі алманың массасы бірдей болып шықты. Алдымен әр қорапта неше килограмм болды? • Берілген: • II-Xkg. • I- 3Xkg. • (3X-4) бірінші қорапта • (X+4) екінші ұяшықта • X-? Шешімі: 3x-4=x+4 3x-x=4+4 2x=8 X=8:2 X=4 Жауабы: бірінші қорапта 12 кг алма, ал екінші қорапта 4 кг алма болды. 1-қосымша 1-тапсырма. Бірінші учаскеде таңқурай бұталары екіншісіне қарағанда 3 есе көп болды. Бірінші учаскеден екіншісіне 20 бұта көшіргенде екі учаскеде де саны бірдей болды. Басында әр учаскеде қанша таңқурай бұталары болды? 2-тапсырма. Шідерта мен Нұраның ұзындығы қосылып 1480 шақырым. Нұра Шідертадан 476 шақырым ұзын. Шідерта мен Нұраның бөлек ұзындығы қанша? Тақтаға бір оқушыны шақырып, тапсырманың толық шешімін жазуын сұраңыз. Оқушылар барлық мысалдарды орнында шешеді және сыныптастарын мұқият тыңдай отырып, тақтадағы жазбалар арқылы шешімдерін тексереді. Математикалық сөйлеуді дамыту үшін оқушылардың бірінен кез келген тапсырманың шешіміне егжей-тегжейлі түсініктеме беруін сұраңыз, олардың назарын шешімдердің негіздемесіне аударыңыз. Оқушыларға тапсырмаларды орындауға жеткілікті уақыт беріңіз. Жауаптардың дұрыстығын тексеріп, қателерін талда. Тапсырмалар бойынша оқушылардың қорытындыларын тыңдау. ОнлайнМектепте тапсырмаларды орындаймыз. |
Оқушылар жаңа сабақты меңгереді
|
|
Слайд, оқулық |
|
Қорытынды
|
Кері
байланысты Оқу тапсырмасы: «Өздік жұмыс: сөздік есептерді теңдеумен шешу» тақырыбына презентация дайындау |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
Қорытынды 5 мин |
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Логарифмдер және оның қасиеттері |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушыларды логарифм ұғымымен таныстыру, логарифмдердің негізгі қасиеттерін математикалық есептерді шығаруда қолдана білуге үйрету. Логикалық ойлауды, ақпаратты талдау және қорытындылау қабілетін, сонымен қатар есептеу дағдыларын дамыту. Математикаға деген қызығушылықтарын арттыру, өз бетімен жұмыс істеу дағдыларын дамыту, топпен жұмыс істеуге дағдыландыру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Сәлемдесу, түгелдеу |
Оқушылар ойын ойнайды
|
Формативті бағалау үнемі жүргізіліп отырады. |
Оқулықтар суреттер, слайдтар кестелер |
|
Сабақтың ортасы 20 минут
|
Мұғалім сұрақтар қояды: 1) Диплом дегеніміз не; дипломның негізі неде; Көрсеткіш дегеніміз не? 2) Дәрежелердің негізгі қасиеттерімен жұмыс. Теңдіктердегі дәрежелер арасындағы қатынасты қарастырыңыз
3) Мысалдарды ауызша
шешу: Логарифмдердің негізгі қасиеттері Бұлар қасиеттері көрсеткіштік функцияның логарифмін және қасиеттерін анықтаудан туындайды.
Кез
келген а > 0 (а) кезінде 1) және кез келген оң x және y теңдіктері орындалады:
кез келген жарамды p үшін. Мысалдарды ауызша шешу. X табу
Ондық және натурал логарифмдер Тәжірибеде логарифмдер әртүрлі негіздер бойынша, атап айтқанда 10-негіз бойынша қарастырылады.
Оң санның логарифмі
бойынша
Мысалға, Натурал логарифммен (белгіленеді In) деп аталады логарифм негізі бойынша e
Ондық логарифмдерді есептеу мысалдары
Логарифмнің бір
негізінен екіншісіне өту формулалары Нал тәжірибеде логарифм әртүрлі негіздер бойынша
қарастырылады. Осыдан бір негізден екінші негіз бойынша логарифмге
өту формуласының қажеттілігі туындайды. Өрнектерді жеңілдету:
a)
б.
б.
Жауап.
a) Зерттелген материалды бекіту Ауызша шешу. Логарифмді негізі бойынша табыңыз a негізі бар дәреже түрінде берілген сандар a
Жұптық жұмыс.
Санды
табыңыз Ауызша шешу. Негізгі логарифмдік сәйкестікті пайдалану арқылы өрнектерді жеңілдетіңіз.
1) |
Оқушылар жаңа сабақты меңгереді
|
|
Оқулықтар суреттер, слайд Кестелер плакаттар
|
|
Қорытынды |
Үйге тапсырма: Негізгі логарифмдік сәйкестікті пайдалану арқылы өрнектерді жеңілдетіңіз.
1)
|
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Рекурсия. Рекурсиялық есептерді шешу |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушыларды рекурсия ұғымымен және оның математикада қолданылуымен таныстыру. Оқушыларды математикалық индукция әдісі арқылы рекурсиялық есептерді шығаруға үйрету. Логикалық ойлауын және есептерді талдау қабілетін дамыту |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Психологиялық ахуал қалыптастыру. Оқушылардың көңілін сабаққа
аудару |
Оқушылар бір-бірімен амандасады. |
Формативті бағалау үнемі жүргізіліп отырады |
Оқулықтар |
|
Сабақтың ортасы |
Арифметиканы түсіну мүмкін емес, оған сенуге мәжбүрміз. Мария Кунциевич. Марияның ұлағатты сөзіне пікір қалдырыңыз.
Сабақтың мақсатын қою Жаңа материалды меңгеруді бастайық. Сабақтың тақырыбын дәптеріңе жаз. Көмекші алгоритмдерді программалау тілдерінде жазу ішкі бағдарламалар арқылы жүзеге асырылады. Бүгін сабақта Паскаль тілінде ішкі программалардың ұйымдастырылуын қарастырамыз. Сабақтың тақырыбын және осы тақырыптың негізгі ұғымдарының анықтамаларын дәптерге жазып алу. Сабақтың тақырыбы бойынша жұмыс Күрделі есепті шешу үшін бағдарлама құру кезінде бағдарламашылар бұл тапсырманы ішкі тапсырмаларға, қосалқы тапсырмаларды одан да кішірек ішкі тапсырмаларға және т.б. оңай бағдарламаланатын қарапайым тапсырмаларға дейін бөледі. Паскаль программалау тілі программаны ішкі бағдарламалар деп аталатын жеке бөліктерге бөлуге мүмкіндік береді. Ішкі программа терминінің өзі оның негізгі программаға ұқсас және бағынышты екенін көрсетеді. Ішкі бағдарламалар бағдарламалауды жеңілдететін үш маңызды тапсырманы орындайды: - бағдарлама мәтініндегі ұқсас фрагменттерді қайталап қайталау қажеттілігін жою, яғни бағдарламаның көлемін азайту; - талдау кезінде түсінуді жеңілдете отырып, бағдарлама құрылымын жақсарту; - қателердің ықтималдығын азайту, бағдарламалау қателеріне және өзгерту кезінде күтпеген салдарға төзімділікті арттыру. Жұмыс жоспары: 1.Жаңа ұғымдарды меңгеру (презентация) 2. Негізгі ұғымдарды дәптеріңе жаз 3. Рекурсиялық есептердің негізгі түрлерін шешу жолдарын қарастырыңыз. (1-қосымша) -Түсіндірмелерді тыңдап, жаңа ұғымдарды дәптерге жазып алу. -Алған білімдерін бекіту үшін зертханалық және практикалық жұмыстарды орындайды. -Жұмысты орындау кезінде түсініксіз мәселелерді анықтау Оқыған материалды бекіту Рекурсиялық есептердің негізгі түрлерін шешу. (1-қосымша) |
|
|
Оқулық, |
|
Қорытынды |
Үйге тапсырма беру: өткенді қайталау |
|
ҚБ қойылады. |
|
Қосымша 1.
Тәжірибелік жұмыс.
Жұмыстың мақсаты: рекурсияға арналған есептерді компьютерді қолданбай шешуге үйрету.
Тапсырмалар:
-
Функцияның мәнін есептеу алгоритмі F(n), қайда n – натурал сан, келесі қатынаспен берілген
F(1)=1
F(n)=F(n-1)*(n+1), кезінде n>1
Функцияның мәні неге тең F(5)? Жауапта тек бүтін санды жазыңыз.
Шешім:
F(1)=1
F(2)=F(1)*3=1*3=3
F(3)=F(2)*4=3*4=12
F(4)=F(3)*5=12*5=60
F(5)=F(4)*6=60*6=360
Жауабы: 360
-
Функцияның мәнін есептеу алгоритмі F(n), қайда n – натурал сан, келесі қатынаспен берілген
F(1)=1
F(n)=F(n-1)*(n+2), кезінде n>1
Функцияның мәні неге тең F(5)? Жауапта тек бүтін санды жазыңыз.
Шешім:
F(1)=1
F(2)=F(1)*4=1*4=4
F(3)=F(2)*5=4*5=20
F(4)=F(3)*6=20*6=120
F(5)=F(4)*7=120*7=840
Жауабы: 840
-
Функцияның мәнін есептеу алгоритмі F(n), қайда n – натурал сан, келесі қатынаспен берілген
F(1)=1
F(n)=F(n-1)*(2*n+1), кезінде n>1
Функцияның мәні неге тең F(4)? Жауапта тек бүтін санды жазыңыз.
Шешім:
F(1)=1
F(2)=F(1)*5=1*5=5
F(3)=F(2)*7=5*7=35
F(4)=F(3)*9=35*9=315
Жауабы: 315
-
Функцияның мәнін есептеу алгоритмі F(n), қайда n – натурал сан, келесі қатынаспен берілген
F(1)=1
F(n)=F(n-1)*(2*n-1), кезінде n>1
Функцияның мәні неге тең F(5)? Жауапта тек бүтін санды жазыңыз.
Шешім:
F(1)=1
F(2)=F(1)*3=1*3=3
F(3)=F(2)*5=3*5=15
F(4)=F(3)*7=15*7=105
F(5)=F(4)*9=105*9=945
Жауабы: 945
-
Функцияның мәнін есептеу алгоритмі F(n), қайда n – натурал сан, келесі қатынаспен берілген
F(1)=1
F(n)=F(n-1)*(3*n-2), кезінде n>1
Функцияның мәні неге тең F(4)? Жауапта тек бүтін санды жазыңыз.
Шешім:
F(1)=1
F(2)=F(1)*4=1*4=4
F(3)=F(2)*7=4*7=28
F(4)=F(3)*10=28*10=280
Жауап: 280
-
Функцияның мәнін есептеу алгоритмі F(n), қайда n – натурал сан, келесі қатынаспен берілген
F(0)=1, F(1)=1
F(n)=F(n-1)+F(n-2), кезінде n>1
Функцияның мәні неге тең F(7)? Жауапта тек бүтін санды жазыңыз.
Шешім:
F(0)=1
F(1)=1
F(2)=F(1)+F(0)=1+1=2
F(3)=F(2)+F(1)=2+1=3
F(4)=F(3)+F(2)=3+2=5
F(5)=F(4)+F(3)=5+3=8
F(6)=F(5)+F(4)=8+5=13
F(7)=F(6)+F(5)=13+8=21
Жауап: 21
-
Функцияның мәнін есептеу алгоритмі F(n), қайда n – натурал сан, келесі қатынаспен берілген
F(0)=1, F(1)=1
F(n)=2*F(n-1)+F(n-2), кезінде n>1
Функцияның мәні неге тең F(6)? Жауапта тек бүтін санды жазыңыз.
Шешім:
F(0)=1
F(1)=1
F(2)=2*F(1)+F(0)=2*1+1=3
F(3)=2*F(2)+F(1)=2*3+1=7
F(4)=2*F(3)+F(2)=2*7+3=17
F(5)=2*F(4)+F(3)=2*17+7=41
F(6)=2*F(5)+F(4)=2*41+17=99
Жауап: 99
-
Функцияның мәнін есептеу алгоритмі F(n), қайда n – натурал сан, келесі қатынаспен берілген
F(0)=1, F(1)=1
F(n)=F(n-1)+2*F(n-1), кезінде n>1
Функцияның мәні неге тең F(6)? Жауапта тек бүтін санды жазыңыз.
Шешім:
F(0)=1
F(1)=1
F(2)=F(1)+2*F(1)=1+2*1=3
F(3)=F(2)+2*F(2)=3+2*3=9
F(4)=F(3)+2*F(3)=9+2*9=27
F(5)=F(4)+2*F(4)=27+2*27=81
F(6)=F(5)+2*F(5)=81+2*81=243
Жауабы: 243
-
Рекурсивті алгоритм берілген:
procedure F(n: integer);
begin
writeln(n);
if n<6 then begin
F(n+2);
F(n*3)
end
end;
Шақырылған кезде шығарылатын сандардың қосындысын табыңыз F(1)
Шешім:
-
алдымен анықтаймыз рекурентті формуланы; арқылы белгілейік F(n) шақырылған кезде болатын сандардың қосындысы F(n)
-
кезінде n>=6 процедура нөмірді шығарады n және рекурсивті қоңырауларсыз жұмысты аяқтайды: F(n)=n, кезінде n>=6
-
кезінде n<6 процедура нөмірді шығарады n және екі рет өзін-өзі шақырады F(n)=n+F(n+2)+F(3n), кезінде n<6
-
шақыру нәтижесінде F(1) аламыз:
F(1)=1+F(3)+F(3)
F(3)=3+F(5)+F(9)=3+F(5)+9
F(5)=5+F(7)+F(15)=5+7+15=27
-
кері алмастыруды қолданамыз
F(3)=3+F(5)+F(9)=3+F(5)+9=3+27+9=39
F(1)=1+2*F(3)=79
-
жауабы: 79
-
Рекурсивті алгоритм берілген:
procedure F(n: integer);
begin
writeln(‘*’);
if n>0 then begin
F(n-2);
F(n div 2)
end
end;
Қанша…
Шешім:
-
алдымен анықтаймыз рекурентті формуланы; арқылы белгілейік F(n), бағдарламаны шақырған кездегі жұлдызшалар саны
-
бағдарламадан біз мұны көреміз
F(n)=1, кезінде n<=0
F(n)=1+F(n-2)+F(n div 2), кезінде n>0
-
еске салайық, бұл n div 2 – бұл бөлудің квотенті n 2-ге
-
осы формулалар бойынша кестені 0-ден бастап толтырамыз:
F(0)=1
F(1)=1+F(-1)+F(0)=1+1+1=3
F(2)=1+F(0)+F(1)=1+1+3=5
F(3)=1+F(1)+F(1)=1+3+3=7
F(4)=1+F(2)+F(2)=1+5+5=11
F(5)=1+F(3)+F(2)=1+7+5=13
F(6)=1+F(4)+F(3)=1+11+7=19
F(7)=1+F(5)+F(3)=1+13+7=21
-
-
n
0
1
2
3
4
5
6
7
F(n)
1
3
5
7
11
13
19
21
-
-
жауабы: 21
-
Функциялардың мәндерін есептеу алгоритмі F(n) және G(n), қайда n – натурал сан, келесі қатынастармен берілген:
F(1)=1, G(1)=1;
F(n)=F(n-1)-G(n-1),
G(n)= F(n-1)+G(n-1), кезінде n>=2
Шаманың мәні неге тең F(5)/G(5)? Жауапта жазыңыз тек бүтін сан
Шешім:
-
іс жүзінде рекурентті формула берілген жұп үшін (F(n);G(n))
-
байқаймыз, бұл F(n) – бұл алдыңғы жұптың вариациясы, жәнеG(n) – бірдей мәндердің қосындысы
-
қосымшакестені белгілі бірінші жұптан бастап сызамыз
-
қажетті мән F(5)/G(5) 1-ге тең
-
Жауабы: 1
|
n |
1 |
2 |
3 |
4 |
5 |
|
F(n) |
1 |
0 |
-2 |
-4 |
-4 |
|
G(n) |
1 |
2 |
2 |
0 |
-4 |
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Тест тапсырмалары. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушылардың алған білімдерін тексеру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
І. Ұйымдастыру
кезеңі. Психологиялық сәт.
|
|
|
Интерактивті тақта, оқулық. |
|
Жаңа білім 15 мин 2 мин Бекіту 15 мин |
1 – нұсқа Тақырыбы: Рекурсия. Рекурсивті есептерді шешу. 1. Сұрақ: Рекурсияға қатысты төмендегі тұжырымдардың қайсысы дұрыс? A) Рекурсия – функция өзін шақыратын процесс. B) Рекурсия – циклдің қайталану санына шектеу қойылмайтын нұсқасы. B) Рекурсия тек массивтің максималды элементін табу үшін қолданылатын алгоритм болып табылады. 2-сұрақ: Әділ тиынды лақтырған кезде елтаңбаны алу ықтималдығы қандай? а) 0 б) 1 в) 0,5 3-сұрақ: Рекурсия тереңдігін шектеу үшін қандай әдіс қолданылады? A) Қайталану санына шектеу қою. B) Рекурсиядан шығу шартын қолдану. C) Қоңырауларды шектеу үшін қосымша мүмкіндікті пайдалану. Тақырыбы: Логарифмдер және олардың қасиеттері. 4-сұрақ: Төмендегі графиктердің қайсысы логарифмдік функцияны дәл көрсетеді? A) А кестесі В) В кестесі B) C кестесі 5-сұрақ: Логарифмдердің қасиеттеріне қатысты төмендегі тұжырымдардың қайсысы дұрыс? A) log a (bc) = log a (b) + log a (c) B) log a (b + c) = log a (b) + log a (c) B) log a (b^c) = c * log a (b) Тақырыбы: Теңдеулерді пайдаланып сөздік есептер жазу. 6-сұрақ: Есепті шешу үшін мына теңдеулердің қайсысын қолдануға болады: "Василий әрқайсысы 15 рубльден бірнеше кәмпит сатып алды. Егер ол 75 рубль төлесе, ол қанша кәмпит сатып алды?" A) 15x = 75 B) 15 - х = 75 B) x/15 = 75 7-сұрақ: Төмендегі теңдеулердің қайсысын есепті шешуге қолдануға болады: «Наталья өзінің бес кітабын екі досына бөледі. Егер әрбір досы х кітап алса, ол әр досына неше кітап сыйлады?». A) 2x = 5 B) 5/2x = 1 B) x - 2 = 5 Тақырыбы: Ньютон биномиясы. Паскаль үшбұрышы. 8-сұрақ: Паскаль үшбұрышының 5-ші қатарындағы 2 санына қандай сан сәйкес келеді? A) 1 В) 10 10-да 9-сұрақ: (a+b)^2 мәні неге тең, мұндағы a=2 және b=3? A) 4 B) 9 B) 25 10-сұрақ: Паскаль үшбұрышының 4-ші қатары неге ұқсайды? А) 1 3 3 1 B) 1 3 6 10 В) 1 2 3 4 2 – нұсқа 1. Рекурсияның негізгі идеясы қандай? а) Қайталанатын амалдар үшін циклдарды қолдану ә) Функцияны өзінен шақыруда в) Программаны тармақтау үшін шартты операторларды қолдануда 2. Қайталанатын цифрлары жоқ неше төрт таңбалы сан бар? а) 524 б) 3024 в) 9 3. Келесі рекурсивті кодты орындаудың нәтижесі қандай болады? нақты факт(n): егер n == 1: қайтару 1 басқа: қайтару n * факт(n-1) басып шығару(факт(5)) а) 10 ә) 120 в) 30 4. Төмендегі қасиеттердің қайсысы логарифмдерге қатысты? а) Қосындының логарифмі логарифмдердің қосындысына тең б) Көбейтіндінің логарифмі логарифмдердің көбейтіндісіне тең в) Бөлу логарифмі логарифмдердің айырмасына тең 5. Теңдеу дегеніміз не? а) Белгісіз шаманы қамтитын математикалық өрнек б) Белгілі бір шартты қанағаттандыратын сандық мәндер жиынтығы в) Белгісіз шаманы білдіретін математикалық таңба 6. Теңдеулерді қолданып сөз есебін қалай жасауға болады? а) Теңдеудегі сандарды сөздермен ауыстыр ә) Жағдайды табиғи тілде сипаттап, оны теңдеу түрінде аудару в) Берілген жағдаятпен сұраққа жауап ретінде теңдеуді қолданыңыз 7. Ньютон биномиясы дегеніміз не? а) Екі айнымалының дәрежелерінің қосындысын қамтитын математикалық өрнек б) Биномдық кеңею коэффициенттерінен тұратын үшбұрыш (a + b)^n в) Теңдеуді мүшелерге жіктеу арқылы шешу әдісі 8. Паскаль үшбұрышының негізгі идеясы қандай? а) (a + b)^n формуласы бойынша биномдық коэффициенттерді кеңейту б) Әрбір сан үстіндегі екі санның қосындысына тең болатын сандық үшбұрышты шығару в) Таңбасы біртіндеп кемулі шексіз қатардың қосындысын табу 9. Паскаль үшбұрышының бесінші қатардағы және үшінші бағандағы элементі қандай сан? а) 3 б) 5 в) 10 10. Паскаль үшбұрышын қолданудың негізгі мақсаты қандай? а) Сандардың комбинацияларын пайдаланып теңдеулерді шешу б) Таңбасы біртіндеп өсетін шексіз қатардың қосындысын табу в) Сан үшбұрышының қасиеттері мен заңдылықтарын оқу |
|
|
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: Өткен тақырыптарды қайталау |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Олимпиада есептерін шешу |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
- логикалық ойлау арқылы стандартты емес есептерді шығаруды үйрену; - есепті және оның шешімін қысқаша жазуды үйрену; - математикаға қызығушылығын дамыту; - сыныптастарының пікіріне құрметпен қарауға тәрбиелеу. |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Психологиялық ахуал қалыптастыру. Оқушылардың көңілін сабаққа
аудару |
Оқушылар бір-бірімен амандасады. |
Формативті бағалау үнемі жүргізіліп отырады |
Оқулықтар |
|
Сабақтың ортасы |
"Математика - бұл мызғымас құрылым және шынайы пайғамбарлық" (Л. Берс). Берстің ұлағатты сөзін талдаңыздар
Бірдей сандар. - Қосу арқылы бес екілік арқылы 28 санын жаз. (Жауабы: 22+2+2+2=28) 1. Цифрларының қосындысы 9-ға тең, 20-дан кіші екі таңбалы санды жаз. Бұл санды тоғыздардың қосындысы ретінде көрсетуге бола ма? Барлық шарттары бірдей бұл санды қосынды ретінде тағы қалай көрсетуге болады? Жауабы: 18, 9+9=18, 6+6+6=18, 3+3+3+3+3+3=18, т.б.) Көңілді үзіліс 1. Алақаныңызды ашып қолыңызды алға созыңыз. Кішкентай саусағыңызды алақанға басыңыз, қалған саусақтар ұзартылуы керек. Қолды ауыстырыңыз. 2. Шеге соғу үшін сол қолыңызды пайдаланыңыз, ал оң қолыңызбен бірдеңені үтіктеңіз. 1. Үштен – төрт. -Қазір мен сендерге әр топқа 3 таяқтан беремін. Тапсырма: 3 таяқшаның 4-ін жасаңыз Жауабы: ///=/V 1. Төрт түзу сызық. - Қағазға 9 нүктені төртбұрыш
түрінде орналастыратындай етіп қойыңыз. Қарындашты қағаздан
көтермей, барлық нүктелерді төрт түзу сызықпен сызып
тастаңыз. Жұмбақ ай. Әрине, бір жылда неше ай бар екенін білесіз бе? Жылдың соңғы айы қалай аталады? Желтоқсан сөзі нені білдіретінін білесіз бе? Бұл сөз гректің «дека» - он сөзінен шыққан. Жыл он екінші айы, желтоқсан айы «оныншы» деп аталады екен. Бұл біздің күнтізбеміз ежелгі римдіктердің күнтізбесінен шыққандықтан болды. Римдіктер жыл басын 1 қаңтар емес, басқа айдың бірінші күні деп есептеді. Бұл қай ай? Оның атын жаз. (наурыз) 7) Сан үшбұрышы Осы үшбұрыштың қабырғаларына 1-ден 9-ға дейінгі сандарды әр жақтың қосындысы 20 болатындай етіп орналастыр.
Көңілді басқатырғыштар. - Балаларға 3 тапсырма беріледі: №1. Піл коньки тепті. Бұл ауыр, сондықтан мен әр аяғыма екі коньки, ал сандықтың ұшына тағы бір коньки қойдым. Піл неше коньки киді? (9) № 2. Чебурашка апельсин қорапшасында саяхаттап жүріп таңғы және түскі асқа 1 апельсин, кешкі асқа 2 апельсин жеді. Сапар аптасында ол қанша апельсин жеді? (20) №3. Федор ағайдың терезелерінде 8 гүл құмыралары бар еді, онда гүлдер өсті. Бір күні Федор ағай келіп, бос гүл құмыраларын көреді. Гүлдерді Мурка сиыр жеді. Құмыраның бір жартысында 2 гүл, екінші жартысында 3 гүл болса, Мурка сиыр неше гүл жеді? (28) Сандық жұмбақтар Сандық жұмбақтарды шешіп,
жауаптарыңызды жазыңыз. |
Оқушылар сұрақтарға жауап беріп, түсінгендерін дәлелдей алу қабілетін көрсетеді; бірін-бірі бағалау, қолданба. үй. асс күнделіктерінде |
Өзін-өзі бағалау және өзара бағалау |
Оқулық, |
|
Қорытынды |
Үйге тапсырма беру: Сандық
жұмбақтарды шешіп, жауаптарыңызды жазыңыз.
|
|
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Олимпиада есептерін шығаруда сандар теориясын қолдану |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Сандар теориясының негізгі ұғымдары мен әдістерін оқып үйрену. Алған білімдерін олимпиада есептерін шығаруда қолдана білуге үйрету. Логикалық ойлауын және математикалық интуициясын дамыту. |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Психологиялық ахуал қалыптастыру. Оқушылардың көңілін сабаққа
аудару |
Оқушылар бір-бірімен амандасады. |
Формативті бағалау үнемі жүргізіліп отырады |
Оқулықтар |
|
Сабақтың ортасы |
«Математиканың қарапайым халыққа пайдасы –
қиындығы» А. Александров. Александрдың қанатты сөзіне
пікір қалдырыңдар. Сәлемдесу, сабақтың мақсатын түсіндіру. Сандар теориясының анықтамасы және оның математикалық және олимпиадалық есептердегі рөлі. Сандар теориясын қолданатын олимпиада есептерінің мысалдарын қарастыру. Олимпиада есептерімен жұмыс: Оқушыларға сандар теориясын қолдануды қажет ететін олимпиада есептерін ұсыну. Бұл есептерді кезең-кезеңмен шешуді көрсету. 1-тапсырманың мысалы: Вася 105 қырыққабатты 5 досына бөлгісі келеді. Әрбір дос ала алатын қырыққабаттың ең аз саны қанша? Мұғалім қалдықпен бөлу теориясын қолдану керектігін түсіндіреді және 5-ке бөлгенде 105 қалдығын табады, ол 0 болады. Сондықтан әрбір дос 21 қырыққабат алады. 2-тапсырманың мысалы: Мектеп олимпиадасына математикадан 100 адам, физикадан 50, информатикадан 48 адам қатысты.Оқушылардың әрқайсысы қанша олимпиадаға қатысқанын сұрағанда, «екі» деген жауап екі есе көп болды. адамдарды «бір» деп, ал «үште» жауабы «бірде» дегеннен үшке аз. Бұл олимпиадаларға қанша адам қатысты? Олимпиадаға математикадан – 100, физикадан – 50, информатикадан – 48, барлығы 100+50+48=198 адам қатысты. 3 олимпиадада адамдар болды, олар 3 рет саналды. x = 3a деп белгілейік. 2 олимпиадада б адам болды, олар 2 рет саналды. y = 2b деп белгілейік. 1-ші олимпиадада адамдар болды, олар 1 рет саналды. Оларды c = z деп белгілейік. Бірақ оқушылардың жауаптарынан a = c/3; b = c/2, яғни x = 3a = 3*c/3 = c = z; y = 2b = 2*c/2 = c = z x + y + z = z + z + z = 3z = 198; z = 198/3 = 1-ші олимпиадаға 66 адам қатысты. b = z/2 = 66/2 = 2 олимпиадаға 33 адам қатысты. a = z/3 = 66/3 = 22 адам 3 олимпиадаға қатысты. Барлығы 22 + 33 + 66 = 121 адам. 3 тапсырма. Параметрдің қандай мәндерінде а теңдеу sin²(x) - 2 (a - 3) sin(x) + a² - 6a + 5 = 0 тамыры жоқ па? Ауыстыру : t = sinx |t|≤ 1 t² - 2 (a - 3) * t + a² - 6a + 5 = 0 D / 4 = (a - 3)² - (a² - 6a + 5) = a² - 6a + 9 - a² + 6a - 5 = 4 = 2² ⇒(шаршы теңдеу бар екі әртүрлі жарамды тамырдың) t₁ = a - 3 - 2 = a - 5 ; t₂ = a - 3 + 2 = a - 1. Мыс. теңдеудің шешімі болмайды, егер қанағаттандырылмаса | t |≤ 1, т. Е. егер : а) { a - 5 < - 1 ; a - 1 2. ⇒a∈( 4 ; ∞). б){ a - 5 > 1 ; a - 1 a - 5 * * * {a> 6 ; a < 0 . ⇒ a∈∅. Жауап : a∈( - ∞ ; 0)∪(2 ; 4)∪(4 ; ∞). болмайды? |
Оқушылар сұрақтарға жауап беріп, түсінгендерін дәлелдей алу қабілетін көрсетеді; бірін-бірі бағалау, қолданба. үй. асс күнделіктерінде |
Өзін-өзі бағалау және өзара бағалау |
Оқулық, |
|
Қорытынды |
Үйге тапсырма беру: сандар теориясының формуласын қайталау. |
|
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Күрделі есептерді қарапайым қосалқы тапсырмаларға бөлу |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Күрделі мәселені анықтаңыз және оны ішкі тапсырмаларға бөлудің не үшін қажет екенін түсіндіріңіз. Ішкі тапсырмаларға бөлу арқылы шешуге болатын есептердің мысалдарын талдаңыз. Оқушыларды есептерді ішкі тапсырмаларға бөлудің негізгі әдістерімен таныстыру. |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Психологиялық ахуал қалыптастыру. Оқушылардың көңілін сабаққа
аудару |
Оқушылар бір-бірімен амандасады. |
Формативті бағалау үнемі жүргізіліп отырады |
Оқулықтар |
|
Сабақтың ортасы |
- Мұғалім күрделі есепті қарапайым ішкі есептерге ыдырату мәселені жақсы түсінуге және оны шешуге мүмкіндік беретінін түсіндіреді. - Күрделі есептерді қарапайым есептерге ыдырату мысалдары (мысалы, алма сатып алу мәселесі, үй салу мәселесі). - Декомпозиция қадамдарын түсіндіру: негізгі ақпарат элементтерін анықтау, олардың шешімге әсерін талдау, ішкі тапсырмаларды шешу ретін құру. Практикалық жұмыс - Сыныпты 3-4 адамнан топтарға бөлу. - Әр топқа қарапайым қосалқы тапсырмаларға бөлу керек тапсырма беру. - Топтар бірлесе отырып тапсырманы талдайды, негізгі элементтерді анықтайды және оны ішкі тапсырмаларға бөледі. - Осыдан кейін әр топ өз нәтижелерін басқа топтарға ұсынып, оның ыдырау логикасын түсіндіреді. Талқылау және кері байланыс - Мұғалім есепті декомпозициялау процесін талқылайды және оқушыларға ыдыраудың сапасы бойынша өзін-өзі бағалауды ұсынады. - Мұғалім әр топ бойынша оң жақтарын атап, жақсарту мүмкіндіктерін көрсете отырып кері байланыс береді. Мәселенің мысалы және оның шешімі: Тапсырма: Петя мен Вася шеңбер бойымен велосипедпен жүреді. Петя 1 сағатта 6 айналым жасайды, ал Вася 45 минутта 4 айналым жасайды. Олардың бастапқы нүктесінде қайтадан кездесуі қанша уақытты алады? Шешімі: 1. Тапсырманың негізгі элементтерін анықтау: - Петя 1 сағатта 6 айналым жасайды. - Вася 45 минутта 4 айналым жасайды. 2. Шешім қабылдауға әрбір элементтің әсерін талдау: - 1 сағатта Петя 6 айналым жасайды, сондықтан 1 айналымға Петя 10 минутты алады (60 минут / 6 айналым). - 45 минутта Вася 4 айналым жасайды, сондықтан 1 революция үшін Васяға 11,25 минут қажет (45 минут / 4 айналым). 3. Ішкі тапсырмаларды шешу ретін құру: - Ұлдардың әрқайсысын айналдыруға қажетті уақыттың LCM (ең кіші ортақ еселік) мәнін табайық. Бұл жағдайда LCM 90 минутты құрайды. - Петя әр 10 минут сайын төңкеріс жасайтындықтан, ол 90 минутта 9 айналым жасайды (бір революцияға 90 минут / 10 минут). - Сол сияқты, Вася 90 минутта 8 айналым жасайды (бір айналымға 90 минут / 11,25 минут). Бұл олардың 90 минуттан кейін бастапқы нүктеде қайта кездесетінін білдіреді. Бұл үлгі есеп пен шешім оқушыларға күрделі мәселені қарапайым ішкі мәселелерге қалай бөлу керектігін түсінуге және дәл және тиімді шешімге жету үшін сол қадамдарды логикалық түрде орындауға көмектеседі. |
Оқушылар сұрақтарға жауап беріп, түсінгендерін дәлелдей алу қабілетін көрсетеді; бірін-бірі бағалау, қолданба. үй. асс күнделіктерінде |
Өзін-өзі бағалау және өзара бағалау |
Оқулық, |
|
Қорытынды |
Үйге тапсырма беру: үйде күрделі мәселені ішкі тапсырмаларға бөліп, келесі сабақта талқылау үшін нәтижелерін жазу. |
|
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Күрделі есептерді қарапайым қосалқы тапсырмаларға бөлу бойынша практикалық жұмыс |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Күрделі есептерді қарапайым ішкі тапсырмаларға бөлшектеу әдісі туралы алған білімдерін бекіту. Осы әдіс арқылы математикалық есептерді өз бетінше шешу дағдыларын дамыту. Оқушылардың математиканы оқуға деген ынтасының деңгейін арттыру. |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Психологиялық ахуал қалыптастыру. Оқушылардың көңілін сабаққа
аудару |
Оқушылар бір-бірімен амандасады. |
Формативті бағалау үнемі жүргізіліп отырады |
Оқулықтар |
|
Сабақтың ортасы |
3 құбыр арқылы толтырылған бассейн мәселесін шешу: түсіндірме және мәліметтер Бассейн бар жағдайды елестетіп көрейік және оны толтыру үшін толтыру жылдамдығы әртүрлі үш құбыр пайдаланылады. Мәселе әрбір құбырдың толтыру жылдамдығын ескере отырып, бассейннің толығымен толтырылатын уақытын анықтау болып табылады. Бұл мәселені шешу үшін әр құбырдың уақыт бірлігіне көлем бірлігімен толтырылу жылдамдығын білу қажет. Бірінші құбырдың жылдамдығы минутына а литрге, екіншісі минутына в литрге, үшіншісі минутына с литрге тең болсын. Бассейн толығымен толтырылатын уақытты t минут ретінде белгілейік. Осы уақыт ішінде әрбір құбыр қанша су көлемін толтыра алатынын қарастырайық. Бірінші құбыр бассейнді минутына литр жылдамдықпен толтырады. Демек, т уақытында ол а * т литр суды толтырады. Сол сияқты, екінші құбыр бассейнді b * t литрмен, ал үшінші құбыр c * t литрмен толтырады. Осылайша, бассейндегі судың жалпы көлемі t уақытынан кейін a * t + b * t + c * t тең болады. Бұл көлем бассейннің көлеміне тең болуы керек екенін ескеру ғана қалады. Бассейннің көлемін V литр деп белгілейік. Сонда t уақытын табудың теңдеуі a * t + b * t + c * t = V түрінде болады. Бұл теңдеуді бассейн толығымен толтырылатын уақыттың мәнін алу арқылы t-ге қатысты шешуге болады. Жоғарыда келтірілген шешім әрбір құбырдың толтыру жылдамдығын ескере отырып, бассейнді толтыруға кететін уақытты анықтауға мүмкіндік береді. Бұл тапсырма бірнеше тәуелді процестер бірге жұмыс істегенде уақытты табу тапсырмасының классикалық мысалы болып табылады. 3 құбыр арқылы толтырылған бассейн туралы тапсырманың сипаттамасы Бірінші құбыр бассейнді бір сағатта, екіншісі екі сағатта, үшіншісі төрт сағатта толтыра алады делік. Егер барлық үш құбыр бір уақытта ашық болса, бассейнді толтыру уақыты t сағатты құрайды. Мәселені шешу үшін t мәнін анықтауымыз керек. Бастау үшін әрбір құбырды жеке қарастырамыз. Егер бірінші құбыр уақыттың бір бөлігінде жұмыс істесе, онда ол осы уақыт ішінде бассейннің т-ші бөлігін толтырады. Сол сияқты, екінші құбыр бассейннің жартысын т/2 сағатта, ал үшінші құбыр бассейннің төрттен бірін т/4 сағатта толтырады. Осы мәндерді қорытындылай келе, келесі теңдеуді аламыз: t + t/2 + t/4 = 1 Теңдеуді жеңілдете отырып, аламыз: 4t + 2t + t = 4 Осылайша, бассейнді толтырудың жалпы уақыты t тең 4/(4+2+1) = 4/7 сағат немесе шамамен 0.57 сағат. Осылайша, 3 құбыр арқылы толтырылған бассейн мәселесі барлық үш құбыр бір уақытта ашық болған жағдайда бассейнді толтыру уақытын есептеуге мүмкіндік береді. Бұл тапсырмада әрбір құбырды толтыру жылдамдығын ескеру және бассейнді толтырудың жалпы уақытын анықтау маңызды. Бассейн мәселесін шешудің алғашқы қадамы Бассейн мәселесін шешу үшін үш құбырдың әрқайсысы арқылы бассейнге қанша су кіретінін анықтауымыз керек. Осы ақпаратты пайдалана отырып, біз белгілі бір уақыттан кейін бассейнде болатын судың жалпы көлемін таба аламыз. Бастау үшін тапсырма шартында берілген деректерді қарастырайық. Бірінші құбыр бассейнді 1 сағатта, екінші құбыр 2 сағатта, үшінші құбыр 3 сағатта толтыра алатынын білеміз. Бұл әр сағат сайын бірінші құбыр бассейн көлемінің 1/1 бөлігін, екінші құбыр бассейн көлемінің 1/2 бөлігін, ал үшінші құбыр бассейн көлемінің 1/3 бөлігін қамтамасыз ететінін білдіреді. Ыңғайлы болу үшін әр құбырды кесте түрінде елестетіп көрейік: Құбыр Уақыт Судың көлемі Судың сағатына көлемі Бірінші 1 сағат 1/1 1 Екінші 2 сағат 1/2 1/2 Үшінші 3 сағат 1/3 1/3 Енді біз үш құбырдың әрқайсысы бассейнге әр сағат сайын қанша су жіберетінін оңай анықтай аламыз. Бұл ақпарат келесі қадамда мәселені шешу үшін пайдалы болады. Аралық есептеулер және бассейн мәселесінің анық емес мәліметтері 3 құбыр арқылы толтырылған бассейн мәселесін шешкен кезде, бір қарағанда түсініксіз болуы мүмкін бірнеше аралық есептеулер мен бөлшектерді ескеру қажет. Біріншіден, әрбір құбырдың өткізу қабілеттілігі тапсырма шартында орнатылғанын есте ұстаған жөн. Бұл әдетте құбырдың бассейннің бір бөлігін толтыратын уақыты. Мысалы, егер бірінші құбырдың өткізу қабілеті 2 сағатты құраса, бұл оның бассейннің 1/2 бөлігін 2 сағатта толтыратынын білдіреді. Екіншіден, құбырлар бір уақытта жұмыс істейтінін ескеру қажет. Бұл бассейнге бір сағатта құйылатын су көлемі әрбір құбырдың бір сағатта құйылатын су көлемінің қосындысына тең екенін білдіреді. Мысалы, егер бірінші құбыр 2 сағат ішінде бассейн көлемінің 1/2 бөлігін қосса, сағатына ол бассейн көлемінің 1/4 бөлігін қосады. Үшіншіден, барлық үш құбыр бір уақытта жұмыс істеген кезде бассейннің толтырылатын уақытын ескеру қажет. Ол үшін барлық үш құбырдың өткізу қабілеттілігінің қосындысының кері мәнін табу керек. Мысалы, егер құбырлардың өткізу қабілеттілігі сәйкесінше 2, 3 және 6 сағатты құраса, онда бұл сандардың қосындысының өзара қатынасы 1/11 болады. Осы аралық есептеулер негізінде бассейнді толтыруға қанша уақыт кететінін анықтауға болады. Ол үшін үш құбырдың өткізу қабілеттілігінің қосындысының өзара қатынасын бассейннің жалпы көлеміне көбейту керек. Мысалы, бассейннің жалпы көлемі тең болса 1000 литр, онда толтыру уақыты 1/11 * 1000 = 90.91 сағатқа тең болады. Осылайша, барлық аралық есептеулер мен тапсырманың егжей-тегжейлерін ескере отырып, барлық үш құбыр бір уақытта жұмыс істеген кезде бассейннің толтырылу уақытын дәл анықтауға болады. 3 құбыр арқылы толтырылған бассейн мәселесінің түпкілікті шешімі Осы ақпараттан, біз келесі формулаларды шығара аламыз: Бірінші құбырдың жұмыс жылдамдығы = сағатына бассейннің 1/5 бөлігі Екінші құбырдың жұмыс жылдамдығы = сағатына бассейннің 1/6 бөлігі Үшінші құбырдың жұмыс жылдамдығы = сағатына бассейннің 1/7 бөлігі Бассейнді толтыруға кететін уақытты табу үшін біз әрбір құбырдың үлесін қосып, олардың бірге жұмыс істеуінің жалпы жылдамдығын табуымыз керек. Барлық үш құбырдың жалпы жұмыс жылдамдығы = бірінші құбырдың жұмыс жылдамдығы + екінші құбырдың жұмыс жылдамдығы + үшінші құбырдың жұмыс жылдамдығы Барлық үш құбырдың жалпы жұмыс жылдамдығы = 1/5 + 1/6 + 1/7 бассейннің сағатына Барлық үш құбырдың жалпы жұмыс жылдамдығын тапқаннан кейін бассейнді толтыруға кететін уақытты таба аламыз. Бассейнді толтыруға кететін уақыт = 1 / (барлық үш құбырдың жалпы жұмыс жылдамдығы) Енді біз есептеуді бастауға болады: Барлық үш құбырдың жалпы жұмыс жылдамдығы = 1/5 + 1/6 + 1/7 = Сағатына 47/210 бассейн Бассейнді толтыруға кететін уақыт = 1 / (47/210) = 210/47 = 4.468 сағат Сонымен, 3 құбыр арқылы толтырылатын бассейн мәселесінің түпкілікті шешімі бассейнді толтыру үшін шамамен 4,468 сағатты қажет етеді.
100А+В=121В 100В+А=84А+14 А=42 В=35 |
Оқушылар сұрақтарға жауап беріп, түсінгендерін дәлелдей алу қабілетін көрсетеді; бірін-бірі бағалау, қолданба. үй. асс күнделіктерінде |
Өзін-өзі бағалау және өзара бағалау |
Оқулық, |
|
Қорытынды |
Үйге тапсырма беру: үйде күрделі мәселені ішкі тапсырмаларға бөліп, келесі сабақта талқылау үшін нәтижелерін жазу. |
|
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Тест тапсырмалары. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушылардың алған білімдерін тексеру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
І. Ұйымдастыру
кезеңі. Психологиялық сәт.
|
|
|
Интерактивті тақта, оқулық. |
|
Жаңа білім 15 мин 2 мин Бекіту 15 мин |
1 – нұсқа 1. Күрделі математикалық есептерді қарапайым ішкі есептерге бөлу үшін қандай әдісті қолдануға болады? а) Индукция әдісі б) Қайшылық арқылы дәлелдеу әдісі в) «Бөл және жең» әдісі 2. Сандар теориясы нені зерттейді? а) Сандардың құрылымы және олардың қасиеттері б) Графиктер және желілер в) Дифференциация және интеграция ережелері 3. Математиканың төмендегі салаларының қайсысы олимпиадалық есептерді шешуде тиімді? а) Геометрия б) Матрицалық есептеулер в) Комбинаторика 4. Математикадан олимпиада есептерін шешуге қандай дағдылар көмектеседі? а) Жақсы есте сақтау б) Математика ұғымдарын терең түсіну в) Мәнерлеп оқу 5. Күрделі математикалық есепті сәтті шешу үшін қандай қадамдар жасау керек? а) Бірден, ойланбастан жауап беріңіз б) Проблеманың қойылымын талдаңыз және негізгі элементтерді анықтаңыз в) Олимпиаданың басқа қатысушыларынан көмек сұрау 6. Математикадан олимпиадаларда қандай есеп түрлері жиі кездеседі? а) Математикалық функцияларды есептеуге арналған есептер б) Теңдеулер мен теңсіздіктерді шешуге арналған есептер в) Функциялардың графиктерін тұрғызуға арналған тапсырмалар 7. Математикадан олимпиада есептерін тапсыру кезінде қандай тәсіл тиімді? а) Бірінші кездескен шешімді тез жазып алыңыз б) Барлық қолда бар деректерді талдап, негізделген шешім қабылдау в) Қатысушының шешімін артына қайта жазыңыз 8. Шығармашылық ойлау олимпиадалық математикалық есептерді шешуде қандай рөл атқарады? а) маңызды емес б) Стандартты емес шешімдерді табуға мүмкіндік береді в) Шешім процесін айтарлықтай баяулатады 9. Математикадан олимпиада есептерін шешу қиын болуының негізгі себебі неде? а) Шешуге уақыт жеткіліксіз б) Тапсырма түсініксіз тұжырымдалған в) Калькуляторларды пайдалануға шектеулер 10. Математикадан олимпиада есептерін шешуге дайындалуға қандай ақпарат көздері көмектеседі? а) Математика оқулықтары б) есептер жинағы бар интернет ресурстары в) Олимпиадаға сәтті қатысқан достардың кеңесі 2 – нұсқа 1. Сұрақ: Төмендегі есептердің қайсысы математикалық олимпиадаға жатады? а) қабырғалары берілген тіктөртбұрыштың ауданын табу; ә) Белгілі қабырғаларды пайдаланып үшбұрыштың периметрін есептеңіз; в) Емтиханнан өткен талапкерлердің санын, егер өту пайызы және топтағы талапкерлердің жалпы саны белгілі болса, анықтаңыз. 2-сұрақ: Функция графиктерін талдауға байланысты олимпиадалық есепті шешу үшін қандай әдісті қолдануға болады? а) Қосу және азайту амалдары; б) Графикалық шешу әдісі; в) Құнды ауыстыру әдісі. 3-сұрақ: Ауданды есептеуге байланысты есептерді шешу үшін қандай алгебралық әдістерді қолдануға болады? а) Факторизация әдісі; б) Толық ыдырау әдісі; в) Көбейту және бөлу әдісі. 4-сұрақ: Төмендегілердің қайсысы математикалық олимпиада есептері болып табылады? а) 3х + 7 = 22 теңдеуін шеш; ә) Екі санның арифметикалық ортасын есептеу; в) cos(x) функциясының туындысын табыңыз. 5-сұрақ: Белгісіз мәнді анықтауға байланысты олимпиадалық есепті шешу үшін қандай әдісті қолдану ұсынылады? а) Құнды ауыстыру әдісі; б) Графикалық шешу әдісі; в) Ортақ көбейткішке бөлу әдісі. 6-сұрақ: Төмендегілердің қайсысы математикалық олимпиада есептері болып табылады? а) Теңдеулер жүйесін шешу; б) Екі санның пайыздық қатынасын анықтау; в) Параллелепипедтің көлемін есептеңдер. 7-сұрақ: Көпмүшелік теңдеулердің түбірін табуға байланысты есептерді қандай алгебралық әдіспен шешуге болады? а) Құнды ауыстыру әдісі; б) Терминдерді жою әдісі; в) Қалдықпен бөлу әдісі. 8-сұрақ: Төмендегі есептердің қайсысы математикалық олимпиадаға жатады? а) Арифметикалық прогрессияның алғашқы N мүшесінің қосындысын табыңыз; б) Берілген радиус негізінде шеңбердің ауданын анықтау; в) Санның бөлгіштерінің санын санау. 9-сұрақ: Геометриялық дизайнға байланысты олимпиадалық есепті шешу үшін қандай әдісті қолдану ұсынылады? а) Мәндерді салыстыру әдісі; б) Терминдерді ауыстыру әдісі; в) Пифагор теоремасын қолдану әдісі. 10-сұрақ: Шексіз кемімелі геометриялық прогрессияның қосындысын есептеуге байланысты есептерді қандай алгебралық әдіспен шешуге болады? а) Күрделі бөлшек әдісі; б) Бөлшектерді ортақ бөлімге келтіру әдісі; в) Шексіз геометриялық прогрессияның қосындысы әдісі. |
|
|
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: Өткен тақырыптарды қайталау |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Стандартты емес есептерді шешу |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушыларды стандартты емес математикалық есептердің әртүрлі түрлерімен таныстыру. Стандартты емес есептерді шығару әдістерін үйрету. Оқушылардың сыни ойлау, шығармашылық қабілеттерін дамыту. |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Психологиялық ахуал қалыптастыру. Оқушылардың көңілін сабаққа
аудару |
Оқушылар бір-бірімен амандасады. |
Формативті бағалау үнемі жүргізіліп отырады |
Оқулықтар |
|
Сабақтың ортасы |
Ауызша логикалық есептерді шығар 3 а д а ч а 1 "Ұлдар мен алмалар". Үш баланың әрқайсысында бірнеше алма бар. Ұлдардың біріншісі басқаларына әрқайсысы қанша алма берсе, сонша береді оларда бар. Содан кейін екінші бала қалған екеуіне әрқайсысында қанша алма болса, сонша береді; өз кезегінде үшіншісі де береді қалған екеуінің әрқайсысына сол сәтте әрқайсысында қанша болса, сонша. Осыдан кейін ұлдардың әрқайсысында 8 алма бар. Басында әр баланың неше алмасы болды? 2-тапсырма
Бұл торайлар қандай геометриялық пішіндерден тұрады? - Қай жерде көбірек айналымдар бар? - Әр торайда неше геометриялық фигура бар? Типтік емес (стандартты емес) тапсырмалар – бұл арифметикалық амалдар мүлде орындалмайтын немесе ең аз мөлшерде орындалатын жауап алуға арналған тапсырмалар.
1. Жылан Горыныч үш батырды шайқасқа шақырды. Жыланда 12 бас болса, ал батырлар оның басын тең бөлсе, әр батырдың неше басын кесу керек? 2. Секірген инелік қызыл жаздың әр күнінің жарты уақытында ұйықтап, уақыттың үштен бірін билеп, алтыдан бірінде ән айтты. Ол қалған уақытын қысқа дайындыққа арнауды шешті. Инелік қыс мезгіліне күніне неше сағат дайындалды? 3. Нәресте 6 минутта 600 грамм джем жей алады, ал Карлсон 2 есе жылдам жей алады. Бұл джемді бірге жеуге қанша уақыт кетеді? 4.Маша аюдан пирогтарды атасы мен әжесіне апарып беруін өтінді. Машаның салмағы 10 кг, әр бәліш жарты килограмм. Аю Машамен бірге қорапты атасы мен әжесіне апарғанда салмағының айырмашылығын байқамауы үшін Маша қораптан қанша пирог алу керек. 5. Мук пен корольдік серуенші үлкен шалғынды айналып өткен 30 шақырымдық жарыста жарысты. Сайыс шарты бойынша тағы бір айналым жүгіріп, екіншісін басып озған адам жеңімпаз атанады. Скороход 10 минутта шеңбер жасайды, ал Кішкентай Мук - 6 минутта. Екеуі бір уақытта жүгіреді. Кішкентай Мук жылдам жүретін адамды неше минутта басып озады? Әзілқой тапсырмалар 1. Қандай сан барлық сандарға (қалдықсыз) бөлінеді? 2. Чайковскийден Пермьге дейін 1 сағат 20 минут, ал кері рейс 80 минутты алады. Бұл айырмашылықты қалай түсіндіре аламыз? 3. Үй шаруашылығы сабағында қыздар нан тілімдерін тосттауды үйренді. 2 минутқа созылған тілімнің бір жағын қуырып болған соң, апам бізге 3 тілім беруге шешім қабылдады, бірақ табаға 2 тілім ғана сыйды. Дегенмен, ол еш қиналмай, 6 минутта 3 тілім қуырды. Ол мұны қалай жасады? 4. Бір бөлке нанның салмағы жарты келі жарты бөлке. Бүкіл нанның салмағы қанша? 5. Үш ат бір сағатта 24 км жүгірді. Әр ат неше км/сағ жүгірді? Логикалық мәселе 6, 5, 4, 3, 2, 1 сандарын әр жол бойындағы сандардың қосындысы 12 болатындай етіп шеңберге орналастыр.
|
Оқушылар сұрақтарға жауап беріп, түсінгендерін дәлелдей алу қабілетін көрсетеді; бірін-бірі бағалау, қолданба. үй. асс күнделіктерінде |
Өзін-өзі бағалау және өзара бағалау |
Оқулық, |
|
Қорытынды |
Үйге тапсырма беру: Ребустар мен жұмбақ түрінде кездесетін есептер жайлы презентация дайындап кел |
|
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Ребустар мен жұмбақ түріндегі олимпиадалық тапсырмалар |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Жұмбақтар мен жұмбақтарды шешу арқылы оқушыларды математикаға қызықтыру және қызықтыру. Жарыс атмосферасын құру және қызықты есептерді шешу арқылы пәнді оқуға деген ынтасын арттыру. Оқушылардың ой-өрісін кеңейтіп, әртүрлі математикалық ұғымдар мен әдістермен таныстыру.. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
«Көңіл - күй неге ұқсас» Сәлемдесу, түгендеу |
Оқушылар ойын ойнайды
|
Формативті бағалау үнемі жүргізіліп отырады. |
Оқулықтар суреттер, слайдтар кестелер |
|
Сабақтың ортасы 20 минут
|
1. Кіріспе (5 минут): - Мұғалім сабақтың мақсаты мен логикалық ойлауын дамытудың маңыздылығын түсіндіреді. - Мұғалім өткен жеңімпаздар сәтті шығарған олимпиада есептеріне мысалдар келтіреді. - Мұғалім әр мәселенің өзіндік нақты шешімі бар екенін, логика мен шығармашылықты қажет ететінін түсіндіреді. 2. Негізгі бөлім (35 минут): - Мұғалім олимпиада есептерімен және жұмбақтармен жұмыс істеу ережелерін түсіндіреді. - Мұғалім топтық жұмысты ұсынады: оқушылар 4-5 адамнан топтарға бөлінеді. - Мұғалім әр топқа ребус немесе жұмбақ түрінде бір олимпиадалық есеп беріп, оны шешуге уақыт береді. - Топтар есептер бойынша жұмыс жасайды, мүмкін болатын шешімдерді талқылайды, логиканы қолданады және жауаптарын тексереді. Мысал тапсырма: Тапсырма: Сізде бір түрдегі 9 монета бар. Оның 8-і жалған, бірақ оны таразы арқылы ғана байқауға болады. Жалған монеталар шынайыға қарағанда жеңіл. 2 таразыда жалған монеталарды табу үшін таразыны пайдаланудың ең тиімді әдісін табыңыз. Шешімі: 1. Тиындарды 3 монетадан 3 топқа бөлу. 2. Осы топтардың екеуін өлшеп көрейік: - Бір топтың салмағы аз болса, онда жалған тиындар бар. 3-қадамға көшейік. - Топтардың салмақтары сәйкес келсе, жалған монеталар пайдаланылмаған үшінші топта. 3-қадамға көшейік. 3. Табылған топтағы екі тиынды өлшеңіз: - Бір тиынның салмағы аз болса, онда жалған монета бар деген сөз. - Егер монеталардың салмақтары сәйкес келсе, онда жалған монета пайдаланылмаған үшінші монета болып табылады. |
Оқушылар жаңа сабақты меңгереді
|
|
Оқулықтар суреттер, слайд Кестелер плакаттар
|
|
Қорытынды |
|
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Ойын теориясы және олимпиада есептері |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушыларға ойын теориясының негізгі принциптерін және оны математикалық есептерді шешуде қолдануды түсіндіру. Әртүрлі деңгейдегі олимпиада есептерін талдау және шешу үшін ойын теориясын қолдануға үйрету. Оқушылардың ойын теориясын өз бетінше оқуға және оны практикада қолдануға ынталандыру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Сәлемдесу, түгендеу |
Оқушылар ойын ойнайды
|
Формативті бағалау үнемі жүргізіліп отырады. |
Оқулықтар суреттер, слайдтар кестелер |
|
Сабақтың ортасы 20 минут
|
"Алгебра ғылымнан артық,
бұл ғылым туралы айтудың тәсілі"
(Н.
Бор).
1. Кіріспе: - Мұғалім сабақтың тақырыбын – ойын теориясы мен математикадан олимпиада есептерін түсіндіреді. - Оқушылар тыңдап, негізгі ұғымдарды жазып алады. 2. Теориялық түсініктеме: - Мұғалім ойын теориясының стратегия, төлем және тепе-теңдік сияқты негізгі ұғымдарын түсіндіреді. - Оқушылар анықтамалар мен мысалдарды жазады. 3. Мысал тапсырманы көрсету: - Мұғалім «Тас, қағаз, қайшы» математикалық ойыны бойынша есеп ұсынып, ойын ережесін түсіндіреді. - Оқушылар жұпқа бөлініп, стратегиялары мен ұтыстарын жазып, бірнеше рет ойнайды. 4. Топтық жұмыс: - Мұғалім оқушылар топтарына математикалық ойындар тақырыбы бойынша олимпиада есептерін таратады. - Оқушылар топ ішінде мәселелерді талқылайды, содан кейін олардың шешімдерін бүкіл сыныпқа ұсынады. Мысал тапсырма: Мәселе: Балаларға арналған тағамның құрамында 10 балмұздақ, 5 шоколад және 4 торт бар. Балалар біріншіден бастап кезекпен таңдайды және олар бір айналымда бірнеше емдік түрін қабылдай алмайды. Бірінші ойыншы әрқашан тортты таңдай алуы үшін балалар қандай стратегияны ұстануы керек? Шешімі: 1. Бірінші қозғалыста тортты таңдауға болатынын тексерейік. Егер балмұздақтар мен шоколадтардың қосындысы 2-ге бөлінетін болса, онда бірінші ойыншы осы тәттілердің бірін таңдайды, ал екінші ойыншы екі бірдей балмұздақ пен шоколадты алуға мәжбүр болады. 2. Егер бірінші жағдайда бірінші ойыншы тортты таңдай алмаса, ол балмұздақ немесе шоколадты таңдау керек. 3. Содан кейін екінші ойыншы бірінші ойыншының кезегін қайталайды. 4. Бірінші ойыншының балмұздақтар мен шоколадтардың қосындысы 2-ге бөлінетін болса, біркелкі бұрылыста қайтадан тортты таңдау мүмкіндігі бар. 5. Егер бірінші де, екінші ойыншы да кез келген бұрылыста тортты таңдай алмаса, олар барлық тәттілер біткенше бір-бірімен айналысады. Осылайша, балмұздақтар мен шоколадтардың қосындысы 2-ге бөлінетін болса, бірінші ойыншы әрқашан біркелкі бұрылыста тортты таңдай алады. |
Оқушылар жаңа сабақты меңгереді
|
|
Оқулықтар суреттер, слайд Кестелер плакаттар
|
|
Қорытынды |
|
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Қайталауға арналған тест тапсырмалары |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Жыл бойына алған білімін тексеру |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
І. Ұйымдастыру
кезеңі. Психологиялық сәт.
|
|
|
Интерактивті тақта, оқулық. |
|
Жаңа білім 15 мин 2 мин Бекіту 15 мин |
1 – нұсқа 1. Рекурсия дегеніміз не? а) Функция өзін шақыратын процесс. b) Функция аргументтерді беретін және нәтижені беретін процесс. в) Функция басқа функцияны шақыратын процесс. 2. Рекурсивті есеп қалай шығарылады? а) Негізгі жағдайды және кіші және үлкен регистрлердің арасындағы байланыстың анықтамасын табыңыз. б) Формуланы есептеу үшін қолдану. в) Талдау және интерполяция әдістерін қолдану. 3. Төмендегі формулалардың қайсысы логарифмнің қасиеті болып табылады? а) ln(ab) = ln(a) + ln(b) б) ln(a/b) = ln(a) - ln(b) c) ln(a^b) = млрд(a) 4. Теңдеулерді пайдаланып сөздік есеп қалай жасалады? а) Жағдайды сипаттап, белгісіз мәнді анықтаңыз. ә) Жағдайды математикалық формулаға аударыңыз. в) Белгісіз мәнді анықтау үшін теңдеулерді пайдаланыңыз. 5. Ньютон биномының қандай қасиеті бар? а) Паскаль үшбұрышының әрбір жолының коэффициенттерінің қосындысы 2^n-ге тең, мұндағы n – жол нөмірі. б) Паскаль үшбұрышының әрбір жолының коэффициенттері биномдық коэффициенттердің қосындысы болып табылады. в) Паскаль үшбұрышының әрбір жолы палиндром болып табылады. 6. Ықтималдықтар теориясы мен статистиканың негізгі міндеті қандай? а) Кездейсоқ құбылыстар мен ықтималдық үлестірімдерін зерттеу. б) Алынған мәліметтердің нақтылығы мен сенімділігін анықтау. в) Статистикалық мәліметтерді талдау және оларды болжау үшін қолдану. 7. Комбинаторикадан көбейту әдісі бойынша олимпиада тапсырмалары қандай? а) Варианттар санын анықтау үшін комбинаторлық формулаларды қолдануды қажет ететін есептер. б) Шешімін табу үшін геометриялық түрлендірулерді қолдануды қажет ететін есептер. в) Графиктерді салуды және олардың қасиеттерін анықтауды қажет ететін тапсырмалар. 8. «Иррационал теңдеу» ұғымы нені білдіреді? а) Тек иррационал сандар болатын теңдеу. б) Иррационал функциясы бар теңдеу. в) Алгебралық әдістер арқылы шешілмейтін және сандық әдістерді қолдануды қажет ететін теңдеу. 9. Рационал теңдеулер мен теңсіздіктер қалай шешіледі? а) Ортақ бөлгішке келтіріп, алынған теңдеуді шеш. б) Шешімдерін анықтау үшін рационал сандардың қасиеттерін және олардың графиктерін қолдану. в) Функцияларды және олардың әрекетін талдау әдістерін қолдану. 10. Функцияның графигі қалай салынады? а) Әр түрлі аргументтер үшін функцияның облысы мен мәндерін анықтаңыз. б) Әр түрлі аргументтер үшін функция мәндеріне сәйкес келетін нүктелерді салу. в) Тегіс қисық алу үшін нүктелерді түзулермен қосыңыз. 2 – нұсқа 1. Рекурсия дегеніміз не? а) Қарапайым ішкі тапсырмаларға кезең-кезеңмен бөлу арқылы есептерді шешу әдісі б) Теңдеулерді қолданып есептер шығару әдісі в) Паскаль үшбұрышының көмегімен есептерді шығару әдісі 2. Көрсеткіштік функцияға кері функция қалай аталады? а) Логарифмдік б) Шаршы в) Тригонометриялық 3. Көбейту кезінде логарифмдердің қандай қасиеті бар? а) Логарифмдердің қосындысы көбейтіндінің логарифміне тең б) Логарифмдердің айырымы бөліктің логарифміне тең в) Көбейтіндінің логарифмі логарифмдердің қосындысына тең 4. Теңдеулерді пайдаланып сөздік есеп қалай жасалады? а) Белгісіз шамаларды орнату және олардың байланысын теңдеу арқылы сипаттау б) Теңдеудің шешімдерінің санын анықтау в) Ньютонның биномдық формуласын қолдану 5. Паскаль үшбұрышы қандай геометриялық объектіні сипаттайды? а) Биномдық коэффициенттерден тұратын үшбұрыш б) Сандардың логарифмінен тұратын үшбұрыш в) Сандардың факториалдарынан тұратын үшбұрыш 6. Ықтималдық теориясы дегеніміз не? а) Кездейсоқ оқиғаларды және олардың ықтималдығын зерттейтін математика саласы б) Рационал теңдеулерді зерттейтін математика саласы в) Комбинаторикадағы есептерді шығару әдісі 7. Комбинаторикадан көбейту әдісі арқылы олимпиада тапсырмаларын шешу үшін қандай әдіс қолданылады? а) Барлық мүмкін комбинациялар арқылы іздеу әдісі б) анықтауыш әдіс в) Кронштейнді орналастыру әдісі 8. Иррационал теңдеу дегеніміз не? а) Белгісіз шамалар тек рационал мәндерді қабылдай алатын теңдеу б) Белгісіз шамалар тек иррационал мәндерді қабылдай алатын теңдеу в) Белгісіз шамалар рационал және иррационал мәндерді қабылдай алатын теңдеу 9. Рационал теңдеу қалай шешіледі? а) Теңдеуді жалпы түрге келтіріп, түбірін тап б) Теңдеудің екі жағын ең кіші ортақ бөлгішке көбейт в) Теңдеуді сызықтық теңдеулер жүйесіне айналдырып, оны шешу 10. Функциялар графиктерде қалай бейнеленген? а) Айнымалылардың тәуелділігін көрсететін қисық сызықтар түрінде б) Координаталық жазықтықтағы нүктелер түрінде в) Функция мәндерінің кестесі түрінде |
|
|
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: Өткен тақырыптарды қайталау |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
Пайдаланылған әдебиеттер:
Мұғалімдерге арналған:
1. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. В 3-х
томах: том 1. – М.: Наука, 1968, с. 157 – 162
2. Ильин В.А. Методы решения функциональных уравнений // Соросовский
образовательный журнал, 2001, № 2, с. 116 – 120
3. Бродский Я. С., Слипенко А. К. Функциональные уравнения. – К.: Вища школа.
Головное издательство, 1983. – 96 с.
4. Андреев А.А., Кузьмин Ю.Н.., Савин А.Н., Саушкин И.Н. Функциональные
уравнения. – Самара: В мире науки, 1999
5. Сабитов К.Б. Функциональные, дифференциальные и интегральные
уравнения.−М.:’’Высшая школа’’,2005,с.190−199
6. Лихтарников Л.М. Элементарное введение в функциональные уравнения.– СПб.:
Лань, 1997. – 160 с.
7.Әбілқасымова А. және т.б. Математиканы оқытудың териясы мен әдістемесі. А, Білім. 1998 ж
8. Бидосов Ә. Математиканы оқыту методикасы. (Жалпы методика). А, Мектеп. 1989ж
9. Рахымбек Д. және т.б. Орта мектепте математиканы оқыту әдістемесіне арналған оқу құралы. Ш, 2003
Оқушыларға арналған:
-
Генкин, С.А., Итенберг, И.В., Фомин, Д.В. (1994). Ленинградские математические кружки. Киров: АСА.
-
Гальперин, Г.А., Толпыго, А.К. (1986). Московские математические олимпиады. Москва: Просвещение.
-
Васильев, Н.Б., Гутенмахер, В.Л., Раббот, Ж.М., Тоом, А.Л. (1981). Заочные математические олимпиады. Москва: Наука.
-
Шарыгин, И.Ф. (1998). Математика: Факультативный курс. Москва: Просвещение.
-
Яглом, И.М. (1981). Математические олимпиады и внеклассная работа по математике. Москва: Просвещение.
Мазмұны
1.Түсінік хаты
2. Тұрақтылау (мазмұндық) бөлімі
3. Нормативтік бөлім
4. Ақпараттық-әдістемелік бөлім
5. Оқу – әдістемелік нұсқаулық
6. Пайдаланылған әдебиеттер
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Математикадан олимпиада есептерін шығару жолдары
Математикадан олимпиада есептерін шығару жолдары
Математикадан олимпиада есептерін шығару жолдары
сынып оқушыларына арналған
аптасына 1 сағат, барлығы 34 сағат
Математика пәні мұғалімі Утешова Жайна Баяновна
Пікір жазған: Абай атындағы ҚазҮПУ, Математика және математикалық модельдеу кафедрасы п.ғ.к., аға оқытушы Б.А.Қадырбаева
2025 ж
Түсінік хаты
Бұл жазбада мен сіздерге оқушыларыңызға пайдалы болуы мүмкін математикалық олимпиада есептерін шешу жолдарын шолуды ұсынғым келеді. Бұл әдістер оқушылардың аналитикалық ойлау, логикалық ойлау және математикалық есептерге есептер шығару тәсілдерін дамытуға мүмкіндік береді, бұл олимпиадаларға қатысудың маңызды бөлігі болып табылады.
1. Декомпозиция және модельдеу әдісі: Бұл әдіс күрделі есепті қарапайым құрамдас бөліктерге бөлуді қамтиды. Содан кейін әрбір компонент жеке талданады және шешіледі. Содан кейін қорытынды жауапқа жету үшін нәтижелер біріктіріледі. Бұл әдіс әсіресе әртүрлі формулалармен және теңдеулермен жұмыс істеуді қажет ететін есептерді шешуде тиімді.
2. Сынақ және қате әдісі: Бұл әдіс мәселені шешудің әртүрлі тәсілдерін жүйелі түрде сынап көруді қамтиды. Қарапайым қадамдардан бастап, оқушылар өз шешімін біртіндеп жақсарту үшін итерациялық процесті пайдалана алады. Бұл әдіс шыдамдылықты, табандылықты және ойлау икемділігін дамытуға ықпал етеді.
3. Аналогтарды қолдану әдісі: Бұл әдіс бұрыннан шешілген ұқсас есептерді табуға негізделген. Оқушылар жалпы үлгілер мен шешімдерді іздеу үшін бұрын орындалған математикалық мысалдарды немесе олимпиада есептерін пайдалана алады. Бұл әдіс аналитикалық ойлауды дамытуға және әртүрлі математикалық ұғымдар арасында байланыс орнатуға көмектеседі.
4. Графиктер мен диаграммалар әдісі: Бұл әдіс графиктер мен диаграммаларды пайдаланып мәселені визуализациялауға баса назар аударады. Оқушылар қандай деректер берілгенін және есепте не қажет екенін жақсы түсіну үшін графикалық бейнені пайдалана алады. Бұл әдіс деректерді талдау және интерпретациялау дағдыларын дамытады.
5. Математикалық индукция әдісі: Бұл әдіс есепті дәлелдеу үшін логикалық пайымдау мен математикалық индукцияны қолдануды қамтиды. Оның көмегімен оқушылар жалпы заңдылықтарды тауып, әртүрлі жағдайларға қолданылатын ережелерді белгілей алады. Бұл әдіс теориялық ойлауды дамытады және күрделі мәселелерді шешуді жеңілдетеді.
Әртүрлі тапсырмалардың бірегей сипаттамаларына байланысты бірнеше әдістердің тіркесімін немесе теңшелген тәсілді қажет ететінін есте ұстаған жөн. Математикадан олимпиада есептеріне қатысу оқушыларға математика саласында дамуға, есептерді шығару және математикалық теоремаларды дәлелдеу дағдыларын жетілдіруге, университеттік сынақтарға және болашақ ғылыми мансапқа дайындалуға мүмкіндік береді.
Мәселені шешудің әртүрлі әдістерін ескере отырып, мен сізге оқушылар осы тәсілдердің әрқайсысын тәжірибеден өткізе алатын тәжірибе сабағын өткізуді ұсынамын. Бұл олардың аналитикалық ойлау қабілеттерін дамытуға көмектеседі, сондай-ақ олимпиада тапсырмаларына қатысу кезінде сенімділігін арттырады.
Математикалық олимпиада есептерін шешудің бұл әдістері оқушыларыңызға тек математикалық ойлауды ғана емес, жалпы есептерді шығару дағдыларын дамытуға көмектеседі деп ойлаймын. Оқушыларіңіз әртүрлі есептерді шешу әдістерін үйреніп, оларды тәжірибеде қолдануды ұнататынына сенімдімін.
Өзектілігі: математикадан олимпиада есептері оқушылардан негізгі ұғымдар мен алгоритмдерді білуді ғана емес, сонымен қатар шешімдердің тривиальды емес тәсілдерін табуды және әртүрлі стратегиялар мен әдістерді қолдана білуді талап етеді. Бұл дағдылар креативті ойлауды дамытудың және әдеттен тыс есептерді шешудің кілті болып табылады, бұл математикада ғана емес, шынайы өмірде де маңызды.
Бағдарламаның мақсаты: оқушылардың күрделі математикалық есептерді талдау және шешу дағдыларын дамыту, олимпиадаларға қатысуға дайындау және математиканы оқуға қызығушылығын арттыру.
Бағдарламаның міндеттері:
1. Оқушыларды математикадан типтік олимпиада есептерімен таныстыру, оларды шешудің әртүрлі тәсілдері мен стратегияларын талдау және талдау.
2. Оқушыларды тривиальды емес шешімдерді табу әдістеріне және олимпиада есептерін шығаруда әртүрлі математикалық тәсілдерді қолдануға жаттықтыру.
3. Математикалық модельдермен жұмыс істеу, логикалық ойлау және шығармашылық ойлау дағдыларын дамыту.
4. Оқушыларды есептерді шешу жолдарын, сонымен қатар басқа олимпиада қатысушыларының шешімдерін талдауға және бағалауға үйрету.
5. Оқушыларды олимпиадалық сынақтарға дайындау және олардың жарыстардағы көрсеткіштерін арттыру.
6. Математикаға және жалпы пәнге деген қызығушылықтың дамуына ықпал ету.
Күтілетін нәтиже:
1. Оқушылардың математикалық дайындық деңгейін арттыру.
2. Логикалық ойлау қабілеттерін дамыту, шығармашылық көзқарас пен күрделі есептерді аналитикалық шешу.
3. Математикадан олимпиадаларға дайын және сәтті өнер көрсететін оқушылардың санын арттыру.
4. Оқушылардың математиканы оқуға деген сенімі мен ынтасын нығайту.
5.Оқушылардың жарыстардағы жетістіктерінің арқасында мектеп пен оқу орнының беделін арттыру.
Бағдарламаның жаңалығы:
Бағдарламаның ғылыми жаңалығы әртүрлі әдістер мен тәсілдерді қолдана отырып, олимпиада есептерін талдау мен шешудің жүйелі тәсілін ұсынуында. Сондай-ақ бағдарлама негізгі есептерден кеңейтілген мәселелерге дейінгі мәселелердің күрделілігінің әртүрлі деңгейлерін қамтиды. Бұл оқушылардың жеке ерекшеліктерін ескере отырып, есептерді шешу дағдыларын біртіндеп дамытуға мүмкіндік береді.
Тұрақтылау (мазмұндық) бөлім
-сынып
Аптасына – 1 сағат. Барлығы – 34 сағат
I – бөлім. Математикадан олимпиада есептерін секциялары бойынша шешу (10 сағат)
Бағдарламаның бірінші бөлімі бөлімдер бойынша математикадан олимпиаданың іріктеу кезеңінің есептерін шешуге арналған. Бұл бөлімнің жетекші идеясы олимпиадалық есептерді сәтті шешу математиканың әртүрлі салаларын терең түсінуді және оларды бірге қолдана білуді талап етеді. Бағдарлама оқушылардың математикалық дағдыларын дамытуға және олимпиаданың ең қиын есептерін шешуге көмектесетін стратегиялар мен есептерді шешу әдістерін ұсынады.
Бағдарламаның бірінші бөлімінің мақсаты – оқушыларды математиканың әртүрлі салаларымен таныстыру және оларды тереңдетіп оқуға көмектесу, осылайша олар алған білімдерін олимпиада есептерін шешуде сәтті қолдана алады. Бұл бөлім математиканың алгебра, геометрия, комбинаторика және сандар теориясы сияқты салаларын қамтиды. Әрбір бөлім оқушыларға олардың жұмысы мен қолданылуын толық түсінуге мүмкіндік беру үшін әртүрлі әдістер мен тәсілдер арқылы зерттеледі.
Бұл авторлық бағдарлама оқушылардың олимпиадалық математикадағы мүмкіндіктерін жүзеге асыруға және жоғары нәтижелерге жетуге көмектеседі деп сенемін. Математиканың әртүрлі салаларындағы есептерді шешуде жүйелі оқу және машықтандыру арқылы ғана адам осы күрделі де қызықты өнердің нағыз шебері бола алады.
II – бөлім. Жоғары қиындық деңгейлі есептерді шешу (10 сағат)
Біздің қолтаңба математикалық бағдарламамыздың екінші бөлімі бізді күрделіліктің жоғары деңгейіндегі есептерді шешудің қызықты және ойландыратын әлемімен таныстырады. Бұл бөлім бізге біліміміз бен дағдыларымыздың көмегімен математикалық жұмбақтардың тереңдігіне үңіліп, олардың жұмбақтарын шешуге бірегей мүмкіндік береді. Мұнда аналитикалық ойлауды, тапқырлықты және шығармашылықты қажет ететін мәселелерге тап боламыз. Әрбір тапсырма жаңа сынақты, әрбір шешім қиындықтарды жеңуді білдіреді. Бізге осы қызықты саяхатқа қосылыңыз, өйткені біз зерттеп, үйреніп, жоғары деңгейдегі міндеттерді шешуде ұлылыққа қол жеткіземіз.
III – бөлім. Ұзақ уақыт алатын есептерді шешу (5 сағат)
Мұғалімнің математикаға арналған бастапқы бағдарламасының үшінші бөлімі арнайы тақырыпқа - көп уақытты қажет ететін есептерді шешуге арналған. Бұл бөлімде біз толық шешу үшін көп уақыт пен күш жұмсауды қажет ететін тапсырмаларға тоқталамыз.
Күрделі математикалық есептерді шешу оқу процесінің маңызды бөлігі болып табылады және оқушылардың аналитикалық ойлауын, есептер шығару және алған білімдерін практикада қолдана білу дағдыларын дамытуға көмектеседі. Дегенмен, біз көптеген тапсырмаларды орындау күрделі және уақытты қажет ететінін түсінеміз.
Авторлық бағдарламаның бұл бөлімінде біздің мақсатымыз – оқушыларға ұзақ уақыт пен терең талдауды қажет ететін есептерді тиімді шешуге үйрету. Біз оқушыларға жұмыстарын ұйымдастыруға, ақпаратты құрылымдауға және шешімге жетудің ең жақсы жолдарын табуға көмектесетін әдістер мен стратегияларды ұсынамыз.
Бағдарлама күрделі математикалық есептерден бастап ұзақ мерзімді жобаларға дейінгі әртүрлі есеп түрлерін қамтиды. Біз оқушыларды көп уақытты қажет ететін есептерді шешу процесін жеңілдету үшін математикалық модельдеу, графикалық бейнелеу және есептеуіш технологияларды пайдалану сияқты әртүрлі құралдарды қолдануға шақырамыз.
Математика пәнінің мұғалімі ретінде біз оқушыларда есеп шығару дағдыларын ғана емес, сонымен қатар олардың қабілетіне деген сенімділікті дамытуға ұмтыламыз. Біз оларды проблемаларды шешуде тәуелсіздік пен ерекшелікті дамытуға көмектесу үшін зерттеу тәсілдері мен балама шешімдерінде қолдаймыз және қолдаймыз.
Бұл бөлімде ұсынылған барлық материалдар мен жаттығулар тапсырмалардың күрделілігін, оқушылар үшін орындылығын және материалды қызықты және қолжетімді түрде ұсынуды ескере отырып әзірленген. Бағдарламаның осы бөлімін меңгеру оқушыларға көп уақытты қажет ететін есептерді шешуде кездесетін қиындықтарды жеңуге көмектесетініне сенімдіміз.
IV – бөлім. Логикалық есептерді шешу (9 сағат)
Логикалық есептерді шешу математиканы оқытудың маңызды кезеңі болып табылады. Ол оқушылардың аналитикалық және сыни тұрғыдан ойлауын, сондай-ақ математикалық дағдылар мен білімдерін өмірлік жағдаяттарда қолдана білуді дамытуға бағытталған.
Біздің меншікті бағдарламамыздың төртінші бөлімінде біз логикалық есептерді зерттеуге терең еніп, оқушыларға оларды сәтті шешуге арналған құралдар жиынтығын ұсынамыз. Біз оқушыларға дерексіз ұғымдармен жұмыс істеуде сенімділік пен дағдыларды дамытуға көмектесетін әртүрлі мәселелерді шешу стратегияларын ұсынамыз.
Логикалық есептерді шешуді зерттеудің бірінші қадамы есептің шарттарын талдау болып табылады. Оқушылар белгілі бір математикалық операциялармен немесе ұғымдармен байланысты болуы мүмкін негізгі сөздер мен сөз тіркестерін анықтауды үйренеді. Бұл мәселені құрылымдауға және оны шешу үшін қажетті операцияларды анықтауға көмектеседі.
Содан кейін біз логикалық ойлау тізбегін құруға көшеміз. Оқушылар маңызды ақпаратты проблемалық мәлімдемеден оқшаулауды және қосымша деректерді шығару үшін логикалық операцияларды қолдануды үйренеді. Сондай-ақ біз оқушыларды ақпаратты жүйелеуге және шешімнің логикалық ағынын оңайырақ қадағалауға көмектесетін кестелер мен диаграммалар сияқты есептерді шешудің әртүрлі әдістерімен таныстырамыз.
Біздің бағдарламамыздың төртінші бөлімінің маңызды бөлігі - дәлелдеу және жауаптарды негіздеу дағдыларын дамыту. Оқушылар өз ойларын және дәлелдемелерін түсінікті және логикалық түрде тұжырымдауға үйренеді. Біз бұл аспектіге үлкен мән береміз, өйткені ол оқушыларға өз ойларын сенімдірек жеткізуге және логикалық ережелерге негізделген дәлелдер құруға көмектеседі.
Нормативті бөлім
|
Бөлім |
Бөлімше |
Тақырып |
Оқу мақсаты |
Барлығы (сағ) |
Теория (сағ) |
Практика (сағ) |
Білім өнімі |
|
I бөлім |
1. Математикадан олимпиада есептеріне кіріспе |
Математикадан олимпиада есептеріне кіріспе |
Олимпиадалық есептердің маңыздылығын түсіну |
1 |
1 |
0 |
Олимпиадалық есептердің ерекшеліктерін білу |
|
|
2. Алгебраны пайдаланып есептер шығару әдістері |
Алгебраны пайдаланып есептер шығару әдістері |
Алгебралық әдістерді есептер шығаруда қолдана білу |
1 |
1 |
0 |
Алгебралық әдістерді қолдану дағдысын меңгеру |
|
|
3. Математикадан олимпиада есептерін шешу |
Математикадан олимпиада есептерін шешу |
Түрлі деңгейдегі олимпиадалық есептерді шеше білу |
1 |
0 |
1 |
Олимпиадалық есептерді шешу тәсілдерін қолдана білу |
|
|
4. Бір айнымалысы бар сызықтық теңдеулерді шешу |
Бір айнымалысы бар сызықтық теңдеулерді шешу |
Бір айнымалысы бар сызықтық теңдеулерді шеше білу |
1 |
1 |
0 |
Сызықтық теңдеулерді шешудің алгоритмін меңгеру |
|
|
5. Тест тапсырмалары |
Тест тапсырмалары |
Өткен материалдарды қайталау және білімді бағалау |
1 |
0 |
1 |
Тақырыптар бойынша білімді тексеру |
|
|
6. Сызықтық теңдеулер жүйесін ауыстыру арқылы шешу |
Сызықтық теңдеулер жүйесін ауыстыру арқылы шешу |
Сызықтық теңдеулер жүйесін ауыстыру әдісімен шешуді меңгеру |
1 |
1 |
0 |
Сызықтық теңдеулер жүйесін шешудің әдістерін білу |
|
|
7. Сызықтық теңдеулер жүйесін қосу және азайту әдісімен шешу |
Сызықтық теңдеулер жүйесін қосу және азайту әдісімен шешу |
Сызықтық теңдеулер жүйесін қосу және азайту әдістерімен шешуді меңгеру |
1 |
1 |
0 |
Сызықтық теңдеулер жүйесін шешудің әдістерін қолдана білу |
|
|
8. Анықтауыш әдісі арқылы сызықтық теңдеулер жүйесін шешу |
Анықтауыш әдісі арқылы сызықтық теңдеулер жүйесін шешу |
Анықтауыш әдісі арқылы сызықтық теңдеулер жүйесін шешуді меңгеру |
1 |
1 |
0 |
Сызықтық теңдеулер жүйесін анықтауыш әдісі арқылы шеше білу |
|
|
9. Функциялар және олардың графиктері |
Функциялар және олардың графиктері |
Функция және оның графигі туралы түсінік қалыптастыру |
1 |
1 |
0 |
Функциялардың негізгі қасиеттерін білу және графиктерді салу |
|
|
10. Тест тапсырмалары |
Тест тапсырмалары |
Өткен материалдарды қайталау және білімді бағалау |
1 |
0 |
1 |
Тақырыптар бойынша білімді тексеру |
|
II бөлім |
11. Арифметикалық және геометриялық прогрессиялар |
Арифметикалық және геометриялық прогрессиялар |
Арифметикалық және геометриялық прогрессиялардың формулаларын қолдана білу |
1 |
1 |
0 |
Прогрессиялардың қасиеттерін қолдануды меңгеру |
|
|
12. Квадрат теңдеулерді шешу |
Квадрат теңдеулерді шешу |
Квадрат теңдеулерді шешудің әдістерін меңгеру |
1 |
1 |
0 |
Квадрат теңдеулерді шешу әдістерін қолдана білу |
|
|
13. Дәреже функциясы, оның қасиеттері және графигі |
Дәреже функциясы, оның қасиеттері және графигі |
Дәреже функциясының қасиеттерін білу және графигін сала білу |
1 |
1 |
0 |
Дәреже функциясының негізгі қасиеттерін қолдану |
|
|
14. Көпмүшені көбейткіштерге бөлу |
Көпмүшені көбейткіштерге бөлу |
Көпмүшені көбейткіштерге бөлудің әдістерін меңгеру |
1 |
1 |
0 |
Көпмүшені көбейткіштерге бөлуді қолдану |
|
|
15. Тест тапсырмалары |
Тест тапсырмалары |
Өткен материалдарды қайталау және білімді бағалау |
1 |
0 |
1 |
Тақырыптар бойынша білімді тексеру |
|
|
16. Рационал теңдеулер мен теңсіздіктерді шешу |
Рационал теңдеулер мен теңсіздіктерді шешу |
Рационал теңдеулер мен теңсіздіктерді шешу әдістерін білу |
1 |
1 |
0 |
Рационал теңдеулер мен теңсіздіктерді шешуді меңгеру |
|
|
17. Иррационал теңдеулер |
Иррационал теңдеулер |
Иррационал теңдеулерді шешу әдістерін меңгеру |
1 |
1 |
0 |
Иррационал теңдеулерді шешуде қасиеттерін қолдануды меңгеру |
|
|
18. Комбинаторикадан көбейту әдісі бойынша олимпиада тапсырмалары |
Комбинаторикадан көбейту әдісі бойынша олимпиада тапсырмалары |
Комбинаториканың көбейту әдісін олимпиадалық есептерде қолдана білу |
1 |
1 |
0 |
Комбинаторикалық есептерді шығарудың әдістерін меңгеру |
|
|
19. Ықтималдықтар теориясы және статистика |
Ықтималдықтар теориясы және статистика |
Ықтималдықтар теориясы мен статистиканың негізгі ұғымдарын білу |
1 |
1 |
0 |
Ықтималдықтар теориясы мен статистика элементтерін есеп шығаруда қолдана білу |
|
|
20. Тест тапсырмалары |
Тест тапсырмалары |
Өткен материалдарды қайталау және білімді бағалау |
1 |
0 |
1 |
Тақырыптар бойынша білімді тексеру |
|
III бөлім |
21. Ньютонның Биномы. Паскаль Үшбұрышы |
Ньютонның Биномы. Паскаль Үшбұрышы |
Ньютонның биномы мен Паскаль үшбұрышын қолдана білу |
1 |
1 |
0 |
Ньютон биномы мен Паскаль үшбұрышын практикада қолдану |
|
|
22. Теңдеулерді пайдаланып сөздік есептерді шығару |
Теңдеулерді пайдаланып сөздік есептерді шығару |
Теңдеулерді қолданып сөздік есептерді шығару дағдыларын дамыту |
1 |
0 |
1 |
Сөздік есептерді шешу үшін теңдеу құрастыру |
|
|
23. Логарифмдер және оның қасиеттері |
Логарифмдер және оның қасиеттері |
Логарифмдердің қасиеттерін білу және есептер шығаруда қолдана білу |
1 |
1 |
0 |
Логарифмдік өрнектерді түрлендіру және есептеу |
|
|
24. Рекурсия. Рекурсиялық есептерді шешу |
Рекурсия. Рекурсиялық есептерді шешу |
Рекурсия ұғымын меңгеру және рекурсиялық есептерді шеше білу |
1 |
1 |
0 |
Рекурсиялық есептерді шығаруды меңгеру |
|
|
25. Тест тапсырмалары |
Тест тапсырмалары |
Өткен материалдарды қайталау және білімді бағалау |
1 |
0 |
1 |
Тақырыптар бойынша білімді тексеру |
|
IV бөлім |
26. Олимпиада есептерін шешу |
Олимпиада есептерін шешу |
Түрлі деңгейдегі олимпиадалық есептерді шешу |
1 |
0 |
1 |
Олимпиадалық есептерді шешу тәсілдерін қолдана білу |
|
|
27. Олимпиада есептерін шығаруда сандар теориясын қолдану |
Олимпиада есептерін шығаруда сандар теориясын қолдану |
Олимпиадалық есептерді шешуде сандар теориясын қолдана білу |
1 |
1 |
0 |
Сандар теориясын қолдану дағдысын меңгеру |
|
|
28. Күрделі есептерді қарапайым қосалқы тапсырмаларға бөлу |
Күрделі есептерді қарапайым қосалқы тапсырмаларға бөлу |
Күрделі есептерді қарапайым қосалқы тапсырмаларға бөлу әдісін меңгеру |
1 |
1 |
0 |
Күрделі есептерді қарапайым есептерге айналдыра білу |
|
|
29. Күрделі есептерді қарапайым қосалқы тапсырмаларға бөлу бойынша практикалық жұмыс |
Күрделі есептерді қарапайым қосалқы тапсырмаларға бөлу бойынша практикалық жұмыс |
Күрделі есептерді қарапайым бөліктерге бөлуді практикада қолдана білу |
1 |
0 |
1 |
Күрделі есептерді шешуде бөлшектеу әдісін қолдану |
|
|
30. Тест тапсырмалары |
Тест тапсырмалары |
Өткен материалдарды қайталау және білімді бағалау |
1 |
0 |
1 |
Тақырыптар бойынша білімді тексеру |
|
|
31. Стандартты емес есептерді шешу |
Стандартты емес есептерді шешу |
Стандартты емес есептерді шығару дағдыларын дамыту |
1 |
0 |
1 |
Стандартты емес есептерді шешудің әдістерін қолдану |
|
|
32. Ребустар мен жұмбақ түріндегі олимпиадалық тапсырмалар |
Ребустар мен жұмбақ түріндегі олимпиадалық тапсырмалар |
Ребустар мен жұмбақ түріндегі олимпиадалық тапсырмаларды шеше білу |
1 |
0 |
1 |
Логикалық ойлауды дамыту |
|
|
33. Ойын теориясы және олимпиада есептері |
Ойын теориясы және олимпиада есептері |
Ойын теориясының негізгі ұғымдарын меңгеру және олимпиадалық есептерге қолдану |
1 |
1 |
0 |
Ойын теориясын олимпиадалық есептерді шығаруда қолдану |
|
|
34. Қайталауға арналған тест тапсырмалары |
Қайталауға арналған тест тапсырмалары |
Барлық өткен материалдарды қайталау және білімді тексеру |
1 |
0 |
1 |
Барлық тақырыптар бойынша білімді тексеру |
Ақпараттық - әдістемелік бөлім
«Математикадан олимпиада есептерін шығару жолдары» авторлық бағдарламасы бойынша сабақтардың әртүрлі формалары көрсетілген, олар оқушылардың математика пәніне деген қызығушылығын арттырып, ойлау қабілеттерін дамытуға бағытталған. Мұндай сабақтардың негізгі формалары:
Дәстүрлі сабақтар (лекциялар және практикалық сабақтар):
-
Мұнда мұғалім теориялық түсініктерді және есеп шығарудың негізгі әдістерін түсіндіреді.
-
Оқушылар топтық немесе жеке түрде есептерді шешіп, түсініктерін тереңдете алады.
-
Жазбаша жұмыстар және есептерді жинақтап шығару.
Талқылау сабақтары:
-
Оқушылар топтарға бөлініп, түрлі олимпиада есептері бойынша пікір алмасып, шешу жолдарын талқылайды.
-
Топтық жұмыс барысында шығармашылық пен сыни ойлау дағдыларын дамытуға мүмкіндік туады.
Кейс-стади әдісі:
-
Математикадағы нақты жағдайларды шешу арқылы әртүрлі олимпиада есептерінің мысалдары ұсынылады.
-
Бұл әдіс нақты өмірмен байланыстыруға және теорияны тәжірибемен байланыстыруға көмектеседі.
Ойын элементтерін қолдану:
-
Математикадан ойындар ұйымдастыру, мысалы, «математикалық викторина», «ойын түріндегі турнирлер».
-
Оқушыларға олимпиада есептерін шешудің қызықты және көңілді тәсілін ұсыну.
Семинарлар мен тренингтер:
-
Олимпиадалық есептердің түрлі категориялары мен шешу әдістері бойынша оқушыларға тереңірек білім беру.
-
Семинарда оқушылар мен мұғалімдер өзара тәжірибе алмасып, күрделі есептерді шешудің тәсілдерімен бөліседі.
Тәжірибелік сабақтар (компьютерлік қолдау):
-
Математикадан олимпиада есептерін шешуде арнайы бағдарламалық құралдарды (мысалы, геогебра, математикалық симуляторлар) қолдану.
-
Бұл тәсіл есептерді визуализациялау мен динамикалық түрде талдауға мүмкіндік береді.
Олимпиадалық сынақтар мен тесттер:
-
Оқушыларға нақты олимпиада тапсырмаларын орындау арқылы өз білімдерін сынау.
-
Бұл түрі оқушылардың дайындық деңгейін бағалауға және оларды тестілеуге көмектеседі.
Қашықтықтан оқыту:
-
Онлайн ресурстар мен платформалар арқылы олимпиадалық есептерді шешу әдістерін үйрету.
-
Бұл әдіс оқушыларға уақыт және кеңістік шектеулерінсіз оқу мүмкіндігін береді.
Әрбір сабақтың формасы оқушылардың жеке қажеттіліктеріне және деңгейіне қарай түрлендірілуі мүмкін, оларды олимпиадаға дайындауда тиімді әрі қызықты тәсілдермен қамтамасыз етуге бағытталған.
«Математикадан олимпиада есептерін шығару жолдары» авторлық бағдарламасында қолданылатын әдіс-тәсілдер оқушылардың математикалық ойлау қабілеттерін дамытуға, олардың олимпиадалық есептерді дұрыс және тиімді шешу дағдыларын қалыптастыруға бағытталған. Мынадай әдіс-тәсілдер қолданылады:
1. Проблемалық оқыту әдісі
-
Мақсаты: Оқушыларды қиыншылықтар мен мәселелерді өздігінен шешуге үйрету.
-
Қолданылуы: Математикадан олимпиада есептерін шешу барысында оқушыларға күрделі есептер ұсынылады, олар мәселенің шешімін табу үшін әртүрлі әдістерді пайдаланады. Бұл әдіс оқушылардың шығармашылық ойлау қабілетін арттырады.
2. Дедуктивті әдіс
-
Мақсаты: Жалпы қағидалар мен ережелерді негізге ала отырып, нақты жағдайларды талдау және шешімдер жасау.
-
Қолданылуы: Олимпиадалық есептерді шешу барысында оқушылар теориялық білімдерін (құралдар, теоремалар) нақты есептерді шешуге қолданады. Теоремалар мен ережелер арқылы шешімдер шығарылады.
3. Индуктивті әдіс
-
Мақсаты: Жеке мысалдар мен тәжірибелер негізінде жалпы қағидаларды тұжырымдау.
-
Қолданылуы: Мұғалім оқушыларға бірнеше жеке есептерді шешуді ұсынып, сол арқылы жалпы ережелер мен шешу тәсілдерін шығаруына көмектеседі. Бұл әдіс оқушылардың интуициясын дамытады.
4. Топтық жұмыс
-
Мақсаты: Оқушылардың бір-бірімен пікір алмасуын, топта жұмыс істей білу дағдыларын дамыту.
-
Қолданылуы: Оқушыларды топтарға бөліп, әр топқа олимпиадалық тапсырма беріледі. Топтар есептерді бірге шешіп, нәтижелерін талқылайды. Бұл әдіс математикалық ойлау мен ынтымақтастықты дамытуға ықпал етеді.
5. Қадамдық шешу әдісі (Алгоритмдік әдіс)
-
Мақсаты: Әрбір есепті бірнеше қадамға бөліп шешу, күрделі есептерді жеңілдету.
-
Қолданылуы: Оқушыларға есепті шешудің қадамдық жоспары ұсынылады. Әр қадамды орындау арқылы есептің шешіміне біртіндеп жақындайды. Бұл әдіс оқушылардың жүйелі түрде ойлау дағдыларын дамытады.
6. Қателерді талдау әдісі
-
Мақсаты: Оқушылардың бұрын жасаған қателерінен сабақ алу.
-
Қолданылуы: Оқушыларға шешімдерді қатемен орындаған жағдайда, олар өз қателіктерін анықтап, сол қателіктерді түзету жолдарын талдайды. Бұл әдіс оқушылардың мәселелерге қатысты сыни тұрғыдан ойлауын дамытады.
7. Геймификация (Ойын әдісі)
-
Мақсаты: Математикадан олимпиадалық тапсырмаларды ойын түрінде шешуге үйрету.
-
Қолданылуы: Оқушылар математикалық тапсырмаларды шешуде ойын элементтерін (мысалы, викториналар, турнирлер, командалық жарыстар) қолдана отырып қызығушылықтарын арттырады. Бұл әдіс оқушылардың мотивациясын жоғарылатады.
8. Кейс-стади әдісі
-
Мақсаты: Математикадан нақты өмірдегі мәселелерді шешу.
-
Қолданылуы: Оқушыларға нақты өмірден алынған олимпиадалық есептер мен тапсырмалар беріледі, олардың шешімі арқылы теория мен практиканың байланысы түсіндіріледі. Бұл әдіс есептердің өмірмен байланысын түсіндіреді.
9. Математикалық модельдеу
-
Мақсаты: Математикадағы теориялық білімді нақты жағдайлармен байланыстыру.
-
Қолданылуы: Оқушыларға математикалық модельдер құруға және оларды олимпиадалық есептерді шешуде қолдануға мүмкіндік беріледі. Бұл әдіс абстрактілі ойлау мен логикалық тұжырым жасау қабілеттерін дамытады.
10. Шығармашылық тапсырмалар
-
Мақсаты: Оқушыларды өз бетімен зерттеуге және жаңа шешу жолдарын табуға ынталандыру.
-
Қолданылуы: Оқушыларға шығармашылық тапсырмалар беріледі, мысалы, жаңа типтегі есептерді ойлап табу немесе есептерді түрлі тәсілдермен шешу. Бұл әдіс оқушылардың шығармашылық дағдыларын дамытады.
11. Бақылау және кері байланыс әдісі
-
Мақсаты: Оқушылардың нәтижелерін бақылап, қателерді анықтап, кері байланыс беру.
-
Қолданылуы: Мұғалім оқушылардың шешімдерін мұқият бақылап, оларға дұрыс бағыт береді, қателерін көрсетіп, оларды түзету жолдарын ұсынады. Кері байланыс оқушылардың қателіктерін жөндеуге және жаңа ақпараттарды терең меңгеруге көмектеседі.
Бұл әдіс-тәсілдер оқушылардың математика пәніне деген қызығушылығын арттырып, олардың олимпиадалық тапсырмаларды тиімді әрі нәтижелі шешуге мүмкіндік береді.
«Математикадан олимпиада есептерін шығару жолдары» авторлық бағдарламасында қолданылатын көрнекі құралдар мен ресурстар оқушылардың математикадан олимпиада есептерін шешу дағдыларын қалыптастыруға және тақырыптарды жақсы меңгеруіне көмектесетін маңызды компонент болып табылады. Мұнда әртүрлі көрнекі құралдар мен ресурстар қолданылып, оқушылардың оқу процесін тиімді және қызықты ету мақсатында түрлі тәсілдер қолданылады.
1. Көрнекі құралдар
-
Интерактивті тақталар: Сабақ барысында интерактивті тақтаны қолдану есептерді шешу процесін визуализациялауға, диаграммаларды, графиктерді көрсетуге және оқушыларды топтық жұмысқа тартуға мүмкіндік береді.
-
Графикалық материалдар: Геометриялық есептерді шешу үшін әртүрлі геометриялық фигуралар мен диаграммалар. Мысалы, көпбұрыштар, дөңгелектер, түзу сызықтар мен қиылысуларды көрсету үшін қолданылады.
-
Математикалық сызбалар мен диаграммалар: Есептерді шешуде қажет болатын сызбалар, графиктер, функциялардың көрнекі графиктері және геометриялық конструкциялар. Бұл әсіресе геометрия және функциялар тақырыптарында пайдалы.
-
Математикалық модельдер: Математикалық есептерді шешу үшін жасалған модельдер. Мысалы, 3D модельдер, геометриялық фигуралардың көлемдерін немесе ауданын есептеу үшін пайдаланылатын көрнекі құралдар.
-
Слайд-презентациялар: Теориялық бөлімдер мен есептерді түсіндіру үшін қолданылатын слайдтар. Презентациялар оқушыларға визуалды ақпаратты жеңіл қабылдауға мүмкіндік береді.
-
Флипчарттар мен постерлер: Есептерді шешудің қадамдарын көрсету үшін уақытша жазылатын немесе сурет салынатын флипчарттар. Бұл құрал оқушыларға тапсырмаларды топтық жұмыс арқылы талқылауға көмектеседі.
-
Таблица мен схемалар: Математикалық формулалар мен теоремалардың қысқаша тізімдерін, шешу әдістерін көрсете отырып, оқушыларға ақпаратты тиімді түрде ұсынуға мүмкіндік береді.
2. Ресурстар
-
Электронды оқулықтар мен әдістемелік материалдар: Онлайн платформалар мен ресурстар арқылы оқушыларға математикадан олимпиада есептерін шешуге арналған электронды оқулықтар мен әдістемелік құралдар ұсынылады. Мысалы, Khan Academy, Brilliant.org сияқты халықаралық платформаларды қолдану.
-
Математика бойынша сайттар: Математика олимпиадасына дайындық үшін ресурстар ұсынатын сайттар. Мысалы, matholymp.kz, artofproblemsolving.com және басқа да олимпиадалық есептерге арналған сайттар.
-
Видеолар мен онлайн курстар: Математикадан олимпиада есептерін шешу әдістерін түсіндіретін видеолар мен онлайн курстар. Бұл ресурстарды пайдалану оқушылардың визуалды және аудио ақпаратты қабылдау мүмкіндігін арттырады.
-
Математикалық бағдарламалар мен қосымшалар: Мысалы, GeoGebra, Wolfram Mathematica сияқты математикалық бағдарламаларды пайдалану. Бұл құралдар геометрияны, алгебраны, функцияларды зерттеу мен модельдеуге көмектеседі.
-
Олимпиадалық есептердің жинақтары мен кітаптар: Математика олимпиадаларының есептерін жинақтаған кітаптар мен жинақтар. Бұл әдебиет түрлері олимпиадалық есептердің үлгілері мен шешу әдістерін ұсынуға арналған. Мысалы, А. С. Алдабергеновтің «Математикадан олимпиада есептерін шешу жолдары» сияқты кітаптар.
-
Математикалық тренажерлар: Әртүрлі онлайн немесе офлайн тренажерлар мен есеп шешу платформалары. Олар оқушыларға тапсырмаларды шешуді жүйелі түрде жаттықтыруға мүмкіндік береді.
-
Математика бойынша журналдар мен мақалалар: Математикалық зерттеулер мен олимпиадалық есептерге қатысты мақалалар жариялайтын арнайы журналдар. Бұл ресурстар студенттердің тереңірек зерттеу жүргізуіне мүмкіндік береді.
-
Қосымша тапсырмалар мен жаттығулар: Әр тақырыпқа қатысты қосымша тапсырмалар мен жаттығулар, олимпиадалық есептер мен шешу тәсілдерін қамтитын жұмыс дәптерлері мен карточкалар.
3. Интерактивті және практикалық құралдар
-
Математика ойындары: Математикалық тапсырмаларды шешу арқылы қызықты түрде білім алуға мүмкіндік беретін ойындар мен викториналар. Бұл әдіс оқушылардың мотивациясын арттырып, пәнге деген қызығушылығын жоғарылатады.
-
Математикалық симуляторлар мен анимациялар: Геометриялық есептерді шешу кезінде қолданылатын анимациялар мен визуализация құралдары. Мысалы, геометриялық фигураларды өзара байланыстырып, олардың қасиеттерін зерттейтін құралдар.
-
Проблемалық-ситуациялық тапсырмалар: Қиын есептер мен нақты өмірден алынған тапсырмалар арқылы оқушыларды өздігінен шешімдер табуға үйрету. Бұл тапсырмалар нақты өмірдегі математикалық мәселелерді шешуге бағытталған.
4. Қосымша ақпараттық құралдар
-
Форумдар мен чаттар: Оқушылар мен мұғалімдер арасында пікір алмасуға мүмкіндік беретін онлайн платформалар, бұл жерлерде олимпиадалық есептерді талқылап, бір-біріне көмек көрсетуге болады.
-
Онлайн тесттер мен сауалнамалар: Оқушылардың білім деңгейін анықтау үшін онлайн тесттер мен сауалнамаларды пайдалану. Бұл құралдар оқушылардың дайындық деңгейін бақылауға мүмкіндік береді.
Бұл көрнекі құралдар мен ресурстар оқушылардың білімін тереңдетуге, олардың олимпиадалық есептерді шешу дағдыларын дамытуға, әрі олардың қызығушылығын арттыруға көмектеседі.
«Математикадан олимпиада есептерін шығару жолдары» авторлық бағдарламасында қолданылатын бағалау түрлері оқушылардың білімін және дағдыларын тиімді әрі жан-жақты бағалауға мүмкіндік береді. Бағалау түрлері оқушылардың жеке жетістіктерін, топтық жұмысқа қатысуын, шығармашылық қабілеттерін, ойлау дағдыларын және тапсырмаларды шешу тәсілдерін бағалауға бағытталған.
1. Қалыптастырушы бағалау
-
Мақсаты: Оқушылардың білімін үнемі бақылау арқылы оқу процесінде қажетті түзетулер енгізу.
-
Қолданылуы: Бұл бағалау түрі оқушылардың әр сабақтағы жетістіктерін бағалауға арналған. Оқушыларға есептерді шығару кезінде мұғалім үнемі кері байланыс беріп, қателіктерді түсіндіріп, дұрыс шешімдер ұсынады. Қалыптастырушы бағалау нәтижесінде оқушылар өз білімін жетілдіруге мүмкіндік алады.
-
Әдістері: Жұмыс нәтижелерін тексеру, ауызша сұрау, тапсырмалар бойынша пікір алмасу, өзара бағалау.
2. Жиынтық бағалау
-
Мақсаты: Оқушылардың белгілі бір оқу кезеңіндегі жалпы нәтижелерін бағалау.
-
Қолданылуы: Оқушылардың оқу кезеңі аяқталғаннан кейін немесе белгілі бір тақырыпты өткен соң, жиынтық бағалау жүргізіледі. Бұл бағалау түрі олимпиада есептері мен тапсырмалары бойынша оқушылардың толық дайындық деңгейін анықтауға көмектеседі.
-
Әдістері: Кешенді тестілеу, олимпиадалық есептерді шешу, жазбаша жұмыстар, жазбаша және ауызша емтихандар.
3. Өзін-өзі бағалау
-
Мақсаты: Оқушыларды өз оқу процесі мен нәтижелерін бағалауға үйрету.
-
Қолданылуы: Оқушылар өздерінің жеке жетістіктерін, қателіктерін, күшті және әлсіз тұстарын бағалайды. Бұл әдіс оқушылардың сыни ойлау қабілетін дамытуға көмектеседі.
-
Әдістері: Өзін-өзі бағалау парақшалары, рефлексиялық жазбалар, оқушының жеке жетістіктерін талқылау.
4. Топтық бағалау
-
Мақсаты: Оқушылардың топтық жұмысын бағалау, ынтымақтастықта жұмыс істеу дағдыларын анықтау.
-
Қолданылуы: Топтық жұмыс барысында оқушылар бірлесіп олимпиадалық есептерді шешеді, нәтижесінде топтың жұмысы бағаланады. Бұл бағалау түрі оқушылардың бір-бірімен өзара әрекеттесуін және топтық жұмысқа қатысуын бағалауға мүмкіндік береді.
-
Әдістері: Топтың жұмысына баға беру, нәтижелерін талқылау, ынтымақтастық деңгейін анықтау.
5. Кері байланыс
-
Мақсаты: Оқушылардың оқу барысында қандай қиындықтар туындайтынын, қандай нәтижелерге жеткенін анықтау.
-
Қолданылуы: Кері байланыс оқушылардың жұмысын бағалау және келешекте дұрыс шешімдер табуға көмектесу үшін қолданылады. Мұғалім оқушыларға өз жұмыстарын жақсарту жолдары мен қосымша тапсырмалар ұсынады.
-
Әдістері: Жазбаша немесе ауызша кері байланыс, жеке пікірлер, топтық талқылаулар.
6. Практикалық бағалау
-
Мақсаты: Оқушылардың практикалық дағдыларын, есептерді шешу қабілетін нақты тапсырмалар арқылы бағалау.
-
Қолданылуы: Бұл бағалау түрі оқушылардың олимпиадалық есептерді шешу кезінде қолданатын техникалық және аналитикалық дағдыларын тексереді.
-
Әдістері: Практикалық тапсырмалар, есептерді шешудің қадамдық процесін бақылау, шешімдер ұсынысы.
7. Қатысу бағасы
-
Мақсаты: Оқушылардың сабаққа қатысуын, белсенділігін және оқу процесіне қатысуын бағалау.
-
Қолданылуы: Сабақтар барысында оқушылардың белсенділігі, сұрақтарға жауап беруі, өз ойларын білдіруі және тапсырмаларды орындау деңгейі бағаланады. Бұл әдіс оқушылардың пәнге деген қызығушылығын анықтауға көмектеседі.
-
Әдістері: Сабаққа қатысу, талқылауға қосылу, сыныптық жұмыстар мен дебаттардағы белсенділік.
8. Шығармашылық және зерттеу бағасы
-
Мақсаты: Оқушылардың шығармашылық ойлауын, математикалық зерттеу дағдыларын бағалау.
-
Қолданылуы: Оқушыларға шығармашылық тапсырмалар мен зерттеу жобалары беріледі, олар өздерінің шешімдер мен ұсыныстарын ұсынады. Бұл бағалау түрі оқушылардың тәуелсіз ойлау қабілетін және математикалық зерттеулерге деген ынтасын бағалауға мүмкіндік береді.
-
Әдістері: Шығармашылық жобалар, зерттеу жұмыстарын қорғау, есептерді шешуде жаңашылдық пен креативтілікті бағалау.
9. Мотивациялық бағалау
-
Мақсаты: Оқушылардың оқу процесіне деген мотивациясын анықтау.
-
Қолданылуы: Оқушылардың тапсырмаларды орындауға деген ынтасы мен қызығушылығын бағалау. Бұл бағалау түрі оқушылардың пәнге деген жалпы қарым-қатынасын және оқуға деген ынтасын өлшеуге бағытталған.
-
Әдістері: Сабаққа қатысу, тапсырмаларды орындау белсенділігі, өз бетімен іздену.
Бұл бағалау түрлері оқушылардың білімін және қабілеттерін жан-жақты және әділ бағалауға мүмкіндік береді. Әр бағалау түрі оқушылардың түрлі дағдыларын, шығармашылық қабілеттерін және пәнге деген ынтасын дамытуға ықпал етеді.
«Математикадан олимпиада есептерін шығару жолдары» авторлық бағдарламасы – оқушылардың математикалық ойлау қабілетін дамытуға, оларды олимпиадалық есептерді шешуге дайындауға бағытталған маңызды оқу құралы. Бұл бағдарламаның маңызы бірнеше аспектілерде көрінеді:
1. Оқушылардың математикалық дағдыларын дамыту
-
Күрделі мәселелерді шешу қабілетін арттыру: Олимпиадалық есептер әдеттегі мектеп бағдарламасынан тыс, ерекше ойлау мен талдау дағдыларын талап етеді. Бұл бағдарламаны оқу оқушылардың күрделі математикалық мәселелерді шешу қабілетін арттырады, сыни ойлау мен аналитикалық дағдыларын дамытады.
-
Шығармашылық ойлауды дамыту: Олимпиада есептерін шешу кезінде стандартты әдістерден тыс тәсілдер қолдануға тура келеді. Бұл оқушыларды шығармашылық тұрғыдан ойлауға, жаңа шешу жолдарын табуға ынталандырады.
2. Теория мен практиканың байланысын нығайту
-
Теориялық білімді практикада қолдану: Бағдарлама оқушыларға математикалық теорияны нақты есептерді шешу кезінде қолдануды үйретеді. Бұл оларға математикалық концепцияларды тереңірек түсінуге көмектеседі.
-
Тәжірибелік дағдыларды қалыптастыру: Оқушылар тек теорияны оқып қоймай, оны әртүрлі олимпиадалық есептерді шешу арқылы қолдану тәжірибесін алады. Бұл олардың білімін тереңдетіп, дағдыларын шыңдайды.
3. Оқушылардың мотивациясын арттыру
-
Математикаға деген қызығушылықты ояту: Олимпиадалық есептерді шешу барысында оқушылардың математикаға деген қызығушылығы мен ынтасы артады. Қиын тапсырмаларды жеңу оқушыларға қанағаттанарлық сезім сыйлап, математиканы жақсы меңгеруге деген құштарлықтарын күшейтеді.
-
Жеке жетістіктерге қол жеткізу: Олимпиадалық жеңістер оқушыларға жеке жетістік сезімін береді. Бұл оларды әрі қарайғы зерттеулер мен білім алуға ынталандырады.
4. Математикалық қабілеттерді бағалау
-
Әртүрлі деңгейдегі тапсырмалар: Бағдарламада олимпиадалық тапсырмалар әртүрлі қиындық деңгейінде ұсынылған, бұл оқушылардың жеке деңгейіне қарай тапсырмаларды орындауға мүмкіндік береді. Бұл дағдыларды объективті бағалауға және жетістіктерді бақылауға мүмкіндік береді.
-
Оқушылардың дайындық деңгейін анықтау: Олимпиадалық есептер оқушылардың тек математикалық білімі ғана емес, сонымен қатар олардың проблемаларды шешу тәсілдерін бағалауға мүмкіндік береді.
5. Оқушылардың ойлау қабілетін кеңейту
-
Логикалық ойлауды дамыту: Олимпиадалық есептер көбінесе логикалық және аналитикалық ойлауды қажет етеді. Бағдарлама оқушылардың ойлау қабілетін кеңейтіп, математикалық логика мен дәлелдеу дағдыларын нығайтады.
-
Стратегиялық ойлауды қалыптастыру: Математикалық есептерді шешу оқушылардың жоспарлау және стратегия құру дағдыларын дамытуға ықпал етеді. Бұл дағдылар олардың тек математикада ғана емес, өмірде де пайдалы болады.
6. Ғылыми зерттеу дағдыларын дамыту
-
Зерттеу дағдыларын қалыптастыру: Олимпиадалық тапсырмаларды шешу барысында оқушылар өз бетімен зерттеу жүргізіп, мәселелерді шешу үшін жаңа идеялар мен тәсілдер ұсынады. Бұл ғылыми зерттеу мен жаңалық ашуға деген қызығушылығын арттырады.
-
Құрылымдық ойлау және дәлелдеу дағдыларын жетілдіру: Олимпиада есептерін шешу көбінесе дәлелдемелер мен шешімдерге негізделеді, бұл оқушыларды математикалық дәлдікке үйретеді.
7. Табиғи дарынды оқушыларды анықтау және дамыту
-
Математикадан талантты оқушыларды таңдау: Бағдарлама олимпиадалық есептер арқылы математикалық дарынды оқушыларды анықтауға көмектеседі. Мұндай оқушыларға арнайы бағдарламалар мен қосымша дайындықтар ұсыну арқылы олардың қабілеттерін одан әрі дамытуға мүмкіндік беріледі.
-
Дарынды балаларға арналған ресурстарды ұсыну: Математикадан дарынды оқушылар үшін арнайы тапсырмалар мен ресурстарды ұсыну олардың білімін тереңдетіп, болашақта жоғары деңгейдегі математик болуына жол ашады.
8. Оқушылардың әлеуметтік дағдыларын дамыту
-
Топтық жұмыс дағдыларын дамыту: Бағдарлама бойынша топтық жұмыстар жүргізу оқушылардың бір-бірімен қарым-қатынас жасау, пікір алмасу және ынтымақтастықта жұмыс істеу дағдыларын қалыптастырады.
-
Жауапкершілік пен көшбасшылық: Олимпиадалық тапсырмаларды шешу кезінде оқушылар бір-біріне көмектесіп, көшбасшылық қасиеттерін көрсету мүмкіндігіне ие болады.
9. Болашаққа дайындық
-
Жоғары оқу орындарына дайындық: Олимпиадалық бағдарламалар жоғары оқу орындарына түсу үшін жақсы дайындық көзі болып табылады. Математикадан олимпиада есептерін шешу университет деңгейінде қажет болатын дағдыларды дамытуға көмектеседі.
-
Халықаралық олимпиадаларға дайындық: Бағдарлама оқушыларды халықаралық олимпиадалар мен конкурстарға дайындалуға ынталандырады, бұл олардың халықаралық аренада жетістіктерге жету мүмкіндігін арттырады.
«Математикадан олимпиада есептерін шығару жолдары» авторлық бағдарламасы оқушылардың математикалық білімдерін тереңдетіп, оларды шығармашылық, аналитикалық және логикалық тұрғыдан дамытады. Бағдарламаның маңызы тек оқушылардың математикалық дағдыларын арттыруда ғана емес, олардың жеке тұлғалық дамуына, сыни ойлау қабілетін қалыптастыруға және болашақтағы ғылыми және кәсіби жетістіктеріне ықпал етуінде жатыр.
Оқу - әдістемелік нұсқаулығы
Қысқа мерзімді жоспары
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Математикадан олимпиада есептеріне кіріспе |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Математикадан олимпиада есептерінің негізгі түрлерімен және оларды шешу стратегияларымен танысу. Математикалық есептерді шешу кезінде логикалық және сыни ойлау қабілеттерін дамыту. Шешімдер мен стратегияларды талқылау кезінде топтық жұмыс пен коммуникация дағдыларын жетілдіріңіз. Ұлы математиктер және олардың ғылымның дамуына қосқан үлесі туралы білімдеріңізді кеңейтіңіз. |
|
|
Сабақтың мақсаты |
Оқушыларды математикалық олимпиадаларға табысты қатысуға дайындау, логикалық және шығармашылық ойлауын дамыту, математикаға ғылым ретінде қызығушылықтарын арттыру. |
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
Ұйымдастыру кезеңі «Қолдағы хат». |
Оқушылар ойын ойнайды
|
Формативті бағалау үнемі жүргізіліп отырады.
Жұлдыздар суреттерін тарату арқылы бағалау жүргізіледі |
Оқулықтар суреттер, слайдтар Кестелер беріледі. |
|
Жаңа білім 15 мин 2 мин Бекіту 15 мин |
Арифметика математиканың, ал математика ғылымдардың патшасы. Карл Фридрих Гаусс Фридрих Гаусстың ұлағатты сөзіне назар аударыңыздар, қалай ойлайсыздар, Фридрих не айтқысы келді?
2 - тапсырма «Постер» әдісімен орындалады.
Математика сөзіне сипаттама
бер
- Мұғалім математикалық олимпиада есептері стандартты емес жағдайларда математикалық білімді қолдана білуді талап ететін күрделі және қызықты тапсырмалар екенін түсіндіреді. - Мұғалім математикалық олимпиадаларға қатысудың артықшылықтары: логикалық ойлауды, шығармашылық әлеуетті дамыту және жоғары оқу орындарына түсуге дайындалу мүмкіндігі туралы айтады. - Мұғалім бастапқы кезеңде оқушыларды олимпиадада кездесетін мәселелердің негізгі түрлерімен танысуға шақырады. 2. Практикалық бөлім: - Мұғалім қолданылған әдістер мен шешу жолдарын түсіндіре отырып, оқушыларға бірнеше мысал есептерді шығаруды ұсынады. Ондықтары бірдей сандарды дөңгелектеңіз: 67, 86, 46, 61, 16, 68, 76, 64 Бірліктері бірдей сандарды дөңгелектеңіз: 84, 48, 74, 47, 58, 85, 64, 46 - Оқушылар алған білімдерін дәлелдеп, қолдана отырып, өз мүмкіндіктері деңгейінде есептерді шешеді. Сандардың ондық құрамын жаз: 5 ұпай (37) (41) (52) (76) (70) - Мұғалім қажет болған жағдайда көмек пен кеңес береді, оқушыларды дұрыс шешім қабылдауға бағыттайды, шығармашылық ойлауды ынталандырады. 3. Рефлексия: - Мұғалім барлық мектеп оқушыларының қатысуымен есептерді шешу жолдарын талқылайды, әдіс-тәсілдері мен шешу жолдарын сұрайды, материалды түсінгенін тексеру үшін сұрақтар қояды. - Мұғалім оқушылардың үлгерімі туралы қорытынды жасайды, дұрыс шешімдерді атап өтеді және сабақты қорытындылайды. |
Оқушылар презентацияны көреді.
Оқушылар құлақ салып тыңдайды
Оқушылар постерді толтырады
|
Дескриптор: Математикадан олимпидалық есептерге кіріспе жасайды ҚБ: Баспалдақ Дескриптор: Оқушылар негізгі терминдерді түсінеді ҚБ: Баспалдақ Оқушылар постерді өз ойларымен толтыра алады ҚБ: Мадақтау |
Оқулықтар суреттер Кестелер Сызғыш қарындаштар Қайшы Қағаздар, плакаттар, графиктер
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: «Математика олимпиадасының маңыздылығы» тақырыбына презентация дайындау. |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Алгебраны пайдаланып есептер шығару әдістері |
|
|
мҰ |
Алгебра арқылы есептерді шешудің негізгі әдістерін үйреніңіз. Осы әдістерді тәжірибеде қолдана білуге үйрету. Логикалық ойлау, талдау қабілеттерін дамыту. |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
І.Ұйымдастыру Оқушылармен сәлемдесу, түгелдеу, сынып бөлмесінің тазалығына көңіл бөлу, оқушылардың сабаққа дайындығын тексеру, оқушылардың назарын сабаққа аудару. Үй жұмысын
сұрау: |
Оқушылар амандасып, сабаққа дайындалады |
Формативті бағалау үнемі жүргізіліп отырады. |
Оқулықтар суреттер Кестелер Слайдтар |
|
Жаңа білім Бекіту |
Математика – барлық ғылымдардың тұңғышы және оларға пайдалы да, қажет те. Роджэр Бэкон
Роджэр Бэконның ұлағатты сөзі бойынша талдау жасаңыздар, Роджэр не айтқысы келді? - Сабақтың мақсатын және оның математикалық әдістерді түсіну және қолдану үшін маңыздылығын түсіндіру. - Оқушылардың есептерді шешу әдістері мен алгебра түсінігі бойынша алдын ала білімдерін тексеру үшін сұрақтар қою. - алмастыру әдісі, теңдеулер әдісі және коэффициенттер әдісі сияқты алгебра көмегімен есептерді шешудің әртүрлі әдістерін түсіндіру. - Әрбір әдісті қолдануға болатын есептерге мысалдар келтіріңіз. - Әр әдістің артықшылықтары мен шектеулерін талқылаңыз. - Әртүрлі әдістерді қолдану арқылы шешілетін күрделілік деңгейі әртүрлі бірнеше есептерді ұсыну. - Есептерді шешуге мысалдар арқылы әр әдісті суреттеңіз. - Сұрақтар қойып, оқушылардан есептерді шешудегі қадамдары мен дәлелдерін түсіндіруді сұраңыз. 1. x-ті басқа айнымалы арқылы өрнектеңіз. 2x = 7 - 3 2x = 4 x = 4/2 x = 2 2. Алынған х мәнін бастапқы теңдеуге ауыстырыңыз және тексеріңіз: 2*2 + 3 = 7 4 + 3 = 7 7 = 7 Сонымен 2x + 3 = 7 теңдеуінің шешімі х = 2 болады. Теңдеулер жүйесін теңдеу әдісімен шешуге мысал: Теңдеулер жүйесін шешейік: 2x + y = 5 x - y = 1 1. x үшін екінші теңдеуді шешейік: x = 1 + y 2. Бірінші теңдеудегі х өрнекті ауыстырыңыз: 2(1 + у) + у = 5 2 + 2ж + у = 5 3ж = 5 - 2 3ж = 3 y = 1 3. Алынған у-ның мәнін х үшін өрнекке ауыстырыңыз: x = 1 + 1 x = 2 Сонымен, 2х + у = 5 және х - у = 1 теңдеулер жүйесінің шешімі х = 2, у = 1 болады. Коэффиценттік әдісті қолданып есепті шешуге мысал: Тапсырма: Әлихан мен Данияр бірге 60 алма жинады. Әлихан Даниярдан 2 есе көп алма жинады. Олардың әрқайсысы неше алма жинады? 1. Данияр жинаған алма саны х болсын. Содан кейін Вася 2 рет алма жинады. 2. Қосындысы 60 болатын теңдеу құрайық: x + 2x = 60 3x = 60 x = 60/3 x = 20 3. Әлиханның өрнекке х мәнін қойыңыз: 2x = 2 * 20 2x = 40 Осылайша Данияр 20 алма, Әлихан 40 алма жинады. - Мектеп оқушыларын 3-4 адамнан топтарға бөлу. - Әр топқа есептер жинағын беру, олар оларды шешуде үйренген әдіс-тәсілдерін қолдана алады. - Топпен жұмыс істеу ережелерін түсіндіріп, тапсырмаларды орындау уақытын белгілеңіз. - Әр топтың үлгерімін бақылап, қажет болған жағдайда көмектесу. - Әр топтың жұмысын жинақтап, есептерді шешу әдістерін қолдануды бағалау. - Дұрыс жауаптар мен тәсілдерді талқылаңыз, сондай-ақ ықтимал қателер мен оларды түзету жолдарын табыңыз. - Оқушылардың материалды қаншалықты меңгергенін және оны тәжірибеде қолдана алатынын түсіну үшін талқылау үшін сұрақтар қойыңыз. |
Оқушылар топқа бөлініп, өздеріне берілген атауларға байланысты ақпаратты сіңіріп талдайды
Оқушылар РАФТ стратегиясы арқылы тапсырма орындайды
|
Дескриптор: ҚБ: Баспалдақ Дескриптор: Оқушы берілген нысанға байланысты өз пікірін жаза алады ҚБ: Смайлик |
Оқулықтар суреттер Кестелер Сызғыш қарындаштар Қайшы Қағаздар, плакаттар, графиктер
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: «есептер шығару әдістері» тақырыбына шағын эссе жазу. |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Математикадан олимпиада есептерін шешу |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Математикадан олимпиада есептерінің әр түрін зерттеу. Логикалық ойлау қабілеттерін дамыту және стандартты емес есептер шығару. Тапсырмаларды талқылау кезінде топтық жұмыс пен тиімді қарым-қатынасқа тәрбиелеу. Ұлы математиктер және олардың жетістіктері туралы білімдерін кеңейту. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру |
І. Ұйымдастыру
кезеңі. Психологиялық сәт. ІІ. Үй тапсырмасын сұрау. |
Қойылған сұрақтарға жауап береді. |
Оқушының жауабын толықтыру немесе тиімді кері байланыс жасау. |
Интерактивті тақта, оқулық. |
|
Жаңа білім Бекіту 15 мин |
1. Сабаққа кірісу Ақыл - ойды тәртіпке келтіретін математика. Михаил Ломоносов
Төбедегі айтылған ұлағат сөз жайлы не ойлайсыздар? Өз пікірлеріңмен бөлісіңдер. 2. Проблеманы баяндау - Мұғалім олимпиадалық есепті ұсынады және барлық оқушылардың есеп шарттарын түсінгеніне көз жеткізе отырып, оны дауыстап оқиды. - Мұғалім оқушыларды сыни тұрғыдан ойлауға, талдауға итермелейтін сұрақтар қою арқылы ойлауға жетелейді. 3. Жеке шешім - Мұғалім әр оқушыға жеткілікті уақыт пен ресурстар бере отырып, мәселені өз бетінше шешуге тырысуға шақырады. - Мұғалім әр оқушының жеке кеңестер мен кеңестер беріп, шешім қабылдау процесіне мән береді. 4. Топтық талқылау - Мұғалім оқушыларды өз шешімдерімен бөлісуге және мәселені шешу әдістерін түсіндіруге шақырады. - Мұғалім шешудің әртүрлі тәсілдерін талқылайды, олардың артықшылықтары мен кемшіліктерін бағалайды. -Мұғалім мәселені шешудің әртүрлі тәсілдерінің тиімділігіне салыстырмалы талдау жүргізеді. 1.Лесовичпен бірге Ракон серуендеп, гүл шоқтарын жинауға шешім қабылдады. Ракон 9 түсті жұлып алды. Бұл орманшының жұлып алғанынан 3 есе көп. Лесовичка букетінен гөрі Ракон букетінде қанша гүл бар? 2 Театр гастрольде тура 3 апта болды. Театрдың гастрольдік сапары неше күнге созылды?
3.Ән құстары байқауында Бұлбұл 12 ән шырқады, түрлі-түсті қарақұйрық сонша ән айтты. Робин бірнеше ән айтты. Барлығы 31 ән айтылды. Робин қанша ән айтты? А) 12 Б) 11 В) 9 Г) 7 4. Сымға 9 шам ілулі. Бірінші және соңғы фонарь арасындағы қашықтық қандай, егер олардың барлығы бір-бірінен бірдей қашықтықта болса және көршілес екі фонарь арасындағы қашықтық 1 м болса?
Есептің аяқталуы - Мұғалім есепті шығара алмаған белгілі бір оқушыларды оны аяқтауға тырысуға шақырады. - Мұғалім оқушыларға мәселені шешудің жаңа идеялары мен әдістерін береді. |
Оқушылар құлақ салып тыңдайды
Оқушылар топқа бөлініп өз арасында жұмыс өткізеді
- шешімдерді жетілдіру туралы айту
|
Дескриптор: Оқушылар лерін біледі ҚБ: Баспалдақ Дескриптор: Ұлағат сөзге талдау - шешімдерді жетілдіру туралы айту ҚБ: Баспалдақ ҚБ: Мадақтау |
интербелсенді тақта, оқулық
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: «Олимпиадағы математикалық есептер» тақырында презентация жасап кел «көлемі 3-4 слайд) |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Бір айнымалысы бар сызықтық теңдеулерді шешу. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Бір айнымалысы бар сызықтық теңдеу түсінігін үйреніңіз және оны анықтауды үйреніңіз. Сызықтық теңдеулердің негізгі қасиеттерін түсіну және қолдануды үйрену. Бір айнымалысы бар сызықтық теңдеулерді әртүрлі әдістер арқылы шешуге үйрету. Сызықтық теңдеуді шешудің дұрыстығын тексеруге үйрету. Сызықтық теңдеулерді шешуге дейінгі есептерді шешу. |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Психологиялық ахуал қалыптастыру. Оқушылардың көңілін сабаққа
аудару Үй жұмысын сұрау. |
Оқушылар бір-бірімен амандасады. |
Формативті бағалау үнемі жүргізіліп отырады |
|
|
Сабақтың ортасы |
Әлем математика тілімен бейнеленген. Галилео Галилей. Төбедегі айтылған ұлағат сөз жайлы не ойлайсыздар? Өз пікірлеріңмен бөлісіңдер. 1 – тапсырма
Fishbone техникасы, оның көмегімен проблемалар мен оларды шешу жолдарын анықтауға, себеп-салдар байланысын анықтауға болады. Сонымен, сіз бен біз сабақта сәтті жұмыс істеу үшін ережелерді қайталауымыз керек: 1) мономиалды көпмүшеге көбейту ережесі Жақшаны ашу ережелері. 3) теңдеуді шешу нені білдіреді? 4) теңдеудің түбірі дегеніміз не? Біз ережелерді қайталаймыз. Мұғалім оқушылардың бірінен ережелерді дауыстап айтуды сұрайды. - Енді өзіңізді бағалаңыз.(ең жоғары балл-3б) Енді біз қаламдарды қойып, ауызша жұмыс жасаймыз.(Слайд) Өрнекті жеңілдетіңіз а) 3 (x-1)=3x-3 б) -5 (2-у)=-10+5у в) 3х*х2=6х3 г) 5х2+3х-6х2=3х-х2 Теңдеуді шешіңіз: а) 5х=-10; б) - 3х+2 = 17 - Балалар, біз теңдеулерді бұрын шешкенбіз. Менде тақтада теңдеулер жазылған. Оларды кім шеше алады? а) 3х+2 (х-3)= - 5х+3 б) 8-5х(х-7)=1-5х2 -Балалар, сендер теңдеулерді шешуді жақсы орындадыңдар, енді жұппен жұмыс істеуге көшеміз, онда сендер қайтадан теңдеулерді шешуге жаттығасыңдар, не істей алмайтыныңды табыңдар. - Жұмысыңызды тексере аласыз. Егер бәрі ойдағыдай болса, сізге жауаптар ұсынылады. Егер сізде қандай да бір қиындықтар болса, кеңес картасын пайдалануға болады. Егер сіз өз жұмысыңызды бәрінен бұрын аяқтаған болсаңыз, картаны қосымша тапсырмамен пайдалана аласыз, сонымен қатар өзіңізді сынай аласыз. Жұппен жұмыс жасау барысында мұғалім жұмыс барысын бақылап, қиындық көрген жұпқа көмек көрсетеді. -Жұптық жұмысты аяқтадық. Егер сіз бәрін дұрыс орындаған болсаңыз, онда сіз өзіңізді бағалау картасына 5 ұпай бересіз. Егер сіз қосымша тапсырманы орындай алсаңыз, «Қосымша тапсырма» бөлімінде өзіңізге ұпай беріңіз: бірінші тапсырма үшін - 3 ұпай, екінші тапсырма үшін - 4 ұпай. -Барлығын дұрыс жасаған оқушылар бар ма? Қолыңызды көтеріңіз. -Енді нұсқалармен өзіңіз жұмыс жасай аласыз. I нұсқа: 3x-5(2x)=54 2) 7(2у-2)-2(3у-3,5)=9 3) 5x(12x-7)-4x(15x-11)=30+29x II нұсқа: 1) 7х-3(4х)=48 2) 5(3ж-1)-4(6ж-0,5)=15 3) 24x-6x(13x-9)= -13-13(6x-1) - Өзіндік жұмысты аяқтады. Тексереміз (слайд). Егер сіз бәрін дұрыс орындасаңыз, біз өзімізге 5 ұпай береміз. Екі мысал – 4 ұпай, бір мысал – 3 ұпай. -Ендеше, балалар, сабақты қорытындылайық. Сіз бүкіл сабақты өзіңізді бағалаумен өткіздіңіз. Енді ұпайларды бағалау парағындағы бағаға айналдырайық (слайд 8). Өзін-өзі бағалау картасы арқылы біз қанша ұпай бар екенін санаймыз. Біз өзімізді бағалаймыз. Бағаға қанағаттансаңыз және оны журналға салғанымды қаласаңыз, оны дөңгелектеп алыңыз. Сабақта мақсатымызға жеттік пе? Сіз біліміңізге жаңа нәрсе қостыңыз ба? |
Болжамдар жасау
Пікірталас
Тапсырманы өз бетінше орындау
Жұппен жұмыс |
ҚБ: Формативті бағалау
Формативті бағалау
Формативті бағалау
|
Оқулық, Бірнеше тар |
|
Қорытынды |
|
|
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Тест тапсырмалары. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушылардың алған білімдерін тексеру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
І. Ұйымдастыру
кезеңі. Психологиялық сәт.
|
|
|
Интерактивті тақта, оқулық. |
|
Жаңа білім 15 мин 2 мин Бекіту 15 мин |
1 – нұсқа 1. Математикадан олимпиадалық есептерді шешу үшін төменде келтірілген әдістердің қайсысын қолдануға болады? а) ауыстыру әдісі б) толық шамадан тыс әдіс в) істерді талдау әдісі 2. Алгебралық есептерді шешуде қандай ұғым қолданылады? а) туынды б) Интеграл в) Коэффициент 3. Бір айнымалы сызықтық теңдеулерді шешу үшін қандай алгоритм қолданылады? а) Гаусс әдісі б) дихотомия әдісі в) Ньютон әдісі 4. Теңдеулердің қайсысы сызықтық? а) x^2 + 2x = 5 б ) 3x + 2 = 7 в) sin (x) + 2 = 3 5. Төмендегі өрнектердің қайсысы сызықтық? а) x^3 + 2x^2 + 3x + 4 б) 3x + 2 в) log (x) + 2x 6. Формулалардың қайсысы тіктөртбұрыштың ауданын табуға мүмкіндік береді? а) S = πr^2 б) S = a * b в) S = 1/2 * a * h 7. Геометриялық прогрессия дегеніміз не? а) әрқайсысы алдыңғы санды прогрессия бөлгіші деп аталатын тұрақты санға көбейту арқылы алынған сандар тізбегі б) әрқайсысы прогрессия қадамы деп аталатын тұрақты санның алдыңғы санына қосу арқылы алынған сандар тізбегі в) сандар тізбегі, олардың әрқайсысы алдыңғы санды прогрессия бөлгіші деп аталатын тұрақты санға бөлу арқылы алынады 8. Теңдеулердің қайсысы квадрат? а) x^3 + 2x = 5 б ) 3x + 2 = 7 в) x^2-3x = 10 9. Төмендегі өрнектердің қайсысы квадрат? а) x^3 + 2x^2 + 3x + 4 б) 3x + 2 в) x^2 + 3x-4 10. Квадрат теңдеудің түбірлерін қалай табуға болады? а) кемсітушілік формуласын қолдану б) Гаусс әдісін қолдану в) Ньютон әдісін қолдану 2 – нұсқа 1. Сұрақ: Төмендегі есептердің қайсысы математикалық олимпиадаға жатады? а) қабырғалары берілген тіктөртбұрыштың ауданын табу; ә) Белгілі қабырғаларды пайдаланып үшбұрыштың периметрін есептеңіз; в) Емтиханнан өткен талапкерлердің санын, егер өту пайызы және топтағы талапкерлердің жалпы саны белгілі болса, анықтаңыз. 2-сұрақ: Функция графиктерін талдауға байланысты олимпиадалық есепті шешу үшін қандай әдісті қолдануға болады? а) Қосу және азайту амалдары; б) Графикалық шешу әдісі; в) Құнды ауыстыру әдісі. 3-сұрақ: Ауданды есептеуге байланысты есептерді шешу үшін қандай алгебралық әдістерді қолдануға болады? а) Факторизация әдісі; б) Толық ыдырау әдісі; в) Көбейту және бөлу әдісі. 4-сұрақ: Төмендегілердің қайсысы математикалық олимпиада есептері болып табылады? а) 3х + 7 = 22 теңдеуін шеш; ә) Екі санның арифметикалық ортасын есептеу; в) cos(x) функциясының туындысын табыңыз. 5-сұрақ: Белгісіз мәнді анықтауға байланысты олимпиадалық есепті шешу үшін қандай әдісті қолдану ұсынылады? а) Құнды ауыстыру әдісі; б) Графикалық шешу әдісі; в) Ортақ көбейткішке бөлу әдісі. 6-сұрақ: Төмендегілердің қайсысы математикалық олимпиада есептері болып табылады? а) Теңдеулер жүйесін шешу; б) Екі санның пайыздық қатынасын анықтау; в) Параллелепипедтің көлемін есептеңдер. 7-сұрақ: Көпмүшелік теңдеулердің түбірін табуға байланысты есептерді қандай алгебралық әдіспен шешуге болады? а) Құнды ауыстыру әдісі; б) Терминдерді жою әдісі; в) Қалдықпен бөлу әдісі. 8-сұрақ: Төмендегі есептердің қайсысы математикалық олимпиадаға жатады? а) Арифметикалық прогрессияның алғашқы N мүшесінің қосындысын табыңыз; б) Берілген радиус негізінде шеңбердің ауданын анықтау; в) Санның бөлгіштерінің санын санау. 9-сұрақ: Геометриялық дизайнға байланысты олимпиадалық есепті шешу үшін қандай әдісті қолдану ұсынылады? а) Мәндерді салыстыру әдісі; б) Терминдерді ауыстыру әдісі; в) Пифагор теоремасын қолдану әдісі. 10-сұрақ: Шексіз кемімелі геометриялық прогрессияның қосындысын есептеуге байланысты есептерді қандай алгебралық әдіспен шешуге болады? а) Күрделі бөлшек әдісі; б) Бөлшектерді ортақ бөлімге келтіру әдісі; в) Шексіз геометриялық прогрессияның қосындысы әдісі. |
|
|
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: Өткен тақырыптарды қайталау |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Сызықтық теңдеулер жүйесін ауыстыру арқылы шешу. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Сызықтық теңдеулер жүйесін шешудің негізгі әдістерінің бірі ретінде алмастыру әдісімен танысыңыз. Сызықтық теңдеулер жүйесін алмастыру арқылы шешу дағдыларын дамыту. Тәжірибелік есептерді шешуде алмастыру әдісін қолдануға үйрету. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
Психологиялық ахуал қалыптастыру.
2.Жағымды көңіл-күйге келу. Тыныс алуға зейін қою. |
Қойылған сұрақтарға жауап береді. |
Оқушының жауабын толықтыру немесе тиімді кері байланыс жасау. |
Интерактивті тақта, оқулық. |
|
Жаңа білім 15 мин 2 мин Бекіту 15 мин |
Математика - ақиқат дүниесінің сандық қатынастары мен кеңістік формалары жайлы ғылым. Фридрих Энгельс. Фридрих Энгельс кім? Фридрихтың ұлағатты сөзін талдаңыздар
Сабақтың тақырыбын тұжырымдау, сабақтың дидактикалық мақсатын қабылдау Сіз үйде жаңа материалмен таныстыңыз. Сонымен, сіз сабақтың тақырыбын өзіңіз атай аласыз: "сызықтық теңдеулер жүйесін алмастыру әдісімен шешу" Бұл сабаққа қандай мақсаттар қоямыз деп ойлайсыз? (Үйде алынған ақпаратты өзіміз жүйелейміз, оны қолдануды үйренеміз) Ақыл-ой әрекетін белсендіру 1. Ұсынылған теңдеулерден Екі айнымалысы бар сызықтық теңдеулерді таңдаңыз: а) 3х + 3у – 1 = 0 г) 1/х +1/у = 3 б) 3х2 + ж = 5 д) х + ж = 3 в) 5х + 5 = 6х е) 1/2х + у-5/6 = 0 Екі айнымалы сызықтық теңдеулер жүйесі дегеніміз не? Сызықтық теңдеулер жүйесін шешу нені білдіреді? Сызықтық теңдеулер жүйесін шешу деп не аталады? Теңдеуден х-ны білдіріңіз: 5х-10у=20; 12х + 3у= 1,2 Өрнек ж теңдеуден: ж+5х=0; 4х-3у=5 Сіз құрастырған алгоритмді атаңыз. Зерттелген нәрсені түсінуді тексеру Опциялар бойынша жұпта жұмыс істеу 1 нұсқа Теңдеулер жүйесін ауыстыру арқылы шешіңіз: а)
б)
в) 2 нұсқа Теңдеулер жүйесін ауыстыру арқылы шешіңіз: а) б) в) Реакция тексеру. Біз реакцияны тексереміз. Астарлы әңгіме ұсынылады: бірде Үнді раджасы өз субъектілері үшін жарыс ұйымдастырды: кім қабырғаға жүгіріп өтіп, басына су құйып, бір тамшы төгілмеді. Қабырғаның астында көптеген адамдар тұрды, олардың әрқайсысы айқайлап, құбырларды үрлеп, барабандарды ұрды. Тек бір адам құмыраны су төгілместен жеткізе алды. Раджа мұны қалай істегенін сұрағанда, ол ештеңе естімегенін айтты, өйткені ол суды алып жүрді. Мұғалім сөздерді атайды (демалыс, емтихан, шешім, рождество, жүйе, Астана, ауыстыру, боран, Токио, теңдеу, мереке, Мәскеу, үстел, Вашингтон, Париж) ал оқушылар естуі керек: 1) математикалық терминдер, 2) Мемлекет астаналары. |
|
|
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: Қазақстанның басқа да көне мәдениеттері туралы білімдерін кеңейту және таңдалған мәдениет туралы шағын презентация дайындау. |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Сызықтық теңдеулер жүйесін қосу және азайту әдісімен шешу. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушыларды сызықтық теңдеулер жүйесін шешу тәсілдерінің бірі ретінде қосу және азайту амалдарымен таныстыру. Оқушыларды сызықтық теңдеулер жүйесін шешуде қосу және азайту амалдарын қолдануға үйрету. Оқу материалдарымен және тапсырмалармен өз бетінше жұмыс істеу дағдыларын дамыту. |
|
|
Сабақтың мақсаты |
Оқушылардың қосу және азайту әдістерін қолдана отырып, сызықтық теңдеулер жүйесін шешу дағдыларын дамыту, логикалық және аналитикалық ойлауын дамыту, сонымен қатар қолданбалы есептердегі математикалық білімдерді қолданудың практикалық дағдыларын дамыту. |
|
|
Сабақ барысы |
Оқытушының іс- әрекеті |
Оқушының іс- әрекеті |
Бағалау |
ресурстар |
|
Сабақтың басы
|
І. Ұйымдастыру кезеңі.
Психологиялық
сәт. ІІ. Үй тапсырмасын сұрау. |
Қойылған сұрақтарға жауап береді.
|
Оқушының жауабын толықтыру немесе тиімді кері байланыс жасау. |
Интерактивті тақта, оқулық. |
|
Сабақтың ортасы 20 минут |
Алгебра біреу. Ол ұлтқа, дінге, мәдениетке, елге, жерге бөлінбейді. «Төрткен төртқараның» айырмашылығы неде? Тек қазақша атауында ғана. Асқар Жұмаділдаев атамыздың ұлағатты сөзі жайлы не ойлайсыздар? Пікірлеріңмен бөлісіңдер
Фронтальды шолу. Екі айнымалысы бар екі сызықтық теңдеулер жүйесі қалай аталады? Екі айнымалысы бар екі сызықтық теңдеулер жүйесінің шешімі қандай? Екі айнымалысы бар теңдеулер жүйесін шешу нені білдіреді? (1;1) сандар жұбы теңдеулер жүйесінің шешімі болып табылады
Екі айнымалысы бар теңдеулер жүйесін шешудің қандай әдістерін білесіз? Теңдеулер жүйесін шешуде не қолданасыз? Ауыстыру әдісі және графикалық әдіс дегеніміз не? (Ережені құрастыру).
Фронтальды зерттеу: Бір айнымалыны екіншісі арқылы өрнектеуге ыңғайлы теңдеуді таңдайық. Бұл жағдайда бұрын зерттелген әдістер бізге сәйкес келмейді. Бұл жағдайдан шығудың жолы қандай? Бірінші жүйені шешкеннен кейін жеткен қорытындыға назар аударыңыз. Бір айнымалысы бар сызықтық теңдеуді алғаннан кейін ғана жүйені шешу мүмкін болды. Теңдеулер жүйесін қараңыз және берілген екі теңдеуден бір айнымалысы бар бір теңдеуді қалай алуға болатынын ойлаңыз. Теңдеулерді қосыңыз. Теңдеулерді қосу деген нені білдіреді? Теңдеулердің сол жақтарының қосындысын, оң жақтарының қосындысын бөлек құрастырып, алынған қосындыларды теңестір. Сабақтың тақырыбы мен мақсатын тұжырымдау Сабақтың тақырыбын жазу Қосу әдісі арқылы сызықтық теңдеулер жүйесін шешу 13x+17y+14x-7y=43+11 27x+0=54 27x=54 ; x=54:27; x=2 |
Оқушылар жаңа сабақты меңгереді Теңдеулерді қосу деген нені білдіретінін біледі |
Теңдеулер жүйесін шешуді үйренеді ҚБ: Гулдер Оқушылар ауыстыру әдісін біледі ҚБ: От шашу |
Слайд, оқулық, Интерактивті тақта, оқулық, фигуралары және тақтасы.
|
|
Сабақтың соңы |
Үйге тапсырма: Сызықтық теңдеулер жүйесін қосу және азайту арқылы шешу жайлы презентация дайындап кел |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Анықтауыш әдісі арқылы сызықтық теңдеулер жүйесін шешу |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Сызықтық теңдеулер жүйесін шешу әдістерінің бірі ретінде анықтауыштар әдісімен оқушыларды таныстыру. Оқушыларға сызықтық теңдеулер жүйесін шешу үшін осы әдісті қолдануға үйрету. Оқу материалымен өз бетінше жұмыс істеу дағдыларын дамыту. Пәннің өмірмен және практикалық іс-әрекетімен байланысын көрсете отырып, математикаға деген қызығушылықтарын арттыру. |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Психологиялық ахуал қалыптастыру. Оқушылардың көңілін сабаққа
аудару |
Оқушылар бір-бірімен амандасады. |
Формативті бағалау үнемі жүргізіліп отырады |
Оқулықтар |
|
Сабақтың ортасы |
Кітапқа енген кез келген формула оны сатып алушылардың санын екі есеге азайтады. Стивен Хокинг. Стивенг Хокингтың ұлағатты сөзі жайлы не
ойлайсыздар? - Мұғалім бүгінгі сабақта сызықтық теңдеулер жүйесін шешу әдісі - анықтауыштар әдісімен танысамыз деп түсіндіреді. - Мұғалім оқушыларға сызықтық теңдеулер жүйесі туралы түсінікті еске салады және мұндай жүйенің бір, шексіз көп немесе шешімдері жоқ болуы мүмкін екенін есіне түсіреді. - Мұғалім анықтауыштар әдісі матрицалардың анықтауыштарын қолдануға негізделгенін түсіндіреді. - Мұғалім оқушыларға матрицаның анықтауышы және оның қасиеттері туралы еске салады. - Мұғалім сызықтық теңдеулер жүйесін бейнелейтін матрицаны қалай құру керектігін түсіндіреді. - Мұғалім сызықтық теңдеулер жүйесін шешу үшін матрицаның анықтауышын қалай қолдану керектігін түсіндіреді. Анықтама 1. Матрица –
сандардан тұратын төртбұрышты кесте. Белгілер: А-матрица, аіj-матрица элементі, i-берілген элемент тұрған жол нөмірі, j-тиісті баған нөмірі; m – матрица жолдарының саны, n – оның бағандарының саны. Анықтама 2. m және n сандары матрицаның өлшемдері деп аталады. Анықтама 3. Егер m = n болса, матрица квадрат деп аталады. Бұл жағдайда n саны шаршы матрицаның реті деп аталады. Әрбір шаршы матрицаны
матрицаның барлық элементтерін пайдаланып бірегей түрде анықталатын
санмен байланыстыруға болады. Бұл сан анықтауыш деп
аталады Крамер әдісі. (Габриэль Крамер (1704-1752) швейцариялық математик) Бұл әдіс айнымалылар саны теңдеулер санымен сәйкес келетін сызықтық теңдеулер жүйесінде ғана қолданылады. Сонымен қатар, жүйе коэффициенттеріне шектеулер енгізу қажет. Барлық теңдеулер сызықтық тәуелсіз болуы қажет, яғни. ешбір теңдеу басқаларының сызықтық комбинациясы болмайды. Ол үшін жүйелік матрицаның анықтауышы 0-ге тең болмауы керек. Шынында да, жүйенің кез келген теңдеуі басқаларының сызықтық комбинациясы болса, онда сызықтық түрлендірулерді пайдалана отырып, бір жолдың элементтеріне басқа жолдың элементтерін кейбір санға көбейтетін қоссаңыз, нөлдік жолды алуға болады. Бұл жағдайда анықтауыш нөлге тең болады. Теорема (Крамер Ережесі). N
белгісіз n теңдеулер жүйесі |
Оқушылар Анықтауыш әдісін талқылайды.
Оқушылар осы материал бойынша өз бетінше жұмыс істейді |
Дескриптор: Оқушылар шын/жалған ойына бойынша ойынға кірісе алады |
|
|
Қорытынды |
Үйге тапсырма беру: Функциялар және графиктер жайлы ақпарат жинап келіңдер |
|
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Функциялар және олардың графиктері |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Функция ұғымын меңгеру, функцияның негізгі элементтерін анықтауды үйрену (аргумент, функция мәні, анықтау облысы және мәндер жиыны). Функциялардың негізгі түрлерін (сызықтық, квадраттық, дәрежелік және т.б.) оқып, оларды ажырата білуге үйрету. Функцияны көрсетудің әртүрлі тәсілдерімен (аналитикалық, графикалық, кестелік) танысыңыз және бір әдістен екіншісіне өтуді үйреніңіз. Әртүрлі функциялардың графиктерін құруды және олардың қасиеттерін талдауды үйрену. Функциялар мен олардың графиктеріне байланысты есептер шығару дағдыларын дамыту. |
|
|
Сабақтың мақсаты |
Функциялардың әртүрлі түрлері, олардың графиктері туралы білімді меңгеру, сонымен қатар ғылым мен техниканың әртүрлі салаларындағы қолданбалы есептерді шешу үшін әртүрлі координаталар жүйесіндегі функциялардың графиктерін оқу, тұрғызу және талдау дағдыларын дамыту. |
|
|
Сабақ барысы |
Оқытушының іс- әрекеті |
Оқушының іс- әрекеті |
Бағалау |
ресурстар |
|
Сабақтың басы 10 минут |
Ұйымдастыру кезеңі «Денелік өзара әрекеттесу» жаттығуы. |
Оқушыларды сабаққа дайындау. Оқушылар ойын ойнау арқылы серпіліп қалады. Оқушылар қойылған сұраққа жауап береді |
Формативті бағалау үнемі жүргізіліп отырады. Гүлдердің суреттерін тарату арқылы бағалау жүргізіледі
|
Оқулықтар суреттер, |
|
Сабақтың ортасы
|
Фрэнсис Бэконның ұлағатты сөзі жайлы не ойлайсыздар? Әкімдік тұрғындарға әрқайсысының ауданы 6 акр (600 м2) болатын саяжай үшін төртбұрышты жер телімін бөлді. Егер ауданның өлшемдерінің бірі х болса, онда оның екінші y өлшемін қалай табуға болады? Анықтама. Х айнымалысының әрбір мәні тәуелді y айнымалысының бір мәнімен байланысты болатын үлгіні функция немесе функционалдық тәуелділік деп атайды. Немесе х айнымалысының әрбір мәні у айнымалысының бір ғана мәніне сәйкес келеді. Талқылау «Графиктерді қай жерде кездестіреміз?» Мысалдар Температураның тәулік уақытына қатысты графигі. 1. График арқылы сағат 4-те ауа температурасы қандай болғанын анықтаңыз? Сағат 12-де? сағат 24-те? Ең жоғары температура қашан болды? Тәуелді айнымалыны атаңыз? Тәуелді айнымалыны атаңыз? Қозғалыс кестесі Тәуелді айнымалыны атаңыз? Тәуелді айнымалыны атаңыз? Функцияның графигін қалай саламыз? Функция мына формуламен берілсін: y = x(4 – x), мұндағы -1 ≤ x ≤ 5 Осы функция үшін мәндер кестесін
құрайық: 3. Кесте деректерін пайдалана отырып, біз координаталық жазықтықта нүктелерді саламыз (презентацияда қалам мен таңдауды қолданамыз және нүктелерді координаталық жазықтыққа орнатамыз) 4. Осы нүктелерді тегіс сызықпен қосамыз, алынған қисық y = x(4 – x) функциясының графигі болады. 5.Бекіту Функция у = 2x – 3 формуласымен берілген, мұндағы -2 ≤ x ≤ 2 К Құрылған графикті тексеру. |
Оқушылар сұрақтарға жауап береді Оқушылар дәрісті мұқият тыңдайды |
Дескриптор: Оқушылар график жайлы біледі. Гүлдердің суреттерін тарату арқылы бағалау жүргізіледі
ҚБ: Бес бармақ
|
Оқулықтар суреттер, слайдтар Кестелер, Интерактивті тақта, оқулық, |
|
Үйге тапсырма беру |
Кері
байланыс: Үйге тапсырма: «Функция және график» тақырыбында ребус жасап кел |
Күнделікке үй тапсырмасын жазады. |
|
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Тест тапсырмалары. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушылардың алған білімдерін тексеру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
І. Ұйымдастыру кезеңі. Сәлемдесу, түгелдеу
|
|
|
Интерактивті тақта, оқулық. |
|
Жаңа білім 15 мин 2 мин Бекіту 15 мин |
1 – нұсқа 1. Функцияның визуализациясы қалай аталады? а) Кесте б) Туынды в) интегралдық 2. Сызықтық теңдеулер жүйесін анықтауыштардың көмегімен шешу үшін қандай әдіс қолданылады? а) Гаусс әдісі б) Крамер әдісі в) Иордан әдісі 3. Сызықтық теңдеулер жүйесін шешудің қандай әдісі теңдеулерді қосу және азайтуға негізделген? а) Иордан әдісі б) Крамер әдісі в) Гаусс әдісі 4. Бір теңдеу екіншісімен ауыстырылатын сызықтық теңдеулер жүйесін шешу әдісі қалай аталады? а) Иордан әдісі б) Крамер әдісі в) Айнымалы ауыстыру әдісі 5. Функцияның координаталық жазықтықта көрінісін бейнелейтін график қалай аталады? а) Сызықтық график б) Көрсеткіштік график в) Функционалдық диаграмма 6. Анықтауыш әдісін қолданғанда сызықтық теңдеулер жүйесінің бірегей шешімі болуы үшін қандай шарт орындалуы керек? а) Жүйе матрицасының анықтауышы нөлге тең болуы керек б) Жүйе матрицасының анықтауышы нөлге тең болмауы керек в) Жүйе матрицасы симметриялы болуы керек 7. Қосу және азайту арқылы шешкенде жүйе қанша теңдеуден тұрады? а) Дәл бір теңдеу б) Екі теңдеу в) Үш теңдеу 8. Математикадағы қандай әдіс теңдеуді шешпей-ақ функциялардың жуық мәндерін табуға мүмкіндік береді? а) жуықтау әдісі б) Ауыстыру әдісі в) Гаусс әдісі 9. Функцияның негізгі сипаттамаларын анықтауға мүмкіндік беретін функцияның сипаттама графигі қалай аталады? а) Функцияның графигі б) Теңдік графигі в) Аналитикалық график 10. Функцияның графигін зерттеу арқылы ол туралы қандай ақпаратты алуға болады? а) Функцияның белгілі бір нүктедегі мәні б) Функцияның туындысының мәні в) Функция облысы 2 – нұсқа 1. Функция дегеніміз не? а) Математикалық өрнек б) Екі шама арасындағы байланыс в) Белгілі бір операцияларды орындағаннан кейін алынған сан 2. Қандай график у = х^2 функциясын көрсетеді? а) (Параболаны көрсететін график) б) (Түзу сызықты бейнелейтін график) в) (Синустық толқынды көрсететін график) 3. Төмендегі теңдеулердің қайсысы функция болып табылады? а) х + у = 5 б) у = 3 в) х^2 + у^2 = 9 Тақырыбы: Анықтауыш әдісі арқылы сызықтық теңдеулер жүйесін шешу 4. Анықтауыш әдісі арқылы сызықтық теңдеулер жүйесінің шешімін қалай табуға болады? а) матрицаның анықтауышын есептеп, оның мәндерін формулаға қойыңыз б) Теңдеулердің коэффициенттерінің қосындысын есептеп, алынған теңдеуді шеш в) Теңдеулердің графиктерінің қиылысу нүктесінің координаталарын табыңдар 5. Сызықтық теңдеулер жүйесінің матрицасының анықтауышы нөлге тең болса, бұл нені білдіреді? а) Жүйенің шешімі жоқ б) Жүйенің шешімдерінің шексіз саны бар в) Жүйенің бірегей шешімі бар 6. Анықтауыш әдісі арқылы сызықтық теңдеулер жүйесінің табылған шешімінің дұрыстығын қалай тексеруге болады? а) Табылған мәндерді жүйенің барлық теңдеулеріне ауыстырыңыз және олардың дұрыстығын тексеріңіз б) Теңдеулер жүйесін басқа түрге айналдырып, алынған нәтижені салыстыру в) Теңдеулердің барлық коэффициенттерін анықтауышқа көбейтіп, қосымша есептеулер жүргізіңдер Тақырыбы: Қосу және азайту әдісі арқылы сызықтық теңдеулер жүйесін шешу 7.Сызықтық теңдеулер жүйесін қосу және азайту әдісі арқылы қалай шешуге болады? а) Екі теңдеуді де белгілі бір санға көбейтіп, оларды қосу/азайту ә) Бір теңдеудегі бір айнымалыны екінші айнымалымен өрнектеп, оны басқа теңдеумен алмастыру в) Берілген жүйеге тән белгілі бір формулалар мен шешу әдістерін қолдану 8.Сызықтық теңдеулер жүйесінің табылған шешімінің дұрыстығын қосу және азайту әдісі арқылы қалай тексеруге болады? а) Табылған мәндерді шешілмеген теңдеулердің орнына қойып, олардың дұрыстығын тексеріңіз б) Теңдеулер жүйесін басқа түрге айналдырып, алынған нәтижені салыстыру в) Ауыстыру әдісін қолданыңыз және алынған шешім жүйенің басқа теңдеулерін де қанағаттандыратынын тексеріңіз Тақырыбы: Сызықтық теңдеулер жүйесін алмастыру әдісі арқылы шешу 9. Сызықтық теңдеулер жүйесін алмастыру әдісі арқылы қалай шешеді? а) Дискриминантты есептеп, оның мәнін теңдеулердің түбірін табу үшін пайдаланыңыз ә) Бір теңдеуді екінші теңдеуге ауыстырып, алынған теңдеуді шеш в) Бір теңдеудегі бір айнымалыны екіншісімен өрнектеп, оны басқа теңдеуге ауыстыр 10. Сызықтық теңдеулер жүйесінің табылған шешімінің дұрыстығын ауыстыру әдісі арқылы қалай тексеруге болады? а) Табылған мәндерді жүйенің барлық теңдеулеріне ауыстырыңыз және олардың дұрыстығын тексеріңіз б) Жүйенің шешілген теңдеулерін пайдаланып қосымша теңдеу құрып, дұрыстығын тексеру в) Теңдеулердің барлық коэффициенттерін белгілі бір санға көбейтіп, қосымша есептеулер жүргізу |
|
|
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: Өткен тақырыптарды қайталау |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Арифметикалық және геометриялық прогрессиялар |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушыларды арифметикалық және геометриялық прогрессия ұғымдарымен және олардың зерттелу тарихымен таныстыру. Оқушыларға прогрессияның n-ші мүшесі және алғашқы n мүшесінің қосындысы формулаларын пайдаланып есептер шығаруға үйрету. Алған білімдерін талдау және жалпылау, әртүрлі күрделіліктегі есептерді шешуде қолдану қабілеттерін дамыту. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
Ұйымдастыру кезеңі:
|
Қойылған сұрақтарға жауап береді. |
Оқушының жауабын толықтыру немесе тиімді кері байланыс жасау. |
Интерактивті тақта, оқулық. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Жаңа білім 15 мин 2 мин Бекіту 15 мин |
Шынайы өмірге қатысы бар
математика заңдылықтары сенімді емес, ал сенімді математика
заңдылықтарының шынайы өмірге түк қатысы
жоқ. Альберт
Эйнштейн. Альберт Энштейн не айтқысы
келді? Ежелгі дәуірдегі арифметикалық прогрессиялар (Тарихи есептер). Вавилондықтардың сына жазу кестелерінде, Египет пирамидаларында (б.з.д. 2 ғ.) арифметикалық прогрессиялардың мысалдары бар. Мысырлық ахмес папирусынан алынған тапсырманың мысалы: "Сізге айтсын: арпаның 10 шарасын 10 адамға бөліңіз, әр адам мен оның көршісі арасындағы айырмашылық шараның 1/8 бөлігіне тең.» Міне, мысырлықтар қолданған формула:
Ежелгі заманнан бізге жеткен прогрессивтік мәселелер шаруашылық өмірінің талаптарымен байланысты болды: өнімді бөлу, мұраны бөлу және т.б. Прогрессияларға қатысты кейбір формулалар қытай және үнді ғалымдарына белгілі болды. Арьябхатта (5 ғасыр) арифмдердің жалпы сандары мен қосындылары үшін формулаларды пайдаланды. Прогрессия. Бірақ ерікті арифмнің мүшелерінің қосындысын табу ережесі. прогрессия алғаш рет 1202 жылы Пизалық Леонардоның «Абак кітабы» еңбегінде кездеседі.
Мәселені шешейік – біздің дәуір басындағы аңыз.
Үнді патшасы Шерам шахмат ойынының өнертапқышы Сетуды тапқыр ойлап тапқаны үшін марапаттау үшін шақырып, оны жомарттықпен марапаттауға уәде берді. Өнертапқыш Сет шахмат тақтасының бірінші шаршысына бір дән, екіншісіне 2, үшіншісіне 4, т.б. беруді сұрады. Қуанған патша осындай «қарапайымды сый» беруді бұйырады. Алайда король өнертапқыш Сетаның тілегін орындай алмағаны белгілі болды, өйткені... астық саны өте көп болды. Есеп шығарайық. (Драмалық қойылым) Берілгені:
Шешілім: Репродуктивті сипаттағы мәселелерді шешу. Өзара бақылауды ұйымдастыру. Енді заманауи мәселелерді шешуге көшейік. Сабақтың күні мен тақырыбын дәптерлеріңе жазып алыңдар. Тапсырмалар жазылған карточкаларды таратып, 2 адамды тақтаға шақырамын, қалған сынып дәптерлеріне жазады. 1) *(сn) реті сn =n/2 -4 формуласымен берілген. c1, c8, c300, ck+1 табыңыз. 2) Арифметикалық прогрессияның әріппен жазылған мүшелерін табыңыз: a1, a2, 15, a4, a5, 33, a7, . . . 3) (– 2,6) тең арифметикалық прогрессияның (xn) мүшесінің санын табыңыз, егер x1 = 8,2 және d = -0,3 болса. 4) Арифметикалық прогрессия берілген -3,6; -3, 3; -3; ...Қай саннан бастап оның мүшелері оң болады? 5) х-1 болатын х мәндерін табыңыз; 4x-3 және x2+1 арифметикалық прогрессияны құрайды ма? 6) a5=6, a12=27 болса, арифметикалық прогрессияның алғашқы жиырма мүшесінің қосындысын табыңыз. 7) Сол жағында жазылған қосындыдағы мүшелер 56+50+44+ …+x=280 арифметикалық прогрессиясын құрайтын теңдеуді шешіңіз.
Енді геометриялық прогрессияны қайталайық. 9) *Геометриялық прогрессияның (bn) бөлімін табыңыз, егер b4 =4, b6 =8 болса. 10)162 саны 2/9 геометриялық прогрессияның мүшесі; 2/3; 2;... Осы мүшенің санын табыңыз. 11) q=3/4, S4 =350 болатын геометриялық прогрессияның b1-ін табыңыз. 12) Геометриялық прогрессияда b1=7, bn =567, Sn =847. q және n табыңыз. 13) Геометриялық прогрессияның бесінші және үшінші мүшелерінің айырмасы 240, ал төртінші мен екінші мүшелерінің айырмасы 60. Осы прогрессияның алғашқы алты мүшесінің қосындысын табыңыз. 14) Оң мүшелері S2=8, S3=26 болатын геометриялық прогрессияда. S5 табыңыз. 15) Кесте бойынша өзіндік жұмыс (жауапты экранда көрсетемін, өзара тексеру жүргізіледі, нәтиже көршінің жеке картасына енгізіледі)
|
Оқушыар жаңа сабақты меңгереді
Оқушылар құлақ салып тыңдайды
|
ҚБ: Оқушылар ортаңғы кезеңнің қыр-сыры мен маңыздылығын ұғады ҚБ: Мадақтау
|
Оқулықтар суреттер Кестелер Сызғыш қарындаштар Қайшы Қағаздар, плакаттар, графиктер
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: «Идеал тапсырма» старегиясы.
(Шығармашылық ізденіс тапсырмасы) – Арифметикалық және геометриялық прогрессиялар жайлы презентация дайындап кел |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Квадрат теңдеулерді шешу. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушыларды квадрат теңдеу ұғымымен және оның негізгі түрлерімен таныстыру. Квадрат теңдеудің түбірін табу формулаларын үйреніңіз. Оқушыларды квадрат теңдеулердің әртүрлі түрлерін шешу үшін осы формулаларды қолдануға үйрету. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақ барысы |
Оқытушының іс- әрекеті |
Оқушының іс- әрекеті |
Бағалау |
ресурстар |
|
Сабақтың басы 10 минут |
Ұйымдастыру кезеңі
Есте қалған қызықты
оқиға |
Оқушылар қимыл іс әркетін орындайды |
Формативті бағалау үнемі жүргізіліп отырады. |
Оқулықтар суреттер, слайдтар Кестелер |
|
Сабақтың ортасы 20 минут |
Үлкен пирамидалы храмдардың архитектурасын мылқау математика десе де болады. Освальд Шпенглер.
Келесі сұрақтарға жауап беріңіз: Сұрақтарға жауап бер: 1. Қай теңдеу квадрат деп аталады? 2. Теңдеуді шешу деген нені білдіреді? 3. Қандай квадрат теңдеулер толық емес, қайсысы толық деп аталады? 4. Толымсыз квадрат теңдеулердің түрлерін көрсетіңіз 5. Толық шаршы урандардың түрлерін атаңыз 6. Толық квадрат теңдеудің қанша түбірі болуы мүмкін? Анықтамалық диаграмманы пайдалана отырып, мәселені талдап, шешеміз. 1 тапсырма. Арман Маратұлы дүкенге өзінің төртбұрышты учаскесіне қоршау алу үшін келгенімен оның өлшемдерін ұмытып кеткен. Арман Маратұлының есінде тек жер учаскесінің ауданы 750 м2 болса, ал жер учаскесінің ұзындығы енінен 5 метр үлкен болса, қанша уақытқа қоршау сатып алуы керек? Шешімі: Ауданның ені х болсын. Көбінесе беймәлім шамалардың кішісі деп х-ті қабылдаған ыңғайлы. Сонда кесіндінің ұзындығы x + 5 болады. Тіктөртбұрыштың ауданы S = x • (x + 5) x • (x + 5) = 750, x² + 5x - 750 = 0. Осы теңдеудің дискриминантын және оның түбірлерін табайық. a = 1, b = 5, c = -750 D = b² - 4ac D = 5² - 4 • 1 • (-750) = 25 + 3000 = 3025 = 552 x₁, ₂ = (-5 ± √3025)/(2 • 1), x1 = (-5 - 55)/2 немесе x2 = (-5 + 55)/2. x₁ = -30 немесе x₂ = 25 Табылған түбірлердің біріншісі мәселенің мағынасында бөгде болып табылады, яғни қиманың ені 25 м-ге тең болады.Демек, ұзындығы 25 + 5 = 30 м-ге тең болады. Енді Арман Маратұлы өз сайтының периметрін есептей алады. P = 2 • (25 + 30) = 110 м Сізге 110 м қоршау сатып алу керек. Әр топқа таблеткалар
дайындалды. Әр топ Kahoot арқылы есептің шешімін
тексереді. Жеке тапсырмалар. Экранда квадрат теңдеулерді көрсетемін: 1. x2 -49=0 2. 64x+4x2 = 0 3. 2x(x+3)=6x-x2 4. 5x2 + 9x –14 = 0; 5. 5x2 + x – 6 = 0; 6. 3х2 – 5х + 2 = 0 7. 2x2 + 5x + 2=0, Мен жеке тапсырмаларды Kahoot порталы арқылы планшеттер арқылы тексеремін. Топтық тапсырма: Бұған дейін сіз екеуміз Арман Маратұлына өз меншігіндегі қоршау үшін қанша материал қажет екенін есептеуге көмектестік, жақсы жұмыс жасағаныңыз үшін Арман Маратұлы бізге жаңа өтінішпен жүгінді. Оған үй салуға, құрылыс материалдарының логистикасына және т.б. көмектесуге тура келеді. Тақтадағы тапсырмаларды тізімдеймін: Арман Маратұлының үйінің құрылысын бастап жатырмыз 1 топ. Үй төртбұрышты пішінді. Бір жағы екіншісінен 4 метрге кіші. Алып жатқан жер аумағы 396 м². Үйдің периметрін табыңыз және бір стандартты панельдің ұзындығы 4 метр болса, үй салу үшін қанша бетон панелі қажет болатынын табыңыз. Шешімі: Үйдің ені х болсын. Сонда үйдің ұзындығы х + 4 болады. Тіктөртбұрыштың ауданы S = x • (x + 4) x • (x + 4) = 396, x² + 4x -396 = 0. Осы теңдеудің дискриминантын және оның түбірлерін табайық. a = 1, b = 4, c=-396 D = b² - 4ac D = 4² - 4 • 1 • (-396) = 16 + 1584 = 1600 x₁, ₂ = (-4 ± √1600)/(2 • 1), x1 = (-4 - 40)/2 немесе x2 = (-4 + 40)/2. x₁ = -22 немесе x₂ = 18 Табылған түбірлердің біріншісі мәселенің мағынасында бөгде, яғни үйдің ені 18 м-ге тең болады.Демек, ұзындығы 18 + 4 = 22 м-ге тең болады. Енді Арман Маратұлы өз сайтының периметрін есептей алады. P = 2 • (18+ 22) = 80 м 80/4=20 дана панельдер Жауап: сізге 20 дана бетон панельдері қажет 2-топ. Құрылыс материалдарына қайда бару керек? Үйден солтүстікке қарай В зауыты, ал шығысында А зауыты орналасқан. Зауыттардың арасы үйден А зауытына дейін 3 км, ал В зауытына қарағанда 6 км артық. Сізге қанша қашықтық қажет. А зауытында блоктарды сатып алу үшін саяхаттаңыз ба? Шешуі: х км – зауыттар арасындағы қашықтық. (x-3) км – А дейін қашықтық (x-6) км – В дейінгі қашықтық Пифагор теоремасы бойынша (x-6)²+(x-3)²=x² x²-12x+36+ x²-6x+9- x²=0 x²-18x+45=0 (x-9)²-81+45=0 (x-9)²=36 x-9=6 x-9=-6 x=15 x=3 3-6 А қондырғысына 15-3=12 км жол жүру керек. Жауабы: А зауытына дейін 12 км 3-топ. Алаңды көгалдандыру Гүлзарға жер учаскесін дайындау керек. Мұны істеу үшін, егер үй иесі тікбұрышты үшбұрыш түрінде гүлзар жасауды шешсе, оның жақтарын табу керек. Оң жақ бұрышқа қарама-қарсы жатқан жағы 5 м. қалған екі жақтың бірі 1 м аз. Гүлзардың белгісіз жақтарын табыңыз. Шешім: Пифагор теоремасы бойынша шешеміз. 1 аяғы=x 2 аяғы=x-1 X2 +(x-1) 2 = 52 X2+x2-2x+1=25 2Х2-2х-24=0 (/2) X2-x-12=0 X1=4, x2=-3 X2 сәйкес келмейді, осы себепті x=4 1 аяғы=4 м, 2 аяғы=5 м Жауап: 4м, 5м. |
Оқушылар жаңа сабақты меңгереді Оқушылар квадратты теңдеулерді шеше алады Оқушылар топта жұмыс жасай алады |
Оқушылар өз болжауын айтады Мадақтау Оқушылар берілген материалды дәптеріне жазады Қолшапалақтау
Дескриптор: Оқушылар ойынның жапырақшалық ойыны арқылы жаңа тақырыпты тиімді меңгереді алады Басбармақ
|
Слайд, оқулық, интерактивті тақта, графиктер, сызбалар, |
|
Сабақтың соңы 10 минут |
Кері байланыс:
Үйге тапсырма: Дәреже функциясы, оның қасиеттері және графигі жайлы сабаққа дайындалып кел |
Оқушылар мұғаліммен кері байланыс жасайды |
|
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Дәреже функциясы, оның қасиеттері және графигі |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Қазақстан жеріндегі алғашқы тайпалардың қалыптасу тарихын зерттеу. Географиялық орнының тайпалардың қалыптасуына әсерін талдау. Тайпалардың мәдени және діни ерекшеліктерін зерттеу. |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 5 мин |
Ынтымақтастық атмосферасын қалыптастыру Сәлемдесу, түгелдеу. Өткен тақырыпқа шолу: -Өткен тақырыпты мазмұндаңдар. -Өткен тақырыптарға байланысты бір-біріңе сұрақ қойып, жауап алыңдар |
Өткен тақырыпқа қатысты сұрақтарға жауап береді. Тақырыпты табады |
Оқушының жауабын толықтыру немесе тиімді кері байланыс жасау. |
Интербел-сенді тақта |
|
Жаңа білім 15 мин 2 мин Бекіту 18 мин |
Тарих дегеніміз — математикаға қатысы жоқ дегеннің бəрінің жиынтығы. Освальд Шпенглер. Ұсынылған ұлағатты сөзге пікір қалдырыңыздар
1. Қуат функциясы. Осы функциялардың барлығында қандай ортақ нәрсе бар? Бұл функциялардың барлығы қуат функциясының ерекше жағдайлары болып табылады. Дәрежелік функцияның анықтамасын берейік. y = xp, мұндағы p – берілген нақты сан. Дәрежелік функцияның қасиеттері мен графигі нақты көрсеткіші бар дәреженің қасиеттеріне, атап айтқанда, xp күші мағынасы бар x және p мәндеріне байланысты. Енді сіздердің әрқайсысыңыз «Қуат функциясы» тақырыбына тірек жазба жасайсыз. Бұл жазбаны аяқтағаннан кейін оны сабаққа дайындалу үшін пайдалану сізге ыңғайлы болады. Қолдау контурында графиктердің эскиздері бар. Сіздің тапсырмаңыз: функциялардың қасиеттерін тұжырымдап, жазбаларыңызға ескертулер жасаңыз. Сыныппен фронтальды жұмыс. Функциялардың қасиеттерін төмендегі жоспар бойынша тізімдейміз. 1. Анықтау аясы. 2. Мәндер ауқымы (мәндер жиыны). 3. Жұп, тақ функция. Жұп, тақ функцияның графикалық иллюстрациясы. Жұп және тақ қасиеттердің аналитикалық белгіленуі. 4. Функцияның өсу және кему аралықтарын жазыңыз. Фронтальды жұмыс кезінде жауаптарды бос орындар немесе теңсіздіктер түрінде жазудың мүмкін нұсқаларына назар аударамын. Слайдтарда р көрсеткіші өзгерген кезде графиктің сыртқы түрі қалай өзгеретінін көрсетемін. 2. Көрсеткіштік функция. Көрсеткіштік функцияның қасиеттерін негіздеу үшін дәрежелердің қасиеттері туралы материалды білу қажет. Сондықтан бұл қасиеттерді қайталауды келесі жаттығуларды ауызша орындау кезінде жасауға болады: 1-жаттығу: 1.
2.
3.
4.
5. 6. 7. 8.
2-тапсырма: Функцияның графигінен оның қасиеттерін анықтауды оқушылармен бірге қайталау тиімді. Осы мақсатта 13-суретте мыналарды табуға болады: 1) функция мәні нөлге тең болатын аргумент мәндері; 2) графтың ордината осімен қиылысу нүктесінің координаталары; 3) функция оң (теріс) мәндерді қабылдайтын аргумент мәндері; 4) функцияның өсу (кему) интервалдары.
Бүгін біз дәреже ұғымын кеңейтуге тырысамыз. Рационал сандармен қатар иррационал сандар да бар екенін білесіздер. Санды иррационал дәрежеге көтеруге бола ма? Кейбір тұрақты a>0 санын бекітейік және рационал сандар жиынындағы әрбір \frac{m}{n} санын a^\frac{m}{n} санымен байланыстырайық. Осылайша, f(x)\ =a^x функциясы туралы айтуға болады. Осы функциямен және оның қасиеттерімен танысу үшін мұғалім оқушыларға нұсқалар бойынша жұмысты ұсынады. Бірінші нұсқа a=2 жағдайын қарастырады. Екінші нұсқа – a=\frac{1}{2}. Оқушылар сәйкес функциялардың графигін салып, олардың қасиеттерін қарастыруы керек. 1. y=2^x функциялары
y=2^x функциясының қасиеттері:
3) жұп та, тақ та емес; 4) өседі; 5) жоғарыдан шектелмеген, төменнен шектелген; 6) ең үлкен немесе ең кіші мәндері жоқ; 7) үздіксіз; 8) дөңес төмен.
3) жұп та, тақ та емес; 4) азаяды; 5) жоғарыдан шектелмеген, төменнен шектелген; 6) ең үлкен немесе ең кіші мәндері жоқ; 7) үздіксіз; 8) дөңес төмен.
Бұл тапсырмаға 10-12 минут беріледі. Төменгі жол: экспоненциалды функцияны анықтау және негізгі қасиеттері. Анықтамасы: |
Қойылған сөздерге ассоцияция жасайды.
Өз пікірлерін білдіреді.
|
Дескриптор: Оқушылардың ассоцияциялау қабілеті жақсы ҚБ:мадақтау Дескриптор: ҚБ:шарлар - Оқушылар топта жұмыс жасай алады. ҚБ:мадақтау |
Оқулық, Карточкалар, Қайшы Қағаздар,
|
|
Қорытынды 5 мин |
Кері
байланысты Оқу тапсырмасы: Дәреже функциясының формуларын қайталау |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Көпмүшені көбейткіштерге бөлу |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушыларды көпмүшелерді көбейткіштерге бөлудің негізгі әдістерімен таныстыру. Алгебралық өрнектерді жеңілдету және теңдеулерді шешу үшін алған білімдерін қолдана білуге үйрету. Оқушылардың логикалық және аналитикалық ойлауын дамыту. |
|
|
Сабақтың мақсаты |
Оқушылардың көпмүшені сызықтық көбейткіштерге жіктеу және осы әдісті өрнектерді жеңілдету, теңдеулер мен теңсіздіктерді шешу үшін қолдану дағдыларын дамыту. |
|
|
Сабақ барысы |
Оқытушының іс- әрекеті |
Оқушының іс- әрекеті |
Бағалау |
ресурстар |
||
|
Сабақтың басы 10 минут |
Ұйымдастыру кезеңі «Денелік өзара әрекеттесу» жаттығуы. |
Оқушыларды сабаққа дайындау. Оқушылар ойын ойнау арқылы серпіліп қалады. Оқушылар қойылған сұраққа жауап береді |
Формативті бағалау үнемі жүргізіліп отырады. Гүлдердің суреттерін тарату арқылы бағалау жүргізіледі
|
Оқулықтар суреттер, слайдтар Кестелер,
|
||
|
Сабақтың ортасы 20 минут |
Математика да —
өнер: оның өз стильдері мен стильді кезеңдері
бар. Освальд Шпенглер. Освальд бізге не айтқысы
келді? Теңдеулерді шешіңіз:
Көпмүшені көбейткіштерге бөлу қажеттілігін ынталандыру.
Теңдеуді шешіңіз: x2 +3x +6 +2x =0
Проблемалық жағдай туады: мәселе бір қарағанда таныс, бірақ оны шешу мүмкін емес. Оң жағы 0 болатын теңдеуді сол жағын көбейткіштерге бөлу арқылы шешу ыңғайлы екенін білеміз.
- Барлық терминдердің ортақ факторы бар ма?
- Демек, бұл факторизация әдісі қолайлы емес.
Оқу тапсырмасының тұжырымы: көпмүшені басқа тәсілмен көбейтуді үйрену.
Жаңа материалды зерттеу:
Жұптық жұмыс: білу үшін көпмүшені қалай көбейтуге болады, егер барлық терминдердің ортақ факторлары болмаса. Мен сізге жұппен жұмыс істеуді және біраз зерттеу жүргізуді ұсынамын.
Шағын зерттеудің дұрыстығын тексеру:
3x +3y +m x +my көпмүшесін қарастырайық.
- Барлық терминдерде ортақ фактор бар ма?
Біз "мұқият қарау әдісін"қолданамыз. Сіз не көрдіңіз?
- Оларды топтарға біріктірейік. - Біз қандай қосу Заңын қолданамыз? ( 3x +3y ) +(m x +my) - Әр топтағы ортақ мультипликатормен не істеуге болады?
- Көбейтудің қандай Заңын қолданамыз?
3(x +y) +m (x +y)
- Қазір қанша термин шықты?
- Алынған өрнекте не қызықты болды? - Біз оны жақшадан шығарамыз. (x +y) (3 +m) - Біз не алдық? - Демек, көпмүшелік өнім түрінде ұсынылған. Қандай жолмен?
- Бұл ыдырау әдісі қалай аталады?
Топтарға бөлу: бірінші партада отырған оқушылар екінші партада отырған оқушыларға қосылады. Үшінші партаның оқушылары төртінші партаның оқушыларына қосылады және әр қатарда.
Топтық жұмыс: көпмүшенің көбейткіштерге ыдырау алгоритмін жасаңыз. Алгоритмдердің құрастырылған нұсқалары тыңдалады. Содан кейін олар түзетіледі. Осылайша, алгоритм моделі, оны талдау, нақтылау жасалады.
Соңғы нұсқа: а) ортақ мультипликаторы бар терминдерді топтастыруды орындау; |
Оқушылар өз пікірлерін білдіреді
Өз тұжырымын айтады
ҚБ: Бес бармақ
Оқушылар топтық жұмыс жасайды
ҚБ: Бес бармақ
Оқушылар сұраққа жауап береді
|
ҚБ: Шарлар
Әр сұрақ – 1 балл
Мадақтау |
Слайд, оқулық, интерактивті тақта, графиктер, сызбалар, |
||
|
Үйге тапсырма беру |
Кері
байланыс: Үйге тапсырма: Өткенді қайталап тестке дайындалып кел |
Күнделікке үй тапсырмасын жазады. |
|
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Тест тапсырмалары. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушылардың алған білімдерін тексеру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
І. Ұйымдастыру
кезеңі. Психологиялық сәт.
|
|
|
Интерактивті тақта, оқулық. |
|
Жаңа білім 15 мин 2 мин Бекіту 15 мин |
1 – нұсқа 1. Көпмүшені көбейткіштерге бөлу процесі қалай аталады? а) факторизация б) интеграция в) дифференциация 2. Төмендегі функциялардың қайсысы қуат функциясы болып табылады? а) f(x) = 2x + 3 б) f(x) = x^2 + 1 c) f(x) = sin(x) 3. Оң көрсеткішті дәрежелік функцияның графигі қандай болады? а) ұлғайту б) төмендеу в) түзу 4. Қай теңдеу квадрат болып табылады? а) 2х + 3 = 0 б) x^2 + 4x + 4 = 0 в) 3x - 1 = 5 5. Екі түрлі нақты түбір болса, квадрат теңдеудің дискриминанты неге тең болады? а) теріс б) нөл в) оң 6. Арифметикалық прогрессия дегеніміз не? а) әрбір элемент алдыңғысынан бірдей санға артық болатын тізбек б) әрбір элемент алдыңғысынан берілген санға артық болатын реттілік в) әрбір элемент алдыңғы екі элементтің қосындысы болатын тізбек 7. 2, 6, 18, ... геометриялық прогрессиясында келесі сан қандай болады? а) 24 б) 54 в) 36 8. Қандай формула арифметикалық прогрессияның алғашқы n мүшесінің қосындысын табуға мүмкіндік береді? а) Sn = n(a1 + an) / 2 б) Sn = 2n + 5 c) Sn = n(a1 + d) 9. Квадрат теңдеудің түбірлерін табу процесі қалай аталады? а) рационалды кеңейту б) қайталау әдісі в) шешім 10. Квадрат теңдеудің қанша түбірі болуы мүмкін? а) 1 б) 2 3-те 2 – нұсқа Тақырыбы: Көпмүшені көбейткіштерге бөлу 1. Көпмүшені көбейткішке бөлгенде қалдықтың дәрежесі қандай болады? а) Көбейткіштің дәрежесінен кем немесе оған тең б) Көбейткіштің қуатынан артық в) Көбейткіштің дәрежесіне тең 2. Көпмүшені көбейткішке бөлудің нәтижесі қандай болады? а) Қалдық + бөлім ә) Қалдық – бөлінді в) Қалдық * факторы Тақырыбы: Дәреже функциясы, оның қасиеттері және графигі 3. График (1, 2) нүктесі арқылы өтетін болса, дәреже функциясының дәрежесі қандай? а) 1 б) 2 в) 3 4. Дәрежесі өскен сайын дәреже функциясының графигі қалай өзгереді? а) Оңға қарай жылжиды б) Солға жылжиды в) өзгермейді Тақырыбы: Квадрат теңдеулерді шешу 5. Квадрат теңдеудегі дискриминант дегеніміз не? а) х^2 коэффициенті b) x кезіндегі коэффициент в) Түбір санын анықтайтын коэффициент 6. Квадрат теңдеудің түбірін табу формуласы қандай? a) x = (-b ± √(b^2 - 4ac)) / (2a) b) x = (-b ± √(b^2 + 4ac)) / (2a) c) x = (-b ± √(b^2 - ac)) / (2a) Тақырыбы: Арифметикалық және геометриялық прогрессиялар 7. Қандай қадам арифметикалық прогрессияның сипаттамасы болып табылады? а) Элементтер арасындағы айырмашылық б) Барлық элементтердің қосындысы в) Барлық элементтердің туындысы 8. Геометриялық прогрессияның n элементінің қосындысын табу формуласы неге ұқсайды? a) S_n = a * r^n ә) S_n = a * (1 - r^n) / (1 - r) в) S_n = a + (n - 1) * d 9. Геометриялық прогрессия өзінің соңғы шегіне қашан жиналады? a) Тек 0 < r < 1 үшін b) Тек r > 1 үшін c) кез келген r мәндері үшін 10. Геометриялық прогрессияның тізбекті мүшелері арасында қандай байланыс бар? а) a_n = a_1 + (n - 1) * d б) a_n = a_1 * r^(n-1) c) a_n = a_1 * n^(n-1) |
|
|
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: Өткен тақырыптарды қайталау |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Рационал теңдеулер мен теңсіздіктерді шешу. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушыларға рационал теңдеулер мен теңсіздіктерді шешудің негізгі әдістерін үйрету; Оқушыларда алгебралық және бөлшек-рационал өрнектерді бірдей түрлендіру дағдыларын қалыптастыру; Оқушыларда қолданбалы есептерді шығаруда алған білімдерін қолдана білу дағдыларын дамыту; Оқушылардың логикалық және аналитикалық ойлауын, сонымен қатар математикалық мәтінмен жұмыс істеу қабілетін дамыту; |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың барысы |
Мұғалімнің іс- әрекеті |
Оқушының іс-әрекеті |
бағалау |
ресурстар |
|
Сабақтың басы
|
І. Ұйымдастыру кезеңі. Психологиялық ахуал. Сәлемдесу, түгелдеу.
|
Психологиялық ахуалға берілген психогиялық жаттығуларды орындау арқылы жаңа сабаққа назар аудару. |
|
Оқулықтар суреттер, кестелер, |
|
Сабақтың ортасы
|
Сұрақтарға жауап беру: 1. Қандай теңдік теңдеу деп аталады? 2. Қай теңдеу квадрат деп аталады? 3. Теңдеуді шешу деген нені білдіреді? 4. Дискриминантты табу формуласы? 5. Қандай теңдеулер толық емес деп аталады? 6. Қандай жағдайда квадрат теңдеудің екі түбірі болады? 7. Қандай жағдайда квадрат теңдеудің бір түбірі болады? 8. Қандай жағдайда квадрат теңдеудің түбірі болмайды? 3. Ауызша санау (тапсырманы экранда көрсету) 3.1. Теңдік дұрыс жазылған ба? Х*18=34 14х=56 2:(х-3)=4
3.2. Теңдеуді шешіңіз: 0*x=0 5x=0 2x-4=2x
3.3. Теңсіздіктерді шеш: X - 2 > 0 X+4 <0 2x<4 X - 5 ≥ 0 X+4≤0 Ауызша есептің соңында сызықтық теңдеулердің бір түбірі, түбірі жоқ немесе олардың шексіз саны болуы мүмкін екеніне назар аударыңыз. Квадрат теңдеулердің екі түрлі түбірі, екі бірдей түбірі болуы немесе түбірі болмауы мүмкін. 3.4. Формула бойынша белгісізді өрнектеңіз: V=? егер S=V*t I=? егер P= I^2*K R=? егер Q=F^2*R*t R_6 =? егер F_1*5 +q*\frac{6}{2} - R_6=0 N_2=? егер N_2*sin30°-C_1=0 t =? егер a=\frac{V-V_0}{t} A=? егер N= \frac{A}{t} V=? егер E= \frac{mV^2}{2}
Топтық жұмыс Топпен жұмыс істеу үшін оқушылардың көпшілігі орындай алмаған тақтадағы тапсырманы орындауға болады. 4. рационал теңдеулер емес
X(x+1) ≠ 0 X+1=0 X ≠ -1 2x+5-2x-2-3 -
3 3-3 -3
|
Оқушылар жаңа сабақты меңгереді
Өз топтарының атынан пікірлерін айтады ҚБ: Екі жұлдыз, бір тілек
Топтық жұмыс жасайды
ҚБ: Шарлар
|
Оқушылар теңдікпен жұмыс жасайды
Теңсіздіктерді шеше алады
|
Интербелсенді тақта, тар, оқулық, жұмыс дәптерлері
|
|
Соңы 10 минут
|
Кері байланыс
Үйге тапсырма беру: келесі есептерді шешіп кел а)4 б) в) г) a) 5(x – 1)+7≤1 – 3(x+2) б)4(a+8) – 7(a – 1)<12 в) (x -2)(x – 5)(x – 12)>0 г) |
Оқушылар мұғаліммен кері байланыс жасайды |
|
Кері байланыс тақтай шасы. |
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Иррационал теңдеулер |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Иррационал теңдеу түсінігін зерттеп, оны шешудің әртүрлі жолдарын қарастырыңыз. Иррационал өрнектерді талдау және түрлендіру қабілеттерін дамыту. Түрлі түрдегі иррационал теңдеулерді шешу дағдыларын дамыту. Математикалық ой-өрісіңізді кеңейтіп, оқытылатын материалға деген қызығушылықты арттырыңыз. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың барысы |
Мұғалімнің іс- әрекеті |
Оқушының іс-әрекеті |
бағалау |
ресурстар |
|
Сабақтың басы 10 минут
|
І. Ұйымдастыру кезеңі. Психологиялық ахуал. Сәлемдесу, түгелдеу.
Өткен сабаққа шолу |
Психологиялық ахуалға берілген психогиялық жаттығуларды орындау арқылы жаңа сабаққа назар аудару. |
Әр дұрыс жауапқа 1 балл
|
Оқулықтар суреттер, кестелер, |
|
Сабақтың ортасы 20 минут
|
Қалыптасқан нәтижелер мен сабақтың мақсаттарын қою. Оқушылардың оқу әрекетіне мотивация - Экранда сіз теңдеулерді көресіз. Мұқият қарап, қандай теңдеулерді шешуді білетініңізді және қайсысы қиын екенін анықтаңыз?
-Өздеріңізге таныс теңдеу түрлерін атаңыздар? Жауабы: квадраттық, сызықтық, бөлшек рационал. Қорытынды: Сіз әлі шеше алмайтын теңдеулер бар. – Бұл теңдеулердің жазылуы біз атаған теңдеулерден несімен ерекшеленеді? Жауабы: белгісіз түбір белгісінің астында. - Дұрыс! Түбір белгісінің астында айнымалысы болатын мұндай теңдеулер иррационал теңдеулер деп аталады. Иррационалдық (латын тілінен Irrationalis – ақылға қонымсыз, бейсаналық) – логикаға қайшы, парасаттылық шегінен тыс нәрсе. Әдетте ұтымдыға парасатты, орынды, негізделген ретінде қарама-қарсы қойылады. Олай болса, сабағымыздың тақырыбы «Иррационал теңдеулер». - Бүгін біз иррационал теңдеудің анықтамасымен танысамыз және иррационал теңдеулерді шешудің әртүрлі әдістерін қарастырамыз. Жаңа материалды меңгеру - «Иррационал теңдеулер» сабағының тақырыбын дәптерлеріңе жазып алыңдар. Анықтамасы: Айнымалысы түбір (радикал) белгісінің астында болатын теңдеулер иррационал деп аталады.
Экранда иррационал теңдеулердің мысалдарын көресіз:
- Экранда сіз үш теңдеуді көресіз «ШЕШУГЕ ОҚЫТАЙЫҚ», оларды шешіңіз. Содан кейін шешімдеріңізді менімен бірге тексеріңіз, ол келесі слайдта болады «ӨЗІҢІЗДІ ТЕКСЕР».
Бекіту: Төмендегі теңдеулерді өзіңіз шешіңіз.
- Енді интерактивті тақтадағы шешімдермен өз шешімдеріңізді тексеріңіз.
|
Оқушылар жаңа сабақты меңгереді
Шілікті және Бесшатыр қорғандарының ортақ белгілерін ашады • Шілікті және Бесшатыр қорғандарының ерекшеліктерін анықтайды
археологиялық олжалардың айрықша белгілерін анықтайды.
Топтық тапсырмаларды орындайды. Оқушылар алған білімдерін практикалық тұрғыда көрсетеді |
Оқушылар концептуалды ойлау мен тың байланысын біледі Мадақтау
«патша қорғандарының» салыну себептеріне дәлел келтіріңіз
Салыстыру сызықтарын анықтай алады
Шілікті және Бесшатыр қорғандарын салыстыра отырып, олардың ұқсастықтары мен айырмашылықтарын табады ҚБ: сэндвич
|
Оқулықтар суреттер, слайд Кестелер Сызғыш қарындаштар Қайшы Қағаздар, плакаттар, , интербелсенді тақта
|
|
Соңы |
|
Оқушылар мұғаліммен кері байланыс жасайды |
|
Кері байланыс тақтай шасы. |
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Комбинаторикадан көбейту әдісі бойынша олимпиада тапсырмалары |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Комбинаторика бойынша олимпиада тапсырмаларын шешу әдістерін меңгеру. Оқушылардың логикалық және сыни ойлауын дамыту. Оқушылардың математиканы оқуға деген қызығушылығын арттыру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақ барысы |
Оқытушының іс- әрекеті |
Оқушының іс- әрекеті |
Бағалау |
ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Сәлемдесу, түгелдеу |
Оқушылар ойын ойнайды
|
Формативті бағалау үнемі жүргізіліп отырады. |
Оқулықтар суреттер, слайдтар кестелер |
|
Сабақтың ортасы 20 минут |
Аксиома – дәлелі аз ақиқат. В. Хмурый Хмурыйдың аксиома жайлы қанатты сөзіне назар аударыңыздар, бұнымен Хмурый не айтқысы келді? «Ребус» мотивациялық кезең - Сабақтың тақырыбын түсіну
үшін жұмбақ шешіңіз: Логика ең түсініксіз математикалық есептерді шешуге көмектеседі! -Бүгін сабақта комбинаторика есептерін көбейту әдісі арқылы шығаруды үйренеміз. - Комбинаторика – берілген ережелер бойынша құрастырылған бастапқы жиыннан элементтерді таңдау және оларды белгілі бір комбинацияда орналастыру есептері зерттелетін және шешілетін математика саласы. - Мұғалім сабақтың мақсатын түсіндіреді және «Олимпиада есептерін шығарудың комбинациялық әдістері» тақырыбын жариялайды. - Мұғалім комбинаторлық әдістерді өмірде қолдану туралы сұрақтар қою арқылы оқушылардың алдыңғы білімдерін белсендіреді. - Мұғалім негізгі комбинаторлық әдістермен таныстырады: ауыстыру, комбинация, орналастыру. - Мұғалім әрбір әдіске мысал келтіріп, олимпиада есептерін шығаруда қолдануды түсіндіреді. - Мұғалім комбинаторлық
әдістерді қолдану арқылы шығарылатын қарапайым есептерді
көрсетеді. Мен комбинаторикадағы бірінші мәселені шешуді ұсынамын: 1-міндет. Әр түрлі сандармен жазылған Үш таңбалы сандар 6, 7, 8 сандарынан қанша тұрады? Мәселені шешуді талдау 1: - Үш санның кез келгені жүздеген санатта тұра ала ма? (үш сан болуы мүмкін) - Қалған екі санның кез келгені ондаған санатта болуы мүмкін? (екі сан болуы мүмкін) - Бірлік санатында қалған бір ғана сан болуы мүмкін? (иә, бір) - Демек, үш сан жүздеген болуы мүмкін; ондықтар санатындағы екі сан және бір Сан санатындағы бір Сан. - Нұсқалардың санын қандай әрекетпен санауға болады? (көбейту арқылы) - Үш таңбалы сандардың мүмкін болатын санын қалай санауға болады? (3 x 2 x 1). - 6, 7, 8 сандарынан әртүрлі сандармен жазылған неше үш таңбалы сандарды жасауға болады? - Барлығы 6 Үш таңбалы сан алынады. - Нақты өмірде қажет комбинаторикаға 2 мәселені шешуге тырысайық: Тапсырма 2. Сәрсенбі күні 3 «М» сыныбында бес сабақта бес түрлі пән бар. Сынып жетекшісі 3 «М» сыныбының сәрсенбі күнінің кестесін неше түрлі жолмен құруы мүмкін? 2 есептің шешімін талдау: - Бірінші сабақ бес пәннің кез келгені болуы мүмкін бе? - Қалған төрт пәннің кез келгені екінші сабақта бола ала ма? - Қалған үш пәннің кез келгені үшінші сабақта бола ала ма? - Төртінші сабақта - қалған екі пәннің қайсысы? - Бесінші сабақта қалған бесінші пән оқытылады. - Опциялардың санын қалай санауға болады? (көбейту арқылы) – Сондықтан сәрсенбінің кестесін 120 тәсілмен жасауға болады. (5x4x3x2x1) - Үшінші комбинаторика есебін мектеп өмірінен көбейту әдісі арқылы шығарамыз: 3-тапсырма.Ағылшын тілі сабағына алты бала келді. Олар қос партаға неше түрлі жолмен жұптасып отыра алады? 3 есептің шешімін талдау: - Сол жақтағы бірінші партаға неше түрлі бала отыруға болады? (алты түрлі бала) -Оң жақтағы бірінші партаға қалған балалардан неше түрлі бала отыра алады? (бес түрлі бала) -Қалған балалардың сол жағындағы екінші партаға неше түрлі бала отыруға болады? (төртеуі отыра алады) -Қалған балалардың оң жағындағы екінші партаға неше түрлі бала отыруға болады? (үшеуі отыра алады) - Қалған балалардың сол жағындағы үшінші партаға неше түрлі бала отыруға болады? (екеуі отыра алады) - Қалған балалардың оң жағындағы үшінші партаға неше түрлі бала отыруға болады? (жалғыз отыруға болады) - Опциялардың санын қалай санауға болады? (көбейту арқылы) - Бұл есепті шешу үшін қандай өрнек қолдануға болады? (6x5x4x3x2x1) - Сабақта алты баланы отырғызудың неше түрі болуы мүмкін? (720) «Жалпы әдісті модельдеу» -Бүгін біз қандай мәселелерді шештік? - Математиканың бұл бөлімі қалай аталады? (комбинаторика) - Бұл тапсырмалардағы нұсқалардың санын қалай санауға болады? (көбейту арқылы) -Егер n есептердегі варианттардың (элементтердің) саны болса, онда комбинаторлық есептерді көбейту әдісімен шешу формуласы қандай болуы керек? n x (n-1) x (n-2) x (n-3) x ..., соңғы көбейткіш бірге тең болғанша көбейтіңіз. - Жарайсың! |
Оқушылар жаңа сабақты меңгереді Оқушылар комбинаторка не екенін меңгереді |
Әр дұрыс жауап 1 балл Мадақтау Қол шапалақтау
|
Слайд, оқулық |
|
Сабақтың соңы |
Үйге тапсырма: Ықтималдық теориясының формулаларын жаттап кел |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Ықтималдықтар теориясы және статистика |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Ықтималдықтар теориясының негізгі ұғымдары мен формулаларын оқып үйрену. Олимпиада есептерін шешу үшін ықтималдықтар теориясын қолдануды үйреніңіз. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақ барысы |
Оқытушының іс- әрекеті |
Оқушының іс- әрекеті |
Бағалау |
ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 5 мин |
Психологиялық ахуал қалыптастыру.
2.Жағымды көңіл-күйге келу. Тыныс алуға зейін қою. |
Психологиялық ахуалға берілген тақпақтарды дауыстап айтып, тілді жаттықтыру және жаңа сабаққа назар аудару. Оқушылар жұмысты берілген түріне қарай орындайды |
Қол шапалақтау арқылы бір бірін бағалайды |
Оқулықтар суреттер Кестелер
|
|
Сабақтың ортасы 20 минут |
Рух пен материя арасында
математика бар. Хуго Штейнхаус. Хуго Штейнхаустың қанатты сөзі
жайлы не ойлайсыздар? Жақында бір журналдан мынадай мәселені оқыдым: «Әйел мен балық ұғымдарының арасындағы арифметикалық ортаны табыңыз?» Қандай жауап бересіз? (Су перісі)
Арифметикалық орта сияқты сипаттамаларды математиканың қай саласы зерттейді? (Статистика) Сабақтан кейін мектептен шығып бара жатқаныңызды елестетіп көріңіз және клуб бақшасында терек бұтағында отырған су перісін көрдіңіз. Мен қандай оқиғаға мысал келтірдім? (мүмкін емес) Осы немесе басқа оқиғаның болуын математиканың қай саласы зерттейді? (ықтималдық теориясы) Қалай ойлайсыңдар, сабағымыздың тақырыбы қандай, егер келесіде есептер шығарудың мысалын қолдана отырып, статистикалық сипаттамалар мен кездейсоқ оқиғалардың пайда болу ықтималдығының қалай табылатынын көрсетуді сұрасам? (Тақырып бойынша жалпы сабақ: Ықтималдық және математикалық статистика) Келесі сабақта осы тақырып бойынша тест болады. Бүгін өзіңізге қандай мақсаттар мен міндеттер қоясыз? (Оқылған материалды қайталау, бекіту және жүйелеу) Негізгі білімді жаңарту. 1) Ассоциацияны қабылдау, түйінді сөз үшін ұсынылған ұғымдарды сипаттайтын сөздерді, формулаларды, фактілерді таңдаңыз. Сыныпты топқа бөлу, тақтада жұмыс жасау. Негізгі сөздер: Статистика, ықтималдық теориясы. 2) Енді оқиғалардың жіктелуін қаншалықты түсінетініңізді тексерейік. Викторина түрінде қозғалмалы үзіліс өткізейік. Түпнұсқа мобильді викторина: Оқиғалардың орын алу мүмкіндігін келесі әрекеттер арқылы бағалаңыз: «сенімді оқиға» (барлығы отырады және тұрмайды), «кездейсоқ оқиға» (қолыңызды көтеріңіз), «мүмкін емес оқиға» (тұруы керек). 1. «Ертең ауа-райы жақсы болады». (кездейсоқ) 2. «Қаңтар айында Климковкада қар жауады». (сенімді) 3. «Сағат 12-де Белая Холуницада жаңбыр жауады, ал 24 сағаттан кейін күн жарқырайды». (кездейсоқ) 4. «Туған күніңізге сөйлейтін қолтырауын аласыз». (мүмкін емес) 5. «Суға лақтырылған тас суға батады». (сенімді) 6. «Сіз ұтыс-жеңіс лотереясына қатысу арқылы ұтпайсыз». (мүмкін емес) IV.Білімді жалпылау және жүйелеу. Есептер шығару (Жұппен жұмыс) тақтада жауап береді. 1-тапсырма: Тоғызыншы сынып оқушылары математикадан тест бойынша келесі ұпайларды алды: 10, 9, 12, 6, 9, 15, 14, 14, 12, 15, 13, 13, 9, 10, 14, 14. Осы нәтижелер бойынша тестілеуден өткен оқушылардың жартысы одан әрі конкурстық тестілеуге іріктелді. Алынған сандар қатарының арифметикалық ортасын (11,81), модасын (14), медианасын (12,5) және диапазонын (9) табыңыз. Жарысқа одан әрі қатысу үшін өту балы қандай болды? (12.5) Табылған сипаттамалардың қайсысы сұраққа нақты жауап береді? «Пирамида» сөзі карточкалардан жасалған. Қай әріптік картаны салу ықтималдығы жоғары? Қандай оқиғалар бірдей ықтимал? (Барлығы 8 әріп бар. “i” әрпі 2 рет кездеседі – P = 2/8 = 1/4; “a” әрпі 2 рет кездеседі – P = 2/8 = 1/4; қалғаны 1 рет – P = 1/8 .) 3-тапсырма. Қосымша. Кездейсоқ экспериментте симметриялы монета үш рет лақтырылады. Бастардың бір рет болса да келмеу ықтималдығын табыңыз.(1/8) Ықтималдықтарды қосу және көбейту А және В екі үйлесімсіз оқиғалардың кем дегенде біреуінің пайда болу ықтималдығы Р(С) олардың ықтималдықтарының қосындысына тең. P(C) = P(A + B) = P(A) + P(B) Қарама-қарсы оқиғаның ықтималдығы: P(A) = 1 - P(A). Екі тәуелсіз А және В оқиғаларының бірігіп пайда болу ықтималдығы Р(С) А және В оқиғаларының ықтималдықтарының көбейтіндісіне тең. P(C) = P(A) P(B) Өзін-өзі бақылау. Өздік жұмыс. ҰБТ-да Ықтималдықтар теориясы бойынша тапсырмалар бар екенін білесіздер, енді мен емтиханға дайындығыңызды тексеріп, осы тақырып бойынша есептер шығару дағдыларыңызды шыңдауды ұсынамын. Мен сізге quar кодын сканерлеп, сынақтан өтуді ұсынамын. Оқиға ықтималдығының классикалық анықтамасын таңдаңыз: Оқиғаның ықтималдығы - … а) бұл оқиғаға қолайлы сынақ нәтижелері санының барлық бірдей ықтимал нәтижелер санына қатынасы. б) бұл оқиға үшін қолайсыз сынақ нәтижелерінің санының барлық бірдей ықтимал нәтижелер санына қатынасы. в) бұл барлық сынақ нәтижелерінің санының оқиғаға қолайлы нәтижелер санына қатынасы. г) бұл барлық сынақ нәтижелерінің санының оқиғаға қолайсыз нәтижелер санына қатынасы 2. Қалтадан еденге тиын түсті. "Елтаңбаның" түсу ықтималдығын табыңыз: а) 0,1 б) 0,2; в) 0,5; г) 1; |
Оқушылар жаңа сабақты меңгереді Түсіндіре отырып, сұрақтарға ауызша жауап беру. |
Мадақтау Қолшапалақтау
мадақтау |
Слайд, оқулық, |
|
Қорытынды |
Кері
байланысты Оқу тапсырмасы: Өткенді қайталап тестке дайындал |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Тест тапсырмалары. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушылардың алған білімдерін тексеру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
І. Ұйымдастыру
кезеңі. Психологиялық сәт. Қайырлы күн болсын! Сәрсенбінің күні Сәттілікке толсын! Біздің алар бағамыз Кілең бестік болсын!
|
|
|
Интерактивті тақта, оқулық. |
|
Жаңа білім 15 мин 2 мин Бекіту 15 мин |
1 – нұсқа 1. Төмендегі формулалардың қайсысы А оқиғасының ықтималдығын сипаттайды? a) P(A) = n(A)/n(S) б) P(A) = n(S)/n(A) c) P(A) = n(A) + n(S) 2. Қайталанатын цифрлары жоқ неше төрт таңбалы сан бар? а) 524 б) 3024 в) 9 3. Төмендегі теңдеулердің қайсысы иррационал болып табылады? а) x^2 = 9 б) x^2 + 4 = 0 в) √x = 5 4. 2х^2 - 3х + 1 = 0 теңдеуінің түбірі қандай? а) х = -1/2, 1/2 б) x = -1, 1 в) x = -1,1/2 5. Төмендегі теңсіздіктердің қайсысы нақты сандар жиынындағы барлық х үшін орындалады? a) x^2 + 3 > 0 б) x^2 - 5 < 0 в) x^2 + 1 < 0 6. Монетада сандардың түсу ықтималдығы қандай? а) 1/2 б) 1 в) 0 7. «ШАР» сөзінің әріптерінен неше түрлі үш әріпті сөз жасауға болады? а) 6 б) 15 в) 24 8. Төмендегі теңдеулердің қайсысы иррационал болып табылады? а) 3х - 5 = 0 б) x^2 = 16 в) x = 2 9. x^2 - 9 = 0 теңдеуінің түбірі неге тең? а) x = -3, 3 б) x = -3,9 в) x = -3,6 10. Төмендегі теңсіздіктердің қайсысы барлық x < -3 үшін орындалады? a) x^2 - 4 > 0 б) x^2 + 5 < 0 c) x^2 + 1 > 0 2 – нұсқа 1. Оқиғаның ықтималдығы 0,8. Қарама-қарсы оқиғаның болу ықтималдығы қандай? (а) 0,2 (b) 0,5 (c) 0,8 2. 10 емтихан нәтижесінің орташа арифметикалық мәні 4,5-ке тең. Тағы 5 нәтиже қосқаннан кейін арифметикалық орта 3,5 болды. Қосылған нәтижелердің көлемі қандай? (а) 10 (b) 15 (c) 25 3. «КОМБИНАТОРИКА» сөзінің әріптерінен неше түрлі сөз жасауға болады? (а) 120 (b) 240 (c) 360 4. 10 адамнан тұратын топта сіз президентті, вице-президентті және хатшыны таңдауыңыз керек. Мұны қанша жолмен жасауға болады? (а) 720 (b) 900 (c) 1120 5. √(x - 3) = 5 теңдеуін шешіңіз: (а) x = 8 (b) x = 28 (c) x = 38 6. √(x + 2) - √(x - 5) = 1 теңдеуінің түбірін табыңыз: (а) x = 1 (b) x = 6 (c) x = 11 7. Теңдеуді шешіңіз: (3х - 5)/(4х + 7) = 5/9 (а) x = 1/4 (b) x = -1/4 (c) x = 1 8. Теңсіздікті шешіңіз: x^2 - 5x + 6 >= 0 (a) (-∞; 2] U [3; ∞) (b) [-2; 3] (c) (2; 3) 9. Төмендегі теңдеулердің қайсысының [0, π] интервалында екі шешімі бар? a) sin(x) = 0 б) sin(x) = 1 c) sin(x) = -1 10. Төмендегі теңдеулердің қайсысының жалғыз бүтін шешімі бар? а) (х - 1) / 2 = 3 б) (x + 2) / 5 = 4 в) (x + 3) / 7 = 2 |
|
|
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: Ньютон Биномы жайлы ақпарат жинап кел |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Ньютонның Биномы. Паскаль Үшбұрышы |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Ньютон биномымен және оның әртүрлі есептерді шығаруда қолданылуымен танысады. Формулалар мен теңдеулермен жұмыс істеу дағдыларын дамыту. Олимпиада есептерін шығару үшін Ньютон биномдық жүйесін қолдануды үйреніңіз. Ньютон биномы мен Паскаль үшбұрышын зерттеу. Логикалық және аналитикалық ойлауды дамыту. Математикалық есептерді шешу үшін алынған білімді қолдану. Жалпы математика мен ғылымдарды оқуға деген қызығушылықты арттыру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақ барысы |
Оқытушының іс- әрекеті |
Оқушының іс- әрекеті |
Бағалау |
ресурстар |
|
Сабақтың басы 5 минут |
Ұйымдастыру кезеңі Ұйымдастыру кезеңі
|
Оқушыларды сабаққа дайындау. Топқа бөлініп отырады Оқушылар ойын ойнау арқылы серпіліп қалады. |
Формативті бағалау үнемі жүргізіліп отырады. Гүлдердің суреттерін тарату арқылы бағалау жүргізіледі
|
Оқулықтар суреттер, слайдтар Кестелер,
|
|
Сабақтың ортасы 20 минут |
Біздің сабағымыздың тақырыбы " Бином Ньютон. Паскаль Үшбұрышы". Бүгін сабақта біз өткен материалды қорытындылап, қайталауымыз керек. Биномдық формулаларды қолдануда алынған білім мен дағдыларды математикалық есептерді шешуге бекітеміз. Сабақ барысында біз топтарда жұмыс істейміз, содан кейін сабақты қорытындылаймыз және сіз үй тапсырмасын аласыз. 1. Кроссвордты шешіңіз. 1. Мономиалды көпмүшеге
көбейту кезінде қолданылатын көбейту қасиеті. 2. Көпмүшені
көбейткіштерге бөлу тәсілі. 3. Теңдеу дұрыс теңдікке айналатын
айнымалының мәні. 4.Айнымалылардың кез-келген мәндеріне сәйкес
келетін теңдік. 5. Мономиалдардың қосындысы болып табылатын өрнек.
6. Бір әріптік бөлігі бар терминдер. 7. Сандық мультипликатор ж o
мономиалдар. Жауаптары: Тарату Топтар Түбір Жеке басын куәландыратын Көпмүшелік Ұқсас Коэффицент Көбейтіндіні көпмүшемен ауыстырыңыз,
нәтижесінде алынған сәйкестік теңсіздік
болады
- Бұл тапсырмада қандай формулаларды қолдандың? Олардың атын атап, тұжырымдап көрейік. 1. Екі өрнектің қосындысы мен айырмасының квадратының формулалары 2. Шаршы айырымының формуласы 3. Кубтардың қосындысы мен айырмасының формулалары 4. Дәреженің қасиеті. Жаңа материалды түсіндіру Қысқартылған көбейту формулалары Ньютон биномының ерекше жағдайы болып табылады. Бүгін сабақта біз алған білімімізді жинақтап, осы формулалармен танысамыз. Ньютон биномының формуласы. Екі терминнің қосындысын N дәрежесіне қалай көтеруге болады? Исаак Ньютон өз заманының нағыз ұлы физигі, мүмкін барлық уақыттар мен халықтардың ең ұлы физигі болған. Бірақ біз оны бағаламаймыз. Алайда, Ньютонның да керемет математик болғанын атап өткен жөн. Айтпақшы, Ньютонның Бином формуласы сол кездегі қазіргі заманның ең үлкен ашылуы ретінде оның қабірінің құлпытасына ойып жазылған! Ньютонның Бином формуласынан басқа, мектеп орындығынан Ньютон-Лейбниц формуласы бәріне белгілі. Осылайша, ұлы Ньютон Лейбницпен бірге дифференциалдық және интегралдық есептеулердің негізін қалады. Шектер теориясының негіздері және математикалық талдаудағы қатаң көзқарас Августин Коши, Георг Кантор, Карл Вейерштрасс сияқты данышпандардың еңбектерінде басталды және дамыды. Әрине, Леонард Эйлердің есімін айналып өту мүмкін емес. Бірақ біз мұнда негізгі ойлау сызығынан алшақтадық. Өйткені, Ньютон биномының формуласы алгебраға, сондай-ақ комбинаторика деп аталатын математика саласына қатысты!
Мысалы - бұл мағына көпмүше Ал екі мүшенің қосындысы Бин деп
аталады! Яғни Ньютон екі мүшенің қосындысын 2-ге тең
көрсеткішпен ғана емес, кез келген көрсеткішпен дәрежеге көтеруге
мүмкіндік беретін формуланы ойлап тапты! Ньютон биномының
формуласының мәнін асыра бағалау мүмкін
емес функциялардың шектерін
шешу. Сондықтан,
дұрыс,
бұл жерде қарастырылып отырған формула биномның дәрежесі үшін Ньютон формуласы деп аталады.
Біз бұл формуланы бірден жалпы түрде жазбаймыз,
алдымен мектеп алгебрасына жүгінеміз!
Бұл қосынды квадратының формуласы немесе биномның квадратының формуласы немесе биномның екінші дәрежесінің формуласы! Ал енді екі мүшенің қосындысын үшінші дәрежеге көтереміз немесе үшінші дәрежелі биномды ашамыз. Жақшаларды алгебраның үлестірімділік немесе үлестірімділік заңын әдеттегідей қолданатындай етіп кеңейтеміз:
Мұнда бізде қазірдің өзінде алты термин бар, дәлірек айтсақ, алты емес, 8 = 23 қосылғыштардың, өйткені екі қосылғыштың коэффициенттері 2-ге тең.
Біз
текшелердің қосындысының формуласын дәлелдедік. Ол сізге мектептегі
алгебра курсынан жақсы таныс болуы керек.
Бұл
жерде біз жақшалардың егжей-тегжейлі кеңейтімдерін жасауды
бастамадық, бірақ кеңейту нәтижесін бірден жазып алдық, өйткені
есептеулер мұны екі рет жасағанымызға ұқсас.
Яғни, биномның төртінші дәрежесінің орнына біз оның бұрын есептелген өрнегін алмастырамыз және жақшаларды қайтадан ашамыз, егжей-тегжейлі есептеулерді қалдырамыз, өйткені олар биномның үшінші және екінші дәрежелерін есептеу кезінде жоғарыда бірнеше рет орындалған.
Сіз сұрайсыз: биномды тұрғызу дәрежесінің ретін осылай көбейтуді қаншаға жалғастыра беруге болады? Жауап: шексіздікке дейін мүмкін! Сол сияқты, мысалы, n=100 болғанда, нәтижені көбейтеміз бойынша 99 дәрежесіне көтеру x+y, сонда біз 100-ге дәрежелеудің нәтижесін аламыз.
Бірақ біз бұл өрнектің барлығын боямаймыз,
өйткені мұндай терминдерді келтіргеннен кейін оның 101 термині
болады және бір жолға сыймайды, ал он жолға оқу өте қиын
болады!
Мұнда біз қарапайым және тапқыр қорытынды жасаймыз: формуласын алу үшін n, үшін осы формуланы білу қажет (n-1). Формуласын білу үшін (n-1) оны алу керек (n-1) біз 2,3,4 және 5-ші дәрежелер үшін жасағандай рет, яғни дәреже үшін бұрыннан белгілі нәтижені берілген дәрежеден кіші бірлікке бірлікке тең дәрежеге көбейттік! Ал енді екінші данышпан қорытынды өзін көрсетеді! Ал егер n-1 дәрежесінің биномдық формуласына әкелетін осы әрекеттердің барлығын бір сәтте жазуға болатын болса ше?! Сонда қайта жазбауға болады (n-1) бір рет іс жүзінде бірдей есептеулер үшін 2, 3, 4, 5, 6,..., биномның n-1 дәрежесі, және оларды бір формуламен жазып, осы формуланы биномның бірінші дәрежесіне тағы бір рет көбейтіп, қажетті формуланы толығымен дәлелдеңдер! Міне, сізде Ньютонның пайымдау алгоритмі бар! Мұнда біз соңғы сөйлемдерді қарамен жаздық, өйткені олар Ньютон биномының формуласын дәлелдеуге негіз болып табылады және біздің барлық пайымдауларымыздағы ең маңызды және күрделі қадам болып табылады. Айтпақшы, бұл қадам индуктивті, ал индуктивті қадамға негізделген әдіс математикалық индукция әдісі деп аталады. Осылайша, біз мұнда математиканың ең іргелі және маңызды әдістерінің бірімен таныстық. Бірақ енді келесі қиындық туындайды: биномның n-1-ге тең дәрежесінің жалпы формуласын қалай жазуға болады? Бұған биномның 3,4 және 5-ке тең дәрежелерінің дәлелденген формулалары көмектеседі.
Биномды дәрежеге көтеру кезінде коэффициенттерді комбинациялар арқылы есептеу өте көп еңбекті қажет ететіндігімен келісіңіз. Бұл есептеулерді жеңілдету үшін мыналарды пайдаланыңыз:
Паскаль үшбұрышы 0 1 1 1 1 2 1 2 1 3 1 3 3 1 4 1 4 6 4 1 5 1 5 10 10 5 1 6 1 6 15 20 15 6 1 … … № Паскаль үшбұрышы 0
1
2
3
4
5
6
Паскаль үшбұрышын құрайтын сандар биномдық коэффициенттер болғандықтан, Паскаль үшбұрышын басқа түрде қайта жазуға болады: 4 Бастапқы бекіту Ньютон биномы мен Паскаль үшбұрышын пайдаланып формуланы жалғастырыңыз.
1/27a³+1/3a²∙2/5b+a∙4/25b²+8/125b³ Жауап: 1/27a³+2a²b/15+4ab²/25+8b³/125
0,8a∙0,027b³+0,0081b4 Жауабы: 0,0016а4-0,0096а³b+0,0216a²b²-0,0216ab³+0,0081b4 3. (1/2a-3/4b)³=(1/2a)³-3(1/2a)²∙3/4b+3(1/2a)(3/4b)²-(3/4b)³= =a³/8-3/8a²∙3/4b+3/2a∙9/16b²-27/64b³= a³/8-9a²b/32+27ab²/32-27b³/64 Жауап: a³/8-9a²b/32+27ab²/32-27b³/64 Оқытушы оқушылардың көмегімен тақтада шешеді. |
Жаңа сабақты меңгереді елдің және хронологиялық шеңберді анықтайды; - контурлық картада Ғұн мемлекетінің бастапқы аумағын көрсетеді; - сұрақтарды дұрыс құрастырады; - өз пікірін білдіре отырып, сұрақтарға жауап береді; |
Гүлдердің тарату арқылы
бағалау жүргізіледі |
Слайд, оқулық, Оқулықтар суреттер, Кестелер, |
|
Соңы
|
Кері байланыс
|
Оқушылар мұғаліммен кері байланыс жасайды |
|
Кері байланыс тақтай шасы. |
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Теңдеулерді пайдаланып сөздік есептерді шығару |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Теңдеулерді қолданып сөздік есептерді шығаруға үйрету. Математикалық ойлау қабілеттерін дамыту. Негізгі математикалық ұғымдар туралы түсінігіңізді арттырыңыз. Есептерді шығару нәтижелерін талдауға және түсіндіруге үйрету. Математикаға ғылым ретінде қызығушылықты арттыру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақ барысы |
Оқытушының іс- әрекеті |
Оқушының іс- әрекеті |
Бағалау |
ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Психологиялық ахуал қалыптастыру.
|
Оқушыларды сабаққа дайындау.оқушылар қимыл қозғалысын жасап көңілдерін көтереді |
Формативті бағалау үнемі жүргізіліп отырады. |
Оқулықтар суреттер, слайдтар Кестелер, |
|
Сабақтың ортасы 20 минут |
Ол ақын болып кетті, математик
болу үшін фантазиясы жетпей қалды. Давид Гильберт. Давидтың қанатты сөзіне
назар аударыңыздар. Давид не айтқысы келді?
Сызықтық теңдеулерді қолданып сөздік есептерді шығаруда негізгі білім мен дағдыларды пайдалана отырып, сабақтың тақырыбын ашады. Біз осындай мәселелерді шешуде осы кезеңдердің барлығын көрсетеміз. 1. Есепте сипатталған жағдайдың математикалық моделін құрастыру 2. Математикалық модельмен жұмыс 3. Негізгі сұраққа жауап Сабақтың тақырыбын түсіну үшін келесі тапсырманы қарастырыңыз: Тапсырма. Бір қорапта екіншісінен 3 есе көп алма болды. Бірінші жәшіктен екіншісіне 4 килограмм алманы ауыстырғанда екі жәшіктегі алманың массасы бірдей болып шықты. Алдымен әр қорапта неше килограмм болды? • Берілген: • II-Xkg. • I- 3Xkg. • (3X-4) бірінші қорапта • (X+4) екінші ұяшықта • X-? Шешімі: 3x-4=x+4 3x-x=4+4 2x=8 X=8:2 X=4 Жауабы: бірінші қорапта 12 кг алма, ал екінші қорапта 4 кг алма болды. 1-қосымша 1-тапсырма. Бірінші учаскеде таңқурай бұталары екіншісіне қарағанда 3 есе көп болды. Бірінші учаскеден екіншісіне 20 бұта көшіргенде екі учаскеде де саны бірдей болды. Басында әр учаскеде қанша таңқурай бұталары болды? 2-тапсырма. Шідерта мен Нұраның ұзындығы қосылып 1480 шақырым. Нұра Шідертадан 476 шақырым ұзын. Шідерта мен Нұраның бөлек ұзындығы қанша? Тақтаға бір оқушыны шақырып, тапсырманың толық шешімін жазуын сұраңыз. Оқушылар барлық мысалдарды орнында шешеді және сыныптастарын мұқият тыңдай отырып, тақтадағы жазбалар арқылы шешімдерін тексереді. Математикалық сөйлеуді дамыту үшін оқушылардың бірінен кез келген тапсырманың шешіміне егжей-тегжейлі түсініктеме беруін сұраңыз, олардың назарын шешімдердің негіздемесіне аударыңыз. Оқушыларға тапсырмаларды орындауға жеткілікті уақыт беріңіз. Жауаптардың дұрыстығын тексеріп, қателерін талда. Тапсырмалар бойынша оқушылардың қорытындыларын тыңдау. ОнлайнМектепте тапсырмаларды орындаймыз. |
Оқушылар жаңа сабақты меңгереді
|
|
Слайд, оқулық |
|
Қорытынды
|
Кері
байланысты Оқу тапсырмасы: «Өздік жұмыс: сөздік есептерді теңдеумен шешу» тақырыбына презентация дайындау |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
Қорытынды 5 мин |
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Логарифмдер және оның қасиеттері |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушыларды логарифм ұғымымен таныстыру, логарифмдердің негізгі қасиеттерін математикалық есептерді шығаруда қолдана білуге үйрету. Логикалық ойлауды, ақпаратты талдау және қорытындылау қабілетін, сонымен қатар есептеу дағдыларын дамыту. Математикаға деген қызығушылықтарын арттыру, өз бетімен жұмыс істеу дағдыларын дамыту, топпен жұмыс істеуге дағдыландыру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Сәлемдесу, түгелдеу |
Оқушылар ойын ойнайды
|
Формативті бағалау үнемі жүргізіліп отырады. |
Оқулықтар суреттер, слайдтар кестелер |
|
Сабақтың ортасы 20 минут
|
Мұғалім сұрақтар қояды: 1) Диплом дегеніміз не; дипломның негізі неде; Көрсеткіш дегеніміз не? 2) Дәрежелердің негізгі қасиеттерімен жұмыс. Теңдіктердегі дәрежелер арасындағы қатынасты қарастырыңыз
3) Мысалдарды ауызша
шешу: Логарифмдердің негізгі қасиеттері Бұлар қасиеттері көрсеткіштік функцияның логарифмін және қасиеттерін анықтаудан туындайды.
Кез
келген а > 0 (а) кезінде 1) және кез келген оң x және y теңдіктері орындалады:
кез келген жарамды p үшін. Мысалдарды ауызша шешу. X табу
Ондық және натурал логарифмдер Тәжірибеде логарифмдер әртүрлі негіздер бойынша, атап айтқанда 10-негіз бойынша қарастырылады.
Оң санның логарифмі
бойынша
Мысалға, Натурал логарифммен (белгіленеді In) деп аталады логарифм негізі бойынша e
Ондық логарифмдерді есептеу мысалдары
Логарифмнің бір
негізінен екіншісіне өту формулалары Нал тәжірибеде логарифм әртүрлі негіздер бойынша
қарастырылады. Осыдан бір негізден екінші негіз бойынша логарифмге
өту формуласының қажеттілігі туындайды. Өрнектерді жеңілдету:
a)
б.
б.
Жауап.
a) Зерттелген материалды бекіту Ауызша шешу. Логарифмді негізі бойынша табыңыз a негізі бар дәреже түрінде берілген сандар a
Жұптық жұмыс.
Санды
табыңыз Ауызша шешу. Негізгі логарифмдік сәйкестікті пайдалану арқылы өрнектерді жеңілдетіңіз.
1) |
Оқушылар жаңа сабақты меңгереді
|
|
Оқулықтар суреттер, слайд Кестелер плакаттар
|
|
Қорытынды |
Үйге тапсырма: Негізгі логарифмдік сәйкестікті пайдалану арқылы өрнектерді жеңілдетіңіз.
1)
|
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Рекурсия. Рекурсиялық есептерді шешу |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушыларды рекурсия ұғымымен және оның математикада қолданылуымен таныстыру. Оқушыларды математикалық индукция әдісі арқылы рекурсиялық есептерді шығаруға үйрету. Логикалық ойлауын және есептерді талдау қабілетін дамыту |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Психологиялық ахуал қалыптастыру. Оқушылардың көңілін сабаққа
аудару |
Оқушылар бір-бірімен амандасады. |
Формативті бағалау үнемі жүргізіліп отырады |
Оқулықтар |
|
Сабақтың ортасы |
Арифметиканы түсіну мүмкін емес, оған сенуге мәжбүрміз. Мария Кунциевич. Марияның ұлағатты сөзіне пікір қалдырыңыз.
Сабақтың мақсатын қою Жаңа материалды меңгеруді бастайық. Сабақтың тақырыбын дәптеріңе жаз. Көмекші алгоритмдерді программалау тілдерінде жазу ішкі бағдарламалар арқылы жүзеге асырылады. Бүгін сабақта Паскаль тілінде ішкі программалардың ұйымдастырылуын қарастырамыз. Сабақтың тақырыбын және осы тақырыптың негізгі ұғымдарының анықтамаларын дәптерге жазып алу. Сабақтың тақырыбы бойынша жұмыс Күрделі есепті шешу үшін бағдарлама құру кезінде бағдарламашылар бұл тапсырманы ішкі тапсырмаларға, қосалқы тапсырмаларды одан да кішірек ішкі тапсырмаларға және т.б. оңай бағдарламаланатын қарапайым тапсырмаларға дейін бөледі. Паскаль программалау тілі программаны ішкі бағдарламалар деп аталатын жеке бөліктерге бөлуге мүмкіндік береді. Ішкі программа терминінің өзі оның негізгі программаға ұқсас және бағынышты екенін көрсетеді. Ішкі бағдарламалар бағдарламалауды жеңілдететін үш маңызды тапсырманы орындайды: - бағдарлама мәтініндегі ұқсас фрагменттерді қайталап қайталау қажеттілігін жою, яғни бағдарламаның көлемін азайту; - талдау кезінде түсінуді жеңілдете отырып, бағдарлама құрылымын жақсарту; - қателердің ықтималдығын азайту, бағдарламалау қателеріне және өзгерту кезінде күтпеген салдарға төзімділікті арттыру. Жұмыс жоспары: 1.Жаңа ұғымдарды меңгеру (презентация) 2. Негізгі ұғымдарды дәптеріңе жаз 3. Рекурсиялық есептердің негізгі түрлерін шешу жолдарын қарастырыңыз. (1-қосымша) -Түсіндірмелерді тыңдап, жаңа ұғымдарды дәптерге жазып алу. -Алған білімдерін бекіту үшін зертханалық және практикалық жұмыстарды орындайды. -Жұмысты орындау кезінде түсініксіз мәселелерді анықтау Оқыған материалды бекіту Рекурсиялық есептердің негізгі түрлерін шешу. (1-қосымша) |
|
|
Оқулық, |
|
Қорытынды |
Үйге тапсырма беру: өткенді қайталау |
|
ҚБ қойылады. |
|
Қосымша 1.
Тәжірибелік жұмыс.
Жұмыстың мақсаты: рекурсияға арналған есептерді компьютерді қолданбай шешуге үйрету.
Тапсырмалар:
-
Функцияның мәнін есептеу алгоритмі F(n), қайда n – натурал сан, келесі қатынаспен берілген
F(1)=1
F(n)=F(n-1)*(n+1), кезінде n>1
Функцияның мәні неге тең F(5)? Жауапта тек бүтін санды жазыңыз.
Шешім:
F(1)=1
F(2)=F(1)*3=1*3=3
F(3)=F(2)*4=3*4=12
F(4)=F(3)*5=12*5=60
F(5)=F(4)*6=60*6=360
Жауабы: 360
-
Функцияның мәнін есептеу алгоритмі F(n), қайда n – натурал сан, келесі қатынаспен берілген
F(1)=1
F(n)=F(n-1)*(n+2), кезінде n>1
Функцияның мәні неге тең F(5)? Жауапта тек бүтін санды жазыңыз.
Шешім:
F(1)=1
F(2)=F(1)*4=1*4=4
F(3)=F(2)*5=4*5=20
F(4)=F(3)*6=20*6=120
F(5)=F(4)*7=120*7=840
Жауабы: 840
-
Функцияның мәнін есептеу алгоритмі F(n), қайда n – натурал сан, келесі қатынаспен берілген
F(1)=1
F(n)=F(n-1)*(2*n+1), кезінде n>1
Функцияның мәні неге тең F(4)? Жауапта тек бүтін санды жазыңыз.
Шешім:
F(1)=1
F(2)=F(1)*5=1*5=5
F(3)=F(2)*7=5*7=35
F(4)=F(3)*9=35*9=315
Жауабы: 315
-
Функцияның мәнін есептеу алгоритмі F(n), қайда n – натурал сан, келесі қатынаспен берілген
F(1)=1
F(n)=F(n-1)*(2*n-1), кезінде n>1
Функцияның мәні неге тең F(5)? Жауапта тек бүтін санды жазыңыз.
Шешім:
F(1)=1
F(2)=F(1)*3=1*3=3
F(3)=F(2)*5=3*5=15
F(4)=F(3)*7=15*7=105
F(5)=F(4)*9=105*9=945
Жауабы: 945
-
Функцияның мәнін есептеу алгоритмі F(n), қайда n – натурал сан, келесі қатынаспен берілген
F(1)=1
F(n)=F(n-1)*(3*n-2), кезінде n>1
Функцияның мәні неге тең F(4)? Жауапта тек бүтін санды жазыңыз.
Шешім:
F(1)=1
F(2)=F(1)*4=1*4=4
F(3)=F(2)*7=4*7=28
F(4)=F(3)*10=28*10=280
Жауап: 280
-
Функцияның мәнін есептеу алгоритмі F(n), қайда n – натурал сан, келесі қатынаспен берілген
F(0)=1, F(1)=1
F(n)=F(n-1)+F(n-2), кезінде n>1
Функцияның мәні неге тең F(7)? Жауапта тек бүтін санды жазыңыз.
Шешім:
F(0)=1
F(1)=1
F(2)=F(1)+F(0)=1+1=2
F(3)=F(2)+F(1)=2+1=3
F(4)=F(3)+F(2)=3+2=5
F(5)=F(4)+F(3)=5+3=8
F(6)=F(5)+F(4)=8+5=13
F(7)=F(6)+F(5)=13+8=21
Жауап: 21
-
Функцияның мәнін есептеу алгоритмі F(n), қайда n – натурал сан, келесі қатынаспен берілген
F(0)=1, F(1)=1
F(n)=2*F(n-1)+F(n-2), кезінде n>1
Функцияның мәні неге тең F(6)? Жауапта тек бүтін санды жазыңыз.
Шешім:
F(0)=1
F(1)=1
F(2)=2*F(1)+F(0)=2*1+1=3
F(3)=2*F(2)+F(1)=2*3+1=7
F(4)=2*F(3)+F(2)=2*7+3=17
F(5)=2*F(4)+F(3)=2*17+7=41
F(6)=2*F(5)+F(4)=2*41+17=99
Жауап: 99
-
Функцияның мәнін есептеу алгоритмі F(n), қайда n – натурал сан, келесі қатынаспен берілген
F(0)=1, F(1)=1
F(n)=F(n-1)+2*F(n-1), кезінде n>1
Функцияның мәні неге тең F(6)? Жауапта тек бүтін санды жазыңыз.
Шешім:
F(0)=1
F(1)=1
F(2)=F(1)+2*F(1)=1+2*1=3
F(3)=F(2)+2*F(2)=3+2*3=9
F(4)=F(3)+2*F(3)=9+2*9=27
F(5)=F(4)+2*F(4)=27+2*27=81
F(6)=F(5)+2*F(5)=81+2*81=243
Жауабы: 243
-
Рекурсивті алгоритм берілген:
procedure F(n: integer);
begin
writeln(n);
if n<6 then begin
F(n+2);
F(n*3)
end
end;
Шақырылған кезде шығарылатын сандардың қосындысын табыңыз F(1)
Шешім:
-
алдымен анықтаймыз рекурентті формуланы; арқылы белгілейік F(n) шақырылған кезде болатын сандардың қосындысы F(n)
-
кезінде n>=6 процедура нөмірді шығарады n және рекурсивті қоңырауларсыз жұмысты аяқтайды: F(n)=n, кезінде n>=6
-
кезінде n<6 процедура нөмірді шығарады n және екі рет өзін-өзі шақырады F(n)=n+F(n+2)+F(3n), кезінде n<6
-
шақыру нәтижесінде F(1) аламыз:
F(1)=1+F(3)+F(3)
F(3)=3+F(5)+F(9)=3+F(5)+9
F(5)=5+F(7)+F(15)=5+7+15=27
-
кері алмастыруды қолданамыз
F(3)=3+F(5)+F(9)=3+F(5)+9=3+27+9=39
F(1)=1+2*F(3)=79
-
жауабы: 79
-
Рекурсивті алгоритм берілген:
procedure F(n: integer);
begin
writeln(‘*’);
if n>0 then begin
F(n-2);
F(n div 2)
end
end;
Қанша…
Шешім:
-
алдымен анықтаймыз рекурентті формуланы; арқылы белгілейік F(n), бағдарламаны шақырған кездегі жұлдызшалар саны
-
бағдарламадан біз мұны көреміз
F(n)=1, кезінде n<=0
F(n)=1+F(n-2)+F(n div 2), кезінде n>0
-
еске салайық, бұл n div 2 – бұл бөлудің квотенті n 2-ге
-
осы формулалар бойынша кестені 0-ден бастап толтырамыз:
F(0)=1
F(1)=1+F(-1)+F(0)=1+1+1=3
F(2)=1+F(0)+F(1)=1+1+3=5
F(3)=1+F(1)+F(1)=1+3+3=7
F(4)=1+F(2)+F(2)=1+5+5=11
F(5)=1+F(3)+F(2)=1+7+5=13
F(6)=1+F(4)+F(3)=1+11+7=19
F(7)=1+F(5)+F(3)=1+13+7=21
-
-
n
0
1
2
3
4
5
6
7
F(n)
1
3
5
7
11
13
19
21
-
-
жауабы: 21
-
Функциялардың мәндерін есептеу алгоритмі F(n) және G(n), қайда n – натурал сан, келесі қатынастармен берілген:
F(1)=1, G(1)=1;
F(n)=F(n-1)-G(n-1),
G(n)= F(n-1)+G(n-1), кезінде n>=2
Шаманың мәні неге тең F(5)/G(5)? Жауапта жазыңыз тек бүтін сан
Шешім:
-
іс жүзінде рекурентті формула берілген жұп үшін (F(n);G(n))
-
байқаймыз, бұл F(n) – бұл алдыңғы жұптың вариациясы, жәнеG(n) – бірдей мәндердің қосындысы
-
қосымшакестені белгілі бірінші жұптан бастап сызамыз
-
қажетті мән F(5)/G(5) 1-ге тең
-
Жауабы: 1
|
n |
1 |
2 |
3 |
4 |
5 |
|
F(n) |
1 |
0 |
-2 |
-4 |
-4 |
|
G(n) |
1 |
2 |
2 |
0 |
-4 |
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Тест тапсырмалары. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушылардың алған білімдерін тексеру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
І. Ұйымдастыру
кезеңі. Психологиялық сәт.
|
|
|
Интерактивті тақта, оқулық. |
|
Жаңа білім 15 мин 2 мин Бекіту 15 мин |
1 – нұсқа Тақырыбы: Рекурсия. Рекурсивті есептерді шешу. 1. Сұрақ: Рекурсияға қатысты төмендегі тұжырымдардың қайсысы дұрыс? A) Рекурсия – функция өзін шақыратын процесс. B) Рекурсия – циклдің қайталану санына шектеу қойылмайтын нұсқасы. B) Рекурсия тек массивтің максималды элементін табу үшін қолданылатын алгоритм болып табылады. 2-сұрақ: Әділ тиынды лақтырған кезде елтаңбаны алу ықтималдығы қандай? а) 0 б) 1 в) 0,5 3-сұрақ: Рекурсия тереңдігін шектеу үшін қандай әдіс қолданылады? A) Қайталану санына шектеу қою. B) Рекурсиядан шығу шартын қолдану. C) Қоңырауларды шектеу үшін қосымша мүмкіндікті пайдалану. Тақырыбы: Логарифмдер және олардың қасиеттері. 4-сұрақ: Төмендегі графиктердің қайсысы логарифмдік функцияны дәл көрсетеді? A) А кестесі В) В кестесі B) C кестесі 5-сұрақ: Логарифмдердің қасиеттеріне қатысты төмендегі тұжырымдардың қайсысы дұрыс? A) log a (bc) = log a (b) + log a (c) B) log a (b + c) = log a (b) + log a (c) B) log a (b^c) = c * log a (b) Тақырыбы: Теңдеулерді пайдаланып сөздік есептер жазу. 6-сұрақ: Есепті шешу үшін мына теңдеулердің қайсысын қолдануға болады: "Василий әрқайсысы 15 рубльден бірнеше кәмпит сатып алды. Егер ол 75 рубль төлесе, ол қанша кәмпит сатып алды?" A) 15x = 75 B) 15 - х = 75 B) x/15 = 75 7-сұрақ: Төмендегі теңдеулердің қайсысын есепті шешуге қолдануға болады: «Наталья өзінің бес кітабын екі досына бөледі. Егер әрбір досы х кітап алса, ол әр досына неше кітап сыйлады?». A) 2x = 5 B) 5/2x = 1 B) x - 2 = 5 Тақырыбы: Ньютон биномиясы. Паскаль үшбұрышы. 8-сұрақ: Паскаль үшбұрышының 5-ші қатарындағы 2 санына қандай сан сәйкес келеді? A) 1 В) 10 10-да 9-сұрақ: (a+b)^2 мәні неге тең, мұндағы a=2 және b=3? A) 4 B) 9 B) 25 10-сұрақ: Паскаль үшбұрышының 4-ші қатары неге ұқсайды? А) 1 3 3 1 B) 1 3 6 10 В) 1 2 3 4 2 – нұсқа 1. Рекурсияның негізгі идеясы қандай? а) Қайталанатын амалдар үшін циклдарды қолдану ә) Функцияны өзінен шақыруда в) Программаны тармақтау үшін шартты операторларды қолдануда 2. Қайталанатын цифрлары жоқ неше төрт таңбалы сан бар? а) 524 б) 3024 в) 9 3. Келесі рекурсивті кодты орындаудың нәтижесі қандай болады? нақты факт(n): егер n == 1: қайтару 1 басқа: қайтару n * факт(n-1) басып шығару(факт(5)) а) 10 ә) 120 в) 30 4. Төмендегі қасиеттердің қайсысы логарифмдерге қатысты? а) Қосындының логарифмі логарифмдердің қосындысына тең б) Көбейтіндінің логарифмі логарифмдердің көбейтіндісіне тең в) Бөлу логарифмі логарифмдердің айырмасына тең 5. Теңдеу дегеніміз не? а) Белгісіз шаманы қамтитын математикалық өрнек б) Белгілі бір шартты қанағаттандыратын сандық мәндер жиынтығы в) Белгісіз шаманы білдіретін математикалық таңба 6. Теңдеулерді қолданып сөз есебін қалай жасауға болады? а) Теңдеудегі сандарды сөздермен ауыстыр ә) Жағдайды табиғи тілде сипаттап, оны теңдеу түрінде аудару в) Берілген жағдаятпен сұраққа жауап ретінде теңдеуді қолданыңыз 7. Ньютон биномиясы дегеніміз не? а) Екі айнымалының дәрежелерінің қосындысын қамтитын математикалық өрнек б) Биномдық кеңею коэффициенттерінен тұратын үшбұрыш (a + b)^n в) Теңдеуді мүшелерге жіктеу арқылы шешу әдісі 8. Паскаль үшбұрышының негізгі идеясы қандай? а) (a + b)^n формуласы бойынша биномдық коэффициенттерді кеңейту б) Әрбір сан үстіндегі екі санның қосындысына тең болатын сандық үшбұрышты шығару в) Таңбасы біртіндеп кемулі шексіз қатардың қосындысын табу 9. Паскаль үшбұрышының бесінші қатардағы және үшінші бағандағы элементі қандай сан? а) 3 б) 5 в) 10 10. Паскаль үшбұрышын қолданудың негізгі мақсаты қандай? а) Сандардың комбинацияларын пайдаланып теңдеулерді шешу б) Таңбасы біртіндеп өсетін шексіз қатардың қосындысын табу в) Сан үшбұрышының қасиеттері мен заңдылықтарын оқу |
|
|
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: Өткен тақырыптарды қайталау |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Олимпиада есептерін шешу |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
- логикалық ойлау арқылы стандартты емес есептерді шығаруды үйрену; - есепті және оның шешімін қысқаша жазуды үйрену; - математикаға қызығушылығын дамыту; - сыныптастарының пікіріне құрметпен қарауға тәрбиелеу. |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Психологиялық ахуал қалыптастыру. Оқушылардың көңілін сабаққа
аудару |
Оқушылар бір-бірімен амандасады. |
Формативті бағалау үнемі жүргізіліп отырады |
Оқулықтар |
|
Сабақтың ортасы |
"Математика - бұл мызғымас құрылым және шынайы пайғамбарлық" (Л. Берс). Берстің ұлағатты сөзін талдаңыздар
Бірдей сандар. - Қосу арқылы бес екілік арқылы 28 санын жаз. (Жауабы: 22+2+2+2=28) 1. Цифрларының қосындысы 9-ға тең, 20-дан кіші екі таңбалы санды жаз. Бұл санды тоғыздардың қосындысы ретінде көрсетуге бола ма? Барлық шарттары бірдей бұл санды қосынды ретінде тағы қалай көрсетуге болады? Жауабы: 18, 9+9=18, 6+6+6=18, 3+3+3+3+3+3=18, т.б.) Көңілді үзіліс 1. Алақаныңызды ашып қолыңызды алға созыңыз. Кішкентай саусағыңызды алақанға басыңыз, қалған саусақтар ұзартылуы керек. Қолды ауыстырыңыз. 2. Шеге соғу үшін сол қолыңызды пайдаланыңыз, ал оң қолыңызбен бірдеңені үтіктеңіз. 1. Үштен – төрт. -Қазір мен сендерге әр топқа 3 таяқтан беремін. Тапсырма: 3 таяқшаның 4-ін жасаңыз Жауабы: ///=/V 1. Төрт түзу сызық. - Қағазға 9 нүктені төртбұрыш
түрінде орналастыратындай етіп қойыңыз. Қарындашты қағаздан
көтермей, барлық нүктелерді төрт түзу сызықпен сызып
тастаңыз. Жұмбақ ай. Әрине, бір жылда неше ай бар екенін білесіз бе? Жылдың соңғы айы қалай аталады? Желтоқсан сөзі нені білдіретінін білесіз бе? Бұл сөз гректің «дека» - он сөзінен шыққан. Жыл он екінші айы, желтоқсан айы «оныншы» деп аталады екен. Бұл біздің күнтізбеміз ежелгі римдіктердің күнтізбесінен шыққандықтан болды. Римдіктер жыл басын 1 қаңтар емес, басқа айдың бірінші күні деп есептеді. Бұл қай ай? Оның атын жаз. (наурыз) 7) Сан үшбұрышы Осы үшбұрыштың қабырғаларына 1-ден 9-ға дейінгі сандарды әр жақтың қосындысы 20 болатындай етіп орналастыр.
Көңілді басқатырғыштар. - Балаларға 3 тапсырма беріледі: №1. Піл коньки тепті. Бұл ауыр, сондықтан мен әр аяғыма екі коньки, ал сандықтың ұшына тағы бір коньки қойдым. Піл неше коньки киді? (9) № 2. Чебурашка апельсин қорапшасында саяхаттап жүріп таңғы және түскі асқа 1 апельсин, кешкі асқа 2 апельсин жеді. Сапар аптасында ол қанша апельсин жеді? (20) №3. Федор ағайдың терезелерінде 8 гүл құмыралары бар еді, онда гүлдер өсті. Бір күні Федор ағай келіп, бос гүл құмыраларын көреді. Гүлдерді Мурка сиыр жеді. Құмыраның бір жартысында 2 гүл, екінші жартысында 3 гүл болса, Мурка сиыр неше гүл жеді? (28) Сандық жұмбақтар Сандық жұмбақтарды шешіп,
жауаптарыңызды жазыңыз. |
Оқушылар сұрақтарға жауап беріп, түсінгендерін дәлелдей алу қабілетін көрсетеді; бірін-бірі бағалау, қолданба. үй. асс күнделіктерінде |
Өзін-өзі бағалау және өзара бағалау |
Оқулық, |
|
Қорытынды |
Үйге тапсырма беру: Сандық
жұмбақтарды шешіп, жауаптарыңызды жазыңыз.
|
|
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Олимпиада есептерін шығаруда сандар теориясын қолдану |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Сандар теориясының негізгі ұғымдары мен әдістерін оқып үйрену. Алған білімдерін олимпиада есептерін шығаруда қолдана білуге үйрету. Логикалық ойлауын және математикалық интуициясын дамыту. |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Психологиялық ахуал қалыптастыру. Оқушылардың көңілін сабаққа
аудару |
Оқушылар бір-бірімен амандасады. |
Формативті бағалау үнемі жүргізіліп отырады |
Оқулықтар |
|
Сабақтың ортасы |
«Математиканың қарапайым халыққа пайдасы –
қиындығы» А. Александров. Александрдың қанатты сөзіне
пікір қалдырыңдар. Сәлемдесу, сабақтың мақсатын түсіндіру. Сандар теориясының анықтамасы және оның математикалық және олимпиадалық есептердегі рөлі. Сандар теориясын қолданатын олимпиада есептерінің мысалдарын қарастыру. Олимпиада есептерімен жұмыс: Оқушыларға сандар теориясын қолдануды қажет ететін олимпиада есептерін ұсыну. Бұл есептерді кезең-кезеңмен шешуді көрсету. 1-тапсырманың мысалы: Вася 105 қырыққабатты 5 досына бөлгісі келеді. Әрбір дос ала алатын қырыққабаттың ең аз саны қанша? Мұғалім қалдықпен бөлу теориясын қолдану керектігін түсіндіреді және 5-ке бөлгенде 105 қалдығын табады, ол 0 болады. Сондықтан әрбір дос 21 қырыққабат алады. 2-тапсырманың мысалы: Мектеп олимпиадасына математикадан 100 адам, физикадан 50, информатикадан 48 адам қатысты.Оқушылардың әрқайсысы қанша олимпиадаға қатысқанын сұрағанда, «екі» деген жауап екі есе көп болды. адамдарды «бір» деп, ал «үште» жауабы «бірде» дегеннен үшке аз. Бұл олимпиадаларға қанша адам қатысты? Олимпиадаға математикадан – 100, физикадан – 50, информатикадан – 48, барлығы 100+50+48=198 адам қатысты. 3 олимпиадада адамдар болды, олар 3 рет саналды. x = 3a деп белгілейік. 2 олимпиадада б адам болды, олар 2 рет саналды. y = 2b деп белгілейік. 1-ші олимпиадада адамдар болды, олар 1 рет саналды. Оларды c = z деп белгілейік. Бірақ оқушылардың жауаптарынан a = c/3; b = c/2, яғни x = 3a = 3*c/3 = c = z; y = 2b = 2*c/2 = c = z x + y + z = z + z + z = 3z = 198; z = 198/3 = 1-ші олимпиадаға 66 адам қатысты. b = z/2 = 66/2 = 2 олимпиадаға 33 адам қатысты. a = z/3 = 66/3 = 22 адам 3 олимпиадаға қатысты. Барлығы 22 + 33 + 66 = 121 адам. 3 тапсырма. Параметрдің қандай мәндерінде а теңдеу sin²(x) - 2 (a - 3) sin(x) + a² - 6a + 5 = 0 тамыры жоқ па? Ауыстыру : t = sinx |t|≤ 1 t² - 2 (a - 3) * t + a² - 6a + 5 = 0 D / 4 = (a - 3)² - (a² - 6a + 5) = a² - 6a + 9 - a² + 6a - 5 = 4 = 2² ⇒(шаршы теңдеу бар екі әртүрлі жарамды тамырдың) t₁ = a - 3 - 2 = a - 5 ; t₂ = a - 3 + 2 = a - 1. Мыс. теңдеудің шешімі болмайды, егер қанағаттандырылмаса | t |≤ 1, т. Е. егер : а) { a - 5 < - 1 ; a - 1 2. ⇒a∈( 4 ; ∞). б){ a - 5 > 1 ; a - 1 a - 5 * * * {a> 6 ; a < 0 . ⇒ a∈∅. Жауап : a∈( - ∞ ; 0)∪(2 ; 4)∪(4 ; ∞). болмайды? |
Оқушылар сұрақтарға жауап беріп, түсінгендерін дәлелдей алу қабілетін көрсетеді; бірін-бірі бағалау, қолданба. үй. асс күнделіктерінде |
Өзін-өзі бағалау және өзара бағалау |
Оқулық, |
|
Қорытынды |
Үйге тапсырма беру: сандар теориясының формуласын қайталау. |
|
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Күрделі есептерді қарапайым қосалқы тапсырмаларға бөлу |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Күрделі мәселені анықтаңыз және оны ішкі тапсырмаларға бөлудің не үшін қажет екенін түсіндіріңіз. Ішкі тапсырмаларға бөлу арқылы шешуге болатын есептердің мысалдарын талдаңыз. Оқушыларды есептерді ішкі тапсырмаларға бөлудің негізгі әдістерімен таныстыру. |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Психологиялық ахуал қалыптастыру. Оқушылардың көңілін сабаққа
аудару |
Оқушылар бір-бірімен амандасады. |
Формативті бағалау үнемі жүргізіліп отырады |
Оқулықтар |
|
Сабақтың ортасы |
- Мұғалім күрделі есепті қарапайым ішкі есептерге ыдырату мәселені жақсы түсінуге және оны шешуге мүмкіндік беретінін түсіндіреді. - Күрделі есептерді қарапайым есептерге ыдырату мысалдары (мысалы, алма сатып алу мәселесі, үй салу мәселесі). - Декомпозиция қадамдарын түсіндіру: негізгі ақпарат элементтерін анықтау, олардың шешімге әсерін талдау, ішкі тапсырмаларды шешу ретін құру. Практикалық жұмыс - Сыныпты 3-4 адамнан топтарға бөлу. - Әр топқа қарапайым қосалқы тапсырмаларға бөлу керек тапсырма беру. - Топтар бірлесе отырып тапсырманы талдайды, негізгі элементтерді анықтайды және оны ішкі тапсырмаларға бөледі. - Осыдан кейін әр топ өз нәтижелерін басқа топтарға ұсынып, оның ыдырау логикасын түсіндіреді. Талқылау және кері байланыс - Мұғалім есепті декомпозициялау процесін талқылайды және оқушыларға ыдыраудың сапасы бойынша өзін-өзі бағалауды ұсынады. - Мұғалім әр топ бойынша оң жақтарын атап, жақсарту мүмкіндіктерін көрсете отырып кері байланыс береді. Мәселенің мысалы және оның шешімі: Тапсырма: Петя мен Вася шеңбер бойымен велосипедпен жүреді. Петя 1 сағатта 6 айналым жасайды, ал Вася 45 минутта 4 айналым жасайды. Олардың бастапқы нүктесінде қайтадан кездесуі қанша уақытты алады? Шешімі: 1. Тапсырманың негізгі элементтерін анықтау: - Петя 1 сағатта 6 айналым жасайды. - Вася 45 минутта 4 айналым жасайды. 2. Шешім қабылдауға әрбір элементтің әсерін талдау: - 1 сағатта Петя 6 айналым жасайды, сондықтан 1 айналымға Петя 10 минутты алады (60 минут / 6 айналым). - 45 минутта Вася 4 айналым жасайды, сондықтан 1 революция үшін Васяға 11,25 минут қажет (45 минут / 4 айналым). 3. Ішкі тапсырмаларды шешу ретін құру: - Ұлдардың әрқайсысын айналдыруға қажетті уақыттың LCM (ең кіші ортақ еселік) мәнін табайық. Бұл жағдайда LCM 90 минутты құрайды. - Петя әр 10 минут сайын төңкеріс жасайтындықтан, ол 90 минутта 9 айналым жасайды (бір революцияға 90 минут / 10 минут). - Сол сияқты, Вася 90 минутта 8 айналым жасайды (бір айналымға 90 минут / 11,25 минут). Бұл олардың 90 минуттан кейін бастапқы нүктеде қайта кездесетінін білдіреді. Бұл үлгі есеп пен шешім оқушыларға күрделі мәселені қарапайым ішкі мәселелерге қалай бөлу керектігін түсінуге және дәл және тиімді шешімге жету үшін сол қадамдарды логикалық түрде орындауға көмектеседі. |
Оқушылар сұрақтарға жауап беріп, түсінгендерін дәлелдей алу қабілетін көрсетеді; бірін-бірі бағалау, қолданба. үй. асс күнделіктерінде |
Өзін-өзі бағалау және өзара бағалау |
Оқулық, |
|
Қорытынды |
Үйге тапсырма беру: үйде күрделі мәселені ішкі тапсырмаларға бөліп, келесі сабақта талқылау үшін нәтижелерін жазу. |
|
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Күрделі есептерді қарапайым қосалқы тапсырмаларға бөлу бойынша практикалық жұмыс |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Күрделі есептерді қарапайым ішкі тапсырмаларға бөлшектеу әдісі туралы алған білімдерін бекіту. Осы әдіс арқылы математикалық есептерді өз бетінше шешу дағдыларын дамыту. Оқушылардың математиканы оқуға деген ынтасының деңгейін арттыру. |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Психологиялық ахуал қалыптастыру. Оқушылардың көңілін сабаққа
аудару |
Оқушылар бір-бірімен амандасады. |
Формативті бағалау үнемі жүргізіліп отырады |
Оқулықтар |
|
Сабақтың ортасы |
3 құбыр арқылы толтырылған бассейн мәселесін шешу: түсіндірме және мәліметтер Бассейн бар жағдайды елестетіп көрейік және оны толтыру үшін толтыру жылдамдығы әртүрлі үш құбыр пайдаланылады. Мәселе әрбір құбырдың толтыру жылдамдығын ескере отырып, бассейннің толығымен толтырылатын уақытын анықтау болып табылады. Бұл мәселені шешу үшін әр құбырдың уақыт бірлігіне көлем бірлігімен толтырылу жылдамдығын білу қажет. Бірінші құбырдың жылдамдығы минутына а литрге, екіншісі минутына в литрге, үшіншісі минутына с литрге тең болсын. Бассейн толығымен толтырылатын уақытты t минут ретінде белгілейік. Осы уақыт ішінде әрбір құбыр қанша су көлемін толтыра алатынын қарастырайық. Бірінші құбыр бассейнді минутына литр жылдамдықпен толтырады. Демек, т уақытында ол а * т литр суды толтырады. Сол сияқты, екінші құбыр бассейнді b * t литрмен, ал үшінші құбыр c * t литрмен толтырады. Осылайша, бассейндегі судың жалпы көлемі t уақытынан кейін a * t + b * t + c * t тең болады. Бұл көлем бассейннің көлеміне тең болуы керек екенін ескеру ғана қалады. Бассейннің көлемін V литр деп белгілейік. Сонда t уақытын табудың теңдеуі a * t + b * t + c * t = V түрінде болады. Бұл теңдеуді бассейн толығымен толтырылатын уақыттың мәнін алу арқылы t-ге қатысты шешуге болады. Жоғарыда келтірілген шешім әрбір құбырдың толтыру жылдамдығын ескере отырып, бассейнді толтыруға кететін уақытты анықтауға мүмкіндік береді. Бұл тапсырма бірнеше тәуелді процестер бірге жұмыс істегенде уақытты табу тапсырмасының классикалық мысалы болып табылады. 3 құбыр арқылы толтырылған бассейн туралы тапсырманың сипаттамасы Бірінші құбыр бассейнді бір сағатта, екіншісі екі сағатта, үшіншісі төрт сағатта толтыра алады делік. Егер барлық үш құбыр бір уақытта ашық болса, бассейнді толтыру уақыты t сағатты құрайды. Мәселені шешу үшін t мәнін анықтауымыз керек. Бастау үшін әрбір құбырды жеке қарастырамыз. Егер бірінші құбыр уақыттың бір бөлігінде жұмыс істесе, онда ол осы уақыт ішінде бассейннің т-ші бөлігін толтырады. Сол сияқты, екінші құбыр бассейннің жартысын т/2 сағатта, ал үшінші құбыр бассейннің төрттен бірін т/4 сағатта толтырады. Осы мәндерді қорытындылай келе, келесі теңдеуді аламыз: t + t/2 + t/4 = 1 Теңдеуді жеңілдете отырып, аламыз: 4t + 2t + t = 4 Осылайша, бассейнді толтырудың жалпы уақыты t тең 4/(4+2+1) = 4/7 сағат немесе шамамен 0.57 сағат. Осылайша, 3 құбыр арқылы толтырылған бассейн мәселесі барлық үш құбыр бір уақытта ашық болған жағдайда бассейнді толтыру уақытын есептеуге мүмкіндік береді. Бұл тапсырмада әрбір құбырды толтыру жылдамдығын ескеру және бассейнді толтырудың жалпы уақытын анықтау маңызды. Бассейн мәселесін шешудің алғашқы қадамы Бассейн мәселесін шешу үшін үш құбырдың әрқайсысы арқылы бассейнге қанша су кіретінін анықтауымыз керек. Осы ақпаратты пайдалана отырып, біз белгілі бір уақыттан кейін бассейнде болатын судың жалпы көлемін таба аламыз. Бастау үшін тапсырма шартында берілген деректерді қарастырайық. Бірінші құбыр бассейнді 1 сағатта, екінші құбыр 2 сағатта, үшінші құбыр 3 сағатта толтыра алатынын білеміз. Бұл әр сағат сайын бірінші құбыр бассейн көлемінің 1/1 бөлігін, екінші құбыр бассейн көлемінің 1/2 бөлігін, ал үшінші құбыр бассейн көлемінің 1/3 бөлігін қамтамасыз ететінін білдіреді. Ыңғайлы болу үшін әр құбырды кесте түрінде елестетіп көрейік: Құбыр Уақыт Судың көлемі Судың сағатына көлемі Бірінші 1 сағат 1/1 1 Екінші 2 сағат 1/2 1/2 Үшінші 3 сағат 1/3 1/3 Енді біз үш құбырдың әрқайсысы бассейнге әр сағат сайын қанша су жіберетінін оңай анықтай аламыз. Бұл ақпарат келесі қадамда мәселені шешу үшін пайдалы болады. Аралық есептеулер және бассейн мәселесінің анық емес мәліметтері 3 құбыр арқылы толтырылған бассейн мәселесін шешкен кезде, бір қарағанда түсініксіз болуы мүмкін бірнеше аралық есептеулер мен бөлшектерді ескеру қажет. Біріншіден, әрбір құбырдың өткізу қабілеттілігі тапсырма шартында орнатылғанын есте ұстаған жөн. Бұл әдетте құбырдың бассейннің бір бөлігін толтыратын уақыты. Мысалы, егер бірінші құбырдың өткізу қабілеті 2 сағатты құраса, бұл оның бассейннің 1/2 бөлігін 2 сағатта толтыратынын білдіреді. Екіншіден, құбырлар бір уақытта жұмыс істейтінін ескеру қажет. Бұл бассейнге бір сағатта құйылатын су көлемі әрбір құбырдың бір сағатта құйылатын су көлемінің қосындысына тең екенін білдіреді. Мысалы, егер бірінші құбыр 2 сағат ішінде бассейн көлемінің 1/2 бөлігін қосса, сағатына ол бассейн көлемінің 1/4 бөлігін қосады. Үшіншіден, барлық үш құбыр бір уақытта жұмыс істеген кезде бассейннің толтырылатын уақытын ескеру қажет. Ол үшін барлық үш құбырдың өткізу қабілеттілігінің қосындысының кері мәнін табу керек. Мысалы, егер құбырлардың өткізу қабілеттілігі сәйкесінше 2, 3 және 6 сағатты құраса, онда бұл сандардың қосындысының өзара қатынасы 1/11 болады. Осы аралық есептеулер негізінде бассейнді толтыруға қанша уақыт кететінін анықтауға болады. Ол үшін үш құбырдың өткізу қабілеттілігінің қосындысының өзара қатынасын бассейннің жалпы көлеміне көбейту керек. Мысалы, бассейннің жалпы көлемі тең болса 1000 литр, онда толтыру уақыты 1/11 * 1000 = 90.91 сағатқа тең болады. Осылайша, барлық аралық есептеулер мен тапсырманың егжей-тегжейлерін ескере отырып, барлық үш құбыр бір уақытта жұмыс істеген кезде бассейннің толтырылу уақытын дәл анықтауға болады. 3 құбыр арқылы толтырылған бассейн мәселесінің түпкілікті шешімі Осы ақпараттан, біз келесі формулаларды шығара аламыз: Бірінші құбырдың жұмыс жылдамдығы = сағатына бассейннің 1/5 бөлігі Екінші құбырдың жұмыс жылдамдығы = сағатына бассейннің 1/6 бөлігі Үшінші құбырдың жұмыс жылдамдығы = сағатына бассейннің 1/7 бөлігі Бассейнді толтыруға кететін уақытты табу үшін біз әрбір құбырдың үлесін қосып, олардың бірге жұмыс істеуінің жалпы жылдамдығын табуымыз керек. Барлық үш құбырдың жалпы жұмыс жылдамдығы = бірінші құбырдың жұмыс жылдамдығы + екінші құбырдың жұмыс жылдамдығы + үшінші құбырдың жұмыс жылдамдығы Барлық үш құбырдың жалпы жұмыс жылдамдығы = 1/5 + 1/6 + 1/7 бассейннің сағатына Барлық үш құбырдың жалпы жұмыс жылдамдығын тапқаннан кейін бассейнді толтыруға кететін уақытты таба аламыз. Бассейнді толтыруға кететін уақыт = 1 / (барлық үш құбырдың жалпы жұмыс жылдамдығы) Енді біз есептеуді бастауға болады: Барлық үш құбырдың жалпы жұмыс жылдамдығы = 1/5 + 1/6 + 1/7 = Сағатына 47/210 бассейн Бассейнді толтыруға кететін уақыт = 1 / (47/210) = 210/47 = 4.468 сағат Сонымен, 3 құбыр арқылы толтырылатын бассейн мәселесінің түпкілікті шешімі бассейнді толтыру үшін шамамен 4,468 сағатты қажет етеді.
100А+В=121В 100В+А=84А+14 А=42 В=35 |
Оқушылар сұрақтарға жауап беріп, түсінгендерін дәлелдей алу қабілетін көрсетеді; бірін-бірі бағалау, қолданба. үй. асс күнделіктерінде |
Өзін-өзі бағалау және өзара бағалау |
Оқулық, |
|
Қорытынды |
Үйге тапсырма беру: үйде күрделі мәселені ішкі тапсырмаларға бөліп, келесі сабақта талқылау үшін нәтижелерін жазу. |
|
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Тест тапсырмалары. |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушылардың алған білімдерін тексеру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
І. Ұйымдастыру
кезеңі. Психологиялық сәт.
|
|
|
Интерактивті тақта, оқулық. |
|
Жаңа білім 15 мин 2 мин Бекіту 15 мин |
1 – нұсқа 1. Күрделі математикалық есептерді қарапайым ішкі есептерге бөлу үшін қандай әдісті қолдануға болады? а) Индукция әдісі б) Қайшылық арқылы дәлелдеу әдісі в) «Бөл және жең» әдісі 2. Сандар теориясы нені зерттейді? а) Сандардың құрылымы және олардың қасиеттері б) Графиктер және желілер в) Дифференциация және интеграция ережелері 3. Математиканың төмендегі салаларының қайсысы олимпиадалық есептерді шешуде тиімді? а) Геометрия б) Матрицалық есептеулер в) Комбинаторика 4. Математикадан олимпиада есептерін шешуге қандай дағдылар көмектеседі? а) Жақсы есте сақтау б) Математика ұғымдарын терең түсіну в) Мәнерлеп оқу 5. Күрделі математикалық есепті сәтті шешу үшін қандай қадамдар жасау керек? а) Бірден, ойланбастан жауап беріңіз б) Проблеманың қойылымын талдаңыз және негізгі элементтерді анықтаңыз в) Олимпиаданың басқа қатысушыларынан көмек сұрау 6. Математикадан олимпиадаларда қандай есеп түрлері жиі кездеседі? а) Математикалық функцияларды есептеуге арналған есептер б) Теңдеулер мен теңсіздіктерді шешуге арналған есептер в) Функциялардың графиктерін тұрғызуға арналған тапсырмалар 7. Математикадан олимпиада есептерін тапсыру кезінде қандай тәсіл тиімді? а) Бірінші кездескен шешімді тез жазып алыңыз б) Барлық қолда бар деректерді талдап, негізделген шешім қабылдау в) Қатысушының шешімін артына қайта жазыңыз 8. Шығармашылық ойлау олимпиадалық математикалық есептерді шешуде қандай рөл атқарады? а) маңызды емес б) Стандартты емес шешімдерді табуға мүмкіндік береді в) Шешім процесін айтарлықтай баяулатады 9. Математикадан олимпиада есептерін шешу қиын болуының негізгі себебі неде? а) Шешуге уақыт жеткіліксіз б) Тапсырма түсініксіз тұжырымдалған в) Калькуляторларды пайдалануға шектеулер 10. Математикадан олимпиада есептерін шешуге дайындалуға қандай ақпарат көздері көмектеседі? а) Математика оқулықтары б) есептер жинағы бар интернет ресурстары в) Олимпиадаға сәтті қатысқан достардың кеңесі 2 – нұсқа 1. Сұрақ: Төмендегі есептердің қайсысы математикалық олимпиадаға жатады? а) қабырғалары берілген тіктөртбұрыштың ауданын табу; ә) Белгілі қабырғаларды пайдаланып үшбұрыштың периметрін есептеңіз; в) Емтиханнан өткен талапкерлердің санын, егер өту пайызы және топтағы талапкерлердің жалпы саны белгілі болса, анықтаңыз. 2-сұрақ: Функция графиктерін талдауға байланысты олимпиадалық есепті шешу үшін қандай әдісті қолдануға болады? а) Қосу және азайту амалдары; б) Графикалық шешу әдісі; в) Құнды ауыстыру әдісі. 3-сұрақ: Ауданды есептеуге байланысты есептерді шешу үшін қандай алгебралық әдістерді қолдануға болады? а) Факторизация әдісі; б) Толық ыдырау әдісі; в) Көбейту және бөлу әдісі. 4-сұрақ: Төмендегілердің қайсысы математикалық олимпиада есептері болып табылады? а) 3х + 7 = 22 теңдеуін шеш; ә) Екі санның арифметикалық ортасын есептеу; в) cos(x) функциясының туындысын табыңыз. 5-сұрақ: Белгісіз мәнді анықтауға байланысты олимпиадалық есепті шешу үшін қандай әдісті қолдану ұсынылады? а) Құнды ауыстыру әдісі; б) Графикалық шешу әдісі; в) Ортақ көбейткішке бөлу әдісі. 6-сұрақ: Төмендегілердің қайсысы математикалық олимпиада есептері болып табылады? а) Теңдеулер жүйесін шешу; б) Екі санның пайыздық қатынасын анықтау; в) Параллелепипедтің көлемін есептеңдер. 7-сұрақ: Көпмүшелік теңдеулердің түбірін табуға байланысты есептерді қандай алгебралық әдіспен шешуге болады? а) Құнды ауыстыру әдісі; б) Терминдерді жою әдісі; в) Қалдықпен бөлу әдісі. 8-сұрақ: Төмендегі есептердің қайсысы математикалық олимпиадаға жатады? а) Арифметикалық прогрессияның алғашқы N мүшесінің қосындысын табыңыз; б) Берілген радиус негізінде шеңбердің ауданын анықтау; в) Санның бөлгіштерінің санын санау. 9-сұрақ: Геометриялық дизайнға байланысты олимпиадалық есепті шешу үшін қандай әдісті қолдану ұсынылады? а) Мәндерді салыстыру әдісі; б) Терминдерді ауыстыру әдісі; в) Пифагор теоремасын қолдану әдісі. 10-сұрақ: Шексіз кемімелі геометриялық прогрессияның қосындысын есептеуге байланысты есептерді қандай алгебралық әдіспен шешуге болады? а) Күрделі бөлшек әдісі; б) Бөлшектерді ортақ бөлімге келтіру әдісі; в) Шексіз геометриялық прогрессияның қосындысы әдісі. |
|
|
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: Өткен тақырыптарды қайталау |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Стандартты емес есептерді шешу |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушыларды стандартты емес математикалық есептердің әртүрлі түрлерімен таныстыру. Стандартты емес есептерді шығару әдістерін үйрету. Оқушылардың сыни ойлау, шығармашылық қабілеттерін дамыту. |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Психологиялық ахуал қалыптастыру. Оқушылардың көңілін сабаққа
аудару |
Оқушылар бір-бірімен амандасады. |
Формативті бағалау үнемі жүргізіліп отырады |
Оқулықтар |
|
Сабақтың ортасы |
Ауызша логикалық есептерді шығар 3 а д а ч а 1 "Ұлдар мен алмалар". Үш баланың әрқайсысында бірнеше алма бар. Ұлдардың біріншісі басқаларына әрқайсысы қанша алма берсе, сонша береді оларда бар. Содан кейін екінші бала қалған екеуіне әрқайсысында қанша алма болса, сонша береді; өз кезегінде үшіншісі де береді қалған екеуінің әрқайсысына сол сәтте әрқайсысында қанша болса, сонша. Осыдан кейін ұлдардың әрқайсысында 8 алма бар. Басында әр баланың неше алмасы болды? 2-тапсырма
Бұл торайлар қандай геометриялық пішіндерден тұрады? - Қай жерде көбірек айналымдар бар? - Әр торайда неше геометриялық фигура бар? Типтік емес (стандартты емес) тапсырмалар – бұл арифметикалық амалдар мүлде орындалмайтын немесе ең аз мөлшерде орындалатын жауап алуға арналған тапсырмалар.
1. Жылан Горыныч үш батырды шайқасқа шақырды. Жыланда 12 бас болса, ал батырлар оның басын тең бөлсе, әр батырдың неше басын кесу керек? 2. Секірген инелік қызыл жаздың әр күнінің жарты уақытында ұйықтап, уақыттың үштен бірін билеп, алтыдан бірінде ән айтты. Ол қалған уақытын қысқа дайындыққа арнауды шешті. Инелік қыс мезгіліне күніне неше сағат дайындалды? 3. Нәресте 6 минутта 600 грамм джем жей алады, ал Карлсон 2 есе жылдам жей алады. Бұл джемді бірге жеуге қанша уақыт кетеді? 4.Маша аюдан пирогтарды атасы мен әжесіне апарып беруін өтінді. Машаның салмағы 10 кг, әр бәліш жарты килограмм. Аю Машамен бірге қорапты атасы мен әжесіне апарғанда салмағының айырмашылығын байқамауы үшін Маша қораптан қанша пирог алу керек. 5. Мук пен корольдік серуенші үлкен шалғынды айналып өткен 30 шақырымдық жарыста жарысты. Сайыс шарты бойынша тағы бір айналым жүгіріп, екіншісін басып озған адам жеңімпаз атанады. Скороход 10 минутта шеңбер жасайды, ал Кішкентай Мук - 6 минутта. Екеуі бір уақытта жүгіреді. Кішкентай Мук жылдам жүретін адамды неше минутта басып озады? Әзілқой тапсырмалар 1. Қандай сан барлық сандарға (қалдықсыз) бөлінеді? 2. Чайковскийден Пермьге дейін 1 сағат 20 минут, ал кері рейс 80 минутты алады. Бұл айырмашылықты қалай түсіндіре аламыз? 3. Үй шаруашылығы сабағында қыздар нан тілімдерін тосттауды үйренді. 2 минутқа созылған тілімнің бір жағын қуырып болған соң, апам бізге 3 тілім беруге шешім қабылдады, бірақ табаға 2 тілім ғана сыйды. Дегенмен, ол еш қиналмай, 6 минутта 3 тілім қуырды. Ол мұны қалай жасады? 4. Бір бөлке нанның салмағы жарты келі жарты бөлке. Бүкіл нанның салмағы қанша? 5. Үш ат бір сағатта 24 км жүгірді. Әр ат неше км/сағ жүгірді? Логикалық мәселе 6, 5, 4, 3, 2, 1 сандарын әр жол бойындағы сандардың қосындысы 12 болатындай етіп шеңберге орналастыр.
|
Оқушылар сұрақтарға жауап беріп, түсінгендерін дәлелдей алу қабілетін көрсетеді; бірін-бірі бағалау, қолданба. үй. асс күнделіктерінде |
Өзін-өзі бағалау және өзара бағалау |
Оқулық, |
|
Қорытынды |
Үйге тапсырма беру: Ребустар мен жұмбақ түрінде кездесетін есептер жайлы презентация дайындап кел |
|
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Ребустар мен жұмбақ түріндегі олимпиадалық тапсырмалар |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Жұмбақтар мен жұмбақтарды шешу арқылы оқушыларды математикаға қызықтыру және қызықтыру. Жарыс атмосферасын құру және қызықты есептерді шешу арқылы пәнді оқуға деген ынтасын арттыру. Оқушылардың ой-өрісін кеңейтіп, әртүрлі математикалық ұғымдар мен әдістермен таныстыру.. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
«Көңіл - күй неге ұқсас» Сәлемдесу, түгендеу |
Оқушылар ойын ойнайды
|
Формативті бағалау үнемі жүргізіліп отырады. |
Оқулықтар суреттер, слайдтар кестелер |
|
Сабақтың ортасы 20 минут
|
1. Кіріспе (5 минут): - Мұғалім сабақтың мақсаты мен логикалық ойлауын дамытудың маңыздылығын түсіндіреді. - Мұғалім өткен жеңімпаздар сәтті шығарған олимпиада есептеріне мысалдар келтіреді. - Мұғалім әр мәселенің өзіндік нақты шешімі бар екенін, логика мен шығармашылықты қажет ететінін түсіндіреді. 2. Негізгі бөлім (35 минут): - Мұғалім олимпиада есептерімен және жұмбақтармен жұмыс істеу ережелерін түсіндіреді. - Мұғалім топтық жұмысты ұсынады: оқушылар 4-5 адамнан топтарға бөлінеді. - Мұғалім әр топқа ребус немесе жұмбақ түрінде бір олимпиадалық есеп беріп, оны шешуге уақыт береді. - Топтар есептер бойынша жұмыс жасайды, мүмкін болатын шешімдерді талқылайды, логиканы қолданады және жауаптарын тексереді. Мысал тапсырма: Тапсырма: Сізде бір түрдегі 9 монета бар. Оның 8-і жалған, бірақ оны таразы арқылы ғана байқауға болады. Жалған монеталар шынайыға қарағанда жеңіл. 2 таразыда жалған монеталарды табу үшін таразыны пайдаланудың ең тиімді әдісін табыңыз. Шешімі: 1. Тиындарды 3 монетадан 3 топқа бөлу. 2. Осы топтардың екеуін өлшеп көрейік: - Бір топтың салмағы аз болса, онда жалған тиындар бар. 3-қадамға көшейік. - Топтардың салмақтары сәйкес келсе, жалған монеталар пайдаланылмаған үшінші топта. 3-қадамға көшейік. 3. Табылған топтағы екі тиынды өлшеңіз: - Бір тиынның салмағы аз болса, онда жалған монета бар деген сөз. - Егер монеталардың салмақтары сәйкес келсе, онда жалған монета пайдаланылмаған үшінші монета болып табылады. |
Оқушылар жаңа сабақты меңгереді
|
|
Оқулықтар суреттер, слайд Кестелер плакаттар
|
|
Қорытынды |
|
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Ойын теориясы және олимпиада есептері |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Оқушыларға ойын теориясының негізгі принциптерін және оны математикалық есептерді шешуде қолдануды түсіндіру. Әртүрлі деңгейдегі олимпиада есептерін талдау және шешу үшін ойын теориясын қолдануға үйрету. Оқушылардың ойын теориясын өз бетінше оқуға және оны практикада қолдануға ынталандыру. |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру |
Сәлемдесу, түгендеу |
Оқушылар ойын ойнайды
|
Формативті бағалау үнемі жүргізіліп отырады. |
Оқулықтар суреттер, слайдтар кестелер |
|
Сабақтың ортасы 20 минут
|
"Алгебра ғылымнан артық,
бұл ғылым туралы айтудың тәсілі"
(Н.
Бор).
1. Кіріспе: - Мұғалім сабақтың тақырыбын – ойын теориясы мен математикадан олимпиада есептерін түсіндіреді. - Оқушылар тыңдап, негізгі ұғымдарды жазып алады. 2. Теориялық түсініктеме: - Мұғалім ойын теориясының стратегия, төлем және тепе-теңдік сияқты негізгі ұғымдарын түсіндіреді. - Оқушылар анықтамалар мен мысалдарды жазады. 3. Мысал тапсырманы көрсету: - Мұғалім «Тас, қағаз, қайшы» математикалық ойыны бойынша есеп ұсынып, ойын ережесін түсіндіреді. - Оқушылар жұпқа бөлініп, стратегиялары мен ұтыстарын жазып, бірнеше рет ойнайды. 4. Топтық жұмыс: - Мұғалім оқушылар топтарына математикалық ойындар тақырыбы бойынша олимпиада есептерін таратады. - Оқушылар топ ішінде мәселелерді талқылайды, содан кейін олардың шешімдерін бүкіл сыныпқа ұсынады. Мысал тапсырма: Мәселе: Балаларға арналған тағамның құрамында 10 балмұздақ, 5 шоколад және 4 торт бар. Балалар біріншіден бастап кезекпен таңдайды және олар бір айналымда бірнеше емдік түрін қабылдай алмайды. Бірінші ойыншы әрқашан тортты таңдай алуы үшін балалар қандай стратегияны ұстануы керек? Шешімі: 1. Бірінші қозғалыста тортты таңдауға болатынын тексерейік. Егер балмұздақтар мен шоколадтардың қосындысы 2-ге бөлінетін болса, онда бірінші ойыншы осы тәттілердің бірін таңдайды, ал екінші ойыншы екі бірдей балмұздақ пен шоколадты алуға мәжбүр болады. 2. Егер бірінші жағдайда бірінші ойыншы тортты таңдай алмаса, ол балмұздақ немесе шоколадты таңдау керек. 3. Содан кейін екінші ойыншы бірінші ойыншының кезегін қайталайды. 4. Бірінші ойыншының балмұздақтар мен шоколадтардың қосындысы 2-ге бөлінетін болса, біркелкі бұрылыста қайтадан тортты таңдау мүмкіндігі бар. 5. Егер бірінші де, екінші ойыншы да кез келген бұрылыста тортты таңдай алмаса, олар барлық тәттілер біткенше бір-бірімен айналысады. Осылайша, балмұздақтар мен шоколадтардың қосындысы 2-ге бөлінетін болса, бірінші ойыншы әрқашан біркелкі бұрылыста тортты таңдай алады. |
Оқушылар жаңа сабақты меңгереді
|
|
Оқулықтар суреттер, слайд Кестелер плакаттар
|
|
Қорытынды |
|
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
|
Бөлім: |
|
|
|
Мұғалімнің аты-жөні |
|
|
|
Күні: |
|
|
|
Сынып: |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы |
Қайталауға арналған тест тапсырмалары |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
Жыл бойына алған білімін тексеру |
|
|
Сабақтың мақсаты |
|
|
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Ұйымдастыру, өзін – өзі тексеру Өткен білімді еске түсіру 8 мин |
І. Ұйымдастыру
кезеңі. Психологиялық сәт.
|
|
|
Интерактивті тақта, оқулық. |
|
Жаңа білім 15 мин 2 мин Бекіту 15 мин |
1 – нұсқа 1. Рекурсия дегеніміз не? а) Функция өзін шақыратын процесс. b) Функция аргументтерді беретін және нәтижені беретін процесс. в) Функция басқа функцияны шақыратын процесс. 2. Рекурсивті есеп қалай шығарылады? а) Негізгі жағдайды және кіші және үлкен регистрлердің арасындағы байланыстың анықтамасын табыңыз. б) Формуланы есептеу үшін қолдану. в) Талдау және интерполяция әдістерін қолдану. 3. Төмендегі формулалардың қайсысы логарифмнің қасиеті болып табылады? а) ln(ab) = ln(a) + ln(b) б) ln(a/b) = ln(a) - ln(b) c) ln(a^b) = млрд(a) 4. Теңдеулерді пайдаланып сөздік есеп қалай жасалады? а) Жағдайды сипаттап, белгісіз мәнді анықтаңыз. ә) Жағдайды математикалық формулаға аударыңыз. в) Белгісіз мәнді анықтау үшін теңдеулерді пайдаланыңыз. 5. Ньютон биномының қандай қасиеті бар? а) Паскаль үшбұрышының әрбір жолының коэффициенттерінің қосындысы 2^n-ге тең, мұндағы n – жол нөмірі. б) Паскаль үшбұрышының әрбір жолының коэффициенттері биномдық коэффициенттердің қосындысы болып табылады. в) Паскаль үшбұрышының әрбір жолы палиндром болып табылады. 6. Ықтималдықтар теориясы мен статистиканың негізгі міндеті қандай? а) Кездейсоқ құбылыстар мен ықтималдық үлестірімдерін зерттеу. б) Алынған мәліметтердің нақтылығы мен сенімділігін анықтау. в) Статистикалық мәліметтерді талдау және оларды болжау үшін қолдану. 7. Комбинаторикадан көбейту әдісі бойынша олимпиада тапсырмалары қандай? а) Варианттар санын анықтау үшін комбинаторлық формулаларды қолдануды қажет ететін есептер. б) Шешімін табу үшін геометриялық түрлендірулерді қолдануды қажет ететін есептер. в) Графиктерді салуды және олардың қасиеттерін анықтауды қажет ететін тапсырмалар. 8. «Иррационал теңдеу» ұғымы нені білдіреді? а) Тек иррационал сандар болатын теңдеу. б) Иррационал функциясы бар теңдеу. в) Алгебралық әдістер арқылы шешілмейтін және сандық әдістерді қолдануды қажет ететін теңдеу. 9. Рационал теңдеулер мен теңсіздіктер қалай шешіледі? а) Ортақ бөлгішке келтіріп, алынған теңдеуді шеш. б) Шешімдерін анықтау үшін рационал сандардың қасиеттерін және олардың графиктерін қолдану. в) Функцияларды және олардың әрекетін талдау әдістерін қолдану. 10. Функцияның графигі қалай салынады? а) Әр түрлі аргументтер үшін функцияның облысы мен мәндерін анықтаңыз. б) Әр түрлі аргументтер үшін функция мәндеріне сәйкес келетін нүктелерді салу. в) Тегіс қисық алу үшін нүктелерді түзулермен қосыңыз. 2 – нұсқа 1. Рекурсия дегеніміз не? а) Қарапайым ішкі тапсырмаларға кезең-кезеңмен бөлу арқылы есептерді шешу әдісі б) Теңдеулерді қолданып есептер шығару әдісі в) Паскаль үшбұрышының көмегімен есептерді шығару әдісі 2. Көрсеткіштік функцияға кері функция қалай аталады? а) Логарифмдік б) Шаршы в) Тригонометриялық 3. Көбейту кезінде логарифмдердің қандай қасиеті бар? а) Логарифмдердің қосындысы көбейтіндінің логарифміне тең б) Логарифмдердің айырымы бөліктің логарифміне тең в) Көбейтіндінің логарифмі логарифмдердің қосындысына тең 4. Теңдеулерді пайдаланып сөздік есеп қалай жасалады? а) Белгісіз шамаларды орнату және олардың байланысын теңдеу арқылы сипаттау б) Теңдеудің шешімдерінің санын анықтау в) Ньютонның биномдық формуласын қолдану 5. Паскаль үшбұрышы қандай геометриялық объектіні сипаттайды? а) Биномдық коэффициенттерден тұратын үшбұрыш б) Сандардың логарифмінен тұратын үшбұрыш в) Сандардың факториалдарынан тұратын үшбұрыш 6. Ықтималдық теориясы дегеніміз не? а) Кездейсоқ оқиғаларды және олардың ықтималдығын зерттейтін математика саласы б) Рационал теңдеулерді зерттейтін математика саласы в) Комбинаторикадағы есептерді шығару әдісі 7. Комбинаторикадан көбейту әдісі арқылы олимпиада тапсырмаларын шешу үшін қандай әдіс қолданылады? а) Барлық мүмкін комбинациялар арқылы іздеу әдісі б) анықтауыш әдіс в) Кронштейнді орналастыру әдісі 8. Иррационал теңдеу дегеніміз не? а) Белгісіз шамалар тек рационал мәндерді қабылдай алатын теңдеу б) Белгісіз шамалар тек иррационал мәндерді қабылдай алатын теңдеу в) Белгісіз шамалар рационал және иррационал мәндерді қабылдай алатын теңдеу 9. Рационал теңдеу қалай шешіледі? а) Теңдеуді жалпы түрге келтіріп, түбірін тап б) Теңдеудің екі жағын ең кіші ортақ бөлгішке көбейт в) Теңдеуді сызықтық теңдеулер жүйесіне айналдырып, оны шешу 10. Функциялар графиктерде қалай бейнеленген? а) Айнымалылардың тәуелділігін көрсететін қисық сызықтар түрінде б) Координаталық жазықтықтағы нүктелер түрінде в) Функция мәндерінің кестесі түрінде |
|
|
|
|
Қорытынды 5 мин |
Кері байланыс
Оқу тапсырмасы: Өткен тақырыптарды қайталау |
Түсінгені туралы ой қорытады. Тапсырманы жазып алады. |
ҚБ қойылады. |
|
Пайдаланылған әдебиеттер:
Мұғалімдерге арналған:
1. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. В 3-х
томах: том 1. – М.: Наука, 1968, с. 157 – 162
2. Ильин В.А. Методы решения функциональных уравнений // Соросовский
образовательный журнал, 2001, № 2, с. 116 – 120
3. Бродский Я. С., Слипенко А. К. Функциональные уравнения. – К.: Вища школа.
Головное издательство, 1983. – 96 с.
4. Андреев А.А., Кузьмин Ю.Н.., Савин А.Н., Саушкин И.Н. Функциональные
уравнения. – Самара: В мире науки, 1999
5. Сабитов К.Б. Функциональные, дифференциальные и интегральные
уравнения.−М.:’’Высшая школа’’,2005,с.190−199
6. Лихтарников Л.М. Элементарное введение в функциональные уравнения.– СПб.:
Лань, 1997. – 160 с.
7.Әбілқасымова А. және т.б. Математиканы оқытудың териясы мен әдістемесі. А, Білім. 1998 ж
8. Бидосов Ә. Математиканы оқыту методикасы. (Жалпы методика). А, Мектеп. 1989ж
9. Рахымбек Д. және т.б. Орта мектепте математиканы оқыту әдістемесіне арналған оқу құралы. Ш, 2003
Оқушыларға арналған:
-
Генкин, С.А., Итенберг, И.В., Фомин, Д.В. (1994). Ленинградские математические кружки. Киров: АСА.
-
Гальперин, Г.А., Толпыго, А.К. (1986). Московские математические олимпиады. Москва: Просвещение.
-
Васильев, Н.Б., Гутенмахер, В.Л., Раббот, Ж.М., Тоом, А.Л. (1981). Заочные математические олимпиады. Москва: Наука.
-
Шарыгин, И.Ф. (1998). Математика: Факультативный курс. Москва: Просвещение.
-
Яглом, И.М. (1981). Математические олимпиады и внеклассная работа по математике. Москва: Просвещение.
Мазмұны
1.Түсінік хаты
2. Тұрақтылау (мазмұндық) бөлімі
3. Нормативтік бөлім
4. Ақпараттық-әдістемелік бөлім
5. Оқу – әдістемелік нұсқаулық
6. Пайдаланылған әдебиеттер

шағым қалдыра аласыз




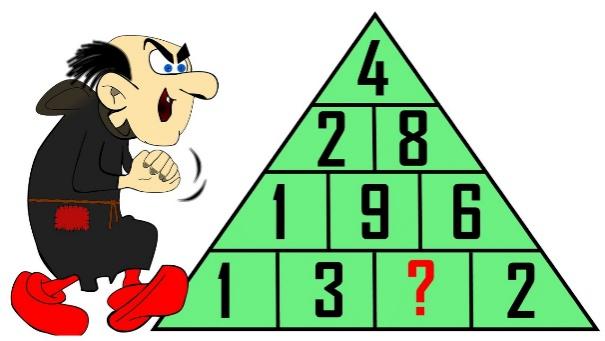







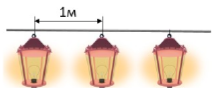


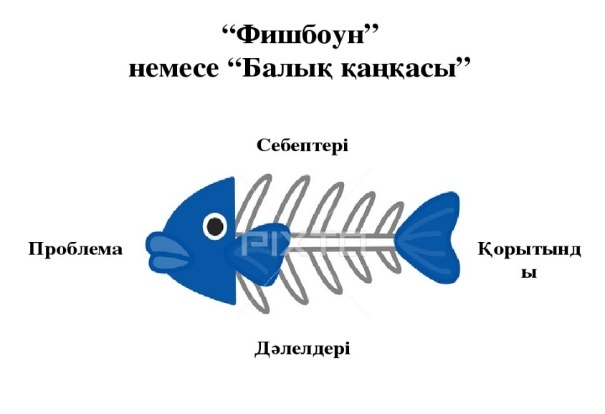












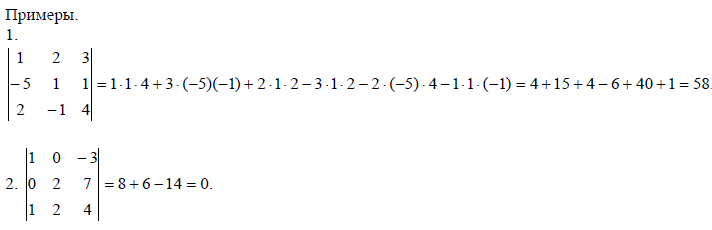


 естені толтырып, графигін
сал.
естені толтырып, графигін
сал.



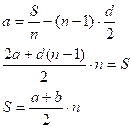



















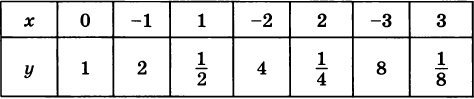
 :
: 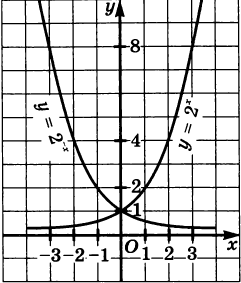
 , где
, где  и
и 






 х=10
х=10 =25
=25










 +
+ =4
=4 -
-  =2
=2 <0
<0