Математикадан регата есептері және шығарылу жолымен

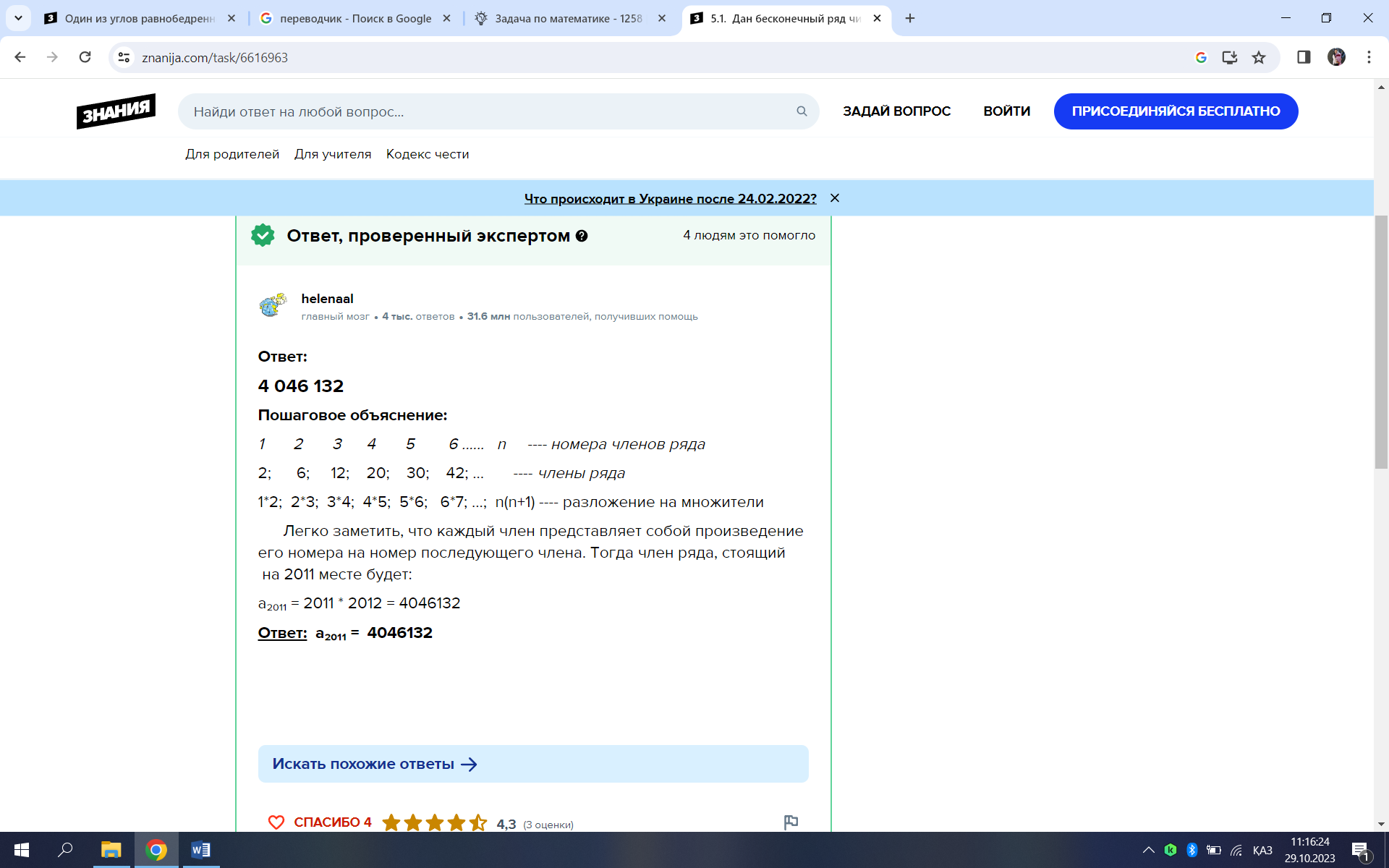
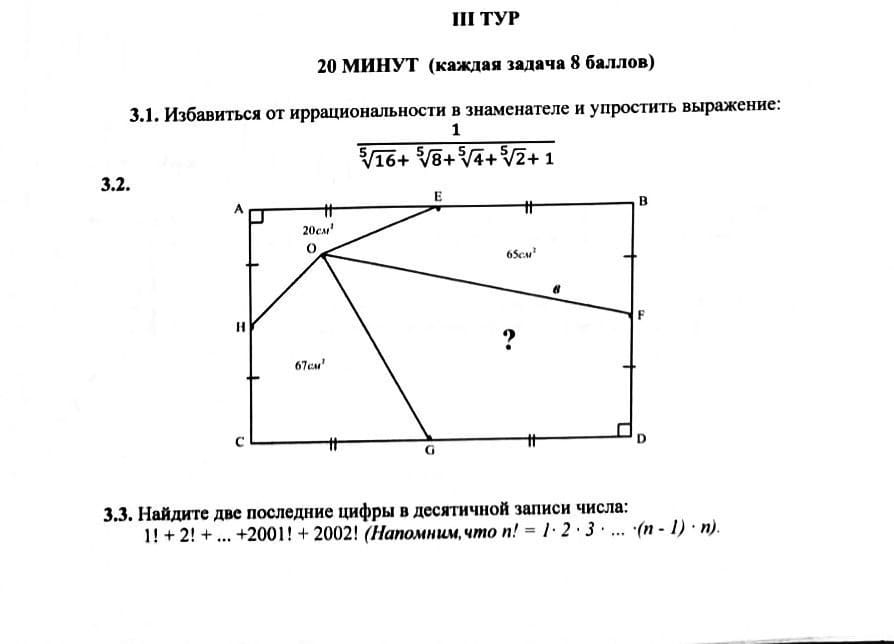1. Дан бесконечный ряд чисел: 2, 6, 12, 20, 30, 42, ... . Укажите закономерность и найдите число, стоящее на 2011 – ем месте.

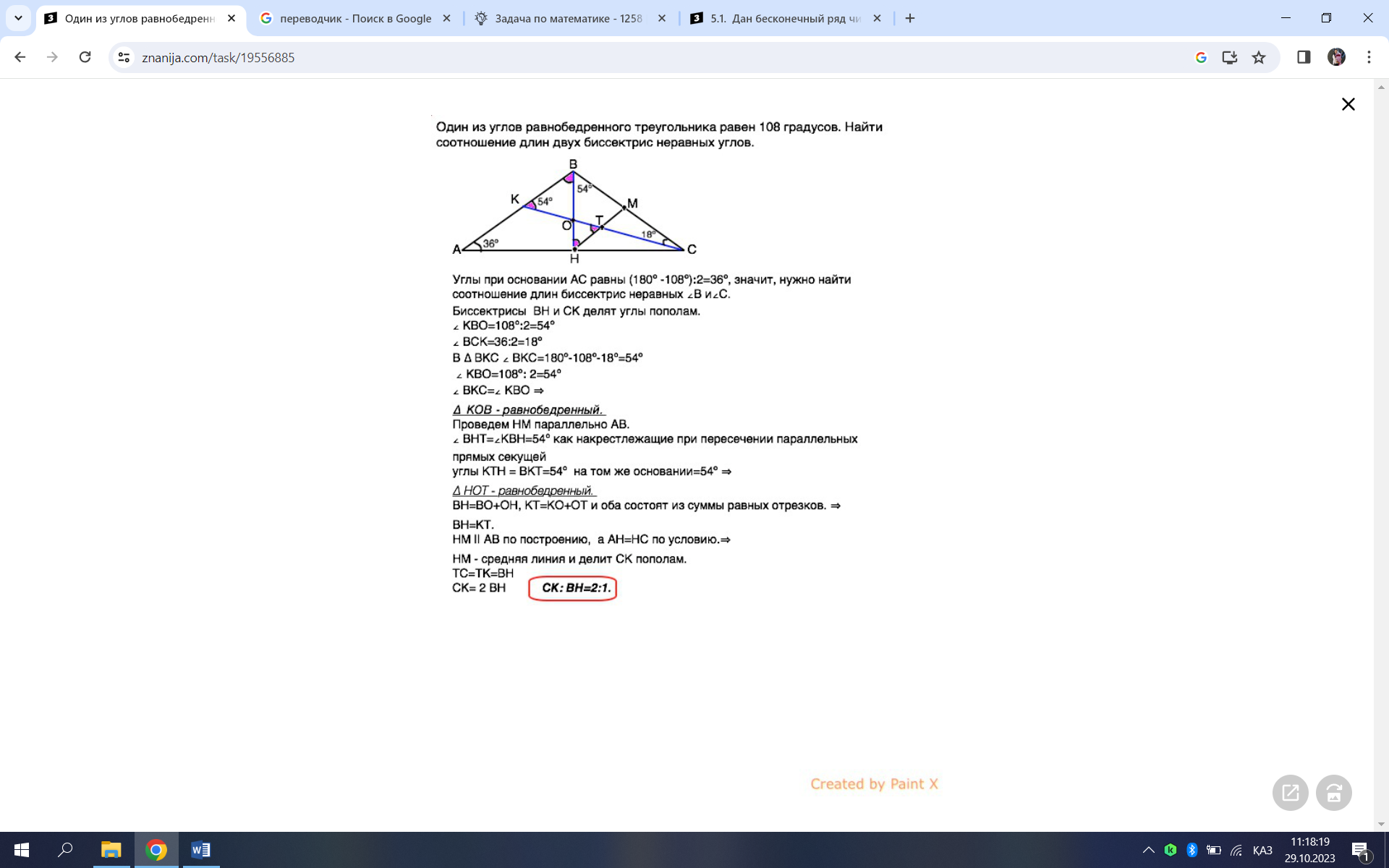
2. Oдин из углов равнобедренного треугольника равен 108 градусов найти соотношение длин двух биссектрис неравных углов

3. У трех членов жюри спросили: «Сколько команд будет участвовать в математической регате?». Один сказал: «Меньше семидесяти двух». Другой: «Меньше семидесяти одной», а третий: «Меньше семидесяти трех». Сколько команд участвовало в регате, если правы были в точности двое членов жюри?

Второе утверждение не может быть верно, так как в этом случае верны и два других утверждения, что противоречит условию. Следовательно, верными являются первое и третье утверждение, а второе - неверно. То есть, данное число меньше 72 и не меньше 71. Единственное число, удовлетворяющее данным условиям - 71. Ответ: 71.

Әділқазылар алқасының үш мүшесіне: «Математикалық регатаға неше команда қатысады?» деген сұрақ қойылды. Біреуі: «Жетпіс екіге жетпейді», – деді. Басқасы: «Жетпіс бірден аз», үшінші: «Жетпіс үштен аз». Егер әділ қазылар алқасының екі мүшесі дұрыс болса, регатаға қанша команда қатысты?

Екінші тұжырым ақиқат бола алмайды, өйткені бұл жағдайда шартқа қайшы келетін басқа екі тұжырым да ақиқат. Сондықтан бірінші және үшінші тұжырымдар дұрыс, ал екіншісі жалған. Яғни, бұл сан 72-ден кем және 71-ден кем емес. Бұл шарттарды қанағаттандыратын жалғыз сан - 71. Жауап: 71.

4. f(cos x) = cos 13x болсын. f(sin x) = sin 13x екенін дәлелдеңдер.

Жауабы: f(sin x) = f(cos (п/2 - x)) = cos13(п/2 - x) = sin13x.

5. функция удовл отношению f(cosx)=cos (17x) Доказать что она также удовл соотнош f(sinx)=sin (17x)

жауабы: f(sinx)=используем формулу приведения=f(cos(pi/2-x))=используем данное отношения для данной функции=cos (17(pi/2-x))=cos (8pi+pi/2-17x)=cos (2*4pi+pi/2-17x)=используем периодичность косинуса=cos(pi/2-17x)=используем формулу приведения=sin (17x)

таким образомf(sinx)=sin (17x), что и требовалось доказать

f(sinx)=азайту формуласын пайдаланыңыз=f(cos(pi/2-x))=осы функция үшін осы қатынасты пайдаланыңыз=cos (17(pi/2-x))=cos (8pi+pi/2-17x ) =cos (2*4pi+pi/2-17x)=косинус кезеңділігін пайдалану=cos(pi/2-17x)=азайту формуласын қолдану=sin (17x)

осылайша f(sinx)=sin (17x), бұл дәлелдеуді қажет етті

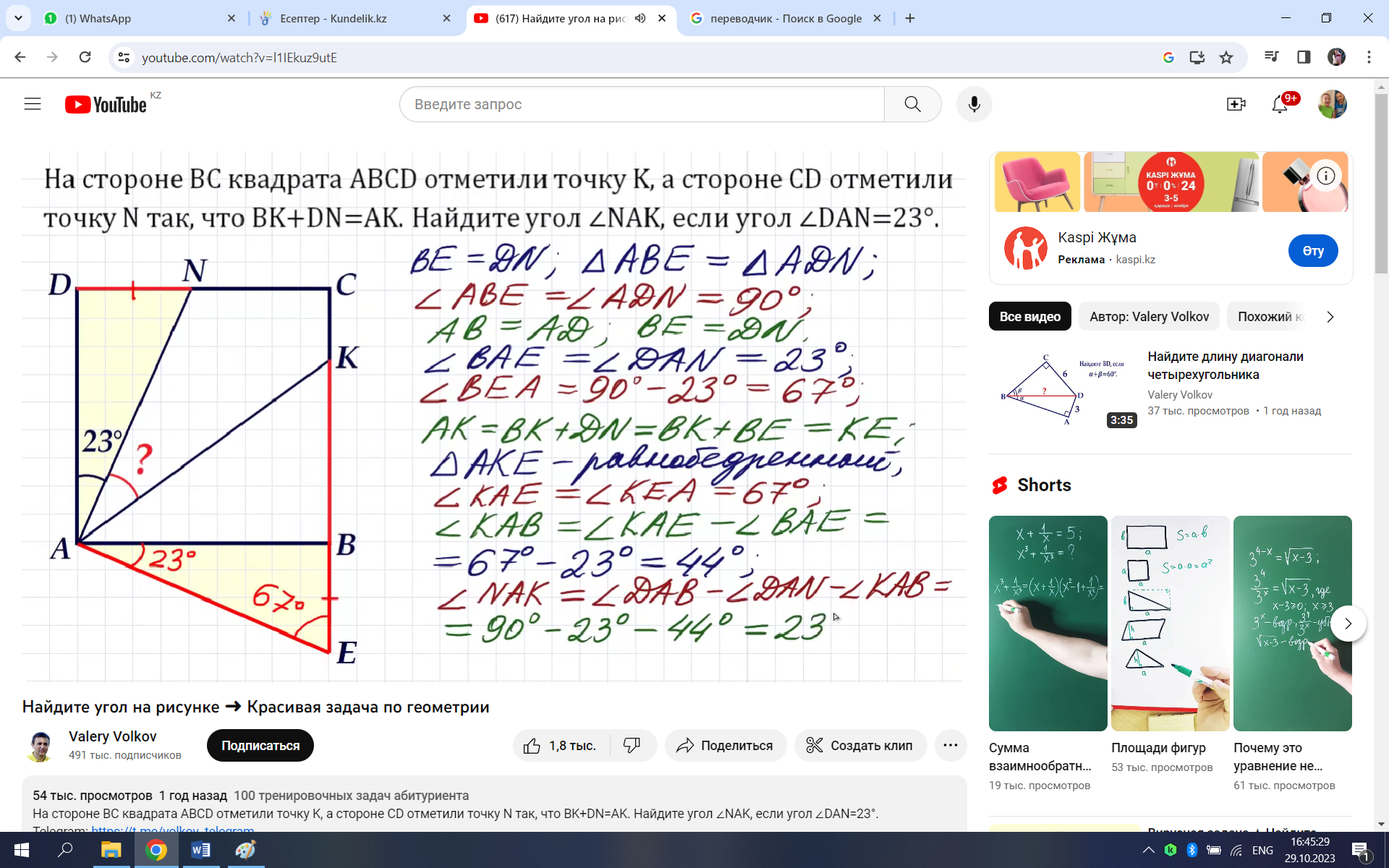
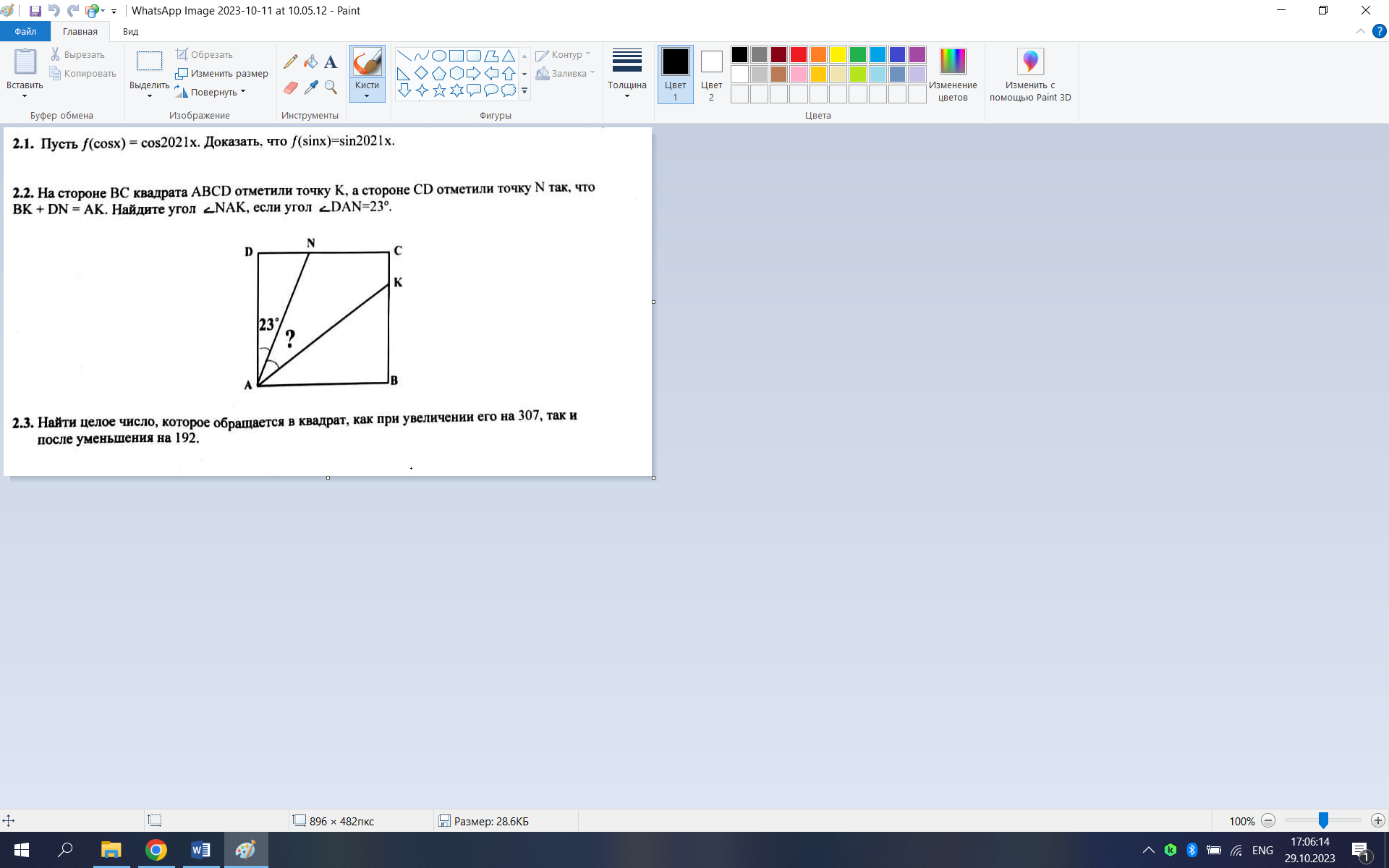
7. найти целое число, которое обращается в квадрат, как при увеличении его на 307, так и после уменьшения на 192

307 ге өсіргенде және 192 ге кеміткенде квадратқа айналатын бүтін санды табыңдар.

х+307=а*а

х-192=(а-1)(а-1)

499=(2а-1)

2а=500

а=250

х=62193

8. 

9. 

10!+11!+..+2011! оканчивается 00 (все числа делятся на 100) 1!+2!+..+8!+9!=1+2+6+24+120+720+5040+40320+362880=...13

10. Найдите последние две цифры в десятичной записи числа 1! + 2!+..+2016!+2017!

Жауабы: 1! + 2! + 3! + 4! + 5! + 6! + 7! + 8! + 9! + 10! + ... + 2017!
Начиная с 10! = 3628800, все факториалы в конце имеют 2 и больше нулей. Поэтому на две последние цифры влияют только от 1! до 9!.
1 + 2 + 6 + 24 + 120 + 720 + 5040 + 40320 + 362880 =
100k + 1 + 2 + 6 + 24 + 20 + 20 + 40 + 20 + 80 = 100k + 213 = 100(k+2) + 13
Ответ: 13

11. Найти сумму чисел
    2+22+222+...+222...2

 n цифр

12. 

ребро куба авсда1в1с1д1 равно 1. прямая m проходит через точку Е-середину ребра С1Д1 и пересекает прямые АД1 и А1В (последнюю -в точке F) Найдите EF

АВСДА1в1с1д1 кубының қыры 1-ге тең m түзу E нүктесінен, C1D1 қырының ортасынан өтіп, AD1 және A1B түзулерін қиып өтеді (соңғысы F нүктесінде) EF табыңыз.

10 машина әрқайсысының салмағы 10 г болатын бірдей резеңке шарларды жасайды.Бір машина зақымдалып, салмағы 5 г болатын шарлар шығара бастады.Бір таразы арқылы сынған машинаны қалай табуға болады?

Зақымдалған көлікті табу үшін қажет: бірінші вагоннан 1 доп, екінші вагоннан 2 доп, үшіншіден 3 доп, ..., оныншы вагоннан 10 шар және барлығын өлшеп алыңыз.

барлық шарлардың салмағы: 10 + 20 + 30 + 40 + 50 + 60 + 70 + 80 + 90 + 100 = 550 г болуы керек

Айталық, егер машина бірінші болып нашар болса, онда массасы 5 г кем және = 545 г, егер машина 4-ші болып нашар болса, онда масса 4 * 5 = 20 г, 20 г аз болады. және = 530 г және т.б.

Надо взять с 1-ой машины 1 мяч. Со 2-ой - 2 мяча. соответственно 3-3мяча, 4-4мяча, ..10-10 мячей. Всего получится 1+2+3+4+5+6+7+8+9+10=55мячей. Если бы все станки были исправны то общий вес составил-бы 55*10=550г. Но т. к. один станок выпускает мячи массой 5г то его определяют следующим образом. Если масса 545г - то это 1ый станок (550-5). Если масса 540г - то это второй станок (550-2*5=540). Если масса 535г - то это 3 ий станок (550-3*5=535). Далее соответственно 530г - 4ый станок. 525г - 5ый станок. 520г - 6ой станок. 515г - 7ой станок. 510г-8ой станок. 505г - 9ый станок. 500г-10ый станок. 1-ші вагоннан 1 доп алу керек. 2-ден - 2 гол. сәйкесінше 3-3 доп, 4-4 доп, ..10-10 доп.

Барлығы 1+2+3+4+5+6+7+8+9+10=55 шар аласыз. Барлық машиналар жақсы жағдайда болса, жалпы салмағы 55*10=550г болар еді. Бірақ бір машина салмағы 5 г болатын шарларды шығаратындықтан, ол келесідей анықталады. Салмағы 545г болса, бұл 1-ші машина (550-5). Егер массасы 540г болса, онда бұл екінші машина (550-2*5=540). Егер массасы 535г болса, онда бұл 3-ші машина (550-3*5=535). Әрі қарай, сәйкесінше, 530 г 4-ші машина. 525 г - 5-ші машина. 520 г - 6-шы машина. 515 г - 7-ші машина. 510г-8-ші машина. 505 г - 9-шы машина. 500г-10-шы машина.

7 класс.

Первый тур (10 минут; каждая задача — 6 баллов).

1.1. Частное от деления двух одночленов равно 9х²у, а их произведение равно х⁸у⁹. Приведите пример таких одночленов.

1.2. В равнобедренном тупоугольном треугольнике проведите четыре отрезка так, чтобы он разделился на шесть прямоугольных треугольников. Поясните ваше решение.

1.3. Найдутся ли различные натуральные числа x, y и z такие, что сумма любых двух из них является простым числом? Объясните ответ.

Второй тур (15 минут; каждая задача — 7 баллов).

2.1. Делегация некоторой страны на Олимпийских играх будет состоять из спортсменов и чиновников. Средний возраст этих спортсменов на начало олимпиады составит 22 года, а чиновников – 47 лет. При этом средний возраст всех членов делегации окажется равным 41 году. Какова в этой делегации доля чиновников, выраженная в процентах?

2.2. Из середины М стороны AB равностороннего треугольника ABC опустили перпендикуляры МK и МL на стороны AC и BC. Найдите KL, если AB = 1.

2.3. Вилли, Билли, Бим и Бом провели круговой турнир по шахматам (каждый сыграл с каждым по одному разу, победа – 1 очко, ничья – 0,5 очка, поражение – 0 очков). Известно, что четыре партии было сыграно вничью, а Вилли набрал 0,5 очка. Бим сказал, что он за турнир набрал 2,5 очка. Могло ли такое быть?

Третий тур (15 минут; каждая задача — 7 баллов).

3.1. Винни-Пух и Пятачок сели за стол немного подкрепиться и начали одновременно есть мед из одного горшка, не отвлекаясь на разговоры. Если бы Винни-Пух ел со скоростью Пятачка, то процесс еды длился бы на 4 минуты дольше, а если бы, наоборот, Пятачок ел со скоростью Винни-Пуха – то сократился бы на 1 минуту. За какое время мед из горшка был полностью съеден?

3.2. Точки А, В, С и D расположены на плоскости так, что никакие три из них не лежат на одной прямой. Известно, что AB = BC = CD и AC = BD. Докажите, что среди прямых, соединяющих данные точки попарно (AB, BC, CD, AC, BD, AD), есть хотя бы две параллельные.

3.3. На клетчатой бумаге нарисовали прямоугольник по линиям сетки. Внутри него оказалось единичных отрезков сетки на 90 больше, чем узлов. Определите размеры прямоугольника.

Четвертый тур (20 минут; каждая задача — 8 баллов).

4.1. Решите уравнение: |65x³ + 12x| = |48x² + 1|.

4.2. Высоты ВР и СQ треугольника АВС пересекаются в точке Н. Оказалось, что BH = AC. Найдите возможные значения угла АВС.

4.3. Десятичная запись числа состоит из десяти различных цифр. Цифра называется «хорошей», если она равна сумме двух своих соседей (слева и справа). Какое наибольшее количество «хороших» цифр может быть в таком числе?

7 класс

Первый тур (10 минут; каждая задача – 6 баллов).

1.1. Частное от деления двух одночленов равно 9х²у, а их произведение равно х⁸у⁹. Приведите пример таких одночленов.

Ответ: и или и .

Получить ответ можно подбором. Можно также использовать уравнения: если А и В – искомые одночлены, то , . Перемножив эти равенства почленно, получим: , откуда . Тогда .

_{1.2. В равнобедренном тупоугольном треугольнике проведите четыре отрезка так, чтобы он разделился на шесть прямоугольных треугольников. Поясните ваше решение.}

_{Рис. 1}

_{Ответ: см., например, рис. 1.}

_{Рассмотрим треугольник АВС, в котором АВ = АС и ВАС > 90. Проведем его высоту AA1, после чего треугольниках ВАА1 и САА1 проведем высоты А1С1 и А1В1 соответственно, а затем проведем отрезок С1В1, который пересечет AA1 в точке Р.}

_{Искомые шесть прямоугольных треугольников: А1С1В, А1В1С, А1С1Р, А1В1Р, АС1Р и АВ1Р.}

_{Прямоугольность всех указанных треугольников очевидна из симметрии. Строгое доказательство можно провести, например, так: из равнобедренности треугольника АВС следует, что равны его углы В и С, а высота AA1 является также медианой и биссектрисой. Значит, А1АС1 = А1АВ1 (по гипотенузе и острому углу). Следовательно, треугольник С1АВ1 также равнобедренный и имеет с данным треугольником общий угол при вершине А. Тогда в треугольниках С1АВ1 и САВ равны и углы при основаниях, поэтому С1В1 || ВС. Так как ВС  АА1, то С1В1  АА1.}

1.3. Найдутся ли различные натуральные числа x, y и z такие, что сумма любых двух из них является простым числом? Объясните ответ.

Ответ: нет, не найдутся.

Среди любых трех натуральных чисел найдутся либо два четных, либо два нечетных числа (по принципу Дирихле). Сумма двух чисел одной четности является четным числом. По условию числа x, y и z различны, поэтому такая сумма отлична от двух, значит она является составным числом.

Второй тур (15 минут; каждая задача – 7 баллов).

_{2.1. Делегация некоторой страны на Олимпийских играх будет состоять из спортсменов и чиновников. Средний возраст этих спортсменов на начало олимпиады составит 22 года, а чиновников – 47 лет. При этом средний возраст всех членов делегации окажется равным 41 году. Какова в этой делегации доля чиновников, выраженная в процентах?}

Ответ: 76%.

Пусть делегация состоит из x спортсменов и y чиновников, тогда суммарный возраст спортсменов равен 22x, а чиновников – 47y. Делегация насчитывает (x + y) человек, поэтому ее суммарный возраст равен 41(x + y). Получим уравнение: 22x + 47y = 41(x + y). Упростив его, получим, что 6y = 19x. Доля чиновников, выраженная в процентах, равна: = = = = 76%.

2.2. Из середины М стороны AB равностороннего треугольника ABC опустили перпендикуляры МK и МL на стороны AC и BC. Найдите KL, если AB = 1.

Ответ: KL = .

_{Рис. 2}

Так как САВ = СВА = 60, то KMА = LMВ = 30 (см. рис. 2). Катет прямоугольного треугольника, лежащий напротив угла величиной 30, равен половине гипотенузы, поэтому AK = AM = и BL = BM = . Следовательно, CK = CL = .

В равнобедренном треугольнике CKL угол СKL равен 60, поэтому этот треугольник – равносторонний, то есть KL = CK = CL = .

В заключительной фазе решения можно было рассуждать и по-другому: АМK = BML (по гипотенузе и острому углу), значит MK = ML. Тогда в равнобедренном треугольнике KML: KML = 120, MKL = MLK = 30. Следовательно, CKL = СLK = 60 (непосредственный подсчет или использование параллельности прямых KL и АВ).

_{2.3. Вилли, Билли, Бим и Бом провели круговой турнир по шахматам (каждый сыграл с каждым по одному разу, победа – 1 очко, ничья – 0,5 очка, поражение – 0 очков). Известно, что четыре партии было сыграно вничью, а Вилли набрал 0,5 очка. Бим сказал, что он за турнир набрал 2,5 очка. Могло ли такое быть?}

Ответ: нет, не могло.

В турнире было сыграно шесть партий, из которых четыре закончились вничью, значит, результативных партий было всего две. Каждый участник провел три партии, поэтому Вилли, набравший пол-очка, двум различным соперникам проиграл.

Таким образом, эти соперники взяли по одному очку в партиях с Вилли и еще по две партии сыграли вничью, то есть набрали по два очка. Это и есть лучший результат, так как оставшийся игрок все три партии свел вничью, то есть набрал 1,5 очка.

Третий тур (15 минут; каждая задача – 7 баллов).

3.1. Винни-Пух и Пятачок сели за стол немного подкрепиться и начали одновременно есть мед из одного горшка, не отвлекаясь на разговоры. Если бы Винни-Пух ел со скоростью Пятачка, то процесс еды длился бы на 4 минуты дольше, а если бы, наоборот, Пятачок ел со скоростью Винни-Пуха – то сократился бы на 1 минуту. За какое время мед из горшка был полностью съеден?

Ответ: за 2 минуты 40 секунд.

Первый способ («арифметический»). Если оба приятеля едят со скоростью Винни-Пуха, то они съедают мёд на 5 минут быстрее, чем если они оба едят со скоростью Пятачка. При этом каждый съедает по половине горшка. Значит, Винни-Пух съедает пол-горшка мёда на 5 минут быстрее, чем Пятачок. Следовательно, когда они ели вместе и Винни-Пух съел пол-горшка, то в горшке оставалось столько мёда, сколько Пятачок съест за 5 минут. Но вместе они доели этот остаток за 1 минуту. За это время Пятачок успел съесть 1/5 остатка, значит, 4/5 остатка съел Винни-Пух, то есть Винни-Пух ест мед в 4 раза быстрее Пятачка.

Таким образом, когда Винни-Пух съел половину горшка, Пятачок съел 1/4 от половины, а на оставшиеся 3/4 от половины горшка ему нужно было еще 5 минут. Следовательно, на половину горшка Пятачку нужно минуты. Если бы оба ели со скоростью Пятачка, то за это время они съели бы весь мёд. Но по условию они съели его на 4 минуты быстрее, то есть за 2 минуты 40 секунд.

Второй способ («алгебраический»). Пусть за минуту Винни-Пух съедает m кг меда, Пятачок  n кг, а процесс их совместной еды длится t минут. Тогда из условия задачи получим два уравнения: (m + n)t = 2n(t + 4) и (m + n)t = 2m(t – 1).

Из первого уравнения: (m – n)t = 8n, а из второго: (m – n)t = 2m. Тогда m = 4n, то есть Винни-Пух ест мед в 4 раза быстрее, чем Пятачок. Подставив полученный результат, например, в первое уравнение, получим: 5nt = 2n(t + 4)  5t = 2t + 8  .

3.2. Точки А, В, С и D расположены на плоскости так, что никакие три из них не лежат на одной прямой. Известно, что AB = BC = CD и AC = BD. Докажите, что среди прямых, соединяющих данные точки попарно (AB, BC, CD, AC, BD, AD), есть хотя бы две параллельные.

_{Рис. 3а}

Возможны два случая расположения данных точек, поскольку отрезки АВ и CD могут лежать в разных полуплоскостях относительно прямой ВС или в одной полуплоскости.

В первом случае (см. рис. 3а) треугольники АВС и DCB равны по трем сторонам, следовательно, АВС = DCB. Так как эти углы – внутренние накрест лежащие для прямых АВ и CD и секущей ВС, то АВ || CD.

Отметим, что в этом случае можно также доказать, что АС || BD. Для этого достаточно из равенства уже рассмотренных треугольников получить, что АСB = DBC.

_{Рис. 3б}

Во втором случае (см. рис. 3б) треугольники АВС и DCB также равны по трем сторонам. Кроме того, эти треугольники – равнобедренные, поэтому BAC = BCA = CBD = CDB.

Заметим также, что ACD = DBA (по трем сторонам), следовательно, CAD = ВDА. Пусть О – точка пересечения АС и BD. Тогда треугольники AOD и BOC – равнобедренные с равными (вертикальными) углами при вершинах, следовательно, и с равными углами при основаниях. Используя любое из равенств CAD = ACB или ADB = CBD, по признаку параллельности прямых получим, что AD || BC.

_{3.3. На клетчатой бумаге нарисовали прямоугольник по линиям сетки. Внутри него оказалось единичных отрезков сетки на 90 больше, чем узлов. Определите размеры прямоугольника.}

Ответ: 713 или 191.

Пусть в данном прямоугольнике n строк и m столбцов. Тогда внутри прямоугольника проходят (n – 1) горизонтальных линий сетки и (m – 1) вертикальных. Далее можно рассуждать по- разному.

Первый способ. Горизонтальные и вертикальные линии пересекаются в (n – 1)(m – 1) точках, которые и являются узлами сетки, лежащими внутри прямоугольника.

Каждая горизонтальная линия внутри прямоугольника делится вертикальными на m единичных отрезков, то есть количество горизонтальных единичных отрезков внутри прямоугольника равно m(n – 1). Аналогично, каждая вертикальная линия внутри прямоугольника делится на n единичных отрезков, то есть количество вертикальных единичных отрезков внутри прямоугольника равно n(m – 1).

_{Рис. 4}

По условию (n – 1)(m – 1) + 90 = m(n – 1) + n(m – 1). Раскрыв скобки и приведя подобные слагаемые, получим, что nm = 91.

Поскольку 91 = 713 = 191, то возможны два варианта ответа.

Второй способ. Из каждого узла сетки, лежащего внутри прямоугольника, проведем вверх единичный вертикальный отрезок (см. рис. 4). Тогда количество проведенных отрезков равно количеству узлов. Остались не проведенными: (n – 1) горизонтальных рядов по m единичных отрезков в каждом и еще (m – 1) вертикальных отрезков. Таким образом, (n – 1)m + (m – 1) = 90, то есть nm = 91.

Дальнейшее решение уже описано.

Четвертый тур (20 минут; каждая задача – 8 баллов).

4.1. Решите уравнение: |65x³ + 12x| = |48x² + 1|.

Ответ: 0,2.

Первый способ. Модули двух чисел равны т. и т. т., когда эти числа равны или противоположны, то есть 65x³ + 12x = 48x² + 1 или 65x³ + 12x = – 48x² – 1.

В первом случае: 65x³ – 48x² + 12x – 1 = 0  x³ + (64x³ – 48x² + 12x – 1) = 0  x³ + (4x – 1)³ = 0  (4x – 1)³ = (–x)³  4x – 1 = –x  x = 0,2.

Во втором случае: 65x³ + 48x² + 12x + 1 = 0  x³ + (64x³ + 48x² + 12x + 1) = 0  x³ + (4x +1)³ = 0  (4x + 1)³ = (–x)³  4x + 1 = –x  x = – 0,2.

Второй способ. 1) Если x  0, то уравнение примет вид: 65x³ + 12x = 48x² + 1. Пусть , тогда y³ – 12y² + 48y – 65 = 0  y³ – 5y² – 7y² + 35y + 13y – 65 = 0  y²(y – 5) – 7y(y – 5) + 13(y – 5) = 0  (y – 5)(y² – 7y + 13) = 0  y = 5, так как y² – 7y + 13 = y² – 23,5y + 12,25 + 0,75 = (y – 3,5)² + 0,75 > 0. Значит, x = 0,2.

2) Если x < 0, то уравнение примет вид: – 65x³ – 12x = 48x² + 1. Пусть , тогда y³ + 12y² + 48y + 65 = 0  y³ + 5y² + 7y² + 35y + 13y + 65 = 0  y²(y + 5) + 7y(y + 5) + 13(y + 5) = 0  (y + 5)(y² + 7y + 13) = 0  y = 5, так как y² + 7y + 13 = y² + 23,5y + 12,25 + 0,75 = (y + 3,5)² + 0,75 > 0. Значит, x = –0,2.

4.2. Высоты ВР и СQ треугольника АВС пересекаются в точке Н. Оказалось, что BH = AC. Найдите возможные значения угла АВС.

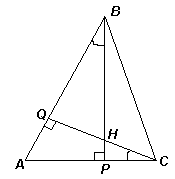
_{Рис. 5а}

Ответ: 45 или 135.

Пусть треугольник АВС – остроугольный, то есть точка Н лежит внутри треугольника (см. рис. 5а). Заметим, что ACQ = 90 – QAC = 90 – BAP = ABP. Тогда прямоугольные треугольники ACQ и HBQ равны по гипотенузе и острому углу (АС = НВ – по условию и ACQ =.HBQ – по доказанному).

Следовательно, CQ = BQ, то есть треугольник BQC – прямоугольный и равнобедренный. В таком треугольнике углы при основании равны 45, поэтому AВC = 45.

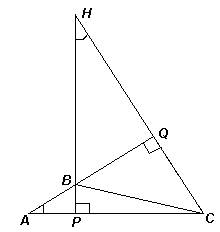
_{Рис. 5б}

В случае, если треугольник АВС – тупоугольный и точка Н лежит вне треугольника (см. рис. 5б), рассуждения аналогичны. Разница состоит в том, что угол BQC, равный 45, является внешним углом треугольника АВС, поэтому AВC = 135.

Для учащихся, знакомых с теоремой о средней линии треугольника, признаками параллелограмма, теоремой об окружности, описанной около треугольника, и свойством углов, вписанных в окружность, можно предложить и другое решение, основанное на следующей лемме:

_{Рис. 5в}

Пусть Н – точка пересечения высот треугольника АВС, О – центр описанной около него окружности, а В₁ – середина стороны АС. Тогда BH = 2OB₁ (см. рис. 5в).

Для доказательства введем следующие обозначения: R – середина отрезка ВН, Т – середина отрезка СН, А₁ – середина отрезка ВС.

В треугольнике ВНС отрезок А₁Т является средней линией, поэтому А₁Т || BH. Отрезок А₁R – также средняя линия этого треугольника, значит, А₁R || CH. Следовательно, четырехугольник RHTА₁ – параллелограмм и BR = RH = A₁T.

Параллелограммом будет являться и четырехугольник OB₁TA₁. Действительно, О – центр окружности, описанной около треугольника АВС, значит ОА₁ и ОВ₁ – серединные перпендикуляры к сторонам ВС и АС соответственно. A₁T || BP, BP  AC, следовательно, A₁T  AC. Таким образом, A₁T || ОВ₁.

Кроме того, В₁Т – средняя линия треугольника АНС, значит В₁Т || АН. Так как три высоты треугольника пересекаются в одной точке, то АН  BC, значит и В₁Т  BC, тогда В₁Т || OA₁. Таким образом получим, что BH = BR = RH = A₁T = ОВ₁.

Применим доказанную лемму к нашей задаче. Так как ОВ₁ = АС, то медиана ОВ₁ треугольника АОС равна половине стороны АС, к которой проведена. Следовательно, треугольник АОС – прямоугольный (АОС = 90, см. рис. 5 г, д).

Далее возможны два случая: точки О и В расположены в одной полуплоскости относительно прямой ВС (см. рис. 5г) или в разных полуплоскостях (см. рис. 5д). По теореме об угле, вписанном в окружность, в первом случае АВС = АОС = 45, а во

_{Рис. 5г}

_{Рис. 5д}

втором случае АВС = 180 – АОС = 135.

4.3. Десятичная запись числа состоит из десяти различных цифр. Цифра называется «хорошей», если она равна сумме двух своих соседей (слева и справа). Какое наибольшее количество «хороших» цифр может быть в таком числе?

Ответ: четыре цифры.

Из условия задачи следует, что «хорошие» цифры не могут быть крайними. Кроме того, соседи «хороших» цифр не могут быть «хорошими», так как «хорошая» цифра должна быть больше каждого из своих соседей (ноль рядом с «хорошей» цифрой стоять не может, иначе «хорошая» цифра будет равна другой соседней, а по условию все цифры различны).

Таким образом, в числе может быть не более четырех «хороших» цифр. Пример: 1439682750 («хорошие» цифры выделены жирным шрифтом).

При построении примера, помимо указанных соображений, полезно учесть еще и такие:

1) ноль должен стоять в конце десятичной записи числа;

2) цифры 1 и 2 «хорошими» быть не могут, а цифры 8 и 9 обязаны быть «хорошими».

Существует всего шесть чисел, состоящих из различных цифр, с четырьмя «хорошими» цифрами (три пары симметричных, если отбросить ноль): 1439682750 и 5728693410; 1547396820 и 2869374510; 7813264950 и 5946231870.

Математическая регата

14.10.2023

9 класс

Первый тур (10 минут; каждая задача – 6 баллов)

1.1. Какое наименьшее натуральное число надо прибавить к сумме 3¹³ + 9¹³, чтобы получить квадрат натурального числа?

Ответ: .

Решение. Так как , то следующий квадрат равен . Следовательно, наименьшее натуральное число, которое надо прибавить к , чтобы получить квадрат натурального числа, равно .

1.2. В прямоугольном треугольнике ABC с прямым углом C проведена медиана AM. Может ли выполняться равенство AB = 2AM?

Ответ: не может.

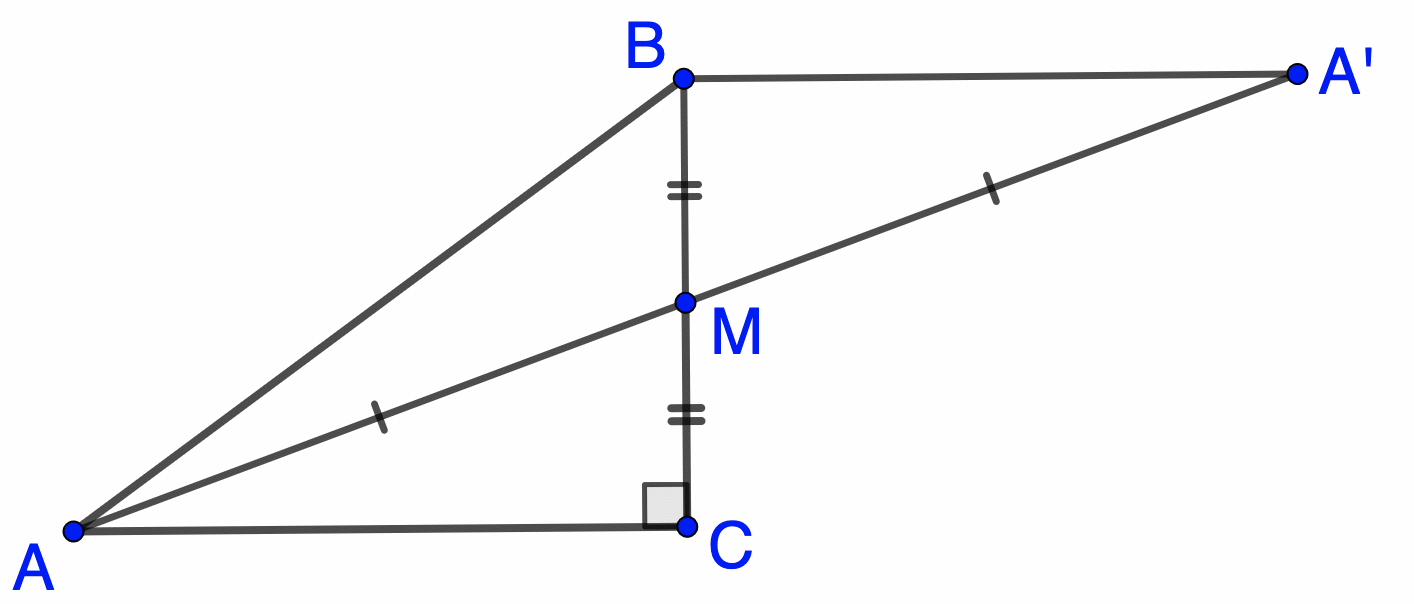
Рис. 1

Решение. Первый способ. Предположим, что AB = 2AM, тогда медиана, проведённая к АВ, равна АМ. Из равенства двух медиан треугольника следует, что АВ = ВС, что невозможно.

Второй способ. Удвоим медиану AM, то есть построим такую точку A’ на луче AM, что AM = MA’, тогда BA’ || AC (см. рис. 1). Следовательно, угол ABA’ – тупой, значит, АА’ – наибольшая сторона треугольника АВА’. Тогда 2AM = АА’ > AB.

Также можно провести через точку М среднюю линию MK треугольника АВС, параллельную АС, и провести аналогичное рассуждение для треугольника AMK.

1.3. Решите в целых числах систему уравнений:

Ответ: (674; 2; 675), (2024; 0; 2023).

Решение. Вычтем из второго уравнения первое: a + bc – ab – c = 1  (b – 1)(c – a) = 1. Из полученного уравнения следует, что b – 1 = c – a = 1 или b – 1 = c – a = –1.

В первом случае b = 2, c = a + 1. Тогда первое уравнение системы можно записать так:
2a + a + 1 = 2023, откуда a = 674, c = 675.

Во втором случае b = 0. Подставив это значение в исходную систему, получим: a = 2024, c = 2023.

Второй тур (15 минут; каждая задача – 7 баллов)

2.1. Для положительных чисел a и b выполняется неравенство a – b > 4. Докажите, что тогда выполняется неравенство .

Решение. Так как a > b + 4 и b > 0, то . Следовательно, достаточно доказать, что . В свою очередь,    .

Эту же идею можно оформить иначе. Рассмотрим разность левой и правой частей доказываемого неравенства: = , так как b > 0. Следовательно, .

2.2. Через точку А окружности с центром О проведена касательная, а через точку В, также лежащую на окружности, проведен луч ОВ, пересекающий эту касательную в точке Е. Из точки А опущен перпендикуляр АС на ОВ, а из точки В – перпендикуляр BD на АЕ. Докажите, что ВС = BD.

Решение. Пусть АОВ = 2, тогда DAB =  (угол между касательной и хордой, см. рис. 2).

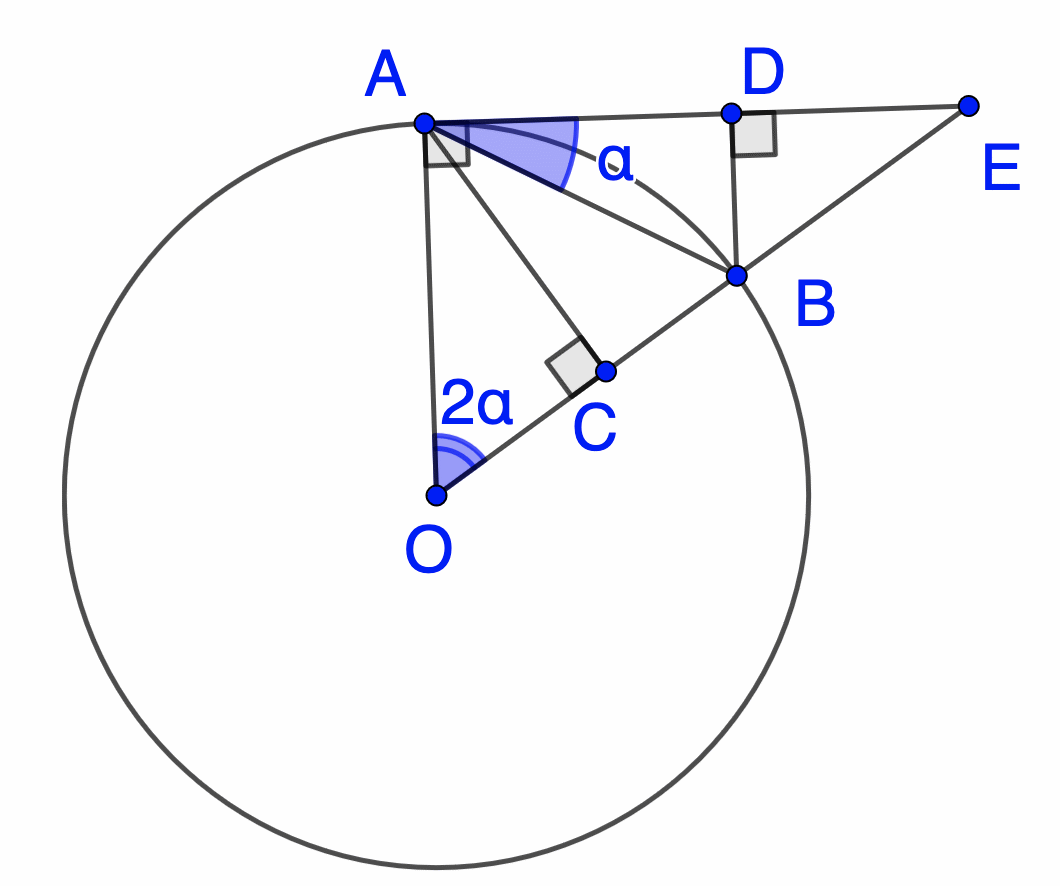
В равнобедренном треугольнике AOB: АВО = ВАО = 90 – , поэтому САВ =  = DAB. Таким образом, прямоугольные треугольники ABС и ABD равны (по гипотенузе и острому углу), откуда BC = BD.

Рис. 2

2.3. На острове проживает 2024 жителя, каждый из которых либо рыцарь (который всегда говорит правду), либо лжец (который всегда лжёт). Однажды все жители острова разбились на пары, и каждый сказал: «Он – рыцарь!» либо «Он – лжец!» про своего соседа по паре. Оказалось, что тех и других фраз произнесено поровну. Какое наименьшее количество лжецов может жить на острове?

Ответ: 506 лжецов.

Решение. Оценка. Заметим, что фразу «Он – рыцарь!» могли сказать друг про друга только люди одного типа, а фразу «Он – лжец!» – люди разных типов. Значит, в каждой паре оба жителя произнесли одинаковые фразы. Тогда «Он – лжец!» сказали люди из 506 пар. В каждой такой паре есть лжец, поэтому их не меньше 506.

Пример. Пусть на острове живет 1518 рыцарей и 506 лжецов. Если 1012 рыцарей разобьются на пары, то в каждой из них будут произнесены только фразы «Он – рыцарь!» Среди остальных 1012 жителей острова поровну рыцарей и лжецов, они могут разбиться на пары рыцарь – лжец, тогда в каждой паре будут произнесены только фразы «Он – лжец!» Таким образом, и тех, и других фраз будет поровну.

Отметим, что пример сразу следует из оценки.

Третий тур (20 минут; каждая задача – 8 баллов)

3.1. Сколько отрицательных корней имеет уравнение: x⁴ – 5x³ – 4x² – 7x + 4 = 0?

Ответ: отрицательных корней нет.

Решение. Перепишем уравнение в виде , что равносильно уравнению . Если теперь x < 0, то , то есть при любых отрицательных значениях x равенство не выполняется.

3.2. В треугольнике АВС отрезки АМ и СР являются биссектрисами углов А и С соответственно, причём АР + СМ = АС. Найдите величину угла В.

Ответ: 60.

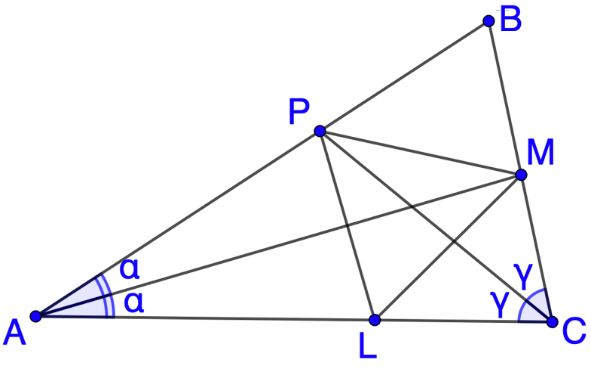
Рис. 3

Решение. Отразим точку P относительно биссектрисы AM (см. рис. 3). Получим точку L на стороне АС, причём треугольник APL – равнобедренный. Из условия AP + CM = AC следует, что CL = CM, то есть CLM – также равнобедренный треугольник. Тогда MA – серединный перпендикуляр к отрезку PL, поэтому MP = ML. Аналогично, PC – серединный перпендикуляр к отрезку ML, поэтому PM = PL. Таким образом, треугольник PML – равносторонний, поэтому PLМ = 60.

Пусть ВАС = 2, ВСА = 2 тогда АLP = 90 – , CLM = 90 – . Значит, 90 –  + 90 –  = 120, откуда  +  = 60. Следовательно, 2 + 2 = 120, поэтому АВС = 60.

3.3. На доске записаны в ряд квадраты натуральных чисел в возрастающем порядке так, что разность любых двух соседних чисел – простое число или квадрат простого числа. Какое наибольшее количество чисел может быть записано?

Ответ: 7 чисел.

Решение. Рассмотрим два соседних числа a² и b². Их разность равна b² – a² = (b – a)(b + a). Простое число p можно представить в виде произведения двух натуральных чисел единственным способом: p = 1·p, а его квадрат – двумя способами: p² = 1·p² = p·p.

Так как числа b – a и b + a различные, то в любом случае b – a = 1, тогда b² – a² = 2a + 1. Следовательно, на доске выписаны квадраты последовательных чисел, а разности соседних выписанных чисел – это последовательные нечётные числа, не меньшие 3.

Если чисел хотя бы четыре, то из первых трёх таких разностей одна делится на 3, поэтому может быть равна только 3 или 9. При этом разности 15 быть не может, поэтому максимальная разность, которую можно получить, равна 13, а всего чисел не больше семи. С другой стороны, можно выписать квадраты первых семи натуральных чисел: 1, 4, 9, 16, 25, 36, 49, получив при этом разности 3, 5, 7, 9, 11, 13.

Четвёртый тур (25 минут; каждая задача – 9 баллов)

4.1. Известно, что для положительных x, y и z выполняются равенства: xy = z + a, yz = x + a, zx = y + a. Какие значения может принимать a?

Ответ: a  – 0,25.

Решение. Вычтем из первого уравнения второе, а из второго – третье. Получим:

 Так как значения всех переменных положительны, то . Тогда каждое из исходных уравнений примет вид: x² – x – a = 0. Это уравнение имеет хотя бы один корень, если D = 1 + 4a  0, то есть при a  – 0,25. Так как сумма корней этого уравнения равна 1, то хотя бы один его корень положителен.

Получив равенство , можно далее рассуждать иначе. Каждое из исходных уравнений можно записать так: a = x² – x. Искомые значения а – ýòî множество значений функции f(x) = x² – x ïðè x > 0. Графиком этой функции является парабола, вершина которой – в точке (0,5; – 0,25), а ветви направлены вверх. Следовательно, a  – 0,25.

4.2. От прямоугольника со сторонами 7 и 10 клеток отрезали два прямоугольных треугольника с катетами 2 и 3 клетки (см. рисунок). Разрежьте получившийся шестиугольник на две части и сложите из них квадрат.

Решение Способ разрезания показан на рис. 4а, а квадрат, сложенный из двух полученных частей, показан на рис. 4б.

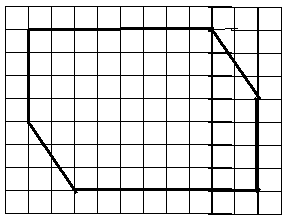
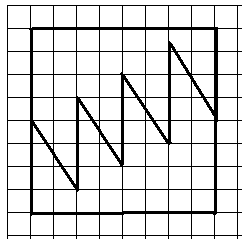
Рис. 4а

Рис. 4б

4.3. На конференцию приехали 200 учёных. Двое из них знают по 21 участнику конференции, ещё двое – по 22, ещё двое – по 23 и так далее, а последние двое – по 120. Может ли оказаться, что их можно посадить в два актовых зала так, чтобы в каждом зале были только незнакомые друг с другом?

Ответ: не может.

Решение. Построим граф, в котором вершины соответствуют учёным, а рёбра соединяют знакомых. Предположим, что полученный граф двудольный. В одной из его долей не менее 120 вершин, поскольку в графе есть вершины степени 120. Значит, в другой доле их не более 80. При этом в графе должно быть ровно 120 вершин, степени которых не превосходят 80. Такое возможно, только если в одной доле ровно 120 вершин – по две вершины каждой степени от 21 до 80, а в другой доле 80 вершин – по две вершины каждой степени от 81 до 120. Тогда сумма степеней вершин первой доли равна 2·(21 + 22 + … + 80) = 6060, а сумма степеней вершин второй доли – 2·(81 + 82 + … + 120) = 8040. Однако эти суммы должны быть равны. Полученное противоречие доказывает, что граф не может быть двудольным, а это равносильно тому, что учёных нельзя рассадить в два зала так, чтобы в каждом зале были только незнакомые.

Пятый тур (15 минут; каждая задача – 7 баллов)

5.1. Разложите на множители, каждый из которых имеет степень не выше двух:

x⁴ + y⁴ + (x + y)⁴.

Ответ: 2(x² + xy + y²)².

Решение. Первый способ. Пусть z = x + y, тогда x² + y² = z² – 2xy, x⁴ + y⁴ = (z² – 2xy)² – 2x²y² = z⁴ – 4xyz² + 2x²y². Следовательно, x⁴ + y⁴ + (x + y)⁴ = x⁴ + y⁴ + z⁴ = 2z⁴ – 4xyz² + 2x²y² = 2(z² – xy)² = 2(x² + xy + y²)².

Второй способ. Раскроем скобки: x⁴ + y⁴ + (x + y)⁴ = x⁴ + y⁴ + (x² + 2xy + y²)² = 2x⁴ + 2y⁴ + 4x²y² + 4x³y + 4xy³ + 2x²y² = 2(x⁴ + y⁴ + x²y² + 2x²y² + 2x³y + 2xy³) = 2(x² + xy + y²)².

После раскрытия скобок можно продолжить и по-другому, если не увидеть формулы квадрата трёхчлена: 2x⁴ + 2y⁴ + 4x²y² + 4x³y + 4xy³ + 2x²y² = (2x⁴ + 2y⁴ + 2x²y²) + (4x²y² + 4x³y + 4xy³) = 2(x⁴ + 2x²y² + y⁴ – x²y²) + 4xy(x² + xy + y²) = 2((x² + y²)² – (xy)²) + 4xy(x² + xy + y²) = 2(x² + xy + y²)(x² – xy + y²) + 4xy(x² + xy + y²) = 2(x² + xy + y²)².

5.2. Существует ли треугольник, в котором окружность, построенная на стороне как на диаметре, касается окружности, проходящей через середины его сторон?

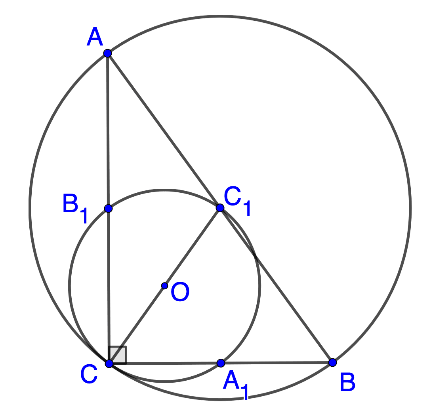
Ответ: существует.

Решение Рассмотрим прямоугольный треугольник ABC и его описанную окружность. Она построена на гипотенузе АВ как на диаметре, поэтому её центр C₁ – середина АВ (см. рис. 5). Далее можно рассуждать по-разному.

Рис. 5

Первый способ. Середины А₁, В₁ и С₁ сторон треугольника и вершина С его прямого угла образуют прямоугольник (А₁С₁ и В₁С₁ – средние линии треугольника АВС), поэтому окружность, проходящая через середины сторон АВС, содержит вершину С, её центр О – середина СС₁.

Таким образом, общая точка С двух указанных окружностей лежит на линии их центров, поэтому касательная, проведённая через эту точку к одной из окружностей, является касательной и к другой. Это и означает, что окружности касаются.

Второй способ. Воспользуемся тем, что при гомотетии с центром в ортоцентре треугольника и коэффициентом 0,5 окружность, описанная около треугольника, переходит в его окружность девяти точек, которая и проходит через середины сторон треугольника. В данном случае, С – центр гомотетии, который является неподвижной точкой. Значит, описанная окружность и её образ касаются в этой точке.

Догадаться рассматривать прямоугольный треугольник можно, исходя из следующих соображений. Окружность, построенная на одной из сторон как на диаметре, – это ГМТ, из которых эта сторона видна под прямым углом, поэтому такая окружность пересекает прямые, содержащие две другие стороны, в основаниях высот. Окружность, проходящая через середины сторон треугольника, – это окружность девяти точек, которая тоже проходит через основания высот. Таким образом, если основания высот к сторонам, которые не являются диаметром, различны, то окружности уже имеют две различных общих точки, а значит касаться не могут. Значит, условие задачи может выполняться только в треугольнике, в котором основания двух высот совпадают, то есть в прямоугольном.

5.3. Существует ли десятизначное число, кратное 7, все цифры в десятичной записи которого различны?

Ответ: существует.

Решение. Проще всего составить такое число из нескольких частей, каждая из которых делится на 7. Возьмём первые четыре числа, кратные 7: 7, 14, 28, 35 – в них нет повторяющихся цифр. Остались цифры 0, 6 и 9, из которых можно составить число 609, также кратное 7. Поэтому условию удовлетворяет, например, число 7142835609.

Понятно, что существует и много других примеров.