
ОРДАБАСЫ АУДАНЫНЫҢ БІЛІМ БӨЛІМІ
АУДАНДЫҚ ПЕДАГОГИКАЛЫҚ-ӘДІСТЕМЕЛІК КАБИНЕТ
МАТЕМАТИКАЛЫҚ ОЛИМПИАДА ЕСЕПТЕРІНІҢ ЖИНАҒЫ
Темірлан
2025
К
М29
Жинақ Ордабасы ауданының білім бөлімінің сараптамалық кеңесінің шешімімен баспаға ұсынылған, №3 хаттама 30.012.2024ж.
Құрастырушылар:
Бейсенбі Г. – Б.Оңтаев атындағы ЖББМ математика пәні мұғалімі
Ибадулла Л. – Б.Оңтаев атындағы ЖББМ математика пәні мұғалімі
Пікір айтушылар:
Бүркіт Ә.Қ. – Қазақстан Педагогикалық академиясы және Жаратылыстану – педагогикалық академиясының академигі, Нобель медалінің иегері
Реңдібаева С. – Ордабасы ауданының білім бөлімінің математика пәні әдіскері, математика ғылымдарының магистры
Нурумбаева К. – Б.Нұрлыбеков атындағы ЖББМ математика пәні мұғалімі, педагог-шебер
Математикалық олимпиада есептерінің жинағы: М29 авторлық/құраст.: Ж.Туккулиева. – Темірлан: Ордабасы
ауданының білім бөлімі, 2024. – 72 б.
Ұсынылып отырған жинақта математикалық олимпиадаларда жиі кездесетін теңсіздіктердің шешу жолдары егжей тегжей көрсетілген. Коши теңсіздігінің қолданысы, санды теңсіздіктерді дәлелдеу әдісі, математикалық индукция принципі, теңсіздіктерді шешуде векторлық әдісті қолдану, геометриялық теңсіздіктер, параметрлі теңсіздіктерді шешу қарастырылған.
Жинақ математика пәні мұғалімдеріне арналған.
К
© Ордабасы ауданының білім бөлімі, 2024
МАЗМҰНЫ
-
Кіріспе..................................................................
4
-
Формулалар.............................................
6
-
Санды теңсіздіктер.................................
8
-
Коши теңсіздігі.......................................
11
-
Қарапайым теңсіздіктер........................
21
-
Геометриялық теңсіздіктер...................
27
-
Параметрмен берілген теңсіздіктер, логарифмдік теңсіздіктер.......................
34
-
Теңсіздіктерді дәлелдеуде векторлық әдістің қолданысы.................................
39
-
Математикалық индукция .....................
43
-
Тапсырмалар ...........................................
49
Қорытынды Әдебиеттер.........................................................
70
-
ІРІСПЕ
Мектеп оқушылары арасында жас таланттарды анықтау мақсатында мектепішілік, аудандық, облыстық, республикалық деңгейде түрлі математикалық олимпиадалар өткізіп тұру дәстүрге айналып келеді. Математикалық олимпиадалардың мақсаты – оқушыларды математикаға қызығушылығын арттыру, оқушыларды терең ойлауға, дәлелдеуге үйрету, талантты жастарды анықтап, математикалық қабілеттерінің дамуына мүмкіндік беру.
Бұл ұсынылып отырған әдістемілік жинақта математикалық олимпиадаларда жиі кездесетін теңсіздіктердің шешу жолдары егжей тегжей көрсетілген. Коши теңсіздігінің қолданысы, санды теңсіздіктерді дәлелдеу әдісі, математикалық индукция принципі, теңсіздіктерді шешуде векторлық әдісті қолдану, геометриялық теңсіздіктер, параметрлі теңсіздіктерді шешу қарастырылған. Сондай-ақ, осы тақырыптар бойынша өздігінен орындауға арналған тапсырмалары және олардың жауаптары қамтылған.
Бұл әдістемелік құралды математикалық олимпиадаға даярлау үшін жалпы білім беретін орта мектептің оқушылары мен математика пәні мұғалімдері, олимпиадалық есептерді шығаруды үйренгісі келген талапкерлердің пайдалануына болады. Сонымен қатар,математика факультетінің студенттері мен болашақ математика пәні мұғалімдері үшін, математиканы тереңдетіліп оқытатын сыныптардың оқушыларына да пайдалы.
-
ФОРМУЛАЛАР
Коши теңсіздігі



Орталар теңсіздігі
min(x1,
x2, … ,
xn)





Мұндағы



 арифметикалық
орта
арифметикалық
орта

n
= 2 деп
алсақ, 






Сонымен,
Гармоникалық
орта  геометриялық
орта
геометриялық
орта  арифметикалық
орта
арифметикалық
орта квадраттық орта
.
квадраттық орта
.
 ≥
≥

 екі жағында 2-ге
көбейткенде
екі жағында 2-ге
көбейткенде  шығады
шығады
Тура солай


 +
+
 өйткені
өйткені 

Коши теңсіздігін теңсіздіктерді дәлелдеу мақсатында теңсіздіктердің сол жақ бөлігін немесе оң жақ бөлігін кішірейтуде немесе үлкейтуде қолданамыз.
2. САНДЫ ТЕҢСІЗДІКТЕР
2.
Теңсіздікті
дәлелдеңдер: 
 +
+  + ... +
+ ... +



Дәлелдеуі: Теңсіздіктің сол жақ бөлігінде қанша мүше бар екенін анықтайық, ол үшін бөлшектің бөліміндегі 3990 санынан 1996 санының алдындағы санды алып тастаймыз:
3990 –
1995  1995
1995
 +
+  +
...
+
+
...
+


 +
...
+
+
...
+

 + ...
+
+ ...
+







 Себебі, алымдары бірдей
бөлшектердің бөлімінің кішісі үлкен
болады.
Себебі, алымдары бірдей
бөлшектердің бөлімінің кішісі үлкен
болады.



Сонымен, теңсіздіктің сол жақ
бөлігінің мүшелері оң жақ бөлігіндегі мүшелерінен үлкен болса, онда
сол жақ бөлігінің мүшелерінің қосындысы да оң жақ бөлігіндегі
мүшелерінен қосындысынан үлкен болады. Олай болса, теңсіздіктің оң
жақ бөлігінің мүшелерінің қосындысы  – ге тең болғандықтан,
сол жақ бөлігі
– ге тең болғандықтан,
сол жақ бөлігі  ден үлкен болады.
Теңсіздік дәлелденді.
ден үлкен болады.
Теңсіздік дәлелденді.
2.Кез келген натурал n саны үшін

 +
+  + ... +
+ ... +

 2 теңсіздігінің
орындалатынын дәлелдеңдер.
2 теңсіздігінің
орындалатынын дәлелдеңдер.
Дәлелдеуі: Теңсіздіктің сол жақ бөлігінің әр мүшесін төмендегіше жіктеп аламыз:

 1
1



 1 -
1 -





 -
-

.......................




 -
-





 -
-

Теңсіздіктің сол жағындағы қосындының орнына үлкейтілген өрнекті апарып қоямыз. Үлкейткен өрнектің өзі 2-ден кіші немесе 2-ге тең болса, онда сол жақтағы кіші өрнек 2-ден кіші болады.
1![]()
![]()
![]()
![]()
![]()
![]()
![]() + 1
-
+ 1
-  +
+
 -
-  +
...
+
+
...
+
 -
-  +
+
 -
- 
 2 -
2 -

 2
2
2 -
 өрнегі 2-ден кіші
болады. Өйткені , 2-ден қандай да бір
өрнегі 2-ден кіші
болады. Өйткені , 2-ден қандай да бір
 санын азайтып
отырмыз. Себебі, шартында n- натурал сан, n натурал сан (теріс сан
болса) болмаса 2-ден үлкен болуы мүмкін. Сонымен, теңсіздігіміз
дәлелденді.
санын азайтып
отырмыз. Себебі, шартында n- натурал сан, n натурал сан (теріс сан
болса) болмаса 2-ден үлкен болуы мүмкін. Сонымен, теңсіздігіміз
дәлелденді.
3.
 -
-  +
+  -
-  + ... -
+ ... -
 +
+ 
 екенін
дәлелдеңдер.
екенін
дәлелдеңдер.
Д![]()
![]()
![]() әлелдеуі: Теңсіздіктің сол жақ бөлігін
есептейік:
әлелдеуі: Теңсіздіктің сол жақ бөлігін
есептейік:
 -
-  +
+
 -
-  +
+
 -
-  +
...
-
+
...
-
 +
+ 
 -
-
 +
+  ) –
(
) –
( -
-
 )
-
)
-  -
-
 ...
-
...
-
 -
- 

 -
-
 -
-  -
-



 - тен қандай да бір
кішкентай санды азайтсақ
- тен қандай да бір
кішкентай санды азайтсақ  – тен кіші сан шығатыны
белгілі. Демек, теңсіздік дәлелденді.
– тен кіші сан шығатыны
белгілі. Демек, теңсіздік дәлелденді.
![]()
![]() 4
4![]()
![]()
![]()
![]()
![]() .Дәлелдеу
керек:
.Дәлелдеу
керек:  <
98
<
98
Дәлелдеуі: ( а + в)2 = а2 + 2ав + в2 қысқаша көбейту формуласын қолдану арқылы дәлелдейміз:
 <
98
<
98




20

20
 49
49
(20 )2
)2
 492
492
2400 2401
дәлелденді.
2401
дәлелденді.
3. КОШИ ТЕҢСІЗДІГІ
1. Айталық
х  1 болсын. Теңсіздікті
дәлелдеңдер:
1 болсын. Теңсіздікті
дәлелдеңдер: 
Дәлелдеуі: Орталар теңсіздігі
формуласынан  теңсіздікті қолдану
арқылы дәлелдейміз.
теңсіздікті қолдану
арқылы дәлелдейміз.  деп алып, формулаға
апарып қоямыз:
деп алып, формулаға
апарып қоямыз:


 =
=
 =
= 

 бұл теңсіздіктің сол жақ
бөлігіндегі 2-ні оң жақ бөлігіне көбейту етіп
өткізсек
бұл теңсіздіктің сол жақ
бөлігіндегі 2-ні оң жақ бөлігіне көбейту етіп
өткізсек  теңсіздігі шығады.
Теңсіздіктің шартында х
теңсіздігі шығады.
Теңсіздіктің шартында х 1 болғандықтан, теңдік
белгісі болмайды. Сонда теңсіздігіміз
1 болғандықтан, теңдік
белгісі болмайды. Сонда теңсіздігіміз
 болады. Сонымен,
теңсіздік дәлелденді.
болады. Сонымен,
теңсіздік дәлелденді.
2. Егер а +
в  1 болса,
онда
1 болса,
онда  +
+ 

 теңсіздігі тура
болатынын дәлелдеңдер.
теңсіздігі тура
болатынын дәлелдеңдер.
Дәлелдеуі: Квадраттық орта арифметикалық ортадан үлкен немесе тең


 формуласын қолданып,
дәлелдейміз.
формуласын қолданып,
дәлелдейміз. 


 =
=





Есептің берілгенінен мына
шарттың а + в  1 екі жағын да 2-ге
бөліп түрлендіріп аламыз.
1 екі жағын да 2-ге
бөліп түрлендіріп аламыз. 



 =>
=> 

 =>
=> 

 Дәлелденді.
Дәлелденді.
3. Оң х және у
үшін: 


 теңсіздігі орындалатынын
дәлелде.
теңсіздігі орындалатынын
дәлелде.
Дәлелдеу Коши
теңсіздігін
Коши
теңсіздігін 

 қолдану арқылы
дәлелдейміз.
қолдану арқылы
дәлелдейміз.


Теңсіздіктің сол жағындағы қосындының бөлімінің орнына кішірейтілген өрнекті апарып қоямыз. Бөлімі кішірейтілсе, өрнектің өзі үлкейтіледі.



 ;
;
 +
+
 ;
;
 +
+ 

 ;
;


 ;
;


 ;
;
Сол жақтағы үлкейтілген
өрнектің өзі  - ге тең болса, онда
кіші болады. Теңсіздік дәлелденді.
- ге тең болса, онда
кіші болады. Теңсіздік дәлелденді.
4.
Дәлелдеңіз: ![]() .
Мұндағы
.
Мұндағы ![]() -кез келген нақты
сандар.
-кез келген нақты
сандар.
Дәлелдеуі: Коши теңсіздігін а +
в 
 қолдану арқылы
дәлелдейміз.
қолдану арқылы
дәлелдейміз.
![]() ,
,
![]() ,
,
![]()
Онда![]() ,
,
![]()
Демек, теңсіздік дәлелденді.
5. Кез келген x,y,z
үшін  теңсіздігі
орындалатынын дәлелдеңіз.
теңсіздігі
орындалатынын дәлелдеңіз.
Дәлелдеуі:  теңсіздігінің екі
жағында 2-ге көбейтеміз, сонда
теңсіздігінің екі
жағында 2-ге көбейтеміз, сонда  одан
одан 
Коши теңсіздігін қолданып, оларды қосамыз



Сонда келесі теңсіздік
шығады 
Сонымен теңсіздіктің сол жағын кішірейту арқылы теңсіздікті дәлелдедік.
6. Теңсіздікті дәлелдеңіз (a+b)(b+c)(a+c)≥8abc, мұндағы a≥0, b≥0, c≥0.
Дәлелдеуі: Коши теңсіздігі бойынша


 олай болса бастапқы
теңсіздікке апарып орын орына қоятын
болсақ
олай болса бастапқы
теңсіздікке апарып орын орына қоятын
болсақ
(a+b)(b+c)(a+c)≥8abc,  ≥8abc шығады ,яғни сол
жағымен оң жағы теңесті, кішірейтілген сол жағы оң жағына тең болып
тұр. Олай болса кішірейтілмеген (a+b)(b+c)(a+c) 8abc-дан үлкен,
яғни (a+b)(b+c)(a+c)≥8abc. Сонымен теңсіздік
дәлелденді.
≥8abc шығады ,яғни сол
жағымен оң жағы теңесті, кішірейтілген сол жағы оң жағына тең болып
тұр. Олай болса кішірейтілмеген (a+b)(b+c)(a+c) 8abc-дан үлкен,
яғни (a+b)(b+c)(a+c)≥8abc. Сонымен теңсіздік
дәлелденді.
7. Кез келген оң таңбалы
a,b,c үшін  екенін
дәлелдеңіз.
екенін
дәлелдеңіз.
Дәлелдеуі: Осы a,b,c үшін Коши теңсіздігін қолданып, келесі теңсіздіктерді жазып алайық
 ,
,  олай
болса
олай
болса 
Коши теңсіздігі бойынша
кішірейтілген сол жағы 3-ке тең болады, яғни, кішірейтілмегені
3-тен үлкен  . Осымен теңсіздік
дәлелденді.
. Осымен теңсіздік
дәлелденді.
8. Егер x+y+z=7 болса
мұндағы  онда
онда
 екенін
дәлелдеңіз.
екенін
дәлелдеңіз.
Дәлелдеуі: (a+b+c) ²=a²+b²+c²+2ab+2bc+2ac сол сияқты

(x+y+z)+2
x+y+z=7
болғандықтан
7+2
енді Коши теңсіздігін қолданып теңсіздіктің сол жағын үлкейтеміз
x+y
≥ , z+y
≥
, z+y
≥ , x+z
≥
, x+z
≥ болғандықтан
болғандықтан
7+x+y+y+z+x+z<25,
7+2(x+y+z) 7+2·7<25, 21<25
демек, теңсіздік дәлелденді.
7+2·7<25, 21<25
демек, теңсіздік дәлелденді.
9. Егер xy+yz+zx=1 болса, онда x²+y²+z²≥1 теңсіздігі орындалатыны дәлелдеңіз.
Дәлелдеуі: x²+y²+z²≥1 теңсіздігінің екі жағында 2-ге көбейтіп алып, Коши теңсіздігін қолданып теңсіздіктің сол жағын кішірейтіп аламыз
2x²+2y²+2z²≥2, (x²+y²)+ (y²+z²)+(x²+z²)≥2
2xy+2yz+2zx≥2, 2(xy+yz+zx)≥2 шарты бойынша xy+yz+zx=1 , сондықтан 2·1=2 дәлелденді, өйткені теңсіздіктің сол жағы кішірейтілгеннің өзінде сол жағының мәніне тең болып тұр. Олай болса теңсіздіктің кішірейтілмеген сол жағы оң жағынан әлбетте үлкен
x²+y²+z²≥1 теңсіздігі дәлелденді.
10. a>0, b>0, c>0
болғанда  екенін
дәлелдеңіз
екенін
дәлелдеңіз
Дәлелдеуі:  теңсіздігінің екі
жағында 2-ге көбейтіп алып келесі теңсіздікті
жазамыз
теңсіздігінің екі
жағында 2-ге көбейтіп алып келесі теңсіздікті
жазамыз

Коши теңсіздігін қолдануға
ыңғайлы етіп мына түріне келтіріп жазып аламыз
( 
Коши теңсіздігін қолданамыз
 ,
, 
 ,
, 
 ,
, 
 осы теңсіздікке Коши
теңсіздігін және қолданамыз, ол үшін алдымен мына түріне келтіріп
аламыз теңсіздікті
осы теңсіздікке Коши
теңсіздігін және қолданамыз, ол үшін алдымен мына түріне келтіріп
аламыз теңсіздікті
(

(

Коши теңсіздігі бойынша
 ,
, 
 ,
,

 ,
,

Олай болса теңсіздіктің сол жағын
 +
+ деп жазып, ортақ
көбейткіштерін жақша сыртына шығарамыз
деп жазып, ортақ
көбейткіштерін жақша сыртына шығарамыз
 =
= осындай теңдік пайда
болады, яғни, теңсіздіктің кішірейтілген сол жағы он жағына тең
болды.Олай болса кішірейтілмеген сол жағы теңсіздіктің оң жаңынан
әлбетте үлкен болады. Сонымен,
осындай теңдік пайда
болады, яғни, теңсіздіктің кішірейтілген сол жағы он жағына тең
болды.Олай болса кішірейтілмеген сол жағы теңсіздіктің оң жаңынан
әлбетте үлкен болады. Сонымен,
 теңсіздігі
дәлелденді.
теңсіздігі
дәлелденді.
11. Егер a+b+c=0 болса, онда ab+ac+bc≤0 болатындығын дәлелдеңдер. Дәлелдеуі: a+b+c=0 теңдігінің екі жағында квадраттаймыз
 ,
,  ,
,
 ,
,  шығады
шығады
Екі жағдай қарастырамыз:
1)
 , олай
болса
, олай
болса 
Яғни
 демек
дәлелденді.
демек
дәлелденді.
12. Егер x+y+z=3 болса онда x²+y²+z² ≥ 3 теңсіздігі орындалатынын дәлелдеңіз
Дәлелдеуі: x+y+z=3 теңдігінің екі жағында квадраттаймыз, сонда
x²+y²+z²+2xy+2yz+2xz=9 шығады (1) одан
2xy+2yz+2xz=9-(x²+y²+z²) шығады (2)
Коши теңсіздігін қолданамыз
x²+y²≥2xy
y²+z²≥2yz
x²+z²≥2xz осы теңсіздіктерді бір біріне мүшелеп қосып келесі теңсіздікке келеміз 2x²+2y²+2z²≥ 2xy+2yz+2xz, 2(x²+y²+z²)≥ 2xy+2yz+2xz
2(x²+y²+z²)≥ 9-(x²+y²+z²)
3(x²+y²+z²)≥ 9
(x²+y²+z²)≥ 3 теңсіздік осымен дәлелденді.
13. Оң таңбалы a,b,c сандары үшін a≥b≥c және a+b+c≤1 болғанда a²+3b²+5c²≤1 теңсіздігі тура болатынын дәлелдеңдер.
Дәлелдеуі: a²+3b²+5c²≤1 теңсіздігін a²+ b² +2b²+2c²+2c²+c²≤1 деп жазып алып, теңсіздіктің сол жағын (a+b+c)² осыған келтіреміз
Алдымен мына теңсіздіктерді жазып алайық
2b²≤2ab, 2bb≤2ab екі жа,ында қыстқартқанда b≤2a қалады
2c²≤2bc, 2cc≤2bc, c≤b,
2a²≤2ac, 2aa≤2ac a≤ c
Сонда a²+ b² +2b²+2c²+2c²+c²≤1 теңсіздігі мынаған келеді
a²+ b² +c²+2ab+2bc+2ac≤1 ал бұл теңсіздікті былай жазсақ болатынын білеміз (a+b+c)² ≤1, олай болса a+b+c ≤1 , теңсіздік дәлелденді
Теңсіздіктің сол жағын Коши теңсіздігін қолданып үлкейту арқылы дәлелдедік.
14. a>b, b>0, c>0
, a+b+c=1 екені белгілі болса, мынаны
дәлелдеңіз 
Дәлелдеуі: 1) a+b+c=1 теңдігін a -ға
бөлеміз, сонда 
2) b-ға
бөлгенде 
3) c -ға бөлгенде

Енді осы теңдікті қосамыз, келесі теңдікті жазамыз

Коши теңсіздігін пайдаланып оң жағын кішейтеміз
 ≥2
≥2
 ≥2
≥2
 ≥2
сонда
≥2
сонда 
 теңсіздік
дәлелденді.
теңсіздік
дәлелденді.
15. a+b=2 шарты қолданылатын кез келген a және b сандары үшін
 +
+ теңсіздігі
орындалатынын дәлелдеңдер.
теңсіздігі
орындалатынын дәлелдеңдер.
Дәлелдеуі: a=1+c деп белгілеп аламыз,
сонда a+b=2 теңдеуіне қойғанда  .
.
Яғни,
мына  +
+ теңсіздікті былай жазуға
болады
теңсіздікті былай жазуға
болады
 +
+ >2 Паскаль үшбұрышын
пайдаланып жақшасын ашамыз
>2 Паскаль үшбұрышын
пайдаланып жақшасын ашамыз  +4
+4 +4a
+4a +
+
 +
+ >2 үшін жақшасын
ашатын болсақ келесі теңсіздік шығады
1+4с
>2 үшін жақшасын
ашатын болсақ келесі теңсіздік шығады
1+4с +
+ +
+ +1-4с
+1-4с -
- +
+ , ықшамдап жіберіп
келесі теңсіздікті жазамыз
, ықшамдап жіберіп
келесі теңсіздікті жазамыз  +12
+12 ,
қысқартып
,
қысқартып  +6
+6 деп аламыз. Теңсіздік
осымен дәлелденеді.
деп аламыз. Теңсіздік
осымен дәлелденеді.
16. Егер x+y+z=1 болса,
онда x²+y²+z²≥ болатынын
дәлелдеңіз.
болатынын
дәлелдеңіз.
Дәлелдеуі: x= ,
y=
,
y= z=
z= деп белгілеп
аламыз,
деп белгілеп
аламыз,
x+y+z=1 шартын қолданамыз,
сонда x+y+z= , яғни 1+a+b+c=1 бұдан
a+b+c=0 олай болса,
, яғни 1+a+b+c=1 бұдан
a+b+c=0 олай болса,
(

 бұдан
бұдан
 +a²+b²+c²≥0,
+a²+b²+c²≥0,  +a²+b²+c²≥0, яғни,
a²+b²+c²≥0 осымен теңсіздік дәлелденді.
+a²+b²+c²≥0, яғни,
a²+b²+c²≥0 осымен теңсіздік дәлелденді.
4. ҚАРАПАЙЫМ ТЕҢСІЗДІКТЕР
1. Теңсіздікті
дәлелдеңіз:  , мұндағы a және b -
нақты сандар.
, мұндағы a және b -
нақты сандар.
Дәлелдеуі:  теңсіздігінің екі
жағында 2-ге көбейтейік. Пайда болған
теңсіздігінің екі
жағында 2-ге көбейтейік. Пайда болған
 теңсіздігін былай
түрлендіріп жазуға болады
теңсіздігін былай
түрлендіріп жазуға болады  . Сол жақтағы жақша
ішіндегі өрнекті қысқаша көбейту формуласы бойынша мына түріне
келеді
. Сол жақтағы жақша
ішіндегі өрнекті қысқаша көбейту формуласы бойынша мына түріне
келеді  . Олай
болса
. Олай
болса 
 , яғни
теңсіздік
, яғни
теңсіздік  дәлелденді
дәлелденді
2. Кез келген x,y,z
үшін  теңсіздігі
орындалатын дәлелдеңіз.
теңсіздігі
орындалатын дәлелдеңіз.
Дәлелдеуі:  теңсіздігінің екі
жағында 2-ге көбейтіп, бір бетіне өткізіп
алайық
теңсіздігінің екі
жағында 2-ге көбейтіп, бір бетіне өткізіп
алайық  .Теңсіздіктің сол
жағын
.Теңсіздіктің сол
жағын
 деп жазуға
болады
деп жазуға
болады

Қысқаша көбейту формуласына салып, келесі теңсіздікті жазамыз



 теңсіздігі
дәлелденді.
теңсіздігі
дәлелденді.
3. Егер xyz >0 , болса,
онда  теңсіздігінің
орындалатынын дәлелдеңдер.
теңсіздігінің
орындалатынын дәлелдеңдер.
Дәлелдеуі:  теңсіздігінің оң жақ
бетіндегі мүшелерін сол жағына өткізіп алып мүшелеп xyz өрнегіне
бөлуді орындаймыз.
теңсіздігінің оң жақ
бетіндегі мүшелерін сол жағына өткізіп алып мүшелеп xyz өрнегіне
бөлуді орындаймыз.
 , қысқартуды
орындаймыз, пайда болған теңсіздіктің екі жағында 2-ге
көбейтіп
, қысқартуды
орындаймыз, пайда болған теңсіздіктің екі жағында 2-ге
көбейтіп

Келесі теңсіздіктің сол жағын
екі мүшенің айырмасы шығатындай етіп
топтастырамыз  ,
бұдан
,
бұдан  , олай болса қысқаша
көбейту формуласы бойынша сол жағын
түрлендіріп
, олай болса қысқаша
көбейту формуласы бойынша сол жағын
түрлендіріп  бұл
теңсіздіктің
бұл
теңсіздіктің
 сондықтан
сондықтан
 теңсіздігі
дәлелденді дейміз.
теңсіздігі
дәлелденді дейміз.
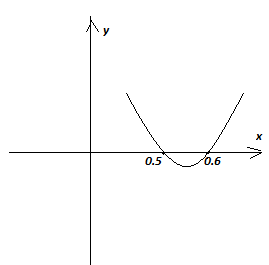
4. Кез келген бүтін n сан
үшін  өрнегінің мәні оң
екенін дәлелдеңіз.
өрнегінің мәні оң
екенін дәлелдеңіз.
Дәлелдеуі: nϵZ, n=1,5,-4,100,….
y(n)= , y>0 1) парабола
тармағы жоғары бағытталған, себебі
, y>0 1) парабола
тармағы жоғары бағытталған, себебі
 y
=
y
= a>0
a>0
2) абцисса осін қандай нүктеде қияды
y
=
 парабола абцисса
осін келесі екі нүктеде қияды
парабола абцисса
осін келесі екі нүктеде қияды

y
= ,
nϵ[
,
nϵ[ ]
y<0, яғни осы аралықта функция
мәні теріс және бұл аралықта n
мәні бүтін
емес.
]
y<0, яғни осы аралықта функция
мәні теріс және бұл аралықта n
мәні бүтін
емес.
nϵ
(-ꚙ; ]
ᴗ[
]
ᴗ[ ꚙ) y>0 демек бұл аралықта y
=
ꚙ) y>0 демек бұл аралықта y
= мәні оң болады, nϵZ
болғанда y>0 екені дәлелденді.
мәні оң болады, nϵZ
болғанда y>0 екені дәлелденді.
5. Егер 4b+a=1 болса,
онда  теңсіздігі
орындалатындығын дәлелдеңіз.
теңсіздігі
орындалатындығын дәлелдеңіз.
Дәлелдеуі: 4b+a=1 теңдігінен
a=1-4b теңсіздігіне a-ның
орнына қойып келесі теңсіздікті жазамыз
теңсіздігіне a-ның
орнына қойып келесі теңсіздікті жазамыз
 . Жақшаны ашып
түрлендіріп
. Жақшаны ашып
түрлендіріп 
 пайда болған
теңсіздіктің екі жағында 5-ке көбейтейік
пайда болған
теңсіздіктің екі жағында 5-ке көбейтейік
 , сосын екі жағында
4-ке бөлеміз
, сосын екі жағында
4-ке бөлеміз
 . Пайда болған
үшмүшені екі мүшенің айырмасының квадраты түрінде
жазамыз
. Пайда болған
үшмүшені екі мүшенің айырмасының квадраты түрінде
жазамыз
25

 .
.
6 . х –тің кез келген мәніндерінде (х-1)(х-3)(х-4)(х-6)+10 өрнегінің оң мәндер қабылдайтынын дәлелдеңдер.
Дәлелдеуі:
(х-1)(х-3)(х-4)(х-6)+10  екені дәлелдеу үшін
бірінші және төртінші жақшадағы өрнектерді, екінші және үшінші
жақшадағы өрнектерді мүшелеп көбейтіп , мынадай түріне келтіріп
аламыз
екені дәлелдеу үшін
бірінші және төртінші жақшадағы өрнектерді, екінші және үшінші
жақшадағы өрнектерді мүшелеп көбейтіп , мынадай түріне келтіріп
аламыз
( )(
)( )+10
)+10

 ал
ал

 a(a+6)+10>0
a(a+6)+10>0
 ,
,
 теңсіздігінен
екімүшенің қосындысының квадратын бөліп алуға әрекет
жасаймыз
теңсіздігінен
екімүшенің қосындысының квадратын бөліп алуға әрекет
жасаймыз

 шығады
шығады  ,
сондықтан
,
сондықтан  теңсіздік дәлелденді
дейміз.
теңсіздік дәлелденді
дейміз.
7. Теңсіздікті
дәлелдеңдер  мұндағы
мұндағы 
Дәлелдеуі:  теңсіздігін дәлелдеу
мақсатында сол жағындағы жақшаны ашып , оң жақ
бетіндегі
теңсіздігін дәлелдеу
мақсатында сол жағындағы жақшаны ашып , оң жақ
бетіндегі  -ті сол жағына өткізіп
аламыз
-ті сол жағына өткізіп
аламыз
 . топтастыру арқылы
көбейткіштерге жіктеп аламыз
. топтастыру арқылы
көбейткіштерге жіктеп аламыз


Теңсіздіктің шарты
бойынша  олай
болса
олай
болса  ,
,
 бұдан
бұдан  екі
жағында
екі
жағында
 / (-1) көбейтеміз
сонда
/ (-1) көбейтеміз
сонда  болады.
болады.
Сонымен
 теңсіздігінде
теңсіздігінде  ,
,

Екеуініңде мәні теріс болып тұр , яғни, теріс сандардың көбейтінсі оң сан болады. Теңсіздік дәлелденді.
8.Теңсіздікті
дәлелдеңіз: 
 +
+ 

Дәлелдеуі:
 анықталу облысын табатын
болсақ, х + 1
анықталу облысын табатын
болсақ, х + 1  0
0
 х
х  -1,
яғни
-1,
яғни
х
 1;
1;
f(-1) =
 +
+  =
=

f(х) =
 +
+ 
 анықталу аймағында монотонды
өспелі ( монотонды өспелі функцияның графигі оң және сол жағында
қатаң өспелі, ал ортасында кемімейді) , сондықтан
f (х
)
≥
f
(-1)
=
анықталу аймағында монотонды
өспелі ( монотонды өспелі функцияның графигі оң және сол жағында
қатаң өспелі, ал ортасында кемімейді) , сондықтан
f (х
)
≥
f
(-1)
=
 >1,4.
Дәлелденді.
>1,4.
Дәлелденді.
9. Теңсіздікті шеш:
(х-1)(х2-1)(х3-1)(х4-1)...(х2002-1)≤0
Шешуі: (-∞; −1] және {1}
xn-1=0 теңдеудің екі түбірі бар егер n –жұп сан болса х=-1 х=1
және бір түбірі бар егер n-тақ болса х=1.
10. Теңсіздікті шешіңдер:



 +(
+(

 кез-келген х үшін,
ал
кез-келген х үшін,
ал кез-келген х үшін
8
кез-келген х үшін
8 болғандықтан, ал
дискриминант теріс. Олай болса
болғандықтан, ал
дискриминант теріс. Олай болса  +(
+( , сондықтан шешімі
жоқ.
, сондықтан шешімі
жоқ.
5. ГЕОМЕТРИЯЛЫҚ ТЕҢСІЗДІКТЕР
1. Ауданы S- ке, ал
қабырғалары а, в, с – ға тең үшбұрыш үшін
 теңсіздігі тура
болатынын дәлелдеңдер.
теңсіздігі тура
болатынын дәлелдеңдер.
Дәлелдеуі:


х

в с
в2



 в
в
 с
с
а

 а
а


 авс теңсіздіктің екі жақ
бөлігін де авс –ға көбейтеміз.
авс теңсіздіктің екі жақ
бөлігін де авс –ға көбейтеміз. 



Үшбұрыштың ауданының
формуласына S =  келтіреміз.
келтіреміз.



 2S·2S·2S
2S·2S·2S 

(2S)3

 Дәлелденді.
Дәлелденді.
2. Егер а, в және с
үшбұрыштың қабырғалары болса, онда
 +
+  +
+ 
 болатындығын
дәлелдеңдер.
болатындығын
дәлелдеңдер.
Дәлелдеуі: Үшбұрыштың кез келген екі қабырғасының қосындысы үшінші қабырғасынан үлкен деген қасиетті қолданып, теңсіздіктің сол жақ бөлігін үлкейтейік:
в + с
 а (в+с) қосамыз,
2(в+с)
а (в+с) қосамыз,
2(в+с) а+в+с => в+с
=
а+в+с => в+с
= 
а + с
 в (а + с) қосамыз,
2(а+с)
в (а + с) қосамыз,
2(а+с)  а+в+с => а+с
=
а+в+с => а+с
= 
а + в
 с (а + в) қосамыз,
2(а+в)
с (а + в) қосамыз,
2(а+в)  а+в+с => а+в
=
а+в+с => а+в
= 
Бастапқы берілген теңсіздіктің сол жақ бөлігінің бөліміне апарып қоямыз:
 +
+  +
+


 +
+  +
+

 =
=
 =
2
=
2
Демек, теңсіздіктің сол жағындағы бөлігін үлкейткендегі теңсіздік 2-ге тең болса, онда бұл теңсіздік 2-ден кіші болады. Демек, теңсіздік дәлелденді.
3. Егер а, в және с
үшбұрыштың қабырғалары болса, онда
в2х2 +
(в2 +
с2 -
а2)х +
с2  0,
(х
0,
(х  R) теңсіздігі
орындалатынын дәлелдеңдер.
R) теңсіздігі
орындалатынын дәлелдеңдер.
Дәлелдеуі:
ах2
+ вх + с
 0 квадрат үшмүшеге
келеді. Яғни, бұл теңсіздік о –ден үлкен болу үшін
D
0 квадрат үшмүшеге
келеді. Яғни, бұл теңсіздік о –ден үлкен болу үшін
D  0
екенін дәлелдесек
жеткілікті.
0
екенін дәлелдесек
жеткілікті.
D = в2 – 4ас = (в2 + с2 - а2)2 - 4·в2·с2 = (в2 + с2 - а2 - 2вс) (в2 + с2 - а2+2вс) = ((в - с)2 – а2) · ((в + с)2 – а2) = (в - с – а)(в - с + + а)(в + с – а)(в + с + а)
Үшбұрыштың кез келген екі қабырғасының қосындысы үшінші қабырғасынан үлкен деген қасиетті қолданамыз:
в + с
 а => в + с –
а > 0
а => в + с –
а > 0
а + с
 в
=> а + с - в
> 0, в – а –
с
в
=> а + с - в
> 0, в – а –
с  0
0
а + в
 с => а + в -
с > 0
с => а + в -
с > 0
(в - с – а)(в - с + а)(в + с –
а)(в + с + а)  0 , в - с +
а > 0, в + с –
а > 0, в + с +
а > 0
0 , в - с +
а > 0, в + с –
а > 0, в + с +
а > 0
(-) · (+) · (+) · (+) = ( - ). Демек, D < 0 болады, теңсіздік дәлелденді.
4.Кез келген үшбұрыш үшін
а3 +
в3 +
с3 + +
+  +
+ 
 4p теңсіздігі орындалатынын
дәлелдеңдер. Мұндағы а,в,с – үшбұрыштың қабырғалары, р - жарты
периметр.
4p теңсіздігі орындалатынын
дәлелдеңдер. Мұндағы а,в,с – үшбұрыштың қабырғалары, р - жарты
периметр.
Дәлелдеуі:  жарты
периметр
жарты
периметр
4р =
4· = 2(а + в +
с)
= 2(а + в +
с)
Теңсіздіктің сол жақ бөлігін Коши теңсіздігін қолданып кішірейтеміз:
Коши теңсіздігі: а +
в  2
2
а3
+
 =
2
=
2 = 2
= 2 = 2а
= 2а
в3
+
 =
2
=
2 = 2
= 2 = 2в
= 2в
с3
+
 =
2
=
2 = 2
= 2 = 2с
= 2с
(а3
+
 в3
в3
 )+
(с3
+
)+
(с3
+
 ) = 2а + 2в +
2с =
2(а + в +
с) =
4р
) = 2а + 2в +
2с =
2(а + в +
с) =
4р
Теңсіздіктің сол жақ бөлігін кішірейткенде 4р – ға тең болса, онда теңсіздік 4р – дан міндетті түрде үлкен болады. Дәлелденді.
5.Айталық а, в – тік бұрышты үшбұрыштың катеттері, ал с – гипотенузасы болсын. Қайсысы үлкен: а3 + в3 немесе с3 ?
Дәлелдеуі: а3 + в3 өрнегі мен с3 өрнегін салыстырайық:
Пифагор теоремасын қолданамыз: а2 + в2 = с2
а2 + в2 = с2 өрнегін мүшелеп с – ға көбейтеміз.
а2с + в2с = с3
Тік бұрышты үшбұрыштың гипотенуза катеттерінен үлкен болады, яғни
с > a, c > в
с > a, а2 - мүшелеп көбейтсек c > в, в2 - мүшелеп көбейтсек
са2 > a3, cв2 > в3
Осы екі теңсіздікті мүшелеп қоссақ,
са2 + св2 > а3 + в3
Теңсіздіктің сол жақ бөлігіне а2с + в2с = с3 теңдіктегі с3 – ты апарып қойсақ, с3 > а3 + в3 болады. Теңсіздік дәлелденді.
6.Теңсіздікті дәлелдеңдер:
R + r 
 , мұндағы R – тік бұрышты
үшбұрышқа сырттай сызылған, ал r – оған іштей сызылған шеңбердің
радиустары, S – оның ауданы.
, мұндағы R – тік бұрышты
үшбұрышқа сырттай сызылған, ал r – оған іштей сызылған шеңбердің
радиустары, S – оның ауданы.
Дәлелдеуі: Тік бұрышты үшбұрыштың төмендегі формулаларын қолдану арқылы дәлелдейміз:
с2 = а2 + в2
S
=  ав
ав
R
= 
r
=  мұндағы р – жарты
периметр
мұндағы р – жарты
периметр
Коши
теңсіздігі 

 .
.
R![]()
![]()
![]()
![]() + r
=
+ r
=  +
+
 =
=  +
+
 ав
ав =
=  +
+  ав
ав =
=
 +
+  =
=
 = =
= =  =
=  =
=
 =
= 

 =
=  =
= 
Коши теңсіздігін қолданып,
теңсіздікті кішірейткенде  – ке тең болса, онда R +
r
– ке тең болса, онда R +
r  болады. Демек, теңсіздік
д
болады. Демек, теңсіздік
д
7.Катеттері а және в, ал
гипотенузасы с болатын кез келген тік бұрышты үшбұрыш үшін
с 
 теңсіздігінің орындалатынын
дәлелдеңдер.
теңсіздігінің орындалатынын
дәлелдеңдер.
Дәлелдеуі:
с2 = а2 + в2 екі жағына да 2-ні көбейтеміз:
2с2 = 2 а2 + 2в2 = а2 + в2 + а2 + в2 + 2ав – 2ав = (а2 + 2ав + в2 ) + (а2 - 2ав + в2 ) = (а + в)2 + (а -в)2
2с2 = (а + в)2 + (а - в)2
с2
=  +
+
 ,
, 
 0
0
с2


с


Сонымен, теңсіздік дәлелденді.
8. Егер үшбұрыштың жарты
периметрі р-ға, ал медианалар
ma,
mв,
mс болса,
онда  р
р ma +
mв +
mс
ma +
mв +
mс  2р арақатысының
орындалатынын дәлелдеңдер.
2р арақатысының
орындалатынын дәлелдеңдер.
Д
mв
әлелдеуі:1) ma + mв + mс
 р
екенін дәлелдейік:
р
екенін дәлелдейік: 

в с
а
Қарсы жоритын
болсақ, ma
+
mв
+
mс

 р
=
р
=  (
( )
=
)
=  (а+в+с) =
(а+в+с) =  =
=

 =
=

Медиана түскен қабырғасын тең
екіге бөлетіндіктен  деп жазып аламыз.
mв
– в қабырғасына түсірілген
медиана. Үшбұрыштың кез келген екі қабырғасының қосындысы үшінші
қабырғасынан үлкен деген қасиетті қолдансақ,
деп жазып аламыз.
mв
– в қабырғасына түсірілген
медиана. Үшбұрыштың кез келген екі қабырғасының қосындысы үшінші
қабырғасынан үлкен деген қасиетті қолдансақ,
 +
с
+
с  mв,
mв,
 +
в
+
в  mс,
mс,
 +
в
+
в  mа
теңсіздігі
шығады.
mа
теңсіздігі
шығады.  =
=
 mа
+
mа
+
 mв
+
mв
+
 mс
mс
 mа
+
mа
+
 mв
+
mв
+
 mс
mс
 ma
+
mв
+
mс. Үшбұрыштың медианаларының
қосындысы жарты медианаларының қосындысынан кіші болып қалды. Олай
болуы мүмкін емес, қарама-қайшылық пайда болды. Бізде
медианаларының қосындысы кіші емес үлкен болуы керек. Демек,
теңсіздік дәлелденді.
ma
+
mв
+
mс. Үшбұрыштың медианаларының
қосындысы жарты медианаларының қосындысынан кіші болып қалды. Олай
болуы мүмкін емес, қарама-қайшылық пайда болды. Бізде
медианаларының қосындысы кіші емес үлкен болуы керек. Демек,
теңсіздік дәлелденді.
2)
ma +
mв +
mс  2р екенін
дәлелдейік:
2р екенін
дәлелдейік:



ma
В в Е
ma
![]() с
с
![]()
А в С
Дәлелдеу үшін үшбұрышты паралелограмға дейін толықтырайық.
в + с
 2mа
mа
2mа
mа


а + с
 2mв
mв
2mв
mв


а + в
 2mс
mс
2mс
mс


Теңсіздіктің екі жағын мүшелеп қосатын болсақ
ma
+
mв
+
mс

 = а + в + с
= 2р
= а + в + с
= 2р
Демек,
ma
+
mв
+
mс
 2р. Сонымен
теңсіздік дәлелденді.
2р. Сонымен
теңсіздік дәлелденді.
6. ПАРАМЕТРМЕН БЕРІЛГЕН ТЕҢСІЗДІКТЕР, ЛОГАРИФМДІК ТЕҢСІЗДІКТЕР
1.а параметрінің қандай
мәнінде  теңсіздігінің шешімі
болмайды.
теңсіздігінің шешімі
болмайды.
Шешуі:  2+
2+ теңсіздігі үшін анықталу
олысын жазып алайық
теңсіздігі үшін анықталу
олысын жазып алайық
 →
→ 
Логарифмдік функция
қасиеттерін пайдаланып келесі теңсіздікке
келеміз 
одан

5x≤5a+30 , x≤a+6 енді мына теңсіздіктер жүйесін шешеміз
 →
→ 
→

→ → a< 2 шешімі болады Яғни,
шешімі (-ꚙ; 2) аралығына тиесілі, сонда
шешімі жатпайтын аралық [2;ꚙ)
болады.
→ a< 2 шешімі болады Яғни,
шешімі (-ꚙ; 2) аралығына тиесілі, сонда
шешімі жатпайтын аралық [2;ꚙ)
болады.
2. а параметрінің барлық
мәні үшін 
 а
а
 теңсіздігін
шешіңіз.
теңсіздігін
шешіңіз.
Дәлелдеуі:
8-х2
 0
0
х2

х
 ±
2
±
2 Яғни, анықталу облысы
х
Яғни, анықталу облысы
х 
 (а
(а  )2
)2
8 -
х2 а2(х -
4)2
а2(х -
4)2
8 -
х2 а2(
х2
- 8х +
16)
а2(
х2
- 8х +
16)
8 -
х2
-
а2х2
+
8а2х -
16а2 0 -1
бөлсек
0 -1
бөлсек
-8 +
х2
+
а2х2
-
8а2х +
16а2 0
0
(1+а2)х2
–
8а2х +
(16а2
- 8)
 0
0
D![]() = 64а4
–
4(1+а2)
(16а2
- 8)
= 64а4
–
4(16а2
-8 +
16а4
–
8а2)
= 64а4
–
64а2
+ 32 –
64а4
+
32а2
=
= 64а4
–
4(1+а2)
(16а2
- 8)
= 64а4
–
4(16а2
-8 +
16а4
–
8а2)
= 64а4
–
64а2
+ 32 –
64а4
+
32а2
=
-64а2 + 32а2 + 32 = 32 - 32а2
-
D < 0 болса, а2 + 1 > 0 (міндетті түрде 0-ден үлкен болады. Себебі, а – ның орнына қандай санды қойсақ та оң сан шығады) болса параболаның тармағы жоғары қарайды да х
 (-
(- ).
).
32 - 32а2 < 0
1 - а2 < 0
а2 – 1 > 0
a1 > 1, a2 < -1
a
 (
-
(
- ;-1)
;-1) (1;
+
(1;
+ )
)
a >1,
x 

-
D

 =
0
=
0
![]() 32
- 32а2
= 0
+
2 +
32
- 32а2
= 0
+
2 +
a =
 , a =
1
, a =
1
x =
 =
=  =
2
=
2
 > 0
x
> 0
x 

-
D > 0, 32 – 32а2 > 0
а


 a
a


х1/2
= =
=  =
= 
а-ның
орнына a

 аралықтағы сандарды
апарып қойып, тексереміз.
аралықтағы сандарды
апарып қойып, тексереміз.
а
= 0 десек,
 =
= 


а
= 1
десек,
 = 2
= 2



Сонымен,
1) a < 0 болған кезде шешімі жоқ.
2)
a
>1,
x


3) а = 1,
x


4)
a

 ,
x
,
x


3. а параметрінің қандай мәнінде теңсіздіктің жалғыз түбірі болады?
 – (2а +
3)
– (2а +
3)  +
6
+
6  0
0
Шешуі:  = t
деп
белгілесек:
= t
деп
белгілесек:
аt2
– (2а +
3)t
+ 6
 0
0
-
а = 0, -3t + 6
 0
0
-3t
 -6
-6
t
 2
2

 2 , анықталу облысы
х > 0.
2 , анықталу облысы
х > 0.
x
 42
x
42
x
 16
16
Есептің шартында жалғыз түбірі
болатынын табу керек. x  16 аралығында шексіз
көп.
16 аралығында шексіз
көп.
Сондықтан, келесі жағдайды қарастырайық:
-
D = (2а + 3)2 - 4a·6 = 4a2 + 12a + 9 – 24a = 4a2 – 12a + 9 = ( 2a – 3)2
Бізде D = 0 болса, жалғыз түбірі болады.
( 2a – 3)2 = 0
2а – 3 = 0
2а = 3
а = 1,5
t
=  =
=  = 2
= 2
 = 2
= 2
x = 42 = 16
Жауабы: а = 1,5 болғанда х = 16.
4.а параметріне байланысты теңсіздікті шешіңіз:
![]()
Шешуі :
![]()
х –
а2
х2
–
а3х + 2ах +
2а2
 0
0
х=а теңсіздіктің а-ға байланысты шешімі :
ах2+(а2-2)х-2а=(х+а)(ах-2)
![]()
шешу үшін мына жағдайларды қарастырамыз:
a) а> 2 ; шешімі {а }
b) 0<а≤ 2 ;
шешімі 
c) а=0; шешімі [0;∞)
d) - 2 ≤а<0 ; шешімі {а }
е) а<-
2 ;
шешімі  )
)
7. ТЕҢСІЗДІКТЕРДІ ДӘЛЕЛДЕУДЕ ВЕКТОРЛЫҚ ӘДІСТІҢ ҚОЛДАНЫСЫ
 ,
, 
 ,
ǀ
,
ǀ ǀ=
ǀ= ,
ǀ
,
ǀ ǀ=
ǀ=
 ǀ
ǀ ǀ
ǀ
Екі вектордың скаляр көбейтіндісі олардың ұзындықтарының көбейтіндісінен кіші немесе тең болады.
1.Теңсіздікті дәлелдеңіз
:  +
+
Дәлелдеуі: 



Векторлық әдіс қолданып келесі теңсіздіктерді шешейік
 ǀ
ǀ ǀ=
ǀ=

 ǀ=
ǀ= =
= =
=
 ǀ
ǀ ǀ
ǀ
 +
+
 +
+ екі жағында квадраттап
келесі теңсіздікті жазамыз
екі жағында квадраттап
келесі теңсіздікті жазамыз 
 , мүшелеп екі жағында 3х-ке
қысқартамыз
, мүшелеп екі жағында 3х-ке
қысқартамыз
 ,
,  ал
ал



олай
болса  демек
демек  +
+ теңсіздігі
дәлелденді.
теңсіздігі
дәлелденді.
2. Теңсіздікті дәлелдеңіз:
х+у+z=1 x²+y²+z²≥
Дәлелдеуі: Векторлық әдіс қолданып
дәлелдейік, олай болса х+у+z=1
 және
және  векторларының скаляр
көбейтіндісі деп қабылдап .
векторларының скаляр
көбейтіндісі деп қабылдап .
 =
=  болады
деп
болады
деп
және
 (x;y;z) , ал
ұзындығы
(x;y;z) , ал
ұзындығы 
 ·
· ≤ǀ
≤ǀ ǀ·ǀ
ǀ·ǀ ǀ теңсіздігін
қолданып
ǀ теңсіздігін
қолданып  ·
· х+у+z
ал ǀ
х+у+z
ал ǀ ǀ·ǀ
ǀ·ǀ ǀ=
ǀ=
Яғни,
х+у+z
≤ немесе 1
≤
немесе 1
≤
Екі жағын
квадраттап 1 ≤
 , x²+y²+z²≥
, x²+y²+z²≥ екеніне көз
жеткіземіз.
екеніне көз
жеткіземіз.
3. Егер
a+b+c=1 
 теңсіздігі орындалатынын
дәлелдеңіз:
теңсіздігі орындалатынын
дәлелдеңіз:
Дәлелдеуі:  теңсіздігінің сол
жағындағы өрнекті
теңсіздігінің сол
жағындағы өрнекті  және
және  векторларының скаляр
көбейтіндісі деп ,ал оң жағындағы өрнекті осы векторлардың
ұзындықтарының көбейтіндісі деп қарастырамыз
.
векторларының скаляр
көбейтіндісі деп ,ал оң жағындағы өрнекті осы векторлардың
ұзындықтарының көбейтіндісі деп қарастырамыз
.
 =
= 
 (
( )
,
)
,
 =
=
 ·
· =
= ,
ал
,
ал  ǀ·ǀ
ǀ·ǀ ǀ=
ǀ=

 =
=
 ·
· ≤ǀ
≤ǀ ǀ·ǀ
ǀ·ǀ ǀ екені белгілі ,
сондықтан
ǀ екені белгілі ,
сондықтан  теісіздігі
орындалады.
теісіздігі
орындалады.
4.
 теңсіздігі
орындалатынын дәлелдеңіз, мұндағы a>0, b>0, c>0 белгілі
болса
теңсіздігі
орындалатынын дәлелдеңіз, мұндағы a>0, b>0, c>0 белгілі
болса
Дәлелдеуі:  теңсіздігін дәлелдеу
үшін векторлық әдіс қолданамыз, яғни , теңсіздіктің сол жақ
бөлігіндегі өрнектен
теңсіздігін дәлелдеу
үшін векторлық әдіс қолданамыз, яғни , теңсіздіктің сол жақ
бөлігіндегі өрнектен  және
және  векторларының
координатоларын бөліп аламыз
векторларының
координатоларын бөліп аламыз

 =(
=(

 =(
=(

 және
және  векторларының
ұзындықтары тең екенін байқаймыз
векторларының
ұзындықтары тең екенін байқаймыз
 =ǀ
=ǀ =
=
 олай болса олардың
ұзындықтарының көбейтіндісі ǀ
олай болса олардың
ұзындықтарының көбейтіндісі ǀ ·ǀ
·ǀ =
= =
=
 ·
· ≤ǀ
≤ǀ ǀ·ǀ
ǀ·ǀ ǀ екі вектордың скаляр
көбейтіндісі олардың ұзындықтарының көбейтіндісінен кіші немесе тең
болғандықтан
ǀ екі вектордың скаляр
көбейтіндісі олардың ұзындықтарының көбейтіндісінен кіші немесе тең
болғандықтан
 теңсіздігі
орындалады. Демек, дәлелденді.
теңсіздігі
орындалады. Демек, дәлелденді.
8. МАТЕМАТИКАЛЫҚ ИНДУКЦИЯ
1. Егер a және b - катет,
ал с- тікбұрышты үшбұрыштың гипотенузасы болса, онда барлық n≥2
натурал сандар үшін  +
+ ≤
≤ теңсіздігі
орындалатындығын дәлелдеңдер.
теңсіздігі
орындалатындығын дәлелдеңдер.
Дәлелдеуі: Математематикалық индукция әдісін қолданып
n=2 үшін
орындалатын  +
+ =
= дұрыс деп
қабылдаймыз,
дұрыс деп
қабылдаймыз,
келесі
n=k  +
+ ≤
≤ дұрыс деп
ұйғарамыз
дұрыс деп
ұйғарамыз
олай болса n=k+1
үшін  +
+ ≤
≤ теңсіздігін
қарастырамыз,
теңсіздігін
қарастырамыз,
дәреже қасиеттерін пайдаланып
мына түріне келтіріп аламыз  +
+ ≤
≤ c. Тік бұрышты үшбұрышта
катеттері a<c, b<c болғандықтан мына түріне келтіріп
жазамыз
c. Тік бұрышты үшбұрышта
катеттері a<c, b<c болғандықтан мына түріне келтіріп
жазамыз  +
+ ≤
≤ , ортақ көбейткішін
жақша сыртына шығарып, екі жағында с-ға қысқартып
c(
, ортақ көбейткішін
жақша сыртына шығарып, екі жағында с-ға қысқартып
c( +
+ ≤
≤ , мына түріне
келтіреміз
, мына түріне
келтіреміз  +
+ ≤
≤ , осымен теңсіздік
дәлелденді.
, осымен теңсіздік
дәлелденді.
2. a ≥-1 Болғанда кез келген натурал сан а үшін мына теңсіздіктің (1+a)≥1+na орындалатындығын дәлелдеңдер.
Дәлелдеуі: математикалық индукция әдісін қолданып n=2 деп алып келесі теңсіздікті (1+a)²≥1+na, 1+2a+a²≥1+na дұрыс деп аламыз
n=k болғанда мына
теңсіздікті  дұрыс деп
үйғарамыз,
дұрыс деп
үйғарамыз,
енді n=k+1 болғанда келесі
теңсіздіктерге келеміз 

3.
Натурал сан n-нің кез
келген n мәндерінде
мәндерінде  теңсіздігі
орындалатынын дәлелдеңдер.
теңсіздігі
орындалатынын дәлелдеңдер.
Дәлелдеуі: n=3 дейік, олай болса 2³>7, яғни 8>7
n=k болса
 деп
үйғарамыз
деп
үйғарамыз
n=k+1
болғанда  жақшасын ашып келесі
теңсіздікті жазамыз
жақшасын ашып келесі
теңсіздікті жазамыз  теңсіздіктің екі жағында
түрлендіріп
теңсіздіктің екі жағында
түрлендіріп  келесі теңсіздіктер
жүйесін қарастырамыз
келесі теңсіздіктер
жүйесін қарастырамыз

 .
.
 яғни,
n
яғни,
n мәндерінде
мәндерінде  теңсіздігі орындалатыны
дәлелденді.
теңсіздігі орындалатыны
дәлелденді.
4.
Теріс емес a,b,c,d сандары
үшін келесі  теңсіздік
орындалатынын дәлелдеңіз
теңсіздік
орындалатынын дәлелдеңіз
Дәлелдеуі:
 ≥
≥ сандардың арифметикалық
ортасы олардың геометриялық ортасынан үлкен
болады
сандардың арифметикалық
ортасы олардың геометриялық ортасынан үлкен
болады
Екі санның арифметикалық
ортасы ≥
≥ ,
,
үш санның арифметикалық
ортасы  , олай
болса
, олай
болса
төрт санның арифметикалық
ортасы  . Теңсіздік
дәлелденді
. Теңсіздік
дәлелденді
5. Кез келген натурал n сан үшін (1+(1:2))(1+(1:5))…(1+(2:(n²+3n))) < 3 теңсіздігі орындалатынын дәлелдеңіз.
Дәлелдеуі: математикалық индукция әдісін қолданып
n=1 (1+(1:2))(1+(1:5))…(1+(2:(1²+3·1))) < 3
n=k (1+(1:2))(1+(1:5))…(1+(2:(k²+3k))) < 3 деп үйғарамыз
n=k+1 (1+(1:2))(1+(1:5))… (1+(2:(k²+3k) (1+(2:((k+1)²+3(k+1))) < 3
(1+ )
(1+
)
(1+ )
...(1+
)
...(1+ )
(1+
)
(1+ ) <
3·1+
) <
3·1+ )
)
(1+ )
(1+
)
(1+ )
...(
)
...( )
(
)
( ) <
3·
) <
3· )
)


 ,
, 
 салыстырамыз, ол ұшін ортақ
бөлімге келтіреміз , сонда
салыстырамыз, ол ұшін ортақ
бөлімге келтіреміз , сонда

 , яғни теңсіздік
дәлелденді.
, яғни теңсіздік
дәлелденді.
6. Кез келген x,y,z сандары
үшін бір мезетте  теңсіздіктері
орындалмайтынын дәлелдеңіз.
теңсіздіктері
орындалмайтынын дәлелдеңіз.
Дәлелдеуі:  теңсіздңктерң орындалады
делік, олай болса осы теңсіздіктердің екі жағында квадраттап, оң
жағындағыларды сол жағына өткізіп жіберіп, көбейткіштерге жіктеп,
пайда болған теңсіздіктерді мүшелеп көбейтіп
көрейік
теңсіздңктерң орындалады
делік, олай болса осы теңсіздіктердің екі жағында квадраттап, оң
жағындағыларды сол жағына өткізіп жіберіп, көбейткіштерге жіктеп,
пайда болған теңсіздіктерді мүшелеп көбейтіп
көрейік
 ,
,  ,
,
(х-у+z)(x+y-z)<0

 ,
,
(y-z+x)(y+z-x)<0

 <
0,
<
0,
(z-x+y)(z+x-y)<0
Соңғы теңсіздіктерді мүшелеп көбейткенде келесі теңсіздік пайда болады
((х-у+z)(x+y-z) (z-x+y
))²<0 яғни, қарамақайшылық
пайда болғанына көз жеткіземіз. Кез келген x,y,z сандары үшін
бір мезетте  теңсіздіктері
орындалмайтыны дәлелденді.
теңсіздіктері
орындалмайтыны дәлелденді.
7. Теңсіздікті дәлелдеңіз:
18( )>
)>
Дәлелдеуі: 18( )>
)> теңсіздігін дәлелдеу
үшін
теңсіздігін дәлелдеу
үшін
(x-y)²≥0 теңсіздігін қолданамыз
x²-2xy+y²≥0
x²+y²≥2xy бұл теңсіздіктің екі жағынада x²+y² қосамыз, сонда
2(x²+y²)≥(х+у)²
x=3a² y=3b² келесі теңсіздікті жазамыз
2(9 +9
+9 )≥(3a²+3b²)²
)≥(3a²+3b²)²
18( +
+ )≥(3a²+3b²)²
)≥(3a²+3b²)²
18( +
+ )≥9(a²+b²)² ,
теңсідіктің оң жағына a²+b²≥2ab деп әрекетті қайталап екі жағынада
a²+b² қосқанда 2(a²+b²)≥(a+b)² шығады.
Яғни,
)≥9(a²+b²)² ,
теңсідіктің оң жағына a²+b²≥2ab деп әрекетті қайталап екі жағынада
a²+b² қосқанда 2(a²+b²)≥(a+b)² шығады.
Яғни,
18( +
+ )≥18(a²+b²)²≥((a+b)²)²
≥
)≥18(a²+b²)²≥((a+b)²)²
≥
Олай болса
18( )>
)> теңсіздігі дәлелденді
десек болады.
теңсіздігі дәлелденді
десек болады.
8. a+b≥1 белгілі болса,
онда  ≥
≥ теңсіздігі
орындалатынын дәлелдеңіз.
теңсіздігі
орындалатынын дәлелдеңіз.
Дәлелдеуі:  ≥
≥ теңсіздігін дәлелдеу
үшін
теңсіздігін дәлелдеу
үшін  ≥
≥ теңсіздігін дәлелдесек
жеткілікті. Ол үшін (x-y)²≥0 теңсіздігін қолданамыз, жақшаны ашамыз
x²-2xy+y²≥0
теңсіздігін дәлелдесек
жеткілікті. Ол үшін (x-y)²≥0 теңсіздігін қолданамыз, жақшаны ашамыз
x²-2xy+y²≥0
x²+y²≥2xy бұл теңсіздіктің екі жағынада x²+y² қосамыз, сонда
2(x²+y²)≥(х+у)²
x=2a² y=2b² алмастыру еңгізіп, келесі теңсіздікті жазамыз
2(4 +4
+4 )≥(2a²+2b²)²
)≥(2a²+2b²)²
8( +
+ )≥(2a²+2b²)²
)≥(2a²+2b²)²
8( +
+ )≥4(a²+b²)² ,
теңсідіктің оң жағына a²+b²≥2ab деп әрекетті қайталап екі жағынада
a²+b² қосқанда 2(a²+b²)≥(a+b)² шығады.
Яғни,
)≥4(a²+b²)² ,
теңсідіктің оң жағына a²+b²≥2ab деп әрекетті қайталап екі жағынада
a²+b² қосқанда 2(a²+b²)≥(a+b)² шығады.
Яғни,
8( +
+ )≥4(2(a²+b²)²)≥8((a+b)²)² ≥
)≥4(2(a²+b²)²)≥8((a+b)²)² ≥ ≥1
≥1
 +
+ )≥
)≥ теңсіздік
дәлелденді.
теңсіздік
дәлелденді.
9. ТАПСЫРМАЛАР
-
Катеттері ? және в, ал гипотенузасы ? болатын тікбұрышты үшбұрыш үшін ?в+??+в?
 2с2
теңсіздігі орындалатынын
дәлелдеңіздер.
2с2
теңсіздігі орындалатынын
дәлелдеңіздер.
Нұсқау: Сол жағына Коши теңсіздігін , ары қарай пифагор теоремасын қолданыңыз.
-
Егер ?,в,? – үшбұрыштың қабырғалары болса, онда ?2+в2+?2 <2(?в+в?+??)
теңсіздігі орындалатынын дәлелдеңіздер.
Нұсқау: Үшбұрыштың екі қабырғасының ұзындығының айырмасы үшінші қабырғасынан кіші деген қасиетін қолданып, ары қарай квадраттаңыз.
-
Жарты периметрі ?−ға тең кез келген үшбұрыштың ауданы ?
 теңсіздігі
орындалатынын дәлелдеңіз.
теңсіздігі
орындалатынын дәлелдеңіз.
Нұсқау: Герон формуласын, сосын Коши теңсіздігін қолданыңыз.
-
Теңсіздікті дәлелдеңіз: ?2 + в2 + ?2 + 2?в?
 2,
мұндағы ?,
в,
?
− периметрі 2−ге тең болатын
үшбұрыштың қабырғалары.
2,
мұндағы ?,
в,
?
− периметрі 2−ге тең болатын
үшбұрыштың қабырғалары.
Нұсқау: ?
+
в
+
?
= 2,
?<1,
?<1,
? . Яғни
(1-а)(1-в)(1-с)
. Яғни
(1-а)(1-в)(1-с) 
 . Ары қарай жақшаларды ашып,
түрлендіріңіз.
. Ары қарай жақшаларды ашып,
түрлендіріңіз.
-
Егер ?, в, ? – үшбұрыштың қабырғалары болса, онда
(? + в − ?)(? + ? − в)(? + в − ?) ≤ ?в? теңсіздігі орындалатынын дәлелдеңіздер.
Нұсқау: ? + в – ? = ?, ? + ? – в = ?, ? + в – ? = ? деп белгілеп алып, ?, в, ?
сандарын ?, ?, ? арқылы өрнектеңіз. Сосын, теңсіздікті қолданыңыз.
-
Кез келген тікбұрышты үшбұрышта 0,4


 0,5
болатынын дәлелдеңіз,
мұндағы r − іштей сызылған шеңбердің
радиусы, ал ℎ − гипотенузаға түсірілген
биіктік.
0,5
болатынын дәлелдеңіз,
мұндағы r − іштей сызылған шеңбердің
радиусы, ал ℎ − гипотенузаға түсірілген
биіктік.
Нұсқау:  hc=pr,
hc=pr,
 =
=  формулаларын
қолданыңыз.
формулаларын
қолданыңыз.
-
Егер ?, в, ? – үшбұрыштың қабырғалары болса, онда 2
 ≤
?
орындалатынын дәлелдеңіз,
мұндағы ?
− жарты
периметр.
≤
?
орындалатынын дәлелдеңіз,
мұндағы ?
− жарты
периметр.
Нұсқау: Коши теңсіздігін дұрыс қолдансаңыз, жеткілікті.
-
Егер ?, в, ? – үшбұрыштың қабырғалары болса, онда
 +
+  +
+
 ≤
≤  орындалатынын
дәлелдеңіз, мұндағы ?
− жарты
периметр.
орындалатынын
дәлелдеңіз, мұндағы ?
− жарты
периметр.
Нұсқау: теңсіздіктің екі жағын квадраттап, Коши теңсіздігін қолданыңыз.
-
Катеттері ? және ?, ал гипотенузасы ? болатын тікбұрышты үшбұрыш үшін
 +
+
 >
>  теңсіздігі орындалатынын
дәлелдеңіздер.
теңсіздігі орындалатынын
дәлелдеңіздер.
Нұсқау: үшбұрыш теңсіздігін қолданыңыз.
-
Қабырғалары ?, в, ?, ? болатын дөңес төртбұрыштың ауданы ? болса, онда ? ≤
 теңсіздігінің
орындалатынын дәлелдеңіз.
теңсіздігінің
орындалатынын дәлелдеңіз.
Нұсқау: дөңес төртбұрышты үшбұрыштардың қосындысы түрінде жазып алып, ол үшбұрыштардың ауданын бағалаңыз.
-
Кез келген натурал n саны үшін 1 +
 теңсіздігі орындалатынын
дәлелдеңіздер.
теңсіздігі орындалатынын
дәлелдеңіздер. -
Теңсіздікті дәлелдеңіздер:


 .
.
-
 болатынын
дәлелдеңдер.
болатынын
дәлелдеңдер.
-
Теңсіздікті дәлелдеңіздер:
1 +
 (
n
(
n  N,
n
N,
n
 2) .
2) .
-
Егер а, в, с - натурал сандар болса, онда ав + вс + са
 3авс болатынын
дәлелдеңіздер.
3авс болатынын
дәлелдеңіздер.
Нұсқау: а, в, с – натурал сан, демек ав саны авс санынан кіші.
-
Теңсіздікті дәлелдеңдер: а2 + в2
 с2
+ ( а + в –
с)2, мұндағы
а > с, с
> в.
с2
+ ( а + в –
с)2, мұндағы
а > с, с
> в. -
Теңсіздікті дәлелдеңдер:


 , мұндағы а, в >
0.
, мұндағы а, в >
0. -
Теңсіздікті дәлелдеңдер:


 , мұндағы а, в >
0.
, мұндағы а, в >
0. -
Теңсіздікті дәлелдеңдер:


 , мұндағы а, в >
0.
, мұндағы а, в >
0. -
а, в > 0 болғанда,
 теңсіздігі орындалатынын
дәлелдеңдер.
теңсіздігі орындалатынын
дәлелдеңдер. -
Теңсіздікті дәлелдеңдер: (х + 1)·(х – 2у + 1) + у2
 0
0 -
х – тің кез келген мәнінде х12 - х9 + х4 – х + 1 > 0 екенін дәлелдеңдер.
-
Теңсіздікті дәлелдеңдер: а + в
 1 + ав, мұндағы
а >1, в
< 1.
1 + ав, мұндағы
а >1, в
< 1. -
Егер а + в = 1 болса, онда а2 + в2
 болатынын
дәлелдеңдер.
болатынын
дәлелдеңдер. -
Егер а + в + с = 1, мұндағы а, в, с > 0 болса, онда (1 – а)(1 – в)(1 – с)
 8авс теңсіздігі
орындалатынын дәлелдеңдер.
8авс теңсіздігі
орындалатынын дәлелдеңдер.
Нұсқау: 1 – а = в + с, ары қарай Коши теңсіздігін қолданыңыз.
-
Айталық а, в, с – теріс емес сандар және а + в + с = 1 болсын. Теңсіздіктің дұрыстығын дәлелдеңдер: (1 + а)(1 + в)(1 + с)
 8(1 – а)(1 – в)(1 –
с)
8(1 – а)(1 – в)(1 –
с)
Нұсқау: 1 + а = 2 – в – с = (1 – в) + (1 – с) ары қарай Коши теңсіздігі.
-
Егер авсd = 1 және а > 0, в > 0, c > 0, d >0 болса, онда а2 + в2 + с2 + d2 + ав + ас + аd + вс + вd + сd
 10 теңсіздігі
орындалатынын дәлелдеңдер.
10 теңсіздігі
орындалатынын дәлелдеңдер.
Нұсқау:  ,
ав + вс
,
ав + вс
 осылай Коши
теңсіздігін қолданыңыз.
осылай Коши
теңсіздігін қолданыңыз.
-
х, у сандары үшін ху = 1 және х > у болса, мына теңсіздіктің
 орындалатынын
дәлелдеңдер.
орындалатынын
дәлелдеңдер.
Нұсқау: сол жағындағы өрнектің алымын х – у квадратына келтіріңіз.
-
Егер а, в, с – көбейтіндісі 1-ге тең нақты сандар болса, онда а + в + с + ав + ас + вс
 6 теңсіздігінің
орындалатынын дәлелдеңдер.
6 теңсіздігінің
орындалатынын дәлелдеңдер.
Нұсқау: авс = 1 болғандықтан ав
=  ...
...
-
Егер а2 + в2 + с2 = 1 болса, онда
 +
+
 +
+  < 4 теңсіздігінің орындалатынын
дәлелдеңдер.
< 4 теңсіздігінің орындалатынын
дәлелдеңдер.
Нұсқау:  осылай Коши теңсіздігін
қолданыңыз.
осылай Коши теңсіздігін
қолданыңыз.
Шешімдері
1.Катеттері ?
және ?, ал
гипотенузасы ?
болатын тікбұрышты үшбұрыш
үшін ??+??+??
 2с2 теңсіздігі орындалатынын
дәлелдеңіздер.
2с2 теңсіздігі орындалатынын
дәлелдеңіздер.
Дәлелдеуі: Сол жағына Коши теңсіздігін қолданып, сосын Пифагор теоремасын қолданамыз:




 ав;
ав;

ав + ас +
вс 
 +
+
 +
+
 =
=
 =
= =
=
 =
2
=
2
Сонымен, теңсіздік дәлелденді.
2.Егер ?,в,? – үшбұрыштың қабырғалары болса, онда ?2+в2+?2 < 2(?в+в?+??) теңсіздігі орындалатынын дәлелдеңіздер.
Дәлелдеуі: Үшбұрыштың екі қабырғасының
ұзындығының айырмасы үшінші қабырғасынан кіші деген қасиетін
қолданып, ары қарай квадраттаймыз: 


2а2
+
2в2
+
2с2
-2(ав + ас +
вс)  ?2+в2+?2
?2+в2+?2
?2+в2+?2
 2(ав + ас +
вс)
2(ав + ас +
вс)
Сонымен, теңсіздік дәлелденді.
3.Жарты
периметрі ?−ға тең кез келген
үшбұрыштың ауданы ?
 теңсіздігі
орындалатынын дәлелдеңіз.
теңсіздігі
орындалатынын дәлелдеңіз.
Дәлелдеуі: Герон
формуласы: S
=  , р
=
, р
= 
 а+в+с
= 2р
а+в+с
= 2р
р(р-а) = а,
(р-в)(р-с) = в деп алып, Коши
теңсіздігін 
 қолданамыз.
қолданамыз. 



 =
=
 =
=  =
=
 =
= 

Сонымен, теңсіздік дәлелденді.
4.Теңсіздікті дәлелдеңіз:
?2 +
в2 +
?2 +
2?в?  2,
мұндағы ?,
в,
?
− периметрі 2−ге тең
болатын үшбұрыштың қабырғалары.
2,
мұндағы ?,
в,
?
− периметрі 2−ге тең
болатын үшбұрыштың қабырғалары.
Дәлелдеуі: ?
+
в
+
?
= 2,
?<1,
?<1,
? . Яғни, (1 - а)(1 - в)(1 -
с)
. Яғни, (1 - а)(1 - в)(1 -
с)  .
Сосын, жақшаларды ашып,
түрлендіріп, (а+в+с)2
=
.
Сосын, жақшаларды ашып,
түрлендіріп, (а+в+с)2
=
 қолданамыз:
қолданамыз:
(1 - а)(1 - в)(1 -
с) = (1 – в – а + ав)(1 –
с) = 1 – с – в + вс – а + ас + ав –
авс = 1 – (а + в + с) + ав + вс + ас
– авс = 1 – 2 +
 -
-  +
+
 + вс + ас –
авс =
-1 +
+ вс + ас –
авс =
-1 +  -
-
 –
авс = -1 +
–
авс = -1 +
 -
-  –
авс = 1 -
–
авс = 1 -
 -
авс
-
авс
1 -
 –
авс
–
авс  0
0
2 -
 –
2авс
–
2авс  0 /
(-1)
0 /
(-1)  +
2авс
+
2авс  2
2
Сонымен, теңсіздік дәлелденді.
5.Егер ?, в, ? – үшбұрыштың қабырғалары болса, онда
(? + в − ?)(? + ? − в)(? + в − ?) ≤ ?в? теңсіздігі орындалатынын дәлелдеңіздер.
Дәлелдеуі: ? + в – ? = ?, ? + ? – в = ?, ? + в – ? = ? деп белгілеп алып, ?, в, ?
сандарын ?, ?, ? арқылы өрнектеп, теңсіздікті қолданамыз:
? + в – ? = ?  а + в = m +
с
а + в = m +
с
 теңдіктің екі жағын
мүшелеп қосамыз
теңдіктің екі жағын
мүшелеп қосамыз
а + в – с + с + а – в + с + в – а = m + n + p
а + в + с = m + n + p
m + c + c = m + n + p
2c = n + p
c =
 ; в =
; в =
 ; a =
; a =

n + p = 2c; m + n = 2в; m + p = 2а
 теңсіздіктің екі
жағын мүшелеп көбейтеміз
теңсіздіктің екі
жағын мүшелеп көбейтеміз



mnp

 =
=

mnp
 авс
авс
(? + в − ?)(? + ? − в)(? + в − ?) ≤ ?в?
Демек, теңсіздік дәлелденді.
-
Кез келген тікбұрышты үшбұрышта 0,4


 0,5 болатынын дәлелдеңіз,
мұндағы r − іштей сызылған шеңбердің
радиусы, ал ℎ − гипотенузаға түсірілген
биіктік.
0,5 болатынын дәлелдеңіз,
мұндағы r − іштей сызылған шеңбердің
радиусы, ал ℎ − гипотенузаға түсірілген
биіктік.
Дәлелдеуі:  hc=pr
,
hc=pr
,
 =
=  формулаларын
қолданамыз:
формулаларын
қолданамыз:
 hc =
hc =


а + в
> с




 0,5
0,5







 /
/  көбейтеміз
көбейтеміз
c
> 
а + в
<  с
с
 >
>  =
= 
 > 0,4
> 0,4
Сонымен, теңсіздік дәлелденді.
7.
Егер ?,
в,
?
– үшбұрыштың қабырғалары
болса, онда 2 ≤ ?
орындалатынын дәлелдеңіз,
мұндағы ?
− жарты
периметр.
≤ ?
орындалатынын дәлелдеңіз,
мұндағы ?
− жарты
периметр.
Дәлелдеуі: Коши теңсіздігін
қолданамыз: а + в
 2
2
Жарты периметріміз
: р
= 
2
 р – с + р – в = 2р – с – в = а + в + с – с
– в = а
р – с + р – в = 2р – с – в = а + в + с – с
– в = а
2
 а. Теңсіздік
дәлелденді.
а. Теңсіздік
дәлелденді.
8.Егер ?, в, ? – үшбұрыштың қабырғалары болса, онда
 +
+  +
+  ≤
≤  орындалатынын
дәлелдеңіз, мұндағы ?
− жарты
периметр.
орындалатынын
дәлелдеңіз, мұндағы ?
− жарты
периметр.
Дәлелдеуі: теңсіздіктің екі жағын квадраттап, Коши теңсіздігін қолданамыз:
 +
+  +
+
 2
≤
2
≤
 )2
)2
р – а + р – в + р – с
+ 2
 3р
3р
3р – а – в – с + р – а + р – в
+ р – а + р – с + р – в + р – с 
9р – 3а – 3в –
3с 
9р – 3(а + в +
с) 
9р – 3 ·
2р 
3р

Демек, теңсіздік дәлелденді.
9.Катеттері ?
және ?, ал
гипотенузасы ?
болатын тікбұрышты үшбұрыш
үшін  +
+  >
>  теңсіздігі
орындалатынын дәлелдеңіздер.
теңсіздігі
орындалатынын дәлелдеңіздер.
Дәлелдеуі: Үшбұрыш теңсіздігін қолданамыз: a + в > c
 +
+  2 >
2 >  2
2
а +
2 + в
> c
+ в
> c
a + в > c
с +
2 > c
> c
2 > 0
> 0
Теңсіздік дәлелденді.
10.
Қабырғалары ?,
в, ?,
?
болатын дөңес төртбұрыштың
ауданы ?
болса,
онда ?
≤
 теңсіздігінің
орындалатынын дәлелдеңіз.
теңсіздігінің
орындалатынын дәлелдеңіз.
Дәлелдеуі: Дөңес төртбұрышты үшбұрыштардың қосындысы түрінде жазып алып, ол үшбұрыштардың ауданын қолданамыз:

![]() в
в
с
 =
= 
а
d
0 <
 <
1
<
1
 =
= 


 =
= 


 =
= 


 =
= 


Осы үшбұрыштың аудандарын мүшелеп қосамыз:
S =


2S


S


S


Теңсіздік дәлелденді.
11. Кез келген натурал n
саны үшін 1 +  теңсіздігі
орындалатынын дәлелдеңіздер.
теңсіздігі
орындалатынын дәлелдеңіздер.
Дәлелдеуі:








 Енді осы түрлендіруді
теңсіздіктің сол жағына жазамыз:
Енді осы түрлендіруді
теңсіздіктің сол жағына жазамыз:
1+ 1 -
 +
+  +...+
+...+ 

-
-



n = 4 деп алатын
болсақ,  =
=

 Теңсіздік
дәлелденді.
Теңсіздік
дәлелденді.
12. Теңсіздікті дәлелдеңіздер:


 .
.
Дәлелдеуі:  =
=
 <
<  =
=
 = 1
-
= 1
-  =
=
 =
= 
Демек, үлкейтілген өрнектің
өзі  тең болса,
онда
тең болса,
онда 
 болады.
Дәлелденді.
болады.
Дәлелденді.
13.  болатынын
дәлелдеңдер.
болатынын
дәлелдеңдер.
Дәлелдеуі: 2000 – 1001 + 1 = 1000 мүше бар

 ( 1000 рет
қоссақ)
( 1000 рет
қоссақ)

 =
=
 Сонымен, теңсіздік
дәлелденді.
Сонымен, теңсіздік
дәлелденді.
14. Теңсіздікті дәлелдеңіздер:
1
+  (
n
(
n  N,
n
N,
n  2)
.
2)
.
Дәлелдеуі: n мүше бар
1 +

 = n
·
= n
·  =
=
 =
=  Дәлелденді.
Дәлелденді.
15. Егер а, в, с - натурал
сандар болса, онда ав + вс + са  3авс болатынын
дәлелдеңіздер.
3авс болатынын
дәлелдеңіздер.
Дәлелдеуі: а, в, с натурал сандар болғандықтан ав саны авс санынан кіші болады. Теңсіздіктің сол жағын үлкейтіп алып, теңсіздіктерін мүшелеп қоссақ:
ав
 авс
авс
вс
 авс
авс
ас
 авс
авс
ав + вс +
ас  3авс
3авс
Демек, теңсіздік дәлелденді.
16.Теңсіздікті дәлелдеңдер:
а2 +
в2  с2 + ( а + в –
с)2, мұндағы
а > с,
с > в.
с2 + ( а + в –
с)2, мұндағы
а > с,
с > в.
Дәлелдеуі:
а2
+
в2
 с2
+
а2
+
в2
с2
+
а2
+
в2
 с2
+ 2ав – 2ас –
2вс
с2
+ 2ав – 2ас –
2вс
с2
+
а2
+
в2
 с2
-
а2
-
в2
+ 2ав – 2ас –
2вс < 0
с2
-
а2
-
в2
+ 2ав – 2ас –
2вс < 0
2c2 + 2ав – 2ас – 2вс < 0 / 2-ге бөлеміз
c2 + ав – ас – вс < 0
(c2 – ас) – (вс – ав) < 0
(c2 – ас) – (вс – ав) < 0
с(с – а) –в(с – а) < 0
(с – а)(с – в) < 0
Берілгенінен а > с, с > в шартын қолдансақ,
а – с
> 0  с –
а < 0, с – в
> 0
болады.
с –
а < 0, с – в
> 0
болады.
Демек, (с – а)(с – в) < 0
( - )·( + ) = ( - ) < 0 Теңсіздік дәлелденді.
17. Теңсіздікті
дәлелдеңдер: 

 , мұндағы а, в >
0.
, мұндағы а, в >
0.
Дәлелдеуі: Теңсіздіктің оң жақ бөлігін түрлендіреміз:


 =
=  =
=
 / (а+в) көбейтеміз.
Себебі, есептің шартында а мен в оң сандар.
/ (а+в) көбейтеміз.
Себебі, есептің шартында а мен в оң сандар.

 2ав
/
2ав
/  бөлсек
бөлсек
а + в


а + в


а + в
 2
2 біздің теңсіздігіміз
Коши теңсіздігіне келеді. Демек, теңсіздік
дәлелденді.
біздің теңсіздігіміз
Коши теңсіздігіне келеді. Демек, теңсіздік
дәлелденді.
18.Теңсіздікті
дәлелдеңдер: 

 , мұндағы а, в >
0.
, мұндағы а, в >
0.
Дәлелдеуі: Теңсіздіктің оң жақ бөлігін түрлендіреміз:


 =
=  =
=
 / (а+в) көбейтеміз.
Себебі, есептің шартында а мен в оң
сандар.
/ (а+в) көбейтеміз.
Себебі, есептің шартында а мен в оң
сандар.

 2ав
2ав
(а +
в)2
 4ав
4ав
а2
+ 2ав +
в2 0
0
а2
- 2ав +
в2 0
0
(а -
в)2
 0
0
Сонымен, теңсіздік дәлелденді.
19. Теңсіздікті
дәлелдеңдер: 

 , мұндағы а, в >
0.
, мұндағы а, в >
0.
Дәлелдеуі:



 / 4-ке
көбейтсек,
/ 4-ке
көбейтсек,
 2а2
+
2в2
2а2
+
2в2
 а2
+ 2ав +
в2
а2
+ 2ав +
в2
2а2
+
2в2
-
а2
- 2ав -
в2
 0
0
а2
- 2ав +
в2
 0
0
(а –
в)2
 0
0
Сонымен, теңсіздік дәлелденді.
20. а, в > 0
болғанда,  теңсіздігі
орындалатынын дәлелдеңдер.
теңсіздігі
орындалатынын дәлелдеңдер.
Дәлелдеуі:
а + в
 2
2 Коши теңсіздігін
қоладанамыз.
Коши теңсіздігін
қоладанамыз.
а2
+
в2 2ав
2ав
Теңсіздіктің сол жақ бөлігін кішірейтсек:
 +
+  =2
·
=2
·



Сол жақ бөлігін кішірейткеннің өзінде теңсіздік оң жағынан үлкен болып тұр. Демек, теңсіздік дәлелденді.
21. Теңсіздікті дәлелдеңдер:
(х + 1)·(х – 2у + 1) +
у2  0
0
Дәлелдеуі:
х2
– 2ху + х + х – 2у + 1 +
у2
 0
0
(
х2
– 2ху +
у2) + (2х – 2у)
+1  0
0
(х –
у)2
+ 2(х – у) +
1  0 х –
у = t
0 х –
у = t
t2 +
2t
+ 1  0
0
(t
+
1)2
 0
0  (х – у +
1)2
(х – у +
1)2
 0
0
Сонымен, теңсіздік дәлелденді.
22. х – тің кез келген мәнінде
х12 - х9 + х4 – х + 1 > 0 екенін дәлелдеңдер.
Дәлелдеуі:
х
 х12
-
х9
+
х4
– х + 1
> 0
х12
-
х9
+
х4
– х + 1
> 0
0
 1 – х +
х4(1 –
х5) +
х12
1 – х +
х4(1 –
х5) +
х12
 0
0
(1 – х)
 0,
х4(1 –
х5)
0,
х4(1 –
х5)
 0,
х12
0,
х12
 0
0
х
 1;
х9(х3
– 1) +
х(х3
– 1) + 1
1;
х9(х3
– 1) +
х(х3
– 1) + 1
 0
0
Теріс санды теріс санға көбейтсек оң сан шығатыны белгілі, олай болса
х9(х3
– 1)
 0 ,
х(х3
– 1)
0 ,
х(х3
– 1)
 0
0
Сонымен, теңсіздік дәлелденді.
23. Теңсіздікті
дәлелдеңдер: а + в  1 + ав, мұндағы
а >1, в
< 1.
1 + ав, мұндағы
а >1, в
< 1.
Дәлелдеуі:
а + в
 1 -
ав
1 -
ав  0
0
(а – 1) –в(а –
1)  0
0
(а – 1)(1 –
в)  0
0
Енді, берілгенінен а >1, в < 1 шартын қолдансақ:
а – 1
 0, в –
1
0, в –
1  0
0
 1 –
в
1 –
в  0
0
Демек, (+)
·(+)  0. Теңсіздік
дәлелденді.
0. Теңсіздік
дәлелденді.
24. Егер а +
в = 1 болса, онда
а2 +
в2  болатынын
дәлелдеңдер.
болатынын
дәлелдеңдер.
Дәлелдеуі:
а + в
= 1  в
= 1 - а
в
= 1 - а
а2
+ (1 –
а)2

а2
+ 1 – 2а +
а2

2а2
– 2а + 1

2а2
– 2а
 -
1
-
1
2а2
– 2а
 / 2-ге
көбейтсек
/ 2-ге
көбейтсек
4а2
– 4а

4а2
– 4а + 1

(2а –
1)2

Сонымен, теңсіздік дәлелденді.
25. Егер а + в +
с = 1, мұндағы а, в,
с > 0 болса, онда (1 – а)(1 –
в)(1 – с)  8авс теңсіздігі
орындалатынын дәлелдеңдер.
8авс теңсіздігі
орындалатынын дәлелдеңдер.
Дәлелдеуі:
1 – а = в + с түрлендіріп, ары қарай Коши теңсіздігін қолданыңыз.
1 – а = в + с, 1 – в = а + с,
1 – с = а + в, в + с =
2 , а + с
= 2
, а + с
= 2 , а +
в =
2
, а +
в =
2
(в + с)(а + с)(а +
в)  2
2 = 8
= 8 =
8
=
8 =
8
=
8 8авс
8авс  8авс
8авс
Теңсіздіктің сол жақ бөлігін кішірейткенде, оң жақ бөлігіне тең болды. Олай болса, теңсіздік дәлелденді.
26. Айталық а, в, с – теріс емес сандар және а + в + с = 1 болсын. Теңсіздіктің дұрыстығын дәлелдеңдер:
(1 + а)(1 + в)(1 +
с)  8(1 – а)(1 – в)(1 –
с)
8(1 – а)(1 – в)(1 –
с)
Дәлелдеуі:
1 + а = 2 – в – с = (1 – в) + (1 – с) деп түрлендіріп алып, ары қарай Коши теңсіздігін қолданамыз.
1 + а
= (1 – в) + (1 –
с)  (1 – в) + (1 –
с)
(1 – в) + (1 –
с) 
1 + в
= 2 – а – с = (1 – а) + (1 –
с)  (1 – а) + (1 –
с)
(1 – а) + (1 –
с) 
1+ с
= 2 – а – в
= (1 – а) + (1 –
в)  (1 – а) + (1 –
в)
(1 – а) + (1 –
в) 
(1 + а)(1 + в)(1 +
с) 
 =
=  = 8(1 – а)(1 – в)(1 –
с)
= 8(1 – а)(1 – в)(1 –
с) 8(1– а) (1 – в)(1 –
с)
8(1– а) (1 – в)(1 –
с)
Теңсіздіктің сол жақ бөлігін кішірейткенде, оң жақ бөлігіне тең болып тұр.
Демек, теңсіздік дәлелденді.
27. Егер авсd = 1 және а > 0, в > 0, c > 0, d >0 болса, онда
а2 +
в2 +
с2 +
d2 + ав + ас + аd + вс + вd +
сd  10 теңсіздігі
орындалатынын дәлелдеңдер.
10 теңсіздігі
орындалатынын дәлелдеңдер.
Дәлелдеуі:
 , ав +
вс
, ав +
вс  осылай Коши теңсіздігін
қолданамыз.
осылай Коши теңсіздігін
қолданамыз.
(а2
+
в2) + (
с2
+
d2) + (ав + сd) + (аd + вс) +
(вd + ас)  10
10
2ав + 2сd
+  +
+
 +
+ 
 10
10
2(ав +
сd) +
6
 10
10
2 +
6
+
6
 10
10
10
 10
10
Есептің шартындағы авсd = 1
апарып қойсақ, 10
 10
10
10
 10
10
Сонымен, теңсіздік дәлелденді.
28. х, у сандары үшін ху =
1 және х > у болса, мына теңсіздіктің
 орындалатынын
дәлелдеңдер.
орындалатынын
дәлелдеңдер.
Дәлелдеуі:
Сол жағындағы өрнектің алымын х – у квадратына келтіреміз.
х2
+
у2
=
х2
– 2ху +
у2
+ 2ху = (х –
у)2
+ 2ху



 (х –
у)
(х –
у)
Теңсіздіктің сол жақ бөлігіне Коши теңсіздігін қолдансақ
2(х –
у)

 (х –
у)
(х –
у)
Демек, теңсіздік дәлелденді.
29.Егер а, в, с –
көбейтіндісі 1-ге тең нақты сандар болса, онда а + в + с + ав + ас
+ вс  6 теңсіздігінің
орындалатынын дәлелдеңдер.
6 теңсіздігінің
орындалатынын дәлелдеңдер.
Дәлелдеуі:
авс = 1 болғандықтан ав
= 
авс = 1 болғандықтан вс
= 
авс = 1 болғандықтан ас
= 
Коши теңсіздігін қолданып, теңсіздіктің сол жақ бөлігін кішірейтеміз:
а +

 =
2
=
2
а + в + с
+  +
+
 +
+ 
 6
6
Демек, кішірейтілген өрнек 6-ға тең болса, онда 6- дан үлкен болады.
Дәлелденді.
30. Егер
а2 +
в2 +
с2 = 1 болса,
онда  +
+  +
+  < 4 теңсіздігінің
орындалатынын дәлелдеңдер.
< 4 теңсіздігінің
орындалатынын дәлелдеңдер.
Дәлелдеуі:
 осылай Коши
теңсіздігін қолданып, теңсіздіктің сол жақ бөлігін
үлкейтеміз.
осылай Коши
теңсіздігін қолданып, теңсіздіктің сол жақ бөлігін
үлкейтеміз. 
 +
+  +
+

 =
=
 =
=  =
4
=
4
Үлкейткендегі өрнек 4 – ке тең болса, онда 4- тен кіші болады. Теңсіздік дәлелденді.
Қорытынды
Қорыта айтқанда, олимпиадалық есептердің арасында жиі кездесетін есептердің қатарында теңсіздіктерді дәлелдеу есептері бар. Сондықтан арифметикалық орта мен геометриялық ортаның арасындағы теңсіздік — Коши теңсіздігін дұрыс қолдана білу маңызды.
Орташа шамалардың арасындағы арақатысты анықтауға байланысты теориялық зерттеулер жүргізілген және теңсіздіктерді әртүрлі тәсілдер мен дәлелдеуді салыстыра отырып, орта мектепте теңсіздіктерді орташа шамалардың қасиетіне сүйеніп дәлелдеудің басқа тәсілдерге қарағанда қолайлы тәсіл екендігі және шығарылу жолы оқушыларға түсінікті екендігі анықталған.
Теңсіздіктерді дәлелдеуге құрастырылған есептерді мұғалім оқушылармен әртүрлі мақсатта – сыныпта, оқушыларға өзіндік тапсырма беруде және одан тыс уақытта оқушыларды деңгейлеп оқыту кезінде пайдалануына болады.
Бұл жинақта қарастырылған көптеген есептерді мұғалім оқушыларды математикалық олимпиадаға даярлау кезінде қолдануына болады.
Жинақта көрсетілген мысалдар мен құрастырылған есептерді орта мектептегі математика пәні мұғалімдері үшін әдістемелік құрал ретінде ұсынуға болады.
ӘДЕБИЕТТЕР
-
Ажгалиев О.А., Отеш А.К. Задачи математических олимпиад. – Алматы, 2001.
-
Бейсеков Ж., Шарипов Т., Тәңірбергенов Ә. 11-сыныптағы оқушыларды математикалық олимпиадаға даярлау. – Шымкент, 2003.
-
Жанасбаева Ұ.Б. Математикалық олимпиада есептері. – Алматы, 2022.
МАТЕМАТИКАЛЫҚ ОЛИМПИАДА ЕСЕПТЕРІНІҢ ЖИНАҒЫ
Басуға 2024ж. қол қойылды
Қағаздың пішімі А4
Офистік қағаз
Есепті баспа табағы 4,5
Таралымы 65 дана
55
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
МАТЕМАТИКАЛЫҚ ОЛИМПИАДА ЕСЕПТЕРІНІҢ ЖИНАҒЫ
МАТЕМАТИКАЛЫҚ ОЛИМПИАДА ЕСЕПТЕРІНІҢ ЖИНАҒЫ
ОРДАБАСЫ АУДАНЫНЫҢ БІЛІМ БӨЛІМІ
АУДАНДЫҚ ПЕДАГОГИКАЛЫҚ-ӘДІСТЕМЕЛІК КАБИНЕТ
МАТЕМАТИКАЛЫҚ ОЛИМПИАДА ЕСЕПТЕРІНІҢ ЖИНАҒЫ
Темірлан
2025
К
М29
Жинақ Ордабасы ауданының білім бөлімінің сараптамалық кеңесінің шешімімен баспаға ұсынылған, №3 хаттама 30.012.2024ж.
Құрастырушылар:
Бейсенбі Г. – Б.Оңтаев атындағы ЖББМ математика пәні мұғалімі
Ибадулла Л. – Б.Оңтаев атындағы ЖББМ математика пәні мұғалімі
Пікір айтушылар:
Бүркіт Ә.Қ. – Қазақстан Педагогикалық академиясы және Жаратылыстану – педагогикалық академиясының академигі, Нобель медалінің иегері
Реңдібаева С. – Ордабасы ауданының білім бөлімінің математика пәні әдіскері, математика ғылымдарының магистры
Нурумбаева К. – Б.Нұрлыбеков атындағы ЖББМ математика пәні мұғалімі, педагог-шебер
Математикалық олимпиада есептерінің жинағы: М29 авторлық/құраст.: Ж.Туккулиева. – Темірлан: Ордабасы
ауданының білім бөлімі, 2024. – 72 б.
Ұсынылып отырған жинақта математикалық олимпиадаларда жиі кездесетін теңсіздіктердің шешу жолдары егжей тегжей көрсетілген. Коши теңсіздігінің қолданысы, санды теңсіздіктерді дәлелдеу әдісі, математикалық индукция принципі, теңсіздіктерді шешуде векторлық әдісті қолдану, геометриялық теңсіздіктер, параметрлі теңсіздіктерді шешу қарастырылған.
Жинақ математика пәні мұғалімдеріне арналған.
К
© Ордабасы ауданының білім бөлімі, 2024
МАЗМҰНЫ
-
Кіріспе..................................................................
4
-
Формулалар.............................................
6
-
Санды теңсіздіктер.................................
8
-
Коши теңсіздігі.......................................
11
-
Қарапайым теңсіздіктер........................
21
-
Геометриялық теңсіздіктер...................
27
-
Параметрмен берілген теңсіздіктер, логарифмдік теңсіздіктер.......................
34
-
Теңсіздіктерді дәлелдеуде векторлық әдістің қолданысы.................................
39
-
Математикалық индукция .....................
43
-
Тапсырмалар ...........................................
49
Қорытынды Әдебиеттер.........................................................
70
-
ІРІСПЕ
Мектеп оқушылары арасында жас таланттарды анықтау мақсатында мектепішілік, аудандық, облыстық, республикалық деңгейде түрлі математикалық олимпиадалар өткізіп тұру дәстүрге айналып келеді. Математикалық олимпиадалардың мақсаты – оқушыларды математикаға қызығушылығын арттыру, оқушыларды терең ойлауға, дәлелдеуге үйрету, талантты жастарды анықтап, математикалық қабілеттерінің дамуына мүмкіндік беру.
Бұл ұсынылып отырған әдістемілік жинақта математикалық олимпиадаларда жиі кездесетін теңсіздіктердің шешу жолдары егжей тегжей көрсетілген. Коши теңсіздігінің қолданысы, санды теңсіздіктерді дәлелдеу әдісі, математикалық индукция принципі, теңсіздіктерді шешуде векторлық әдісті қолдану, геометриялық теңсіздіктер, параметрлі теңсіздіктерді шешу қарастырылған. Сондай-ақ, осы тақырыптар бойынша өздігінен орындауға арналған тапсырмалары және олардың жауаптары қамтылған.
Бұл әдістемелік құралды математикалық олимпиадаға даярлау үшін жалпы білім беретін орта мектептің оқушылары мен математика пәні мұғалімдері, олимпиадалық есептерді шығаруды үйренгісі келген талапкерлердің пайдалануына болады. Сонымен қатар,математика факультетінің студенттері мен болашақ математика пәні мұғалімдері үшін, математиканы тереңдетіліп оқытатын сыныптардың оқушыларына да пайдалы.
-
ФОРМУЛАЛАР
Коши теңсіздігі



Орталар теңсіздігі
min(x1,
x2, … ,
xn)





Мұндағы



 арифметикалық
орта
арифметикалық
орта

n
= 2 деп
алсақ, 






Сонымен,
Гармоникалық
орта  геометриялық
орта
геометриялық
орта  арифметикалық
орта
арифметикалық
орта квадраттық орта
.
квадраттық орта
.
 ≥
≥

 екі жағында 2-ге
көбейткенде
екі жағында 2-ге
көбейткенде  шығады
шығады
Тура солай


 +
+
 өйткені
өйткені 

Коши теңсіздігін теңсіздіктерді дәлелдеу мақсатында теңсіздіктердің сол жақ бөлігін немесе оң жақ бөлігін кішірейтуде немесе үлкейтуде қолданамыз.
2. САНДЫ ТЕҢСІЗДІКТЕР
2.
Теңсіздікті
дәлелдеңдер: 
 +
+  + ... +
+ ... +



Дәлелдеуі: Теңсіздіктің сол жақ бөлігінде қанша мүше бар екенін анықтайық, ол үшін бөлшектің бөліміндегі 3990 санынан 1996 санының алдындағы санды алып тастаймыз:
3990 –
1995  1995
1995
 +
+  +
...
+
+
...
+


 +
...
+
+
...
+

 + ...
+
+ ...
+







 Себебі, алымдары бірдей
бөлшектердің бөлімінің кішісі үлкен
болады.
Себебі, алымдары бірдей
бөлшектердің бөлімінің кішісі үлкен
болады.



Сонымен, теңсіздіктің сол жақ
бөлігінің мүшелері оң жақ бөлігіндегі мүшелерінен үлкен болса, онда
сол жақ бөлігінің мүшелерінің қосындысы да оң жақ бөлігіндегі
мүшелерінен қосындысынан үлкен болады. Олай болса, теңсіздіктің оң
жақ бөлігінің мүшелерінің қосындысы  – ге тең болғандықтан,
сол жақ бөлігі
– ге тең болғандықтан,
сол жақ бөлігі  ден үлкен болады.
Теңсіздік дәлелденді.
ден үлкен болады.
Теңсіздік дәлелденді.
2.Кез келген натурал n саны үшін

 +
+  + ... +
+ ... +

 2 теңсіздігінің
орындалатынын дәлелдеңдер.
2 теңсіздігінің
орындалатынын дәлелдеңдер.
Дәлелдеуі: Теңсіздіктің сол жақ бөлігінің әр мүшесін төмендегіше жіктеп аламыз:

 1
1



 1 -
1 -





 -
-

.......................




 -
-





 -
-

Теңсіздіктің сол жағындағы қосындының орнына үлкейтілген өрнекті апарып қоямыз. Үлкейткен өрнектің өзі 2-ден кіші немесе 2-ге тең болса, онда сол жақтағы кіші өрнек 2-ден кіші болады.
1![]()
![]()
![]()
![]()
![]()
![]()
![]() + 1
-
+ 1
-  +
+
 -
-  +
...
+
+
...
+
 -
-  +
+
 -
- 
 2 -
2 -

 2
2
2 -
 өрнегі 2-ден кіші
болады. Өйткені , 2-ден қандай да бір
өрнегі 2-ден кіші
болады. Өйткені , 2-ден қандай да бір
 санын азайтып
отырмыз. Себебі, шартында n- натурал сан, n натурал сан (теріс сан
болса) болмаса 2-ден үлкен болуы мүмкін. Сонымен, теңсіздігіміз
дәлелденді.
санын азайтып
отырмыз. Себебі, шартында n- натурал сан, n натурал сан (теріс сан
болса) болмаса 2-ден үлкен болуы мүмкін. Сонымен, теңсіздігіміз
дәлелденді.
3.
 -
-  +
+  -
-  + ... -
+ ... -
 +
+ 
 екенін
дәлелдеңдер.
екенін
дәлелдеңдер.
Д![]()
![]()
![]() әлелдеуі: Теңсіздіктің сол жақ бөлігін
есептейік:
әлелдеуі: Теңсіздіктің сол жақ бөлігін
есептейік:
 -
-  +
+
 -
-  +
+
 -
-  +
...
-
+
...
-
 +
+ 
 -
-
 +
+  ) –
(
) –
( -
-
 )
-
)
-  -
-
 ...
-
...
-
 -
- 

 -
-
 -
-  -
-



 - тен қандай да бір
кішкентай санды азайтсақ
- тен қандай да бір
кішкентай санды азайтсақ  – тен кіші сан шығатыны
белгілі. Демек, теңсіздік дәлелденді.
– тен кіші сан шығатыны
белгілі. Демек, теңсіздік дәлелденді.
![]()
![]() 4
4![]()
![]()
![]()
![]()
![]() .Дәлелдеу
керек:
.Дәлелдеу
керек:  <
98
<
98
Дәлелдеуі: ( а + в)2 = а2 + 2ав + в2 қысқаша көбейту формуласын қолдану арқылы дәлелдейміз:
 <
98
<
98




20

20
 49
49
(20 )2
)2
 492
492
2400 2401
дәлелденді.
2401
дәлелденді.
3. КОШИ ТЕҢСІЗДІГІ
1. Айталық
х  1 болсын. Теңсіздікті
дәлелдеңдер:
1 болсын. Теңсіздікті
дәлелдеңдер: 
Дәлелдеуі: Орталар теңсіздігі
формуласынан  теңсіздікті қолдану
арқылы дәлелдейміз.
теңсіздікті қолдану
арқылы дәлелдейміз.  деп алып, формулаға
апарып қоямыз:
деп алып, формулаға
апарып қоямыз:


 =
=
 =
= 

 бұл теңсіздіктің сол жақ
бөлігіндегі 2-ні оң жақ бөлігіне көбейту етіп
өткізсек
бұл теңсіздіктің сол жақ
бөлігіндегі 2-ні оң жақ бөлігіне көбейту етіп
өткізсек  теңсіздігі шығады.
Теңсіздіктің шартында х
теңсіздігі шығады.
Теңсіздіктің шартында х 1 болғандықтан, теңдік
белгісі болмайды. Сонда теңсіздігіміз
1 болғандықтан, теңдік
белгісі болмайды. Сонда теңсіздігіміз
 болады. Сонымен,
теңсіздік дәлелденді.
болады. Сонымен,
теңсіздік дәлелденді.
2. Егер а +
в  1 болса,
онда
1 болса,
онда  +
+ 

 теңсіздігі тура
болатынын дәлелдеңдер.
теңсіздігі тура
болатынын дәлелдеңдер.
Дәлелдеуі: Квадраттық орта арифметикалық ортадан үлкен немесе тең


 формуласын қолданып,
дәлелдейміз.
формуласын қолданып,
дәлелдейміз. 


 =
=





Есептің берілгенінен мына
шарттың а + в  1 екі жағын да 2-ге
бөліп түрлендіріп аламыз.
1 екі жағын да 2-ге
бөліп түрлендіріп аламыз. 



 =>
=> 

 =>
=> 

 Дәлелденді.
Дәлелденді.
3. Оң х және у
үшін: 


 теңсіздігі орындалатынын
дәлелде.
теңсіздігі орындалатынын
дәлелде.
Дәлелдеу Коши
теңсіздігін
Коши
теңсіздігін 

 қолдану арқылы
дәлелдейміз.
қолдану арқылы
дәлелдейміз.


Теңсіздіктің сол жағындағы қосындының бөлімінің орнына кішірейтілген өрнекті апарып қоямыз. Бөлімі кішірейтілсе, өрнектің өзі үлкейтіледі.



 ;
;
 +
+
 ;
;
 +
+ 

 ;
;


 ;
;


 ;
;
Сол жақтағы үлкейтілген
өрнектің өзі  - ге тең болса, онда
кіші болады. Теңсіздік дәлелденді.
- ге тең болса, онда
кіші болады. Теңсіздік дәлелденді.
4.
Дәлелдеңіз: ![]() .
Мұндағы
.
Мұндағы ![]() -кез келген нақты
сандар.
-кез келген нақты
сандар.
Дәлелдеуі: Коши теңсіздігін а +
в 
 қолдану арқылы
дәлелдейміз.
қолдану арқылы
дәлелдейміз.
![]() ,
,
![]() ,
,
![]()
Онда![]() ,
,
![]()
Демек, теңсіздік дәлелденді.
5. Кез келген x,y,z
үшін  теңсіздігі
орындалатынын дәлелдеңіз.
теңсіздігі
орындалатынын дәлелдеңіз.
Дәлелдеуі:  теңсіздігінің екі
жағында 2-ге көбейтеміз, сонда
теңсіздігінің екі
жағында 2-ге көбейтеміз, сонда  одан
одан 
Коши теңсіздігін қолданып, оларды қосамыз



Сонда келесі теңсіздік
шығады 
Сонымен теңсіздіктің сол жағын кішірейту арқылы теңсіздікті дәлелдедік.
6. Теңсіздікті дәлелдеңіз (a+b)(b+c)(a+c)≥8abc, мұндағы a≥0, b≥0, c≥0.
Дәлелдеуі: Коши теңсіздігі бойынша


 олай болса бастапқы
теңсіздікке апарып орын орына қоятын
болсақ
олай болса бастапқы
теңсіздікке апарып орын орына қоятын
болсақ
(a+b)(b+c)(a+c)≥8abc,  ≥8abc шығады ,яғни сол
жағымен оң жағы теңесті, кішірейтілген сол жағы оң жағына тең болып
тұр. Олай болса кішірейтілмеген (a+b)(b+c)(a+c) 8abc-дан үлкен,
яғни (a+b)(b+c)(a+c)≥8abc. Сонымен теңсіздік
дәлелденді.
≥8abc шығады ,яғни сол
жағымен оң жағы теңесті, кішірейтілген сол жағы оң жағына тең болып
тұр. Олай болса кішірейтілмеген (a+b)(b+c)(a+c) 8abc-дан үлкен,
яғни (a+b)(b+c)(a+c)≥8abc. Сонымен теңсіздік
дәлелденді.
7. Кез келген оң таңбалы
a,b,c үшін  екенін
дәлелдеңіз.
екенін
дәлелдеңіз.
Дәлелдеуі: Осы a,b,c үшін Коши теңсіздігін қолданып, келесі теңсіздіктерді жазып алайық
 ,
,  олай
болса
олай
болса 
Коши теңсіздігі бойынша
кішірейтілген сол жағы 3-ке тең болады, яғни, кішірейтілмегені
3-тен үлкен  . Осымен теңсіздік
дәлелденді.
. Осымен теңсіздік
дәлелденді.
8. Егер x+y+z=7 болса
мұндағы  онда
онда
 екенін
дәлелдеңіз.
екенін
дәлелдеңіз.
Дәлелдеуі: (a+b+c) ²=a²+b²+c²+2ab+2bc+2ac сол сияқты

(x+y+z)+2
x+y+z=7
болғандықтан
7+2
енді Коши теңсіздігін қолданып теңсіздіктің сол жағын үлкейтеміз
x+y
≥ , z+y
≥
, z+y
≥ , x+z
≥
, x+z
≥ болғандықтан
болғандықтан
7+x+y+y+z+x+z<25,
7+2(x+y+z) 7+2·7<25, 21<25
демек, теңсіздік дәлелденді.
7+2·7<25, 21<25
демек, теңсіздік дәлелденді.
9. Егер xy+yz+zx=1 болса, онда x²+y²+z²≥1 теңсіздігі орындалатыны дәлелдеңіз.
Дәлелдеуі: x²+y²+z²≥1 теңсіздігінің екі жағында 2-ге көбейтіп алып, Коши теңсіздігін қолданып теңсіздіктің сол жағын кішірейтіп аламыз
2x²+2y²+2z²≥2, (x²+y²)+ (y²+z²)+(x²+z²)≥2
2xy+2yz+2zx≥2, 2(xy+yz+zx)≥2 шарты бойынша xy+yz+zx=1 , сондықтан 2·1=2 дәлелденді, өйткені теңсіздіктің сол жағы кішірейтілгеннің өзінде сол жағының мәніне тең болып тұр. Олай болса теңсіздіктің кішірейтілмеген сол жағы оң жағынан әлбетте үлкен
x²+y²+z²≥1 теңсіздігі дәлелденді.
10. a>0, b>0, c>0
болғанда  екенін
дәлелдеңіз
екенін
дәлелдеңіз
Дәлелдеуі:  теңсіздігінің екі
жағында 2-ге көбейтіп алып келесі теңсіздікті
жазамыз
теңсіздігінің екі
жағында 2-ге көбейтіп алып келесі теңсіздікті
жазамыз

Коши теңсіздігін қолдануға
ыңғайлы етіп мына түріне келтіріп жазып аламыз
( 
Коши теңсіздігін қолданамыз
 ,
, 
 ,
, 
 ,
, 
 осы теңсіздікке Коши
теңсіздігін және қолданамыз, ол үшін алдымен мына түріне келтіріп
аламыз теңсіздікті
осы теңсіздікке Коши
теңсіздігін және қолданамыз, ол үшін алдымен мына түріне келтіріп
аламыз теңсіздікті
(

(

Коши теңсіздігі бойынша
 ,
, 
 ,
,

 ,
,

Олай болса теңсіздіктің сол жағын
 +
+ деп жазып, ортақ
көбейткіштерін жақша сыртына шығарамыз
деп жазып, ортақ
көбейткіштерін жақша сыртына шығарамыз
 =
= осындай теңдік пайда
болады, яғни, теңсіздіктің кішірейтілген сол жағы он жағына тең
болды.Олай болса кішірейтілмеген сол жағы теңсіздіктің оң жаңынан
әлбетте үлкен болады. Сонымен,
осындай теңдік пайда
болады, яғни, теңсіздіктің кішірейтілген сол жағы он жағына тең
болды.Олай болса кішірейтілмеген сол жағы теңсіздіктің оң жаңынан
әлбетте үлкен болады. Сонымен,
 теңсіздігі
дәлелденді.
теңсіздігі
дәлелденді.
11. Егер a+b+c=0 болса, онда ab+ac+bc≤0 болатындығын дәлелдеңдер. Дәлелдеуі: a+b+c=0 теңдігінің екі жағында квадраттаймыз
 ,
,  ,
,
 ,
,  шығады
шығады
Екі жағдай қарастырамыз:
1)
 , олай
болса
, олай
болса 
Яғни
 демек
дәлелденді.
демек
дәлелденді.
12. Егер x+y+z=3 болса онда x²+y²+z² ≥ 3 теңсіздігі орындалатынын дәлелдеңіз
Дәлелдеуі: x+y+z=3 теңдігінің екі жағында квадраттаймыз, сонда
x²+y²+z²+2xy+2yz+2xz=9 шығады (1) одан
2xy+2yz+2xz=9-(x²+y²+z²) шығады (2)
Коши теңсіздігін қолданамыз
x²+y²≥2xy
y²+z²≥2yz
x²+z²≥2xz осы теңсіздіктерді бір біріне мүшелеп қосып келесі теңсіздікке келеміз 2x²+2y²+2z²≥ 2xy+2yz+2xz, 2(x²+y²+z²)≥ 2xy+2yz+2xz
2(x²+y²+z²)≥ 9-(x²+y²+z²)
3(x²+y²+z²)≥ 9
(x²+y²+z²)≥ 3 теңсіздік осымен дәлелденді.
13. Оң таңбалы a,b,c сандары үшін a≥b≥c және a+b+c≤1 болғанда a²+3b²+5c²≤1 теңсіздігі тура болатынын дәлелдеңдер.
Дәлелдеуі: a²+3b²+5c²≤1 теңсіздігін a²+ b² +2b²+2c²+2c²+c²≤1 деп жазып алып, теңсіздіктің сол жағын (a+b+c)² осыған келтіреміз
Алдымен мына теңсіздіктерді жазып алайық
2b²≤2ab, 2bb≤2ab екі жа,ында қыстқартқанда b≤2a қалады
2c²≤2bc, 2cc≤2bc, c≤b,
2a²≤2ac, 2aa≤2ac a≤ c
Сонда a²+ b² +2b²+2c²+2c²+c²≤1 теңсіздігі мынаған келеді
a²+ b² +c²+2ab+2bc+2ac≤1 ал бұл теңсіздікті былай жазсақ болатынын білеміз (a+b+c)² ≤1, олай болса a+b+c ≤1 , теңсіздік дәлелденді
Теңсіздіктің сол жағын Коши теңсіздігін қолданып үлкейту арқылы дәлелдедік.
14. a>b, b>0, c>0
, a+b+c=1 екені белгілі болса, мынаны
дәлелдеңіз 
Дәлелдеуі: 1) a+b+c=1 теңдігін a -ға
бөлеміз, сонда 
2) b-ға
бөлгенде 
3) c -ға бөлгенде

Енді осы теңдікті қосамыз, келесі теңдікті жазамыз

Коши теңсіздігін пайдаланып оң жағын кішейтеміз
 ≥2
≥2
 ≥2
≥2
 ≥2
сонда
≥2
сонда 
 теңсіздік
дәлелденді.
теңсіздік
дәлелденді.
15. a+b=2 шарты қолданылатын кез келген a және b сандары үшін
 +
+ теңсіздігі
орындалатынын дәлелдеңдер.
теңсіздігі
орындалатынын дәлелдеңдер.
Дәлелдеуі: a=1+c деп белгілеп аламыз,
сонда a+b=2 теңдеуіне қойғанда  .
.
Яғни,
мына  +
+ теңсіздікті былай жазуға
болады
теңсіздікті былай жазуға
болады
 +
+ >2 Паскаль үшбұрышын
пайдаланып жақшасын ашамыз
>2 Паскаль үшбұрышын
пайдаланып жақшасын ашамыз  +4
+4 +4a
+4a +
+
 +
+ >2 үшін жақшасын
ашатын болсақ келесі теңсіздік шығады
1+4с
>2 үшін жақшасын
ашатын болсақ келесі теңсіздік шығады
1+4с +
+ +
+ +1-4с
+1-4с -
- +
+ , ықшамдап жіберіп
келесі теңсіздікті жазамыз
, ықшамдап жіберіп
келесі теңсіздікті жазамыз  +12
+12 ,
қысқартып
,
қысқартып  +6
+6 деп аламыз. Теңсіздік
осымен дәлелденеді.
деп аламыз. Теңсіздік
осымен дәлелденеді.
16. Егер x+y+z=1 болса,
онда x²+y²+z²≥ болатынын
дәлелдеңіз.
болатынын
дәлелдеңіз.
Дәлелдеуі: x= ,
y=
,
y= z=
z= деп белгілеп
аламыз,
деп белгілеп
аламыз,
x+y+z=1 шартын қолданамыз,
сонда x+y+z= , яғни 1+a+b+c=1 бұдан
a+b+c=0 олай болса,
, яғни 1+a+b+c=1 бұдан
a+b+c=0 олай болса,
(

 бұдан
бұдан
 +a²+b²+c²≥0,
+a²+b²+c²≥0,  +a²+b²+c²≥0, яғни,
a²+b²+c²≥0 осымен теңсіздік дәлелденді.
+a²+b²+c²≥0, яғни,
a²+b²+c²≥0 осымен теңсіздік дәлелденді.
4. ҚАРАПАЙЫМ ТЕҢСІЗДІКТЕР
1. Теңсіздікті
дәлелдеңіз:  , мұндағы a және b -
нақты сандар.
, мұндағы a және b -
нақты сандар.
Дәлелдеуі:  теңсіздігінің екі
жағында 2-ге көбейтейік. Пайда болған
теңсіздігінің екі
жағында 2-ге көбейтейік. Пайда болған
 теңсіздігін былай
түрлендіріп жазуға болады
теңсіздігін былай
түрлендіріп жазуға болады  . Сол жақтағы жақша
ішіндегі өрнекті қысқаша көбейту формуласы бойынша мына түріне
келеді
. Сол жақтағы жақша
ішіндегі өрнекті қысқаша көбейту формуласы бойынша мына түріне
келеді  . Олай
болса
. Олай
болса 
 , яғни
теңсіздік
, яғни
теңсіздік  дәлелденді
дәлелденді
2. Кез келген x,y,z
үшін  теңсіздігі
орындалатын дәлелдеңіз.
теңсіздігі
орындалатын дәлелдеңіз.
Дәлелдеуі:  теңсіздігінің екі
жағында 2-ге көбейтіп, бір бетіне өткізіп
алайық
теңсіздігінің екі
жағында 2-ге көбейтіп, бір бетіне өткізіп
алайық  .Теңсіздіктің сол
жағын
.Теңсіздіктің сол
жағын
 деп жазуға
болады
деп жазуға
болады

Қысқаша көбейту формуласына салып, келесі теңсіздікті жазамыз



 теңсіздігі
дәлелденді.
теңсіздігі
дәлелденді.
3. Егер xyz >0 , болса,
онда  теңсіздігінің
орындалатынын дәлелдеңдер.
теңсіздігінің
орындалатынын дәлелдеңдер.
Дәлелдеуі:  теңсіздігінің оң жақ
бетіндегі мүшелерін сол жағына өткізіп алып мүшелеп xyz өрнегіне
бөлуді орындаймыз.
теңсіздігінің оң жақ
бетіндегі мүшелерін сол жағына өткізіп алып мүшелеп xyz өрнегіне
бөлуді орындаймыз.
 , қысқартуды
орындаймыз, пайда болған теңсіздіктің екі жағында 2-ге
көбейтіп
, қысқартуды
орындаймыз, пайда болған теңсіздіктің екі жағында 2-ге
көбейтіп

Келесі теңсіздіктің сол жағын
екі мүшенің айырмасы шығатындай етіп
топтастырамыз  ,
бұдан
,
бұдан  , олай болса қысқаша
көбейту формуласы бойынша сол жағын
түрлендіріп
, олай болса қысқаша
көбейту формуласы бойынша сол жағын
түрлендіріп  бұл
теңсіздіктің
бұл
теңсіздіктің
 сондықтан
сондықтан
 теңсіздігі
дәлелденді дейміз.
теңсіздігі
дәлелденді дейміз.
4. Кез келген бүтін n сан
үшін  өрнегінің мәні оң
екенін дәлелдеңіз.
өрнегінің мәні оң
екенін дәлелдеңіз.
Дәлелдеуі: nϵZ, n=1,5,-4,100,….
y(n)= , y>0 1) парабола
тармағы жоғары бағытталған, себебі
, y>0 1) парабола
тармағы жоғары бағытталған, себебі
 y
=
y
= a>0
a>0
2) абцисса осін қандай нүктеде қияды
y
=
 парабола абцисса
осін келесі екі нүктеде қияды
парабола абцисса
осін келесі екі нүктеде қияды

y
= ,
nϵ[
,
nϵ[ ]
y<0, яғни осы аралықта функция
мәні теріс және бұл аралықта n
мәні бүтін
емес.
]
y<0, яғни осы аралықта функция
мәні теріс және бұл аралықта n
мәні бүтін
емес.
nϵ
(-ꚙ; ]
ᴗ[
]
ᴗ[ ꚙ) y>0 демек бұл аралықта y
=
ꚙ) y>0 демек бұл аралықта y
= мәні оң болады, nϵZ
болғанда y>0 екені дәлелденді.
мәні оң болады, nϵZ
болғанда y>0 екені дәлелденді.
5. Егер 4b+a=1 болса,
онда  теңсіздігі
орындалатындығын дәлелдеңіз.
теңсіздігі
орындалатындығын дәлелдеңіз.
Дәлелдеуі: 4b+a=1 теңдігінен
a=1-4b теңсіздігіне a-ның
орнына қойып келесі теңсіздікті жазамыз
теңсіздігіне a-ның
орнына қойып келесі теңсіздікті жазамыз
 . Жақшаны ашып
түрлендіріп
. Жақшаны ашып
түрлендіріп 
 пайда болған
теңсіздіктің екі жағында 5-ке көбейтейік
пайда болған
теңсіздіктің екі жағында 5-ке көбейтейік
 , сосын екі жағында
4-ке бөлеміз
, сосын екі жағында
4-ке бөлеміз
 . Пайда болған
үшмүшені екі мүшенің айырмасының квадраты түрінде
жазамыз
. Пайда болған
үшмүшені екі мүшенің айырмасының квадраты түрінде
жазамыз
25

 .
.
6 . х –тің кез келген мәніндерінде (х-1)(х-3)(х-4)(х-6)+10 өрнегінің оң мәндер қабылдайтынын дәлелдеңдер.
Дәлелдеуі:
(х-1)(х-3)(х-4)(х-6)+10  екені дәлелдеу үшін
бірінші және төртінші жақшадағы өрнектерді, екінші және үшінші
жақшадағы өрнектерді мүшелеп көбейтіп , мынадай түріне келтіріп
аламыз
екені дәлелдеу үшін
бірінші және төртінші жақшадағы өрнектерді, екінші және үшінші
жақшадағы өрнектерді мүшелеп көбейтіп , мынадай түріне келтіріп
аламыз
( )(
)( )+10
)+10

 ал
ал

 a(a+6)+10>0
a(a+6)+10>0
 ,
,
 теңсіздігінен
екімүшенің қосындысының квадратын бөліп алуға әрекет
жасаймыз
теңсіздігінен
екімүшенің қосындысының квадратын бөліп алуға әрекет
жасаймыз

 шығады
шығады  ,
сондықтан
,
сондықтан  теңсіздік дәлелденді
дейміз.
теңсіздік дәлелденді
дейміз.
7. Теңсіздікті
дәлелдеңдер  мұндағы
мұндағы 
Дәлелдеуі:  теңсіздігін дәлелдеу
мақсатында сол жағындағы жақшаны ашып , оң жақ
бетіндегі
теңсіздігін дәлелдеу
мақсатында сол жағындағы жақшаны ашып , оң жақ
бетіндегі  -ті сол жағына өткізіп
аламыз
-ті сол жағына өткізіп
аламыз
 . топтастыру арқылы
көбейткіштерге жіктеп аламыз
. топтастыру арқылы
көбейткіштерге жіктеп аламыз


Теңсіздіктің шарты
бойынша  олай
болса
олай
болса  ,
,
 бұдан
бұдан  екі
жағында
екі
жағында
 / (-1) көбейтеміз
сонда
/ (-1) көбейтеміз
сонда  болады.
болады.
Сонымен
 теңсіздігінде
теңсіздігінде  ,
,

Екеуініңде мәні теріс болып тұр , яғни, теріс сандардың көбейтінсі оң сан болады. Теңсіздік дәлелденді.
8.Теңсіздікті
дәлелдеңіз: 
 +
+ 

Дәлелдеуі:
 анықталу облысын табатын
болсақ, х + 1
анықталу облысын табатын
болсақ, х + 1  0
0
 х
х  -1,
яғни
-1,
яғни
х
 1;
1;
f(-1) =
 +
+  =
=

f(х) =
 +
+ 
 анықталу аймағында монотонды
өспелі ( монотонды өспелі функцияның графигі оң және сол жағында
қатаң өспелі, ал ортасында кемімейді) , сондықтан
f (х
)
≥
f
(-1)
=
анықталу аймағында монотонды
өспелі ( монотонды өспелі функцияның графигі оң және сол жағында
қатаң өспелі, ал ортасында кемімейді) , сондықтан
f (х
)
≥
f
(-1)
=
 >1,4.
Дәлелденді.
>1,4.
Дәлелденді.
9. Теңсіздікті шеш:
(х-1)(х2-1)(х3-1)(х4-1)...(х2002-1)≤0
Шешуі: (-∞; −1] және {1}
xn-1=0 теңдеудің екі түбірі бар егер n –жұп сан болса х=-1 х=1
және бір түбірі бар егер n-тақ болса х=1.
10. Теңсіздікті шешіңдер:



 +(
+(

 кез-келген х үшін,
ал
кез-келген х үшін,
ал кез-келген х үшін
8
кез-келген х үшін
8 болғандықтан, ал
дискриминант теріс. Олай болса
болғандықтан, ал
дискриминант теріс. Олай болса  +(
+( , сондықтан шешімі
жоқ.
, сондықтан шешімі
жоқ.
5. ГЕОМЕТРИЯЛЫҚ ТЕҢСІЗДІКТЕР
1. Ауданы S- ке, ал
қабырғалары а, в, с – ға тең үшбұрыш үшін
 теңсіздігі тура
болатынын дәлелдеңдер.
теңсіздігі тура
болатынын дәлелдеңдер.
Дәлелдеуі:


х

в с
в2



 в
в
 с
с
а

 а
а


 авс теңсіздіктің екі жақ
бөлігін де авс –ға көбейтеміз.
авс теңсіздіктің екі жақ
бөлігін де авс –ға көбейтеміз. 



Үшбұрыштың ауданының
формуласына S =  келтіреміз.
келтіреміз.



 2S·2S·2S
2S·2S·2S 

(2S)3

 Дәлелденді.
Дәлелденді.
2. Егер а, в және с
үшбұрыштың қабырғалары болса, онда
 +
+  +
+ 
 болатындығын
дәлелдеңдер.
болатындығын
дәлелдеңдер.
Дәлелдеуі: Үшбұрыштың кез келген екі қабырғасының қосындысы үшінші қабырғасынан үлкен деген қасиетті қолданып, теңсіздіктің сол жақ бөлігін үлкейтейік:
в + с
 а (в+с) қосамыз,
2(в+с)
а (в+с) қосамыз,
2(в+с) а+в+с => в+с
=
а+в+с => в+с
= 
а + с
 в (а + с) қосамыз,
2(а+с)
в (а + с) қосамыз,
2(а+с)  а+в+с => а+с
=
а+в+с => а+с
= 
а + в
 с (а + в) қосамыз,
2(а+в)
с (а + в) қосамыз,
2(а+в)  а+в+с => а+в
=
а+в+с => а+в
= 
Бастапқы берілген теңсіздіктің сол жақ бөлігінің бөліміне апарып қоямыз:
 +
+  +
+


 +
+  +
+

 =
=
 =
2
=
2
Демек, теңсіздіктің сол жағындағы бөлігін үлкейткендегі теңсіздік 2-ге тең болса, онда бұл теңсіздік 2-ден кіші болады. Демек, теңсіздік дәлелденді.
3. Егер а, в және с
үшбұрыштың қабырғалары болса, онда
в2х2 +
(в2 +
с2 -
а2)х +
с2  0,
(х
0,
(х  R) теңсіздігі
орындалатынын дәлелдеңдер.
R) теңсіздігі
орындалатынын дәлелдеңдер.
Дәлелдеуі:
ах2
+ вх + с
 0 квадрат үшмүшеге
келеді. Яғни, бұл теңсіздік о –ден үлкен болу үшін
D
0 квадрат үшмүшеге
келеді. Яғни, бұл теңсіздік о –ден үлкен болу үшін
D  0
екенін дәлелдесек
жеткілікті.
0
екенін дәлелдесек
жеткілікті.
D = в2 – 4ас = (в2 + с2 - а2)2 - 4·в2·с2 = (в2 + с2 - а2 - 2вс) (в2 + с2 - а2+2вс) = ((в - с)2 – а2) · ((в + с)2 – а2) = (в - с – а)(в - с + + а)(в + с – а)(в + с + а)
Үшбұрыштың кез келген екі қабырғасының қосындысы үшінші қабырғасынан үлкен деген қасиетті қолданамыз:
в + с
 а => в + с –
а > 0
а => в + с –
а > 0
а + с
 в
=> а + с - в
> 0, в – а –
с
в
=> а + с - в
> 0, в – а –
с  0
0
а + в
 с => а + в -
с > 0
с => а + в -
с > 0
(в - с – а)(в - с + а)(в + с –
а)(в + с + а)  0 , в - с +
а > 0, в + с –
а > 0, в + с +
а > 0
0 , в - с +
а > 0, в + с –
а > 0, в + с +
а > 0
(-) · (+) · (+) · (+) = ( - ). Демек, D < 0 болады, теңсіздік дәлелденді.
4.Кез келген үшбұрыш үшін
а3 +
в3 +
с3 + +
+  +
+ 
 4p теңсіздігі орындалатынын
дәлелдеңдер. Мұндағы а,в,с – үшбұрыштың қабырғалары, р - жарты
периметр.
4p теңсіздігі орындалатынын
дәлелдеңдер. Мұндағы а,в,с – үшбұрыштың қабырғалары, р - жарты
периметр.
Дәлелдеуі:  жарты
периметр
жарты
периметр
4р =
4· = 2(а + в +
с)
= 2(а + в +
с)
Теңсіздіктің сол жақ бөлігін Коши теңсіздігін қолданып кішірейтеміз:
Коши теңсіздігі: а +
в  2
2
а3
+
 =
2
=
2 = 2
= 2 = 2а
= 2а
в3
+
 =
2
=
2 = 2
= 2 = 2в
= 2в
с3
+
 =
2
=
2 = 2
= 2 = 2с
= 2с
(а3
+
 в3
в3
 )+
(с3
+
)+
(с3
+
 ) = 2а + 2в +
2с =
2(а + в +
с) =
4р
) = 2а + 2в +
2с =
2(а + в +
с) =
4р
Теңсіздіктің сол жақ бөлігін кішірейткенде 4р – ға тең болса, онда теңсіздік 4р – дан міндетті түрде үлкен болады. Дәлелденді.
5.Айталық а, в – тік бұрышты үшбұрыштың катеттері, ал с – гипотенузасы болсын. Қайсысы үлкен: а3 + в3 немесе с3 ?
Дәлелдеуі: а3 + в3 өрнегі мен с3 өрнегін салыстырайық:
Пифагор теоремасын қолданамыз: а2 + в2 = с2
а2 + в2 = с2 өрнегін мүшелеп с – ға көбейтеміз.
а2с + в2с = с3
Тік бұрышты үшбұрыштың гипотенуза катеттерінен үлкен болады, яғни
с > a, c > в
с > a, а2 - мүшелеп көбейтсек c > в, в2 - мүшелеп көбейтсек
са2 > a3, cв2 > в3
Осы екі теңсіздікті мүшелеп қоссақ,
са2 + св2 > а3 + в3
Теңсіздіктің сол жақ бөлігіне а2с + в2с = с3 теңдіктегі с3 – ты апарып қойсақ, с3 > а3 + в3 болады. Теңсіздік дәлелденді.
6.Теңсіздікті дәлелдеңдер:
R + r 
 , мұндағы R – тік бұрышты
үшбұрышқа сырттай сызылған, ал r – оған іштей сызылған шеңбердің
радиустары, S – оның ауданы.
, мұндағы R – тік бұрышты
үшбұрышқа сырттай сызылған, ал r – оған іштей сызылған шеңбердің
радиустары, S – оның ауданы.
Дәлелдеуі: Тік бұрышты үшбұрыштың төмендегі формулаларын қолдану арқылы дәлелдейміз:
с2 = а2 + в2
S
=  ав
ав
R
= 
r
=  мұндағы р – жарты
периметр
мұндағы р – жарты
периметр
Коши
теңсіздігі 

 .
.
R![]()
![]()
![]()
![]() + r
=
+ r
=  +
+
 =
=  +
+
 ав
ав =
=  +
+  ав
ав =
=
 +
+  =
=
 = =
= =  =
=  =
=
 =
= 

 =
=  =
= 
Коши теңсіздігін қолданып,
теңсіздікті кішірейткенде  – ке тең болса, онда R +
r
– ке тең болса, онда R +
r  болады. Демек, теңсіздік
д
болады. Демек, теңсіздік
д
7.Катеттері а және в, ал
гипотенузасы с болатын кез келген тік бұрышты үшбұрыш үшін
с 
 теңсіздігінің орындалатынын
дәлелдеңдер.
теңсіздігінің орындалатынын
дәлелдеңдер.
Дәлелдеуі:
с2 = а2 + в2 екі жағына да 2-ні көбейтеміз:
2с2 = 2 а2 + 2в2 = а2 + в2 + а2 + в2 + 2ав – 2ав = (а2 + 2ав + в2 ) + (а2 - 2ав + в2 ) = (а + в)2 + (а -в)2
2с2 = (а + в)2 + (а - в)2
с2
=  +
+
 ,
, 
 0
0
с2


с


Сонымен, теңсіздік дәлелденді.
8. Егер үшбұрыштың жарты
периметрі р-ға, ал медианалар
ma,
mв,
mс болса,
онда  р
р ma +
mв +
mс
ma +
mв +
mс  2р арақатысының
орындалатынын дәлелдеңдер.
2р арақатысының
орындалатынын дәлелдеңдер.
Д
mв
әлелдеуі:1) ma + mв + mс
 р
екенін дәлелдейік:
р
екенін дәлелдейік: 

в с
а
Қарсы жоритын
болсақ, ma
+
mв
+
mс

 р
=
р
=  (
( )
=
)
=  (а+в+с) =
(а+в+с) =  =
=

 =
=

Медиана түскен қабырғасын тең
екіге бөлетіндіктен  деп жазып аламыз.
mв
– в қабырғасына түсірілген
медиана. Үшбұрыштың кез келген екі қабырғасының қосындысы үшінші
қабырғасынан үлкен деген қасиетті қолдансақ,
деп жазып аламыз.
mв
– в қабырғасына түсірілген
медиана. Үшбұрыштың кез келген екі қабырғасының қосындысы үшінші
қабырғасынан үлкен деген қасиетті қолдансақ,
 +
с
+
с  mв,
mв,
 +
в
+
в  mс,
mс,
 +
в
+
в  mа
теңсіздігі
шығады.
mа
теңсіздігі
шығады.  =
=
 mа
+
mа
+
 mв
+
mв
+
 mс
mс
 mа
+
mа
+
 mв
+
mв
+
 mс
mс
 ma
+
mв
+
mс. Үшбұрыштың медианаларының
қосындысы жарты медианаларының қосындысынан кіші болып қалды. Олай
болуы мүмкін емес, қарама-қайшылық пайда болды. Бізде
медианаларының қосындысы кіші емес үлкен болуы керек. Демек,
теңсіздік дәлелденді.
ma
+
mв
+
mс. Үшбұрыштың медианаларының
қосындысы жарты медианаларының қосындысынан кіші болып қалды. Олай
болуы мүмкін емес, қарама-қайшылық пайда болды. Бізде
медианаларының қосындысы кіші емес үлкен болуы керек. Демек,
теңсіздік дәлелденді.
2)
ma +
mв +
mс  2р екенін
дәлелдейік:
2р екенін
дәлелдейік:



ma
В в Е
ma
![]() с
с
![]()
А в С
Дәлелдеу үшін үшбұрышты паралелограмға дейін толықтырайық.
в + с
 2mа
mа
2mа
mа


а + с
 2mв
mв
2mв
mв


а + в
 2mс
mс
2mс
mс


Теңсіздіктің екі жағын мүшелеп қосатын болсақ
ma
+
mв
+
mс

 = а + в + с
= 2р
= а + в + с
= 2р
Демек,
ma
+
mв
+
mс
 2р. Сонымен
теңсіздік дәлелденді.
2р. Сонымен
теңсіздік дәлелденді.
6. ПАРАМЕТРМЕН БЕРІЛГЕН ТЕҢСІЗДІКТЕР, ЛОГАРИФМДІК ТЕҢСІЗДІКТЕР
1.а параметрінің қандай
мәнінде  теңсіздігінің шешімі
болмайды.
теңсіздігінің шешімі
болмайды.
Шешуі:  2+
2+ теңсіздігі үшін анықталу
олысын жазып алайық
теңсіздігі үшін анықталу
олысын жазып алайық
 →
→ 
Логарифмдік функция
қасиеттерін пайдаланып келесі теңсіздікке
келеміз 
одан

5x≤5a+30 , x≤a+6 енді мына теңсіздіктер жүйесін шешеміз
 →
→ 
→

→ → a< 2 шешімі болады Яғни,
шешімі (-ꚙ; 2) аралығына тиесілі, сонда
шешімі жатпайтын аралық [2;ꚙ)
болады.
→ a< 2 шешімі болады Яғни,
шешімі (-ꚙ; 2) аралығына тиесілі, сонда
шешімі жатпайтын аралық [2;ꚙ)
болады.
2. а параметрінің барлық
мәні үшін 
 а
а
 теңсіздігін
шешіңіз.
теңсіздігін
шешіңіз.
Дәлелдеуі:
8-х2
 0
0
х2

х
 ±
2
±
2 Яғни, анықталу облысы
х
Яғни, анықталу облысы
х 
 (а
(а  )2
)2
8 -
х2 а2(х -
4)2
а2(х -
4)2
8 -
х2 а2(
х2
- 8х +
16)
а2(
х2
- 8х +
16)
8 -
х2
-
а2х2
+
8а2х -
16а2 0 -1
бөлсек
0 -1
бөлсек
-8 +
х2
+
а2х2
-
8а2х +
16а2 0
0
(1+а2)х2
–
8а2х +
(16а2
- 8)
 0
0
D![]() = 64а4
–
4(1+а2)
(16а2
- 8)
= 64а4
–
4(16а2
-8 +
16а4
–
8а2)
= 64а4
–
64а2
+ 32 –
64а4
+
32а2
=
= 64а4
–
4(1+а2)
(16а2
- 8)
= 64а4
–
4(16а2
-8 +
16а4
–
8а2)
= 64а4
–
64а2
+ 32 –
64а4
+
32а2
=
-64а2 + 32а2 + 32 = 32 - 32а2
-
D < 0 болса, а2 + 1 > 0 (міндетті түрде 0-ден үлкен болады. Себебі, а – ның орнына қандай санды қойсақ та оң сан шығады) болса параболаның тармағы жоғары қарайды да х
 (-
(- ).
).
32 - 32а2 < 0
1 - а2 < 0
а2 – 1 > 0
a1 > 1, a2 < -1
a
 (
-
(
- ;-1)
;-1) (1;
+
(1;
+ )
)
a >1,
x 

-
D

 =
0
=
0
![]() 32
- 32а2
= 0
+
2 +
32
- 32а2
= 0
+
2 +
a =
 , a =
1
, a =
1
x =
 =
=  =
2
=
2
 > 0
x
> 0
x 

-
D > 0, 32 – 32а2 > 0
а


 a
a


х1/2
= =
=  =
= 
а-ның
орнына a

 аралықтағы сандарды
апарып қойып, тексереміз.
аралықтағы сандарды
апарып қойып, тексереміз.
а
= 0 десек,
 =
= 


а
= 1
десек,
 = 2
= 2



Сонымен,
1) a < 0 болған кезде шешімі жоқ.
2)
a
>1,
x


3) а = 1,
x


4)
a

 ,
x
,
x


3. а параметрінің қандай мәнінде теңсіздіктің жалғыз түбірі болады?
 – (2а +
3)
– (2а +
3)  +
6
+
6  0
0
Шешуі:  = t
деп
белгілесек:
= t
деп
белгілесек:
аt2
– (2а +
3)t
+ 6
 0
0
-
а = 0, -3t + 6
 0
0
-3t
 -6
-6
t
 2
2

 2 , анықталу облысы
х > 0.
2 , анықталу облысы
х > 0.
x
 42
x
42
x
 16
16
Есептің шартында жалғыз түбірі
болатынын табу керек. x  16 аралығында шексіз
көп.
16 аралығында шексіз
көп.
Сондықтан, келесі жағдайды қарастырайық:
-
D = (2а + 3)2 - 4a·6 = 4a2 + 12a + 9 – 24a = 4a2 – 12a + 9 = ( 2a – 3)2
Бізде D = 0 болса, жалғыз түбірі болады.
( 2a – 3)2 = 0
2а – 3 = 0
2а = 3
а = 1,5
t
=  =
=  = 2
= 2
 = 2
= 2
x = 42 = 16
Жауабы: а = 1,5 болғанда х = 16.
4.а параметріне байланысты теңсіздікті шешіңіз:
![]()
Шешуі :
![]()
х –
а2
х2
–
а3х + 2ах +
2а2
 0
0
х=а теңсіздіктің а-ға байланысты шешімі :
ах2+(а2-2)х-2а=(х+а)(ах-2)
![]()
шешу үшін мына жағдайларды қарастырамыз:
a) а> 2 ; шешімі {а }
b) 0<а≤ 2 ;
шешімі 
c) а=0; шешімі [0;∞)
d) - 2 ≤а<0 ; шешімі {а }
е) а<-
2 ;
шешімі  )
)
7. ТЕҢСІЗДІКТЕРДІ ДӘЛЕЛДЕУДЕ ВЕКТОРЛЫҚ ӘДІСТІҢ ҚОЛДАНЫСЫ
 ,
, 
 ,
ǀ
,
ǀ ǀ=
ǀ= ,
ǀ
,
ǀ ǀ=
ǀ=
 ǀ
ǀ ǀ
ǀ
Екі вектордың скаляр көбейтіндісі олардың ұзындықтарының көбейтіндісінен кіші немесе тең болады.
1.Теңсіздікті дәлелдеңіз
:  +
+
Дәлелдеуі: 



Векторлық әдіс қолданып келесі теңсіздіктерді шешейік
 ǀ
ǀ ǀ=
ǀ=

 ǀ=
ǀ= =
= =
=
 ǀ
ǀ ǀ
ǀ
 +
+
 +
+ екі жағында квадраттап
келесі теңсіздікті жазамыз
екі жағында квадраттап
келесі теңсіздікті жазамыз 
 , мүшелеп екі жағында 3х-ке
қысқартамыз
, мүшелеп екі жағында 3х-ке
қысқартамыз
 ,
,  ал
ал



олай
болса  демек
демек  +
+ теңсіздігі
дәлелденді.
теңсіздігі
дәлелденді.
2. Теңсіздікті дәлелдеңіз:
х+у+z=1 x²+y²+z²≥
Дәлелдеуі: Векторлық әдіс қолданып
дәлелдейік, олай болса х+у+z=1
 және
және  векторларының скаляр
көбейтіндісі деп қабылдап .
векторларының скаляр
көбейтіндісі деп қабылдап .
 =
=  болады
деп
болады
деп
және
 (x;y;z) , ал
ұзындығы
(x;y;z) , ал
ұзындығы 
 ·
· ≤ǀ
≤ǀ ǀ·ǀ
ǀ·ǀ ǀ теңсіздігін
қолданып
ǀ теңсіздігін
қолданып  ·
· х+у+z
ал ǀ
х+у+z
ал ǀ ǀ·ǀ
ǀ·ǀ ǀ=
ǀ=
Яғни,
х+у+z
≤ немесе 1
≤
немесе 1
≤
Екі жағын
квадраттап 1 ≤
 , x²+y²+z²≥
, x²+y²+z²≥ екеніне көз
жеткіземіз.
екеніне көз
жеткіземіз.
3. Егер
a+b+c=1 
 теңсіздігі орындалатынын
дәлелдеңіз:
теңсіздігі орындалатынын
дәлелдеңіз:
Дәлелдеуі:  теңсіздігінің сол
жағындағы өрнекті
теңсіздігінің сол
жағындағы өрнекті  және
және  векторларының скаляр
көбейтіндісі деп ,ал оң жағындағы өрнекті осы векторлардың
ұзындықтарының көбейтіндісі деп қарастырамыз
.
векторларының скаляр
көбейтіндісі деп ,ал оң жағындағы өрнекті осы векторлардың
ұзындықтарының көбейтіндісі деп қарастырамыз
.
 =
= 
 (
( )
,
)
,
 =
=
 ·
· =
= ,
ал
,
ал  ǀ·ǀ
ǀ·ǀ ǀ=
ǀ=

 =
=
 ·
· ≤ǀ
≤ǀ ǀ·ǀ
ǀ·ǀ ǀ екені белгілі ,
сондықтан
ǀ екені белгілі ,
сондықтан  теісіздігі
орындалады.
теісіздігі
орындалады.
4.
 теңсіздігі
орындалатынын дәлелдеңіз, мұндағы a>0, b>0, c>0 белгілі
болса
теңсіздігі
орындалатынын дәлелдеңіз, мұндағы a>0, b>0, c>0 белгілі
болса
Дәлелдеуі:  теңсіздігін дәлелдеу
үшін векторлық әдіс қолданамыз, яғни , теңсіздіктің сол жақ
бөлігіндегі өрнектен
теңсіздігін дәлелдеу
үшін векторлық әдіс қолданамыз, яғни , теңсіздіктің сол жақ
бөлігіндегі өрнектен  және
және  векторларының
координатоларын бөліп аламыз
векторларының
координатоларын бөліп аламыз

 =(
=(

 =(
=(

 және
және  векторларының
ұзындықтары тең екенін байқаймыз
векторларының
ұзындықтары тең екенін байқаймыз
 =ǀ
=ǀ =
=
 олай болса олардың
ұзындықтарының көбейтіндісі ǀ
олай болса олардың
ұзындықтарының көбейтіндісі ǀ ·ǀ
·ǀ =
= =
=
 ·
· ≤ǀ
≤ǀ ǀ·ǀ
ǀ·ǀ ǀ екі вектордың скаляр
көбейтіндісі олардың ұзындықтарының көбейтіндісінен кіші немесе тең
болғандықтан
ǀ екі вектордың скаляр
көбейтіндісі олардың ұзындықтарының көбейтіндісінен кіші немесе тең
болғандықтан
 теңсіздігі
орындалады. Демек, дәлелденді.
теңсіздігі
орындалады. Демек, дәлелденді.
8. МАТЕМАТИКАЛЫҚ ИНДУКЦИЯ
1. Егер a және b - катет,
ал с- тікбұрышты үшбұрыштың гипотенузасы болса, онда барлық n≥2
натурал сандар үшін  +
+ ≤
≤ теңсіздігі
орындалатындығын дәлелдеңдер.
теңсіздігі
орындалатындығын дәлелдеңдер.
Дәлелдеуі: Математематикалық индукция әдісін қолданып
n=2 үшін
орындалатын  +
+ =
= дұрыс деп
қабылдаймыз,
дұрыс деп
қабылдаймыз,
келесі
n=k  +
+ ≤
≤ дұрыс деп
ұйғарамыз
дұрыс деп
ұйғарамыз
олай болса n=k+1
үшін  +
+ ≤
≤ теңсіздігін
қарастырамыз,
теңсіздігін
қарастырамыз,
дәреже қасиеттерін пайдаланып
мына түріне келтіріп аламыз  +
+ ≤
≤ c. Тік бұрышты үшбұрышта
катеттері a<c, b<c болғандықтан мына түріне келтіріп
жазамыз
c. Тік бұрышты үшбұрышта
катеттері a<c, b<c болғандықтан мына түріне келтіріп
жазамыз  +
+ ≤
≤ , ортақ көбейткішін
жақша сыртына шығарып, екі жағында с-ға қысқартып
c(
, ортақ көбейткішін
жақша сыртына шығарып, екі жағында с-ға қысқартып
c( +
+ ≤
≤ , мына түріне
келтіреміз
, мына түріне
келтіреміз  +
+ ≤
≤ , осымен теңсіздік
дәлелденді.
, осымен теңсіздік
дәлелденді.
2. a ≥-1 Болғанда кез келген натурал сан а үшін мына теңсіздіктің (1+a)≥1+na орындалатындығын дәлелдеңдер.
Дәлелдеуі: математикалық индукция әдісін қолданып n=2 деп алып келесі теңсіздікті (1+a)²≥1+na, 1+2a+a²≥1+na дұрыс деп аламыз
n=k болғанда мына
теңсіздікті  дұрыс деп
үйғарамыз,
дұрыс деп
үйғарамыз,
енді n=k+1 болғанда келесі
теңсіздіктерге келеміз 

3.
Натурал сан n-нің кез
келген n мәндерінде
мәндерінде  теңсіздігі
орындалатынын дәлелдеңдер.
теңсіздігі
орындалатынын дәлелдеңдер.
Дәлелдеуі: n=3 дейік, олай болса 2³>7, яғни 8>7
n=k болса
 деп
үйғарамыз
деп
үйғарамыз
n=k+1
болғанда  жақшасын ашып келесі
теңсіздікті жазамыз
жақшасын ашып келесі
теңсіздікті жазамыз  теңсіздіктің екі жағында
түрлендіріп
теңсіздіктің екі жағында
түрлендіріп  келесі теңсіздіктер
жүйесін қарастырамыз
келесі теңсіздіктер
жүйесін қарастырамыз

 .
.
 яғни,
n
яғни,
n мәндерінде
мәндерінде  теңсіздігі орындалатыны
дәлелденді.
теңсіздігі орындалатыны
дәлелденді.
4.
Теріс емес a,b,c,d сандары
үшін келесі  теңсіздік
орындалатынын дәлелдеңіз
теңсіздік
орындалатынын дәлелдеңіз
Дәлелдеуі:
 ≥
≥ сандардың арифметикалық
ортасы олардың геометриялық ортасынан үлкен
болады
сандардың арифметикалық
ортасы олардың геометриялық ортасынан үлкен
болады
Екі санның арифметикалық
ортасы ≥
≥ ,
,
үш санның арифметикалық
ортасы  , олай
болса
, олай
болса
төрт санның арифметикалық
ортасы  . Теңсіздік
дәлелденді
. Теңсіздік
дәлелденді
5. Кез келген натурал n сан үшін (1+(1:2))(1+(1:5))…(1+(2:(n²+3n))) < 3 теңсіздігі орындалатынын дәлелдеңіз.
Дәлелдеуі: математикалық индукция әдісін қолданып
n=1 (1+(1:2))(1+(1:5))…(1+(2:(1²+3·1))) < 3
n=k (1+(1:2))(1+(1:5))…(1+(2:(k²+3k))) < 3 деп үйғарамыз
n=k+1 (1+(1:2))(1+(1:5))… (1+(2:(k²+3k) (1+(2:((k+1)²+3(k+1))) < 3
(1+ )
(1+
)
(1+ )
...(1+
)
...(1+ )
(1+
)
(1+ ) <
3·1+
) <
3·1+ )
)
(1+ )
(1+
)
(1+ )
...(
)
...( )
(
)
( ) <
3·
) <
3· )
)


 ,
, 
 салыстырамыз, ол ұшін ортақ
бөлімге келтіреміз , сонда
салыстырамыз, ол ұшін ортақ
бөлімге келтіреміз , сонда

 , яғни теңсіздік
дәлелденді.
, яғни теңсіздік
дәлелденді.
6. Кез келген x,y,z сандары
үшін бір мезетте  теңсіздіктері
орындалмайтынын дәлелдеңіз.
теңсіздіктері
орындалмайтынын дәлелдеңіз.
Дәлелдеуі:  теңсіздңктерң орындалады
делік, олай болса осы теңсіздіктердің екі жағында квадраттап, оң
жағындағыларды сол жағына өткізіп жіберіп, көбейткіштерге жіктеп,
пайда болған теңсіздіктерді мүшелеп көбейтіп
көрейік
теңсіздңктерң орындалады
делік, олай болса осы теңсіздіктердің екі жағында квадраттап, оң
жағындағыларды сол жағына өткізіп жіберіп, көбейткіштерге жіктеп,
пайда болған теңсіздіктерді мүшелеп көбейтіп
көрейік
 ,
,  ,
,
(х-у+z)(x+y-z)<0

 ,
,
(y-z+x)(y+z-x)<0

 <
0,
<
0,
(z-x+y)(z+x-y)<0
Соңғы теңсіздіктерді мүшелеп көбейткенде келесі теңсіздік пайда болады
((х-у+z)(x+y-z) (z-x+y
))²<0 яғни, қарамақайшылық
пайда болғанына көз жеткіземіз. Кез келген x,y,z сандары үшін
бір мезетте  теңсіздіктері
орындалмайтыны дәлелденді.
теңсіздіктері
орындалмайтыны дәлелденді.
7. Теңсіздікті дәлелдеңіз:
18( )>
)>
Дәлелдеуі: 18( )>
)> теңсіздігін дәлелдеу
үшін
теңсіздігін дәлелдеу
үшін
(x-y)²≥0 теңсіздігін қолданамыз
x²-2xy+y²≥0
x²+y²≥2xy бұл теңсіздіктің екі жағынада x²+y² қосамыз, сонда
2(x²+y²)≥(х+у)²
x=3a² y=3b² келесі теңсіздікті жазамыз
2(9 +9
+9 )≥(3a²+3b²)²
)≥(3a²+3b²)²
18( +
+ )≥(3a²+3b²)²
)≥(3a²+3b²)²
18( +
+ )≥9(a²+b²)² ,
теңсідіктің оң жағына a²+b²≥2ab деп әрекетті қайталап екі жағынада
a²+b² қосқанда 2(a²+b²)≥(a+b)² шығады.
Яғни,
)≥9(a²+b²)² ,
теңсідіктің оң жағына a²+b²≥2ab деп әрекетті қайталап екі жағынада
a²+b² қосқанда 2(a²+b²)≥(a+b)² шығады.
Яғни,
18( +
+ )≥18(a²+b²)²≥((a+b)²)²
≥
)≥18(a²+b²)²≥((a+b)²)²
≥
Олай болса
18( )>
)> теңсіздігі дәлелденді
десек болады.
теңсіздігі дәлелденді
десек болады.
8. a+b≥1 белгілі болса,
онда  ≥
≥ теңсіздігі
орындалатынын дәлелдеңіз.
теңсіздігі
орындалатынын дәлелдеңіз.
Дәлелдеуі:  ≥
≥ теңсіздігін дәлелдеу
үшін
теңсіздігін дәлелдеу
үшін  ≥
≥ теңсіздігін дәлелдесек
жеткілікті. Ол үшін (x-y)²≥0 теңсіздігін қолданамыз, жақшаны ашамыз
x²-2xy+y²≥0
теңсіздігін дәлелдесек
жеткілікті. Ол үшін (x-y)²≥0 теңсіздігін қолданамыз, жақшаны ашамыз
x²-2xy+y²≥0
x²+y²≥2xy бұл теңсіздіктің екі жағынада x²+y² қосамыз, сонда
2(x²+y²)≥(х+у)²
x=2a² y=2b² алмастыру еңгізіп, келесі теңсіздікті жазамыз
2(4 +4
+4 )≥(2a²+2b²)²
)≥(2a²+2b²)²
8( +
+ )≥(2a²+2b²)²
)≥(2a²+2b²)²
8( +
+ )≥4(a²+b²)² ,
теңсідіктің оң жағына a²+b²≥2ab деп әрекетті қайталап екі жағынада
a²+b² қосқанда 2(a²+b²)≥(a+b)² шығады.
Яғни,
)≥4(a²+b²)² ,
теңсідіктің оң жағына a²+b²≥2ab деп әрекетті қайталап екі жағынада
a²+b² қосқанда 2(a²+b²)≥(a+b)² шығады.
Яғни,
8( +
+ )≥4(2(a²+b²)²)≥8((a+b)²)² ≥
)≥4(2(a²+b²)²)≥8((a+b)²)² ≥ ≥1
≥1
 +
+ )≥
)≥ теңсіздік
дәлелденді.
теңсіздік
дәлелденді.
9. ТАПСЫРМАЛАР
-
Катеттері ? және в, ал гипотенузасы ? болатын тікбұрышты үшбұрыш үшін ?в+??+в?
 2с2
теңсіздігі орындалатынын
дәлелдеңіздер.
2с2
теңсіздігі орындалатынын
дәлелдеңіздер.
Нұсқау: Сол жағына Коши теңсіздігін , ары қарай пифагор теоремасын қолданыңыз.
-
Егер ?,в,? – үшбұрыштың қабырғалары болса, онда ?2+в2+?2 <2(?в+в?+??)
теңсіздігі орындалатынын дәлелдеңіздер.
Нұсқау: Үшбұрыштың екі қабырғасының ұзындығының айырмасы үшінші қабырғасынан кіші деген қасиетін қолданып, ары қарай квадраттаңыз.
-
Жарты периметрі ?−ға тең кез келген үшбұрыштың ауданы ?
 теңсіздігі
орындалатынын дәлелдеңіз.
теңсіздігі
орындалатынын дәлелдеңіз.
Нұсқау: Герон формуласын, сосын Коши теңсіздігін қолданыңыз.
-
Теңсіздікті дәлелдеңіз: ?2 + в2 + ?2 + 2?в?
 2,
мұндағы ?,
в,
?
− периметрі 2−ге тең болатын
үшбұрыштың қабырғалары.
2,
мұндағы ?,
в,
?
− периметрі 2−ге тең болатын
үшбұрыштың қабырғалары.
Нұсқау: ?
+
в
+
?
= 2,
?<1,
?<1,
? . Яғни
(1-а)(1-в)(1-с)
. Яғни
(1-а)(1-в)(1-с) 
 . Ары қарай жақшаларды ашып,
түрлендіріңіз.
. Ары қарай жақшаларды ашып,
түрлендіріңіз.
-
Егер ?, в, ? – үшбұрыштың қабырғалары болса, онда
(? + в − ?)(? + ? − в)(? + в − ?) ≤ ?в? теңсіздігі орындалатынын дәлелдеңіздер.
Нұсқау: ? + в – ? = ?, ? + ? – в = ?, ? + в – ? = ? деп белгілеп алып, ?, в, ?
сандарын ?, ?, ? арқылы өрнектеңіз. Сосын, теңсіздікті қолданыңыз.
-
Кез келген тікбұрышты үшбұрышта 0,4


 0,5
болатынын дәлелдеңіз,
мұндағы r − іштей сызылған шеңбердің
радиусы, ал ℎ − гипотенузаға түсірілген
биіктік.
0,5
болатынын дәлелдеңіз,
мұндағы r − іштей сызылған шеңбердің
радиусы, ал ℎ − гипотенузаға түсірілген
биіктік.
Нұсқау:  hc=pr,
hc=pr,
 =
=  формулаларын
қолданыңыз.
формулаларын
қолданыңыз.
-
Егер ?, в, ? – үшбұрыштың қабырғалары болса, онда 2
 ≤
?
орындалатынын дәлелдеңіз,
мұндағы ?
− жарты
периметр.
≤
?
орындалатынын дәлелдеңіз,
мұндағы ?
− жарты
периметр.
Нұсқау: Коши теңсіздігін дұрыс қолдансаңыз, жеткілікті.
-
Егер ?, в, ? – үшбұрыштың қабырғалары болса, онда
 +
+  +
+
 ≤
≤  орындалатынын
дәлелдеңіз, мұндағы ?
− жарты
периметр.
орындалатынын
дәлелдеңіз, мұндағы ?
− жарты
периметр.
Нұсқау: теңсіздіктің екі жағын квадраттап, Коши теңсіздігін қолданыңыз.
-
Катеттері ? және ?, ал гипотенузасы ? болатын тікбұрышты үшбұрыш үшін
 +
+
 >
>  теңсіздігі орындалатынын
дәлелдеңіздер.
теңсіздігі орындалатынын
дәлелдеңіздер.
Нұсқау: үшбұрыш теңсіздігін қолданыңыз.
-
Қабырғалары ?, в, ?, ? болатын дөңес төртбұрыштың ауданы ? болса, онда ? ≤
 теңсіздігінің
орындалатынын дәлелдеңіз.
теңсіздігінің
орындалатынын дәлелдеңіз.
Нұсқау: дөңес төртбұрышты үшбұрыштардың қосындысы түрінде жазып алып, ол үшбұрыштардың ауданын бағалаңыз.
-
Кез келген натурал n саны үшін 1 +
 теңсіздігі орындалатынын
дәлелдеңіздер.
теңсіздігі орындалатынын
дәлелдеңіздер. -
Теңсіздікті дәлелдеңіздер:


 .
.
-
 болатынын
дәлелдеңдер.
болатынын
дәлелдеңдер.
-
Теңсіздікті дәлелдеңіздер:
1 +
 (
n
(
n  N,
n
N,
n
 2) .
2) .
-
Егер а, в, с - натурал сандар болса, онда ав + вс + са
 3авс болатынын
дәлелдеңіздер.
3авс болатынын
дәлелдеңіздер.
Нұсқау: а, в, с – натурал сан, демек ав саны авс санынан кіші.
-
Теңсіздікті дәлелдеңдер: а2 + в2
 с2
+ ( а + в –
с)2, мұндағы
а > с, с
> в.
с2
+ ( а + в –
с)2, мұндағы
а > с, с
> в. -
Теңсіздікті дәлелдеңдер:


 , мұндағы а, в >
0.
, мұндағы а, в >
0. -
Теңсіздікті дәлелдеңдер:


 , мұндағы а, в >
0.
, мұндағы а, в >
0. -
Теңсіздікті дәлелдеңдер:


 , мұндағы а, в >
0.
, мұндағы а, в >
0. -
а, в > 0 болғанда,
 теңсіздігі орындалатынын
дәлелдеңдер.
теңсіздігі орындалатынын
дәлелдеңдер. -
Теңсіздікті дәлелдеңдер: (х + 1)·(х – 2у + 1) + у2
 0
0 -
х – тің кез келген мәнінде х12 - х9 + х4 – х + 1 > 0 екенін дәлелдеңдер.
-
Теңсіздікті дәлелдеңдер: а + в
 1 + ав, мұндағы
а >1, в
< 1.
1 + ав, мұндағы
а >1, в
< 1. -
Егер а + в = 1 болса, онда а2 + в2
 болатынын
дәлелдеңдер.
болатынын
дәлелдеңдер. -
Егер а + в + с = 1, мұндағы а, в, с > 0 болса, онда (1 – а)(1 – в)(1 – с)
 8авс теңсіздігі
орындалатынын дәлелдеңдер.
8авс теңсіздігі
орындалатынын дәлелдеңдер.
Нұсқау: 1 – а = в + с, ары қарай Коши теңсіздігін қолданыңыз.
-
Айталық а, в, с – теріс емес сандар және а + в + с = 1 болсын. Теңсіздіктің дұрыстығын дәлелдеңдер: (1 + а)(1 + в)(1 + с)
 8(1 – а)(1 – в)(1 –
с)
8(1 – а)(1 – в)(1 –
с)
Нұсқау: 1 + а = 2 – в – с = (1 – в) + (1 – с) ары қарай Коши теңсіздігі.
-
Егер авсd = 1 және а > 0, в > 0, c > 0, d >0 болса, онда а2 + в2 + с2 + d2 + ав + ас + аd + вс + вd + сd
 10 теңсіздігі
орындалатынын дәлелдеңдер.
10 теңсіздігі
орындалатынын дәлелдеңдер.
Нұсқау:  ,
ав + вс
,
ав + вс
 осылай Коши
теңсіздігін қолданыңыз.
осылай Коши
теңсіздігін қолданыңыз.
-
х, у сандары үшін ху = 1 және х > у болса, мына теңсіздіктің
 орындалатынын
дәлелдеңдер.
орындалатынын
дәлелдеңдер.
Нұсқау: сол жағындағы өрнектің алымын х – у квадратына келтіріңіз.
-
Егер а, в, с – көбейтіндісі 1-ге тең нақты сандар болса, онда а + в + с + ав + ас + вс
 6 теңсіздігінің
орындалатынын дәлелдеңдер.
6 теңсіздігінің
орындалатынын дәлелдеңдер.
Нұсқау: авс = 1 болғандықтан ав
=  ...
...
-
Егер а2 + в2 + с2 = 1 болса, онда
 +
+
 +
+  < 4 теңсіздігінің орындалатынын
дәлелдеңдер.
< 4 теңсіздігінің орындалатынын
дәлелдеңдер.
Нұсқау:  осылай Коши теңсіздігін
қолданыңыз.
осылай Коши теңсіздігін
қолданыңыз.
Шешімдері
1.Катеттері ?
және ?, ал
гипотенузасы ?
болатын тікбұрышты үшбұрыш
үшін ??+??+??
 2с2 теңсіздігі орындалатынын
дәлелдеңіздер.
2с2 теңсіздігі орындалатынын
дәлелдеңіздер.
Дәлелдеуі: Сол жағына Коши теңсіздігін қолданып, сосын Пифагор теоремасын қолданамыз:




 ав;
ав;

ав + ас +
вс 
 +
+
 +
+
 =
=
 =
= =
=
 =
2
=
2
Сонымен, теңсіздік дәлелденді.
2.Егер ?,в,? – үшбұрыштың қабырғалары болса, онда ?2+в2+?2 < 2(?в+в?+??) теңсіздігі орындалатынын дәлелдеңіздер.
Дәлелдеуі: Үшбұрыштың екі қабырғасының
ұзындығының айырмасы үшінші қабырғасынан кіші деген қасиетін
қолданып, ары қарай квадраттаймыз: 


2а2
+
2в2
+
2с2
-2(ав + ас +
вс)  ?2+в2+?2
?2+в2+?2
?2+в2+?2
 2(ав + ас +
вс)
2(ав + ас +
вс)
Сонымен, теңсіздік дәлелденді.
3.Жарты
периметрі ?−ға тең кез келген
үшбұрыштың ауданы ?
 теңсіздігі
орындалатынын дәлелдеңіз.
теңсіздігі
орындалатынын дәлелдеңіз.
Дәлелдеуі: Герон
формуласы: S
=  , р
=
, р
= 
 а+в+с
= 2р
а+в+с
= 2р
р(р-а) = а,
(р-в)(р-с) = в деп алып, Коши
теңсіздігін 
 қолданамыз.
қолданамыз. 



 =
=
 =
=  =
=
 =
= 

Сонымен, теңсіздік дәлелденді.
4.Теңсіздікті дәлелдеңіз:
?2 +
в2 +
?2 +
2?в?  2,
мұндағы ?,
в,
?
− периметрі 2−ге тең
болатын үшбұрыштың қабырғалары.
2,
мұндағы ?,
в,
?
− периметрі 2−ге тең
болатын үшбұрыштың қабырғалары.
Дәлелдеуі: ?
+
в
+
?
= 2,
?<1,
?<1,
? . Яғни, (1 - а)(1 - в)(1 -
с)
. Яғни, (1 - а)(1 - в)(1 -
с)  .
Сосын, жақшаларды ашып,
түрлендіріп, (а+в+с)2
=
.
Сосын, жақшаларды ашып,
түрлендіріп, (а+в+с)2
=
 қолданамыз:
қолданамыз:
(1 - а)(1 - в)(1 -
с) = (1 – в – а + ав)(1 –
с) = 1 – с – в + вс – а + ас + ав –
авс = 1 – (а + в + с) + ав + вс + ас
– авс = 1 – 2 +
 -
-  +
+
 + вс + ас –
авс =
-1 +
+ вс + ас –
авс =
-1 +  -
-
 –
авс = -1 +
–
авс = -1 +
 -
-  –
авс = 1 -
–
авс = 1 -
 -
авс
-
авс
1 -
 –
авс
–
авс  0
0
2 -
 –
2авс
–
2авс  0 /
(-1)
0 /
(-1)  +
2авс
+
2авс  2
2
Сонымен, теңсіздік дәлелденді.
5.Егер ?, в, ? – үшбұрыштың қабырғалары болса, онда
(? + в − ?)(? + ? − в)(? + в − ?) ≤ ?в? теңсіздігі орындалатынын дәлелдеңіздер.
Дәлелдеуі: ? + в – ? = ?, ? + ? – в = ?, ? + в – ? = ? деп белгілеп алып, ?, в, ?
сандарын ?, ?, ? арқылы өрнектеп, теңсіздікті қолданамыз:
? + в – ? = ?  а + в = m +
с
а + в = m +
с
 теңдіктің екі жағын
мүшелеп қосамыз
теңдіктің екі жағын
мүшелеп қосамыз
а + в – с + с + а – в + с + в – а = m + n + p
а + в + с = m + n + p
m + c + c = m + n + p
2c = n + p
c =
 ; в =
; в =
 ; a =
; a =

n + p = 2c; m + n = 2в; m + p = 2а
 теңсіздіктің екі
жағын мүшелеп көбейтеміз
теңсіздіктің екі
жағын мүшелеп көбейтеміз



mnp

 =
=

mnp
 авс
авс
(? + в − ?)(? + ? − в)(? + в − ?) ≤ ?в?
Демек, теңсіздік дәлелденді.
-
Кез келген тікбұрышты үшбұрышта 0,4


 0,5 болатынын дәлелдеңіз,
мұндағы r − іштей сызылған шеңбердің
радиусы, ал ℎ − гипотенузаға түсірілген
биіктік.
0,5 болатынын дәлелдеңіз,
мұндағы r − іштей сызылған шеңбердің
радиусы, ал ℎ − гипотенузаға түсірілген
биіктік.
Дәлелдеуі:  hc=pr
,
hc=pr
,
 =
=  формулаларын
қолданамыз:
формулаларын
қолданамыз:
 hc =
hc =


а + в
> с




 0,5
0,5







 /
/  көбейтеміз
көбейтеміз
c
> 
а + в
<  с
с
 >
>  =
= 
 > 0,4
> 0,4
Сонымен, теңсіздік дәлелденді.
7.
Егер ?,
в,
?
– үшбұрыштың қабырғалары
болса, онда 2 ≤ ?
орындалатынын дәлелдеңіз,
мұндағы ?
− жарты
периметр.
≤ ?
орындалатынын дәлелдеңіз,
мұндағы ?
− жарты
периметр.
Дәлелдеуі: Коши теңсіздігін
қолданамыз: а + в
 2
2
Жарты периметріміз
: р
= 
2
 р – с + р – в = 2р – с – в = а + в + с – с
– в = а
р – с + р – в = 2р – с – в = а + в + с – с
– в = а
2
 а. Теңсіздік
дәлелденді.
а. Теңсіздік
дәлелденді.
8.Егер ?, в, ? – үшбұрыштың қабырғалары болса, онда
 +
+  +
+  ≤
≤  орындалатынын
дәлелдеңіз, мұндағы ?
− жарты
периметр.
орындалатынын
дәлелдеңіз, мұндағы ?
− жарты
периметр.
Дәлелдеуі: теңсіздіктің екі жағын квадраттап, Коши теңсіздігін қолданамыз:
 +
+  +
+
 2
≤
2
≤
 )2
)2
р – а + р – в + р – с
+ 2
 3р
3р
3р – а – в – с + р – а + р – в
+ р – а + р – с + р – в + р – с 
9р – 3а – 3в –
3с 
9р – 3(а + в +
с) 
9р – 3 ·
2р 
3р

Демек, теңсіздік дәлелденді.
9.Катеттері ?
және ?, ал
гипотенузасы ?
болатын тікбұрышты үшбұрыш
үшін  +
+  >
>  теңсіздігі
орындалатынын дәлелдеңіздер.
теңсіздігі
орындалатынын дәлелдеңіздер.
Дәлелдеуі: Үшбұрыш теңсіздігін қолданамыз: a + в > c
 +
+  2 >
2 >  2
2
а +
2 + в
> c
+ в
> c
a + в > c
с +
2 > c
> c
2 > 0
> 0
Теңсіздік дәлелденді.
10.
Қабырғалары ?,
в, ?,
?
болатын дөңес төртбұрыштың
ауданы ?
болса,
онда ?
≤
 теңсіздігінің
орындалатынын дәлелдеңіз.
теңсіздігінің
орындалатынын дәлелдеңіз.
Дәлелдеуі: Дөңес төртбұрышты үшбұрыштардың қосындысы түрінде жазып алып, ол үшбұрыштардың ауданын қолданамыз:

![]() в
в
с
 =
= 
а
d
0 <
 <
1
<
1
 =
= 


 =
= 


 =
= 


 =
= 


Осы үшбұрыштың аудандарын мүшелеп қосамыз:
S =


2S


S


S


Теңсіздік дәлелденді.
11. Кез келген натурал n
саны үшін 1 +  теңсіздігі
орындалатынын дәлелдеңіздер.
теңсіздігі
орындалатынын дәлелдеңіздер.
Дәлелдеуі:








 Енді осы түрлендіруді
теңсіздіктің сол жағына жазамыз:
Енді осы түрлендіруді
теңсіздіктің сол жағына жазамыз:
1+ 1 -
 +
+  +...+
+...+ 

-
-



n = 4 деп алатын
болсақ,  =
=

 Теңсіздік
дәлелденді.
Теңсіздік
дәлелденді.
12. Теңсіздікті дәлелдеңіздер:


 .
.
Дәлелдеуі:  =
=
 <
<  =
=
 = 1
-
= 1
-  =
=
 =
= 
Демек, үлкейтілген өрнектің
өзі  тең болса,
онда
тең болса,
онда 
 болады.
Дәлелденді.
болады.
Дәлелденді.
13.  болатынын
дәлелдеңдер.
болатынын
дәлелдеңдер.
Дәлелдеуі: 2000 – 1001 + 1 = 1000 мүше бар

 ( 1000 рет
қоссақ)
( 1000 рет
қоссақ)

 =
=
 Сонымен, теңсіздік
дәлелденді.
Сонымен, теңсіздік
дәлелденді.
14. Теңсіздікті дәлелдеңіздер:
1
+  (
n
(
n  N,
n
N,
n  2)
.
2)
.
Дәлелдеуі: n мүше бар
1 +

 = n
·
= n
·  =
=
 =
=  Дәлелденді.
Дәлелденді.
15. Егер а, в, с - натурал
сандар болса, онда ав + вс + са  3авс болатынын
дәлелдеңіздер.
3авс болатынын
дәлелдеңіздер.
Дәлелдеуі: а, в, с натурал сандар болғандықтан ав саны авс санынан кіші болады. Теңсіздіктің сол жағын үлкейтіп алып, теңсіздіктерін мүшелеп қоссақ:
ав
 авс
авс
вс
 авс
авс
ас
 авс
авс
ав + вс +
ас  3авс
3авс
Демек, теңсіздік дәлелденді.
16.Теңсіздікті дәлелдеңдер:
а2 +
в2  с2 + ( а + в –
с)2, мұндағы
а > с,
с > в.
с2 + ( а + в –
с)2, мұндағы
а > с,
с > в.
Дәлелдеуі:
а2
+
в2
 с2
+
а2
+
в2
с2
+
а2
+
в2
 с2
+ 2ав – 2ас –
2вс
с2
+ 2ав – 2ас –
2вс
с2
+
а2
+
в2
 с2
-
а2
-
в2
+ 2ав – 2ас –
2вс < 0
с2
-
а2
-
в2
+ 2ав – 2ас –
2вс < 0
2c2 + 2ав – 2ас – 2вс < 0 / 2-ге бөлеміз
c2 + ав – ас – вс < 0
(c2 – ас) – (вс – ав) < 0
(c2 – ас) – (вс – ав) < 0
с(с – а) –в(с – а) < 0
(с – а)(с – в) < 0
Берілгенінен а > с, с > в шартын қолдансақ,
а – с
> 0  с –
а < 0, с – в
> 0
болады.
с –
а < 0, с – в
> 0
болады.
Демек, (с – а)(с – в) < 0
( - )·( + ) = ( - ) < 0 Теңсіздік дәлелденді.
17. Теңсіздікті
дәлелдеңдер: 

 , мұндағы а, в >
0.
, мұндағы а, в >
0.
Дәлелдеуі: Теңсіздіктің оң жақ бөлігін түрлендіреміз:


 =
=  =
=
 / (а+в) көбейтеміз.
Себебі, есептің шартында а мен в оң сандар.
/ (а+в) көбейтеміз.
Себебі, есептің шартында а мен в оң сандар.

 2ав
/
2ав
/  бөлсек
бөлсек
а + в


а + в


а + в
 2
2 біздің теңсіздігіміз
Коши теңсіздігіне келеді. Демек, теңсіздік
дәлелденді.
біздің теңсіздігіміз
Коши теңсіздігіне келеді. Демек, теңсіздік
дәлелденді.
18.Теңсіздікті
дәлелдеңдер: 

 , мұндағы а, в >
0.
, мұндағы а, в >
0.
Дәлелдеуі: Теңсіздіктің оң жақ бөлігін түрлендіреміз:


 =
=  =
=
 / (а+в) көбейтеміз.
Себебі, есептің шартында а мен в оң
сандар.
/ (а+в) көбейтеміз.
Себебі, есептің шартында а мен в оң
сандар.

 2ав
2ав
(а +
в)2
 4ав
4ав
а2
+ 2ав +
в2 0
0
а2
- 2ав +
в2 0
0
(а -
в)2
 0
0
Сонымен, теңсіздік дәлелденді.
19. Теңсіздікті
дәлелдеңдер: 

 , мұндағы а, в >
0.
, мұндағы а, в >
0.
Дәлелдеуі:



 / 4-ке
көбейтсек,
/ 4-ке
көбейтсек,
 2а2
+
2в2
2а2
+
2в2
 а2
+ 2ав +
в2
а2
+ 2ав +
в2
2а2
+
2в2
-
а2
- 2ав -
в2
 0
0
а2
- 2ав +
в2
 0
0
(а –
в)2
 0
0
Сонымен, теңсіздік дәлелденді.
20. а, в > 0
болғанда,  теңсіздігі
орындалатынын дәлелдеңдер.
теңсіздігі
орындалатынын дәлелдеңдер.
Дәлелдеуі:
а + в
 2
2 Коши теңсіздігін
қоладанамыз.
Коши теңсіздігін
қоладанамыз.
а2
+
в2 2ав
2ав
Теңсіздіктің сол жақ бөлігін кішірейтсек:
 +
+  =2
·
=2
·



Сол жақ бөлігін кішірейткеннің өзінде теңсіздік оң жағынан үлкен болып тұр. Демек, теңсіздік дәлелденді.
21. Теңсіздікті дәлелдеңдер:
(х + 1)·(х – 2у + 1) +
у2  0
0
Дәлелдеуі:
х2
– 2ху + х + х – 2у + 1 +
у2
 0
0
(
х2
– 2ху +
у2) + (2х – 2у)
+1  0
0
(х –
у)2
+ 2(х – у) +
1  0 х –
у = t
0 х –
у = t
t2 +
2t
+ 1  0
0
(t
+
1)2
 0
0  (х – у +
1)2
(х – у +
1)2
 0
0
Сонымен, теңсіздік дәлелденді.
22. х – тің кез келген мәнінде
х12 - х9 + х4 – х + 1 > 0 екенін дәлелдеңдер.
Дәлелдеуі:
х
 х12
-
х9
+
х4
– х + 1
> 0
х12
-
х9
+
х4
– х + 1
> 0
0
 1 – х +
х4(1 –
х5) +
х12
1 – х +
х4(1 –
х5) +
х12
 0
0
(1 – х)
 0,
х4(1 –
х5)
0,
х4(1 –
х5)
 0,
х12
0,
х12
 0
0
х
 1;
х9(х3
– 1) +
х(х3
– 1) + 1
1;
х9(х3
– 1) +
х(х3
– 1) + 1
 0
0
Теріс санды теріс санға көбейтсек оң сан шығатыны белгілі, олай болса
х9(х3
– 1)
 0 ,
х(х3
– 1)
0 ,
х(х3
– 1)
 0
0
Сонымен, теңсіздік дәлелденді.
23. Теңсіздікті
дәлелдеңдер: а + в  1 + ав, мұндағы
а >1, в
< 1.
1 + ав, мұндағы
а >1, в
< 1.
Дәлелдеуі:
а + в
 1 -
ав
1 -
ав  0
0
(а – 1) –в(а –
1)  0
0
(а – 1)(1 –
в)  0
0
Енді, берілгенінен а >1, в < 1 шартын қолдансақ:
а – 1
 0, в –
1
0, в –
1  0
0
 1 –
в
1 –
в  0
0
Демек, (+)
·(+)  0. Теңсіздік
дәлелденді.
0. Теңсіздік
дәлелденді.
24. Егер а +
в = 1 болса, онда
а2 +
в2  болатынын
дәлелдеңдер.
болатынын
дәлелдеңдер.
Дәлелдеуі:
а + в
= 1  в
= 1 - а
в
= 1 - а
а2
+ (1 –
а)2

а2
+ 1 – 2а +
а2

2а2
– 2а + 1

2а2
– 2а
 -
1
-
1
2а2
– 2а
 / 2-ге
көбейтсек
/ 2-ге
көбейтсек
4а2
– 4а

4а2
– 4а + 1

(2а –
1)2

Сонымен, теңсіздік дәлелденді.
25. Егер а + в +
с = 1, мұндағы а, в,
с > 0 болса, онда (1 – а)(1 –
в)(1 – с)  8авс теңсіздігі
орындалатынын дәлелдеңдер.
8авс теңсіздігі
орындалатынын дәлелдеңдер.
Дәлелдеуі:
1 – а = в + с түрлендіріп, ары қарай Коши теңсіздігін қолданыңыз.
1 – а = в + с, 1 – в = а + с,
1 – с = а + в, в + с =
2 , а + с
= 2
, а + с
= 2 , а +
в =
2
, а +
в =
2
(в + с)(а + с)(а +
в)  2
2 = 8
= 8 =
8
=
8 =
8
=
8 8авс
8авс  8авс
8авс
Теңсіздіктің сол жақ бөлігін кішірейткенде, оң жақ бөлігіне тең болды. Олай болса, теңсіздік дәлелденді.
26. Айталық а, в, с – теріс емес сандар және а + в + с = 1 болсын. Теңсіздіктің дұрыстығын дәлелдеңдер:
(1 + а)(1 + в)(1 +
с)  8(1 – а)(1 – в)(1 –
с)
8(1 – а)(1 – в)(1 –
с)
Дәлелдеуі:
1 + а = 2 – в – с = (1 – в) + (1 – с) деп түрлендіріп алып, ары қарай Коши теңсіздігін қолданамыз.
1 + а
= (1 – в) + (1 –
с)  (1 – в) + (1 –
с)
(1 – в) + (1 –
с) 
1 + в
= 2 – а – с = (1 – а) + (1 –
с)  (1 – а) + (1 –
с)
(1 – а) + (1 –
с) 
1+ с
= 2 – а – в
= (1 – а) + (1 –
в)  (1 – а) + (1 –
в)
(1 – а) + (1 –
в) 
(1 + а)(1 + в)(1 +
с) 
 =
=  = 8(1 – а)(1 – в)(1 –
с)
= 8(1 – а)(1 – в)(1 –
с) 8(1– а) (1 – в)(1 –
с)
8(1– а) (1 – в)(1 –
с)
Теңсіздіктің сол жақ бөлігін кішірейткенде, оң жақ бөлігіне тең болып тұр.
Демек, теңсіздік дәлелденді.
27. Егер авсd = 1 және а > 0, в > 0, c > 0, d >0 болса, онда
а2 +
в2 +
с2 +
d2 + ав + ас + аd + вс + вd +
сd  10 теңсіздігі
орындалатынын дәлелдеңдер.
10 теңсіздігі
орындалатынын дәлелдеңдер.
Дәлелдеуі:
 , ав +
вс
, ав +
вс  осылай Коши теңсіздігін
қолданамыз.
осылай Коши теңсіздігін
қолданамыз.
(а2
+
в2) + (
с2
+
d2) + (ав + сd) + (аd + вс) +
(вd + ас)  10
10
2ав + 2сd
+  +
+
 +
+ 
 10
10
2(ав +
сd) +
6
 10
10
2 +
6
+
6
 10
10
10
 10
10
Есептің шартындағы авсd = 1
апарып қойсақ, 10
 10
10
10
 10
10
Сонымен, теңсіздік дәлелденді.
28. х, у сандары үшін ху =
1 және х > у болса, мына теңсіздіктің
 орындалатынын
дәлелдеңдер.
орындалатынын
дәлелдеңдер.
Дәлелдеуі:
Сол жағындағы өрнектің алымын х – у квадратына келтіреміз.
х2
+
у2
=
х2
– 2ху +
у2
+ 2ху = (х –
у)2
+ 2ху



 (х –
у)
(х –
у)
Теңсіздіктің сол жақ бөлігіне Коши теңсіздігін қолдансақ
2(х –
у)

 (х –
у)
(х –
у)
Демек, теңсіздік дәлелденді.
29.Егер а, в, с –
көбейтіндісі 1-ге тең нақты сандар болса, онда а + в + с + ав + ас
+ вс  6 теңсіздігінің
орындалатынын дәлелдеңдер.
6 теңсіздігінің
орындалатынын дәлелдеңдер.
Дәлелдеуі:
авс = 1 болғандықтан ав
= 
авс = 1 болғандықтан вс
= 
авс = 1 болғандықтан ас
= 
Коши теңсіздігін қолданып, теңсіздіктің сол жақ бөлігін кішірейтеміз:
а +

 =
2
=
2
а + в + с
+  +
+
 +
+ 
 6
6
Демек, кішірейтілген өрнек 6-ға тең болса, онда 6- дан үлкен болады.
Дәлелденді.
30. Егер
а2 +
в2 +
с2 = 1 болса,
онда  +
+  +
+  < 4 теңсіздігінің
орындалатынын дәлелдеңдер.
< 4 теңсіздігінің
орындалатынын дәлелдеңдер.
Дәлелдеуі:
 осылай Коши
теңсіздігін қолданып, теңсіздіктің сол жақ бөлігін
үлкейтеміз.
осылай Коши
теңсіздігін қолданып, теңсіздіктің сол жақ бөлігін
үлкейтеміз. 
 +
+  +
+

 =
=
 =
=  =
4
=
4
Үлкейткендегі өрнек 4 – ке тең болса, онда 4- тен кіші болады. Теңсіздік дәлелденді.
Қорытынды
Қорыта айтқанда, олимпиадалық есептердің арасында жиі кездесетін есептердің қатарында теңсіздіктерді дәлелдеу есептері бар. Сондықтан арифметикалық орта мен геометриялық ортаның арасындағы теңсіздік — Коши теңсіздігін дұрыс қолдана білу маңызды.
Орташа шамалардың арасындағы арақатысты анықтауға байланысты теориялық зерттеулер жүргізілген және теңсіздіктерді әртүрлі тәсілдер мен дәлелдеуді салыстыра отырып, орта мектепте теңсіздіктерді орташа шамалардың қасиетіне сүйеніп дәлелдеудің басқа тәсілдерге қарағанда қолайлы тәсіл екендігі және шығарылу жолы оқушыларға түсінікті екендігі анықталған.
Теңсіздіктерді дәлелдеуге құрастырылған есептерді мұғалім оқушылармен әртүрлі мақсатта – сыныпта, оқушыларға өзіндік тапсырма беруде және одан тыс уақытта оқушыларды деңгейлеп оқыту кезінде пайдалануына болады.
Бұл жинақта қарастырылған көптеген есептерді мұғалім оқушыларды математикалық олимпиадаға даярлау кезінде қолдануына болады.
Жинақта көрсетілген мысалдар мен құрастырылған есептерді орта мектептегі математика пәні мұғалімдері үшін әдістемелік құрал ретінде ұсынуға болады.
ӘДЕБИЕТТЕР
-
Ажгалиев О.А., Отеш А.К. Задачи математических олимпиад. – Алматы, 2001.
-
Бейсеков Ж., Шарипов Т., Тәңірбергенов Ә. 11-сыныптағы оқушыларды математикалық олимпиадаға даярлау. – Шымкент, 2003.
-
Жанасбаева Ұ.Б. Математикалық олимпиада есептері. – Алматы, 2022.
МАТЕМАТИКАЛЫҚ ОЛИМПИАДА ЕСЕПТЕРІНІҢ ЖИНАҒЫ
Басуға 2024ж. қол қойылды
Қағаздың пішімі А4
Офистік қағаз
Есепті баспа табағы 4,5
Таралымы 65 дана
55

шағым қалдыра аласыз















