
Маңғыстау облысының білім басқармасының Жаңаөзен қаласы бойынша білім бөлімінің «№15 жалпы білім беретін мектеп» КММ
МАТЕМАТИКАНЫ ОҚЫТУДА АРИФМЕТИКАЛЫҚ АМАЛДАРДЫҢ ЖАЗБАША ӘДІСТЕРІ
(оқу-әдістемелік құрал)
Адыканова Аққу Жалғасқызы
Маңғыстау облысының білім басқармасының
Жаңаөзен қаласы бойынша білім бөлімінің
«№15 жалпы білім беретін мектеп» КММ
математика пәнінің мұғалімі
Педагог
Жаңаөзен 2026
«Бекітемін»
Жаңаөзен қаласы бойынша білім бөлімінің
«№15 жалпы білім беретін мектеп» КММ
_____________________Есбосинов Б.С.
«____» _____________________2026 ж.
Құрастырушы автор: Жаңаөзен қаласы бойынша білім бөлімінің
«№15 жалпы білім беретін мектеп» КММ – Адыканова Аққу Жалғасқызы математика пәнінін мұғалімі, педагог.
Аннотация: Ұсынылған, «Математиканы оқытуда арифметикалық амалдарды жазбаша тәсілдері» оқу-әдістемелік құралында математикалық сауаттылықтың негізгі тақырыптары, оның ішінде аныктамалар, тақырыпқа байланысты есептер оқушыларға түсінікті түрде берілген. Сонымен қатар, ережелер кеңінен түсіндіріліп, және сол тақырыпқа байланысты есептер жинақтары оқушылардың математикалық сауаттылығын арттыруға септігін тигізетіндей жасакталған. Бұл әдістемелік құрал 4 бөлімнен тұрады.Алдымен математикалық сауаттылық курсындағы негізгі тақырыптар мен әдістер түсіндіріліп, әрі карай есеп жинақтарымен толықтырылған. Бұл оқу-әдістемелік құрал 5-6 сынып оқушылар мен математика мұғалімдері, жалпылама көпшілікке арналған.
«Ұсынылды»
Сараптау комиссиясының кеңесі
Хаттама № ____
«____» ________ 2026 ж
Мазмұны
Түсінік хат..................................................................................... 4
-
Математиканы оқытудағы арифметикалық амалдар............... 5
-
Қосу мен азайту амалдарының жазбаша әдістері ................... 8
-
Көбейту мен бөлу амалдарының жазбаша әдістері................. 15
-
Есептеулер................................................................................... 22
Пайдаланылған әдебиеттер тізімі.................................................... 25
Түсінік хат
Математиканы оқытудың мақсаты - практикалық іс-әрекетте пайдалануға, сабақтас пәндерді оқып үйренуге, білім алуды жалғастыруға қажетті нақты математикалық білімді меңгерту және оқушылардың логикалық ойлауын, дәлелдеулер жасай білу, есептерді шығару біліктері мен дағдыларын дамыту, математикалық сауаттылығын қалыптастыру.
Математикалық сауаттылықты қалыптастырудың негізі ретінде арифметикалық амалдарды қолдануды айтады. Арифметикалық амалдарды қолдану дағдыларынсыз математикада күрделі есептеулерді шешу мүмкін емес. Сондықтан да, арифметикалық төрт амал негізгі амалдар болып табылады.
Математика сан ғасырдан бері қалыптасып, зерттелінген ғылым. Оны үйренуде арифметикалық амалдардың түрлі әдістері мен тәсілдері қалыптасқан. Арифметикалық амалдарды оқытып-үйрету есептердің жаңа түрлерін қосу мен азайту,көбейту, бөлу амалдарының мән-мағынасын ашу, белгісіз қосылғыштарды, белгісіз азайғышты, белгісіз азайтқышты табу, т.б. шығарумен байланысты.
Арифметикалық амалдарды үйрену математиканы оқытудағы негізгі деңгейлерімен сипатталадыы:
-
Қосу және азайту амалын білу және оның қасиеттерін қолдану;
-
Көбейту және бөлу амалын есептеулерде қолдану.
Білім беру жүйесінде математикалық сауаттылықта арифметикалық амалдар ретімен үйретіледі. Себебі бұл оқушылардың даму деңгейімен (білу, қолдану, ойлау) байланысты. Оқушының танымдық деңгейі мен ойлау қабілеті әр түрлі болғандықтан, әрбір арифметикалық амалды үйренудің негізгі әрі практикалық әдістерін тиімді қолдану арқылы үйрету керек. Осы оқу-әдістемелік құралда арифметикалық амалдардың негізгі жазбаша әдістері қарастырылады.
1. МАТЕМАТИКАНЫ ОҚЫТУДАҒЫ АРИФМЕТИКАЛЫҚ АМАЛДАР
Арифметикалық амалдар, математиканың бастауыш курсынан бастап оқытылады. Мұның өзі күрделі де сан қырлы – мәселе. Оған арифметикалық амалдардың, заңдардың және амалдар қасиеттерінің, амалдардың компоненттері мен нәтижелерінің арасындағы және амалдардың өздерінің арасындағы байланыстар мен тәуелділіктердің нақтылы мағынасын ашып көрсету, сондай-ақ есептеу дағдыларын, арифметикалық есептерді шығара алу шеберліктерін қалыптастыру мәселесі енеді. Әрбір арифметикалық амал, басқа да математикалық ұғымдар сияқты, жиындарға қолданылатын операцияларды орындау процесінде нақтылы негізге сүйеніп айқындалады:
қосу амалы – ортақ элементтері жоқ жиындарды біріктіру операциясына;
азайту амалы – жиынның бір бөлігін (ішкі жиынды ) айырып алу операциясына;
көбейту – элементтерінің саны бірдей жиындарды біріктіру;
бөлу – жиынды саны бірдей қиылыспайтын жиындарға айыру операциясына сүйеніп айқындалады.
Арифметикалық амалдар және олардың қасиеттерімен таныстыру практикалық жұмыс нәтижесінде, яғни оқушылар жиындарға амалдар қолданғанда, сондай-ақ есептерді шығару барысында жүзеге асырылады. Оқушыларды жаңа материалды игеруге дайындаудың тағы бір маңызды жағы бар – оның ой операцияларын орындай алу білігін қалыптастыру:
-
анализ ( талдау );
-
синтез жасай білуін, объектілерді салыстыра білуін, елеусізге көңіл бөлмей, негізгі жалпы мәселені айыра білуін ( жалпы қорытынды жасай білуін ) қалыптастыру.
Осы аталған оймен орындалатын операцияларды қалыптастыру жөнінен істелетін жұмыс балаларды мектепте оқытудың алғашқы күндерінен басталуы және материалды оқып үйренумен органикалық байланыста болуы тиіс. Объектілерді салыстыра білуге үйретуге ерекше назар аударылуы керек, өйткені салыстыру үшін анализ-талдау және синтез жасай білулері керек, ал салыстыру операциясының өзі жалпылама қорытынды жасау негізінде алынған. Оқушылардың салыстыра алу білігін қалыптастыруда математикалық өрнектерді, сандарды, есептерді, геометриялық фигураларды т.б. салыстыруға арналған жаттығуларды көбірек беріп отыру керек.
Мағлұматтар ( өрнектердегі арифметикалық амалдардың орындалу тәртібінің ережесі, терминдермен таныстыру т.с.с ) түріндегі теориялық, материалмен таныстыру кезінде, есептеулердің ( 2 санын қосу және азайту т.с.с ) кейбір әдістермен таныстыру кезінде оқушыларға құралдарды ( сызғышты, циркульді т.с.с ) пайдалану жөнінде нұсқау бергенде және басқа да сондай жағдайларда мұғалімнің жаңа материалды баяндау ( түсіндіру ) әдісі қолданылады. Мұнда мұғалім материалды баяндайды ( түсіндіреді ), ал оқушылар оны қабылдайды, яғни білімді дайын күйінде игеріп алады.
Математиканы оқытуда қосу амалын оқып – үйрену заттардың әр түрлері топтарын біріктірумен, ал азайту – заттардың тобынан қандай да бір белгісіне қарай біраз заттарды алып тастаумен байланысты орындалатын практикалық жұмыс болып табылады. Сонда заттардың тобымен жүргізілетін нақты іс - әрекеттермен санау қатар жүргізіледі. Мұндай жаттығуларды орындау қосу және азайту амалдарын оқып – үйренуге дайындайды, яғни олардың мән – мағынасын ашуға негіз қалайды да, әрі қарай мәтінді жай есептерді шығару барысында жалғасады.
Арифметикалық амалдың бірі көбейту қосу арқылы,ал бөлу азайту арқылы анықталады және олардың да мән мағынасына қарапайым мәтінді жай есептер арқылы ашылады. Сонда көбейту амалы элементтері бірдей топтарды біріктіру ,яғни қосу амалы арқылы жүзеге асырылады. Ал бөлу жайындағы түсінік заттардың тобымен жүргізілетін практикалық екі іс әрекетке :тең бөліктерге бөлуге сүйеніп қалыптастырылады.Арифметикалық амалдардың мән мағынасын ашу , олардың таңбаларын және сәйкес терминдерді енгізумен жалғасады.
Арифметикалық амалдардың компоненттері мен нәтижелері арсындағы байланыстар, арифметикалық амалддардың дұрыс орындалғанын тексеру және белгісіз компоненттерін табу үшін пайдаланылады. Сондықтан әрбір арифметикалық амалдың нақтылығы мағынасын айқындаумен бірге ,олардың белгіленуі,яғни амал таңбасы және терминалогия ,амалдардың ,амалдардың компоненттері мен нәтижелерінің атаулары енгізіледі. Матеметикада арифметикалық амалдарды орындау реті туралы ережелерлің маңызы зор. Ол ережелердің өзі математикалық заңдылық емес ,тек солай қолданып қалыптасып кеткен келісім екенін ескерген жөн.
Арифметика математиканың алгебра, геометрия және тригонометрия сияқты күрделі салаларының негізі болып табылады. Негізгі арифметикалық амалдар мен сандармен жұмыс істеу ережелерін түсінбестен, күрделі математикалық ұғымдарды түсіну және қолдану мүмкін емес. Сонымен қатар, арифметика адамдардың күнделікті өмірінде маңызды рөл атқарады. Негізгі математикалық операцияларды білу және сандармен жұмыс істей білу қаржыға, бюджетті жоспарлауға, өлшеуге және т. б. байланысты көптеген мәселелерді шешу үшін қажет. Арифметика математиканың ажырамас бөлігі болып табылады және ғылыми зерттеулер үшін , күнделікті өмір үшін де үлкен маңызға ие. Арифметика математиканың көне салаларының бірі болып табылады. Ол математикамен бірге қалыптасып, дамыды.
Арифметиканың дамуы әр уақытта халықтар арасында әр түрлі болды. Мысалы, үндістер текше түбірін алуды қарапайым арифметикалық амалдарға жатқызды. Арифметикалық әрекеттерді арифметикалық амалдар деп атауы алғаш рет XIII ғасырдың қолжазбаларында кездеседі. XVI ғасырда ол жалпы қолданысқа енді және арифметикалық амал термині қалыптасты (лат. рагѕ arthmetika). Үнді математиктері алты арифметикалық әрекетті қарастырды: қосу, азайту, көбейту, бөлу, дәрежелеу және түбір астына алу. Мысырлықтар сандар бойынша төрт амалды қосу, екі есе көбейту және екіге бөлу арқылы жүзеге асырды. Екі еселену Египетте негізгі операция болды және Египет тілі бұл үшін қос санның ерекше формасын қолданды. Ал азайту амалы болса азайтылғанға дейін азайтқанды қосу арқылы жүзеге асырылды. Гректер көбейту амалын білгенменен, күнделікті тәжірибеде Египеттің екі еселену әдісін қолданды. Бұл елдерде сандарға амал қолдану үшін арифметикалық әрекеттерді қолданды. Бәрімізге белгілі, қазіргі қарапайым арифметикалық амалдардың негізін үнді халқы қалыптастырған болатын.
Арифметиканың пайда болуының себебі – санауға, қарапайым өлшеулер мен есептеулерге практикалық қажеттіліктің болуы еді. Математика нақтылықты, сандарды, фигуралар мен кеңістіктегі заттарды зерттейді. Осы аталғандарды зерттеу үшн математикада арифметикалық амалдар қолданылады. Сондықтан да арифметикалық амалдар математиканың ажырамас бөлігі болып саналады.
1. ҚОСУ МЕН АЗАЙТУ АМАЛДАРЫНЫҢ ЖАЗБАША ӘДІСТЕРІ
Математикада сан және цифр ұғымдарымен танысқаннан кейін, осы сан мен цифрға математикалық амалдар, яғни арифметикалық амалдарды қолдануды үйретеді. Арифметикалық амалдарды үйретуде ең алдымен қосу және азайту амалдары үйретіледі. Қосу мен азайту амалдары арифметикалық амалдардың ішіндегі үйретілуі оңай амалдар. Бұл екі амал бір-біріне кері амалдар болып табылады. Сондықтан қосу мен азайту амалдарын үйрету қатар жүреді. Осы екі амалды үйретуде оқушыларда алғашқы математикалық негіз қалыптасады. Қосу амалын үйрену заттардың, сандардың әр түрлі топтарын біріктірумен, ал азайту – заттардың, сандардың тобынан затты не санды алып тастаумен байланысты үйретіледі.
-
Қосу – екі немесе одан да көп элементтерді біріктіру процесі.
Математикадағы қосу – екі немесе одан да көп сандардың қосындысын есептеу әдісі. Қосу амалын орындағанда қосудың өзінің құрамды бөліктері болады: қосылғыш, қосылғыш, қосындының мәні. Мысалы 2 + 5 = 7 теңдігін қарастырайық. Бұл теңдікте 2 – қосылғыш, 5 – қосылғыш, ал 7 – қосындының мәні. Қосу амалымен сандарды өрнектеу қосынды деп аталады.
-
Азайту – бұл бір санды екіншісінен алу процесі.
Бұл негізгі арифметикалық амал, ол азайту (-) белгісімен белгіленеді және екі сан арасындағы айырмашылықты есептеу әдісі болып табылады. Азайту амалының бөліктері: азайғыш, азайтқыш, айырманың мәні. Мысалы: 9 – 3 = 6. 9 – азайғыш, 2 – азайтқыш, 7 – айырманың мәні болып табылады. Азайту амалымен сандарды өрнектеу айырма деп аталады.
Қосу амалын орындау кезінде оның қасиеттерін қолданамыз:
1.Ауыстырымдылық
қасиеті: ![]() ;
;![]() – қосылғыштардың орны
ауысқанымен қосындының мәні өзгермейді. Мысалы: 36 + 14 = 50; 14 +
36 = 50.
– қосылғыштардың орны
ауысқанымен қосындының мәні өзгермейді. Мысалы: 36 + 14 = 50; 14 +
36 = 50.
2. Терімділік
қасиеті: ![]()
Мысалы: (25 + 13) + 14 = 25 + (13 + 14) = 52
3. Қосылғышқа 0 –ді қосса, қосындының мәні қосылғышқа тең болады.
Азайту амалының қасиеттері:1. Азайғыштан 0 – ді азайтса, айырманың мәні азайғышқа тең болады.
Мысалы: 26 – 0 = 26.
2. Азайғыш пен азайтқыш бірдей сан болса, онда айырманың мән 0-ге тең болады. Мысалы: 26 – 26 = 0.
Математикалық өрнектерде арифметикалық амалдар жақша арқылы да орындалды. Жақшаға арқылы орындалатын екі ереже:
1. жақшасыз өрнекте бірінші солдан оңға қарай көбейту мен бөлі, ал содан кейін қосу мен азайту амалдары орындалады.
2. Егер өрнекте жақша болса, онда жақша ішіндегі амалдар бірінші орындалады.
Қосу мен азайту амалдарын жазбаша орындау әдістері
Арифметикалық амалдарды орындау ауызша және жазбаша орындалады. Амалдарды ауызша орындау әдістерінде оқушылар ойша есептеп, логикалық ойлауын тез дамыта алады. Бірақ та амалдарды ауызша орындау жазбаша орындауды үйренгеннен кейін ғана оңай әрі тез үйретіледі. Сондықтан бірінші кезекте есептеуде арифметикалық амалдарды жазбаша орындау әдістерін қолданады. Жазбаша есептеу тәсілдерінде өзіндік алгоритмдер қолданылады. Жазбаша қосу және азайту амалдарын орындау алгоритмдерінің қарапайымдылығына қарамастан, оқушылар көптеген қателіктер жібереді. Жазбаша орындау тәсілдерін үйрету кезінде амалдардың әрқайсысын жазбаша орындаудың рет-тәртібі көрсетіліп орындалады. Оқушыларға амалдарды жазбаша орындауды үйрету кезінде алгоритмдер мен есептер шешімдерінің дұрыстығын мұқият қадағалау керек. Сандарды жазбаша қосу және азайту алгоритмін білгеннен кейін, оқушылар өздері қорытынды ережені тұжырымдай алады. Амалдарды жазбаша орындау әдістері арқылы есепті жылдам әрі дұрыс шығара біледі. Математика сабағында арифметикалық амалдарды жазбаша орындау әдістерінің көмегімен оқушыларды сабаққа, есеп шығаруға деген қызығушылығын арттыра аламыз.
Қосу мен азайту амалдарын жазбаша орындау әдістеріне: кестелік қосу- азайту әдісі, бағандау әдісі, қосылғыштарға жіктеу әдісі.
Кестелік қосу азайту әдісі. The method of tabular of addition and substraction.
Кестелік қосу азайту әдісі 1 ден 9-ға дейінгі сандарды қосып, азайту кезінде қолданылады. Бастауыш сынып математикасында натурал сандарға арифметикалық амалдар қолдануды осы кестелік қосу азайту әдісімен есептеу арқылы бастайды. Кестелік қосу азайту әдісінде ең алдымен сандарға 1-санын қосып, азайтуды көрсету арқылы санға 1-ді қосқанда сол саннан кейінгі сан шығатынын, керісінше саннан 1-ді азайтқанда сол саннан алдыңғы санның шығатыны туралы ережені дәлелдейді.
Кестелік қосу азайту әдісінде әрбір санға 1-ден 9-ға дейінгі сандарды қосу азайту кестесі беріледі. Амалдардың кестелік әдісін оқып-үйренуде 10-ға дейінгі сандардың құрамын білу өте маңызды. Қосу амалының кестелік әдісінің тиімділігі – сандарды орын ауыстырып қоса алады, қосудың ауыстырымдылық қасиетін қолданады. Бұл әдіс арқылы бала сан құрамын тез жаттап, қосудың ауыстырымдылық қасиетін қолдануды тез үйренеді.
1 – ден 5-ке дейінгі қосу кестесі
|
+ |
1 |
2 |
3 |
4 |
5 |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
2 |
3 |
4 |
5 |
6 |
7 |
|
3 |
4 |
5 |
6 |
7 |
8 |
|
4 |
5 |
6 |
7 |
8 |
9 |
Кестелік әдісті білгеннен кейін бала сандарды қосылғыштарға жіктеп жаза алады. Мысалы 5-санының қосылғыштарын айтып бере алады: 5 = 1+4 және 5 = 2 +3
Бағандаy тәсілі
Математикада екітаңбалы немесе одан да көп таңбалы сандарды қосу-азайту амалдарын орындау үшін бағандау тәсілін жиі қолданады. Бұл тәсіл бастауыш математикасында екітаңбалы сандарға амалдар қолдану кезінде үйретіледі. Бағандау тәсілі қосу мен азайту амалдарын үйретуде оқушылар үшін тиімді әрі жылдам тәсіл, бірақ бағандап қосу-азайту кезінде міндетті түрде сандардың разрядтық бірліктерін (бірлік, ондық, жүздік) мұқият үйренген жөн. Бұл әдістің ерекшелігі сандардың рет ретімен разрядына қарай жазылуына байланысты. Қосу не азайту, көбейту амалы болсын бағандау әдісінде бірлік бірліктің астында, ондық ондықтың астында, жүздік жүздіктің астында жазылады. Осы разрядтың қатардың реті дұрыс жазылмаса, мән дұрыс шықпайды.
Қосу мен азайту амалын бағандау тәсілімен орындау алгоритмі:
-
Сандарды екі жолға бір-бірінің астына жазу;
-
Орындау керек амалдың таңбасын салу;
-
Ең кіші бірліктен бастап амалды орындау;
-
Бірліктерді қосқанда ондық сан шықса, онда ондық санды ойға алып, бірлік санды жазамыз. Ойдағы ондықты ондықтарға қосамыз.
Егер азайту кезінде азайғыш азайтқыштан кіші болса, онда бірліктен не ондықтан қарыз сұралып алынады.
Қосу амалына мысал:

Азайту амалына мысал:

Қосылғыштарға жіктеу тәсілі. Еxtended column method.
Бағандау тәсілі арқылы қосу – азайту амалдарын орындауды үйренгеннен кейін оқушылар тез есептеп үйренеді. Бірақ бағандап қосу-азайту кезінде бірліктер мен ондықтарға амалдар орындауда көп қателеседі. Сондықтан сандарды қосылғыштарға (разрядтарға) жіктеу арқылы қосуға да болады. Мысалы: 756 + 489 =
1) сандарды қосылғыштарға жіктеп аламыз;
756 = 7 жүздік 5 ондық 6 бірлік
489 = 4 жүздік 8 ондық 9 бірлік
2) бірліктерді, ондықтарды, жұздіктерді жеке жеке қосамыз.
7 жүздік 5 ондық 6 бірлік
+
4 жүздік 8 ондық 9 бірлік
![]()
1 мыңдық 2 жүздік 4 ондық 5 бірлік
Жуықтау тәсілі
Бұл тәсіл қосу амалы арқылы азайту амалын тиімді орындау тәсілі болып табылады. Азайту амалында азайтқышты ондыққа, жүздікке немесе мыңдыққа жуықтау арқылы уақытты үнемдеп тез шығаруға болады. Жуықтау тәсілінің орындалу жолы қарапайым: азайтқышты ондықтан, жүздіктен азайтамыз; шыққан мәнді азайғышқа қосамыз; осыдан шыққан мәннің алдындағы 1 цифрын алып тастаймыз, сонда қалған сан айырманың мәні болады.
Мысалы: 653 – 372 = 281
1) 653
 1000
1000
1000 – 372 = 628
2)653 + 628 = 1281
3) 1281
 281
281
Жай бөлшектерді қосу мен азайтудың әдістері
Жай бөлшек – натурал санның бір немесе бірнеше тең бөліктерінен құралған сан. Жай бөлшек тақырыбы 5-6 сынып оқушылары үшін күрделі тақырып. Жай бөлшектерді қосу мен азайтуда олардың қасиеттерін ескерген жөн. Арифметикалық амалдарды орындауда жай бөлшектердің түріне қарай амалдар орындалады.
Жай бөлшек дұрыс, бқрыс
және аралас жай бөлшек деп бөлінеді. Бірақ біз оларға амал
қолданғанда бөлімдеріне назар аударамыз. Жай бөлшектің бөлімі –
санның неше бөлікке бөлінгенін көрсетеді.
Мысалы: санның үштен бір бөлігі.
санның үштен бір бөлігі.
Бөлімдері бірдей сандарды қосу мен азайту қарапайым қосу-азайту әдістерімен шы,арылады. Жай бөлшектің бөлімдері өзгерісссіз қалып, алымдарына амал қолданамыз. Үлгі:
Жай бөлшекті азайту:

Жай бөлшекті қосу:


Бөлімдері әр түрлі жай бөлшекті қосу-азайтуда көбелек әдісін қолдану тиімді. Көбелек әдісінде қарама-қарсы алымдары мен бөлімдерін көбейтіп, қосу немесе азайтуды орындаймыз.
Үлгі:
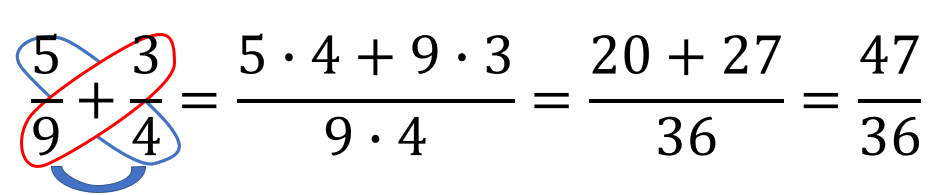
3. КӨБЕЙТУ МЕН БӨЛУ АМАЛДАРЫНЫҢ ЖАЗБАША ӘДІСТЕРІ
Көбейту – қосу, азайту және бөлумен қатар төрт негізгі арифметикалық әрекеттің бірі.
Математикада көбейту бірдей топтарды бірнеше рет қосуды білдіреді. Көбейтілетін сандар көбейткіштер деп аталады, ал екі немесе одан да көп сандарды көбейткеннен кейін алынған нәтиже сол сандардың көбейтіндісі деп аталады. Көбейту бір санды бірнеше рет қосу мәселесін жеңілдету үшін қолданылады . Мысалы: егер 6 қорап шар болса және әр қорапта 9 шардан болса, шардың жалпы санын табыңыз.
Шешуі: Қосу амалы арқылы: 9+9+9+9+9+9 = 54
Енді көбейту амалымен есептейік. Біз қораптар санын әр қораптағы шарлар санына көбейтеміз. Егер біз 6 × 9 көбейтсек, онда біз шарлардың жалпы санын аламыз, бұл 6 × 9 = 54. Осылайша, қысқа уақыт ішінде бірдей нәтиже аламыз.
Математикада бізде әртүрлі белгілер бар. Көбейту символы – ең көп қолданылатын математикалық белгілердің бірі. Жоғарыдағы мысалда біз 6 және 9 екі санды көбейту туралы білдік. Егер көбейту өрнегін (6 × 9 = 54) қарастыратын болсақ, онда (× ) таңбасы екі санды қосып, берілген өрнекті аяқтайтынын көреміз. Крест белгісінен басқа ( × ) көбейту нүкте (•) және жұлдызша (*) белгісімен де белгіленеді.
Көбейту амалының алгоритмі
Көбейтінді * көбейткіш = көбейтіндінің мәні
Көбейтінді – көбейтілетін сан, көбейткіш – көбейтетін сан, ал көбейтіндінің мәні көбейту амалынан алынған шешім.
Көбейтудің қасиеттері:
-
ауыстырымдылық қасиеті: көбейткіштердің орнын ауыстырғанымен көбейтіндінің мәні өзгермейді.
-
терімділік қасиеті: санды екі санның көбейтіндісіне көбейту үшін , алдымен бірінші көбейткішке көбейтіп, шыққан мәнді екінші көбейткішге көбейтеді.
-
қосуға қатысты үлестірімділік қасиеті: қосындыны санға көбейту үшін әр қосылғышты сол санға көбейтіп, шыққан көбейтіндінің мәндерін қосу.
Бөлу – математикадағы негізгі арифметикалық амалдардың бірі, онда үлкен сан элементтердің саны бірдей кіші топтарға бөлінеді, тең топтастыру және тең бөлу үшін қолданылатын операция.
Бөлу қайталанатын азайту амалы және көбейту амалына кері амал. Бөлу сызықтың үстінде және астында нүктелері бар шағын көлденең сызықтан тұратын математикалық таңбамен белгіленеді. Екі санның бөлінуін білдіретін екі негізгі бөлу таңбасы бар. Бұл ÷ және /.
Бөлу амалының алгоритмі
Бөлінгіш/бөлгіш = бөліндінің мәні
Бөлу бөліктері бөлу процесіне қатысты терминдердің атауын білдіреді. Бөлудің төрт бөлігі бар: бөлінгіш, бөлгіш, бөліндінің мәні және қалдық. Бөлінгіш – бөлінетін сан, ал бөлгіш санды бөлетін сан. Бөлу амалы арқылы алынған мән бөліндінің мәні болып табылады. Қалдық дегеніміз бөлу кезінде бөлінбей қалған артық сан. Мысалы: 24 / 4 = 6. 24 – бөлінгіш, 4 – бөлгіш, 6 – бөліндінің мәні.
Көбейту кестесі. Көбейту амалын орындау үшін көбейту кестесі қолданылады. Кесте бойынша көбейтуді алғаш рет вавилон математиктері енгізді. Алайда, бұл ондық санау жүйесіндегі дәстүрлі көбейту емес, әлем халықтары арасында кең орын алмаған алпысыншы санау жүйесіндегі дайын кестелер бойынша көбейту болды. Көбейту кестесінің күнделікті формасы бағаналар түрінде жасалған Паламеда кестелерінде (б.з. д. III ғасырға дейін) және квадрат түрінде жасалған Никомах кестесінде (б. з. I ғ.) қолданылды. Кестелік көбейтудің қазіргі заманғы өзгеруі үнділердің ондық позициялық санау жүйесін ойлап тапқаннан және олардың нөлді енгізген кезінен, сондай-ақ ерікті сандарды көбейтудің неғұрлым жетілдірілген тәсілдерін ойлап тапқаннан басталады (V-VI ғғ.). Бүгінгі таңда көбейту әрекетін жазудың өзгеретін түрін Н.Г.Курганов өзінің "әмбебап арифметикасында" (1757) енгізді.
Көбейту кестесі – бұл 1-ден 9-ға дейінгі сандарды бір-біріне көбейтудің көбейтіндісін алу үшін қолданатын математикалық кесте. Қазір көбейту кестесінің ондық үлгісі қолданылады. Ең танымал кесте, оның негізі ондық жүйе, бамбук жолақтарындағы қытайлық көбейту кестесі болып саналады. Қытайдың ең көне көбейту кестелері б.з.д. 221-206 жылдар аралығындағы Цинь әулетінің кезеңде пайда болды. Бұл қарапайым көбейтуге мүмкіндік беретін қысқа сөйлемдер сериясы (мысалы, «алты сегіздік қырық сегізді тудырады»).
Көбейту кестесін бастауыш мектеп математикасында үйретеді. Көбейту кестесі арқылы көбейтуді жазбаша орындаудың басқа да тәсілдері қарастырылады.
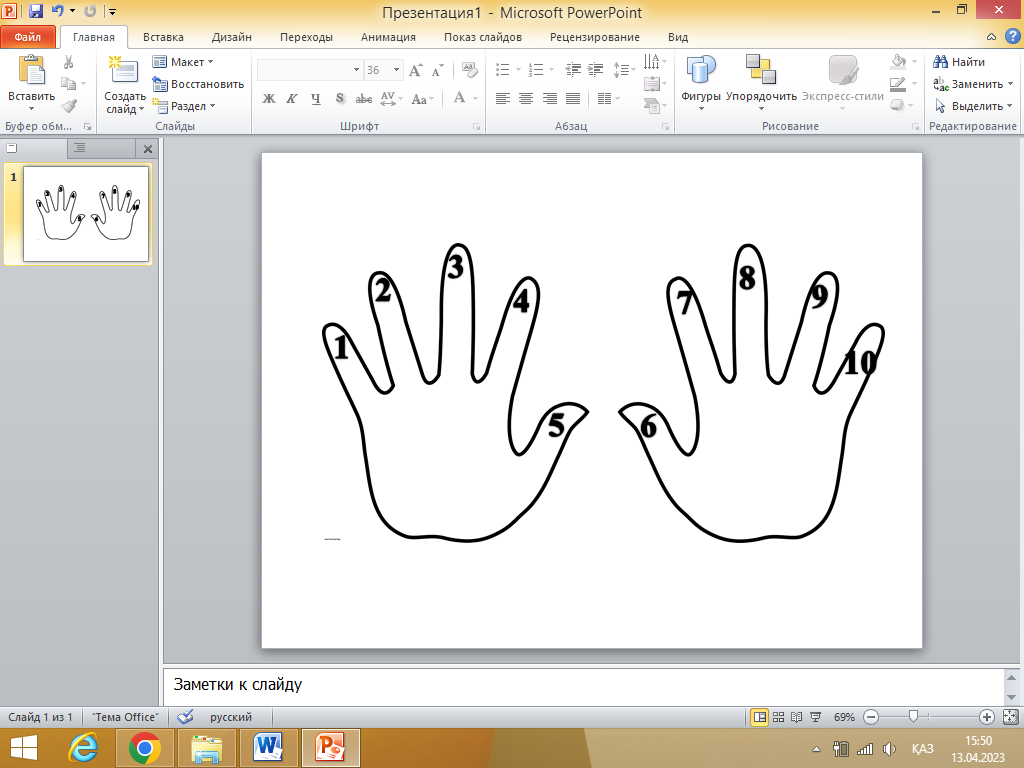
9-ға көбейту тәсілі.
Адамдардың ең алғашқы санау құралдарының бірі олардың саусақтары болған. Осы саусақтар арқылы ондық санау жүйесі қалыптасқан. Көбейту амалында таяқтар пен басқа заттардың көмегінсіз саусақтар арқылы орындаған. Оған айқын мысал 9-ға көбейту тәсілі. Бұл өте қарапайым тәсіл. Кез келген 1-ден 9-ға дейінгі санды 9-ға көбейту үшін қолыңызға қараңыз. 9*3 табайық. Бізде көбейткіш 3-ке тең болғандықтан, қолымыздың сол жағынан 3-ке дейін санап, сол саусақты бүгеміз. Бүгілген саусаққа дейін 2 саусақ, ал кейін 7 саусақ қалды. Сонда бізде 27 саны шықты.
Бағандау тәсілімен көбейту.
Көбейту кестесі мектепте 1-ден 9-ға дейінгі сандар аралығында ғана үйретіледі. Бұл сандар бізде тек қана бір таңбалы сандар. Ал екітаңбалы сандарға көбейту амалын қолдануда бағандау тәсілі қолданылады және Әдетте бұл әдіс мектеп оқушыларына үлкен сандарды көбейту әдісі ретінде оқытылады және арифметика негіздерін нығайту үшін білім беру мақсатында қолданылады. Бағандап көбейту тәсілі көбейтудің тиімді тәсілі болғанымен, бұл тәсілдің орындалу жолы күрделі, сондықтан бұл көбейтудің ұзақ тәсілі деп те аталады. Бағандау тәсілінде көбейту кестесін білу керек. Бұл тәсілдің алгоритмі көбейту амалында да өзгеріссіз қалады:
•Сандарды жазыңыз;
•Көбейту амалының таңбасы қойылады;
•Көбейтіндіні көбейткіштің бірлігіне көбейтіңіз;
•Көбейтіндіні көбейткіштің ондық цифрына көбейтеміз және бірліктен шыққан мәннің ондық цифрынан бастап жазамыз;
•Шыққан мәндерді қосамыз.
Үлгі:

|
|
|
|
|
° |
|
|
|
|
|
5 |
6 |
|
|
|
|
x |
8 |
3 |
1 |
|
|
|
1 |
6 |
8 |
|
|
+ |
4 |
4 |
8 |
|
1 |
|
|
4 |
6 |
4 |
8 |
|
Кестелік көбейту тәсілі.
Кестелік көбейту тәсілі бағандап көбейту тәсілімен ұқсас болып келеді. Бұл тәсілдің ерекшелігі сандарды көбейткіштерге жіктеп алып, жеке көбейтіледі. Мысалы екі таңбалы сандарды осы тәсіл арқылы көбейтіп көрейік:
Бірінші, сандарды көбейткіштерге жіктеп жазамыз;
Екінші, сандарды кестеге салып көбейтеміз;
Үшінші, шыққан мәндердің барлығын қосамыз.
Мысалы: 43 * 21 = 903
1) 43 = 40+3; 21 = 20+1.
2)
|
х |
20 |
1 |
|
40 |
800 |
40 |
|
3 |
60 |
3 |
3) 800+40+60+3 = 903
Бхаскара тәсілі. Мethod of Bhaskara.
Бұл XII ғасырда өмір сүрген үнді математигі Бхаскараның көбейту амалына қолданған ежелгі тәсілі.
Бұл әдісте сандарды жоғарғы солдан оңға қарай сызылған диагональдармен екіге бөлінген квадраттарда есептейді. Әрбір шаршының үстінде бірінші көбейткіштің сандары, ал сол жақта төменнен жоғарыға қарай екінші көбейткіштің сандары жазылады. Квадраттың басқа жақтарынан жоғары оң жақтан бастап көбейткіштердің цифрларының көбейтіндісі жазылады. Әр жеке өнімнің бірліктері шаршының диагоналінің үстіне толтырылады. Бір жолдағы сандар қосылады. Егер қосынды оннан көп болса, онда қосындының бірлік цифры ғана жазылады, ал келесі қосындыға ондық цифры қосылады. Егер қосынды оннан аз болса, онда ол жолақтың төменгі цифрының астына жазылады. Әр жолдан шыққан цифрлар көбейтіндінің мәні болып табылады.
Мысалы: 256 * 83 =
|
x |
2 |
5 |
6 |
|
|
|
3 |
6 |
5 1 |
8 1 |
8 |
|
|
8 |
6 1 |
0 4 |
8 4 |
4 |
|
|
|
2 |
1 |
2 |
|
|
Қарапайым бөлу тәсілі. Азайту амалы арқылы бөлу амалын орындауда қолданылатын оңай тәсілді қарапайым бөлу тәсілі деп атайды. Қарапайым бөлу тәсілінде бөлінгіштен бөлгішті бөліндінің мәні 0-ге тең болғанша немесе қалдық шыққанша азайтады. Бұл тәсіл бастауыш оқушыларына бөлу туралы негізгі тұжырымдаманы үйретуде қолданылады. Қарапайым бөлу тәсілінің алгоритмі:
-
Бөлінді мен бөлгішті анықтау;
-
Бөліндіден бөлгішті азайту;
-
Айырмадан бөлгішті азайту;
-
Бөліндінің мәні 0-ге тең болғанша немесе қалдық шыққанша азайтуды жалғастырады;
Мысалы: 15 / 3 =
1) 15 – 3 = 12
2) 12 – 3 = 9
3) 9 – 3 = 6
4) 6 – 3 = 3
5) 3 – 3 = 0
Бағандап бөлу тәсілі. Бөлу амалы 4 амалдың ішіндегі үйретілуі күрделі, қиын амал. Бөлу амалы тікелей көбейту амалымен байланысты және осы амалға кері амал. Бағандап бөлу тәсілінде бөлінгішті жоғары разрядтан бастап бөледі және бөліндінің мәні 0-ге тең болғанша азайтады. Егер толымсыз бөлінгіш болса,онда келесі разрядқа қосылып бөлінеді.
4. ЕСЕПТЕУЛЕР
№1. Бағандау тәсілі арқылы қосу амалын орындаңдар.
1) 263+458
|
|
|
° |
° |
|
|
2 |
6 |
3 |
|
+ |
4 |
5 |
8 |
|
|
7 |
2 |
1 |
263+458 = 721
2) 4539+716
|
|
|
° |
|
° |
|
|
4 |
5 |
3 |
9 |
|
+ |
|
7 |
1 |
6 |
|
|
5 |
2 |
5 |
5 |
4539 + 716 = 5255
3) 3568 + 57
|
|
|
|
° |
° |
|
|
3 |
5 |
6 |
8 |
|
+ |
|
|
5 |
7 |
|
|
3 |
6 |
2 |
5 |
3568 + 57 = 3625
№2 Жуықтау тәсілімен азайту амалын орындаңдар.
1) 896 – 584;
Шешуі:
896  1000
1000
1000 – 584 = 416
416 + 896 = 1312
896 – 584 = 312
Жауабы: : 312
2) 956 – 327;
Шешуі:
956  1000
1000
1000 – 327 = 673
956 + 673 = 1629
956 – 327 = 629
№3. Кестелік көбейту тәсілімен көбейту амалын орындаңдар.
1) 452 * 53;
Шешуі: 452 = 400+50+2
53 = 50 +3
|
x |
400 |
50 |
2 |
|
50 |
20000 |
2500 |
100 |
|
3 |
1200 |
150 |
6 |
20000+2500+1200+150+100+6 = 23956
Жауабы: 23956
2) 125 * 36;
Шешуі: 125 = 100+20+5;
36 = 30+6.
|
x |
100 |
20 |
5 |
|
30 |
3000 |
600 |
150 |
|
6 |
600 |
120 |
30 |
3000+600+600+150+120+30 = 4500
Жауабы: 4500
№3.Бхаскара тәсілі арқылы көбейту амалын орындаңдар.
1)456*24;
456 * 24 = 10944
2) 562 * 34;
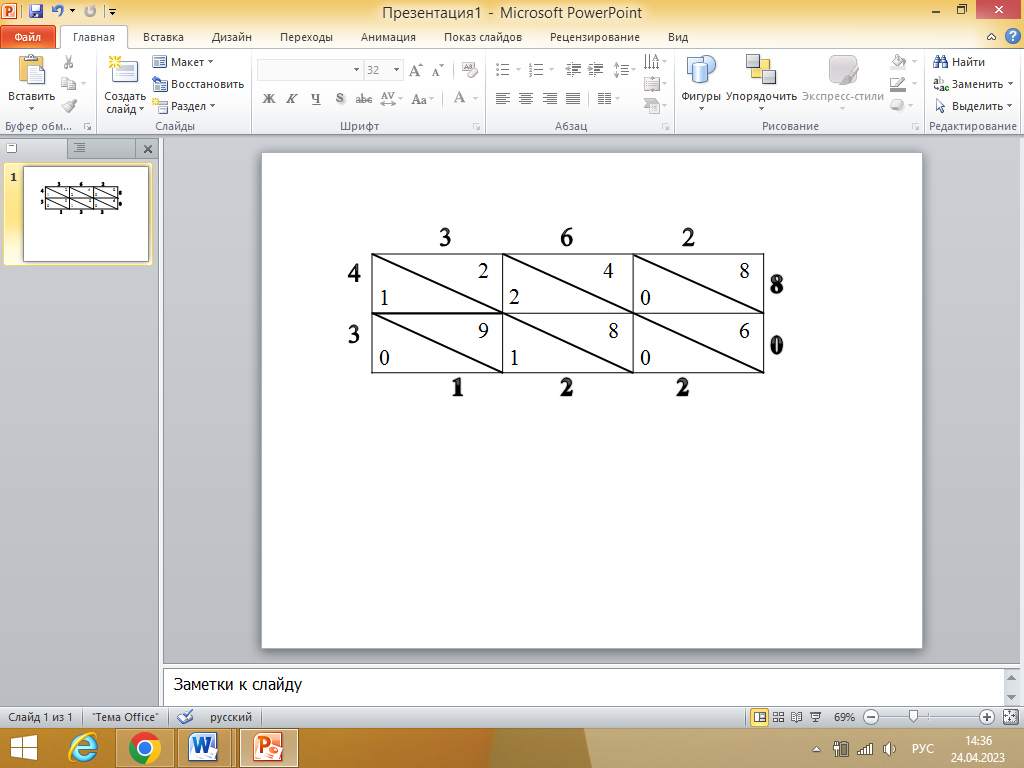
562 * 34 = 12208
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ
1. Әбілқасымова А.Е. Математиканы оқытудың теориясы мен әдістемесі:дидактиалық әдістеме негіздері. – Алматы: Мектеп, 2014. -214 бет.
2. Билялова Ж.Т. Бастауыш сыныптарда математиканы оқытуда оқу есептерін пайдалану әдістемесі. – Алматы: 2000. – 26бет
3. Бидосов Э. Математиканы оқыту методикасы. – Алматы: Мектеп, 1989. – 300 бет.
4. Абылкасымова А.Е. және т.б. Орта мектепте математика есептерін шығаруға үйретудің әдістемелік негіздері. –Алматы, 2004. -125 бет.
5. Андронов И. К., Брадис В. М. Арифметика: пособие для средней школы. — 1957
6. Шохор-Троцкий С.И. Методика арифметики: пособие для учителей средней школы – 1935, 343 с.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Математиканы оқытуда арифметикалық амалдардың жазбаша әдістері
Математиканы оқытуда арифметикалық амалдардың жазбаша әдістері
Маңғыстау облысының білім басқармасының Жаңаөзен қаласы бойынша білім бөлімінің «№15 жалпы білім беретін мектеп» КММ
МАТЕМАТИКАНЫ ОҚЫТУДА АРИФМЕТИКАЛЫҚ АМАЛДАРДЫҢ ЖАЗБАША ӘДІСТЕРІ
(оқу-әдістемелік құрал)
Адыканова Аққу Жалғасқызы
Маңғыстау облысының білім басқармасының
Жаңаөзен қаласы бойынша білім бөлімінің
«№15 жалпы білім беретін мектеп» КММ
математика пәнінің мұғалімі
Педагог
Жаңаөзен 2026
«Бекітемін»
Жаңаөзен қаласы бойынша білім бөлімінің
«№15 жалпы білім беретін мектеп» КММ
_____________________Есбосинов Б.С.
«____» _____________________2026 ж.
Құрастырушы автор: Жаңаөзен қаласы бойынша білім бөлімінің
«№15 жалпы білім беретін мектеп» КММ – Адыканова Аққу Жалғасқызы математика пәнінін мұғалімі, педагог.
Аннотация: Ұсынылған, «Математиканы оқытуда арифметикалық амалдарды жазбаша тәсілдері» оқу-әдістемелік құралында математикалық сауаттылықтың негізгі тақырыптары, оның ішінде аныктамалар, тақырыпқа байланысты есептер оқушыларға түсінікті түрде берілген. Сонымен қатар, ережелер кеңінен түсіндіріліп, және сол тақырыпқа байланысты есептер жинақтары оқушылардың математикалық сауаттылығын арттыруға септігін тигізетіндей жасакталған. Бұл әдістемелік құрал 4 бөлімнен тұрады.Алдымен математикалық сауаттылық курсындағы негізгі тақырыптар мен әдістер түсіндіріліп, әрі карай есеп жинақтарымен толықтырылған. Бұл оқу-әдістемелік құрал 5-6 сынып оқушылар мен математика мұғалімдері, жалпылама көпшілікке арналған.
«Ұсынылды»
Сараптау комиссиясының кеңесі
Хаттама № ____
«____» ________ 2026 ж
Мазмұны
Түсінік хат..................................................................................... 4
-
Математиканы оқытудағы арифметикалық амалдар............... 5
-
Қосу мен азайту амалдарының жазбаша әдістері ................... 8
-
Көбейту мен бөлу амалдарының жазбаша әдістері................. 15
-
Есептеулер................................................................................... 22
Пайдаланылған әдебиеттер тізімі.................................................... 25
Түсінік хат
Математиканы оқытудың мақсаты - практикалық іс-әрекетте пайдалануға, сабақтас пәндерді оқып үйренуге, білім алуды жалғастыруға қажетті нақты математикалық білімді меңгерту және оқушылардың логикалық ойлауын, дәлелдеулер жасай білу, есептерді шығару біліктері мен дағдыларын дамыту, математикалық сауаттылығын қалыптастыру.
Математикалық сауаттылықты қалыптастырудың негізі ретінде арифметикалық амалдарды қолдануды айтады. Арифметикалық амалдарды қолдану дағдыларынсыз математикада күрделі есептеулерді шешу мүмкін емес. Сондықтан да, арифметикалық төрт амал негізгі амалдар болып табылады.
Математика сан ғасырдан бері қалыптасып, зерттелінген ғылым. Оны үйренуде арифметикалық амалдардың түрлі әдістері мен тәсілдері қалыптасқан. Арифметикалық амалдарды оқытып-үйрету есептердің жаңа түрлерін қосу мен азайту,көбейту, бөлу амалдарының мән-мағынасын ашу, белгісіз қосылғыштарды, белгісіз азайғышты, белгісіз азайтқышты табу, т.б. шығарумен байланысты.
Арифметикалық амалдарды үйрену математиканы оқытудағы негізгі деңгейлерімен сипатталадыы:
-
Қосу және азайту амалын білу және оның қасиеттерін қолдану;
-
Көбейту және бөлу амалын есептеулерде қолдану.
Білім беру жүйесінде математикалық сауаттылықта арифметикалық амалдар ретімен үйретіледі. Себебі бұл оқушылардың даму деңгейімен (білу, қолдану, ойлау) байланысты. Оқушының танымдық деңгейі мен ойлау қабілеті әр түрлі болғандықтан, әрбір арифметикалық амалды үйренудің негізгі әрі практикалық әдістерін тиімді қолдану арқылы үйрету керек. Осы оқу-әдістемелік құралда арифметикалық амалдардың негізгі жазбаша әдістері қарастырылады.
1. МАТЕМАТИКАНЫ ОҚЫТУДАҒЫ АРИФМЕТИКАЛЫҚ АМАЛДАР
Арифметикалық амалдар, математиканың бастауыш курсынан бастап оқытылады. Мұның өзі күрделі де сан қырлы – мәселе. Оған арифметикалық амалдардың, заңдардың және амалдар қасиеттерінің, амалдардың компоненттері мен нәтижелерінің арасындағы және амалдардың өздерінің арасындағы байланыстар мен тәуелділіктердің нақтылы мағынасын ашып көрсету, сондай-ақ есептеу дағдыларын, арифметикалық есептерді шығара алу шеберліктерін қалыптастыру мәселесі енеді. Әрбір арифметикалық амал, басқа да математикалық ұғымдар сияқты, жиындарға қолданылатын операцияларды орындау процесінде нақтылы негізге сүйеніп айқындалады:
қосу амалы – ортақ элементтері жоқ жиындарды біріктіру операциясына;
азайту амалы – жиынның бір бөлігін (ішкі жиынды ) айырып алу операциясына;
көбейту – элементтерінің саны бірдей жиындарды біріктіру;
бөлу – жиынды саны бірдей қиылыспайтын жиындарға айыру операциясына сүйеніп айқындалады.
Арифметикалық амалдар және олардың қасиеттерімен таныстыру практикалық жұмыс нәтижесінде, яғни оқушылар жиындарға амалдар қолданғанда, сондай-ақ есептерді шығару барысында жүзеге асырылады. Оқушыларды жаңа материалды игеруге дайындаудың тағы бір маңызды жағы бар – оның ой операцияларын орындай алу білігін қалыптастыру:
-
анализ ( талдау );
-
синтез жасай білуін, объектілерді салыстыра білуін, елеусізге көңіл бөлмей, негізгі жалпы мәселені айыра білуін ( жалпы қорытынды жасай білуін ) қалыптастыру.
Осы аталған оймен орындалатын операцияларды қалыптастыру жөнінен істелетін жұмыс балаларды мектепте оқытудың алғашқы күндерінен басталуы және материалды оқып үйренумен органикалық байланыста болуы тиіс. Объектілерді салыстыра білуге үйретуге ерекше назар аударылуы керек, өйткені салыстыру үшін анализ-талдау және синтез жасай білулері керек, ал салыстыру операциясының өзі жалпылама қорытынды жасау негізінде алынған. Оқушылардың салыстыра алу білігін қалыптастыруда математикалық өрнектерді, сандарды, есептерді, геометриялық фигураларды т.б. салыстыруға арналған жаттығуларды көбірек беріп отыру керек.
Мағлұматтар ( өрнектердегі арифметикалық амалдардың орындалу тәртібінің ережесі, терминдермен таныстыру т.с.с ) түріндегі теориялық, материалмен таныстыру кезінде, есептеулердің ( 2 санын қосу және азайту т.с.с ) кейбір әдістермен таныстыру кезінде оқушыларға құралдарды ( сызғышты, циркульді т.с.с ) пайдалану жөнінде нұсқау бергенде және басқа да сондай жағдайларда мұғалімнің жаңа материалды баяндау ( түсіндіру ) әдісі қолданылады. Мұнда мұғалім материалды баяндайды ( түсіндіреді ), ал оқушылар оны қабылдайды, яғни білімді дайын күйінде игеріп алады.
Математиканы оқытуда қосу амалын оқып – үйрену заттардың әр түрлері топтарын біріктірумен, ал азайту – заттардың тобынан қандай да бір белгісіне қарай біраз заттарды алып тастаумен байланысты орындалатын практикалық жұмыс болып табылады. Сонда заттардың тобымен жүргізілетін нақты іс - әрекеттермен санау қатар жүргізіледі. Мұндай жаттығуларды орындау қосу және азайту амалдарын оқып – үйренуге дайындайды, яғни олардың мән – мағынасын ашуға негіз қалайды да, әрі қарай мәтінді жай есептерді шығару барысында жалғасады.
Арифметикалық амалдың бірі көбейту қосу арқылы,ал бөлу азайту арқылы анықталады және олардың да мән мағынасына қарапайым мәтінді жай есептер арқылы ашылады. Сонда көбейту амалы элементтері бірдей топтарды біріктіру ,яғни қосу амалы арқылы жүзеге асырылады. Ал бөлу жайындағы түсінік заттардың тобымен жүргізілетін практикалық екі іс әрекетке :тең бөліктерге бөлуге сүйеніп қалыптастырылады.Арифметикалық амалдардың мән мағынасын ашу , олардың таңбаларын және сәйкес терминдерді енгізумен жалғасады.
Арифметикалық амалдардың компоненттері мен нәтижелері арсындағы байланыстар, арифметикалық амалддардың дұрыс орындалғанын тексеру және белгісіз компоненттерін табу үшін пайдаланылады. Сондықтан әрбір арифметикалық амалдың нақтылығы мағынасын айқындаумен бірге ,олардың белгіленуі,яғни амал таңбасы және терминалогия ,амалдардың ,амалдардың компоненттері мен нәтижелерінің атаулары енгізіледі. Матеметикада арифметикалық амалдарды орындау реті туралы ережелерлің маңызы зор. Ол ережелердің өзі математикалық заңдылық емес ,тек солай қолданып қалыптасып кеткен келісім екенін ескерген жөн.
Арифметика математиканың алгебра, геометрия және тригонометрия сияқты күрделі салаларының негізі болып табылады. Негізгі арифметикалық амалдар мен сандармен жұмыс істеу ережелерін түсінбестен, күрделі математикалық ұғымдарды түсіну және қолдану мүмкін емес. Сонымен қатар, арифметика адамдардың күнделікті өмірінде маңызды рөл атқарады. Негізгі математикалық операцияларды білу және сандармен жұмыс істей білу қаржыға, бюджетті жоспарлауға, өлшеуге және т. б. байланысты көптеген мәселелерді шешу үшін қажет. Арифметика математиканың ажырамас бөлігі болып табылады және ғылыми зерттеулер үшін , күнделікті өмір үшін де үлкен маңызға ие. Арифметика математиканың көне салаларының бірі болып табылады. Ол математикамен бірге қалыптасып, дамыды.
Арифметиканың дамуы әр уақытта халықтар арасында әр түрлі болды. Мысалы, үндістер текше түбірін алуды қарапайым арифметикалық амалдарға жатқызды. Арифметикалық әрекеттерді арифметикалық амалдар деп атауы алғаш рет XIII ғасырдың қолжазбаларында кездеседі. XVI ғасырда ол жалпы қолданысқа енді және арифметикалық амал термині қалыптасты (лат. рагѕ arthmetika). Үнді математиктері алты арифметикалық әрекетті қарастырды: қосу, азайту, көбейту, бөлу, дәрежелеу және түбір астына алу. Мысырлықтар сандар бойынша төрт амалды қосу, екі есе көбейту және екіге бөлу арқылы жүзеге асырды. Екі еселену Египетте негізгі операция болды және Египет тілі бұл үшін қос санның ерекше формасын қолданды. Ал азайту амалы болса азайтылғанға дейін азайтқанды қосу арқылы жүзеге асырылды. Гректер көбейту амалын білгенменен, күнделікті тәжірибеде Египеттің екі еселену әдісін қолданды. Бұл елдерде сандарға амал қолдану үшін арифметикалық әрекеттерді қолданды. Бәрімізге белгілі, қазіргі қарапайым арифметикалық амалдардың негізін үнді халқы қалыптастырған болатын.
Арифметиканың пайда болуының себебі – санауға, қарапайым өлшеулер мен есептеулерге практикалық қажеттіліктің болуы еді. Математика нақтылықты, сандарды, фигуралар мен кеңістіктегі заттарды зерттейді. Осы аталғандарды зерттеу үшн математикада арифметикалық амалдар қолданылады. Сондықтан да арифметикалық амалдар математиканың ажырамас бөлігі болып саналады.
1. ҚОСУ МЕН АЗАЙТУ АМАЛДАРЫНЫҢ ЖАЗБАША ӘДІСТЕРІ
Математикада сан және цифр ұғымдарымен танысқаннан кейін, осы сан мен цифрға математикалық амалдар, яғни арифметикалық амалдарды қолдануды үйретеді. Арифметикалық амалдарды үйретуде ең алдымен қосу және азайту амалдары үйретіледі. Қосу мен азайту амалдары арифметикалық амалдардың ішіндегі үйретілуі оңай амалдар. Бұл екі амал бір-біріне кері амалдар болып табылады. Сондықтан қосу мен азайту амалдарын үйрету қатар жүреді. Осы екі амалды үйретуде оқушыларда алғашқы математикалық негіз қалыптасады. Қосу амалын үйрену заттардың, сандардың әр түрлі топтарын біріктірумен, ал азайту – заттардың, сандардың тобынан затты не санды алып тастаумен байланысты үйретіледі.
-
Қосу – екі немесе одан да көп элементтерді біріктіру процесі.
Математикадағы қосу – екі немесе одан да көп сандардың қосындысын есептеу әдісі. Қосу амалын орындағанда қосудың өзінің құрамды бөліктері болады: қосылғыш, қосылғыш, қосындының мәні. Мысалы 2 + 5 = 7 теңдігін қарастырайық. Бұл теңдікте 2 – қосылғыш, 5 – қосылғыш, ал 7 – қосындының мәні. Қосу амалымен сандарды өрнектеу қосынды деп аталады.
-
Азайту – бұл бір санды екіншісінен алу процесі.
Бұл негізгі арифметикалық амал, ол азайту (-) белгісімен белгіленеді және екі сан арасындағы айырмашылықты есептеу әдісі болып табылады. Азайту амалының бөліктері: азайғыш, азайтқыш, айырманың мәні. Мысалы: 9 – 3 = 6. 9 – азайғыш, 2 – азайтқыш, 7 – айырманың мәні болып табылады. Азайту амалымен сандарды өрнектеу айырма деп аталады.
Қосу амалын орындау кезінде оның қасиеттерін қолданамыз:
1.Ауыстырымдылық
қасиеті: ![]() ;
;![]() – қосылғыштардың орны
ауысқанымен қосындының мәні өзгермейді. Мысалы: 36 + 14 = 50; 14 +
36 = 50.
– қосылғыштардың орны
ауысқанымен қосындының мәні өзгермейді. Мысалы: 36 + 14 = 50; 14 +
36 = 50.
2. Терімділік
қасиеті: ![]()
Мысалы: (25 + 13) + 14 = 25 + (13 + 14) = 52
3. Қосылғышқа 0 –ді қосса, қосындының мәні қосылғышқа тең болады.
Азайту амалының қасиеттері:1. Азайғыштан 0 – ді азайтса, айырманың мәні азайғышқа тең болады.
Мысалы: 26 – 0 = 26.
2. Азайғыш пен азайтқыш бірдей сан болса, онда айырманың мән 0-ге тең болады. Мысалы: 26 – 26 = 0.
Математикалық өрнектерде арифметикалық амалдар жақша арқылы да орындалды. Жақшаға арқылы орындалатын екі ереже:
1. жақшасыз өрнекте бірінші солдан оңға қарай көбейту мен бөлі, ал содан кейін қосу мен азайту амалдары орындалады.
2. Егер өрнекте жақша болса, онда жақша ішіндегі амалдар бірінші орындалады.
Қосу мен азайту амалдарын жазбаша орындау әдістері
Арифметикалық амалдарды орындау ауызша және жазбаша орындалады. Амалдарды ауызша орындау әдістерінде оқушылар ойша есептеп, логикалық ойлауын тез дамыта алады. Бірақ та амалдарды ауызша орындау жазбаша орындауды үйренгеннен кейін ғана оңай әрі тез үйретіледі. Сондықтан бірінші кезекте есептеуде арифметикалық амалдарды жазбаша орындау әдістерін қолданады. Жазбаша есептеу тәсілдерінде өзіндік алгоритмдер қолданылады. Жазбаша қосу және азайту амалдарын орындау алгоритмдерінің қарапайымдылығына қарамастан, оқушылар көптеген қателіктер жібереді. Жазбаша орындау тәсілдерін үйрету кезінде амалдардың әрқайсысын жазбаша орындаудың рет-тәртібі көрсетіліп орындалады. Оқушыларға амалдарды жазбаша орындауды үйрету кезінде алгоритмдер мен есептер шешімдерінің дұрыстығын мұқият қадағалау керек. Сандарды жазбаша қосу және азайту алгоритмін білгеннен кейін, оқушылар өздері қорытынды ережені тұжырымдай алады. Амалдарды жазбаша орындау әдістері арқылы есепті жылдам әрі дұрыс шығара біледі. Математика сабағында арифметикалық амалдарды жазбаша орындау әдістерінің көмегімен оқушыларды сабаққа, есеп шығаруға деген қызығушылығын арттыра аламыз.
Қосу мен азайту амалдарын жазбаша орындау әдістеріне: кестелік қосу- азайту әдісі, бағандау әдісі, қосылғыштарға жіктеу әдісі.
Кестелік қосу азайту әдісі. The method of tabular of addition and substraction.
Кестелік қосу азайту әдісі 1 ден 9-ға дейінгі сандарды қосып, азайту кезінде қолданылады. Бастауыш сынып математикасында натурал сандарға арифметикалық амалдар қолдануды осы кестелік қосу азайту әдісімен есептеу арқылы бастайды. Кестелік қосу азайту әдісінде ең алдымен сандарға 1-санын қосып, азайтуды көрсету арқылы санға 1-ді қосқанда сол саннан кейінгі сан шығатынын, керісінше саннан 1-ді азайтқанда сол саннан алдыңғы санның шығатыны туралы ережені дәлелдейді.
Кестелік қосу азайту әдісінде әрбір санға 1-ден 9-ға дейінгі сандарды қосу азайту кестесі беріледі. Амалдардың кестелік әдісін оқып-үйренуде 10-ға дейінгі сандардың құрамын білу өте маңызды. Қосу амалының кестелік әдісінің тиімділігі – сандарды орын ауыстырып қоса алады, қосудың ауыстырымдылық қасиетін қолданады. Бұл әдіс арқылы бала сан құрамын тез жаттап, қосудың ауыстырымдылық қасиетін қолдануды тез үйренеді.
1 – ден 5-ке дейінгі қосу кестесі
|
+ |
1 |
2 |
3 |
4 |
5 |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
2 |
3 |
4 |
5 |
6 |
7 |
|
3 |
4 |
5 |
6 |
7 |
8 |
|
4 |
5 |
6 |
7 |
8 |
9 |
Кестелік әдісті білгеннен кейін бала сандарды қосылғыштарға жіктеп жаза алады. Мысалы 5-санының қосылғыштарын айтып бере алады: 5 = 1+4 және 5 = 2 +3
Бағандаy тәсілі
Математикада екітаңбалы немесе одан да көп таңбалы сандарды қосу-азайту амалдарын орындау үшін бағандау тәсілін жиі қолданады. Бұл тәсіл бастауыш математикасында екітаңбалы сандарға амалдар қолдану кезінде үйретіледі. Бағандау тәсілі қосу мен азайту амалдарын үйретуде оқушылар үшін тиімді әрі жылдам тәсіл, бірақ бағандап қосу-азайту кезінде міндетті түрде сандардың разрядтық бірліктерін (бірлік, ондық, жүздік) мұқият үйренген жөн. Бұл әдістің ерекшелігі сандардың рет ретімен разрядына қарай жазылуына байланысты. Қосу не азайту, көбейту амалы болсын бағандау әдісінде бірлік бірліктің астында, ондық ондықтың астында, жүздік жүздіктің астында жазылады. Осы разрядтың қатардың реті дұрыс жазылмаса, мән дұрыс шықпайды.
Қосу мен азайту амалын бағандау тәсілімен орындау алгоритмі:
-
Сандарды екі жолға бір-бірінің астына жазу;
-
Орындау керек амалдың таңбасын салу;
-
Ең кіші бірліктен бастап амалды орындау;
-
Бірліктерді қосқанда ондық сан шықса, онда ондық санды ойға алып, бірлік санды жазамыз. Ойдағы ондықты ондықтарға қосамыз.
Егер азайту кезінде азайғыш азайтқыштан кіші болса, онда бірліктен не ондықтан қарыз сұралып алынады.
Қосу амалына мысал:

Азайту амалына мысал:

Қосылғыштарға жіктеу тәсілі. Еxtended column method.
Бағандау тәсілі арқылы қосу – азайту амалдарын орындауды үйренгеннен кейін оқушылар тез есептеп үйренеді. Бірақ бағандап қосу-азайту кезінде бірліктер мен ондықтарға амалдар орындауда көп қателеседі. Сондықтан сандарды қосылғыштарға (разрядтарға) жіктеу арқылы қосуға да болады. Мысалы: 756 + 489 =
1) сандарды қосылғыштарға жіктеп аламыз;
756 = 7 жүздік 5 ондық 6 бірлік
489 = 4 жүздік 8 ондық 9 бірлік
2) бірліктерді, ондықтарды, жұздіктерді жеке жеке қосамыз.
7 жүздік 5 ондық 6 бірлік
+
4 жүздік 8 ондық 9 бірлік
![]()
1 мыңдық 2 жүздік 4 ондық 5 бірлік
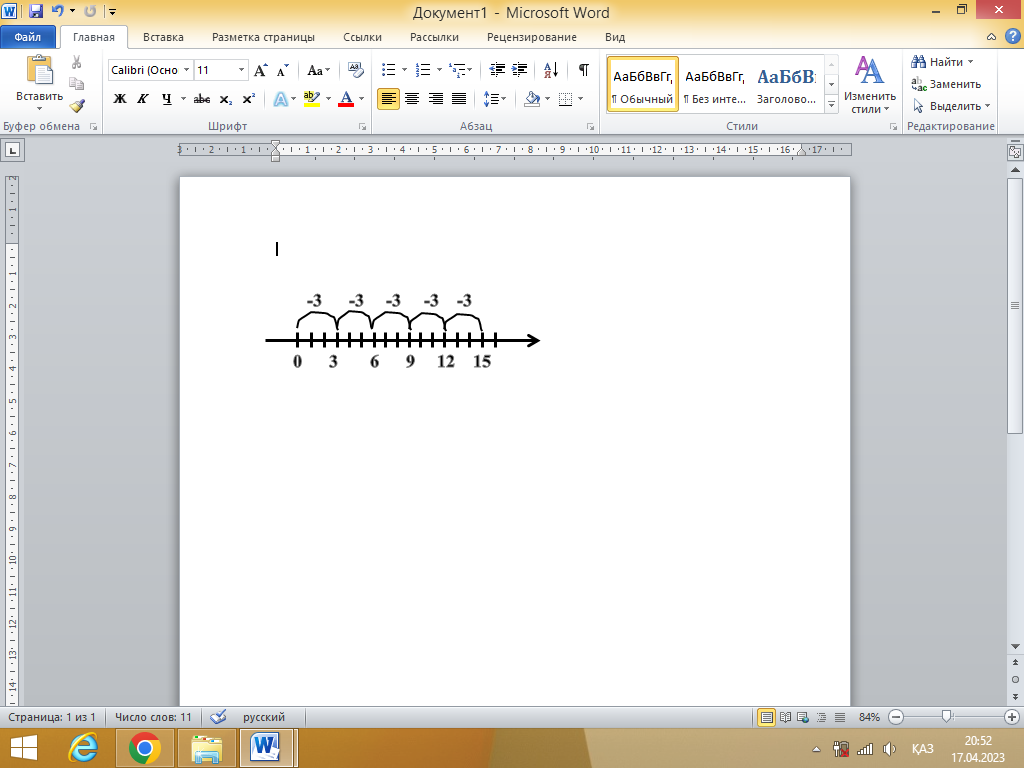
Жуықтау тәсілі
Бұл тәсіл қосу амалы арқылы азайту амалын тиімді орындау тәсілі болып табылады. Азайту амалында азайтқышты ондыққа, жүздікке немесе мыңдыққа жуықтау арқылы уақытты үнемдеп тез шығаруға болады. Жуықтау тәсілінің орындалу жолы қарапайым: азайтқышты ондықтан, жүздіктен азайтамыз; шыққан мәнді азайғышқа қосамыз; осыдан шыққан мәннің алдындағы 1 цифрын алып тастаймыз, сонда қалған сан айырманың мәні болады.
Мысалы: 653 – 372 = 281
1) 653
 1000
1000
1000 – 372 = 628
2)653 + 628 = 1281
3) 1281
 281
281
Жай бөлшектерді қосу мен азайтудың әдістері
Жай бөлшек – натурал санның бір немесе бірнеше тең бөліктерінен құралған сан. Жай бөлшек тақырыбы 5-6 сынып оқушылары үшін күрделі тақырып. Жай бөлшектерді қосу мен азайтуда олардың қасиеттерін ескерген жөн. Арифметикалық амалдарды орындауда жай бөлшектердің түріне қарай амалдар орындалады.
Жай бөлшек дұрыс, бқрыс
және аралас жай бөлшек деп бөлінеді. Бірақ біз оларға амал
қолданғанда бөлімдеріне назар аударамыз. Жай бөлшектің бөлімі –
санның неше бөлікке бөлінгенін көрсетеді.
Мысалы: санның үштен бір бөлігі.
санның үштен бір бөлігі.
Бөлімдері бірдей сандарды қосу мен азайту қарапайым қосу-азайту әдістерімен шы,арылады. Жай бөлшектің бөлімдері өзгерісссіз қалып, алымдарына амал қолданамыз. Үлгі:
Жай бөлшекті азайту:

Жай бөлшекті қосу:


Бөлімдері әр түрлі жай бөлшекті қосу-азайтуда көбелек әдісін қолдану тиімді. Көбелек әдісінде қарама-қарсы алымдары мен бөлімдерін көбейтіп, қосу немесе азайтуды орындаймыз.
Үлгі:
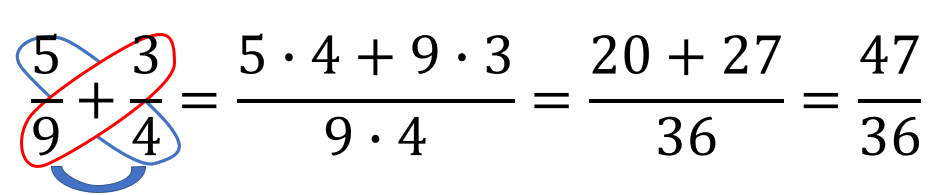
3. КӨБЕЙТУ МЕН БӨЛУ АМАЛДАРЫНЫҢ ЖАЗБАША ӘДІСТЕРІ
Көбейту – қосу, азайту және бөлумен қатар төрт негізгі арифметикалық әрекеттің бірі.
Математикада көбейту бірдей топтарды бірнеше рет қосуды білдіреді. Көбейтілетін сандар көбейткіштер деп аталады, ал екі немесе одан да көп сандарды көбейткеннен кейін алынған нәтиже сол сандардың көбейтіндісі деп аталады. Көбейту бір санды бірнеше рет қосу мәселесін жеңілдету үшін қолданылады . Мысалы: егер 6 қорап шар болса және әр қорапта 9 шардан болса, шардың жалпы санын табыңыз.
Шешуі: Қосу амалы арқылы: 9+9+9+9+9+9 = 54
Енді көбейту амалымен есептейік. Біз қораптар санын әр қораптағы шарлар санына көбейтеміз. Егер біз 6 × 9 көбейтсек, онда біз шарлардың жалпы санын аламыз, бұл 6 × 9 = 54. Осылайша, қысқа уақыт ішінде бірдей нәтиже аламыз.
Математикада бізде әртүрлі белгілер бар. Көбейту символы – ең көп қолданылатын математикалық белгілердің бірі. Жоғарыдағы мысалда біз 6 және 9 екі санды көбейту туралы білдік. Егер көбейту өрнегін (6 × 9 = 54) қарастыратын болсақ, онда (× ) таңбасы екі санды қосып, берілген өрнекті аяқтайтынын көреміз. Крест белгісінен басқа ( × ) көбейту нүкте (•) және жұлдызша (*) белгісімен де белгіленеді.
Көбейту амалының алгоритмі
Көбейтінді * көбейткіш = көбейтіндінің мәні
Көбейтінді – көбейтілетін сан, көбейткіш – көбейтетін сан, ал көбейтіндінің мәні көбейту амалынан алынған шешім.
Көбейтудің қасиеттері:
-
ауыстырымдылық қасиеті: көбейткіштердің орнын ауыстырғанымен көбейтіндінің мәні өзгермейді.
-
терімділік қасиеті: санды екі санның көбейтіндісіне көбейту үшін , алдымен бірінші көбейткішке көбейтіп, шыққан мәнді екінші көбейткішге көбейтеді.
-
қосуға қатысты үлестірімділік қасиеті: қосындыны санға көбейту үшін әр қосылғышты сол санға көбейтіп, шыққан көбейтіндінің мәндерін қосу.
Бөлу – математикадағы негізгі арифметикалық амалдардың бірі, онда үлкен сан элементтердің саны бірдей кіші топтарға бөлінеді, тең топтастыру және тең бөлу үшін қолданылатын операция.
Бөлу қайталанатын азайту амалы және көбейту амалына кері амал. Бөлу сызықтың үстінде және астында нүктелері бар шағын көлденең сызықтан тұратын математикалық таңбамен белгіленеді. Екі санның бөлінуін білдіретін екі негізгі бөлу таңбасы бар. Бұл ÷ және /.
Бөлу амалының алгоритмі
Бөлінгіш/бөлгіш = бөліндінің мәні
Бөлу бөліктері бөлу процесіне қатысты терминдердің атауын білдіреді. Бөлудің төрт бөлігі бар: бөлінгіш, бөлгіш, бөліндінің мәні және қалдық. Бөлінгіш – бөлінетін сан, ал бөлгіш санды бөлетін сан. Бөлу амалы арқылы алынған мән бөліндінің мәні болып табылады. Қалдық дегеніміз бөлу кезінде бөлінбей қалған артық сан. Мысалы: 24 / 4 = 6. 24 – бөлінгіш, 4 – бөлгіш, 6 – бөліндінің мәні.
Көбейту кестесі. Көбейту амалын орындау үшін көбейту кестесі қолданылады. Кесте бойынша көбейтуді алғаш рет вавилон математиктері енгізді. Алайда, бұл ондық санау жүйесіндегі дәстүрлі көбейту емес, әлем халықтары арасында кең орын алмаған алпысыншы санау жүйесіндегі дайын кестелер бойынша көбейту болды. Көбейту кестесінің күнделікті формасы бағаналар түрінде жасалған Паламеда кестелерінде (б.з. д. III ғасырға дейін) және квадрат түрінде жасалған Никомах кестесінде (б. з. I ғ.) қолданылды. Кестелік көбейтудің қазіргі заманғы өзгеруі үнділердің ондық позициялық санау жүйесін ойлап тапқаннан және олардың нөлді енгізген кезінен, сондай-ақ ерікті сандарды көбейтудің неғұрлым жетілдірілген тәсілдерін ойлап тапқаннан басталады (V-VI ғғ.). Бүгінгі таңда көбейту әрекетін жазудың өзгеретін түрін Н.Г.Курганов өзінің "әмбебап арифметикасында" (1757) енгізді.
Көбейту кестесі – бұл 1-ден 9-ға дейінгі сандарды бір-біріне көбейтудің көбейтіндісін алу үшін қолданатын математикалық кесте. Қазір көбейту кестесінің ондық үлгісі қолданылады. Ең танымал кесте, оның негізі ондық жүйе, бамбук жолақтарындағы қытайлық көбейту кестесі болып саналады. Қытайдың ең көне көбейту кестелері б.з.д. 221-206 жылдар аралығындағы Цинь әулетінің кезеңде пайда болды. Бұл қарапайым көбейтуге мүмкіндік беретін қысқа сөйлемдер сериясы (мысалы, «алты сегіздік қырық сегізді тудырады»).
Көбейту кестесін бастауыш мектеп математикасында үйретеді. Көбейту кестесі арқылы көбейтуді жазбаша орындаудың басқа да тәсілдері қарастырылады.
9-ға көбейту тәсілі.
Адамдардың ең алғашқы санау құралдарының бірі олардың саусақтары болған. Осы саусақтар арқылы ондық санау жүйесі қалыптасқан. Көбейту амалында таяқтар пен басқа заттардың көмегінсіз саусақтар арқылы орындаған. Оған айқын мысал 9-ға көбейту тәсілі. Бұл өте қарапайым тәсіл. Кез келген 1-ден 9-ға дейінгі санды 9-ға көбейту үшін қолыңызға қараңыз. 9*3 табайық. Бізде көбейткіш 3-ке тең болғандықтан, қолымыздың сол жағынан 3-ке дейін санап, сол саусақты бүгеміз. Бүгілген саусаққа дейін 2 саусақ, ал кейін 7 саусақ қалды. Сонда бізде 27 саны шықты.

Бағандау тәсілімен көбейту.
Көбейту кестесі мектепте 1-ден 9-ға дейінгі сандар аралығында ғана үйретіледі. Бұл сандар бізде тек қана бір таңбалы сандар. Ал екітаңбалы сандарға көбейту амалын қолдануда бағандау тәсілі қолданылады және Әдетте бұл әдіс мектеп оқушыларына үлкен сандарды көбейту әдісі ретінде оқытылады және арифметика негіздерін нығайту үшін білім беру мақсатында қолданылады. Бағандап көбейту тәсілі көбейтудің тиімді тәсілі болғанымен, бұл тәсілдің орындалу жолы күрделі, сондықтан бұл көбейтудің ұзақ тәсілі деп те аталады. Бағандау тәсілінде көбейту кестесін білу керек. Бұл тәсілдің алгоритмі көбейту амалында да өзгеріссіз қалады:
•Сандарды жазыңыз;
•Көбейту амалының таңбасы қойылады;
•Көбейтіндіні көбейткіштің бірлігіне көбейтіңіз;
•Көбейтіндіні көбейткіштің ондық цифрына көбейтеміз және бірліктен шыққан мәннің ондық цифрынан бастап жазамыз;
•Шыққан мәндерді қосамыз.
Үлгі:

|
|
|
|
|
° |
|
|
|
|
|
5 |
6 |
|
|
|
|
x |
8 |
3 |
1 |
|
|
|
1 |
6 |
8 |
|
|
+ |
4 |
4 |
8 |
|
1 |
|
|
4 |
6 |
4 |
8 |
|
Кестелік көбейту тәсілі.
Кестелік көбейту тәсілі бағандап көбейту тәсілімен ұқсас болып келеді. Бұл тәсілдің ерекшелігі сандарды көбейткіштерге жіктеп алып, жеке көбейтіледі. Мысалы екі таңбалы сандарды осы тәсіл арқылы көбейтіп көрейік:
Бірінші, сандарды көбейткіштерге жіктеп жазамыз;
Екінші, сандарды кестеге салып көбейтеміз;
Үшінші, шыққан мәндердің барлығын қосамыз.
Мысалы: 43 * 21 = 903
1) 43 = 40+3; 21 = 20+1.
2)
|
х |
20 |
1 |
|
40 |
800 |
40 |
|
3 |
60 |
3 |
3) 800+40+60+3 = 903
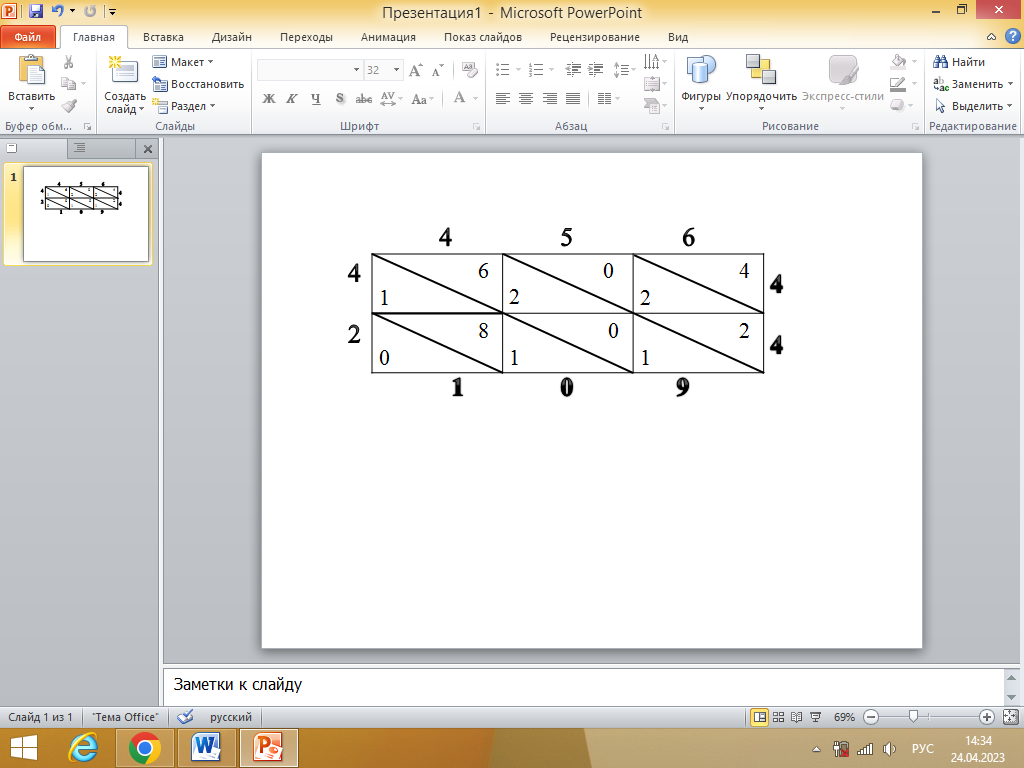
Бхаскара тәсілі. Мethod of Bhaskara.
Бұл XII ғасырда өмір сүрген үнді математигі Бхаскараның көбейту амалына қолданған ежелгі тәсілі.
Бұл әдісте сандарды жоғарғы солдан оңға қарай сызылған диагональдармен екіге бөлінген квадраттарда есептейді. Әрбір шаршының үстінде бірінші көбейткіштің сандары, ал сол жақта төменнен жоғарыға қарай екінші көбейткіштің сандары жазылады. Квадраттың басқа жақтарынан жоғары оң жақтан бастап көбейткіштердің цифрларының көбейтіндісі жазылады. Әр жеке өнімнің бірліктері шаршының диагоналінің үстіне толтырылады. Бір жолдағы сандар қосылады. Егер қосынды оннан көп болса, онда қосындының бірлік цифры ғана жазылады, ал келесі қосындыға ондық цифры қосылады. Егер қосынды оннан аз болса, онда ол жолақтың төменгі цифрының астына жазылады. Әр жолдан шыққан цифрлар көбейтіндінің мәні болып табылады.
Мысалы: 256 * 83 =
|
x |
2 |
5 |
6 |
|
|
|
3 |
6 |
5 1 |
8 1 |
8 |
|
|
8 |
6 1 |
0 4 |
8 4 |
4 |
|
|
|
2 |
1 |
2 |
|
|
Қарапайым бөлу тәсілі. Азайту амалы арқылы бөлу амалын орындауда қолданылатын оңай тәсілді қарапайым бөлу тәсілі деп атайды. Қарапайым бөлу тәсілінде бөлінгіштен бөлгішті бөліндінің мәні 0-ге тең болғанша немесе қалдық шыққанша азайтады. Бұл тәсіл бастауыш оқушыларына бөлу туралы негізгі тұжырымдаманы үйретуде қолданылады. Қарапайым бөлу тәсілінің алгоритмі:
-
Бөлінді мен бөлгішті анықтау;
-
Бөліндіден бөлгішті азайту;
-
Айырмадан бөлгішті азайту;
-
Бөліндінің мәні 0-ге тең болғанша немесе қалдық шыққанша азайтуды жалғастырады;
Мысалы: 15 / 3 =
1) 15 – 3 = 12
2) 12 – 3 = 9
3) 9 – 3 = 6
4) 6 – 3 = 3
5) 3 – 3 = 0

Бағандап бөлу тәсілі. Бөлу амалы 4 амалдың ішіндегі үйретілуі күрделі, қиын амал. Бөлу амалы тікелей көбейту амалымен байланысты және осы амалға кері амал. Бағандап бөлу тәсілінде бөлінгішті жоғары разрядтан бастап бөледі және бөліндінің мәні 0-ге тең болғанша азайтады. Егер толымсыз бөлінгіш болса,онда келесі разрядқа қосылып бөлінеді.
4. ЕСЕПТЕУЛЕР
№1. Бағандау тәсілі арқылы қосу амалын орындаңдар.
1) 263+458
|
|
|
° |
° |
|
|
2 |
6 |
3 |
|
+ |
4 |
5 |
8 |
|
|
7 |
2 |
1 |
263+458 = 721
2) 4539+716
|
|
|
° |
|
° |
|
|
4 |
5 |
3 |
9 |
|
+ |
|
7 |
1 |
6 |
|
|
5 |
2 |
5 |
5 |
4539 + 716 = 5255
3) 3568 + 57
|
|
|
|
° |
° |
|
|
3 |
5 |
6 |
8 |
|
+ |
|
|
5 |
7 |
|
|
3 |
6 |
2 |
5 |
3568 + 57 = 3625
№2 Жуықтау тәсілімен азайту амалын орындаңдар.
1) 896 – 584;
Шешуі:
896  1000
1000
1000 – 584 = 416
416 + 896 = 1312
896 – 584 = 312
Жауабы: : 312
2) 956 – 327;
Шешуі:
956  1000
1000
1000 – 327 = 673
956 + 673 = 1629
956 – 327 = 629
№3. Кестелік көбейту тәсілімен көбейту амалын орындаңдар.
1) 452 * 53;
Шешуі: 452 = 400+50+2
53 = 50 +3
|
x |
400 |
50 |
2 |
|
50 |
20000 |
2500 |
100 |
|
3 |
1200 |
150 |
6 |
20000+2500+1200+150+100+6 = 23956
Жауабы: 23956
2) 125 * 36;
Шешуі: 125 = 100+20+5;
36 = 30+6.
|
x |
100 |
20 |
5 |
|
30 |
3000 |
600 |
150 |
|
6 |
600 |
120 |
30 |
3000+600+600+150+120+30 = 4500
Жауабы: 4500
№3.Бхаскара тәсілі арқылы көбейту амалын орындаңдар.
1)456*24;

456 * 24 = 10944
2) 562 * 34;

562 * 34 = 12208
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ
1. Әбілқасымова А.Е. Математиканы оқытудың теориясы мен әдістемесі:дидактиалық әдістеме негіздері. – Алматы: Мектеп, 2014. -214 бет.
2. Билялова Ж.Т. Бастауыш сыныптарда математиканы оқытуда оқу есептерін пайдалану әдістемесі. – Алматы: 2000. – 26бет
3. Бидосов Э. Математиканы оқыту методикасы. – Алматы: Мектеп, 1989. – 300 бет.
4. Абылкасымова А.Е. және т.б. Орта мектепте математика есептерін шығаруға үйретудің әдістемелік негіздері. –Алматы, 2004. -125 бет.
5. Андронов И. К., Брадис В. М. Арифметика: пособие для средней школы. — 1957
6. Шохор-Троцкий С.И. Методика арифметики: пособие для учителей средней школы – 1935, 343 с.

шағым қалдыра аласыз















