
Железинский аграрно-технический колледж
План учебного занятия №
56
(теоретического обучения)
Многогранники.
(тема
занятия)
Наименование модуля /дисциплины Математика
Подготовил педагог Аплашова Акмарал Кайратовна
«___» __________ 2025 года
1. Общие
сведения
Курс 1, группа _______
Тип занятия: Изучение нового материала
2. Цели,
задачи
1)Дать понятия правильного многогранника, рассмотреть свойства многогранников, познакомить с историей возникновения и развития теории многогранников, рассмотреть виды многогранников.
2) Формирование пространственных представлений, математической культуры, культуры общения
3)Развитие практических навыков учащихся по изготовлению правильных, полуправильных, многогранников
3. Перечень ожидаемых результатов и (или) профессиональных умений, которыми овладеют обучающиеся в процессе учебного занятия
1) Раскрывает содержание понятия многогранника и его элементов;
2) Объясняет свойства многогранников по видам.
4. Необходимые ресурсы
Геометрия 11 кл, изд «Алматы мектеп» общественно-гуманитарное направление - В.Гусев,Ж.Кайдасов, А.Кагазбаева. раздаточный материал, карточки с заданиями, презентация к теме урока, компьютер, интерактивная доска, проектор.
5. Ход занятия
5.1 Организационный момент
Взаимоприветствие. Фиксация отсутствующих. Проверка подготовленности к уроку. Создание благоприятной среды. Психологический настрой на урок.
Прием «Винегрет» – вопросы из разных областей знаний, например:
- За сколькими зайцами нельзя угнаться? (За двумя.)
- Какая нога собаке ни к чему? (Пятая.)
- Золотое колесо в синем небе? (Солнце.)
- Сколько букв в русском алфавите? (33)
- Назовите три последние буквы алфавита. (Э, ю, я.)
- Какой сегодня день? (Вторник, 19 января.)
- Записываем в тетради: 7 декабря. Классная работа.
5.3 Объяснение нового материала
B – НАВЕДЕНИЕ МОСТОВ
Просмотрите пожалуйста фрагменты видео и ответьте на следующие вопросы: https://bilimland.kz/ru/courses/math-ru/geometriya/stereometriya/mnogogranniki/lesson/ponyatie-mnogogrannika-obshie-svoi-stva-obemov
1.Что вы увидели в данном видеоролике?
2. Скажите, в повседней жизни часто ли мы пользуемся многогранниками?
3. Как вы думаете чем отличаются друг от друга многогранники?
4. Сформулируйте определение многогранника.
Отвечая на вопросы вы должны были догадаться, что сегодня на уроке мы будем с вами изучать!
Давайте вместе сформулируем тему нашего урока…( формулируют тему урока «Многогранники» и записывают в тетради)
Давайте ребята запишем новые слова и переводы к ним:
|
На русском: |
На казахском: |
На английском: |
|
Многогранники |
көпжақтар |
polyhedron |
|
Грань |
қыр |
facets |
|
Ребро |
қабырғалар |
slats |
|
Вершина |
шын |
vertex |
O – ОЖИДАЕМЫЕ РЕЗУЛЬТАТЫ
По окончании урока студенты будут знать определение многогранника, виды многогранников и применять полученные знания на практике
Задание №1. Работа в паре
Прочитать текст учебника §1 стр. 6-7 и выполнить задание. (Приложение 1).
Метод «Составление конспекта»
Цель: изложить основные мысли из прочитанного в учебнике текста
1) Записать определение понятий: многогранника, ребра,вершины, правильный многогранник, выпуклый и невыпуклый многоранник.
2) Составить схему классификаций видов многогранников.
Ответы обучающихся
Критериальное оценивание: самооценивание по ответу
Дескрипторы:
- записывает определение понятий
- составляет схему по классификации видов многогранников
Существует пять правильных многогранников. Почему же многогранники получили такие имена? Названия этих многогранников пришли из Древней Греции, и в них указывается число граней: «эдра» - грань,«тетра» - 4,«гекса» - 6,«окта» - 8,«додека» - 12, «икоса» - 20.
Познакомимся с теоремой Эйлера. Леонард Эйлер – один из величайших математиков 18 века, академик Санкт-Петербургской академии наук. Ему принадлежит более 850 научных работ в разных областях.
Обозначим число граней многогранника буквой Г, число вершин – В, число ребер- Р. Оказывается эти 3 числа для любого простого многогранника связаны одним и тем же соотношением: В+Г-Р=2. Например, у куба В=8, Г=6, Р=12. Тогда 8+6-12=2.
Теорема Эйлера звучит так: «У любого простого многогранника сумма числа граней и вершин на две единицы больше числа ребер».
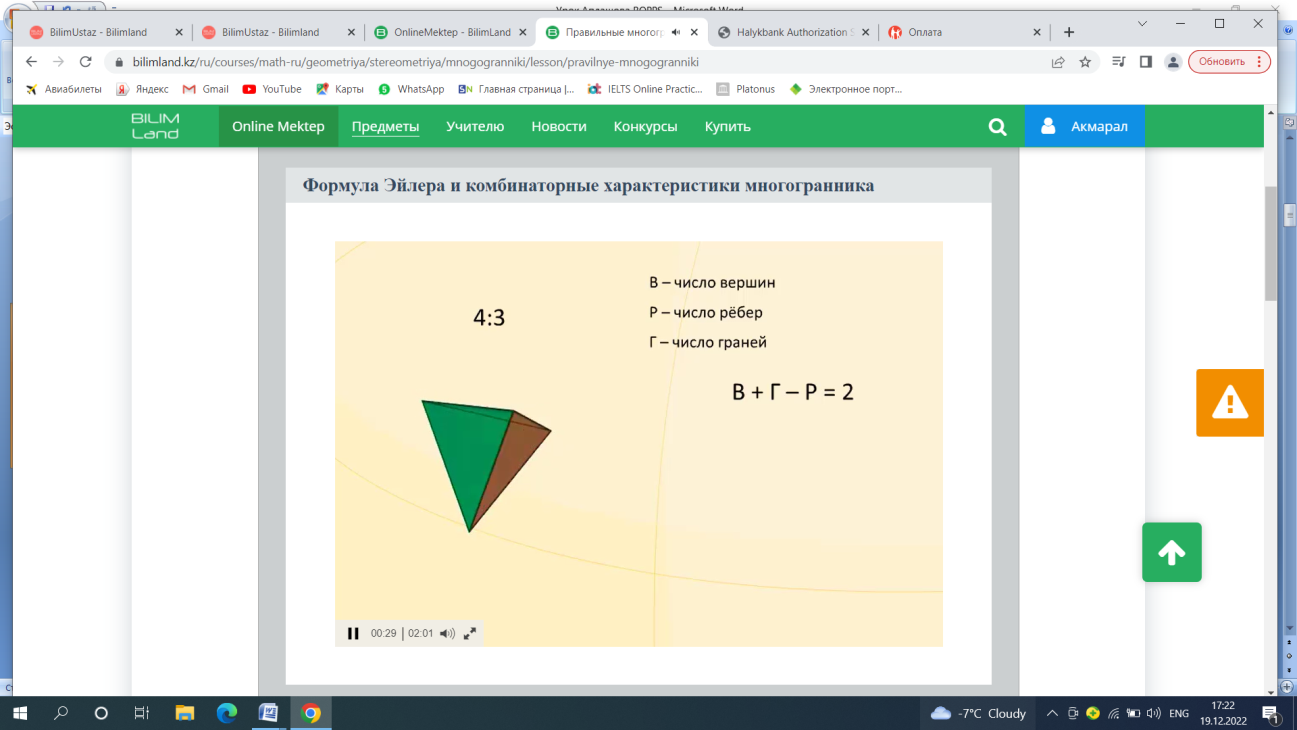
Исследуем многогранники подробнее. Возьмите в руки тетраэдр. Давайте посчитаем вместе количество граней, ребер и вершин. Подсчитаем число указанных элементов правильных многогранников.
( Тетраэдр. Число граней – 4, число вершин – 4, число ребер – 6).
Формативное оценивание . Прием «Светофор»
Задание №2. Работа в группах
Прием «Составление таблицы»
Цель: определяет и знает различие элементов многогранника.
А теперь поработаем по группам: 1 группа работает с кубом, 2 группа – с октаэдром, 3 группа – с додекаэдром. Результаты занести в таблицу. (Приложение 2).
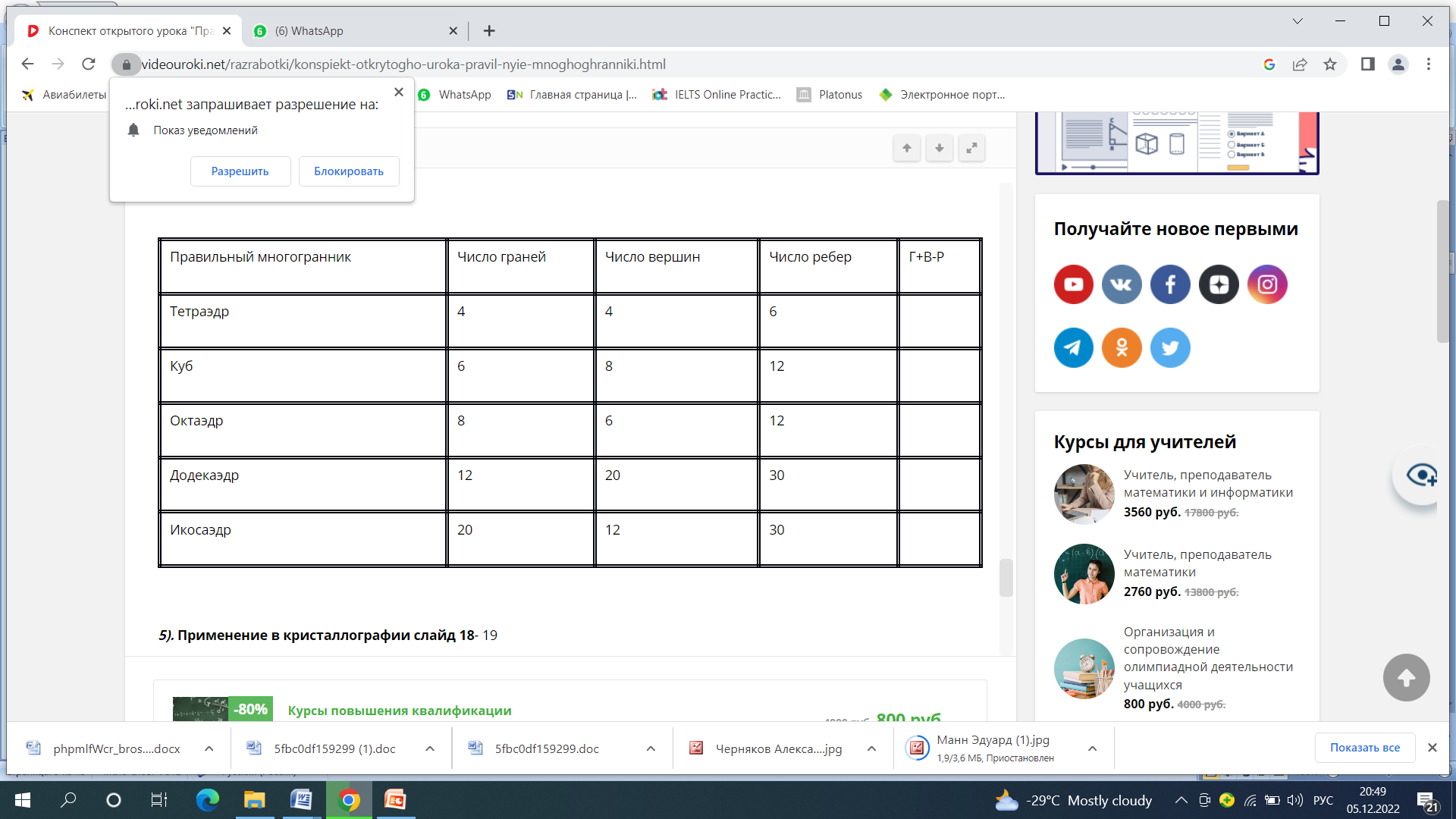
Дескрипторы:
- считает число граней многогранника;
- считает число вершин многогранника;
-считает число ребер многогранника;
P – ПРЕДВАРИТЕЛЬНАЯ ОЦЕНКА
Для того чтобы предварительно оценить работу студентов используем игру Kahoot. https://play.kahoot.it/v2/?quizId=8c7c7779-7994-4989-8c9a-c4ba9ca2d28a
В данном уроке использовались элементы современных педагогических технологий:
-
мобильное обучение (обучение с использованием персональных электронных устройств);
Игра Kahoot позволяет разнообразить работу на уроке, что, в свою очередь, помогает удержать внимание учащихся на проблемах, изучаемых на уроке, и добиться наилучшего результата.
5.4 Закрепление нового материала
P – АКТИВНОЕ ОБУЧЕНИЕ
Задание №3. Будем работать по группам. 1 группа – 1 задача, 2 группа – 2 задача, 3 группа – 3 задача.
Задача 1. Гранями выпуклого многогранника являются только треугольники. Сколько у него вершин и граней, если он имеет 12 ребер? Нарисуйте такой многогранник.
Решение. Пусть у данного многогранника будет В вершин, Р ребер и Г граней. Тогда ЗГ = 2Р, где Р = 12, значит, Г = 8. Применяем теорему Эйлера, из которой следует, что В = 2 + Р - Г. В нашем случае В = 2 +12-8 = 6. Итак, В = 6, Р = 12, Г = 8. Примером такого многогранника является октаэдр.
Задача 2. Из каждой вершины выпуклого многогранника выходит три ребра. Сколько он имеет вершин и граней, если число ребер равно 12? Нарисуйте такой многогранник.
Решение. ЗВ = 2Р, учитывая, что Р = 12, имеем: В = 8. По теореме Эйлера
Г=2-В + Р, Г = 2- 8 + 12 = 6.
Таким образом, у данного выпуклого многогранника В = 8, Р=12 и Г = 6. Примером такого многогранника является куб.
Задача 3. Из каждой вершины выпуклого многогранника выходит четыре ребра. Сколько он имеет вершин и граней, если число ребер равно 12? Нарисуйте такой многогранник.
Решение. 4В = 2Р, учитывая, что Р = 12, имеем: В = 6. По теореме Эйлера
Г=2-В + Р, Г = 2- 6 + 12 = 8.
Таким образом, у данного выпуклого многогранника В = 6, Р=12 и Г = 8. Примером такого многогранника является октаэдр.
Дескрипторы:
- различает грани, вершины и ребра многогранников
-считает количество ребер многогранника
-считает количество вершин многоранника
- определяет вид многогранника
-применяет теорему Эйлера при решении задач
Критериальное оценивание: взаимооценивание, группы оценивают работу друг друга
Прием «Стена Граффити».
C помощью плаката, маркеров, студенты разрисовывают стену информацией, которой владеют о многогранниках.
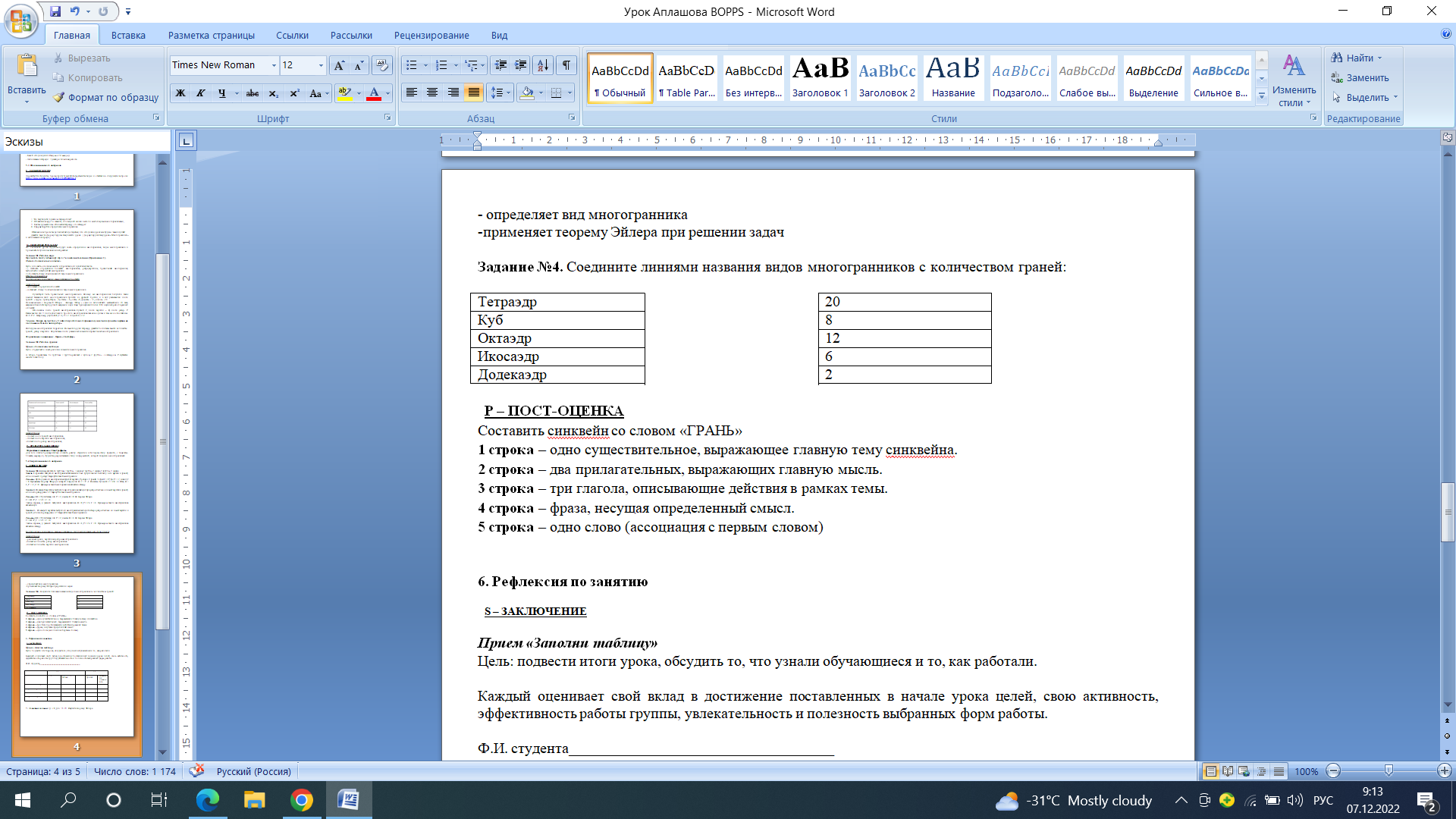
Задание №4. Соедините линиями названия видов многогранников с количеством граней
( Приложение 3).
|
Тетраэдр |
|
20 |
|
Куб |
|
8 |
|
Октаэдр |
|
12 |
|
Икосаэдр |
|
6 |
|
Додекаэдр |
|
4 |
P – ПОСТ-ОЦЕНКА
Составить синквейн со словом «ГРАНЬ»
1 строка – одно существительное, выражающее главную тему cинквейна.
2 строка – два прилагательных, выражающих главную мысль.
3 строка – три глагола, описывающие действия в рамках темы.
4 строка – фраза, несущая определенный смысл.
5 строка – одно слово (ассоциация с первым словом)
6. Рефлексия по занятию
S – ЗАКЛЮЧЕНИЕ
Прием «Заполни таблицу». (Приложение 4).
Цель: подвести итоги урока, обсудить то, что узнали обучающиеся и то, как работали.
Каждый оценивает свой вклад в достижение поставленных в начале урока целей, свою активность, эффективность работы группы, увлекательность и полезность выбранных форм работы.
Ф.И. студента___________________________________
|
|
В начале урока |
В конце урока |
|||
|
Я знаю |
хорошо |
удовлетвори-тельно |
не знаю |
узнал лучше |
знания не изменились |
|
Что такое многогранник? |
|
|
|
|
|
|
Виды многогранников? |
|
|
|
|
|
|
Элементы многогранника |
|
|
|
|
|
|
Теорема Эйлера |
|
|
|
|
|
7. Домашнее задание: §1 с. 8, §6 с. 31-33. Выучить теорему Эйлера.
Оценочный лист
по предмету: Математика
на тему: №56 Многогранники
Критерии для оценки результатов учебных достижений
|
Оценка по буквенной системе |
Максимальное количество баллов |
Критерии |
|
|
Отлично |
Оценка «А» |
95-100 |
Знает понятие многогранника Знает основные свойства многогранников Применяет методы решения задач по нахождению свойств многогранников Умеет отличать элементы многогранников Знает теорему Эйлера. Умеет применять формулы Эйлера для нахождения элементов многогранников |
|
Оценка «А-» |
90-94 |
Знает понятие многогранника Знает основные свойства многогранников Применяет методы решения задач по нахождению свойств многогранников Умеет отличать элементы многогранников Знает теорему Эйлера. Умеет применять формулы Эйлера для нахождения элементов многогранников Допускает 1 ошибку. |
|
|
Хорошо
|
Оценка «В+» |
85-89 |
Знает понятие многогранника Называет основные свойства многогранников Применяет методы решения задач по нахождению свойств многогранников Умеет отличать элементы многогранников Знает теорему Эйлера. Допускает 2-3 ошибок |
|
Оценка «В» |
80-84 |
Знает понятие многогранника Называет основные свойства многогранников Применяет методы решения задач по нахождению свойств многогранников Умеет отличать элементы многогранников Знает теорему Эйлера.
|
|
|
Оценка В- |
75-79 |
Знает понятие многогранника Называет основные свойства многогранников Применяет методы решения задач по нахождению свойств многогранников Умеет отличать элементы многогранников Допускает 2-3 ошибок |
|
|
Оценка С+ |
70-74 |
Знает понятие многогранника Называет основные свойства многогранников Применяет методы решения задач по нахождению свойств многогранников Умеет отличать элементы многогранников Допускает 4-5 ошибок |
|
|
Удовлет.
|
Оценка С |
65-69 |
Знает понятие многогранника Называет основные свойства многогранников Умеет отличать элементы многогранников |
|
Оценка С- |
60-64 |
Знает понятие многогранника Называет основные свойства многогранников Умеет отличать элементы многогранников Допускает 2-3 ошибок. |
|
|
Оценка D+ |
55-59 |
Знает понятие многогранника Называет основные свойства многогранников Умеет отличать элементы многогранников Допускает 1-2 ошибок.
|
|
|
Оценка D |
50-54 |
Знает понятие многогранника Умеет отличать элементы многогранников.
|
|
|
Неуд.
|
Оценка F |
0-49 |
Знает понятие многогранника Умеет отличать элементы многогранников |
Примечание: * критерии определяются согласно таксономии Блума:
-
Знание - D (конкретного материала, терминологии, фактов, способов и средств обращения с конкретным материалом, определений, тенденций и результатов, системы понятий и категорий, критериев, методологии и т.п.);
-
Понимание - С, С-,D+ (объяснение, интерпретация, экстраполяция и т.п.);
-
Применение – В-, С+ (применение знаний не только в стандартных, но в новых ситуациях и т.п.);
-
Анализ – В (элементов, взаимосвязей, принципов построения, частей целого и взаимосвязи между ними, нарушений в логике рассуждений, различий между фактами и следствиями, значимости данных и т.п.);
-
Синтез - В+(знаний из нескольких областей, экспериментирование, творческая переработка информации для создания нового целого, получение системы абстрактных отношений и т.п.);
-
Оценка – А, А- (суждение на основе имеющих данных, суждение на основе внешних критериев,
-
видение различий между фактами и оценочными суждениями и т.п.).
Группа: ____________
|
№ |
ФИ обучающегося |
Максимальное количество баллов |
Оценка по буквенной системе |
Достигнутый уровень |
Комментарий |
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
9 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
11 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
13 |
|
|
|
|
|
|
14 |
|
|
|
|
|
|
15 |
|
|
|
|
|
Приложение 1.
Многогранники представляют собой простейшие тела в пространстве, подобно тому, как многоугольники – простейшие фигуры на плоскости. Многогранные формы мы видим ежедневно: спичечный коробок, книга, комната, многоэтажные дома, а также - граненый карандаш, гайка и т.п.
Многогранники обладают богатой историей, которая связана с такими знаменитыми учеными древности, как Архимед, Евклид, Пифагор(слайд10.
С древнейших времен наши представления о красоте связаны с понятием симметрия. Наверное, этим объясняется интерес человека к многогранникам – удивительным символам симметрии, привлекавшим внимание выдающихся мыслителей.
Существует пять правильных многогранников. Почему же многогранники получили такие имена? Названия этих многогранников пришли из Древней Греции, и в них указывается число граней: «эдра» - грань,«тетра» - 4,«гекса» - 6,«окта» - 8,«додека» - 12, «икоса» - 20.
Исследуем многогранники подробнее. Подсчитаем число указанных элементов правильных многогранников и занесём результаты в таблицу (раздаточный материал). Возьмите в руки тетраэдр. Давайте посчитаем вместе количество граней, ребер и вершин.
Теорема Эйлера звучит так: «У любого простого многогранника сумма числа граней и вершин на две единицы больше числа ребер».
Приложение 2.
Задача №2. Посчитать число элементов правильного многоугольника и заполнить таблицу.
|
Правильный многогранник |
Число граней |
Число вершин |
Число ребер |
|
Тетраэдр |
4 |
4 |
6 |
|
Куб |
|
|
|
|
Октаэдр |
|
|
|
|
Додекаэдр |
|
|
|
Задача №2. Посчитать число элементов правильного многоугольника и заполнить таблицу.
|
Правильный многогранник |
Число граней |
Число вершин |
Число ребер |
|
Тетраэдр |
4 |
4 |
6 |
|
Куб |
|
|
|
|
Октаэдр |
|
|
|
|
Додекаэдр |
|
|
|
Задача №2. Посчитать число элементов правильного многоугольника и заполнить таблицу.
|
Правильный многогранник |
Число граней |
Число вершин |
Число ребер |
|
Тетраэдр |
4 |
4 |
6 |
|
Куб |
|
|
|
|
Октаэдр |
|
|
|
|
Додекаэдр |
|
|
|
Задача №2. Посчитать число элементов правильного многоугольника и заполнить таблицу.
|
Правильный многогранник |
Число граней |
Число вершин |
Число ребер |
|
Тетраэдр |
4 |
4 |
6 |
|
Куб |
|
|
|
|
Октаэдр |
|
|
|
|
Додекаэдр |
|
|
|
Задание №3. Выполнить задачи по группам. 1 группа-задача №1, 2 группа-задача №2 3 группа-задача №3.
Задача 1. Гранями выпуклого многогранника являются только треугольники. Сколько у него вершин и граней, если он имеет 12 ребер? Нарисуйте такой многогранник.
Задание №3. Выполнить задачи по группам. 1 группа-задача №1, 2 группа-задача №2 3 группа-задача №3.
Задача 3. Из каждой вершины выпуклого многогранника выходит четыре ребра. Сколько он имеет вершин и граней, если число ребер равно 12? Нарисуйте такой многогранник.
Задание №3. Выполнить задачи по группам. 1 группа-задача №1, 2 группа-задача №2 3 группа-задача №3.
Задача 2. Из каждой вершины выпуклого многогранника выходит три ребра. Сколько он имеет вершин и граней, если число ребер равно 12? Нарисуйте такой многогранник.
Приложение 3.




Приложение 4.
Ф.И. студента___________________________________
|
|
В начале урока |
В конце урока |
|||
|
Я знаю |
хорошо |
удовлетвори-тельно |
не знаю |
узнал лучше |
знания не изменились |
|
Что такое многогранник? |
|
|
|
|
|
|
Виды многогранников? |
|
|
|
|
|
|
Элементы многогранника |
|
|
|
|
|
|
Теорема Эйлера |
|
|
|
|
|
Ф.И. студента___________________________________
|
|
В начале урока |
В конце урока |
|||
|
Я знаю |
хорошо |
удовлетвори-тельно |
не знаю |
узнал лучше |
знания не изменились |
|
Что такое многогранник? |
|
|
|
|
|
|
Виды многогранников? |
|
|
|
|
|
|
Элементы многогранника |
|
|
|
|
|
|
Теорема Эйлера |
|
|
|
|
|
Ф.И. студента___________________________________
|
|
В начале урока |
В конце урока |
|||
|
Я знаю |
хорошо |
удовлетвори-тельно |
не знаю |
узнал лучше |
знания не изменились |
|
Что такое многогранник? |
|
|
|
|
|
|
Виды многогранников? |
|
|
|
|
|
|
Элементы многогранника |
|
|
|
|
|
|
Теорема Эйлера |
|
|
|
|
|
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Многогранники
Многогранники
Железинский аграрно-технический колледж
План учебного занятия №
56
(теоретического обучения)
Многогранники.
(тема
занятия)
Наименование модуля /дисциплины Математика
Подготовил педагог Аплашова Акмарал Кайратовна
«___» __________ 2025 года
1. Общие
сведения
Курс 1, группа _______
Тип занятия: Изучение нового материала
2. Цели,
задачи
1)Дать понятия правильного многогранника, рассмотреть свойства многогранников, познакомить с историей возникновения и развития теории многогранников, рассмотреть виды многогранников.
2) Формирование пространственных представлений, математической культуры, культуры общения
3)Развитие практических навыков учащихся по изготовлению правильных, полуправильных, многогранников
3. Перечень ожидаемых результатов и (или) профессиональных умений, которыми овладеют обучающиеся в процессе учебного занятия
1) Раскрывает содержание понятия многогранника и его элементов;
2) Объясняет свойства многогранников по видам.
4. Необходимые ресурсы
Геометрия 11 кл, изд «Алматы мектеп» общественно-гуманитарное направление - В.Гусев,Ж.Кайдасов, А.Кагазбаева. раздаточный материал, карточки с заданиями, презентация к теме урока, компьютер, интерактивная доска, проектор.
5. Ход занятия
5.1 Организационный момент
Взаимоприветствие. Фиксация отсутствующих. Проверка подготовленности к уроку. Создание благоприятной среды. Психологический настрой на урок.
Прием «Винегрет» – вопросы из разных областей знаний, например:
- За сколькими зайцами нельзя угнаться? (За двумя.)
- Какая нога собаке ни к чему? (Пятая.)
- Золотое колесо в синем небе? (Солнце.)
- Сколько букв в русском алфавите? (33)
- Назовите три последние буквы алфавита. (Э, ю, я.)
- Какой сегодня день? (Вторник, 19 января.)
- Записываем в тетради: 7 декабря. Классная работа.
5.3 Объяснение нового материала
B – НАВЕДЕНИЕ МОСТОВ
Просмотрите пожалуйста фрагменты видео и ответьте на следующие вопросы: https://bilimland.kz/ru/courses/math-ru/geometriya/stereometriya/mnogogranniki/lesson/ponyatie-mnogogrannika-obshie-svoi-stva-obemov
1.Что вы увидели в данном видеоролике?
2. Скажите, в повседней жизни часто ли мы пользуемся многогранниками?
3. Как вы думаете чем отличаются друг от друга многогранники?
4. Сформулируйте определение многогранника.
Отвечая на вопросы вы должны были догадаться, что сегодня на уроке мы будем с вами изучать!
Давайте вместе сформулируем тему нашего урока…( формулируют тему урока «Многогранники» и записывают в тетради)
Давайте ребята запишем новые слова и переводы к ним:
|
На русском: |
На казахском: |
На английском: |
|
Многогранники |
көпжақтар |
polyhedron |
|
Грань |
қыр |
facets |
|
Ребро |
қабырғалар |
slats |
|
Вершина |
шын |
vertex |
O – ОЖИДАЕМЫЕ РЕЗУЛЬТАТЫ
По окончании урока студенты будут знать определение многогранника, виды многогранников и применять полученные знания на практике
Задание №1. Работа в паре
Прочитать текст учебника §1 стр. 6-7 и выполнить задание. (Приложение 1).
Метод «Составление конспекта»
Цель: изложить основные мысли из прочитанного в учебнике текста
1) Записать определение понятий: многогранника, ребра,вершины, правильный многогранник, выпуклый и невыпуклый многоранник.
2) Составить схему классификаций видов многогранников.
Ответы обучающихся
Критериальное оценивание: самооценивание по ответу
Дескрипторы:
- записывает определение понятий
- составляет схему по классификации видов многогранников
Существует пять правильных многогранников. Почему же многогранники получили такие имена? Названия этих многогранников пришли из Древней Греции, и в них указывается число граней: «эдра» - грань,«тетра» - 4,«гекса» - 6,«окта» - 8,«додека» - 12, «икоса» - 20.
Познакомимся с теоремой Эйлера. Леонард Эйлер – один из величайших математиков 18 века, академик Санкт-Петербургской академии наук. Ему принадлежит более 850 научных работ в разных областях.
Обозначим число граней многогранника буквой Г, число вершин – В, число ребер- Р. Оказывается эти 3 числа для любого простого многогранника связаны одним и тем же соотношением: В+Г-Р=2. Например, у куба В=8, Г=6, Р=12. Тогда 8+6-12=2.
Теорема Эйлера звучит так: «У любого простого многогранника сумма числа граней и вершин на две единицы больше числа ребер».

Исследуем многогранники подробнее. Возьмите в руки тетраэдр. Давайте посчитаем вместе количество граней, ребер и вершин. Подсчитаем число указанных элементов правильных многогранников.
( Тетраэдр. Число граней – 4, число вершин – 4, число ребер – 6).
Формативное оценивание . Прием «Светофор»
Задание №2. Работа в группах
Прием «Составление таблицы»
Цель: определяет и знает различие элементов многогранника.
А теперь поработаем по группам: 1 группа работает с кубом, 2 группа – с октаэдром, 3 группа – с додекаэдром. Результаты занести в таблицу. (Приложение 2).

Дескрипторы:
- считает число граней многогранника;
- считает число вершин многогранника;
-считает число ребер многогранника;
P – ПРЕДВАРИТЕЛЬНАЯ ОЦЕНКА
Для того чтобы предварительно оценить работу студентов используем игру Kahoot. https://play.kahoot.it/v2/?quizId=8c7c7779-7994-4989-8c9a-c4ba9ca2d28a
В данном уроке использовались элементы современных педагогических технологий:
-
мобильное обучение (обучение с использованием персональных электронных устройств);
Игра Kahoot позволяет разнообразить работу на уроке, что, в свою очередь, помогает удержать внимание учащихся на проблемах, изучаемых на уроке, и добиться наилучшего результата.
5.4 Закрепление нового материала
P – АКТИВНОЕ ОБУЧЕНИЕ
Задание №3. Будем работать по группам. 1 группа – 1 задача, 2 группа – 2 задача, 3 группа – 3 задача.
Задача 1. Гранями выпуклого многогранника являются только треугольники. Сколько у него вершин и граней, если он имеет 12 ребер? Нарисуйте такой многогранник.
Решение. Пусть у данного многогранника будет В вершин, Р ребер и Г граней. Тогда ЗГ = 2Р, где Р = 12, значит, Г = 8. Применяем теорему Эйлера, из которой следует, что В = 2 + Р - Г. В нашем случае В = 2 +12-8 = 6. Итак, В = 6, Р = 12, Г = 8. Примером такого многогранника является октаэдр.
Задача 2. Из каждой вершины выпуклого многогранника выходит три ребра. Сколько он имеет вершин и граней, если число ребер равно 12? Нарисуйте такой многогранник.
Решение. ЗВ = 2Р, учитывая, что Р = 12, имеем: В = 8. По теореме Эйлера
Г=2-В + Р, Г = 2- 8 + 12 = 6.
Таким образом, у данного выпуклого многогранника В = 8, Р=12 и Г = 6. Примером такого многогранника является куб.
Задача 3. Из каждой вершины выпуклого многогранника выходит четыре ребра. Сколько он имеет вершин и граней, если число ребер равно 12? Нарисуйте такой многогранник.
Решение. 4В = 2Р, учитывая, что Р = 12, имеем: В = 6. По теореме Эйлера
Г=2-В + Р, Г = 2- 6 + 12 = 8.
Таким образом, у данного выпуклого многогранника В = 6, Р=12 и Г = 8. Примером такого многогранника является октаэдр.
Дескрипторы:
- различает грани, вершины и ребра многогранников
-считает количество ребер многогранника
-считает количество вершин многоранника
- определяет вид многогранника
-применяет теорему Эйлера при решении задач
Критериальное оценивание: взаимооценивание, группы оценивают работу друг друга
Прием «Стена Граффити».
C помощью плаката, маркеров, студенты разрисовывают стену информацией, которой владеют о многогранниках.
Задание №4. Соедините линиями названия видов многогранников с количеством граней
( Приложение 3).
|
Тетраэдр |
|
20 |
|
Куб |
|
8 |
|
Октаэдр |
|
12 |
|
Икосаэдр |
|
6 |
|
Додекаэдр |
|
4 |
P – ПОСТ-ОЦЕНКА
Составить синквейн со словом «ГРАНЬ»
1 строка – одно существительное, выражающее главную тему cинквейна.
2 строка – два прилагательных, выражающих главную мысль.
3 строка – три глагола, описывающие действия в рамках темы.
4 строка – фраза, несущая определенный смысл.
5 строка – одно слово (ассоциация с первым словом)
6. Рефлексия по занятию
S – ЗАКЛЮЧЕНИЕ
Прием «Заполни таблицу». (Приложение 4).
Цель: подвести итоги урока, обсудить то, что узнали обучающиеся и то, как работали.
Каждый оценивает свой вклад в достижение поставленных в начале урока целей, свою активность, эффективность работы группы, увлекательность и полезность выбранных форм работы.
Ф.И. студента___________________________________
|
|
В начале урока |
В конце урока |
|||
|
Я знаю |
хорошо |
удовлетвори-тельно |
не знаю |
узнал лучше |
знания не изменились |
|
Что такое многогранник? |
|
|
|
|
|
|
Виды многогранников? |
|
|
|
|
|
|
Элементы многогранника |
|
|
|
|
|
|
Теорема Эйлера |
|
|
|
|
|
7. Домашнее задание: §1 с. 8, §6 с. 31-33. Выучить теорему Эйлера.
Оценочный лист
по предмету: Математика
на тему: №56 Многогранники
Критерии для оценки результатов учебных достижений
|
Оценка по буквенной системе |
Максимальное количество баллов |
Критерии |
|
|
Отлично |
Оценка «А» |
95-100 |
Знает понятие многогранника Знает основные свойства многогранников Применяет методы решения задач по нахождению свойств многогранников Умеет отличать элементы многогранников Знает теорему Эйлера. Умеет применять формулы Эйлера для нахождения элементов многогранников |
|
Оценка «А-» |
90-94 |
Знает понятие многогранника Знает основные свойства многогранников Применяет методы решения задач по нахождению свойств многогранников Умеет отличать элементы многогранников Знает теорему Эйлера. Умеет применять формулы Эйлера для нахождения элементов многогранников Допускает 1 ошибку. |
|
|
Хорошо
|
Оценка «В+» |
85-89 |
Знает понятие многогранника Называет основные свойства многогранников Применяет методы решения задач по нахождению свойств многогранников Умеет отличать элементы многогранников Знает теорему Эйлера. Допускает 2-3 ошибок |
|
Оценка «В» |
80-84 |
Знает понятие многогранника Называет основные свойства многогранников Применяет методы решения задач по нахождению свойств многогранников Умеет отличать элементы многогранников Знает теорему Эйлера.
|
|
|
Оценка В- |
75-79 |
Знает понятие многогранника Называет основные свойства многогранников Применяет методы решения задач по нахождению свойств многогранников Умеет отличать элементы многогранников Допускает 2-3 ошибок |
|
|
Оценка С+ |
70-74 |
Знает понятие многогранника Называет основные свойства многогранников Применяет методы решения задач по нахождению свойств многогранников Умеет отличать элементы многогранников Допускает 4-5 ошибок |
|
|
Удовлет.
|
Оценка С |
65-69 |
Знает понятие многогранника Называет основные свойства многогранников Умеет отличать элементы многогранников |
|
Оценка С- |
60-64 |
Знает понятие многогранника Называет основные свойства многогранников Умеет отличать элементы многогранников Допускает 2-3 ошибок. |
|
|
Оценка D+ |
55-59 |
Знает понятие многогранника Называет основные свойства многогранников Умеет отличать элементы многогранников Допускает 1-2 ошибок.
|
|
|
Оценка D |
50-54 |
Знает понятие многогранника Умеет отличать элементы многогранников.
|
|
|
Неуд.
|
Оценка F |
0-49 |
Знает понятие многогранника Умеет отличать элементы многогранников |
Примечание: * критерии определяются согласно таксономии Блума:
-
Знание - D (конкретного материала, терминологии, фактов, способов и средств обращения с конкретным материалом, определений, тенденций и результатов, системы понятий и категорий, критериев, методологии и т.п.);
-
Понимание - С, С-,D+ (объяснение, интерпретация, экстраполяция и т.п.);
-
Применение – В-, С+ (применение знаний не только в стандартных, но в новых ситуациях и т.п.);
-
Анализ – В (элементов, взаимосвязей, принципов построения, частей целого и взаимосвязи между ними, нарушений в логике рассуждений, различий между фактами и следствиями, значимости данных и т.п.);
-
Синтез - В+(знаний из нескольких областей, экспериментирование, творческая переработка информации для создания нового целого, получение системы абстрактных отношений и т.п.);
-
Оценка – А, А- (суждение на основе имеющих данных, суждение на основе внешних критериев,
-
видение различий между фактами и оценочными суждениями и т.п.).
Группа: ____________
|
№ |
ФИ обучающегося |
Максимальное количество баллов |
Оценка по буквенной системе |
Достигнутый уровень |
Комментарий |
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
9 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
11 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
13 |
|
|
|
|
|
|
14 |
|
|
|
|
|
|
15 |
|
|
|
|
|
Приложение 1.
Многогранники представляют собой простейшие тела в пространстве, подобно тому, как многоугольники – простейшие фигуры на плоскости. Многогранные формы мы видим ежедневно: спичечный коробок, книга, комната, многоэтажные дома, а также - граненый карандаш, гайка и т.п.
Многогранники обладают богатой историей, которая связана с такими знаменитыми учеными древности, как Архимед, Евклид, Пифагор(слайд10.
С древнейших времен наши представления о красоте связаны с понятием симметрия. Наверное, этим объясняется интерес человека к многогранникам – удивительным символам симметрии, привлекавшим внимание выдающихся мыслителей.
Существует пять правильных многогранников. Почему же многогранники получили такие имена? Названия этих многогранников пришли из Древней Греции, и в них указывается число граней: «эдра» - грань,«тетра» - 4,«гекса» - 6,«окта» - 8,«додека» - 12, «икоса» - 20.
Исследуем многогранники подробнее. Подсчитаем число указанных элементов правильных многогранников и занесём результаты в таблицу (раздаточный материал). Возьмите в руки тетраэдр. Давайте посчитаем вместе количество граней, ребер и вершин.
Теорема Эйлера звучит так: «У любого простого многогранника сумма числа граней и вершин на две единицы больше числа ребер».
Приложение 2.
Задача №2. Посчитать число элементов правильного многоугольника и заполнить таблицу.
|
Правильный многогранник |
Число граней |
Число вершин |
Число ребер |
|
Тетраэдр |
4 |
4 |
6 |
|
Куб |
|
|
|
|
Октаэдр |
|
|
|
|
Додекаэдр |
|
|
|
Задача №2. Посчитать число элементов правильного многоугольника и заполнить таблицу.
|
Правильный многогранник |
Число граней |
Число вершин |
Число ребер |
|
Тетраэдр |
4 |
4 |
6 |
|
Куб |
|
|
|
|
Октаэдр |
|
|
|
|
Додекаэдр |
|
|
|
Задача №2. Посчитать число элементов правильного многоугольника и заполнить таблицу.
|
Правильный многогранник |
Число граней |
Число вершин |
Число ребер |
|
Тетраэдр |
4 |
4 |
6 |
|
Куб |
|
|
|
|
Октаэдр |
|
|
|
|
Додекаэдр |
|
|
|
Задача №2. Посчитать число элементов правильного многоугольника и заполнить таблицу.
|
Правильный многогранник |
Число граней |
Число вершин |
Число ребер |
|
Тетраэдр |
4 |
4 |
6 |
|
Куб |
|
|
|
|
Октаэдр |
|
|
|
|
Додекаэдр |
|
|
|
Задание №3. Выполнить задачи по группам. 1 группа-задача №1, 2 группа-задача №2 3 группа-задача №3.
Задача 1. Гранями выпуклого многогранника являются только треугольники. Сколько у него вершин и граней, если он имеет 12 ребер? Нарисуйте такой многогранник.
Задание №3. Выполнить задачи по группам. 1 группа-задача №1, 2 группа-задача №2 3 группа-задача №3.
Задача 3. Из каждой вершины выпуклого многогранника выходит четыре ребра. Сколько он имеет вершин и граней, если число ребер равно 12? Нарисуйте такой многогранник.
Задание №3. Выполнить задачи по группам. 1 группа-задача №1, 2 группа-задача №2 3 группа-задача №3.
Задача 2. Из каждой вершины выпуклого многогранника выходит три ребра. Сколько он имеет вершин и граней, если число ребер равно 12? Нарисуйте такой многогранник.
Приложение 3.





Приложение 4.
Ф.И. студента___________________________________
|
|
В начале урока |
В конце урока |
|||
|
Я знаю |
хорошо |
удовлетвори-тельно |
не знаю |
узнал лучше |
знания не изменились |
|
Что такое многогранник? |
|
|
|
|
|
|
Виды многогранников? |
|
|
|
|
|
|
Элементы многогранника |
|
|
|
|
|
|
Теорема Эйлера |
|
|
|
|
|
Ф.И. студента___________________________________
|
|
В начале урока |
В конце урока |
|||
|
Я знаю |
хорошо |
удовлетвори-тельно |
не знаю |
узнал лучше |
знания не изменились |
|
Что такое многогранник? |
|
|
|
|
|
|
Виды многогранников? |
|
|
|
|
|
|
Элементы многогранника |
|
|
|
|
|
|
Теорема Эйлера |
|
|
|
|
|
Ф.И. студента___________________________________
|
|
В начале урока |
В конце урока |
|||
|
Я знаю |
хорошо |
удовлетвори-тельно |
не знаю |
узнал лучше |
знания не изменились |
|
Что такое многогранник? |
|
|
|
|
|
|
Виды многогранников? |
|
|
|
|
|
|
Элементы многогранника |
|
|
|
|
|
|
Теорема Эйлера |
|
|
|
|
|

шағым қалдыра аласыз

















