Қазақстандағы ең үлкен материалдар базасынан іздеу
Сіз үшін 400 000 ұстаздардың еңбегі мен тәжірибесін біріктіріп, ең үлкен материалдар базасын жасадық. Төменде керек материалды іздеп, жүктеп алып сабағыңызға қолдана аласыз
Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз!

Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз!

Министірлікпен келісілген курстар тізімі



 функциясының
графигі.
функциясының
графигі. болғандықтан, берілген функция жұп функция.
Сондықтан оның графигі
болғандықтан, берілген функция жұп функция.
Сондықтан оның графигі  осіне қатысты симметриялы болады. Бұл
функцияның графигін алдымен
осіне қатысты симметриялы болады. Бұл
функцияның графигін алдымен  жағдай үшін салып аламыз да, функция жұп
болғандықтан
жағдай үшін салып аламыз да, функция жұп
болғандықтан  үшін салынған графикті
үшін салынған графикті
 функциясының графигін
салыңдар.
функциясының графигін
салыңдар. болғандықтан берілген
функция
болғандықтан берілген
функция  түріне келеді. Бұл функция жұп
болғандықтан,
түріне келеді. Бұл функция жұп
болғандықтан,  графигін салып,
графигін салып,  функциясының
функциясының 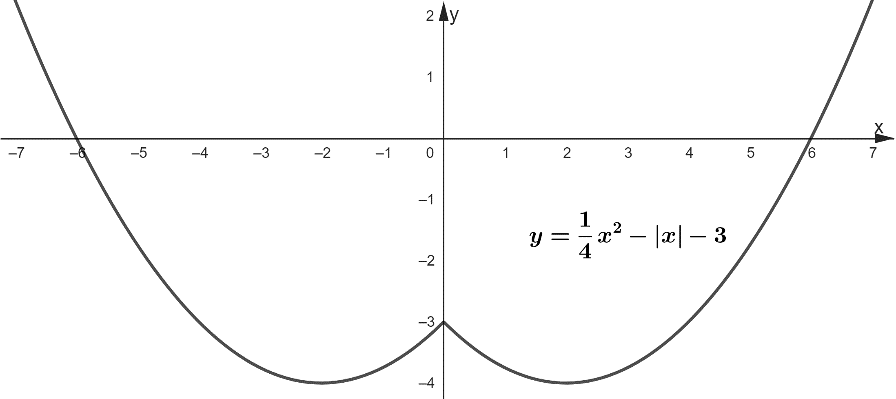 )
параболаның
)
параболаның  төбесінің координаталарын
табайық:
төбесінің координаталарын
табайық: ;
;  ;
; параболаның
төбесі.
параболаның
төбесі. осін қиятын
нүктесі:
осін қиятын
нүктесі:

 .
. функциясының графигін
салыңдар.
функциясының графигін
салыңдар.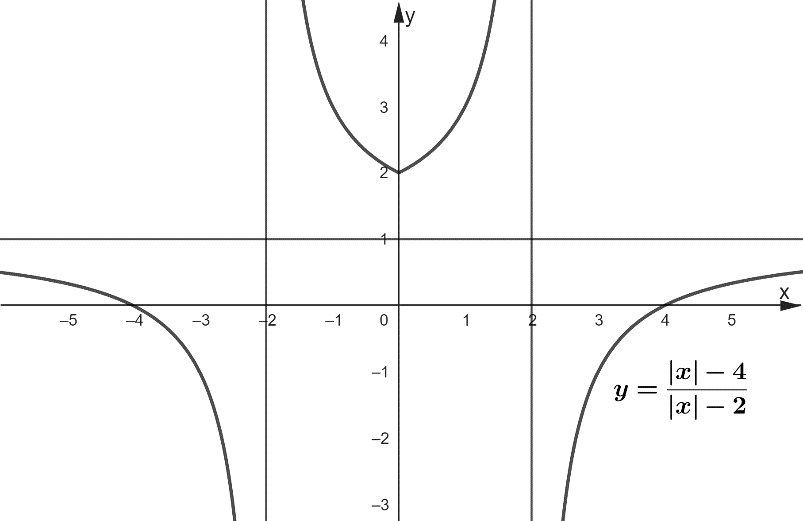 ешуі.
ешуі.  функциясының графигін
салып, салынған графикті
функциясының графигін
салып, салынған графикті  функциясының графигін салайық. Ол
үшін
функциясының графигін салайық. Ол
үшін  координаталар басын
координаталар басын  нүктесіне көшіріп,
нүктесіне көшіріп,  жаңа координаталар жүйесін
сызамыз.
жаңа координаталар жүйесін
сызамыз. гиперболасын жаңа
гиперболасын жаңа  функциясының
функциясының  жазықтығындағы графигі болады. Шыққан
графиктің
жазықтығындағы графигі болады. Шыққан
графиктің  функциясының
графигі.
функциясының
графигі.
 болғандықтан,
болғандықтан,  функциясының графигін салып алып, сонан
кейін оның
функциясының графигін салып алып, сонан
кейін оның  функциясының графигін
салыңдар.
функциясының графигін
салыңдар.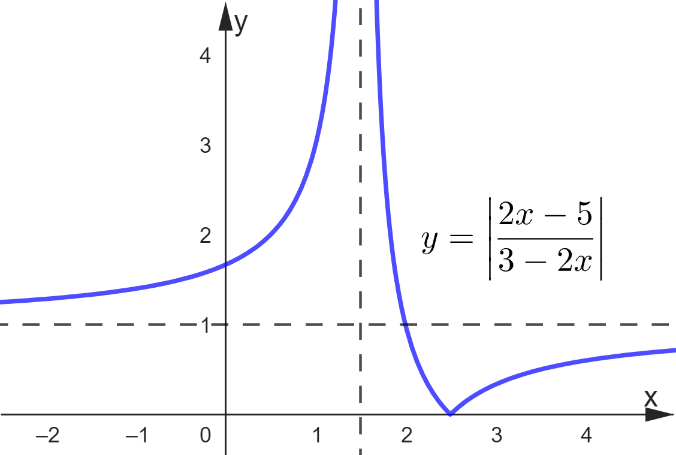 ешуі.
ешуі.  функциясының графигін
саламыз.
функциясының графигін
саламыз.
 функциясының графигін
салайық.
функциясының графигін
салайық. нүктесіне көшіріп,
нүктесіне көшіріп,  гиперболасын жаңа
гиперболасын жаңа
 функциясының
графигі.
функциясының
графигі. функциясының графигін салып аламыз
да,
функциясының графигін салып аламыз
да,  болғандықтан,
болғандықтан, 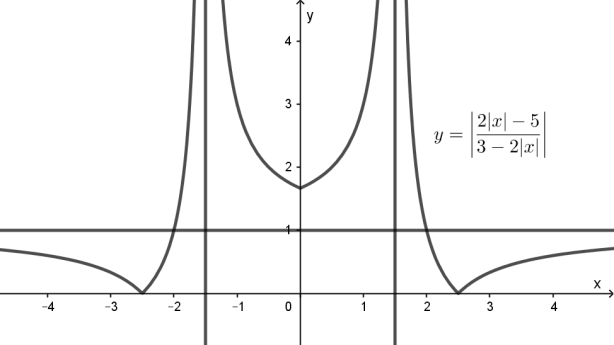 ысал
ысал  функциясының графигін
салыңдар.
функциясының графигін
салыңдар. функциясының графигін
салып,
функциясының графигін
салып,  теңдігінің
графигі.
теңдігінің
графигі. :
:
 .
. ⇔
⇔ 
 болатын жағдай үшін
болатын жағдай үшін  үшін салынған графикті
үшін салынған графикті  теңдігін қанағаттандыратын нүктелер жиынын
жазықтықта кескіндеңдер.
теңдігін қанағаттандыратын нүктелер жиынын
жазықтықта кескіндеңдер. графигін сызып,
графигін сызып, 

 теңдігінің
графигі.
теңдігінің
графигі.
 функциясының графигін сызып, шыққан
графикті
функциясының графигін сызып, шыққан
графикті  теңдігін қанағаттандыратын нүктелер жиынын
жазықтықта кескіндеңдер.
теңдігін қанағаттандыратын нүктелер жиынын
жазықтықта кескіндеңдер.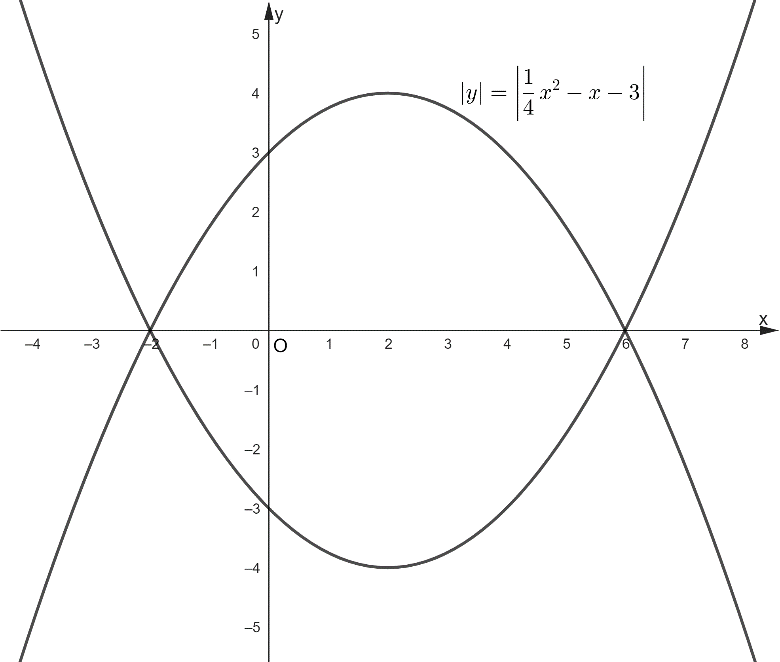 ешуі.
ешуі. 
 функциясының графигін
сызамыз.
функциясының графигін
сызамыз. теңдігінің
графигі.
теңдігінің
графигі. үшін сызып (I ширекте), салынған
графикті
үшін сызып (I ширекте), салынған
графикті  осьтеріне қатысты симметриялы көшіреміз.
Яғни,
осьтеріне қатысты симметриялы көшіреміз.
Яғни,
 теңдігін қанағаттандыратын нүктелер жиынын
жазықтықта кескіндеңдер.
теңдігін қанағаттандыратын нүктелер жиынын
жазықтықта кескіндеңдер.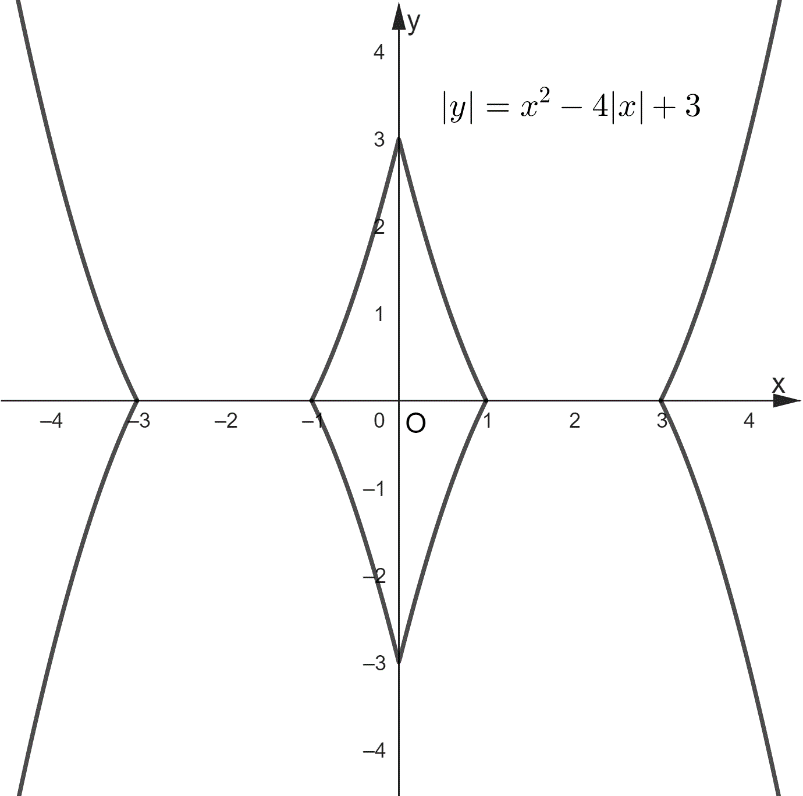 ешуі.
ешуі.  функциясының графигін
сызып,
функциясының графигін
сызып, теңдігінің
графигі.
теңдігінің
графигі.
 функцияcының графигін саламыз
да,
функцияcының графигін саламыз
да,  теңдігін қанағаттандыратын нүктелер жиынын
жазықтықта кескіндеңдер.
теңдігін қанағаттандыратын нүктелер жиынын
жазықтықта кескіндеңдер.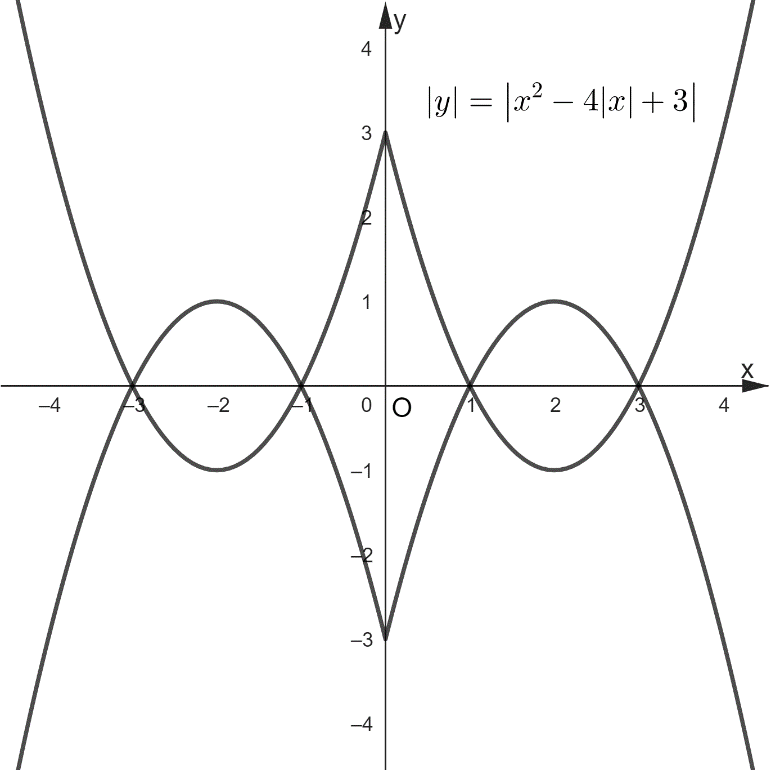 ешуі.
ешуі.  функцияларының графиктерін
саламыз.
функцияларының графиктерін
саламыз. функциясының графигін салып, оның
графигін
функциясының графигін салып, оның
графигін  функциясының графигін
саламыз.
функциясының графигін
саламыз. түріндегі функцияларының
графиктері
түріндегі функцияларының
графиктері функциясының
графигі.
функциясының
графигі. – сынық сызықтың сыну нүктелері
табамыз;
– сынық сызықтың сыну нүктелері
табамыз; функциясының графигін
салыңдар.
функциясының графигін
салыңдар.











