
Сызу 9-сынып күні : 14.10.2018ж.
Сабақтың тақырыбы: Бір, екі және үш проекция жазықтығына тік
бұрыштап проекциялау. Монж эпюрі.
Мақсат:
1. Білімділік: Монж эпюрі жүйесінде нүктенің нәрсе бетіндегі проекциясын салу жолдарымен таныстыру.
2. Дамытушылық: Оқушыларды сызба есептерді шешу, кеңістікте ойлау қабілеттерін, визуалды қабылдау дағдыларын дамыту.
3. Тәрбиелік: Монж эпюрі жүйесі негіздерін сызба геометриясында игерту арқылы оқушыларды техникалық мамандықтарға тәрбиелеу
Сабақ типі: жаңа сабақ
Сабақ түрі: лекция, машықтық сабақ
Құрал-жабдықтар: Транспортир, циркуль, қарындаштардың түрлері, өшіргіш, сызғыш түрлері, бұрыштықтар
Көрнекілігі: таратпа
Сабақ барысы
І. Ұйымдастыру кезеңі
Оқушылармен сәлемдесу. Сабақта жоқ оқушыларды түгендеп, журналға белгілеу.
ІІ. Жаңа сабақты меңгеруге дайындау кезеңі
Оқушыларды сабақтың тақырыбымен, мақсатымен, таныстыру.
Сендер бүгін сабақта Монж эпюрі жүйесінде нүктенің нәрсе бетіндегі проекциясын орындап оның өмірде инженерлік графикада пайдалану негіздерімен танысасыңдар.
III. Өткен тақырыпты қайталау
Әр оқушыға жеке таратпа тарату арқылы өткен сабақты қаншалықты түсінгендеріне бақылау жасаймын.
ІV. Жаңа сабақты меңгеру кезеңі
Монж эпюрі
Өзара перпендикуляр екі жазықтықта тік бұрыштап проекцилау тәсілін француз ғалымы геометр Гапар Монж (1746-1818жж.) XVIII ғасырдың аяғында жетілдірген.
Сондықтан мұндай тәсілді Монж эпюрі деп атайды. Г. Монж сызба геометрияның –нәрселерді кескіндеу турала жаңа ғылымның дамуына жол салды. Сызба геометрия сызудың теориялық негізі болып саналады. 1798ж. Г. Монж-«Сызба геметриясы» алғашқы ғылыми еңбегін жарыққа келтірді. 1, 2 және 3 жазықтықтарының 1-сурет біреуін олардың қиылысу сызығынан айналдырып, екіншісімен беттестіреміз. Сонда беттескен 1 = 2 = 3 жазықтықты сызба салынатын қағаз болады 2-сурет. Біз эпюр деудің орнына сызба дейтін боламыз.
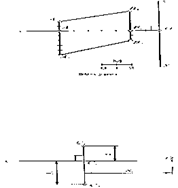
Үштарының координаталары бойынша АВ кесіндісінің сызбасын салуды көрсетейік. А(7; 5; 2) жөне В(2; 2; 4) болсын. Горизонталь түзу жүргізіп, оны абсциссалар осі деп қарастырамыз. Осы х осінің О нүктесі арқылы оған перпендикуляр түзу жүргізейік. Осы түзудің О нүктесінен жоғарғы бөлігін аппликаталар осі, ал төменгі бөлігін ординаталар осі ретінде карастыруға болады. Абсциссалар осіне бас нүктеден бастап 7 және 2 бірлік кесінділер салып, Ах және Вх нүктелерін аламыз (1-сурет). Ах нүктесі аркылы х осіне перпендикуляр түзу жүргізіп, оның бойына жоғары карай 2 кесінді салып, А нүктесінің фронталь проекциясын (Аг), ал темен карай 5 кесінді салып, А нүктесінің горизонталь проекциясын (А2) аламыз. Вх нүктесін бастыра абсциссалар осіне перпендикуляр түзу жүргізіп, оған жоғары қарай Вх нүктесінен бастап 4 кесінді салсақ, В1 нүктесін, ал төмен қарай Вх нүктесінен бастап 2 кесінді салсақ, В2 нүктесін аламыз. В1 нүктесі-В нүктесінін фронталь проекциясы, ал В2 оның горизонталь проекциясы. А1 нүктесін В1 нүктесімен қосатын А1В1 кесіндісі-АВ кесіндісінің фронталь проекциясы, ал А және В нүктелерінің горизонталь проекцияларьш қосатын А2В2 кесіндісі-оның горизонталь проекциясы. Сонымен біз берілген кесіндінің екі проекциядан түратын сызбасын (эпюрін) салдық.
Енді өзара перпендикуляр үш жазықтық алып, нәрсені оларға тік бұрыштап проекциялайық. Бұл жазықтықтардың екеуімен таныспыз: олар 1 -фронталь проекциялар жазықтығы да, ал 2 -горизонталь проекциялар жазықтығы. Үшінші жазықтық 3 профиль проекциялар жазықтығы деп, ал онда алынған проекция нәрсенің профилъ проекциясы деп аталады. Профилъ -француз сөзі-қазақша бүйірінен қарағандағы түрі дегенді білдіреді. А3 нүктесі -А нүктесінің профиль проекциясы. 3 1, 2 3, 3 х. Горизонталь және профиль проекциялар жазықтықтарының қиылысу сызығын ординаталар осі, фронталь жөне профиль проекциялар жазықтықтарының қиылысу сызығын аппликаталар осі ретінде қарастыратын боламыз. 2 3 =y; 1 3=z; y 1; z 2 . Сызба салғанда 1 жазыктығын қағаз бетімен беттескен деп қарастырады, ал 2 және 3 жазықтықтарын оларға сәйкес абсцисса және аппликата осьтерінен айналдырып, оларды 1 жазықтығымен беттестіреді. Сонда алынған жазық фигураны (2, ә-сурет) эпюр деп атайды. Сызбада х осін горизонталь, z осін вертикаль орналастырады, ал у осі екіге бөлінеді. Ординаталар осінің бір жартысы z осінің, ал екінші жартысы х осінің жалғасы болады. Бір нүктенің фронталь және горизонталь проекциялары х осіне перпендикуляр түзудің бойында орналасады. Бүл түзуді вертикалъ байланыс сызығы деп атайтын боламыз. Бір нүктенің фронталь және профиль проекциялары горизонталъ байланыс сызығы деп аталатын, z осіне перпендикуляр түзудің бойында орналасулары керек. (А1А2)-вертикаль байланыс сызығы; (А1А2)-горизонталь байланыс сызығы. Нүктенің горизонталь проекциясынан абсциссалар осіне дейінгі қашықтық оның профиль проекциясынан аппликаталар осіне дейінгі қашықтыққа тең: /А2АХ / = /А3Аz /. Сондықтан сызбада нүктенің екі проекциясы берілсе, оның үшінші проекциясын табуға болады. Мысалы, А нүктесінің фронталь және горизонталь проекциялары берілсе, оның профиль проекциясын оңай тұрғызуға болады.
V. Жаңа сабақты бекіту
Тапсырма: Әр қатарға тақтаға үш мысал жазамын, әр қатар берілген мән бойынша жұмыс дәптерлеріне тапсырманы орындаулары қажет.
VI. Қорытынды осы сабақта оқушылар координата жүйесінде жұмыс жасау әдісін игерді, жұмыстары бағаланады
VII. Үйге тапсырма, Монж эпюрі тақырыбын қайталау.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Монж эпюрі.
Монж эпюрі.
Сызу 9-сынып күні : 14.10.2018ж.
Сабақтың тақырыбы: Бір, екі және үш проекция жазықтығына тік
бұрыштап проекциялау. Монж эпюрі.
Мақсат:
1. Білімділік: Монж эпюрі жүйесінде нүктенің нәрсе бетіндегі проекциясын салу жолдарымен таныстыру.
2. Дамытушылық: Оқушыларды сызба есептерді шешу, кеңістікте ойлау қабілеттерін, визуалды қабылдау дағдыларын дамыту.
3. Тәрбиелік: Монж эпюрі жүйесі негіздерін сызба геометриясында игерту арқылы оқушыларды техникалық мамандықтарға тәрбиелеу
Сабақ типі: жаңа сабақ
Сабақ түрі: лекция, машықтық сабақ
Құрал-жабдықтар: Транспортир, циркуль, қарындаштардың түрлері, өшіргіш, сызғыш түрлері, бұрыштықтар
Көрнекілігі: таратпа
Сабақ барысы
І. Ұйымдастыру кезеңі
Оқушылармен сәлемдесу. Сабақта жоқ оқушыларды түгендеп, журналға белгілеу.
ІІ. Жаңа сабақты меңгеруге дайындау кезеңі
Оқушыларды сабақтың тақырыбымен, мақсатымен, таныстыру.
Сендер бүгін сабақта Монж эпюрі жүйесінде нүктенің нәрсе бетіндегі проекциясын орындап оның өмірде инженерлік графикада пайдалану негіздерімен танысасыңдар.
III. Өткен тақырыпты қайталау
Әр оқушыға жеке таратпа тарату арқылы өткен сабақты қаншалықты түсінгендеріне бақылау жасаймын.
ІV. Жаңа сабақты меңгеру кезеңі
Монж эпюрі
Өзара перпендикуляр екі жазықтықта тік бұрыштап проекцилау тәсілін француз ғалымы геометр Гапар Монж (1746-1818жж.) XVIII ғасырдың аяғында жетілдірген.
Сондықтан мұндай тәсілді Монж эпюрі деп атайды. Г. Монж сызба геометрияның –нәрселерді кескіндеу турала жаңа ғылымның дамуына жол салды. Сызба геометрия сызудың теориялық негізі болып саналады. 1798ж. Г. Монж-«Сызба геметриясы» алғашқы ғылыми еңбегін жарыққа келтірді. 1, 2 және 3 жазықтықтарының 1-сурет біреуін олардың қиылысу сызығынан айналдырып, екіншісімен беттестіреміз. Сонда беттескен 1 = 2 = 3 жазықтықты сызба салынатын қағаз болады 2-сурет. Біз эпюр деудің орнына сызба дейтін боламыз.

Үштарының координаталары бойынша АВ кесіндісінің сызбасын салуды көрсетейік. А(7; 5; 2) жөне В(2; 2; 4) болсын. Горизонталь түзу жүргізіп, оны абсциссалар осі деп қарастырамыз. Осы х осінің О нүктесі арқылы оған перпендикуляр түзу жүргізейік. Осы түзудің О нүктесінен жоғарғы бөлігін аппликаталар осі, ал төменгі бөлігін ординаталар осі ретінде карастыруға болады. Абсциссалар осіне бас нүктеден бастап 7 және 2 бірлік кесінділер салып, Ах және Вх нүктелерін аламыз (1-сурет). Ах нүктесі аркылы х осіне перпендикуляр түзу жүргізіп, оның бойына жоғары карай 2 кесінді салып, А нүктесінің фронталь проекциясын (Аг), ал темен карай 5 кесінді салып, А нүктесінің горизонталь проекциясын (А2) аламыз. Вх нүктесін бастыра абсциссалар осіне перпендикуляр түзу жүргізіп, оған жоғары қарай Вх нүктесінен бастап 4 кесінді салсақ, В1 нүктесін, ал төмен қарай Вх нүктесінен бастап 2 кесінді салсақ, В2 нүктесін аламыз. В1 нүктесі-В нүктесінін фронталь проекциясы, ал В2 оның горизонталь проекциясы. А1 нүктесін В1 нүктесімен қосатын А1В1 кесіндісі-АВ кесіндісінің фронталь проекциясы, ал А және В нүктелерінің горизонталь проекцияларьш қосатын А2В2 кесіндісі-оның горизонталь проекциясы. Сонымен біз берілген кесіндінің екі проекциядан түратын сызбасын (эпюрін) салдық.
Енді өзара перпендикуляр үш жазықтық алып, нәрсені оларға тік бұрыштап проекциялайық. Бұл жазықтықтардың екеуімен таныспыз: олар 1 -фронталь проекциялар жазықтығы да, ал 2 -горизонталь проекциялар жазықтығы. Үшінші жазықтық 3 профиль проекциялар жазықтығы деп, ал онда алынған проекция нәрсенің профилъ проекциясы деп аталады. Профилъ -француз сөзі-қазақша бүйірінен қарағандағы түрі дегенді білдіреді. А3 нүктесі -А нүктесінің профиль проекциясы. 3 1, 2 3, 3 х. Горизонталь және профиль проекциялар жазықтықтарының қиылысу сызығын ординаталар осі, фронталь жөне профиль проекциялар жазықтықтарының қиылысу сызығын аппликаталар осі ретінде қарастыратын боламыз. 2 3 =y; 1 3=z; y 1; z 2 . Сызба салғанда 1 жазыктығын қағаз бетімен беттескен деп қарастырады, ал 2 және 3 жазықтықтарын оларға сәйкес абсцисса және аппликата осьтерінен айналдырып, оларды 1 жазықтығымен беттестіреді. Сонда алынған жазық фигураны (2, ә-сурет) эпюр деп атайды. Сызбада х осін горизонталь, z осін вертикаль орналастырады, ал у осі екіге бөлінеді. Ординаталар осінің бір жартысы z осінің, ал екінші жартысы х осінің жалғасы болады. Бір нүктенің фронталь және горизонталь проекциялары х осіне перпендикуляр түзудің бойында орналасады. Бүл түзуді вертикалъ байланыс сызығы деп атайтын боламыз. Бір нүктенің фронталь және профиль проекциялары горизонталъ байланыс сызығы деп аталатын, z осіне перпендикуляр түзудің бойында орналасулары керек. (А1А2)-вертикаль байланыс сызығы; (А1А2)-горизонталь байланыс сызығы. Нүктенің горизонталь проекциясынан абсциссалар осіне дейінгі қашықтық оның профиль проекциясынан аппликаталар осіне дейінгі қашықтыққа тең: /А2АХ / = /А3Аz /. Сондықтан сызбада нүктенің екі проекциясы берілсе, оның үшінші проекциясын табуға болады. Мысалы, А нүктесінің фронталь және горизонталь проекциялары берілсе, оның профиль проекциясын оңай тұрғызуға болады.
V. Жаңа сабақты бекіту
Тапсырма: Әр қатарға тақтаға үш мысал жазамын, әр қатар берілген мән бойынша жұмыс дәптерлеріне тапсырманы орындаулары қажет.
VI. Қорытынды осы сабақта оқушылар координата жүйесінде жұмыс жасау әдісін игерді, жұмыстары бағаланады
VII. Үйге тапсырма, Монж эпюрі тақырыбын қайталау.

шағым қалдыра аласыз















