
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ ҒЫЛЫМ ЖӘНЕ БІЛІМ МИНИСТРЛІГІ
Қызылорда облыстық білім басқармасы
Жаңақорған ауданы
№110 мектеп-лицей
Математика секциясы
ҒЫЛЫМИ-ЗЕРТТЕУ ЖҰМЫСЫ
Тақырыбы: НАТУРАЛ ҚАТАРДЫҢ ЖІКТЕЛУІ
Орындаған: Білалова Гүлжахан Мейрамқызы. 11-сынып
Ғылыми жетекші: Сейлова Зоя Төлеубайқызы, п.ғ.к., доцент
Пән мұғалімі: Райымбекова Сағима Жақыпқызы
ҚЫЗЫЛОРДА 2015-2016 оқу жылы.
МАЗМҰНЫ
Кіріспе 3
§1. Негізгі ұғымдар және анықтамалар 4-5
§2. Өзара қиылыспайтын тізбектер. Олардың қасиеттері 6-9
§3. Жаттығулар 10-12
§4. Геометриялық интерпретациялау 13-14
§5. Кейбір қолданыстары (Палиндромдар) 15-18
Қорытынды 19
Пайдаланылған әдебиеттер 20
КІРІСПЕ
Леонардо-да Винчи, Фибоначи қатары, пентакл, қасиетті пропорция немесе «Алтын қима» сияқты математика тарихында ерекше орын алатын ұғымдар бар. Осыларды өнер тарихындағы ең бір фундаментальды ұғымдардың бірі PHI санымен байланыстырады. PHI (айтылуы фи-и саны) деген қандай сан?
PHI саны шамамен 1,618-ге тең және бейнелеу өнерінде ең маңызды және мәнді сан болып табылады. Бұл сан дүниедегі ең «әдемі сан» деп есептеледі.
PHI саны Фибоначчи қатарынан шығады. Ал, Фибоначчи қатары дегеніміз бірінші және екінші мүшелерінің әрқайсысы 1-ге тең,ал үшінші мүшесінен бастап,әрбір мүшесі алдыңғы екі мүшесінің қосындысына тең болатын математикалық прогрессия:
1,1,2,3,5,8,13,21,34,55,89,144,...
Бұл прогрессияның тағы бір қасиеті қатарда тұрған көршілес екі санның қатынасы ерекше қасиетке ие болады-ол оның 1,618 санына, яғни PHI санына жуықтауы.
PHI санының басқа да қасиеттері көп. Бұл сан жер бетіндегі барлық тірі нәрселердің негізі қаланатын фундаменттің кірпіші сияқты. Барлық өсімдіктер, жануарлар тіпті адамдар да физикалық жағынан шамамен осы PHI санының негізі 1 санына жуық пропорциямен байланысты болады.
PHI санының табиғатта көптен кездесуі барлық тірі нәрселердің арасында байланыс бар екенін көрсетеді. Бұрын PHI санын «дүниені жаратушы орнатқан» деген пікір болған. Ертедегі оқымыстылар бір бүтін жүз мыңнан алты жүз он сегізді «құдай жартқан пропорция» деп те атаған.
Табиғаттан осы пропорцияға мысал келтірейік: аралардың ұясындағы аналық түрлер саны аталық түрлер санынан басым. Дүниедегі кез-келген ара ұяларындағы аналық түрлер санын аталық түрлер санына бөлсек тағы да сол PHI саны, яғни шамамен 1,618 саны шығады. Бұған мысалдар көп. Мысалы, жүзу қасиетіне ие болу үшін қабыршағына газ толтыратын және басын аяқ ететін спираль бейнелі теңіз малюскасі-наутилустың бақалшығын қарастырайық. Оның спиралінің әрбір орамының ішке қарай бақалшағының келесі орамына қатынасы тағы да осы PHI санын, яғни 1,618-ді береді екен. Сол сияқты, күнбағыс өсімдігінің піскен дәндерінің сағат тіліне қарсы бағыт бойынша спираль бойымен орналасқан орсдар диаметрінің келесі орамның диаметріне қатынасы шамамен 1,618-ге тең жүгері сабағының оралған жапырақтары, өсімдіктердің сабақтарындағы жапырақтарының орналасу арақашықтықтары, жәндіктердің денелерінің сегменттік бөліктері т.б.-осылардың бәрі өздерінің құрылысыда «қасиетті пропорцияға» бағынады.
Леонардо да Винчи және Витрувиан адамы. Енді, осының бәрінің сәулет өнеріне қандай қатысы бар екенін қарастырайық. Леонардо да Винчидің, өзінің «сәулет өнері жайындағы он кітап» атты еңбегінде «құдай жаратқан» пропорцияны мадақтаған данышпан рим сәулетшісі Маркус Витрувийге арнап сызған, шеңберге іштей сызылған жалаңаш адам бейнесі « Витрувиан адамы» деген суретінде адам денесінің қасиетті құрылысы мен құрамын терең түсінгенін көрсетеді. Өзінің білімін жетілдіру үшін Леонардо да Винчи адам анатомиясын зерттеп, өлген адам сүйектерінің пропорциясын өлшеген. Ол алғаш рет адам денесінің «құрылыс блоктарынан» тұратынын және олардың қатынасының пропорциясы біз айтып отырған «қасиетті санға» тең болатынын көрсеткен. Бұны әрбір адам өз денесінің биіктігінің ұзындығын кіндігінен табанына дейінгі ұзындыққа бөліп, немесе, иықтан саусақтарының ұшына дейінгі ұзындықты, шынтақтан тағы да сол саусақтардың ұшына дейінгі ұзындыққа бөліп тексеруіне болады.
Жұмыстың мақсаты математикаға қызығушылығы жоғары оқушыларға мектепте оқылатын сан қатарларынан (арифметикалық және геометриялық прогрессиялар) өзге қатарларды оқып үйренуге, оларды есеп шығаруда қолданыстарын қарастыру. Оның ішінде натурал қатардың әр түрлі екі қатарға жіктелуі туралы сұрақтарға жауап беру.
Жұмыста қарастырылған және дәлелденетін теореманың бірқатар қолданыстарына тоқталу. «Алтын қима» тұрақтысының 1,618-ге жуық иррационал сан екендігі дәлелденеді.
Жұмыс бес параграфтан тұрады.
Бірінші параграф бүкіл жұмыста басшылыққа алатын негізгі ұғымдар мен анықтамаларға арналады.
Екінші параграфта бір-бірімен қиылыспайтын қатарлар және Акулич гипотезасы туралы баяндалады.
Үшінші параграфта жаттығулар мен мысалдар келтірілген.
§1 Негізгі ұғымдар және анықтамалар
Санның бүтін және бөлшек бөлігі
1.Анықтама x санының бүтін бөлігі деп, x санынан артпайтын r ең үлкен бүтін санды айтамыз.
x санының бүтін бөлігі [x] немесе (кейде) E(x) (фр. entier "антье" — бүтін сөзінен алынған) деп белгіленеді.
Егер x [r; r +1) аралығына тиісті болса, мұндағы r — бүтін сан, онда [x]=r, яғни x [ [x]; [x]+1) аралығында жатады. Сандық теңсіздіктер қасиеттері бойынша x-[x] айырмасы [0; 1) аралығына тиісті болады.
2.Анықтама q = x - [x] санын x санының бөлшек бөлігі деп аталады және {x} деп белгіленеді. Сондықтан, санның бөлшек бөлігі әрдайым оң және 1-ден аспайды, ал бүтін бөлігі оң және теріс мәндерге ие болады. Сонымен, {x} = x - [x], сондықтан, x = [x] + {x}.
Мысалы:
|
[5]=5 |
[7,2]=7 |
[-3]=-3 |
[-4,2]=-5 |
[0]=0 |
|
{5}=0 |
{7,2}=0,2 |
{-3}=0 |
{-4,2}=0,8 |
{0}=0 |
Бүтін бөлігінің қасиеттері
[x+n] = [x]+n, мұндағы n – натурал сан
Рационал және иррационал сандар және олардың қасиеттері
3.Анықтама  түрінде жазуға болатын
санды рационал сан деп атаймыз, мұндағы m –
бүтін
сан,
ал
n
– натурал сан.
түрінде жазуға болатын
санды рационал сан деп атаймыз, мұндағы m –
бүтін
сан,
ал
n
– натурал сан.
4.Анықтама Егер санды  түрінде жазуға
болмаса,
онда бұл
сан иррационал сан деп
аталады.
түрінде жазуға
болмаса,
онда бұл
сан иррационал сан деп
аталады.
1Теорема. Кез келген рационал санды шектелген немесе шектеусіз периодты бөлшек түрінде жазуға болады.
Сол сияқты кез келген иррационал санды шектелген немесе шектеусіз периодты бөлшек түрінде жазуға болады.
Мысалы:
0,5= -рационал
сан
-рационал
сан
0,(3)=  - рационал
сан
- рационал
сан
1,0123456789101112…- иррационал сан
 -
иррационал сан
-
иррационал сан
Рационал және иррационал сандарға қолданылатын арифметикалық амалдардың қасиеттері
1. Егер  - рационал сандар
болса, онда
- рационал сандар
болса, онда  ,
,  ,
,  ,
,  ,
, - рационал сандар.
- рационал сандар.
Берілгені:  ;
; 
Дәлелдеу:  - рационал сан
- рационал сан
2. Егер r-рационал сан,  -иррационал сан болса, онда
-иррационал сан болса, онда  - иррационал сандар.
- иррационал сандар.
Дәлелдеу: (қарсы жору арқылы)
 болсын,
бірақ
болсын,
бірақ  - қарама-қайшылыққа
келдік.
- қарама-қайшылыққа
келдік.
3. Егер  ,онда
,онда  сандары жайлы
айқындалған тұжырым жоқ.
сандары жайлы
айқындалған тұжырым жоқ.
Мысалы:

§2 Өзара қиылыспайтын тізбектер. Олардың қасиеттері
Бұл параграфта әңгіме натурал қатарды тізбектерге жіктеу туралы есептерге және оларды дәлелдейтін теоремаларға арналады.
Натурал қатарды екі  және
және  өспелі қиылыспайтын тізбектерге жіктеудің бір әдісін
қарастырамыз, мұндағы
өспелі қиылыспайтын тізбектерге жіктеудің бір әдісін
қарастырамыз, мұндағы  кез-келген натурал үшін шартын
қанағаттандырады.
кез-келген натурал үшін шартын
қанағаттандырады.
Натурал қатар арқылы жылжи отырып, екі тізбектің мүшелерін біртіндеп есептей аламыз.

Шарт
бойынша  болғандықтан, онда ең кіші натурал сан,
яғни
1-
болғандықтан, онда ең кіші натурал сан,
яғни
1-  -ге тең
болады.
-ге тең
болады.
Мұнан,  және
солай жалғаса
береді.
Осылай, ең кіші натурал санды таңдағанда
оны
және
солай жалғаса
береді.
Осылай, ең кіші натурал санды таңдағанда
оны  -ге тең деп есептей
отырып,
-ге тең деп есептей
отырып,
 -ді
-ді
 формуласы арқылы тауып
тізбектерді
құрастырамыз.
формуласы арқылы тауып
тізбектерді
құрастырамыз.
Бұлай құрылған тізбектер математиктердің натурал сандар теориясында қызығушылық тудырған, көптеген қолданыстарына жол ашқан.
Мәселен, бұл туралы 1877
жылы лорд Рэлейдің «Дыбыстар теориясы» еңбегінде былай жазған
болатын: «егер x бір санынан кіші болатын, қандай да бір оң
иррационал сан болса, онда n/x және n/(x-1) шамаларынан тұратын екі
қатар құруға болады, мұндағы n = 1,2,3…; қатарлардың біреуіне
тиісті әрбір сан, тек осы сан ғана, қатар тұрған екі натурал
сандардың арсында болады». Яғни,  және
және
 , егер 0<x<1 және
x
, егер 0<x<1 және
x Q болса, бүкіл натурал
қатарды толтырады.
Q болса, бүкіл натурал
қатарды толтырады.
Акулич гипотезасы және айқын формулалар
И.Ф. Акулич
гипотезасы: a-сандар мөлшерінің
b-сандар мөлшеріне
қатынасы «алтын
қимаға» ұмтылады  (мұндағы a,
(мұндағы a,
 тізбегіне тиісті
сандар,
b
тізбегіне тиісті
сандар,
b
 тізбегіне тиісті
сандар).
тізбегіне тиісті
сандар).
 [(1+
[(1+ )n/2]
)n/2]
 =[(1+
=[(1+ )n/2]+n=[(3+
)n/2]+n=[(3+ )n/2]
)n/2]
Акулич гипотезасын жоғарыдағы формулаларды пайдаланып, дәлелдейміз.
 ;
; тең
болсын.
тең
болсын.
Егер тізбектер:

 ;
; формулалары арқылы
берілсін.
формулалары арқылы
берілсін.
Алғашқы N натурал сандары үшін қанша a-саны және b-саны бар екендігін есептейік.
 теңсіздігі санның бүтін
бөлігі анықтамасы бойынша,
теңсіздігі санның бүтін
бөлігі анықтамасы бойынша,  <N+1теңсіздігіне тең
күштес, яғни n<(N+1)/
<N+1теңсіздігіне тең
күштес, яғни n<(N+1)/ теңсіздігіне де. Демек,
a-саны алғашқы N натурал сандар арасында
[(N+1)/
теңсіздігіне де. Демек,
a-саны алғашқы N натурал сандар арасында
[(N+1)/ ] рет кездеседі. Осыған
ұқсас, b-саны [(N+1)/
] рет кездеседі. Осыған
ұқсас, b-саны [(N+1)/ ].
].
Олай болса, a-сандар мөлшерінің b-сандар мөлшеріне қатынасы

N –ді шексіздікке ұмтылдыра отырып:

Гипотезаның  және
және
 тізбектерінің айқын
формулалар арқылы берілген жағдайда дұрыс екендігіне көз
жеткіздік.
тізбектерінің айқын
формулалар арқылы берілген жағдайда дұрыс екендігіне көз
жеткіздік.
 [(1+
[(1+ )n/2]
)n/2]
 =[(3+
=[(3+ )n/2]
)n/2]
Бірақ Акулич  және
және
 тізбектерінің
[
тізбектерінің
[ ] және [
] және [ ] түрінде жазуға болатынын білген
математиктердің біріншісі емес еді.
] түрінде жазуға болатынын білген
математиктердің біріншісі емес еді.
Дәл осы айқын
формулаларды Рэлейдің x =
2/(1+ )
мәнінде алуға болады,
себебі, 1-ншілердің мәні
2/(3+
)
мәнінде алуға болады,
себебі, 1-ншілердің мәні
2/(3+ )-ке тең, яғни
)-ке тең, яғни 
Бұл жағдайда N жиынын екі тізбекке жіктеу есебі шешімінің жалғыздығы туралы сұрақ туындайды.
Баабабовтың [2] статьясында бұл теорема толық дәлелденіп, оның қорытындысын жалпылай келе натурал қатарды мұндай жіктеу шексіз көп екндігін көрсеткен.
Төменде осы теореманы және оның толық дәлелдемесін келтіреміз.
 деп
белгілейік.
деп
белгілейік.
Теорема.
Егер  және
және
 - оң иррационал сандар болса және мына арақатынас
арқылы
- оң иррационал сандар болса және мына арақатынас
арқылы  байланыссын, онда мына түрдегі сандардың
арасынан [
байланыссын, онда мына түрдегі сандардың
арасынан [ ] және [
] және [ ] , мұндағы n
] , мұндағы n  , әрбір натурал сан бірақ рет
кездеседі.
, әрбір натурал сан бірақ рет
кездеседі.
Дәлелдеу:
 > 1 болғандықтан,
> 1 болғандықтан,  тізбегінде бірде-бір сан
қайталанбайды.
тізбегінде бірде-бір сан
қайталанбайды.
Осыған
ұқсас  >1
үшін
>1
үшін  тізбегі де қатаң түрде
өспелі болады.
тізбегі де қатаң түрде
өспелі болады.
Шынында,
[ ]
– k
болсын,
]
– k
болсын, 
Мұнан, 
Енді әрбір натурал санның
бір рет қана кездесетініне көз жеткіземіз.
Қандай да
бір k натурал саны екі тізбектің де мүшесі болсын
деп есептейік, яғни, k =
 , мұндағы m,n –
натурал сандар. Олай болса төмендегі теңсіздіктер
орындалады:
, мұндағы m,n –
натурал сандар. Олай болса төмендегі теңсіздіктер
орындалады:
k< < k +
1, k<
< k +
1, k< <k +
1,
<k +
1,
яғни,


Теңсіздіктерді мүшелеп
қосамыз,  екендігін
ескерсек
екендігін
ескерсек
 аламыз,
аламыз,
мұнан k<m+n<k+1.
Алайда, қатар орналасқан екі натурал сандардың аралығында басқа натурал сан болуы мүмкін емес. Демек, k саны екі тізбекке бір мезгілде тиіс емес.
Енді k саны екі тізбектің де құрамында болмаған жағдайын қарастырайық. Онда қандайда бір m және n натурал сандары үшін төмендегі теңсіздіктер орындалады.
 m
< k <k+1<
m
< k <k+1<  (m+1),
(m+1),
 n
< k <k+1<
n
< k <k+1<  (n+1),
(n+1),
Түрлендіріп мына түрдегі
теңсіздіктерді аламыз 
Мүшелеп
қосып,
 аламыз,
аламыз,
Мұнан m+n<k және k+1<m+n+2  m+n<k және m+n>k-1
m+n<k және m+n>k-1
Бұл тағы да қайшылыққа әкелді, яғни теорема толық дәлелденді.
Келесі параграфте натурал қатарды жіктеуге арналған жаттығулар қарастырылады. Оларды шешу үшін осы теоремалардың қорытындылары қалай қолданатынын көрсетеді.
§3. Жаттығулар
1 - жаттығу.
Тізбек  формуласымен
берілсін.
формуласымен
берілсін.
 табу
керек.
табу
керек.








1 … 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48















49 50

Дәл
осылай,
a -нің кез-келген мәнін
табуға болады.
-нің кез-келген мәнін
табуға болады.
2- жаттығу.
Есепте:
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
[(1+ |
1 |
3 |
4 |
6 |
8 |
9 |
11 |
12 |
14 |
16 |
17 |
19 |
21 |
22 |
24 |
25 |
27 |
29 |
|
[(3+ |
2 |
5 |
7 |
10 |
13 |
15 |
18 |
20 |
23 |
26 |
28 |
31 |
34 |
36 |
39 |
41 |
44 |
47 |
3- жаттығу.
 және
және
 формулаларын пайдаланып,
натурал қатарды толық жабатын тізбектерді
құрастыр.
формулаларын пайдаланып,
натурал қатарды толық жабатын тізбектерді
құрастыр.

 ,
,  ,
,  …
…
… ,
,  ,
,  …
…






1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21















Мұндағы 
4-жаттығу.
Натурал қатарды толық жабатын
 және
және
 өспелі тізбектердің айқын
формулаларын тап, егер олар барлық n=
1,2,3…үшін мына
өспелі тізбектердің айқын
формулаларын тап, егер олар барлық n=
1,2,3…үшін мына  арақатынаспен
байланысса.
арақатынаспен
байланысса.


Сонымен, берілген шартты қанағаттандыратын айқын формулалар дәлелденді.
§4.Геометриялық интерпретациялау
Қарапайым және көрнекі дәлелдемесі.
§ 1 теоремадан, егер геометриялық интерпретациясын қарастырсақ, төмендегідей сурет аламыз.
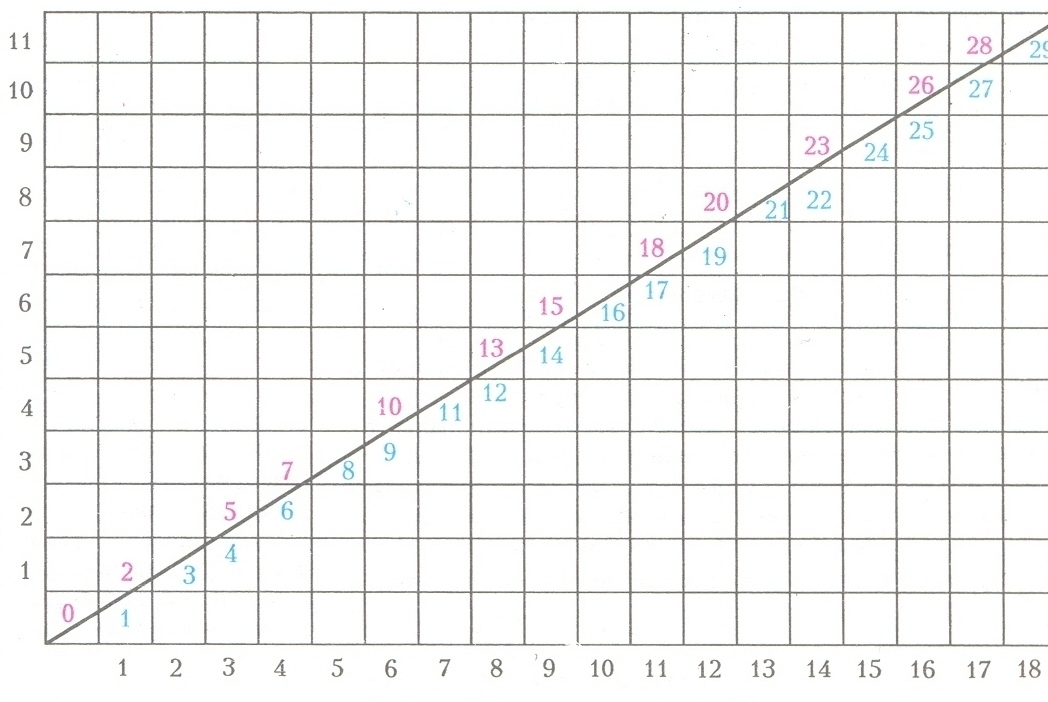
Әрине, α және β бұрынғыша– оң иррационал сандар болсын
Мұндағы  .
Сонда
.
Сонда  ,
мұнан
,
мұнан  . Бір парақ қағаз бетіне,
координат жазықтығына салғандай етіп,
у=(α-1)x формуласымен берілген
l түзуін саламыз. Бұл түзуді мына түрде де жаза
аламыз x=(β-1)y.
. Бір парақ қағаз бетіне,
координат жазықтығына салғандай етіп,
у=(α-1)x формуласымен берілген
l түзуін саламыз. Бұл түзуді мына түрде де жаза
аламыз x=(β-1)y.
Бас нүктеден
бастап, l түзуін қиятын барлық
α= (
немесе β...) мәні
үшін пайда болған нүктелерді
нөмірлейміз.
(
немесе β...) мәні
үшін пайда болған нүктелерді
нөмірлейміз.
Түзудің жоғары жағында орналасқан нүктелерді a-деп, керісінше төменгі жағында орналасқан нүктелерді b–деп есептесек §1 айтылған екі тізбектер пайда болады.
Ал α иррационал болғандықтан, l түзуі тор көздердің төбелері арқылы өтпейді. Яғни, l түзуі суретте көріп отырғанымыздай, әр тор көзді вертикаль сызығын сол жағынан қиып, немесе горизонталь сызығын төменгі жағынан қия орналасады.
Егер l тор көзді вертикаль сызығын сол жағынан қиса және х=n болса, онда түзудің тор көзді қию нөмірі n+[( α-1)n]=[ αn] –ға тең.
Егер керісінше, яғни l түзуі тордың горизонталь сызығын төменгі жағынан қиса және y=m, онда ол тордың нөмірі [(β-1)m]+m=[βm] –ға тең.
5. Кейбір қолданыстары (Палиндромдар).
a тізбегіне тиісті натурал
сандарды А
әрпімен
белгілейік, ал
тізбегіне тиісті натурал
сандарды А
әрпімен
белгілейік, ал  -ға тиістілерді
В әрпімен белгілейміз.
-ға тиістілерді
В әрпімен белгілейміз.
Сонда төмендегідей тізбек пайда болады:
АВААВАВААВААВАВААВАВААВААВАВААВААВАВААВАВААВААВАВА…
Тізбекке мұқият қарасақ, оны полиндромдарға бөлуге болады.
Анықтама: Палиндромдар – бұл оңнан соға оқыса да, солдан оңға оқысада өзгеріссіз қалатын сөздер.
Мысалы:
Шалаш, ротор, қазақ немесе АВВАВАВВА.
Палиндромдармен байланысты бір есеп қарастырайық, осыған ұқсас есепті Акулич кезінде өзінің статьясында қарастырған.
Есеп.
А және В әріптерінен тұратын 2010-әріптен тұратын сөз құрастырылған. Осы сөзді 900 –дан аспайтын жуық қысқа сөздерге бөлуге болатынын дәлелдеңдер.
Дәлелдеу:
Кез-келген 2010-әріптен тұратын сөз қарастырайық, және оны сөздерге бөліп жазамыз, олардың саны – барлығы 402 болады. 5-әріптік сөздерді кезегінде екі палиндромнан аспайтын сөздерге бөлуге болады. Сондықтан еркін алынған 2010-әріптен тұратын сөзден 804-тен аспайтын палиндром құрастыруға болады деген сөз, яғни бұл 900-ден аз, дәлелдеу керегі де осы.
Осыған ұқсас есептерді шығару үшін, f(n) функциясын енгіземіз.
Ол арқылы ұзақтығы n-ге тең, А және В әріптерінен құрылған сөзді бөлуге болатын палиндром сандарының ең кішісін белгілейміз. Яғни бұл сөзді саны f(n) –нен аспайтын палиндромдарға бөлуге болады.
1-жаттығу.
А және В әріптерінен тұратын, саны 3-тен артпайтын палиндромға бөлуге болатын, бірақ оның оң жағынан немесе сол жағынан А және В әріптерінің бірін жазып, өзгеткеннен кейін, оны тек 2 палиндромға ғана бөлуге болатын сөзді құрастыр?
АВААВВ+А
Бұл есепті жалпы жағдайда шешуге болады. Ол үшін f(n) функциясын ендіреміз.
Ол арқылы ұзақтығы n-ге тең, А және В әріптерінен құрылған сөзді бөлуге болатын палиндром сандарының ең кішісін белгілейміз. Яғни бұл сөзді саны f(n) –нен аспайтын палиндромдарға бөлуге болады.
Мысалы:
f(6)-ны есептейік. Алты әріпті сөздің саны
барлығы  бірақ А және В әріптерінің тізбекте кездесуі бірдей
болғандықтан, А
әрпінен басталатын сөзді
қарастыру жеткілікті:
бірақ А және В әріптерінің тізбекте кездесуі бірдей
болғандықтан, А
әрпінен басталатын сөзді
қарастыру жеткілікті:
АААААА
ААААА+В
ААА+АВА
АААА+ВВ
А+ААВАА
ААА+ВАВ
АА+АВВА
ААА+ВВВ
ААВАА+А
АА+ВААВ
А+АВАВА
АА+ВАВ+В!
ААВВАА
А+АВВА+В!
А+АВВВА
АА+ВВВ
АВА+ААА
А+ВАААВ
АВА+АВА
АВА+А+ВВ!
АВАВА+А
АВАВА+В
АВА+ВВ+А!
АВА+ВВВ
АВВА+АА
АА+ВААВ
АВВА+В+А!
АВВА+ВВ
АВВВА+А
АВВВА+В
АВВВВА
А+ВВВВВ
Леп белгісі бар сөздер, саны 3-тен кем емес палиндромға жіктелетіндер.
Мұнан, алты әріпті сөзді 3 палиндромнан артыққа жіктеуге болмайтынын көріп тұрмыз.
Кестеде f функциясының 10 мәнін есептейміз:
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
f(n) |
1 |
2 |
2 |
2 |
2 |
3 |
3 |
4 |
4 |
4 |
|
n/f(n) |
1 |
1 |
1.5 |
2 |
2.5 |
2 |
2.33 |
2 |
2.25 |
2.5 |
n/f(n) – бұл палиндромдардың ұзындықтарының орта мәні, мұның көмегімен ең қиын бөлінетін n-әріпті сөздердегі палиндромдардың ұзындығын есептей аламыз.
2-жаттығу.
Әрбір n- 1,2,3,…10 үшін ұзындығы n-ге тең букв А және В-дан тұратын сөзді құрастыр, бұл сөзді саны f(n)-нен кем емес палиндромдарға жіктеуге болатыны белгілі.
n=1 А
n=2 ВВ
n=3 АВВ
n=4 ААВВ
n=5 АВАВВ
n=6 АВААВВ
n=7 ВАВААВВ
n=8 ВВААВВАА
n=9 АВАВАВААВ
n=10 АВАВАВАВВВ
Теорема:
Кез-келген натурал n үшін f(3n)=n+1, f(3n+1)=n+1, f(6n+2)=2n+2
ал, n>1 үшін f(6n+5)=2n+2, f(11)=5 мәнінен өзге.
Теоремадан шығатын салдар:
 шегі бар және 3-ке
тең.
шегі бар және 3-ке
тең.
А және В n әріптен тұратын әрбір сөз, саны [(n+4)/3]-нан аспайтын палиндромдарға бөлінеді.



4)f(6k+5) = 2k+2
 .
.
Көріп отырғанымыздай, барлық жағдайда шектің мәні 3-ке тең.
Мұнан,  .
.
ҚОРЫТЫНДЫ
Таңдалған тақырыптың мақсатына жету үшін, натурал қатарды екі қиылыспайтын өспелі тізбектерге жіктеу туралы сұрақтар қарастырылды.
6 жаттығуды өз бетімше шығарып, § 3 теорема дәлелденді.
Осы тақырыпты таңдағандағы мақсатымыз, математикадан олимпиадада палиндромдарға есептер жиі келіп жүр, арнайы даярланбаған оқушыларға бұл есептерді шешу әдістерін оқу көп қиындық келтіреді. Сондықтан сол есептерді шешу үшін, жұмыста келтірілген теоремалар, жаттығулар қорытындыларын оқушылар өз бетінше оқып үйрене алады. Сонымен қатар, «алтын қима» тұрақтысы туралы да бірқатар мағлұматтар ала алады.
Ұсыныс
1. Математика адамзат тарихында тұрмыстық мұқтаждықты қанағаттандыру мақсатында пайда болған ең алғашқы ғылым. Олай дейтініміз адамзат өзін айнала қоршаған ортадан күнкөрістік тағамдық заттардың қорын жинағанда олардың мөлшерін білу үшін санауға мәжбүр болған. Санаудың нәтижесінен сан ұғымы қалыптасқан.Сонымен,сан адамзаттың ақыл-ойының жалаң туындысы емес,тұрмыстық қажеттіліктерінен бастау алған ұғым.Сандар математика ғылымының түп қазығы.Сондықтан натурал сандар қатарының жіктелуін оқушыларға жеңіл тәсілдермен үйрету қажет.
2. Адамзаттың математикамен тығыз байланыстылығын анықтай білу, көре білу, қолдану аясын кеңейту, математикалық іс-әрекетке тән ойлау сапасын қалыптастыру керек.
3. Осы тақырыпты алдағы уақытта математикадан олимпиадаларға дайындық жұмыстарында қолдана отырып, оқушыларға полиндромдық есептерді оңай шешу әдістерін түсіндіріп, оқыту керек.
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР
1. Акулич И.Ф. Ум хорошо, а пять лучше // Квант. – 1998. - №6
2.Баобабов А. «Пентиум» хорошо, а ум лучше // Квант.-1999. - №4,№5
3. Зайцев В.В., Рыжков В.В., Сканави М.И. Элементарная математика М.Наука, 1976
4. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра 8 класс. М. Просвещение, 1996
5. Маркушевич А.И. Ряды М.Наука, 1979
6. Игнатьев Е.И. В царстве смекалки. М.Наука, 1987
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
НАТУРАЛ ҚАТАРДЫҢ ЖІКТЕЛУІ
НАТУРАЛ ҚАТАРДЫҢ ЖІКТЕЛУІ
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ ҒЫЛЫМ ЖӘНЕ БІЛІМ МИНИСТРЛІГІ
Қызылорда облыстық білім басқармасы
Жаңақорған ауданы
№110 мектеп-лицей
Математика секциясы
ҒЫЛЫМИ-ЗЕРТТЕУ ЖҰМЫСЫ
Тақырыбы: НАТУРАЛ ҚАТАРДЫҢ ЖІКТЕЛУІ
Орындаған: Білалова Гүлжахан Мейрамқызы. 11-сынып
Ғылыми жетекші: Сейлова Зоя Төлеубайқызы, п.ғ.к., доцент
Пән мұғалімі: Райымбекова Сағима Жақыпқызы
ҚЫЗЫЛОРДА 2015-2016 оқу жылы.
МАЗМҰНЫ
Кіріспе 3
§1. Негізгі ұғымдар және анықтамалар 4-5
§2. Өзара қиылыспайтын тізбектер. Олардың қасиеттері 6-9
§3. Жаттығулар 10-12
§4. Геометриялық интерпретациялау 13-14
§5. Кейбір қолданыстары (Палиндромдар) 15-18
Қорытынды 19
Пайдаланылған әдебиеттер 20
КІРІСПЕ
Леонардо-да Винчи, Фибоначи қатары, пентакл, қасиетті пропорция немесе «Алтын қима» сияқты математика тарихында ерекше орын алатын ұғымдар бар. Осыларды өнер тарихындағы ең бір фундаментальды ұғымдардың бірі PHI санымен байланыстырады. PHI (айтылуы фи-и саны) деген қандай сан?
PHI саны шамамен 1,618-ге тең және бейнелеу өнерінде ең маңызды және мәнді сан болып табылады. Бұл сан дүниедегі ең «әдемі сан» деп есептеледі.
PHI саны Фибоначчи қатарынан шығады. Ал, Фибоначчи қатары дегеніміз бірінші және екінші мүшелерінің әрқайсысы 1-ге тең,ал үшінші мүшесінен бастап,әрбір мүшесі алдыңғы екі мүшесінің қосындысына тең болатын математикалық прогрессия:
1,1,2,3,5,8,13,21,34,55,89,144,...
Бұл прогрессияның тағы бір қасиеті қатарда тұрған көршілес екі санның қатынасы ерекше қасиетке ие болады-ол оның 1,618 санына, яғни PHI санына жуықтауы.
PHI санының басқа да қасиеттері көп. Бұл сан жер бетіндегі барлық тірі нәрселердің негізі қаланатын фундаменттің кірпіші сияқты. Барлық өсімдіктер, жануарлар тіпті адамдар да физикалық жағынан шамамен осы PHI санының негізі 1 санына жуық пропорциямен байланысты болады.
PHI санының табиғатта көптен кездесуі барлық тірі нәрселердің арасында байланыс бар екенін көрсетеді. Бұрын PHI санын «дүниені жаратушы орнатқан» деген пікір болған. Ертедегі оқымыстылар бір бүтін жүз мыңнан алты жүз он сегізді «құдай жартқан пропорция» деп те атаған.
Табиғаттан осы пропорцияға мысал келтірейік: аралардың ұясындағы аналық түрлер саны аталық түрлер санынан басым. Дүниедегі кез-келген ара ұяларындағы аналық түрлер санын аталық түрлер санына бөлсек тағы да сол PHI саны, яғни шамамен 1,618 саны шығады. Бұған мысалдар көп. Мысалы, жүзу қасиетіне ие болу үшін қабыршағына газ толтыратын және басын аяқ ететін спираль бейнелі теңіз малюскасі-наутилустың бақалшығын қарастырайық. Оның спиралінің әрбір орамының ішке қарай бақалшағының келесі орамына қатынасы тағы да осы PHI санын, яғни 1,618-ді береді екен. Сол сияқты, күнбағыс өсімдігінің піскен дәндерінің сағат тіліне қарсы бағыт бойынша спираль бойымен орналасқан орсдар диаметрінің келесі орамның диаметріне қатынасы шамамен 1,618-ге тең жүгері сабағының оралған жапырақтары, өсімдіктердің сабақтарындағы жапырақтарының орналасу арақашықтықтары, жәндіктердің денелерінің сегменттік бөліктері т.б.-осылардың бәрі өздерінің құрылысыда «қасиетті пропорцияға» бағынады.
Леонардо да Винчи және Витрувиан адамы. Енді, осының бәрінің сәулет өнеріне қандай қатысы бар екенін қарастырайық. Леонардо да Винчидің, өзінің «сәулет өнері жайындағы он кітап» атты еңбегінде «құдай жаратқан» пропорцияны мадақтаған данышпан рим сәулетшісі Маркус Витрувийге арнап сызған, шеңберге іштей сызылған жалаңаш адам бейнесі « Витрувиан адамы» деген суретінде адам денесінің қасиетті құрылысы мен құрамын терең түсінгенін көрсетеді. Өзінің білімін жетілдіру үшін Леонардо да Винчи адам анатомиясын зерттеп, өлген адам сүйектерінің пропорциясын өлшеген. Ол алғаш рет адам денесінің «құрылыс блоктарынан» тұратынын және олардың қатынасының пропорциясы біз айтып отырған «қасиетті санға» тең болатынын көрсеткен. Бұны әрбір адам өз денесінің биіктігінің ұзындығын кіндігінен табанына дейінгі ұзындыққа бөліп, немесе, иықтан саусақтарының ұшына дейінгі ұзындықты, шынтақтан тағы да сол саусақтардың ұшына дейінгі ұзындыққа бөліп тексеруіне болады.
Жұмыстың мақсаты математикаға қызығушылығы жоғары оқушыларға мектепте оқылатын сан қатарларынан (арифметикалық және геометриялық прогрессиялар) өзге қатарларды оқып үйренуге, оларды есеп шығаруда қолданыстарын қарастыру. Оның ішінде натурал қатардың әр түрлі екі қатарға жіктелуі туралы сұрақтарға жауап беру.
Жұмыста қарастырылған және дәлелденетін теореманың бірқатар қолданыстарына тоқталу. «Алтын қима» тұрақтысының 1,618-ге жуық иррационал сан екендігі дәлелденеді.
Жұмыс бес параграфтан тұрады.
Бірінші параграф бүкіл жұмыста басшылыққа алатын негізгі ұғымдар мен анықтамаларға арналады.
Екінші параграфта бір-бірімен қиылыспайтын қатарлар және Акулич гипотезасы туралы баяндалады.
Үшінші параграфта жаттығулар мен мысалдар келтірілген.
§1 Негізгі ұғымдар және анықтамалар
Санның бүтін және бөлшек бөлігі
1.Анықтама x санының бүтін бөлігі деп, x санынан артпайтын r ең үлкен бүтін санды айтамыз.
x санының бүтін бөлігі [x] немесе (кейде) E(x) (фр. entier "антье" — бүтін сөзінен алынған) деп белгіленеді.
Егер x [r; r +1) аралығына тиісті болса, мұндағы r — бүтін сан, онда [x]=r, яғни x [ [x]; [x]+1) аралығында жатады. Сандық теңсіздіктер қасиеттері бойынша x-[x] айырмасы [0; 1) аралығына тиісті болады.
2.Анықтама q = x - [x] санын x санының бөлшек бөлігі деп аталады және {x} деп белгіленеді. Сондықтан, санның бөлшек бөлігі әрдайым оң және 1-ден аспайды, ал бүтін бөлігі оң және теріс мәндерге ие болады. Сонымен, {x} = x - [x], сондықтан, x = [x] + {x}.
Мысалы:
|
[5]=5 |
[7,2]=7 |
[-3]=-3 |
[-4,2]=-5 |
[0]=0 |
|
{5}=0 |
{7,2}=0,2 |
{-3}=0 |
{-4,2}=0,8 |
{0}=0 |
Бүтін бөлігінің қасиеттері
[x+n] = [x]+n, мұндағы n – натурал сан
Рационал және иррационал сандар және олардың қасиеттері
3.Анықтама  түрінде жазуға болатын
санды рационал сан деп атаймыз, мұндағы m –
бүтін
сан,
ал
n
– натурал сан.
түрінде жазуға болатын
санды рационал сан деп атаймыз, мұндағы m –
бүтін
сан,
ал
n
– натурал сан.
4.Анықтама Егер санды  түрінде жазуға
болмаса,
онда бұл
сан иррационал сан деп
аталады.
түрінде жазуға
болмаса,
онда бұл
сан иррационал сан деп
аталады.
1Теорема. Кез келген рационал санды шектелген немесе шектеусіз периодты бөлшек түрінде жазуға болады.
Сол сияқты кез келген иррационал санды шектелген немесе шектеусіз периодты бөлшек түрінде жазуға болады.
Мысалы:
0,5= -рационал
сан
-рационал
сан
0,(3)=  - рационал
сан
- рационал
сан
1,0123456789101112…- иррационал сан
 -
иррационал сан
-
иррационал сан
Рационал және иррационал сандарға қолданылатын арифметикалық амалдардың қасиеттері
1. Егер  - рационал сандар
болса, онда
- рационал сандар
болса, онда  ,
,  ,
,  ,
,  ,
, - рационал сандар.
- рационал сандар.
Берілгені:  ;
; 
Дәлелдеу:  - рационал сан
- рационал сан
2. Егер r-рационал сан,  -иррационал сан болса, онда
-иррационал сан болса, онда  - иррационал сандар.
- иррационал сандар.
Дәлелдеу: (қарсы жору арқылы)
 болсын,
бірақ
болсын,
бірақ  - қарама-қайшылыққа
келдік.
- қарама-қайшылыққа
келдік.
3. Егер  ,онда
,онда  сандары жайлы
айқындалған тұжырым жоқ.
сандары жайлы
айқындалған тұжырым жоқ.
Мысалы:

§2 Өзара қиылыспайтын тізбектер. Олардың қасиеттері
Бұл параграфта әңгіме натурал қатарды тізбектерге жіктеу туралы есептерге және оларды дәлелдейтін теоремаларға арналады.
Натурал қатарды екі  және
және  өспелі қиылыспайтын тізбектерге жіктеудің бір әдісін
қарастырамыз, мұндағы
өспелі қиылыспайтын тізбектерге жіктеудің бір әдісін
қарастырамыз, мұндағы  кез-келген натурал үшін шартын
қанағаттандырады.
кез-келген натурал үшін шартын
қанағаттандырады.
Натурал қатар арқылы жылжи отырып, екі тізбектің мүшелерін біртіндеп есептей аламыз.

Шарт
бойынша  болғандықтан, онда ең кіші натурал сан,
яғни
1-
болғандықтан, онда ең кіші натурал сан,
яғни
1-  -ге тең
болады.
-ге тең
болады.
Мұнан,  және
солай жалғаса
береді.
Осылай, ең кіші натурал санды таңдағанда
оны
және
солай жалғаса
береді.
Осылай, ең кіші натурал санды таңдағанда
оны  -ге тең деп есептей
отырып,
-ге тең деп есептей
отырып,
 -ді
-ді
 формуласы арқылы тауып
тізбектерді
құрастырамыз.
формуласы арқылы тауып
тізбектерді
құрастырамыз.
Бұлай құрылған тізбектер математиктердің натурал сандар теориясында қызығушылық тудырған, көптеген қолданыстарына жол ашқан.
Мәселен, бұл туралы 1877
жылы лорд Рэлейдің «Дыбыстар теориясы» еңбегінде былай жазған
болатын: «егер x бір санынан кіші болатын, қандай да бір оң
иррационал сан болса, онда n/x және n/(x-1) шамаларынан тұратын екі
қатар құруға болады, мұндағы n = 1,2,3…; қатарлардың біреуіне
тиісті әрбір сан, тек осы сан ғана, қатар тұрған екі натурал
сандардың арсында болады». Яғни,  және
және
 , егер 0<x<1 және
x
, егер 0<x<1 және
x Q болса, бүкіл натурал
қатарды толтырады.
Q болса, бүкіл натурал
қатарды толтырады.
Акулич гипотезасы және айқын формулалар
И.Ф. Акулич
гипотезасы: a-сандар мөлшерінің
b-сандар мөлшеріне
қатынасы «алтын
қимаға» ұмтылады  (мұндағы a,
(мұндағы a,
 тізбегіне тиісті
сандар,
b
тізбегіне тиісті
сандар,
b
 тізбегіне тиісті
сандар).
тізбегіне тиісті
сандар).
 [(1+
[(1+ )n/2]
)n/2]
 =[(1+
=[(1+ )n/2]+n=[(3+
)n/2]+n=[(3+ )n/2]
)n/2]
Акулич гипотезасын жоғарыдағы формулаларды пайдаланып, дәлелдейміз.
 ;
; тең
болсын.
тең
болсын.
Егер тізбектер:

 ;
; формулалары арқылы
берілсін.
формулалары арқылы
берілсін.
Алғашқы N натурал сандары үшін қанша a-саны және b-саны бар екендігін есептейік.
 теңсіздігі санның бүтін
бөлігі анықтамасы бойынша,
теңсіздігі санның бүтін
бөлігі анықтамасы бойынша,  <N+1теңсіздігіне тең
күштес, яғни n<(N+1)/
<N+1теңсіздігіне тең
күштес, яғни n<(N+1)/ теңсіздігіне де. Демек,
a-саны алғашқы N натурал сандар арасында
[(N+1)/
теңсіздігіне де. Демек,
a-саны алғашқы N натурал сандар арасында
[(N+1)/ ] рет кездеседі. Осыған
ұқсас, b-саны [(N+1)/
] рет кездеседі. Осыған
ұқсас, b-саны [(N+1)/ ].
].
Олай болса, a-сандар мөлшерінің b-сандар мөлшеріне қатынасы

N –ді шексіздікке ұмтылдыра отырып:

Гипотезаның  және
және
 тізбектерінің айқын
формулалар арқылы берілген жағдайда дұрыс екендігіне көз
жеткіздік.
тізбектерінің айқын
формулалар арқылы берілген жағдайда дұрыс екендігіне көз
жеткіздік.
 [(1+
[(1+ )n/2]
)n/2]
 =[(3+
=[(3+ )n/2]
)n/2]
Бірақ Акулич  және
және
 тізбектерінің
[
тізбектерінің
[ ] және [
] және [ ] түрінде жазуға болатынын білген
математиктердің біріншісі емес еді.
] түрінде жазуға болатынын білген
математиктердің біріншісі емес еді.
Дәл осы айқын
формулаларды Рэлейдің x =
2/(1+ )
мәнінде алуға болады,
себебі, 1-ншілердің мәні
2/(3+
)
мәнінде алуға болады,
себебі, 1-ншілердің мәні
2/(3+ )-ке тең, яғни
)-ке тең, яғни 
Бұл жағдайда N жиынын екі тізбекке жіктеу есебі шешімінің жалғыздығы туралы сұрақ туындайды.
Баабабовтың [2] статьясында бұл теорема толық дәлелденіп, оның қорытындысын жалпылай келе натурал қатарды мұндай жіктеу шексіз көп екндігін көрсеткен.
Төменде осы теореманы және оның толық дәлелдемесін келтіреміз.
 деп
белгілейік.
деп
белгілейік.
Теорема.
Егер  және
және
 - оң иррационал сандар болса және мына арақатынас
арқылы
- оң иррационал сандар болса және мына арақатынас
арқылы  байланыссын, онда мына түрдегі сандардың
арасынан [
байланыссын, онда мына түрдегі сандардың
арасынан [ ] және [
] және [ ] , мұндағы n
] , мұндағы n  , әрбір натурал сан бірақ рет
кездеседі.
, әрбір натурал сан бірақ рет
кездеседі.
Дәлелдеу:
 > 1 болғандықтан,
> 1 болғандықтан,  тізбегінде бірде-бір сан
қайталанбайды.
тізбегінде бірде-бір сан
қайталанбайды.
Осыған
ұқсас  >1
үшін
>1
үшін  тізбегі де қатаң түрде
өспелі болады.
тізбегі де қатаң түрде
өспелі болады.
Шынында,
[ ]
– k
болсын,
]
– k
болсын, 
Мұнан, 
Енді әрбір натурал санның
бір рет қана кездесетініне көз жеткіземіз.
Қандай да
бір k натурал саны екі тізбектің де мүшесі болсын
деп есептейік, яғни, k =
 , мұндағы m,n –
натурал сандар. Олай болса төмендегі теңсіздіктер
орындалады:
, мұндағы m,n –
натурал сандар. Олай болса төмендегі теңсіздіктер
орындалады:
k< < k +
1, k<
< k +
1, k< <k +
1,
<k +
1,
яғни,


Теңсіздіктерді мүшелеп
қосамыз,  екендігін
ескерсек
екендігін
ескерсек
 аламыз,
аламыз,
мұнан k<m+n<k+1.
Алайда, қатар орналасқан екі натурал сандардың аралығында басқа натурал сан болуы мүмкін емес. Демек, k саны екі тізбекке бір мезгілде тиіс емес.
Енді k саны екі тізбектің де құрамында болмаған жағдайын қарастырайық. Онда қандайда бір m және n натурал сандары үшін төмендегі теңсіздіктер орындалады.
 m
< k <k+1<
m
< k <k+1<  (m+1),
(m+1),
 n
< k <k+1<
n
< k <k+1<  (n+1),
(n+1),
Түрлендіріп мына түрдегі
теңсіздіктерді аламыз 
Мүшелеп
қосып,
 аламыз,
аламыз,
Мұнан m+n<k және k+1<m+n+2  m+n<k және m+n>k-1
m+n<k және m+n>k-1
Бұл тағы да қайшылыққа әкелді, яғни теорема толық дәлелденді.
Келесі параграфте натурал қатарды жіктеуге арналған жаттығулар қарастырылады. Оларды шешу үшін осы теоремалардың қорытындылары қалай қолданатынын көрсетеді.
§3. Жаттығулар
1 - жаттығу.
Тізбек  формуласымен
берілсін.
формуласымен
берілсін.
 табу
керек.
табу
керек.








1 … 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48















49 50

Дәл
осылай,
a -нің кез-келген мәнін
табуға болады.
-нің кез-келген мәнін
табуға болады.
2- жаттығу.
Есепте:
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
[(1+ |
1 |
3 |
4 |
6 |
8 |
9 |
11 |
12 |
14 |
16 |
17 |
19 |
21 |
22 |
24 |
25 |
27 |
29 |
|
[(3+ |
2 |
5 |
7 |
10 |
13 |
15 |
18 |
20 |
23 |
26 |
28 |
31 |
34 |
36 |
39 |
41 |
44 |
47 |
3- жаттығу.
 және
және
 формулаларын пайдаланып,
натурал қатарды толық жабатын тізбектерді
құрастыр.
формулаларын пайдаланып,
натурал қатарды толық жабатын тізбектерді
құрастыр.

 ,
,  ,
,  …
…
… ,
,  ,
,  …
…






1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21















Мұндағы 
4-жаттығу.
Натурал қатарды толық жабатын
 және
және
 өспелі тізбектердің айқын
формулаларын тап, егер олар барлық n=
1,2,3…үшін мына
өспелі тізбектердің айқын
формулаларын тап, егер олар барлық n=
1,2,3…үшін мына  арақатынаспен
байланысса.
арақатынаспен
байланысса.


Сонымен, берілген шартты қанағаттандыратын айқын формулалар дәлелденді.
§4.Геометриялық интерпретациялау
Қарапайым және көрнекі дәлелдемесі.
§ 1 теоремадан, егер геометриялық интерпретациясын қарастырсақ, төмендегідей сурет аламыз.

Әрине, α және β бұрынғыша– оң иррационал сандар болсын
Мұндағы  .
Сонда
.
Сонда  ,
мұнан
,
мұнан  . Бір парақ қағаз бетіне,
координат жазықтығына салғандай етіп,
у=(α-1)x формуласымен берілген
l түзуін саламыз. Бұл түзуді мына түрде де жаза
аламыз x=(β-1)y.
. Бір парақ қағаз бетіне,
координат жазықтығына салғандай етіп,
у=(α-1)x формуласымен берілген
l түзуін саламыз. Бұл түзуді мына түрде де жаза
аламыз x=(β-1)y.
Бас нүктеден
бастап, l түзуін қиятын барлық
α= (
немесе β...) мәні
үшін пайда болған нүктелерді
нөмірлейміз.
(
немесе β...) мәні
үшін пайда болған нүктелерді
нөмірлейміз.
Түзудің жоғары жағында орналасқан нүктелерді a-деп, керісінше төменгі жағында орналасқан нүктелерді b–деп есептесек §1 айтылған екі тізбектер пайда болады.
Ал α иррационал болғандықтан, l түзуі тор көздердің төбелері арқылы өтпейді. Яғни, l түзуі суретте көріп отырғанымыздай, әр тор көзді вертикаль сызығын сол жағынан қиып, немесе горизонталь сызығын төменгі жағынан қия орналасады.
Егер l тор көзді вертикаль сызығын сол жағынан қиса және х=n болса, онда түзудің тор көзді қию нөмірі n+[( α-1)n]=[ αn] –ға тең.
Егер керісінше, яғни l түзуі тордың горизонталь сызығын төменгі жағынан қиса және y=m, онда ол тордың нөмірі [(β-1)m]+m=[βm] –ға тең.
5. Кейбір қолданыстары (Палиндромдар).
a тізбегіне тиісті натурал
сандарды А
әрпімен
белгілейік, ал
тізбегіне тиісті натурал
сандарды А
әрпімен
белгілейік, ал  -ға тиістілерді
В әрпімен белгілейміз.
-ға тиістілерді
В әрпімен белгілейміз.
Сонда төмендегідей тізбек пайда болады:
АВААВАВААВААВАВААВАВААВААВАВААВААВАВААВАВААВААВАВА…
Тізбекке мұқият қарасақ, оны полиндромдарға бөлуге болады.
Анықтама: Палиндромдар – бұл оңнан соға оқыса да, солдан оңға оқысада өзгеріссіз қалатын сөздер.
Мысалы:
Шалаш, ротор, қазақ немесе АВВАВАВВА.
Палиндромдармен байланысты бір есеп қарастырайық, осыған ұқсас есепті Акулич кезінде өзінің статьясында қарастырған.
Есеп.
А және В әріптерінен тұратын 2010-әріптен тұратын сөз құрастырылған. Осы сөзді 900 –дан аспайтын жуық қысқа сөздерге бөлуге болатынын дәлелдеңдер.
Дәлелдеу:
Кез-келген 2010-әріптен тұратын сөз қарастырайық, және оны сөздерге бөліп жазамыз, олардың саны – барлығы 402 болады. 5-әріптік сөздерді кезегінде екі палиндромнан аспайтын сөздерге бөлуге болады. Сондықтан еркін алынған 2010-әріптен тұратын сөзден 804-тен аспайтын палиндром құрастыруға болады деген сөз, яғни бұл 900-ден аз, дәлелдеу керегі де осы.
Осыған ұқсас есептерді шығару үшін, f(n) функциясын енгіземіз.
Ол арқылы ұзақтығы n-ге тең, А және В әріптерінен құрылған сөзді бөлуге болатын палиндром сандарының ең кішісін белгілейміз. Яғни бұл сөзді саны f(n) –нен аспайтын палиндромдарға бөлуге болады.
1-жаттығу.
А және В әріптерінен тұратын, саны 3-тен артпайтын палиндромға бөлуге болатын, бірақ оның оң жағынан немесе сол жағынан А және В әріптерінің бірін жазып, өзгеткеннен кейін, оны тек 2 палиндромға ғана бөлуге болатын сөзді құрастыр?
АВААВВ+А
Бұл есепті жалпы жағдайда шешуге болады. Ол үшін f(n) функциясын ендіреміз.
Ол арқылы ұзақтығы n-ге тең, А және В әріптерінен құрылған сөзді бөлуге болатын палиндром сандарының ең кішісін белгілейміз. Яғни бұл сөзді саны f(n) –нен аспайтын палиндромдарға бөлуге болады.
Мысалы:
f(6)-ны есептейік. Алты әріпті сөздің саны
барлығы  бірақ А және В әріптерінің тізбекте кездесуі бірдей
болғандықтан, А
әрпінен басталатын сөзді
қарастыру жеткілікті:
бірақ А және В әріптерінің тізбекте кездесуі бірдей
болғандықтан, А
әрпінен басталатын сөзді
қарастыру жеткілікті:
АААААА
ААААА+В
ААА+АВА
АААА+ВВ
А+ААВАА
ААА+ВАВ
АА+АВВА
ААА+ВВВ
ААВАА+А
АА+ВААВ
А+АВАВА
АА+ВАВ+В!
ААВВАА
А+АВВА+В!
А+АВВВА
АА+ВВВ
АВА+ААА
А+ВАААВ
АВА+АВА
АВА+А+ВВ!
АВАВА+А
АВАВА+В
АВА+ВВ+А!
АВА+ВВВ
АВВА+АА
АА+ВААВ
АВВА+В+А!
АВВА+ВВ
АВВВА+А
АВВВА+В
АВВВВА
А+ВВВВВ
Леп белгісі бар сөздер, саны 3-тен кем емес палиндромға жіктелетіндер.
Мұнан, алты әріпті сөзді 3 палиндромнан артыққа жіктеуге болмайтынын көріп тұрмыз.
Кестеде f функциясының 10 мәнін есептейміз:
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
f(n) |
1 |
2 |
2 |
2 |
2 |
3 |
3 |
4 |
4 |
4 |
|
n/f(n) |
1 |
1 |
1.5 |
2 |
2.5 |
2 |
2.33 |
2 |
2.25 |
2.5 |
n/f(n) – бұл палиндромдардың ұзындықтарының орта мәні, мұның көмегімен ең қиын бөлінетін n-әріпті сөздердегі палиндромдардың ұзындығын есептей аламыз.
2-жаттығу.
Әрбір n- 1,2,3,…10 үшін ұзындығы n-ге тең букв А және В-дан тұратын сөзді құрастыр, бұл сөзді саны f(n)-нен кем емес палиндромдарға жіктеуге болатыны белгілі.
n=1 А
n=2 ВВ
n=3 АВВ
n=4 ААВВ
n=5 АВАВВ
n=6 АВААВВ
n=7 ВАВААВВ
n=8 ВВААВВАА
n=9 АВАВАВААВ
n=10 АВАВАВАВВВ
Теорема:
Кез-келген натурал n үшін f(3n)=n+1, f(3n+1)=n+1, f(6n+2)=2n+2
ал, n>1 үшін f(6n+5)=2n+2, f(11)=5 мәнінен өзге.
Теоремадан шығатын салдар:
 шегі бар және 3-ке
тең.
шегі бар және 3-ке
тең.
А және В n әріптен тұратын әрбір сөз, саны [(n+4)/3]-нан аспайтын палиндромдарға бөлінеді.



4)f(6k+5) = 2k+2
 .
.
Көріп отырғанымыздай, барлық жағдайда шектің мәні 3-ке тең.
Мұнан,  .
.
ҚОРЫТЫНДЫ
Таңдалған тақырыптың мақсатына жету үшін, натурал қатарды екі қиылыспайтын өспелі тізбектерге жіктеу туралы сұрақтар қарастырылды.
6 жаттығуды өз бетімше шығарып, § 3 теорема дәлелденді.
Осы тақырыпты таңдағандағы мақсатымыз, математикадан олимпиадада палиндромдарға есептер жиі келіп жүр, арнайы даярланбаған оқушыларға бұл есептерді шешу әдістерін оқу көп қиындық келтіреді. Сондықтан сол есептерді шешу үшін, жұмыста келтірілген теоремалар, жаттығулар қорытындыларын оқушылар өз бетінше оқып үйрене алады. Сонымен қатар, «алтын қима» тұрақтысы туралы да бірқатар мағлұматтар ала алады.
Ұсыныс
1. Математика адамзат тарихында тұрмыстық мұқтаждықты қанағаттандыру мақсатында пайда болған ең алғашқы ғылым. Олай дейтініміз адамзат өзін айнала қоршаған ортадан күнкөрістік тағамдық заттардың қорын жинағанда олардың мөлшерін білу үшін санауға мәжбүр болған. Санаудың нәтижесінен сан ұғымы қалыптасқан.Сонымен,сан адамзаттың ақыл-ойының жалаң туындысы емес,тұрмыстық қажеттіліктерінен бастау алған ұғым.Сандар математика ғылымының түп қазығы.Сондықтан натурал сандар қатарының жіктелуін оқушыларға жеңіл тәсілдермен үйрету қажет.
2. Адамзаттың математикамен тығыз байланыстылығын анықтай білу, көре білу, қолдану аясын кеңейту, математикалық іс-әрекетке тән ойлау сапасын қалыптастыру керек.
3. Осы тақырыпты алдағы уақытта математикадан олимпиадаларға дайындық жұмыстарында қолдана отырып, оқушыларға полиндромдық есептерді оңай шешу әдістерін түсіндіріп, оқыту керек.
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР
1. Акулич И.Ф. Ум хорошо, а пять лучше // Квант. – 1998. - №6
2.Баобабов А. «Пентиум» хорошо, а ум лучше // Квант.-1999. - №4,№5
3. Зайцев В.В., Рыжков В.В., Сканави М.И. Элементарная математика М.Наука, 1976
4. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра 8 класс. М. Просвещение, 1996
5. Маркушевич А.И. Ряды М.Наука, 1979
6. Игнатьев Е.И. В царстве смекалки. М.Наука, 1987

шағым қалдыра аласыз















