
Сабақ жоспар
Сынып: 8 «A» пәні: Геометрия Өтілген күні:
Сабақ тақырыбы: Негізгі тригонометриялық тепе-теңдіктер (Формулалары)
Сабақтың мақсаты:
І. Білімділік мақсаты: Негізгі триогонометриялық тепе –теңдіктердің шығу жолымен таныстыру. Бір тригонометриялық функцияның мәні бойынша қалғандарының мәнін табуға есептер шығаруды үйрету.
ІІ. Дамытушылық мақсаты: Тік бұрышты үшбұрыштың сүйір бұрыштарының синусын, косинусын , тангенсін, котангенсін анықтауды,формулаларды есептеуде қолдана білу дағдысын қалыптастыру, пәнге қызығушылығын арттыру.
ІІІ. Тәрбиелік мақсаты: Оқушылардың ойлау қабілетін жетілдіру, шыншылдыққа, жауапкершілікке, еңбек етуге тәрбиелеу.
Сабақтың түрі : жаңа сабақ
Сабақтың көрнекілігі: интербелсенді тақта, құрал – жабдықтар
Сабақтың барысы:
1. Ұйымдастыру кезеңі:
а) Сәлемдесу
ә) Оқушылар тізімін тексеру
б) Сабақтың мақсатын нұсқау
2. Өткен тақырыпты қайталау:
1. Пифагор теоремасы бойынша сұрақтар
2. Тік бұрышты үшбұрыштың.....
|
Сүйір бұрыштың синусы деп... |
|
Сүйір бұрыштың косинусы деп... |
|
Сүйір бұрыштың тангенсі деп... |
|
Сүйір бұрыштың котангенсі деп... |
Жауаптары:
1. Анықтама: Тікбұрышты үшбұрыштың сүйір бұрышына іргелес жатқан катеттің гипотенузаға қатынасы осы бұрыштың косинусы деп аталады.
2. Анықтама: Тік бұрышты үшбұрыштың сүйір бұрышына қарсы жатқан катеттің гипотенузаға қатынасы сол бұрыштың с и н у с ы деп аталады
3. Анықтама: Тік бұрышты ұшбұрыштың сүйір бұрышына қарсы жатқан катеттің іргелес жатқан катетке қатынасы сол бұрыштың т а н г е н с і деп аталады.
4. Анықтама: Тік бұрышты ұшбұрыштың сүйір бұрышына іргелес жатқан катетке қатынасы сол бұрыштың к о т а н г е н с і деп аталады.
3. Тригонометрияның шығу тарихы.
“Тригонометрия” сөзі грек тілінен аударғанда “Үшбұрыштарды шешу” ұғымды білдіреді.Тригонометрия ғылыми терминін адамдар бұрынғы кезде практикалық әрекеттерге қолданылған емес.
Географиялық карталарды жер қыртыстарын өлшеуде қолданған.Ең алғаш рет Ежелгі грек ғалымы белгілі Клавдий Птоломей «Альмагест»атты еңбегінде «Хорда тригонометриясы»атты еңбегін ойлап тапқан.
Санды шеңберде кез келген бұрыштың тригонометриялық функциясымен таныстыңдар және sinα, cosα, tgα, ctgα мәндері радиустың ұзындығына тәуелді бола алмайды.
Сондықтанда тригонометриялық функцияларда қарастырған кезде радиусы 1-ге тең шеңберді алу жеткілікті.
Мысалы жылжымалы ОВ радиусының соңғы нүктесіндегі синус функциясы тек ордината у-пен,ал В нүктесіндегі косинустың мәні абсцисса х-пен анықталатын болады.ОВС тікбұрышты үшбұрышын қарастырайық.
Сонда Пифагор теоремасы бойынша ОВ=ОС²+ВС²,мұндағы ОВ= 1,ОС=х,ВС=у немесе ОС=х= sinα,ВС=у= cosα .
sin²α + cos²α =1, (1)
4. Жаңа тақырыпты түсіндіру
Білімдерін пысықтау: Негізгі тригонометриялық теп-теңдіктер
|
1)
соs 2 соs sin 2)
tg |
3)
ctg 4)
tg tg ctg |
5) 1+
tg2 6) 1+
ctg2
|
Өрнекті ықшамда:
|
|
|
Есептер шығару:
1 – ші есеп: ( «А» - тобының есептері)


 Ромбтың қабырғаларын тап, егер
оның дигональдары 16 дм және 30 дм
болса.
Ромбтың қабырғаларын тап, егер
оның дигональдары 16 дм және 30 дм
болса.
б) Тең бүйірлі АВС үшбұрыштың бүйір қабырғасы АВ 17 см, ал табаны АС 16 см. Үшбұрыштың В төбесінен табанына түсірілген биіктікті тап.
в) Тікбұрышты үшбұрыштың бір катеті 8 см – ге, ал оған қарсы жатқан бұрыштың синусы 0,8-ге тең. Гипатинузасы мен екінші катетін тапбыңдар.
2 – ші есеп: ( «Б» - тобының есептері)








3 – ші есеп: ( «C» тобының есептері)
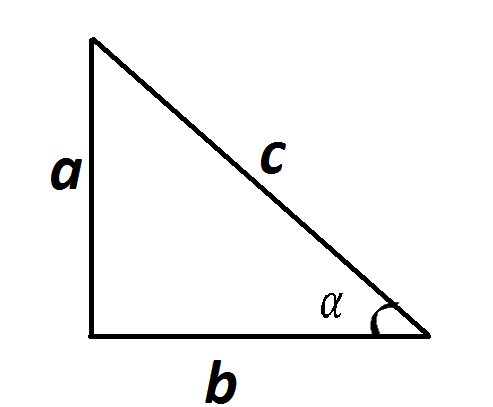
 -бұрышы арқылы белгісіз
тригонометриялық функциялардың мәндерін
тап
-бұрышы арқылы белгісіз
тригонометриялық функциялардың мәндерін
тап
а) 



4 – ші есеп.
Ойын сабақ.
Интербелсенді тақтада әртүрлі 5 ұяшық беріледі. Әр ұяшықта 1 есеп және анықтама беріледі, дұрыс жауап берген оқушы 1 ұпай иеленеді.
-
Өрнекті ықшамдаңыз:

Тік бұрышты
үшбұрыштың  анықтамасы
анықтамасы
-
Өрнекті ықшамдаңыз: (sin
 –
cos
–
cos )
) +
2sin
+
2sin cos
cos .
.
Тік бұрышты
үшбұрыштың  анықтамасы
анықтамасы
-
Өрнекті ықшамдаңыз:

Тік бұрышты
үшбұрыштың  анықтамасы
анықтамасы
-
Өрнекті ықшамдаңыз: (sin
 –
cos
–
cos )
) +
2sin
+
2sin cos
cos .
.
Тік бұрышты
үшбұрыштың  анықтамасы
анықтамасы
-
Есептеңіз: sin
 80
80
 + cos
+ cos
 80
80

Пифагор теоремасы
Сабақты қорытындылау.
Өтілген тақырыптан анықтама және формулалар қайталау.
Негізгі тригонометриялық формулаларды қолданып, тік бұрышты үшбұрыштардың белгісіз қабырғаларын және бұрыштарын анықтауда оқушылардың білім дағдысын дамыту.
Үйге тапсырма:
-
Тригонометриялық функциялардың арасында қандай байланыстар бар?
-
Негізгі тригонометриялық тепе теңдіктер
-
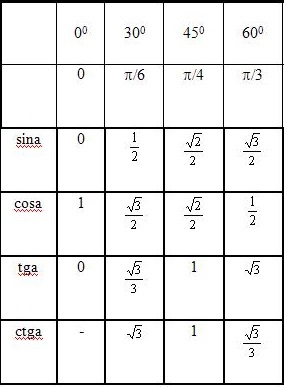
Тригонометриялық функциялардың мәндерін кесте бойынша қалай анықтауға болады?
-
Қандай үшбұрыш пифагорлық үшбұрыштар деп аталады?
Пайдаланған әдебиеттер:
Геометрия 8 сынып Алматы. Атамұры 2012 ж Авторы: Ә.Н.Шыныбеков
Геометрия 7-9 сынып. Алматы. Мектеп 2001 ж Авторы: Л.С Атанасян. В.Ф.Бутузов. И.И.Юдина
Геометрия 7-11 сыныптар. Алматы 2002 ж Авторы: Р.Бөкейханов
Геометрия 7-9 сынып. Алматы. Рауан. 1996 ж Авторы: Л.С Атанасян. В.Ф.Бутузов. И.И.Юдина
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Негізгі тригонаметриялық тепе-теңдіктер
Негізгі тригонаметриялық тепе-теңдіктер
Сабақ жоспар
Сынып: 8 «A» пәні: Геометрия Өтілген күні:
Сабақ тақырыбы: Негізгі тригонометриялық тепе-теңдіктер (Формулалары)
Сабақтың мақсаты:
І. Білімділік мақсаты: Негізгі триогонометриялық тепе –теңдіктердің шығу жолымен таныстыру. Бір тригонометриялық функцияның мәні бойынша қалғандарының мәнін табуға есептер шығаруды үйрету.
ІІ. Дамытушылық мақсаты: Тік бұрышты үшбұрыштың сүйір бұрыштарының синусын, косинусын , тангенсін, котангенсін анықтауды,формулаларды есептеуде қолдана білу дағдысын қалыптастыру, пәнге қызығушылығын арттыру.
ІІІ. Тәрбиелік мақсаты: Оқушылардың ойлау қабілетін жетілдіру, шыншылдыққа, жауапкершілікке, еңбек етуге тәрбиелеу.
Сабақтың түрі : жаңа сабақ
Сабақтың көрнекілігі: интербелсенді тақта, құрал – жабдықтар
Сабақтың барысы:
1. Ұйымдастыру кезеңі:
а) Сәлемдесу
ә) Оқушылар тізімін тексеру
б) Сабақтың мақсатын нұсқау
2. Өткен тақырыпты қайталау:
1. Пифагор теоремасы бойынша сұрақтар
2. Тік бұрышты үшбұрыштың.....
|
Сүйір бұрыштың синусы деп... |
|
Сүйір бұрыштың косинусы деп... |
|
Сүйір бұрыштың тангенсі деп... |
|
Сүйір бұрыштың котангенсі деп... |
Жауаптары:
1. Анықтама: Тікбұрышты үшбұрыштың сүйір бұрышына іргелес жатқан катеттің гипотенузаға қатынасы осы бұрыштың косинусы деп аталады.
2. Анықтама: Тік бұрышты үшбұрыштың сүйір бұрышына қарсы жатқан катеттің гипотенузаға қатынасы сол бұрыштың с и н у с ы деп аталады
3. Анықтама: Тік бұрышты ұшбұрыштың сүйір бұрышына қарсы жатқан катеттің іргелес жатқан катетке қатынасы сол бұрыштың т а н г е н с і деп аталады.
4. Анықтама: Тік бұрышты ұшбұрыштың сүйір бұрышына іргелес жатқан катетке қатынасы сол бұрыштың к о т а н г е н с і деп аталады.
3. Тригонометрияның шығу тарихы.
“Тригонометрия” сөзі грек тілінен аударғанда “Үшбұрыштарды шешу” ұғымды білдіреді.Тригонометрия ғылыми терминін адамдар бұрынғы кезде практикалық әрекеттерге қолданылған емес.
Географиялық карталарды жер қыртыстарын өлшеуде қолданған.Ең алғаш рет Ежелгі грек ғалымы белгілі Клавдий Птоломей «Альмагест»атты еңбегінде «Хорда тригонометриясы»атты еңбегін ойлап тапқан.
Санды шеңберде кез келген бұрыштың тригонометриялық функциясымен таныстыңдар және sinα, cosα, tgα, ctgα мәндері радиустың ұзындығына тәуелді бола алмайды.
Сондықтанда тригонометриялық функцияларда қарастырған кезде радиусы 1-ге тең шеңберді алу жеткілікті.
Мысалы жылжымалы ОВ радиусының соңғы нүктесіндегі синус функциясы тек ордината у-пен,ал В нүктесіндегі косинустың мәні абсцисса х-пен анықталатын болады.ОВС тікбұрышты үшбұрышын қарастырайық.
Сонда Пифагор теоремасы бойынша ОВ=ОС²+ВС²,мұндағы ОВ= 1,ОС=х,ВС=у немесе ОС=х= sinα,ВС=у= cosα .
sin²α + cos²α =1, (1)
4. Жаңа тақырыпты түсіндіру
Білімдерін пысықтау: Негізгі тригонометриялық теп-теңдіктер
|
1)
соs 2 соs sin 2)
tg |
3)
ctg 4)
tg tg ctg |
5) 1+
tg2 6) 1+
ctg2
|
Өрнекті ықшамда:
|
|
|
Есептер шығару:
1 – ші есеп: ( «А» - тобының есептері)


 Ромбтың қабырғаларын тап, егер
оның дигональдары 16 дм және 30 дм
болса.
Ромбтың қабырғаларын тап, егер
оның дигональдары 16 дм және 30 дм
болса.
б) Тең бүйірлі АВС үшбұрыштың бүйір қабырғасы АВ 17 см, ал табаны АС 16 см. Үшбұрыштың В төбесінен табанына түсірілген биіктікті тап.
в) Тікбұрышты үшбұрыштың бір катеті 8 см – ге, ал оған қарсы жатқан бұрыштың синусы 0,8-ге тең. Гипатинузасы мен екінші катетін тапбыңдар.
2 – ші есеп: ( «Б» - тобының есептері)









3 – ші есеп: ( «C» тобының есептері)

 -бұрышы арқылы белгісіз
тригонометриялық функциялардың мәндерін
тап
-бұрышы арқылы белгісіз
тригонометриялық функциялардың мәндерін
тап
а) 



4 – ші есеп.
Ойын сабақ.
Интербелсенді тақтада әртүрлі 5 ұяшық беріледі. Әр ұяшықта 1 есеп және анықтама беріледі, дұрыс жауап берген оқушы 1 ұпай иеленеді.
-
Өрнекті ықшамдаңыз:

Тік бұрышты
үшбұрыштың  анықтамасы
анықтамасы
-
Өрнекті ықшамдаңыз: (sin
 –
cos
–
cos )
) +
2sin
+
2sin cos
cos .
.
Тік бұрышты
үшбұрыштың  анықтамасы
анықтамасы
-
Өрнекті ықшамдаңыз:

Тік бұрышты
үшбұрыштың  анықтамасы
анықтамасы
-
Өрнекті ықшамдаңыз: (sin
 –
cos
–
cos )
) +
2sin
+
2sin cos
cos .
.
Тік бұрышты
үшбұрыштың  анықтамасы
анықтамасы
-
Есептеңіз: sin
 80
80
 + cos
+ cos
 80
80

Пифагор теоремасы
Сабақты қорытындылау.
Өтілген тақырыптан анықтама және формулалар қайталау.
Негізгі тригонометриялық формулаларды қолданып, тік бұрышты үшбұрыштардың белгісіз қабырғаларын және бұрыштарын анықтауда оқушылардың білім дағдысын дамыту.
Үйге тапсырма:
-
Тригонометриялық функциялардың арасында қандай байланыстар бар?
-
Негізгі тригонометриялық тепе теңдіктер
-
Тригонометриялық функциялардың мәндерін кесте бойынша қалай анықтауға болады?
-
Қандай үшбұрыш пифагорлық үшбұрыштар деп аталады?
Пайдаланған әдебиеттер:
Геометрия 8 сынып Алматы. Атамұры 2012 ж Авторы: Ә.Н.Шыныбеков
Геометрия 7-9 сынып. Алматы. Мектеп 2001 ж Авторы: Л.С Атанасян. В.Ф.Бутузов. И.И.Юдина
Геометрия 7-11 сыныптар. Алматы 2002 ж Авторы: Р.Бөкейханов
Геометрия 7-9 сынып. Алматы. Рауан. 1996 ж Авторы: Л.С Атанасян. В.Ф.Бутузов. И.И.Юдина

шағым қалдыра аласыз







































