
МАЗМҰНЫ
КІРІСПЕ ........................................................................................................................3
І. НЕГІЗГІ ТҮСІНІКТЕР...............................................................................................4
1.1. Көлденең күш пен июші моменттер.....................................................................4
1.2. Қиғаш иілу............................................................................................................13
ІІ. Кез келген күш әсерінен сырықтар жүйелеріндегі орын ауыстырулар...........16
2.1. Кез келген күш түсірілген брустың поетнциялық энергиясы.........................18
2.2. Цилиндр тәрізді оралған серіппелерді есептеу.................................................24
ҚОРЫТЫНДЫ ............................................................................................................26
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР........................................................................27
КІРІСПЕ
Бойлық өс арқылы өтетін жазықтықтарда (өс жазықтықтарында) жатқан көлденең күштер мен моменттердің (жұп күштердің) әсерінен сырықта пайда болған деформацияны иілу деп атайды.
Яғни, сыртқы күштің әсер ету сызығы мен бейтарап сызық өзара перпендикуляр. Әсер ету сызығы координаттар жүйесінің бас нүктесі арқылы өтетін кез келген күштің әсерінен мұндай аркалықтар жазық иіледі.
Сыртқы күш пен қауіпсіз кернеу белгілі болса, қиғаш иілген арқалықтың қима өлшемдерін беріктік шартынан келесі тәртіппен анықтайды қиманың өлшемдері алдын ала белгілі деп қарастырылып қандайда бір мәндері (4) теңсіздігіне енгізіледі.
Есептеліп анықталған теңсіздіктің сол жағы оң жағына қарағанда айтарлықтай кіші болса, қима өлшемдерін үлкейтіп, ал айтарлықтай үлкен болса кішірейтіп аркалықтың беріктігі қайта тексеріледі
Басты жазықтықтардан басқа, бойлық өс арқылы өтетін, кез келген жазықтықтарда жатқан сыртқы күштердің әсерінен конструкция элементі қиғаш иіледі. Қиғаш иілген арқалықты беріктікке есептеу тәртібі келесі мысалда көрсетілген. Бір ұшы қатаң бекітілген арқалықтың екінші ұшына Р күші әсер етсін
Екінші беріктік теориясын ең үлкен сызықтық деформация теориясы деп атайды. ¤йткені, бұл теорияда беріктік нышаны ретінде сызықтық деформация қабылданған.
Оның негізін Мариотт салып, Сен-Венан жалғастырған. Ол былай тұжырымдалады:
Күрделі кернеулі күйдегі материал көлеміндегі ең үлкен сызықтық деформация шамасы қауіпті шегіне жеткенде өзінің жұмыс істеу қабілетін жоғалтады.
Жазық иілген арқалықтың көлденең қималарында ішкі күштер — көлденең күш пен июші момент пайда болады.
Егер иілген арқалықтың көлденең қималарында июші моменттен басқа ішкі күштер жоқ болса, яғни көлденең күш нөлге тең болса, ондай иілу таза иілу деп аталады.
І. НЕГІЗГІ ТҮСІНІКТЕР
-
Көлденең күш пен июші моменттер
Беріктік кепілдігі. Межелік (сындырушы) күштің немесе кернеудің іс жүзінде әсер етіп тұрған күшке немесе кернеуге қатынасы. Син. – Беріктік кепілдігінің еселігі; күрделі кернеулі күй жағдайында кернеулі күйдің құраушыларының барлығын бірге кернеулі күй межелік кернеулі күй болу үшін неше өсе көбейту керек екенін көрсететін өселік.
Беріктік шегі. Үлгі төтеп бере алатын ең үлкен күштің үлгінің көлденең қимасының бастапқы (күш түсірілмеген кездегі) ауданына қатынасы.
Беріктік. Қатты дененің сыртқы күштер әсеріне сынбай төтеп беру қабілеті. Кең мағынада беріктік - материалдың сынуға төтеп берумен қатар оның өз формасын қайтымсыз (пластикалық) өзгертуге қарсыласу қабілеті.
Верещагин әдісі. Екі функцияның көбейтіндісінен алынатын интегралды сол функциялардың графиктерін арнаулы жолмен “көбейтумен” алмастыру.
Даламбер қағидасы. Қозғалыстағы материялық нүктелер жүйесі үшін барлық пәрменді күштердің, реакция күштерінің, инерция күштерінің векторлық қосындысы және осы аталған күштердің бас моменттерінің қосындысы нольге тең болады.
Деформация. Сыртқы күштер әсерінен туындайтын дене нүктелерінің өзара орналасуының өзгеруі.
Деформацияның потенциалдық энергиясы. Деформацияның серпімді құраушыларының арқасында пайда болып, күшті алып тастаған кезде жүйенің сыртқы жұмысына айнала алатын деформация энергиясы.
Динамикалық түрде күш түсіру. 1. Деформацияланатын дене бөлшектерінің жылдамдығы едеуір болып, яғни қозғалыстағы массаның кинетикалық энергиясы сыртқы күштер жұмысының айтарлықтай бөлігін құрайтындай жағдай туғызатын күш түсіру түрі. 2. Пластикалық деформациялар толық пайда бола алмайтындай күш түсіру түрі. Син. – Тез өзгеремді жүктеме.
Есептеу сүлбесі. Қарастырылатын нақты объектінің есептеу мақсатына айтарлықтай әсері жоқ ерекшеліктері алып тасталған түрі (Модель дегенді де қараңыз).
Жазық қималар болжамы. Сырықтың көлденең қимасы күш түсірілгенге дейін жазық және бойлық өске перпендикуляр болса, күш түсірілгеннен кейін де жазық және бойлық еске перпендикуляр күйінде қалады деген тұжырымға негізделген болжам. Қараңыз. – Бернулли болжамы.
Жазық фигураның бас инерция моменті. Жазық фигураның бас өстеріне қатысты инерция моменттері.
Жазық фигураның орталық бас өстері. Қиманың ауырлық орталығынан өтетін бас өстері.
Жанама кернеу. Берілген қимадағы толық кернеу векторының қима жазықтығына проекциясы.
Жаншылу. Шекті өлшемді беттескен беттердегі тік кернеудің әсерінен бұйым материалының беткі қабатының пластикалық деформация алуы.
Жұмсару шегі. Үлгідегі деформацияның кернеуге тәуелсіз едеуір өсетін кезіне сәйкес кернеудің мәні.
Жылжу жолақтары (Людерс-Чернов сызықтары). Беті жылтырата тегістелген үлгіні жалпы жұмсару аймағында созуға сынау кезінде оның бетінде бойлық оске 45 градус көлбеу бағытта пайда градус көлбеу бағытта пайда болатын сызықтар.
Изотроптық. Денеден бөліп алынған үлгінің қасиеттерінің кеңістіктегі бағыттардан тәуелсіздігі. Керісінше дененің материалы анизотропты деп аталады.
Иілу. Сырықтың көлденең қимасында июші момент туындататын күш түсіру түрі; иілу тік (жазық) және қиғаш болып бөлінеді; сонымен қатар бойлық және бойлық-көлденең иілу түрлері кездеседі.
Ішкі күштер. Сыртқы күштер әсерінен туындайтын жүйенің элементтерінің немесе дененің бөліктерінің өз-ара әсер күштері. Олар қарастырырылатын көлемдегі немесе нүкте маңындағы сыртқы күштер өсерін теңгереді.
Қабық. Бір өлшемі (қалындығы) басқа өлшемдерінен әлдеқайда кіші дене.
Қажуға беріктік. Құрылма элементінің, материалының айнымалы кернеу әсеріне төтеп беру қабілеті; айнымалы күштержүйесі әсеріне беріктік.
Кастилиано теоремасы. Серпімді жүйенің толық потенциялық энергиясынан күшке қатысты алынған дербес туынды сол күш түсірілген нүктенің күш бағытындағы орын ауыстыруына тең болады.
Қатаңдық. Қатты дененің сыртқы әсерлерді өзінің бастапқы геометриялық формасы мен өлшөемдерін айтарлықтай өзгертпей төтеп беру қабілеті.
Кернеулер эллипсоиды. Нүктедегі толық кернеу векторының ұшының геометриялық орны.
Кернеулі күйдің бас алаңдары. Кернеулі күйдің бас өстеріне сәйкес өзара перпендикуляр жазықтықтар.
Кесілу. Жанама кернеудің әсерінен бұйым материалының бір бөлігінің екінші бөлігіне қарағанда жазықтық бойымен ығысуының нәтижесінде сынуы.
Қима өзегі. Көлденең қиманың барлық ңүктелерінде бір таңбалы кернеу туындататын орталықтан тыс түсірілген бойлық күштердің түсу нүктелерінің жиынтығы.
Қималар тәсілі. Жүйедегі (денедегі) ішкі күштерді табу төсілі. Ол үшін жүйені қажет жерден ойша кесіп, бір бөлігін алып тастаса, оның қалған бөліктің тепе-теңдігін қамтамасыз өтетін әсері ішкі күшті береді.
Кернеу. Сыртқы күштер әсерінен туатын денедегі ішкі күштердің таралуын сипаттайтын шама; аудан бірлігіне келетін ішкі күштер үлесі.
Күштер әсерлерінің тәуелсіздігі қағидасы. Бірнеше сыртқы әсердің (күштер, температура, қысым және т.б.) нәтижесі сол әсерлердің әрқайсысының нәтижелерінің қосымдысына теңдігі және оларды түсіру тәртібіне тәуелсіздігі болжамына негізделген қағида. Син. – Қондыра қосу қағидасы.
Күшті статикалық түрде түсіру. Күштің өзгеру жылдамдағы дене бөліктерінің кинетикалық энергиясына айтарлықтай әсер етпейтіндей күш түсіру түрі.
Мор интегралы. Сызықты серпімді жүйелердегі орын ауыстыруды табу үшін Мор тәсілін қолданғанда пайдаланылатын интегралдар.
Нүктедегі кернеулі күй. Нүктеден өтетін барлық жазықтардағы кернеулердің жиынтығы; басы қарастырылатын нүктеде орналасқан тікбұрышты координаттар жүйесіндігі кернеулі күй құраушылары арқылы толық анықталады. Син. - Кернеулер тензоры.
Орнықтылық. Жүйенің сыртқы әсерлерге төтеп бере отырып өзінің бастапқы қалпын сақтау қабілеті.
Орталықтан тыс созылу (сығылу). Тең әсерлісі сырықтың көлденең қимасының ауырлық орталығынан тыс жерден өтетін бойлық бағытпен түсірілген күштер жүйесінен туындайтын деформация; мұны созылу (сығылу) және бір немесе екі бас өске қатысты иілудің біріккен әсері деп қарастыру ыңғайлы.
Пластикалық материалдар. Стандартталған үлгілері қалыпты температурада статикалық түрде үзілуге дейін созылуға сынағанда салыстырмалы ұзаруы мен салыстырмалы жіңішкеруі (10...60) % - тен кем болмайтын материалдар. Кей жағдайларда пластикалық материалдан жасалған бөлшектердің де морт сынуы мүмкін.
Полюстік инерция моменті. Дөңгелек немесе сақина тәрізді қималы сырықтардағы бұралу кезіндегі кернеулер мен деформацияларды табу үшін қолданылатын геометриялық сипаттама.
Полюстік қарсыласу моменті. Дөңгелек немесе сақина тәрізді қималы сырықтардың бұралу кезінде ең үлкен жанама кернеулерді анықтауцға пайдаланылатын шама; өлшем бірлігі -ұзындық өлшемінің үшінші дәрежесі.
Пропорционалдық шегі. Материалдың қасиеттерінің Гук заңына бағынатын аралығындағы ең үлкен кернеу.
Сен-Венан қағидасы. Жүйенің (дененің) күш түсірілген нүктесінен жеткілікті дәрежеде алыс жатқан нүктелердегі кернеулер мен деформациялар күштің нақты түсірілу әдісіне тәуелсіздігі жайындағы ереже. Бұл қағидаға сүйеніп түсірілген күш жүйесін оған барабар қарапайым жүйемен алмастыруға болады.
Серпімділік. Дененің өлшемдері мен формасын сыртқы күш әсері тоқтағаннан кейін қайтадан қалпына келтіре алу қабілеті.
Бойлық өс арқылы өтетін жазықтықтарда (өс жазықтықтарында) жатқан көлденең күштер мен моменттердің (жұп күштердің) әсерінен сырықта пайда болған деформацияны иілу деп атайды. Иіліп деформацияланған сырықтар арқалық деп аталады. Арқалықтың бойлық өсі мен көлденең қималарының баст инерция өстері арқылы екі баст жазықтык (V, Н) жүргізуге болады (1, а-сурет). Июші күштер бас жазықтықтардың бірінде жатса, онда иілу көлденең жазық иілу деп аталады. Көлденең жазық иілу кезінде арқалықтың майысқан бойлық өсі күш жазықтығында жатады. Сыртқы күштер бас жазықтықтардан басқа кез келген өс жазықтықтарында жатса, онда иілу қиғаш иілу деп аталады. Арқалық қиғаш иілгенде, оның майысқан бойлық өсі мен әсер етуші күштер әр түрлі жазықтықтарда жатады. Жазық иілген арқалықтың көлденең қималарында ішкі күштер — көлденең күш пен июші момент пайда болады.
Егер иілген арқалықтың көлденең қималарында июші моменттен басқа ішкі күштер жоқ болса, яғни көлденең күш нөлге тең болса, ондай иілу таза иілу деп аталады. Таза иілу кезінде арқалық 1-сурет шеңбер доғасы бойымен майысады.

1-сурет
Элементтері иіле деформацияланып, өзара қатаң немесе топса арқылы жалғасқан сырықтар жүйесі жақтау деп аталады. Жақтау элементтерінің көлденең қималарында көлденең күш, ию момент, сондай-ақ бойлық күш те пайда болуы мүмкін. Арқалықтар мен жақтаулар есептелгенде, олар есептеу сүлбелерімен алмастырылады. Есептеу сүлбелері бойлық өстер мен әсер етуші сырткы күштерден құралады (1, б-сурет).
К
өлденең күштер мен июші
моменттер
Қос тұғырлы иілген арқалықтың көлденен қималарындағы ішкі күштерді анықтайық (1-cypeт). Кез келген m-m қимасындағы ішкі күштерді табу үшін қималар тәсілі бойынша, сол қима арқылы арқалықты екіге бөліп, бір бөлігін алып тастаймыз. Алып тасталынған бөліктің қалған бөлікке әсерін көлденең күш пен июші моментпен алмастырамыз (1,б-сурет). Қалған бөлік сыртқы күштер мен ішкі күштердің әсерінен тепе-теңдік күйде болуы тиіс.
Статиканың бірінші теңдеуі

![]()
осыдан
![]()
![]()
яғни кез келген m-m қимасындағы көлденең күш Q(z) сол қиманың бір жағында әсер етуші сыртқы күштердің y осіне түсірілген проекцияларының алгебралық қосындысына тең.
Статиканың екінші теңдеуі
![]()
осыдан
![]()
яғни кез келген m-m қимасыңдағы ию моменті M(z) сол қиманың бір жағында жатқан сыртқы күштердің С нүктесіне қарағандағы моменттерінің алгебралық қосындысына тең (С нүктесі m-m қимасының ауырлық орталығы).
Бір қалыпты таралған күштерді y өсіне проекциялау үшін немесе С нүктесіне қарағаңдағы моментін анықтау үшін, 1-суретте оларды биіктігі q-ға, ұзындығы z-ке тең, тік төртбұрыштың ауырлық центрі арқылы өтетін қорытынды Rq = qz күшімен алмастырылған.
К өлденең күш пен июші моменттің таңбалары туралы
келесі ережелер
қабылданады.
Көлденең
m-m қимасының сол жағында әсер етіп тұрған сыртқы күштердің
қорытынды күші
(R)
төменнен жоғары
қарай,
ал оң
жақтағы сыртқы
күштердің қорытынды күші (R) жоғарыдан төмен қарай бағытталған болса, ол қимадагы жанама күш Q(z) оң таңбалы болып саналады. Кері жағдайда жанама күш теріс таңбалы (2, б-сурет).
өлденең күш пен июші моменттің таңбалары туралы
келесі ережелер
қабылданады.
Көлденең
m-m қимасының сол жағында әсер етіп тұрған сыртқы күштердің
қорытынды күші
(R)
төменнен жоғары
қарай,
ал оң
жақтағы сыртқы
күштердің қорытынды күші (R) жоғарыдан төмен қарай бағытталған болса, ол қимадагы жанама күш Q(z) оң таңбалы болып саналады. Кері жағдайда жанама күш теріс таңбалы (2, б-сурет).
К
өлденең m-m қимасының сол
жағындағы әсер етуші сыртқы күштердің осы қиманың ауырлық
орталығына қарағандағы қорытынды моменті (М) сағат тілінің бағытымен
бағыттас, ал оң жағындағы күштердің корытынды моменті сағат тілінің
бағытына қарама-қарсы бағытта болса, ол қимадағы июші момент оң
таңбалы деп саналады (3,
а-сурет). Кері
жағдайда июші момент М(z) теріс таңбалы (3, б-сурет) болады.
Таралған күштің қарқындылығы, көолденең күш, июші момент араларындағы дифференциалдық байланыс
Б
іркелкі таралған күштің
қарқындылығы, жанама күш, июші момент араларындағы дифференциалдық
байланыстарды анықтау үшін 1-суреттегі арқалықты қарастырайық. Сол
жақтағы A тірегінен z-ке тең
қашықтықта жатқан көлденең қимада пайда болатын
жанама күш
![]() , (1)
, (1)
ал z + dz қашықтығында жатқан көлденең қимадағы жанама күш
![]() (2)
(2)
Соңғы (2) теңдеу мен (1) теңдеуінің айырмасынан
![]() немесе
немесе ![]() (3)
(3)
екенін көреміз.
Демек, кез келген қимадағы жанама күштің өрнегінен z бойынша алынған бірінші туынды, сол аралықтағы әсер етуші бір қалыпты таралған күштің қарқындылығына тең.
Абсциссасы z-ке тең көлденең қимадағы июші момент
![]() (4)
(4)
ал абсциссасы z + dz-ке тең көлденең қимадағы ию моментінің өрнегі
![]() (5)
(5)
Соңғы (5) теңдігінен (4) теңдігін алып тастап
![]() (6)
(6)
екенін көреміз.
Демек, кез келген көлденең қимадағы июші моменттің өрнегінен z бойынша алынған бірінші туынды, осы қимадағы жанама күшке тең. Олай болса
![]() (7)
(7)
Көлденең қимадағы июші моменттің өрнегінен z бойынша алынған екінші туынды осы аралықта єсер етуші бір қалыпты таралған күштің қарқындылығына тең.

Тік кернеуді анықтау. Тік кенреу бойынша беріктік пен қатандыққа есептеу
Июші момент — арқалыктың көлденең қимасындағы ішкі тік кернеулердің қорытынды моменті. Тік кернеулердің шамасы мен қима бетіндегі таралу заңдылығын анықтау үшін таза иілген арқалықты қарастырайық (1, а-сурет).
Есептің статикалық жағы. Таза иілген арқалықтың кез келген көлденең қимасында июші моменттен басқа ішкі күштер нөлге тең. Июші момент ішкі күштердің қорытынды моменті болғандықтан, көлденең кимада (m — m) жатқан кез келген нүктеде тек қана тік кернеу әсер етеді. Қима жазықтығынан бөлініп алынған шексіз кіші аудандағы (dА) кернеулердің қорытынды күші мен y және x өсіне қарағандағы моменттерін анықтайық (1, б-сурет)
![]() , осыдан
, осыдан
![]()
Арқалық таза иіліп деформацияланғанда
N=0, Mx =M, My=0,
демек,
![]() (1)
(1)
Берілген арқалықтың бетіне, бойлық өске параллель жєне
көлденең
сызықтар ж ү ргіземіз (1, а-сурет). Деформацияға
дейінгі m –m, n - n т
түзу сызықтары
деформациядан кейін өзара ![]() бұрышына бұрылып, түзу күйінде қалады. Демек,
деформацияға дейінгі жазық қималар деформациядан кейін де
арқалықтың бойлық талшықтарына перпендикуляр жазық күйінде
қалады.
бұрышына бұрылып, түзу күйінде қалады. Демек,
деформацияға дейінгі жазық қималар деформациядан кейін де
арқалықтың бойлық талшықтарына перпендикуляр жазық күйінде
қалады.
Деформацияға дейінгі арқалықтың өзара тең ab, dc, ef талшықтары деформациядан кейін шеңбер доғасы бойынша иіліп, ef қысқарады (сығылады) да, ab ұзарады (созылады), ал dc талшығының ұзындығы өзгермейді (1,б-сурет). Арқалықтың ұзындығы өзгеріссіз қалатын талшықтарының геометриялық орны бейтарап жазықтық деп, ал бейтарап жазықтықтың кез келген көлденең қимамен қиылысу сызығы, қиманаң бейтарап сызығы деп аталады (2 в-сурет)
Деформациядан кейінгі бейтарап
жазықтықта жатқан dc
талшығы радиусы![]() -ға тең, ал ab талшығы радиусы
ρ +y-ке тең доғаларға
айналады.
-ға тең, ал ab талшығы радиусы
ρ +y-ке тең доғаларға
айналады.
аb талшығының салыстырмалы созылуы
![]() ,
,
мұндағы аb1 =(![]() )
)![]() , ал аb=dz
болғандықтан
, ал аb=dz
болғандықтан
![]() (2)
(2)
Б ейтарап жазықтықта жатқан
dc = dz талшығы
деформациядан кейін шеңбердін доғасы бойынша иіліп, ұ зындығы
өзгермейді
ейтарап жазықтықта жатқан
dc = dz талшығы
деформациядан кейін шеңбердін доғасы бойынша иіліп, ұ зындығы
өзгермейді
![]() (3)
(3)
Олай болса, (2) теңдігін (3) тендігіне енгізіп
![]() (4)
(4)
екенін көреміз.
Яғни талшықтың салыстырмалы бойлық деформациясы оның бейтарап өске дейінгі ара қашықтығына тура пропорционал.
Еңді есептің физикалық жағын қарастырайық. Көлденең қимада жанама кернеу жоқ
болғандықтан, жанама кернеулердің жұ птық заңы бойынша, ол бойлық
қималарда да жоқ. Сондықтан, бойлық талшықтар өзара әсерлеспейді деп
қарастыруға болады. Олай болса, аb талшығы сызықтық
кернеулі күйде. Сызықтық кернеулі күй үшін Гук заңы
![]() = E
= E![]() .
.
Енді синтез жасайық. Гук заңына (4) тендігін енгізіп
![]() , (5)
, (5)
кернеу қарастырылған нүкте мен бейтарап өстің ара қашықтығына (у) тура пропорционал өзгеретінін көреміз. Бейтарап өсте жатқан нүктедегі кернеулер нөлге тең, ал қиманың ең жоғарғы және ең төменгі нүктелерінде ең үлкен кернеулер әсер етеді (2, в-сурет).
Статикалық (1) тендеуіне (5) теңдігін енгізіп'
![]()
![]() ,
,
ал теңдіктегі интеграл
![]() -қиманың
x -өcіне
қатысты өстік
инерция моменті екенін ескерсек,
-қиманың
x -өcіне
қатысты өстік
инерция моменті екенін ескерсек,
![]() (6)
(6)
Мұндағы
![]() -арқалықтың қатаңдығы,
-арқалықтың қатаңдығы, ![]() — арқалықтың
қисықтығы.
— арқалықтың
қисықтығы.
Гук заңынан (5)
![]() (7)
(7)
яғни
![]() (8)
(8)
Соңғы формула таза иілген арқалықтың көлденең қимасыңда жатқан кез келген нүктедегі тік кернеуді анықтауға мүмкіндік береді.
Еңді (8) формуласын (1) тендеулеріне кезекпен енгізейік:
![]() болғандықтан
болғандықтан ![]()
Бұл интеграл – қиманың бейтарап өске қарағандағы статикалық моменті. Статикалық моменті нөлге тең болғандықтан, бейтарап өс қиманың ауырлық орталығы арқылы өтіп, x -сінің үстінде жатады.
2. ![]() болғандықтан,
болғандықтан,
![]()
Бұл иyтеграл — қиманың x, ү өстеріне қатысты өрістік инерция моменті. Өрістік инерция моменті нөлге тең болғандықтан x, ү өстері баст, ал сыртқы момент бас ү өсі арқылы өтетін жазыктықта әсер етуі тиіс. Демек, жазық иілудегі ү өсімен сәйкес келетін сырты күштердің әсер ету сызығы мен бейтарап сызық өзара перпендикуляр.
Теориялық және тәжірибе жүзіндегі зерттеулердің нәтижелеріне қарағанда, (8) формуланы көлденең жазық, иілген арқалықтар үшін де қолдануға болады.
Иілген арқалықтң беріктігін тексеру үшін М(z) эпюрі салынып, қауіпті қимасы анықталады.
Қауіпті деп, июші моменттердің ең үлкені (абсолюттік шамасы) (Mmax ) әсер етіп тұрған қиманы айтады. Қауіпті қимадағы қауіпті кернеу
![]()
мұндағы ymax - бейтарап өстен ең шеткі нүктеге дейінгі кашықтық; Jmax /ymax =Wx - геометриялық сипаттама, өстік қарсылық моменті деп аталады.
Созылу мен сығылуға бірдей қарсыласатын пластикалық материалдары үшін тік кернеу бойынша беріктік шарты
![]() (9)
(9)
Созылу мен сығылуға қарсыласу кабілеті әр түрлі морт материалдардың беріктігі ең үлкен созушы және сығушы тік кернеулер бойынша есептеледі.
Созушы тік кернеу бойынша беріктік шарты
![]() (10)
(10)
Сығушы тік кернеу бойышпа беріктік шарты
![]() (11)
(11)
мұндағы
![]() - созылған жөне сығылған талшықтар үшін
анықталатын қарсылық моменті.
- созылған жөне сығылған талшықтар үшін
анықталатын қарсылық моменті.
а) Дөңгелек пішінді қима үшін
![]()
б) Тіктөртбұ рышты қима үшін
![]()
Стандартталған қималар үшін Wx -тің мәндері анықтамалықтарда арнайы сортамент кестелерінде беріледі.
1.2. Қиғаш иілу
Басты жазықтықтардан басқа,
бойлық өс арқылы өтетін, кез келген жазықтықтарда жатқан сыртқы
күштердің әсерінен конструкция элементі қиғаш иіледі. Қиғаш иілген
арқалықты беріктікке есептеу тәртібі келесі мысалда көрсетілген.
Бір ұшы қатаң бекітілген арқалықтың екінші ұшына Р күші әсер етсін.
Күштің әсер ету сызығы x
өсімен ![]() бұрышын жасап өтетіндіктен арқалық қиғаш
иіледі (1, а-сурет). Сыртқы күшті басты өстерге проекциялап
құраушыларын табайық
бұрышын жасап өтетіндіктен арқалық қиғаш
иіледі (1, а-сурет). Сыртқы күшті басты өстерге проекциялап
құраушыларын табайық
![]()
Құраушы Рх, Ру күштерініњ әсерінен берілген арќалық өзара перпендикуляр басты жазықтықтарда жазық иіліп, көлденең қималарыңда июші моменттер пайда болады

мұндағы M = Pz.
Тұғыр қимасында жатқан Е нүктесіндегі кернеуді табу үшін күш әрекеттерінің тәуелсіздік приціпін пайдаланамыз (1, а-сурет). Вертикаль жазықтықтағы Мх -тің әсерінен Е нүктесінде пайда болған кернеу
![]()
Горизонталь жазықтықтағы Му -тің әсерінен пайда болған кернеу
![]()
Нүктедегі толық кернеу
![]() (1)
(1)
немесе
![]()

м±ндағы хе, уе— Е нүктесінің координаталары.
Алынған (1) формуланы пайдаланып кез келген пішінді қиманың нүктелеріндегі кернеулерді анықтауға болады. Бұл формуладағы, бірінші квадранттың нүктелерінде созушы кернеу тудыратын июші моменттер оң таңбалы деп қарастырылып, ал нүктелерінің координаттары өз таңбаларымен жазылады. Нүктелерінде тек созушы кернеулер пайда болатын квадрант бірінші квадрант ретінде қабылданады.
Қимадағы кернеулер х, у координаттына тәуелді болғандықтан, қауіпті қимадағы ең үлкен созушы кернеу әсер етіп тұрған бұрыштағы А мен ең үлкен сығушы кернеу әсер етіп тұрған бұрыштағы С нүктелері қауіпті болып саналады.
Арқалықтың беріктігін А нүктесі үшін беріктік шартын құрып тексереміз
![]()
мұндағы х а = хmax , ya =ymax болғандықтан
![]()
Бұрыштардағы А, С нүктелеріндегі кернеулердің абсолют шамалары бірдей.
Арқалық морт материалдан жасалса, оның беріктігі A нүктесімен қатар С нүктесі бойынша да тексеріледі.
Е нді
бұрышы жоқ 2-суреттегі қиманы қарастырайық. Қиманың қауіпті нүктелерін табу үшін алдымен бейтарап
сызықтың орны анықталады. Бейтарап сызық, тік кернеуі нөлге тек
нүктелердің геометриялық орны. Олай болса, кернеудің шамасын (1)
нөлге теңестіріп, координаттар басы арқылы өтетін, бейтарап
сызықтың теңдеуін аламыз
нді
бұрышы жоқ 2-суреттегі қиманы қарастырайық. Қиманың қауіпті нүктелерін табу үшін алдымен бейтарап
сызықтың орны анықталады. Бейтарап сызық, тік кернеуі нөлге тек
нүктелердің геометриялық орны. Олай болса, кернеудің шамасын (1)
нөлге теңестіріп, координаттар басы арқылы өтетін, бейтарап
сызықтың теңдеуін аламыз
![]()
мұндағы х0 ,у0 - бейтарап өс нүктелерінің айнымалы координаттары.
Бұл теңдеуді
![]() шамасына көбейтіп келесі түрге
келтірейік:
шамасына көбейтіп келесі түрге
келтірейік:
![]() (2)
(2)
Енді ![]() екенін ескеріп, бейтарап
сызықтың орнын анықтайтын формуланы
аламыз
екенін ескеріп, бейтарап
сызықтың орнын анықтайтын формуланы
аламыз
![]() .
(3)
.
(3)
Бейтарап сызықтың x өсіне қарағандағы бұрышы теріс таңбалы болғандықтан, ол сағат тілі бағыты бойымен салынып П, IV квадранттар арқылы өтеді (2-сурет).
Алынға3) теңдеуінде
![]() болғандықтан,
болғандықтан, ![]() . Демек, сыртқы күштің әсер
ету сызығы (ә. с) мен бейтарап сызық (б. с.) өзара перпендикуляр
емес (2-сурет).
. Демек, сыртқы күштің әсер
ету сызығы (ә. с) мен бейтарап сызық (б. с.) өзара перпендикуляр
емес (2-сурет).
Қиманың контурына, бейтарап сызыққа параллель жанамалар жүргізіп қауіпті А, В нүктелерін табамыз (2-сурет). Суреттегі кернеудің эпюрі ежелгі тәртіппен салынған.
Қауіпті нүктелер үшін беріктік шарты келесі түрде жазылады
![]() (4)
(4)
![]() (5)
(5)
Конструкция элементтерінің көлденең қималары дөңгелек, квадрат пішінді болса, Jx =Jy .
![]() .
.
Яғни, сыртқы күштің әсер ету сызығы мен бейтарап сызық өзара перпендикуляр. Әсер ету сызығы координаттар жүйесінің бас нүктесі арқылы өтетін кез келген күштің әсерінен мұндай аркалықтар жазық иіледі.
Сыртқы күш пен қауіпсіз кернеу белгілі болса, қиғаш иілген арқалықтың қима өлшемдерін беріктік шартынан келесі тәртіппен анықтайды қиманың өлшемдері алдын ала белгілі деп қарастырылып қандайда бір мәндері (4) теңсіздігіне енгізіледі.
Есептеліп анықталған теңсіздіктің сол жағы оң жағына қарағанда айтарлықтай кіші болса, қима өлшемдерін үлкейтіп, ал айтарлықтай үлкен болса кішірейтіп аркалықтың беріктігі қайта тексеріледі. Тексеру теңсіздіктің сол жағы мен оң жағының арасындағы айырым 4—5%-ке жуықтағанша қайталанады.
Қиғаш иілген арқалықтың деформациясы, иілу өсінің дифференциалдық теңдеуін интегралдау немесе басқа әдістермен анықталады. Ол үшін күш әсерлерінің тәуелсіздік принципі пайдаланылып, қиғаш иілу бас жазықтықтардағы екі жазық иілудің қосындысы ретінде қарастырылады. Қиғаш иілген арқалықтың кез келген қимасындағы ойысу, бас жазықтықтардағы ойысулардың геометриялық қосындысына тең
![]() (6)
(6)
мұндағы yвер — вертикаль жазықтықтағы ойысу, угор— горизонталь жазықтықтағы ойысу. Қатаңдық шарты келесі түрде жазылады
![]()
мұндағы [у] — қауіпсіз ойысу.
Қиғаш иілген арқалықтың серпімді сызығы мен сыртқы күштің әсер ету сызығы әр түрлі өс жазықтықтарында жатады. Ойысу мен күш бағыттары өзара сәйкес келмейді.
Орталықтан тыс созылу (сығылу)
Орталықтан тыс созылу (сығылу) деп қиманың ауырлық орталығынан басқа кез келген нүкте арқылы берілетін, бойлық өске параллель күштің әсерінен сырықтың деформациялануын айтады (3-сурет).
Күш түскен нүкте (р) полюс деп аталады. Полюстің координаталарын хр , ур арқылы белгілейік. Полюстен координаттар жүйесінің басына дейінгі ара қашықтық эксцентриситет деп аталып, е арқылы белгіленеді. Орталықтан тыс созылған сырықтың кез келген қималарында Nz = Р, Мx = Руp , Мy = Рхp ішкі факторлары пайда болады (3-сурет).
Б
ерілген қиманың Е нүктесіндегі
кернеуді анықтайық. Күш әрекеттерінің тәуелсіздік принципі
бойынша Nz бойлық күшінің
әсерінен
![]() - июші моменттің әсерінен
- июші моменттің әсерінен
![]() - июші моменттің әсерінен
- июші моменттің әсерінен![]() тік кернеулері пайда
болады.
тік кернеулері пайда
болады.
Сонымен Е нүктесіндегі қорытынды кернеу
 (7)
(7)
Алынған (7) формуласымен қиманың кез келген нүктесіндегі кернеуді табуға болады. Кернеудің таңбасын дұрыс анықтау үшін полюс жаткан квадрант бірінші квадрант деп қарастырылып, ішкі факторлар мен нүктенің координаталары (7) формуласына өз таңбаларымен енгізіледі. Бірінші квадранттағы нүктелерде созушы кернеулер тудыратын июші моменттер оң таңбалы деп саналады.
Қауіпті кернеулер бұрыштағы A, C нүктелерінде пайда болады. Соңдықтан сырықтың беріктігі А нүктесі үшін жазылған беріктік шарты бойынша тексеріледі
![]()
немесе
![]() ,
,
мұндағы хa , ya - A нүктесінің координаталары.
Морт материалдардан жасалған брустар тек созушы емес ең үлкен сығушы кернеу бойынша да тексеріледі
![]()
Енді бұрыштық нүктелері жоқ 4-суретіндегі қиманы қарастырайық. Бұрыштық нүктелері жоқ қиманың қауіпті нүктелерін табу үшін алдымен бейтарап сызықтың орны анықталады. Бейтарап сызықтың бойында жатқан нүктелерде кернеу нөлге тең. Олай болса
 (8
а)
(8
а)
Мұндағы хб,
yб —
бейтарап сызық нүктелерінің айнымалы
координаталары. Есептің бастапқы шарты бойынша, ![]() болғандықтан
болғандықтан
 (8
б)
(8
б)
Енді хб, yб координаталарын кезекпен нөлге теңестіріп, X пен У осьтерінің бейтарап сызықпен қиылған кесінділерін табамыз
 (9)
(9)
Кесінділерді (таңбаларын ескеріп) X, Ү осьтеріне өлшеп салып, алынған m, n нүктелері арқылы бейтарап сызықты жүргіземіз (4-сурет). Суретте, бейтарап сызық (б.с.) арќылы белгіленген. Бейтарап сызық координата осьтерін бірінші квадрантқа қарсы үшінші квадрант арқылы қиып өтеді. Қиманың контур бейтарап сызыққа параллель, жанамалар жүргізіп қауіпті А, нүктелерін табамыз.
Қауіпті нүктелер үшін беріктік шарты келесі түрде жазылады
![]() (10)
(10)
![]() (11)
(11)
Мұндағы ха ,уа - А нүктесінің координаталары, хб, yб- -B нүктесінің координаталары.
Кернеудің (7) формуласы бойынша салынған эпюрі 4- суретте көрсетілген.
Қима өзегі. Алынған (9) формуласы бойынша, бейтарап сызық координаттар басы (қиманың ауырлық орталығы) арқылы өтпейді. Сыртқы күштің эксцентриситеті неғұрлым үлкен болса, бейтарап сызық координаттар басына соғұрлым жақын, неғұрлым кіші болса — соғұрлым алыс. Эксцентриситет нөлге тең болғанда бейтарап сызық пен координаттар басы ара қашықтығы шексіздікке ұмтылып, сырық Орталық созылу деформациясына ұшырайды.
Бейтарап сызықтың бұл қасиеті инженерлік практикада кеңінен қолданылады. Морт материалдардың көбісінің сығылуға қарағанда созылуға қарсыласу қабілеті төмен екені бізге белгілі. Бетон, тас, күйдірілгген қыш сияқты материалдардан жасалған азаматтық немесе өндірістік құрылыс элементтерінде, шамасы мардымсыз, созушы кернеулердің пайда болуы сыну қаупін туғызуы мүмкін. Соңдықтан мұндай құрылыс элементтері үшін қима ядросы тұрғызылады.
Қима өзегі деп, ауырлық центрін қоршаған, келесі қасиеті бар аймақты айтады: сыртқы күштің әсер ету нүктесі осы аймақта жатса, қиманың барлық нүктелерінде таңбалары бірдей кернеулер пайда болады.
ІІ. Кез келген күш әсерінен сырықтар жүйелеріндегі орын ауыстырулар
2.1. Кез келген күш түсірілген брустың поетнциялық энергиясы
Жоғарыда түзу сырықтың созылу, бұралу және иiлу кезінде орын ауыстыруы анықталған ды. Ендi сырыққа күш түсiрiлген кезде көлденен қимасында бip мезгiлде тiк және көлденен күштер, июшi және бұраушы моменттер пайда болуын қарастырайық. Сонымен бipгe сырық тек қана түзу болмай қисықтығы аз, сондай-ак жазык немесе кеңiстiк жүйелердi жасайтын түзу. бөліктерден тұрады деп есептеп қарастырылатын мәселелер ауқымын кеңейтемiз. Қарастырылатын есептердi шешу тек орын ауыстыру шамаларын ғана анықтаумен бipгe конструкция қатаңдығын бағалау үшiн де қажет.
К үш түcipiлгeн сырықтар жүйесінің потенциялық энергиясының жалпы
өрнегіне сүйенiп, энергетикалық қатынастар арқылы орын ауыстыруды
оңай табуға болады.
үш түcipiлгeн сырықтар жүйесінің потенциялық энергиясының жалпы
өрнегіне сүйенiп, энергетикалық қатынастар арқылы орын ауыстыруды
оңай табуға болады.
Потенциялық энергияньң анықталуы сырықта пайда болатын iшкi күш әсерлерін талдаудан туындайды. Бұл талдау, әдетте, қималар тәсілiмен жүргiзiледі де, июші және бұраушы моменттердің әпюрлерiн, ал қажет жағдайда бойлық және көлденең күш эпюрлерiн салумен анықталады.
Барлық жағдайда iшкi күш әсерлерiнiң эпюрлерi сырықтың өсіне салынады (1-сурет). Кеңістiктегі сырық үшiн өс сызығы, әдетте, аксонометрияда сызылады және июші моменттердің эпюрлерi иiлу жазықтықтарына сәйкес бейнеленедi (2-сурет). Бұраушы моменттердің эпюрi белгілi бip жазықтықпен байланыстырылмайды да, июші моменттердiң эпюрiнен ерекшеленіп бұранда сызықпен шабақталады.
Потенциялық энергияны анықтау үшін сырықтан ұзындығы dz-ке тең әлементар бөлікті бөліп алайық (3-сурет). Сырық түзу және бастапқы қисықтығы кіші түрде болуы мүмкін. Күш түcipiлгeн жалпы жағдайда әpбip көлденең қимада алты әсер (үш момент және үш күш) пайда болады. Бөлiп алынған бөлікке қатысты осы күш әсерлерін сыртқы күштер деп санап, олардьң элементтi деформациялау кезiнде iстеген жұмысын ықтаймыз.
Б ұл жұмыс сырықтың элементар бөлігiнде жинақталған потенциялық
энергияға тең болады. Сол жаққа
түсiрiлген барлық күш әсерлерiнiң жұмысы нөлге тең болуы үшін
элементтiң сол қимасын шартты түрде қозғалмайтын деп қарастырамыз
(3-сурет). Оң қиманьң күш түcipiлгeн нүктесi элементтiң
деформациясы салдарынан шамалы орын ауыстырып, iздеп отырған жұмыс
істелiнедi. Алты күш әсеріне жеке-жеке сәйкес келетiн орын ауыстыру
кезiнде қалған бес әсердің бipeyi де жұмыс істемейтіндей болуының
үлкен маңызы бар. Мысалы, Мδ моментi
әсерiнен z осіне сәйкес қиманың бұралу бұрышы пайда болады. Осы
бұрыштық орын ауыстыруда жұмыс тек Ms моментімен iстелiнедi.
у oci бойынша
сызықтық орын ауыстыру Qу күш әсерінен болады да, орын ауыстыру
кезінде тек осы күш жұмыс атқарады. Демек, элементтiң потенциялық
энергиясы алты күш әсерiнің әрқайсысының атқарған тәуелсiз
жұмыстарының қосындысы, яғни буралу,
иілу, созылу және ығысу энергияла-
ұл жұмыс сырықтың элементар бөлігiнде жинақталған потенциялық
энергияға тең болады. Сол жаққа
түсiрiлген барлық күш әсерлерiнiң жұмысы нөлге тең болуы үшін
элементтiң сол қимасын шартты түрде қозғалмайтын деп қарастырамыз
(3-сурет). Оң қиманьң күш түcipiлгeн нүктесi элементтiң
деформациясы салдарынан шамалы орын ауыстырып, iздеп отырған жұмыс
істелiнедi. Алты күш әсеріне жеке-жеке сәйкес келетiн орын ауыстыру
кезiнде қалған бес әсердің бipeyi де жұмыс істемейтіндей болуының
үлкен маңызы бар. Мысалы, Мδ моментi
әсерiнен z осіне сәйкес қиманың бұралу бұрышы пайда болады. Осы
бұрыштық орын ауыстыруда жұмыс тек Ms моментімен iстелiнедi.
у oci бойынша
сызықтық орын ауыстыру Qу күш әсерінен болады да, орын ауыстыру
кезінде тек осы күш жұмыс атқарады. Демек, элементтiң потенциялық
энергиясы алты күш әсерiнің әрқайсысының атқарған тәуелсiз
жұмыстарының қосындысы, яғни буралу,
иілу, созылу және ығысу энергияла-
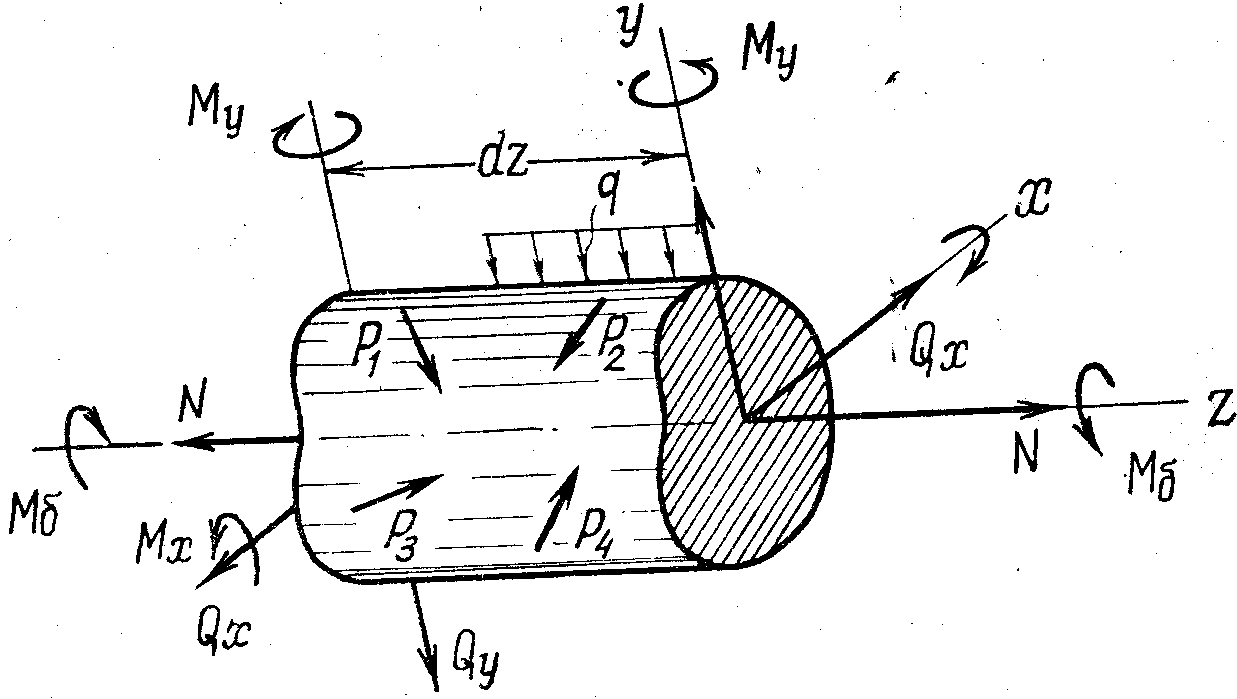
3 - сурет
рының қосындысы ретінде қарастыруға болады:
![]()
Алғашқы төрт қосылғыш өрнектерi бiзге белгілi:
 .
.
Тек ![]() және
және ![]() ығысу энергиясын табу
қажет.
ығысу энергиясын табу
қажет. ![]() шамасын анықтау үшін табан ауданы
шамасын анықтау үшін табан ауданы
![]() және ұзындығы
және ұзындығы ![]() болатын элементар призманы
қарастырамыз. Бұл көлемдегі энергия
болатын элементар призманы
қарастырамыз. Бұл көлемдегі энергия ![]() тең, мұндағы
тең, мұндағы
![]() -
ығысу кезiндегі меншiкті потенциялық энергия.
(6.15') (§ 3, VI тарау) өрнегіне сәйкес
-
ығысу кезiндегі меншiкті потенциялық энергия.
(6.15') (§ 3, VI тарау) өрнегіне сәйкес ![]() . Сонымен,
. Сонымен,
![]() .
.
![]() аудан бойынша интегралдасақ:
аудан бойынша интегралдасақ:
![]()
Бipaқ Журавский формуласы бойынша ![]() Демеқ,
Демеқ,
![]() , немесе
, немесе ![]() .
. ![]() (1)
(1)
деп белгілейік. Сонда
![]() , осыған ұқсас
, осыған ұқсас ![]() .
.
![]() және
және ![]() коэффициенттерi қиманың геометриялық түрiне
байланысты өлшемсiз шамалар. Мысалы, өлшемдерi
коэффициенттерi қиманың геометриялық түрiне
байланысты өлшемсiз шамалар. Мысалы, өлшемдерi
![]() және
және ![]() .
.
болатын тiк бұрыш үшін шабақталған ауданның
![]() статикалық моментi
статикалық моментi ![]() өсіне сәйкес
өсіне сәйкес  .
.
Одан
ары ![]() .
.
Түрлендiру (2) формуласы бойынша
![]() .
.
Тұтас дөңгелек қима үшін Жұка
қабырғалы дөңгелек профиль үшін ![]() және т.
с. с. Енді (1) өрнегі мынадай түрде болады:
және т.
с. с. Енді (1) өрнегі мынадай түрде болады:
 .
.
Брустьн потенциалық энергиясын алу үшiн бұл өрнектi брустың ұзындығы бойынша интегралдау керек:
 (3)
(3)
Егер конструкция күрделi болып, ол сырық тәрiздi бiрнеше әлементтерден құралса, онда интегралдаудан кейiн әр сырық шегінде құраушы элементтер санына сәйкес энергияларды қосу қажет болады.
(3) өрнектегі барлық қосылғыштар маңызды болмайды. Іс жүзінде көптеген жүйелерде құраушы элементтер иiлy не бұралуға жұмыс істейді, сондықтан (3) өрнегiндегі соңғы үш қосылғыш алғашқы үшеуіне қарағанда айтарлықтай аз болады. Басқаша айтқанда, созылу және ығысу энергиясы, әдетте иілу және бұралу энергиясынан айтарлықтай аз болады.
Бipaқ, сонымен бipгe қосылғыштардың шамалары бiрдей болуы да ықтимал. Мысалы, көрсетiлген иіні шағын орталықтан тыс созылған сырық үшiн созылу және иілу энергиясы бiр шамада болады.
Кастилиано теоремасы
Сырықтың орын ауыстыруын анықтау үшiн Кастилиано теоремасын қолдануға болады: жүйенің потенциялық энергиясының күш бойынша дербес туындысы күш түсiрiлген нүктенің оның бағыты бойынша орын ауыстыруына тең. Бepiлгeн бағытта орын ауыстыруды сол бағыттағы толық орын ауыстырудың проекциясы болып табылады. Кез келген күш жүйесi түсiрілген және орын ауыстыру болмайтын тұтастай қатаң бекiтiлген серпімді дененi қарастырайық. Сыртқы күштер жұмысының нәтижесінде дене көлемінде деформацияның жинақталған потенциялық энергиясы U-ға тең болсын.
Мысалы, Рn күш 3yt өсiмше берейiк. Сонда U потенциялық энергия мына шамаға өзгереді
![]()
Ендi күш түcipy тәpтiбiн
өзгертемiз. Серпiмдi денеге
алдымен dPn күштi түсiремiз. Күштiң түсу нүктесiнде шексіз аз орын ауыстыру пайда
болады, оның dP проекциясы күш бағытында да dδ-ға тең. ![]() күшінiң жұмысы
күшінiң жұмысы
![]() -ға
тең болады.
-ға
тең болады.
Сыртқы күштер жүйесін тұтастай
түсiремiз. ![]() күші
болмаса, жүйенiң потенциялық энергиясы кайтадан U-ға тең болар
едi. Бірақ
бұл энергия сыртқы күштер жүйесi әсерінен
күші
болмаса, жүйенiң потенциялық энергиясы кайтадан U-ға тең болар
едi. Бірақ
бұл энергия сыртқы күштер жүйесi әсерінен
![]() орын ауыстыру кезiнде
орын ауыстыру кезiнде ![]() күш тудыратын
күш тудыратын
![]() қосымша жұмыстың шамасына өзгередi.
қосымша жұмыстың шамасына өзгередi.
![]() шамасы қайтадан Рn күші бағытында
толық орын ауыстыру проекциясын бейнелейдi. dPn
шамасы қайтадан Рn күші бағытында
толық орын ауыстыру проекциясын бейнелейдi. dPn![]() көбейтiндiсiнiң алдына
көбейтiндiсiнiң алдына ![]() көбейткіш
3 қойылмайды, өйткенi
көбейткіш
3 қойылмайды, өйткенi ![]() проекциясында
проекциясында
![]() өзгepicciз қалады.
өзгepicciз қалады.
Күш түсiрудiң керi тәртiбiнде потенциялық энергияның өрнегі келесi түрде болады:
![]() (5)
(5)
Бұл өрнектi (4) өрнегiне теңестiрiп, ![]() көбейтіндiсін аздығына байланысты ескермей алып
тастағанда.
көбейтіндiсін аздығына байланысты ескермей алып
тастағанда.
![]() (6)
(6)
болады. Сонымен, потенциялық энергияны сыртқы күштердiң бipeyiне қатысты дербес туындысы сол күштің түсу нүктесiнiң күш бағыты бойынша орын ауыстыруына тең болады.
(6) өрнегінде
![]() күшiн жалпыланған күш, яғни күш факторы ретінде
түсiндiруге болады. Сонда
күшiн жалпыланған күш, яғни күш факторы ретінде
түсiндiруге болады. Сонда ![]() -ді жалпыланған орын ауыстыру, яғни
-ді жалпыланған орын ауыстыру, яғни ![]() жалпыланған күш жұмыс iстейтiн
геометриялық параметр ретінде қарастыру керек. Егер
жалпыланған күш жұмыс iстейтiн
геометриялық параметр ретінде қарастыру керек. Егер
![]() деп сыртқы моментті
деп сыртқы моментті ![]() түсінсек, онда
түсінсек, онда
![]() момент түcipiлгeн нүктенiң момент бағытындағы
бұрыштық орын ауыстыруын бейнелейдi. Егер денеге гидростатикалық
қысым күштерi түcipiлce, онда потенциалық энергияны қысым бойынша
дифференциалдап дене көлемінің өзгерісін
анықтаймыз.
момент түcipiлгeн нүктенiң момент бағытындағы
бұрыштық орын ауыстыруын бейнелейдi. Егер денеге гидростатикалық
қысым күштерi түcipiлce, онда потенциалық энергияны қысым бойынша
дифференциалдап дене көлемінің өзгерісін
анықтаймыз.
Кастилиано теоремасын дәлелдеу
кезінде дене түріне, сыртқы күштер жүйесіне ешқандай шектеулер
қойылған жоқ. Оған қоса, материал Гук заңына
бағына ма, жоқ па, ол да қарастырылмады. Дегенмен, бұл шектеулер
бар. Егер күш пен орын ауыстыру арасында сызықты
тәуелдiлiк болса, онда сыртқы күштер
жүйесінің атқарған жұмысы күштер жүйесi ![]() күшіне дейін не одан кейін
түсiрілгеніне байланысты әр
түрлi
болады.
Басқаша айтсақ (4) және (5) өрнектерінің қосылғыштары
бiрдей болады. Бұл жағдайда
Кастилиано теоремасы орындалмайды. Практикада кездесетін көптеген
есептерде күш пен орын ауыстырудың қатынасы сызықты болады, ал
мұндай есептердi шешуге Кастилиано теоремасын
пайдалануға болады. Бастапқы өлшемдерi өзгермеу және күш әсерінің
тәуелсiздік
принциптерiн қолдануға болмайтын
жүйелерде орын ауыстыруды анықтау кeзiндe Кастилиано теоремасын
жоғарыдарыдай түрде пайдалануға болмайды.
күшіне дейін не одан кейін
түсiрілгеніне байланысты әр
түрлi
болады.
Басқаша айтсақ (4) және (5) өрнектерінің қосылғыштары
бiрдей болады. Бұл жағдайда
Кастилиано теоремасы орындалмайды. Практикада кездесетін көптеген
есептерде күш пен орын ауыстырудың қатынасы сызықты болады, ал
мұндай есептердi шешуге Кастилиано теоремасын
пайдалануға болады. Бастапқы өлшемдерi өзгермеу және күш әсерінің
тәуелсiздік
принциптерiн қолдануға болмайтын
жүйелерде орын ауыстыруды анықтау кeзiндe Кастилиано теоремасын
жоғарыдарыдай түрде пайдалануға болмайды.
Мор интегралы
Кастилиано теоремасының көмегімен тек сыртқы күштер түcipiлгeн нүктесінің және тек күш бағытында ғана орын ауыстыруын анықтайтындығымызға қарастырылған мысалдардан көзiмiз жеттi. Ал іс жүзінде жүйенiң кез келген нүктелерiнiң әр түрлi бағытта орын ауыстыруын анықтау керек болады.
 Егер сыртқы күштер түcipiлмеген нүктеде орын ауыстыруды анықтау
керек болса, онда нүктеге керек бағытта Ж сыртқы күшті түсіремiз
(4-сурет). Одан ары жүйенің потенциялық энергиясының өрнегін
Ж күшін ескере
отырып жазамыз. Энергияның Ж бойынша дифференциалдап,
нүктенiң Ж күші түcipiлгeн бағыты бойынша орын ауыстыруын табамыз.
Содан кейiн Ж күшін нөлге теңеймiз, сонда табылған шама iзделген орын
ауыстыру болып табылады.
Егер сыртқы күштер түcipiлмеген нүктеде орын ауыстыруды анықтау
керек болса, онда нүктеге керек бағытта Ж сыртқы күшті түсіремiз
(4-сурет). Одан ары жүйенің потенциялық энергиясының өрнегін
Ж күшін ескере
отырып жазамыз. Энергияның Ж бойынша дифференциалдап,
нүктенiң Ж күші түcipiлгeн бағыты бойынша орын ауыстыруын табамыз.
Содан кейiн Ж күшін нөлге теңеймiз, сонда табылған шама iзделген орын
ауыстыру болып табылады.
С
нүктесінің ![]() өci бағытындағы орын
ауыстыруын анықтайық. Кез келген сыртқы күштер жүйесi түсiрiлген
брус үшiн
өci бағытындағы орын
ауыстыруын анықтайық. Кез келген сыртқы күштер жүйесi түсiрiлген
брус үшiн ![]() бағыты бойынша С нүктесіне
Ж күшiн
түсiрейік. Күш факторларының Ж күшіне байланысты
шамалары, мысалы, қайсыбiр көлденең қимада бұраушы момент мынадай
түрде болады:
бағыты бойынша С нүктесіне
Ж күшiн
түсiрейік. Күш факторларының Ж күшіне байланысты
шамалары, мысалы, қайсыбiр көлденең қимада бұраушы момент мынадай
түрде болады: ![]() мұндағы бiрiншi қосылғыш түcipiлгeн сырт-қы күштердiң әсерінен пайда болатын момент,
ал екінші қосылғыш түсiрілген
Ж күшінің
нәтижесінде пайда болған қосымша момент
мұндағы бiрiншi қосылғыш түcipiлгeн сырт-қы күштердiң әсерінен пайда болатын момент,
ал екінші қосылғыш түсiрілген
Ж күшінің
нәтижесінде пайда болған қосымша момент ![]() мен
мен ![]() брустың ұзындығы бойынша
өзгеретiндіктен z-тің функциялары екендiгi өзiнен-өзi бeлгiлi. Осыған ұқсас
қалған iшкi күш әcepлepi үшін де қосымша қосылғыштар пайда
болады:
брустың ұзындығы бойынша
өзгеретiндіктен z-тің функциялары екендiгi өзiнен-өзi бeлгiлi. Осыған ұқсас
қалған iшкi күш әcepлepi үшін де қосымша қосылғыштар пайда
болады: ![]() және т. б.
және т. б.
Қосымша
![]() т. б. күш, әсерлерi Ж күшіне пропорционал
екендiгi айкын. Сондықтан,
т. б. күш, әсерлерi Ж күшіне пропорционал
екендiгi айкын. Сондықтан,
 (7)
(7)
мұндағы
![]() және т. б. байланысты пропорционалдық еселіктер,
яғни қарастырылмақшы қиманың күйiне,
сырықтың ұзындығына байланысты айнымалылар. Егер сыртқы күштер
жүйесін алып тастап және күштi бiрлiк күшпен ауыстырса, онда
және т. б. байланысты пропорционалдық еселіктер,
яғни қарастырылмақшы қиманың күйiне,
сырықтың ұзындығына байланысты айнымалылар. Егер сыртқы күштер
жүйесін алып тастап және күштi бiрлiк күшпен ауыстырса, онда
![]() және т. б.
және т. б.
меқ
![]() — қарастырылатын нүктеге берiлген бағытта түсiрiлген бiрлiк
күштiң әсерiнен сырықтың көлденең қимасында пайда болатын iшкi күш
факторлары болып шыкты.
— қарастырылатын нүктеге берiлген бағытта түсiрiлген бiрлiк
күштiң әсерiнен сырықтың көлденең қимасында пайда болатын iшкi күш
факторлары болып шыкты.
Энергия өрнегіндегі iшкi күш әсерлерін (7) формуладағы жаңа мәндерiмен ауыстырамыз. Сонда,
 (8)
(8)
С өрнегін Ж бойынша дифференциалдап, содан кейін Ж=0 қойсақ, С нүктесінің орын ауыстыруын табамыз:
Алынған интегралдар Mop интегралы деп аталады.
Верещагин әдісі
Орын ауыстыруды Мор интегралының көмегiмен анықтағанда интеграл астындағы функциялардың аналитикалық өрнегін құру қажеттiгi оның негiзгi кемшілігі болып саналады. Бұл әciресе көп бөлікті сырықта орын ауыстыруды анықтағанда тиiмciз. Бipaқ сырық әрқайсысының қатаңдығы алынған шекте тұрақты болатын бөліктерден құралса, онда интегралдауды оңайлатуға болады. Ол бiрлiк күш әсерлерінің эпюрлерi сырықтың түзу өсті бөліктерінде түзу сызықты сызықты болатындығына негiзделедi.
Ұзындығы
а-ға тең бөлікте
![]() екi функцияның көбейтiндiсiнен интеграл алу
керек болсын делiк:
екi функцияның көбейтiндiсiнен интеграл алу
керек болсын делiк:
 (9)
(9)
Функциялардың бipeyi сызықты
болсын: ![]() .(8.9) өрнегi мына түрге енедi:
.(8.9) өрнегi мына түрге енедi:
 .
.
Бipiншi интеграл
![]() қисығымен шектелген ауданды, басқаша
айтсақ,
қисығымен шектелген ауданды, басқаша
айтсақ, ![]() эпюрi ауданын бередi (5-сурет):
эпюрi ауданын бередi (5-сурет):
 . Екіншi интеграл ауданның
. Екіншi интеграл ауданның
![]() өciнe сәйкес статикалық моментiн
бейнелейдi
өciнe сәйкес статикалық моментiн
бейнелейдi  , мұндағы
, мұндағы ![]() - бipiнші эпюрдiң ауырлық орталығының координаты.
Сонда
- бipiнші эпюрдiң ауырлық орталығының координаты.
Сонда ![]() , немесе
, немесе ![]() .
.
Сонымен, Верещагин әдісі
бойынша интегралдау бiрінші эпюрдiң ауданың өзінің ауырлық
орталығының тұсындағы екiнші (сызықты) эпюрдің ординатасына
көбейтумен алмастырылады. ![]() және
және
![]() функциялары сызықты болғанда көбейту операциясы
коммутативтiк қасиетке ие
болады.
функциялары сызықты болғанда көбейту операциясы
коммутативтiк қасиетке ие
болады.
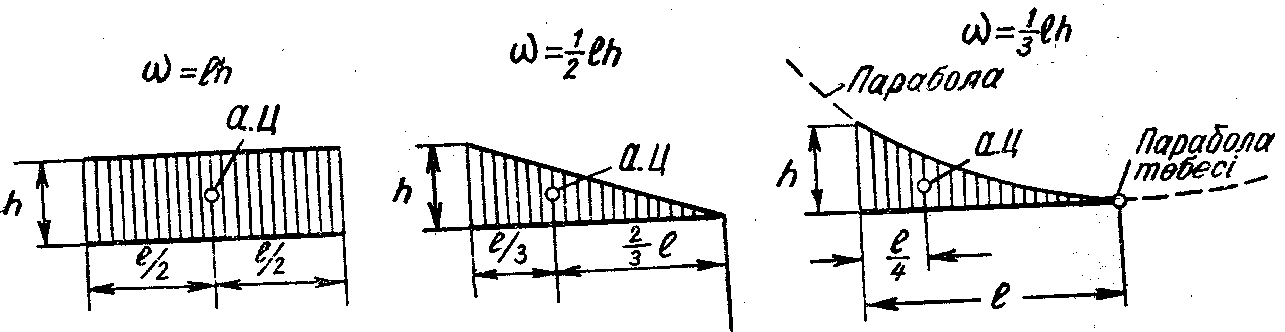
5-сурет
Мор интегралдарының
әрқайсысына ![]() т.с.с. көбейтіндiлер кiредi. Верещагин тәсілін алты интегралдың кез келгеніне қолдануға
болады, олардың эпюрлерін көбейту июші не бұраушы моменттер,
немесе бойлық
және көлденең күштер үшін бiрдей. Айырмашылығы:
эпюрлер көбейтіндiсi иілудегідей EJ
қатаңдығына
емес, бұралудағы
т.с.с. көбейтіндiлер кiредi. Верещагин тәсілін алты интегралдың кез келгеніне қолдануға
болады, олардың эпюрлерін көбейту июші не бұраушы моменттер,
немесе бойлық
және көлденең күштер үшін бiрдей. Айырмашылығы:
эпюрлер көбейтіндiсi иілудегідей EJ
қатаңдығына
емес, бұралудағы ![]() қатандығына, немесе созылу және ығысу
кезіне сәйкес EА не GА-ға
бөлінеді.
қатандығына, немесе созылу және ығысу
кезіне сәйкес EА не GА-ға
бөлінеді.
Былай
қарағанда Верещагин тәсілі айтарлықтай ықшамдау бермейтін сияқты.
Оны қолдану үшін ішкі күштер эпюрлерінің ayданы мен ауырлық
орталығының орнын табу керек. Эпюр күрделi болғанда тікелей
интегралдау қажет болады. Бірақ іс жүзінде кездесетін ішкі күштер
эпюрлepiн әдетте қарапайым фигураларға: тiктөртбұрышка, үшбұрышқа,
параболалық үшбұрышқа жіктеуге болады (5-сурет), сонан соң олардың
ауданының шамасы ![]() және ауырлық орталығының орны
бeлгiлi болады. Бұралу, созылу және ығысу кезінде эпюрлер тіптi
қарапайым болады. Олар әдетте сызықты болып және әр түрлi
комбинацияда тіктөртбұрыштар мен үшбұрыштардан
тұрады.
және ауырлық орталығының орны
бeлгiлi болады. Бұралу, созылу және ығысу кезінде эпюрлер тіптi
қарапайым болады. Олар әдетте сызықты болып және әр түрлi
комбинацияда тіктөртбұрыштар мен үшбұрыштардан
тұрады.
2.2. Цилиндр тәрізді оралған серіппелерді есептеу
Машина жасауда серiппелердiң атқаратын қызметi үлкен. Көптеген механизмдер конструкциясында ондаған, жүздеген cepiппeлep болады. Орам саны аз винттiк цилиндрлi cepiппенi есептеу теориясын қарастырайық. Атап айтқанда, мұндай cepiппелердiң осiне перпендикуляр жазықтыққа орамның көлбеу бұрышы кiшi, демек орамды сол жазықтықта жатыр деп есептеуге болады.
d, r - cepiппе дайындалған сымның диаметрi және радиусы;
D - серiппенiң орташа диаметрi; R – серiппе орамының радиусы,n -орам саны болсын (6, a-сурет).
Cepiппенi екi бөлiкке бөлемiз (6, б-сурет). Төменгi бөлiгiн алып тастап, оның жоғарғы бөлiкке әсерiн көлденең күшпен Q және бұраушы моментпен М ауыстырамыз. Онда Q=P; ал M=P·R. Сонымен, аз орамды cepiппe қиюға және бұралуға ұшырайды. Қиюда жанама кернеулер cepiппe орамының қимасы бойынша бiрқалыпты үлестiрiлген деп есептеймiз

![]() (3)
(3)
n орамы бар cepiппенi дайындауға жұмсалған сымның ұзындығы мына формуламен анықталады. l=2Rn сондықтан
![]()
А жұмыс пен U потенциялық энергияны теңестiрiп және
![]()
ескерiп
![]() (4)
(4)
Созылу және сығылу теориясында сырықтың көлденең қимасының өлшемi және формасы қарапайым геометриялық сипаттамамен, яғни қима ауданымен өрнектеледi. Иiлу және бұралу теориясында қиманың күрделiрек геометриялық сипаттамалары қарастырылады.
Сырықтың кез келген көлденең қимасын аламыз (1-сурет). Оны х,у координаттар жүйесiмен байланыстырып, мына екi интегралды қарастырамыз:
ҚОРЫТЫНДЫ
Сыртқы күш пен қауіпсіз кернеу белгілі болса, қиғаш иілген арқалықтың қима өлшемдерін беріктік шартынан келесі тәртіппен анықтайды қиманың өлшемдері алдын ала белгілі деп қарастырылып қандайда бір мәндері (4) теңсіздігіне енгізіледі.
Есептеліп анықталған теңсіздіктің сол жағы оң жағына қарағанда айтарлықтай кіші болса, қима өлшемдерін үлкейтіп, ал айтарлықтай үлкен болса кішірейтіп аркалықтың беріктігі қайта тексеріледі
Басты жазықтықтардан басқа, бойлық өс арқылы өтетін, кез келген жазықтықтарда жатқан сыртқы күштердің әсерінен конструкция элементі қиғаш иіледі. Қиғаш иілген арқалықты беріктікке есептеу тәртібі келесі мысалда көрсетілген. Бір ұшы қатаң бекітілген арқалықтың екінші ұшына Р күші әсер етсін
Екінші беріктік теориясын ең үлкен сызықтық деформация теориясы деп атайды. ¤йткені, бұл теорияда беріктік нышаны ретінде сызықтық деформация қабылданған.
Оның негізін Мариотт салып, Сен-Венан жалғастырған. Ол былай тұжырымдалады:
Потенциялық энергияньң анықталуы сырықта пайда болатын iшкi күш әсерлерін талдаудан туындайды. Бұл талдау, әдетте, қималар тәсілiмен жүргiзiледі де, июші және бұраушы моменттердің әпюрлерiн, ал қажет жағдайда бойлық және көлденең күш эпюрлерiн салумен анықталады.
Созылу және сығылу теориясында сырықтың көлденең қимасының өлшемi және формасы қарапайым геометриялық сипаттамамен, яғни қима ауданымен өрнектеледi. Иiлу және бұралу теориясында қиманың күрделiрек геометриялық сипаттамалары қарастырылады.
Орын ауыстыруды Мор интегралының көмегiмен анықтағанда интеграл астындағы функциялардың аналитикалық өрнегін құру қажеттiгi оның негiзгi кемшілігі болып саналады. Бұл әciресе көп бөлікті сырықта орын ауыстыруды анықтағанда тиiмciз. Бipaқ сырық әрқайсысының қатаңдығы алынған шекте тұрақты болатын бөліктерден құралса, онда интегралдауды оңайлатуға болады. Ол бiрлiк күш әсерлерінің эпюрлерi сырықтың түзу өсті бөліктерінде түзу сызықты сызықты болатындығына негiзделедi.
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР
-
Н.Қожаспаев, С.Кешуов, И.Мухитов Электротехника /оқу құралы/ - Алматы. Республикалық баспа кабинеті, 1996 ж., 300 бет
-
Электротехника /Под ред- проф. В. Г. Герасимова.— М.: Высшая школа. 1935.
-
Волынский Б. А., Зейн Е. Н..Шатерников В. Е.Электротехника.— Москва.:Эпергоатомиздат, 1987.
-
Борисов Ю.М., Липатов Д.Н., Зорин Ю.Н., Электротехника —Москва.:Эпергоатомиздат, 1985.
-
Касаткин А. С., Немцов М. В..Электротехника.— М.: Энерогоатомиздат. 1983.
-
Иванов И. И., Равдоник С. С. Электротехника.— М.: Высшее школа, 1984.
-
Электротехника. Программированное учебное пособие /Под ред. проф. В. Г. Герасимова.— М.: Высшая школа, 1983.
-
Основы промышленной электроники. /Под ред. проф. А Г. Герасимова.— М.:Высшая школа, 1986.
31
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
НЕГІЗГІ ТҮСІНІКТЕР
НЕГІЗГІ ТҮСІНІКТЕР
МАЗМҰНЫ
КІРІСПЕ ........................................................................................................................3
І. НЕГІЗГІ ТҮСІНІКТЕР...............................................................................................4
1.1. Көлденең күш пен июші моменттер.....................................................................4
1.2. Қиғаш иілу............................................................................................................13
ІІ. Кез келген күш әсерінен сырықтар жүйелеріндегі орын ауыстырулар...........16
2.1. Кез келген күш түсірілген брустың поетнциялық энергиясы.........................18
2.2. Цилиндр тәрізді оралған серіппелерді есептеу.................................................24
ҚОРЫТЫНДЫ ............................................................................................................26
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР........................................................................27
КІРІСПЕ
Бойлық өс арқылы өтетін жазықтықтарда (өс жазықтықтарында) жатқан көлденең күштер мен моменттердің (жұп күштердің) әсерінен сырықта пайда болған деформацияны иілу деп атайды.
Яғни, сыртқы күштің әсер ету сызығы мен бейтарап сызық өзара перпендикуляр. Әсер ету сызығы координаттар жүйесінің бас нүктесі арқылы өтетін кез келген күштің әсерінен мұндай аркалықтар жазық иіледі.
Сыртқы күш пен қауіпсіз кернеу белгілі болса, қиғаш иілген арқалықтың қима өлшемдерін беріктік шартынан келесі тәртіппен анықтайды қиманың өлшемдері алдын ала белгілі деп қарастырылып қандайда бір мәндері (4) теңсіздігіне енгізіледі.
Есептеліп анықталған теңсіздіктің сол жағы оң жағына қарағанда айтарлықтай кіші болса, қима өлшемдерін үлкейтіп, ал айтарлықтай үлкен болса кішірейтіп аркалықтың беріктігі қайта тексеріледі
Басты жазықтықтардан басқа, бойлық өс арқылы өтетін, кез келген жазықтықтарда жатқан сыртқы күштердің әсерінен конструкция элементі қиғаш иіледі. Қиғаш иілген арқалықты беріктікке есептеу тәртібі келесі мысалда көрсетілген. Бір ұшы қатаң бекітілген арқалықтың екінші ұшына Р күші әсер етсін
Екінші беріктік теориясын ең үлкен сызықтық деформация теориясы деп атайды. ¤йткені, бұл теорияда беріктік нышаны ретінде сызықтық деформация қабылданған.
Оның негізін Мариотт салып, Сен-Венан жалғастырған. Ол былай тұжырымдалады:
Күрделі кернеулі күйдегі материал көлеміндегі ең үлкен сызықтық деформация шамасы қауіпті шегіне жеткенде өзінің жұмыс істеу қабілетін жоғалтады.
Жазық иілген арқалықтың көлденең қималарында ішкі күштер — көлденең күш пен июші момент пайда болады.
Егер иілген арқалықтың көлденең қималарында июші моменттен басқа ішкі күштер жоқ болса, яғни көлденең күш нөлге тең болса, ондай иілу таза иілу деп аталады.
І. НЕГІЗГІ ТҮСІНІКТЕР
-
Көлденең күш пен июші моменттер
Беріктік кепілдігі. Межелік (сындырушы) күштің немесе кернеудің іс жүзінде әсер етіп тұрған күшке немесе кернеуге қатынасы. Син. – Беріктік кепілдігінің еселігі; күрделі кернеулі күй жағдайында кернеулі күйдің құраушыларының барлығын бірге кернеулі күй межелік кернеулі күй болу үшін неше өсе көбейту керек екенін көрсететін өселік.
Беріктік шегі. Үлгі төтеп бере алатын ең үлкен күштің үлгінің көлденең қимасының бастапқы (күш түсірілмеген кездегі) ауданына қатынасы.
Беріктік. Қатты дененің сыртқы күштер әсеріне сынбай төтеп беру қабілеті. Кең мағынада беріктік - материалдың сынуға төтеп берумен қатар оның өз формасын қайтымсыз (пластикалық) өзгертуге қарсыласу қабілеті.
Верещагин әдісі. Екі функцияның көбейтіндісінен алынатын интегралды сол функциялардың графиктерін арнаулы жолмен “көбейтумен” алмастыру.
Даламбер қағидасы. Қозғалыстағы материялық нүктелер жүйесі үшін барлық пәрменді күштердің, реакция күштерінің, инерция күштерінің векторлық қосындысы және осы аталған күштердің бас моменттерінің қосындысы нольге тең болады.
Деформация. Сыртқы күштер әсерінен туындайтын дене нүктелерінің өзара орналасуының өзгеруі.
Деформацияның потенциалдық энергиясы. Деформацияның серпімді құраушыларының арқасында пайда болып, күшті алып тастаған кезде жүйенің сыртқы жұмысына айнала алатын деформация энергиясы.
Динамикалық түрде күш түсіру. 1. Деформацияланатын дене бөлшектерінің жылдамдығы едеуір болып, яғни қозғалыстағы массаның кинетикалық энергиясы сыртқы күштер жұмысының айтарлықтай бөлігін құрайтындай жағдай туғызатын күш түсіру түрі. 2. Пластикалық деформациялар толық пайда бола алмайтындай күш түсіру түрі. Син. – Тез өзгеремді жүктеме.
Есептеу сүлбесі. Қарастырылатын нақты объектінің есептеу мақсатына айтарлықтай әсері жоқ ерекшеліктері алып тасталған түрі (Модель дегенді де қараңыз).
Жазық қималар болжамы. Сырықтың көлденең қимасы күш түсірілгенге дейін жазық және бойлық өске перпендикуляр болса, күш түсірілгеннен кейін де жазық және бойлық еске перпендикуляр күйінде қалады деген тұжырымға негізделген болжам. Қараңыз. – Бернулли болжамы.
Жазық фигураның бас инерция моменті. Жазық фигураның бас өстеріне қатысты инерция моменттері.
Жазық фигураның орталық бас өстері. Қиманың ауырлық орталығынан өтетін бас өстері.
Жанама кернеу. Берілген қимадағы толық кернеу векторының қима жазықтығына проекциясы.
Жаншылу. Шекті өлшемді беттескен беттердегі тік кернеудің әсерінен бұйым материалының беткі қабатының пластикалық деформация алуы.
Жұмсару шегі. Үлгідегі деформацияның кернеуге тәуелсіз едеуір өсетін кезіне сәйкес кернеудің мәні.
Жылжу жолақтары (Людерс-Чернов сызықтары). Беті жылтырата тегістелген үлгіні жалпы жұмсару аймағында созуға сынау кезінде оның бетінде бойлық оске 45 градус көлбеу бағытта пайда градус көлбеу бағытта пайда болатын сызықтар.
Изотроптық. Денеден бөліп алынған үлгінің қасиеттерінің кеңістіктегі бағыттардан тәуелсіздігі. Керісінше дененің материалы анизотропты деп аталады.
Иілу. Сырықтың көлденең қимасында июші момент туындататын күш түсіру түрі; иілу тік (жазық) және қиғаш болып бөлінеді; сонымен қатар бойлық және бойлық-көлденең иілу түрлері кездеседі.
Ішкі күштер. Сыртқы күштер әсерінен туындайтын жүйенің элементтерінің немесе дененің бөліктерінің өз-ара әсер күштері. Олар қарастырырылатын көлемдегі немесе нүкте маңындағы сыртқы күштер өсерін теңгереді.
Қабық. Бір өлшемі (қалындығы) басқа өлшемдерінен әлдеқайда кіші дене.
Қажуға беріктік. Құрылма элементінің, материалының айнымалы кернеу әсеріне төтеп беру қабілеті; айнымалы күштержүйесі әсеріне беріктік.
Кастилиано теоремасы. Серпімді жүйенің толық потенциялық энергиясынан күшке қатысты алынған дербес туынды сол күш түсірілген нүктенің күш бағытындағы орын ауыстыруына тең болады.
Қатаңдық. Қатты дененің сыртқы әсерлерді өзінің бастапқы геометриялық формасы мен өлшөемдерін айтарлықтай өзгертпей төтеп беру қабілеті.
Кернеулер эллипсоиды. Нүктедегі толық кернеу векторының ұшының геометриялық орны.
Кернеулі күйдің бас алаңдары. Кернеулі күйдің бас өстеріне сәйкес өзара перпендикуляр жазықтықтар.
Кесілу. Жанама кернеудің әсерінен бұйым материалының бір бөлігінің екінші бөлігіне қарағанда жазықтық бойымен ығысуының нәтижесінде сынуы.
Қима өзегі. Көлденең қиманың барлық ңүктелерінде бір таңбалы кернеу туындататын орталықтан тыс түсірілген бойлық күштердің түсу нүктелерінің жиынтығы.
Қималар тәсілі. Жүйедегі (денедегі) ішкі күштерді табу төсілі. Ол үшін жүйені қажет жерден ойша кесіп, бір бөлігін алып тастаса, оның қалған бөліктің тепе-теңдігін қамтамасыз өтетін әсері ішкі күшті береді.
Кернеу. Сыртқы күштер әсерінен туатын денедегі ішкі күштердің таралуын сипаттайтын шама; аудан бірлігіне келетін ішкі күштер үлесі.
Күштер әсерлерінің тәуелсіздігі қағидасы. Бірнеше сыртқы әсердің (күштер, температура, қысым және т.б.) нәтижесі сол әсерлердің әрқайсысының нәтижелерінің қосымдысына теңдігі және оларды түсіру тәртібіне тәуелсіздігі болжамына негізделген қағида. Син. – Қондыра қосу қағидасы.
Күшті статикалық түрде түсіру. Күштің өзгеру жылдамдағы дене бөліктерінің кинетикалық энергиясына айтарлықтай әсер етпейтіндей күш түсіру түрі.
Мор интегралы. Сызықты серпімді жүйелердегі орын ауыстыруды табу үшін Мор тәсілін қолданғанда пайдаланылатын интегралдар.
Нүктедегі кернеулі күй. Нүктеден өтетін барлық жазықтардағы кернеулердің жиынтығы; басы қарастырылатын нүктеде орналасқан тікбұрышты координаттар жүйесіндігі кернеулі күй құраушылары арқылы толық анықталады. Син. - Кернеулер тензоры.
Орнықтылық. Жүйенің сыртқы әсерлерге төтеп бере отырып өзінің бастапқы қалпын сақтау қабілеті.
Орталықтан тыс созылу (сығылу). Тең әсерлісі сырықтың көлденең қимасының ауырлық орталығынан тыс жерден өтетін бойлық бағытпен түсірілген күштер жүйесінен туындайтын деформация; мұны созылу (сығылу) және бір немесе екі бас өске қатысты иілудің біріккен әсері деп қарастыру ыңғайлы.
Пластикалық материалдар. Стандартталған үлгілері қалыпты температурада статикалық түрде үзілуге дейін созылуға сынағанда салыстырмалы ұзаруы мен салыстырмалы жіңішкеруі (10...60) % - тен кем болмайтын материалдар. Кей жағдайларда пластикалық материалдан жасалған бөлшектердің де морт сынуы мүмкін.
Полюстік инерция моменті. Дөңгелек немесе сақина тәрізді қималы сырықтардағы бұралу кезіндегі кернеулер мен деформацияларды табу үшін қолданылатын геометриялық сипаттама.
Полюстік қарсыласу моменті. Дөңгелек немесе сақина тәрізді қималы сырықтардың бұралу кезінде ең үлкен жанама кернеулерді анықтауцға пайдаланылатын шама; өлшем бірлігі -ұзындық өлшемінің үшінші дәрежесі.
Пропорционалдық шегі. Материалдың қасиеттерінің Гук заңына бағынатын аралығындағы ең үлкен кернеу.
Сен-Венан қағидасы. Жүйенің (дененің) күш түсірілген нүктесінен жеткілікті дәрежеде алыс жатқан нүктелердегі кернеулер мен деформациялар күштің нақты түсірілу әдісіне тәуелсіздігі жайындағы ереже. Бұл қағидаға сүйеніп түсірілген күш жүйесін оған барабар қарапайым жүйемен алмастыруға болады.
Серпімділік. Дененің өлшемдері мен формасын сыртқы күш әсері тоқтағаннан кейін қайтадан қалпына келтіре алу қабілеті.
Бойлық өс арқылы өтетін жазықтықтарда (өс жазықтықтарында) жатқан көлденең күштер мен моменттердің (жұп күштердің) әсерінен сырықта пайда болған деформацияны иілу деп атайды. Иіліп деформацияланған сырықтар арқалық деп аталады. Арқалықтың бойлық өсі мен көлденең қималарының баст инерция өстері арқылы екі баст жазықтык (V, Н) жүргізуге болады (1, а-сурет). Июші күштер бас жазықтықтардың бірінде жатса, онда иілу көлденең жазық иілу деп аталады. Көлденең жазық иілу кезінде арқалықтың майысқан бойлық өсі күш жазықтығында жатады. Сыртқы күштер бас жазықтықтардан басқа кез келген өс жазықтықтарында жатса, онда иілу қиғаш иілу деп аталады. Арқалық қиғаш иілгенде, оның майысқан бойлық өсі мен әсер етуші күштер әр түрлі жазықтықтарда жатады. Жазық иілген арқалықтың көлденең қималарында ішкі күштер — көлденең күш пен июші момент пайда болады.
Егер иілген арқалықтың көлденең қималарында июші моменттен басқа ішкі күштер жоқ болса, яғни көлденең күш нөлге тең болса, ондай иілу таза иілу деп аталады. Таза иілу кезінде арқалық 1-сурет шеңбер доғасы бойымен майысады.

1-сурет
Элементтері иіле деформацияланып, өзара қатаң немесе топса арқылы жалғасқан сырықтар жүйесі жақтау деп аталады. Жақтау элементтерінің көлденең қималарында көлденең күш, ию момент, сондай-ақ бойлық күш те пайда болуы мүмкін. Арқалықтар мен жақтаулар есептелгенде, олар есептеу сүлбелерімен алмастырылады. Есептеу сүлбелері бойлық өстер мен әсер етуші сырткы күштерден құралады (1, б-сурет).
К
өлденең күштер мен июші
моменттер
Қос тұғырлы иілген арқалықтың көлденен қималарындағы ішкі күштерді анықтайық (1-cypeт). Кез келген m-m қимасындағы ішкі күштерді табу үшін қималар тәсілі бойынша, сол қима арқылы арқалықты екіге бөліп, бір бөлігін алып тастаймыз. Алып тасталынған бөліктің қалған бөлікке әсерін көлденең күш пен июші моментпен алмастырамыз (1,б-сурет). Қалған бөлік сыртқы күштер мен ішкі күштердің әсерінен тепе-теңдік күйде болуы тиіс.
Статиканың бірінші теңдеуі

![]()
осыдан
![]()
![]()
яғни кез келген m-m қимасындағы көлденең күш Q(z) сол қиманың бір жағында әсер етуші сыртқы күштердің y осіне түсірілген проекцияларының алгебралық қосындысына тең.
Статиканың екінші теңдеуі
![]()
осыдан
![]()
яғни кез келген m-m қимасыңдағы ию моменті M(z) сол қиманың бір жағында жатқан сыртқы күштердің С нүктесіне қарағандағы моменттерінің алгебралық қосындысына тең (С нүктесі m-m қимасының ауырлық орталығы).
Бір қалыпты таралған күштерді y өсіне проекциялау үшін немесе С нүктесіне қарағаңдағы моментін анықтау үшін, 1-суретте оларды биіктігі q-ға, ұзындығы z-ке тең, тік төртбұрыштың ауырлық центрі арқылы өтетін қорытынды Rq = qz күшімен алмастырылған.
К өлденең күш пен июші моменттің таңбалары туралы
келесі ережелер
қабылданады.
Көлденең
m-m қимасының сол жағында әсер етіп тұрған сыртқы күштердің
қорытынды күші
(R)
төменнен жоғары
қарай,
ал оң
жақтағы сыртқы
күштердің қорытынды күші (R) жоғарыдан төмен қарай бағытталған болса, ол қимадагы жанама күш Q(z) оң таңбалы болып саналады. Кері жағдайда жанама күш теріс таңбалы (2, б-сурет).
өлденең күш пен июші моменттің таңбалары туралы
келесі ережелер
қабылданады.
Көлденең
m-m қимасының сол жағында әсер етіп тұрған сыртқы күштердің
қорытынды күші
(R)
төменнен жоғары
қарай,
ал оң
жақтағы сыртқы
күштердің қорытынды күші (R) жоғарыдан төмен қарай бағытталған болса, ол қимадагы жанама күш Q(z) оң таңбалы болып саналады. Кері жағдайда жанама күш теріс таңбалы (2, б-сурет).
К
өлденең m-m қимасының сол
жағындағы әсер етуші сыртқы күштердің осы қиманың ауырлық
орталығына қарағандағы қорытынды моменті (М) сағат тілінің бағытымен
бағыттас, ал оң жағындағы күштердің корытынды моменті сағат тілінің
бағытына қарама-қарсы бағытта болса, ол қимадағы июші момент оң
таңбалы деп саналады (3,
а-сурет). Кері
жағдайда июші момент М(z) теріс таңбалы (3, б-сурет) болады.
Таралған күштің қарқындылығы, көолденең күш, июші момент араларындағы дифференциалдық байланыс
Б
іркелкі таралған күштің
қарқындылығы, жанама күш, июші момент араларындағы дифференциалдық
байланыстарды анықтау үшін 1-суреттегі арқалықты қарастырайық. Сол
жақтағы A тірегінен z-ке тең
қашықтықта жатқан көлденең қимада пайда болатын
жанама күш
![]() , (1)
, (1)
ал z + dz қашықтығында жатқан көлденең қимадағы жанама күш
![]() (2)
(2)
Соңғы (2) теңдеу мен (1) теңдеуінің айырмасынан
![]() немесе
немесе ![]() (3)
(3)
екенін көреміз.
Демек, кез келген қимадағы жанама күштің өрнегінен z бойынша алынған бірінші туынды, сол аралықтағы әсер етуші бір қалыпты таралған күштің қарқындылығына тең.
Абсциссасы z-ке тең көлденең қимадағы июші момент
![]() (4)
(4)
ал абсциссасы z + dz-ке тең көлденең қимадағы ию моментінің өрнегі
![]() (5)
(5)
Соңғы (5) теңдігінен (4) теңдігін алып тастап
![]() (6)
(6)
екенін көреміз.
Демек, кез келген көлденең қимадағы июші моменттің өрнегінен z бойынша алынған бірінші туынды, осы қимадағы жанама күшке тең. Олай болса
![]() (7)
(7)
Көлденең қимадағы июші моменттің өрнегінен z бойынша алынған екінші туынды осы аралықта єсер етуші бір қалыпты таралған күштің қарқындылығына тең.

Тік кернеуді анықтау. Тік кенреу бойынша беріктік пен қатандыққа есептеу
Июші момент — арқалыктың көлденең қимасындағы ішкі тік кернеулердің қорытынды моменті. Тік кернеулердің шамасы мен қима бетіндегі таралу заңдылығын анықтау үшін таза иілген арқалықты қарастырайық (1, а-сурет).
Есептің статикалық жағы. Таза иілген арқалықтың кез келген көлденең қимасында июші моменттен басқа ішкі күштер нөлге тең. Июші момент ішкі күштердің қорытынды моменті болғандықтан, көлденең кимада (m — m) жатқан кез келген нүктеде тек қана тік кернеу әсер етеді. Қима жазықтығынан бөлініп алынған шексіз кіші аудандағы (dА) кернеулердің қорытынды күші мен y және x өсіне қарағандағы моменттерін анықтайық (1, б-сурет)
![]() , осыдан
, осыдан
![]()
Арқалық таза иіліп деформацияланғанда
N=0, Mx =M, My=0,
демек,
![]() (1)
(1)
Берілген арқалықтың бетіне, бойлық өске параллель жєне
көлденең
сызықтар ж ү ргіземіз (1, а-сурет). Деформацияға
дейінгі m –m, n - n т
түзу сызықтары
деформациядан кейін өзара ![]() бұрышына бұрылып, түзу күйінде қалады. Демек,
деформацияға дейінгі жазық қималар деформациядан кейін де
арқалықтың бойлық талшықтарына перпендикуляр жазық күйінде
қалады.
бұрышына бұрылып, түзу күйінде қалады. Демек,
деформацияға дейінгі жазық қималар деформациядан кейін де
арқалықтың бойлық талшықтарына перпендикуляр жазық күйінде
қалады.
Деформацияға дейінгі арқалықтың өзара тең ab, dc, ef талшықтары деформациядан кейін шеңбер доғасы бойынша иіліп, ef қысқарады (сығылады) да, ab ұзарады (созылады), ал dc талшығының ұзындығы өзгермейді (1,б-сурет). Арқалықтың ұзындығы өзгеріссіз қалатын талшықтарының геометриялық орны бейтарап жазықтық деп, ал бейтарап жазықтықтың кез келген көлденең қимамен қиылысу сызығы, қиманаң бейтарап сызығы деп аталады (2 в-сурет)
Деформациядан кейінгі бейтарап
жазықтықта жатқан dc
талшығы радиусы![]() -ға тең, ал ab талшығы радиусы
ρ +y-ке тең доғаларға
айналады.
-ға тең, ал ab талшығы радиусы
ρ +y-ке тең доғаларға
айналады.
аb талшығының салыстырмалы созылуы
![]() ,
,
мұндағы аb1 =(![]() )
)![]() , ал аb=dz
болғандықтан
, ал аb=dz
болғандықтан
![]() (2)
(2)
Б ейтарап жазықтықта жатқан
dc = dz талшығы
деформациядан кейін шеңбердін доғасы бойынша иіліп, ұ зындығы
өзгермейді
ейтарап жазықтықта жатқан
dc = dz талшығы
деформациядан кейін шеңбердін доғасы бойынша иіліп, ұ зындығы
өзгермейді
![]() (3)
(3)
Олай болса, (2) теңдігін (3) тендігіне енгізіп
![]() (4)
(4)
екенін көреміз.
Яғни талшықтың салыстырмалы бойлық деформациясы оның бейтарап өске дейінгі ара қашықтығына тура пропорционал.
Еңді есептің физикалық жағын қарастырайық. Көлденең қимада жанама кернеу жоқ
болғандықтан, жанама кернеулердің жұ птық заңы бойынша, ол бойлық
қималарда да жоқ. Сондықтан, бойлық талшықтар өзара әсерлеспейді деп
қарастыруға болады. Олай болса, аb талшығы сызықтық
кернеулі күйде. Сызықтық кернеулі күй үшін Гук заңы
![]() = E
= E![]() .
.
Енді синтез жасайық. Гук заңына (4) тендігін енгізіп
![]() , (5)
, (5)
кернеу қарастырылған нүкте мен бейтарап өстің ара қашықтығына (у) тура пропорционал өзгеретінін көреміз. Бейтарап өсте жатқан нүктедегі кернеулер нөлге тең, ал қиманың ең жоғарғы және ең төменгі нүктелерінде ең үлкен кернеулер әсер етеді (2, в-сурет).
Статикалық (1) тендеуіне (5) теңдігін енгізіп'
![]()
![]() ,
,
ал теңдіктегі интеграл
![]() -қиманың
x -өcіне
қатысты өстік
инерция моменті екенін ескерсек,
-қиманың
x -өcіне
қатысты өстік
инерция моменті екенін ескерсек,
![]() (6)
(6)
Мұндағы
![]() -арқалықтың қатаңдығы,
-арқалықтың қатаңдығы, ![]() — арқалықтың
қисықтығы.
— арқалықтың
қисықтығы.
Гук заңынан (5)
![]() (7)
(7)
яғни
![]() (8)
(8)
Соңғы формула таза иілген арқалықтың көлденең қимасыңда жатқан кез келген нүктедегі тік кернеуді анықтауға мүмкіндік береді.
Еңді (8) формуласын (1) тендеулеріне кезекпен енгізейік:
![]() болғандықтан
болғандықтан ![]()
Бұл интеграл – қиманың бейтарап өске қарағандағы статикалық моменті. Статикалық моменті нөлге тең болғандықтан, бейтарап өс қиманың ауырлық орталығы арқылы өтіп, x -сінің үстінде жатады.
2. ![]() болғандықтан,
болғандықтан,
![]()
Бұл иyтеграл — қиманың x, ү өстеріне қатысты өрістік инерция моменті. Өрістік инерция моменті нөлге тең болғандықтан x, ү өстері баст, ал сыртқы момент бас ү өсі арқылы өтетін жазыктықта әсер етуі тиіс. Демек, жазық иілудегі ү өсімен сәйкес келетін сырты күштердің әсер ету сызығы мен бейтарап сызық өзара перпендикуляр.
Теориялық және тәжірибе жүзіндегі зерттеулердің нәтижелеріне қарағанда, (8) формуланы көлденең жазық, иілген арқалықтар үшін де қолдануға болады.
Иілген арқалықтң беріктігін тексеру үшін М(z) эпюрі салынып, қауіпті қимасы анықталады.
Қауіпті деп, июші моменттердің ең үлкені (абсолюттік шамасы) (Mmax ) әсер етіп тұрған қиманы айтады. Қауіпті қимадағы қауіпті кернеу
![]()
мұндағы ymax - бейтарап өстен ең шеткі нүктеге дейінгі кашықтық; Jmax /ymax =Wx - геометриялық сипаттама, өстік қарсылық моменті деп аталады.
Созылу мен сығылуға бірдей қарсыласатын пластикалық материалдары үшін тік кернеу бойынша беріктік шарты
![]() (9)
(9)
Созылу мен сығылуға қарсыласу кабілеті әр түрлі морт материалдардың беріктігі ең үлкен созушы және сығушы тік кернеулер бойынша есептеледі.
Созушы тік кернеу бойынша беріктік шарты
![]() (10)
(10)
Сығушы тік кернеу бойышпа беріктік шарты
![]() (11)
(11)
мұндағы
![]() - созылған жөне сығылған талшықтар үшін
анықталатын қарсылық моменті.
- созылған жөне сығылған талшықтар үшін
анықталатын қарсылық моменті.
а) Дөңгелек пішінді қима үшін
![]()
б) Тіктөртбұ рышты қима үшін
![]()
Стандартталған қималар үшін Wx -тің мәндері анықтамалықтарда арнайы сортамент кестелерінде беріледі.
1.2. Қиғаш иілу
Басты жазықтықтардан басқа,
бойлық өс арқылы өтетін, кез келген жазықтықтарда жатқан сыртқы
күштердің әсерінен конструкция элементі қиғаш иіледі. Қиғаш иілген
арқалықты беріктікке есептеу тәртібі келесі мысалда көрсетілген.
Бір ұшы қатаң бекітілген арқалықтың екінші ұшына Р күші әсер етсін.
Күштің әсер ету сызығы x
өсімен ![]() бұрышын жасап өтетіндіктен арқалық қиғаш
иіледі (1, а-сурет). Сыртқы күшті басты өстерге проекциялап
құраушыларын табайық
бұрышын жасап өтетіндіктен арқалық қиғаш
иіледі (1, а-сурет). Сыртқы күшті басты өстерге проекциялап
құраушыларын табайық
![]()
Құраушы Рх, Ру күштерініњ әсерінен берілген арќалық өзара перпендикуляр басты жазықтықтарда жазық иіліп, көлденең қималарыңда июші моменттер пайда болады

мұндағы M = Pz.
Тұғыр қимасында жатқан Е нүктесіндегі кернеуді табу үшін күш әрекеттерінің тәуелсіздік приціпін пайдаланамыз (1, а-сурет). Вертикаль жазықтықтағы Мх -тің әсерінен Е нүктесінде пайда болған кернеу
![]()
Горизонталь жазықтықтағы Му -тің әсерінен пайда болған кернеу
![]()
Нүктедегі толық кернеу
![]() (1)
(1)
немесе
![]()

м±ндағы хе, уе— Е нүктесінің координаталары.
Алынған (1) формуланы пайдаланып кез келген пішінді қиманың нүктелеріндегі кернеулерді анықтауға болады. Бұл формуладағы, бірінші квадранттың нүктелерінде созушы кернеу тудыратын июші моменттер оң таңбалы деп қарастырылып, ал нүктелерінің координаттары өз таңбаларымен жазылады. Нүктелерінде тек созушы кернеулер пайда болатын квадрант бірінші квадрант ретінде қабылданады.
Қимадағы кернеулер х, у координаттына тәуелді болғандықтан, қауіпті қимадағы ең үлкен созушы кернеу әсер етіп тұрған бұрыштағы А мен ең үлкен сығушы кернеу әсер етіп тұрған бұрыштағы С нүктелері қауіпті болып саналады.
Арқалықтың беріктігін А нүктесі үшін беріктік шартын құрып тексереміз
![]()
мұндағы х а = хmax , ya =ymax болғандықтан
![]()
Бұрыштардағы А, С нүктелеріндегі кернеулердің абсолют шамалары бірдей.
Арқалық морт материалдан жасалса, оның беріктігі A нүктесімен қатар С нүктесі бойынша да тексеріледі.
Е нді
бұрышы жоқ 2-суреттегі қиманы қарастырайық. Қиманың қауіпті нүктелерін табу үшін алдымен бейтарап
сызықтың орны анықталады. Бейтарап сызық, тік кернеуі нөлге тек
нүктелердің геометриялық орны. Олай болса, кернеудің шамасын (1)
нөлге теңестіріп, координаттар басы арқылы өтетін, бейтарап
сызықтың теңдеуін аламыз
нді
бұрышы жоқ 2-суреттегі қиманы қарастырайық. Қиманың қауіпті нүктелерін табу үшін алдымен бейтарап
сызықтың орны анықталады. Бейтарап сызық, тік кернеуі нөлге тек
нүктелердің геометриялық орны. Олай болса, кернеудің шамасын (1)
нөлге теңестіріп, координаттар басы арқылы өтетін, бейтарап
сызықтың теңдеуін аламыз
![]()
мұндағы х0 ,у0 - бейтарап өс нүктелерінің айнымалы координаттары.
Бұл теңдеуді
![]() шамасына көбейтіп келесі түрге
келтірейік:
шамасына көбейтіп келесі түрге
келтірейік:
![]() (2)
(2)
Енді ![]() екенін ескеріп, бейтарап
сызықтың орнын анықтайтын формуланы
аламыз
екенін ескеріп, бейтарап
сызықтың орнын анықтайтын формуланы
аламыз
![]() .
(3)
.
(3)
Бейтарап сызықтың x өсіне қарағандағы бұрышы теріс таңбалы болғандықтан, ол сағат тілі бағыты бойымен салынып П, IV квадранттар арқылы өтеді (2-сурет).
Алынға3) теңдеуінде
![]() болғандықтан,
болғандықтан, ![]() . Демек, сыртқы күштің әсер
ету сызығы (ә. с) мен бейтарап сызық (б. с.) өзара перпендикуляр
емес (2-сурет).
. Демек, сыртқы күштің әсер
ету сызығы (ә. с) мен бейтарап сызық (б. с.) өзара перпендикуляр
емес (2-сурет).
Қиманың контурына, бейтарап сызыққа параллель жанамалар жүргізіп қауіпті А, В нүктелерін табамыз (2-сурет). Суреттегі кернеудің эпюрі ежелгі тәртіппен салынған.
Қауіпті нүктелер үшін беріктік шарты келесі түрде жазылады
![]() (4)
(4)
![]() (5)
(5)
Конструкция элементтерінің көлденең қималары дөңгелек, квадрат пішінді болса, Jx =Jy .
![]() .
.
Яғни, сыртқы күштің әсер ету сызығы мен бейтарап сызық өзара перпендикуляр. Әсер ету сызығы координаттар жүйесінің бас нүктесі арқылы өтетін кез келген күштің әсерінен мұндай аркалықтар жазық иіледі.
Сыртқы күш пен қауіпсіз кернеу белгілі болса, қиғаш иілген арқалықтың қима өлшемдерін беріктік шартынан келесі тәртіппен анықтайды қиманың өлшемдері алдын ала белгілі деп қарастырылып қандайда бір мәндері (4) теңсіздігіне енгізіледі.
Есептеліп анықталған теңсіздіктің сол жағы оң жағына қарағанда айтарлықтай кіші болса, қима өлшемдерін үлкейтіп, ал айтарлықтай үлкен болса кішірейтіп аркалықтың беріктігі қайта тексеріледі. Тексеру теңсіздіктің сол жағы мен оң жағының арасындағы айырым 4—5%-ке жуықтағанша қайталанады.
Қиғаш иілген арқалықтың деформациясы, иілу өсінің дифференциалдық теңдеуін интегралдау немесе басқа әдістермен анықталады. Ол үшін күш әсерлерінің тәуелсіздік принципі пайдаланылып, қиғаш иілу бас жазықтықтардағы екі жазық иілудің қосындысы ретінде қарастырылады. Қиғаш иілген арқалықтың кез келген қимасындағы ойысу, бас жазықтықтардағы ойысулардың геометриялық қосындысына тең
![]() (6)
(6)
мұндағы yвер — вертикаль жазықтықтағы ойысу, угор— горизонталь жазықтықтағы ойысу. Қатаңдық шарты келесі түрде жазылады
![]()
мұндағы [у] — қауіпсіз ойысу.
Қиғаш иілген арқалықтың серпімді сызығы мен сыртқы күштің әсер ету сызығы әр түрлі өс жазықтықтарында жатады. Ойысу мен күш бағыттары өзара сәйкес келмейді.
Орталықтан тыс созылу (сығылу)
Орталықтан тыс созылу (сығылу) деп қиманың ауырлық орталығынан басқа кез келген нүкте арқылы берілетін, бойлық өске параллель күштің әсерінен сырықтың деформациялануын айтады (3-сурет).
Күш түскен нүкте (р) полюс деп аталады. Полюстің координаталарын хр , ур арқылы белгілейік. Полюстен координаттар жүйесінің басына дейінгі ара қашықтық эксцентриситет деп аталып, е арқылы белгіленеді. Орталықтан тыс созылған сырықтың кез келген қималарында Nz = Р, Мx = Руp , Мy = Рхp ішкі факторлары пайда болады (3-сурет).
Б
ерілген қиманың Е нүктесіндегі
кернеуді анықтайық. Күш әрекеттерінің тәуелсіздік принципі
бойынша Nz бойлық күшінің
әсерінен
![]() - июші моменттің әсерінен
- июші моменттің әсерінен
![]() - июші моменттің әсерінен
- июші моменттің әсерінен![]() тік кернеулері пайда
болады.
тік кернеулері пайда
болады.
Сонымен Е нүктесіндегі қорытынды кернеу
 (7)
(7)
Алынған (7) формуласымен қиманың кез келген нүктесіндегі кернеуді табуға болады. Кернеудің таңбасын дұрыс анықтау үшін полюс жаткан квадрант бірінші квадрант деп қарастырылып, ішкі факторлар мен нүктенің координаталары (7) формуласына өз таңбаларымен енгізіледі. Бірінші квадранттағы нүктелерде созушы кернеулер тудыратын июші моменттер оң таңбалы деп саналады.
Қауіпті кернеулер бұрыштағы A, C нүктелерінде пайда болады. Соңдықтан сырықтың беріктігі А нүктесі үшін жазылған беріктік шарты бойынша тексеріледі
![]()
немесе
![]() ,
,
мұндағы хa , ya - A нүктесінің координаталары.
Морт материалдардан жасалған брустар тек созушы емес ең үлкен сығушы кернеу бойынша да тексеріледі
![]()
Енді бұрыштық нүктелері жоқ 4-суретіндегі қиманы қарастырайық. Бұрыштық нүктелері жоқ қиманың қауіпті нүктелерін табу үшін алдымен бейтарап сызықтың орны анықталады. Бейтарап сызықтың бойында жатқан нүктелерде кернеу нөлге тең. Олай болса
 (8
а)
(8
а)
Мұндағы хб,
yб —
бейтарап сызық нүктелерінің айнымалы
координаталары. Есептің бастапқы шарты бойынша, ![]() болғандықтан
болғандықтан
 (8
б)
(8
б)
Енді хб, yб координаталарын кезекпен нөлге теңестіріп, X пен У осьтерінің бейтарап сызықпен қиылған кесінділерін табамыз
 (9)
(9)
Кесінділерді (таңбаларын ескеріп) X, Ү осьтеріне өлшеп салып, алынған m, n нүктелері арқылы бейтарап сызықты жүргіземіз (4-сурет). Суретте, бейтарап сызық (б.с.) арќылы белгіленген. Бейтарап сызық координата осьтерін бірінші квадрантқа қарсы үшінші квадрант арқылы қиып өтеді. Қиманың контур бейтарап сызыққа параллель, жанамалар жүргізіп қауіпті А, нүктелерін табамыз.
Қауіпті нүктелер үшін беріктік шарты келесі түрде жазылады
![]() (10)
(10)
![]() (11)
(11)
Мұндағы ха ,уа - А нүктесінің координаталары, хб, yб- -B нүктесінің координаталары.
Кернеудің (7) формуласы бойынша салынған эпюрі 4- суретте көрсетілген.
Қима өзегі. Алынған (9) формуласы бойынша, бейтарап сызық координаттар басы (қиманың ауырлық орталығы) арқылы өтпейді. Сыртқы күштің эксцентриситеті неғұрлым үлкен болса, бейтарап сызық координаттар басына соғұрлым жақын, неғұрлым кіші болса — соғұрлым алыс. Эксцентриситет нөлге тең болғанда бейтарап сызық пен координаттар басы ара қашықтығы шексіздікке ұмтылып, сырық Орталық созылу деформациясына ұшырайды.
Бейтарап сызықтың бұл қасиеті инженерлік практикада кеңінен қолданылады. Морт материалдардың көбісінің сығылуға қарағанда созылуға қарсыласу қабілеті төмен екені бізге белгілі. Бетон, тас, күйдірілгген қыш сияқты материалдардан жасалған азаматтық немесе өндірістік құрылыс элементтерінде, шамасы мардымсыз, созушы кернеулердің пайда болуы сыну қаупін туғызуы мүмкін. Соңдықтан мұндай құрылыс элементтері үшін қима ядросы тұрғызылады.
Қима өзегі деп, ауырлық центрін қоршаған, келесі қасиеті бар аймақты айтады: сыртқы күштің әсер ету нүктесі осы аймақта жатса, қиманың барлық нүктелерінде таңбалары бірдей кернеулер пайда болады.
ІІ. Кез келген күш әсерінен сырықтар жүйелеріндегі орын ауыстырулар
2.1. Кез келген күш түсірілген брустың поетнциялық энергиясы
Жоғарыда түзу сырықтың созылу, бұралу және иiлу кезінде орын ауыстыруы анықталған ды. Ендi сырыққа күш түсiрiлген кезде көлденен қимасында бip мезгiлде тiк және көлденен күштер, июшi және бұраушы моменттер пайда болуын қарастырайық. Сонымен бipгe сырық тек қана түзу болмай қисықтығы аз, сондай-ак жазык немесе кеңiстiк жүйелердi жасайтын түзу. бөліктерден тұрады деп есептеп қарастырылатын мәселелер ауқымын кеңейтемiз. Қарастырылатын есептердi шешу тек орын ауыстыру шамаларын ғана анықтаумен бipгe конструкция қатаңдығын бағалау үшiн де қажет.
К үш түcipiлгeн сырықтар жүйесінің потенциялық энергиясының жалпы
өрнегіне сүйенiп, энергетикалық қатынастар арқылы орын ауыстыруды
оңай табуға болады.
үш түcipiлгeн сырықтар жүйесінің потенциялық энергиясының жалпы
өрнегіне сүйенiп, энергетикалық қатынастар арқылы орын ауыстыруды
оңай табуға болады.
Потенциялық энергияньң анықталуы сырықта пайда болатын iшкi күш әсерлерін талдаудан туындайды. Бұл талдау, әдетте, қималар тәсілiмен жүргiзiледі де, июші және бұраушы моменттердің әпюрлерiн, ал қажет жағдайда бойлық және көлденең күш эпюрлерiн салумен анықталады.
Барлық жағдайда iшкi күш әсерлерiнiң эпюрлерi сырықтың өсіне салынады (1-сурет). Кеңістiктегі сырық үшiн өс сызығы, әдетте, аксонометрияда сызылады және июші моменттердің эпюрлерi иiлу жазықтықтарына сәйкес бейнеленедi (2-сурет). Бұраушы моменттердің эпюрi белгілi бip жазықтықпен байланыстырылмайды да, июші моменттердiң эпюрiнен ерекшеленіп бұранда сызықпен шабақталады.
Потенциялық энергияны анықтау үшін сырықтан ұзындығы dz-ке тең әлементар бөлікті бөліп алайық (3-сурет). Сырық түзу және бастапқы қисықтығы кіші түрде болуы мүмкін. Күш түcipiлгeн жалпы жағдайда әpбip көлденең қимада алты әсер (үш момент және үш күш) пайда болады. Бөлiп алынған бөлікке қатысты осы күш әсерлерін сыртқы күштер деп санап, олардьң элементтi деформациялау кезiнде iстеген жұмысын ықтаймыз.
Б ұл жұмыс сырықтың элементар бөлігiнде жинақталған потенциялық
энергияға тең болады. Сол жаққа
түсiрiлген барлық күш әсерлерiнiң жұмысы нөлге тең болуы үшін
элементтiң сол қимасын шартты түрде қозғалмайтын деп қарастырамыз
(3-сурет). Оң қиманьң күш түcipiлгeн нүктесi элементтiң
деформациясы салдарынан шамалы орын ауыстырып, iздеп отырған жұмыс
істелiнедi. Алты күш әсеріне жеке-жеке сәйкес келетiн орын ауыстыру
кезiнде қалған бес әсердің бipeyi де жұмыс істемейтіндей болуының
үлкен маңызы бар. Мысалы, Мδ моментi
әсерiнен z осіне сәйкес қиманың бұралу бұрышы пайда болады. Осы
бұрыштық орын ауыстыруда жұмыс тек Ms моментімен iстелiнедi.
у oci бойынша
сызықтық орын ауыстыру Qу күш әсерінен болады да, орын ауыстыру
кезінде тек осы күш жұмыс атқарады. Демек, элементтiң потенциялық
энергиясы алты күш әсерiнің әрқайсысының атқарған тәуелсiз
жұмыстарының қосындысы, яғни буралу,
иілу, созылу және ығысу энергияла-
ұл жұмыс сырықтың элементар бөлігiнде жинақталған потенциялық
энергияға тең болады. Сол жаққа
түсiрiлген барлық күш әсерлерiнiң жұмысы нөлге тең болуы үшін
элементтiң сол қимасын шартты түрде қозғалмайтын деп қарастырамыз
(3-сурет). Оң қиманьң күш түcipiлгeн нүктесi элементтiң
деформациясы салдарынан шамалы орын ауыстырып, iздеп отырған жұмыс
істелiнедi. Алты күш әсеріне жеке-жеке сәйкес келетiн орын ауыстыру
кезiнде қалған бес әсердің бipeyi де жұмыс істемейтіндей болуының
үлкен маңызы бар. Мысалы, Мδ моментi
әсерiнен z осіне сәйкес қиманың бұралу бұрышы пайда болады. Осы
бұрыштық орын ауыстыруда жұмыс тек Ms моментімен iстелiнедi.
у oci бойынша
сызықтық орын ауыстыру Qу күш әсерінен болады да, орын ауыстыру
кезінде тек осы күш жұмыс атқарады. Демек, элементтiң потенциялық
энергиясы алты күш әсерiнің әрқайсысының атқарған тәуелсiз
жұмыстарының қосындысы, яғни буралу,
иілу, созылу және ығысу энергияла-

3 - сурет
рының қосындысы ретінде қарастыруға болады:
![]()
Алғашқы төрт қосылғыш өрнектерi бiзге белгілi:
 .
.
Тек ![]() және
және ![]() ығысу энергиясын табу
қажет.
ығысу энергиясын табу
қажет. ![]() шамасын анықтау үшін табан ауданы
шамасын анықтау үшін табан ауданы
![]() және ұзындығы
және ұзындығы ![]() болатын элементар призманы
қарастырамыз. Бұл көлемдегі энергия
болатын элементар призманы
қарастырамыз. Бұл көлемдегі энергия ![]() тең, мұндағы
тең, мұндағы
![]() -
ығысу кезiндегі меншiкті потенциялық энергия.
(6.15') (§ 3, VI тарау) өрнегіне сәйкес
-
ығысу кезiндегі меншiкті потенциялық энергия.
(6.15') (§ 3, VI тарау) өрнегіне сәйкес ![]() . Сонымен,
. Сонымен,
![]() .
.
![]() аудан бойынша интегралдасақ:
аудан бойынша интегралдасақ:
![]()
Бipaқ Журавский формуласы бойынша ![]() Демеқ,
Демеқ,
![]() , немесе
, немесе ![]() .
. ![]() (1)
(1)
деп белгілейік. Сонда
![]() , осыған ұқсас
, осыған ұқсас ![]() .
.
![]() және
және ![]() коэффициенттерi қиманың геометриялық түрiне
байланысты өлшемсiз шамалар. Мысалы, өлшемдерi
коэффициенттерi қиманың геометриялық түрiне
байланысты өлшемсiз шамалар. Мысалы, өлшемдерi
![]() және
және ![]() .
.
болатын тiк бұрыш үшін шабақталған ауданның
![]() статикалық моментi
статикалық моментi ![]() өсіне сәйкес
өсіне сәйкес  .
.
Одан
ары ![]() .
.
Түрлендiру (2) формуласы бойынша
![]() .
.
Тұтас дөңгелек қима үшін Жұка
қабырғалы дөңгелек профиль үшін ![]() және т.
с. с. Енді (1) өрнегі мынадай түрде болады:
және т.
с. с. Енді (1) өрнегі мынадай түрде болады:
 .
.
Брустьн потенциалық энергиясын алу үшiн бұл өрнектi брустың ұзындығы бойынша интегралдау керек:
 (3)
(3)
Егер конструкция күрделi болып, ол сырық тәрiздi бiрнеше әлементтерден құралса, онда интегралдаудан кейiн әр сырық шегінде құраушы элементтер санына сәйкес энергияларды қосу қажет болады.
(3) өрнектегі барлық қосылғыштар маңызды болмайды. Іс жүзінде көптеген жүйелерде құраушы элементтер иiлy не бұралуға жұмыс істейді, сондықтан (3) өрнегiндегі соңғы үш қосылғыш алғашқы үшеуіне қарағанда айтарлықтай аз болады. Басқаша айтқанда, созылу және ығысу энергиясы, әдетте иілу және бұралу энергиясынан айтарлықтай аз болады.
Бipaқ, сонымен бipгe қосылғыштардың шамалары бiрдей болуы да ықтимал. Мысалы, көрсетiлген иіні шағын орталықтан тыс созылған сырық үшiн созылу және иілу энергиясы бiр шамада болады.
Кастилиано теоремасы
Сырықтың орын ауыстыруын анықтау үшiн Кастилиано теоремасын қолдануға болады: жүйенің потенциялық энергиясының күш бойынша дербес туындысы күш түсiрiлген нүктенің оның бағыты бойынша орын ауыстыруына тең. Бepiлгeн бағытта орын ауыстыруды сол бағыттағы толық орын ауыстырудың проекциясы болып табылады. Кез келген күш жүйесi түсiрілген және орын ауыстыру болмайтын тұтастай қатаң бекiтiлген серпімді дененi қарастырайық. Сыртқы күштер жұмысының нәтижесінде дене көлемінде деформацияның жинақталған потенциялық энергиясы U-ға тең болсын.
Мысалы, Рn күш 3yt өсiмше берейiк. Сонда U потенциялық энергия мына шамаға өзгереді
![]()
Ендi күш түcipy тәpтiбiн
өзгертемiз. Серпiмдi денеге
алдымен dPn күштi түсiремiз. Күштiң түсу нүктесiнде шексіз аз орын ауыстыру пайда
болады, оның dP проекциясы күш бағытында да dδ-ға тең. ![]() күшінiң жұмысы
күшінiң жұмысы
![]() -ға
тең болады.
-ға
тең болады.
Сыртқы күштер жүйесін тұтастай
түсiремiз. ![]() күші
болмаса, жүйенiң потенциялық энергиясы кайтадан U-ға тең болар
едi. Бірақ
бұл энергия сыртқы күштер жүйесi әсерінен
күші
болмаса, жүйенiң потенциялық энергиясы кайтадан U-ға тең болар
едi. Бірақ
бұл энергия сыртқы күштер жүйесi әсерінен
![]() орын ауыстыру кезiнде
орын ауыстыру кезiнде ![]() күш тудыратын
күш тудыратын
![]() қосымша жұмыстың шамасына өзгередi.
қосымша жұмыстың шамасына өзгередi.
![]() шамасы қайтадан Рn күші бағытында
толық орын ауыстыру проекциясын бейнелейдi. dPn
шамасы қайтадан Рn күші бағытында
толық орын ауыстыру проекциясын бейнелейдi. dPn![]() көбейтiндiсiнiң алдына
көбейтiндiсiнiң алдына ![]() көбейткіш
3 қойылмайды, өйткенi
көбейткіш
3 қойылмайды, өйткенi ![]() проекциясында
проекциясында
![]() өзгepicciз қалады.
өзгepicciз қалады.
Күш түсiрудiң керi тәртiбiнде потенциялық энергияның өрнегі келесi түрде болады:
![]() (5)
(5)
Бұл өрнектi (4) өрнегiне теңестiрiп, ![]() көбейтіндiсін аздығына байланысты ескермей алып
тастағанда.
көбейтіндiсін аздығына байланысты ескермей алып
тастағанда.
![]() (6)
(6)
болады. Сонымен, потенциялық энергияны сыртқы күштердiң бipeyiне қатысты дербес туындысы сол күштің түсу нүктесiнiң күш бағыты бойынша орын ауыстыруына тең болады.
(6) өрнегінде
![]() күшiн жалпыланған күш, яғни күш факторы ретінде
түсiндiруге болады. Сонда
күшiн жалпыланған күш, яғни күш факторы ретінде
түсiндiруге болады. Сонда ![]() -ді жалпыланған орын ауыстыру, яғни
-ді жалпыланған орын ауыстыру, яғни ![]() жалпыланған күш жұмыс iстейтiн
геометриялық параметр ретінде қарастыру керек. Егер
жалпыланған күш жұмыс iстейтiн
геометриялық параметр ретінде қарастыру керек. Егер
![]() деп сыртқы моментті
деп сыртқы моментті ![]() түсінсек, онда
түсінсек, онда
![]() момент түcipiлгeн нүктенiң момент бағытындағы
бұрыштық орын ауыстыруын бейнелейдi. Егер денеге гидростатикалық
қысым күштерi түcipiлce, онда потенциалық энергияны қысым бойынша
дифференциалдап дене көлемінің өзгерісін
анықтаймыз.
момент түcipiлгeн нүктенiң момент бағытындағы
бұрыштық орын ауыстыруын бейнелейдi. Егер денеге гидростатикалық
қысым күштерi түcipiлce, онда потенциалық энергияны қысым бойынша
дифференциалдап дене көлемінің өзгерісін
анықтаймыз.
Кастилиано теоремасын дәлелдеу
кезінде дене түріне, сыртқы күштер жүйесіне ешқандай шектеулер
қойылған жоқ. Оған қоса, материал Гук заңына
бағына ма, жоқ па, ол да қарастырылмады. Дегенмен, бұл шектеулер
бар. Егер күш пен орын ауыстыру арасында сызықты
тәуелдiлiк болса, онда сыртқы күштер
жүйесінің атқарған жұмысы күштер жүйесi ![]() күшіне дейін не одан кейін
түсiрілгеніне байланысты әр
түрлi
болады.
Басқаша айтсақ (4) және (5) өрнектерінің қосылғыштары
бiрдей болады. Бұл жағдайда
Кастилиано теоремасы орындалмайды. Практикада кездесетін көптеген
есептерде күш пен орын ауыстырудың қатынасы сызықты болады, ал
мұндай есептердi шешуге Кастилиано теоремасын
пайдалануға болады. Бастапқы өлшемдерi өзгермеу және күш әсерінің
тәуелсiздік
принциптерiн қолдануға болмайтын
жүйелерде орын ауыстыруды анықтау кeзiндe Кастилиано теоремасын
жоғарыдарыдай түрде пайдалануға болмайды.
күшіне дейін не одан кейін
түсiрілгеніне байланысты әр
түрлi
болады.
Басқаша айтсақ (4) және (5) өрнектерінің қосылғыштары
бiрдей болады. Бұл жағдайда
Кастилиано теоремасы орындалмайды. Практикада кездесетін көптеген
есептерде күш пен орын ауыстырудың қатынасы сызықты болады, ал
мұндай есептердi шешуге Кастилиано теоремасын
пайдалануға болады. Бастапқы өлшемдерi өзгермеу және күш әсерінің
тәуелсiздік
принциптерiн қолдануға болмайтын
жүйелерде орын ауыстыруды анықтау кeзiндe Кастилиано теоремасын
жоғарыдарыдай түрде пайдалануға болмайды.
Мор интегралы
Кастилиано теоремасының көмегімен тек сыртқы күштер түcipiлгeн нүктесінің және тек күш бағытында ғана орын ауыстыруын анықтайтындығымызға қарастырылған мысалдардан көзiмiз жеттi. Ал іс жүзінде жүйенiң кез келген нүктелерiнiң әр түрлi бағытта орын ауыстыруын анықтау керек болады.
 Егер сыртқы күштер түcipiлмеген нүктеде орын ауыстыруды анықтау
керек болса, онда нүктеге керек бағытта Ж сыртқы күшті түсіремiз
(4-сурет). Одан ары жүйенің потенциялық энергиясының өрнегін
Ж күшін ескере
отырып жазамыз. Энергияның Ж бойынша дифференциалдап,
нүктенiң Ж күші түcipiлгeн бағыты бойынша орын ауыстыруын табамыз.
Содан кейiн Ж күшін нөлге теңеймiз, сонда табылған шама iзделген орын
ауыстыру болып табылады.
Егер сыртқы күштер түcipiлмеген нүктеде орын ауыстыруды анықтау
керек болса, онда нүктеге керек бағытта Ж сыртқы күшті түсіремiз
(4-сурет). Одан ары жүйенің потенциялық энергиясының өрнегін
Ж күшін ескере
отырып жазамыз. Энергияның Ж бойынша дифференциалдап,
нүктенiң Ж күші түcipiлгeн бағыты бойынша орын ауыстыруын табамыз.
Содан кейiн Ж күшін нөлге теңеймiз, сонда табылған шама iзделген орын
ауыстыру болып табылады.
С
нүктесінің ![]() өci бағытындағы орын
ауыстыруын анықтайық. Кез келген сыртқы күштер жүйесi түсiрiлген
брус үшiн
өci бағытындағы орын
ауыстыруын анықтайық. Кез келген сыртқы күштер жүйесi түсiрiлген
брус үшiн ![]() бағыты бойынша С нүктесіне
Ж күшiн
түсiрейік. Күш факторларының Ж күшіне байланысты
шамалары, мысалы, қайсыбiр көлденең қимада бұраушы момент мынадай
түрде болады:
бағыты бойынша С нүктесіне
Ж күшiн
түсiрейік. Күш факторларының Ж күшіне байланысты
шамалары, мысалы, қайсыбiр көлденең қимада бұраушы момент мынадай
түрде болады: ![]() мұндағы бiрiншi қосылғыш түcipiлгeн сырт-қы күштердiң әсерінен пайда болатын момент,
ал екінші қосылғыш түсiрілген
Ж күшінің
нәтижесінде пайда болған қосымша момент
мұндағы бiрiншi қосылғыш түcipiлгeн сырт-қы күштердiң әсерінен пайда болатын момент,
ал екінші қосылғыш түсiрілген
Ж күшінің
нәтижесінде пайда болған қосымша момент ![]() мен
мен ![]() брустың ұзындығы бойынша
өзгеретiндіктен z-тің функциялары екендiгi өзiнен-өзi бeлгiлi. Осыған ұқсас
қалған iшкi күш әcepлepi үшін де қосымша қосылғыштар пайда
болады:
брустың ұзындығы бойынша
өзгеретiндіктен z-тің функциялары екендiгi өзiнен-өзi бeлгiлi. Осыған ұқсас
қалған iшкi күш әcepлepi үшін де қосымша қосылғыштар пайда
болады: ![]() және т. б.
және т. б.
Қосымша
![]() т. б. күш, әсерлерi Ж күшіне пропорционал
екендiгi айкын. Сондықтан,
т. б. күш, әсерлерi Ж күшіне пропорционал
екендiгi айкын. Сондықтан,
 (7)
(7)
мұндағы
![]() және т. б. байланысты пропорционалдық еселіктер,
яғни қарастырылмақшы қиманың күйiне,
сырықтың ұзындығына байланысты айнымалылар. Егер сыртқы күштер
жүйесін алып тастап және күштi бiрлiк күшпен ауыстырса, онда
және т. б. байланысты пропорционалдық еселіктер,
яғни қарастырылмақшы қиманың күйiне,
сырықтың ұзындығына байланысты айнымалылар. Егер сыртқы күштер
жүйесін алып тастап және күштi бiрлiк күшпен ауыстырса, онда
![]() және т. б.
және т. б.
меқ
![]() — қарастырылатын нүктеге берiлген бағытта түсiрiлген бiрлiк
күштiң әсерiнен сырықтың көлденең қимасында пайда болатын iшкi күш
факторлары болып шыкты.
— қарастырылатын нүктеге берiлген бағытта түсiрiлген бiрлiк
күштiң әсерiнен сырықтың көлденең қимасында пайда болатын iшкi күш
факторлары болып шыкты.
Энергия өрнегіндегі iшкi күш әсерлерін (7) формуладағы жаңа мәндерiмен ауыстырамыз. Сонда,
 (8)
(8)
С өрнегін Ж бойынша дифференциалдап, содан кейін Ж=0 қойсақ, С нүктесінің орын ауыстыруын табамыз:
Алынған интегралдар Mop интегралы деп аталады.
Верещагин әдісі
Орын ауыстыруды Мор интегралының көмегiмен анықтағанда интеграл астындағы функциялардың аналитикалық өрнегін құру қажеттiгi оның негiзгi кемшілігі болып саналады. Бұл әciресе көп бөлікті сырықта орын ауыстыруды анықтағанда тиiмciз. Бipaқ сырық әрқайсысының қатаңдығы алынған шекте тұрақты болатын бөліктерден құралса, онда интегралдауды оңайлатуға болады. Ол бiрлiк күш әсерлерінің эпюрлерi сырықтың түзу өсті бөліктерінде түзу сызықты сызықты болатындығына негiзделедi.
Ұзындығы
а-ға тең бөлікте
![]() екi функцияның көбейтiндiсiнен интеграл алу
керек болсын делiк:
екi функцияның көбейтiндiсiнен интеграл алу
керек болсын делiк:
 (9)
(9)
Функциялардың бipeyi сызықты
болсын: ![]() .(8.9) өрнегi мына түрге енедi:
.(8.9) өрнегi мына түрге енедi:
 .
.
Бipiншi интеграл
![]() қисығымен шектелген ауданды, басқаша
айтсақ,
қисығымен шектелген ауданды, басқаша
айтсақ, ![]() эпюрi ауданын бередi (5-сурет):
эпюрi ауданын бередi (5-сурет):
 . Екіншi интеграл ауданның
. Екіншi интеграл ауданның
![]() өciнe сәйкес статикалық моментiн
бейнелейдi
өciнe сәйкес статикалық моментiн
бейнелейдi  , мұндағы
, мұндағы ![]() - бipiнші эпюрдiң ауырлық орталығының координаты.
Сонда
- бipiнші эпюрдiң ауырлық орталығының координаты.
Сонда ![]() , немесе
, немесе ![]() .
.
Сонымен, Верещагин әдісі
бойынша интегралдау бiрінші эпюрдiң ауданың өзінің ауырлық
орталығының тұсындағы екiнші (сызықты) эпюрдің ординатасына
көбейтумен алмастырылады. ![]() және
және
![]() функциялары сызықты болғанда көбейту операциясы
коммутативтiк қасиетке ие
болады.
функциялары сызықты болғанда көбейту операциясы
коммутативтiк қасиетке ие
болады.
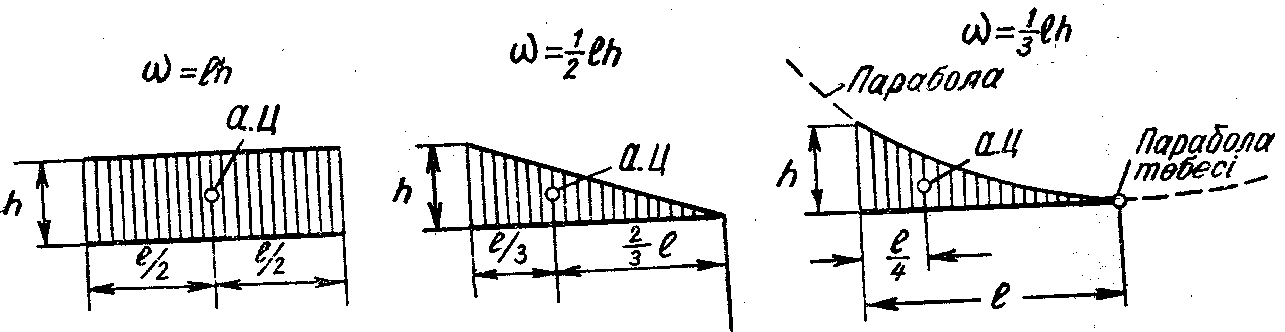
5-сурет
Мор интегралдарының
әрқайсысына ![]() т.с.с. көбейтіндiлер кiредi. Верещагин тәсілін алты интегралдың кез келгеніне қолдануға
болады, олардың эпюрлерін көбейту июші не бұраушы моменттер,
немесе бойлық
және көлденең күштер үшін бiрдей. Айырмашылығы:
эпюрлер көбейтіндiсi иілудегідей EJ
қатаңдығына
емес, бұралудағы
т.с.с. көбейтіндiлер кiредi. Верещагин тәсілін алты интегралдың кез келгеніне қолдануға
болады, олардың эпюрлерін көбейту июші не бұраушы моменттер,
немесе бойлық
және көлденең күштер үшін бiрдей. Айырмашылығы:
эпюрлер көбейтіндiсi иілудегідей EJ
қатаңдығына
емес, бұралудағы ![]() қатандығына, немесе созылу және ығысу
кезіне сәйкес EА не GА-ға
бөлінеді.
қатандығына, немесе созылу және ығысу
кезіне сәйкес EА не GА-ға
бөлінеді.
Былай
қарағанда Верещагин тәсілі айтарлықтай ықшамдау бермейтін сияқты.
Оны қолдану үшін ішкі күштер эпюрлерінің ayданы мен ауырлық
орталығының орнын табу керек. Эпюр күрделi болғанда тікелей
интегралдау қажет болады. Бірақ іс жүзінде кездесетін ішкі күштер
эпюрлepiн әдетте қарапайым фигураларға: тiктөртбұрышка, үшбұрышқа,
параболалық үшбұрышқа жіктеуге болады (5-сурет), сонан соң олардың
ауданының шамасы ![]() және ауырлық орталығының орны
бeлгiлi болады. Бұралу, созылу және ығысу кезінде эпюрлер тіптi
қарапайым болады. Олар әдетте сызықты болып және әр түрлi
комбинацияда тіктөртбұрыштар мен үшбұрыштардан
тұрады.
және ауырлық орталығының орны
бeлгiлi болады. Бұралу, созылу және ығысу кезінде эпюрлер тіптi
қарапайым болады. Олар әдетте сызықты болып және әр түрлi
комбинацияда тіктөртбұрыштар мен үшбұрыштардан
тұрады.
2.2. Цилиндр тәрізді оралған серіппелерді есептеу
Машина жасауда серiппелердiң атқаратын қызметi үлкен. Көптеген механизмдер конструкциясында ондаған, жүздеген cepiппeлep болады. Орам саны аз винттiк цилиндрлi cepiппенi есептеу теориясын қарастырайық. Атап айтқанда, мұндай cepiппелердiң осiне перпендикуляр жазықтыққа орамның көлбеу бұрышы кiшi, демек орамды сол жазықтықта жатыр деп есептеуге болады.
d, r - cepiппе дайындалған сымның диаметрi және радиусы;
D - серiппенiң орташа диаметрi; R – серiппе орамының радиусы,n -орам саны болсын (6, a-сурет).
Cepiппенi екi бөлiкке бөлемiз (6, б-сурет). Төменгi бөлiгiн алып тастап, оның жоғарғы бөлiкке әсерiн көлденең күшпен Q және бұраушы моментпен М ауыстырамыз. Онда Q=P; ал M=P·R. Сонымен, аз орамды cepiппe қиюға және бұралуға ұшырайды. Қиюда жанама кернеулер cepiппe орамының қимасы бойынша бiрқалыпты үлестiрiлген деп есептеймiз

![]() (3)
(3)
n орамы бар cepiппенi дайындауға жұмсалған сымның ұзындығы мына формуламен анықталады. l=2Rn сондықтан
![]()
А жұмыс пен U потенциялық энергияны теңестiрiп және
![]()
ескерiп
![]() (4)
(4)
Созылу және сығылу теориясында сырықтың көлденең қимасының өлшемi және формасы қарапайым геометриялық сипаттамамен, яғни қима ауданымен өрнектеледi. Иiлу және бұралу теориясында қиманың күрделiрек геометриялық сипаттамалары қарастырылады.
Сырықтың кез келген көлденең қимасын аламыз (1-сурет). Оны х,у координаттар жүйесiмен байланыстырып, мына екi интегралды қарастырамыз:
ҚОРЫТЫНДЫ
Сыртқы күш пен қауіпсіз кернеу белгілі болса, қиғаш иілген арқалықтың қима өлшемдерін беріктік шартынан келесі тәртіппен анықтайды қиманың өлшемдері алдын ала белгілі деп қарастырылып қандайда бір мәндері (4) теңсіздігіне енгізіледі.
Есептеліп анықталған теңсіздіктің сол жағы оң жағына қарағанда айтарлықтай кіші болса, қима өлшемдерін үлкейтіп, ал айтарлықтай үлкен болса кішірейтіп аркалықтың беріктігі қайта тексеріледі
Басты жазықтықтардан басқа, бойлық өс арқылы өтетін, кез келген жазықтықтарда жатқан сыртқы күштердің әсерінен конструкция элементі қиғаш иіледі. Қиғаш иілген арқалықты беріктікке есептеу тәртібі келесі мысалда көрсетілген. Бір ұшы қатаң бекітілген арқалықтың екінші ұшына Р күші әсер етсін
Екінші беріктік теориясын ең үлкен сызықтық деформация теориясы деп атайды. ¤йткені, бұл теорияда беріктік нышаны ретінде сызықтық деформация қабылданған.
Оның негізін Мариотт салып, Сен-Венан жалғастырған. Ол былай тұжырымдалады:
Потенциялық энергияньң анықталуы сырықта пайда болатын iшкi күш әсерлерін талдаудан туындайды. Бұл талдау, әдетте, қималар тәсілiмен жүргiзiледі де, июші және бұраушы моменттердің әпюрлерiн, ал қажет жағдайда бойлық және көлденең күш эпюрлерiн салумен анықталады.
Созылу және сығылу теориясында сырықтың көлденең қимасының өлшемi және формасы қарапайым геометриялық сипаттамамен, яғни қима ауданымен өрнектеледi. Иiлу және бұралу теориясында қиманың күрделiрек геометриялық сипаттамалары қарастырылады.
Орын ауыстыруды Мор интегралының көмегiмен анықтағанда интеграл астындағы функциялардың аналитикалық өрнегін құру қажеттiгi оның негiзгi кемшілігі болып саналады. Бұл әciресе көп бөлікті сырықта орын ауыстыруды анықтағанда тиiмciз. Бipaқ сырық әрқайсысының қатаңдығы алынған шекте тұрақты болатын бөліктерден құралса, онда интегралдауды оңайлатуға болады. Ол бiрлiк күш әсерлерінің эпюрлерi сырықтың түзу өсті бөліктерінде түзу сызықты сызықты болатындығына негiзделедi.
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР
-
Н.Қожаспаев, С.Кешуов, И.Мухитов Электротехника /оқу құралы/ - Алматы. Республикалық баспа кабинеті, 1996 ж., 300 бет
-
Электротехника /Под ред- проф. В. Г. Герасимова.— М.: Высшая школа. 1935.
-
Волынский Б. А., Зейн Е. Н..Шатерников В. Е.Электротехника.— Москва.:Эпергоатомиздат, 1987.
-
Борисов Ю.М., Липатов Д.Н., Зорин Ю.Н., Электротехника —Москва.:Эпергоатомиздат, 1985.
-
Касаткин А. С., Немцов М. В..Электротехника.— М.: Энерогоатомиздат. 1983.
-
Иванов И. И., Равдоник С. С. Электротехника.— М.: Высшее школа, 1984.
-
Электротехника. Программированное учебное пособие /Под ред. проф. В. Г. Герасимова.— М.: Высшая школа, 1983.
-
Основы промышленной электроники. /Под ред. проф. А Г. Герасимова.— М.:Высшая школа, 1986.
31

шағым қалдыра аласыз















