Непер таяқшалары. Маңызы және қолданылу жолдары.

«НЕПЕР ТАЯҚШАЛАРЫ. МАҢЫЗЫ ЖӘНЕ ҚОЛДАНЫЛУ ЖОЛДАРЫ»

Жагипарова Арай Бакытовна

Математика және информатика пәнінің мұғалімі

В статье рассматривается практическое использование «палочки Непера», занимающих важную роль в повышении качества знаний, в организации самостоятельной деятельности личности.

The subject of the article is the practical use of the «sticks of Neper» which takes a good role in improving the knowledge quality of individual s activity of organization.

Дана қазақ уақытты күнге қарап, бағытын жұлдызға қарап белгiлесе, өзге елдерде есептеу құралдары ретiнде есеп таяқшаларын пайдаланды. Мұның нәтижесi бүгiнгi калькуляторға, одан соң компьютерлерге алып келдi.

Есептеуіш техника есептеу және мәліметтерді өңдеу процесінің маңызды компоненті болып табылады. Есептеуге арналған алғашқы құрал ретінде есептеу таяқшаларын атауға болады, бұл құрал қазіргі кезде де бастауыш сынып оқушыларын есепке үйрету үшін қолданылады. Даму жолында бұл құралдар күрделене түсті (мысалы, финикиялық саз фигуралары).

Уақыт өте келе, қарапайым құрылғылардан күрделі құралдар пайда бола бастады: абак, логарифмдік сызғыш, механикалық арифмометр, электронды компьютер. Алғашқы есептеуіш құрылғылардың қарапайымдылығына қарамастан, олармен жұмыс жасауға үйренген адам, қазіргі заманғы калькуляторларды пайдаланғаннан да жылдам есептер жүргізе алады. Әрине, қазіргі заманғы есептеуіш құрылғыларының жұмыс өнімділігі және есептеу жылдамдығы ең жылдам есептегіш адамның өзін шаң қаптырып кетеді.

Әйтсе де біз бүгін «Математикадағы есептеулер үшін көбейту, бөлу, үлкен сандардан квадрат, куб түбірлер шығару амалдары көптеген қиыншылықтар туғызып, жұмысқа бөгет жасап, шаршатып және есепшілердің басын қатырып, қыруар уақыт алып, сөйте тұра сан алуан қателіктерге ұрындырып жүргеніне көзім жеткеннен кейін, мен осы бейнеттерден құтқарар оңай жолдарды іздеп, ойлана бастадым. Осы мақсатқа жеткізетін әр түрлі тәсілдерді қарастыра келіп, мен, ақырында, жан қинамайтын, келешекте қолдануға болатын тамаша ережелер таптым. Бұл ережелердің ішіндегі өте-мөте пайдалылары... сандардың бірін біріне көбейтіп жатудан, бөлуден немесе түбір шығарудан құтқаратын олардың орнына басқа бір сандарды қосып, азайтып немесе екіге яки үшке ғана бөліп, оңай амалдар арқылы шығаруға мүмкіндік беретін ережелер»,-деп Д.Непердің өзі айтқандай Непер таяқшалары арқылы қалай тез есептеуге болатындығы жөнінде айтпақпыз.

«Непер таяқшалары» атауының дамуына шотландиялық математик Д. Непердiң ойлап тапқан арнайы есеп таяқшалары негiз болды. Ол таяқшалар арқылы жұмыс iстеу жеңiл болды. Тек қана кемшiлiгi, жиналған қосындыларды механикалық түрде ауыстыру мүмкiндiгi болмады. Дегенмен, бұл таяқшалар Еуропада кеңiнен таралды. Непердiң жолын қуып таяқшаларды дамытушылар көп болды. Олар қателiктердi жөндеп, өзгерiстер жасады. Сондықтан, осы тақырыпты алған мақсатым Непер таяқшасымен есептеу арқылы оқушының шапшаң есептеуіне, ақыл-ойының дамуына септігімді тигізу болып табылады.

Н епер таяқшалары есептеу құралы ретінде астрономияда, артиллерияда және басқа да салаларда кеңінен қолданылды. ХҮІ ғасырдың 70-ші жылдарында өмір сүрген ағылшын философы Томас Морені «Барлық уақыттағы адам» деп атап, фильм түсірілген болатын. Ал, егер одан бірнеше онжыл кейін өмір сүрген отандасы туралы фильм түсірілсе, оны «Уақыттан озған адам» деп айтуға болушы еді. Біз оның есімін атақты Галилео Галилеймен, Николай Коперникпен тіпті мүмкін болса Леонардо да Винчи мен қатар қоюға болатын сэр Джон Непер туралы айтпақпыз.

Непер – шотландық математик және теолог- протестант (теологиямен шұғылданушы, ал теология-діннің хадистері туралы ілім. Протестант – протестантизмді жақтаушы, ал протентантизм христиан дініндегі үшінші бағыт) – ақсүйек, дворян әулетінен. 1550 жылы Мерчистон бекінісінде Эдинбург маңайында дүниеге келген, осы жерде 1617 жылы 4 сәуірде дүниеден өткен.

Ол Эдинбург университетінде білім алды, содан соң білім іздеу жолында ұзақ уақыт Европаға саяхат жасады. Қорыта келе ұзақ саяхаттағанннан кейін сол кездегі көпшілік ғалымдар секілді Непер жан-жақты, бесаспап, кең профильді маман болып шықты. Кейінгі өмірінің көп уақытын Непер дін іліміне арнаған, нағыз шотландықтар тәрізді құдайға табыну жөніндегі айтыстарға қатысқан.

1593 жылы теолог ретінде ол «Иоанн Богословтың қарапайым түсіндірмесі» атты еңбегі жарыққа шыққаннан кейін танымал болды. Сонымен бірге ол астрономия мен алхимия ғылымдарымен де шұғылданған. Осы әуестігіне қарамастан ол инженер де болған. Жерді өңдейтін машиналар, жер суғаруға арналған су насосын ойлап тапқан. Сонымен бірге, Непер бірнеше «құпия» құрылғылар, оның ішінде айна мен линзалар жүйесі негізінде жасалған сәулелік қаруды - нысанаға дәл тигізуге бағытталған «өлім қаруын», су астында қолданатын құрылғыны (акваланг), оқ өтпейтін арбаны (танк) ойлап тапқан.

Өмірінің соңғы жылдарында математика ғылымында жаңалықтар ашпаса, мүмкін оның аты әлі де біздің ұрпаққа жетпей қалар ма еді?.

Оның ең алғашқы математикалық еңбегі – «Ғажайып логарифм кестесінің түсіндірмесі» (1614ж). Бұл еңбегінде логарифмдер кестесі мен «логарифм» терминіне түсіндірме берілді. Кейінірек, 1619 жылы «Ғажайып логарифм кестесінің құрылымы» еңбегінде логарифмдер қасиеттері ашып көрсетілді. Бұл еңбегінің жарыққа шығуына Грэшем колледжінің профессоры Генри Бригс тікелей ықпал жасады, кейін ол кісі Непердің сенімді ізбасары, өмірбаяншысы, еңбегін жария етушісі болды. Бригс Непердің осы еңбегімен танысқаннан кейін ол кісімен жүзбе-жүз кездесу үшін Шотландияға саяхатқа шығады, өмірін Непердің ісін жалғастырумен, насихаттаумен өткізді.

Математика тарихында осы екі атаулы жұмыстар көптеген қызығушылық тудырды, ал есептеу техникасы тарихы үшін қарпайым бірақ ең маңызды техникалық құрал болды. Оны кейіннен «Непер таяқшалары» (немесе сүйегі) деп атады. Ол абактан кейінгі екінші орындағы есептеуіш құрылғысы болды. Ақиқатында бұдан бұрын Леонардо да Винчидің салған суретінен есептеуіш машинасының сызбасы табылған, тіпті кейінгі өңделген нұсқасы да бар, бірақ ол калькулятордың практикалық тұрғыдан қолданылуы, сипаттамасының куәлігі жоқ болғандықтан таралмаған. Қарпайымдылығына қарамастан Непердің таяқшасынан құрылғылар тізбегі басталып осы заманғы ДК-ге әкелді.

Бұл туындысының маңыздылығын түсінген Непер өмірінің соңғы жылында «Рабдология немесе таяқшалармен есептеудің Екі кітабы» атты қорытынды трактатын жариялауға дайындаумен болды.

« Рабдология немесе таяқшалармен есептеудің Екі кітабы» трактатында таяқшалар арқылы сандарды көбейту тәсілін көрсеткен. Бұл таяқшалармен көбейту ежелгі gelosia (гелоси) деп аталған көбейту ережесіне өте ұқсас. Қазір бұл арифметикалық есептеудің түп-төркініне ешкім де көңіл бөлмейді, тіпті олар үшін «көбейту ережесі» біртүрлі қызық естіледі, себебі қазіргі баған бойынша көбейту ережесін 3 класста қарастырады ғой. Ал, сол бір алыс заманда бұл көптеген трактаттар арналған үлкен ғылым болған. Бұл жөнінде көпке танымал еңбектің бірі Луки Пачолидің «Summa de arithmetica» (Зумма де аризметик) еңбегінде, көптеген есептеулермен бірге Индияда ойлап табылған, ХІҮ ғасырда парсылар мен арабтар арқылы Европаға таралған gelosia туралы да айтылған.Непер таяқшалары өте танымал және көптеген өнертапқыш ғалымдарды қызықтырды. Ғасыр соңына дейін оның қолданылуы көптеген жаңартуларға ұшырап, басқа құралдың пайда болуына әкелді.

Непердің бұл әдісі өте қарапайым: ол үшін көбейту кестесін тігінен қиып алу керек. Таяқшалар пайда болады, әрине жинақта мұндай таяқшалардан бірнешеу болуы керек, себебі сандарда цифрлар қайталануы мүмкін. Осылайша көбейту түкке тұрмайтын оңай есеп болып шыға келеді, жаңалығы жоқ сияқты болып көрінгенімен таяқшалар өз маңызын жоймайды. Олармен бөлуді де, дәрежеге шығаруды да, тіпті түбір табу амалын да, қосу мен есептеулерге сүйеніп логарифмді есептеуге де болады.

Таяқшалар әдісі Германияда жалғасын тапты. «Рабдология немесе таяқшалармен есептеудің Екі кітабы» жарыққа шыққан кейінгі он жылдан соң Тюбинген университетінің шығыс тілдерінің профессоры Вильгельм Шиккард таяқшалармен жеңіл жұмыс жасауға болатын механизм ойлап тапты. Ол машинаның құрылысы жасалды ма, жоқ па, ол жөнінде айту қиын, бірақ бұл ең алғашқы калькулятордың математикалық моделі болғаны сөзсіз.

Шотланд ғалымы Джон Непер 1617 жылы шыққан кітабында таяқшалар арқылы көбейту тәсілін сипаттаған. Осыдан кейін оны «Непер таяқшалары» деп атаған. Бұл құрылғының негізіне ХҮІІ ғасырда кеңінен таралған торшамен көбейту принципі жатады.

Торшамен көбейту үшін көбейгіштің разрядына сай бағаннан және көбейткіштің разрядына сай жолдан тұратын кесте қолданылады. (бұл кәдімгі көбейту кестесі). Кесте бағанының үстіне көбейгіш разряд бірліктері жазылады. Кестенің оң жағына әр көбейткішке еселіктері қарсы орналасатындай жазылады. әрбір ұяшыққа әр бағандағы көбейгішпен, әр жолдағы көбейткіштің көбейтінділері жазылады. Ұяшықтың нәтижелері диагональ бойынша екі бөлікке бөлінеді. Жоғары бөлігіне үлкен разряд бірлігі, ал астына кіші разряд бірлігі жазылады. Кейін көбейтінді оңнан солға қарай көлбеу бойынша қосындыланады. Табылған қосынды нақты нәтиже болып табылады.

О сындай көбейту тәсілін қолдану арқылы Джон непер «Непер таяқшалары» деп аталатын құрылғы ойлап тапты. Бұл құрылғы таяқшалар жиынтығынан тұрады. Оған 1-ден 9-ға дейінгі сандар жазылған (жол көрсеткіш) бір таяқша және 1-ден 9-ға дейінгі сандардың көбейту кестесі жазылған (көбейгіш разрядтары) тоғыз таяқша кіреді. Осы таяқшалар 1-ден 9-ға дейін нөмірленген, бағана бойына осы көбейгіш разрядының көбейтінділері жазылған. Осыған қарап Непер таяқшалары 123456789 сандарының 123456789 сандарына көбей тіндісін баған бойынша қиып алынған десе болады.

Бұл құралмен көбейту амалын орындау үшін көбейгіш разрядына сай таяқшаларды таңдап алу керек. Сонда таяқшалардың үстінде тұрған сандар көбейгішті құрауы керек. Кейде көбейгіш разрядтары қайталануы мүмкін, мұндай жағдайда әр разрядтың бірнешеуі болуы керек. Сол жағына жол көрсеткіш таяқшаны орналастырамыз, ол арқылы көбейткіштің сәйкес разрядтары алынады. Содан соң таңдалған жол көлбеу бойынша оңнан солға қарай қосындыланады. Табылған нәтиже үлкен разрядтан бастап жазылады.

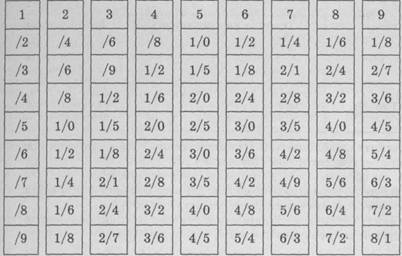
Непер таяқшаларымен көбейту техникасын мысал арқылы қарастырайық: 4938*385

1. 3, 4, 8 және 9 таяқшаларын таңдаймыз.

2. Оларды қатарға 4938 саны шығатындай орналастырамыз.

3. С 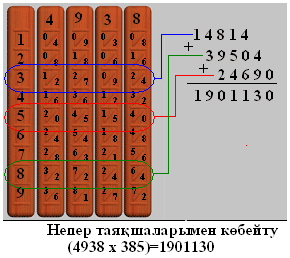ол жағына жол көрсеткіш таяқшаны орналастырамыз.

4. Сол жақ шеткі таяқшаны басшылыққа алып, 3-жолдағы сандарды көлбеу бойынша қосамыз. Қосынды нәтижесі – 14814.

5. Осыған ұқсас жағдайды 8- жолмен де орындаймыз. Нәтиже – 39504.

6. Осы әрекетті көбейгіштің кіші разряды бойынша, яғни 5 - жолмен орындаймыз. Қосынды нәтижесі – 24690.

7. Алынған нәтижелерді көбейгіштің разрядтарын есепке алып орналастырамыз. Бірінші қосынды жүздік разряд үшін табылғандықтан, оны 100-ге көбейтеміз. Екінші қосындыны 10-ға, ал үшіншісін өзгеріссіз қалдырамыз. Сонда 1481400+395040+24690=1901130.

Табылған қосынды 49380*385 көбейтіндісінің нәтижесі.

Бөлу

Непер таяқшалары арқылы тек көбейтуді ғана емес, бөлу, түбір табу амалдарын да орындауға болады. Бөлу техникасын 491756/3852 мысалы арқылы түсіндірейік.

1. Кестеден 2, 3, 5 және 8 сандарына сәйкес таяқшаларды аламыз.

2. Оларды цифрлары бөлгішті құрайтындай етіп орналастырамыз. (3852).

3. К өлбеу сызық бойымен қосып, нәтижесін оң жаққа, қатар тұсына жазамыз. Осы әрекетті қалған қатарлармен де жүргіземіз.

4. Енді тікелей бөлуге кірісеміз. Бұл қадамда бөлінгіштен аспайтын ең үлкен қосындыны аламыз. Біздің мысал үшін бұл сан -3852. Табылған санды бөлінгіштен азайтамыз да, бөліндінің үлкен разрядын табамыз және қалдықты табамыз. Үлкен разряд 1 болады, себебі таңдаған сан 1-ші жолда тұр. Қалдықта 106556 қалады.

5. 4- пункттегі әрекетті қайталаймыз. Нәтижесінде бөліндінің екінші разряды 2-ні және 29516 қалдығын табамыз. Бұл әрекетті қалдық бөлгіштен артық болса, қайталай береміз. Ал қалдық бөлгіштен кем болғанда, нәтиженің бүтін бөлігі табылды деп есептеледі. Біздің мысал үшін бұл жағдай үш итерациядан табылады және бүтін бөлік 127 болады.

6. Қалдықты 10 есе арттырып жоғарыда айтылған әрекетті қайталаймыз. Нәтижеде ондық үлесті, яғни 6-ны және қалдықты табамыз. Бұл әрекет нақты бөлінді табылғанша немесе қалдық 0-ге тең болғанша қайталана береді.

Түбір табу

К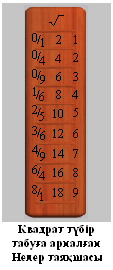 авдрат түбірден шығару үшін үш бағаннан тұратын қосымша таяқша керек. Бұл таяқшаның 1-ші бағаны жол көрсеткіш бағанның квадрат дәрежесінің диагональ бойынша бөлінген нәтижесінен тұрады. Ал екінші баған жол көрсеткіш бағанды екі еселеген сандарынан тұрады. Үшінші баған 1-ден 9-ға дейінгі сандарды құрайды.

Непер таяқшаларымен түбір табу амалының орындалуын мысал арқылы түсіндірейік. Мысал: 56349 санының квадрат түбірін табайық.

Квадрат түбірден шығару бірнеше қадамнан тұрады. Берілген санды оңнан солға қарай 2 цифрдан топтарға бөлеміз, олар әр қадамда жұбымен әрекет жасайды. Яғни бір қадамнан екінші қадамға өту үшін қалдыққа жұбымен тіркеліп жазылады да, түбір табу әрекеті жалғасады. Топтардың саны нәтижеде шығатын цифрлардың санын білдіреді.

Қ адам 1. 56349 саны топтарға келесідегідей бөлінеді: 5’63’49’. Квадрат түбірден шығаруды сол жақтағы топтан басталады, біздің жағдайда бұл

сан – 5.

Таяқшаның бірінші қатарынан 5-тен артпайтын үлкен санды таңдаймыз. Бұл сан- 4. Яғни 4<5<9. 4 саны 2-ші жолда тұрғандықтан, нәтиженің үлкен разряды - 2 болады.

Қалдықты 5-4=1 орындау арқылы табамыз. Квадрат түбірден шығарудың 2- қадамына қалдықпен (1) 2-ші топты (63) біріктіріп 163 санын дайындаймыз.

Таяқшаның 2- бағаны мен 2- жолының қиылысуындағы мәнді қараймыз. Ол – 4 саны. Осы санға сәйкес 4-ші таяқшаны осы таяқшаның сол жағына қоямыз. Сурет «Квадрат түбірден шығару. Қадам-1.»

Квадрат түбір табу таяқшасының 2, 3- бағандарын елемей, барлық қатардың қосындысын есептейміз. Қосындыны таяқшаның оң жағына жазамыз.

Қ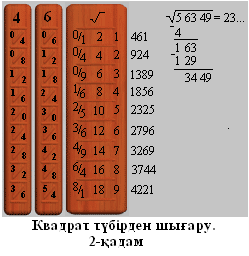 адам 2. қосындылардың ішінен 163 санынан артпайтын үлкен санды іздейміз. Ол 129<163<176 шартын қанағаттандыратын 3- жолда орналасқан 129 саны. Сондықтан нәтиженің келесі разряды 3 болады.

Қалдықты 163-129= 34 табамыз. Қалдықты біле отырып 3 қадамның мәнін анықтаймыз. Қалдық (34) пен үшінші топ (49) санын біріктіру арқылы 3449 санын аламыз.

Квадрат түбір табу таяқшасының 2-ші бағанынан 3-ші жолдың мәнін табамыз. Ол 6 саны. Осы санға сәйкес таяқшаны негізгі таяқшаның сол жағынан қоямыз. Сурет «Квадрат түбірден шығару. Қадам-2».

2, 3-ші бағандарды елемей, қатарларды көлбеу сызық бойымен қосып, нәтижесін таяқшаның оң жағына жазамыз.

Қ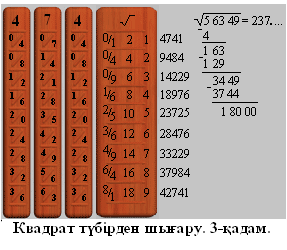 адам 3. Қосындылардың арасынан 3449 санынан артпайтын үлкен санды табамыз. Бұл 3269 (3269<3449<3744) саны, 7-ші қатарда орналасқан. Осы себепті нәтиженің келесі разряды 7 болады.

Азайтуды орындап қалдықты табамыз. Қалдық 3449-3269=180 болады. Қалдықты біле отырып, 4-қадамның мәнін анықтаймыз. 4-қадамға сандар жұбы қалмағандықтан, бұл қадамның нәтижесі ондық үлес шамасы болады. Есептеуді ары қарай жүргізу үшін қалдыққа екі нөлден (00) тұратын топ қосылып жазылады. Демек, 4-қадамдағы сан 18000 болады.

Квадрат түбір табу таяқшасының 2-ші бағанының 7-ші жолмен қиылысуындағы мәніне қараймыз. Ол 14 саны. 4, 6 - таяқшаларынан құралған 46 санын 14 санымен келесі ереже бойынша біріктіреміз. 46 санына 14 санының ондығын қосып (46+1=47), бірлігін (4) тіркеп жазамыз, сонда 474 саны шығады. Осы таяқшаларды квадрат түбір табу таяқшасының сол жағына орналастырамыз. Сурет «Квадрат түбірден шығару. Қадам-3».

Квадрат түбір табу таяқшасының 2,3 - бағандарын елемей, көлбеу сызық бойымен қатарлардың қосындысын тауып, таяқшаның оң жағына жазамыз.

Қадам 4. Көлбеу сызық бойымен қосылған қосындылардың арасынан 18000 санынан артпайтын үлкен санды табамыз. Ол 14229 (14229<18000<18976) шартын қанағаттандыратын 3- жолда тұрған сан. Сол себепті ондық үлестің шамасы 3 болады. Осыдан келіп 56349 санының квадрат түбірі 237,3... болады.

Ары қарай 3-қадамдағы жағдайды қайталаймыз. Осы әрекетті ізделінді дәлдікке дейін немесе қалдық нөлге тең болмағанда қайталай береміз. Егер қалдық нөлге тең болса, онда түбір нақты табылды деп есептеледі.

Қорытындылай келе, оқушылардың біліктілігін оқу материалын тек қабылдау мен есте сақтау ретиінде ғана емес, оқушылардың өзіндік іс-әрекеті арқылы қол жеткізуге болатындығына, берілген материалды ой-елегінен өткізуге бағытталған белсенді танымдық іс-әрекет ретінде қарастыру қажеттігіне назар аударылды. Оқыту процесінде шығарылатын әрбір есептің үйренушілік сипаты бар, өйткені олар әртүрлі проблемалық жағдаяттарға бағдарланады, ал оқушылар осы проблемаларды шешеді, білімдерін толықтырады, тәжірибе жинақтайды, математикалық іс-әрекеттерге машықтанады.

Ал, Непер таяқшалары арқылы есептеу оқушының теориялық білімін практикада жүзеге асыру үшін маңызды. Яғни оқушы жылдам көбейтуді, бөлуді, квадрат түбір табуды жан-жақты меңгереді. Математикалық есептер шығару оған енді қиын іс емес, қызықты іс болады деп есептеймін.

Пайдаланылған әдебиеттер тізімі.

1. М.М.Лиман. Оқушыларға математика және математиктер жайлы – Алматы «Мектеп»,1984, 44 бет.

2. А.Көбесов. Математика тарихы – Алматы, «Қазақ университеті», 1993, 178-180 беттер.

3. Г.А.Бордовский, В.А.Извозчиков, Ю.В.Исаев, В.В.Морозов. Информатика в понятиях и терминах – Москва «Просвещение», 1991, 16-17 беттер.

4. Г.И.Глейзер. Мектептегі математика тарихы. IV-VI кластар – Алматы «Мектеп», 1985, 153-155 беттер.

5. Интернет беттерінен:

1. http://osp.ru

2. http://museum.iu4.bmstu.ru

3. Ru.wikipedia.org

4. Diary.ru

5. Istoria2.narod.ru

6. Istraswt.narod.ru

7. Fedotov.nsu.ru

8. Psf-ccko.ru