Неравенство треугольника 7 класс

КГУ «Гимназия №34»

Предмет: геометрия

3 четверть

Урок №35

ФИО педагога:

Байбосынова С.Т.

Дата:

24.02.2023 г.

Класс: 7

Тема урока:

Неравенство треугольника

Раздел:

Взаимное расположение прямых

Цели обучения в соответствии
с учебной программой

7.1.1.20 знать соотношение между сторонами и углами треугольника и применять его при решении задач;

Цели урока

- рассмотреть теорему о неравенстве треугольника и показать ее применение при решении задач

Этап урока/ Время

Действия педагога

Действия ученика

Оценивание

Ресурсы

Начало урока

7 минут

Организационный момент.

В начале урока учитель и учащиеся приветствуют друг друга.

Актуализация знаний

Устный опрос на разгадывание кроссворда.

1. Сторона прямоугольного треугольника, лежащая против прямого угла, называется (гипотенузой).

2. Стороны прямоугольного треугольника, заключающие прямой угол называются (катетами).

3. Если все три угла треугольника острые, то он называется?

4. В равнобедренном треугольнике две стороны (равны)

5.  Если два угла треугольника равны, то треугольник (равнобедренный).

6. Внешний угол треугольника равен сумме двух углов треугольника не (смежных) с ним.

7.  Если одни из углов треугольника тупой, то треугольник называется (тупоугольный).

8. Чему равна градусная мера третьего угла треугольника, если два других угла равны 60 градусов и 20 градусов?(сто)

9.  В треугольнике против меньшего угла лежит меньшая (сторона).

10. В равнобедренном треугольнике углы при основании (равны)

11. В треугольнике против большей стороны лежит (больший) угол?

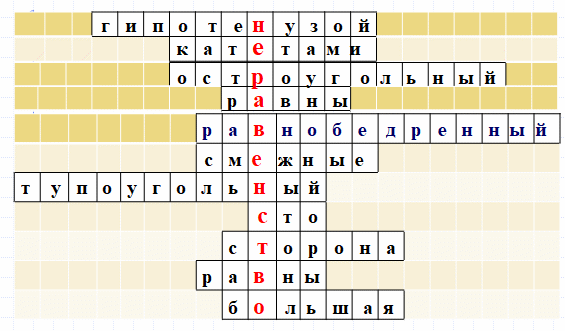
Какое слово получилось? (неравенство)

Разгадайте ребус

Приветствие

Учащийся отвечает на вопросы

ФО

Презентация

Середина урока

20 минут

15 минут

Как Вы думаете, какую фигуру мы с вами будем сегодня рассматривать?

Сегодня на уроке мы с вами будем изучать неравенство треугольников.

Посмотрите видеоурок:

https://www.youtube.com/watch?v=7gYeA9zjVWM

- Скажите, а где еще в повседневной жизни вам встречались треугольные формы? В архитектуре? 

- Всегда, ли можно построить треугольник по трём сторонам? В каких случаях это сделать нельзя?

Гипотеза урока: каждая сторона треугольника меньше суммы двух других сторон.

Итак, рассмотрим теорему о неравенстве треугольника и найдем применение при решении задач

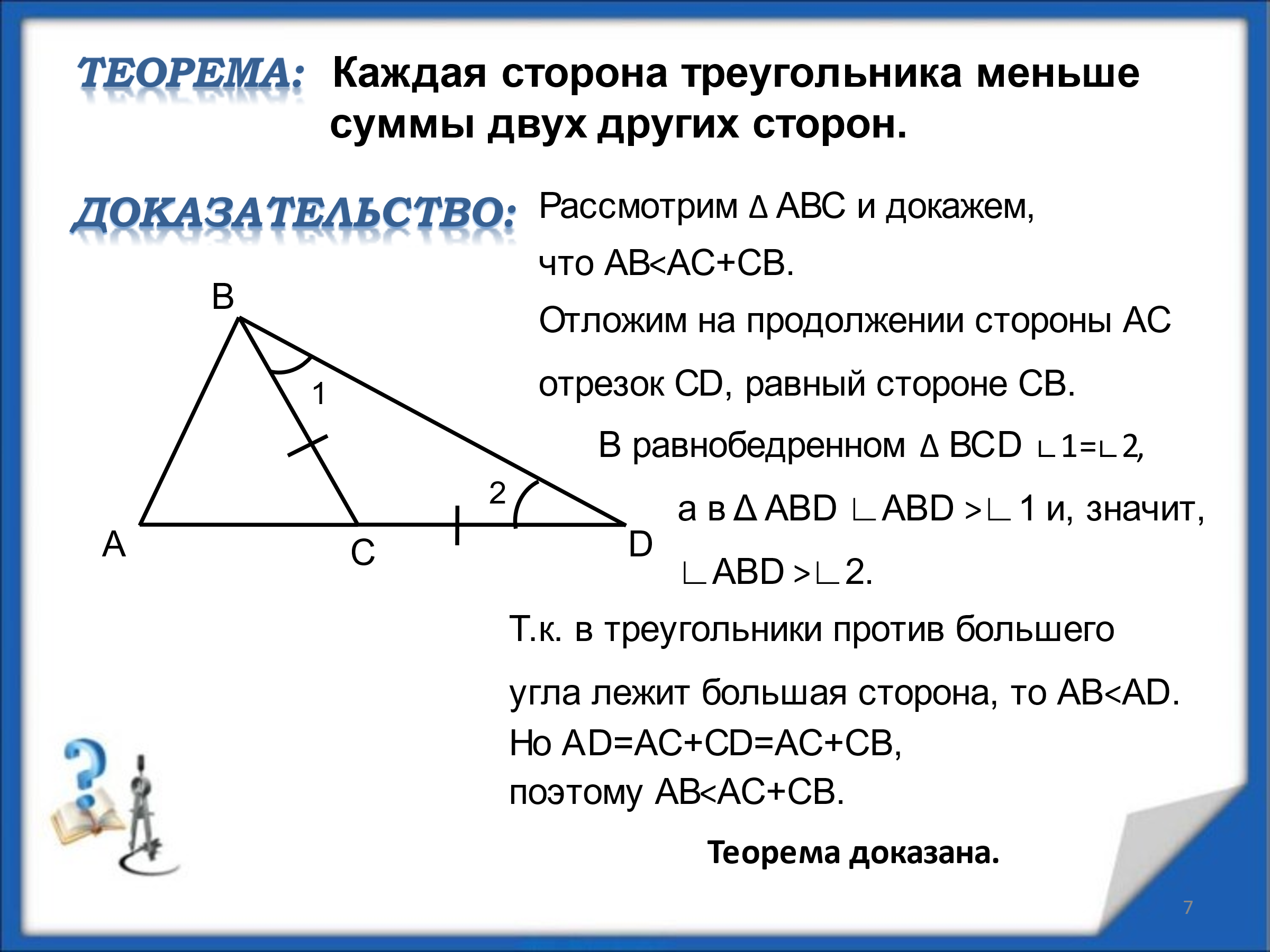
Следствие:

• Для любых трех точек А, В, С.

АВ С+АС

АС + ВС

ВС + АС

Пример: могут ли существовать треугольник у которого стороны равны 3, 4 и 5.

Проверим с помощью теоремы неравенства треугольника:

• 3 4 + 5

• 4 3 + 5

• 5 3 + 4

По данному неравенству следует, что «да, существует».

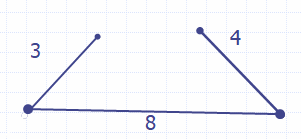
Существует ли треугольник со сторонами

3, 4 и 8.

Проверим с помощью теоремы неравенства треугольника:

• 8 3 + 4

НЕ СУЩЕСТВУЕТ.

Таким образом, мы с помощью теоремы неравенств треугольника можем проверят существует ли такой треугольник заданными сторонами.

Каждая сторона треугольника меньше суммы двух других сторон.

Найдите треугольники, которые не существуют.

Достаточно проверить выполнение неравенства

для большей стороны.

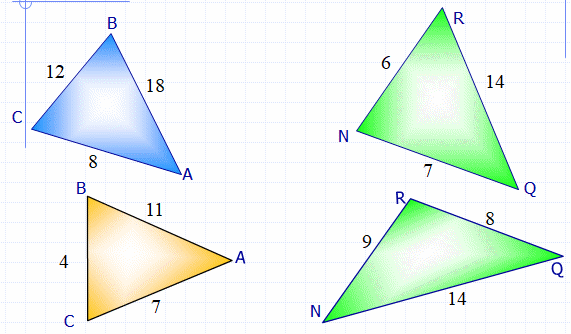
14<9+8 (Верно)

Определите вид треугольника

У треугольника не хватает одной стороны.

Какое из предложенных чисел подойдет?

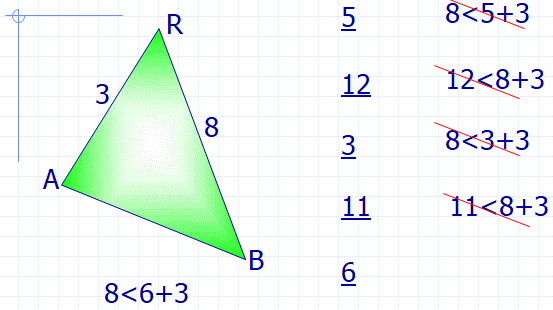
Пример:

Два внешних угла при разных вершинах равны. P=74см. Одна из сторон 16см. Найти две другие стороны треугольника.

Решение:

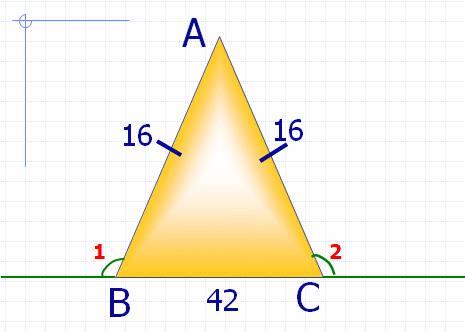
АВ=АС=16см

ВС=74 – (16+16)= 42см

42<16+16 (Н)

Пример:

Два внешних угла при разных вершинах равны. P=74см. Одна из сторон 16см. Найти две другие стороны треугольника.

Решение:

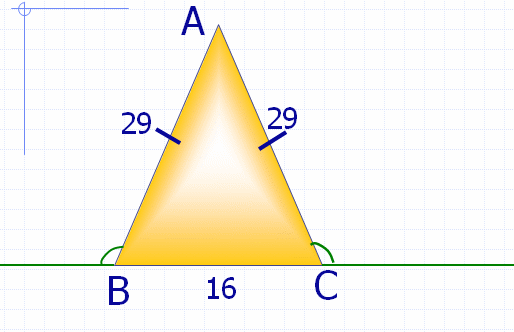
АВ=(74 –16):2=29см

29<29+16 (В)

Ответ: стороны треугольника 29, 29, 16см

Выполните задание:

№№ 17.1; 17.6 стр 95

п.17 на стр 92

Учащийся просматривает видеоурок

Учащийся работает совместно с учителем

Учащийся работают вместе с учителем

Учащийся отвечают на вопросы устно по слайду

Учащийся определяют вид треугольника

Учащийся работают совместно с учителем, разбирают пример, отвечают устно

Выполняют задание с учебника

ФО

ФО

ФО

ФО