
Нүктеден жазықтыққа дейінгі арақашықтық
Дайындаған: «РФММ» КеАҚ-ның математика пәнінің мұғалімі
Сқақов Марғұлан Қызайбайұлы
Алматы-2024 жыл
Нүктеден жазықтыққа перпендикуляр жүргізу үшін келесі алгоритмді қолдануға болады:

-
 нүктесінен
нүктесінен  түзуіне
түзуіне  перпендикулярын жүргіземіз;
перпендикулярын жүргіземіз; -
 жазықтығында
жазықтығында  түзіне
түзіне  перпендикулярын жүргіземіз;
перпендикулярын жүргіземіз; -
 нүктесінен
нүктесінен  түзуіне жүргізілген
түзуіне жүргізілген  перпендикуляры ізделінді
перпендикуляр.
перпендикуляры ізделінді
перпендикуляр.
 екенін
дәлелдейік.
екенін
дәлелдейік.
 олай болса түзу мен
жазықтықтың перпендикулярлық белгісі бойынша,
олай болса түзу мен
жазықтықтың перпендикулярлық белгісі бойынша,
 Түзу мен жазықтықтың
перпендикулярлығының анықтамасы бойынша
Түзу мен жазықтықтың
перпендикулярлығының анықтамасы бойынша  болғандықтан түзу мен жазықтықтың перпендикулярлығының
белігісі бойынша,
болғандықтан түзу мен жазықтықтың перпендикулярлығының
белігісі бойынша, 
1 Есеп.
 кубының
кубының  ,
,  және
және  қырларының орталарынан сәйкесінше
P, Q
және R
нүктелері алынған. Кубтың қыры a-ға
тең.
қырларының орталарынан сәйкесінше
P, Q
және R
нүктелері алынған. Кубтың қыры a-ға
тең.  нүктесінен PQR жазықтығына дейінгі ара қашықтықты
табыңыз.
нүктесінен PQR жазықтығына дейінгі ара қашықтықты
табыңыз.
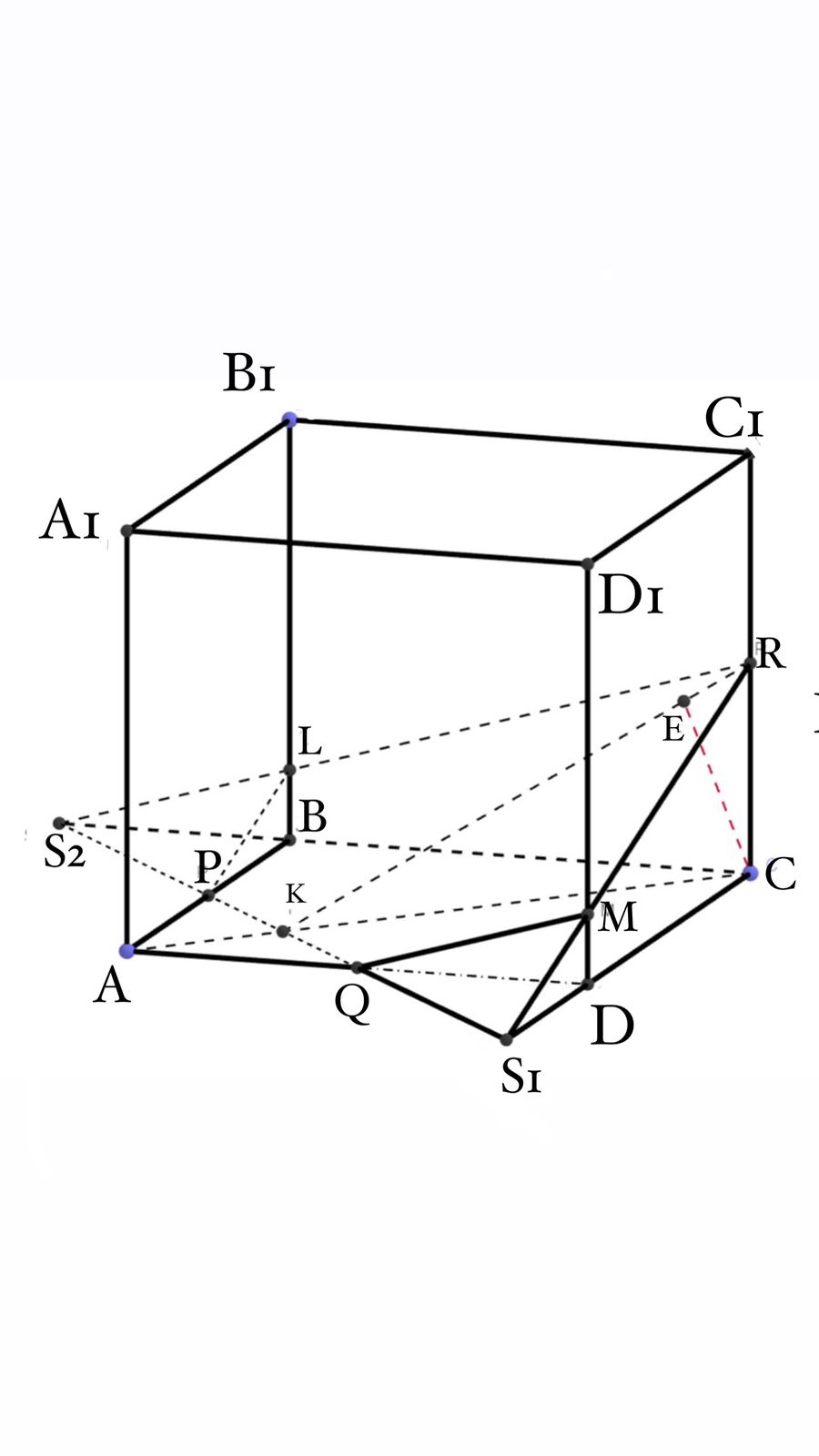
Шешуі:
Кубтың қимасы (PQMRL) екені белгілі.  нүктесінен (PQMRL) жазықтығына дейінгі ара қашықтық -С
нүктесінен осы жазықтыққа дейінгі ара қашықтыққа
тең.
нүктесінен (PQMRL) жазықтығына дейінгі ара қашықтық -С
нүктесінен осы жазықтыққа дейінгі ара қашықтыққа
тең.
 .
.



Жауабы:  .
.
2
есеп. Тік бұрышты  параллелепипедінің қырлары
параллелепипедінің қырлары  қатынасындай. Р нүктесі
қатынасындай. Р нүктесі  қырының ортасы.
қырының ортасы.  тең.
тең.  нүктесінен
нүктесінен  жазықтығына дейінгі ара қашықтықты
табыңыз.
жазықтығына дейінгі ара қашықтықты
табыңыз.
Шешуі:
Кубтың қимасы ( ) екені белгілі.
) екені белгілі.  . Егер
. Егер  квадратын қарастырсақ
квадратын қарастырсақ 
Олай
болса,  нүктесінен (
нүктесінен ( ) жазықтығына дейінгі ара қашықтық, С нүктесінен осы
жазықтыққа дейінгі ара қашықтықтан 2 есе үлкен
болады.
) жазықтығына дейінгі ара қашықтық, С нүктесінен осы
жазықтыққа дейінгі ара қашықтықтан 2 есе үлкен
болады.
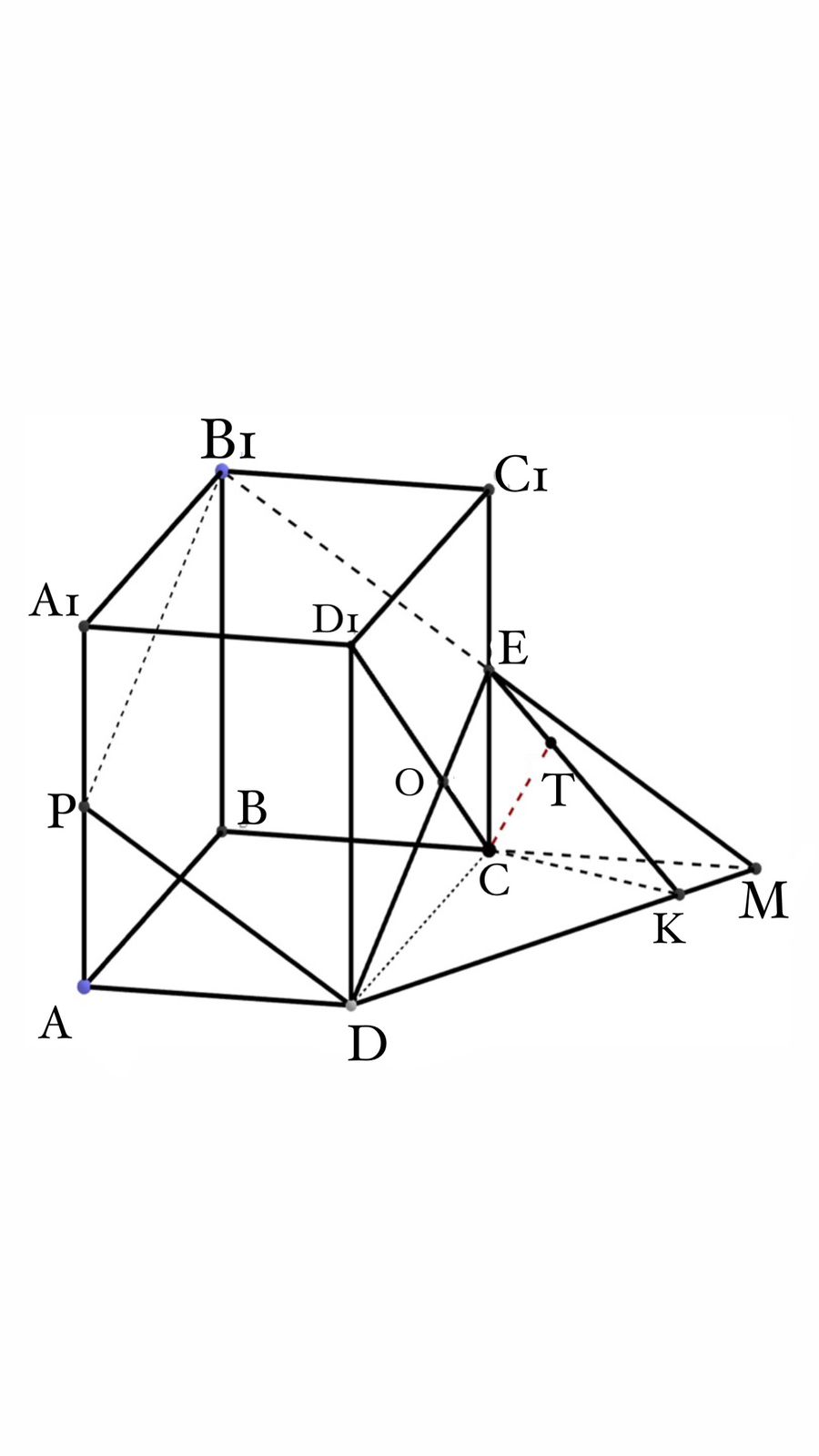
 MCD үшбұрышы тік бұрышты
үшбұрыш.
MCD үшбұрышы тік бұрышты
үшбұрыш.
 екенін аңғаруға
болады.
екенін аңғаруға
болады.
 .
.
ECK үшбұрышы тік бұрышты үшбұрыш.
 .
.

 .
.
 Жауабы:
Жауабы:

3 есеп.  пирамидасының табанында С бұрышы тік болатын тең бүйірлі
үшбұрыш жатыр.
пирамидасының табанында С бұрышы тік болатын тең бүйірлі
үшбұрыш жатыр.  бүйір жағы табан жазықтығына перпендикуляр, әрі S бұрышы
тік болатын тең бүйірлі үшбұрыш.
бүйір жағы табан жазықтығына перпендикуляр, әрі S бұрышы
тік болатын тең бүйірлі үшбұрыш.  нүктесі
нүктесі  қырының ортасы.
қырының ортасы.  нүктесі
нүктесі  үшбұрышының центроиды. Пирамидаға
үшбұрышының центроиды. Пирамидаға
 қырына параллель
болатын
қырына параллель
болатын  және
және  нүктелері арқылы өтетін қима жүргізілген.
Егер
нүктелері арқылы өтетін қима жүргізілген.
Егер  болса, онда А нүктесінен осы қимаға дейінгі ара
қашықтықты табыңыз.
болса, онда А нүктесінен осы қимаға дейінгі ара
қашықтықты табыңыз.
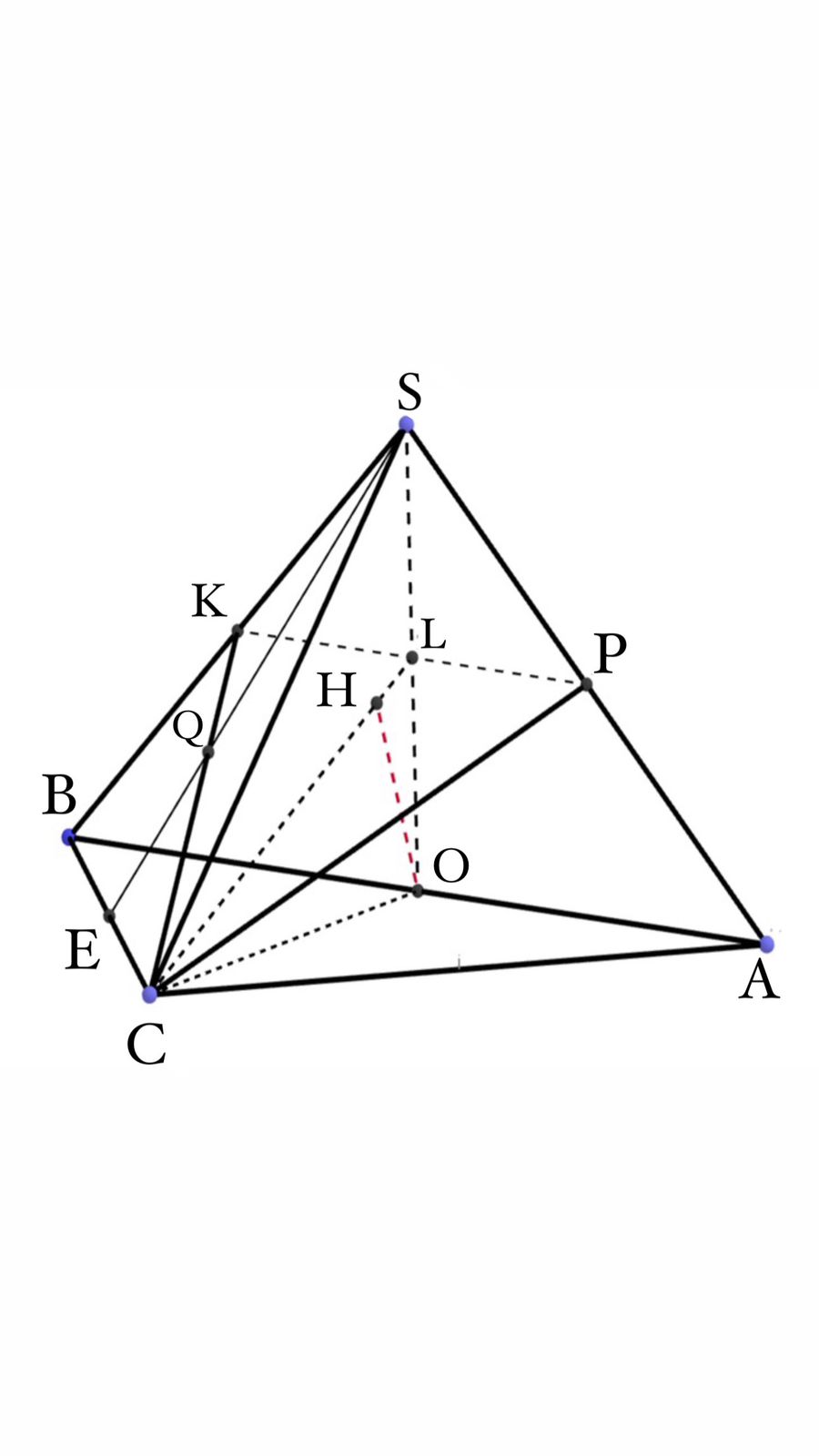
Шешуі:
 болғандықтан
болғандықтан  .
.  медиана ⇒
медиана ⇒ .
.


 тең бүйірлі
үшбұрыш.
тең бүйірлі
үшбұрыш. 
 жүргізейік.
жүргізейік.


Демек
ізделінді ара қашықтыққа  алынады.
алынады. .
.

 .
.
Жауабы: 
4
Есеп.  тік призмасының табанында С бұрышы тік болатын тең
бүйірлі үшбұрыш жатыр.
тік призмасының табанында С бұрышы тік болатын тең
бүйірлі үшбұрыш жатыр.  және
және  қырларының орталарынан P және K нүктелері алынған. К
нүктесі арқылы өтетін қима
қырларының орталарынан P және K нүктелері алынған. К
нүктесі арқылы өтетін қима  және
және  түзулеріне параллель.
түзулеріне параллель.  деп алып,
деп алып,  нүктесінен осы қимаға дейінгі ара қашықтықты
табыңыз.
нүктесінен осы қимаға дейінгі ара қашықтықты
табыңыз.
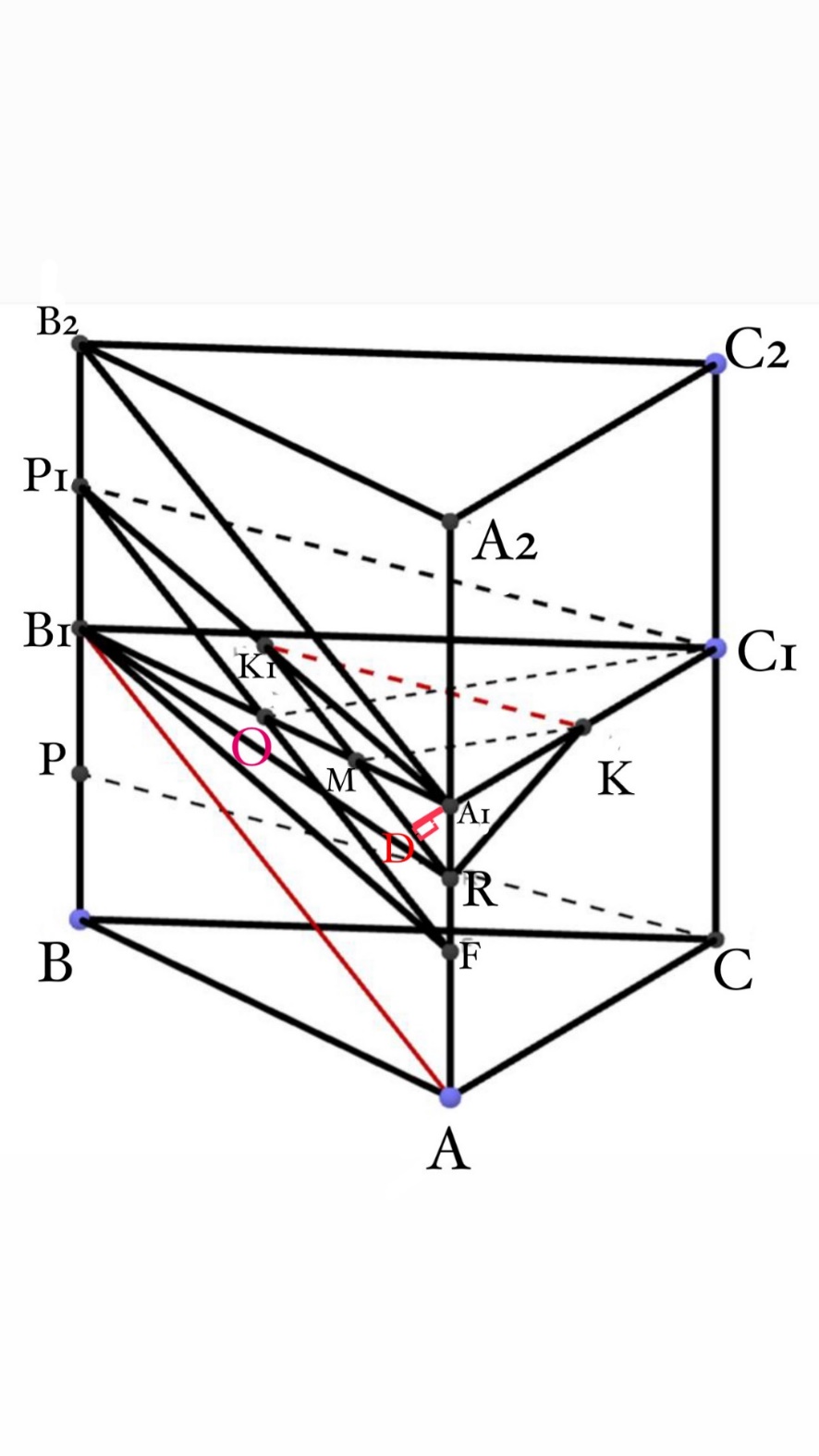
Шешуі:  призмасын
призмасын  призмасына дейін толықтырайық.
призмасына дейін толықтырайық.

 .
.
 нүктесі
нүктесі
 дің ортасы
болсын.
дің ортасы
болсын.  ‖
‖ екені белгілі.
екені белгілі.


 .
Онда
ізделінді қима
.
Онда
ізделінді қима 
 -төртбұрышы
параллелограмм.
-төртбұрышы
параллелограмм.  , (
, ( параллелограммның диагональдары)
параллелограммның диагональдары)
 .
. болғандықтан Фалес
болғандықтан Фалес
теоремасы бойынша  .
.
 тік бұрышты тең бүйірлі
үшбұрыш болғандықтан,
тік бұрышты тең бүйірлі
үшбұрыш болғандықтан, медиана да, биіктік те болып
табылады.
медиана да, биіктік те болып
табылады.
Онда  MK-орта сызық болып
табылады.
MK-орта сызық болып
табылады.
Әрі, 

 жүргізейік.
жүргізейік.

 ⇒
⇒ 






Демек ізделінді ара қашықтыққа
 алынады.
алынады.
 ;
;
 .
.

 .
.

 =
= Жауабы:
Жауабы: 
№5.  пирамидасының табанында қабырғасы
a-ға тең
пирамидасының табанында қабырғасы
a-ға тең
 ромбы
жатыр.
ромбы
жатыр.  .
Пирамиданың
биіктігі
.
Пирамиданың
биіктігі  және
және  .
.
 қырынан
қырынан
 болатындай
болатындай  нүктесі алынған.
нүктесі алынған.  және
және  түзулерінің ара қашықтығын
табыңыз.
түзулерінің ара қашықтығын
табыңыз.
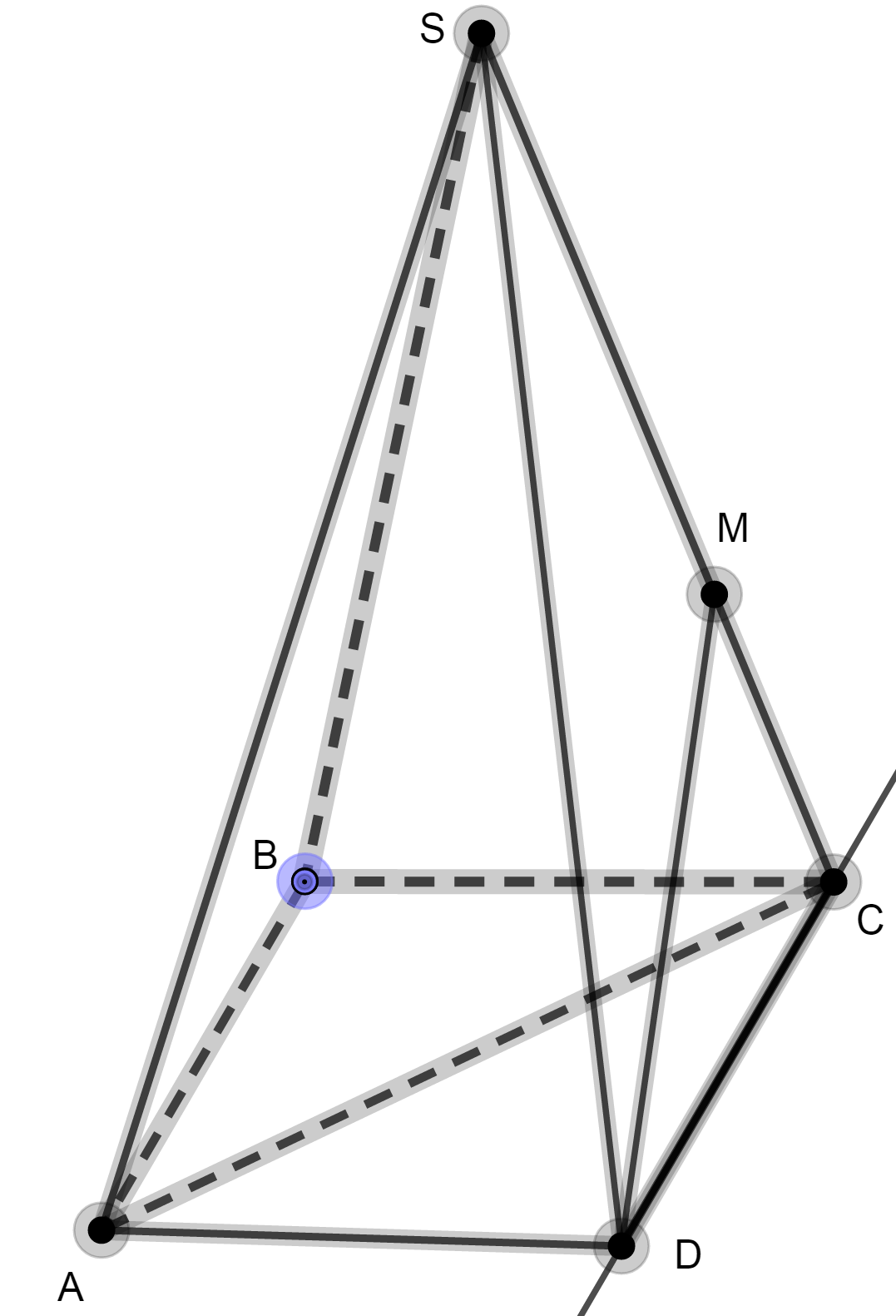
Шешуі:
АС мен  түзулерінің ара қашықтығына М нүктесінен АС ға параллель
түзу жүргізіп алып, содан кейін АС ның кез келген нүктесінен осы
пайда болған жазықтыққа (DMN) дейінгі қашықтықты тапсақ
жеткілікті болады.
түзулерінің ара қашықтығына М нүктесінен АС ға параллель
түзу жүргізіп алып, содан кейін АС ның кез келген нүктесінен осы
пайда болған жазықтыққа (DMN) дейінгі қашықтықты тапсақ
жеткілікті болады.  , әрі
, әрі  болғандықтан
болғандықтан  . Осыдан
. Осыдан  пирамидасының
пирамидасының  төбесінен
төбесінен  табан жазықтығына жүргізілген
перпендикуляры
табан жазықтығына жүргізілген
перпендикуляры  бұрышының биссектрисасының бойына түсетінін дәлелдеуге
болады. Сонымен
бұрышының биссектрисасының бойына түсетінін дәлелдеуге
болады. Сонымен  .
.
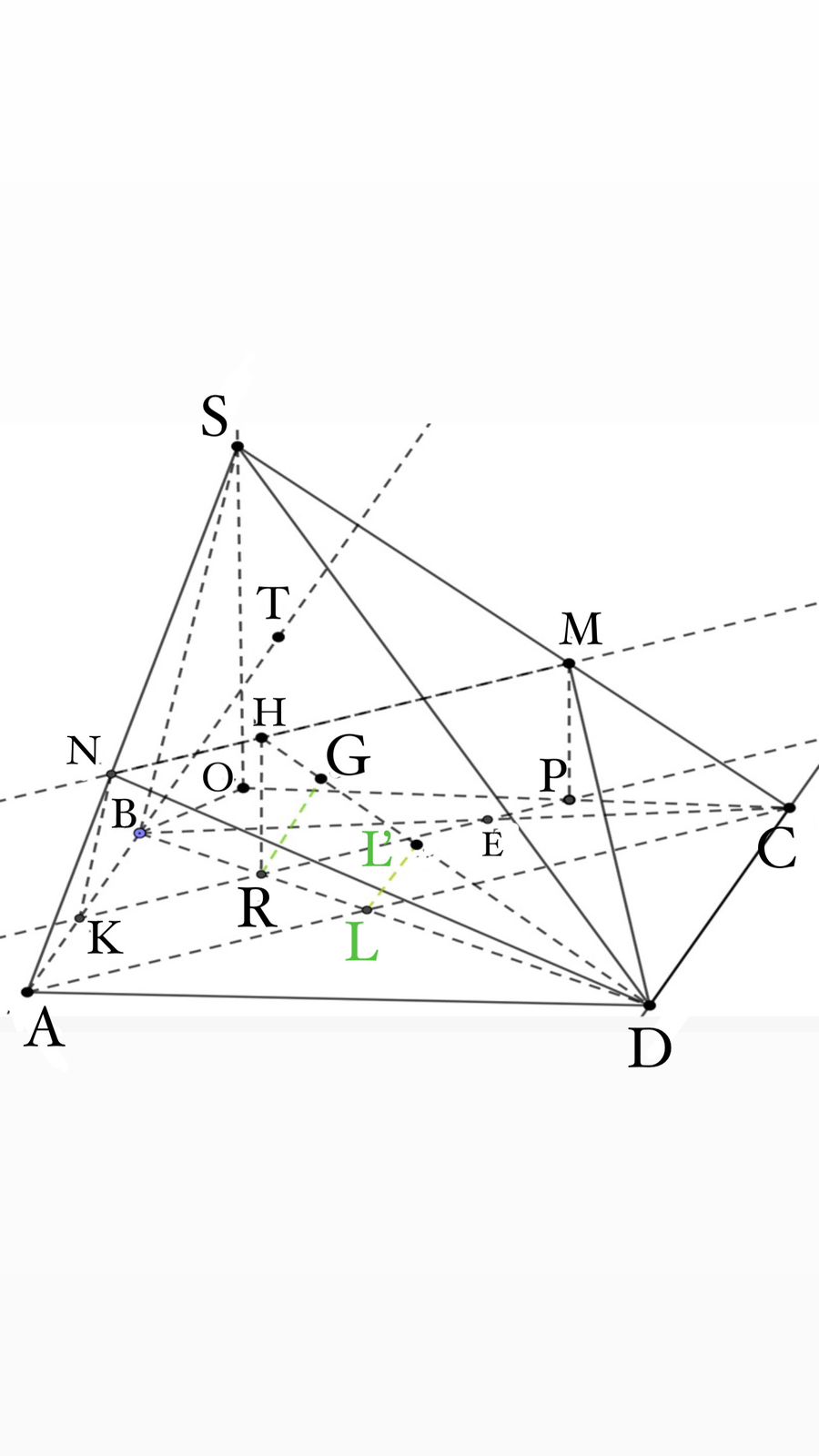
M
нүктесінен  жазықтығына перпендикуляр жүргізейік,
жазықтығына перпендикуляр жүргізейік,
 . P нүктесінен АС –ға
параллель PK түзуін жүргізейік, ВС мен қиылысу нүктесі
Е,
. P нүктесінен АС –ға
параллель PK түзуін жүргізейік, ВС мен қиылысу нүктесі
Е,  мен қиылысу нүктесі R болсын.
мен қиылысу нүктесі R болсын.
 .
.
 нүктелері бір жазықтықта
жататыны белгілі болады.
нүктелері бір жазықтықта
жататыны белгілі болады.  жүргізейік. Онда
жүргізейік. Онда  . Осыдан HRD тік бұрышты үшбұрышының
. Осыдан HRD тік бұрышты үшбұрышының
 биіктігін жүргізсек,
ол
биіктігін жүргізсек,
ол  жазықтығына жүргізілген перпендикуляр болып
табылады.
жазықтығына жүргізілген перпендикуляр болып
табылады.  жүргізсек, онда ізделінді
жүргізсек, онда ізделінді  .
.
 ,
,
 .
.


жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Нүктеден жазықтыққа дейінгі ара қашықтық
Нүктеден жазықтыққа дейінгі ара қашықтық
Нүктеден жазықтыққа дейінгі арақашықтық
Дайындаған: «РФММ» КеАҚ-ның математика пәнінің мұғалімі
Сқақов Марғұлан Қызайбайұлы
Алматы-2024 жыл
Нүктеден жазықтыққа перпендикуляр жүргізу үшін келесі алгоритмді қолдануға болады:

-
 нүктесінен
нүктесінен  түзуіне
түзуіне  перпендикулярын жүргіземіз;
перпендикулярын жүргіземіз; -
 жазықтығында
жазықтығында  түзіне
түзіне  перпендикулярын жүргіземіз;
перпендикулярын жүргіземіз; -
 нүктесінен
нүктесінен  түзуіне жүргізілген
түзуіне жүргізілген  перпендикуляры ізделінді
перпендикуляр.
перпендикуляры ізделінді
перпендикуляр.
 екенін
дәлелдейік.
екенін
дәлелдейік.
 олай болса түзу мен
жазықтықтың перпендикулярлық белгісі бойынша,
олай болса түзу мен
жазықтықтың перпендикулярлық белгісі бойынша,
 Түзу мен жазықтықтың
перпендикулярлығының анықтамасы бойынша
Түзу мен жазықтықтың
перпендикулярлығының анықтамасы бойынша  болғандықтан түзу мен жазықтықтың перпендикулярлығының
белігісі бойынша,
болғандықтан түзу мен жазықтықтың перпендикулярлығының
белігісі бойынша, 
1 Есеп.
 кубының
кубының  ,
,  және
және  қырларының орталарынан сәйкесінше
P, Q
және R
нүктелері алынған. Кубтың қыры a-ға
тең.
қырларының орталарынан сәйкесінше
P, Q
және R
нүктелері алынған. Кубтың қыры a-ға
тең.  нүктесінен PQR жазықтығына дейінгі ара қашықтықты
табыңыз.
нүктесінен PQR жазықтығына дейінгі ара қашықтықты
табыңыз.

Шешуі:
Кубтың қимасы (PQMRL) екені белгілі.  нүктесінен (PQMRL) жазықтығына дейінгі ара қашықтық -С
нүктесінен осы жазықтыққа дейінгі ара қашықтыққа
тең.
нүктесінен (PQMRL) жазықтығына дейінгі ара қашықтық -С
нүктесінен осы жазықтыққа дейінгі ара қашықтыққа
тең.
 .
.



Жауабы:  .
.
2
есеп. Тік бұрышты  параллелепипедінің қырлары
параллелепипедінің қырлары  қатынасындай. Р нүктесі
қатынасындай. Р нүктесі  қырының ортасы.
қырының ортасы.  тең.
тең.  нүктесінен
нүктесінен  жазықтығына дейінгі ара қашықтықты
табыңыз.
жазықтығына дейінгі ара қашықтықты
табыңыз.
Шешуі:
Кубтың қимасы ( ) екені белгілі.
) екені белгілі.  . Егер
. Егер  квадратын қарастырсақ
квадратын қарастырсақ 
Олай
болса,  нүктесінен (
нүктесінен ( ) жазықтығына дейінгі ара қашықтық, С нүктесінен осы
жазықтыққа дейінгі ара қашықтықтан 2 есе үлкен
болады.
) жазықтығына дейінгі ара қашықтық, С нүктесінен осы
жазықтыққа дейінгі ара қашықтықтан 2 есе үлкен
болады.

 MCD үшбұрышы тік бұрышты
үшбұрыш.
MCD үшбұрышы тік бұрышты
үшбұрыш.
 екенін аңғаруға
болады.
екенін аңғаруға
болады.
 .
.
ECK үшбұрышы тік бұрышты үшбұрыш.
 .
.

 .
.
 Жауабы:
Жауабы:

3 есеп.  пирамидасының табанында С бұрышы тік болатын тең бүйірлі
үшбұрыш жатыр.
пирамидасының табанында С бұрышы тік болатын тең бүйірлі
үшбұрыш жатыр.  бүйір жағы табан жазықтығына перпендикуляр, әрі S бұрышы
тік болатын тең бүйірлі үшбұрыш.
бүйір жағы табан жазықтығына перпендикуляр, әрі S бұрышы
тік болатын тең бүйірлі үшбұрыш.  нүктесі
нүктесі  қырының ортасы.
қырының ортасы.  нүктесі
нүктесі  үшбұрышының центроиды. Пирамидаға
үшбұрышының центроиды. Пирамидаға
 қырына параллель
болатын
қырына параллель
болатын  және
және  нүктелері арқылы өтетін қима жүргізілген.
Егер
нүктелері арқылы өтетін қима жүргізілген.
Егер  болса, онда А нүктесінен осы қимаға дейінгі ара
қашықтықты табыңыз.
болса, онда А нүктесінен осы қимаға дейінгі ара
қашықтықты табыңыз.

Шешуі:
 болғандықтан
болғандықтан  .
.  медиана ⇒
медиана ⇒ .
.


 тең бүйірлі
үшбұрыш.
тең бүйірлі
үшбұрыш. 
 жүргізейік.
жүргізейік.


Демек
ізделінді ара қашықтыққа  алынады.
алынады. .
.

 .
.
Жауабы: 
4
Есеп.  тік призмасының табанында С бұрышы тік болатын тең
бүйірлі үшбұрыш жатыр.
тік призмасының табанында С бұрышы тік болатын тең
бүйірлі үшбұрыш жатыр.  және
және  қырларының орталарынан P және K нүктелері алынған. К
нүктесі арқылы өтетін қима
қырларының орталарынан P және K нүктелері алынған. К
нүктесі арқылы өтетін қима  және
және  түзулеріне параллель.
түзулеріне параллель.  деп алып,
деп алып,  нүктесінен осы қимаға дейінгі ара қашықтықты
табыңыз.
нүктесінен осы қимаға дейінгі ара қашықтықты
табыңыз.

Шешуі:  призмасын
призмасын  призмасына дейін толықтырайық.
призмасына дейін толықтырайық.

 .
.
 нүктесі
нүктесі
 дің ортасы
болсын.
дің ортасы
болсын.  ‖
‖ екені белгілі.
екені белгілі.


 .
Онда
ізделінді қима
.
Онда
ізделінді қима 
 -төртбұрышы
параллелограмм.
-төртбұрышы
параллелограмм.  , (
, ( параллелограммның диагональдары)
параллелограммның диагональдары)
 .
. болғандықтан Фалес
болғандықтан Фалес
теоремасы бойынша  .
.
 тік бұрышты тең бүйірлі
үшбұрыш болғандықтан,
тік бұрышты тең бүйірлі
үшбұрыш болғандықтан, медиана да, биіктік те болып
табылады.
медиана да, биіктік те болып
табылады.
Онда  MK-орта сызық болып
табылады.
MK-орта сызық болып
табылады.
Әрі, 

 жүргізейік.
жүргізейік.

 ⇒
⇒ 






Демек ізделінді ара қашықтыққа
 алынады.
алынады.
 ;
;
 .
.

 .
.

 =
= Жауабы:
Жауабы: 
№5.  пирамидасының табанында қабырғасы
a-ға тең
пирамидасының табанында қабырғасы
a-ға тең
 ромбы
жатыр.
ромбы
жатыр.  .
Пирамиданың
биіктігі
.
Пирамиданың
биіктігі  және
және  .
.
 қырынан
қырынан
 болатындай
болатындай  нүктесі алынған.
нүктесі алынған.  және
және  түзулерінің ара қашықтығын
табыңыз.
түзулерінің ара қашықтығын
табыңыз.

Шешуі:
АС мен  түзулерінің ара қашықтығына М нүктесінен АС ға параллель
түзу жүргізіп алып, содан кейін АС ның кез келген нүктесінен осы
пайда болған жазықтыққа (DMN) дейінгі қашықтықты тапсақ
жеткілікті болады.
түзулерінің ара қашықтығына М нүктесінен АС ға параллель
түзу жүргізіп алып, содан кейін АС ның кез келген нүктесінен осы
пайда болған жазықтыққа (DMN) дейінгі қашықтықты тапсақ
жеткілікті болады.  , әрі
, әрі  болғандықтан
болғандықтан  . Осыдан
. Осыдан  пирамидасының
пирамидасының  төбесінен
төбесінен  табан жазықтығына жүргізілген
перпендикуляры
табан жазықтығына жүргізілген
перпендикуляры  бұрышының биссектрисасының бойына түсетінін дәлелдеуге
болады. Сонымен
бұрышының биссектрисасының бойына түсетінін дәлелдеуге
болады. Сонымен  .
.

M
нүктесінен  жазықтығына перпендикуляр жүргізейік,
жазықтығына перпендикуляр жүргізейік,
 . P нүктесінен АС –ға
параллель PK түзуін жүргізейік, ВС мен қиылысу нүктесі
Е,
. P нүктесінен АС –ға
параллель PK түзуін жүргізейік, ВС мен қиылысу нүктесі
Е,  мен қиылысу нүктесі R болсын.
мен қиылысу нүктесі R болсын.
 .
.
 нүктелері бір жазықтықта
жататыны белгілі болады.
нүктелері бір жазықтықта
жататыны белгілі болады.  жүргізейік. Онда
жүргізейік. Онда  . Осыдан HRD тік бұрышты үшбұрышының
. Осыдан HRD тік бұрышты үшбұрышының
 биіктігін жүргізсек,
ол
биіктігін жүргізсек,
ол  жазықтығына жүргізілген перпендикуляр болып
табылады.
жазықтығына жүргізілген перпендикуляр болып
табылады.  жүргізсек, онда ізделінді
жүргізсек, онда ізделінді  .
.
 ,
,
 .
.



шағым қалдыра аласыз















