
ОЛИМПИАДА ЕСЕПТЕРІ
5 сынып
1. 13-ке бөлгенде қалдықпен және бөліндісі 17-ге тең болатын ең үлкен
бүтін санды табыңдар.
Шешуі: а=13*17+12=33.
2. Бақа тереңдігі 25м құдыққа түсіп кетті. Ол құдықтан шығу үшін күніне 5м көтеріліп, 4м қайта түсіп отырды. Бақа неше күнде құдықтан шығады?
Шешуі: 21 күнде. Бақа 20 күнде 20м шығады, 5м көтерілетіндіктен 21 күні 20+5=25м болады, олай болса құдықтың басына шыққандықтан қайта түспейді.
3. Алынған сан 36-ға бөлінетіндей 52*2* жазбадағы жұлдызшаларды цифрлармен алмастырыңдар.
Шешуі: Сан 36-ға бөлінеді, егер ол 4-ке де 9-ға да бөлінетін болса. 5,2,2 цифрларының қосындысы 9-ға тең болғандықтан, жетіспей тұрған екі цифрлардың қосындысы 0,9 немесе 18 болуы керек. Алынатын сан 4-ке бөлінетінін, ал соңғының алдындағы цифр 2-ге тең екенін ескерсек, онда соңғы цифр тек 0 мен 4 немесе 8 болуы мүмкін. Онда жауабы мына сандар болады: 52524, 52128, 52020, 52920.
4. Сыныпта математиканы ұнататын қыздардың саны математиканы ұнатпайтын ұлдардың санымен бірдей. Сыныпта кімдер көп: математиканы ұнататын оқушылар ма, әлде ұлдар ма?
Шешуі: Барлық оқушыларды екі топқа бөлеміз: біріншісінде – ұлдар, екіншісінде – қыздар. Осыдан кейін математиканы ұнатпайтын ұлдарды – екінші, ал математиканы ұнататын қыздарды бірінші топқа ауыстырамыз. Топтардың саны бұдан өзгермейді. Бірақ бірінші топта математиканы ұнататын оқушылардың барлығы болады, сондықтан математиканы ұнататын оқушылар саны ұлдардың санымен бірдей.
5. Кітапханада ағылшын, француз және неміс тілінде кітаптар бар.Ағылшын тіліндегі кітаптар барлық шет тіліндегі кітаптардың 40%-ын, француз тіліндегілер ағылшын тіліндегінің 75%-ын құрайды, ал қалған 210 кітап неміс тіліндегілер. Кітапханада шет тілінде неше кітап бар?
Шешуі: Барлық кітап саны - х болсын, есеп шартынан
0,4х + 0,75*0,4х + 210 = х бұдан х = 700 Жауабы :700
1
6. 9 тиынның біреуі жалған және ол басқаларынан жеңіл. Табақты
таразы арқылы гирсіз екі өлшегеннен жалған тиынды қалай анықтауға
болады?
Шешуі: 9 тиынды 3 тиыннан 3 бөлікке бөлеміз. Кез-келген 2 бөлікті өлшейміз,егер таразының екі жағы тең болса, онда жалған тиын үшінші бөлікте болғаны. Оны 1 тиыннан тағы да 3 бөлікке бөлеміз де екеуін таразыға салып өлшейміз, қайсысы жеңіл сол жалған.Ал бұл екеуі тең болса, онда қалған тиын жалған болғаны.
7. 5 л және 7 л-ік ыдыс арқылы 6 л суды қалай құяды?
Шешуі: a) 7 л толтырып 5л құяды, сонан соң оны төгіп , қалған 2 л қайта 5л құяды.
b) 7 л толтырып 5л-ге құяды. 7л-де →4л қалады 5л төгіп 4л →5л құяды
c)7л толтырып 1л→5л құяды. Сонда 7л→6л қалады
8 .Осы фигураны төрт тең фигураларға бөл:

Шешуі:

9. Екі сағат бір уақытта соғуды бірге бастап, бірге аяқтады. Бірінші сағат – әрбір екі секунд сайын, екінші сағат – әрбір үш секунд сайын соғады. Есептегенде барлығы 13 соғу болды (бірігіп қалған соғулар бір соғу деп есептелінеді). Бірінші соғу мен соңғы соғудың арасында қанша уақыт өтті?
Шешуі: 18с.
10. Қарбыздың салмағы 20 кг болды, ал ондағы құрғақ зат 1% - ын құрайды. Біраздан кейін қарбыз құрғап қалды да, құрғақ зат 2% болды. Қарбыздың соңғы салмағы қандай?
Шешуі: Құрғақ заттың 0,2 кг-мы , қарбыздың салмағы 10 кг болатын болды.
2
11. Үш жұмысшы ботқа пісірді. Бірінші 2 кесе жарма, екінші 1 кесе
жарма, ал үшіншісінде ешқандай жарма болмады. Ботқаны барлығы тең бөліп жеді. Үшінші жұмысшы: «Ботқаларыңа рахмет, мен сендерге 50 теңге беремін, сонда менің жеген ботқамды сендер салған жармамен қалай бөліп аласыңдар?» - деді.
Шешуі: Ботқаны 3 кеседен пісіріп, тең бӛліп жегендіктен, әр қайсысы 1 кесе жейді. Сондықтан үшіншінің ақшасын біріншіге беру керек.
12. Кез келген үш натурал санның арасынан әрқашанда қосындысы 2-ге бөлінетін 2 сан табуға болатынын дәлелдеңдер.
Шешуі: Үш санның ең болмағанда екеуі бірдей жұп, ендеше олардың қосындысы 2-ге бөлінеді.
13. Ең үлкен бір орынды санға, ең үлкен екі орынды санды неше рет қосқанда, ең үлкен үш орынды сан шығады?
Шешуі: 1) 9+n*99=999 n=10 Жауабы : 10 рет.
14. 7*9+12:3-2-ге жақшаны қойғанда а) 23 ә) 75 шығу керек.
Шешуі: а) (9*7+12):3-2=23 ә) (7*9+12):(3-2)=75
15. Серік мектепке автобуспен барып, қайтқанда жаяу келеді, сонда
барлық жолға 1 сағ 30 минут уақыт жыбереді. Егер автобуспен жүрсе 30 минут уақыт жібереді. Егер Серік мектепке жаяу барып қайтса, оған қанша уақыт жібереді?
Шешуі: 30мин:2=15мин. Серік мектепке автобуспен барады 1сағ 30мин-15мин=1сағ15мин Серік жаяу жүреді 1сағ15мин+1сағ15мин=2сағ30мин
Жауабы: 2сағ30мин.
16.Қалған саны ең үлкен болатындай етіп берілген 123456789101112131415... ............5657585960 санының 100 цифрын сызып таста.
Шешуі: 99999785960
17. Кеме дүйсенбі күні түсте жүзуге кетті. Жүзу 100 сағатқа созылса, онда
кеме қай күні қандай сағатта оралады?
Шешуі: сөткеде 24 сағат бар 100сағ=4*24сағ+4сағ=4сөтке+4сағ Ендеше кеме жұмада 16 сағ. келеді.
3
18. Ұзындығы 16 см, ені 9см тік төртбұрышты қалай тең екі бөлікке бөлуге және одан квадрат құруға болады?
Шешуі:

19. Есепте: 101101*999-101*999999
Шешуі: 6) 101101*999-101*999 999= 101*1001*999-101*999*1001=0
20. 3п+1 сандарының ішінен 5-ке еселік болатын үш санды табыңдар.
Шешуі: 10,25,40.
21. 9 бет қағаз болған, оның кейбіреуін 3 бөлікке бөлгенде 15 бет қағаз болды. Қанша бет қағазды бөлген?
Шешуі: әр бетті 3 бөлікке кескенде беттер 2-ге артады, 15-9=6 (бет)
6:2=3 (бетті кескен)
22. Өрнектің мәнін тап:
26*25-25*24+24*23-23*22+22*21-21*20+20*19-19*18+18*17-17*16+16*15-15*14.
Шешуі: 26*25-25*24+24*23-23*22+22*21-21*20+20*19-19*18+18*17-17*16+16*1515*14= =25(26-24)+23(24-22)+21(22-20)+19(20-18)+17(18-16)+15(16-14)= =2*(25+23+21+19+17+15)=2*120=240.
23. Жанұяда 4 бала бар, олар 5,8,13 және 15 жаста. Олардың аттары
Айнур, Болат , Әсем Әсель. Олардың біреуі бала бақшасына барады , Айнур Болаттан үлкен және Айнур мен Әсемнің жастарының қосындысы 3-ке бөлінеді. Әр қайсысы неше жаста?
Шешуі: В-5жас ,Б-8жас, А-13 жас, Г- 15 жас.
4
24. Азайғыш, азайтқыш және айырманың қосындысы 26 болса, азай-ғышты тап.
Шешуі: Азайтқыш пен айырманың қосындысы азайғыш болады ,онда екі азайғыш 26 болса, азайғыш 13 болады.
25. Балықшылар салмағы 100гр, 200гр, ...., 1900гр 19 балық ұстады. 10 балықшы балықты тең бөліп ала ма? Егер бөлсе қалай? Бөле алмаса неге?
Шешуі: (1900+100)*9+1000=19000(гр) барлық балық салмағы.
Әр балықшыға 1900гр .
1900гр;100гр;1800гр;......900гр+1000гр
6 сынып
1. Барлық үш орынды авс санын тап, егер мына теңдік орындалса:
авс =2(ав+вс+ас).
Шешуі: 138;144;150;288;294.
2. Оқушы кітапты үш күнде оқыды.Бірінші күні кітаптің 0,2 -сін және 16
бетті, екінші күні қалғанының 0,3-ін және 20 бетін, үшінші күні қалғанының 0,75-ін және 30 бетін оқыды. Кітапта неше бет бар?
Шешуі: х –кітап бетінің саны 1-ші күні 0,2х+16 бет оқылды 2-ші және3-ші күндеріне қалғаныны 0,8х-16 2-ш күні 0,3(0,8х-16)+20 бет оқылды 3-ші күні 0,56х-31,2 бет оқылды Сонда 3-ші күні 0,75 қалғанының және 30 бет оқылса онда қалдық 120 бет 0,56х-31,2=120, х=270 бет
3. Көйлек 500 теңге тұрады. Осы бағаны 10% арттырып, 10% кемітті. Енді көйлектің бағасы неше теңге болды?
Шешуі: 550-55 = 495 (теңге)
4. 15 санының алдына және соңына бір цифр қойғанда, шыққан сан 15-ке
бөлінуі керек.
Шешуі: 1155;3150;4155;6150;7155;9150.
5. Мектепте 33 сынып, 1150 оқушы бар. 35 оқушыдан кем оқушысы бар
сынып табыла ма?
Шешуі: Барлық сыныпта 35 оқушы болса, онда 35*33=1155 оқушы болады, бұл есеп шартына қайшы, ендеше 35 –тен кем оқушы бар сынып бар.
5
6. Дөңгелекке 2009 натурал сан жазылған. Қосындысы жұп сан болатын
екі көрші сан табылатынын дәлелдеңдер.
Шешуі: Көршілес натурал сандардың қосындысы әрқашанда тақ болады және натурал сандар саны жұп болса, ал дөңгелекке 2009 сан орналастырылған, ол – тақ сан сондықтан, 1 мен 2009 көршілес, ал олардың қосындысы 2010 – жұп сан.
7. Гаражда 54 жүргізуші бар.Егер әр күні гараждағы 60 машинаның 25%-ы өз ақауларын жөндеу үшін жұмысқа шықпай қалса, онда бір айда (30 күн) әр жүргізушінің неше бос күні болады?
Шешуі: Әр күні 0,25*60 = 15 машина гаражда қалады. 60 – 15 = 45 машина жұмысқа шығады, 54 – 45 = 9 жұмыстан бос қалады. Бір айда 30*9=270 адам-күн бос. Әр жүргізушінің 270 : 54 = 5 бос күні болады. Жауабы: 5
8. Сүтімен шелектің массасы 32 кг, сүтсіз -2кг. Шелектің жартысы
сүтпен толтырылса оның массасы қандай?
Шешуі: 17 кг.
9. Үш қыз ақ, көк, жасыл көйлек және сондай туфли киды. Егер
Айгүлдің көйлегі мен туфлиі бірдей болса, ал Гулнардың не көйлегі не туфлиі ақ емес, Нүргүлдікі жасыл туфли болды. Әр қыздың көйлегі мен туфлилерінің түрін анықта.
Шешуі: Айгүл-ақ көйлек , ақ туфли Гүлнар- жасыл көйлек, көк туфли Нұргүл-көк көйлек, жасыл туфли.
10. Екі өзара жай сандардың көбейтіндісі 3232. Ең кіші ортақ еселігін және осы сандарды тап.
Шешуі: 3232=32*101=2*2*2*2*2*101 еселігі 3232.
11. х-тің 13,5%, у-тің 12,5%-не тең болса, х және у сандарын салыстыр.
Шешуі: 13,5х=12,5у, х<у, егер х және у оң сан болса; х=у, егер х= у=0 болса; х>у, егер х және у-теріс сан болса.
12. Өлшемі 2х2х2 кубты бояу үшін 2 грамм бояу керек. Өлшемі 6х6х6 кубты бояу үшін қанша бояу керек?
Шешуі: Кубиктің үлкен жағы кіші кубиктің жағынан 9 есе үлкен болса , онда бояу да 9 есе көп кетеді , ендеше 18 гр.
6
13. 2008 натурал санның қосындысы – тақ сан. Осы сандардың
көбейтінділері тақ па, әлдә жұп сан бола ма?
Шешуі: 2008 натурал санның барлығы жұп, тақ , жұп және тақ болады. Бірінші және екіншіcі болмайды, себебі олардың қосындысы тақ, ендеше 2008 натурал сандарының ішінде тақ та, жұп та сандар бар , сондықтан олардың көбейтінділері жұп болады.
14. 1-ден 12-ге дейінгі сандарды пайдаланып екі тіктөртбұрыш пен бір шаршының төбелеріндегі сандардың қосындысы бірдей болатындай етіп жазыңдар.

![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 1-ден 12-ге дейінгі
сандардың қосындысы 78-ге тең. Онда тіктөртбұрыш пен шаршының
төбелеріндегі сандардың қосындысы 26-ға тең болады. Мүмкін
жағдайлар: 12,9,1,4 - шаршының төбелері 11,8,2,5 және 10,7,3,6 -
тіктөртбұрыш төбелері.
1-ден 12-ге дейінгі
сандардың қосындысы 78-ге тең. Онда тіктөртбұрыш пен шаршының
төбелеріндегі сандардың қосындысы 26-ға тең болады. Мүмкін
жағдайлар: 12,9,1,4 - шаршының төбелері 11,8,2,5 және 10,7,3,6 -
тіктөртбұрыш төбелері.
15. Сыныпта 25 оқушы бар, олардың жастарының қосындысы 270 жыл.
Сыныпта 20 оқушы табыла ма, олардың жастарының қосындысы 260 тан
артық болатын?
Шешуі: 20 оқушы табылсын , қалған 5 оқушының жастарының қосындысы 10 үлкен болмайды , сонда орташа жастары 2 ден артық болмайды . Бүл қайшы , ендеше ондай оқушылар жоқ.
16. Көлде 1 лилия гүлдеді. Әр күні гүлдер саны көбейді де 10 -шы күні барлық өзенді гүлдер көмкерді.Көлдің жартысын гүлдер нешінші күні көмкереді?
Шешуі: Тоғызыншы.
7
17. Ерік дүкеннен 1 қаламды 1 теңге 80 тиынға және 6 қарандаш алуға барды. Дүкенші Еріктен 5 теңге бересің, сонда Ерік мен қателестім деді. Еріктікі дұрыс па және неге?
Шешуі: 5 теңге-1 теңге 80т=3 теңге 20 тиын=320 тиын 320 бөлінбейді 6-ға.
18. 11*21*31*41*51*61*71*81*91-1 10-ға бөліне ме? Неге?
Шешуі: Көбейтіндінің соңғы цифры 1-ге аяқталады, онда айырма 0-мен аяқталады , ендеше 10-ға бөлінеді.
19. Есептеңдер: -90-89-88-....-1+0+1+2+....98+99+100
Шешуі: -90-89-88-...-1+0+1+2+3+...+98+99+100=(91+100)*5=955.
20. Алматыдан Талдықорғанға дейін 40 км/сағ жылдамдықпен машина
шықты және 1 сағат жүрді. Кері қайтқанда ол 60 км/сағ жылдамдықпен жүрді. Машинаның орташа жылдамдығын тап.
Шешуі: 48 км/сағ.
21. 4х4 метр өлшемі бар кілемді 15 тесік жасап құрт жеді. Өлшемі 1х1 метр кілемді кесіп алуға бола ма? Және оның ішінде тесік болмау керек.
Шешуі: 16 кілемшелерге 1х1 бөлеміз 16>15 сонда бір кілемше тесіксіз қалады.
22. Жеті алманы 12 адамға, бір алманы 4 тен артық бөлікке бөлмей тең беруге бола ма?
Шешуі: 7:12
= =
=
 +
+  онда 3 алманы 4 бөлікке
, ал 4 алманы 3 бөлікке бөлуге болады.
онда 3 алманы 4 бөлікке
, ал 4 алманы 3 бөлікке бөлуге болады.
23. Бөлінгіш пен бөлгішті 3 есе арттырғанда, бөлінді мен қалдық өзгере
ме?
Шешуі: a=bq+r 3-ке көбейтеміз 3a=3bq+3r ендеше қалдық 3 есе өседі, ал бөлінді өзгермейді 5=3*1+2 5*3=15 3*3=9 15=9*1+6 қалдық өзгерді.
24.





 сандарын кему ретімен
орналастырыңдар.
сандарын кему ретімен
орналастырыңдар.
Шешуі: 1- =
= ;
1-
;
1- =
= 1-
1- =
= 1-
1- =
=




 болса,
онда
болса,
онда 




Жауабы:


8
25. Бір тәулікте сағаттың және минуттың тілдері неше рет тік бұрыш
жасайды?
Шешуі: Шарт бойынша 3 сағ,9сағ ,15сағ ,21сағ. 1 сөткеде бұл 11*4=44 болады.
7 сынып
1. Поезд бағдаршамның жанынан 5 сек, ал ұзындығы 150 м көпірден 15 сек өтеді. Поездың ұзындығы мен оның жылдамдығын тап.
Шешуі:  =
5;
=
5;  = 15, S=75м,
v=15м/с
= 15, S=75м,
v=15м/с
2. 101 жылқыны 15 қораға орналастырған. Сонда неге ең болмағанда бір
қорада тақ санды жылқылар саны болады?
Шешуі: Кері дәлелдейміз.Әр қорада жұп сан жылқылар бар, онда қосынды жұп. Шарт бойынша 101 жылқы бар – тақ, ендеше ең болмағанда 1 қорада тақ сан жылқылар бар.
3. Натурал санды өзінің әрбір цифрларына көбейткенде 1995 шықты. Ол
қандай сан?
Шешуі: 1995 –ті көбейткіштерге жіктеу керек 1995=3*5*7*19 ізделінді сан бір орынды, үш орынды бола алмайды , ендеше ол екі орынды.1995=57*7*5
4. Үстелде 60 кәмпит бар. Екі оқушы кезек-кезек бір алғанда 4 тен артық
емес кәмпит алады. Кім соңында алса сол жеңеді. Дұрыс ойында кім жеңеді?
Шешуі: Екінші жеңеді. Ол әрқашан біріншінің алған конфеттерінің қосындысын 5-ке тең деп алу керек.
5. Жазықтықта төрт тең үшбұрыштар берілген және екеуінің ортақ екі
төбелері бар. Барлығының ортақ төбесі бар деген дұрыс па?
Шешуі: АВСД төртбұрышынан ΔАВС ΔДВС ΔАДС ΔАВД алу керек, бұл үшбұрыштарда ортақ төбе болмайды , ендеше дұрыс емес.
6. Жәшіктен барлық жұмыртқаның жартысын, сонан соң қалғанының
жартысын, тағы жаңа қалғанының жартысын соңында тағы қалғанының
жартысын алды, сонда жәшікте 10 жұмыртқа қалды. Барлығы қанша
жүмыртқа еді?
Шешуі: 160 жұмыртқа
9
7. 4 қара және 3 сары сиырлар 5 күнде қанша сүт берсе , 3 қара және 3 сары сиырлар 4 күнде сондай сүт береді. Қара сиырдың ба, әлде сары
сиырдың сүті көп болады?
Шешуі: 20 қара, 15 сары, сиырлардың бір күнде беретін сүтін 12 қара және 20 сары сиырлар береді, ендеше 8 қара сиырдың бергенін 5 сары сиыр береді. Сары сиыр сүтті көп береді.
8. Егер ұзындығын 20%-ке, енін10%-ке өсірсе тік төртбұрыштың ауданы
қанша пайызға өседі?
Шешуі: 32%-ға
9. Теңдеуді шешіңдер: 2(3-2х)=3х-4(1+3х);
Шешуі: х= -2
10. (а+в)х+(а-в)х-2ах=0 тең екенін дәлелдеңдер.
Шешуі: Жақшаны ашып ұқсас қосылғыштарды біріктіру керек.
11. Жәшікте 24кг шеге бар. Табақшалы таразы мен гирсыз 9 кг шегені
қалай алуға болады?
Шешуі: 24 кг-ды екі бөлікке бөледі , таразымен 12 кг шегені өлшеу керек. Біреуін өзін қалдырып екінші үймекті тағы тең бөлу керек . Тағы 6кг екі үймек шықты , сонда 12;6;3;3кг 3*3=9 кг
12. Тақтаға 321321321321 саны жазылған. Қай цифрды өшіргенде ең
үлкен және 9-ға бөлінетін сан шығады?
Шешуі: 9-дың бөлінгіштік қасиеті бойынша сызылған цифр 6. Екі үштікті сызу керек, тағы тізбектес екі үштікті сыз.
13.Егер а=в+1 болса,
онда (а+в)( +
+ )(
)( +
+ )...(
)...( +
+ )=
)= теңдігі орындалатынын
дәлелде.
теңдігі орындалатынын
дәлелде.
 а-в=1,
а-в=1,  =(
=( +
+ )(
)( +
+ )(
)( +
+ )(
)(
 +
+ )( а+в
)( а-в ).
)( а+в
)( а-в ).
14. АВС тең қабырғалы үшбұрыштың АВ,ВС және АС қабырғаларына сәйкесінше Д,Е,F нүктелері алынған және АД = ВЕ = СF болса, онда пайда болған ДЕF тең қабырғалы үшбұрыш екенін дәлелдеңдер.
 Мына
Мына  ВЕ
=
ВЕ
=  FАД тең болғандықтан
(екі қабырғасы мен арасындағы бұрышы бойынша) ДЕ = ЕF = FД
қабырғалары тең болады. Сондықтан ,
FАД тең болғандықтан
(екі қабырғасы мен арасындағы бұрышы бойынша) ДЕ = ЕF = FД
қабырғалары тең болады. Сондықтан ,  ДЕF тең қабырғалы
үшбұрыш болып табылады.
ДЕF тең қабырғалы
үшбұрыш болып табылады.
10
15.Сыныпта 27 оқушы бар. Әр бала 4 қызбен, әр қыз 5 баламен достасады. Сыныпта қанша бала, қанша қыз бар?
 Сыныпта х – бала, у –
қыз болсын. Жалпы достықты санасақ, 4х және 5у бұдан
4х = 5у, ал
х+у=27. Есептеуді орындағанда
х=15, у=12.
Сыныпта х – бала, у –
қыз болсын. Жалпы достықты санасақ, 4х және 5у бұдан
4х = 5у, ал
х+у=27. Есептеуді орындағанда
х=15, у=12.
16. АС және ВД кесінділері қиылысады және АВ=ВС=СД=АД. АС және ВД перпендикуляр екенін дәлелде және АВСД фигурасының ауданын тап, егер АС= 10см, ВД=15 см болса.
Шешуі: ΔАВС=ΔСДА және тең бүйірлі.ДАС = ВСА = АСД СА
ΔВСД-ның биссектрисасы және CA
биіктік, АС![]() ВД . А және С нүктелері арқылы
ВД параллель , В және Д нүктелері арқылы АС-ға параллель жүргізу
керек. Тіктөртбұрыш ауданы АВСД-дан 2 есе артық
шықты.
ВД . А және С нүктелері арқылы
ВД параллель , В және Д нүктелері арқылы АС-ға параллель жүргізу
керек. Тіктөртбұрыш ауданы АВСД-дан 2 есе артық
шықты.
Жауабы:
SАВСД = ВД*АС=75см2
ВД*АС=75см2
17. Арман шаршы пішіндегі үйінің көлемін сол бұрынғы шаршы пішінін сақтай отырып екі есе кеңейткісі келді. Үйінің төрт бұрышында 4 ағаш өсіп тұр. Арман ағаштарды қалдыруды ойлады. Жаңа қабат та, басқа жерден жаңа үй де салғысы келмеді. Ол үйін қалай үлкейткен?
![]()
![]()

![]()
![]()


![]()
![]()
![]()
![]()
18. Есептеңдер:
1+2-3-4+5+6-7-8+9+10-.....+2002-2003-2004+2005+2006-2007-+2008+2009-2010
Шешуі: 2-ден бастап барлық сандарды төрт-төрттен топтау керек. Барлық төрттіктер 501. Әрбір төрттіктердің қосындысы 0.Ендеше өрнектердің қосындысы 1.
11
19. Кітаптың бірінші бетінен соңғы бетіне дейін нөмірленген. Бұзық Самат кітаптың әр жерінен 25 жыртып алып, 50 беттің барлық нөмірлерін қосады. Сонда ол сандардың қосындысы 2002-ге тең болады.Бұл туралы Қанат естігенде, ол Саматтың есептеуде қателескенін айтады.Қанат неге бұлай айтты ойланыңдар.
Шешуі: Әрбір жыртылған парақта екі бет бар болады.Бір беттің номері тақ сан болса, екінші беттің номері жұп сан болады.Ендеше 25 тақ нөмерлі 25 жұп нөмер беттерінің қосындысынан тұрады. Ал бұлардың қосындысы тақ сан болады, ал онда ол 2002-ге тең болмайды, өйткені бұл жұп сан.
20.
Есептеңдер:  ;
;

 =
=
 =
= 
 ;
;
21. Екі дос
мынандай  сандардың екінші
дәрежелерінің айырымын есептеп отырып осы санның негіздерінің
қосындысына тең екенін байқап қалады.Өздерінің жаңалықтарын басқа
10 және 11 санына пайдаланып қорытындысына көздері
жетеді:
сандардың екінші
дәрежелерінің айырымын есептеп отырып осы санның негіздерінің
қосындысына тең екенін байқап қалады.Өздерінің жаңалықтарын басқа
10 және 11 санына пайдаланып қорытындысына көздері
жетеді:  ал, сен қалай
дәлелдейсің?
ал, сен қалай
дәлелдейсің?

 формуласымен
дәлелденеді.
формуласымен
дәлелденеді.
22. Теңдік ақиқат болатындай модуль таңбасын қойыңдар:
1 – 2 – 4 – 8 – 16 = 19

 = 19.
= 19.
23. 1000 м қашықтыққа жүгіруде алға Марат озып шықты, екінші боп Ерлан келе жатты, ал үшіншісі – Самат. Жүгіру барысында Марат пен Ерлан – 6 рет, Ерлан мен Самат – 5 рет, Марат пен Самат – 4 рет орындарымен ауысты. Спортсмендер қандай ретпен жүгірісті аяқтады? Неге?
Шешуі: Марат пен Ерлан орындарымен жұп сан рет ауысты, сондықтан Марат Ерланның алдында қала берді. Марат пен Самат та жұп сан рет ауысып, орындары өзгерген жоқ, Марат Саматтың алдында. Ерлан мен Самат тақ сан рет ауысқандықтан, Самат Ерланның алдында келеді. Сонда мәредегі спортсмендердің реттері мынандай: Марат, Самат, Ерлан.
24. Сандарды
салыстыр:  және
және  *
*


12
25. АВС үшбұрышының А
бұрышы  , ал В
бұрышы
, ал В
бұрышы , АВ - ВС=4 болса С
бұрышының биссектрисасының ұзындығын тап.
, АВ - ВС=4 болса С
бұрышының биссектрисасының ұзындығын тап.

С


![]()
![]()
![]()
А Д Е В
АВ қабырғасына ВД=ВС кесіндісін салып , оны Д және С нүктелерімен қосады
ΔВСД ; ВД=ВС ДСВ = СДВ=80°
ΔАВС ; СЕ биссектрисасы болсын С=120° АСЕ=60° АЕС=80°
ΔДЕС ; Е = Д=80° ендеше АСД=40°
ΔАСД ; СЕ=СД=АД=АВ-ВС=4, сонымен СЕ = 4.
8 сынып
1. Натурал n санның екі а және в бөлгіші бар, сонда (а-1)(в+2)= n -2 болса,
2 n – натурал санның квадраты екенін дәлелде.
Шешуі: ав=2а-в=n а және в n-нің әр түрлі бӛлгіші.в:а, 2а:в, в=2а және 2n=4а2=(2а)2;
2. Дүкенде консервленген жемісі бар шыны 0,5л; 0,7л; 1 л ыдыс бар.
Сонда дүкенде 2600 шыны ыдыс массасы 2002 л бар. Дүкенде ең болмағанда бір 1,5л ыдыс бар екенін дәлелде.
Шешуі: Дүкенде көлемі 0,7 л а шыны және көлемі 1л ыдыс бар.
3. Жәшікте 16 алма бар. Бір рет өлшеу арқылы үш алманың масса-ларының қосындысын табуға болады. Қалай 8 рет өлшегенде барлығы-ның массасын табуға болады?
Шешуі: mi i= 1,….,16 осы шамалардың массасы. 4-рет өлшеп (m1+m2+m3)+(m1+m2+m4)+(m1+m3+m4)+(m2+m3+m4)=3(m1+m2+m3+m4)Қалған 12 алманың массаларының қосындысы (m5+m6+m7)+ (m8+m9+m10)+ (m11+m12+m13)+ (m14+m15+m16).
13
4. Төрт әр түрлі натурал сан таңдап алуға бола ма ,әрбір екеуінің
қосындысы 3-тің дәрежесі болатын?
Шешуі: Дирихле принципі бойынша сандардың ішінде екі сан бар , қосындысы жүп , сондықтан 3-тің дәрежесі болмайды.
5. Барлық теріс емес m және n сандарының парын тап, ол mn-n+m=2004
теңдігіне қанағаттандыратындай.
Шешуі: Жауабы: m=2 ,n=2002, m=2004 ,n=0 нұсқау ; бастапқы теңдеуді мына түрде жаз (m-1)(n+1) =2003, Жауабы:2003 жай сан.
6. АВС ұшбұрышының АҒ медианасы. АВ қабырғасының созындысы В
нүктесінен кейін Д нүктесін белгілеп, ал Е нүктесі ДҒ пен АС-нің қиылысу
нүктесі болса, онда АВ=ВД=АҒ болса СЕ=ЕҒ болатынын дәлелде.
А
![]()


 Е
Е
![]() С
В
С
В
F
Д
Шешуі:
ДFВ=ϒ=ЕFС (вертикаль) АВ=АF АВF=АFВ=α ДВF=180°-α
ДВС=ВАС+ВСА=ВAF+(FАС+FСА)=180°-2α+α=180°-α.
ΔАFС=ΔДFВ ВFД=FСЕ=ϒ бұдан СЕ=ЕҒ.
7. Жылдамдығы 60км/сағ поездағы адам терезеден жанынан өткен поезді
4 сек көрді. Егер өткен поездің ұзындығы 120 м болса, жылдамдығын тап.
Шешуі: 48 км/сағ.
8. 1 ден 100 дейінгі бүтін сандардың көбейтіндісі қанша нольмен
аяқталады?
Шешуі: 1 ден 100-ге дейінгі сандарда 24 бестік бар. 10;20;30;40;60;70;80;90;5;15;35;45;55;65;85;95;25;50;75;100.
Барлық сан 5 пен көбейткенде нольге аяқталады. Ендеше 24 нольмен аяқталады. Жауабы:24
14
9. 1997*** саны 1996-ға бөлінеді. *** цифрларын қанша тәсілмен ауыстырады?
 Бір ғана тәсіл бар және
1997996 ізделінді сан болып табылады.
Бір ғана тәсіл бар және
1997996 ізделінді сан болып табылады.
10. Теңдеуді шеш, мұндағы Р – А және В сандарының арифметикалық ортасы.
А
= және В =
және В = ,
,

 5
5
А
= В
=
В
= болса, Р
=
болса, Р
= =
= =
=
 =
= ,
Жауабы: х =
5.
,
Жауабы: х =
5.
11.
Ең үлкен ортақ бөлгіш тап:
а= және в=
және в=
 ЕҮОБ(а;в)=3
ЕҮОБ(а;в)=3
Ортақ бөлгіш в-2а=3 санының да бөлгіші, сондықтан берілген сандар 3-ке бөлінеді.
12. Бес бала 9 саңырауқұлақ тауып алды. Осы балалардың ең болмағанда екеуі тең шамада саңырауқұлақ тауып алғанын дәлелдеу керек.
 Балалар әртүрлі шамада
саңырауқұлақ тауып алды дейік, олардың
Балалар әртүрлі шамада
саңырауқұлақ тауып алды дейік, олардың
тауып алған саңырауқұлақтарын өсу ретімен айтайық: біріншісі нөлден кем емес, екіншісі бірден кем емес,үшіншісі екіден кем емес,төртіншісі үштен кем емес,бесіншісі төрттен кем емес.Барлығы оннан кем емес, бұл – қайшылық.
13. Жүйені бүтін сандар
жиынында

Екінші теңдеуден біріншіні шегеріп: (z-x)(y-1) =1 x,y,z бүтін сан болса, онда екі жағдай қарастырылады:
а) z-x =1 және y-1=1
z=х+1 у=2 жүйеге қойып 2х+х+1=2005 х=668 z=669
ә) z-x = -1 және y-1= -1
x =1+z және y=0 z=2005 х=2006
15
14. АВСД шаршының АВ қабырғасына іштей теңбүйірлі АВЕ үшбұрышын салған, АВ табанындағы бұрыштары 15°-қа тең. СДЕ үшбұрышының дұрыс үшбұрыш екенін дәлелдеңдер.
 Кері есеп шығарайық:
егер СДЕ1
дұрыс үшбұрыш болатын болса,
АВЕ1
үшбұрышының АВ табанындағы
бұрыштары 15°-қа тең екенін
дәлелдейік.
Кері есеп шығарайық:
егер СДЕ1
дұрыс үшбұрыш болатын болса,
АВЕ1
үшбұрышының АВ табанындағы
бұрыштары 15°-қа тең екенін
дәлелдейік.
Д С


![]()
![]()
![]()
![]()
![]()
![]()
60°
30°
![]()
![]()
![]() 75° Е1
75° Е1
75°
![]()
![]() 15°
15°
![]() А В
А В
АДЕ1=30° және ДЕ1=АД, онда Е1АД = А Е1Д = 75° олай болса, Е1АВ=15°, сол сияқты Е1ВА=15°. Сонымен біз СДЕ1 дұрыс үшбұрышының Е1 төбесі есептің берілгеніндегі Е нүктесімен дәл беттеседі, олай болса СДЕ - дұрыс үшбұрыш .
15.Дәлелдеу
керек:  < 98
< 98
 <
98,
<
98,

 49+
49+
2400 2401
дәлелденді.
2401
дәлелденді.
16. Егер
 = 7 болса,
онда
= 7 болса,
онда  неге
тең?
неге
тең?


17. Теңдеуді
шеш:  +
+
 2;
6
2;
6
16
18.
Оң х және у
үшін: 


 теңсіздігі орындалатынын
дәлелде.
теңсіздігі орындалатынын
дәлелде.





 +
+
 ;
х = у
=1
;
х = у
=1
19.
 қосындысының 85-ке
бөлгенде қалдығын тап.
қосындысының 85-ке
бөлгенде қалдығын тап.

169 = 85*2-1
және  =
85*3+1
=
85*3+1
 =к*85+
=к*85+
 Жауабы:
0
Жауабы:
0
20. Өрнектің мәні рационал сан болатынын дәлелдеңдер:



 -
-

21. Мектепте 25 сынып және 850 оқушы бар болса, 34 оқушыдан кем емес сынып бар екенін дәлелдеңдер:
 Айталық мектепте мұндай
сынып жоқ делік, сонда барлық сыныпта 33 немесе одан да аз оқушылар
бар болады. Сондықтан, мектептегі барлық оқушылар 33*25=825-тен
артық болмайды. Ал, бұл берілген шартқа қайшы, демек біздің ұйғарым
шын емес.Сондықтан, мектепте 34-тен кем емес сыныптар болады
екен.
Айталық мектепте мұндай
сынып жоқ делік, сонда барлық сыныпта 33 немесе одан да аз оқушылар
бар болады. Сондықтан, мектептегі барлық оқушылар 33*25=825-тен
артық болмайды. Ал, бұл берілген шартқа қайшы, демек біздің ұйғарым
шын емес.Сондықтан, мектепте 34-тен кем емес сыныптар болады
екен.
22. х-тің кез-келген мәнінде а мен в-ның мәнін табыңдар:
 =
= +
+
 Теңдіктің оң жағының
бөлімін ортақ бөлімге келтірсек, ол сол жағының ортақ бөліміне тең
болады. Сондықтан: 5х+31= ах+2а+вх-5в
бұдан
Теңдіктің оң жағының
бөлімін ортақ бөлімге келтірсек, ол сол жағының ортақ бөліміне тең
болады. Сондықтан: 5х+31= ах+2а+вх-5в
бұдан
5х+31= (а+в)х+(2а-5в) әрі қарай мына жүйені шешеміз:

 Жауабы:
а = 8, в =
-3.
Жауабы:
а = 8, в =
-3.
17
23. (Безу есебі). Біреу жылқы сатып алып, біраз уақыт өткізіп, оны 24 пистолға сатып жібереді. Сонда ол жылқыны сатып алғандағы бағамен бірдей болатын пайызға ұтылып қалады. Жылқыны қандай бағаға сатып алды?
 Жылқыны х – пистолмен
белгілесек. Сату барысында х% жоғалтады десек,онда мынадай теңдеу
құрамыз: х-
Жылқыны х – пистолмен
белгілесек. Сату барысында х% жоғалтады десек,онда мынадай теңдеу
құрамыз: х- = 24 бұдан х = 40
немесе
= 24 бұдан х = 40
немесе
х = 60 , сонымен жылқыны 40 пистолға немесе 60 пистолға сатып алады.
24. Дөңес төртбұрыштың диагональдары оны төрт үшбұрышқа бөледі. Қарама-қарсы үшбұрыштың ауданының көбейтіндісі, екінші қарама-қарсы үшбұрыштың ауданының көбейтіндісіне тең екендігін дәлелдеңдер.
 Айталық АВСД - берілген
төртбұрыш, онда S1
=
Айталық АВСД - берілген
төртбұрыш, онда S1
=
 ;
;
S2
=
 ; S3
=
; S3
=
 ; S4
=
; S4
=
 ; Сондықтан
; Сондықтан
S1*
S3
=
S2*
S4
=
 дәлелдеу керегі де
осы.
дәлелдеу керегі де
осы.
25.
Егерде  қосындысы 3-ке бөлінетін
болса және х, у – бүтін сандар болса, онда х және у 3-ке
бөлінетіндігін дәлелдеңдер.
қосындысы 3-ке бөлінетін
болса және х, у – бүтін сандар болса, онда х және у 3-ке
бөлінетіндігін дәлелдеңдер.
 Айталық х =
3q+r1 ,
y =
3p+r2
.
r1
мен
r2
3-ке бөлгендегі қалдықтар
болса, онда 0, 1, 2 сандар болады. Онда:
Айталық х =
3q+r1 ,
y =
3p+r2
.
r1
мен
r2
3-ке бөлгендегі қалдықтар
болса, онда 0, 1, 2 сандар болады. Онда:
 =
=
 3-ке
бөлінетіндіктен
3-ке
бөлінетіндіктен  - де 3-ке бөлінеді.
Бірақ
- де 3-ке бөлінеді.
Бірақ 
0, 1, 2, 4, 5 немесе 8 қабылдайтындықтан, бұлардан 0 ғана 3-ке бөлінеді. Бұдан . r1 = r2 = 0. Демек х және у 3-ке бөлінеді.
9 сынып
1. Машина 600км жол жүрді. Ол жолдың бірінші жартысын 100км/сағ
жылдамдықпен, екінші жартысын 60км/сағ жылдамдықпен жүрды.
Машинаның орташа жылдамдығын тап.
Шешуі: Жарты жол 600:2=300(км) бұған жіберген уақыт 300:100=3(сағ). Екінші жартысына жіберілген уақыт 300:60=5(сағ). Машинаның жүрген уақыты 3+5=8(сағ). Орташа жылдамдық 600:8=75(км/сағ)
Жауабы : 75(км/сағ)
18
2. Екі үш орынды сандарды тап, олардың қосындысы 498-ге еселік, ал
бөліндісі 5-ке еселік болатын.
Шешуі: а кіші , в үлкен ізделінді үш орынды сан 100≤а<в<1000, а+в=498к, в=5а немесе 6а=498, а=83к, в=415к, к≥2 және к≤2, к=2 а=166 в=830
Жауабы: а=166, в=830
3. Бір санның квадраты 0, 2, 3, 5 цифрларынан түрады, осы санды тап. Шешуі: Санның квадраты 2 немесе 3 немесе бір нольмен аяқталмайды. Ендеше соңғы цифр 5, ондық 2-ге тең. (10а+5)2=100а2+100а+25 3025=552
Жауабы: 3025=552
4. Бірнеше санның қосындысы 1-ге тең, олардың квадратарының
қосындысы 0,01-ден кіші бола ма?
Шешуі: Әрбір n
саны  -ге тең болса , онда осы
сандардың қосындысы 1-ге тең , ал квадраттарының
қосындысы
-ге тең болса , онда осы
сандардың қосындысы 1-ге тең , ал квадраттарының
қосындысы  -ге тең , n>10
квадраттың қосындысы 0,01ден кіші. Жауабы:
болады
-ге тең , n>10
квадраттың қосындысы 0,01ден кіші. Жауабы:
болады
5. Дөңес АВСД төртбұрышының диагональдарының қиылысу нүктесі Е.
SABE=SCDE болса АС А бұрышының биссектрисасы, АВ =4 болса, онда ВС -ны тап.
В С
![]()




4
Е
![]()
![]()
![]()
![]() А
Д
А
Д
Шешуі: SABE=SCDE, SABD=SCВD AD||BС, ABCD- трапеция ВСА=САД ВСА=САВ берілгені бойынша АД және ВС=АВ=4
Жауабы: ВС=4
6. Алты адамның ішінен үш бір-бірін танитын немесе үшеуі бір-бірін
танымайтынын дәлелде.
Шешуі: А,В,С,Д,Е,М алтауы А: «таныс», «таныс емес» В,С,Д болсын. Бұның біреуі «таныс», «таныс емес» болса, онда екеуі А мен ізделінді үштік немесе В,С,Д болады.
19
7. Дөңес төртбұрыштың диагональдары оны төрт үшбұрышқа бөледі.
Қарама-қарсы екі үшбұрыштың аудандарының көбейтіндісі, қалған екі
үшбұрышының аудандарының көбейтіндісіне тең екенін дәлелде.
Шешуі: ?1=
 ?2=
?2= ?3=
?3= ?4=
?4= ?1*?3=?2*?4
?1*?3=?2*?4
8. 100 санын қанша тәсілмен тібектес бірнеше санның қосындысы
түрінде жазуға болады?
Шешуі: Бірінші сан n, соңғы n+к қосындыны n+(n+1)+(n+2)+...+(n+к) =100 арифметикалық прогрессияның сол жақтағы қосындысын тауып: (2n+к)(к+1) =200 200=2*100=1*200=4*50=5*40=8*25 Бірінші көбейткіш екіншіден үлкен және біреуі жұп, екіншісі – тақ
2n+k=25 немесе 2n+k=40
k+1=8 k+1=5
n=9 k=7 n=18 k=4
Жауабы: 9+10+11+12+13+14+15+16=100 немесе 18+19+20+21+22=100
9.Бірінші мүшесі 1-ге, ал айырмасы 2-ге тең болатын арифметикалық прогрессияның алғашқы он мүшесінің көбейтіндісі қандай цифрмен аяқталады?
Шешуі: (![]() ) - арифметикалық
прогрессия.
) - арифметикалық
прогрессия. ![]() . Онда 1; 3; 5; 7; 9; 11; 13;
15;17; 19. Бұл прогрессия арасында 5 және 15 сандары тақ сандар.
Тақ сандардың 5 пен көбейтіндісі 5 цифрымен
аяқталады.
. Онда 1; 3; 5; 7; 9; 11; 13;
15;17; 19. Бұл прогрессия арасында 5 және 15 сандары тақ сандар.
Тақ сандардың 5 пен көбейтіндісі 5 цифрымен
аяқталады.
1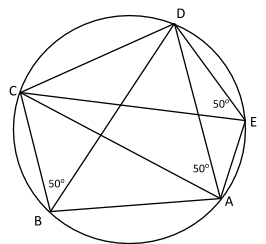 0. АВСДЕ дөңес бесбұрышы шеңберге іштей
сызылған.
0. АВСДЕ дөңес бесбұрышы шеңберге іштей
сызылған. ![]() екені
белгілі.
екені
белгілі. ![]() қосындысын
табыңыз.
қосындысын
табыңыз.
Шешуі: CD доғасына
тірелген![]() болса, онда
.
болса, онда
. ![]() 50
0
50
0
![]()
деп білейік
![]()
болады.
АС доғасына қарама-қарсы тірелген бұрыштардың қосындысы
![]() 0 , олай
болса
0 , олай
болса
![]() , бұдан
, бұдан ![]()
![]()
Жауабы: 230о
20
11. ![]() теңдігін
қанағаттандыратын
теңдігін
қанағаттандыратын ![]() саны табылатындай, барлық
жай
саны табылатындай, барлық
жай ![]() сандарын
табыңыз.
сандарын
табыңыз.
Шешуі: ![]() теңдеуі
теңдеуі ![]() квадрат теңдеуіне
келеді.
квадрат теңдеуіне
келеді.
D=![]()
![]() ,
p жай сан болуы
үшін,
,
p жай сан болуы
үшін,
![]() жай сан емес
жай сан емес
![]() жай сан,
жай сан,
![]() жай сан емес,
жай сан емес,
![]() жай сан емес Жауабы: р=2
жай сан емес Жауабы: р=2
12. Оқушылар емтихан тапсырғанда оларға 3 есеп берілді. Оқушылардың 98 % - бірінші, 90 % - екінші және 85 % - үшінші есепті шығарды. Барлық үш есепті оқушылардың х% шығарды. х - тің ең кіші және ең үлкен мәнін табыңыз.
Шешуі: Бірінші есепті 2%-ы шығармады.Екінші есепті 10%-ы шығармады.
Үшінші есепті 15%-ы шығармады. Осы есептерді шығармаған оқушылар әртүрлі болса, онда үш есептің біреуін шығармаған оқушылар 2%+10%+15%=27% онда x%=100%-27%=73% Үшінші есепті шығарғандар ең азы 85%-ы, сол үшінші есепті шығарғандардың барлығы бірінші және екінші есепті шығарған болса, x%=85% болады.
Жауабы: xmax=85, xmin=73
13. 512... алты таңбалы санның соңғы үш цифрын табу керек, сонда шыққан сан 7-ге, 8-ге және 9-ға бөлінетін болсын.
Шешуі: Ізделінді сан мынадай шарттарды қанағаттандыру керек:
1.
![]() санына бөлінетін жұп сан болуы
керек;
санына бөлінетін жұп сан болуы
керек;
2. 8-ге бөлінетін болғандықтан соңғы үш цифры 8-ге бөліну керек.
3. 9-ға бөлінетіндіктен ізделінді алты таңбалы снның цифрларының қосындысы 9-ға бөлінетін, 18-ге және 27-ге тең болуы қажет.
Онда ізделінді сан 512064 және 512568.
21
14.![]() саны қандай цифрмен
аяқталады?
саны қандай цифрмен
аяқталады?
Шешуі: 1-тәсіл.

Енді 9 дың бірнеше дәрежесінің қандай цифрмен аяқталатынын анықтаймыз:
-
-

1 цифрымен аяқталатын санның дәрежелері 1 цифрымен аяқталады. Онда
 және
және  1
цифрымен аяқталады. Демек, 1х1х9=9.
1
цифрымен аяқталады. Демек, 1х1х9=9. саны 9 цифрымен аяқталады.
саны 9 цифрымен аяқталады.
-
2-тәсіл. 9-дың тақ көрсеткішті дәрежелері 9 цифрымен,
ал жұп көрсеткіштідәрежелері 1 цифрымен
аяқталатынын байқаймыз. Дәреже көрсеткіштері 1; 3; 5 ;… және 2; 4;
6 арифметикалық прогрессия құрайды, айырмасы
![]() болады.
болады. ![]() арифметикалық
прогрессияның
арифметикалық
прогрессияның
![]() - ші мүшесінің
формуласы бойынша
- ші мүшесінің
формуласы бойынша
![]() .
Онда
.
Онда
![]() айырмасы 2-ге бөлінуі
үшін
айырмасы 2-ге бөлінуі
үшін ![]() болуы керек. 1 тақ сан,
ендеше
болуы керек. 1 тақ сан,
ендеше ![]() саны 9 цифрымен
аяқталады.
саны 9 цифрымен
аяқталады.
15.Теңдеулер жүйесін
шешіңдер: 
Шешуі:  жүйедегі 1-теңдеуді 1-ге,
2-теңдеуді 3-ке көбейтіп
жүйедегі 1-теңдеуді 1-ге,
2-теңдеуді 3-ке көбейтіп  жүйенің теңдеулерін
қосып,
жүйенің теңдеулерін
қосып, ![]() теңдеуін аламыз.
Онда,
теңдеуін аламыз.
Онда,![]()
![]() болады.
болады.
Виет теоремасы бойынша квадрат
теңдеуді шешіп ![]() . Демек,
. Демек,


Жауабы:
![]()
16. Егер
![]() - кез келген бүтін сан
болса,
- кез келген бүтін сан
болса, ![]() өрнегі 19-ға бөлінетінін
дәлелдеңдер.
өрнегі 19-ға бөлінетінін
дәлелдеңдер.
22
Шешуі![]() деп алып,
деп алып,
![]() , яғни
, яғни
![]() саны 19-ға бөлінеді
және
саны 19-ға бөлінеді
және ![]() саны да 19-ға
бөлінеді.
саны да 19-ға
бөлінеді.
17.Қосындыны
табыңдар: 
Шешуі:
1-тәсіл:

2-тәсіл:

18.![]() мен
мен
![]() сандарын
салыстырыңдар.
сандарын
салыстырыңдар.
Шешуі: ![]() және
және
![]() жазып, осы бөлшектерге кері
бөлшектерді қарастырайық
жазып, осы бөлшектерге кері
бөлшектерді қарастырайық ![]() және
және
![]() . Осы бөлшектердің екеуінен
де
. Осы бөлшектердің екеуінен
де ![]() -ді азайтып
жазайық:
-ді азайтып
жазайық:  .
.
 Ал,
Ал,
![]() екені белгілі,
онда
екені белгілі,
онда ![]() немесе
немесе
![]() <
<
![]() .
.
23
19. Өрнектің мәнін табыңдар:
(1+ )(1+
)(1+ )
)(1+
)
)(1+ )
)(1+
)
)(1+ )
)(1+
)
)(1+ )
)(1-
)
)(1- ),
а = 2003
),
а = 2003

 =
= формуласы бойынша ең ақырғы
екі көбейткіш мына түрге келеді: (1 -
формуласы бойынша ең ақырғы
екі көбейткіш мына түрге келеді: (1 -
 )(
1+
)(
1+ ) = 1 – а 1 – а = 1 –
2003 = -2002, Жауабы: -2002.
) = 1 – а 1 – а = 1 –
2003 = -2002, Жауабы: -2002.
20.Есептеңдер: ![]()
Шешуі: 1-тәсіл:
![]() деп алып,
деп алып,
![]() .
.
2-тәсіл:
![]() деп алып,
деп алып,
![]()
21.
Көбейткіштерге
жіктеңдер: ![]()
Шешуі:

22. Дипломаттың иесі дипломаттың үш таңбалы саннан тұратын кодын ұмытып қалыпты. Оның есінде сол санның цифларының қосындысы 15 екені ғана есінде қалыпты. Дипломатты кепілді түрде ашу үшін оған ең аз легенде қанша вариант қарап шығу керек?
Шешуі:Цифрларының қосындысы 15-ке тең болатын үш таңбалы санның варианттарын қарастырайық:
-
Осы цифрлардан тұратын 6 сан бар: 096; 069; 960; 906; 609; 690.
-
087 6 вариант 195 6 вариант 186 6 вариант
294 - І - 285 - І - 276 - І -
384 - І - 375 - І - 366 3 вариант
177 3 вариант 393 3 вариант 474 3 вариант
465 6 вариант 555 1 вариант
24
23.
Дәлелдеңіз: ![]() .
Мұндағы
.
Мұндағы
![]() -кез келген нақты
сандар.
-кез келген нақты
сандар.
Шешуі:
![]() ,
,
![]() ,
,

![]()
Онда![]() ,
,
![]() .
.
24.
Қайсысы
үлкен: ![]() және
және
![]()
Шешуі:

![]()
![]() .
Демек,
.
Демек,
![]() немесе
немесе
![]()
![]()
25.Теңсіздікті
шешіңдер: 


 +(
+(
 бірақ
бірақ
 кез-келген х үшін,
ал
кез-келген х үшін,
ал кез-келген х үшін
8
кез-келген х үшін
8 болғандықтан, ал
дискриминант – теріс. Олай болса
болғандықтан, ал
дискриминант – теріс. Олай болса
 +(
+( , сондықтан шешімі
жоқ.
, сондықтан шешімі
жоқ.
10 сынып
1. 3р4+5q4+15=13p 2q2 теңдігі орындалатын p және q жай сандарын тап.
Шешуі : p және q тақ болса , онда сол жағы модулі 4 бойынша 3-ке тең, оң жағы модулі 4 бойынша 1-тең,бұл жағдай болмайды. Ендеше p= q=2 есеп шартына қанағаттандырылмайды p=2 болса q=3 болады, ал q=2 болса
p болмайды.
Жауабы: p= 2 ; q=3
25
2.Дұрыс
па?  =
2000;
=
2000;

 Сол жағын
түрлендіреміз:
Сол жағын
түрлендіреміз:
 =
= =
=

= =
= =
2000; 2000 =
2000 Жауабы:
дұрыс.
=
2000; 2000 =
2000 Жауабы:
дұрыс.
3. ABCD шаршысының A төбесі және CD қабырғасының ортасы l түзуіне қарағанда симметриялы. l түзуі ABCD шаршысының бөлген бөліктердің аудандарының қатнасын табыңыз.
Шешуі: AB=a, BN=x, DM=y деп белгілейміз.
![]()
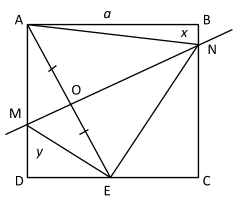 болғандықтан
MA=ME=a–y
болғандықтан
MA=ME=a–y
![]() тікбұрышты ұшбұрыш
сондықтан
тікбұрышты ұшбұрыш
сондықтан
![]()
![]()
![]()
![]()
![]() болғандықтан AN=EN
болғандықтан AN=EN
![]() тікбұрышты үшбұрыш сондықтан
тікбұрышты үшбұрыш сондықтан
![]()
![]() тікбұрышты үшбұрыш сондықтан
тікбұрышты үшбұрыш сондықтан
![]()
AN=EN болғандықтан
![]()
![]()
![]()
ABNM трапецияның ауданы ![]()
DMNC трапецияның ауданы ![]()
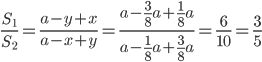 Жауабы:
Жауабы:  .
.
26
4. 2015 санын қандай санға көбейткенде, сол санның бөлгіштерінің саны дәл 12-ге ( бір мен сол санның өзін қоса есептегенде) тең болады?
Шешуі: 2015 санын көбейткіштерге жіктейміз. 2015=5·13·31
2015-тің бөлгіштері сегіз: 1, 5, 13, 31, 5·13, 5·31, 13·31, 5·13·31
Егер 2015 санын оның жай көбейткіштерінен басқа кез-келген бір жай санға көбейтсек, мысалы: 3-ке, 2015·3=3·5·13·31
2015·3 санының бөлгіштері:1, 3, 5,
13, 31, ![]()
![]() бөлгіштерінің саны 15-ке тең
болады.
бөлгіштерінің саны 15-ке тең
болады.
Демек өзінің жай көбейткіштерінен басқа келкелген санға көбейткенде оның бөлгіштерінің саны 12-ден артық болады.
Енді 2015 санының жай көбейткіштеріне көбейтсек бөлгіштерінің саны дәл 12-ге тең болады.
2015·5=5·5·13·31 2015·5 санының бөлгіштері: 1,5,13,31,5·5,5·13,5·31,13·31,5·5·13,5·5·31,5·13·31,5·5·13·31 саны 12-ге тең болды.
Демек, 2015 санының жай көбейткіштерінің біріне көбейтсек ол санның бөлгіштері дәл 12-ге тең болады.
Жауабы: 5, 13, 31
5. АВСД дөңес төртбұрышы
берілген. Сонда ![]() , ал Ғ нүктесі АД кесіндінің
ортасы. ВҒ түзуі АС түзуімен Р нүктесінде қиылысады және ВС=СР
екенін дәлелде.
, ал Ғ нүктесі АД кесіндінің
ортасы. ВҒ түзуі АС түзуімен Р нүктесінде қиылысады және ВС=СР
екенін дәлелде.
Шешуі: А,В,С және F нүктелерінің бір шеңберге тиіс екенін дәлелдеу керек.
ΔАВF=ΔАСF = ᴪ, бұдан Δ СBL=90°-ᴪ.
6. Теңдеулер жүйесін
шешіңіз: ![]()
Шешуі:
1-ші әдісі:
![]()
![]()
![]()
Соңғы жүйедегі теңдеулерді
өзара көбейтсек: ![]() болып
болып ![]() шығады. Осы теңдеуді соңғы
жүйенің бірінші теңдеуіне бөлсек
шығады. Осы теңдеуді соңғы
жүйенің бірінші теңдеуіне бөлсек
![]()
Тура осыған ұқсас жолмен
![]()
![]() шығады.
шығады.
Жауабы: ![]() және
және ![]()
27
2-ші әдісі:
![]()
![]()
![]()
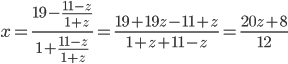

![]()
![]()
![]() теңдеуінің
шешімі
теңдеуінің
шешімі ![]() .
.
![]() теңдеуіне x-ті
қойып,
теңдеуіне x-ті
қойып, ![]()
![]() теңдеуіне z-ті
қойып,
теңдеуіне z-ті
қойып, ![]()
Жауабы: ![]() және
және ![]()
![]()
7. ![]() рационал санның кубы болатындай барлық
бүтін n санын табыңыз.
рационал санның кубы болатындай барлық
бүтін n санын табыңыз.
Рационал санның кубы болу үшін, алымы бүтін санның кубы, ал бөлімі натурал санның кубы болуы керек.
Шешуі: ![]() мұндағы m бүтін сан, k натурал сан.
мұндағы m бүтін сан, k натурал сан.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
болатындай төрт жағдайын қарастырамыз.
1. ![]() бұл жүйені шешуде
бұл жүйені шешуде ![]() теңдеуін аламыз.
теңдеуін аламыз. ![]() болып, теңдеу бүтін шешімге ие
емес.
болып, теңдеу бүтін шешімге ие
емес.
2.
![]() бұл жүйені
шешуде
бұл жүйені
шешуде ![]() теңдеуін
аламыз.
теңдеуін
аламыз. ![]() шешімі
жоқ.
шешімі
жоқ.
3.
![]() бұл жүйені
шешуде
бұл жүйені
шешуде ![]() теңдеуін
аламыз.
теңдеуін
аламыз. ![]()
![]() осыдан
осыдан ![]() шешімін
аламыз.
шешімін
аламыз.
Шарт
бойынша m бүтін
сан, k натурал сан.
Сондықтан![]()
Жауабы: n=3
28
8.
![]() функциясының
функциясының ![]() аралығындағы ең кіші мәнін
табыңдар.
аралығындағы ең кіші мәнін
табыңдар.
Шешуі:1-ші әдісі:
Өрнектітүрлендіреміз. Енді осы өрнекке Коши теңсіздігін қолданамыз, сонда мынадай болады.
![]()
Жауабы: 4
2-ші әдісі:
Берілген функцияның кері функциясының анықталу облысын табу арқылы шешеміз.
![]()
![]()
теңдеудің екі жағында х2-қа бөлеміз.
![]()
Жаңа айнымалы енгіземіз.
![]() ,
, ![]() осыдан
осыдан
![]() шығады.
шығады.
![]()
![]()
![]()
![]() теңсіздігінің шешімінің
теңсіздігінің шешімінің
![]() аралығындағы ең кіші мәнін
аламыз.
аралығындағы ең кіші мәнін
аламыз.
![]()
![]()
![]()
Теңсіздіктің шешімі
![]() аралығы болады.
аралығы болады.
Бұл аралықтың ең кіші мәні 4.
Жауабы: 4
9.Теңсіздікті шеш: (х-1)(х2-1)(х3-1)(х4-1)...(х2002-1)≤0
Шешуі: (-∞; −1] {1}
xn-1=0 теңдеудің екі түбірі бар егер n –жұп сан болса х=-1 х=1
және бір түбірі бар егер n-тақ болса х=1.
29
10. ![]() шахмат тақтасында барлық қара
шаршы таңдалып алынатындай және әрбір жол мен әрбір бағаннан дәл 7
шаршыдан таңдалып алынатындай 56 әр түрлі шаршыны қанша тәсілмен
таңдап алуға болады?
шахмат тақтасында барлық қара
шаршы таңдалып алынатындай және әрбір жол мен әрбір бағаннан дәл 7
шаршыдан таңдалып алынатындай 56 әр түрлі шаршыны қанша тәсілмен
таңдап алуға болады?
-
-
-
-
a
b
c
d
e
f
g
h
1
2
3
4
5
6
7
8
-
-
-
Шешуі: Таңдалмайтын ақ шаршыны іріктеп алайық. Әрбір жолмен әрбір бағанда 4 ақ шаршы бар екені белгілі. Әрбір жолдан және әрбір бағаннан 1 ден артық ақ шаршы алып тасталынбайды.
1-ші жолда ақ түсті шаршыны алып тастау мүмкіндігі 4-ке тең. 2-ші жолдан алып тасталынатын ақ шаршы, 1-ші жолдан алып тасталған ақ шаршы бағанында болмауы керек. 2-ші жолда мұндай мүмкіндік саны–4.
3-ші жолда әртүрлі мүмкіндік саны 3 тең болады. Себебі 1-ші жолда алынған бір бағанға кеміді.
4-ші жолда әртүрлі мүмкіндік саны 3 тең болады. Себебі 2-ші жолда алынған бір бағанға кеміді.
5-ші жолда әртүрлі мүмкіндік саны 2 тең болады. Себебі 1-ші және 3-ші жолдардағы 2 бағанға кеміді.
6-шы жолда әртүрлі мүмкіндік саны 2 тең болады. Себебі 2-ші және 4-ші жолдардағы 2 бағанға кеміді.
7-ші жолда әртүрлі мүмкіндік саны 1 тең болады. Себебі 1-ші, 3-ші және 5-ші жолдардағы 3 бағанға кеміді.
8-ші жолда әртүрлі мүмкіндік саны 1 тең болады. Себебі 2-ші, 4-ші және 6-шы жолдардағы 3 бағанға кеміді.
Сонымен жалпы мүмкіндіктер саны 4·4·3·3·2·2·1·1=576
Жауабы: 576
11.Жай сандар р2-2; 2р2-1 және 3р2+4 үшін барлық жай р санын тап.
Шешуі : р=3 р=7 2-ден 7-ге дейінгі жай сандарды тексеру керек.
Ары р>7 осылардың біреуі 7-ге бөлінетінін дәлелдеу керек.
30
12. ![]() интервалында х және у сандары тиіс. Дәлелдеу
керек:
интервалында х және у сандары тиіс. Дәлелдеу
керек:
xcosx+ycosy≤ycosx+xcosy
Шешуі : Оң және сол жақтың айырымын тексеріп, оны көбейткіштерге жіктеп және берілген аралықта косинустың кемитінін қарастыру керек.
13. Натурал п саны табылады ма, егер пп+(п+1)п 2003-ке бөлінсе.
Шешуі : п=1001 иә орындалады.
14. а, в, с және x, y, z -оң нақты сандар болып, a+x=b+y=c+z=1 болса, онда
(abc+xyz) ![]() теңсіздігін дәлелде.
теңсіздігін дәлелде.
Шешуі : Жақшаны ашып, сол жақтың  екенін көрсетіп ары қарай
екенін көрсетіп ары қарай ![]() ,мұндағы m;n>0 қолдану
жеткілікті.
,мұндағы m;n>0 қолдану
жеткілікті.
15.Функцияның графигін
сал ![]()
Шешуі :
![]() формуланы қолданып модульді
ашу керек :
формуланы қолданып модульді
ашу керек :

16. а-нақты сан болып, а2+а және а+2а рационал сан болса, онда а саны
да рационал болатынын дәләлде.
Шешуі : А=а2+а , В=а3+2а рационал сандар болса , онда В=а(А+3)-А.
Бұдан а 2+а+3=0 теңдеудің нақты түбірі жоқ , онда А≠ -3, ендеше
![]() болады.
болады.
17. О центрлі шеңбердің АС және ВД хордалары К нүктесінде қиылысады. М және Н ΔАВК және ΔСДК-ға сырттай сызылған шеңберлердіңцентрі болса, онда ОМ=КН екенін дәлелде.
Шешуі
: ОМ![]() АВ орта перпендикуляр
болғандықтан АВ-ға , НК-ның созындысы АВ мен Р нүктесінде
қиылысады.
АВ орта перпендикуляр
болғандықтан АВ-ға , НК-ның созындысы АВ мен Р нүктесінде
қиылысады.
Сонда
РАК+РКА=КДС+СКН=
 КНС+
КНС+ (СКН+КСН)=90°
(СКН+КСН)=90°
КН ||АВ болғандықтан КМ||ОН ендеше КНОМ – параллелограмм, ОМ=КН.
31
18. Егер
2tg2α+tgα-3=0
болып π/2<α<π аралығында болса
sin2α-ны тап.
Шешуі :
![]()
19. Есепте: tg200 tg400 tg800
Шешуі : sin20°sin40°sin80°=½(cos20°-cos60°)sin80°=½cos20°sin80°-¼sin80°=
=¼(sin100°+sin60°)-¼sin80°=![]()
Енді cos20°cos40°cos80°=![]() tg200tg400tg800=
tg200tg400tg800= ;
;
20. а
параметріне байланысты теңсіздікті шеш: ![]()
Шешуі : х=а теңсіздіктің а-ға байланысты шешімі :
ах2+(а2-2)х-2а=(х+а)(ах-2)
![]()
шешу үшін мына жағдайларды қарастырамыз:
a) а> 2 ; шешімі {а }
b) 0<а≤ 2 ;
шешімі 
c) а=0; шешімі [0;∞)
d) - 2 ≤а<0 ;шешімі {а }
i) а<-
2 ;шешімі
 )
)
21. ![]() және
және![]() сандары бүтін сан болу үшін натурал а және
в
сандары бүтін сан болу үшін натурал а және
в
жұптарын тап.
Шешуі : (2;2),(3;3),(1;2),(2;1),(2;3),(3;2).
а≥в. Егер а>в+1 болса , онда а(а-1)>в(в+1) және а 2-в>а+в 2
бұл орындалмайды.Ендеше а=в немесе а=в +1.
а=в (2;2)(3;3) болады.
Ал а=в +1 болса , бүтін
сан![]() болады в≥6
в 2
-в-1>4в+2,
1≤в≤5 , онда тексер.
болады в≥6
в 2
-в-1>4в+2,
1≤в≤5 , онда тексер.
22. 13!-11! Өрнегі 31-ге еселік екенін дәлелде.
Шешуі: 5) 13! =1*2*3*....*13=1*2*3*....*11(12*13) =11!*12*13.
Ендеше 13!-11! =11!(12*13-1) =11!*155=11!*31*5. 31-ге еселік болады.
32
23.
а, в, с>0 болса,
 теңсіздігін дәлелде.
теңсіздігін дәлелде.
Шешуі: Теңсіздіктің арифметикалық және гармониялық оң сан үшін қолданып шығатыны:
 ; Бұдан кейін теңсіздікті
шеш.
; Бұдан кейін теңсіздікті
шеш.
24.
Ықшамда: ![]() ;
;
Шешуі
: ![]()
![]() ;
;
25. Дұрыс жетібұрыштың неше диагоналі бар?
Шешуі : Әрбір төбеден 4 диагональ жүргізуге болады, бірақ 2 диагональ үйлеседі,ендеше 14 диагональ жүргізуге болады.
Жауабы: 14 диагональ.
![]()
1. Мына функциялардың графиктерін салыңдар:
а) y=sin(arcsinx)
б)
y=arccos
Шешуі: 


2. ax2002+вх1111+с=0 теңдеуінде а, в, с нақты сандар болса үш нақты түбірі бола ма?
Шешуі:
 Жоқ.
Жоқ.
у=ах2002+вх1111+с және оның бір экстремалды нүктесі болатынын дәлелде.Осыдан берілген теңдеудің екіден артық емес әр түрлі түбірі болады.
33
3. Теріс емес нақты сандар жиынында теңдеу жүйесін шеш:

Шешуі:  (0;0;0),
(1;1;1)
(0;0;0),
(1;1;1)
Нұсқау: үш теңдеуді мүшелеп қосу керек.
4. sinх ≤ sin2х ≤ sin4х теңсіздігі орындалатын х-тың барлық нақты сан мәнін тап.
Шешуі:
 Берілген қос теңсіздікті былай
жазуға болады:
Берілген қос теңсіздікті былай
жазуға болады:

Интервал әдісін қолданып және периодтылығын ескеріп, жауабын жаз.
х , n
, n
5. 0 және 1 цифрлары мен жазылған және 15-ке бөлінетін жеті орынды сандардың қосындысын тап.
Шешуі: 11 555 550
3-ке және 5-ке бөлінгіштік қасиетін қолдан.
6.Теңдік орындалатын ең кіші натурал n санын тап:
sin(n°+80°)+sin(n°-40°)+sin(n°+70°)=sin65°
Шешуі: 105
Берілген теңдікті тең
түрлендіру арқылы келтір. sin( n+450) =  ;
;
7.Теңдеуді шеш: (х2+х-1002,5)2+х2=2005
Шешуі: 1002,5=а деп белгілеп, теңдеуді
(х2-а)(х2+2х+2-а) =0 түріне келтір. Сонда
х1,2= ±  және
х3,4= -1 ±
және
х3,4= -1 ± 
у(х) = х2+х-а, у(у(х)) = х; у(х) = х; х2-а=0.
8. Пирамиданың төбесіндегі жазық бұрыш 180°-тан үлкен. Бір бүйір қабырғасы табанының жарты периметрінен кіші екенін дәлелде.
Шешуі: АS ең үлкен пирамиданың бүйір қыры. Бүйір жағының жазбасы АS қыры арқылы жасалған бүйір жағы, осы кесіндіге орта перпендикуляр жүргізу керек және ол S арқылы өтсе , олардың қиылысуы М нүктесі болады. Осыдан Р > 2, АМ > 2АS екенін дәлелдеу керек.
34
9.Теңсіздікті
шеш:  +
+

 ;
;
Шешуі:1;
f(х) =
 +
+ 
 анықталу аймағында монотонды
өспелі, сондықтан f (х
)
≥
f
(-1)
=
анықталу аймағында монотонды
өспелі, сондықтан f (х
)
≥
f
(-1)
=
 >1.4
>1.4
10.Теңсіздікті
дәлелде:  ,
х
,
х
Шешуі:
q(x) = x
- -
-  оң жарты осьте монотонды кемитіндігін көрсет qᴵ(x) ≥ 0, х ≥
0 qᴵ(x) =
оң жарты осьте монотонды кемитіндігін көрсет qᴵ(x) ≥ 0, х ≥
0 qᴵ(x) =  болса теңсіздік
дәлелденді.
болса теңсіздік
дәлелденді.
11. Фукцияның графигін салыңдар:
y =  +
+  ;
;
 +
+  ,
,
 +
+  ,
,
 +
+ 
 +
+
 ,
,
 ,
,

Жауабы:
Графигі  түзу
сызық.
түзу
сызық.
12.
Теңдеудің бүтін түбірін тап:
2 -1=2ху
-1=2ху
 Берілген теңдеудің
шешімі жоқ, себебі сол жағы тақ сан, ал оң жағы жұп
сан.
Берілген теңдеудің
шешімі жоқ, себебі сол жағы тақ сан, ал оң жағы жұп
сан.
13. Төрт таңбалы санның цифрларын кері жазғанда шыққан сан берілген саннан 4 есе кем болатын санды тап.
 1000а+100в+10с+d деп белгілеу керек
сонда
1000а+100в+10с+d деп белгілеу керек
сонда
4(1000а+100в+10с+d)=1000d+100c+10b+a
Сол жағы жұп болғандықтан , оң жағы да жұп болады , ендеше
а-жұп цифр. а=2 басқа цифрды қойсақ бес орынды болады.
4d 2-ге аяқталады d=8.
4(1000*2+100в+10с+8) =1000*8+100с+10в+2 , 4(10в+с)+3=10с+в
40в+4с+3=10с+в , 13в+1=2с, в=1 ,с=7 і зделінді сан 2178
Жауабы: 2178
35
14. Тепе-теңдікті дәлелдеңдер:
 =
=


 =
=

 =
=

 =
=




15. Теңдеуді
шеш:  +
+ =
= ;
;
 Сол жағы барлық нақты сан
жиынында өспелі функция, сондықтан барлық мәнді бір рет
қабылдайды.
Сол жағы барлық нақты сан
жиынында өспелі функция, сондықтан барлық мәнді бір рет
қабылдайды.
мәнін
функция х= -1 –ге тең
болғанда қабылдайды.  мәнін функция х=-1 –ге тең болғанда қабылдайды.
Жауабы: х=
-1.
мәнін функция х=-1 –ге тең болғанда қабылдайды.
Жауабы: х=
-1.
16. а-нің қандай
мәнінде 
теңдеу жүйесінің бір шешімі бар?
 а=7
а=7
Координата жазықтығында
у=4- және
және  графиктерін салу керек.
(0;а) және R=3 шеңбер теңдеуі болады.
графиктерін салу керек.
(0;а) және R=3 шеңбер теңдеуі болады.
17.
 теңсіздігін
дәлелде.
теңсіздігін
дәлелде.
 1+cos1° =
2
1+cos1° =
2 =
=
 =
=
 бағала . Бірлік дөңгелектің
секторын х (0 < х <
бағала . Бірлік дөңгелектің
секторын х (0 < х < ) катеттері а=1 , в =
tgx тік бұрышты үшбұрышпен жауып сектор ауданы мен үшбұрыш ауданын
салыстырып, tgx>х, 0<х<
) катеттері а=1 , в =
tgx тік бұрышты үшбұрышпен жауып сектор ауданы мен үшбұрыш ауданын
салыстырып, tgx>х, 0<х<  .
.
 >
> >
> және 1+cos1°
=
және 1+cos1°
= <
<  =
= ;
Теңсіздік
дәлелденді.
;
Теңсіздік
дәлелденді.
18. Теңдеуді
шеш: ((х-3)
((х-3) )
)

 ((х-3)
((х-3) )
) және
және 
Екінші теңдеу  -5х+6=0
-5х+6=0  ((х-3) sinх) = 1
((х-3) sinх) = 1
Х1=3; х2=2 х=3 Жауабы: х=3.
36
19. Теңдеу жүйесін
шеш: 
 Бірнеше жағдайды
қарастыр:
Бірнеше жағдайды
қарастыр:
1) х=0 және у=0 болса z өз бетінше қалады,
2) у=0 және х=0 болса z өз бетінше қалады,
3) z=0 онда х және у≠0
х=с, у=-с с кез келген сан с≠0
сондықтан бірінші теңдеуді 3у-ке, екіншіні (-у)-ке, үшіншіні х-ке көбейтіп қос.
 +3
+3
 у+3х
у+3х  +
+ -
-
 =0
=0
( 
х+у=уz бірінші теңдеуден
 +ху+у(х+у) =
+ху+у(х+у) =  (
(  z=3
z=3
үшіншіден хуz+у =0
х=- z =-3 x=-3
z=3
=0
х=- z =-3 x=-3
z=3
20. Екі құбыр бірге бассейнді 4 сағатта толтырады. Алдымен бірінші құбыр бассейннің жартысын толтырғаннан кейін оны жауып , екінші құбырды ашса, онда бассейн 9 сағатта толады. Жеке-жеке толтырса әр құбыр неше сағатта толтыра алады?
 Біріншісі – х, екіншісі
– у болсын. Мынандай жүйе құрамыз:
Біріншісі – х, екіншісі
– у болсын. Мынандай жүйе құрамыз:



 және
және

Жауабы: 6 сағат және 12 сағат.
21. Егер α, β, γ үшбұрыштың бұрыштары болса, онда мына теңдіктің дұрыс екенін дәлелдеңдер: cos2α + cos2β + cos2γ + 2 cosα cosβ cosγ = 1
 α +
β +
γ =
π, мына формулаларды қолдана
отырып, cos2x
=
α +
β +
γ =
π, мына формулаларды қолдана
отырып, cos2x
=  , cosx = -
cos(π - x), cosx + cosy = 2
cos
, cosx = -
cos(π - x), cosx + cosy = 2
cos cos
cos дәлелдейміз.
дәлелдейміз.
22. Кіші картопты тазалағанша үлкен картопты тазалаған неге оңайырақ?
 Бұнда ( картоп шар
сияқты деп алса) онда көлемі және массасы радиустың кубына
пропорционалды , беті радиустың квадратына пропорционал
болады.
Бұнда ( картоп шар
сияқты деп алса) онда көлемі және массасы радиустың кубына
пропорционалды , беті радиустың квадратына пропорционал
болады.
37
23. Теңдікті дәлелдеңдер:
arctg1+ arctg +
arctg
+
arctg =
=
 ;
;
 arctg
arctg +
arctg
+
arctg =
=
 -
- 
tg(arctg +
arctg
+
arctg =
tg
=
tg 
 =
1
=
1
 = 1
= 1
 1 = 1
дәлелденді.
1 = 1
дәлелденді.
24. Мынандай қатынастар
орындалатындай: АВ=СД=8см; АС=ВД=10см; АВ=ВС=13см; кеңістікте
фигура табуға бола ма? (төбелері А, В, С, Д болатын көпбұрыштан
тұрады.
 Ондай фигура бар. Оларды
екі ұшбұрыш АВС және ВСД-дан алуға болады, екеуі бір-біріне тең
беттеседі.
Ондай фигура бар. Оларды
екі ұшбұрыш АВС және ВСД-дан алуға болады, екеуі бір-біріне тең
беттеседі.

![]()
![]() Д
Д

![]()
![]()
![]()
![]()
![]() С
С
![]()
![]() А
А
В
25. xy = 2006 (x+y) теңдеуінің бүтін шешімі болатынын дәлелдеу керек.
 Берілген теңдеуді мына түрге
келтіреміз: (х – 2006)(у - 2006) =
20062 одан х = у = 4012.
Берілген теңдеуді мына түрге
келтіреміз: (х – 2006)(у - 2006) =
20062 одан х = у = 4012.
38
Қолданылған әдебиеттер:
-
Агаханов Н.Х, О.К.Полипский «Математика Районные олимпиады», Москва Просвещение, 2010.
-
Бугулов Е.А , Б.А.Толасов «Сборник задач для подготовки к математическим олимпиадам».
Северо-Осетинское книжное издательство, 1962.
-
Горбачев Н.В. «Сборник олимпиадных задач по математике» – М.: МЦНМО, 2004.
-
Муштари Д.Х. «Подготовка к математическим олимпиадам» Муштари Д.К. – Казань: Изд-во Казан. матем. об-ва, 2000.
-
Фарков А.В. «Математические олимпиады в школе 5-11 классы», Москва Айрис-пресс, 2009.
39
Құрастырған:
А.С.Жасекеева, А.М. Кенжегалиева, М.К.Нигметуллин,
Р.А.Каратаева – Орал қаласы №46жалпы орта білім беретін
мектебінің математика пәні мұғалімдері.
Пікір жазғандар:
З.Ж.Жұбанышева – М.Өтемісов атындағы БҚМУ физика және
математика кафедрасының аға оқытушысы.
Г.Х.Хусаинова - №41 жаратылыстану-математика бағытындағы
мектеп-лицейінің жоғарғы санатты математика пәні мұғалімі.
Бұл жинақта оқушылардың теориялық білімін нығайтып, қиындығы жоғары есептерді шығару дағдысын қалыптастыру мақсатында мектеп программасында қарастырылмайтын стандартты емес есеп түрлерін , логикалық тапсырмаларды , күрделі теңдеулер мен теңсіздіктерді шешудің жолдары нақты көрсетілген. Математика пәні мұғалімдеріне әдістемелік көмек ретінде ұсынылады.
Мазмұны:
-
Кіріспе
-
5 сынып ......................................................................... 1 бет
-
6 сынып ......................................................................... 5 бет
-
7 сынып ........................................................................ 9 бет
-
8 сынып ........................................................................ 13 бет
-
9 сынып ........................................................................ 18 бет
-
10 сынып ........................................................................ 25 бет
-
11 сынып ........................................................................ 33 бет
-
Қолданылған әдебиеттер .............................................. 39 бет
2. Бақа тереңдігі 25м құдыққа түсіп кетті. Ол құдықтан шығу үшін күніне 5м көтеріліп, 4м қайта түсіп отырды. Бақа неше күнде құдықтан шығады?
4. Сыныпта математиканы ұнататын қыздардың саны математиканы ұнатпайтын ұлдардың санымен бірдей. Сыныпта кімдер көп: математиканы ұнататын оқушылар ма, әлде ұлдар ма?
Екі сағат бір уақытта соғуды бірге бастап,біргеаяқтады.Бірінші сағат–әрбірекісекундсайын, екінші сағат–әрбірүшсекундсайынсоғады.Есептегендебарлығы13 соғу болды (бірігіп қалғансоғуларбірсоғудепесептелінеді). Бірінші соғу мен соңғы соғудың арасында қанша уақыт өтті?
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Олимпиадалық есептер жинағы
Олимпиадалық есептер жинағы
ОЛИМПИАДА ЕСЕПТЕРІ
5 сынып
1. 13-ке бөлгенде қалдықпен және бөліндісі 17-ге тең болатын ең үлкен
бүтін санды табыңдар.
Шешуі: а=13*17+12=33.
2. Бақа тереңдігі 25м құдыққа түсіп кетті. Ол құдықтан шығу үшін күніне 5м көтеріліп, 4м қайта түсіп отырды. Бақа неше күнде құдықтан шығады?
Шешуі: 21 күнде. Бақа 20 күнде 20м шығады, 5м көтерілетіндіктен 21 күні 20+5=25м болады, олай болса құдықтың басына шыққандықтан қайта түспейді.
3. Алынған сан 36-ға бөлінетіндей 52*2* жазбадағы жұлдызшаларды цифрлармен алмастырыңдар.
Шешуі: Сан 36-ға бөлінеді, егер ол 4-ке де 9-ға да бөлінетін болса. 5,2,2 цифрларының қосындысы 9-ға тең болғандықтан, жетіспей тұрған екі цифрлардың қосындысы 0,9 немесе 18 болуы керек. Алынатын сан 4-ке бөлінетінін, ал соңғының алдындағы цифр 2-ге тең екенін ескерсек, онда соңғы цифр тек 0 мен 4 немесе 8 болуы мүмкін. Онда жауабы мына сандар болады: 52524, 52128, 52020, 52920.
4. Сыныпта математиканы ұнататын қыздардың саны математиканы ұнатпайтын ұлдардың санымен бірдей. Сыныпта кімдер көп: математиканы ұнататын оқушылар ма, әлде ұлдар ма?
Шешуі: Барлық оқушыларды екі топқа бөлеміз: біріншісінде – ұлдар, екіншісінде – қыздар. Осыдан кейін математиканы ұнатпайтын ұлдарды – екінші, ал математиканы ұнататын қыздарды бірінші топқа ауыстырамыз. Топтардың саны бұдан өзгермейді. Бірақ бірінші топта математиканы ұнататын оқушылардың барлығы болады, сондықтан математиканы ұнататын оқушылар саны ұлдардың санымен бірдей.
5. Кітапханада ағылшын, француз және неміс тілінде кітаптар бар.Ағылшын тіліндегі кітаптар барлық шет тіліндегі кітаптардың 40%-ын, француз тіліндегілер ағылшын тіліндегінің 75%-ын құрайды, ал қалған 210 кітап неміс тіліндегілер. Кітапханада шет тілінде неше кітап бар?
Шешуі: Барлық кітап саны - х болсын, есеп шартынан
0,4х + 0,75*0,4х + 210 = х бұдан х = 700 Жауабы :700
1
6. 9 тиынның біреуі жалған және ол басқаларынан жеңіл. Табақты
таразы арқылы гирсіз екі өлшегеннен жалған тиынды қалай анықтауға
болады?
Шешуі: 9 тиынды 3 тиыннан 3 бөлікке бөлеміз. Кез-келген 2 бөлікті өлшейміз,егер таразының екі жағы тең болса, онда жалған тиын үшінші бөлікте болғаны. Оны 1 тиыннан тағы да 3 бөлікке бөлеміз де екеуін таразыға салып өлшейміз, қайсысы жеңіл сол жалған.Ал бұл екеуі тең болса, онда қалған тиын жалған болғаны.
7. 5 л және 7 л-ік ыдыс арқылы 6 л суды қалай құяды?
Шешуі: a) 7 л толтырып 5л құяды, сонан соң оны төгіп , қалған 2 л қайта 5л құяды.
b) 7 л толтырып 5л-ге құяды. 7л-де →4л қалады 5л төгіп 4л →5л құяды
c)7л толтырып 1л→5л құяды. Сонда 7л→6л қалады
8 .Осы фигураны төрт тең фигураларға бөл:

Шешуі:

9. Екі сағат бір уақытта соғуды бірге бастап, бірге аяқтады. Бірінші сағат – әрбір екі секунд сайын, екінші сағат – әрбір үш секунд сайын соғады. Есептегенде барлығы 13 соғу болды (бірігіп қалған соғулар бір соғу деп есептелінеді). Бірінші соғу мен соңғы соғудың арасында қанша уақыт өтті?
Шешуі: 18с.
10. Қарбыздың салмағы 20 кг болды, ал ондағы құрғақ зат 1% - ын құрайды. Біраздан кейін қарбыз құрғап қалды да, құрғақ зат 2% болды. Қарбыздың соңғы салмағы қандай?
Шешуі: Құрғақ заттың 0,2 кг-мы , қарбыздың салмағы 10 кг болатын болды.
2
11. Үш жұмысшы ботқа пісірді. Бірінші 2 кесе жарма, екінші 1 кесе
жарма, ал үшіншісінде ешқандай жарма болмады. Ботқаны барлығы тең бөліп жеді. Үшінші жұмысшы: «Ботқаларыңа рахмет, мен сендерге 50 теңге беремін, сонда менің жеген ботқамды сендер салған жармамен қалай бөліп аласыңдар?» - деді.
Шешуі: Ботқаны 3 кеседен пісіріп, тең бӛліп жегендіктен, әр қайсысы 1 кесе жейді. Сондықтан үшіншінің ақшасын біріншіге беру керек.
12. Кез келген үш натурал санның арасынан әрқашанда қосындысы 2-ге бөлінетін 2 сан табуға болатынын дәлелдеңдер.
Шешуі: Үш санның ең болмағанда екеуі бірдей жұп, ендеше олардың қосындысы 2-ге бөлінеді.
13. Ең үлкен бір орынды санға, ең үлкен екі орынды санды неше рет қосқанда, ең үлкен үш орынды сан шығады?
Шешуі: 1) 9+n*99=999 n=10 Жауабы : 10 рет.
14. 7*9+12:3-2-ге жақшаны қойғанда а) 23 ә) 75 шығу керек.
Шешуі: а) (9*7+12):3-2=23 ә) (7*9+12):(3-2)=75
15. Серік мектепке автобуспен барып, қайтқанда жаяу келеді, сонда
барлық жолға 1 сағ 30 минут уақыт жыбереді. Егер автобуспен жүрсе 30 минут уақыт жібереді. Егер Серік мектепке жаяу барып қайтса, оған қанша уақыт жібереді?
Шешуі: 30мин:2=15мин. Серік мектепке автобуспен барады 1сағ 30мин-15мин=1сағ15мин Серік жаяу жүреді 1сағ15мин+1сағ15мин=2сағ30мин
Жауабы: 2сағ30мин.
16.Қалған саны ең үлкен болатындай етіп берілген 123456789101112131415... ............5657585960 санының 100 цифрын сызып таста.
Шешуі: 99999785960
17. Кеме дүйсенбі күні түсте жүзуге кетті. Жүзу 100 сағатқа созылса, онда
кеме қай күні қандай сағатта оралады?
Шешуі: сөткеде 24 сағат бар 100сағ=4*24сағ+4сағ=4сөтке+4сағ Ендеше кеме жұмада 16 сағ. келеді.
3
18. Ұзындығы 16 см, ені 9см тік төртбұрышты қалай тең екі бөлікке бөлуге және одан квадрат құруға болады?
Шешуі:

19. Есепте: 101101*999-101*999999
Шешуі: 6) 101101*999-101*999 999= 101*1001*999-101*999*1001=0
20. 3п+1 сандарының ішінен 5-ке еселік болатын үш санды табыңдар.
Шешуі: 10,25,40.
21. 9 бет қағаз болған, оның кейбіреуін 3 бөлікке бөлгенде 15 бет қағаз болды. Қанша бет қағазды бөлген?
Шешуі: әр бетті 3 бөлікке кескенде беттер 2-ге артады, 15-9=6 (бет)
6:2=3 (бетті кескен)
22. Өрнектің мәнін тап:
26*25-25*24+24*23-23*22+22*21-21*20+20*19-19*18+18*17-17*16+16*15-15*14.
Шешуі: 26*25-25*24+24*23-23*22+22*21-21*20+20*19-19*18+18*17-17*16+16*1515*14= =25(26-24)+23(24-22)+21(22-20)+19(20-18)+17(18-16)+15(16-14)= =2*(25+23+21+19+17+15)=2*120=240.
23. Жанұяда 4 бала бар, олар 5,8,13 және 15 жаста. Олардың аттары
Айнур, Болат , Әсем Әсель. Олардың біреуі бала бақшасына барады , Айнур Болаттан үлкен және Айнур мен Әсемнің жастарының қосындысы 3-ке бөлінеді. Әр қайсысы неше жаста?
Шешуі: В-5жас ,Б-8жас, А-13 жас, Г- 15 жас.
4
24. Азайғыш, азайтқыш және айырманың қосындысы 26 болса, азай-ғышты тап.
Шешуі: Азайтқыш пен айырманың қосындысы азайғыш болады ,онда екі азайғыш 26 болса, азайғыш 13 болады.
25. Балықшылар салмағы 100гр, 200гр, ...., 1900гр 19 балық ұстады. 10 балықшы балықты тең бөліп ала ма? Егер бөлсе қалай? Бөле алмаса неге?
Шешуі: (1900+100)*9+1000=19000(гр) барлық балық салмағы.
Әр балықшыға 1900гр .
1900гр;100гр;1800гр;......900гр+1000гр
6 сынып
1. Барлық үш орынды авс санын тап, егер мына теңдік орындалса:
авс =2(ав+вс+ас).
Шешуі: 138;144;150;288;294.
2. Оқушы кітапты үш күнде оқыды.Бірінші күні кітаптің 0,2 -сін және 16
бетті, екінші күні қалғанының 0,3-ін және 20 бетін, үшінші күні қалғанының 0,75-ін және 30 бетін оқыды. Кітапта неше бет бар?
Шешуі: х –кітап бетінің саны 1-ші күні 0,2х+16 бет оқылды 2-ші және3-ші күндеріне қалғаныны 0,8х-16 2-ш күні 0,3(0,8х-16)+20 бет оқылды 3-ші күні 0,56х-31,2 бет оқылды Сонда 3-ші күні 0,75 қалғанының және 30 бет оқылса онда қалдық 120 бет 0,56х-31,2=120, х=270 бет
3. Көйлек 500 теңге тұрады. Осы бағаны 10% арттырып, 10% кемітті. Енді көйлектің бағасы неше теңге болды?
Шешуі: 550-55 = 495 (теңге)
4. 15 санының алдына және соңына бір цифр қойғанда, шыққан сан 15-ке
бөлінуі керек.
Шешуі: 1155;3150;4155;6150;7155;9150.
5. Мектепте 33 сынып, 1150 оқушы бар. 35 оқушыдан кем оқушысы бар
сынып табыла ма?
Шешуі: Барлық сыныпта 35 оқушы болса, онда 35*33=1155 оқушы болады, бұл есеп шартына қайшы, ендеше 35 –тен кем оқушы бар сынып бар.
5
6. Дөңгелекке 2009 натурал сан жазылған. Қосындысы жұп сан болатын
екі көрші сан табылатынын дәлелдеңдер.
Шешуі: Көршілес натурал сандардың қосындысы әрқашанда тақ болады және натурал сандар саны жұп болса, ал дөңгелекке 2009 сан орналастырылған, ол – тақ сан сондықтан, 1 мен 2009 көршілес, ал олардың қосындысы 2010 – жұп сан.
7. Гаражда 54 жүргізуші бар.Егер әр күні гараждағы 60 машинаның 25%-ы өз ақауларын жөндеу үшін жұмысқа шықпай қалса, онда бір айда (30 күн) әр жүргізушінің неше бос күні болады?
Шешуі: Әр күні 0,25*60 = 15 машина гаражда қалады. 60 – 15 = 45 машина жұмысқа шығады, 54 – 45 = 9 жұмыстан бос қалады. Бір айда 30*9=270 адам-күн бос. Әр жүргізушінің 270 : 54 = 5 бос күні болады. Жауабы: 5
8. Сүтімен шелектің массасы 32 кг, сүтсіз -2кг. Шелектің жартысы
сүтпен толтырылса оның массасы қандай?
Шешуі: 17 кг.
9. Үш қыз ақ, көк, жасыл көйлек және сондай туфли киды. Егер
Айгүлдің көйлегі мен туфлиі бірдей болса, ал Гулнардың не көйлегі не туфлиі ақ емес, Нүргүлдікі жасыл туфли болды. Әр қыздың көйлегі мен туфлилерінің түрін анықта.
Шешуі: Айгүл-ақ көйлек , ақ туфли Гүлнар- жасыл көйлек, көк туфли Нұргүл-көк көйлек, жасыл туфли.
10. Екі өзара жай сандардың көбейтіндісі 3232. Ең кіші ортақ еселігін және осы сандарды тап.
Шешуі: 3232=32*101=2*2*2*2*2*101 еселігі 3232.
11. х-тің 13,5%, у-тің 12,5%-не тең болса, х және у сандарын салыстыр.
Шешуі: 13,5х=12,5у, х<у, егер х және у оң сан болса; х=у, егер х= у=0 болса; х>у, егер х және у-теріс сан болса.
12. Өлшемі 2х2х2 кубты бояу үшін 2 грамм бояу керек. Өлшемі 6х6х6 кубты бояу үшін қанша бояу керек?
Шешуі: Кубиктің үлкен жағы кіші кубиктің жағынан 9 есе үлкен болса , онда бояу да 9 есе көп кетеді , ендеше 18 гр.
6
13. 2008 натурал санның қосындысы – тақ сан. Осы сандардың
көбейтінділері тақ па, әлдә жұп сан бола ма?
Шешуі: 2008 натурал санның барлығы жұп, тақ , жұп және тақ болады. Бірінші және екіншіcі болмайды, себебі олардың қосындысы тақ, ендеше 2008 натурал сандарының ішінде тақ та, жұп та сандар бар , сондықтан олардың көбейтінділері жұп болады.
14. 1-ден 12-ге дейінгі сандарды пайдаланып екі тіктөртбұрыш пен бір шаршының төбелеріндегі сандардың қосындысы бірдей болатындай етіп жазыңдар.

![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 1-ден 12-ге дейінгі
сандардың қосындысы 78-ге тең. Онда тіктөртбұрыш пен шаршының
төбелеріндегі сандардың қосындысы 26-ға тең болады. Мүмкін
жағдайлар: 12,9,1,4 - шаршының төбелері 11,8,2,5 және 10,7,3,6 -
тіктөртбұрыш төбелері.
1-ден 12-ге дейінгі
сандардың қосындысы 78-ге тең. Онда тіктөртбұрыш пен шаршының
төбелеріндегі сандардың қосындысы 26-ға тең болады. Мүмкін
жағдайлар: 12,9,1,4 - шаршының төбелері 11,8,2,5 және 10,7,3,6 -
тіктөртбұрыш төбелері.
15. Сыныпта 25 оқушы бар, олардың жастарының қосындысы 270 жыл.
Сыныпта 20 оқушы табыла ма, олардың жастарының қосындысы 260 тан
артық болатын?
Шешуі: 20 оқушы табылсын , қалған 5 оқушының жастарының қосындысы 10 үлкен болмайды , сонда орташа жастары 2 ден артық болмайды . Бүл қайшы , ендеше ондай оқушылар жоқ.
16. Көлде 1 лилия гүлдеді. Әр күні гүлдер саны көбейді де 10 -шы күні барлық өзенді гүлдер көмкерді.Көлдің жартысын гүлдер нешінші күні көмкереді?
Шешуі: Тоғызыншы.
7
17. Ерік дүкеннен 1 қаламды 1 теңге 80 тиынға және 6 қарандаш алуға барды. Дүкенші Еріктен 5 теңге бересің, сонда Ерік мен қателестім деді. Еріктікі дұрыс па және неге?
Шешуі: 5 теңге-1 теңге 80т=3 теңге 20 тиын=320 тиын 320 бөлінбейді 6-ға.
18. 11*21*31*41*51*61*71*81*91-1 10-ға бөліне ме? Неге?
Шешуі: Көбейтіндінің соңғы цифры 1-ге аяқталады, онда айырма 0-мен аяқталады , ендеше 10-ға бөлінеді.
19. Есептеңдер: -90-89-88-....-1+0+1+2+....98+99+100
Шешуі: -90-89-88-...-1+0+1+2+3+...+98+99+100=(91+100)*5=955.
20. Алматыдан Талдықорғанға дейін 40 км/сағ жылдамдықпен машина
шықты және 1 сағат жүрді. Кері қайтқанда ол 60 км/сағ жылдамдықпен жүрді. Машинаның орташа жылдамдығын тап.
Шешуі: 48 км/сағ.
21. 4х4 метр өлшемі бар кілемді 15 тесік жасап құрт жеді. Өлшемі 1х1 метр кілемді кесіп алуға бола ма? Және оның ішінде тесік болмау керек.
Шешуі: 16 кілемшелерге 1х1 бөлеміз 16>15 сонда бір кілемше тесіксіз қалады.
22. Жеті алманы 12 адамға, бір алманы 4 тен артық бөлікке бөлмей тең беруге бола ма?
Шешуі: 7:12
= =
=
 +
+  онда 3 алманы 4 бөлікке
, ал 4 алманы 3 бөлікке бөлуге болады.
онда 3 алманы 4 бөлікке
, ал 4 алманы 3 бөлікке бөлуге болады.
23. Бөлінгіш пен бөлгішті 3 есе арттырғанда, бөлінді мен қалдық өзгере
ме?
Шешуі: a=bq+r 3-ке көбейтеміз 3a=3bq+3r ендеше қалдық 3 есе өседі, ал бөлінді өзгермейді 5=3*1+2 5*3=15 3*3=9 15=9*1+6 қалдық өзгерді.
24.





 сандарын кему ретімен
орналастырыңдар.
сандарын кему ретімен
орналастырыңдар.
Шешуі: 1- =
= ;
1-
;
1- =
= 1-
1- =
= 1-
1- =
=




 болса,
онда
болса,
онда 




Жауабы:


8
25. Бір тәулікте сағаттың және минуттың тілдері неше рет тік бұрыш
жасайды?
Шешуі: Шарт бойынша 3 сағ,9сағ ,15сағ ,21сағ. 1 сөткеде бұл 11*4=44 болады.
7 сынып
1. Поезд бағдаршамның жанынан 5 сек, ал ұзындығы 150 м көпірден 15 сек өтеді. Поездың ұзындығы мен оның жылдамдығын тап.
Шешуі:  =
5;
=
5;  = 15, S=75м,
v=15м/с
= 15, S=75м,
v=15м/с
2. 101 жылқыны 15 қораға орналастырған. Сонда неге ең болмағанда бір
қорада тақ санды жылқылар саны болады?
Шешуі: Кері дәлелдейміз.Әр қорада жұп сан жылқылар бар, онда қосынды жұп. Шарт бойынша 101 жылқы бар – тақ, ендеше ең болмағанда 1 қорада тақ сан жылқылар бар.
3. Натурал санды өзінің әрбір цифрларына көбейткенде 1995 шықты. Ол
қандай сан?
Шешуі: 1995 –ті көбейткіштерге жіктеу керек 1995=3*5*7*19 ізделінді сан бір орынды, үш орынды бола алмайды , ендеше ол екі орынды.1995=57*7*5
4. Үстелде 60 кәмпит бар. Екі оқушы кезек-кезек бір алғанда 4 тен артық
емес кәмпит алады. Кім соңында алса сол жеңеді. Дұрыс ойында кім жеңеді?
Шешуі: Екінші жеңеді. Ол әрқашан біріншінің алған конфеттерінің қосындысын 5-ке тең деп алу керек.
5. Жазықтықта төрт тең үшбұрыштар берілген және екеуінің ортақ екі
төбелері бар. Барлығының ортақ төбесі бар деген дұрыс па?
Шешуі: АВСД төртбұрышынан ΔАВС ΔДВС ΔАДС ΔАВД алу керек, бұл үшбұрыштарда ортақ төбе болмайды , ендеше дұрыс емес.
6. Жәшіктен барлық жұмыртқаның жартысын, сонан соң қалғанының
жартысын, тағы жаңа қалғанының жартысын соңында тағы қалғанының
жартысын алды, сонда жәшікте 10 жұмыртқа қалды. Барлығы қанша
жүмыртқа еді?
Шешуі: 160 жұмыртқа
9
7. 4 қара және 3 сары сиырлар 5 күнде қанша сүт берсе , 3 қара және 3 сары сиырлар 4 күнде сондай сүт береді. Қара сиырдың ба, әлде сары
сиырдың сүті көп болады?
Шешуі: 20 қара, 15 сары, сиырлардың бір күнде беретін сүтін 12 қара және 20 сары сиырлар береді, ендеше 8 қара сиырдың бергенін 5 сары сиыр береді. Сары сиыр сүтті көп береді.
8. Егер ұзындығын 20%-ке, енін10%-ке өсірсе тік төртбұрыштың ауданы
қанша пайызға өседі?
Шешуі: 32%-ға
9. Теңдеуді шешіңдер: 2(3-2х)=3х-4(1+3х);
Шешуі: х= -2
10. (а+в)х+(а-в)х-2ах=0 тең екенін дәлелдеңдер.
Шешуі: Жақшаны ашып ұқсас қосылғыштарды біріктіру керек.
11. Жәшікте 24кг шеге бар. Табақшалы таразы мен гирсыз 9 кг шегені
қалай алуға болады?
Шешуі: 24 кг-ды екі бөлікке бөледі , таразымен 12 кг шегені өлшеу керек. Біреуін өзін қалдырып екінші үймекті тағы тең бөлу керек . Тағы 6кг екі үймек шықты , сонда 12;6;3;3кг 3*3=9 кг
12. Тақтаға 321321321321 саны жазылған. Қай цифрды өшіргенде ең
үлкен және 9-ға бөлінетін сан шығады?
Шешуі: 9-дың бөлінгіштік қасиеті бойынша сызылған цифр 6. Екі үштікті сызу керек, тағы тізбектес екі үштікті сыз.
13.Егер а=в+1 болса,
онда (а+в)( +
+ )(
)( +
+ )...(
)...( +
+ )=
)= теңдігі орындалатынын
дәлелде.
теңдігі орындалатынын
дәлелде.
 а-в=1,
а-в=1,  =(
=( +
+ )(
)( +
+ )(
)( +
+ )(
)(
 +
+ )( а+в
)( а-в ).
)( а+в
)( а-в ).
14. АВС тең қабырғалы үшбұрыштың АВ,ВС және АС қабырғаларына сәйкесінше Д,Е,F нүктелері алынған және АД = ВЕ = СF болса, онда пайда болған ДЕF тең қабырғалы үшбұрыш екенін дәлелдеңдер.
 Мына
Мына  ВЕ
=
ВЕ
=  FАД тең болғандықтан
(екі қабырғасы мен арасындағы бұрышы бойынша) ДЕ = ЕF = FД
қабырғалары тең болады. Сондықтан ,
FАД тең болғандықтан
(екі қабырғасы мен арасындағы бұрышы бойынша) ДЕ = ЕF = FД
қабырғалары тең болады. Сондықтан ,  ДЕF тең қабырғалы
үшбұрыш болып табылады.
ДЕF тең қабырғалы
үшбұрыш болып табылады.
10
15.Сыныпта 27 оқушы бар. Әр бала 4 қызбен, әр қыз 5 баламен достасады. Сыныпта қанша бала, қанша қыз бар?
 Сыныпта х – бала, у –
қыз болсын. Жалпы достықты санасақ, 4х және 5у бұдан
4х = 5у, ал
х+у=27. Есептеуді орындағанда
х=15, у=12.
Сыныпта х – бала, у –
қыз болсын. Жалпы достықты санасақ, 4х және 5у бұдан
4х = 5у, ал
х+у=27. Есептеуді орындағанда
х=15, у=12.
16. АС және ВД кесінділері қиылысады және АВ=ВС=СД=АД. АС және ВД перпендикуляр екенін дәлелде және АВСД фигурасының ауданын тап, егер АС= 10см, ВД=15 см болса.
Шешуі: ΔАВС=ΔСДА және тең бүйірлі.ДАС = ВСА = АСД СА
ΔВСД-ның биссектрисасы және CA
биіктік, АС![]() ВД . А және С нүктелері арқылы
ВД параллель , В және Д нүктелері арқылы АС-ға параллель жүргізу
керек. Тіктөртбұрыш ауданы АВСД-дан 2 есе артық
шықты.
ВД . А және С нүктелері арқылы
ВД параллель , В және Д нүктелері арқылы АС-ға параллель жүргізу
керек. Тіктөртбұрыш ауданы АВСД-дан 2 есе артық
шықты.
Жауабы:
SАВСД = ВД*АС=75см2
ВД*АС=75см2
17. Арман шаршы пішіндегі үйінің көлемін сол бұрынғы шаршы пішінін сақтай отырып екі есе кеңейткісі келді. Үйінің төрт бұрышында 4 ағаш өсіп тұр. Арман ағаштарды қалдыруды ойлады. Жаңа қабат та, басқа жерден жаңа үй де салғысы келмеді. Ол үйін қалай үлкейткен?
![]()
![]()

![]()
![]()


![]()
![]()
![]()
![]()
18. Есептеңдер:
1+2-3-4+5+6-7-8+9+10-.....+2002-2003-2004+2005+2006-2007-+2008+2009-2010
Шешуі: 2-ден бастап барлық сандарды төрт-төрттен топтау керек. Барлық төрттіктер 501. Әрбір төрттіктердің қосындысы 0.Ендеше өрнектердің қосындысы 1.
11
19. Кітаптың бірінші бетінен соңғы бетіне дейін нөмірленген. Бұзық Самат кітаптың әр жерінен 25 жыртып алып, 50 беттің барлық нөмірлерін қосады. Сонда ол сандардың қосындысы 2002-ге тең болады.Бұл туралы Қанат естігенде, ол Саматтың есептеуде қателескенін айтады.Қанат неге бұлай айтты ойланыңдар.
Шешуі: Әрбір жыртылған парақта екі бет бар болады.Бір беттің номері тақ сан болса, екінші беттің номері жұп сан болады.Ендеше 25 тақ нөмерлі 25 жұп нөмер беттерінің қосындысынан тұрады. Ал бұлардың қосындысы тақ сан болады, ал онда ол 2002-ге тең болмайды, өйткені бұл жұп сан.
20.
Есептеңдер:  ;
;

 =
=
 =
= 
 ;
;
21. Екі дос
мынандай  сандардың екінші
дәрежелерінің айырымын есептеп отырып осы санның негіздерінің
қосындысына тең екенін байқап қалады.Өздерінің жаңалықтарын басқа
10 және 11 санына пайдаланып қорытындысына көздері
жетеді:
сандардың екінші
дәрежелерінің айырымын есептеп отырып осы санның негіздерінің
қосындысына тең екенін байқап қалады.Өздерінің жаңалықтарын басқа
10 және 11 санына пайдаланып қорытындысына көздері
жетеді:  ал, сен қалай
дәлелдейсің?
ал, сен қалай
дәлелдейсің?

 формуласымен
дәлелденеді.
формуласымен
дәлелденеді.
22. Теңдік ақиқат болатындай модуль таңбасын қойыңдар:
1 – 2 – 4 – 8 – 16 = 19

 = 19.
= 19.
23. 1000 м қашықтыққа жүгіруде алға Марат озып шықты, екінші боп Ерлан келе жатты, ал үшіншісі – Самат. Жүгіру барысында Марат пен Ерлан – 6 рет, Ерлан мен Самат – 5 рет, Марат пен Самат – 4 рет орындарымен ауысты. Спортсмендер қандай ретпен жүгірісті аяқтады? Неге?
Шешуі: Марат пен Ерлан орындарымен жұп сан рет ауысты, сондықтан Марат Ерланның алдында қала берді. Марат пен Самат та жұп сан рет ауысып, орындары өзгерген жоқ, Марат Саматтың алдында. Ерлан мен Самат тақ сан рет ауысқандықтан, Самат Ерланның алдында келеді. Сонда мәредегі спортсмендердің реттері мынандай: Марат, Самат, Ерлан.
24. Сандарды
салыстыр:  және
және  *
*


12
25. АВС үшбұрышының А
бұрышы  , ал В
бұрышы
, ал В
бұрышы , АВ - ВС=4 болса С
бұрышының биссектрисасының ұзындығын тап.
, АВ - ВС=4 болса С
бұрышының биссектрисасының ұзындығын тап.

С


![]()
![]()
![]()
А Д Е В
АВ қабырғасына ВД=ВС кесіндісін салып , оны Д және С нүктелерімен қосады
ΔВСД ; ВД=ВС ДСВ = СДВ=80°
ΔАВС ; СЕ биссектрисасы болсын С=120° АСЕ=60° АЕС=80°
ΔДЕС ; Е = Д=80° ендеше АСД=40°
ΔАСД ; СЕ=СД=АД=АВ-ВС=4, сонымен СЕ = 4.
8 сынып
1. Натурал n санның екі а және в бөлгіші бар, сонда (а-1)(в+2)= n -2 болса,
2 n – натурал санның квадраты екенін дәлелде.
Шешуі: ав=2а-в=n а және в n-нің әр түрлі бӛлгіші.в:а, 2а:в, в=2а және 2n=4а2=(2а)2;
2. Дүкенде консервленген жемісі бар шыны 0,5л; 0,7л; 1 л ыдыс бар.
Сонда дүкенде 2600 шыны ыдыс массасы 2002 л бар. Дүкенде ең болмағанда бір 1,5л ыдыс бар екенін дәлелде.
Шешуі: Дүкенде көлемі 0,7 л а шыны және көлемі 1л ыдыс бар.
3. Жәшікте 16 алма бар. Бір рет өлшеу арқылы үш алманың масса-ларының қосындысын табуға болады. Қалай 8 рет өлшегенде барлығы-ның массасын табуға болады?
Шешуі: mi i= 1,….,16 осы шамалардың массасы. 4-рет өлшеп (m1+m2+m3)+(m1+m2+m4)+(m1+m3+m4)+(m2+m3+m4)=3(m1+m2+m3+m4)Қалған 12 алманың массаларының қосындысы (m5+m6+m7)+ (m8+m9+m10)+ (m11+m12+m13)+ (m14+m15+m16).
13
4. Төрт әр түрлі натурал сан таңдап алуға бола ма ,әрбір екеуінің
қосындысы 3-тің дәрежесі болатын?
Шешуі: Дирихле принципі бойынша сандардың ішінде екі сан бар , қосындысы жүп , сондықтан 3-тің дәрежесі болмайды.
5. Барлық теріс емес m және n сандарының парын тап, ол mn-n+m=2004
теңдігіне қанағаттандыратындай.
Шешуі: Жауабы: m=2 ,n=2002, m=2004 ,n=0 нұсқау ; бастапқы теңдеуді мына түрде жаз (m-1)(n+1) =2003, Жауабы:2003 жай сан.
6. АВС ұшбұрышының АҒ медианасы. АВ қабырғасының созындысы В
нүктесінен кейін Д нүктесін белгілеп, ал Е нүктесі ДҒ пен АС-нің қиылысу
нүктесі болса, онда АВ=ВД=АҒ болса СЕ=ЕҒ болатынын дәлелде.
А
![]()


 Е
Е
![]() С
В
С
В
F
Д
Шешуі:
ДFВ=ϒ=ЕFС (вертикаль) АВ=АF АВF=АFВ=α ДВF=180°-α
ДВС=ВАС+ВСА=ВAF+(FАС+FСА)=180°-2α+α=180°-α.
ΔАFС=ΔДFВ ВFД=FСЕ=ϒ бұдан СЕ=ЕҒ.
7. Жылдамдығы 60км/сағ поездағы адам терезеден жанынан өткен поезді
4 сек көрді. Егер өткен поездің ұзындығы 120 м болса, жылдамдығын тап.
Шешуі: 48 км/сағ.
8. 1 ден 100 дейінгі бүтін сандардың көбейтіндісі қанша нольмен
аяқталады?
Шешуі: 1 ден 100-ге дейінгі сандарда 24 бестік бар. 10;20;30;40;60;70;80;90;5;15;35;45;55;65;85;95;25;50;75;100.
Барлық сан 5 пен көбейткенде нольге аяқталады. Ендеше 24 нольмен аяқталады. Жауабы:24
14
9. 1997*** саны 1996-ға бөлінеді. *** цифрларын қанша тәсілмен ауыстырады?
 Бір ғана тәсіл бар және
1997996 ізделінді сан болып табылады.
Бір ғана тәсіл бар және
1997996 ізделінді сан болып табылады.
10. Теңдеуді шеш, мұндағы Р – А және В сандарының арифметикалық ортасы.
А
= және В =
және В = ,
,

 5
5
А
= В
=
В
= болса, Р
=
болса, Р
= =
= =
=
 =
= ,
Жауабы: х =
5.
,
Жауабы: х =
5.
11.
Ең үлкен ортақ бөлгіш тап:
а= және в=
және в=
 ЕҮОБ(а;в)=3
ЕҮОБ(а;в)=3
Ортақ бөлгіш в-2а=3 санының да бөлгіші, сондықтан берілген сандар 3-ке бөлінеді.
12. Бес бала 9 саңырауқұлақ тауып алды. Осы балалардың ең болмағанда екеуі тең шамада саңырауқұлақ тауып алғанын дәлелдеу керек.
 Балалар әртүрлі шамада
саңырауқұлақ тауып алды дейік, олардың
Балалар әртүрлі шамада
саңырауқұлақ тауып алды дейік, олардың
тауып алған саңырауқұлақтарын өсу ретімен айтайық: біріншісі нөлден кем емес, екіншісі бірден кем емес,үшіншісі екіден кем емес,төртіншісі үштен кем емес,бесіншісі төрттен кем емес.Барлығы оннан кем емес, бұл – қайшылық.
13. Жүйені бүтін сандар
жиынында

Екінші теңдеуден біріншіні шегеріп: (z-x)(y-1) =1 x,y,z бүтін сан болса, онда екі жағдай қарастырылады:
а) z-x =1 және y-1=1
z=х+1 у=2 жүйеге қойып 2х+х+1=2005 х=668 z=669
ә) z-x = -1 және y-1= -1
x =1+z және y=0 z=2005 х=2006
15
14. АВСД шаршының АВ қабырғасына іштей теңбүйірлі АВЕ үшбұрышын салған, АВ табанындағы бұрыштары 15°-қа тең. СДЕ үшбұрышының дұрыс үшбұрыш екенін дәлелдеңдер.
 Кері есеп шығарайық:
егер СДЕ1
дұрыс үшбұрыш болатын болса,
АВЕ1
үшбұрышының АВ табанындағы
бұрыштары 15°-қа тең екенін
дәлелдейік.
Кері есеп шығарайық:
егер СДЕ1
дұрыс үшбұрыш болатын болса,
АВЕ1
үшбұрышының АВ табанындағы
бұрыштары 15°-қа тең екенін
дәлелдейік.
Д С


![]()
![]()
![]()
![]()
![]()
![]()
60°
30°
![]()
![]()
![]() 75° Е1
75° Е1
75°
![]()
![]() 15°
15°
![]() А В
А В
АДЕ1=30° және ДЕ1=АД, онда Е1АД = А Е1Д = 75° олай болса, Е1АВ=15°, сол сияқты Е1ВА=15°. Сонымен біз СДЕ1 дұрыс үшбұрышының Е1 төбесі есептің берілгеніндегі Е нүктесімен дәл беттеседі, олай болса СДЕ - дұрыс үшбұрыш .
15.Дәлелдеу
керек:  < 98
< 98
 <
98,
<
98,

 49+
49+
2400 2401
дәлелденді.
2401
дәлелденді.
16. Егер
 = 7 болса,
онда
= 7 болса,
онда  неге
тең?
неге
тең?


17. Теңдеуді
шеш:  +
+
 2;
6
2;
6
16
18.
Оң х және у
үшін: 


 теңсіздігі орындалатынын
дәлелде.
теңсіздігі орындалатынын
дәлелде.





 +
+
 ;
х = у
=1
;
х = у
=1
19.
 қосындысының 85-ке
бөлгенде қалдығын тап.
қосындысының 85-ке
бөлгенде қалдығын тап.

169 = 85*2-1
және  =
85*3+1
=
85*3+1
 =к*85+
=к*85+
 Жауабы:
0
Жауабы:
0
20. Өрнектің мәні рационал сан болатынын дәлелдеңдер:



 -
-

21. Мектепте 25 сынып және 850 оқушы бар болса, 34 оқушыдан кем емес сынып бар екенін дәлелдеңдер:
 Айталық мектепте мұндай
сынып жоқ делік, сонда барлық сыныпта 33 немесе одан да аз оқушылар
бар болады. Сондықтан, мектептегі барлық оқушылар 33*25=825-тен
артық болмайды. Ал, бұл берілген шартқа қайшы, демек біздің ұйғарым
шын емес.Сондықтан, мектепте 34-тен кем емес сыныптар болады
екен.
Айталық мектепте мұндай
сынып жоқ делік, сонда барлық сыныпта 33 немесе одан да аз оқушылар
бар болады. Сондықтан, мектептегі барлық оқушылар 33*25=825-тен
артық болмайды. Ал, бұл берілген шартқа қайшы, демек біздің ұйғарым
шын емес.Сондықтан, мектепте 34-тен кем емес сыныптар болады
екен.
22. х-тің кез-келген мәнінде а мен в-ның мәнін табыңдар:
 =
= +
+
 Теңдіктің оң жағының
бөлімін ортақ бөлімге келтірсек, ол сол жағының ортақ бөліміне тең
болады. Сондықтан: 5х+31= ах+2а+вх-5в
бұдан
Теңдіктің оң жағының
бөлімін ортақ бөлімге келтірсек, ол сол жағының ортақ бөліміне тең
болады. Сондықтан: 5х+31= ах+2а+вх-5в
бұдан
5х+31= (а+в)х+(2а-5в) әрі қарай мына жүйені шешеміз:

 Жауабы:
а = 8, в =
-3.
Жауабы:
а = 8, в =
-3.
17
23. (Безу есебі). Біреу жылқы сатып алып, біраз уақыт өткізіп, оны 24 пистолға сатып жібереді. Сонда ол жылқыны сатып алғандағы бағамен бірдей болатын пайызға ұтылып қалады. Жылқыны қандай бағаға сатып алды?
 Жылқыны х – пистолмен
белгілесек. Сату барысында х% жоғалтады десек,онда мынадай теңдеу
құрамыз: х-
Жылқыны х – пистолмен
белгілесек. Сату барысында х% жоғалтады десек,онда мынадай теңдеу
құрамыз: х- = 24 бұдан х = 40
немесе
= 24 бұдан х = 40
немесе
х = 60 , сонымен жылқыны 40 пистолға немесе 60 пистолға сатып алады.
24. Дөңес төртбұрыштың диагональдары оны төрт үшбұрышқа бөледі. Қарама-қарсы үшбұрыштың ауданының көбейтіндісі, екінші қарама-қарсы үшбұрыштың ауданының көбейтіндісіне тең екендігін дәлелдеңдер.
 Айталық АВСД - берілген
төртбұрыш, онда S1
=
Айталық АВСД - берілген
төртбұрыш, онда S1
=
 ;
;
S2
=
 ; S3
=
; S3
=
 ; S4
=
; S4
=
 ; Сондықтан
; Сондықтан
S1*
S3
=
S2*
S4
=
 дәлелдеу керегі де
осы.
дәлелдеу керегі де
осы.
25.
Егерде  қосындысы 3-ке бөлінетін
болса және х, у – бүтін сандар болса, онда х және у 3-ке
бөлінетіндігін дәлелдеңдер.
қосындысы 3-ке бөлінетін
болса және х, у – бүтін сандар болса, онда х және у 3-ке
бөлінетіндігін дәлелдеңдер.
 Айталық х =
3q+r1 ,
y =
3p+r2
.
r1
мен
r2
3-ке бөлгендегі қалдықтар
болса, онда 0, 1, 2 сандар болады. Онда:
Айталық х =
3q+r1 ,
y =
3p+r2
.
r1
мен
r2
3-ке бөлгендегі қалдықтар
болса, онда 0, 1, 2 сандар болады. Онда:
 =
=
 3-ке
бөлінетіндіктен
3-ке
бөлінетіндіктен  - де 3-ке бөлінеді.
Бірақ
- де 3-ке бөлінеді.
Бірақ 
0, 1, 2, 4, 5 немесе 8 қабылдайтындықтан, бұлардан 0 ғана 3-ке бөлінеді. Бұдан . r1 = r2 = 0. Демек х және у 3-ке бөлінеді.
9 сынып
1. Машина 600км жол жүрді. Ол жолдың бірінші жартысын 100км/сағ
жылдамдықпен, екінші жартысын 60км/сағ жылдамдықпен жүрды.
Машинаның орташа жылдамдығын тап.
Шешуі: Жарты жол 600:2=300(км) бұған жіберген уақыт 300:100=3(сағ). Екінші жартысына жіберілген уақыт 300:60=5(сағ). Машинаның жүрген уақыты 3+5=8(сағ). Орташа жылдамдық 600:8=75(км/сағ)
Жауабы : 75(км/сағ)
18
2. Екі үш орынды сандарды тап, олардың қосындысы 498-ге еселік, ал
бөліндісі 5-ке еселік болатын.
Шешуі: а кіші , в үлкен ізделінді үш орынды сан 100≤а<в<1000, а+в=498к, в=5а немесе 6а=498, а=83к, в=415к, к≥2 және к≤2, к=2 а=166 в=830
Жауабы: а=166, в=830
3. Бір санның квадраты 0, 2, 3, 5 цифрларынан түрады, осы санды тап. Шешуі: Санның квадраты 2 немесе 3 немесе бір нольмен аяқталмайды. Ендеше соңғы цифр 5, ондық 2-ге тең. (10а+5)2=100а2+100а+25 3025=552
Жауабы: 3025=552
4. Бірнеше санның қосындысы 1-ге тең, олардың квадратарының
қосындысы 0,01-ден кіші бола ма?
Шешуі: Әрбір n
саны  -ге тең болса , онда осы
сандардың қосындысы 1-ге тең , ал квадраттарының
қосындысы
-ге тең болса , онда осы
сандардың қосындысы 1-ге тең , ал квадраттарының
қосындысы  -ге тең , n>10
квадраттың қосындысы 0,01ден кіші. Жауабы:
болады
-ге тең , n>10
квадраттың қосындысы 0,01ден кіші. Жауабы:
болады
5. Дөңес АВСД төртбұрышының диагональдарының қиылысу нүктесі Е.
SABE=SCDE болса АС А бұрышының биссектрисасы, АВ =4 болса, онда ВС -ны тап.
В С
![]()




4
Е
![]()
![]()
![]()
![]() А
Д
А
Д
Шешуі: SABE=SCDE, SABD=SCВD AD||BС, ABCD- трапеция ВСА=САД ВСА=САВ берілгені бойынша АД және ВС=АВ=4
Жауабы: ВС=4
6. Алты адамның ішінен үш бір-бірін танитын немесе үшеуі бір-бірін
танымайтынын дәлелде.
Шешуі: А,В,С,Д,Е,М алтауы А: «таныс», «таныс емес» В,С,Д болсын. Бұның біреуі «таныс», «таныс емес» болса, онда екеуі А мен ізделінді үштік немесе В,С,Д болады.
19
7. Дөңес төртбұрыштың диагональдары оны төрт үшбұрышқа бөледі.
Қарама-қарсы екі үшбұрыштың аудандарының көбейтіндісі, қалған екі
үшбұрышының аудандарының көбейтіндісіне тең екенін дәлелде.
Шешуі: ?1=
 ?2=
?2= ?3=
?3= ?4=
?4= ?1*?3=?2*?4
?1*?3=?2*?4
8. 100 санын қанша тәсілмен тібектес бірнеше санның қосындысы
түрінде жазуға болады?
Шешуі: Бірінші сан n, соңғы n+к қосындыны n+(n+1)+(n+2)+...+(n+к) =100 арифметикалық прогрессияның сол жақтағы қосындысын тауып: (2n+к)(к+1) =200 200=2*100=1*200=4*50=5*40=8*25 Бірінші көбейткіш екіншіден үлкен және біреуі жұп, екіншісі – тақ
2n+k=25 немесе 2n+k=40
k+1=8 k+1=5
n=9 k=7 n=18 k=4
Жауабы: 9+10+11+12+13+14+15+16=100 немесе 18+19+20+21+22=100
9.Бірінші мүшесі 1-ге, ал айырмасы 2-ге тең болатын арифметикалық прогрессияның алғашқы он мүшесінің көбейтіндісі қандай цифрмен аяқталады?
Шешуі: (![]() ) - арифметикалық
прогрессия.
) - арифметикалық
прогрессия. ![]() . Онда 1; 3; 5; 7; 9; 11; 13;
15;17; 19. Бұл прогрессия арасында 5 және 15 сандары тақ сандар.
Тақ сандардың 5 пен көбейтіндісі 5 цифрымен
аяқталады.
. Онда 1; 3; 5; 7; 9; 11; 13;
15;17; 19. Бұл прогрессия арасында 5 және 15 сандары тақ сандар.
Тақ сандардың 5 пен көбейтіндісі 5 цифрымен
аяқталады.
1 0. АВСДЕ дөңес бесбұрышы шеңберге іштей
сызылған.
0. АВСДЕ дөңес бесбұрышы шеңберге іштей
сызылған. ![]() екені
белгілі.
екені
белгілі. ![]() қосындысын
табыңыз.
қосындысын
табыңыз.
Шешуі: CD доғасына
тірелген![]() болса, онда
.
болса, онда
. ![]() 50
0
50
0
![]()
деп білейік
![]()
болады.
АС доғасына қарама-қарсы тірелген бұрыштардың қосындысы
![]() 0 , олай
болса
0 , олай
болса
![]() , бұдан
, бұдан ![]()
![]()
Жауабы: 230о
20
11. ![]() теңдігін
қанағаттандыратын
теңдігін
қанағаттандыратын ![]() саны табылатындай, барлық
жай
саны табылатындай, барлық
жай ![]() сандарын
табыңыз.
сандарын
табыңыз.
Шешуі: ![]() теңдеуі
теңдеуі ![]() квадрат теңдеуіне
келеді.
квадрат теңдеуіне
келеді.
D=![]()
![]() ,
p жай сан болуы
үшін,
,
p жай сан болуы
үшін,
![]() жай сан емес
жай сан емес
![]() жай сан,
жай сан,
![]() жай сан емес,
жай сан емес,
![]() жай сан емес Жауабы: р=2
жай сан емес Жауабы: р=2
12. Оқушылар емтихан тапсырғанда оларға 3 есеп берілді. Оқушылардың 98 % - бірінші, 90 % - екінші және 85 % - үшінші есепті шығарды. Барлық үш есепті оқушылардың х% шығарды. х - тің ең кіші және ең үлкен мәнін табыңыз.
Шешуі: Бірінші есепті 2%-ы шығармады.Екінші есепті 10%-ы шығармады.
Үшінші есепті 15%-ы шығармады. Осы есептерді шығармаған оқушылар әртүрлі болса, онда үш есептің біреуін шығармаған оқушылар 2%+10%+15%=27% онда x%=100%-27%=73% Үшінші есепті шығарғандар ең азы 85%-ы, сол үшінші есепті шығарғандардың барлығы бірінші және екінші есепті шығарған болса, x%=85% болады.
Жауабы: xmax=85, xmin=73
13. 512... алты таңбалы санның соңғы үш цифрын табу керек, сонда шыққан сан 7-ге, 8-ге және 9-ға бөлінетін болсын.
Шешуі: Ізделінді сан мынадай шарттарды қанағаттандыру керек:
1.
![]() санына бөлінетін жұп сан болуы
керек;
санына бөлінетін жұп сан болуы
керек;
2. 8-ге бөлінетін болғандықтан соңғы үш цифры 8-ге бөліну керек.
3. 9-ға бөлінетіндіктен ізделінді алты таңбалы снның цифрларының қосындысы 9-ға бөлінетін, 18-ге және 27-ге тең болуы қажет.
Онда ізделінді сан 512064 және 512568.
21
14.![]() саны қандай цифрмен
аяқталады?
саны қандай цифрмен
аяқталады?
Шешуі: 1-тәсіл.

Енді 9 дың бірнеше дәрежесінің қандай цифрмен аяқталатынын анықтаймыз:
-
-

1 цифрымен аяқталатын санның дәрежелері 1 цифрымен аяқталады. Онда
 және
және  1
цифрымен аяқталады. Демек, 1х1х9=9.
1
цифрымен аяқталады. Демек, 1х1х9=9. саны 9 цифрымен аяқталады.
саны 9 цифрымен аяқталады.
-
2-тәсіл. 9-дың тақ көрсеткішті дәрежелері 9 цифрымен,
ал жұп көрсеткіштідәрежелері 1 цифрымен
аяқталатынын байқаймыз. Дәреже көрсеткіштері 1; 3; 5 ;… және 2; 4;
6 арифметикалық прогрессия құрайды, айырмасы
![]() болады.
болады. ![]() арифметикалық
прогрессияның
арифметикалық
прогрессияның
![]() - ші мүшесінің
формуласы бойынша
- ші мүшесінің
формуласы бойынша
![]() .
Онда
.
Онда
![]() айырмасы 2-ге бөлінуі
үшін
айырмасы 2-ге бөлінуі
үшін ![]() болуы керек. 1 тақ сан,
ендеше
болуы керек. 1 тақ сан,
ендеше ![]() саны 9 цифрымен
аяқталады.
саны 9 цифрымен
аяқталады.
15.Теңдеулер жүйесін
шешіңдер: 
Шешуі:  жүйедегі 1-теңдеуді 1-ге,
2-теңдеуді 3-ке көбейтіп
жүйедегі 1-теңдеуді 1-ге,
2-теңдеуді 3-ке көбейтіп  жүйенің теңдеулерін
қосып,
жүйенің теңдеулерін
қосып, ![]() теңдеуін аламыз.
Онда,
теңдеуін аламыз.
Онда,![]()
![]() болады.
болады.
Виет теоремасы бойынша квадрат
теңдеуді шешіп ![]() . Демек,
. Демек,


Жауабы:
![]()
16. Егер
![]() - кез келген бүтін сан
болса,
- кез келген бүтін сан
болса, ![]() өрнегі 19-ға бөлінетінін
дәлелдеңдер.
өрнегі 19-ға бөлінетінін
дәлелдеңдер.
22
Шешуі![]() деп алып,
деп алып,
![]() , яғни
, яғни
![]() саны 19-ға бөлінеді
және
саны 19-ға бөлінеді
және ![]() саны да 19-ға
бөлінеді.
саны да 19-ға
бөлінеді.
17.Қосындыны
табыңдар: 
Шешуі:
1-тәсіл:

2-тәсіл:

18.![]() мен
мен
![]() сандарын
салыстырыңдар.
сандарын
салыстырыңдар.
Шешуі: ![]() және
және
![]() жазып, осы бөлшектерге кері
бөлшектерді қарастырайық
жазып, осы бөлшектерге кері
бөлшектерді қарастырайық ![]() және
және
![]() . Осы бөлшектердің екеуінен
де
. Осы бөлшектердің екеуінен
де ![]() -ді азайтып
жазайық:
-ді азайтып
жазайық:  .
.
 Ал,
Ал,
![]() екені белгілі,
онда
екені белгілі,
онда ![]() немесе
немесе
![]() <
<
![]() .
.
23
19. Өрнектің мәнін табыңдар:
(1+ )(1+
)(1+ )
)(1+
)
)(1+ )
)(1+
)
)(1+ )
)(1+
)
)(1+ )
)(1-
)
)(1- ),
а = 2003
),
а = 2003

 =
= формуласы бойынша ең ақырғы
екі көбейткіш мына түрге келеді: (1 -
формуласы бойынша ең ақырғы
екі көбейткіш мына түрге келеді: (1 -
 )(
1+
)(
1+ ) = 1 – а 1 – а = 1 –
2003 = -2002, Жауабы: -2002.
) = 1 – а 1 – а = 1 –
2003 = -2002, Жауабы: -2002.
20.Есептеңдер: ![]()
Шешуі: 1-тәсіл:
![]() деп алып,
деп алып,
![]() .
.
2-тәсіл:
![]() деп алып,
деп алып,
![]()
21.
Көбейткіштерге
жіктеңдер: ![]()
Шешуі:

22. Дипломаттың иесі дипломаттың үш таңбалы саннан тұратын кодын ұмытып қалыпты. Оның есінде сол санның цифларының қосындысы 15 екені ғана есінде қалыпты. Дипломатты кепілді түрде ашу үшін оған ең аз легенде қанша вариант қарап шығу керек?
Шешуі:Цифрларының қосындысы 15-ке тең болатын үш таңбалы санның варианттарын қарастырайық:
-
Осы цифрлардан тұратын 6 сан бар: 096; 069; 960; 906; 609; 690.
-
087 6 вариант 195 6 вариант 186 6 вариант
294 - І - 285 - І - 276 - І -
384 - І - 375 - І - 366 3 вариант
177 3 вариант 393 3 вариант 474 3 вариант
465 6 вариант 555 1 вариант
24
23.
Дәлелдеңіз: ![]() .
Мұндағы
.
Мұндағы
![]() -кез келген нақты
сандар.
-кез келген нақты
сандар.
Шешуі:
![]() ,
,
![]() ,
,

![]()
Онда![]() ,
,
![]() .
.
24.
Қайсысы
үлкен: ![]() және
және
![]()
Шешуі:

![]()
![]() .
Демек,
.
Демек,
![]() немесе
немесе
![]()
![]()
25.Теңсіздікті
шешіңдер: 


 +(
+(
 бірақ
бірақ
 кез-келген х үшін,
ал
кез-келген х үшін,
ал кез-келген х үшін
8
кез-келген х үшін
8 болғандықтан, ал
дискриминант – теріс. Олай болса
болғандықтан, ал
дискриминант – теріс. Олай болса
 +(
+( , сондықтан шешімі
жоқ.
, сондықтан шешімі
жоқ.
10 сынып
1. 3р4+5q4+15=13p 2q2 теңдігі орындалатын p және q жай сандарын тап.
Шешуі : p және q тақ болса , онда сол жағы модулі 4 бойынша 3-ке тең, оң жағы модулі 4 бойынша 1-тең,бұл жағдай болмайды. Ендеше p= q=2 есеп шартына қанағаттандырылмайды p=2 болса q=3 болады, ал q=2 болса
p болмайды.
Жауабы: p= 2 ; q=3
25
2.Дұрыс
па?  =
2000;
=
2000;

 Сол жағын
түрлендіреміз:
Сол жағын
түрлендіреміз:
 =
= =
=

= =
= =
2000; 2000 =
2000 Жауабы:
дұрыс.
=
2000; 2000 =
2000 Жауабы:
дұрыс.
3. ABCD шаршысының A төбесі және CD қабырғасының ортасы l түзуіне қарағанда симметриялы. l түзуі ABCD шаршысының бөлген бөліктердің аудандарының қатнасын табыңыз.
Шешуі: AB=a, BN=x, DM=y деп белгілейміз.
![]()
 болғандықтан
MA=ME=a–y
болғандықтан
MA=ME=a–y
![]() тікбұрышты ұшбұрыш
сондықтан
тікбұрышты ұшбұрыш
сондықтан
![]()
![]()
![]()
![]()
![]() болғандықтан AN=EN
болғандықтан AN=EN
![]() тікбұрышты үшбұрыш сондықтан
тікбұрышты үшбұрыш сондықтан
![]()
![]() тікбұрышты үшбұрыш сондықтан
тікбұрышты үшбұрыш сондықтан
![]()
AN=EN болғандықтан
![]()
![]()
![]()
ABNM трапецияның ауданы ![]()
DMNC трапецияның ауданы ![]()
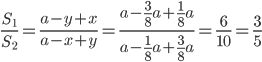 Жауабы:
Жауабы:  .
.
26
4. 2015 санын қандай санға көбейткенде, сол санның бөлгіштерінің саны дәл 12-ге ( бір мен сол санның өзін қоса есептегенде) тең болады?
Шешуі: 2015 санын көбейткіштерге жіктейміз. 2015=5·13·31
2015-тің бөлгіштері сегіз: 1, 5, 13, 31, 5·13, 5·31, 13·31, 5·13·31
Егер 2015 санын оның жай көбейткіштерінен басқа кез-келген бір жай санға көбейтсек, мысалы: 3-ке, 2015·3=3·5·13·31
2015·3 санының бөлгіштері:1, 3, 5,
13, 31, ![]()
![]() бөлгіштерінің саны 15-ке тең
болады.
бөлгіштерінің саны 15-ке тең
болады.
Демек өзінің жай көбейткіштерінен басқа келкелген санға көбейткенде оның бөлгіштерінің саны 12-ден артық болады.
Енді 2015 санының жай көбейткіштеріне көбейтсек бөлгіштерінің саны дәл 12-ге тең болады.
2015·5=5·5·13·31 2015·5 санының бөлгіштері: 1,5,13,31,5·5,5·13,5·31,13·31,5·5·13,5·5·31,5·13·31,5·5·13·31 саны 12-ге тең болды.
Демек, 2015 санының жай көбейткіштерінің біріне көбейтсек ол санның бөлгіштері дәл 12-ге тең болады.
Жауабы: 5, 13, 31
5. АВСД дөңес төртбұрышы
берілген. Сонда ![]() , ал Ғ нүктесі АД кесіндінің
ортасы. ВҒ түзуі АС түзуімен Р нүктесінде қиылысады және ВС=СР
екенін дәлелде.
, ал Ғ нүктесі АД кесіндінің
ортасы. ВҒ түзуі АС түзуімен Р нүктесінде қиылысады және ВС=СР
екенін дәлелде.
Шешуі: А,В,С және F нүктелерінің бір шеңберге тиіс екенін дәлелдеу керек.
ΔАВF=ΔАСF = ᴪ, бұдан Δ СBL=90°-ᴪ.
6. Теңдеулер жүйесін
шешіңіз: ![]()
Шешуі:
1-ші әдісі:
![]()
![]()
![]()
Соңғы жүйедегі теңдеулерді
өзара көбейтсек: ![]() болып
болып ![]() шығады. Осы теңдеуді соңғы
жүйенің бірінші теңдеуіне бөлсек
шығады. Осы теңдеуді соңғы
жүйенің бірінші теңдеуіне бөлсек
![]()
Тура осыған ұқсас жолмен
![]()
![]() шығады.
шығады.
Жауабы: ![]() және
және ![]()
27
2-ші әдісі:
![]()
![]()
![]()
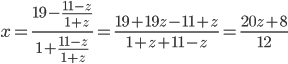

![]()
![]()
![]() теңдеуінің
шешімі
теңдеуінің
шешімі ![]() .
.
![]() теңдеуіне x-ті
қойып,
теңдеуіне x-ті
қойып, ![]()
![]() теңдеуіне z-ті
қойып,
теңдеуіне z-ті
қойып, ![]()
Жауабы: ![]() және
және ![]()
![]()
7. ![]() рационал санның кубы болатындай барлық
бүтін n санын табыңыз.
рационал санның кубы болатындай барлық
бүтін n санын табыңыз.
Рационал санның кубы болу үшін, алымы бүтін санның кубы, ал бөлімі натурал санның кубы болуы керек.
Шешуі: ![]() мұндағы m бүтін сан, k натурал сан.
мұндағы m бүтін сан, k натурал сан.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
болатындай төрт жағдайын қарастырамыз.
1. ![]() бұл жүйені шешуде
бұл жүйені шешуде ![]() теңдеуін аламыз.
теңдеуін аламыз. ![]() болып, теңдеу бүтін шешімге ие
емес.
болып, теңдеу бүтін шешімге ие
емес.
2.
![]() бұл жүйені
шешуде
бұл жүйені
шешуде ![]() теңдеуін
аламыз.
теңдеуін
аламыз. ![]() шешімі
жоқ.
шешімі
жоқ.
3.
![]() бұл жүйені
шешуде
бұл жүйені
шешуде ![]() теңдеуін
аламыз.
теңдеуін
аламыз. ![]()
![]() осыдан
осыдан ![]() шешімін
аламыз.
шешімін
аламыз.
Шарт
бойынша m бүтін
сан, k натурал сан.
Сондықтан![]()
Жауабы: n=3
28
8.
![]() функциясының
функциясының ![]() аралығындағы ең кіші мәнін
табыңдар.
аралығындағы ең кіші мәнін
табыңдар.
Шешуі:1-ші әдісі:
Өрнектітүрлендіреміз. Енді осы өрнекке Коши теңсіздігін қолданамыз, сонда мынадай болады.
![]()
Жауабы: 4
2-ші әдісі:
Берілген функцияның кері функциясының анықталу облысын табу арқылы шешеміз.
![]()
![]()
теңдеудің екі жағында х2-қа бөлеміз.
![]()
Жаңа айнымалы енгіземіз.
![]() ,
, ![]() осыдан
осыдан
![]() шығады.
шығады.
![]()
![]()
![]()
![]() теңсіздігінің шешімінің
теңсіздігінің шешімінің
![]() аралығындағы ең кіші мәнін
аламыз.
аралығындағы ең кіші мәнін
аламыз.
![]()
![]()
![]()
Теңсіздіктің шешімі
![]() аралығы болады.
аралығы болады.
Бұл аралықтың ең кіші мәні 4.
Жауабы: 4
9.Теңсіздікті шеш: (х-1)(х2-1)(х3-1)(х4-1)...(х2002-1)≤0
Шешуі: (-∞; −1] {1}
xn-1=0 теңдеудің екі түбірі бар егер n –жұп сан болса х=-1 х=1
және бір түбірі бар егер n-тақ болса х=1.
29
10. ![]() шахмат тақтасында барлық қара
шаршы таңдалып алынатындай және әрбір жол мен әрбір бағаннан дәл 7
шаршыдан таңдалып алынатындай 56 әр түрлі шаршыны қанша тәсілмен
таңдап алуға болады?
шахмат тақтасында барлық қара
шаршы таңдалып алынатындай және әрбір жол мен әрбір бағаннан дәл 7
шаршыдан таңдалып алынатындай 56 әр түрлі шаршыны қанша тәсілмен
таңдап алуға болады?
-
-
-
-
a
b
c
d
e
f
g
h
1
2
3
4
5
6
7
8
-
-
-
Шешуі: Таңдалмайтын ақ шаршыны іріктеп алайық. Әрбір жолмен әрбір бағанда 4 ақ шаршы бар екені белгілі. Әрбір жолдан және әрбір бағаннан 1 ден артық ақ шаршы алып тасталынбайды.
1-ші жолда ақ түсті шаршыны алып тастау мүмкіндігі 4-ке тең. 2-ші жолдан алып тасталынатын ақ шаршы, 1-ші жолдан алып тасталған ақ шаршы бағанында болмауы керек. 2-ші жолда мұндай мүмкіндік саны–4.
3-ші жолда әртүрлі мүмкіндік саны 3 тең болады. Себебі 1-ші жолда алынған бір бағанға кеміді.
4-ші жолда әртүрлі мүмкіндік саны 3 тең болады. Себебі 2-ші жолда алынған бір бағанға кеміді.
5-ші жолда әртүрлі мүмкіндік саны 2 тең болады. Себебі 1-ші және 3-ші жолдардағы 2 бағанға кеміді.
6-шы жолда әртүрлі мүмкіндік саны 2 тең болады. Себебі 2-ші және 4-ші жолдардағы 2 бағанға кеміді.
7-ші жолда әртүрлі мүмкіндік саны 1 тең болады. Себебі 1-ші, 3-ші және 5-ші жолдардағы 3 бағанға кеміді.
8-ші жолда әртүрлі мүмкіндік саны 1 тең болады. Себебі 2-ші, 4-ші және 6-шы жолдардағы 3 бағанға кеміді.
Сонымен жалпы мүмкіндіктер саны 4·4·3·3·2·2·1·1=576
Жауабы: 576
11.Жай сандар р2-2; 2р2-1 және 3р2+4 үшін барлық жай р санын тап.
Шешуі : р=3 р=7 2-ден 7-ге дейінгі жай сандарды тексеру керек.
Ары р>7 осылардың біреуі 7-ге бөлінетінін дәлелдеу керек.
30
12. ![]() интервалында х және у сандары тиіс. Дәлелдеу
керек:
интервалында х және у сандары тиіс. Дәлелдеу
керек:
xcosx+ycosy≤ycosx+xcosy
Шешуі : Оң және сол жақтың айырымын тексеріп, оны көбейткіштерге жіктеп және берілген аралықта косинустың кемитінін қарастыру керек.
13. Натурал п саны табылады ма, егер пп+(п+1)п 2003-ке бөлінсе.
Шешуі : п=1001 иә орындалады.
14. а, в, с және x, y, z -оң нақты сандар болып, a+x=b+y=c+z=1 болса, онда
(abc+xyz) ![]() теңсіздігін дәлелде.
теңсіздігін дәлелде.
Шешуі : Жақшаны ашып, сол жақтың  екенін көрсетіп ары қарай
екенін көрсетіп ары қарай ![]() ,мұндағы m;n>0 қолдану
жеткілікті.
,мұндағы m;n>0 қолдану
жеткілікті.
15.Функцияның графигін
сал ![]()
Шешуі :
![]() формуланы қолданып модульді
ашу керек :
формуланы қолданып модульді
ашу керек :

16. а-нақты сан болып, а2+а және а+2а рационал сан болса, онда а саны
да рационал болатынын дәләлде.
Шешуі : А=а2+а , В=а3+2а рационал сандар болса , онда В=а(А+3)-А.
Бұдан а 2+а+3=0 теңдеудің нақты түбірі жоқ , онда А≠ -3, ендеше
![]() болады.
болады.
17. О центрлі шеңбердің АС және ВД хордалары К нүктесінде қиылысады. М және Н ΔАВК және ΔСДК-ға сырттай сызылған шеңберлердіңцентрі болса, онда ОМ=КН екенін дәлелде.
Шешуі
: ОМ![]() АВ орта перпендикуляр
болғандықтан АВ-ға , НК-ның созындысы АВ мен Р нүктесінде
қиылысады.
АВ орта перпендикуляр
болғандықтан АВ-ға , НК-ның созындысы АВ мен Р нүктесінде
қиылысады.
Сонда
РАК+РКА=КДС+СКН=
 КНС+
КНС+ (СКН+КСН)=90°
(СКН+КСН)=90°
КН ||АВ болғандықтан КМ||ОН ендеше КНОМ – параллелограмм, ОМ=КН.
31
18. Егер
2tg2α+tgα-3=0
болып π/2<α<π аралығында болса
sin2α-ны тап.
Шешуі :
![]()
19. Есепте: tg200 tg400 tg800
Шешуі : sin20°sin40°sin80°=½(cos20°-cos60°)sin80°=½cos20°sin80°-¼sin80°=
=¼(sin100°+sin60°)-¼sin80°=![]()
Енді cos20°cos40°cos80°=![]() tg200tg400tg800=
tg200tg400tg800= ;
;
20. а
параметріне байланысты теңсіздікті шеш: ![]()
Шешуі : х=а теңсіздіктің а-ға байланысты шешімі :
ах2+(а2-2)х-2а=(х+а)(ах-2)
![]()
шешу үшін мына жағдайларды қарастырамыз:
a) а> 2 ; шешімі {а }
b) 0<а≤ 2 ;
шешімі 
c) а=0; шешімі [0;∞)
d) - 2 ≤а<0 ;шешімі {а }
i) а<-
2 ;шешімі
 )
)
21. ![]() және
және![]() сандары бүтін сан болу үшін натурал а және
в
сандары бүтін сан болу үшін натурал а және
в
жұптарын тап.
Шешуі : (2;2),(3;3),(1;2),(2;1),(2;3),(3;2).
а≥в. Егер а>в+1 болса , онда а(а-1)>в(в+1) және а 2-в>а+в 2
бұл орындалмайды.Ендеше а=в немесе а=в +1.
а=в (2;2)(3;3) болады.
Ал а=в +1 болса , бүтін
сан![]() болады в≥6
в 2
-в-1>4в+2,
1≤в≤5 , онда тексер.
болады в≥6
в 2
-в-1>4в+2,
1≤в≤5 , онда тексер.
22. 13!-11! Өрнегі 31-ге еселік екенін дәлелде.
Шешуі: 5) 13! =1*2*3*....*13=1*2*3*....*11(12*13) =11!*12*13.
Ендеше 13!-11! =11!(12*13-1) =11!*155=11!*31*5. 31-ге еселік болады.
32
23.
а, в, с>0 болса,
 теңсіздігін дәлелде.
теңсіздігін дәлелде.
Шешуі: Теңсіздіктің арифметикалық және гармониялық оң сан үшін қолданып шығатыны:
 ; Бұдан кейін теңсіздікті
шеш.
; Бұдан кейін теңсіздікті
шеш.
24.
Ықшамда: ![]() ;
;
Шешуі
: ![]()
![]() ;
;
25. Дұрыс жетібұрыштың неше диагоналі бар?
Шешуі : Әрбір төбеден 4 диагональ жүргізуге болады, бірақ 2 диагональ үйлеседі,ендеше 14 диагональ жүргізуге болады.
Жауабы: 14 диагональ.
![]()
1. Мына функциялардың графиктерін салыңдар:
а) y=sin(arcsinx)
б)
y=arccos
Шешуі: 


2. ax2002+вх1111+с=0 теңдеуінде а, в, с нақты сандар болса үш нақты түбірі бола ма?
Шешуі:
 Жоқ.
Жоқ.
у=ах2002+вх1111+с және оның бір экстремалды нүктесі болатынын дәлелде.Осыдан берілген теңдеудің екіден артық емес әр түрлі түбірі болады.
33
3. Теріс емес нақты сандар жиынында теңдеу жүйесін шеш:

Шешуі:  (0;0;0),
(1;1;1)
(0;0;0),
(1;1;1)
Нұсқау: үш теңдеуді мүшелеп қосу керек.
4. sinх ≤ sin2х ≤ sin4х теңсіздігі орындалатын х-тың барлық нақты сан мәнін тап.
Шешуі:
 Берілген қос теңсіздікті былай
жазуға болады:
Берілген қос теңсіздікті былай
жазуға болады:

Интервал әдісін қолданып және периодтылығын ескеріп, жауабын жаз.
х , n
, n
5. 0 және 1 цифрлары мен жазылған және 15-ке бөлінетін жеті орынды сандардың қосындысын тап.
Шешуі: 11 555 550
3-ке және 5-ке бөлінгіштік қасиетін қолдан.
6.Теңдік орындалатын ең кіші натурал n санын тап:
sin(n°+80°)+sin(n°-40°)+sin(n°+70°)=sin65°
Шешуі: 105
Берілген теңдікті тең
түрлендіру арқылы келтір. sin( n+450) =  ;
;
7.Теңдеуді шеш: (х2+х-1002,5)2+х2=2005
Шешуі: 1002,5=а деп белгілеп, теңдеуді
(х2-а)(х2+2х+2-а) =0 түріне келтір. Сонда
х1,2= ±  және
х3,4= -1 ±
және
х3,4= -1 ± 
у(х) = х2+х-а, у(у(х)) = х; у(х) = х; х2-а=0.
8. Пирамиданың төбесіндегі жазық бұрыш 180°-тан үлкен. Бір бүйір қабырғасы табанының жарты периметрінен кіші екенін дәлелде.
Шешуі: АS ең үлкен пирамиданың бүйір қыры. Бүйір жағының жазбасы АS қыры арқылы жасалған бүйір жағы, осы кесіндіге орта перпендикуляр жүргізу керек және ол S арқылы өтсе , олардың қиылысуы М нүктесі болады. Осыдан Р > 2, АМ > 2АS екенін дәлелдеу керек.
34
9.Теңсіздікті
шеш:  +
+

 ;
;
Шешуі:1;
f(х) =
 +
+ 
 анықталу аймағында монотонды
өспелі, сондықтан f (х
)
≥
f
(-1)
=
анықталу аймағында монотонды
өспелі, сондықтан f (х
)
≥
f
(-1)
=
 >1.4
>1.4
10.Теңсіздікті
дәлелде:  ,
х
,
х
Шешуі:
q(x) = x
- -
-  оң жарты осьте монотонды кемитіндігін көрсет qᴵ(x) ≥ 0, х ≥
0 qᴵ(x) =
оң жарты осьте монотонды кемитіндігін көрсет qᴵ(x) ≥ 0, х ≥
0 qᴵ(x) =  болса теңсіздік
дәлелденді.
болса теңсіздік
дәлелденді.
11. Фукцияның графигін салыңдар:
y =  +
+  ;
;
 +
+  ,
,
 +
+  ,
,
 +
+ 
 +
+
 ,
,
 ,
,

Жауабы:
Графигі  түзу
сызық.
түзу
сызық.
12.
Теңдеудің бүтін түбірін тап:
2 -1=2ху
-1=2ху
 Берілген теңдеудің
шешімі жоқ, себебі сол жағы тақ сан, ал оң жағы жұп
сан.
Берілген теңдеудің
шешімі жоқ, себебі сол жағы тақ сан, ал оң жағы жұп
сан.
13. Төрт таңбалы санның цифрларын кері жазғанда шыққан сан берілген саннан 4 есе кем болатын санды тап.
 1000а+100в+10с+d деп белгілеу керек
сонда
1000а+100в+10с+d деп белгілеу керек
сонда
4(1000а+100в+10с+d)=1000d+100c+10b+a
Сол жағы жұп болғандықтан , оң жағы да жұп болады , ендеше
а-жұп цифр. а=2 басқа цифрды қойсақ бес орынды болады.
4d 2-ге аяқталады d=8.
4(1000*2+100в+10с+8) =1000*8+100с+10в+2 , 4(10в+с)+3=10с+в
40в+4с+3=10с+в , 13в+1=2с, в=1 ,с=7 і зделінді сан 2178
Жауабы: 2178
35
14. Тепе-теңдікті дәлелдеңдер:
 =
=


 =
=

 =
=

 =
=




15. Теңдеуді
шеш:  +
+ =
= ;
;
 Сол жағы барлық нақты сан
жиынында өспелі функция, сондықтан барлық мәнді бір рет
қабылдайды.
Сол жағы барлық нақты сан
жиынында өспелі функция, сондықтан барлық мәнді бір рет
қабылдайды.
мәнін
функция х= -1 –ге тең
болғанда қабылдайды.  мәнін функция х=-1 –ге тең болғанда қабылдайды.
Жауабы: х=
-1.
мәнін функция х=-1 –ге тең болғанда қабылдайды.
Жауабы: х=
-1.
16. а-нің қандай
мәнінде 
теңдеу жүйесінің бір шешімі бар?
 а=7
а=7
Координата жазықтығында
у=4- және
және  графиктерін салу керек.
(0;а) және R=3 шеңбер теңдеуі болады.
графиктерін салу керек.
(0;а) және R=3 шеңбер теңдеуі болады.
17.
 теңсіздігін
дәлелде.
теңсіздігін
дәлелде.
 1+cos1° =
2
1+cos1° =
2 =
=
 =
=
 бағала . Бірлік дөңгелектің
секторын х (0 < х <
бағала . Бірлік дөңгелектің
секторын х (0 < х < ) катеттері а=1 , в =
tgx тік бұрышты үшбұрышпен жауып сектор ауданы мен үшбұрыш ауданын
салыстырып, tgx>х, 0<х<
) катеттері а=1 , в =
tgx тік бұрышты үшбұрышпен жауып сектор ауданы мен үшбұрыш ауданын
салыстырып, tgx>х, 0<х<  .
.
 >
> >
> және 1+cos1°
=
және 1+cos1°
= <
<  =
= ;
Теңсіздік
дәлелденді.
;
Теңсіздік
дәлелденді.
18. Теңдеуді
шеш: ((х-3)
((х-3) )
)

 ((х-3)
((х-3) )
) және
және 
Екінші теңдеу  -5х+6=0
-5х+6=0  ((х-3) sinх) = 1
((х-3) sinх) = 1
Х1=3; х2=2 х=3 Жауабы: х=3.
36
19. Теңдеу жүйесін
шеш: 
 Бірнеше жағдайды
қарастыр:
Бірнеше жағдайды
қарастыр:
1) х=0 және у=0 болса z өз бетінше қалады,
2) у=0 және х=0 болса z өз бетінше қалады,
3) z=0 онда х және у≠0
х=с, у=-с с кез келген сан с≠0
сондықтан бірінші теңдеуді 3у-ке, екіншіні (-у)-ке, үшіншіні х-ке көбейтіп қос.
 +3
+3
 у+3х
у+3х  +
+ -
-
 =0
=0
( 
х+у=уz бірінші теңдеуден
 +ху+у(х+у) =
+ху+у(х+у) =  (
(  z=3
z=3
үшіншіден хуz+у =0
х=- z =-3 x=-3
z=3
=0
х=- z =-3 x=-3
z=3
20. Екі құбыр бірге бассейнді 4 сағатта толтырады. Алдымен бірінші құбыр бассейннің жартысын толтырғаннан кейін оны жауып , екінші құбырды ашса, онда бассейн 9 сағатта толады. Жеке-жеке толтырса әр құбыр неше сағатта толтыра алады?
 Біріншісі – х, екіншісі
– у болсын. Мынандай жүйе құрамыз:
Біріншісі – х, екіншісі
– у болсын. Мынандай жүйе құрамыз:



 және
және

Жауабы: 6 сағат және 12 сағат.
21. Егер α, β, γ үшбұрыштың бұрыштары болса, онда мына теңдіктің дұрыс екенін дәлелдеңдер: cos2α + cos2β + cos2γ + 2 cosα cosβ cosγ = 1
 α +
β +
γ =
π, мына формулаларды қолдана
отырып, cos2x
=
α +
β +
γ =
π, мына формулаларды қолдана
отырып, cos2x
=  , cosx = -
cos(π - x), cosx + cosy = 2
cos
, cosx = -
cos(π - x), cosx + cosy = 2
cos cos
cos дәлелдейміз.
дәлелдейміз.
22. Кіші картопты тазалағанша үлкен картопты тазалаған неге оңайырақ?
 Бұнда ( картоп шар
сияқты деп алса) онда көлемі және массасы радиустың кубына
пропорционалды , беті радиустың квадратына пропорционал
болады.
Бұнда ( картоп шар
сияқты деп алса) онда көлемі және массасы радиустың кубына
пропорционалды , беті радиустың квадратына пропорционал
болады.
37
23. Теңдікті дәлелдеңдер:
arctg1+ arctg +
arctg
+
arctg =
=
 ;
;
 arctg
arctg +
arctg
+
arctg =
=
 -
- 
tg(arctg +
arctg
+
arctg =
tg
=
tg 
 =
1
=
1
 = 1
= 1
 1 = 1
дәлелденді.
1 = 1
дәлелденді.
24. Мынандай қатынастар
орындалатындай: АВ=СД=8см; АС=ВД=10см; АВ=ВС=13см; кеңістікте
фигура табуға бола ма? (төбелері А, В, С, Д болатын көпбұрыштан
тұрады.
 Ондай фигура бар. Оларды
екі ұшбұрыш АВС және ВСД-дан алуға болады, екеуі бір-біріне тең
беттеседі.
Ондай фигура бар. Оларды
екі ұшбұрыш АВС және ВСД-дан алуға болады, екеуі бір-біріне тең
беттеседі.

![]()
![]() Д
Д

![]()
![]()
![]()
![]()
![]() С
С
![]()
![]() А
А
В
25. xy = 2006 (x+y) теңдеуінің бүтін шешімі болатынын дәлелдеу керек.
 Берілген теңдеуді мына түрге
келтіреміз: (х – 2006)(у - 2006) =
20062 одан х = у = 4012.
Берілген теңдеуді мына түрге
келтіреміз: (х – 2006)(у - 2006) =
20062 одан х = у = 4012.
38
Қолданылған әдебиеттер:
-
Агаханов Н.Х, О.К.Полипский «Математика Районные олимпиады», Москва Просвещение, 2010.
-
Бугулов Е.А , Б.А.Толасов «Сборник задач для подготовки к математическим олимпиадам».
Северо-Осетинское книжное издательство, 1962.
-
Горбачев Н.В. «Сборник олимпиадных задач по математике» – М.: МЦНМО, 2004.
-
Муштари Д.Х. «Подготовка к математическим олимпиадам» Муштари Д.К. – Казань: Изд-во Казан. матем. об-ва, 2000.
-
Фарков А.В. «Математические олимпиады в школе 5-11 классы», Москва Айрис-пресс, 2009.
39
Құрастырған:
А.С.Жасекеева, А.М. Кенжегалиева, М.К.Нигметуллин,
Р.А.Каратаева – Орал қаласы №46жалпы орта білім беретін
мектебінің математика пәні мұғалімдері.
Пікір жазғандар:
З.Ж.Жұбанышева – М.Өтемісов атындағы БҚМУ физика және
математика кафедрасының аға оқытушысы.
Г.Х.Хусаинова - №41 жаратылыстану-математика бағытындағы
мектеп-лицейінің жоғарғы санатты математика пәні мұғалімі.
Бұл жинақта оқушылардың теориялық білімін нығайтып, қиындығы жоғары есептерді шығару дағдысын қалыптастыру мақсатында мектеп программасында қарастырылмайтын стандартты емес есеп түрлерін , логикалық тапсырмаларды , күрделі теңдеулер мен теңсіздіктерді шешудің жолдары нақты көрсетілген. Математика пәні мұғалімдеріне әдістемелік көмек ретінде ұсынылады.
Мазмұны:
-
Кіріспе
-
5 сынып ......................................................................... 1 бет
-
6 сынып ......................................................................... 5 бет
-
7 сынып ........................................................................ 9 бет
-
8 сынып ........................................................................ 13 бет
-
9 сынып ........................................................................ 18 бет
-
10 сынып ........................................................................ 25 бет
-
11 сынып ........................................................................ 33 бет
-
Қолданылған әдебиеттер .............................................. 39 бет
2. Бақа тереңдігі 25м құдыққа түсіп кетті. Ол құдықтан шығу үшін күніне 5м көтеріліп, 4м қайта түсіп отырды. Бақа неше күнде құдықтан шығады?
4. Сыныпта математиканы ұнататын қыздардың саны математиканы ұнатпайтын ұлдардың санымен бірдей. Сыныпта кімдер көп: математиканы ұнататын оқушылар ма, әлде ұлдар ма?
Екі сағат бір уақытта соғуды бірге бастап,біргеаяқтады.Бірінші сағат–әрбірекісекундсайын, екінші сағат–әрбірүшсекундсайынсоғады.Есептегендебарлығы13 соғу болды (бірігіп қалғансоғуларбірсоғудепесептелінеді). Бірінші соғу мен соңғы соғудың арасында қанша уақыт өтті?

шағым қалдыра аласыз















