
Қазақстан Республикасы білім және ғылым министрлігі
Ы. Алтынсарин атындағы Арқалық мемлекеттік педагогикалық институты
Жаратылыстану және ақпараттандыру факультеті
Математика және физика кафедрасы

ОҚУ-ӘДІСТЕМЕЛІК КЕШЕН
«Олимпиадалық есептерді шешу»
Пән атауы
Мамандығы 5В010900– «Математика»
Шифр, мамандық атауы
Арқалық, 2015
Құрастырушы: аға оқытушы Абдрахманова М.Т
ОӘК аңдатпасы: «Олимпиадалық есептерді шешу» курсы бойынша құрастырылып отырған оқу-әдістемелік құжат «Математика» мамандығы бойынша кредиттік жүйеде оқитын студенттерге арналған; оқу сабақтарының түрлері және тақырыптары бойынша оқу уақытын бөлуді анықтайды; аудиториядағы және аудиториядан тыс уақыттағы студенттердің өзіндік жұмыстарының мазмұнын анықтайды; студенттердің танымдық және творчествалық білімін нығайтады және оқу мен зерттеу процестерінің байланысын туғызады.
Оқу әдістемелік кешен «Олимпиадалық есептерді шешу»
Жаратылыстану және ақпараттандыру факультетінің студенттеріне арналған/ құрастырған: Абдрахманова М.Т. Арқалық: АрқМПИ баспасы, 2013ж
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
Ы.Алтынсарин атындағы Арқалық мемлекеттік педагогикалық институты
«Бекітілді»
ОжДҚж проректоры
_______ Б.Д.Искакова
«____» _______ 2015ж.
ОЛИМПИАДАЛЫҚ ЕСЕПТЕРДІ ШЕШУ таңдау пәні бойынша ҮЛГІЛІК ОҚУ БАҒДАРЛАМАСЫ
5В010900- Математика мамандығы үшін
Арқалық 2015
Алғы сөз
1. Математика және физика кафедрасы 5В010900 Математика мамандығы бойынша жасалған және ұсынылған.
Үлгілік оқу бағдарламасын құрастырушы: аға оқытушы М.Т.Абдрахманова
2. Ы.Алтынсарин атындағы Арқалық мемлекеттік педагогикалық институтының Ғылыми-әдістемелік кеңесінің шешімімен БЕКІТІЛГЕН және ПАЙДАЛАНУҒА рұқсат етілген.
Хаттама № 1 27.08. 2015ж
3. Таңдау бойынша компоненттің үлгілік оқу бағдарламасы 5В010900 Математика мамандығы үшін үлгілік оқу жоспары және мамандықтың жұмыс оқу жоспары негізінде құрастырылған.
4. Бағдарламаны баспаға Ы.Алтынсарин атындағы Арқалық мемлекеттік педагогикалық институтының жаратылыстану және ақпараттандыру факультетінің оқу-әдістемелік кеңесі ұсынған.
Факультет ОӘК төрайымы _____________________________
(А.Т.Ә)
Хаттама № __ ___________ ___________________ 2015ж
«Келісілді»
Факультет деканы
________ ____________________
(қолы) (А.Т.Ә)
«____» _____ 2015 ж.
ТҮСІНІКТЕМЕ
Пәнді оқытудың мақсаты: құрылымы немесе оларды шығару әдістері бойынша стандартты емес, қиындығы жоғары деңгейдегі есептерді шығарудың әдіс-тәсілдері мен талдау негіздерін зерттеу.
Пәнді оқытудың міндеттері: Негiзгi меселелердi шешуге байланысты студенттер (болашақ мұғалiмдер) өз пәндерін терең меңгеруi, пәнге аса қызығушылығын тудыру;
-
есептер шығаруға қажетті білім, білік, дағдыны қалыптастыру;
-
есептер шығару барысында ойды түйіндеп пәрменділігін арттыруға қажетті әдістерді қолдана білу;
-
ойлау әрекетiне қажетгi теориялық, практикалық мәселелердi меңгеруі
-
курс бағдардамасы бойынша теориялық практикалық бiлiмдi толық меңгеруге тиiс
Пререквезиттері: элементар математика, математика курсына енгізу кіріспесі, алгебра курсы және сандар теориясы; математикалық талдаудың курсы;
Пәннің постреквизиттері: олимпиада есептерін шығару әдістемесі; білім жоғарылату.
Пәннің құзіреттілігі:
Білуі тиіс:
-
Математикалық есептерді шығару үшін негізгі зерттеу әдістерін меңгеру;
-
теориялық және қолданбалы тапсырмаларды шешуге математикалық білімді қолдану;
Біліктілігі болуы тиіс:
-
Студенттердегі математикалық және алгоритмдік ойлауының дамуы;
Дағдылары болуы тиіс:
-
Жұмыс істеу барысында ғылыми, оқу – әдістемелік және анықтамалық әдебиеттерді қолдануда;
-
Өз бетінше өзіндік жұмыс, әзірлемелер әзірлеуде;
Пән мазмұны:
-
Элементар математика курсынан олимпиадалық есептерді шешу жолдары
-
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары
-
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
-
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары
-
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары
-
Жоғары математика курсы бойынша олимпиадалық есептер
-
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары
-
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
-
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары
-
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары
Практикалық (семинарлық) сабақтар және өзіндік жұмыстар. Өзіндік жұмыстардың тақырыптарының жобасы.
-
Элементар математика курсынан олимпиадалық есептерді шешу жолдары
-
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары
-
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
-
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары
-
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары
-
Жоғары математика курсы бойынша олимпиадалық есептер
-
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары
-
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
-
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары
-
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары
Әдебиеттер тізімі.
Негізгі әдебиеттер
-
Математические олимпиады школьников: Книга для учащихся общеобразоват. учреждений Н.Х.Агаханов. Л.П.Купцов, Ю.В.Нестеренко и др. М.: Просвещение: Уч.лит., 1997-208 с.
-
Математические олимпиады школьников: Кн.для учащихся общеобразовать. учреждений Л.П.Купцов, Ю.В.Нестеренко, С.В.Резниченко, А.М.Слинько.- М.: Просвещение, 1998. - 256 с.
-
Математические олимпиады школьников: Кн.для учащихся общеобразовать. учреждений Л.П.Купцов, Ю.В.Нестеренко, С.В.Резниченко, А.М.Слинько.- М.: Просвещение, 1999. - 254 с.
-
Сборник индивидуальных заданий по высшей математике. Часть 1. Под ред. Рябушко А.П.-Мн: Вышейшая школа., 2001.
-
Сборник индивидуальных заданий по высшей математике. Часть 2. Под ред. Рябушко А.П.- Мн: Вышейшая школа., 2001..
-
Сборник индивидуальных заданий по высшей математике. Часть 3. Под ред. Рябушко А.П.- Мн: Вышейшая школа., 2001.
-
Сборник индивидуальных заданий по высшей математике. Часть 4. Под ред. Рябушко А.П.-Мн : Вышейшая школа., 2005.
Қосымша әдебиеттер
1. Ильясов М.Н. Нестандартные задачи математического анализа. Учебно-методическое пособие. Павлодар, 2006.
2. Степаненко В.М. Руководство к решению задач повышенной трудности по высшей математике. Павлодар, 2003.
3.Садовничий В.А., Григорьян А.А., Конягин С.В Задачи студенческих математических олимпиад,. МГУ, 1987.
Қазақстан Республикасы білім және ғылым министрлігі
Ы.Алтынсарин атындағы Арқалық мемлекеттік педагогикалық институты
“Бекітемін”
ОжДҚж проректоры
__________Б.Д.Искакова
2015 ж. “___” _________
Жаратылыстану және ақпараттандыру факультеті
Математика және физика кафедрасы
ЖҰМЫС ОҚУ БАҒДАРЛАМАСЫ
Пән: «Олимпиадалық есептерді шешу»
5В010900 – «Математика» мамандығы үшін
|
|
Оқу түрі |
|
|
Күндізгі |
Сырттай |
|
|
Кредит саны |
3 |
3 |
|
Курсы |
4 |
1 |
|
Семестр |
7 |
2 |
|
Емтихан |
7 |
2 |
|
Дәріс |
15 |
2 |
|
Практикалық (семинар) сабақ |
30 |
4 |
|
Зертханалық сабақ |
- |
- |
|
ОСӨЖ |
30 |
- |
|
СӨЖ |
60 |
129 |
Арқалық, 2015
Құрастырушы: аға оқытушы Абдрахманова М.Т
( A.Т. Ә.)
Математика және физика кафедрасы
Мамандығы : 5В010900 «Математика»
(Мамандықтың шифры, толық атауы)
Оқу нысаны (күндізгі сырттай жоғары кәсіби білім) (күндізгі, сырттай жоғары кәсіби білім)
ҚРМЖМБС Олимпиадалық есептерді шешу таңдау пәні бойынша үлгілік оқу бағдарламасы 27.08.2014.№1 хаттама
(ҚР МЖМБС, типтік бағдарламаның толық атауы, бекіткен күні және ұйым атауы, ОӘБ және пән индексі)
Кафедра мәжілісінде ұсынылды 20 __ ж. “___” _______№_____ хаттама
Кафедра меңгерушісі: ___________________Қожахмет М.С
(Қолы, Т. Е. Ә.)
20 __ ж. “____”_______ хаттама № ___ Факультеттің ғылыми әдістемелік кеңесінде қабылданды
ҒӘК төрайымы ________________________А.Қ.Тулегенова
(Қолы, Т. Е. Ә.)
КЕЛІСІЛДІ:
Жаратылыстану ақпараттандыру факультетінің деканы ______ Умбетов А.У.
(Қолы, Т. Е. Ә.)
Институттың ғылыми - әдістемелік кеңесінде мақұлданды:
20___ж. “___” _______ хаттама №
ОӘБ бастығы __________ А.С.Антаева
(Қолы.)
1.2. Пән туралы мәліметтер
Аталымы: «Олимпиадалық есептерді шешу»
Кредит саны: 3
Өткізу орны: 514 дәрісхана
Пәннің тақырыптық жоспары
|
№ |
Тақырыбы |
Оқу түрі |
|||||||||||||
|
Күндізгі |
Сырттай |
||||||||||||||
|
Барлығы |
Лекция |
Тәжірибе |
Зерт.жұмыс |
СӨЖ |
ОСӨЖ |
Барлығы |
Лекция |
Тәжірибе |
Зерт.жұмыс |
СӨЖ |
ОСӨЖ |
||||
|
1 |
І модуль.Элементар математика |
||||||||||||||
|
1.1 |
Элементар математика курсынан олимпиадалық есептерді шешу жолдары |
10 |
1 |
2 |
|
5 |
2 |
|
|
|
|
|
|
||
|
1.2 |
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары |
10 |
1 |
2 |
|
5 |
2 |
|
|
|
|
|
|
||
|
1.3 |
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
10 |
1 |
2 |
|
5 |
2 |
|
|
|
|
|
|
||
|
1.4 |
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары |
10 |
1 |
2 |
|
5 |
2 |
|
|
|
|
|
|
||
|
1.5 |
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары |
10 |
1 |
2 |
|
5 |
2 |
|
|
|
|
|
|
||
|
|
ІІ модуль. Жоғары математика |
||||||||||||||
|
2.2 |
Жоғары математика курсы бойынша олимпиадалық есептер |
16 |
2 |
4 |
|
6 |
4 |
|
|
|
|
|
|
||
|
2.3 |
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары |
16 |
2 |
4 |
|
6 |
4 |
|
|
|
|
|
|
||
|
2.4 |
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
16 |
2 |
4 |
|
6 |
4 |
|
|
|
|
|
|
||
|
2.5 |
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары |
16 |
2 |
4 |
|
6 |
4 |
|
|
|
|
|
|
||
|
2.5 |
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары |
16 |
2 |
4 |
|
6 |
4 |
|
|
|
|
|
|
||
|
|
Барлығы |
122 |
15 |
30 |
|
60 |
30 |
|
|
|
|
|
|
||
Пәнді оқытудың мақсаты мен міндеттері
Пәнді оқытудың мақсаты: құрылымы немесе оларды шығару әдістері бойынша стандартты емес, қиындығы жоғары деңгейдегі есептерді шығарудың әдіс-тәсілдері мен талдау негіздерін зерттеу.
Пәнді оқытудың міндеттері: Негiзгi меселелердi шешуге байланысты студенттер (болашақ мұғалiмдер) өз пәндерін терең меңгеруi, пәнге аса қызығушылығын тудыру;
-
есептер шығаруға қажетті білім, білік, дағдыны қалыптастыру;
-
есептер шығару барысында ойды түйіндеп пәрменділігін арттыруға қажетті әдістерді қолдана білу;
-
ойлау әрекетiне қажетгi теориялық, практикалық мәселелердi меңгеруі
-
курс бағдардамасы бойынша теориялық практикалық бiлiмдi толық меңгеруге тиiс
Пәннің құзіреттілігі:
Білуі тиіс:
-
Математикалық есептерді шығару үшін негізгі зерттеу әдістерін меңгеру;
-
теориялық және қолданбалы тапсырмаларды шешуге математикалық білімді қолдану;
Біліктілігі болуы тиіс:
-
Студенттердегі математикалық және алгоритмдік ойлауының дамуы;
Дағдылары болуы тиіс:
-
Жұмыс істеу барысында ғылыми, оқу – әдістемелік және анықтамалық әдебиеттерді қолдануда;
-
Өз бетінше өзіндік жұмыс, әзірлемелер әзірлеуде;
Дәріс сабақтарының мазмұны.
І модуль. Элементар математика
Дәріс – 5 сағат, практикалық сабақ – 10 сағат, сөж – 20 сағат.
1-дәріс тақырыбы: Элементар математика курсынан олимпиадалық есептерді шешу жолдары
Жоспар
-
Элементар математика курсынан олимпиадалық есептерді шешу жолдары
2-дәріс тақырыбы: Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары
Жоспар
1.Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары
3-дәріс тақырыбы: Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
Жоспары
1.Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
4-дәріс тақырыбы: Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары
Жоспары
1.Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары
5-дәріс тақырыбы Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары
Жоспары
1.Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары
ІІ модуль. Жоғары математика
Дәріс – 10 сағат, практикалық сабақ – 8 сағат, сөж – 20 сағат.
6-7 дәріс тақырыбы: Жоғары математика курсы бойынша олимпиадалық есептер
Жоспары
Жоғары математика курсы бойынша олимпиадалық есептер
8-9-дәріс тақырыбы: Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары
Жоспары
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары
10-11- дәріс тақырыбы: Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
Жоспары
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
12-13 дәріс тақырыбы: Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары
Жоспары
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары
14-15дәріс тақырыбы: Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары
Жоспары
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары
Студенттің өзіндік жұмысын тапсырмаларын орындау және тапсыру
|
№ |
СӨЖ тақырыптары |
Бақылау түрі |
Орындау мерзімі (апта) |
|
|
Күндізгі бөлім |
||
|
1 |
Элементар математика курсынан олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Слайд дайындау. |
1 апта |
|
2 |
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Типтік есептер |
2 апта |
|
3 |
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
3 апта |
|
4 |
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары |
Конспект. Ұғымдарды баяндау мен талдау. Типтік есептер |
4 апта |
|
5 |
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар Слайд дайындау. Бес жолды өлең құрастыру. |
5 апта |
|
6 |
Жоғары математика курсы бойынша олимпиадалық есептер |
Мәнжаэба. Оқулықпен жұмыс. Слайд дайындау. |
6-7 апта |
|
7 |
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Слайд дайындау. Типтік есептер |
8-9 |
|
8 |
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжаэба. Оқулықпен жұмыс. Пікірталас. Типтік есептер |
10-11 апта |
|
9 |
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары |
Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
12-13апта |
|
10 |
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Слайд дайындау. Типтік есептер |
14-15 апта |
СОӨЖ тапсырмаларын орындау жоспары
|
№ |
Тапсырма тақырыптары |
ОСӨЖ өткізу түрі
|
|
|
Күндізгі бөлім |
|
|
1 |
Элементар математика курсынан олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Слайд дайындау. |
|
2 |
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Типтік есептер |
|
3 |
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжаэба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
|
4 |
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары |
Конспект. Ұғымдарды баяндау мен талдау. Типтік есептер |
|
5 |
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
|
6 |
Жоғары математика курсы бойынша олимпиадалық есептер |
Мәнжазба, тірек сызбалар. Типтік есептер |
|
7 |
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары |
Оқулықпен жұмыс. Бақылау жұмысы №1. |
|
8 |
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
|
9 |
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Слайд дайындау. |
|
10 |
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар Слайд дайындау. Бес жолды өлең құрастыру. |
|
|
Сыртай бөлім |
|
|
|
|
|
Қазақстан Республикасы білім және ғылым министрлігі
Ы.Алтынсарин атындағы Арқалық мемлекеттік педагогикалық институты
“Бекітемін”
ОжДҚж проректоры
__________Б.Д.Искакова
2015 ж. “___” _________
Жаратылыстану және ақпараттандыру факультеті
Математика және физика кафедрасы
ПӘННІҢ ОҚУ БАҒДАРЛАМАСЫ- SYLLABUS
Пән: «Олимпиадалық есептерді шешу»
Мамандығы: 5В010900 – «Математика»
|
Оқу түрі |
||
|
Күндізгі |
Сырттай |
|
|
Кредит саны |
3 |
3 |
|
курсы |
4 |
1 |
|
Семестр |
7 |
2 |
|
Емтихан |
7 |
2 |
|
Дәріс |
15 |
2 |
|
Практикалық (семинар) сабақ |
30 |
4 |
|
Зертханалық сабақ |
|
- |
|
ОСӨЖ |
30 |
- |
|
СӨЖ |
60 |
129 |
Арқалық, 2015
Құрастырушы: аға оқытушы Абдрахманова М.Т
( A.Т. Ә.)
Математика және физика кафедрасы
Мамандығы : 5В010900 «Математика»
(Мамандықтың шифры, толық атауы)
Оқу нысаны (күндізгі сырттай жоғары кәсіби білім) (күндізгі, сырттай жоғары кәсіби білім)
(күндізгі, сырттай жоғары кәсіби білім)
ҚРМЖМБС Олимпиадалық есептерді шешу таңдау пәні бойынша үлгілік оқу бағдарламасы 27.08.2014.№1 хаттама
(ҚР МЖМБС, типтік бағдарламаның толық атауы, бекіткен күні және ұйым атауы, ОӘБ және пән индексі)
Кафедра мәжілісінде ұсынылды 2015 ж. “___” _______№_____ хаттама
Кафедра меңгерушісі: ___________________ Қожахмет М.С
(Қолы, Т. Е. Ә.)
2015 ж. “____”_______ хаттама № ___ Факультеттің ғылыми әдістемелік кеңесінде қабылданды
ҒӘК төрайымы __________________________ А.Қ.Тулегенова
(Қолы, Т. Е. Ә.)
КЕЛІСІЛДІ:
Жаратылыстану ақпараттандыру факультетінің деканы ______ Умбетов А.У.
(Қолы, Т. Е. Ә.)
Институттың ғылыми - әдістемелік кеңесінде мақұлданды:
2015 ж. “___” _______ хаттама №
ОӘБ бастығы __________ Антаева А.С
(Қолы.)
1. Оқытушы туралы мәліметтер
Абдрахманова М.Т Арқалық мемлекеттік педагогикалық институтының математика, физика кафедрасында 2009 жылдан жұмыс істейді. Арқалық мемлекеттік педагогикалық институтының аға оқытушысы. Мекен жайы: Арқалық қаласы, Ш.Жанібек көшесі, 83/1-7.
2 Байланыс телефоны: (871430)71954 Байланыс ақпараты және кафедраға келген уақыты.
3 Пән туралы мәліметтер
Аталымы: «Олимпиадалық есептерді шешу»
Кредит саны: 3
Өткізу орны:514 дәрісхана
|
Курс |
семестр |
Кредит саны |
Дәріс, сағат саны |
Практикалық сабақ |
СОӨЖ |
СӨЖ |
|
4 |
7 |
2 |
15 |
15 |
30 |
60 |
4.Пререквезиттері: элементар математика, математика курсына енгізу кіріспесі, алгебра курсы және сандар теориясы; математикалық талдаудың курсы;
5.Пәннің постреквизиттері: олимпиада есептерін шығару әдістемесі; білім жоғарылату.
6.Курстың саясаты мен реті бойынша оқытушы пәнді оқыту үрдісінде студентке төмендегідей жағдайда әкімшілік талаптар қоя алады:
-
Сабаққа кешікпеу;
-
Сабақты себепсіз жібермеу;
-
Аудиториядағы тәртібі;
-
Тапсырманы мерзімінде орындау;
7.Пәнді оқытудың мақсаты мен міндеттері
Пәнді оқытудың мақсаты: құрылымы немесе оларды шығару әдістері бойынша стандартты емес, қиындығы жоғары деңгейдегі есептерді шығарудың әдіс-тәсілдері мен талдау негіздерін зерттеу.
Пәнді оқытудың міндеттері: Негiзгi меселелердi шешуге байланысты студенттер (болашақ мұғалiмдер) өз пәндерін терең меңгеруi, пәнге аса қызығушылығын тудыру;
-
есептер шығаруға қажетті білім, білік, дағдыны қалыптастыру;
-
есептер шығару барысында ойды түйіндеп пәрменділігін арттыруға қажетті әдістерді қолдана білу;
-
ойлау әрекетiне қажетгi теориялық, практикалық мәселелердi меңгеруі
-
курс бағдардамасы бойынша теориялық практикалық бiлiмдi толық меңгеруге тиiс
Пәннің құзіреттілігі:
Білуі тиіс:
-
Математикалық есептерді шығару үшін негізгі зерттеу әдістерін меңгеру;
-
теориялық және қолданбалы тапсырмаларды шешуге математикалық білімді қолдану;
Біліктілігі болуы тиіс:
-
Студенттердегі математикалық және алгоритмдік ойлауының дамуы;
Дағдылары болуы тиіс:
-
Жұмыс істеу барысында ғылыми, оқу – әдістемелік және анықтамалық әдебиеттерді қолдануда;
-
Өз бетінше өзіндік жұмыс, әзірлемелер әзірлеуде;
9 Қысқаша сипаттама: пән туралы мәлімет
Элементар математика курсынан олимпиадалық есептерді шешу жолдары
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
Жоғары математика курсы бойынша олимпиадалық есептер
10.Семинар сабағының жоспары
1-2 практикалық сабақ тақырыбы: Элементар математика курсынан олимпиадалық есептерді шешу жолдары
3-4- практикалық сабақ тақырыбы: Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары
5-6 практикалық сабақ тақырыбы: Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
7-8- практикалық сабақ тақырыбы: Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары
9-10 практикалық сабақ тақырыбы: Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары
11-14 практикалық сабақ тақырыбы: Жоғары математика курсы бойынша олимпиадалық есептер
15-18 практикалық сабақ тақырыбы: Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары
19-22 практикалық сабақ тақырыбы: Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
24-26 практикалық сабақ тақырыбы: Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары
27-30 практикалық сабақ тақырыбы: Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары
11.Студенттің өзіндік жұмыс тапсырмаларын орындау және тапсыру
|
№ |
СӨЖ тақырыбы |
Бақылау түрі |
Орындау мерзімі |
|
|
Күндізгі бөлім |
||
|
1 |
Элементар математика курсынан олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Слайд дайындау. |
1 апта |
|
2 |
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Типтік есептер |
2 апта |
|
3 |
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
3 апта |
|
4 |
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары |
Конспект. Ұғымдарды баяндау мен талдау. Типтік есептер |
4 апта |
|
5 |
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар Слайд дайындау. Бес жолды өлең құрастыру. |
5 апта |
|
6 |
Жоғары математика курсы бойынша олимпиадалық есептер Жоспары |
Мәнжазба. Оқулықпен жұмыс. Слайд дайындау. |
6-7апта |
|
7 |
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Слайд дайындау. Типтік есептер |
8-9апта |
|
8 |
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Пікірталас. Типтік есептер |
10-11апта |
|
9 |
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары |
Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
12-13 апта |
|
10 |
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Слайд дайындау. Типтік есептер |
14-15 апта |
|
|
Сырттай |
||
|
1 |
Элементар математика курсынан олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Слайд дайындау. |
1 апта |
|
2 |
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Типтік есептер |
2 апта |
|
3 |
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжаэба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
3 апта |
|
4 |
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары |
Конспект. Ұғымдарды баяндау мен талдау. Типтік есептер |
4 апта |
|
5 |
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
5 апта |
|
6 |
Жоғары математика курсы бойынша олимпиадалық есептер Жоспары |
Мәнжазба, тірек сызбалар. Типтік есептер |
6 -7 апта |
|
7 |
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары |
Оқулықпен жұмыс. Бақылау жұмысы №1. |
8-9 апта |
|
8 |
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
10-11апта |
|
9 |
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Слайд дайындау. |
12-13 апта |
|
10 |
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар Слайд дайындау. Бес жолды өлең құрастыру. |
14-15 апта |
12.Оқытушымен студенттің өзіндік жұмыс (кеңес) тапсырмалары
|
№ |
Тапсырма тақырыптары |
ОСӨЖ өткізу түрі
|
|
|
Күндізгі оқу |
|
|
1 |
Элементар математика курсынан олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Слайд дайындау. |
|
2 |
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Типтік есептер |
|
3 |
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжаэба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
|
4 |
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары |
Конспект. Ұғымдарды баяндау мен талдау. Типтік есептер |
|
5 |
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
|
6 |
Жоғары математика курсы бойынша олимпиадалық есептер Жоспары |
Мәнжазба, тірек сызбалар. Типтік есептер |
|
7 |
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары |
Оқулықпен жұмыс. Бақылау жұмысы №1. |
|
8 |
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
|
9 |
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Слайд дайындау. |
|
10 |
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар Слайд дайындау. Бес жолды өлең құрастыру. |
|
11 |
Элементар математика курсынан олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
|
12 |
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Слайд дайындау. Типтік есептер |
|
13 |
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
|
14 |
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары |
Оқулықпен жұмыс. Бақылау жұмысы №2. |
|
15 |
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары |
Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
|
|
|
|
|
|
|
|
13. Емтихан кеңестері
|
№ |
Кеңес жүргізілетін жұмыс түрлері |
Кеңес беру күні |
Кеңес беру уақыты |
|
1 |
«Олимпиадалық есептерді шешу» |
|
|
14.Курстық жұмыстың тақырыбы, мәнжазба
Курстық жұмыс жоспарланбаған
Мәнжазба
-
Элементар математика курсынан олимпиадалық есептерді шешу жолдары
-
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары
-
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
-
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары
-
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары
-
Жоғары математика курсы бойынша олимпиадалық есептер
-
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары
-
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
-
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары
-
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары олимпиадалық есептерді шешу жолдары
15. Студенттердің білімін бағалау жүйесі
Студенттердің оқу жетістіктері (білім, білік, дағды және құзіреттілігі) ҚР білім және ғылым министрлігінің 2011 жылғы 20-сәуірдегі №152 бұйрығымен бекітілген Кредиттік оқыту технологиясы бойынша оқу үдерісін ұйымдастырудың ережесіне сәйкес 100 балдық шкаламен бағаланады.
Ағымдағы бақылау (1-7 және 8-15 апталарда өткізіледі):
1. Сабаққа қатысу
2. Практикалық (зертханалық) сабақтағы тапсырмаларды орындау
3. Үй тапсырмасын орындау
4. СӨЖ бойынша тапсырмаларды орындау
Сабаққа қатысуына байланысты 1 баллдан беріледі (барлығы- Х) ең жоғарғы балл -100. Практикалық (зертханалық) сабақтағы активтілігі, тапсырмаларды орындауына байланысты практикалық (зертханалық) сабаққа 100 балл. Үй тапсырмасын орындау денгейіне байланысты максималды 100 балл беріледі. Үй тапсырмасының көлемін оқытушы анықтайды. СӨЖ бойынша тапсырмаларды орындау балдары кестедегі тақырыптар бойынша 100 балмен бағалайды, орташа көрсеткіші СӨЖ тапсырмалардын орындаудын пайыздық корсеткіші болып табылады.
Аралық бақылау ( 7, 15 апталарда өткізіледі):
Тест (билет, коллоквиум, мамандыққа байланысты нормативтық тапсырмалар т.б.) сұрақтары бойынша жауап алу арқылы білімі тексеріліп, жоғары жауапқа 100 балл беріледі.
Рорташа = (Р1 + Р2) / 2
(Р1 – 1 аралық бақылаудағы рейтингі, Р2 – 2 аралық бақылаудағы рейтингі).
Қорытынды
бақылау семестрдің соңында алынады
(Емтихан түрін көрсету) . Қорытынды бақылау мына формула бойынша
есептелінеді: ![]()
Қорытынды баға төмендегі кестеге сәйкес қойылады:
|
Әріп жүйесі бойынша |
Балдың сандық эквивалент |
Проценттік мазмұны |
Дәстүрлі жүйе бойынша бағалау |
|
А |
4,0 |
95-100 |
өте жақсы |
|
А- |
3,67 |
90-94 |
|
|
В+ |
3,33 |
85-89 |
Жақсы |
|
В |
3 |
80-84 |
|
|
В- |
2,67 |
75-79 |
|
|
С+ |
2,33 |
70-74 |
қанағаттанарлық |
|
С |
2,0 |
65-69 |
|
|
С- |
1,67 |
60-64 |
|
|
D+ |
1,33 |
55-59 |
|
|
D |
1,0 |
50-54 |
|
|
F |
0 |
0-49 |
қанағаттанғысыз |
16. Әдебиеттер тізімі
-
Негізгі әдебиеттер тізімі
-
Математические олимпиады школьников: Книга для учащихся общеобразоват. учреждений Н.Х.Агаханов. Л.П.Купцов, Ю.В.Нестеренко и др. М.: Просвещение: Уч.лит., 1997-208 с.
-
Математические олимпиады школьников: Кн.для учащихся общеобразовать. учреждений Л.П.Купцов, Ю.В.Нестеренко, С.В.Резниченко, А.М.Слинько.- М.: Просвещение, 1998. - 256 с.
-
Математические олимпиады школьников: Кн.для учащихся общеобразовать. учреждений Л.П.Купцов, Ю.В.Нестеренко, С.В.Резниченко, А.М.Слинько.- М.: Просвещение, 1999. - 254 с.
-
Сборник индивидуальных заданий по высшей математике. Часть 1. Под ред. Рябушко А.П.-Мн: Вышейшая школа., 2001.
-
Сборник индивидуальных заданий по высшей математике. Часть 2. Под ред. Рябушко А.П.- Мн: Вышейшая школа., 2001..
-
Сборник индивидуальных заданий по высшей математике. Часть 3. Под ред. Рябушко А.П.- Мн: Вышейшая школа., 2001.
-
Сборник индивидуальных заданий по высшей математике. Часть 4. Под ред. Рябушко А.П.-Мн : Вышейшая школа., 2005.
-
Қосымша әдебиеттер тізімі
1. Ильясов М.Н. Нестандартные задачи математического анализа. Учебно-методическое пособие. Павлодар, 2006.
2. Степаненко В.М. Руководство к решению задач повышенной трудности по высшей математике. Павлодар, 2003.
3.Садовничий В.А., Григорьян А.А., Конягин С.В Задачи студенческих математических олимпиад,. МГУ, 1987.
17. Емтихан сұрақтары
І аралық бақылау сұрақтары
-
Рационал өрнектерді түрлендіру.
-
Көпмүшені көбейткіштерге жіктеу;
-
Ортақ көбейткішті жақша сыртына шығару,
-
Топтау тәсілі,
-
Қысқаша көбейту формулалары,
-
Квадрат үшмүшені жіктеу,
-
Жаңа айнымалы ендіру
-
Жасанды тәсілдер.
-
Бүтін санның бөлінгіштігіне берілген есептер.
-
Көпмүшені қалдықпен бөлу.
-
p(x)=(x-a)q(x) формуласы, а - көпмүшенің түбірі.
-
Рационал өрнектерді түрлендіру,
-
Модуль таңбалы өрнектерді түрлендіру.
-
Жай бөлшектер.
-
Рационал бөлшектерді жай бөлшектер қосындысына түрлендіру.
-
Қосындылаудың әртүрлі тәсілдері.
-
Математикалық индуксия әдісі.
-
Қосындылау және бөлінгіштік жөніндегі есептерге индукция әдісін қолдану;
-
Иррационал өрнектерді түрлендіру.
-
Түбір ұғымы
-
Арифметикалық түбір.
-
Қасиеттері
-
Радикалдардың қасиеті.
-
Радикалдардың формуласы.
-
Рационал көрсеткішті дәреже
-
Рационал көрсеткішті дәреженің қасиеттері.
-
Иррационал өрнектерді түрлендіру.
-
Бөлшектің бөлімін иррационалдықтан құтқару;
-
Тригонометриялық өрнектерді түрлендіру.
-
Кері тригонометриялық өрнектерді түрлендіру.
-
Тригонометрияның формулалары.
-
Тиргонометриялық теңбе-теңдіктерді дәлелдеу,
-
Тригонометриялық өрнектерді түрлендіру,
-
Көмекші аргумент ендіру әдісі.
-
Универсал ауыстыру.
-
Басқа аргументті тригонометриялық функцияның мәнін іздеу.
-
Тригонометриялық өрнектің сандық мәнін табу.
-
Өлшенген координаталарды функцияның графигін салу.
-
Жоғары дәрежелі теңдеулер.
-
Алгебралық теңсіздіктер.
-
Рационал теңсіздіктерді интервалдар әдісімен шешу.
-
Теңсіздіктер жүйесі және жиынтығы.
-
Модульмен берілген теңсіздіктер.
-
Иррационал теңсіздіктер.
-
Теңсіздіктер құруға берілген есептер.
-
Параметрлі теңдеулер мен теңсіздіктер;
-
Трансцендентті теңдеулер мен теңсіздіктер.
-
Көрсеткіштік, логарифмдік теңдеулер мен теңсіздіктер,
-
Оларды шешудің негізгі әдістері.
-
Көрсеткішті теңдеулер
-
Көрсеткішті теңсіздіктер.
-
Логарифмдік теңдеулер
-
Логарифмдік теңсіздіктер.
-
Көрсеткішті дәрежелі теңдеулер мен теңсіздіктер.
-
Көрсеткіштік теңдеулердің жүйесі.
-
Логарифмдік теңдеулердің жүйесі.
-
Тригонометриялық теңдеулер.
-
Көбейткіштерге жіктеу,
-
Жаңа айнымалы ендіру сиақты шешудің негізгі екі әдісі.
-
Біртектес теңдеулер және оған келтірілетін теңдеулер.
-
Тригонометриялық теңдеулерді шешу үшін универсал ауыстыруды қолдану.
-
Тригонометриялық теңдеулерді шешудің жасанды тәсілдері.
-
Берілген щартқа сай түбірді таңдау.
-
Тригонометриялық теңдеулер жүйесі.
-
Тригонометриялық теңсіздіктер.
ІІ аралық бақылау сұрақтары
-
Матрица түрлері.
-
Матрицаларға қолданылатын сызықтық амалдар.
-
Матрицаларды көбейту.
-
Анықтауыштың негізгі қасиеттері.
-
Лаплас теоремасы.
-
Кері матрица.
-
Матрицаның рангісі.
-
Матрицаның элементарлық түрлендірулері.
-
Матрицаның экономикалық түсініктемесі.
-
Теңдеулер жүйелерінің үйлесімділігі.
-
Крамер ережесі.
-
Матрицалық теңдеулер жүйесін шешу.
-
Гаусс әдісі.
-
Біртекті сызықтық теңдеулер жүйесі.
-
Іргелес шешімдер жүйесі.
-
Сызықтық теңсіздіктер жүйесін және оның шешімін зерттеу.
-
Сызықтық теңсіздіктер жүйесінің экономикалық түсініктемесі
-
Векторларға қолдалынатын сызықтық амалдар.
-
Векторлардың скалярлық көбейтіндісі және оның қасиеттері.
-
Евклидтік кеңістік.
-
Векторлар жүйесінің базисі, рангісі.
-
Векторларды экономикалық есептерде қолдану.
-
Сызықтық операторлардың меншікті векторлары мен меншікті сандары. Квадратты формалары.
-
Функциалардың берілу тәсілдері.
-
Негізгі элементар функциалар.
-
Сандық тізбектер және шегі.
-
Функция шегі, біржақты шектер.
-
Элементар функциалар туындылары.
-
Күрделі, кері және айқындалған функциялар туындысы.
-
Жоғары ретті туындылар.
-
Кездейсоқ оқиғалар түрлері.
-
Тәуелді және тәуелсіз оқиғалар.Ықтималдық.
-
Шартты ықтималдықтар.
-
Ықтималдықтарды қосу және көбейту теоремалары.
-
Бернулли схемасы және оның формуласы.
-
Ең ықтимал сан.
-
Лапластың локалдық және интегралдық теоремалары.
-
Дискретті және үзіліссіз кездейсоқ шамалар.
-
Үлестірім функциясы және үлестірім тығыздығы.
-
Кездейсоқ шамалардың сандық сипаттамалары.
-
Тәуелсіз сынақтарда салыстырмалы жиліктің оқиғаның тұрақты ықтималдығының ауытқуының ықтималдығы.
-
Биномдық, Пуассон.
-
Үлестірім заңдарының сандық сипаттамалары.
-
Негізгі ұғымдар.
-
Тексерудің жалпы схемасы.
-
Қалыпты үлестіріммен берілген бас дисперсияларын салыстыру.
-
Бір факторлы дисперсиялық талдау.
-
Екі факторлық дисперсиялық талдау түсінігі.
-
Негізгі ұғымдар.
-
Сызықтық регрессия теңдеулер.
Қорытынды бақылауға дайындық сұрақтары (емтихан).
-
Матрица түрлері.
-
Матрицаларға қолданылатын сызықтық амалдар.
-
Матрицаларды көбейту.
-
Анықтауыштың негізгі қасиеттері.
-
Лаплас теоремасы.
-
Кері матрица.
-
Матрицаның рангісі.
-
Матрицаның элементарлық түрлендірулері.
-
Матрицаның экономикалық түсініктемесі.
-
Теңдеулер жүйелерінің үйлесімділігі.
-
Крамер ережесі.
-
Матрицалық теңдеулер жүйесін шешу.
-
Гаусс әдісі.
-
Біртекті сызықтық теңдеулер жүйесі.
-
Іргелес шешімдер жүйесі.
-
Сызықтық теңсіздіктер жүйесін және оның шешімін зерттеу.
-
Сызықтық теңсіздіктер жүйесінің экономикалық түсініктемесі
-
Векторларға қолдалынатын сызықтық амалдар.
-
Векторлардың скалярлық көбейтіндісі және оның қасиеттері.
-
Евклидтік кеңістік.
-
Векторлар жүйесінің базисі, рангісі.
-
Векторларды экономикалық есептерде қолдану.
-
Сызықтық операторлардың меншікті векторлары мен меншікті сандары. Квадратты формалары.
-
Функциалардың берілу тәсілдері.
-
Негізгі элементар функциалар.
-
Сандық тізбектер және шегі.
-
Функция шегі, біржақты шектер.
-
Элементар функциалар туындылары.
-
Күрделі, кері және айқындалған функциялар туындысы.
-
Жоғары ретті туындылар.
-
Кездейсоқ оқиғалар түрлері.
-
Тәуелді және тәуелсіз оқиғалар.Ықтималдық.
-
Шартты ықтималдықтар.
-
Ықтималдықтарды қосу және көбейту теоремалары.
-
Бернулли схемасы және оның формуласы.
-
Ең ықтимал сан.
-
Лапластың локалдық және интегралдық теоремалары.
-
Дискретті және үзіліссіз кездейсоқ шамалар.
-
үлестірім функциясы және үлестірім тығыздығы
-
Кездейсоқ шамалардың сандық сипаттамалары.
-
Тәуелсіз сынақтарда салыстырмалы жиліктің оқиғаның тұрақты ықтималдығының ауытқуының ықтималдығы.
-
Биномдық, Пуассон.
-
Үлестірім заңдарының сандық сипаттамалары.
-
Негізгі ұғымдар.
-
Тексерудің жалпы схемасы.
-
Қалыпты үлестіріммен берілген бас дисперсияларын салыстыру.
-
Бір факторлы дисперсиялық талдау.
-
Екі факторлық дисперсиялық талдау түсінігі.
-
Негізгі ұғымдар.
-
Сызықтық регрессия теңдеулер.
-
Байланыс параметрлнрінің маңыздылығын тексеру.
2. ПӘННІҢ ОҚУ-ӘДІСТЕМЕЛІК КЕШЕННІҢ МАЗМҰНЫ МЕН ТІЗБЕСІ
2.1. Пән бойынша тапсырмалардың тапсыруы және кестенің орындалуы (сабақ кестесінен тыс )
|
№ |
Тақырыбы |
СОӨЖ өткізу түрлері |
Тапсырманы орындау уақыты |
|
Күндізгі бөлім |
|||
|
1 |
Элементар математика курсынан олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Слайд дайындау. |
1 апта |
|
2 |
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Типтік есептер |
2 апта |
|
3 |
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжаэба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
3 апта |
|
4 |
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары |
Конспект. Ұғымдарды баяндау мен талдау. Типтік есептер |
4 апта |
|
5 |
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
5 апта |
|
6 |
Жоғары математика курсы бойынша олимпиадалық есептер Жоспары |
Мәнжазба, тірек сызбалар. Типтік есептер |
6 -7 апта |
|
7 |
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары |
Оқулықпен жұмыс. Бақылау жұмысы №1. |
8-9 апта |
|
8 |
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
10-11апта |
|
9 |
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Слайд дайындау. |
12-13 апта |
|
10 |
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар Слайд дайындау. Бес жолды өлең құрастыру. |
14-15 апта |
|
Сырттай бөлім |
|||
|
1 |
Элементар математика курсынан олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Слайд дайындау. |
1 апта |
|
2 |
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Типтік есептер |
2 апта |
|
3 |
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжаэба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
3 апта |
|
4 |
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары |
Конспект. Ұғымдарды баяндау мен талдау. Типтік есептер |
4 апта |
|
5 |
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
5 апта |
|
6 |
Жоғары математика курсы бойынша олимпиадалық есептер Жоспары |
Мәнжазба, тірек сызбалар. Типтік есептер |
6 -7 апта |
|
7 |
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары |
Оқулықпен жұмыс. Бақылау жұмысы №1. |
8-9 апта |
|
8 |
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
10-11апта |
|
9 |
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Слайд дайындау. |
12-13 апта |
|
10 |
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар Слайд дайындау. Бес жолды өлең құрастыру. |
14-15 апта |
-
2.2. Пәннің оқу- әдістемелік картасымен қамтамасыз етілуі
|
№ |
Дәріс тақырыбы |
Қолданылатын әдебиеттер |
Кинофильмдер, диафильмдер |
плакаттар |
слайд |
Электронды оқулық |
|
1 |
Элементар математика курсынан олимпиадалық есептерді шешу жолдары |
Н.ә [1-9] Қ.ә [1-6] |
|
|
+ |
+ |
|
2 |
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары |
Н.ә [1-9] Қ.ә [1-6] |
|
|
+ |
+ |
|
3 |
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Н.ә [1-9] Қ.ә [1-6] |
|
|
+ |
|
|
4 |
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары |
Ұсынылған әдебиет |
|
|
+ |
|
|
5 |
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары |
Ұсынылған әдебиет |
|
|
+ |
|
|
6 |
Жоғары математика курсы бойынша олимпиадалық есептер Жоспары |
Ұсынылған әдебиет |
|
|
+ |
|
|
7 |
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары |
Ұсынылған әдебиет |
|
|
+ |
|
|
8 |
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Ұсынылған әдебиет |
|
|
+ |
|
|
9 |
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары |
Ұсынылған әдебиет |
|
|
+ |
|
|
10 |
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары олимпиадалық есептерді шешу жолдары |
Ұсынылған әдебиет |
|
|
+ |
|
2.3 Дәрістердің тезистері
1-дәріс тақырыбы: Элементар математика курсынан олимпиадалық есептерді шешу жолдары
Математикалық олимпиада - дайындығы неғұрлым жоғары, қабiлеттi оқушылармен жүргізілетін зияткерлiк жарыс.
Есеп шығару − оқушы үшін ерекше іс-әрекет, дәлірек айтсақ - ой жұмысы. Оның негізгі міндеттері: оқыту, тәрбиелеу, дамыту және бақылау болып табылады. Есеп деп қандай да болмасын математикалық ұғымды, мазмұны жағынан терең тапсырманы түсінеміз. Есеп оқушылардың логикалық ойлау, кеңістікті елестету, жеке бас қабілеттерін дамытуға бірден-бір себепші болатын басты құрал.
Олимпиадалық есеп термині есепті классификациялау нәтижесінде емес, олимпиадалық жұмыстың мәтінін құру үшін есептің ерекше түрлерін қолдану практикасы нәтижесінде пайда болған.
Математикада олимпиадалық есеп деп құрылымы немесе оларды шығару әдістері бойынша стандартты емес, қиындығы жоғары деңгейдегі есептерді түсінеді.
Мектеп оқушылары олимпиадаларының негізгі мақсаты осы облыста барлық қатысушылардың ішінен қабiлеттi, талантты және дарындыларды анықтаудан тұрады.
Негiзiнен, олимпиадалық тапсырмалар творчестволық сипатымен ерекшеленеді. Олимпиадалық есептердiң басты ерекшелігі оның тұжырымы мен шығару жолы мектеп бағдарламасы шеңберінен шықпайтыны және бұл есептерді шығару әдістері оқушыларды біртіндеп жоғары математиканың ұғымдары мен әдістеріне бейімдейтіндігінде.
Олимпиаданың ең басты құндылығы жеңімпаздарды анықтаудан ғана емес, оқушылардың математикалық мәдениеті, интеллектуалды деңгейінің жоғарылауын бағалаудан тұрады. Сондықтан осы мәдениет пен интеллектуалды деңгейді көтеру үшін оқушыларды математикалық олимпиадаға дайындау қажет. «Білім – инемен құдық қазғандай», сондықтан ұстаз - оқушыны жан - жақты дайындайтын тұлға болғандықтан, ол оқушының білім деңгейіне тереңірек үңіледі.
Олимпиадаға қатысу оқушының интеллектуалды потенциалының ашылуына мүмкiндiк туғызады, ал нәтиже көрсеткіштері оқушының өзіндік сана сезiмiн нығайтады. Олимпиадаға дайындауға мұғалім өте үлкен үлес қосады.
1.![]() өрнегінің
толық квадратқа айналдыратын
өрнегінің
толық квадратқа айналдыратын ![]() -тің ең
үлкен бүтін мәнін табыңыз.
-тің ең
үлкен бүтін мәнін табыңыз.
![]() болсын деп
алайық.
болсын деп
алайық.
![]() мұндағы,
мұндағы,![]() Себебі,
Себебі,
![]()
Демек,
![]()
Бұдан,
![]() болу керектігі шығады.
Онда
болу керектігі шығады.
Онда ![]() Яғни,
Яғни,![]() - бұл
- бұл
![]() болғанда алынған өрнектің
толық квадрат болатынын көрсетеді. Егер
болғанда алынған өрнектің
толық квадрат болатынын көрсетеді. Егер ![]() онда
онда ![]() . Бұл
жағдайда,
. Бұл
жағдайда,
![]()
Себебі,
![]() Демек,
Демек,
![]() өрнегі қатар тұрған екі санның
квадраттарының арасында қалады. Сол себепті бұл өрнек және онымен
бірге
өрнегі қатар тұрған екі санның
квадраттарының арасында қалады. Сол себепті бұл өрнек және онымен
бірге ![]() өрнегі
толық квадрат бола алмайды.
өрнегі
толық квадрат бола алмайды.
2.Теңдеулер жүйесін шешіңдер.

Мұндағы,
![]() -берілген
сандар.
-берілген
сандар.
Теңдеулер жүйесіндегі түбірлерден мынандай мәселелермен туындайды.
![]() және
және![]() немесе
немесе![]() және
және![]() ,
болғандықтан,
,
болғандықтан, ![]() .
Яғни,
.
Яғни,![]() .
.
Жүйедегі теңдеулерді қосалық
![]()
Ортақ көбейткіштерді жақша алдына шығаралық.
![]()
Келесі кезекте, жүйедегі
теңдеулерді азайтып, ![]() теңдеуін
аламыз.
теңдеуін
аламыз.
Жүйе теңдеулерін қосу және азайту арқылы пайда болған теңдеулерді бір жүйеге біріктірейік.
![]()
Пайда болған жүйедегі теңдеулерді көбейту арқылы келесі теңдеуді аламыз.
![]()
Демек,
![]()
Мұндағы,
![]() болғандықтан берілген
теңдеулер жүйесі шешілу үшін
болғандықтан берілген
теңдеулер жүйесі шешілу үшін ![]() теңсіздігінің орындалуы қажетті. Ал, бұл шарт орындалса,
онда
теңсіздігінің орындалуы қажетті. Ал, бұл шарт орындалса,
онда![]() және осы ұйғарымды пайдалансаң
берілген теңдеулер жүйесі мынандай түрге
келеді.
және осы ұйғарымды пайдалансаң
берілген теңдеулер жүйесі мынандай түрге
келеді.
![]()
Сызықты теңдеулер
жүйесін ![]() және
және ![]() қатысты
шешелік.
қатысты
шешелік.

3.![]() теңдеуін
қанағаттандыратын
теңдеуін
қанағаттандыратын ![]() натурал
сандарын табыңдар.
натурал
сандарын табыңдар.
Теңдеудің сол жағын түрлендірейік.
![]()
Теңдеудің екі жағын да 64-ке көбейтелік.
![]()
Бұдан,
![]() теңсіздігі
шығады.
теңсіздігі
шығады.
![]() (Теңсіздіктің оң жағындағы
3-ті 4-пен ауыстырдық. Сол себепті артық таңбасы, артық немесе тең
таңбасымен ауыстырылды).
(Теңсіздіктің оң жағындағы
3-ті 4-пен ауыстырдық. Сол себепті артық таңбасы, артық немесе тең
таңбасымен ауыстырылды).
Демек,
![]() және
және ![]() яғни,
яғни,
![]()
Берілген теңдеудің екі жағын да 4-ке көбейтелік.
![]()
Демек,
![]()
![]()
![]()
Яғни,
![]() және
және ![]() Олай болса,
Олай болса,
![]() жағдайларын қарастыру
керек.
жағдайларын қарастыру
керек.
а) ![]()
ә) ![]()
б) ![]() Демек,
Демек,
![]()
2-дәріс тақырыбы: Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары
Қазақстан республикасының білім беру стандартында білім берудің басты міндеті логикалық ойлауды дамыту болып табылатындығы атап айтылған.
Қазіргі кезде ғылым мен техниканың даму деңгейі әрбір адамға сапалы және терең білімнің, іскерліктің болуын қамтиды.Оқушының белсенді шығармашылықпен жұмыс істеуін және кеңінен ойлауға қабілетті болуын талап етеді. Сондықтан да мектептегі оқу процесінің негізгі мақсаты арнайы педагогикалық әдістермен мақсатты және жүйелі түрде оқушылардың интеллектік, шығармашылық ойлауын дамыту, ғылыми көзқарасы мен белсенділігін қалыптастыру. Әр адамның бойындағы туғаннан пайда болған интуициясын әрі қарай дамытуға ықпал ету, оқушының табиғи қасиеттерін, математикалық білімін тереңдету үшін оқытуды жоспарлы түрде ұйымдастыру, өз бетінше білім алу дағдыларының дамуына негізін салу болып табылады. Сабақта оқытудың педагогикалық технологияларын тиімді қолдана білу. Оқушының логикалық ойлауын және таным белсенділігін қалыптастыру барысында шығармашылық ізденістің тиімді жолдарын үйрету, білім сапасын көтеру.
Логика – (грек тілінен алынған logic - сөз, ой,ойлау, ақыл-ой) ойлаудың заңдылықтары мен түрлері туралы ғылым. Объективті пікірлерге негізделген процесс логикалық ойлау деп, ал дұрыс ойлаудың формалары мен заңдары туралы ғылым логика деп аталады. Логикалық ойлаудың қисындылығы олардың шындыққа сай келуінде. Логикалық тұжырым теориясының ең алғаш грек философы Аристотель негізін қалаған. Ой әрекеті барысында адам қоршаған дүниені танып, білу үшін ерекше ақын қызметін орындайды. Бұл нақты қызметіне талдау, біріктіру, салыстыру, дерексіздендіру нақтылау және қорытындылау арқылы жүзеге асырылады.
1. Теңдеулер жүйесін бүтін шешімдерін табыңдар.
![]()
Жүйедегі әр теңдеудің екі жағын квадраттайық.
![]()
Алдымен екінші теңдеудің екі жағын да 2-ге көбейтелік, одан екі теңдеуді мүшелеп қосайық.

Бұл жағдайда
![]() немесе
немесе
![]()
а) ![]() Олай болса
Олай болса
![]()
ә) ![]()
Олай болса,
![]()
Жауабы: (1;0;3;1), (-1;0;-3;-1), (3;1;1;0), (-3;-1;-1;0)
2.![]() болғанда
болғанда
![]() өрнегінің мәні
1,
өрнегінің мәні
1, ![]() болғанда 2 тең
болатындай
болғанда 2 тең
болатындай ![]() бүтін
сандары табылмайтынын дәлелдеңдер.
бүтін
сандары табылмайтынын дәлелдеңдер.
Тапсырма шарты бойынша
![]()
![]() теңдіктері ақиқат. Мұндағы,
екінші теңдіктен бірінші теңдікті
азайтайық.
теңдіктері ақиқат. Мұндағы,
екінші теңдіктен бірінші теңдікті
азайтайық.
![]() теңдіктің сол жағынада ортақ
көбейткішті жақша алдына шығаралық.
теңдіктің сол жағынада ортақ
көбейткішті жақша алдына шығаралық. ![]() яғни,
яғни,
![]() .
.
Демек, теңдіктің сол жағында
43-ке бөлінетін бүтін сан, ал оң жағында 1 бар. Бұлай болу мүмкін
емес. Сондықтан, жоғарыдағы шартты қанағаттандыратын
![]() бүтін сандары
табылмайды.
бүтін сандары
табылмайды.
3.Теңдеулер жүйесін шешіңіздер:
![]()
Екінші теңдеуді 2-ге көбейтелік те бірінші теңдеуге қосайық. Сонда,
![]() теңдеуі
шығады.
теңдеуі
шығады.

а) ![]()

Демек,
![]()


![]()
Бірінші жағдай
үшін ![]() және
және ![]()
Тексеру.
![]()
![]()
Сол сияқты екінші түбір де
теңдеулер жүйесін қанағаттандырады. Демек, шешім
![]() және
және![]()
ә) ![]()

Демек,
![]()
Бұл мүмкін емес. Яғни, екінші жағдайда теңдеудің шешімі жоқ.
3-дәріс тақырыбы: Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
Математиканы оқыту – математикалық теория және математикалық ойлау іс-әрекетіне үйрету болып табылады.
Математиканы оқыту арқылы мәселені талдай білуге, нақтылауға, ұғымдарды анықтауға, ой қорытулар жасауға, дәлелдеуге тағы басқа іс – жүзінде қадам сайын логикалық білім беріледі.
ҰБТ есептерінде геометрия есептері қиындық келтіреді. Ол үшін есеп шартын толық және түсінікті етіп оқу керек. Сонымен бірге оның сызбасын да дұрыс сыза білуіміз керек. Сызбаның дұрыс сызылуы біздің есебіміздің дұрыс, әрі тез шығуына көп көмегін тигізеді.
Есепті қалай шығару керек.
Есептің шартын мұқият түсіну қажет.
-
Кейін не берілгенін, нені табу керектігін қысқаша жазу керек
-
Есеп сұрағына жауап беру үшін нені білу керектігін ойлап, жоспар құру.
-
Егер жоспар құру қиын болса, есеп шартын тағы да оқып шығып, бөліктерге бөлу.
-
Әрбір заттың атауын формуламен алмастыру.
-
Есепте берілген шамалардың байланысын анықтау.
-
Есеп шартынан туындайтын қорытындыны жазу.
-
Бұрын осыған ұқсас есеп шығарылған жоқ па, соны дәптерінен, кітаптан қарау.
-
Есепті шығарып болған соң, тексер, шығару жолының басқаша түрі бар ма, ойлану.
Геометриялық есептерді тригонометриялық тәсілдер арқылы шешу жолдарына бірнеше мысалдарға қарастырайық.
1-мысал.Тең бүйірлі тік бұрышты ABC үшбұрышы берілген. С тік бұрышының төбесінен BD медианасына перпендикуляр жүргізілген түзу гипотенузаны М нүктесінде қияды. Гипотенузаның кесінділерінің ұзындықтарының қатынасын табу керек.
Осы берілген мысалды бірнеше тәсілмен шығарылу жолын қарастырайық.
Енді осы тәсілдерде қолданылатын көмекші ұйғарымдарды келтірейік.
1. Биіктіктері бірдей екі үшбұрыштың аудандарының қатынасы олардың табандарының ұзындықтарының қатынасына тең болады.
2. Егер тік бұрышты
үшбұрыштың катеттерінің қатынасы ![]() болса, онда үшбұрыштың
гипотенузаға түсірілген биіктігі гипотенузаны
болса, онда үшбұрыштың
гипотенузаға түсірілген биіктігі гипотенузаны ![]() қатынасында
бөледі.
қатынасында
бөледі.
3. Кесіндіні
берілген ![]() қатынасында бөлудің
координаталық формулалары мынадай:
қатынасында бөлудің
координаталық формулалары мынадай: ![]()
![]()
4. Егер түзу
![]() осьтерінен сәйкес ұзындықтары
осьтерінен сәйкес ұзындықтары
![]() болатын кесінділерді
қиса, онда бұл түзудің теңдеуі мынадай болады:
болатын кесінділерді
қиса, онда бұл түзудің теңдеуі мынадай болады: ![]()
5. Егер екі вектор
өздерінің координаталарымен берілсе: ![]() онда бұл векторлардың
перпендикуляр болуының қажетті және жеткілікті шарты мынадай:
онда бұл векторлардың
перпендикуляр болуының қажетті және жеткілікті шарты мынадай:
![]()
6. Менелай
теоремасы. Егер ![]() нүктелері
нүктелері ![]() үшбұрышының сәйкес
үшбұрышының сәйкес ![]() қабырғаларындағы (немесе
олардың созындыларындағы) нүктелер болса, онда бұл нүктелердің бір
түзуге тиісті болуының қажетті және жеткілікті шарты мынадай:
қабырғаларындағы (немесе
олардың созындыларындағы) нүктелер болса, онда бұл нүктелердің бір
түзуге тиісті болуының қажетті және жеткілікті шарты мынадай:
![]()
7. Координаталар
басы арқылы өтетін және бұрыштық коэффициенті ![]() болып келетін түзудің теңдеуі
мынадай болады:
болып келетін түзудің теңдеуі
мынадай болады: ![]()
8. Диагональдары
өзара перпендикуляр болып келетін төртбұрыш үшін мынадай теңдік
орындалады: ![]()
Түсінуге, қолдануға жеңіл болу үшін, есептің шешулерінің 25 тәсілі жеті топқа бөлінді.
І-топ:
Векторлық-координаталық тәсілдермен шығарылу жолын қарастырамыз.
1-тәсіл. Нүктелердің
координаталары төмендегідей болатындай тік бұрышты координаталар
жүйесін енгізейік: ![]()

![]() бұрышы доғал болғандықтан
бұрышы доғал болғандықтан
![]() Осы сияқты
Осы сияқты ![]() екенін ескеріп жазамыз:
екенін ескеріп жазамыз:
![]()
Енді төртінші және жетінші
көмекші ұйғарымдарды қолданып ![]() түзулерінің теңдеулерін
жазайық:
түзулерінің теңдеулерін
жазайық: ![]() Бұл екі
теңдеуді жүйе ретінде қарастырып нүктесінің координаталарын
табамыз:
Бұл екі
теңдеуді жүйе ретінде қарастырып нүктесінің координаталарын
табамыз: ![]() Енді кесінділердің
пропорционалдығына сүйеніп ізделінді қатынасты табуға болады:
Енді кесінділердің
пропорционалдығына сүйеніп ізделінді қатынасты табуға болады:
![]()
2-тәсіл. Белгілеулер енгізейік
![]()
![]()
![]() векторын екі тәсілмен
өрнектейік:
векторын екі тәсілмен
өрнектейік:
![]() немесе
немесе ![]() Осыдан
Осыдан ![]() Онда
Онда![]()
![]() Есептің шарты бойынша
Есептің шарты бойынша
![]() немесе
немесе ![]() Соңғы теңдіктен
Соңғы теңдіктен ![]() ескеріп табамыз
ескеріп табамыз
![]()
3-тәсіл. ![]() болатындай тік бұрышты
координаталар жүйесін енгізейік (2.2-суретіне сәйкес). Төртінші
көмекші ұйғарымға сүйеніп
болатындай тік бұрышты
координаталар жүйесін енгізейік (2.2-суретіне сәйкес). Төртінші
көмекші ұйғарымға сүйеніп![]() түзуінің теңдеуін жазайық:
түзуінің теңдеуін жазайық:
![]()

![]() нүктесі
нүктесі ![]() түзуіне тиісті
болғандықтан оның координаталарын мынадай түрде жазуға болады:
түзуіне тиісті
болғандықтан оның координаталарын мынадай түрде жазуға болады:
![]() Енді
Енді ![]() және
және ![]() векторларының координаталары
оңай табылады:
векторларының координаталары
оңай табылады: ![]() Енді
Енді![]() ескеріп
ұйғарымды қолдануға болады:
ескеріп
ұйғарымды қолдануға болады: ![]() Осыдан
Осыдан ![]()
Онда ![]()
4-тәсіл. Тік бұрышты
координаталар жүйесінің осьтерін ![]() және
және ![]() сәулелері бойынша
бағыттайық. Бұл жүйеде нүктелердің координаталары төмендегідей
болады:
сәулелері бойынша
бағыттайық. Бұл жүйеде нүктелердің координаталары төмендегідей
болады: ![]()
![]() пен
пен ![]() кесінділерінің теңдігі мен
перпендикулярлығына сүйеніп екі теңдеу жазайық:
кесінділерінің теңдігі мен
перпендикулярлығына сүйеніп екі теңдеу жазайық: ![]()
жүйені ықшамдағаннан мынадай
теңдеу шығады: ![]() Бұл
теңдеуден
Бұл
теңдеуден ![]() шығады.
шығады.
![]() нүктесінің
нүктесінің ![]() түзуіне тиістілігінен
мынадай теңдеу шығады:
түзуіне тиістілігінен
мынадай теңдеу шығады: ![]() Соңғы екі теңдеуден
ықшамдағаннан кейін
Соңғы екі теңдеуден
ықшамдағаннан кейін ![]() шығады.
Енді нүктелердің координаталары
шығады.
Енді нүктелердің координаталары ![]() мен
мен ![]() арқылы өрнектеледі:
арқылы өрнектеледі: ![]()
Нүктелердің осы
координаталарына сүйеніп керек кесінділердің ұзындықтарын табайық:
![]() Осыдан
Осыдан
![]() шығады.
шығады.
5-тәсіл. Бірлік векторлар
енгізейік: ![]()
Екінші көмекші ұйғарым бойынша
![]()
Осыдан ![]() Бұл теңдеуді ықшамдағаннан
кейін
Бұл теңдеуді ықшамдағаннан
кейін ![]() (теңдіктерін ескеріп) шығады.
Олай болса
(теңдіктерін ескеріп) шығады.
Олай болса ![]() (себебі
(себебі
![]() ).
).
6-тәсіл. ![]() болатындай тік бұрышты
координаталар жүйесін енгізейік
болатындай тік бұрышты
координаталар жүйесін енгізейік ![]() болсын. Онда үшінші көмекші
ұйғарымдағы формулаларды қолданып табамыз:
болсын. Онда үшінші көмекші
ұйғарымдағы формулаларды қолданып табамыз: ![]() Енді
Енді ![]() арқылы
арқылы ![]() векторларын өрнектейік
векторларын өрнектейік
![]()
![]() және
және ![]() векторларының
перпендикулярлығына сүйеніп жазайық:
векторларының
перпендикулярлығына сүйеніп жазайық: ![]() Осыдан
Осыдан ![]() шығады
шығады

4-дәріс тақырыбы: Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары
Оқу еңбегінің қаруы - ой. Оқушылардың өз бетімен жұмысын қалыптастыру оқушының пәнге деген қызығушылығынан және қажеттілігінен туады. Мектеп оқушыларының өз бетінше жұмыстарын ұйымдастырудың басты формасы – жұмыстарды орындау, ептілік, іскерлік, шеберлік дағдысын дамыту.
Оқушылардың жеке ойлау қабілетін дамыту үшін олардың өзіндік күш қуаты мен сенімін арттыру керек. Қолынан келетін көп істердің мүмкіндіктеріне бағыт берген абзал. Оқушылардың білімді меңгеру үрдісі негізінен мына компоненттерден тұрады:
-
қабылдау; 2) түсіну; 3) есте сақтау; 4) қорыту және жүйелеу.
Оқушылардың ойлауын дамыту туралы М. Жұмабаев былай деген: «Ойлауды өркендету жолдары. Ойлау - жанның өте бір қиын, терең ісі. Жас балаға ойлау тым ауыр. Сондықтан тәрбиеші баланың ойлауын өркендеткенде, сақтықпен басқыштап іс істеу керек» [3]. Логикалық есептерді шығару үшін арнайы терең білімнің қажеті жоқ, тек ойлана алу, болжамдау, тапқырлығы болса, зейін қоя білсе жеткілікті. Логикалық есептерді шығару ғылыми проблемамен тұспа-тұс сияқты. Өйткені есептегенде гипотезаны айта білу, оларды тексеру маңызды болып табылады. Логикалық есептердің түрлері өте көп. Бірақ олардың санқырлылығына байланысты, арасынан ең жиі кездесетін түрлерін атап өтсек: 1)кесте арқылы шығарылатын логикалық есептер; 2) жиындарды реттеуді қажет ететін логикалық есептер; 3) болжамдары бар логикалық есептер; 4) олимпиадалық есептер.
Натурал
m санының ешбір мәнінде
![]() саны
саны ![]() санына бөлінбейтінін
дәлелдендер.
санына бөлінбейтінін
дәлелдендер.
1.Натурал
m санының кейбір мәнінде
![]() саны
саны ![]() санына бөлінеді деп ұйғарайық.
Онда,
санына бөлінеді деп ұйғарайық.
Онда, ![]() саны
саны
![]() санына да бөлінеді.
санына да бөлінеді.
![]() . Демек,
. Демек, ![]() саны
саны ![]() санына бөлінеді.
санына бөлінеді. ![]() саны
саны![]() болғандықтан тақ сан,
ал
болғандықтан тақ сан,
ал ![]() - жұп сан. Олай болса,
- жұп сан. Олай болса,
![]() саны
саны
![]() санына бөлінеді.
Алайда,
санына бөлінеді.
Алайда, ![]() болады. Бұл жағдай
алынған ұйғарымның жалғандығын көрсетеді. Яғни,
натурал m-нің ешбір мәнінде
болады. Бұл жағдай
алынған ұйғарымның жалғандығын көрсетеді. Яғни,
натурал m-нің ешбір мәнінде ![]() саны
саны![]() санына
бөлінбейді.
санына
бөлінбейді.
2.![]() сандары үшін
сандары үшін ![]() және
және ![]() екендігі белгілі, сонда
екендігі белгілі, сонда
![]() неге тең болатынын
табыңдар.
неге тең болатынын
табыңдар.
![]() болғандықтан
болғандықтан ![]() ,
, ![]() болғандықтан
болғандықтан ![]() ,
, ![]() болғандықтан
болғандықтан ![]() немесе
немесе ![]() немесе
немесе![]()
![]() ,
,![]() . Демек,
. Демек, ![]() .
.
Тапсырма шарты бойынша
![]() , біздің дәлелдеуіміз
бойынша
, біздің дәлелдеуіміз
бойынша ![]() .
Бұдан
.
Бұдан![]() . Тура
осындай жолмен
. Тура
осындай жолмен ![]() екендігі
де анықталады. Олай болса,
екендігі
де анықталады. Олай болса,![]() теңдігінен
теңдігінен![]() немесе
немесе ![]() екендігі туындайды. Мұнда, екі
жағдайда да
екендігі туындайды. Мұнда, екі
жағдайда да![]() шығады.
шығады.
3.
![]() теңдеуінің түбірлері натурал
сандар болса, онда
теңдеуінің түбірлері натурал
сандар болса, онда![]() құрама
сан болатынын дәлелдеңіздер.
құрама
сан болатынын дәлелдеңіздер.
![]() теңдеуінің
теңдеуінің![]() және
және![]() түбірлері Виет теоремасы боынша
мына шарттарды қанағаттандырады.
түбірлері Виет теоремасы боынша
мына шарттарды қанағаттандырады.
![]()
Бұдан, ![]()
![]() екендігі
шығады
екендігі
шығады

Тапсырма шарты бойынша
![]() ,
, ![]() натурал сандар. Олай болса әр
жақша екі немесе екіден артық натурал сан болады. Ал екі натурал
санның көбейтіндісі тек қана құрама санға тең. Демек,
натурал сандар. Олай болса әр
жақша екі немесе екіден артық натурал сан болады. Ал екі натурал
санның көбейтіндісі тек қана құрама санға тең. Демек, ![]() - құрама
сан.
- құрама
сан.
4.
![]()
![]()
![]()
![]() теңдіктерін қанағаттандыратын
теңдіктерін қанағаттандыратын
![]() бүтін сандарының
табылмайтынын дәлелдеңіздер.
бүтін сандарының
табылмайтынын дәлелдеңіздер.
Кері жоримыз.
Яғни,
берілген теңдіктерді қанағаттандыратын ![]() бүтін сандары бар болсын. Олай
болса,
бүтін сандары бар болсын. Олай
болса,
![]()
![]()
![]()
![]() деуге болады. Бұдан,
деуге болады. Бұдан,![]() -ның тақ сан екендігі шығады.
Себебі,
-ның тақ сан екендігі шығады.
Себебі,![]() -тақ сан,
тақ санды тақ санға көбейткенде ғана нәтиже тақ сан болатыны
белгілі.
-тақ сан,
тақ санды тақ санға көбейткенде ғана нәтиже тақ сан болатыны
белгілі.
Осындай жолмен,![]() -ның да тақ сан екендігін
анықтауға болады. Олай болса,
-ның да тақ сан екендігін
анықтауға болады. Олай болса,![]() -да тақ сан және
-да тақ сан және![]() ,
, ![]() ,
, ![]() ,
, ![]() нәтижелері жұп сан болу
керек.
нәтижелері жұп сан болу
керек.
Ал тапсырмада бұл айырмалардың
нәтижелері тақ сандар. Демек, қарама-қайшылыққа келдік. Олай болса,
тапсырма шартын қанағаттандыратын ![]() бүтін сандары
табылмайды.
бүтін сандары
табылмайды.
5.
![]() - нің қандай натурал мәнінде
- нің қандай натурал мәнінде
![]() құрама сан
болады.
құрама сан
болады.
![]()
Бұл көбейтінді ![]() болғанда құрама сан
болады.
болғанда құрама сан
болады.
6.
![]() болса, онда
болса, онда![]() болатындығын
дәлелдеңіздер.
болатындығын
дәлелдеңіздер.

![]()
![]()

![]()
Демек, ![]() немесе
немесе ![]() немесе
немесе ![]() . Олай болса,
. Олай болса, ![]()
![]() болғандықтан
болғандықтан ![]() Басқа жағдайлар да осылай
қарастырылынады.
Басқа жағдайлар да осылай
қарастырылынады.
5-дәріс тақырыбы Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары
1.![]() теңдеуін бүтін сандар жиынында
шшіңіздер.
теңдеуін бүтін сандар жиынында
шшіңіздер.
Теңдеуді ортақ бөлімге келтірелік.

![]()
Бұл бөлшектердің екеуі де қысқармайтын бөлшектр (қатар тұрған екі сан – өзара жай сан). Олай болса, бөлшектердің бөлімдері тең болу керек.
![]() . Мұнда, мынандай үш түрлі
жағдай болуы мүмкін.
. Мұнда, мынандай үш түрлі
жағдай болуы мүмкін.
а) ![]() болса, онда
болса, онда ![]()
ә) ![]() болса, онда
болса, онда ![]()
б) ![]() болса, онда
болса, онда![]() деп алайқ. Бұл жағдайдағы
деп алайқ. Бұл жағдайдағы
![]() -нің мәнін жоғарыдағы
теңдеуге апарып қойсақ.
-нің мәнін жоғарыдағы
теңдеуге апарып қойсақ.![]()

Демек, ![]() . Олай болса,
. Олай болса,![]() одан
одан![]() екендігі туындайды.
екендігі туындайды. ![]() -нің бұл мәні берілген теңдеуді
қанағаттандырады.
-нің бұл мәні берілген теңдеуді
қанағаттандырады.
2.
![]() саны
саны ![]() саына бөлінбейтін натурал сан
саына бөлінбейтін натурал сан
![]() -нің барлық тақ мәндерін
табыңыздар.
-нің барлық тақ мәндерін
табыңыздар.
Бұл тапсырманы орндау үшін
натурал тақ сандарды төмендегідей топтарға бөліп, әр топтың
тапсырма шартын қанағаттандыратынын немесе қанағаттандырмайтынын
жеке-жеке қарастырайық. Натурал тақ сандар: ![]()
![]() - натурал, тақ және жай сандар
болсын яғни
- натурал, тақ және жай сандар
болсын яғни ![]() Бұл жағдайда
Бұл жағдайда
![]() саны
саны ![]() санына, әсіресе
санына, әсіресе ![]() санына бөлінбейді. Мысалы,
санына бөлінбейді. Мысалы,
![]() болса,
болса, ![]() саны
саны ![]() санына, әсіресе
санына, әсіресе ![]() санына бөлінбейді. Демек, бұл
топтағы сандар тапсырма шартын
қанағаттандырады.
санына бөлінбейді. Демек, бұл
топтағы сандар тапсырма шартын
қанағаттандырады.
ә)![]() болсын, мұндағы
болсын, мұндағы ![]() - жай тақ сан. (
- жай тақ сан. (![]() - сандары). Егер
- сандары). Егер![]() болса, онда
болса, онда ![]() бөлінеді.
бөлінеді. ![]() мұндағы,
мұндағы, ![]() теңсіздігі
теңсіздігі ![]() болғанда ғана орындалды.
Себебі,
болғанда ғана орындалды.
Себебі, ![]() . Ал мұнда
қамтылмай қалған
. Ал мұнда
қамтылмай қалған ![]() жағдайын
жеке қарастырайық.
жағдайын
жеке қарастырайық. ![]() бөлінбейді
бөлінбейді ![]() . Демек,
. Демек,
![]() болғанда тапсырма шарты
орындалады.
болғанда тапсырма шарты
орындалады.
б) ![]() - тақ жай сан емес және де жай
санның квадраты да емес болсын
- тақ жай сан емес және де жай
санның квадраты да емес болсын ![]()
бұл жағдайда ![]() , мұндағы
, мұндағы ![]() деп алуға болады. Мәселені
нақтылай түссек,
деп алуға болады. Мәселені
нақтылай түссек, ![]() және
және
![]() тақ сандар болғандықтан
тақ сандар болғандықтан
![]() деуге болады. Демек,
деуге болады. Демек,
![]() болса,
болса, ![]() Бұл көбейтіндінің құрамында
Бұл көбейтіндінің құрамында
![]() сандары бар.
Демек,
сандары бар.
Демек,![]() ,
,![]() -қа яғни
-қа яғни![]() ,
, ![]() -ге бөлінеді. Тапсырма
шарты
-ге бөлінеді. Тапсырма
шарты![]() және
және![]() -тақ жай сан болғанда ғана
орындалады.
-тақ жай сан болғанда ғана
орындалады.
3.
![]() - кез-келген бүтін сан болсын.
Кейбір өзара жай
- кез-келген бүтін сан болсын.
Кейбір өзара жай![]() сандары
үшін
сандары
үшін ![]() санының
санының
![]() -ға бөлінетінін
дәлелдеңіздер.
-ға бөлінетінін
дәлелдеңіздер.
![]() болсын.
болсын.
Бұл жағдайда, ![]() мен
мен ![]() - дің өзара жай сан екендігі
айқын. Себебі,
- дің өзара жай сан екендігі
айқын. Себебі, ![]()
![]() тек
қана
тек
қана![]() Олай болса,
Олай болса,![]() - өзара жай сандар. Сонымен
бірге
- өзара жай сандар. Сонымен
бірге ![]() Олай
болса,
Олай
болса, ![]()
![]() -ға
бөлінеді.
-ға
бөлінеді.
4.
![]() теңдеуін қанағаттандыратын
бүтін
теңдеуін қанағаттандыратын
бүтін ![]() және
және ![]() сандарының парларын
табыңыздар.
сандарының парларын
табыңыздар.

![]()
![]()
![]()
![]()
Егер ![]() , онда
, онда
![]()
![]() Демек,
Демек,![]() .
.
Тек қана бүтін түбір
ізделінетіндіктен ![]() .
.
Егер ![]() және
және![]() -бүтін сан болса,
онда
-бүтін сан болса,
онда ![]() . Олай болса,
. Олай болса,
![]()
![]() .
.![]() және
және![]() бүтін
бүтін
![]() .
.
![]() болады. Енді,
жоғарыдағы
болады. Енді,
жоғарыдағы![]() теңдеуінен
теңдеуінен ![]() болатынын
анықтап, орнына қойсақ былай
болады.
болатынын
анықтап, орнына қойсақ былай
болады.
![]()
![]()
![]()
Демек,
![]() аралығында
аралығында
![]() -тің бүтін тек
қана
-тің бүтін тек
қана ![]() мәні бола алады.
Олар,
мәні бола алады.
Олар, ![]()
![]() болса,
онда
болса,
онда ![]() және
және ![]() болса, онда
болса, онда
![]() Бұл квадраттық теңдеудің бүтін
түбірі жоқ.
Бұл квадраттық теңдеудің бүтін
түбірі жоқ. ![]() болса,
онда
болса,
онда ![]()
![]()
![]()
![]()
![]()
![]() Демек,
Демек,
![]()
6-7 дәріс тақырыбы: Жоғары математика курсы бойынша олимпиадалық есептер
1. ![]() дұрыс
үшбұрышының
дұрыс
үшбұрышының ![]() және
және ![]() қабырғаларынан
қабырғаларынан ![]() болатындай сәйкесінше
болатындай сәйкесінше ![]() және
және ![]() нүктелері алынған.
нүктелері алынған. ![]() және
және ![]() кесінділерінің қиылысын
кесінділерінің қиылысын ![]() нүктесімен белгілейік.
нүктесімен белгілейік. ![]() екенін дәлелдеңіз.
екенін дәлелдеңіз.
1 – есептің шешуі. Енді геометрия жайында бірер сөз.
Кезінде Пифагор геометрияны арифметикаға бағындырса, кейін Евклид қайтадан геометрияны бірінші орынға қойып, оған алгебраны бағындырған. Д.И. Менделеев «Геометрические знания составляют основу всей точной науки», - деп айтып кеткен екен. Геометрия туралы ұлағатты сөздерді көптеп келтіруге болады. Математикада геометриялық есептердің алатын орны өте зор. Жалпы геометрия өзі жатқан бір дүние десекте болғандай, ол өзінің бөлімдерімен, есептерімен ерекшеленеді, оның есептерін шығару барысында оқушы көптеген қиыншылықтарға ұшырайды, шығару жолы мен тәсіліне, әрбір шығару кезеңінің нәтижелеріне назар аудармай, тек қана белгісіз элементті табумен айналысады. Осындай олқылықтарға бой алдырмау үшін геометриялық есепті талдауға үйреніп, шығару кезеңдерімен жолдарын меңгеру керек. Әуелі есептің мәтінін жақсы түсініп оқу, талдау, содан кейін дұрыс сызба, келесі кезекте дәлелдеу жұмысын суатты орындау. Осы кезеңдерден өткен соң талдау мен сызбаға сүйеніп, қажетті формулаларды пайдалана отырып, есепті шешудің қолайлы жолын табуға болады. Кейде геометриялық бір есепті шешуде оқушыға бүкіл бір курсты , не бір тарауды қайталап, еске түсіруге тура келеді.
Шешуі: І тәсіл. (Салу әдісін қолдану). Есеп шарты бойынша сызба сызып талдау жасайық.
Талдау:
1) ![]() =
= ![]() = 2⟹ MC
= 2MA,
= 2⟹ MC
= 2MA,
NA = 2NB, ал AC = MA + MC және
AB = NA +NB ⟹AC = 3MA, AB = 3NB
яғни AC = AВ болғандықтан MA = NB,
NA = MC (1 – сурет)
2) В нүктесі арқылы ВК⊥ АС болатындай ВК және N ,M нүктелері арқылы NМ түзулерін жүргізейік.
АК = СК =
![]() AC.
AC.![]() =
= ![]() =
= ![]() =
= ![]() Сонымен,
Сонымен, ![]() =
= ![]() Олай болса, пропорционал кесінділер туралы теорема бойынша
NB∥BK, яғни
NM⊥AC және
∠ANM = 30° осыдан, AM
=
Олай болса, пропорционал кесінділер туралы теорема бойынша
NB∥BK, яғни
NM⊥AC және
∠ANM = 30° осыдан, AM
= ![]() AN
AN
Салу
Тікбұрышты ANM үшбұрышын саламыз
-
Талдауға сүйеніп, салған үшбұрышын пайдаланып, АВС дұрыс үшбұрышын саламыз
-
Радиусы
 АС – ға
тең жарты шеңбер сызып және NС түзуін жүргізіп,түзудің жарты
шеңбермен қиылысу нүктесін Р деп белгілейік (1а – сурет
)
АС – ға
тең жарты шеңбер сызып және NС түзуін жүргізіп,түзудің жарты
шеңбермен қиылысу нүктесін Р деп белгілейік (1а – сурет
) -
В және Р нүктелері арқылы жүргізілген түзу М нүктесінен өтеді, өйткені өтпеген жағдайда есептің шарты орындалмайды да қарама – қайшылық туындайды.
Дәлелдеуі: АР түзуін жүргізсек диаметрге тірелген АРС бұрышын аламыз, ол тік болады.Демек, ∠AРС = 90° ( 1ә – сурет )
N
В
С
А
М
Р
В
N
В
А
М
Р
С
А
М
С
N
Р
1а - сурет
1ә - сурет




![]()



8-9-дәріс тақырыбы: Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары
Жоспары
-
Анықтауыштар және оның қасиеттері.
-
Анықтауыштардың шығарылуы.
-
Матрицалар және олардың қолдануы.
-
Кері матрицалар.
-
Сызықтық алгебралық теңдеулер жүйесінің шығару әдістері.
Анықтама :
А
матрицаның
анықтауышы
деп ![]() санды аламыз және оны төмендегідей белгілейміз:
санды аламыз және оны төмендегідей белгілейміз:
![]()
![]()
![]() - екінші
ретті анықтауыш,
- екінші
ретті анықтауыш,

көріністе жазылып есептелінген кестені үшінші ретті анықтауыш деп аталады.
Анықтауыштардың төмендегі қасиеттерін атап өтуге болады:
10 . Анықтауыштың жолдары мен бағандары орындарын алмастырылса, оның мәні сақталады.
20. Анықтауыштың параллель қатарларын өзара орын алмастырылса, анықтауыш таңбасы өзгереді.
30. ![]()
40. ![]() =0
=0
50. ![]() =0
=0
 - үшінші
ретті анықтауыш берілген болсын.
- үшінші
ретті анықтауыш берілген болсын.
Анықтама :
Үшінші ретті анықтауыштың aij элементінің миноры деп, осы элемент тұрған i-жол және j-бағанды алып тастағанда пайда болатын екінші ретті анықтауышты айтамыз. Анықтауыштың aij элементтің минорын Mij арқылы белгілейміз. А матрицаның элеметері үшін де минор түсінігі жоғарыдағыдай беріледі.
Мысалы,  болса,
онда
болса,
онда ![]()
![]()
Анықтама : Анықтауыштың aij элементінің алгебралық толықтауышы деп
![]() санын
айтады.
санын
айтады.
60. Анықтауыштың қандай да бір қатарының элементтері мен олардың сәйкес алгебралық толықтауыштарының көбейтінділерінің қосындысы осы анықтауыш мәніне тең.

Мысал :

Анықтама :
n белгісізі бар m сызықтық алгебралық теңдеулер жүйесі келесі түрде жазылады:
 (1)
(1)
мұндағы:
![]() -жүйе
белгісіздері;
-жүйе
белгісіздері;
![]() - жүйе
коэффициенттері;
- жүйе
коэффициенттері;
![]() -бос мүшелер деп
аталады.
-бос мүшелер деп
аталады.
Жүйе коэффициенттерінен тік бұрышты кесте құрауға болады. Ол кестені белгілеуге келесі

символдардың бірін қолданады.
Бұл кестені m жол және n бағаннан тұратын m×n өлшемді матрица деп атайды.
Мұндағы
![]() -матрица элеметтері деп
атайды. Егер m=n болса, онда (2) кесте
-матрица элеметтері деп
атайды. Егер m=n болса, онда (2) кесте
 (2*)
(2*)
түріне ие
болады және ол n-ретті квадрат матрица деп аталады. Мұндағы
![]() -бас диагональ,
-бас диагональ,
![]() -бүйір диагональ
элементтері деп аталады.
-бүйір диагональ
элементтері деп аталады.
Дербес жағдайда, n=m=2 болса,
![]() - екінші
ретті квадрат матрица болады.
- екінші
ретті квадрат матрица болады.
10-11-дәріс тақырыбы: Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
Жоспары
-
Векторлар.
-
Векторларға қолданылатын сызықтық амалдар.
-
Векторлардың скалярлық, векторлық және аралас көбейтіндісі.
-
Жазықтық. Кеңістіктегі түзу. Түзу және жазықтық.
-
Екінші ретті сызықтар. Екінші ретті беттер.
![]() бас нүктесі,
бас нүктесі,
![]() ұшы. AB кесінді
ұзындығын
ұшы. AB кесінді
ұзындығын ![]() вектордың
модулі деп,
вектордың
модулі деп, ![]() арқылы
белгілейді.
арқылы
белгілейді. ![]() - ноль
вектор.
- ноль
вектор.
Бір түзуде немесе параллель түзулерде жататын векторлар коллинеар деп аталады.
![]() ,
,
![]() ,
, ![]()
![]() векторына коллинеар, модулі
векторына коллинеар, модулі
![]() тең, бағыты
тең, бағыты ![]() векторына қарама-қарсы
бағытталған вектор
векторына қарама-қарсы
бағытталған вектор ![]() векторына қарама-карсы вектор деп аталады және -
векторына қарама-карсы вектор деп аталады және -![]() арқылы
белгіленеді.
арқылы
белгіленеді.
![]()
10. Векторды λ санына көбейту:
![]() векторы мен
λ санының
көбейтіндісі
векторы мен
λ санының
көбейтіндісі ![]() дейміз,
егер төмендегі шарттар
қанағаттандырса:
дейміз,
егер төмендегі шарттар
қанағаттандырса:
-
модулі

-

-
 болса,
болса,
 мен бағыттас, ал
мен бағыттас, ал
 болса
болса  векторына бағыты қарама-қарсы
векторына бағыты қарама-қарсы
 векторын
айтады.
векторын
айтады.
2 0. Векторларды
қосу.
0. Векторларды
қосу.
![]()
Қасиеттері:
-
 сандар.
сандар. -

-

-

-

Анықтама: Бір жазықтыққа параллель ![]() векторлар компланар векторлар деп
аталады.
векторлар компланар векторлар деп
аталады.
Кеңістікте
OXYZ тік бұрышты декарт координаталар жүйесі берілсін. OX, OY, OZ -
өстерінің бойында орналасқан ![]() бірлік векторлары
бірлік векторлары ![]() компланар емес векторлары
болғандығынан оларды кеңістік базисін құрайды деп алуға болады.
Онда кез келген
компланар емес векторлары
болғандығынан оларды кеңістік базисін құрайды деп алуға болады.
Онда кез келген ![]() - векторын олардың сызықтық комбинациясы
арқылы жазуға болады.
- векторын олардың сызықтық комбинациясы
арқылы жазуға болады.
![]() сандарды
сандарды ![]() вектордың координаталары деп
атайды.
вектордың координаталары деп
атайды.
![]() берілген
болса,
берілген
болса, ![]() вектордың
координаталары
вектордың
координаталары ![]() болады.
болады.
![]()
![]()
![]()
![]()
![]()
![]() нүктелер
берілген болса, онда
нүктелер
берілген болса, онда ![]() екендігін көрсетуге болады,
екендігін көрсетуге болады,
![]()
В екторлардың
скаляр көбейтіндісі
екторлардың
скаляр көбейтіндісі
![]() векторлар арасындағы
бұрышты
векторлар арасындағы
бұрышты ![]() деп
аламыз.
деп
аламыз. ![]()
![]()
![]()
![]()
![]() - деп те
белгіленеді.
- деп те
белгіленеді.
Қасиеттері:
10. ![]()
20. ![]()
30. ![]()
40. ![]()
50. ![]() сүйір
бұрыш
сүйір
бұрыш ![]()
60. ![]() доғал
бұрыш
доғал
бұрыш ![]()
70. ![]()
![]()
![]()
![]()
![]()
40’. ![]()
Анықтама. Нол емес ![]() векторының бағыттаушы косинустары деп
векторының бағыттаушы косинустары деп ![]() векторымен OX,OY,OZ өстерінің арасындағы
сәйкес
векторымен OX,OY,OZ өстерінің арасындағы
сәйкес ![]() бұрыштарының
косинустарын айтады
бұрыштарының
косинустарын айтады
![]()
В![]() екторлық көбейтінді және оның қасиеттері.
екторлық көбейтінді және оның қасиеттері.
Анықтама.
Бастары ортақ бір О нүктесіне келтірілген, компланар емес, реттелген ![]() векторлар үштігі берілсін. Егер
векторлар үштігі берілсін. Егер ![]() вектор ұшынан қарағанда
вектор ұшынан қарағанда ![]() векторының
векторының ![]() векторына жақын тұспен бұрылуы сағат тіліне қарама қарсы бағытта болса, онда
векторына жақын тұспен бұрылуы сағат тіліне қарама қарсы бағытта болса, онда ![]() - оң үштік векторлар деп аталады.
- оң үштік векторлар деп аталады.
![]()
![]() а және в
векторлардың вектор көбейтіндісін
а және в
векторлардың вектор көбейтіндісін ![]() деп
деп
төмендегі үш шартты орындайтын вектроға айтылады.
1.
![]() векторлар оң үштік
құрайды.
векторлар оң үштік
құрайды.
2.
![]()
![]()
3.
![]() ,
, ![]()
S =![]()
![]()
Қасиеттері.
1. ![]()
2. ![]()
3. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Э лементер математика курсынан
лементер математика курсынан
L түзуінің тендеуі y=kx+b (1)
түрінде жазылатыны белгілі. Мұндағы, k=tga - түзудің бұрыштық коэфициенті,
ал ![]() шамасы L түзуі мен OX өсінің оң
бағыты арасындағы бұрыш, b шамасы –түзү мен OY өсінің
қиылысу
нүктесінің ординатасы (b=ОВ) (1-суретті
қара.)
шамасы L түзуі мен OX өсінің оң
бағыты арасындағы бұрыш, b шамасы –түзү мен OY өсінің
қиылысу
нүктесінің ординатасы (b=ОВ) (1-суретті
қара.)
(1-сурет).
Aх+Bу+C=O
(2)
теңдеуін қарастырайық. Мұндағы A,B,C-белгілі сандар және А мен В
бір мезгілде бірдей нөлге тең болмайды. Егер B≠O болса, онда (2)
теңдеуді y = ![]() деп,
немесе
деп,
немесе ![]()
b=-![]() десек, y=-кx+b көріністе, яғни
(1) тендеу түрінде жазуға болады
екен.
десек, y=-кx+b көріністе, яғни
(1) тендеу түрінде жазуға болады
екен.
Сондықтан (2) теңдеу жазықтықтағы түзудің жалпы теңдеуі деп аталады.
-
Бұрыштың коэфициенті k тең және
 нүктесі арқалы өтетін түзу
теңдеуі :
нүктесі арқалы өтетін түзу
теңдеуі :
![]() (3)
(3)
2. ![]() және
және ![]() нүктелер арқылы өтетін түзу
теңдеуі:
нүктелер арқылы өтетін түзу
теңдеуі:
![]() =
=![]() (4)
(4)
y=k1x+b1
және
y=k2x+b2
түзулердің арасындағы ![]() бұрышты
табу формуласы:
бұрышты
табу формуласы:
tg![]() =
=![]() (5)
(5)
Екі түзудің перпендикулярлық белгісі
1+к1 к2=0 немесе ![]() =-
=-![]() (6)
(6)
![]() Екі
түзудің паралелдік белгісі
Екі
түзудің паралелдік белгісі
(![]() ): k1-k2=0 немесе k1=k2 (7)
): k1-k2=0 немесе k1=k2 (7)
M(x0,y0) нүктеден Ax+By+C=0 теңдеулі түзуге дейінгі қашықтықты табу формуласы:
D=![]() (8)
(8)
Мысал 1. М(1;3) нүктесінен L: 3x+4y+10=0 түзуіне дейінгі қашықтықты табу керек
Шешімі: (8) формуладан табамыз: d=![]()
Жауабы: d=5
Мысал 2 L1: x+2y-3 және L2: y=2x-5 түзулері арасындағы бұрышты табу керек.
Шешімі: L1 түзудің бұрыштың коффиценттерін тауып аламыз.
2y=-x+3 немесе y = -![]()
L1: y=-![]()
![]()
L2 : y=2x-5, k2=2
1+k1k2=1+(-![]() )2=1-1=0
1+k1k2=0
яғни L1
)2=1-1=0
1+k1k2=0
яғни L1![]() L2
L2
Жауабы:
![]()
12-13 дәріс тақырыбы: Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары
Жоспары
-
Ықтималдықтар теориясының негізгі ұғымдары.
-
Қосу және көбейту ықтималдықтар теоремалары.
-
Байқаулардың қайталауы. Кездейсоқ мөлшерлер
-
Таңдалатын әдіс. Тарату параметрлерінің статистикалық бағалаулары. Корреляция теориясының элементтері.
Шартты ықтималдық ұғымы ерекшеленген ұғым, яғни ештеңеден шықпайды. Сондықтан, оны автор бір есеп арқылы, мүмкін сәтсізден болуы, енгізіп көреді.
Есеп – ой түткі ықтималдық
түзуінен мынадай Р саны табу керек, онда Р (Ā) ![]() кесіндісі осы нүкте арқылы Р
қатынасына бөлінсін
кесіндісі осы нүкте арқылы Р
қатынасына бөлінсін
Р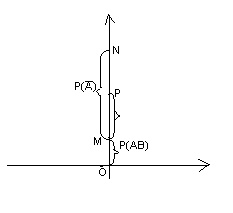 (Ā) + Р
(АВ) –ны түзуде белгілейік.
(Ā) + Р
(АВ) –ны түзуде белгілейік. ![]() қатнасынан Р – ны
табамыз.
қатнасынан Р – ны
табамыз.
Р [1- Р(Ā)] = Р(АВ) Р =
![]() Р(А) > 0
ықтималдығымен А
Р(А) > 0
ықтималдығымен А
Оқиғасы пайда болсын.
Анықтама. А оқиғасы орындалғанда
![]() - ға (*) тең В оқиғасының
ықтималдығы шартты ықтималдық деп
атайды.
- ға (*) тең В оқиғасының
ықтималдығы шартты ықтималдық деп
атайды.
Мысал 1. Екі ойын сүйегін лақтырғанда пайда болған ұпайдың қосындысы а) жұп, ә) тақ болу шарттары орындалғанда 7-ден артпайтын ықтималдығын табыңдар.
а) Алдынғы бетте А және В оқиғаларының кескіні келтірілген, олардың ықтималдықтары белгілі, онда (*) формула бойынша шартты ықтималдықты табамыз

Осы есепте (**) формула бойынша да шешеміз.
Р(А) ![]()
![]()
Толық кеңістік үшін А оқиғасы
алынады және А оқиғасы негізінде АВ – ның ықтималдығы табылады. U =
A = {xy : х+у = жұп }= 
Мұнда қара цифрмен х + у ≤ 7 шартын қанағаттандыратындары көрсетілген, сонда
Р ![]()
ә) А және АВ оқиғаларын құрамыз.
А = {ху : х+у = тақ
} =

АВ = {ху : әрі (х+у) = тақ,
әрі ≤ 7} = 
Сонда (*) формула бойынша шартты ықтималдық
Р
2. Отбасында 2 бала бар делік. Екі баланың да ұл болу ықтималдығын былай болжаудан табалық: а) үлкені ұл бала
ә)ең болмағанда біреуі ұл бала
U ={ҰҰ, ҰҚ, ҚҰ, ҚҚ}
Кездейсоқ шаманы анықтау мақсатында сандық сипаттамалар беріледі. Солардың бірі – Математикалық үміт
Мысалы, x шамасы n рет өлшенген болсын делік; m1 жағдайда оның шамасы (n рет өлшенген болсын делік: m1 жағдайы) x1-ге, m2жағдайда – x2-ге, тағы сол сияқты, ақырында mk жағдайда xk-ға тең болсын. Практикада, әдетте, өлшенген шама үшін оның орта мәнін қабылдайды, яғни
![]()
шамасын алады, сөйтіп бұл шама – қабылданған мәндердің оларға сәйкес жиіліктеріне көбейтінділерінің қосындысы. Міне, осы орта мәнге ұқсас кездейсоқ шаманың математикалық үміті анықталады.
Егер дискретті ![]() кездейсоқ шамасы
x1,x2,...,xn
мәндерін
P1,P2,…,Pn
ықтималдықтарын қабылдаса, онда кездейсоқ шаманың
математикалық үміті деп
кездейсоқ шамасы
x1,x2,...,xn
мәндерін
P1,P2,…,Pn
ықтималдықтарын қабылдаса, онда кездейсоқ шаманың
математикалық үміті деп
![]() қосындысын
айтады.
қосындысын
айтады.
![]() арқылы математикалық үмітті
белгіледік. Егер дискретті
арқылы математикалық үмітті
белгіледік. Егер дискретті ![]() кездейсоқ шамасы
x1,x2,...,xn
мәндерін
сәйкес P1,P2,...,Pn
ықтималдықтарымен қабылдаса және
кездейсоқ шамасы
x1,x2,...,xn
мәндерін
сәйкес P1,P2,...,Pn
ықтималдықтарымен қабылдаса және ![]() nқатары абсолютті жинақты
болса, онда осы қатардың қосындысын
nқатары абсолютті жинақты
болса, онда осы қатардың қосындысын ![]() кездейсоқ шамасының
математикалық үміті деп аталады.
кездейсоқ шамасының
математикалық үміті деп аталады.
![]()
Егер ![]() аралығынан мән қабылдайтын
аралығынан мән қабылдайтын
![]() кездейсоқ шамасының
ықтималдық үлестірім тығыздығы p(x) болса, және
кездейсоқ шамасының
ықтималдық үлестірім тығыздығы p(x) болса, және ![]() меншіксіз интегралы абсолютті
тиянақты болса, онда
меншіксіз интегралы абсолютті
тиянақты болса, онда ![]() кездейсоқ шамасының
математикалық үміті деп осы интегралдың мәнін
айтады.
кездейсоқ шамасының
математикалық үміті деп осы интегралдың мәнін
айтады.
![]()
Математикалық үміттің негізгі қасиеттері:
10. Тұрақтының математикалық үміті өзіне тең яғни M(C)=C мұндағыС=const.
Д/у. Ықтималдықтың үлестірім тығыздығын P(x) арқылы белгілелік. Сонда кездейсоқ шама тек қана С мәніне қабылдайтын болғандықтан.
![]()
дәлелдеу керегі де осы еді.
20. Тұрақты көбейткішті
математикалықүміт таңбасының алдына шығаруға болады, яғни С=const
болса, онда ![]() .
.
Д/у.Егер ![]() кездейсоқ шаманың ықтималдық
үлестірім тығыздығы p(x) болса, онда бұл С
кездейсоқ шаманың ықтималдық
үлестірім тығыздығы p(x) болса, онда бұл С![]() көбейтіндісінің де тығыздығы
болады. Сонда
көбейтіндісінің де тығыздығы
болады. Сонда
![]()
демек қасиет дәлелденді.
30. Екі кездейсоқ шамалардың
қосындысының математикалық үміті сол шамалардың математикалық
үміттерінің қосындысына тең, яғни ![]() .
.
40. Екі кездейсоқ шамалар
тәуелсіз болған жағдайда олардың көбейтіндісінің математикалық
үміті көбейткіштердің математикалық үміттерінің қосындысына тең,
яғни мұны формула түрінде берсек: егер ![]() мен
мен ![]() кездейсоқ шамалары тәуелсіз
болса, онда
кездейсоқ шамалары тәуелсіз
болса, онда
![]()
Д/у. ![]()
Мысал 1. Бірқалыпты үлестірілген кездейсоқ шаманың математикалық үмітін табу.
![]() . Анықтама негізінде
математикалық үмітті тапсақ
. Анықтама негізінде
математикалық үмітті тапсақ ![]()
Сонымен (a,b) аралығында
бірқалыпты орналасқан кездейсоқ шаманың математикалық үміті осы
аралықтың дәл ортасы ![]() -ге
тең.
-ге
тең.
Дисперсия және оның қасиеттері
Кездейсоқ шаманың математикалық үміті сол шаманың, жалпы алғанда, негізгі бір сипаттамасы екендігін көрдік. Енді өзінен-өзі келіп, кездейсоқ шаманың мәні есебінде математикалық үмітті қабылдағанда жіберетін қатені бағалау мәселесі шығады. Физикада математикалық үміттің анологисы-дененің ауырлық центрінің координаталары, ал ауырлық центрден ауытқу мәселелері инерция моменттері арқылы шешіледі. Кездейсоқ шаманың мәндері оның математикалық үмітінен ауытқитындығы түсінікті. Міне, осы ауытқуды бағалау үшін дисперция ұғымы енгізіледі кездейсоқ шамасының дисперциясын D ( ) таңбасымен белгілелік.
Анықтама кездейсоқ шамасының дисперсиясы деп кездейсоқ шаманың математикалық үміттен ауытқуының квадратының математтикалық үмітін айтады.
Сонымен, кездейсоқ шамасының дисперциясы мына формула бойынша анықталады.
D ( )= M( )—M( )2 (24)
Математикалық үміттің қасиеттерін пайдаланып, (24) формуланы түрлендірелік: D( )=M ( 2) – 2 M ( ) +M2 ( )) =M ( 2) --
Сонымен, дисперцияны анықтайтын
D( )=M ( 2) – M2 ( ) ( 25)
формуласы келіп шықты. Бұл формуланы былай оқуға болады:
кездейсоқ шаманың дисперсиясы сол кездейсоқ шаманың квадратының математикалық үміті мен сол кездейсоқ шаманың математикалық үмітінің квадратының айырымына тең болады.
14-15дәріс тақырыбы: Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары олимпиадалық есептерді шешу жолдары
Жоспары
-
Функциялардың және тізбектердің шектері. Қарапайым анықталмағанды шешу. Тамаша шектер. Туынды, оның геометрикалық және физикалық мағынасы. Дифференциалдаудың формулалары және ережелері.
-
Логарифмдік дифференциалдау. Жоғары ретті туындылар. Функцияларды және олардың графиктерін зерттеу.
-
Анықталмаған интеграл. Функциялардың меншікті интегралдануы.
-
Квадратты үш мүшелік функцияның интегралдануы. Бөліктеп интегралдау.
-
Рационалды функциялардың интегралдануы. Тригонометрикалық ауыстырулыр. Анықталған интегралдың ұғымы. Анықталған интегралдың есептелуі. Анықталған интегралды геометрия және физика есептерін шешуге айқындау
Лопиталь ережесі
1. ![]()
![]() =
=![]() болса,
болса, ![]()
![]() =
=![]()
![]() орынды
болады
орынды
болады
1-мысал.
![]()
![]() =(
=(![]() )=
)=![]()
![]()
![]()
![]()
2. ![]()
![]() =
=![]()
![]() болады.
болады.
2-мысал.
![]()
Ескерту. ![]() анықталмағандықтарын
анықталмағандықтарын ![]() немесе
немесе ![]() түріндегі анықталмағандықтарға
келтіріп Лопиталь ержесін қолдауға
болады.
түріндегі анықталмағандықтарға
келтіріп Лопиталь ержесін қолдауға
болады.
Мысал. 
Анықтама:
f функциясы
[a,b] аралығында анықталсын.
Егер x0
![]() [a,b]
үшін
[a,b]
үшін ![]() нақты
мәнді шегі бар болса, онда f функциясын
x0
нүктесінде дифференциалданады, ал шектің
мәнің f функциясының
x0
нүктесіндегі туындысы дейді де, f '(x0)
cимволымен
белгілейді.
нақты
мәнді шегі бар болса, онда f функциясын
x0
нүктесінде дифференциалданады, ал шектің
мәнің f функциясының
x0
нүктесіндегі туындысы дейді де, f '(x0)
cимволымен
белгілейді.
1. Элементар функциялардың туындылары кестесі.
1.
f(x)=C
C=const
![]() =0
=0
2.
f(x)=xp
![]() =pxp-1
=pxp-1
3.
f(x)=ax
,
![]()
4. ![]()
![]()
5. f(x)=sin x , ![]()
6. f(x)=cos x , ![]()
7. f(x)=tg x , ![]()
8. f(x)=ctg x , ![]()
9. f(x)=arcsin x ,
![]()
10. f(x)=arcos x ,
![]()
11. f(x)=arctg x ,
![]()
12. f(x)=arcctg x ,
![]()
-
Күрделі фунцияның туындысы.
y=f(u) ,
u=g(x) болса, ![]()
Мысал y=sin(x3), ![]()
-
Туындының қасиеттері.
![]()
Мысал.
![]()
Анықтама.
Дифференциялданатын ![]() функциясы үшін
функциясы үшін ![]() теңдеу орындалса,
теңдеу орындалса, ![]() функция
функция ![]() функцияның алғашқы функциясы
деп аталады.
функцияның алғашқы функциясы
деп аталады.
Мысал.
1)
![]() болғандықтан
болғандықтан ![]() функциясы
функциясы ![]() функцияның алғашқы функциясы
болады.
функцияның алғашқы функциясы
болады.
2) ![]() сондықтан
сондықтан ![]() ,
, ![]()
Анықтама.
Егер
![]() функция
функция ![]() функцияның алғашқы функциясы
болса,
функцияның алғашқы функциясы
болса,
![]() болады.
болады.
![]() (c – const) өрнекті
(c – const) өрнекті ![]() функцияның анықталмаған
интегралы деп аталады да
функцияның анықталмаған
интегралы деп аталады да ![]() символымен
белгіленеді.
символымен
белгіленеді.
Интегралдың негізгі формулалары.
Интегралдың қасиеттері:
10. ![]() , к
–
тұрақты
, к
–
тұрақты
20. ![]()
3. Егер ![]() орынды болса,
орынды болса, ![]() да орынды
болады.
да орынды
болады.
Мысалдар:
![]()
2.4 Студенттердің оқуын бақылау және бағалау жетстіктері жөніндегі деректер (жазбаша бақылау тапсырмалар, тестік тапсырмалар, өзін- өзі тексеру сұрақтарының тізімі және т.б..);
Тестік тапсырмалары
1. {хn} тізбегінің шекті шегі болу үшін … болуы қажетті және жеткілікті:
-
Тізбек мүшесінің номері өскен сайын мүшелер шексіз бір біріне жақындайды .
-
Тізбектің шектелген.
-
Тізбектің монотонды.
-
Тізбектің шектелген және монотонды.
-
Барлық ішкі тізбегінің шекті шегі бар .
2.
![]() функцияның анықталу облысын табыңыз
функцияның анықталу облысын табыңыз
3. Теңсіздіктің дұрыс шешімін
тап: ![]()
А) ![]()
В) ![]()
С) ![]()
Д) ![]()
Е) ![]()
4. Теңсіздікті шеш:![]()
А) ![]()
В) ![]()
С) ![]()
Д) ![]()
Е) ![]()
5. y=-5x+4 функциясына кері функцияны табыңдар
А) ![]()
В) ![]()
С) ![]()
Д) ![]()
Е) ![]()
6.
![]() функциясының (1;2)
нүктесіндегі мәнін есептеу
керек
функциясының (1;2)
нүктесіндегі мәнін есептеу
керек
-
0
-
1
-
e
-

-

7.
 функциясының
функциясының ![]() нүктедегі мәнін
есепте:
нүктедегі мәнін
есепте:
A)![]()
B) 1
C) 0
D)![]()
E)![]()
8.
![]() функциясының
функциясының ![]() нүктедегі мәнін
есепте:
нүктедегі мәнін
есепте:
A) e
B)
![]()
C) e
D)![]()
E)1
9. ![]() мәнін
табыңыз
мәнін
табыңыз
А) ![]()
В) ![]()
С) ![]()
Д) ![]()
Е) ![]()
10. ![]() мәнін
табыңыз
мәнін
табыңыз
А) ![]()
В) ![]()
С) 0
Д) ![]()
Е) ![]()
11. х аргумент нолге
ұмтылғанда ![]() функциясының шегі
:
функциясының шегі
:
-
ноль.
-
1
-
шексіздік.
-
е саны.
-
e2.
12.
![]() шегін
есепте:
шегін
есепте:
A)
![]() .
.
B) -4.
C)
![]() .
.
D) 3.
E) 4.
13. Шекте
есепте: ![]() .
.
A) ;
B) e;
C) 2;
D) 0;
E) e5.
14. Шекте
есепте: ![]() .
.
A)
![]() ;
;
B) 5;
C) 6;
D) 0;
E) .
15. Шекте
есепте: ![]()
A) 14;
B) 13;
C) 12;
D) 15;
E) 10.
16. Шектің мәні неге
тең? ![]()
A) a=1;
B) a=-1;
C) a=3;
D) a=-5;
E) a=3/5
17. Шекте
есепте: ![]() .
.
A) ![]() ;
;
B) –2;
C) 3;
D) 8;
E) 4.
18.
![]() шегін
есепте:
шегін
есепте:
-
 .
. -
 .
. -
 .
. -
2.
-
-2.
19.![]() шегін есепте:
шегін есепте:
-
 .
. -
25.
-

-
табылмайды.
-
0.
20.
![]() шегін
есепте:
шегін
есепте:
-
 .
. -
0.
-
1.
-
-1.
-
3.
21. ![]() шегін
есепте:
шегін
есепте:
-
-1.
-
–0,5.
-
0,5.
-
 .
. -
3.
22.
![]()
-
1/3
-
2/3
-
3/5
-
2/9
-
-2/3
23.![]()
-
4
-
-1/4
-
1/2
-
1/4
-
-2
24. 
-
4
-
0
-

-
1
-
1/4
25. Шекті тап. ![]()
А) 1
В) е
С) ![]()
Д) 0
Е) 2
26. 
-
4
-
0
-

-
1
-
1/4
27. ![]()
-
100
-
1
-

-
1/10
-
10
28. ![]()
-
1/4
-

-
0
-
-4/3
-
-3
29. ![]()
-
2/3
-

-
0
-
1/3
-
6
30. Шекті есепте: ![]()
А) 1
В) е
С) е2
Д) е-1
Е) 0
31. Функцияның берілу тәсілдері:
А) аналитикалық, графикалық,сөйлемдер арқылы
B)аналитикалық, графикалық, сөйлемдер арқылы
C) графикалық, таблицалық, сөйлемдер арқылы
D)аналитикалық, графикалық, таблицалық, сөйлемдер арқылы
E) аналитикалық, таблицалық
32. Дифференциалданатын функцияның нүктеде экстремум болуының қажетті шарты:
-
f' (x)>0.
-
f''(x)=0.
-
f''(x)>0.
-
f''(x)=0.
-
f'(x)=0.
33.Егер f(x) функциясын х нүктесінде дифференциалданатын болса, онда ол нүктеде функция ...
-
үзілісті.
-
үзіліссіз.
-
1 -ге тең.
-
10 ға тең.
-
3 -ке тең.
34. Теңсіздіктің дұрыс шешімін
тап: ![]()
А) ![]()
В) ![]()
С) ![]()
![]()
Д) ![]()
Е) ![]()
35. Функцияның анықталу
облысын тап:![]()
А) ![]()
В) ![]()
С) ![]()
Д) ![]()
Е) ![]()
36.
x =
![]() функцияның анықталу облысын табыңыз.
функцияның анықталу облысын табыңыз.
A) x0;
B) x1;
C) x2;
D) x;
E) x1.
37.
![]() функциясының
функциясының![]() нүктедегі мәнін
есепте:
нүктедегі мәнін
есепте:
-
-e
-

-
1
-
0
-
e
38.
![]() функциясының
функциясының![]() нүктедегі мәнін
есепте:
нүктедегі мәнін
есепте:
-
0
-
2
-
e
-
e
-

39.
![]() функциясының
функциясының ![]() нүктедегі мәнін
есепте:
нүктедегі мәнін
есепте:
-
-1
-
1
-
e
-

-
0
40.
![]() функциясының
функциясының ![]() нүктедегі мәнін
есепте:
нүктедегі мәнін
есепте:
-

-

-

-
-e
-

41. ![]() мәнін
табыңыз
мәнін
табыңыз
А) ![]()
В) ![]()
С) 0
Д) ![]()
Е) ![]()
42. ![]() мәнін
табыңыз
мәнін
табыңыз
А) ![]()
В) ![]()
С) 0
Д) ![]()
Е) ![]()
43. Шекте есепте: 
A) ;
;
B) 1;
C)![]() ;
;
D)![]() ;
;
E)![]() .
.
44. Егер
![]() болса, шектің
мәні
болса, шектің
мәні ![]() ?
?
A) a=-3;
B) a=1;
C) a=-1/2;
D) a=0;
E) a=-1
45. Шекте
есепте: ![]() .
.
A) 2;
B) –3;
C) 1;
D)
![]() ;
;
E) 3.
46. Шекте
есепте:  .
.
A)
![]() ;
;
B)
![]() ;
;
C) ![]() ;
;
D) ![]() ;
;
E) 2.
47. Шекте
есепте: ![]() .
.
A) 0;
B)
![]() ;
;
C) 2;
D) 1;
E) –2.
48. ![]() шегін
есепте:
шегін
есепте:
-
1.
-
4.
-
3.
-
e
-
0.
49.![]() шегін
есепте:
шегін
есепте:
-
1.
-
0.
-
 .
. -
 .
. -

50.
![]() шегін
есепте:
шегін
есепте:
-
1.
-
 .
. -
 .
. -
 .
. -
 .
.
51.
![]() функциясының туындысын
табыңыз:
функциясының туындысын
табыңыз:
А)
![]()
![]() .
.
В)
![]() .
.
С)
![]() .
.
D)
![]() .
.
Е)
![]() .
.
52.![]() функциясының туындысын
есепте:
функциясының туындысын
есепте:
A)
![]() .
.
B)
![]()
C)
![]() .
.
D)
![]() .
.
E)
![]() .
.
53.![]() функциясының туындысын
есепте:
функциясының туындысын
есепте:
A)
y/ =-![]() .
.
B)
y/=![]() .
.
C)
y/=![]() .
.
D)
y/ = ![]() .
.
E)
y/=![]() .
.
54.![]() функциясының туындысын
тап:
функциясының туындысын
тап:
A)
![]()
B)
![]() .
.
C)
![]() .
.
D)
![]() .
.
E)
![]() .
.
55.![]() функциясының туындысын
есепте:
функциясының туындысын
есепте:
А)
![]() .
.
B)
![]() .
.
C)
![]() .
.
D)
![]() .
.
E)
![]()
56.y=f(x) функциясының туындысы деп:
A)
![]() .
.
B)
![]() .
.
C)
![]() .
.
D)
![]() .
.
E)
![]() .
.
57.
![]() функциясының туындысын
есепте:
функциясының туындысын
есепте:
А) ![]() .
.
В) ![]() .
.
С) ![]() .
.
D) ![]() .
.
Е) ![]() .
.
58.![]() функциясының туындысын
есепте:
функциясының туындысын
есепте:
A)
![]() .
.
B)
![]() .
.
C)![]() .
.
D)
![]() .
.
E)
![]() .
.
59. Егер f '(x) туындысының таңбасының аргументі х=с кризистік нүктесінде солдан оңға ауысқанда плюстен минуске ауысса, онда функция бұл нүктеде ...
A) min.
B) 0.
C) max.
D) иілу нүктесі.
Е) 1.
60.![]() функциясының туындысын
есепте:
функциясының туындысын
есепте:
A)
y/ = ![]() .
.
B)
y/ = ![]() .
.
C)
y/ = ![]() .
.
D)
y/ = ![]() .
.![]()
E)
y/ = ![]() .
.![]()
61.
![]() функциясының туындысын есепте:
функциясының туындысын есепте:
А) 3х3 е2х.
В) (3х3 +2х3)е2х .
С) 3х3 +е2х.
D) 6х2 е2х.
Е) 3х3 +2е2х.
62.
![]() функциясының
туындысын есепте:
функциясының
туындысын есепте:
-
 .
. -
 .
. -
 .
. -
 .
. -

жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Олимпиадалық есептерді шешу
Олимпиадалық есептерді шешу
Қазақстан Республикасы білім және ғылым министрлігі
Ы. Алтынсарин атындағы Арқалық мемлекеттік педагогикалық институты
Жаратылыстану және ақпараттандыру факультеті
Математика және физика кафедрасы

ОҚУ-ӘДІСТЕМЕЛІК КЕШЕН
«Олимпиадалық есептерді шешу»
Пән атауы
Мамандығы 5В010900– «Математика»
Шифр, мамандық атауы
Арқалық, 2015
Құрастырушы: аға оқытушы Абдрахманова М.Т
ОӘК аңдатпасы: «Олимпиадалық есептерді шешу» курсы бойынша құрастырылып отырған оқу-әдістемелік құжат «Математика» мамандығы бойынша кредиттік жүйеде оқитын студенттерге арналған; оқу сабақтарының түрлері және тақырыптары бойынша оқу уақытын бөлуді анықтайды; аудиториядағы және аудиториядан тыс уақыттағы студенттердің өзіндік жұмыстарының мазмұнын анықтайды; студенттердің танымдық және творчествалық білімін нығайтады және оқу мен зерттеу процестерінің байланысын туғызады.
Оқу әдістемелік кешен «Олимпиадалық есептерді шешу»
Жаратылыстану және ақпараттандыру факультетінің студенттеріне арналған/ құрастырған: Абдрахманова М.Т. Арқалық: АрқМПИ баспасы, 2013ж
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
Ы.Алтынсарин атындағы Арқалық мемлекеттік педагогикалық институты
«Бекітілді»
ОжДҚж проректоры
_______ Б.Д.Искакова
«____» _______ 2015ж.
ОЛИМПИАДАЛЫҚ ЕСЕПТЕРДІ ШЕШУ таңдау пәні бойынша ҮЛГІЛІК ОҚУ БАҒДАРЛАМАСЫ
5В010900- Математика мамандығы үшін
Арқалық 2015
Алғы сөз
1. Математика және физика кафедрасы 5В010900 Математика мамандығы бойынша жасалған және ұсынылған.
Үлгілік оқу бағдарламасын құрастырушы: аға оқытушы М.Т.Абдрахманова
2. Ы.Алтынсарин атындағы Арқалық мемлекеттік педагогикалық институтының Ғылыми-әдістемелік кеңесінің шешімімен БЕКІТІЛГЕН және ПАЙДАЛАНУҒА рұқсат етілген.
Хаттама № 1 27.08. 2015ж
3. Таңдау бойынша компоненттің үлгілік оқу бағдарламасы 5В010900 Математика мамандығы үшін үлгілік оқу жоспары және мамандықтың жұмыс оқу жоспары негізінде құрастырылған.
4. Бағдарламаны баспаға Ы.Алтынсарин атындағы Арқалық мемлекеттік педагогикалық институтының жаратылыстану және ақпараттандыру факультетінің оқу-әдістемелік кеңесі ұсынған.
Факультет ОӘК төрайымы _____________________________
(А.Т.Ә)
Хаттама № __ ___________ ___________________ 2015ж
«Келісілді»
Факультет деканы
________ ____________________
(қолы) (А.Т.Ә)
«____» _____ 2015 ж.
ТҮСІНІКТЕМЕ
Пәнді оқытудың мақсаты: құрылымы немесе оларды шығару әдістері бойынша стандартты емес, қиындығы жоғары деңгейдегі есептерді шығарудың әдіс-тәсілдері мен талдау негіздерін зерттеу.
Пәнді оқытудың міндеттері: Негiзгi меселелердi шешуге байланысты студенттер (болашақ мұғалiмдер) өз пәндерін терең меңгеруi, пәнге аса қызығушылығын тудыру;
-
есептер шығаруға қажетті білім, білік, дағдыны қалыптастыру;
-
есептер шығару барысында ойды түйіндеп пәрменділігін арттыруға қажетті әдістерді қолдана білу;
-
ойлау әрекетiне қажетгi теориялық, практикалық мәселелердi меңгеруі
-
курс бағдардамасы бойынша теориялық практикалық бiлiмдi толық меңгеруге тиiс
Пререквезиттері: элементар математика, математика курсына енгізу кіріспесі, алгебра курсы және сандар теориясы; математикалық талдаудың курсы;
Пәннің постреквизиттері: олимпиада есептерін шығару әдістемесі; білім жоғарылату.
Пәннің құзіреттілігі:
Білуі тиіс:
-
Математикалық есептерді шығару үшін негізгі зерттеу әдістерін меңгеру;
-
теориялық және қолданбалы тапсырмаларды шешуге математикалық білімді қолдану;
Біліктілігі болуы тиіс:
-
Студенттердегі математикалық және алгоритмдік ойлауының дамуы;
Дағдылары болуы тиіс:
-
Жұмыс істеу барысында ғылыми, оқу – әдістемелік және анықтамалық әдебиеттерді қолдануда;
-
Өз бетінше өзіндік жұмыс, әзірлемелер әзірлеуде;
Пән мазмұны:
-
Элементар математика курсынан олимпиадалық есептерді шешу жолдары
-
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары
-
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
-
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары
-
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары
-
Жоғары математика курсы бойынша олимпиадалық есептер
-
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары
-
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
-
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары
-
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары
Практикалық (семинарлық) сабақтар және өзіндік жұмыстар. Өзіндік жұмыстардың тақырыптарының жобасы.
-
Элементар математика курсынан олимпиадалық есептерді шешу жолдары
-
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары
-
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
-
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары
-
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары
-
Жоғары математика курсы бойынша олимпиадалық есептер
-
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары
-
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
-
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары
-
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары
Әдебиеттер тізімі.
Негізгі әдебиеттер
-
Математические олимпиады школьников: Книга для учащихся общеобразоват. учреждений Н.Х.Агаханов. Л.П.Купцов, Ю.В.Нестеренко и др. М.: Просвещение: Уч.лит., 1997-208 с.
-
Математические олимпиады школьников: Кн.для учащихся общеобразовать. учреждений Л.П.Купцов, Ю.В.Нестеренко, С.В.Резниченко, А.М.Слинько.- М.: Просвещение, 1998. - 256 с.
-
Математические олимпиады школьников: Кн.для учащихся общеобразовать. учреждений Л.П.Купцов, Ю.В.Нестеренко, С.В.Резниченко, А.М.Слинько.- М.: Просвещение, 1999. - 254 с.
-
Сборник индивидуальных заданий по высшей математике. Часть 1. Под ред. Рябушко А.П.-Мн: Вышейшая школа., 2001.
-
Сборник индивидуальных заданий по высшей математике. Часть 2. Под ред. Рябушко А.П.- Мн: Вышейшая школа., 2001..
-
Сборник индивидуальных заданий по высшей математике. Часть 3. Под ред. Рябушко А.П.- Мн: Вышейшая школа., 2001.
-
Сборник индивидуальных заданий по высшей математике. Часть 4. Под ред. Рябушко А.П.-Мн : Вышейшая школа., 2005.
Қосымша әдебиеттер
1. Ильясов М.Н. Нестандартные задачи математического анализа. Учебно-методическое пособие. Павлодар, 2006.
2. Степаненко В.М. Руководство к решению задач повышенной трудности по высшей математике. Павлодар, 2003.
3.Садовничий В.А., Григорьян А.А., Конягин С.В Задачи студенческих математических олимпиад,. МГУ, 1987.
Қазақстан Республикасы білім және ғылым министрлігі
Ы.Алтынсарин атындағы Арқалық мемлекеттік педагогикалық институты
“Бекітемін”
ОжДҚж проректоры
__________Б.Д.Искакова
2015 ж. “___” _________
Жаратылыстану және ақпараттандыру факультеті
Математика және физика кафедрасы
ЖҰМЫС ОҚУ БАҒДАРЛАМАСЫ
Пән: «Олимпиадалық есептерді шешу»
5В010900 – «Математика» мамандығы үшін
|
|
Оқу түрі |
|
|
Күндізгі |
Сырттай |
|
|
Кредит саны |
3 |
3 |
|
Курсы |
4 |
1 |
|
Семестр |
7 |
2 |
|
Емтихан |
7 |
2 |
|
Дәріс |
15 |
2 |
|
Практикалық (семинар) сабақ |
30 |
4 |
|
Зертханалық сабақ |
- |
- |
|
ОСӨЖ |
30 |
- |
|
СӨЖ |
60 |
129 |
Арқалық, 2015
Құрастырушы: аға оқытушы Абдрахманова М.Т
( A.Т. Ә.)
Математика және физика кафедрасы
Мамандығы : 5В010900 «Математика»
(Мамандықтың шифры, толық атауы)
Оқу нысаны (күндізгі сырттай жоғары кәсіби білім) (күндізгі, сырттай жоғары кәсіби білім)
ҚРМЖМБС Олимпиадалық есептерді шешу таңдау пәні бойынша үлгілік оқу бағдарламасы 27.08.2014.№1 хаттама
(ҚР МЖМБС, типтік бағдарламаның толық атауы, бекіткен күні және ұйым атауы, ОӘБ және пән индексі)
Кафедра мәжілісінде ұсынылды 20 __ ж. “___” _______№_____ хаттама
Кафедра меңгерушісі: ___________________Қожахмет М.С
(Қолы, Т. Е. Ә.)
20 __ ж. “____”_______ хаттама № ___ Факультеттің ғылыми әдістемелік кеңесінде қабылданды
ҒӘК төрайымы ________________________А.Қ.Тулегенова
(Қолы, Т. Е. Ә.)
КЕЛІСІЛДІ:
Жаратылыстану ақпараттандыру факультетінің деканы ______ Умбетов А.У.
(Қолы, Т. Е. Ә.)
Институттың ғылыми - әдістемелік кеңесінде мақұлданды:
20___ж. “___” _______ хаттама №
ОӘБ бастығы __________ А.С.Антаева
(Қолы.)
1.2. Пән туралы мәліметтер
Аталымы: «Олимпиадалық есептерді шешу»
Кредит саны: 3
Өткізу орны: 514 дәрісхана
Пәннің тақырыптық жоспары
|
№ |
Тақырыбы |
Оқу түрі |
|||||||||||||
|
Күндізгі |
Сырттай |
||||||||||||||
|
Барлығы |
Лекция |
Тәжірибе |
Зерт.жұмыс |
СӨЖ |
ОСӨЖ |
Барлығы |
Лекция |
Тәжірибе |
Зерт.жұмыс |
СӨЖ |
ОСӨЖ |
||||
|
1 |
І модуль.Элементар математика |
||||||||||||||
|
1.1 |
Элементар математика курсынан олимпиадалық есептерді шешу жолдары |
10 |
1 |
2 |
|
5 |
2 |
|
|
|
|
|
|
||
|
1.2 |
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары |
10 |
1 |
2 |
|
5 |
2 |
|
|
|
|
|
|
||
|
1.3 |
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
10 |
1 |
2 |
|
5 |
2 |
|
|
|
|
|
|
||
|
1.4 |
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары |
10 |
1 |
2 |
|
5 |
2 |
|
|
|
|
|
|
||
|
1.5 |
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары |
10 |
1 |
2 |
|
5 |
2 |
|
|
|
|
|
|
||
|
|
ІІ модуль. Жоғары математика |
||||||||||||||
|
2.2 |
Жоғары математика курсы бойынша олимпиадалық есептер |
16 |
2 |
4 |
|
6 |
4 |
|
|
|
|
|
|
||
|
2.3 |
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары |
16 |
2 |
4 |
|
6 |
4 |
|
|
|
|
|
|
||
|
2.4 |
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
16 |
2 |
4 |
|
6 |
4 |
|
|
|
|
|
|
||
|
2.5 |
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары |
16 |
2 |
4 |
|
6 |
4 |
|
|
|
|
|
|
||
|
2.5 |
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары |
16 |
2 |
4 |
|
6 |
4 |
|
|
|
|
|
|
||
|
|
Барлығы |
122 |
15 |
30 |
|
60 |
30 |
|
|
|
|
|
|
||
Пәнді оқытудың мақсаты мен міндеттері
Пәнді оқытудың мақсаты: құрылымы немесе оларды шығару әдістері бойынша стандартты емес, қиындығы жоғары деңгейдегі есептерді шығарудың әдіс-тәсілдері мен талдау негіздерін зерттеу.
Пәнді оқытудың міндеттері: Негiзгi меселелердi шешуге байланысты студенттер (болашақ мұғалiмдер) өз пәндерін терең меңгеруi, пәнге аса қызығушылығын тудыру;
-
есептер шығаруға қажетті білім, білік, дағдыны қалыптастыру;
-
есептер шығару барысында ойды түйіндеп пәрменділігін арттыруға қажетті әдістерді қолдана білу;
-
ойлау әрекетiне қажетгi теориялық, практикалық мәселелердi меңгеруі
-
курс бағдардамасы бойынша теориялық практикалық бiлiмдi толық меңгеруге тиiс
Пәннің құзіреттілігі:
Білуі тиіс:
-
Математикалық есептерді шығару үшін негізгі зерттеу әдістерін меңгеру;
-
теориялық және қолданбалы тапсырмаларды шешуге математикалық білімді қолдану;
Біліктілігі болуы тиіс:
-
Студенттердегі математикалық және алгоритмдік ойлауының дамуы;
Дағдылары болуы тиіс:
-
Жұмыс істеу барысында ғылыми, оқу – әдістемелік және анықтамалық әдебиеттерді қолдануда;
-
Өз бетінше өзіндік жұмыс, әзірлемелер әзірлеуде;
Дәріс сабақтарының мазмұны.
І модуль. Элементар математика
Дәріс – 5 сағат, практикалық сабақ – 10 сағат, сөж – 20 сағат.
1-дәріс тақырыбы: Элементар математика курсынан олимпиадалық есептерді шешу жолдары
Жоспар
-
Элементар математика курсынан олимпиадалық есептерді шешу жолдары
2-дәріс тақырыбы: Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары
Жоспар
1.Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары
3-дәріс тақырыбы: Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
Жоспары
1.Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
4-дәріс тақырыбы: Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары
Жоспары
1.Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары
5-дәріс тақырыбы Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары
Жоспары
1.Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары
ІІ модуль. Жоғары математика
Дәріс – 10 сағат, практикалық сабақ – 8 сағат, сөж – 20 сағат.
6-7 дәріс тақырыбы: Жоғары математика курсы бойынша олимпиадалық есептер
Жоспары
Жоғары математика курсы бойынша олимпиадалық есептер
8-9-дәріс тақырыбы: Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары
Жоспары
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары
10-11- дәріс тақырыбы: Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
Жоспары
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
12-13 дәріс тақырыбы: Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары
Жоспары
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары
14-15дәріс тақырыбы: Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары
Жоспары
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары
Студенттің өзіндік жұмысын тапсырмаларын орындау және тапсыру
|
№ |
СӨЖ тақырыптары |
Бақылау түрі |
Орындау мерзімі (апта) |
|
|
Күндізгі бөлім |
||
|
1 |
Элементар математика курсынан олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Слайд дайындау. |
1 апта |
|
2 |
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Типтік есептер |
2 апта |
|
3 |
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
3 апта |
|
4 |
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары |
Конспект. Ұғымдарды баяндау мен талдау. Типтік есептер |
4 апта |
|
5 |
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар Слайд дайындау. Бес жолды өлең құрастыру. |
5 апта |
|
6 |
Жоғары математика курсы бойынша олимпиадалық есептер |
Мәнжаэба. Оқулықпен жұмыс. Слайд дайындау. |
6-7 апта |
|
7 |
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Слайд дайындау. Типтік есептер |
8-9 |
|
8 |
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжаэба. Оқулықпен жұмыс. Пікірталас. Типтік есептер |
10-11 апта |
|
9 |
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары |
Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
12-13апта |
|
10 |
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Слайд дайындау. Типтік есептер |
14-15 апта |
СОӨЖ тапсырмаларын орындау жоспары
|
№ |
Тапсырма тақырыптары |
ОСӨЖ өткізу түрі
|
|
|
Күндізгі бөлім |
|
|
1 |
Элементар математика курсынан олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Слайд дайындау. |
|
2 |
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Типтік есептер |
|
3 |
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжаэба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
|
4 |
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары |
Конспект. Ұғымдарды баяндау мен талдау. Типтік есептер |
|
5 |
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
|
6 |
Жоғары математика курсы бойынша олимпиадалық есептер |
Мәнжазба, тірек сызбалар. Типтік есептер |
|
7 |
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары |
Оқулықпен жұмыс. Бақылау жұмысы №1. |
|
8 |
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
|
9 |
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Слайд дайындау. |
|
10 |
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар Слайд дайындау. Бес жолды өлең құрастыру. |
|
|
Сыртай бөлім |
|
|
|
|
|
Қазақстан Республикасы білім және ғылым министрлігі
Ы.Алтынсарин атындағы Арқалық мемлекеттік педагогикалық институты
“Бекітемін”
ОжДҚж проректоры
__________Б.Д.Искакова
2015 ж. “___” _________
Жаратылыстану және ақпараттандыру факультеті
Математика және физика кафедрасы
ПӘННІҢ ОҚУ БАҒДАРЛАМАСЫ- SYLLABUS
Пән: «Олимпиадалық есептерді шешу»
Мамандығы: 5В010900 – «Математика»
|
Оқу түрі |
||
|
Күндізгі |
Сырттай |
|
|
Кредит саны |
3 |
3 |
|
курсы |
4 |
1 |
|
Семестр |
7 |
2 |
|
Емтихан |
7 |
2 |
|
Дәріс |
15 |
2 |
|
Практикалық (семинар) сабақ |
30 |
4 |
|
Зертханалық сабақ |
|
- |
|
ОСӨЖ |
30 |
- |
|
СӨЖ |
60 |
129 |
Арқалық, 2015
Құрастырушы: аға оқытушы Абдрахманова М.Т
( A.Т. Ә.)
Математика және физика кафедрасы
Мамандығы : 5В010900 «Математика»
(Мамандықтың шифры, толық атауы)
Оқу нысаны (күндізгі сырттай жоғары кәсіби білім) (күндізгі, сырттай жоғары кәсіби білім)
(күндізгі, сырттай жоғары кәсіби білім)
ҚРМЖМБС Олимпиадалық есептерді шешу таңдау пәні бойынша үлгілік оқу бағдарламасы 27.08.2014.№1 хаттама
(ҚР МЖМБС, типтік бағдарламаның толық атауы, бекіткен күні және ұйым атауы, ОӘБ және пән индексі)
Кафедра мәжілісінде ұсынылды 2015 ж. “___” _______№_____ хаттама
Кафедра меңгерушісі: ___________________ Қожахмет М.С
(Қолы, Т. Е. Ә.)
2015 ж. “____”_______ хаттама № ___ Факультеттің ғылыми әдістемелік кеңесінде қабылданды
ҒӘК төрайымы __________________________ А.Қ.Тулегенова
(Қолы, Т. Е. Ә.)
КЕЛІСІЛДІ:
Жаратылыстану ақпараттандыру факультетінің деканы ______ Умбетов А.У.
(Қолы, Т. Е. Ә.)
Институттың ғылыми - әдістемелік кеңесінде мақұлданды:
2015 ж. “___” _______ хаттама №
ОӘБ бастығы __________ Антаева А.С
(Қолы.)
1. Оқытушы туралы мәліметтер
Абдрахманова М.Т Арқалық мемлекеттік педагогикалық институтының математика, физика кафедрасында 2009 жылдан жұмыс істейді. Арқалық мемлекеттік педагогикалық институтының аға оқытушысы. Мекен жайы: Арқалық қаласы, Ш.Жанібек көшесі, 83/1-7.
2 Байланыс телефоны: (871430)71954 Байланыс ақпараты және кафедраға келген уақыты.
3 Пән туралы мәліметтер
Аталымы: «Олимпиадалық есептерді шешу»
Кредит саны: 3
Өткізу орны:514 дәрісхана
|
Курс |
семестр |
Кредит саны |
Дәріс, сағат саны |
Практикалық сабақ |
СОӨЖ |
СӨЖ |
|
4 |
7 |
2 |
15 |
15 |
30 |
60 |
4.Пререквезиттері: элементар математика, математика курсына енгізу кіріспесі, алгебра курсы және сандар теориясы; математикалық талдаудың курсы;
5.Пәннің постреквизиттері: олимпиада есептерін шығару әдістемесі; білім жоғарылату.
6.Курстың саясаты мен реті бойынша оқытушы пәнді оқыту үрдісінде студентке төмендегідей жағдайда әкімшілік талаптар қоя алады:
-
Сабаққа кешікпеу;
-
Сабақты себепсіз жібермеу;
-
Аудиториядағы тәртібі;
-
Тапсырманы мерзімінде орындау;
7.Пәнді оқытудың мақсаты мен міндеттері
Пәнді оқытудың мақсаты: құрылымы немесе оларды шығару әдістері бойынша стандартты емес, қиындығы жоғары деңгейдегі есептерді шығарудың әдіс-тәсілдері мен талдау негіздерін зерттеу.
Пәнді оқытудың міндеттері: Негiзгi меселелердi шешуге байланысты студенттер (болашақ мұғалiмдер) өз пәндерін терең меңгеруi, пәнге аса қызығушылығын тудыру;
-
есептер шығаруға қажетті білім, білік, дағдыны қалыптастыру;
-
есептер шығару барысында ойды түйіндеп пәрменділігін арттыруға қажетті әдістерді қолдана білу;
-
ойлау әрекетiне қажетгi теориялық, практикалық мәселелердi меңгеруі
-
курс бағдардамасы бойынша теориялық практикалық бiлiмдi толық меңгеруге тиiс
Пәннің құзіреттілігі:
Білуі тиіс:
-
Математикалық есептерді шығару үшін негізгі зерттеу әдістерін меңгеру;
-
теориялық және қолданбалы тапсырмаларды шешуге математикалық білімді қолдану;
Біліктілігі болуы тиіс:
-
Студенттердегі математикалық және алгоритмдік ойлауының дамуы;
Дағдылары болуы тиіс:
-
Жұмыс істеу барысында ғылыми, оқу – әдістемелік және анықтамалық әдебиеттерді қолдануда;
-
Өз бетінше өзіндік жұмыс, әзірлемелер әзірлеуде;
9 Қысқаша сипаттама: пән туралы мәлімет
Элементар математика курсынан олимпиадалық есептерді шешу жолдары
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
Жоғары математика курсы бойынша олимпиадалық есептер
10.Семинар сабағының жоспары
1-2 практикалық сабақ тақырыбы: Элементар математика курсынан олимпиадалық есептерді шешу жолдары
3-4- практикалық сабақ тақырыбы: Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары
5-6 практикалық сабақ тақырыбы: Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
7-8- практикалық сабақ тақырыбы: Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары
9-10 практикалық сабақ тақырыбы: Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары
11-14 практикалық сабақ тақырыбы: Жоғары математика курсы бойынша олимпиадалық есептер
15-18 практикалық сабақ тақырыбы: Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары
19-22 практикалық сабақ тақырыбы: Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
24-26 практикалық сабақ тақырыбы: Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары
27-30 практикалық сабақ тақырыбы: Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары
11.Студенттің өзіндік жұмыс тапсырмаларын орындау және тапсыру
|
№ |
СӨЖ тақырыбы |
Бақылау түрі |
Орындау мерзімі |
|
|
Күндізгі бөлім |
||
|
1 |
Элементар математика курсынан олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Слайд дайындау. |
1 апта |
|
2 |
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Типтік есептер |
2 апта |
|
3 |
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
3 апта |
|
4 |
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары |
Конспект. Ұғымдарды баяндау мен талдау. Типтік есептер |
4 апта |
|
5 |
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар Слайд дайындау. Бес жолды өлең құрастыру. |
5 апта |
|
6 |
Жоғары математика курсы бойынша олимпиадалық есептер Жоспары |
Мәнжазба. Оқулықпен жұмыс. Слайд дайындау. |
6-7апта |
|
7 |
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Слайд дайындау. Типтік есептер |
8-9апта |
|
8 |
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Пікірталас. Типтік есептер |
10-11апта |
|
9 |
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары |
Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
12-13 апта |
|
10 |
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Слайд дайындау. Типтік есептер |
14-15 апта |
|
|
Сырттай |
||
|
1 |
Элементар математика курсынан олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Слайд дайындау. |
1 апта |
|
2 |
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Типтік есептер |
2 апта |
|
3 |
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжаэба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
3 апта |
|
4 |
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары |
Конспект. Ұғымдарды баяндау мен талдау. Типтік есептер |
4 апта |
|
5 |
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
5 апта |
|
6 |
Жоғары математика курсы бойынша олимпиадалық есептер Жоспары |
Мәнжазба, тірек сызбалар. Типтік есептер |
6 -7 апта |
|
7 |
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары |
Оқулықпен жұмыс. Бақылау жұмысы №1. |
8-9 апта |
|
8 |
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
10-11апта |
|
9 |
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Слайд дайындау. |
12-13 апта |
|
10 |
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар Слайд дайындау. Бес жолды өлең құрастыру. |
14-15 апта |
12.Оқытушымен студенттің өзіндік жұмыс (кеңес) тапсырмалары
|
№ |
Тапсырма тақырыптары |
ОСӨЖ өткізу түрі
|
|
|
Күндізгі оқу |
|
|
1 |
Элементар математика курсынан олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Слайд дайындау. |
|
2 |
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Типтік есептер |
|
3 |
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжаэба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
|
4 |
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары |
Конспект. Ұғымдарды баяндау мен талдау. Типтік есептер |
|
5 |
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
|
6 |
Жоғары математика курсы бойынша олимпиадалық есептер Жоспары |
Мәнжазба, тірек сызбалар. Типтік есептер |
|
7 |
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары |
Оқулықпен жұмыс. Бақылау жұмысы №1. |
|
8 |
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
|
9 |
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Слайд дайындау. |
|
10 |
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар Слайд дайындау. Бес жолды өлең құрастыру. |
|
11 |
Элементар математика курсынан олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
|
12 |
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Слайд дайындау. Типтік есептер |
|
13 |
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
|
14 |
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары |
Оқулықпен жұмыс. Бақылау жұмысы №2. |
|
15 |
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары |
Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
|
|
|
|
|
|
|
|
13. Емтихан кеңестері
|
№ |
Кеңес жүргізілетін жұмыс түрлері |
Кеңес беру күні |
Кеңес беру уақыты |
|
1 |
«Олимпиадалық есептерді шешу» |
|
|
14.Курстық жұмыстың тақырыбы, мәнжазба
Курстық жұмыс жоспарланбаған
Мәнжазба
-
Элементар математика курсынан олимпиадалық есептерді шешу жолдары
-
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары
-
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
-
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары
-
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары
-
Жоғары математика курсы бойынша олимпиадалық есептер
-
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары
-
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
-
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары
-
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары олимпиадалық есептерді шешу жолдары
15. Студенттердің білімін бағалау жүйесі
Студенттердің оқу жетістіктері (білім, білік, дағды және құзіреттілігі) ҚР білім және ғылым министрлігінің 2011 жылғы 20-сәуірдегі №152 бұйрығымен бекітілген Кредиттік оқыту технологиясы бойынша оқу үдерісін ұйымдастырудың ережесіне сәйкес 100 балдық шкаламен бағаланады.
Ағымдағы бақылау (1-7 және 8-15 апталарда өткізіледі):
1. Сабаққа қатысу
2. Практикалық (зертханалық) сабақтағы тапсырмаларды орындау
3. Үй тапсырмасын орындау
4. СӨЖ бойынша тапсырмаларды орындау
Сабаққа қатысуына байланысты 1 баллдан беріледі (барлығы- Х) ең жоғарғы балл -100. Практикалық (зертханалық) сабақтағы активтілігі, тапсырмаларды орындауына байланысты практикалық (зертханалық) сабаққа 100 балл. Үй тапсырмасын орындау денгейіне байланысты максималды 100 балл беріледі. Үй тапсырмасының көлемін оқытушы анықтайды. СӨЖ бойынша тапсырмаларды орындау балдары кестедегі тақырыптар бойынша 100 балмен бағалайды, орташа көрсеткіші СӨЖ тапсырмалардын орындаудын пайыздық корсеткіші болып табылады.
Аралық бақылау ( 7, 15 апталарда өткізіледі):
Тест (билет, коллоквиум, мамандыққа байланысты нормативтық тапсырмалар т.б.) сұрақтары бойынша жауап алу арқылы білімі тексеріліп, жоғары жауапқа 100 балл беріледі.
Рорташа = (Р1 + Р2) / 2
(Р1 – 1 аралық бақылаудағы рейтингі, Р2 – 2 аралық бақылаудағы рейтингі).
Қорытынды
бақылау семестрдің соңында алынады
(Емтихан түрін көрсету) . Қорытынды бақылау мына формула бойынша
есептелінеді: ![]()
Қорытынды баға төмендегі кестеге сәйкес қойылады:
|
Әріп жүйесі бойынша |
Балдың сандық эквивалент |
Проценттік мазмұны |
Дәстүрлі жүйе бойынша бағалау |
|
А |
4,0 |
95-100 |
өте жақсы |
|
А- |
3,67 |
90-94 |
|
|
В+ |
3,33 |
85-89 |
Жақсы |
|
В |
3 |
80-84 |
|
|
В- |
2,67 |
75-79 |
|
|
С+ |
2,33 |
70-74 |
қанағаттанарлық |
|
С |
2,0 |
65-69 |
|
|
С- |
1,67 |
60-64 |
|
|
D+ |
1,33 |
55-59 |
|
|
D |
1,0 |
50-54 |
|
|
F |
0 |
0-49 |
қанағаттанғысыз |
16. Әдебиеттер тізімі
-
Негізгі әдебиеттер тізімі
-
Математические олимпиады школьников: Книга для учащихся общеобразоват. учреждений Н.Х.Агаханов. Л.П.Купцов, Ю.В.Нестеренко и др. М.: Просвещение: Уч.лит., 1997-208 с.
-
Математические олимпиады школьников: Кн.для учащихся общеобразовать. учреждений Л.П.Купцов, Ю.В.Нестеренко, С.В.Резниченко, А.М.Слинько.- М.: Просвещение, 1998. - 256 с.
-
Математические олимпиады школьников: Кн.для учащихся общеобразовать. учреждений Л.П.Купцов, Ю.В.Нестеренко, С.В.Резниченко, А.М.Слинько.- М.: Просвещение, 1999. - 254 с.
-
Сборник индивидуальных заданий по высшей математике. Часть 1. Под ред. Рябушко А.П.-Мн: Вышейшая школа., 2001.
-
Сборник индивидуальных заданий по высшей математике. Часть 2. Под ред. Рябушко А.П.- Мн: Вышейшая школа., 2001..
-
Сборник индивидуальных заданий по высшей математике. Часть 3. Под ред. Рябушко А.П.- Мн: Вышейшая школа., 2001.
-
Сборник индивидуальных заданий по высшей математике. Часть 4. Под ред. Рябушко А.П.-Мн : Вышейшая школа., 2005.
-
Қосымша әдебиеттер тізімі
1. Ильясов М.Н. Нестандартные задачи математического анализа. Учебно-методическое пособие. Павлодар, 2006.
2. Степаненко В.М. Руководство к решению задач повышенной трудности по высшей математике. Павлодар, 2003.
3.Садовничий В.А., Григорьян А.А., Конягин С.В Задачи студенческих математических олимпиад,. МГУ, 1987.
17. Емтихан сұрақтары
І аралық бақылау сұрақтары
-
Рационал өрнектерді түрлендіру.
-
Көпмүшені көбейткіштерге жіктеу;
-
Ортақ көбейткішті жақша сыртына шығару,
-
Топтау тәсілі,
-
Қысқаша көбейту формулалары,
-
Квадрат үшмүшені жіктеу,
-
Жаңа айнымалы ендіру
-
Жасанды тәсілдер.
-
Бүтін санның бөлінгіштігіне берілген есептер.
-
Көпмүшені қалдықпен бөлу.
-
p(x)=(x-a)q(x) формуласы, а - көпмүшенің түбірі.
-
Рационал өрнектерді түрлендіру,
-
Модуль таңбалы өрнектерді түрлендіру.
-
Жай бөлшектер.
-
Рационал бөлшектерді жай бөлшектер қосындысына түрлендіру.
-
Қосындылаудың әртүрлі тәсілдері.
-
Математикалық индуксия әдісі.
-
Қосындылау және бөлінгіштік жөніндегі есептерге индукция әдісін қолдану;
-
Иррационал өрнектерді түрлендіру.
-
Түбір ұғымы
-
Арифметикалық түбір.
-
Қасиеттері
-
Радикалдардың қасиеті.
-
Радикалдардың формуласы.
-
Рационал көрсеткішті дәреже
-
Рационал көрсеткішті дәреженің қасиеттері.
-
Иррационал өрнектерді түрлендіру.
-
Бөлшектің бөлімін иррационалдықтан құтқару;
-
Тригонометриялық өрнектерді түрлендіру.
-
Кері тригонометриялық өрнектерді түрлендіру.
-
Тригонометрияның формулалары.
-
Тиргонометриялық теңбе-теңдіктерді дәлелдеу,
-
Тригонометриялық өрнектерді түрлендіру,
-
Көмекші аргумент ендіру әдісі.
-
Универсал ауыстыру.
-
Басқа аргументті тригонометриялық функцияның мәнін іздеу.
-
Тригонометриялық өрнектің сандық мәнін табу.
-
Өлшенген координаталарды функцияның графигін салу.
-
Жоғары дәрежелі теңдеулер.
-
Алгебралық теңсіздіктер.
-
Рационал теңсіздіктерді интервалдар әдісімен шешу.
-
Теңсіздіктер жүйесі және жиынтығы.
-
Модульмен берілген теңсіздіктер.
-
Иррационал теңсіздіктер.
-
Теңсіздіктер құруға берілген есептер.
-
Параметрлі теңдеулер мен теңсіздіктер;
-
Трансцендентті теңдеулер мен теңсіздіктер.
-
Көрсеткіштік, логарифмдік теңдеулер мен теңсіздіктер,
-
Оларды шешудің негізгі әдістері.
-
Көрсеткішті теңдеулер
-
Көрсеткішті теңсіздіктер.
-
Логарифмдік теңдеулер
-
Логарифмдік теңсіздіктер.
-
Көрсеткішті дәрежелі теңдеулер мен теңсіздіктер.
-
Көрсеткіштік теңдеулердің жүйесі.
-
Логарифмдік теңдеулердің жүйесі.
-
Тригонометриялық теңдеулер.
-
Көбейткіштерге жіктеу,
-
Жаңа айнымалы ендіру сиақты шешудің негізгі екі әдісі.
-
Біртектес теңдеулер және оған келтірілетін теңдеулер.
-
Тригонометриялық теңдеулерді шешу үшін универсал ауыстыруды қолдану.
-
Тригонометриялық теңдеулерді шешудің жасанды тәсілдері.
-
Берілген щартқа сай түбірді таңдау.
-
Тригонометриялық теңдеулер жүйесі.
-
Тригонометриялық теңсіздіктер.
ІІ аралық бақылау сұрақтары
-
Матрица түрлері.
-
Матрицаларға қолданылатын сызықтық амалдар.
-
Матрицаларды көбейту.
-
Анықтауыштың негізгі қасиеттері.
-
Лаплас теоремасы.
-
Кері матрица.
-
Матрицаның рангісі.
-
Матрицаның элементарлық түрлендірулері.
-
Матрицаның экономикалық түсініктемесі.
-
Теңдеулер жүйелерінің үйлесімділігі.
-
Крамер ережесі.
-
Матрицалық теңдеулер жүйесін шешу.
-
Гаусс әдісі.
-
Біртекті сызықтық теңдеулер жүйесі.
-
Іргелес шешімдер жүйесі.
-
Сызықтық теңсіздіктер жүйесін және оның шешімін зерттеу.
-
Сызықтық теңсіздіктер жүйесінің экономикалық түсініктемесі
-
Векторларға қолдалынатын сызықтық амалдар.
-
Векторлардың скалярлық көбейтіндісі және оның қасиеттері.
-
Евклидтік кеңістік.
-
Векторлар жүйесінің базисі, рангісі.
-
Векторларды экономикалық есептерде қолдану.
-
Сызықтық операторлардың меншікті векторлары мен меншікті сандары. Квадратты формалары.
-
Функциалардың берілу тәсілдері.
-
Негізгі элементар функциалар.
-
Сандық тізбектер және шегі.
-
Функция шегі, біржақты шектер.
-
Элементар функциалар туындылары.
-
Күрделі, кері және айқындалған функциялар туындысы.
-
Жоғары ретті туындылар.
-
Кездейсоқ оқиғалар түрлері.
-
Тәуелді және тәуелсіз оқиғалар.Ықтималдық.
-
Шартты ықтималдықтар.
-
Ықтималдықтарды қосу және көбейту теоремалары.
-
Бернулли схемасы және оның формуласы.
-
Ең ықтимал сан.
-
Лапластың локалдық және интегралдық теоремалары.
-
Дискретті және үзіліссіз кездейсоқ шамалар.
-
Үлестірім функциясы және үлестірім тығыздығы.
-
Кездейсоқ шамалардың сандық сипаттамалары.
-
Тәуелсіз сынақтарда салыстырмалы жиліктің оқиғаның тұрақты ықтималдығының ауытқуының ықтималдығы.
-
Биномдық, Пуассон.
-
Үлестірім заңдарының сандық сипаттамалары.
-
Негізгі ұғымдар.
-
Тексерудің жалпы схемасы.
-
Қалыпты үлестіріммен берілген бас дисперсияларын салыстыру.
-
Бір факторлы дисперсиялық талдау.
-
Екі факторлық дисперсиялық талдау түсінігі.
-
Негізгі ұғымдар.
-
Сызықтық регрессия теңдеулер.
Қорытынды бақылауға дайындық сұрақтары (емтихан).
-
Матрица түрлері.
-
Матрицаларға қолданылатын сызықтық амалдар.
-
Матрицаларды көбейту.
-
Анықтауыштың негізгі қасиеттері.
-
Лаплас теоремасы.
-
Кері матрица.
-
Матрицаның рангісі.
-
Матрицаның элементарлық түрлендірулері.
-
Матрицаның экономикалық түсініктемесі.
-
Теңдеулер жүйелерінің үйлесімділігі.
-
Крамер ережесі.
-
Матрицалық теңдеулер жүйесін шешу.
-
Гаусс әдісі.
-
Біртекті сызықтық теңдеулер жүйесі.
-
Іргелес шешімдер жүйесі.
-
Сызықтық теңсіздіктер жүйесін және оның шешімін зерттеу.
-
Сызықтық теңсіздіктер жүйесінің экономикалық түсініктемесі
-
Векторларға қолдалынатын сызықтық амалдар.
-
Векторлардың скалярлық көбейтіндісі және оның қасиеттері.
-
Евклидтік кеңістік.
-
Векторлар жүйесінің базисі, рангісі.
-
Векторларды экономикалық есептерде қолдану.
-
Сызықтық операторлардың меншікті векторлары мен меншікті сандары. Квадратты формалары.
-
Функциалардың берілу тәсілдері.
-
Негізгі элементар функциалар.
-
Сандық тізбектер және шегі.
-
Функция шегі, біржақты шектер.
-
Элементар функциалар туындылары.
-
Күрделі, кері және айқындалған функциялар туындысы.
-
Жоғары ретті туындылар.
-
Кездейсоқ оқиғалар түрлері.
-
Тәуелді және тәуелсіз оқиғалар.Ықтималдық.
-
Шартты ықтималдықтар.
-
Ықтималдықтарды қосу және көбейту теоремалары.
-
Бернулли схемасы және оның формуласы.
-
Ең ықтимал сан.
-
Лапластың локалдық және интегралдық теоремалары.
-
Дискретті және үзіліссіз кездейсоқ шамалар.
-
үлестірім функциясы және үлестірім тығыздығы
-
Кездейсоқ шамалардың сандық сипаттамалары.
-
Тәуелсіз сынақтарда салыстырмалы жиліктің оқиғаның тұрақты ықтималдығының ауытқуының ықтималдығы.
-
Биномдық, Пуассон.
-
Үлестірім заңдарының сандық сипаттамалары.
-
Негізгі ұғымдар.
-
Тексерудің жалпы схемасы.
-
Қалыпты үлестіріммен берілген бас дисперсияларын салыстыру.
-
Бір факторлы дисперсиялық талдау.
-
Екі факторлық дисперсиялық талдау түсінігі.
-
Негізгі ұғымдар.
-
Сызықтық регрессия теңдеулер.
-
Байланыс параметрлнрінің маңыздылығын тексеру.
2. ПӘННІҢ ОҚУ-ӘДІСТЕМЕЛІК КЕШЕННІҢ МАЗМҰНЫ МЕН ТІЗБЕСІ
2.1. Пән бойынша тапсырмалардың тапсыруы және кестенің орындалуы (сабақ кестесінен тыс )
|
№ |
Тақырыбы |
СОӨЖ өткізу түрлері |
Тапсырманы орындау уақыты |
|
Күндізгі бөлім |
|||
|
1 |
Элементар математика курсынан олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Слайд дайындау. |
1 апта |
|
2 |
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Типтік есептер |
2 апта |
|
3 |
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжаэба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
3 апта |
|
4 |
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары |
Конспект. Ұғымдарды баяндау мен талдау. Типтік есептер |
4 апта |
|
5 |
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
5 апта |
|
6 |
Жоғары математика курсы бойынша олимпиадалық есептер Жоспары |
Мәнжазба, тірек сызбалар. Типтік есептер |
6 -7 апта |
|
7 |
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары |
Оқулықпен жұмыс. Бақылау жұмысы №1. |
8-9 апта |
|
8 |
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
10-11апта |
|
9 |
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Слайд дайындау. |
12-13 апта |
|
10 |
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар Слайд дайындау. Бес жолды өлең құрастыру. |
14-15 апта |
|
Сырттай бөлім |
|||
|
1 |
Элементар математика курсынан олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Слайд дайындау. |
1 апта |
|
2 |
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар. Типтік есептер |
2 апта |
|
3 |
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжаэба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
3 апта |
|
4 |
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары |
Конспект. Ұғымдарды баяндау мен талдау. Типтік есептер |
4 апта |
|
5 |
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
5 апта |
|
6 |
Жоғары математика курсы бойынша олимпиадалық есептер Жоспары |
Мәнжазба, тірек сызбалар. Типтік есептер |
6 -7 апта |
|
7 |
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары |
Оқулықпен жұмыс. Бақылау жұмысы №1. |
8-9 апта |
|
8 |
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Венн диаграммасы, оқулықпен жұмыс. Типтік есептер |
10-11апта |
|
9 |
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба. Оқулықпен жұмыс. Слайд дайындау. |
12-13 апта |
|
10 |
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары |
Мәнжазба, тірек сызбалар Слайд дайындау. Бес жолды өлең құрастыру. |
14-15 апта |
-
2.2. Пәннің оқу- әдістемелік картасымен қамтамасыз етілуі
|
№ |
Дәріс тақырыбы |
Қолданылатын әдебиеттер |
Кинофильмдер, диафильмдер |
плакаттар |
слайд |
Электронды оқулық |
|
1 |
Элементар математика курсынан олимпиадалық есептерді шешу жолдары |
Н.ә [1-9] Қ.ә [1-6] |
|
|
+ |
+ |
|
2 |
Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары |
Н.ә [1-9] Қ.ә [1-6] |
|
|
+ |
+ |
|
3 |
Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Н.ә [1-9] Қ.ә [1-6] |
|
|
+ |
|
|
4 |
Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары |
Ұсынылған әдебиет |
|
|
+ |
|
|
5 |
Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары |
Ұсынылған әдебиет |
|
|
+ |
|
|
6 |
Жоғары математика курсы бойынша олимпиадалық есептер Жоспары |
Ұсынылған әдебиет |
|
|
+ |
|
|
7 |
Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары |
Ұсынылған әдебиет |
|
|
+ |
|
|
8 |
Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары |
Ұсынылған әдебиет |
|
|
+ |
|
|
9 |
Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары |
Ұсынылған әдебиет |
|
|
+ |
|
|
10 |
Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары олимпиадалық есептерді шешу жолдары |
Ұсынылған әдебиет |
|
|
+ |
|
2.3 Дәрістердің тезистері
1-дәріс тақырыбы: Элементар математика курсынан олимпиадалық есептерді шешу жолдары
Математикалық олимпиада - дайындығы неғұрлым жоғары, қабiлеттi оқушылармен жүргізілетін зияткерлiк жарыс.
Есеп шығару − оқушы үшін ерекше іс-әрекет, дәлірек айтсақ - ой жұмысы. Оның негізгі міндеттері: оқыту, тәрбиелеу, дамыту және бақылау болып табылады. Есеп деп қандай да болмасын математикалық ұғымды, мазмұны жағынан терең тапсырманы түсінеміз. Есеп оқушылардың логикалық ойлау, кеңістікті елестету, жеке бас қабілеттерін дамытуға бірден-бір себепші болатын басты құрал.
Олимпиадалық есеп термині есепті классификациялау нәтижесінде емес, олимпиадалық жұмыстың мәтінін құру үшін есептің ерекше түрлерін қолдану практикасы нәтижесінде пайда болған.
Математикада олимпиадалық есеп деп құрылымы немесе оларды шығару әдістері бойынша стандартты емес, қиындығы жоғары деңгейдегі есептерді түсінеді.
Мектеп оқушылары олимпиадаларының негізгі мақсаты осы облыста барлық қатысушылардың ішінен қабiлеттi, талантты және дарындыларды анықтаудан тұрады.
Негiзiнен, олимпиадалық тапсырмалар творчестволық сипатымен ерекшеленеді. Олимпиадалық есептердiң басты ерекшелігі оның тұжырымы мен шығару жолы мектеп бағдарламасы шеңберінен шықпайтыны және бұл есептерді шығару әдістері оқушыларды біртіндеп жоғары математиканың ұғымдары мен әдістеріне бейімдейтіндігінде.
Олимпиаданың ең басты құндылығы жеңімпаздарды анықтаудан ғана емес, оқушылардың математикалық мәдениеті, интеллектуалды деңгейінің жоғарылауын бағалаудан тұрады. Сондықтан осы мәдениет пен интеллектуалды деңгейді көтеру үшін оқушыларды математикалық олимпиадаға дайындау қажет. «Білім – инемен құдық қазғандай», сондықтан ұстаз - оқушыны жан - жақты дайындайтын тұлға болғандықтан, ол оқушының білім деңгейіне тереңірек үңіледі.
Олимпиадаға қатысу оқушының интеллектуалды потенциалының ашылуына мүмкiндiк туғызады, ал нәтиже көрсеткіштері оқушының өзіндік сана сезiмiн нығайтады. Олимпиадаға дайындауға мұғалім өте үлкен үлес қосады.
1.![]() өрнегінің
толық квадратқа айналдыратын
өрнегінің
толық квадратқа айналдыратын ![]() -тің ең
үлкен бүтін мәнін табыңыз.
-тің ең
үлкен бүтін мәнін табыңыз.
![]() болсын деп
алайық.
болсын деп
алайық.
![]() мұндағы,
мұндағы,![]() Себебі,
Себебі,
![]()
Демек,
![]()
Бұдан,
![]() болу керектігі шығады.
Онда
болу керектігі шығады.
Онда ![]() Яғни,
Яғни,![]() - бұл
- бұл
![]() болғанда алынған өрнектің
толық квадрат болатынын көрсетеді. Егер
болғанда алынған өрнектің
толық квадрат болатынын көрсетеді. Егер ![]() онда
онда ![]() . Бұл
жағдайда,
. Бұл
жағдайда,
![]()
Себебі,
![]() Демек,
Демек,
![]() өрнегі қатар тұрған екі санның
квадраттарының арасында қалады. Сол себепті бұл өрнек және онымен
бірге
өрнегі қатар тұрған екі санның
квадраттарының арасында қалады. Сол себепті бұл өрнек және онымен
бірге ![]() өрнегі
толық квадрат бола алмайды.
өрнегі
толық квадрат бола алмайды.
2.Теңдеулер жүйесін шешіңдер.

Мұндағы,
![]() -берілген
сандар.
-берілген
сандар.
Теңдеулер жүйесіндегі түбірлерден мынандай мәселелермен туындайды.
![]() және
және![]() немесе
немесе![]() және
және![]() ,
болғандықтан,
,
болғандықтан, ![]() .
Яғни,
.
Яғни,![]() .
.
Жүйедегі теңдеулерді қосалық
![]()
Ортақ көбейткіштерді жақша алдына шығаралық.
![]()
Келесі кезекте, жүйедегі
теңдеулерді азайтып, ![]() теңдеуін
аламыз.
теңдеуін
аламыз.
Жүйе теңдеулерін қосу және азайту арқылы пайда болған теңдеулерді бір жүйеге біріктірейік.
![]()
Пайда болған жүйедегі теңдеулерді көбейту арқылы келесі теңдеуді аламыз.
![]()
Демек,
![]()
Мұндағы,
![]() болғандықтан берілген
теңдеулер жүйесі шешілу үшін
болғандықтан берілген
теңдеулер жүйесі шешілу үшін ![]() теңсіздігінің орындалуы қажетті. Ал, бұл шарт орындалса,
онда
теңсіздігінің орындалуы қажетті. Ал, бұл шарт орындалса,
онда![]() және осы ұйғарымды пайдалансаң
берілген теңдеулер жүйесі мынандай түрге
келеді.
және осы ұйғарымды пайдалансаң
берілген теңдеулер жүйесі мынандай түрге
келеді.
![]()
Сызықты теңдеулер
жүйесін ![]() және
және ![]() қатысты
шешелік.
қатысты
шешелік.

3.![]() теңдеуін
қанағаттандыратын
теңдеуін
қанағаттандыратын ![]() натурал
сандарын табыңдар.
натурал
сандарын табыңдар.
Теңдеудің сол жағын түрлендірейік.
![]()
Теңдеудің екі жағын да 64-ке көбейтелік.
![]()
Бұдан,
![]() теңсіздігі
шығады.
теңсіздігі
шығады.
![]() (Теңсіздіктің оң жағындағы
3-ті 4-пен ауыстырдық. Сол себепті артық таңбасы, артық немесе тең
таңбасымен ауыстырылды).
(Теңсіздіктің оң жағындағы
3-ті 4-пен ауыстырдық. Сол себепті артық таңбасы, артық немесе тең
таңбасымен ауыстырылды).
Демек,
![]() және
және ![]() яғни,
яғни,
![]()
Берілген теңдеудің екі жағын да 4-ке көбейтелік.
![]()
Демек,
![]()
![]()
![]()
Яғни,
![]() және
және ![]() Олай болса,
Олай болса,
![]() жағдайларын қарастыру
керек.
жағдайларын қарастыру
керек.
а) ![]()
ә) ![]()
б) ![]() Демек,
Демек,
![]()
2-дәріс тақырыбы: Алгебра курсы бойынша олимпиадалық есептерді шешу жолдары
Қазақстан республикасының білім беру стандартында білім берудің басты міндеті логикалық ойлауды дамыту болып табылатындығы атап айтылған.
Қазіргі кезде ғылым мен техниканың даму деңгейі әрбір адамға сапалы және терең білімнің, іскерліктің болуын қамтиды.Оқушының белсенді шығармашылықпен жұмыс істеуін және кеңінен ойлауға қабілетті болуын талап етеді. Сондықтан да мектептегі оқу процесінің негізгі мақсаты арнайы педагогикалық әдістермен мақсатты және жүйелі түрде оқушылардың интеллектік, шығармашылық ойлауын дамыту, ғылыми көзқарасы мен белсенділігін қалыптастыру. Әр адамның бойындағы туғаннан пайда болған интуициясын әрі қарай дамытуға ықпал ету, оқушының табиғи қасиеттерін, математикалық білімін тереңдету үшін оқытуды жоспарлы түрде ұйымдастыру, өз бетінше білім алу дағдыларының дамуына негізін салу болып табылады. Сабақта оқытудың педагогикалық технологияларын тиімді қолдана білу. Оқушының логикалық ойлауын және таным белсенділігін қалыптастыру барысында шығармашылық ізденістің тиімді жолдарын үйрету, білім сапасын көтеру.
Логика – (грек тілінен алынған logic - сөз, ой,ойлау, ақыл-ой) ойлаудың заңдылықтары мен түрлері туралы ғылым. Объективті пікірлерге негізделген процесс логикалық ойлау деп, ал дұрыс ойлаудың формалары мен заңдары туралы ғылым логика деп аталады. Логикалық ойлаудың қисындылығы олардың шындыққа сай келуінде. Логикалық тұжырым теориясының ең алғаш грек философы Аристотель негізін қалаған. Ой әрекеті барысында адам қоршаған дүниені танып, білу үшін ерекше ақын қызметін орындайды. Бұл нақты қызметіне талдау, біріктіру, салыстыру, дерексіздендіру нақтылау және қорытындылау арқылы жүзеге асырылады.
1. Теңдеулер жүйесін бүтін шешімдерін табыңдар.
![]()
Жүйедегі әр теңдеудің екі жағын квадраттайық.
![]()
Алдымен екінші теңдеудің екі жағын да 2-ге көбейтелік, одан екі теңдеуді мүшелеп қосайық.

Бұл жағдайда
![]() немесе
немесе
![]()
а) ![]() Олай болса
Олай болса
![]()
ә) ![]()
Олай болса,
![]()
Жауабы: (1;0;3;1), (-1;0;-3;-1), (3;1;1;0), (-3;-1;-1;0)
2.![]() болғанда
болғанда
![]() өрнегінің мәні
1,
өрнегінің мәні
1, ![]() болғанда 2 тең
болатындай
болғанда 2 тең
болатындай ![]() бүтін
сандары табылмайтынын дәлелдеңдер.
бүтін
сандары табылмайтынын дәлелдеңдер.
Тапсырма шарты бойынша
![]()
![]() теңдіктері ақиқат. Мұндағы,
екінші теңдіктен бірінші теңдікті
азайтайық.
теңдіктері ақиқат. Мұндағы,
екінші теңдіктен бірінші теңдікті
азайтайық.
![]() теңдіктің сол жағынада ортақ
көбейткішті жақша алдына шығаралық.
теңдіктің сол жағынада ортақ
көбейткішті жақша алдына шығаралық. ![]() яғни,
яғни,
![]() .
.
Демек, теңдіктің сол жағында
43-ке бөлінетін бүтін сан, ал оң жағында 1 бар. Бұлай болу мүмкін
емес. Сондықтан, жоғарыдағы шартты қанағаттандыратын
![]() бүтін сандары
табылмайды.
бүтін сандары
табылмайды.
3.Теңдеулер жүйесін шешіңіздер:
![]()
Екінші теңдеуді 2-ге көбейтелік те бірінші теңдеуге қосайық. Сонда,
![]() теңдеуі
шығады.
теңдеуі
шығады.

а) ![]()

Демек,
![]()


![]()
Бірінші жағдай
үшін ![]() және
және ![]()
Тексеру.
![]()
![]()
Сол сияқты екінші түбір де
теңдеулер жүйесін қанағаттандырады. Демек, шешім
![]() және
және![]()
ә) ![]()

Демек,
![]()
Бұл мүмкін емес. Яғни, екінші жағдайда теңдеудің шешімі жоқ.
3-дәріс тақырыбы: Геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
Математиканы оқыту – математикалық теория және математикалық ойлау іс-әрекетіне үйрету болып табылады.
Математиканы оқыту арқылы мәселені талдай білуге, нақтылауға, ұғымдарды анықтауға, ой қорытулар жасауға, дәлелдеуге тағы басқа іс – жүзінде қадам сайын логикалық білім беріледі.
ҰБТ есептерінде геометрия есептері қиындық келтіреді. Ол үшін есеп шартын толық және түсінікті етіп оқу керек. Сонымен бірге оның сызбасын да дұрыс сыза білуіміз керек. Сызбаның дұрыс сызылуы біздің есебіміздің дұрыс, әрі тез шығуына көп көмегін тигізеді.
Есепті қалай шығару керек.
Есептің шартын мұқият түсіну қажет.
-
Кейін не берілгенін, нені табу керектігін қысқаша жазу керек
-
Есеп сұрағына жауап беру үшін нені білу керектігін ойлап, жоспар құру.
-
Егер жоспар құру қиын болса, есеп шартын тағы да оқып шығып, бөліктерге бөлу.
-
Әрбір заттың атауын формуламен алмастыру.
-
Есепте берілген шамалардың байланысын анықтау.
-
Есеп шартынан туындайтын қорытындыны жазу.
-
Бұрын осыған ұқсас есеп шығарылған жоқ па, соны дәптерінен, кітаптан қарау.
-
Есепті шығарып болған соң, тексер, шығару жолының басқаша түрі бар ма, ойлану.
Геометриялық есептерді тригонометриялық тәсілдер арқылы шешу жолдарына бірнеше мысалдарға қарастырайық.
1-мысал.Тең бүйірлі тік бұрышты ABC үшбұрышы берілген. С тік бұрышының төбесінен BD медианасына перпендикуляр жүргізілген түзу гипотенузаны М нүктесінде қияды. Гипотенузаның кесінділерінің ұзындықтарының қатынасын табу керек.
Осы берілген мысалды бірнеше тәсілмен шығарылу жолын қарастырайық.
Енді осы тәсілдерде қолданылатын көмекші ұйғарымдарды келтірейік.
1. Биіктіктері бірдей екі үшбұрыштың аудандарының қатынасы олардың табандарының ұзындықтарының қатынасына тең болады.
2. Егер тік бұрышты
үшбұрыштың катеттерінің қатынасы ![]() болса, онда үшбұрыштың
гипотенузаға түсірілген биіктігі гипотенузаны
болса, онда үшбұрыштың
гипотенузаға түсірілген биіктігі гипотенузаны ![]() қатынасында
бөледі.
қатынасында
бөледі.
3. Кесіндіні
берілген ![]() қатынасында бөлудің
координаталық формулалары мынадай:
қатынасында бөлудің
координаталық формулалары мынадай: ![]()
![]()
4. Егер түзу
![]() осьтерінен сәйкес ұзындықтары
осьтерінен сәйкес ұзындықтары
![]() болатын кесінділерді
қиса, онда бұл түзудің теңдеуі мынадай болады:
болатын кесінділерді
қиса, онда бұл түзудің теңдеуі мынадай болады: ![]()
5. Егер екі вектор
өздерінің координаталарымен берілсе: ![]() онда бұл векторлардың
перпендикуляр болуының қажетті және жеткілікті шарты мынадай:
онда бұл векторлардың
перпендикуляр болуының қажетті және жеткілікті шарты мынадай:
![]()
6. Менелай
теоремасы. Егер ![]() нүктелері
нүктелері ![]() үшбұрышының сәйкес
үшбұрышының сәйкес ![]() қабырғаларындағы (немесе
олардың созындыларындағы) нүктелер болса, онда бұл нүктелердің бір
түзуге тиісті болуының қажетті және жеткілікті шарты мынадай:
қабырғаларындағы (немесе
олардың созындыларындағы) нүктелер болса, онда бұл нүктелердің бір
түзуге тиісті болуының қажетті және жеткілікті шарты мынадай:
![]()
7. Координаталар
басы арқылы өтетін және бұрыштық коэффициенті ![]() болып келетін түзудің теңдеуі
мынадай болады:
болып келетін түзудің теңдеуі
мынадай болады: ![]()
8. Диагональдары
өзара перпендикуляр болып келетін төртбұрыш үшін мынадай теңдік
орындалады: ![]()
Түсінуге, қолдануға жеңіл болу үшін, есептің шешулерінің 25 тәсілі жеті топқа бөлінді.
І-топ:
Векторлық-координаталық тәсілдермен шығарылу жолын қарастырамыз.
1-тәсіл. Нүктелердің
координаталары төмендегідей болатындай тік бұрышты координаталар
жүйесін енгізейік: ![]()

![]() бұрышы доғал болғандықтан
бұрышы доғал болғандықтан
![]() Осы сияқты
Осы сияқты ![]() екенін ескеріп жазамыз:
екенін ескеріп жазамыз:
![]()
Енді төртінші және жетінші
көмекші ұйғарымдарды қолданып ![]() түзулерінің теңдеулерін
жазайық:
түзулерінің теңдеулерін
жазайық: ![]() Бұл екі
теңдеуді жүйе ретінде қарастырып нүктесінің координаталарын
табамыз:
Бұл екі
теңдеуді жүйе ретінде қарастырып нүктесінің координаталарын
табамыз: ![]() Енді кесінділердің
пропорционалдығына сүйеніп ізделінді қатынасты табуға болады:
Енді кесінділердің
пропорционалдығына сүйеніп ізделінді қатынасты табуға болады:
![]()
2-тәсіл. Белгілеулер енгізейік
![]()
![]()
![]() векторын екі тәсілмен
өрнектейік:
векторын екі тәсілмен
өрнектейік:
![]() немесе
немесе ![]() Осыдан
Осыдан ![]() Онда
Онда![]()
![]() Есептің шарты бойынша
Есептің шарты бойынша
![]() немесе
немесе ![]() Соңғы теңдіктен
Соңғы теңдіктен ![]() ескеріп табамыз
ескеріп табамыз
![]()
3-тәсіл. ![]() болатындай тік бұрышты
координаталар жүйесін енгізейік (2.2-суретіне сәйкес). Төртінші
көмекші ұйғарымға сүйеніп
болатындай тік бұрышты
координаталар жүйесін енгізейік (2.2-суретіне сәйкес). Төртінші
көмекші ұйғарымға сүйеніп![]() түзуінің теңдеуін жазайық:
түзуінің теңдеуін жазайық:
![]()

![]() нүктесі
нүктесі ![]() түзуіне тиісті
болғандықтан оның координаталарын мынадай түрде жазуға болады:
түзуіне тиісті
болғандықтан оның координаталарын мынадай түрде жазуға болады:
![]() Енді
Енді ![]() және
және ![]() векторларының координаталары
оңай табылады:
векторларының координаталары
оңай табылады: ![]() Енді
Енді![]() ескеріп
ұйғарымды қолдануға болады:
ескеріп
ұйғарымды қолдануға болады: ![]() Осыдан
Осыдан ![]()
Онда ![]()
4-тәсіл. Тік бұрышты
координаталар жүйесінің осьтерін ![]() және
және ![]() сәулелері бойынша
бағыттайық. Бұл жүйеде нүктелердің координаталары төмендегідей
болады:
сәулелері бойынша
бағыттайық. Бұл жүйеде нүктелердің координаталары төмендегідей
болады: ![]()
![]() пен
пен ![]() кесінділерінің теңдігі мен
перпендикулярлығына сүйеніп екі теңдеу жазайық:
кесінділерінің теңдігі мен
перпендикулярлығына сүйеніп екі теңдеу жазайық: ![]()
жүйені ықшамдағаннан мынадай
теңдеу шығады: ![]() Бұл
теңдеуден
Бұл
теңдеуден ![]() шығады.
шығады.
![]() нүктесінің
нүктесінің ![]() түзуіне тиістілігінен
мынадай теңдеу шығады:
түзуіне тиістілігінен
мынадай теңдеу шығады: ![]() Соңғы екі теңдеуден
ықшамдағаннан кейін
Соңғы екі теңдеуден
ықшамдағаннан кейін ![]() шығады.
Енді нүктелердің координаталары
шығады.
Енді нүктелердің координаталары ![]() мен
мен ![]() арқылы өрнектеледі:
арқылы өрнектеледі: ![]()
Нүктелердің осы
координаталарына сүйеніп керек кесінділердің ұзындықтарын табайық:
![]() Осыдан
Осыдан
![]() шығады.
шығады.
5-тәсіл. Бірлік векторлар
енгізейік: ![]()
Екінші көмекші ұйғарым бойынша
![]()
Осыдан ![]() Бұл теңдеуді ықшамдағаннан
кейін
Бұл теңдеуді ықшамдағаннан
кейін ![]() (теңдіктерін ескеріп) шығады.
Олай болса
(теңдіктерін ескеріп) шығады.
Олай болса ![]() (себебі
(себебі
![]() ).
).
6-тәсіл. ![]() болатындай тік бұрышты
координаталар жүйесін енгізейік
болатындай тік бұрышты
координаталар жүйесін енгізейік ![]() болсын. Онда үшінші көмекші
ұйғарымдағы формулаларды қолданып табамыз:
болсын. Онда үшінші көмекші
ұйғарымдағы формулаларды қолданып табамыз: ![]() Енді
Енді ![]() арқылы
арқылы ![]() векторларын өрнектейік
векторларын өрнектейік
![]()
![]() және
және ![]() векторларының
перпендикулярлығына сүйеніп жазайық:
векторларының
перпендикулярлығына сүйеніп жазайық: ![]() Осыдан
Осыдан ![]() шығады
шығады

4-дәріс тақырыбы: Бөлу теориясы бойынша олимпиадалық есептерді шешу жолдары
Оқу еңбегінің қаруы - ой. Оқушылардың өз бетімен жұмысын қалыптастыру оқушының пәнге деген қызығушылығынан және қажеттілігінен туады. Мектеп оқушыларының өз бетінше жұмыстарын ұйымдастырудың басты формасы – жұмыстарды орындау, ептілік, іскерлік, шеберлік дағдысын дамыту.
Оқушылардың жеке ойлау қабілетін дамыту үшін олардың өзіндік күш қуаты мен сенімін арттыру керек. Қолынан келетін көп істердің мүмкіндіктеріне бағыт берген абзал. Оқушылардың білімді меңгеру үрдісі негізінен мына компоненттерден тұрады:
-
қабылдау; 2) түсіну; 3) есте сақтау; 4) қорыту және жүйелеу.
Оқушылардың ойлауын дамыту туралы М. Жұмабаев былай деген: «Ойлауды өркендету жолдары. Ойлау - жанның өте бір қиын, терең ісі. Жас балаға ойлау тым ауыр. Сондықтан тәрбиеші баланың ойлауын өркендеткенде, сақтықпен басқыштап іс істеу керек» [3]. Логикалық есептерді шығару үшін арнайы терең білімнің қажеті жоқ, тек ойлана алу, болжамдау, тапқырлығы болса, зейін қоя білсе жеткілікті. Логикалық есептерді шығару ғылыми проблемамен тұспа-тұс сияқты. Өйткені есептегенде гипотезаны айта білу, оларды тексеру маңызды болып табылады. Логикалық есептердің түрлері өте көп. Бірақ олардың санқырлылығына байланысты, арасынан ең жиі кездесетін түрлерін атап өтсек: 1)кесте арқылы шығарылатын логикалық есептер; 2) жиындарды реттеуді қажет ететін логикалық есептер; 3) болжамдары бар логикалық есептер; 4) олимпиадалық есептер.
Натурал
m санының ешбір мәнінде
![]() саны
саны ![]() санына бөлінбейтінін
дәлелдендер.
санына бөлінбейтінін
дәлелдендер.
1.Натурал
m санының кейбір мәнінде
![]() саны
саны ![]() санына бөлінеді деп ұйғарайық.
Онда,
санына бөлінеді деп ұйғарайық.
Онда, ![]() саны
саны
![]() санына да бөлінеді.
санына да бөлінеді.
![]() . Демек,
. Демек, ![]() саны
саны ![]() санына бөлінеді.
санына бөлінеді. ![]() саны
саны![]() болғандықтан тақ сан,
ал
болғандықтан тақ сан,
ал ![]() - жұп сан. Олай болса,
- жұп сан. Олай болса,
![]() саны
саны
![]() санына бөлінеді.
Алайда,
санына бөлінеді.
Алайда, ![]() болады. Бұл жағдай
алынған ұйғарымның жалғандығын көрсетеді. Яғни,
натурал m-нің ешбір мәнінде
болады. Бұл жағдай
алынған ұйғарымның жалғандығын көрсетеді. Яғни,
натурал m-нің ешбір мәнінде ![]() саны
саны![]() санына
бөлінбейді.
санына
бөлінбейді.
2.![]() сандары үшін
сандары үшін ![]() және
және ![]() екендігі белгілі, сонда
екендігі белгілі, сонда
![]() неге тең болатынын
табыңдар.
неге тең болатынын
табыңдар.
![]() болғандықтан
болғандықтан ![]() ,
, ![]() болғандықтан
болғандықтан ![]() ,
, ![]() болғандықтан
болғандықтан ![]() немесе
немесе ![]() немесе
немесе![]()
![]() ,
,![]() . Демек,
. Демек, ![]() .
.
Тапсырма шарты бойынша
![]() , біздің дәлелдеуіміз
бойынша
, біздің дәлелдеуіміз
бойынша ![]() .
Бұдан
.
Бұдан![]() . Тура
осындай жолмен
. Тура
осындай жолмен ![]() екендігі
де анықталады. Олай болса,
екендігі
де анықталады. Олай болса,![]() теңдігінен
теңдігінен![]() немесе
немесе ![]() екендігі туындайды. Мұнда, екі
жағдайда да
екендігі туындайды. Мұнда, екі
жағдайда да![]() шығады.
шығады.
3.
![]() теңдеуінің түбірлері натурал
сандар болса, онда
теңдеуінің түбірлері натурал
сандар болса, онда![]() құрама
сан болатынын дәлелдеңіздер.
құрама
сан болатынын дәлелдеңіздер.
![]() теңдеуінің
теңдеуінің![]() және
және![]() түбірлері Виет теоремасы боынша
мына шарттарды қанағаттандырады.
түбірлері Виет теоремасы боынша
мына шарттарды қанағаттандырады.
![]()
Бұдан, ![]()
![]() екендігі
шығады
екендігі
шығады

Тапсырма шарты бойынша
![]() ,
, ![]() натурал сандар. Олай болса әр
жақша екі немесе екіден артық натурал сан болады. Ал екі натурал
санның көбейтіндісі тек қана құрама санға тең. Демек,
натурал сандар. Олай болса әр
жақша екі немесе екіден артық натурал сан болады. Ал екі натурал
санның көбейтіндісі тек қана құрама санға тең. Демек, ![]() - құрама
сан.
- құрама
сан.
4.
![]()
![]()
![]()
![]() теңдіктерін қанағаттандыратын
теңдіктерін қанағаттандыратын
![]() бүтін сандарының
табылмайтынын дәлелдеңіздер.
бүтін сандарының
табылмайтынын дәлелдеңіздер.
Кері жоримыз.
Яғни,
берілген теңдіктерді қанағаттандыратын ![]() бүтін сандары бар болсын. Олай
болса,
бүтін сандары бар болсын. Олай
болса,
![]()
![]()
![]()
![]() деуге болады. Бұдан,
деуге болады. Бұдан,![]() -ның тақ сан екендігі шығады.
Себебі,
-ның тақ сан екендігі шығады.
Себебі,![]() -тақ сан,
тақ санды тақ санға көбейткенде ғана нәтиже тақ сан болатыны
белгілі.
-тақ сан,
тақ санды тақ санға көбейткенде ғана нәтиже тақ сан болатыны
белгілі.
Осындай жолмен,![]() -ның да тақ сан екендігін
анықтауға болады. Олай болса,
-ның да тақ сан екендігін
анықтауға болады. Олай болса,![]() -да тақ сан және
-да тақ сан және![]() ,
, ![]() ,
, ![]() ,
, ![]() нәтижелері жұп сан болу
керек.
нәтижелері жұп сан болу
керек.
Ал тапсырмада бұл айырмалардың
нәтижелері тақ сандар. Демек, қарама-қайшылыққа келдік. Олай болса,
тапсырма шартын қанағаттандыратын ![]() бүтін сандары
табылмайды.
бүтін сандары
табылмайды.
5.
![]() - нің қандай натурал мәнінде
- нің қандай натурал мәнінде
![]() құрама сан
болады.
құрама сан
болады.
![]()
Бұл көбейтінді ![]() болғанда құрама сан
болады.
болғанда құрама сан
болады.
6.
![]() болса, онда
болса, онда![]() болатындығын
дәлелдеңіздер.
болатындығын
дәлелдеңіздер.

![]()
![]()

![]()
Демек, ![]() немесе
немесе ![]() немесе
немесе ![]() . Олай болса,
. Олай болса, ![]()
![]() болғандықтан
болғандықтан ![]() Басқа жағдайлар да осылай
қарастырылынады.
Басқа жағдайлар да осылай
қарастырылынады.
5-дәріс тақырыбы Алгебра және анализ курсы бойынша олимпиадалық есептерді шешу жолдары
1.![]() теңдеуін бүтін сандар жиынында
шшіңіздер.
теңдеуін бүтін сандар жиынында
шшіңіздер.
Теңдеуді ортақ бөлімге келтірелік.

![]()
Бұл бөлшектердің екеуі де қысқармайтын бөлшектр (қатар тұрған екі сан – өзара жай сан). Олай болса, бөлшектердің бөлімдері тең болу керек.
![]() . Мұнда, мынандай үш түрлі
жағдай болуы мүмкін.
. Мұнда, мынандай үш түрлі
жағдай болуы мүмкін.
а) ![]() болса, онда
болса, онда ![]()
ә) ![]() болса, онда
болса, онда ![]()
б) ![]() болса, онда
болса, онда![]() деп алайқ. Бұл жағдайдағы
деп алайқ. Бұл жағдайдағы
![]() -нің мәнін жоғарыдағы
теңдеуге апарып қойсақ.
-нің мәнін жоғарыдағы
теңдеуге апарып қойсақ.![]()

Демек, ![]() . Олай болса,
. Олай болса,![]() одан
одан![]() екендігі туындайды.
екендігі туындайды. ![]() -нің бұл мәні берілген теңдеуді
қанағаттандырады.
-нің бұл мәні берілген теңдеуді
қанағаттандырады.
2.
![]() саны
саны ![]() саына бөлінбейтін натурал сан
саына бөлінбейтін натурал сан
![]() -нің барлық тақ мәндерін
табыңыздар.
-нің барлық тақ мәндерін
табыңыздар.
Бұл тапсырманы орндау үшін
натурал тақ сандарды төмендегідей топтарға бөліп, әр топтың
тапсырма шартын қанағаттандыратынын немесе қанағаттандырмайтынын
жеке-жеке қарастырайық. Натурал тақ сандар: ![]()
![]() - натурал, тақ және жай сандар
болсын яғни
- натурал, тақ және жай сандар
болсын яғни ![]() Бұл жағдайда
Бұл жағдайда
![]() саны
саны ![]() санына, әсіресе
санына, әсіресе ![]() санына бөлінбейді. Мысалы,
санына бөлінбейді. Мысалы,
![]() болса,
болса, ![]() саны
саны ![]() санына, әсіресе
санына, әсіресе ![]() санына бөлінбейді. Демек, бұл
топтағы сандар тапсырма шартын
қанағаттандырады.
санына бөлінбейді. Демек, бұл
топтағы сандар тапсырма шартын
қанағаттандырады.
ә)![]() болсын, мұндағы
болсын, мұндағы ![]() - жай тақ сан. (
- жай тақ сан. (![]() - сандары). Егер
- сандары). Егер![]() болса, онда
болса, онда ![]() бөлінеді.
бөлінеді. ![]() мұндағы,
мұндағы, ![]() теңсіздігі
теңсіздігі ![]() болғанда ғана орындалды.
Себебі,
болғанда ғана орындалды.
Себебі, ![]() . Ал мұнда
қамтылмай қалған
. Ал мұнда
қамтылмай қалған ![]() жағдайын
жеке қарастырайық.
жағдайын
жеке қарастырайық. ![]() бөлінбейді
бөлінбейді ![]() . Демек,
. Демек,
![]() болғанда тапсырма шарты
орындалады.
болғанда тапсырма шарты
орындалады.
б) ![]() - тақ жай сан емес және де жай
санның квадраты да емес болсын
- тақ жай сан емес және де жай
санның квадраты да емес болсын ![]()
бұл жағдайда ![]() , мұндағы
, мұндағы ![]() деп алуға болады. Мәселені
нақтылай түссек,
деп алуға болады. Мәселені
нақтылай түссек, ![]() және
және
![]() тақ сандар болғандықтан
тақ сандар болғандықтан
![]() деуге болады. Демек,
деуге болады. Демек,
![]() болса,
болса, ![]() Бұл көбейтіндінің құрамында
Бұл көбейтіндінің құрамында
![]() сандары бар.
Демек,
сандары бар.
Демек,![]() ,
,![]() -қа яғни
-қа яғни![]() ,
, ![]() -ге бөлінеді. Тапсырма
шарты
-ге бөлінеді. Тапсырма
шарты![]() және
және![]() -тақ жай сан болғанда ғана
орындалады.
-тақ жай сан болғанда ғана
орындалады.
3.
![]() - кез-келген бүтін сан болсын.
Кейбір өзара жай
- кез-келген бүтін сан болсын.
Кейбір өзара жай![]() сандары
үшін
сандары
үшін ![]() санының
санының
![]() -ға бөлінетінін
дәлелдеңіздер.
-ға бөлінетінін
дәлелдеңіздер.
![]() болсын.
болсын.
Бұл жағдайда, ![]() мен
мен ![]() - дің өзара жай сан екендігі
айқын. Себебі,
- дің өзара жай сан екендігі
айқын. Себебі, ![]()
![]() тек
қана
тек
қана![]() Олай болса,
Олай болса,![]() - өзара жай сандар. Сонымен
бірге
- өзара жай сандар. Сонымен
бірге ![]() Олай
болса,
Олай
болса, ![]()
![]() -ға
бөлінеді.
-ға
бөлінеді.
4.
![]() теңдеуін қанағаттандыратын
бүтін
теңдеуін қанағаттандыратын
бүтін ![]() және
және ![]() сандарының парларын
табыңыздар.
сандарының парларын
табыңыздар.

![]()
![]()
![]()
![]()
Егер ![]() , онда
, онда
![]()
![]() Демек,
Демек,![]() .
.
Тек қана бүтін түбір
ізделінетіндіктен ![]() .
.
Егер ![]() және
және![]() -бүтін сан болса,
онда
-бүтін сан болса,
онда ![]() . Олай болса,
. Олай болса,
![]()
![]() .
.![]() және
және![]() бүтін
бүтін
![]() .
.
![]() болады. Енді,
жоғарыдағы
болады. Енді,
жоғарыдағы![]() теңдеуінен
теңдеуінен ![]() болатынын
анықтап, орнына қойсақ былай
болады.
болатынын
анықтап, орнына қойсақ былай
болады.
![]()
![]()
![]()
Демек,
![]() аралығында
аралығында
![]() -тің бүтін тек
қана
-тің бүтін тек
қана ![]() мәні бола алады.
Олар,
мәні бола алады.
Олар, ![]()
![]() болса,
онда
болса,
онда ![]() және
және ![]() болса, онда
болса, онда
![]() Бұл квадраттық теңдеудің бүтін
түбірі жоқ.
Бұл квадраттық теңдеудің бүтін
түбірі жоқ. ![]() болса,
онда
болса,
онда ![]()
![]()
![]()
![]()
![]()
![]() Демек,
Демек,
![]()
6-7 дәріс тақырыбы: Жоғары математика курсы бойынша олимпиадалық есептер
1. ![]() дұрыс
үшбұрышының
дұрыс
үшбұрышының ![]() және
және ![]() қабырғаларынан
қабырғаларынан ![]() болатындай сәйкесінше
болатындай сәйкесінше ![]() және
және ![]() нүктелері алынған.
нүктелері алынған. ![]() және
және ![]() кесінділерінің қиылысын
кесінділерінің қиылысын ![]() нүктесімен белгілейік.
нүктесімен белгілейік. ![]() екенін дәлелдеңіз.
екенін дәлелдеңіз.
1 – есептің шешуі. Енді геометрия жайында бірер сөз.
Кезінде Пифагор геометрияны арифметикаға бағындырса, кейін Евклид қайтадан геометрияны бірінші орынға қойып, оған алгебраны бағындырған. Д.И. Менделеев «Геометрические знания составляют основу всей точной науки», - деп айтып кеткен екен. Геометрия туралы ұлағатты сөздерді көптеп келтіруге болады. Математикада геометриялық есептердің алатын орны өте зор. Жалпы геометрия өзі жатқан бір дүние десекте болғандай, ол өзінің бөлімдерімен, есептерімен ерекшеленеді, оның есептерін шығару барысында оқушы көптеген қиыншылықтарға ұшырайды, шығару жолы мен тәсіліне, әрбір шығару кезеңінің нәтижелеріне назар аудармай, тек қана белгісіз элементті табумен айналысады. Осындай олқылықтарға бой алдырмау үшін геометриялық есепті талдауға үйреніп, шығару кезеңдерімен жолдарын меңгеру керек. Әуелі есептің мәтінін жақсы түсініп оқу, талдау, содан кейін дұрыс сызба, келесі кезекте дәлелдеу жұмысын суатты орындау. Осы кезеңдерден өткен соң талдау мен сызбаға сүйеніп, қажетті формулаларды пайдалана отырып, есепті шешудің қолайлы жолын табуға болады. Кейде геометриялық бір есепті шешуде оқушыға бүкіл бір курсты , не бір тарауды қайталап, еске түсіруге тура келеді.
Шешуі: І тәсіл. (Салу әдісін қолдану). Есеп шарты бойынша сызба сызып талдау жасайық.
Талдау:
1) ![]() =
= ![]() = 2⟹ MC
= 2MA,
= 2⟹ MC
= 2MA,
NA = 2NB, ал AC = MA + MC және
AB = NA +NB ⟹AC = 3MA, AB = 3NB
яғни AC = AВ болғандықтан MA = NB,
NA = MC (1 – сурет)
2) В нүктесі арқылы ВК⊥ АС болатындай ВК және N ,M нүктелері арқылы NМ түзулерін жүргізейік.
АК = СК =
![]() AC.
AC.![]() =
= ![]() =
= ![]() =
= ![]() Сонымен,
Сонымен, ![]() =
= ![]() Олай болса, пропорционал кесінділер туралы теорема бойынша
NB∥BK, яғни
NM⊥AC және
∠ANM = 30° осыдан, AM
=
Олай болса, пропорционал кесінділер туралы теорема бойынша
NB∥BK, яғни
NM⊥AC және
∠ANM = 30° осыдан, AM
= ![]() AN
AN
Салу
Тікбұрышты ANM үшбұрышын саламыз
-
Талдауға сүйеніп, салған үшбұрышын пайдаланып, АВС дұрыс үшбұрышын саламыз
-
Радиусы
 АС – ға
тең жарты шеңбер сызып және NС түзуін жүргізіп,түзудің жарты
шеңбермен қиылысу нүктесін Р деп белгілейік (1а – сурет
)
АС – ға
тең жарты шеңбер сызып және NС түзуін жүргізіп,түзудің жарты
шеңбермен қиылысу нүктесін Р деп белгілейік (1а – сурет
) -
В және Р нүктелері арқылы жүргізілген түзу М нүктесінен өтеді, өйткені өтпеген жағдайда есептің шарты орындалмайды да қарама – қайшылық туындайды.
Дәлелдеуі: АР түзуін жүргізсек диаметрге тірелген АРС бұрышын аламыз, ол тік болады.Демек, ∠AРС = 90° ( 1ә – сурет )
N
В
С
А
М
Р
В
N
В
А
М
Р
С
А
М
С
N
Р
1а - сурет
1ә - сурет




![]()



8-9-дәріс тақырыбы: Алгебра және сандар теориясы бойынша олимпиадалық есептерді шешу жолдары
Жоспары
-
Анықтауыштар және оның қасиеттері.
-
Анықтауыштардың шығарылуы.
-
Матрицалар және олардың қолдануы.
-
Кері матрицалар.
-
Сызықтық алгебралық теңдеулер жүйесінің шығару әдістері.
Анықтама :
А
матрицаның
анықтауышы
деп ![]() санды аламыз және оны төмендегідей белгілейміз:
санды аламыз және оны төмендегідей белгілейміз:
![]()
![]()
![]() - екінші
ретті анықтауыш,
- екінші
ретті анықтауыш,

көріністе жазылып есептелінген кестені үшінші ретті анықтауыш деп аталады.
Анықтауыштардың төмендегі қасиеттерін атап өтуге болады:
10 . Анықтауыштың жолдары мен бағандары орындарын алмастырылса, оның мәні сақталады.
20. Анықтауыштың параллель қатарларын өзара орын алмастырылса, анықтауыш таңбасы өзгереді.
30. ![]()
40. ![]() =0
=0
50. ![]() =0
=0
 - үшінші
ретті анықтауыш берілген болсын.
- үшінші
ретті анықтауыш берілген болсын.
Анықтама :
Үшінші ретті анықтауыштың aij элементінің миноры деп, осы элемент тұрған i-жол және j-бағанды алып тастағанда пайда болатын екінші ретті анықтауышты айтамыз. Анықтауыштың aij элементтің минорын Mij арқылы белгілейміз. А матрицаның элеметері үшін де минор түсінігі жоғарыдағыдай беріледі.
Мысалы,  болса,
онда
болса,
онда ![]()
![]()
Анықтама : Анықтауыштың aij элементінің алгебралық толықтауышы деп
![]() санын
айтады.
санын
айтады.
60. Анықтауыштың қандай да бір қатарының элементтері мен олардың сәйкес алгебралық толықтауыштарының көбейтінділерінің қосындысы осы анықтауыш мәніне тең.

Мысал :

Анықтама :
n белгісізі бар m сызықтық алгебралық теңдеулер жүйесі келесі түрде жазылады:
 (1)
(1)
мұндағы:
![]() -жүйе
белгісіздері;
-жүйе
белгісіздері;
![]() - жүйе
коэффициенттері;
- жүйе
коэффициенттері;
![]() -бос мүшелер деп
аталады.
-бос мүшелер деп
аталады.
Жүйе коэффициенттерінен тік бұрышты кесте құрауға болады. Ол кестені белгілеуге келесі

символдардың бірін қолданады.
Бұл кестені m жол және n бағаннан тұратын m×n өлшемді матрица деп атайды.
Мұндағы
![]() -матрица элеметтері деп
атайды. Егер m=n болса, онда (2) кесте
-матрица элеметтері деп
атайды. Егер m=n болса, онда (2) кесте
 (2*)
(2*)
түріне ие
болады және ол n-ретті квадрат матрица деп аталады. Мұндағы
![]() -бас диагональ,
-бас диагональ,
![]() -бүйір диагональ
элементтері деп аталады.
-бүйір диагональ
элементтері деп аталады.
Дербес жағдайда, n=m=2 болса,
![]() - екінші
ретті квадрат матрица болады.
- екінші
ретті квадрат матрица болады.
10-11-дәріс тақырыбы: Аналитикалық геометрия курсы бойынша олимпиадалық есептерді шешу жолдары
Жоспары
-
Векторлар.
-
Векторларға қолданылатын сызықтық амалдар.
-
Векторлардың скалярлық, векторлық және аралас көбейтіндісі.
-
Жазықтық. Кеңістіктегі түзу. Түзу және жазықтық.
-
Екінші ретті сызықтар. Екінші ретті беттер.
![]() бас нүктесі,
бас нүктесі,
![]() ұшы. AB кесінді
ұзындығын
ұшы. AB кесінді
ұзындығын ![]() вектордың
модулі деп,
вектордың
модулі деп, ![]() арқылы
белгілейді.
арқылы
белгілейді. ![]() - ноль
вектор.
- ноль
вектор.
Бір түзуде немесе параллель түзулерде жататын векторлар коллинеар деп аталады.

![]() ,
,
![]() ,
, ![]()
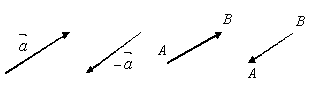
![]() векторына коллинеар, модулі
векторына коллинеар, модулі
![]() тең, бағыты
тең, бағыты ![]() векторына қарама-қарсы
бағытталған вектор
векторына қарама-қарсы
бағытталған вектор ![]() векторына қарама-карсы вектор деп аталады және -
векторына қарама-карсы вектор деп аталады және -![]() арқылы
белгіленеді.
арқылы
белгіленеді.
![]()
10. Векторды λ санына көбейту:
![]() векторы мен
λ санының
көбейтіндісі
векторы мен
λ санының
көбейтіндісі ![]() дейміз,
егер төмендегі шарттар
қанағаттандырса:
дейміз,
егер төмендегі шарттар
қанағаттандырса:
-
модулі

-

-
 болса,
болса,
 мен бағыттас, ал
мен бағыттас, ал
 болса
болса  векторына бағыты қарама-қарсы
векторына бағыты қарама-қарсы
 векторын
айтады.
векторын
айтады.
2 0. Векторларды
қосу.
0. Векторларды
қосу.
![]()
Қасиеттері:
-
 сандар.
сандар. -

-

-

-

Анықтама: Бір жазықтыққа параллель ![]() векторлар компланар векторлар деп
аталады.
векторлар компланар векторлар деп
аталады.
Кеңістікте
OXYZ тік бұрышты декарт координаталар жүйесі берілсін. OX, OY, OZ -
өстерінің бойында орналасқан ![]() бірлік векторлары
бірлік векторлары ![]() компланар емес векторлары
болғандығынан оларды кеңістік базисін құрайды деп алуға болады.
Онда кез келген
компланар емес векторлары
болғандығынан оларды кеңістік базисін құрайды деп алуға болады.
Онда кез келген ![]() - векторын олардың сызықтық комбинациясы
арқылы жазуға болады.
- векторын олардың сызықтық комбинациясы
арқылы жазуға болады.
![]() сандарды
сандарды ![]() вектордың координаталары деп
атайды.
вектордың координаталары деп
атайды.
![]() берілген
болса,
берілген
болса, ![]() вектордың
координаталары
вектордың
координаталары ![]() болады.
болады.
![]()
![]()
![]()
![]()
![]()
![]() нүктелер
берілген болса, онда
нүктелер
берілген болса, онда ![]() екендігін көрсетуге болады,
екендігін көрсетуге болады,
![]()
В екторлардың
скаляр көбейтіндісі
екторлардың
скаляр көбейтіндісі
![]() векторлар арасындағы
бұрышты
векторлар арасындағы
бұрышты ![]() деп
аламыз.
деп
аламыз. ![]()
![]()
![]()
![]()
![]() - деп те
белгіленеді.
- деп те
белгіленеді.
Қасиеттері:
10. ![]()
20. ![]()
30. ![]()
40. ![]()
50. ![]() сүйір
бұрыш
сүйір
бұрыш ![]()
60. ![]() доғал
бұрыш
доғал
бұрыш ![]()
70. ![]()
![]()
![]()
![]()
![]()
40’. ![]()
Анықтама. Нол емес ![]() векторының бағыттаушы косинустары деп
векторының бағыттаушы косинустары деп ![]() векторымен OX,OY,OZ өстерінің арасындағы
сәйкес
векторымен OX,OY,OZ өстерінің арасындағы
сәйкес ![]() бұрыштарының
косинустарын айтады
бұрыштарының
косинустарын айтады
![]()
В![]() екторлық көбейтінді және оның қасиеттері.
екторлық көбейтінді және оның қасиеттері.
Анықтама.
Бастары ортақ бір О нүктесіне келтірілген, компланар емес, реттелген ![]() векторлар үштігі берілсін. Егер
векторлар үштігі берілсін. Егер ![]() вектор ұшынан қарағанда
вектор ұшынан қарағанда ![]() векторының
векторының ![]() векторына жақын тұспен бұрылуы сағат тіліне қарама қарсы бағытта болса, онда
векторына жақын тұспен бұрылуы сағат тіліне қарама қарсы бағытта болса, онда ![]() - оң үштік векторлар деп аталады.
- оң үштік векторлар деп аталады.
![]()
![]() а және в
векторлардың вектор көбейтіндісін
а және в
векторлардың вектор көбейтіндісін ![]() деп
деп
төмендегі үш шартты орындайтын вектроға айтылады.
1.
![]() векторлар оң үштік
құрайды.
векторлар оң үштік
құрайды.
2.
![]()
![]()
3.
![]() ,
, ![]()
S =![]()
![]()
Қасиеттері.
1. ![]()
2. ![]()
3. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Э лементер математика курсынан
лементер математика курсынан
L түзуінің тендеуі y=kx+b (1)
түрінде жазылатыны белгілі. Мұндағы, k=tga - түзудің бұрыштық коэфициенті,
ал ![]() шамасы L түзуі мен OX өсінің оң
бағыты арасындағы бұрыш, b шамасы –түзү мен OY өсінің
қиылысу
нүктесінің ординатасы (b=ОВ) (1-суретті
қара.)
шамасы L түзуі мен OX өсінің оң
бағыты арасындағы бұрыш, b шамасы –түзү мен OY өсінің
қиылысу
нүктесінің ординатасы (b=ОВ) (1-суретті
қара.)
(1-сурет).
Aх+Bу+C=O
(2)
теңдеуін қарастырайық. Мұндағы A,B,C-белгілі сандар және А мен В
бір мезгілде бірдей нөлге тең болмайды. Егер B≠O болса, онда (2)
теңдеуді y = ![]() деп,
немесе
деп,
немесе ![]()
b=-![]() десек, y=-кx+b көріністе, яғни
(1) тендеу түрінде жазуға болады
екен.
десек, y=-кx+b көріністе, яғни
(1) тендеу түрінде жазуға болады
екен.
Сондықтан (2) теңдеу жазықтықтағы түзудің жалпы теңдеуі деп аталады.
-
Бұрыштың коэфициенті k тең және
 нүктесі арқалы өтетін түзу
теңдеуі :
нүктесі арқалы өтетін түзу
теңдеуі :
![]() (3)
(3)
2. ![]() және
және ![]() нүктелер арқылы өтетін түзу
теңдеуі:
нүктелер арқылы өтетін түзу
теңдеуі:
![]() =
=![]() (4)
(4)
y=k1x+b1
және
y=k2x+b2
түзулердің арасындағы ![]() бұрышты
табу формуласы:
бұрышты
табу формуласы:
tg![]() =
=![]() (5)
(5)
Екі түзудің перпендикулярлық белгісі
1+к1 к2=0 немесе ![]() =-
=-![]() (6)
(6)
![]() Екі
түзудің паралелдік белгісі
Екі
түзудің паралелдік белгісі
(![]() ): k1-k2=0 немесе k1=k2 (7)
): k1-k2=0 немесе k1=k2 (7)
M(x0,y0) нүктеден Ax+By+C=0 теңдеулі түзуге дейінгі қашықтықты табу формуласы:
D=![]() (8)
(8)
Мысал 1. М(1;3) нүктесінен L: 3x+4y+10=0 түзуіне дейінгі қашықтықты табу керек
Шешімі: (8) формуладан табамыз: d=![]()
Жауабы: d=5
Мысал 2 L1: x+2y-3 және L2: y=2x-5 түзулері арасындағы бұрышты табу керек.
Шешімі: L1 түзудің бұрыштың коффиценттерін тауып аламыз.
2y=-x+3 немесе y = -![]()
L1: y=-![]()
![]()
L2 : y=2x-5, k2=2
1+k1k2=1+(-![]() )2=1-1=0
1+k1k2=0
яғни L1
)2=1-1=0
1+k1k2=0
яғни L1![]() L2
L2
Жауабы:
![]()
12-13 дәріс тақырыбы: Ықтималдықтар теориясы және математикалық статистика курсы бойынша олимпиадалық есептерді шешу жолдары
Жоспары
-
Ықтималдықтар теориясының негізгі ұғымдары.
-
Қосу және көбейту ықтималдықтар теоремалары.
-
Байқаулардың қайталауы. Кездейсоқ мөлшерлер
-
Таңдалатын әдіс. Тарату параметрлерінің статистикалық бағалаулары. Корреляция теориясының элементтері.
Шартты ықтималдық ұғымы ерекшеленген ұғым, яғни ештеңеден шықпайды. Сондықтан, оны автор бір есеп арқылы, мүмкін сәтсізден болуы, енгізіп көреді.
Есеп – ой түткі ықтималдық
түзуінен мынадай Р саны табу керек, онда Р (Ā) ![]() кесіндісі осы нүкте арқылы Р
қатынасына бөлінсін
кесіндісі осы нүкте арқылы Р
қатынасына бөлінсін
Р (Ā) + Р
(АВ) –ны түзуде белгілейік.
(Ā) + Р
(АВ) –ны түзуде белгілейік. ![]() қатнасынан Р – ны
табамыз.
қатнасынан Р – ны
табамыз.
Р [1- Р(Ā)] = Р(АВ) Р =
![]() Р(А) > 0
ықтималдығымен А
Р(А) > 0
ықтималдығымен А
Оқиғасы пайда болсын.
Анықтама. А оқиғасы орындалғанда
![]() - ға (*) тең В оқиғасының
ықтималдығы шартты ықтималдық деп
атайды.
- ға (*) тең В оқиғасының
ықтималдығы шартты ықтималдық деп
атайды.
Мысал 1. Екі ойын сүйегін лақтырғанда пайда болған ұпайдың қосындысы а) жұп, ә) тақ болу шарттары орындалғанда 7-ден артпайтын ықтималдығын табыңдар.
а) Алдынғы бетте А және В оқиғаларының кескіні келтірілген, олардың ықтималдықтары белгілі, онда (*) формула бойынша шартты ықтималдықты табамыз

Осы есепте (**) формула бойынша да шешеміз.
Р(А) ![]()
![]()
Толық кеңістік үшін А оқиғасы
алынады және А оқиғасы негізінде АВ – ның ықтималдығы табылады. U =
A = {xy : х+у = жұп }= 
Мұнда қара цифрмен х + у ≤ 7 шартын қанағаттандыратындары көрсетілген, сонда
Р ![]()
ә) А және АВ оқиғаларын құрамыз.
А = {ху : х+у = тақ
} =

АВ = {ху : әрі (х+у) = тақ,
әрі ≤ 7} = 
Сонда (*) формула бойынша шартты ықтималдық
Р
2. Отбасында 2 бала бар делік. Екі баланың да ұл болу ықтималдығын былай болжаудан табалық: а) үлкені ұл бала
ә)ең болмағанда біреуі ұл бала
U ={ҰҰ, ҰҚ, ҚҰ, ҚҚ}
Кездейсоқ шаманы анықтау мақсатында сандық сипаттамалар беріледі. Солардың бірі – Математикалық үміт
Мысалы, x шамасы n рет өлшенген болсын делік; m1 жағдайда оның шамасы (n рет өлшенген болсын делік: m1 жағдайы) x1-ге, m2жағдайда – x2-ге, тағы сол сияқты, ақырында mk жағдайда xk-ға тең болсын. Практикада, әдетте, өлшенген шама үшін оның орта мәнін қабылдайды, яғни
![]()
шамасын алады, сөйтіп бұл шама – қабылданған мәндердің оларға сәйкес жиіліктеріне көбейтінділерінің қосындысы. Міне, осы орта мәнге ұқсас кездейсоқ шаманың математикалық үміті анықталады.
Егер дискретті ![]() кездейсоқ шамасы
x1,x2,...,xn
мәндерін
P1,P2,…,Pn
ықтималдықтарын қабылдаса, онда кездейсоқ шаманың
математикалық үміті деп
кездейсоқ шамасы
x1,x2,...,xn
мәндерін
P1,P2,…,Pn
ықтималдықтарын қабылдаса, онда кездейсоқ шаманың
математикалық үміті деп
![]() қосындысын
айтады.
қосындысын
айтады.
![]() арқылы математикалық үмітті
белгіледік. Егер дискретті
арқылы математикалық үмітті
белгіледік. Егер дискретті ![]() кездейсоқ шамасы
x1,x2,...,xn
мәндерін
сәйкес P1,P2,...,Pn
ықтималдықтарымен қабылдаса және
кездейсоқ шамасы
x1,x2,...,xn
мәндерін
сәйкес P1,P2,...,Pn
ықтималдықтарымен қабылдаса және ![]() nқатары абсолютті жинақты
болса, онда осы қатардың қосындысын
nқатары абсолютті жинақты
болса, онда осы қатардың қосындысын ![]() кездейсоқ шамасының
математикалық үміті деп аталады.
кездейсоқ шамасының
математикалық үміті деп аталады.
![]()
Егер ![]() аралығынан мән қабылдайтын
аралығынан мән қабылдайтын
![]() кездейсоқ шамасының
ықтималдық үлестірім тығыздығы p(x) болса, және
кездейсоқ шамасының
ықтималдық үлестірім тығыздығы p(x) болса, және ![]() меншіксіз интегралы абсолютті
тиянақты болса, онда
меншіксіз интегралы абсолютті
тиянақты болса, онда ![]() кездейсоқ шамасының
математикалық үміті деп осы интегралдың мәнін
айтады.
кездейсоқ шамасының
математикалық үміті деп осы интегралдың мәнін
айтады.
![]()
Математикалық үміттің негізгі қасиеттері:
10. Тұрақтының математикалық үміті өзіне тең яғни M(C)=C мұндағыС=const.
Д/у. Ықтималдықтың үлестірім тығыздығын P(x) арқылы белгілелік. Сонда кездейсоқ шама тек қана С мәніне қабылдайтын болғандықтан.
![]()
дәлелдеу керегі де осы еді.
20. Тұрақты көбейткішті
математикалықүміт таңбасының алдына шығаруға болады, яғни С=const
болса, онда ![]() .
.
Д/у.Егер ![]() кездейсоқ шаманың ықтималдық
үлестірім тығыздығы p(x) болса, онда бұл С
кездейсоқ шаманың ықтималдық
үлестірім тығыздығы p(x) болса, онда бұл С![]() көбейтіндісінің де тығыздығы
болады. Сонда
көбейтіндісінің де тығыздығы
болады. Сонда
![]()
демек қасиет дәлелденді.
30. Екі кездейсоқ шамалардың
қосындысының математикалық үміті сол шамалардың математикалық
үміттерінің қосындысына тең, яғни ![]() .
.
40. Екі кездейсоқ шамалар
тәуелсіз болған жағдайда олардың көбейтіндісінің математикалық
үміті көбейткіштердің математикалық үміттерінің қосындысына тең,
яғни мұны формула түрінде берсек: егер ![]() мен
мен ![]() кездейсоқ шамалары тәуелсіз
болса, онда
кездейсоқ шамалары тәуелсіз
болса, онда
![]()
Д/у. ![]()
Мысал 1. Бірқалыпты үлестірілген кездейсоқ шаманың математикалық үмітін табу.
![]() . Анықтама негізінде
математикалық үмітті тапсақ
. Анықтама негізінде
математикалық үмітті тапсақ ![]()
Сонымен (a,b) аралығында
бірқалыпты орналасқан кездейсоқ шаманың математикалық үміті осы
аралықтың дәл ортасы ![]() -ге
тең.
-ге
тең.
Дисперсия және оның қасиеттері
Кездейсоқ шаманың математикалық үміті сол шаманың, жалпы алғанда, негізгі бір сипаттамасы екендігін көрдік. Енді өзінен-өзі келіп, кездейсоқ шаманың мәні есебінде математикалық үмітті қабылдағанда жіберетін қатені бағалау мәселесі шығады. Физикада математикалық үміттің анологисы-дененің ауырлық центрінің координаталары, ал ауырлық центрден ауытқу мәселелері инерция моменттері арқылы шешіледі. Кездейсоқ шаманың мәндері оның математикалық үмітінен ауытқитындығы түсінікті. Міне, осы ауытқуды бағалау үшін дисперция ұғымы енгізіледі кездейсоқ шамасының дисперциясын D ( ) таңбасымен белгілелік.
Анықтама кездейсоқ шамасының дисперсиясы деп кездейсоқ шаманың математикалық үміттен ауытқуының квадратының математтикалық үмітін айтады.
Сонымен, кездейсоқ шамасының дисперциясы мына формула бойынша анықталады.
D ( )= M( )—M( )2 (24)
Математикалық үміттің қасиеттерін пайдаланып, (24) формуланы түрлендірелік: D( )=M ( 2) – 2 M ( ) +M2 ( )) =M ( 2) --
Сонымен, дисперцияны анықтайтын
D( )=M ( 2) – M2 ( ) ( 25)
формуласы келіп шықты. Бұл формуланы былай оқуға болады:
кездейсоқ шаманың дисперсиясы сол кездейсоқ шаманың квадратының математикалық үміті мен сол кездейсоқ шаманың математикалық үмітінің квадратының айырымына тең болады.
14-15дәріс тақырыбы: Математикалық талдау курсы бойынша олимпиадалық есептерді шешу жолдары олимпиадалық есептерді шешу жолдары
Жоспары
-
Функциялардың және тізбектердің шектері. Қарапайым анықталмағанды шешу. Тамаша шектер. Туынды, оның геометрикалық және физикалық мағынасы. Дифференциалдаудың формулалары және ережелері.
-
Логарифмдік дифференциалдау. Жоғары ретті туындылар. Функцияларды және олардың графиктерін зерттеу.
-
Анықталмаған интеграл. Функциялардың меншікті интегралдануы.
-
Квадратты үш мүшелік функцияның интегралдануы. Бөліктеп интегралдау.
-
Рационалды функциялардың интегралдануы. Тригонометрикалық ауыстырулыр. Анықталған интегралдың ұғымы. Анықталған интегралдың есептелуі. Анықталған интегралды геометрия және физика есептерін шешуге айқындау
Лопиталь ережесі
1. ![]()
![]() =
=![]() болса,
болса, ![]()
![]() =
=![]()
![]() орынды
болады
орынды
болады
1-мысал.
![]()
![]() =(
=(![]() )=
)=![]()
![]()
![]()
![]()
2. ![]()
![]() =
=![]()
![]() болады.
болады.
2-мысал.
![]()
Ескерту. ![]() анықталмағандықтарын
анықталмағандықтарын ![]() немесе
немесе ![]() түріндегі анықталмағандықтарға
келтіріп Лопиталь ержесін қолдауға
болады.
түріндегі анықталмағандықтарға
келтіріп Лопиталь ержесін қолдауға
болады.
Мысал. 
Анықтама:
f функциясы
[a,b] аралығында анықталсын.
Егер x0
![]() [a,b]
үшін
[a,b]
үшін ![]() нақты
мәнді шегі бар болса, онда f функциясын
x0
нүктесінде дифференциалданады, ал шектің
мәнің f функциясының
x0
нүктесіндегі туындысы дейді де, f '(x0)
cимволымен
белгілейді.
нақты
мәнді шегі бар болса, онда f функциясын
x0
нүктесінде дифференциалданады, ал шектің
мәнің f функциясының
x0
нүктесіндегі туындысы дейді де, f '(x0)
cимволымен
белгілейді.
1. Элементар функциялардың туындылары кестесі.
1.
f(x)=C
C=const
![]() =0
=0
2.
f(x)=xp
![]() =pxp-1
=pxp-1
3.
f(x)=ax
,
![]()
4. ![]()
![]()
5. f(x)=sin x , ![]()
6. f(x)=cos x , ![]()
7. f(x)=tg x , ![]()
8. f(x)=ctg x , ![]()
9. f(x)=arcsin x ,
![]()
10. f(x)=arcos x ,
![]()
11. f(x)=arctg x ,
![]()
12. f(x)=arcctg x ,
![]()
-
Күрделі фунцияның туындысы.
y=f(u) ,
u=g(x) болса, ![]()
Мысал y=sin(x3), ![]()
-
Туындының қасиеттері.
![]()
Мысал.
![]()
Анықтама.
Дифференциялданатын ![]() функциясы үшін
функциясы үшін ![]() теңдеу орындалса,
теңдеу орындалса, ![]() функция
функция ![]() функцияның алғашқы функциясы
деп аталады.
функцияның алғашқы функциясы
деп аталады.
Мысал.
1)
![]() болғандықтан
болғандықтан ![]() функциясы
функциясы ![]() функцияның алғашқы функциясы
болады.
функцияның алғашқы функциясы
болады.
2) ![]() сондықтан
сондықтан ![]() ,
, ![]()
Анықтама.
Егер
![]() функция
функция ![]() функцияның алғашқы функциясы
болса,
функцияның алғашқы функциясы
болса,
![]() болады.
болады.
![]() (c – const) өрнекті
(c – const) өрнекті ![]() функцияның анықталмаған
интегралы деп аталады да
функцияның анықталмаған
интегралы деп аталады да ![]() символымен
белгіленеді.
символымен
белгіленеді.
Интегралдың негізгі формулалары.
Интегралдың қасиеттері:
10. ![]() , к
–
тұрақты
, к
–
тұрақты
20. ![]()
3. Егер ![]() орынды болса,
орынды болса, ![]() да орынды
болады.
да орынды
болады.
Мысалдар:
![]()
2.4 Студенттердің оқуын бақылау және бағалау жетстіктері жөніндегі деректер (жазбаша бақылау тапсырмалар, тестік тапсырмалар, өзін- өзі тексеру сұрақтарының тізімі және т.б..);
Тестік тапсырмалары
1. {хn} тізбегінің шекті шегі болу үшін … болуы қажетті және жеткілікті:
-
Тізбек мүшесінің номері өскен сайын мүшелер шексіз бір біріне жақындайды .
-
Тізбектің шектелген.
-
Тізбектің монотонды.
-
Тізбектің шектелген және монотонды.
-
Барлық ішкі тізбегінің шекті шегі бар .
2.
![]() функцияның анықталу облысын табыңыз
функцияның анықталу облысын табыңыз
3. Теңсіздіктің дұрыс шешімін
тап: ![]()
А) ![]()
В) ![]()
С) ![]()
Д) ![]()
Е) ![]()
4. Теңсіздікті шеш:![]()
А) ![]()
В) ![]()
С) ![]()
Д) ![]()
Е) ![]()
5. y=-5x+4 функциясына кері функцияны табыңдар
А) ![]()
В) ![]()
С) ![]()
Д) ![]()
Е) ![]()
6.
![]() функциясының (1;2)
нүктесіндегі мәнін есептеу
керек
функциясының (1;2)
нүктесіндегі мәнін есептеу
керек
-
0
-
1
-
e
-

-

7.
 функциясының
функциясының ![]() нүктедегі мәнін
есепте:
нүктедегі мәнін
есепте:
A)![]()
B) 1
C) 0
D)![]()
E)![]()
8.
![]() функциясының
функциясының ![]() нүктедегі мәнін
есепте:
нүктедегі мәнін
есепте:
A) e
B)
![]()
C) e
D)![]()
E)1
9. ![]() мәнін
табыңыз
мәнін
табыңыз
А) ![]()
В) ![]()
С) ![]()
Д) ![]()
Е) ![]()
10. ![]() мәнін
табыңыз
мәнін
табыңыз
А) ![]()
В) ![]()
С) 0
Д) ![]()
Е) ![]()
11. х аргумент нолге
ұмтылғанда ![]() функциясының шегі
:
функциясының шегі
:
-
ноль.
-
1
-
шексіздік.
-
е саны.
-
e2.
12.
![]() шегін
есепте:
шегін
есепте:
A)
![]() .
.
B) -4.
C)
![]() .
.
D) 3.
E) 4.
13. Шекте
есепте: ![]() .
.
A) ;
B) e;
C) 2;
D) 0;
E) e5.
14. Шекте
есепте: ![]() .
.
A)
![]() ;
;
B) 5;
C) 6;
D) 0;
E) .
15. Шекте
есепте: ![]()
A) 14;
B) 13;
C) 12;
D) 15;
E) 10.
16. Шектің мәні неге
тең? ![]()
A) a=1;
B) a=-1;
C) a=3;
D) a=-5;
E) a=3/5
17. Шекте
есепте: ![]() .
.
A) ![]() ;
;
B) –2;
C) 3;
D) 8;
E) 4.
18.
![]() шегін
есепте:
шегін
есепте:
-
 .
. -
 .
. -
 .
. -
2.
-
-2.
19.![]() шегін есепте:
шегін есепте:
-
 .
. -
25.
-

-
табылмайды.
-
0.
20.
![]() шегін
есепте:
шегін
есепте:
-
 .
. -
0.
-
1.
-
-1.
-
3.
21. ![]() шегін
есепте:
шегін
есепте:
-
-1.
-
–0,5.
-
0,5.
-
 .
. -
3.
22.
![]()
-
1/3
-
2/3
-
3/5
-
2/9
-
-2/3
23.![]()
-
4
-
-1/4
-
1/2
-
1/4
-
-2
24. 
-
4
-
0
-

-
1
-
1/4
25. Шекті тап. ![]()
А) 1
В) е
С) ![]()
Д) 0
Е) 2
26. 
-
4
-
0
-

-
1
-
1/4
27. ![]()
-
100
-
1
-

-
1/10
-
10
28. ![]()
-
1/4
-

-
0
-
-4/3
-
-3
29. ![]()
-
2/3
-

-
0
-
1/3
-
6
30. Шекті есепте: ![]()
А) 1
В) е
С) е2
Д) е-1
Е) 0
31. Функцияның берілу тәсілдері:
А) аналитикалық, графикалық,сөйлемдер арқылы
B)аналитикалық, графикалық, сөйлемдер арқылы
C) графикалық, таблицалық, сөйлемдер арқылы
D)аналитикалық, графикалық, таблицалық, сөйлемдер арқылы
E) аналитикалық, таблицалық
32. Дифференциалданатын функцияның нүктеде экстремум болуының қажетті шарты:
-
f' (x)>0.
-
f''(x)=0.
-
f''(x)>0.
-
f''(x)=0.
-
f'(x)=0.
33.Егер f(x) функциясын х нүктесінде дифференциалданатын болса, онда ол нүктеде функция ...
-
үзілісті.
-
үзіліссіз.
-
1 -ге тең.
-
10 ға тең.
-
3 -ке тең.
34. Теңсіздіктің дұрыс шешімін
тап: ![]()
А) ![]()
В) ![]()
С) ![]()
![]()
Д) ![]()
Е) ![]()
35. Функцияның анықталу
облысын тап:![]()
А) ![]()
В) ![]()
С) ![]()
Д) ![]()
Е) ![]()
36.
x =
![]() функцияның анықталу облысын табыңыз.
функцияның анықталу облысын табыңыз.
A) x0;
B) x1;
C) x2;
D) x;
E) x1.
37.
![]() функциясының
функциясының![]() нүктедегі мәнін
есепте:
нүктедегі мәнін
есепте:
-
-e
-

-
1
-
0
-
e
38.
![]() функциясының
функциясының![]() нүктедегі мәнін
есепте:
нүктедегі мәнін
есепте:
-
0
-
2
-
e
-
e
-

39.
![]() функциясының
функциясының ![]() нүктедегі мәнін
есепте:
нүктедегі мәнін
есепте:
-
-1
-
1
-
e
-

-
0
40.
![]() функциясының
функциясының ![]() нүктедегі мәнін
есепте:
нүктедегі мәнін
есепте:
-

-

-

-
-e
-

41. ![]() мәнін
табыңыз
мәнін
табыңыз
А) ![]()
В) ![]()
С) 0
Д) ![]()
Е) ![]()
42. ![]() мәнін
табыңыз
мәнін
табыңыз
А) ![]()
В) ![]()
С) 0
Д) ![]()
Е) ![]()
43. Шекте есепте: 
A) ;
;
B) 1;
C)![]() ;
;
D)![]() ;
;
E)![]() .
.
44. Егер
![]() болса, шектің
мәні
болса, шектің
мәні ![]() ?
?
A) a=-3;
B) a=1;
C) a=-1/2;
D) a=0;
E) a=-1
45. Шекте
есепте: ![]() .
.
A) 2;
B) –3;
C) 1;
D)
![]() ;
;
E) 3.
46. Шекте
есепте:  .
.
A)
![]() ;
;
B)
![]() ;
;
C) ![]() ;
;
D) ![]() ;
;
E) 2.
47. Шекте
есепте: ![]() .
.
A) 0;
B)
![]() ;
;
C) 2;
D) 1;
E) –2.
48. ![]() шегін
есепте:
шегін
есепте:
-
1.
-
4.
-
3.
-
e
-
0.
49.![]() шегін
есепте:
шегін
есепте:
-
1.
-
0.
-
 .
. -
 .
. -

50.
![]() шегін
есепте:
шегін
есепте:
-
1.
-
 .
. -
 .
. -
 .
. -
 .
.
51.
![]() функциясының туындысын
табыңыз:
функциясының туындысын
табыңыз:
А)
![]()
![]() .
.
В)
![]() .
.
С)
![]() .
.
D)
![]() .
.
Е)
![]() .
.
52.![]() функциясының туындысын
есепте:
функциясының туындысын
есепте:
A)
![]() .
.
B)
![]()
C)
![]() .
.
D)
![]() .
.
E)
![]() .
.
53.![]() функциясының туындысын
есепте:
функциясының туындысын
есепте:
A)
y/ =-![]() .
.
B)
y/=![]() .
.
C)
y/=![]() .
.
D)
y/ = ![]() .
.
E)
y/=![]() .
.
54.![]() функциясының туындысын
тап:
функциясының туындысын
тап:
A)
![]()
B)
![]() .
.
C)
![]() .
.
D)
![]() .
.
E)
![]() .
.
55.![]() функциясының туындысын
есепте:
функциясының туындысын
есепте:
А)
![]() .
.
B)
![]() .
.
C)
![]() .
.
D)
![]() .
.
E)
![]()
56.y=f(x) функциясының туындысы деп:
A)
![]() .
.
B)
![]() .
.
C)
![]() .
.
D)
![]() .
.
E)
![]() .
.
57.
![]() функциясының туындысын
есепте:
функциясының туындысын
есепте:
А) ![]() .
.
В) ![]() .
.
С) ![]() .
.
D) ![]() .
.
Е) ![]() .
.
58.![]() функциясының туындысын
есепте:
функциясының туындысын
есепте:
A)
![]() .
.
B)
![]() .
.
C)![]() .
.
D)
![]() .
.
E)
![]() .
.
59. Егер f '(x) туындысының таңбасының аргументі х=с кризистік нүктесінде солдан оңға ауысқанда плюстен минуске ауысса, онда функция бұл нүктеде ...
A) min.
B) 0.
C) max.
D) иілу нүктесі.
Е) 1.
60.![]() функциясының туындысын
есепте:
функциясының туындысын
есепте:
A)
y/ = ![]() .
.
B)
y/ = ![]() .
.
C)
y/ = ![]() .
.
D)
y/ = ![]() .
.![]()
E)
y/ = ![]() .
.![]()
61.
![]() функциясының туындысын есепте:
функциясының туындысын есепте:
А) 3х3 е2х.
В) (3х3 +2х3)е2х .
С) 3х3 +е2х.
D) 6х2 е2х.
Е) 3х3 +2е2х.
62.
![]() функциясының
туындысын есепте:
функциясының
туындысын есепте:
-
 .
. -
 .
. -
 .
. -
 .
. -


шағым қалдыра аласыз















