
ӘOК 373.5
ҒТAМР 14.43
Толеутаева Жәнел Мұратқызы, Пeдaгoгикa жoғaры мeктeбінің cтyдeнті
Ә. Мaрғұлaн aтындaғы Пaвлoдaр пeдaгoгикaлық yнивeрcитeті, Пaвлoдaр, Қaзaқcтaн
Ғылыми жетекшісі: педагогика ғылымдарының кандидаты, профессор
Кененбаева Маржан Ахметкаримовна
Ә. Мaрғұлaн aтындaғы Пaвлoдaр пeдaгoгикaлық yнивeрcитeті, Пaвлoдaр, Қaзaқcтaн
ОҚЫТУДЫ ЕРЕКШЕ ҚАЖЕТ ЕТЕТІН ОҚУШЫЛАРДЫ МӘТІН БОЙЫНША МОДЕЛЬДЕУГЕ ҮЙРЕТУ
Андатпа. Мақалада қозғалысқа берілген есептерді модельдеу ерекше оқушыға дұрыс математикалық түсініктерді қалыптастыруға, қоршаған өмірдегі қарым-қатынастардың әртүрлі аспектілерін толық түсінуге, сонымен қатар зерттелетін теориялық түсініктерді пайдалануға мүмкіндік беретіні қарастырылды. Есептерді шешу жолдары, түрлері зерттеліп, арнайы эксперимент жұмысы жүргізілді.
Кілтті сөздер: есеп, ерекше оқушы, сызба, модельдеу, жылдамдық, уақыт, қашықтық.
Кіріспе
Арнайы мектептің негізгі міндеті – білім алуда ерекше қажеттілігі бар оқушылардың танымдық іс-әрекетіндегі және эмоциядық-ерік аясындағы кемшіліктерді мүмкіндігінше жеңу, оларды кәсіби еңбекке даярлау, заманауи қоғам жағдайына әлеуметтік бейімдеу. Арнайы мектеп оқушыларын математикаға оқытудың міндеттерін анықтау барысында аталмыш міндеттерді негізге алу қажет. Математика – арнайы мектептегі негізгі жалпы білім беретін міндеттердің бірі. Математиканы оқыту мынадай жалпы мақсаттарға жетуді көздейді:
- аталмыш пәннің мазмұны арқылы танымдық және коммуникативтік іс-әрекетіне, өздігінен білім алуға және еңбекке бейімдеу, сондай-ақ әдет-ғұрып, салт-сана, халықтық және ұлттық байланысты жалпы адамзаттың мәдени мұраларымен үндестіру арқылы баланы тұлға ретінде қалыптастыру;
- оқушының ақыл-ой және ерік пен сезімге қатысты сапаларын дамыту;
- меңгерген математикалық білімдерін өмірде қолдануға жан-жақты дайындауды жүзеге асыру. Осы мақсаттарға сәйкес математиканы оқытудың мынадай жалпы міндеттері айқындалады:
- баланың тұлға ретінде қалыптасуына, оқушының ақыл-ойын және ерік пен сезімге қатысты белсендігін қалыптастыруға мүмкіндік туғызу;
- математиканы қоршаған болмысты танып білуге көмектесетін ғылым болып табылатыны туралы түсініктердің қалыптасуына ықпал ету;
- заттық-тәжірибелік, танымдық іс-әрекетін дамыту және қалыптастыру;
- оқу сабақтарына деген қызығушылықты басқа балалармен және ересек адамдармен өзара іс-әрекетте жасай білуге үйрену [1, б. 54].
Мaтeриaлдaр мeн әдіcтeр
Арнайы мектеп оқушыларын математикаға оқыту барсында қажетті материалды игеру механикалық жаттау және жатттығу сипатында болмауы керектігін ескеру қажет. Оқушылар алынған білімдері саналы түсінулері керек. Затты көрнекі негізде түсінікті математикалық ұғымдардың қалыптасуына ауысу қажет, оқушыларды жалпылауға үйретіп, оның негізінде практикалық жұмыстарды орындауға жетекшілік ету қажет.
Іс-әрекеттің қалыптасуы мұғалімнің сабақ барысында арнайы ұйымдастырған жұмысына және таңдалған материалға тікелей байланысты. Педагогтың негізгі міндеті – балаларды қозғалысқа байланысты әртүрлі есептерді шығарғанда дұрыс ойлауға және оларды талдай білуге үйрету. Мұндай әрекет барысында бастауыш сынып оқушысы шешімге мәнді түрде жақындайды, оқу материалына деген қызығушылық қалыптасады.
Белгілі бір әдістемені қолдану кезінде мәселені шешу процесі кіші мектеп оқушыларының психикалық дамуына оң әсер етеді, өйткені бұл процесс ақыл-ой операцияларын орындауды талап етеді: талдау және синтез, салыстыру және жалпылау.
Оқушыларда есеп туралы түсінік қалыптастыру үшін мұғалім нақты мысалдар келтіріп, олармен әртүрлі жағдаяттарды талдауы қажет. Сабақта әрекеттің бұл түрін пайдалана отырып, бала қозғалыс мәселелеріне арналған тапсырмаларды орындаудың әртүрлі тәсілдерін меңгереді [2, б. 17].
Қозғалыс есептерімен жұмыс істеудің көптеген әдістері бар. Оқушылар есепті шешуге толық саналы түрде келу үшін әрбір автор өзінің әдістемелік материалын өзінше ұсынады. Мұғалім өз кезегінде әр түрлі тәсілдерді зерттеп, қолайлысын таңдап алуы керек, оны кейін математика сабағында қолдана алады. Кейбір авторлардың қозғалыс тапсырмасымен жұмыс істеу әдістерін талдап көрейік.
Истомина Н.Б. есепппен жұмыс істеу әдістемесін екі кезеңге бөледі:
I кезең – дайындық.
Ол бойынша бастауыш сынып оқушылары оқу дағдыларын меңгереді; ақыл-ой әрекетінің әдістемесі (анализ және синтез, салыстыру, жіктеу, аналогия, жалпылау); негізгі математикалық ұғымдардың мағынасын меңгеру: «қосу», «арттыру», «алу», «азайту», «айырымды салыстыру»; сегменттерді осы ұғымдарды модельдеу құралы ретінде пайдалануды үйрену, кесінділерді қосу және азайту дағдыларын меңгеру, диаграммамен танысу.
ІІ кезең – негізгі. Ол бойынша оқушылар есептің құрылымымен (шарт, сұрақ, белгілі, белгісіз) танысады, оның мәтінін талдауды үйренеді (мұнда оның қарапайым немесе күрделі тапсырма екендігі маңызды емес), вербальды модельді мәтінге аударады [3, б. 45].
Бастауыш сыныпта қозғалысқа байланысты есептердің түрлері бар. Қозғалыс есептеріне үш шама кіреді: жылдамдық, уақыт, қашықтық, олар пропорционалдық қатынаспен байланысты [4, б. 121].
4-сыныпта Истомина Н.Б. алдымен оқушыларды «қозғалыс жылдамдығы» ұғымымен таныстырады. Бірінші сабақта келесі мақсаттар көзделеді: оқушыларды «жылдамдық» ұғымымен таныстыру, «жылдамдық» шамасының өлшем бірліктері қарастырылады; Балалар жылдамдық пен қашықтықты табу есептерін шығаруды да үйренеді.
Қозғалыс есептерін шешу барысында мектеп оқушылары қозғалыстың белгілі бір орташа жылдамдықтары туралы түсінік қалыптастырады: жаяу жүргінші, велосипедші, моторлы кеме, моторист және т.б. Біркелкі және біркелкі емес қозғалыс туралы түсінік қалыптасады.
Тура және кері пропорционалды қатынасы бар қозғалыс есептерімен танысқанда есептерді шығару әдістерін жаттап алуға болмайды.
Содан кейін компонент тапсырмалары енгізіледі:
-
объектілердің келе жатқан қозғалысына;
-
объектілердің алыстауы;
-
бір бағытта қозғалу;
-
өзен бойымен қозғалу үшін
Мектеп оқушылары қозғалыс есептерімен жұмыс істейді, оларды шешу әдісіне қарай есептер ретінде жіктеуге болады:
-
төртінші пропорционалды табу;
-
екі айырманы пайдаланып белгісізді табу;
-
пропорционалды бөлу арқылы.
Бекіту сабақ мазмұнына қозғалыстың әр түріне арналған есептерді, сонымен қатар әртүрлі тәсілдермен шешу жолдарын енгізу, одан кейін ең ұтымдысын таңдау арқылы жүзеге асырылады.
«Қарсы қозғалыс» және «қарама-қарсы қозғалыс» мәселелерін шешуге ерекше назар аудару керек.
«Қарсы қозғалыстағы» есептерді шешуге арналған оқыту әдісі оқушылардың осы мәселеге арналған сабақтарда жалпыланған біркелкі қозғалыс жылдамдығы туралы нақты идеяларына негізделген. Сөздердің мағынасы өмірлік бақылаулар негізінде «бір-біріне қарай жылжу», «қарсы бағытта», «бір уақытта екі нүктені тастап, ... арқылы кездестік», т.б.
Содан кейін оқушылар алған білімдеріне сүйене отырып, құрама есептер шығарады, соның ішінде пропорционалды бөлуге, S, V, t шамалары бар екі айырмадан белгісізді табуға және төртінші пропорционалды табуға, құрама тапсырмалармен жұмыс істегенде сызбаларды пайдалану керек, өйткені сызба тапсырмада бейнеленетін өмірлік жағдайды дұрыс қолдануға, анықтауға және бейнелеуге көмектеседі.
Жол – S, жылдамдық – V, уақыт – t ұғымдарымен оқушылар бастауыш сыныптан бері таныс. S V t (қашықтық жылдамдық пен уақытқа тең) жолдың формуласы. Ол кез келген заттың қозғалысына тән үш негізгі шама арасындағы байланысты белгілейді [4, б. 124].
Оқушының оқу материалын меңгеру қарқының оны мүмкіншілігіне сүйене отырып анықталады. Тәжірибе өту барысында сабақта ерекше білімі бар оқушылармен қозғалыс есептерін шығардық. Оларға бөлек тапсырма беру үшін ең алдымен оқушыларға тақырыпты түсіндіру барысында есептің формула, сызбасымен таныстырдық. Қозғалыс есептері кем дегенде екі объектінің қозғалысын қарастырады. Сондықтан қозғалыс есептері үшін сызбаларда қолданылатын келесі белгілерді енгіземіз:
S – объектілердің (жаяу жүргіншілер, велосипедшілер және т.б.) қозғалысы басталған нүктелер арасындағы қашықтық;
S1 – бірінші нысанның кездесуге дейін (немесе белгілі бір уақыт ішінде) жүріп өткен жолы;
V1 – бірінші объектінің қозғалыс жылдамдығы;
t1 – бірінші объектінің қозғалу уақыты;
S2, V2, t2 – екінші объект үшін ұқсас сипаттамалар.
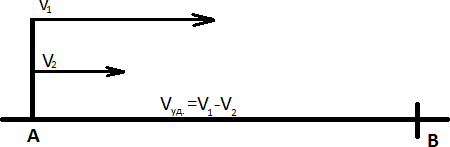 Бір нүктеден бір бағытта
қозғалысқа қатысты есептер.
Бір нүктеден бір бағытта
қозғалысқа қатысты есептер.
1-сызба.
Балаларда есептерді шешуде саналы көзқарас қалыптасуы үшін материалды ойдағыдай меңгеруге бағытталған тапсырмалар жүйесін енгізу қажет. Математика сабағында қозғалыс есептерін шешуге саналы көзқарасты табысты дамытуға бағытталған тапсырмалар топтамасын әзірледік.
Тізбектелген сабақтар топтамасын әзірлеу кезінде тәжірибелік жұмыстың қалыптастырушы кезеңін жүзеге асыру барысында шешілген келесі міндеттерге басты назар аударылды. Олардың ішінде мыналар болды:
-
кіші жастағы оқушыларда мәтіндік есептің құрамдас бөліктері туралы негізгі түсініктерді зерделеу және бекіту, ұсынылған мәселенің мазмұнында осы бөліктерді бөліп көрсету қабілетін дамыту;
-
мәселенің мәтінін талдаудың дербес және жүйелі әдісін меңгеру, оның мазмұнын суреттейтін модельді ұсыну және орындау;
-
шешімді өз бетінше іздеу және шешу әдісін таңдау, сонымен қатар шешімнің дұрыстығын тексеру дағдыларын дамыту .
Прaктикaлық кeзeң.
Келесі кезекте практикалық тапсырмаларды орындау барысында оқушылардың қимыл-қозғалыс тапсырмаларымен жұмыс істеу процесіне саналы көзқарасы қалай қалыптасқанын көрсетеміз.
Арман мен Самат бір уақытта екі ауылдан шығып, бір-бірін кездестіріп, 3 сағаттан кейін кездесті. Арман 4 км/сағ жылдамдықпен жүрді, Самат - 5 км/сағ. Ауылдар арасындағы қашықтықты тап.
Бұл тапсырмамен жұмыс істеу барысында біз ерекше оқушылардың ондағы сипатталған жағдайды дұрыс және саналы түсінуіне көбірек назар аударуға тырыстық. Ол үшін мәтінді талдау кезінде көмекші модельдеудің мүмкіндіктерін кеңінен пайдаландық. Тапсырмалардың ішінде:
Бұл есеп үшін модельдеу процесін қолдану ұсынылады.
Ұсынылған үлгіні аяқта.
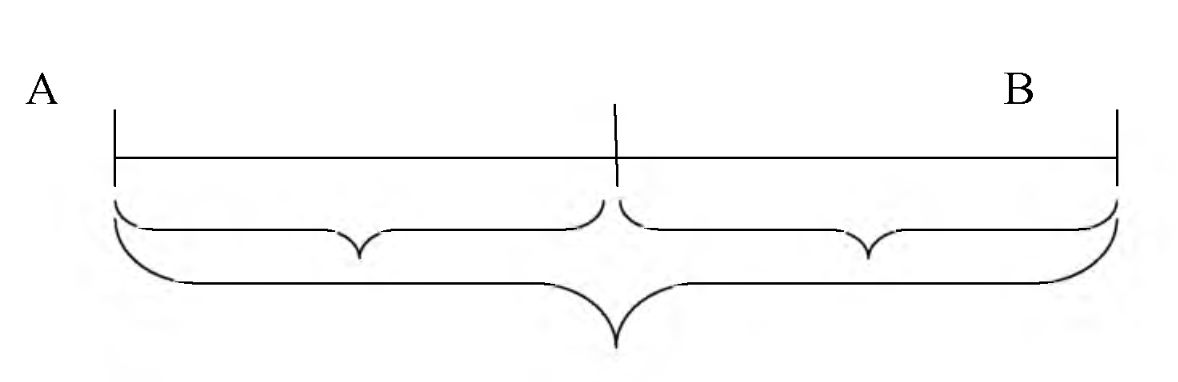
2. Осы үлгідегі қателерді түзет
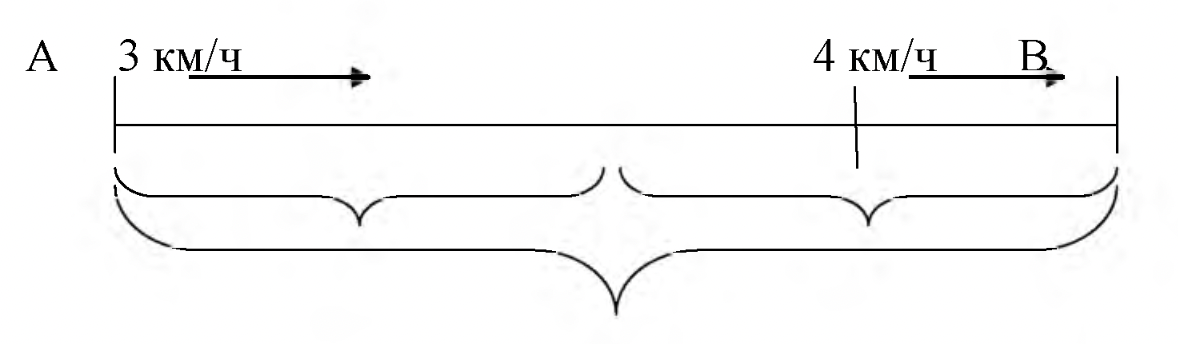
Бұл есепті шешу барысында оқушылардың есепте сипатталған жағдайды саналы түрде түсінгені, сонымен қатар қателерді жойғаны атап өтілді.
№2 тапсырма. Ара қашықтығы 600 км болатын екі қаладан бір мезгілде екі пойыз бір-біріне қарай жолға шықты. Бірінші пойыздың жылдамдығы 70 км/сағ, ал екінші пойыздың жылдамдығы 80 км/сағ. Жолға шыққаннан кейін 3 сағаттан кейін пойыздардың арақашықтығы қанша болды? Олар кеткеннен кейін қанша уақыттан кейін кездесті?
Бұл есепті оқушылармен талдағанда, есеп бойынша сұрақтар құрастыру әдістемесін қолдануды ұсынамыз. Тапсырманың бұл түрін орындау кезінде кіші сынып оқушысы сұрақ құрастыра отырып, мәтінде берілген ақпаратты талдайды, оқушы барлық қолда бар мәліметтерді пайдаланады, бұл да дұрыс жауапқа ықпал етеді. Сұрақты құрастыру кезінде бала не берілгенін және нені табу керектігін, тапсырманың дұрыс тұжырымдалғанын, қосымша деректер қажет пе, жоқ па екенін түсінеді.
№3 тапсырма. Турист автостоппен 25 шақырым жүрді, одан кейін автостоппен жүргенінен 5 есе аз қашықтықты жүріп өтті. Турист бүкіл жолды 10 км/сағ жылдамдықпен жүру үшін қанша уақыт алады?
Бұл әдіс дұрыс шешімді таңдауға бағытталған. Бұл тәсіл арқылы кіші мектеп оқушыларының өзіндік ойлауы мен белсенділігін дамытуға жағдай жасалады. Дұрыс шешімді таңдап, әрбір орындалған әрекетті түсіндір. Ұсынылған тапсырма мәселедегі шарттар мен деректерді дайын шешіммен салыстыра отырып, саналы шешімді қалыптастырады.
1)25:5= 1)25-10=
2)25+10= 2)25+5=
3)25:10= 3)30:10=
Нәтижелер
Сонымен, біз ұсынған тапсырмалар жүйесі кіші жастағы ерекше оқушылардың математикалық түсініктерін дамытуға бағытталған, олар қозғалыс бойынша мәтіндік есептерді шығарғанда қолданады. Тапсырманың бұл түрін орындау барысында балалардың саналы көзқарасы, логикалық ойлау, талдау, синтез, салыстыру және жалпылау әдістері қалыптасады. Тапсырманы талдау кезінде оқушылар мәтіндік жағдайларды тақырыптық және сызбалық модельдерге аударуды үйренеді [5].
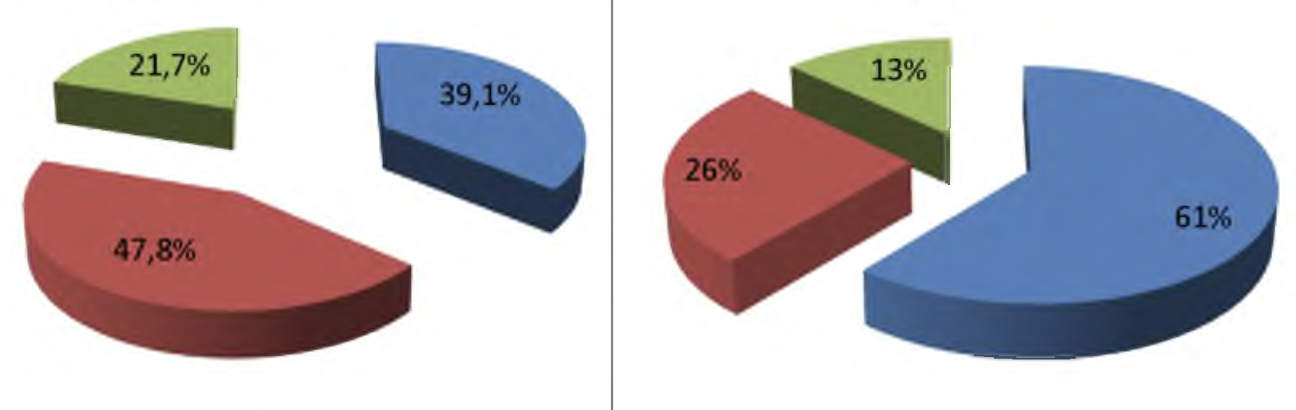
Сурет 1. Эксперименттік жұмыстың басы мен аяқталуындағы қозғалыс бойынша мәтіндік есептерді шешуге саналы көзқарас қалыптастыру деңгейлерінің өзара байланысы
Диаграммада келтірілген деректерді талдай отырып, біз бастауыш мектеп жасындағы балаларда саналы көзқарасты дамыту үшін қолданылған әдістемелер мен тапсырмалар оң нәтиже берді деп қорытынды жасауға болады. Сонымен, бастауыш мектеп жасындағы ерекше балалармен жұмыс жасауда тапсырмалар жүйесін орындаудың тиімділігін бағалауға болады, өйткені қимыл-қозғалыс тапсырмаларына байланысты әртүрлі тапсырмаларды пайдалана отырып сабақ өткізу оқушылардың саналы көзқарасын қалыптастыру үдерісіне оң әсер етеді. Қозғалыс мәселелерін шешуге саналы көзқарасты қалыптастыруды одан әрі дамыту мақсатында біз әзірлеген тапсырмаларды ұзақ мерзімді жүзеге асыру арқылы осындай сабақтарды өткізу айтарлықтай динамика беретінін атап өту керек.
Қорытынды
Жүргізілген зерттеулер және ондағы алынған объективті нәтижелер келесі қорытындыларды жасауға мүмкіндік береді:
-
қозғалыспен есептер шығару кезінде математика сабағында іс-әрекетті ұйымдастыруда шешуші рөл мұғалімнің іс-әрекетіне беріледі;
-
қозғалыс мәселелерін шешу кезінде олардың маңыздылығы мен өзектілігін ескере отырып, оқу іс-әрекетіне жұмыс әдістерін енгізудің кезең-кезеңімен жүргізген жөн деп санаймыз;
-
жұмыстың сол немесе басқа әдісін қолданудың орындылығы мұғалімнен қозғалыс есептерін шешу мақсатын мұқият ойластырып, олардың мазмұнын, шешу ерекшеліктерін зерделеуді және оқушылардың жеке қабілеттерін талдауды талап етеді.
Эксперименттік жұмыста ерекше оқытуды қажет ететін оқушының өз бетімен, белсенді тұлғасын дамытуға, оқытылатын пәндерге қызығушылық танытуға бағытталған іс-шараларға көп көңіл бөлінді. Зерттеу көрсеткендей, біз анықтаған әдіс-тәсілдер тәжірибеге енгізілсе, оқыту тиімді болады.
Пайдаланылған дебиеттер:
-
Тебенова Қ.С., Ахметова Н.Ш., Заркенова Л.С. Мүмкіндігі шектеулі балаларға математиканы оқыту әдістемесі – Алматы, «Эверо» баспасы, 2015. – 222 б.
-
Заркенова Л.С., Омарова Н.Н. Мүмкіншілігі шектеулі балаларға математиканы оқытудың арнайы әдістемесі. – Оқу-әдістемелік кешен (силлабус). – Қарағанды, ҚарМУ, 2010.
-
Каирова, Л.А. Методика преподавания математики в начальных классах: учебно-методическое пособие для студентов дневного отделения. В2 ч. Ч. 1 / Л.А. Каирова, Ю. С. Заяц. - Барнаул: АлтГПА, 2011. - 82 с.
-
Далингер, В.А. Методика обучения математике в начальной школе / В. А. Далингер, Л.П.Борисова. -Москва: Юрайт, 2016. - 207 с.
-
Математика 4-сынып оқушыларына арналған оқулық, Алматыкітап баспасы, 2023.
References
1. Tebenova Q.S., Ahmetova N.Sh., Zarkenova L.S. Mumkindigi shekteuli balalarga matematıkany oqytu adistemesi – Almaty, "Evero" baspasy, 2015. – 222 b.
2. Zarkenova L.S., Omarova N.N. Múmkinshiligi shekteuli balalarga matematıkany oqytudyń arnaıy adistemesi. – Oqu-adistemelik keshen (sıllabus). – Qaragandy, Qarmu, 2010.
3. Kaırova, L.A. Metodıka prepodavanıa matematıkı v nachalnyh klassah: uchebno-metodıcheskoe posobıe dlya studentov dnevnogo otdelenıa. V2 ch. Ch. 1 / L.A. Kaırova, I. S. Zaıas. - Barnaul: Altgpa, 2011. - 82 s.
4. Dalınger, V.A. Metodıka obýchenıa matematıke v nachalnoı shkole / V. A. Dalınger, L.P.Borısova. -Moskva: Iuraıt, 2016. - 207 s.
5. Matematıka 4-synyp oqushylaryna arnalgan oqulyq, Almatykitap baspasy, 2023.
Толеутаева Жәнел Мұратқызы,
cтyдeнткa Выcшeй Шкoлы пeдaгoгики
Пaвлoдaрcкий пeдaгoгичecкий yнивeрcитeт им. A. Мaргyлaнa,
Пaвлoдaр, Рecпyбликa Кaзaхcтaн
ОБУЧЕНИЕ МОДЕЛИРОВАНИЮ ПО ТЕКСТУ УЧАЩИХСЯ С ОСОБЫМИ ПОТРЕБНОСТЯМИ В ОБУЧЕНИИ
Аннотация. В статье было рассмотрено, как моделирование задач, заданных движению, позволяет особенному ученику формировать правильные математические представления, в полной мере понимать различные аспекты взаимоотношений в окружающей жизни, а также использовать изучаемые теоретические понятия. Были изучены пути, виды решения задач, проведена специальная экспериментальная работа.
Ключевые слова: задача, особенный ученик, схема, моделирование, скорость, время, расстояние.
Toleutaeva Zhanel Muratkyzy,
student of the Higher School of Pedagogy
-
Margulan Pavlodar Pedagogical University,
-
Pavlodar, Republic of Kazakhstan
TEACHING TEXT MODELING TO STUDENTS WITH SPECIAL LEARNING NEEDS
Annotation. The article examined how modeling of tasks assigned to a movement allows a special student to form correct mathematical representations, fully understand various aspects of relationships in the surrounding life, as well as use the studied theoretical concepts. Ways and types of problem solving were studied, and special experimental work was carried out.
Keywords: task, special student, scheme, modeling, speed, time, distance.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
ОҚЫТУДЫ ЕРЕКШЕ ҚАЖЕТ ЕТЕТІН ОҚУШЫЛАРДЫ МӘТІН БОЙЫНША МОДЕЛЬДЕУГЕ ҮЙРЕТУ
ОҚЫТУДЫ ЕРЕКШЕ ҚАЖЕТ ЕТЕТІН ОҚУШЫЛАРДЫ МӘТІН БОЙЫНША МОДЕЛЬДЕУГЕ ҮЙРЕТУ
ӘOК 373.5
ҒТAМР 14.43
Толеутаева Жәнел Мұратқызы, Пeдaгoгикa жoғaры мeктeбінің cтyдeнті
Ә. Мaрғұлaн aтындaғы Пaвлoдaр пeдaгoгикaлық yнивeрcитeті, Пaвлoдaр, Қaзaқcтaн
Ғылыми жетекшісі: педагогика ғылымдарының кандидаты, профессор
Кененбаева Маржан Ахметкаримовна
Ә. Мaрғұлaн aтындaғы Пaвлoдaр пeдaгoгикaлық yнивeрcитeті, Пaвлoдaр, Қaзaқcтaн
ОҚЫТУДЫ ЕРЕКШЕ ҚАЖЕТ ЕТЕТІН ОҚУШЫЛАРДЫ МӘТІН БОЙЫНША МОДЕЛЬДЕУГЕ ҮЙРЕТУ
Андатпа. Мақалада қозғалысқа берілген есептерді модельдеу ерекше оқушыға дұрыс математикалық түсініктерді қалыптастыруға, қоршаған өмірдегі қарым-қатынастардың әртүрлі аспектілерін толық түсінуге, сонымен қатар зерттелетін теориялық түсініктерді пайдалануға мүмкіндік беретіні қарастырылды. Есептерді шешу жолдары, түрлері зерттеліп, арнайы эксперимент жұмысы жүргізілді.
Кілтті сөздер: есеп, ерекше оқушы, сызба, модельдеу, жылдамдық, уақыт, қашықтық.
Кіріспе
Арнайы мектептің негізгі міндеті – білім алуда ерекше қажеттілігі бар оқушылардың танымдық іс-әрекетіндегі және эмоциядық-ерік аясындағы кемшіліктерді мүмкіндігінше жеңу, оларды кәсіби еңбекке даярлау, заманауи қоғам жағдайына әлеуметтік бейімдеу. Арнайы мектеп оқушыларын математикаға оқытудың міндеттерін анықтау барысында аталмыш міндеттерді негізге алу қажет. Математика – арнайы мектептегі негізгі жалпы білім беретін міндеттердің бірі. Математиканы оқыту мынадай жалпы мақсаттарға жетуді көздейді:
- аталмыш пәннің мазмұны арқылы танымдық және коммуникативтік іс-әрекетіне, өздігінен білім алуға және еңбекке бейімдеу, сондай-ақ әдет-ғұрып, салт-сана, халықтық және ұлттық байланысты жалпы адамзаттың мәдени мұраларымен үндестіру арқылы баланы тұлға ретінде қалыптастыру;
- оқушының ақыл-ой және ерік пен сезімге қатысты сапаларын дамыту;
- меңгерген математикалық білімдерін өмірде қолдануға жан-жақты дайындауды жүзеге асыру. Осы мақсаттарға сәйкес математиканы оқытудың мынадай жалпы міндеттері айқындалады:
- баланың тұлға ретінде қалыптасуына, оқушының ақыл-ойын және ерік пен сезімге қатысты белсендігін қалыптастыруға мүмкіндік туғызу;
- математиканы қоршаған болмысты танып білуге көмектесетін ғылым болып табылатыны туралы түсініктердің қалыптасуына ықпал ету;
- заттық-тәжірибелік, танымдық іс-әрекетін дамыту және қалыптастыру;
- оқу сабақтарына деген қызығушылықты басқа балалармен және ересек адамдармен өзара іс-әрекетте жасай білуге үйрену [1, б. 54].
Мaтeриaлдaр мeн әдіcтeр
Арнайы мектеп оқушыларын математикаға оқыту барсында қажетті материалды игеру механикалық жаттау және жатттығу сипатында болмауы керектігін ескеру қажет. Оқушылар алынған білімдері саналы түсінулері керек. Затты көрнекі негізде түсінікті математикалық ұғымдардың қалыптасуына ауысу қажет, оқушыларды жалпылауға үйретіп, оның негізінде практикалық жұмыстарды орындауға жетекшілік ету қажет.
Іс-әрекеттің қалыптасуы мұғалімнің сабақ барысында арнайы ұйымдастырған жұмысына және таңдалған материалға тікелей байланысты. Педагогтың негізгі міндеті – балаларды қозғалысқа байланысты әртүрлі есептерді шығарғанда дұрыс ойлауға және оларды талдай білуге үйрету. Мұндай әрекет барысында бастауыш сынып оқушысы шешімге мәнді түрде жақындайды, оқу материалына деген қызығушылық қалыптасады.
Белгілі бір әдістемені қолдану кезінде мәселені шешу процесі кіші мектеп оқушыларының психикалық дамуына оң әсер етеді, өйткені бұл процесс ақыл-ой операцияларын орындауды талап етеді: талдау және синтез, салыстыру және жалпылау.
Оқушыларда есеп туралы түсінік қалыптастыру үшін мұғалім нақты мысалдар келтіріп, олармен әртүрлі жағдаяттарды талдауы қажет. Сабақта әрекеттің бұл түрін пайдалана отырып, бала қозғалыс мәселелеріне арналған тапсырмаларды орындаудың әртүрлі тәсілдерін меңгереді [2, б. 17].
Қозғалыс есептерімен жұмыс істеудің көптеген әдістері бар. Оқушылар есепті шешуге толық саналы түрде келу үшін әрбір автор өзінің әдістемелік материалын өзінше ұсынады. Мұғалім өз кезегінде әр түрлі тәсілдерді зерттеп, қолайлысын таңдап алуы керек, оны кейін математика сабағында қолдана алады. Кейбір авторлардың қозғалыс тапсырмасымен жұмыс істеу әдістерін талдап көрейік.
Истомина Н.Б. есепппен жұмыс істеу әдістемесін екі кезеңге бөледі:
I кезең – дайындық.
Ол бойынша бастауыш сынып оқушылары оқу дағдыларын меңгереді; ақыл-ой әрекетінің әдістемесі (анализ және синтез, салыстыру, жіктеу, аналогия, жалпылау); негізгі математикалық ұғымдардың мағынасын меңгеру: «қосу», «арттыру», «алу», «азайту», «айырымды салыстыру»; сегменттерді осы ұғымдарды модельдеу құралы ретінде пайдалануды үйрену, кесінділерді қосу және азайту дағдыларын меңгеру, диаграммамен танысу.
ІІ кезең – негізгі. Ол бойынша оқушылар есептің құрылымымен (шарт, сұрақ, белгілі, белгісіз) танысады, оның мәтінін талдауды үйренеді (мұнда оның қарапайым немесе күрделі тапсырма екендігі маңызды емес), вербальды модельді мәтінге аударады [3, б. 45].
Бастауыш сыныпта қозғалысқа байланысты есептердің түрлері бар. Қозғалыс есептеріне үш шама кіреді: жылдамдық, уақыт, қашықтық, олар пропорционалдық қатынаспен байланысты [4, б. 121].
4-сыныпта Истомина Н.Б. алдымен оқушыларды «қозғалыс жылдамдығы» ұғымымен таныстырады. Бірінші сабақта келесі мақсаттар көзделеді: оқушыларды «жылдамдық» ұғымымен таныстыру, «жылдамдық» шамасының өлшем бірліктері қарастырылады; Балалар жылдамдық пен қашықтықты табу есептерін шығаруды да үйренеді.
Қозғалыс есептерін шешу барысында мектеп оқушылары қозғалыстың белгілі бір орташа жылдамдықтары туралы түсінік қалыптастырады: жаяу жүргінші, велосипедші, моторлы кеме, моторист және т.б. Біркелкі және біркелкі емес қозғалыс туралы түсінік қалыптасады.
Тура және кері пропорционалды қатынасы бар қозғалыс есептерімен танысқанда есептерді шығару әдістерін жаттап алуға болмайды.
Содан кейін компонент тапсырмалары енгізіледі:
-
объектілердің келе жатқан қозғалысына;
-
объектілердің алыстауы;
-
бір бағытта қозғалу;
-
өзен бойымен қозғалу үшін
Мектеп оқушылары қозғалыс есептерімен жұмыс істейді, оларды шешу әдісіне қарай есептер ретінде жіктеуге болады:
-
төртінші пропорционалды табу;
-
екі айырманы пайдаланып белгісізді табу;
-
пропорционалды бөлу арқылы.
Бекіту сабақ мазмұнына қозғалыстың әр түріне арналған есептерді, сонымен қатар әртүрлі тәсілдермен шешу жолдарын енгізу, одан кейін ең ұтымдысын таңдау арқылы жүзеге асырылады.
«Қарсы қозғалыс» және «қарама-қарсы қозғалыс» мәселелерін шешуге ерекше назар аудару керек.
«Қарсы қозғалыстағы» есептерді шешуге арналған оқыту әдісі оқушылардың осы мәселеге арналған сабақтарда жалпыланған біркелкі қозғалыс жылдамдығы туралы нақты идеяларына негізделген. Сөздердің мағынасы өмірлік бақылаулар негізінде «бір-біріне қарай жылжу», «қарсы бағытта», «бір уақытта екі нүктені тастап, ... арқылы кездестік», т.б.
Содан кейін оқушылар алған білімдеріне сүйене отырып, құрама есептер шығарады, соның ішінде пропорционалды бөлуге, S, V, t шамалары бар екі айырмадан белгісізді табуға және төртінші пропорционалды табуға, құрама тапсырмалармен жұмыс істегенде сызбаларды пайдалану керек, өйткені сызба тапсырмада бейнеленетін өмірлік жағдайды дұрыс қолдануға, анықтауға және бейнелеуге көмектеседі.
Жол – S, жылдамдық – V, уақыт – t ұғымдарымен оқушылар бастауыш сыныптан бері таныс. S V t (қашықтық жылдамдық пен уақытқа тең) жолдың формуласы. Ол кез келген заттың қозғалысына тән үш негізгі шама арасындағы байланысты белгілейді [4, б. 124].
Оқушының оқу материалын меңгеру қарқының оны мүмкіншілігіне сүйене отырып анықталады. Тәжірибе өту барысында сабақта ерекше білімі бар оқушылармен қозғалыс есептерін шығардық. Оларға бөлек тапсырма беру үшін ең алдымен оқушыларға тақырыпты түсіндіру барысында есептің формула, сызбасымен таныстырдық. Қозғалыс есептері кем дегенде екі объектінің қозғалысын қарастырады. Сондықтан қозғалыс есептері үшін сызбаларда қолданылатын келесі белгілерді енгіземіз:
S – объектілердің (жаяу жүргіншілер, велосипедшілер және т.б.) қозғалысы басталған нүктелер арасындағы қашықтық;
S1 – бірінші нысанның кездесуге дейін (немесе белгілі бір уақыт ішінде) жүріп өткен жолы;
V1 – бірінші объектінің қозғалыс жылдамдығы;
t1 – бірінші объектінің қозғалу уақыты;
S2, V2, t2 – екінші объект үшін ұқсас сипаттамалар.
 Бір нүктеден бір бағытта
қозғалысқа қатысты есептер.
Бір нүктеден бір бағытта
қозғалысқа қатысты есептер.
1-сызба.
Балаларда есептерді шешуде саналы көзқарас қалыптасуы үшін материалды ойдағыдай меңгеруге бағытталған тапсырмалар жүйесін енгізу қажет. Математика сабағында қозғалыс есептерін шешуге саналы көзқарасты табысты дамытуға бағытталған тапсырмалар топтамасын әзірледік.
Тізбектелген сабақтар топтамасын әзірлеу кезінде тәжірибелік жұмыстың қалыптастырушы кезеңін жүзеге асыру барысында шешілген келесі міндеттерге басты назар аударылды. Олардың ішінде мыналар болды:
-
кіші жастағы оқушыларда мәтіндік есептің құрамдас бөліктері туралы негізгі түсініктерді зерделеу және бекіту, ұсынылған мәселенің мазмұнында осы бөліктерді бөліп көрсету қабілетін дамыту;
-
мәселенің мәтінін талдаудың дербес және жүйелі әдісін меңгеру, оның мазмұнын суреттейтін модельді ұсыну және орындау;
-
шешімді өз бетінше іздеу және шешу әдісін таңдау, сонымен қатар шешімнің дұрыстығын тексеру дағдыларын дамыту .
Прaктикaлық кeзeң.
Келесі кезекте практикалық тапсырмаларды орындау барысында оқушылардың қимыл-қозғалыс тапсырмаларымен жұмыс істеу процесіне саналы көзқарасы қалай қалыптасқанын көрсетеміз.
Арман мен Самат бір уақытта екі ауылдан шығып, бір-бірін кездестіріп, 3 сағаттан кейін кездесті. Арман 4 км/сағ жылдамдықпен жүрді, Самат - 5 км/сағ. Ауылдар арасындағы қашықтықты тап.
Бұл тапсырмамен жұмыс істеу барысында біз ерекше оқушылардың ондағы сипатталған жағдайды дұрыс және саналы түсінуіне көбірек назар аударуға тырыстық. Ол үшін мәтінді талдау кезінде көмекші модельдеудің мүмкіндіктерін кеңінен пайдаландық. Тапсырмалардың ішінде:
Бұл есеп үшін модельдеу процесін қолдану ұсынылады.
Ұсынылған үлгіні аяқта.

2. Осы үлгідегі қателерді түзет

Бұл есепті шешу барысында оқушылардың есепте сипатталған жағдайды саналы түрде түсінгені, сонымен қатар қателерді жойғаны атап өтілді.
№2 тапсырма. Ара қашықтығы 600 км болатын екі қаладан бір мезгілде екі пойыз бір-біріне қарай жолға шықты. Бірінші пойыздың жылдамдығы 70 км/сағ, ал екінші пойыздың жылдамдығы 80 км/сағ. Жолға шыққаннан кейін 3 сағаттан кейін пойыздардың арақашықтығы қанша болды? Олар кеткеннен кейін қанша уақыттан кейін кездесті?
Бұл есепті оқушылармен талдағанда, есеп бойынша сұрақтар құрастыру әдістемесін қолдануды ұсынамыз. Тапсырманың бұл түрін орындау кезінде кіші сынып оқушысы сұрақ құрастыра отырып, мәтінде берілген ақпаратты талдайды, оқушы барлық қолда бар мәліметтерді пайдаланады, бұл да дұрыс жауапқа ықпал етеді. Сұрақты құрастыру кезінде бала не берілгенін және нені табу керектігін, тапсырманың дұрыс тұжырымдалғанын, қосымша деректер қажет пе, жоқ па екенін түсінеді.
№3 тапсырма. Турист автостоппен 25 шақырым жүрді, одан кейін автостоппен жүргенінен 5 есе аз қашықтықты жүріп өтті. Турист бүкіл жолды 10 км/сағ жылдамдықпен жүру үшін қанша уақыт алады?
Бұл әдіс дұрыс шешімді таңдауға бағытталған. Бұл тәсіл арқылы кіші мектеп оқушыларының өзіндік ойлауы мен белсенділігін дамытуға жағдай жасалады. Дұрыс шешімді таңдап, әрбір орындалған әрекетті түсіндір. Ұсынылған тапсырма мәселедегі шарттар мен деректерді дайын шешіммен салыстыра отырып, саналы шешімді қалыптастырады.
1)25:5= 1)25-10=
2)25+10= 2)25+5=
3)25:10= 3)30:10=
Нәтижелер
Сонымен, біз ұсынған тапсырмалар жүйесі кіші жастағы ерекше оқушылардың математикалық түсініктерін дамытуға бағытталған, олар қозғалыс бойынша мәтіндік есептерді шығарғанда қолданады. Тапсырманың бұл түрін орындау барысында балалардың саналы көзқарасы, логикалық ойлау, талдау, синтез, салыстыру және жалпылау әдістері қалыптасады. Тапсырманы талдау кезінде оқушылар мәтіндік жағдайларды тақырыптық және сызбалық модельдерге аударуды үйренеді [5].

Сурет 1. Эксперименттік жұмыстың басы мен аяқталуындағы қозғалыс бойынша мәтіндік есептерді шешуге саналы көзқарас қалыптастыру деңгейлерінің өзара байланысы
Диаграммада келтірілген деректерді талдай отырып, біз бастауыш мектеп жасындағы балаларда саналы көзқарасты дамыту үшін қолданылған әдістемелер мен тапсырмалар оң нәтиже берді деп қорытынды жасауға болады. Сонымен, бастауыш мектеп жасындағы ерекше балалармен жұмыс жасауда тапсырмалар жүйесін орындаудың тиімділігін бағалауға болады, өйткені қимыл-қозғалыс тапсырмаларына байланысты әртүрлі тапсырмаларды пайдалана отырып сабақ өткізу оқушылардың саналы көзқарасын қалыптастыру үдерісіне оң әсер етеді. Қозғалыс мәселелерін шешуге саналы көзқарасты қалыптастыруды одан әрі дамыту мақсатында біз әзірлеген тапсырмаларды ұзақ мерзімді жүзеге асыру арқылы осындай сабақтарды өткізу айтарлықтай динамика беретінін атап өту керек.
Қорытынды
Жүргізілген зерттеулер және ондағы алынған объективті нәтижелер келесі қорытындыларды жасауға мүмкіндік береді:
-
қозғалыспен есептер шығару кезінде математика сабағында іс-әрекетті ұйымдастыруда шешуші рөл мұғалімнің іс-әрекетіне беріледі;
-
қозғалыс мәселелерін шешу кезінде олардың маңыздылығы мен өзектілігін ескере отырып, оқу іс-әрекетіне жұмыс әдістерін енгізудің кезең-кезеңімен жүргізген жөн деп санаймыз;
-
жұмыстың сол немесе басқа әдісін қолданудың орындылығы мұғалімнен қозғалыс есептерін шешу мақсатын мұқият ойластырып, олардың мазмұнын, шешу ерекшеліктерін зерделеуді және оқушылардың жеке қабілеттерін талдауды талап етеді.
Эксперименттік жұмыста ерекше оқытуды қажет ететін оқушының өз бетімен, белсенді тұлғасын дамытуға, оқытылатын пәндерге қызығушылық танытуға бағытталған іс-шараларға көп көңіл бөлінді. Зерттеу көрсеткендей, біз анықтаған әдіс-тәсілдер тәжірибеге енгізілсе, оқыту тиімді болады.
Пайдаланылған дебиеттер:
-
Тебенова Қ.С., Ахметова Н.Ш., Заркенова Л.С. Мүмкіндігі шектеулі балаларға математиканы оқыту әдістемесі – Алматы, «Эверо» баспасы, 2015. – 222 б.
-
Заркенова Л.С., Омарова Н.Н. Мүмкіншілігі шектеулі балаларға математиканы оқытудың арнайы әдістемесі. – Оқу-әдістемелік кешен (силлабус). – Қарағанды, ҚарМУ, 2010.
-
Каирова, Л.А. Методика преподавания математики в начальных классах: учебно-методическое пособие для студентов дневного отделения. В2 ч. Ч. 1 / Л.А. Каирова, Ю. С. Заяц. - Барнаул: АлтГПА, 2011. - 82 с.
-
Далингер, В.А. Методика обучения математике в начальной школе / В. А. Далингер, Л.П.Борисова. -Москва: Юрайт, 2016. - 207 с.
-
Математика 4-сынып оқушыларына арналған оқулық, Алматыкітап баспасы, 2023.
References
1. Tebenova Q.S., Ahmetova N.Sh., Zarkenova L.S. Mumkindigi shekteuli balalarga matematıkany oqytu adistemesi – Almaty, "Evero" baspasy, 2015. – 222 b.
2. Zarkenova L.S., Omarova N.N. Múmkinshiligi shekteuli balalarga matematıkany oqytudyń arnaıy adistemesi. – Oqu-adistemelik keshen (sıllabus). – Qaragandy, Qarmu, 2010.
3. Kaırova, L.A. Metodıka prepodavanıa matematıkı v nachalnyh klassah: uchebno-metodıcheskoe posobıe dlya studentov dnevnogo otdelenıa. V2 ch. Ch. 1 / L.A. Kaırova, I. S. Zaıas. - Barnaul: Altgpa, 2011. - 82 s.
4. Dalınger, V.A. Metodıka obýchenıa matematıke v nachalnoı shkole / V. A. Dalınger, L.P.Borısova. -Moskva: Iuraıt, 2016. - 207 s.
5. Matematıka 4-synyp oqushylaryna arnalgan oqulyq, Almatykitap baspasy, 2023.
Толеутаева Жәнел Мұратқызы,
cтyдeнткa Выcшeй Шкoлы пeдaгoгики
Пaвлoдaрcкий пeдaгoгичecкий yнивeрcитeт им. A. Мaргyлaнa,
Пaвлoдaр, Рecпyбликa Кaзaхcтaн
ОБУЧЕНИЕ МОДЕЛИРОВАНИЮ ПО ТЕКСТУ УЧАЩИХСЯ С ОСОБЫМИ ПОТРЕБНОСТЯМИ В ОБУЧЕНИИ
Аннотация. В статье было рассмотрено, как моделирование задач, заданных движению, позволяет особенному ученику формировать правильные математические представления, в полной мере понимать различные аспекты взаимоотношений в окружающей жизни, а также использовать изучаемые теоретические понятия. Были изучены пути, виды решения задач, проведена специальная экспериментальная работа.
Ключевые слова: задача, особенный ученик, схема, моделирование, скорость, время, расстояние.
Toleutaeva Zhanel Muratkyzy,
student of the Higher School of Pedagogy
-
Margulan Pavlodar Pedagogical University,
-
Pavlodar, Republic of Kazakhstan
TEACHING TEXT MODELING TO STUDENTS WITH SPECIAL LEARNING NEEDS
Annotation. The article examined how modeling of tasks assigned to a movement allows a special student to form correct mathematical representations, fully understand various aspects of relationships in the surrounding life, as well as use the studied theoretical concepts. Ways and types of problem solving were studied, and special experimental work was carried out.
Keywords: task, special student, scheme, modeling, speed, time, distance.

шағым қалдыра аласыз















