Орта мектеп курсында "Интеграл" тақырыбын оқытудың әдістемелік ерекшеліктері

Орта мектепте «Интеграл» тақырыбын оқытудың әдістемелік ерекшеліктері

№152 мектеп – гимназияның математика пәнінің мұғалімі Тұратбек Меруерт Семетейқызы(Алматы қаласы. Алатау ауданы)

Қазақстан Республикасы Президенті Н.Ә.Назарбаевтың Қазақстан халқына 2014 жылғы «Қазақстан жолы – 2050: «Бір мақсат, бір мүдде, бір болашақ» атты Жолдауында негізгі бағыттарды білім берудің маңызын көтеру, инновацияларға қолайлы жағдай жасау керектігін атап көрсетті. «Әлемдік білім кеңістігіне толығымен кіру білім беру жүйесін халықаралық деңгейге көтеруді талап ететіні сөзсіз» – деп көрсетілген. Сондықтан елімізді дамытудың қазіргі әлеуметтік – экономикалық, саяси жағдайлары және жоғары дамыған елдердің тәжірибесі білім берудің мазмұнын, әдістерін жаңарту және жетілдіру қажеттілігін тудыруда. Соның бірі білім беру саласының қазіргі заман талаптарына сай болуды талап етіп отыр.

«Басты мақсат – Қазақстанның әлемдегі ең дамыған 30 мемлекеттің қатарына қосылуы! Ол – «Мәңгілік Қазақстан» жобасы, ел тарихындағы біз аяқ басатын жаңа дәуірдің кемел келбеті. «Қазақстан-2050» Стратегиясы – барлық саланы қамтитын және үздіксіз өсуді қамтамасыз ететін жаңғыру жолы. Ол – елдігіміз бен бірлігіміз, ерлігіміз бен еңбегіміз сыналатын, сынала жүріп шыңдалатын үлкен емтихан. Стратегияны мүлтіксіз орындап, емтиханнан мүдірмей өту – ортақ парыз, абыройлы міндет!», деп атап айтты.

Ұлы ғалым – педагогтар (Әл-Фараби, Я.А.Коменский, И.Г. Песталоций, Ж.Ж.Руссо, И.Герберт, А.Дистерверг, К.Д.Ушинский, Ы.Алтынсарин т.б) оқыту әдістері арқылы оқушылардың ақыл-ой қабілеттері мен дербестігін дамытуған назар аударғаны да тегін емес.

Жалпы, интегралды оқыту әдістерінің өзіне тән тарихы бар. Интеграл және интегралдау ұғымдары туралы алғашқы жүйелі түсініктер И. Ньютон жәнеГ. Лейбниц еңбектерінде келтірілген. Интегралдық есептеуді дамытуға қомақты үлес қосқан ғалымдар қатарына орыс математиктері М.В. Остроградский, В.Я. Буняковский, П.Л.Чебышев, А.Я.Хинчин, көрнекті неміс математигі Б.Риман, француз математиктері Г.Дарбу, А.Лебег және т.б көптеген ғалымдар болған.

Мектеп оқушыларына интеграл тақырыбын түсіндіру әдістемесінің негізгі мақсаты – білім бере отырып, олардың танымдық деңгейін және ой – өрісін кеңейту, оқуға және математикаға деген қызығушылығын арттыру, ынтасын ояту, тәрбиелікке, патриоттыққа және шығармашылыққа баулу. Сабақ өту кездерінде алған білімдерін оқушылар практикалық жұмыстарда пайдалануға машықтанады және білімдерін тереңдете түседі, интегралдың геометриялық және физикалық мағынасын терең түсінудің себебін және салдарын анықтайды, оқушылардың логикалық ойлау қабілетінің дамуы анық көріне бастайды және олар жүйелі абстрактылы ойлауға көшеді, орындаған жұмыстарын дәлелдеуге және саналы түсінуге тырысады.

Интегралдау тақырыбын оқытудың әдістемесі мектепте оқытылатын пәндік білімдерді және оларды тәжірибе жүзінде қолдану арқылы жүзеге асырылады. Математика пәнін басқа пәндермен байланыстыра оқығанда оқушылар тек есепті шығарып қана қоймай, олар сол есепті түбегейлі дәлелдеуге және практика жүзінде пайдалануға үйренеді, оқулық қызметінде

сенімділік орнығады, келешек өзіндік тұлға ретінде қалыптасады.

1997 – 98 оқу жылынан бастап мектептерде оқытудың жаңа мазмұнына көше бастады. Осыған орай жалпы мектепте берілетін білімнің тұжырымдамасы, мемлекеттік стандарты, жаңа типтік оқу жоспары мен бағдарламалары жасалды. Қазақстан Республикасы жалпы орта білім беру стандартында көрсетілгендей білімнің мазмұны өзгерумен бірге әр пән бойынша білім мазмұнын оқытудың әдістемесі де қазіргі таңда түбегейлі өзгеріп отыр. Мектеп тәжірибесіне енгізіліп отырған төл оқулықтардың жаңа толқынында дамыта оқыту технологиясының мүмкіндіктері ұсынылған. Сол себептен жаңа материалды түсіндіру кезеңдерінде қолданылатын әр алуан әдістерді де жетілдіру қажеттігі байқалады.

Дегенмен, оқыту әдістерінің қолайлы етіп таңдаудың теориялық қағидалары мен тәжірибесінде бірізділіктің болмауы байқалуда. Осыдан келіп оқыту әдістерін тиімді қолданудың теориясы мен тәжірибесі арасындағы қарама - қайшылық орын алып отыр.

Кез– келген жиынында өзгеретін үшін

(1.1)

теңдігі орындалса, онда функциясы үшін функциясының алғашқы функциясы деп аталады.

Кез – келген функция сиякты алғашқы функция да барлық нақты сандар жиынында немесе белгілі бір аралықта қарастырылуы мүмкін. Берілген функцияның туындысын табуды біз 10 сыныпта өткеніміз белгілі. Сонымен қатар, кез келген функцияның туындысы функция (тұрақты немесе айнымалы) болатыны білеміз. Енді «Туындысы белгілі болған жағдайда бастапқы функцияны қалай табуға болады? » деген сұрақ туындап отыр. функциясы қандай функцияның туындысы екенін анықтап көрейік. Туындысы болатын бастапқы функцияны қалай анықтауға болады?

Егер ондай функцияны шартты түрде F(х) деп белгілеп алсақ, онда ізделінді функция болады, себебі, .

Интегралдау амалы дифференциялдау амалына кері амал. Интегралдаудың негізгі мақсаты интегралданатын функцияның балық алғашқы функцияларын табу.

Мысал – 1.1 Барлық нақты сандар жиынында функциясы функциясы үшін алғашқы функция болады, өйткені

Теорема 1.1 Егер белгілі бір аралықта F(x) және Ф(х) функциялары функциясы үшін алғашқы функция болса, онда осы аралықта ол функциялар бір-бірінен тек тұрақты санға ғана ерекшеленеді.

Дәлелдеу. Ол үшін

Ф(х) - F(x) (1.2)

деп алайық. Теорема бойынша берілген аралықта F'(x)= және Ф'(х) теңдіктері орындалады. Онда Ф'(х) - F'(x)=

Туынды табу ережесі бойынша тұрақты санның ғана туындысы нөлге тең екені белгілі. Демек, Енді -дің мәнін (1.2) теңдікке қоямыз. Сонда Ф(х)= F(x)+C шығады.

Сонымен, егер F'(x)= және С – кез – келген тұрақты сан болса, онда F(x)+C қосындысы да алғашқы функциясы болады.

Ф(х)=F(x)+C теңдігі алғашқы функцияның негізгі қасиеті болып табылады.

Анықтама 1.2 функциясының барлық алғашқы функцияларының жалпы түрін, яғниF(x)+Cөрнегін осы функцияның анықталмаған интегралы деп аталады.

Белгіленуі:

(1.3)

мұндағы - интеграл таңбасының ішіндегі функция, - интеграл таңбасының ішіндегі өрнек, интеграл белгісі.

Анықтама бойынша:

= F(x)+C (1.4)

С–тұрақтысының орнына кез келген санды алуға болады, яғни оның мәні анықталмаған. Сондықтан анықталмағанинтегралболып есептеледі.

Анықталмаған интегралдың мәнін табу операциясын функцияны интегралдау дейді.

Енді кейбір функциялардың алғашқы функцияларының кестесін келтірейік:

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

Интеграл астындағы функцияны ықшамдау арқылы кейбір анықталмаған интегралдар 1-18 кестелік интегралды қолданып есептеледі. Осыған мысалдар келтірейік.

Есептердің шығару жолдарымен:

№1.  есептеңіз.

Шешуі: Интегралды есептеуде таблицалық интегралды бірден пайдалануға болады. Мұнда   Сондықтан кестелік интегралдың (3) – формуласы бойынша:

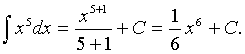
№2.  есептеңіз.

Шешуі: Анықталмаған интегралдың 2⁰ қасиетін және 3 формуланы пайдалансақ, онда

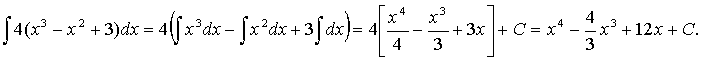Мектептің математика курсында тура және оған кері амалдар орын алатыны белгілі, яғни қосу мен азайту, көбейту мен бөлу, дәрежеге шығару мен түбірді табу. Тура осылайша туындыны табуға (дифференциалдауға) өзара кері амал алғашқы функцияны табу (интегралдау) екеніне көз жеткіздік.

Мысалы, берілген қозғалыс теңдеуі бойынша туындының көмегімен берілген ақыт мезетінде материялық нүкте қозғалысының жылдамдығын табуға болады. Материялық нүктенің жылдамдығын табу үшін қозғалыс теңдеуінен уақыт бойынша туынды табу керек.

Алғашқы функцияны табудың үш ережесі:

1)Егер F(x) функциясы f(x) функциясының, ал Р(х) функциясы р(х) функциясының алғашқы функциялары болса, онда F(x)+ P(x) функциясы f(x)+ р(х) функциясының алғашқы функциясы болады.

2)Егер F(x) функциясы f(x) функциясының алғашқы функциясы,ал k – тұрақты болса, онда kF(x) функциясы kf(x)функциясы үшін алғашқы функция болады.

3) Егер F(x) функциясы f(x) функциясының алғашқы функциясы,ал k және b – тұрақтылар болса, онда функциясы f (kx+b)функциясы үшін алғашқы функция болады.

Мысал :Анықталмаған интегралдың мәнін табайық:

; 2) 3)

Шешуі. 1) функциясы функциясы үшін алғашқы функциялардың бірі болып табылады. Олай болса, екінші ереже бойынша:

функциясының алғашқы функцияларының бірі функциясы, ал х⁴ функциясы үшін алғашқы функция болып табылады. Бірінші ережені қолдансақ,

шығады.

функциясы функциясы үшін алғашқы функциялардың бірі. Үшінші ережені қолданып,мынаны аламыз:

Геометриялық және физикалық есептерде интегралды қолдану

Геометрия мен физика курстарында анықталған интегралдың кейбір қолдануларын қарастырайық. анықталған интегралы жоғарыдан функциясының графигімен, төменгі жағынан Ох осіне тиісті кесіндісімен, ал екі жағынан =а, = түзулерімен шектелгенқисықсызықты трапецияның ауданын беретінін білеміз.

Кейбір жағдайларда жоғарыдан да, төменнен де әртүрлі функциялардың графиктерімен (әртүрлі қисықтар) шектелген жазық фигураның ауданын табуға тура келеді.

Жазық фигураның ауданын кескіндеу үшін жоғарыдан функциясының графигімен шектелген қисықсызықты трапецияның ауданынан жоғарыдан функциясының графигімен шектелген қисықсызықты трапецияның ауданын азайту керек.

Сонда ізделінді ауданды былай табамыз:

Кейбір дербес жағдайларда Ох осіне параллель түзулерімен, =0 түзуі және бір бүйір жағынан қисықпен = (у) функциясының графигімен) шектелген фигураның ауданын есептеу қажет болады.

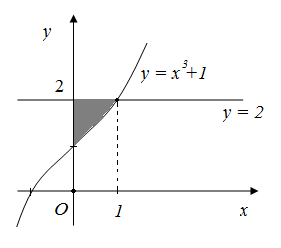
Шешуі. Берілген жазық фигураның ауданын (1.6) формула бойынша есептейміз:

Алғашқы функция, анықталмаған интеграл және олардың қасиеттерін оқыту әдістемесі

Алғашқы функциялардың жалпы түрі.

Интегралдау есебі дегеніміз – берілген функция үшін оның барлық алғашқы функцияларын табу. Бұл есепті шығарғандамына ұйғарымның атқарар ролі зор.

Функцияның тұрақтылық белгісі.Егер қандай да бір І аралықта болса, онда функциясы осы аралықта тұрақты шама болады.

Дәлелдеу. І аралығынан қандай да бір х₀ нүктесін белгілеп қояйық. Сонда осы аралықтағы кез келген х саны үшін Лагранж теоремасы бойынша х пен х₀ арасында жататын және

теңдігі орындалатындай с санын көрсетуге болады. Ал с болғандықтан, , демек,

Сонымен, І аралығынан алынған барлық үшін

яғни F функциясы тұрақты мәнін сақтайды.

Барлық алғашқы F функцияларды бір ғана формуланың көмегімен жазып көрсетуге болады, оны функциясы үшін алғашқы функциялардың жалпы түрі деп атайды. Мына теорема тура (алғашқы функциялардың қасиеті).

Теорема: І аралығында функциясы үшін алғашқы функциялардың кез келгенін мына түрде

жазып көрсетуге болады, мұндағы С – кез келген тұрақты шама, ал I аралығындағы функциясы үшін алғашқы функциялардың бірі.

Осы пікірді түсіндірейік. Бұл пікір алғашқы функцияның екі қасиетін қысқаша тұжырымдап отыр:

сол өрнектегі С – нің орнына қандай санды қойсақ та, І аралығындағы үшін алғашқы функция шығады;

І аралығында үшін қандай алғашқы функция Ф– ті алсақ та, І аралығындағы барлық х үшін

Ф(х)

теңдігі орындалатындай, бір С санын таңдап алуға болады.

Дәлелдеу.1) Шарт бойынша Ғ функциясы функция үшін I аралығында алғашқы функция. Олай болса, кез келген х үшін

Сондықтан

функциясы - функция үшін алғашқы функция.

Интегралдың қолданылуы

1.Дененің көлемін есептеу. КөлеміV-ға тең, дене берілген және оған коса 6ip тузу бар, ол тузуге перпендикуляр өтетін қандай жазыктықты алсақ та, дененің осы жазықтықпен қимасыныц S ауданы бізге белгілі делік (125-сурет). Ал Ох осше перпендикуляр жазықтық ол ocьтi қандай да 6ip х нуктесінде қиып өтеді. Олай болса, әрбip х санына ([a;b] кесіндісіндегі, 125-суретке қара) жалғыз ғана S(x) саны — дененің, осы жазықтықпен қимасының ауданы — сәйкес койылады. Енді, сонымен [а;b] кесіндісінде S(x) функциясы берілген болады. Егер S функциясы [а;b] кесіндісінде үзіліссіз болса, онда мына формула дұрыс:

Бұл мақалада орта мектепте «Ингеграл» тақырыбын оқытудың әдістемелік ерекшеліктері тақырыбы қарастырылған.Мектеп интегралдау тақырыбын оқыту әдістемесін дамытуда оқушылардың жас ерекшеліктері , психологиялық – педагогикалық, әдістемелік негіздемелеріне сүйенеотырып келесідей қорытындыға келдік:

Оқулықтар мен бағдарламаларға талдау жасау мектептік интегралдау тақырыбын оқыту әдістемесін дамытудың мүмкіндіктерінің мол екендігін көрсетті;

мектеп оқулықтарындағы есептер мен жаттығуларды қайта өңдеп жаңа мазмұн беру арқылы оқушылардың ойлау қабілетін және танымдық деңгейін дамытуға қолданбалы есептерді шешуге және оқыту үрдісін, оқу – танымдық іс-әрекетерін, дидактикалық міндеттерін тиімді пайдалануға болатындығы айқындалды;

Интегралдау тақырыбын оқытуға бағытталған және ұсынылып отырған әдістемелердің ұтымдылығы педагогикалық практика барысында расталды;

орта мектепте математикалық білім берудің өзіндік ерекшелігін және математика пәнінің табиғаты, өзіндік орны мен мақсатына сәйкес, осы пән бойынша орта сыныптың сабақтарында “түсіндіру,” “түсіндірме,” “әңгіме,” “әңгімелесу,” “проблемалы баяндау,” “ішінара іздену немесе эвристикалық әңгімелеу” сияқты әдіс түрлерін тиімді қолдануға болаындығы тұжырымдалды.

Сонымен қатар, мақалада интеграл тақырыбын оқытуда қазіргі заман дидактикалық ерекшеліктері анықталып, тақырыпты оқытудың технологиялық деңгейлері көрсеткіштері болашақта оқушының ойлау қабілеттерін және танымдық деңгейлерін дамытудың алғышарты болып табылатыны негізделді.

Дегенмен бұл мақалада қарастырылып отырған мәселенің шешімі толығымен анықталды деп айтуға болмайды.

Алдағы уақытта мектеп математика курсында интеграл тақырыбын оқытудың бағытын және мазмұнын қолданбалық жағдайға бейімдеп оқыту негізгі мәселелердің бірі ретінде қарастырылып, зерттеу жұмысының жаңа бағытарын анықтауы мүмкін.

«Интеграл»тақырыбын оқытудағы әртүрлі авторлардың (оқулықтардың) әдістемелері бойынша оқыту үрдісін анағұрлым тереңірек зерделеу, жалпы білім беретін аталмыш мәселені қарастырудағы жаңа оңтайлы бағыттар мен технологияларды анықтау сияқты мәселелер зерттеу жұмысының жаңа бағытын анықтайды, деп ойлаймын.

Біздің осы мақалада ұсынып отырған идеялар мен ұсыныстар мектеп пән мұғалімдері мен жоғары курс студенттерін қызықтырады деп ойлаймын. Осыған байланысты келешекте осы интеграл тақырыбын оқытудың тиімділік сапасын жақсартуда ұсыныс болса автор қанағатырарлық сезіммен қабылдап, ұсыныс берген оқырманмен бірге жұмыс істеуге дайын.

Түйіндеме

Бұл мақалада мектеп математикасы курсында интеграл тақырыбын оқытудың маңызы, әртүрлі авторлардың ұсынған тәсілдері және оларды пайдаланудың қазіргі заманғы талаптарына сай әдістемелік мәселелері қарастырылған. Осы тақырыпты тиімді оқытудың кейбір әдістемелік идеялары және нақты үлгілері ұсынылады.

Резюме

В данной статье работе рассматриваются различные методические подходы различных авторов учебников по изучению темы “Интеграл” в школьном курсе математики, с учетом совремменных требований к обучению. Автором предлагается свой варинат изложения и планирования изучения указанный темы.

Sumary

This articleinteractive methods the various methodological approaches of different authors of different books the study topics integrals of school mathematics by taking into account the current requirements for training. The author offers his own version of the presentation and planning study of this topic.