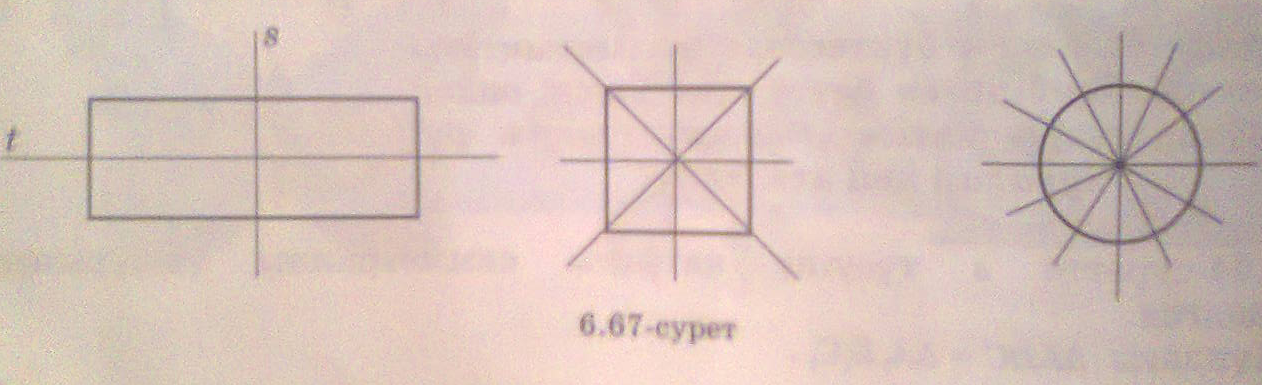Ақтөбе облысы
Шалқар қаласы
№ 6 орта мектебі
Пән мұғалімі: Р.О.Бахытова
|
ПӘН |
математика |
6 Б сынып |
|
||||||||||||
|
ТАҚЫРЫП |
Осьтік симметрия |
||||||||||||||
|
Сілтеме |
Математика оқулығы |
||||||||||||||
|
Жалпы мақсаты |
Симметрия туралы түсінік бере отырып, түзуге қатысты фигураларды, центрлік симметриялы фигураларды, осьтік симметриялы фигураларды және де симметриялы фигуралардың өзара теңдігін үйрену. |
||||||||||||||
|
Күтілетін нәтиже |
Өздігінен оқу дағдыларын қалыптастырады. Жаңа тақырыптың мазмұнын өз бетімен аша алады, салыстыра біледі, талдай алады, ой қорытуды үйренеді. |
||||||||||||||
|
Мұғалімнің іс-әрекеті |
Оқушының іс-әрекеті |
Бағалау |
Ресурстар |
||||||||||||
|
Үй тапсырмасын тексеру Жауаптардың дұрыстығын тексереді |
Жауаптарын салыстырады |
Критериалды бағалау |
Оқушы дәптері |
||||||||||||
|
Қызығушылықты ояту |
|||||||||||||||
|
Өтілген материалды еске түсіру |
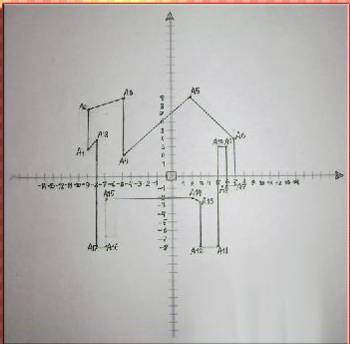
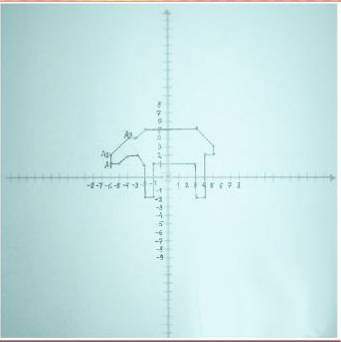
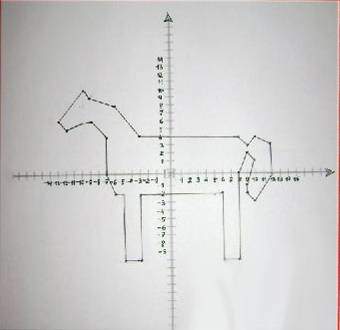
Координаталық жазықтықта берілген суреттің нүктелерін анықта
|
Мұға лім жауап тарды тыңдап, форма тивті баға лайды. |
Сын ып тақ тасы, оқу Шы дәп те рі |
||||||||||||
|
Мағынаны тану |
|||||||||||||||
|
Мәтінді бөліктерге бөледі. Тақырыптың түйінді мәселелеріне назар аудартады. |
1. «Симметрия» грек
сөзінен алынған, ол «гармония» сөзі сияқты бірдей өлшемділікті,
белгілі бір реттілікпен орналасқан деген ұғымды білдіреді.
Симметрия әр түрлі болады. Симметрияның ең қарапайым түрі - түзуге
қатысты симметрия. Ол үшін:
|
Жұптық бағалау Критериал ды бағалау |
Жалпы білім беретін мектептің 6-сыныбы на арналған «оқулығы. |
||||||||||||
|
Ой толғаныс |
|||||||||||||||
|
Тақырып тың түйінді мәселелеріне назар аудартады. |
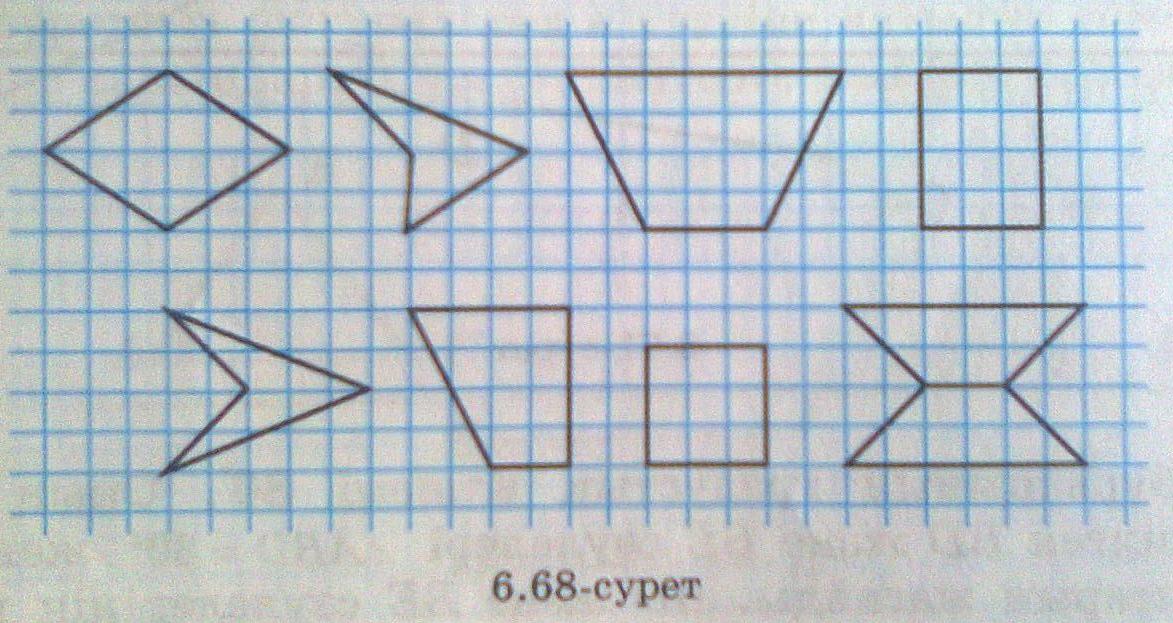
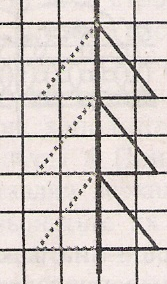
№1206. Мына фигуралардан осьтік симметриялы фигураларды таңдап алыңдар. Оларды дәптерге көшіріп салып, симметрия осьтерін сызыңдар (6.68-сурет).
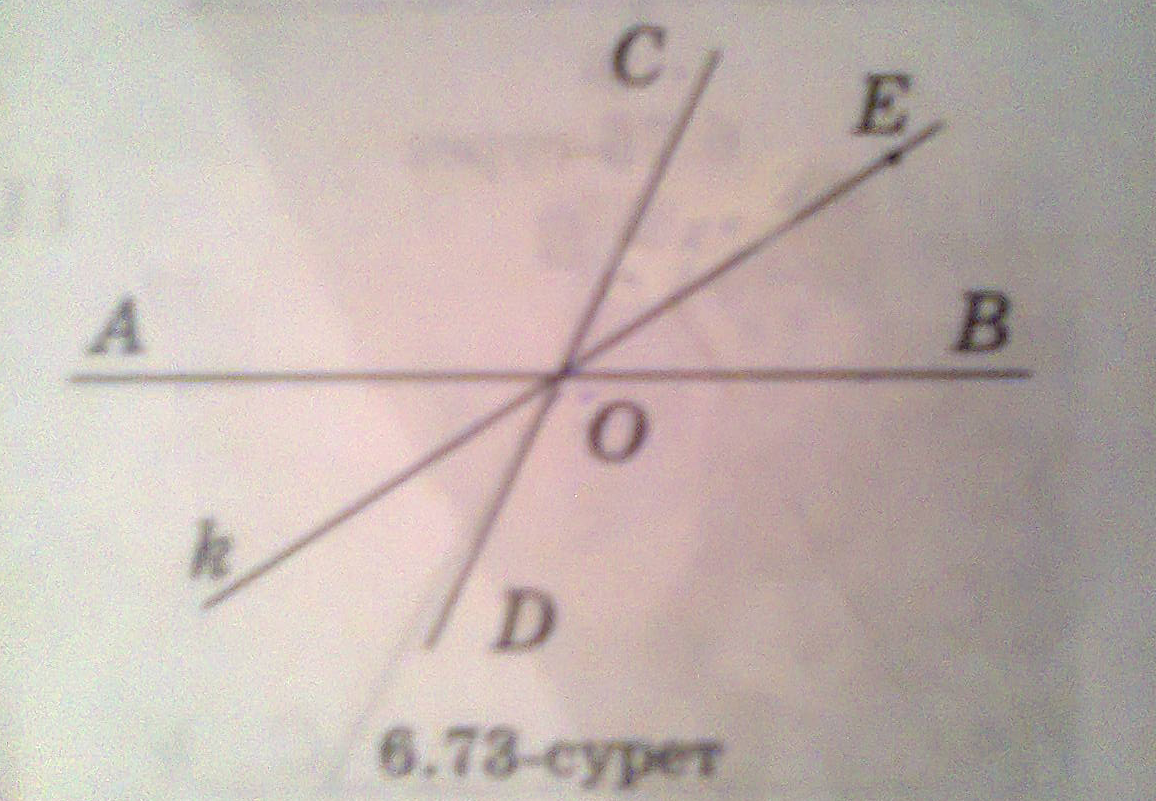
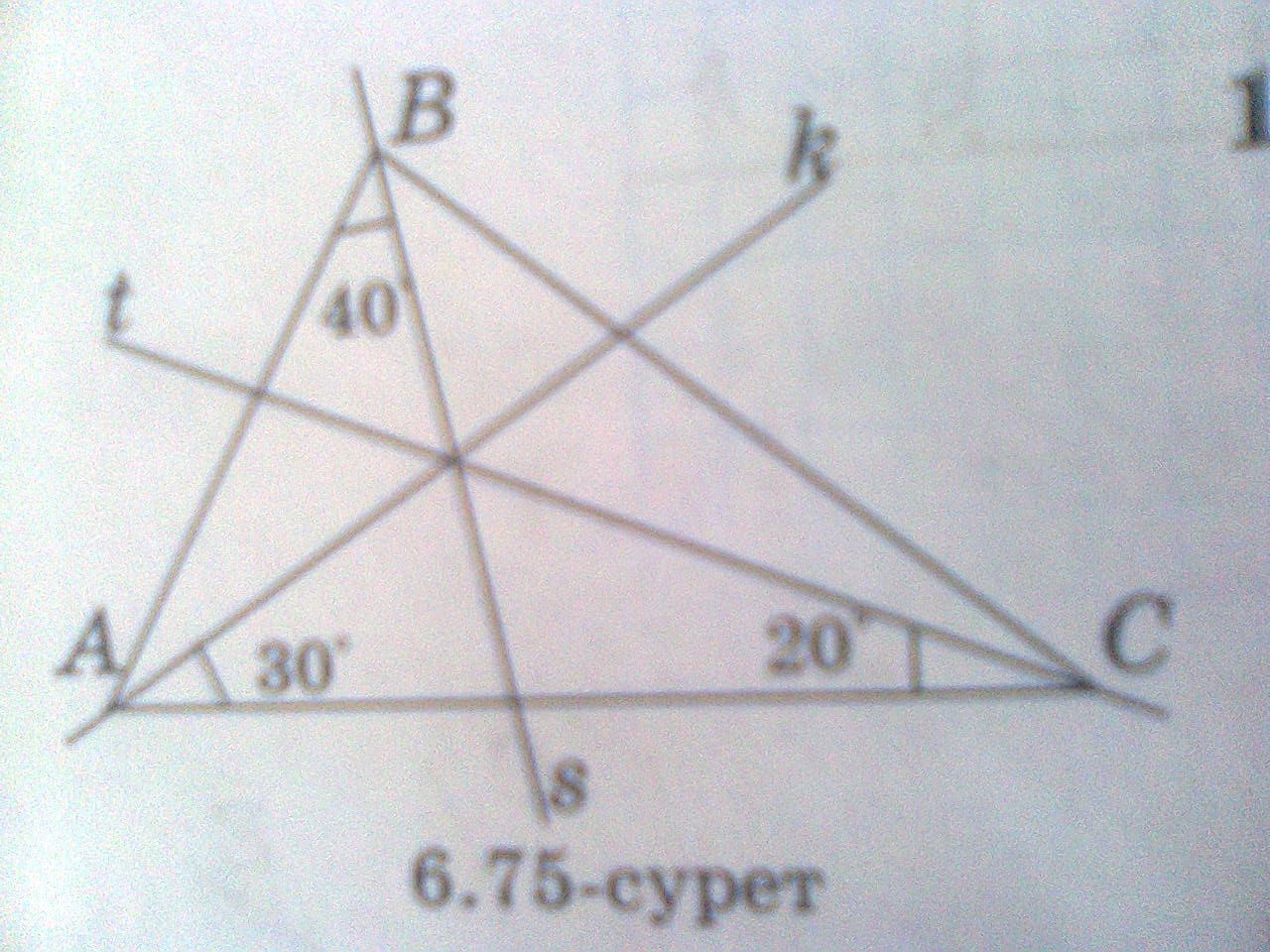
АВ және СД түзулері О нүктесінде қиылысады (6.73-сурет). k түзуі - АОД және СОВ вертикаль бұрыштарының симметрия осі. Е нүктесі k түзуіндегі нүкте. СОЕ бұрышының градустық өлшемі 300. АОД бұрышының градустық өлшемін табыңдар. Шешуі: k түзуі симметрия осі болғандықтан СОЕ=ЕОВ=300 СОВ=СОЕ+ЕОВ; 300+300=600 АОД және СОВ өзара вертикаль бұрыштар болғандықтан олар тең бұрыштар АОД=СОВ=600 Жауабы: АОД=600 «С» тобы. №1186. 6.75-суреттегі АВС үшбұрышының В бұрышының, А бұрышының, С бұрышының биссектрисалары оларды градустық өлшемдері 400; 300; 200 бұрыштарға бөледі. В, А және С бұрыштарының градустық өлшемдерінің қосындысы неше градус? Шешуі: Үшбұрыштың ішкі бұрыштарының қосындысы 1800-қа тең. s, t, k – түзулері симметрия остері. ∟В=400+400, ∟А=300+300, ∟С=200+200 ∟A+∟B+∟C = 1800 800+600+400=1800 Жауабы: 1800 |
Критериал ды бағалау |
|
||||||||||||
|
Кері байланыс |
|||||||||||||||
|
Сабақта нені түсініп, нені игере алмағанына кері байланыс беруді тапсырады. |
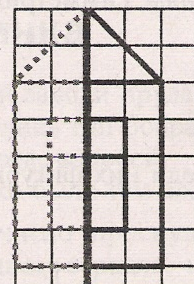
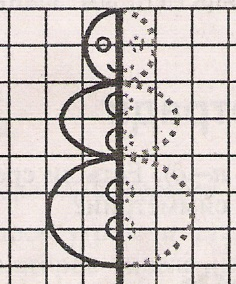
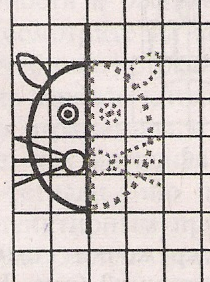
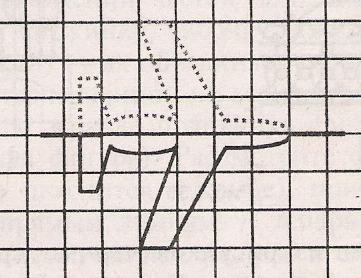
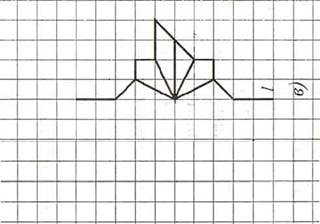
Кері байланыс ұсынады Фигуралар өзара симметриялы болатындай суретті аяқта
|
Критериалды бағалау |
Кері байланыс парағы |
||||||||||||
|
Үйге тапсырма: §13, № 8 жаттығу(4-6), 60-бет |
|||||||||||||||
|
Бағалау |
Күнделікке баға қойдырады |
Жиынтық бағалау |
Күнделік |
||||||||||||
|
Сабақтан кейін ойланатын сұрақтар: |
|||||||||||||||
|
Не сәтті болды? |
|
||||||||||||||
|
Не сәтсіз болды? |
|
||||||||||||||
|
Нені жақсартуға болады? |
|
||||||||||||||
|
Мен өз дағдымда нені дамыта алдым: Нені өзгертуге болады? |
|||||||||||||||
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Осьтік симметрия
Осьтік симметрия
Ақтөбе облысы
Шалқар қаласы
№ 6 орта мектебі
Пән мұғалімі: Р.О.Бахытова
|
ПӘН |
математика |
6 Б сынып |
|
||||||||||||
|
ТАҚЫРЫП |
Осьтік симметрия |
||||||||||||||
|
Сілтеме |
Математика оқулығы |
||||||||||||||
|
Жалпы мақсаты |
Симметрия туралы түсінік бере отырып, түзуге қатысты фигураларды, центрлік симметриялы фигураларды, осьтік симметриялы фигураларды және де симметриялы фигуралардың өзара теңдігін үйрену. |
||||||||||||||
|
Күтілетін нәтиже |
Өздігінен оқу дағдыларын қалыптастырады. Жаңа тақырыптың мазмұнын өз бетімен аша алады, салыстыра біледі, талдай алады, ой қорытуды үйренеді. |
||||||||||||||
|
Мұғалімнің іс-әрекеті |
Оқушының іс-әрекеті |
Бағалау |
Ресурстар |
||||||||||||
|
Үй тапсырмасын тексеру Жауаптардың дұрыстығын тексереді |
Жауаптарын салыстырады |
Критериалды бағалау |
Оқушы дәптері |
||||||||||||
|
Қызығушылықты ояту |
|||||||||||||||
|
Өтілген материалды еске түсіру |
Координаталық жазықтықта берілген суреттің нүктелерін анықта
|
Мұға лім жауап тарды тыңдап, форма тивті баға лайды. |
Сын ып тақ тасы, оқу Шы дәп те рі |
||||||||||||
|
Мағынаны тану |
|||||||||||||||
|
Мәтінді бөліктерге бөледі. Тақырыптың түйінді мәселелеріне назар аудартады. |
1. «Симметрия» грек
сөзінен алынған, ол «гармония» сөзі сияқты бірдей өлшемділікті,
белгілі бір реттілікпен орналасқан деген ұғымды білдіреді.
Симметрия әр түрлі болады. Симметрияның ең қарапайым түрі - түзуге
қатысты симметрия. Ол үшін:
|
Жұптық бағалау Критериал ды бағалау |
Жалпы білім беретін мектептің 6-сыныбы на арналған «оқулығы. |
||||||||||||
|
Ой толғаныс |
|||||||||||||||
|
Тақырып тың түйінді мәселелеріне назар аудартады. |
№1206. Мына фигуралардан осьтік симметриялы фигураларды таңдап алыңдар. Оларды дәптерге көшіріп салып, симметрия осьтерін сызыңдар (6.68-сурет).
АВ және СД түзулері О нүктесінде қиылысады (6.73-сурет). k түзуі - АОД және СОВ вертикаль бұрыштарының симметрия осі. Е нүктесі k түзуіндегі нүкте. СОЕ бұрышының градустық өлшемі 300. АОД бұрышының градустық өлшемін табыңдар. Шешуі: k түзуі симметрия осі болғандықтан СОЕ=ЕОВ=300 СОВ=СОЕ+ЕОВ; 300+300=600 АОД және СОВ өзара вертикаль бұрыштар болғандықтан олар тең бұрыштар АОД=СОВ=600 Жауабы: АОД=600 «С» тобы. №1186. 6.75-суреттегі АВС үшбұрышының В бұрышының, А бұрышының, С бұрышының биссектрисалары оларды градустық өлшемдері 400; 300; 200 бұрыштарға бөледі. В, А және С бұрыштарының градустық өлшемдерінің қосындысы неше градус? Шешуі: Үшбұрыштың ішкі бұрыштарының қосындысы 1800-қа тең. s, t, k – түзулері симметрия остері. ∟В=400+400, ∟А=300+300, ∟С=200+200 ∟A+∟B+∟C = 1800 800+600+400=1800 Жауабы: 1800 |
Критериал ды бағалау |
|
||||||||||||
|
Кері байланыс |
|||||||||||||||
|
Сабақта нені түсініп, нені игере алмағанына кері байланыс беруді тапсырады. |
Кері байланыс ұсынады Фигуралар өзара симметриялы болатындай суретті аяқта
|
Критериалды бағалау |
Кері байланыс парағы |
||||||||||||
|
Үйге тапсырма: §13, № 8 жаттығу(4-6), 60-бет |
|||||||||||||||
|
Бағалау |
Күнделікке баға қойдырады |
Жиынтық бағалау |
Күнделік |
||||||||||||
|
Сабақтан кейін ойланатын сұрақтар: |
|||||||||||||||
|
Не сәтті болды? |
|
||||||||||||||
|
Не сәтсіз болды? |
|
||||||||||||||
|
Нені жақсартуға болады? |
|
||||||||||||||
|
Мен өз дағдымда нені дамыта алдым: Нені өзгертуге болады? |
|||||||||||||||




шағым қалдыра аласыз