|
Раздел долгосрочного плана: 8.2A Соотношения между сторонами и углами прямоугольного треугольника |
||
|
Дата: |
ФИО учителя: Тихова Л.В. |
|
|
Класс: 8 |
Количество присутствующих: Отсутствующих: |
|
|
Тема урока |
Теорема Пифагора |
|
|
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) |
8.1.3.3 доказывать и применять теорему Пифагора |
|
|
Цели урока |
Учащиеся могут:
|
|
|
Критерии оценивания |
Учащиеся :
|
|
|
Языковые цели
|
Учащиеся могут: Называть элементы прямоугольного треугольника; Формулировать теорему Пифагора; Устно обозначить неизвестные элементы треугольника. Письменно формулировать вопросы. Лексика и терминология, специфичная для предмета: Прямоугольный треугольник, катет, гипотенуза, острый угол, прямой угол, квадрат гипотенузы, сумма квадратов катетов. Полезные выражения для диалогов и письма: В прямоугольном треугольнике квадрат гипотенузы равен …… |
|
|
Привитие ценностей
|
Данный урок направлен на развитие ценностей академической честности, сплоченности и умения работать в команде, ответственности и лидерства. Привитие ценностей осуществляется посредством установления правил работы в группе, паре, оказания поддержки менее способным учащимся. |
|
|
Межпредметные связи |
Связь с архитектурой, с физикой, связь с историей |
|
|
Предварительные знания
|
Знание определения прямоугольного треугольника и его элементов; знание и умение применять признаки равенства прямоугольных треугольников; знание неравенства треугольника и соотношения между сторонами и углами треугольника. |
|
|
Ход урока |
||||||||||||||||||||
|
Запланированные этапы урока |
Запланированная деятельность на уроке |
Ресурсы |
||||||||||||||||||
|
Начало урока 0-2
3-5
6-12 |
1. Организационный момент. Сообщение темы и цели урока, в том числе и языковых целей. Ознакомление с планом урока.
2. Актуализации знаний. «Мозговой шторм»: А) Какой треугольник называется прямоугольным? Б) Как называются стороны такого треугольника? В) Где находится гипотенуза? Г) Какие свойства прямоугольного треугольника вы знаете? Д) Сформулируйте теорему Пифагора.
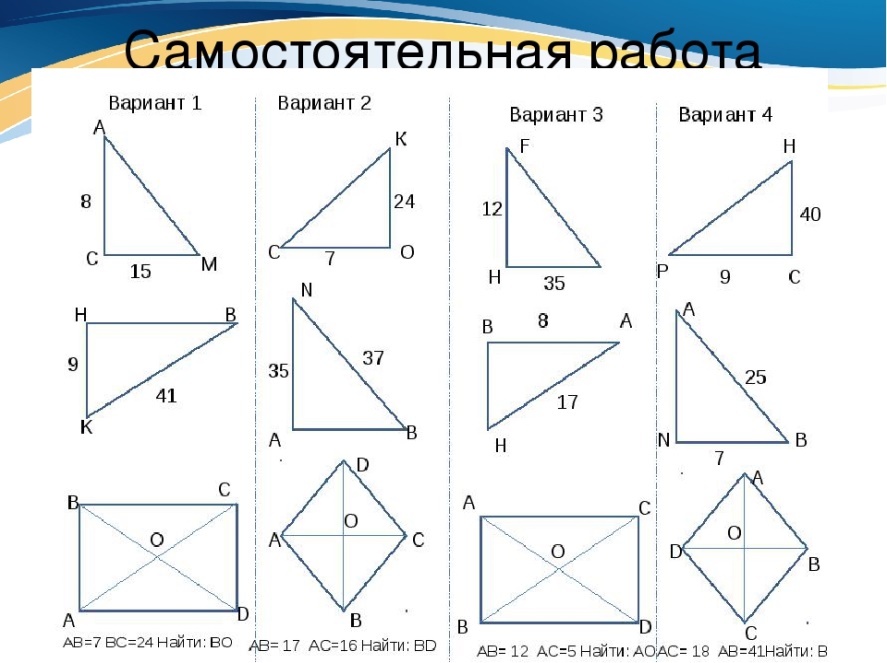
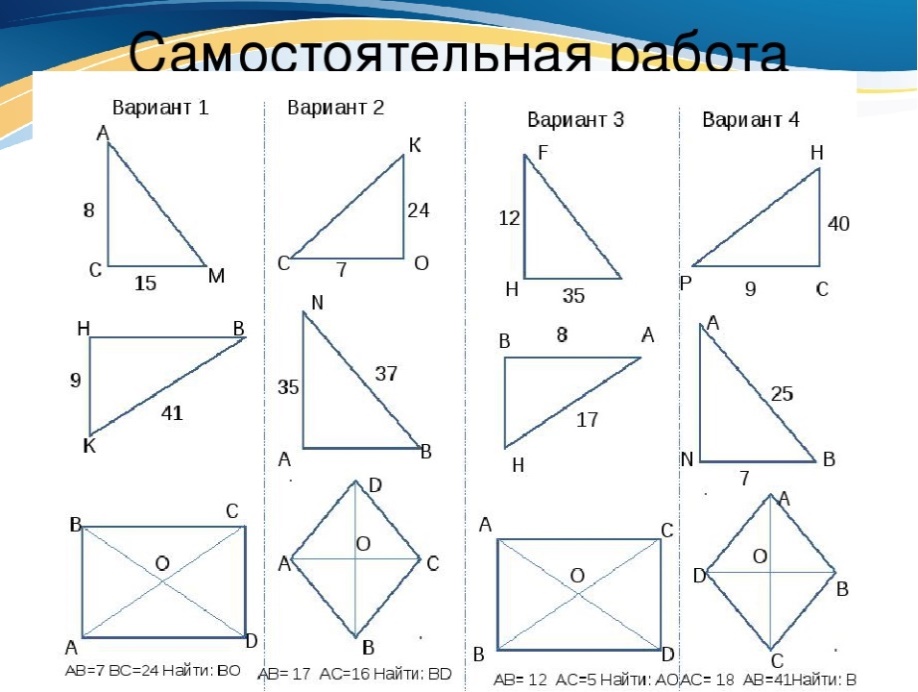
3.Повторение «Задачи по готовым чертежам» Учащиеся работают в парах, совместно решая и обсуждая решения задач. Каждый ряд решает свой вариант и сверяют ответы учащихся.
Критерии оценивания: Верно определена неизвестная сторона треугольника.
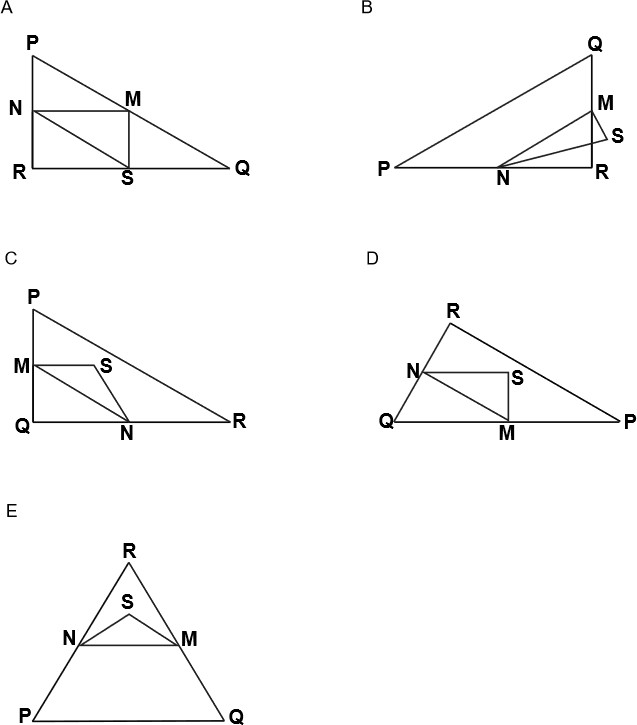
3*) Для более сильных учащихся из каждого ряда приготовлена задача на карточке с последующим объяснением решения для класса: Обведите букву, которой обозначена фигура, подходящая под описание ниже. Треугольник PQR – прямоугольный с
прямым углом R. Сторона RQ меньше стороны PR. M – середина стороны
PQ, а N – середина стороны QR. S – точка внутри данного
треугольника. Отрезок MN больше отрезка MS. |
Задача из Piza: математическая грамотность.-Минск: РИКЗ, 2020, стр 36
|
||||||||||||||||||
|
13-14
15-17
18-30
31-36
37-40
|
4. Деление на группы. Учащимся на столях предложены различные фигуры (треугольник, квадрат , ромб, прямоугольник и трапеция). Те учащиеся, которые выбрали одинаковые фигуры, образуют группу. 5. Физмунутка
6. Решение задач в группах. Каждая группа получает 3 задачи. Учащиеся решают задачи, применяя теорему Пифагора и другие геомет рические знания и оформляют решение на листах А2 в виде постеров.
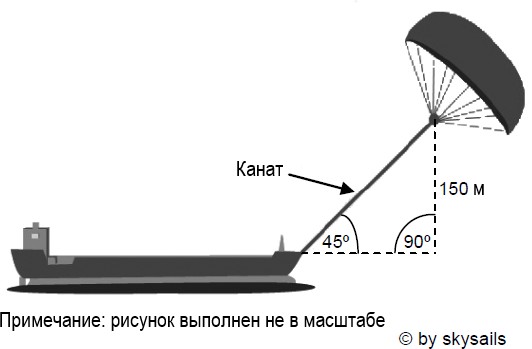
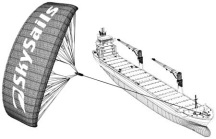
Инженеры планируют разработать поддержку кораблей, используя силу ветра. Их предложение заключается в прикреплении к кораблям кайтов (парящих в воздухе парусов) и использовании силы ветра, чтобы уменьшить расход дизельного топлива и его влияние на окружающую среду. Вопрос:
Чему примерно должна быть равна длина каната у кайта, чтобы он
тянул корабль под углом в 45° и находился на высоте в 150 м по
вертикали, как показано на рисунке?
3)
7. Защита постеров. Каждая группа демонстрируют свое решение, объясняя остальным учащимся.
8. Оценивание достижения уровня достижения учебной цели с помощью упражнения «Муравейник». Учащиеся записывают на стикере один вопрос, который для них остался непонятным по новой теме. Если у учащихся нет затруднений, то они могут придумать интересный вопрос для одноклассников. По завершению задания организуется предоставление обратной связи по уровню ответов учащихся.
9. Подведение итогов урока. Рефлексия. Учитель возвращается к целям урока, обсуждая уровень их достижения.
10. Домашнее задание: Повторить теорему Пифагора ее доказательство, решить задачу №1 Задача №1.На одной прямой на равном расстоянии друг от друга стоят три телеграфных столба. Крайние находятся от дороги на расстояниях 18 м и 45 м. найдите расстояние, на котором находится от дороги средние столб.
|
Задача из Piza: математическая грамотность.-Минск: РИКЗ, 2020, стр 36
|
||||||||||||||||||
|
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? |
Оценивание – как Вы планируете проверить уровень усвоения материала учащихся? |
Здоровье и соблюдение техники
безопасности |
|
На этапе повторения материала используются дифференцированные задачи с учетом индивидуальных особенностей учащихся. Для работы в группе учащимся предложены дифференцированные задания по источнику. |
На этапе повторения учащиеся оцениваются по критериям, которые позволяют оценить навык применение теоремы Пифагора при решении задач. Учитель оценивает практические результаты группы по дескрипторам. |
Соблюдение техники безопасности при передвижении учащихся по классу во время групповой работы у доски и упражнения «Муравейник». |
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Открытый урок 8 класс, Тема урока: Теорема Пифагора
Открытый урок 8 класс, Тема урока: Теорема Пифагора
|
Раздел долгосрочного плана: 8.2A Соотношения между сторонами и углами прямоугольного треугольника |
||
|
Дата: |
ФИО учителя: Тихова Л.В. |
|
|
Класс: 8 |
Количество присутствующих: Отсутствующих: |
|
|
Тема урока |
Теорема Пифагора |
|
|
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) |
8.1.3.3 доказывать и применять теорему Пифагора |
|
|
Цели урока |
Учащиеся могут:
|
|
|
Критерии оценивания |
Учащиеся :
|
|
|
Языковые цели
|
Учащиеся могут: Называть элементы прямоугольного треугольника; Формулировать теорему Пифагора; Устно обозначить неизвестные элементы треугольника. Письменно формулировать вопросы. Лексика и терминология, специфичная для предмета: Прямоугольный треугольник, катет, гипотенуза, острый угол, прямой угол, квадрат гипотенузы, сумма квадратов катетов. Полезные выражения для диалогов и письма: В прямоугольном треугольнике квадрат гипотенузы равен …… |
|
|
Привитие ценностей
|
Данный урок направлен на развитие ценностей академической честности, сплоченности и умения работать в команде, ответственности и лидерства. Привитие ценностей осуществляется посредством установления правил работы в группе, паре, оказания поддержки менее способным учащимся. |
|
|
Межпредметные связи |
Связь с архитектурой, с физикой, связь с историей |
|
|
Предварительные знания
|
Знание определения прямоугольного треугольника и его элементов; знание и умение применять признаки равенства прямоугольных треугольников; знание неравенства треугольника и соотношения между сторонами и углами треугольника. |
|
|
Ход урока |
||||||||||||||||||||
|
Запланированные этапы урока |
Запланированная деятельность на уроке |
Ресурсы |
||||||||||||||||||
|
Начало урока 0-2
3-5
6-12 |
1. Организационный момент. Сообщение темы и цели урока, в том числе и языковых целей. Ознакомление с планом урока.
2. Актуализации знаний. «Мозговой шторм»: А) Какой треугольник называется прямоугольным? Б) Как называются стороны такого треугольника? В) Где находится гипотенуза? Г) Какие свойства прямоугольного треугольника вы знаете? Д) Сформулируйте теорему Пифагора.
3.Повторение «Задачи по готовым чертежам» Учащиеся работают в парах, совместно решая и обсуждая решения задач. Каждый ряд решает свой вариант и сверяют ответы учащихся.
Критерии оценивания: Верно определена неизвестная сторона треугольника.
3*) Для более сильных учащихся из каждого ряда приготовлена задача на карточке с последующим объяснением решения для класса: Обведите букву, которой обозначена фигура, подходящая под описание ниже. Треугольник PQR – прямоугольный с
прямым углом R. Сторона RQ меньше стороны PR. M – середина стороны
PQ, а N – середина стороны QR. S – точка внутри данного
треугольника. Отрезок MN больше отрезка MS. |
Задача из Piza: математическая грамотность.-Минск: РИКЗ, 2020, стр 36
|
||||||||||||||||||
|
13-14
15-17
18-30
31-36
37-40
|
4. Деление на группы. Учащимся на столях предложены различные фигуры (треугольник, квадрат , ромб, прямоугольник и трапеция). Те учащиеся, которые выбрали одинаковые фигуры, образуют группу. 5. Физмунутка
6. Решение задач в группах. Каждая группа получает 3 задачи. Учащиеся решают задачи, применяя теорему Пифагора и другие геомет рические знания и оформляют решение на листах А2 в виде постеров.
Инженеры планируют разработать поддержку кораблей, используя силу ветра. Их предложение заключается в прикреплении к кораблям кайтов (парящих в воздухе парусов) и использовании силы ветра, чтобы уменьшить расход дизельного топлива и его влияние на окружающую среду. Вопрос:
Чему примерно должна быть равна длина каната у кайта, чтобы он
тянул корабль под углом в 45° и находился на высоте в 150 м по
вертикали, как показано на рисунке?
3)
7. Защита постеров. Каждая группа демонстрируют свое решение, объясняя остальным учащимся.
8. Оценивание достижения уровня достижения учебной цели с помощью упражнения «Муравейник». Учащиеся записывают на стикере один вопрос, который для них остался непонятным по новой теме. Если у учащихся нет затруднений, то они могут придумать интересный вопрос для одноклассников. По завершению задания организуется предоставление обратной связи по уровню ответов учащихся.
9. Подведение итогов урока. Рефлексия. Учитель возвращается к целям урока, обсуждая уровень их достижения.
10. Домашнее задание: Повторить теорему Пифагора ее доказательство, решить задачу №1 Задача №1.На одной прямой на равном расстоянии друг от друга стоят три телеграфных столба. Крайние находятся от дороги на расстояниях 18 м и 45 м. найдите расстояние, на котором находится от дороги средние столб.
|
Задача из Piza: математическая грамотность.-Минск: РИКЗ, 2020, стр 36
|
||||||||||||||||||
|
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? |
Оценивание – как Вы планируете проверить уровень усвоения материала учащихся? |
Здоровье и соблюдение техники
безопасности |
|
На этапе повторения материала используются дифференцированные задачи с учетом индивидуальных особенностей учащихся. Для работы в группе учащимся предложены дифференцированные задания по источнику. |
На этапе повторения учащиеся оцениваются по критериям, которые позволяют оценить навык применение теоремы Пифагора при решении задач. Учитель оценивает практические результаты группы по дескрипторам. |
Соблюдение техники безопасности при передвижении учащихся по классу во время групповой работы у доски и упражнения «Муравейник». |

шағым қалдыра аласыз



 Девяносто пять процентов товаров в мире
перевозят по морю примерно 50 000 танкеров, грузовых кораблей и
контейнеровозов. Большинство этих кораблей используют дизельное
топливо.
Девяносто пять процентов товаров в мире
перевозят по морю примерно 50 000 танкеров, грузовых кораблей и
контейнеровозов. Большинство этих кораблей используют дизельное
топливо.