
Краткосрочный план
|
Раздел 7.3С: Взаимное расположение прямых |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Дата: |
Ф.И.О. учителя: Нуркеева А О СШ № 44 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Класс: 7 Урок |
Количество присутствующих: |
отсутствующих: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Тема урока |
Теорема о сумме внутренних углов треугольника |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) |
7.3.1.16 доказывать теорему о сумме внутренних углов треугольника и следствия из неё; 7.3.1.17 применять теорему о сумме внутренних углов треугольника и следствия из неё при решении задач; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Цели урока |
Выдвинуть гипотезу о сумме углов треугольника; Сформулировать и доказать теорему о сумме углов треугольника; Научиться решать задачи, используя данную теорему. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Критерии оценивания |
Учащийся достиг цель, если
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Языковые цели
|
Учащиеся будут: - комментировать доказательство теорем и решения задач; - оперировать понятиями и терминами раздела; - описывать данные чертежа. Предметная лексика и терминология - параллельные, пересекающиеся, перпендикулярные прямые; - секущая; - внутренние накрест лежащие углы, внутренние односторонние углы, соответственные углы; - перпендикуляр, наклонная, проекция. Серия полезных фраз для диалога/письма - при пересечении секущей двух параллельных прямых образуются ... ; - если внутренние накрест лежащие углы при … ; - если сумма внутренних односторонних углов при … ; - если соответственные углы при … ; - сумма острых углов прямоугольного треугольника … ; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Привитие ценностей |
Академическая честность: уважение идей и мыслей других людей, заключающееся в соблюдении принципов академической честности, нетерпимости к плагиату и копированию информации без указания ее источника. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Межпредметные связи |
Использование навыков черчения при построении отрезков и чертежей |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Предварительные знания |
Свойства и признаки параллельных прямых |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ход урока |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Запланированные этапы урока |
Запланированная деятельность на уроке |
Ресурсы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Начало урока 3 минут
3 минут
5 минут
2 минуты
Середина урока
2 минуты
4 минуты
2 минуты
3 минуты
2 минуты
1 минуты
7 минут
Конец урока Рефлексия Домашнее задание
|
I.Организационный момент Стартер « Я …….» и деление на групп с помощью блиц опроса учащихся 1 )прямоугольный треугольник: какой треугольник называется прямоугольным? Как называется сторона против лежащий прямого угла? Сколько прямых углов в прямоугольном треугольнике? Сколько острых углов? Сколько катетов? 2 ) Равносторонний треугольник: какой треугольник называется равносторонним? Сколько углов в равностороннем треугольнике? Какими свойствами обладают стороны равностороннего треугольника? Одна сторона 6см , чему равен периметр? Сколько вершин в равностороннем треугольнике? 3 )Равнобедренный треугольник: какой треугольник называется равнобедренном? как называются его стороны? Какие стороны равны? Какие свойства углов при основании? Чем является медиана проведенная к основанию равнобедренного треугольника? Проверка домашней работы ІІ. Повторение М -Назовите пары односторонних углов. Назовите пары накрест лежащих углов. Назовите пары соответственных углов. -Найдите все углы, если прямая а ‖‖ в и угол 1 равен 700.
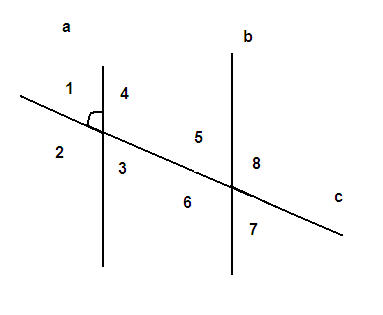
-Найдите углы 3,4,5, если АС ‖‖ m и угол 1 равен 600, Угол 2 равен 500.
III. Расскрытие новый темы Сегодня урок я начну стихотворением: Знает даже и дошкольник, – И сегодня на уроке мы выясним, чему равна сумма углов треугольника. И используя эти знания будем решать задачи. Карнавал геометрических фигур. (Слайд 6) Говорят три маски.( в роли маски выступают девочки) 1 маска: - Мы дочери одной матери. Живем в одном семействе, но силы и свойства у нас разные. 2 маска: - Я очень правильная фигура. У меня все углы и стороны равны. К тому же у меня три оси симметрии. 3 маска: - А я тоже имею две равные стороны. У меня так же есть ось симметрии, а потому у меня два равных угла при основании. 1 маска: - Зато я имею прямой угол. Вот какие мы сильные и важные! - Подумаешь, расхвастались,- сказали две маски, стоящие неподалеку,- мы тоже из вашего семейства. У меня, например, все уголки острые, а у моего друга есть один тупой угол. Но все мы обладаем замечательным свойством, которое сегодня откроют ребята. Учитель: Ребята, как вы думаете, что скрывается за масками? Каким свойством обладают все треугольники? (Обучающиеся высказывают предположения, что это за маски и каким свойством они обладают) Практическая работа Ребята, мы с вами измеряли углы и с помощью транспортира, теперь предлагаю найти сумму углов треугольника двумя другими способами. У каждой из вас есть на парте по одному треугольнику разных цветов. Возьмите их. Они желтого или розового цвета. Обозначьте углы треугольника цифрами 1, 2, 3. Учащиеся с желтыми треугольниками: отрежьте два угла треугольника и приложите их к сторонам третьего угла так, чтобы все вершины были в одной точке. Учащиеся с розовыми треугольниками: сложите углы во внутрь треугольника. Заметим, что перегибать треугольник надо по прямой параллельной к стороне, того угла, который мы будем сгибать первым, а данный угол должен касаться данной стороны. - Посмотрите, на получившуюся фигуру и скажите, какой угол образуют в сумме все углы треугольника? - Замечаем, что все углы треугольника в сумме образуют развернутый угол. - Чему равна градусная мера развернутого угла? - К какому выводу мы пришли? - Сумма углов треугольника равна 180 градусов. - Выполнив практическую работу, мы установили, что сумма углов треугольника равна 180 градусов. Итак, тема нашего урока « сумме углов треугольника» Указываются цели урока: Можно ли быть уверенным в том, что в каждом треугольнике сумма углов равна 1800. Можно ли измерить углы любого треугольника? - Посмотрите карту звёздного неба. Найдите созвездие Большой Медведицы и Малой Медведицы. Найдите Полярную звезду – ориентир для путешественников и мореплавателей, - которая указывает направление на север. Найдём ещё две яркие звезды: α-звезда Капелла в созвездии Возничего и α- звезда Вега в созвездии Лира. Мысленно соединим их отрезками, получим треугольник. Можно ли измерить углы этого треугольника? В математике практическая работа дает возможность лишь сделать какое-то утверждение – гипотезу. Чтобы она стала истиной, её нужно доказать, убедиться, что она справедлива для любого треугольника. Как называется утверждение, справедливость которого устанавливается с помощью доказательства? (Утверждение, справедливость, которого устанавливается путем доказательства, называется теоремой.) - Какую теорему нам нужно доказать? Сумма внутренних углов треугольника равна 180 градусов. Доказательство теоремы. Итак, дан треугольник АВС, нужно доказать, что сумма его внутренних углов А, В, С равна 1800. Давайте оформим теорему. Теорема: Сумма внутренних углов треугольников равна 1800. - Как доказать данную теорему? Перед вами опорная схема, заполните пропуски в ней. Т Самооценивание Дано: ∆ АВС Доказать: А + В+ С =180° Доказательство: 1) Проведём через вершину В прямую MN II …..; (1балл) 2) 1= Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Краткосрочный план Раздел 7.3С:
Взаимное расположение
прямых
Дата:
Ф.И.О. учителя: Нуркеева А О
СШ № 44
Класс: 7
Урок
Количество
присутствующих:
отсутствующих:
Тема
урока Теорема о сумме внутренних
углов треугольника Цели обучения, которые достигаются
на данном уроке (ссылка на учебную программу) 7.3.1.16 доказывать теорему о сумме внутренних углов
треугольника и следствия из неё; 7.3.1.17 применять теорему о сумме внутренних углов
треугольника и следствия из неё при решении
задач; Цели урока
Выдвинуть гипотезу о сумме
углов треугольника;
Сформулировать и доказать
теорему о сумме углов треугольника; Научиться решать задачи,
используя данную теорему. Критерии оценивания Учащийся достиг цель,
если Доказывает теорему о сумме углов
треугольника; Применяет теорему о сумме углов треугольника при
решении задач; Решает задачи на вычисление и
доказательство
Языковые цели
Учащиеся будут: -
комментировать доказательство теорем и решения
задач; -
оперировать понятиями и терминами
раздела; -
описывать данные чертежа.
Предметная лексика и
терминология -
параллельные, пересекающиеся, перпендикулярные
прямые; -
секущая; -
внутренние накрест лежащие углы,
внутренние односторонние углы, соответственные
углы;
- перпендикуляр, наклонная,
проекция.
Серия полезных фраз для
диалога/письма -
при пересечении секущей
двух параллельных прямых образуются ...
; -
если внутренние накрест лежащие углы при …
; -
если сумма внутренних односторонних углов при
… ; - если соответственные углы при
… ; - сумма острых углов прямоугольного треугольника …
; Привитие ценностей Академическая
честность:
уважение идей и мыслей других людей, заключающееся в соблюдении
принципов академической честности, нетерпимости к плагиату и
копированию информации без указания ее источника. Межпредметные
связи Использование навыков черчения при
построении отрезков и чертежей Предварительные знания Свойства и признаки параллельных
прямых Ход урока Запланированные этапы
урока Запланированная деятельность на
уроке Ресурсы
Начало урока
3 минут
3 минут
5 минут
2 минуты
Середина урока
2 минуты
4 минуты
2
минуты
3 минуты
2 минуты
1 минуты
7 минут
Конец урока
Рефлексия
Домашнее задание
I.Организационный момент Стартер « Я …….» и
деление на групп с помощью блиц опроса учащихся 1
)прямоугольный
треугольник:
какой треугольник называется прямоугольным? Как называется сторона
против лежащий прямого угла? Сколько прямых углов в прямоугольном
треугольнике? Сколько острых углов? Сколько
катетов? 2
) Равносторонний
треугольник:
какой треугольник называется равносторонним? Сколько углов в
равностороннем треугольнике? Какими свойствами обладают стороны
равностороннего треугольника? Одна сторона 6см , чему равен
периметр? Сколько вершин в равностороннем
треугольнике? 3
)Равнобедренный
треугольник: какой треугольник называется равнобедренном? как
называются его стороны? Какие стороны равны? Какие свойства углов
при основании? Чем является медиана проведенная к основанию
равнобедренного треугольника? Проверка домашней работы ІІ.
Повторение М -Назовите пары односторонних
углов. Назовите пары накрест лежащих
углов. Назовите пары соответственных
углов. -Найдите все углы, если прямая а ‖‖ в и угол 1
равен 700. -Найдите углы 3,4,5, если АС ‖‖
m
и угол 1 равен 600,
Угол 2 равен 500. III. Расскрытие новый
темы Сегодня урок я начну
стихотворением: Знает даже и дошкольник, – И
сегодня на уроке мы выясним, чему равна сумма углов треугольника. И
используя эти знания будем решать задачи.
Карнавал геометрических
фигур. (Слайд 6) Говорят три маски.( в роли маски выступают
девочки) 1 маска: -
Мы дочери одной матери. Живем в одном семействе, но силы и свойства
у нас разные. 2 маска: - Я
очень правильная фигура. У меня все углы и стороны равны. К тому же
у меня три оси симметрии. 3 маска: - А
я тоже имею две равные стороны. У меня так же есть ось симметрии, а
потому у меня два равных угла при основании. 1 маска: -
Зато я имею прямой угол. Вот какие мы сильные и
важные! -
Подумаешь, расхвастались,- сказали две маски, стоящие неподалеку,-
мы тоже из вашего семейства. У меня, например, все уголки острые, а
у моего друга есть один тупой угол. Но все мы обладаем
замечательным свойством, которое сегодня откроют
ребята. Учитель: Ребята, как вы думаете, что скрывается за
масками? Каким свойством обладают все
треугольники? (Обучающиеся высказывают предположения, что это
за маски и каким свойством они обладают) Практическая
работа Ребята, мы с вами измеряли углы и с помощью
транспортира, теперь предлагаю найти сумму углов треугольника двумя
другими способами. У каждой из вас есть на парте по одному
треугольнику разных цветов. Возьмите их. Они желтого или
розового цвета. Обозначьте углы треугольника цифрами 1, 2,
3. Учащиеся с желтыми
треугольниками:
отрежьте два угла треугольника и приложите их к сторонам третьего
угла так, чтобы все вершины были в одной точке. Учащиеся с розовыми треугольниками: сложите углы
во внутрь треугольника. Заметим, что перегибать треугольник надо по
прямой параллельной к стороне, того угла, который мы будем сгибать
первым, а данный угол должен касаться данной
стороны. -
Посмотрите, на получившуюся фигуру и скажите, какой угол образуют в
сумме все углы треугольника? -
Замечаем, что все углы треугольника в сумме образуют развернутый
угол. -
Чему равна градусная мера развернутого угла? - К
какому выводу мы пришли? -
Сумма углов треугольника равна 180 градусов. -
Выполнив практическую работу, мы установили, что сумма углов
треугольника равна 180 градусов. Итак, тема нашего урока « сумме углов
треугольника» Указываются цели урока: Можно ли быть уверенным в том, что в каждом
треугольнике сумма углов равна 1800. Можно ли измерить углы любого
треугольника? -
Посмотрите карту звёздного неба. Найдите созвездие Большой
Медведицы и Малой Медведицы. Найдите Полярную звезду – ориентир для
путешественников и мореплавателей, - которая указывает
направление на север. Найдём ещё две яркие звезды: α-звезда Капелла в
созвездии Возничего и α- звезда Вега в созвездии Лира. Мысленно
соединим их отрезками, получим треугольник. Можно ли
измерить углы этого треугольника? В
математике практическая работа дает возможность лишь сделать
какое-то утверждение – гипотезу. Чтобы она стала истиной, её
нужно доказать, убедиться, что она справедлива для любого
треугольника. Как
называется утверждение, справедливость которого устанавливается с
помощью доказательства? (Утверждение, справедливость, которого
устанавливается путем доказательства, называется
теоремой.) -
Какую теорему нам нужно доказать? Сумма внутренних углов треугольника равна 180
градусов. Доказательство
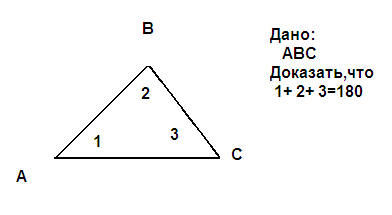
теоремы. Итак, дан треугольник АВС, нужно доказать, что
сумма его внутренних углов А, В, С равна
1800.
Давайте оформим теорему. Теорема: Сумма внутренних углов треугольников
равна 1800. - Как
доказать данную теорему? Перед вами опорная схема, заполните пропуски в
ней. Т Самооценивание Дано: ∆ АВС Доказать: А
+ В+ С
=180° Доказательство: 1)
Проведём через вершину В прямую MN
II
…..; (1балл) 2) 1= | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 ы
ы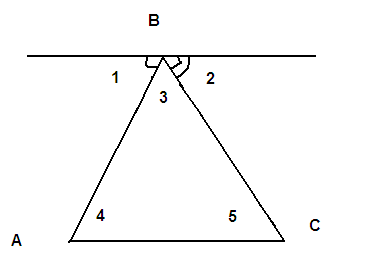
 еперь проверим
еперь проверим













