
Параметрі бар көрсеткіштік теңдеулерді шешу
Көрсеткіштік теңдеу — дәреже көрсеткіші
белгісіз болатын теңдеу. Қарапайым көрсекткіш теңдеулердің
түрі:  мұндағы
мұндағы
 ,
,  . Көрсеткіштік теңдеулерді шешу
үшін теңдеудің екі жақ бөлігін логарифмдеу, айнымалыларды
алмастыру, негіздері бірдей дәрежелерді
теңестіру, графиктік шешу, т. б. тәсілдер
қолданылады.
. Көрсеткіштік теңдеулерді шешу
үшін теңдеудің екі жақ бөлігін логарифмдеу, айнымалыларды
алмастыру, негіздері бірдей дәрежелерді
теңестіру, графиктік шешу, т. б. тәсілдер
қолданылады.
Көрсеткіштік теңдеулерді шешу кезінде негізгі екі әдіс қолданылады:
1. түріндегі
теңдеуден
түріндегі
теңдеуден  түріндегі теңдеуге
ауысу;
түріндегі теңдеуге
ауысу;
2.Жаңа айнымалылар енгізу. Кейде жасанды әдістерді қолдануға тура келеді.
Бірдей негізге келтіру арқылы шығарылатын теңдеу.
-
ax=b ( a>0, a≠1)
Егер b>0 болса, теңдеудің жалғыз ғана түбірі бар болады.
Егер b≤0 болса, теңдеудің түбірі жоқ болады.
-
af(x)=ag(x) мұндағы (a>0, a≠1) теңдеуінің сол және оң бөліктерінің
негіздері бірдей болғандықтан, af(x)=ag(x) теңдеуі f(x)=g(x) теңдеуімен мәндес болады.
36- мысал. 5x=125
Шешуі: , 125>0, 125=53,5x=53, x=3Жауабы: 3
Жаңа айнымалы енгізу арқылы жиі шығарылатын теңдеулер.
-
A∙a2x+B∙ax+C=0 a>0, a≠1
ax=y, y>0 деп белгілесек, у-ке қатысты квадрат теңдеуге келеді. Ay2+By+C=0
37- мысал. 52x-6∙5x+5=0
Шешуі: 5x=y, y>0 белгілесек у-ке байланысты y2-6y+5=0 квадрат теңдеуіне келеміз. Бұдан y1=1, y2=5 екенін табамыз.
у-тің екі мәніне сәйкес екі көрсеткіштік теңдеу шығады.
-
5x=1, x=0
-
5x=5, x=1
Бұл теңдеулерден есептің екі жауабы шығады. Жауабы: 0; 1
Графиктік тәсілмен шығарылатын теңдеулер.
aφ(x)=f(x) түріндегі теңдеулер
Ал мұндай теңдеулер түбірлерінің жуық мәндерін графиктік тәсілмен табуға болады.
ax=b a>0, a≠1, b>0
y=b түзуі y=axфункциясының графигін бір ғана нүктеде қиып өтеді. Қиылысу нүктесінің абсциссасы берілген көрсеткіштік теңдеудің түбірі болады.
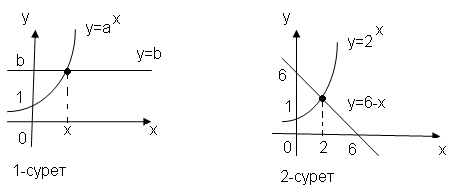
38- мысал. 2x=6-x
Шешуі: y=6-x түзуі y=2xфункциясының графиктерін сызып, олардың қиылысу нүктесінің абсциссасын табайық. Екі графиктің қиылысу нүктесінің абсциссасы x=2.
Жауабы: 2
Негіздері әр түрлі болып келген көрсеткіштік теңдеулерді шешу мысалдары.
39- мысал. 2x=3x
Шешуі: 3x>0,  =1,
=1,
 =
= , x=0
Жауабы: 0
, x=0
Жауабы: 0
Параметрі бар көрсеткіштік теңдеулер
Келесі
 (2.2.1)
(2.2.1)
теңдеуін
көрсеткіштік теңдеу деп атайды, мұнда
Бұл
теңдеудің анықталу облысы  функцияларының анықталу облыстарының
ортақ жиыны
функцияларының анықталу облыстарының
ортақ жиыны  болады.
Егер
болады.
Егер  болса, онда (2.2.1)
теңдеудің шешімі
болса, онда (2.2.1)
теңдеудің шешімі  жиынын құрайтын сандар
болады.
жиынын құрайтын сандар
болады.
Егер  болса, онда
(2.2.1) теңдеу
болса, онда
(2.2.1) теңдеу

жүйесіне парапар болады.
Егер  болса, онда
(2.2.1) теңдеу
болса, онда
(2.2.1) теңдеу

жүйесіне парапар болады.
Егер  болса, онда
(2.2.1)-ден
болса, онда
(2.2.1)-ден

теңдеуін аламыз.
Егер  болса, онда
(2.2.1)-ден
болса, онда
(2.2.1)-ден
 (2.2.2)
(2.2.2)
парапар
теңдеуін аламыз. Бұл жерде логарифм негізі ретінде  немесе
немесе  мәнін алсақ, онда (2.2.2)
теңдеуді
мәнін алсақ, онда (2.2.2)
теңдеуді


теңдеулері түрінде жазуға болады.
Кез келген көрсеткіштік теңдеуді шешу қарапайым көрсеткіштік теңдеудің шешімін табуға әкелінеді.
40- мысал.
Теңдеудің шешімін тап: 
Шешуі:
Берілген теңдеудің  болғанда ғана мағынасы болады. Бұл
теңдеудің анықталу облысы барлық нақты сандар жиыны
болғанда ғана мағынасы болады. Бұл
теңдеудің анықталу облысы барлық нақты сандар жиыны
 болады. Теңдеуді
болады. Теңдеуді

түрінде
жазуға болады. Бұдан егер  болса, онда
болса, онда кезкелген сан болады. Егер
кезкелген сан болады. Егер
 болса, онда
болса, онда теңдеуін аламыз. Бұдан
теңдеуін аламыз. Бұдан
 шешімін аламыз.
шешімін аламыз.
Жауабы:
Егер  болса, онда
шешімі
болса, онда
шешімі  - кезкелген нақты сан
болады;
- кезкелген нақты сан
болады;
Егер  болса,
онда
болса,
онда шешімі
болады.
шешімі
болады.
41- мысал.
Теңдеудің шешімін тап: 
Шешуі:
Берілген теңдеудің  болғанда мағынасы болады. Бұл
теңдеудің анықталу облысы
болғанда мағынасы болады. Бұл
теңдеудің анықталу облысы  жиыны болады. Осы шарттар орындалған
жағдайда берілген теңдеуді
жиыны болады. Осы шарттар орындалған
жағдайда берілген теңдеуді

түрге келтіреміз. Бұдан

теңдеуін
аламыз. Оның шешімі  сандары болады.
сандары болады.
Жауабы:
Егер  болса, онда
шешімі
болса, онда
шешімі  - нақты сандар жиыны
болады;
- нақты сандар жиыны
болады;
Егер  болса,
онда
болса,
онда шешімі
болады.
шешімі
болады.
42- мысал.
Теңдеудің шешімін тап: 
Шешуі:
Берілген теңдеудің  болғанда мағынасы болады. Егер,
болғанда мағынасы болады. Егер,
 болса, онда онда
болса, онда онда кезкелген сан болады. Егер
кезкелген сан болады. Егер
 болса, онда
болса, онда шешім болады. Егер
шешім болады. Егер  болса, онда онда
болса, онда онда шешім болады. Енді
шешім болады. Енді  болсын. Онда
болсын. Онда
 ~
~ 
теңдеуін
табамыз. Егер  яғни
яғни  болса, ондасоңғы теңдеудің оң жағы
4-ке, ал сол жағы нөлге тең болады. Бұл жағдайда шешімі болмайды.
Егер
болса, ондасоңғы теңдеудің оң жағы
4-ке, ал сол жағы нөлге тең болады. Бұл жағдайда шешімі болмайды.
Егер  болса,
онда
болса,
онда шешімін
табамыз.
шешімін
табамыз.
Жауабы:
Егер,  болса, онда онда
болса, онда онда кезкелген сан болады.
кезкелген сан болады.
Егер  болса,
онда
болса,
онда шешім
болады.
шешім
болады.
Егер  болса, онда
онда
болса, онда
онда шешім
болады.
шешім
болады.
Егер болса, онда
теңдеудің шешімі болмайды;
болса, онда
теңдеудің шешімі болмайды;
Егер болса,
онда
болса,
онда шешім
болады.
шешім
болады.
43- мысал.
 теңдеуінің төрт жауабы болатындай, а
параметрінің барлық мәнін табыңдар.
теңдеуінің төрт жауабы болатындай, а
параметрінің барлық мәнін табыңдар.
Шешуі:  деп белгілеп аламыз. Бастапқы
теңдеуіміз мына түрге келеді:
деп белгілеп аламыз. Бастапқы
теңдеуіміз мына түрге келеді:
 (t > 0, t ≠ 1, E(t) = [1; +∞]
)
(t > 0, t ≠ 1, E(t) = [1; +∞]
)
 осы теңдеуді қарастырайық.
осы теңдеуді қарастырайық.
 болған жағдайда теңдеудің бір ғана
шешімі болады , яғни
болған жағдайда теңдеудің бір ғана
шешімі болады , яғни  .
.
 болған кезде
болған кезде  . Сол себепті
. Сол себепті  теңдеудің екі шешімі болады:
теңдеудің екі шешімі болады:


Егер
алынған квадрат теңдеудің екі түбірі болса және
және  ,
,

демек, бастапқы теңдеудің төрт шешімі бар.
Жаттығулар. Төмендегі теңдеулерді  айнымалысына қарағанда
шешіңдер.
айнымалысына қарағанда
шешіңдер.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12.  -
- =
= -
-
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Параметрі бар көрсеткіштік теңдеулерді шешу
Параметрі бар көрсеткіштік теңдеулерді шешу
Параметрі бар көрсеткіштік теңдеулерді шешу
Көрсеткіштік теңдеу — дәреже көрсеткіші
белгісіз болатын теңдеу. Қарапайым көрсекткіш теңдеулердің
түрі:  мұндағы
мұндағы
 ,
,  . Көрсеткіштік теңдеулерді шешу
үшін теңдеудің екі жақ бөлігін логарифмдеу, айнымалыларды
алмастыру, негіздері бірдей дәрежелерді
теңестіру, графиктік шешу, т. б. тәсілдер
қолданылады.
. Көрсеткіштік теңдеулерді шешу
үшін теңдеудің екі жақ бөлігін логарифмдеу, айнымалыларды
алмастыру, негіздері бірдей дәрежелерді
теңестіру, графиктік шешу, т. б. тәсілдер
қолданылады.
Көрсеткіштік теңдеулерді шешу кезінде негізгі екі әдіс қолданылады:
1. түріндегі
теңдеуден
түріндегі
теңдеуден  түріндегі теңдеуге
ауысу;
түріндегі теңдеуге
ауысу;
2.Жаңа айнымалылар енгізу. Кейде жасанды әдістерді қолдануға тура келеді.
Бірдей негізге келтіру арқылы шығарылатын теңдеу.
-
ax=b ( a>0, a≠1)
Егер b>0 болса, теңдеудің жалғыз ғана түбірі бар болады.
Егер b≤0 болса, теңдеудің түбірі жоқ болады.
-
af(x)=ag(x) мұндағы (a>0, a≠1) теңдеуінің сол және оң бөліктерінің
негіздері бірдей болғандықтан, af(x)=ag(x) теңдеуі f(x)=g(x) теңдеуімен мәндес болады.
36- мысал. 5x=125
Шешуі: , 125>0, 125=53,5x=53, x=3Жауабы: 3
Жаңа айнымалы енгізу арқылы жиі шығарылатын теңдеулер.
-
A∙a2x+B∙ax+C=0 a>0, a≠1
ax=y, y>0 деп белгілесек, у-ке қатысты квадрат теңдеуге келеді. Ay2+By+C=0
37- мысал. 52x-6∙5x+5=0
Шешуі: 5x=y, y>0 белгілесек у-ке байланысты y2-6y+5=0 квадрат теңдеуіне келеміз. Бұдан y1=1, y2=5 екенін табамыз.
у-тің екі мәніне сәйкес екі көрсеткіштік теңдеу шығады.
-
5x=1, x=0
-
5x=5, x=1
Бұл теңдеулерден есептің екі жауабы шығады. Жауабы: 0; 1
Графиктік тәсілмен шығарылатын теңдеулер.
aφ(x)=f(x) түріндегі теңдеулер
Ал мұндай теңдеулер түбірлерінің жуық мәндерін графиктік тәсілмен табуға болады.
ax=b a>0, a≠1, b>0
y=b түзуі y=axфункциясының графигін бір ғана нүктеде қиып өтеді. Қиылысу нүктесінің абсциссасы берілген көрсеткіштік теңдеудің түбірі болады.

38- мысал. 2x=6-x
Шешуі: y=6-x түзуі y=2xфункциясының графиктерін сызып, олардың қиылысу нүктесінің абсциссасын табайық. Екі графиктің қиылысу нүктесінің абсциссасы x=2.
Жауабы: 2
Негіздері әр түрлі болып келген көрсеткіштік теңдеулерді шешу мысалдары.
39- мысал. 2x=3x
Шешуі: 3x>0,  =1,
=1,
 =
= , x=0
Жауабы: 0
, x=0
Жауабы: 0
Параметрі бар көрсеткіштік теңдеулер
Келесі
 (2.2.1)
(2.2.1)
теңдеуін
көрсеткіштік теңдеу деп атайды, мұнда
Бұл
теңдеудің анықталу облысы  функцияларының анықталу облыстарының
ортақ жиыны
функцияларының анықталу облыстарының
ортақ жиыны  болады.
Егер
болады.
Егер  болса, онда (2.2.1)
теңдеудің шешімі
болса, онда (2.2.1)
теңдеудің шешімі  жиынын құрайтын сандар
болады.
жиынын құрайтын сандар
болады.
Егер  болса, онда
(2.2.1) теңдеу
болса, онда
(2.2.1) теңдеу

жүйесіне парапар болады.
Егер  болса, онда
(2.2.1) теңдеу
болса, онда
(2.2.1) теңдеу

жүйесіне парапар болады.
Егер  болса, онда
(2.2.1)-ден
болса, онда
(2.2.1)-ден

теңдеуін аламыз.
Егер  болса, онда
(2.2.1)-ден
болса, онда
(2.2.1)-ден
 (2.2.2)
(2.2.2)
парапар
теңдеуін аламыз. Бұл жерде логарифм негізі ретінде  немесе
немесе  мәнін алсақ, онда (2.2.2)
теңдеуді
мәнін алсақ, онда (2.2.2)
теңдеуді


теңдеулері түрінде жазуға болады.
Кез келген көрсеткіштік теңдеуді шешу қарапайым көрсеткіштік теңдеудің шешімін табуға әкелінеді.
40- мысал.
Теңдеудің шешімін тап: 
Шешуі:
Берілген теңдеудің  болғанда ғана мағынасы болады. Бұл
теңдеудің анықталу облысы барлық нақты сандар жиыны
болғанда ғана мағынасы болады. Бұл
теңдеудің анықталу облысы барлық нақты сандар жиыны
 болады. Теңдеуді
болады. Теңдеуді

түрінде
жазуға болады. Бұдан егер  болса, онда
болса, онда кезкелген сан болады. Егер
кезкелген сан болады. Егер
 болса, онда
болса, онда теңдеуін аламыз. Бұдан
теңдеуін аламыз. Бұдан
 шешімін аламыз.
шешімін аламыз.
Жауабы:
Егер  болса, онда
шешімі
болса, онда
шешімі  - кезкелген нақты сан
болады;
- кезкелген нақты сан
болады;
Егер  болса,
онда
болса,
онда шешімі
болады.
шешімі
болады.
41- мысал.
Теңдеудің шешімін тап: 
Шешуі:
Берілген теңдеудің  болғанда мағынасы болады. Бұл
теңдеудің анықталу облысы
болғанда мағынасы болады. Бұл
теңдеудің анықталу облысы  жиыны болады. Осы шарттар орындалған
жағдайда берілген теңдеуді
жиыны болады. Осы шарттар орындалған
жағдайда берілген теңдеуді

түрге келтіреміз. Бұдан

теңдеуін
аламыз. Оның шешімі  сандары болады.
сандары болады.
Жауабы:
Егер  болса, онда
шешімі
болса, онда
шешімі  - нақты сандар жиыны
болады;
- нақты сандар жиыны
болады;
Егер  болса,
онда
болса,
онда шешімі
болады.
шешімі
болады.
42- мысал.
Теңдеудің шешімін тап: 
Шешуі:
Берілген теңдеудің  болғанда мағынасы болады. Егер,
болғанда мағынасы болады. Егер,
 болса, онда онда
болса, онда онда кезкелген сан болады. Егер
кезкелген сан болады. Егер
 болса, онда
болса, онда шешім болады. Егер
шешім болады. Егер  болса, онда онда
болса, онда онда шешім болады. Енді
шешім болады. Енді  болсын. Онда
болсын. Онда
 ~
~ 
теңдеуін
табамыз. Егер  яғни
яғни  болса, ондасоңғы теңдеудің оң жағы
4-ке, ал сол жағы нөлге тең болады. Бұл жағдайда шешімі болмайды.
Егер
болса, ондасоңғы теңдеудің оң жағы
4-ке, ал сол жағы нөлге тең болады. Бұл жағдайда шешімі болмайды.
Егер  болса,
онда
болса,
онда шешімін
табамыз.
шешімін
табамыз.
Жауабы:
Егер,  болса, онда онда
болса, онда онда кезкелген сан болады.
кезкелген сан болады.
Егер  болса,
онда
болса,
онда шешім
болады.
шешім
болады.
Егер  болса, онда
онда
болса, онда
онда шешім
болады.
шешім
болады.
Егер болса, онда
теңдеудің шешімі болмайды;
болса, онда
теңдеудің шешімі болмайды;
Егер болса,
онда
болса,
онда шешім
болады.
шешім
болады.
43- мысал.
 теңдеуінің төрт жауабы болатындай, а
параметрінің барлық мәнін табыңдар.
теңдеуінің төрт жауабы болатындай, а
параметрінің барлық мәнін табыңдар.
Шешуі:  деп белгілеп аламыз. Бастапқы
теңдеуіміз мына түрге келеді:
деп белгілеп аламыз. Бастапқы
теңдеуіміз мына түрге келеді:
 (t > 0, t ≠ 1, E(t) = [1; +∞]
)
(t > 0, t ≠ 1, E(t) = [1; +∞]
)
 осы теңдеуді қарастырайық.
осы теңдеуді қарастырайық.
 болған жағдайда теңдеудің бір ғана
шешімі болады , яғни
болған жағдайда теңдеудің бір ғана
шешімі болады , яғни  .
.
 болған кезде
болған кезде  . Сол себепті
. Сол себепті  теңдеудің екі шешімі болады:
теңдеудің екі шешімі болады:


Егер
алынған квадрат теңдеудің екі түбірі болса және
және  ,
,

демек, бастапқы теңдеудің төрт шешімі бар.
Жаттығулар. Төмендегі теңдеулерді  айнымалысына қарағанда
шешіңдер.
айнымалысына қарағанда
шешіңдер.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12.  -
- =
= -
-

шағым қалдыра аласыз















