
К.К.Есмуханова –БҚО,Ақжайық ауданы,Тайпақ орта жалпы білім беретін мектебі,жоғарғы санатты математика пәні мұғалімі
«Параметрлі теңдеулер мен теңсіздіктерді шешу»
Бұл қолданбалы курстың бағдарламасы жаратылыстану-математика бағытында оқитын оқушыларға және мұғалімдерге арналған.
Бағдарламада математиканың маңызды тақырыптарының бірі параметрлі теңдеулер мен теңсіздіктерді шешу әдіс-тәсілдері қарастырылған.
Бағыты: Жаратылыстану-математика
Өзектілігі: «Параметрлі теңдеулер мен теңсіздіктерді шешу» қолданбалы бағдарлы оқыту курсының бағдарламасы оқушылардың теориялық білімін нығайтып, математикалық заңдылықтарды терең біліп, дәлелдей алуға ,өздігінен іздендіру арқылы шығармашылық дамуын шыңдау мақсатында құрылған.
Курс бағдарламасы бойынша оқушылар параметрі бар сызықтық теңдеулер мен теңсіздіктерді, бүтін теңдеулер мен теңсіздіктерді , квадрат теңдеулер мен теңсіздіктерді, бөлшек-рационал теңдеулер мен теңсіздіктерді, рационал теңдеулер мен теңсіздіктерді, иррационал теңдеулер мен теңсіздіктерді, жоғары дәрежелі теңдеулер мен теңсіздіктерді,трансценденттік теңдеулер,яғни ,параметрі бар тригонометриялық теңдеулер мен теңсіздіктерді, көрсеткіштік теңдеулер мен теңсіздіктерді, логарифмдік теңдеулер мен теңсіздіктерді шешу арқылы математикадан терең білім алуға мүмкіндігі мол.
Бағдарлама : 11- сынып оқушыларына және мұғалімдерге арналған.
Қажеттілігі: Математика пәні жалпы білім берудің негізгі компоненті болып табылады. Оның оқушыға қатысты басты мақсаты –оқушылардың математикалық сауаттылығын арттыру ,олардың білімдерінің тиянақты болуын қамтамасыз ету болып саналады. Математикалық білім- оқушының жоғары деңгейде дамуы мен шығармашылық іс-әрекет тәжірибесімен қаруланған , бүгінгі жағдайда бағдарлама алуға дайын тұлға ретінде қалыптасуы үшін қажет. Оқушының ойлау қабілетін дамытуға, олардың математиканы оқуға деген ынта –талабын арттыруға жәрдем етеді.
Түсінік хат
Математиканы оқыту процесінің мақсаты–жеке оқушының есеп шығару қабілетін дамыту және математикалық ойлау қабілетін дамыту үшін жаратылыстану –математикалық бағыттағы оқытуға сәйкес мектептегі білім сапасын арттыру болып табылады.
Қазіргі заман математика ғылымының өте кең тараған кезеңі . Ал талапқа сай математикалық білім берудің басты шарты математикалық мәдениеттің деңгейін көтеру болып табылады.
Математикалық есептерді шешу , теоремаларды дәлелдеу оқушылардың ойын оятып , ойлау, есте сақ-тау қабілеттерін дамытуда , батыл қимылдар жасауға , шығармашылық ізденіске тәрбиелейді.
Ендеше оқушылардың математикаға дайындығын жан-жақты жетілдіру қазіргі аса маңызды міндеттердің бірі.
11- сыныптағы жаратылыстану–математикалық бағыттағы математика курсында қосымша түрде қолданбалы курс қарастырылады.
Бейіндік оқытудың мақсаты – математика пәні мазмұны ғылыми жетістігіне сай болып, оны түсініп қолдануға және әрі қарай дамытуға жағдай жасай-тындай болуға және де жаңа ғылымдарды жай ғана меңгеру емес, жеке тұлғаның интеллектуалдық қорын ұлғайту. Математиканың ерекше орны басқа ғылымдарды меңгеруде негіз болатын ойлаудың сапалық та, сандық та дамытуына әсер етуінен көрінеді.
Есеп шығара білу – математикадан алған білім деңгейінің , оқу материалын қаншалықты терең меңгергенінің көрсеткіші.
Сондықтан кез келген емтихан мен білімді тексеру математика курсында теңдеулер мен теңсіздіктерді, олардың жүйелерін шешу, есептерді теңдеу құру арқылы шығару оқушы меңгеруге тиісті материалдың бірі болып табылады.
Бұл қолданбалы курста 11- сынып оқушыларына сабақта алған білімдеріне қосымша білім беруге, оқыған материалдарын тереңдетуге және мектеп курсында көп мағлұмат берілмейтін мынадай: «Параметрлі теңдеулер мен теңсіздіктер» тақырыптарын меңгеруге бағытталған.
Есептердің шығарылу жолдары алдымен әртүрлі тәсілдермен көрсетіліп, ал қалған есептерді оқушылардың өздерінің тиімді тәсілді таңдап алуына баса назар аударылады. Шешімдерді іздеудің математикалық методтарын, логикалық пайымдаулардың , математикалық модельдердің , адекваттылық мәселелерін оқушылар меңгеріп алуларына зор көңіл бөлінеді. Бұл курс орта мектептері түлектеріне теңдеу шешуге қажетті және жеткілікті білім жинақтауға мүмкіндік бере отырып, математика негізгі пән болып келетін ҰБТ есептерін шығаруға дайындық болып табылады.
Мақсаттары:
-
Жалпы теңдеулер мен теңсіздіктерді және оларды шешу әдістері туралы толық мағлұмат алу, алған білімдерін тереңдету;
-
Жалпы мәдениеттің ішінде ойлау мәдениетінің логикалық және әдістемелік тұрғыдан дамуы;
-
Жалпы логикалық ойлау мәдениетін дамыта отырып , оқушының
математикаға қызығушылығын арттыру;
-
Орта мектепті бітіруші түлектердің жоғары оқу орындарында білімдерін жалғастыру үшін математикалық білімдерін
жүйелеу,тереңдету, тұжырымдау және нақтылау;
-
Жоғары математика мен элементар математиканың арасындағы байланысты түсіне білу, арифметика, алгебра, математикалық анализдің, жалпы математиканың бірлігі туралы білу;
-
Оқушылардың математика және оның салалары бойынша мамандық таңдауға көмектесу
Оқушылардың дайындығына қойылатын талаптар:
-
Теңдеулер мен теңсіздіктерді шеше білу;
-
Алгебралық теңдеулер мен теңсіздіктер жүйелерінің шешімдерін анықтай білу;
-
Трансценденттік параметрлі теңдеулер мен теңсіздіктерді шеше білу;
-
Тереңірек білім беру;
-
Ойлау , есте сақтау қабілеттерін дамыту;
-
Игерген білімдерін болашақта қолдана білу, жетілдіру;
-
Әртүрлі ақпарат көздерімен жұмыс жасауға; қорытынды ой жасау және нәтижені сараптауды,пікірталасқа қатысу , өз қызметінің нәтижесін көре білу , параметрлері берілген теңдеулер мен теңсіздіктерді әртүрлі әдістермен шешу;
-
есеп шығарудың ұтымды жолын таңдау.
Курсты жүргізудегі негізгі принциптер:
-
Жүйелілік (негізгі жұмысты оқушы үйде өз бетімен орындауы керек);
-
Ілгерілемелі күрделілік (үйде орындауға аптасына 5-10 есептер беріледі, мұндағы, 3-5 есептер барлығы шығара алатындай, 1-3 есеп оқушылардың кейбірі шығара алатындай және 1-2 есеп ешкім шығара алмайтындай );
-
Вариативтік (бір теңдеудің немесе есептің бірнеше тәсілмен алынған шешімдерін салыстыру);
-
Басымдылықтың ауысымы (қиындау есептерді шешкенде ойлау идеясына басымдылық берілсе, оңай , стандартты есептердің тек дұрыс жауптарына басымдылық беріледі).
Күтілетін нәтиже:
-оқушылардың мектеп курсындағы сызықтық, квадрат және рационал теңдеулер мен теңсіздіктерді әртүрлі, тиімді тәсілдермен шеше алулары;
- параметрлі сызықтық, квадрат және рационал теңдеулер мен теңсіздіктерді шеше алулары;
- тригонометриялық теңдеулерді шеше алулары, бірлік шеңберді тригонометриялық теңсіздіктерді шешуде қолдана алулары;
- мәтінмен берілген есептерге теңдеу құрып, оны шеше алулары;
-оқушылардың математикалық білімінің жоғарылауы;
-қиындығы жоғары есептер шығару арқылы
шығармашылық жұмыстану деңгейінің жоғарылауы;
- білімдерін ұшқырлау арқылы ҰБТ –дан жоғарғы
нәтижеге жету.
Пәнаралық кіріктіру:
Алгебра, физика, сызу, информатика
Кәсіпке бағдарлау:
Математика, информатика, инженер, экономист, бухгалтер, менеджер т.б. мамандықтарын таңдайтын оқушылардың білімдерінің терең де мазмұнды болуына ықпалын тигізеді.
Оқу уақытының көлемі, сабақтың мерзімділігі:
Сағат саны-34, аптасына 1 рет.
Оқу материалының мазмұны мен құрылымы:
-
Алгебралық теңдеулер мен теңсіздіктер-25 сағат(теорияға-14 сағат, практикаға-11 сағат)
-
Параметрі бар сызықтық теңдеулер мен теңсіздіктерді шешу-1 сағат
-
Параметрі бар бүтін теңдеулер мен теңсіздіктерді шешу-1 сағат
-
Квадрат үшмүшені зерттеу. Параметрі бар квадрат теңдеулер мен теңсіздіктерді шешу-2 сағат
-
Параметрі бар бөлшек-рационал теңдеулер мен теңсіздіктерді шешу-2 сағат
-
Параметрі бар рационал теңдеулер мен теңсіздіктерді шешу-2 сағат
-
Параметрі бар иррационал теңдеулер мен теңсіздіктерді шешу-2 сағат
-
Параметрі бар жоғары дәрежелі теңдеулер мен теңсіздіктерді шешу-2 сағат
Трансценденттік теңдеулер-9 сағат(теорияға 3 сағат,практикаға-3 сағат,қорытындығы-3 сағат)
-
Параметрі бар тригонометриялық теңдеулер мен теңсіздіктерді шешу-2 сағат
-
Параметрі бар көрсеткіштік теңдеулер мен теңсіздіктерді шешу-2сағат
-
Параметрі бар логарифмдік теңдеулер мен теңсіздіктерді шешу-2 сағат
|
№ |
сабақ № |
Сабақтың тақырыбы |
сағат саны |
||
|
барлығы |
теориялық бөлім |
практикалық бөлім |
|||
|
Алгебралық теңдеулер мен теңсіздіктер -25 сағат |
|||||
|
1 |
1 |
Параметрі бар сызықтық теңдеулерді шешу |
1 |
1 |
|
|
2 |
2 |
Параметрі бар бүтін теңдеулерді шешу |
1 |
1 |
|
|
3 |
3,4 |
Квадрат үшмүшені зерттеу. Параметрі бар квадрат теңдеулерді шешу |
2 |
1 |
1 |
|
3 |
5,6 |
Параметрі бар бөлшек-рационал теңдеулерді шешу |
2 |
1 |
1 |
|
5 |
7,8 |
Параметрі бар рационал теңдеулерді шешу |
2 |
1 |
1 |
|
6 |
9,10,11 |
Параметрі бар иррационал теңдеулерді шешу |
3 |
1 |
2 |
|
7 |
12,13 |
Параметрі бар жоғары дәрежелі теңдеулерді шешу |
2 |
1 |
1 |
|
8 |
14 |
Параметрі бар сызықтық теңсіздіктерді шешу |
1 |
1 |
|
|
9 |
15 |
Параметрі бар бүтін теңсіздіктерді шешу |
1 |
1 |
|
|
10 |
16,17 |
Параметрі бар квадрат теңсіздіктерді шешу |
2 |
1 |
1 |
|
11 |
18,19 |
Параметрі бар бөлшек-рационал теңсіздіктерді шешу |
2 |
1 |
1 |
|
12 |
20,21 |
Параметрі бар рационал теңсіздіктерді шешу |
2 |
1 |
1 |
|
13 |
22,23 |
Параметрі бар иррационал теңсіздіктерді шешу |
2 |
1 |
1 |
|
14 |
24,25 |
Параметрі бар жоғары дәрежелі теңсіздіктерді шешу |
2 |
1 |
1 |
|
Трансценденттік теңдеулер мен теңсіздіктер -9 сағат |
|||||
|
15 |
26,27 |
Параметрі бар тригонометриялық теңдеулер мен теңсіздіктерді шешу |
2 |
1 |
1 |
|
16 |
28,29 |
Параметрі бар көрсеткіштік теңдеулер мен теңсіздіктерді шешу |
2 |
1 |
1 |
|
17 |
30,31 |
Параметрі бар логарифмдік теңдеулер мен теңсіздіктерді шешу |
2 |
1 |
1 |
|
18 |
32, 33,34 |
Қорытынды сабақ |
3 |
1 |
2 |
|
барлығы |
34 |
18 |
16 |
||
Курсты ұйымдастыру формасын анықтау:
-интерактивті әдіс;
-топтық жұмыстар;
-жеке жұмыстар;
-практикум;
Курсты оқытуды аяқтау формасы:
-қорытынды аттестаттау;
Оқушылардың оқу жетістіктерін бағалау жүйесі:
-сынақ
Параметрлі сызықтық бөлшек-рационал теңдеулер мен теңсіздіктерді шешу
1. жүйеде а-ның қандай мәндерінде
тек бір ғана шешім болады?
жүйеде а-ның қандай мәндерінде
тек бір ғана шешім болады?
 Жауабы:
Жауабы: 
2.  жүйеде а-ның қандай мәндерінде
тек бір ғана шешім болады?
жүйеде а-ның қандай мәндерінде
тек бір ғана шешім болады?
Шешуі: 

Жауабы: 
Өз беттерімен шығаруға:
 жүйеде а-ның қандай мәндерінде
тек бір ғана шешім болады?
жүйеде а-ның қандай мәндерінде
тек бір ғана шешім болады?
Шешуі: 

Жауабы: 
4.  теңдеулер жүйесінің m-нің қандай
мәнінде а)бір шешімі ә)екі шешімі болады?
теңдеулер жүйесінің m-нің қандай
мәнінде а)бір шешімі ә)екі шешімі болады?
5. а параметрінің әрбір мәні үшін теңдеуді
шеш: 
1)a=-2 болса,онда берілген теңдеу 0*x=0 түріне көшеді.Бұл теңдеуді x-тің кез келген нақты мәні қанағаттандырады
2) болса,онда
берілген теңдеу бір ғана x=a-2 түріндегі шешімі бар сызықтық
теңдеуді береді
болса,онда
берілген теңдеу бір ғана x=a-2 түріндегі шешімі бар сызықтық
теңдеуді береді
Жауабы: a=-2 болғанда теңдеудің түбірі кез келген сан
 болғанда теңдеудің түбірі
x=a-2
болғанда теңдеудің түбірі
x=a-2
6. Теңдеуді шеш: 
 жағдайларын қарастырамыз ,егер a=0
болса,теңдеу 0*x=-2 болады,яғни шешімі жоқ
жағдайларын қарастырамыз ,егер a=0
болса,теңдеу 0*x=-2 болады,яғни шешімі жоқ
2. a=2 болса, теңдеу 0*x=0 болады,шешімі кез келген сан
3. 
Жауабы: a=0 болса,шешімі жоқ, a=2 болса, шешімі кез
келген сан,
7. Анықталу облысы: (m-1)(x+3)
Анықталу облысы: (m-1)(x+3)
3mx-5+(3m-11)(x+3)=(2x+7)(m-1);(4m-9)x=31-2m;
Ж:1)x=-3 -0,4 болғанда теңдеудің
бір ғана шешімі бар. m=2,25 және m=-0,4 болғанда
шешуі жоқ,m-1
болғанда теңдеудің мағынасы
болмайды.
-0,4 болғанда теңдеудің
бір ғана шешімі бар. m=2,25 және m=-0,4 болғанда
шешуі жоқ,m-1
болғанда теңдеудің мағынасы
болмайды.
8.
теңдеудің мағынасы бойынша

a=b болғанда 0*x=0;x= x-тің кез келген нақты мәнін
қанағаттандырады.
x-тің кез келген нақты мәнін
қанағаттандырады.  болғанда x=
болғанда x= Енді
Енді  болатын а мен в –ның мәндерін
табамыз.
болатын а мен в –ның мәндерін
табамыз.
1)  яғни
a=
яғни
a=
2)  яғни
a=
яғни
a=
Жауабы:1)  a
a ,a
,a болғанда x=
болғанда x=
2) a=b болғанда  –тан басқа
x –кез
келген сан.
–тан басқа
x –кез
келген сан.
3)
a= болғанда шешуі
жоқ
болғанда шешуі
жоқ
Өз бетімен орындауға берілетін тапсырмалар:
1. в-ның қандай мәндерінде (2-b)(b+x)=15-7b теңдеуінің түбірі 3-тен артық немесе тең? Жауапта осы мәндердің ең үлкенін көрсет
2. а-ның қандай мәндерінде (x-1)( теңдеуінің түбірі 0-ден артық
немесе тең? Жауапта осы мәндердің ең үлкенін көрсет
теңдеуінің түбірі 0-ден артық
немесе тең? Жауапта осы мәндердің ең үлкенін көрсет
3. k коэффициентінің қандай мәндерінде  теңдеудің түбірі
болмайды?
теңдеудің түбірі
болмайды?
4. p коэффициентінің қандай мәндерінде  теңдеудің 2 түбірі
болады?
теңдеудің 2 түбірі
болады?
5.  теңдеуінің
түбірлерінің бірі 3-ке тең болатындай а-ның мәнін тап?
теңдеуінің
түбірлерінің бірі 3-ке тең болатындай а-ның мәнін тап?
6. k -ның қандай мәнінде  теңдеуінің
теңдеуінің  –ге тең түбірі болады?
–ге тең түбірі болады?
7.  k-ның қандай
мәндерінде теңдеуінің түбірлерінің кубтарының қосындысы 7-ге тең
болады?
k-ның қандай
мәндерінде теңдеуінің түбірлерінің кубтарының қосындысы 7-ге тең
болады?
8. k , k-ның
қандай мәндерінде теңдеуінің түбірлерінің кубтарының қосындысы
72-ге тең болады?
, k-ның
қандай мәндерінде теңдеуінің түбірлерінің кубтарының қосындысы
72-ге тең болады?
9. а параметрінің қандай мәнінде теңсіздігінің шешімдері болмайды?
1.ax>9x+6
2. ax<8x-7
10. а параметрінің қандай мәнінде теңсіздігінің шешімі кез келген нақты сан?
1.ax>4x-5
2.ax<3x+6
11. а параметрінің әрбір мәнінде теңсіздігін шешіңдер ?
1.ax+5a<4-6x
2.ax-6a<5x+3
7.  а-ның қандай мәндерінде теңсіздігі
кез келген х үшін орындалады?
а-ның қандай мәндерінде теңсіздігі
кез келген х үшін орындалады?
Берілген теңсіздіктің сол жағындағы өрнекті
түрлендірейік: емесе
емесе

Кез келген х үшін  себебі квадрат үшмүшеліктің
дискриминанты 0-ден кіші.
себебі квадрат үшмүшеліктің
дискриминанты 0-ден кіші.
 теңсіздігін шешейік. Квадрат
үшмүшеліктің таңбасы
теңсіздігін шешейік. Квадрат
үшмүшеліктің таңбасы  –тың коэффицентінің таңбасымен
бірдей болады,егер оның дискриминанты 0-ден кіші болса,яғни
–тың коэффицентінің таңбасымен
бірдей болады,егер оның дискриминанты 0-ден кіші болса,яғни
 Демек,-6<a<2
Демек,-6<a<2
8. Теңдеуді шеш: 
1. a
2.а
9.  жауабы: (a;3]
жауабы: (a;3]
Квадрат үшмүшеліктерді зерттеу. Параметрі бар квадрат теңдеулерді шешу
 вадрат үшмүшелігіне сәйкес
функцияның графигі парабола ,оның тармақтары а коэффициентінің
таңбасына байланысты.
вадрат үшмүшелігіне сәйкес
функцияның графигі парабола ,оның тармақтары а коэффициентінің
таңбасына байланысты.
а) a>0 болса,парабола тармағы жоғары, a<0 болса парабола тармағы төмен қарайды.
2. D = дискриминантына байланысты
параболаның абсцисса өсін қиятыны не қимайтыны белгілі
болады. f(x)=
дискриминантына байланысты
параболаның абсцисса өсін қиятыны не қимайтыны белгілі
болады. f(x)= -
-

3. y= үшмүшелігінің
түбірлері мен графигіне сәйкес келесі кестені қолданған
тиімді:
үшмүшелігінің
түбірлері мен графигіне сәйкес келесі кестені қолданған
тиімді:

 вадрат үшмүшелігінің түбірлері мен
коэффициенттерінің арасындағы тәуелділікті Виет теоремасы
/келтірілген квадрат үшмүше үшін / кез келген үшмүше үшін
береді:
вадрат үшмүшелігінің түбірлері мен
коэффициенттерінің арасындағы тәуелділікті Виет теоремасы
/келтірілген квадрат үшмүше үшін / кез келген үшмүше үшін
береді:

Салдар1:  квадрат үшмүшеліктің әртүрлі екі
нақты түбірлері бар болып және олардың таңбалары бірдей болуы
үшін
квадрат үшмүшеліктің әртүрлі екі
нақты түбірлері бар болып және олардың таңбалары бірдей болуы
үшін  және
және яғни
яғни
 шарттарының орындалуы қажет
және жеткілікті
шарттарының орындалуы қажет
және жеткілікті
Салдар 2:  болуы үшін ,
болуы үшін ,

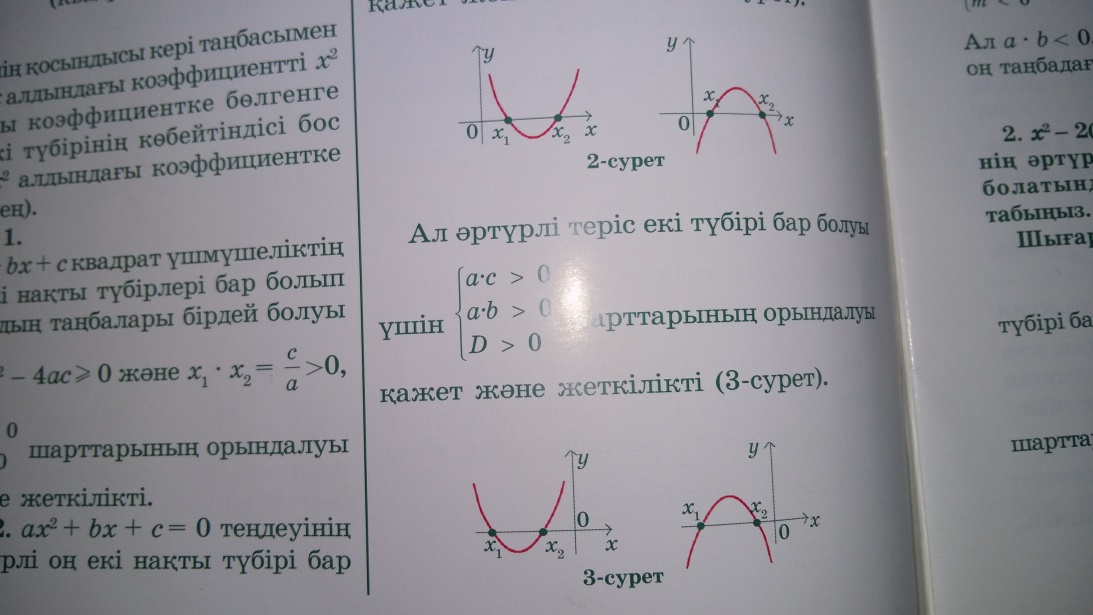
 шарттарының орындалуы қажет және жеткілікті .
шарттарының орындалуы қажет және жеткілікті .
Ал әртүрлі теріс екі түбірі бар болуы үшін
 шарттарының орындалуы қажет және
жеткілікті.
шарттарының орындалуы қажет және
жеткілікті.
Салдар 3: квадрат теңдеуінің әртүрлі нақты
екі түбірі бар болып және олардың таңбалары әртүрлі болуы
үшін
квадрат теңдеуінің әртүрлі нақты
екі түбірі бар болып және олардың таңбалары әртүрлі болуы
үшін  ,
,
яғни  теңсіздіктержүйесі орындалуы қажет және жеткілікті ,
теңсіздіктержүйесі орындалуы қажет және жеткілікті ,
 болса,
болса,
 болса, теріс түбірдің модулі үлкен
болады.
болса, теріс түбірдің модулі үлкен
болады.
Сабақта берілетін денгейлік тапсырмалар:
1.m параметрінің қандай мәнінде  теңдеуінің түбірлерінің
таңбалары әртүрлі болады? Қандай таңбадағы түбірдің абсолют шамасы
ең үлкен?
теңдеуінің түбірлерінің
таңбалары әртүрлі болады? Қандай таңбадағы түбірдің абсолют шамасы
ең үлкен?
Шешуі:  үшмүшелігі үшін 3-салдарды
пайдалансақ, түбірлердің таңбалары әртүрлі болу үшін
үшмүшелігі үшін 3-салдарды
пайдалансақ, түбірлердің таңбалары әртүрлі болу үшін
 шарттары бойынша
шарттары бойынша
 болады.
болады.
Ал a*b<0 ,яғни -5<0 болғандықтан оң таңбадағы түбірдің модулі үлкен.
Жауабы: m<0,оң түбірдікі
 теңдеуінің әртүрлі нақты екі оң
түбірі бар болатындай а параметрінің мәнін тап
теңдеуінің әртүрлі нақты екі оң
түбірі бар болатындай а параметрінің мәнін тап
 2-салдар бойынша (екі оң түбірі бар
болуы үшін)
2-салдар бойынша (екі оң түбірі бар
болуы үшін)  шарттарынан
шарттарынан 


Ескерту: бұл есепті графиктік-аналитикалық тәсілмен шығаруға болады /оқушыларға жеке жұмыстануға/
3.Қандай b үшін  теңдеуінің а) теріс екі түбірі
болады? б)оң екі түбірі болады? в) әртүрлі таңбадағы екі түбірі бар
болады?
теңдеуінің а) теріс екі түбірі
болады? б)оң екі түбірі болады? в) әртүрлі таңбадағы екі түбірі бар
болады?
Шешуі: 1-3 салдарларды пайдалансақ:
а) 
б) 
 болса,
болса,
b)
Жауабы: 
Ескерту: бұл есепті графиктік-аналитикалық тәсілмен шығаруға болады /оқушыларға жеке жұмыстануға/
4.f(x)=(2a-3) үшмүшелігінің түбірлері теріс
болатындай барлық а мәндерін табыңдар.
үшмүшелігінің түбірлері теріс
болатындай барлық а мәндерін табыңдар.
Шешуі: 1) 2a-3=0
2) a 2-салдарды
пайдаланып,теңсіздіктер жүйесін құрамыз.
2-салдарды
пайдаланып,теңсіздіктер жүйесін құрамыз. 
Жауабы:a
5.y=a үшмүшелігінің графигі ОХ өсімен
ортақ екі оң нүктесі бар болатындай а параметрінің мәндерінің
жиынын тап
үшмүшелігінің графигі ОХ өсімен
ортақ екі оң нүктесі бар болатындай а параметрінің мәндерінің
жиынын тап
Шешуі: 1)егер a=0 болса,сызықтық теңдеу шығады,ОХ өсі бір ғана нүктеде қиылады, есеп шарты орындалмайды.
2)үшмүшеліктің  алдындағы коэффициенттер оң немесе
теріс болуы мүмкін.
алдындағы коэффициенттер оң немесе
теріс болуы мүмкін.
а) a>0 болсын. Тармағы жоғары қарайды, ( төбесі ІУ ширекте ,яғни
төбесі ІУ ширекте ,яғни
 ал f(0)>0 болуы
керек.
ал f(0)>0 болуы
керек.
Жүйе құрсақ:
б) a<0 болсын. Тармағы төмен қарайды, ( өбесі І ширекте ,яғни
өбесі І ширекте ,яғни
 ал f(0) <0 болуы
керек.
ал f(0) <0 болуы
керек. Шешімі:
Шешімі:
 Жауабы: a
Жауабы: a
6.  теңдеуінің бір түбірі -3 тен
кіші,екіншісі 2-ден артық болатындай р параметрінің бүтін
мәндерінің қосындысын тап
теңдеуінің бір түбірі -3 тен
кіші,екіншісі 2-ден артық болатындай р параметрінің бүтін
мәндерінің қосындысын тап
Шешуі:  үшмүшелігінің графигі тармақтары
жоғары қараған парабола ,
үшмүшелігінің графигі тармақтары
жоғары қараған парабола , оның түбірлері болсын,және
оның түбірлері болсын,және
 болғандықтан
[
болғандықтан
[ кесіндісі
[
кесіндісі
[ кесіндісін
қамтиды. Сондықтан тармағы жоғары параболаның
кесіндісін
қамтиды. Сондықтан тармағы жоғары параболаның
f(-3) . Сәйкес
жүйе құрайық:
. Сәйкес
жүйе құрайық:


Жауабы:-3
7. теңдеуінің түбірлерінің
таңбалары әртүрлі ,және оң түбірі теріс түбірдің модулінен үлкен
болатындай a
мәнін тап.
теңдеуінің түбірлерінің
таңбалары әртүрлі ,және оң түбірі теріс түбірдің модулінен үлкен
болатындай a
мәнін тап.
Шешуі: 3-салдар көмегімен шығарамыз:  Жауабы: a
Жауабы: a
І І-тәсіл:
І-тәсіл:  үшмүшелігінің графигі тармағы жоғары қараған парабола,
төбесі
үшмүшелігінің графигі тармағы жоғары қараған парабола,
төбесі  және
және
 болады. Жүйе
құрсақ:
болады. Жүйе
құрсақ:
 Жауабы: a
Жауабы: a
 -ден үлкен
-ден үлкен
болатындай а мәнін тап.
Шешуі: графиктік –аналитикалық тәсілмен шығарсақ:
1) болса, квадрат
теңдеу сызықтық теңдеуге айналады,ендеше
болса, квадрат
теңдеу сызықтық теңдеуге айналады,ендеше 
2) 2-a>0 болсын,тармағы жоғары қараған парабола
 теңсіздіктер жүйесі есептің
барлық шарттарын қанағаттандырады.
теңсіздіктер жүйесі есептің
барлық шарттарын қанағаттандырады.  Шешімі:
Шешімі:
3) 2-a<0 парабола тармақтары төмен қарайды
 шешімі:
шешімі: Жауабы:
Жауабы: 
9. 8 саны  теңдеуінің екі түбірінің
арасында болатындай а параметрінің мәнін тап.
теңдеуінің екі түбірінің
арасында болатындай а параметрінің мәнін тап.
Шешуі: 1) a=0 болса,сызықтық теңдеу шығады,оның түбірі
біреу ғана,есеп шартын қанағаттандырмайды. Ендеше ,
a
2) a>0 болсын, онда f(8) <0
болса,жеткілікті. f(8)
=64a-24a-24-2<0 ,20a<13, 0<a<
Шешімі: 0<a<
3) a<0 болcын .f(8)>0  . Жауабы: 0<a<
. Жауабы: 0<a<
11. теңдеуінің дәл бір түбірі
теңсіздігін қанағаттандыратын параметрінің барлық мәнін
тап.
теңдеуінің дәл бір түбірі
теңсіздігін қанағаттандыратын параметрінің барлық мәнін
тап.
Шешуі: берілген  үшмүшелігінің екі түбірінің дәл
бірі x<-1 теңсіздігін қанағаттандыру үшін D
үшмүшелігінің екі түбірінің дәл
бірі x<-1 теңсіздігін қанағаттандыру үшін D орындалуы қажет,яғни
D
орындалуы қажет,яғни
D
а)r=0 болса,онда  Ол x<-1 шартын
қанағаттандырмайды.
Ол x<-1 шартын
қанағаттандырмайды.
Б) r=5 болса,
 шартын қанағаттандырады.
шартын қанағаттандырады.
В)  болса, D>0. Бұл жағдайда дәл бір түбірі x<-1 орындалуы үшін
f(-1)<0,яғни
болса, D>0. Бұл жағдайда дәл бір түбірі x<-1 орындалуы үшін
f(-1)<0,яғни
1-2r+2+3r+1=r+4<0 болуы қажет немесе үлкен
түбірі
болуы қажет немесе үлкен
түбірі  болуы мүмкін
,яғни
болуы мүмкін
,яғни
1-2r+2+3r+1=r+4=0 болуы мүмкін .Берілген теңдеуге
r=-4 қоямыз:
болуы мүмкін .Берілген теңдеуге
r=-4 қоямыз:  Бірақ,
Бірақ, және бұл x<-1 шартын
қанағаттандырмайды. Жауабы: r<-4;r=5
және бұл x<-1 шартын
қанағаттандырмайды. Жауабы: r<-4;r=5
Параметрі бар екінші дәрежелі теңдеулерді шешу
Сабақта берілетін теориялық білім:
Егер  болса,
0*
болса,
0* теңдігі кез
келген х үшін орындалады.
теңдігі кез
келген х үшін орындалады.
Шешімі 
 болса, 0*
болса, 0* теңдігі ақиқат емес. Шешімі
жоқ
теңдігі ақиқат емес. Шешімі
жоқ
 болса, квадрат теңдеу сызықтық
теңдеуге айналады, bx+c=0
болса, квадрат теңдеу сызықтық
теңдеуге айналады, bx+c=0  түбірі біреу:
түбірі біреу:
егер  болса,
a*
болса,
a* ,екі түбірі
бар.
,екі түбірі
бар.
егер  болса,
болса, екі түбірі бар,біреуі 0-ге
тең
екі түбірі бар,біреуі 0-ге
тең
егер  болса
,
болса
, формуласымен
табылады,мұндағы D- дискриминант
формуласымен
табылады,мұндағы D- дискриминант
Сабақты бекітуге берілетін денгейлік тапсырмалар:
1.қандай а мәнінде  теңдеуінің түбірлері шексіз көп
болады?
теңдеуінің түбірлері шексіз көп
болады?
Шешуі: Теңдеу
0* түріне келсе кез
келген х үшін теңдік орындалады.
түріне келсе кез
келген х үшін теңдік орындалады.
Мұнда ,а =1 болса,x
Жауабы:a=1
2. теңдеуінің а параметрінің қандай
мәндерінде түбірлері екіден көп болады?
теңдеуінің а параметрінің қандай
мәндерінде түбірлері екіден көп болады?
Шешуі: Егер теңдеу
 түріне келсе,теңдеудің шексіз
көп шешімі болады, ендеше оның түбірлерінің саны 2-ден көп.
Коэффициенттерін көбейткіштерге жіктейік.
түріне келсе,теңдеудің шексіз
көп шешімі болады, ендеше оның түбірлерінің саны 2-ден көп.
Коэффициенттерін көбейткіштерге жіктейік.


10-3a-
Берілген теңдеу келесі түрге келеді: 
Егер a=2 болса,теңдеу 0* түріне келеді. Жауабы:
a=2
түріне келеді. Жауабы:
a=2
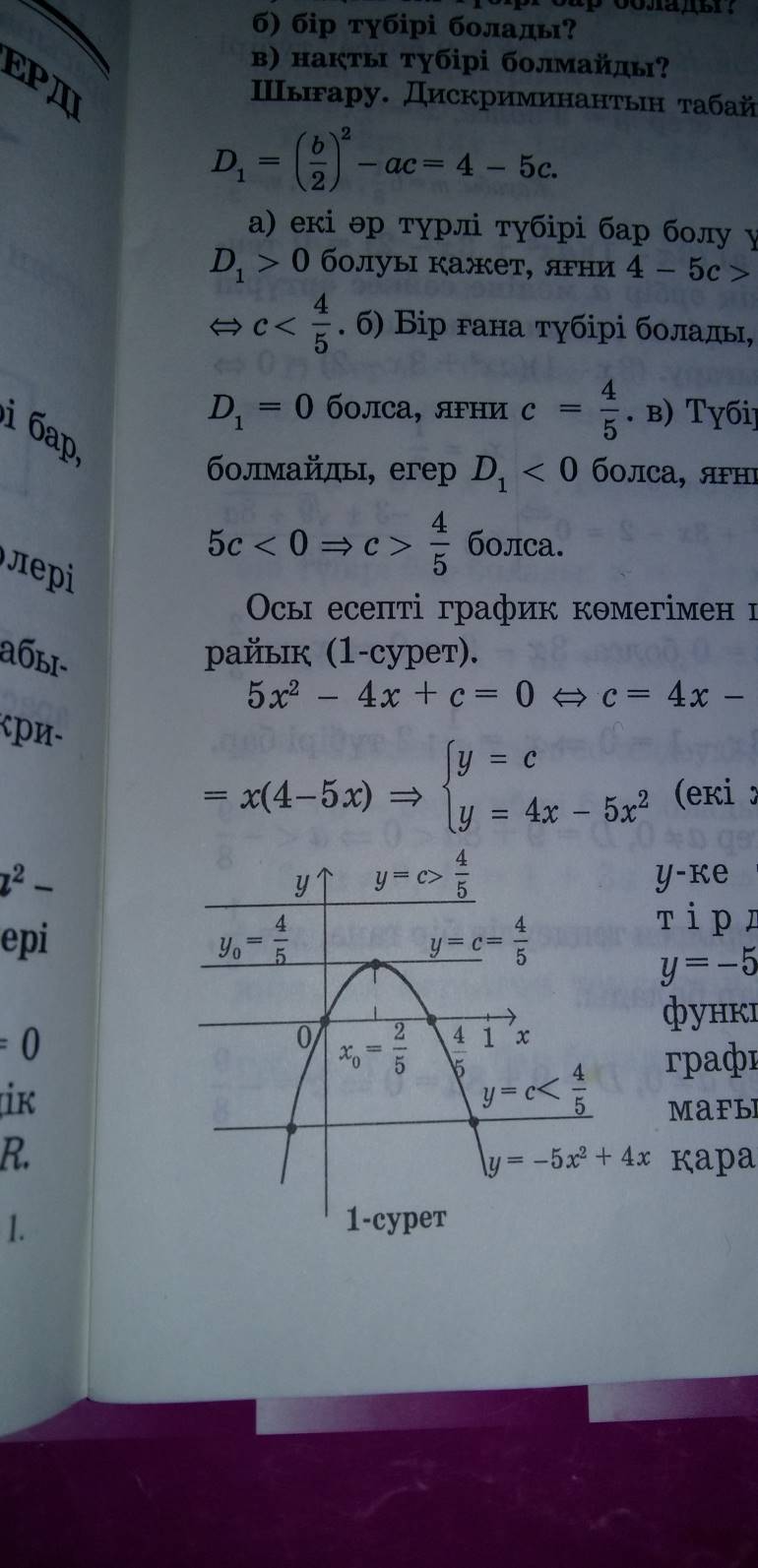 с параметрінің қандай мәнінде
с параметрінің қандай мәнінде  теңдеуінің
теңдеуінің
а)нақты екі түбірі бар болады?
б)бір түбірі болады?
в)нақты түбірі болмайды?
Шешуі:Дискриминантын
табайық:D=
а)екі әр түрлі түбірі бар болу үшін  болуы қажет,яғни
4-5c
болуы қажет,яғни
4-5c
б)бір ғана түбірі болады,егер  болса,яғни c=
болса,яғни c=
в) түбірлері болмайды,егер  болса,яғни 4-5c<0
болса,яғни 4-5c<0 болса.
болса.
Осы есепті графиктік тәсілмен шығарайық:
 4x-5
4x-5
 функциясының графигі тармағы төмен
қараған парабола, төбесінің координаттары:
функциясының графигі тармағы төмен
қараған парабола, төбесінің координаттары: 
 қиылыспайды,егер
c>
қиылыспайды,егер
c> болса.
болса.
б) түзу мен парабола 1 нүктеде қиылысады,егер
c= болса
болса
в)түзу және парабола 2 нүктеде қиылысады,егер с болса.
болса.
Жауабы: 1)c болса,шешімі жоқ
2)c=
болса,шешімі жоқ
2)c= болса,1 шешім
3)
болса,1 шешім
3)  болса,2
шешім
болса,2
шешім
3.Қандай а мәнінде  теңдеуінің түбірі біреу ғана
болады?
теңдеуінің түбірі біреу ғана
болады?
Шешеуі: 1)a=0 болса,берілген квадрат теңдеу сызықтық
теңдеуге айналады: -x-1=0
2)D=0 болса,1 шешім болады:D=
4.  теңдеуінің түбірі біреу ғана
болатындай а параметрінің барлық мәнін
табыңыз.
теңдеуінің түбірі біреу ғана
болатындай а параметрінің барлық мәнін
табыңыз.
Шешуі: 1)  болса,берілген теңдеу сызықтық
теңдеуге айналады:-1,5x+0,5
=0,x=
болса,берілген теңдеу сызықтық
теңдеуге айналады:-1,5x+0,5
=0,x= жалғыз шешімі болады
жалғыз шешімі болады
2) болсын,берілген квадрат теңдеудің жалғыз түбірі болады,егер
оның дискриминанты 0-ге тең болса: D=9
болсын,берілген квадрат теңдеудің жалғыз түбірі болады,егер
оның дискриминанты 0-ге тең болса: D=9 егер,
егер,  немесе
немесе  Есеп шартын а параметрінің үш мәні
қанағаттандырады.
Есеп шартын а параметрінің үш мәні
қанағаттандырады.
Жауабы:-5;-1;-0,5
9. ,егер
,егер  болса,а-ны
табыңдар
болса,а-ны
табыңдар
Виет теоремасы бойынша  ,
,
5 =
=

а-ның қандай мәндерінде теңдеудің нақты түбірлері болмайды?
1) 
7. Теңдеуді шеш:  +2(2a+1)x+(4a+3)=0
+2(2a+1)x+(4a+3)=0
1.егер a=1 онда теңдеу 6x+7=0 болады, x=-
2. 
a

Жауабы: a=1
болса, x=- ,
,  ,
,  б
б
Параметрі бар екінші дәрежелі теңсіздіктерді шешу
Әрбір нақты а мәні үшін келесі теңсіздіктерді шешеміз:
1.
2.
3.
4.
5.
6.Қандай нақты m мәндері үшін  үшін орындалады?
үшін орындалады?
1. y=


2) егер
a=
3)егер
a> D<0 ,
D<0 , себебі парабола ОХ өсін қимайды,әр
уақытта функция оң.
себебі парабола ОХ өсін қимайды,әр
уақытта функция оң.
Жауабы:
2.y= үшмүшелігінің графигі тармағы
.Төбесінің координаттары
үшмүшелігінің графигі тармағы
.Төбесінің координаттары 
 болса,ОХ
өсімен
болса,ОХ
өсімен  екі нүктеде
қияды.
екі нүктеде
қияды.  >0
теңсіздігінің шешімі:
>0
теңсіздігінің шешімі: 
Егер  болса,
болса, шешімі
шешімі  .Егер
.Егер  болса,парабола ОХ өсін
қимайды,
болса,парабола ОХ өсін
қимайды,  >0
теңсіздігі
>0
теңсіздігі  яғни кез
келген х үшін орындалады. Жауабы: егер |a|
яғни кез
келген х үшін орындалады. Жауабы: егер |a| ,егер a|<2 болса,x-кез келген
сан.
,егер a|<2 болса,x-кез келген
сан.
1) егер a=0 болса, x+1>0
2) егер  болса,тармағы төмен қараған
парабола ОХ өсін
болса,тармағы төмен қараған
парабола ОХ өсін  екі нүктеде қияды, мұнда
екі нүктеде қияды, мұнда
 ; шешімі:
; шешімі: 
 егер
егер  болса, яғни
болса, яғни  болса,яғни
0<a<
болса,яғни
0<a< болса,
болса,
 егер
егер  болса,
болса, болғанда ,парабола ОХ өсін
қимайды,ендеше
болғанда ,парабола ОХ өсін
қимайды,ендеше 

 болса,
болса,

 болса,
болса, x<-2,x>-2
x<-2,x>-2
 ал егер
ал егер  болса,
болса, шешімі жоқ
шешімі жоқ
Жауабы: 1) болса,
болса, 2)
2) болса, x<-2,x>-2
болса, x<-2,x>-2
 0<a<
0<a< болса,
болса,
 a=0 болса,x>-1
a=0 болса,x>-1

 a<0 болса,
a<0 болса,
4.
a=0 болса, x+1>0  .Егер
.Егер  болса,D=
болса,D= кез келген
кез келген  үшін түбірлері
үшін түбірлері 
1.a<0 болса,  және
және түбірлерінің өзара орналасуының екі
жағдайы болуы мүмкін:
түбірлерінің өзара орналасуының екі
жағдайы болуы мүмкін:  <
< немесе
немесе  яғни
яғни  немесе -1-(-
немесе -1-(- Сандар өсіне осы екі жағдайды
салып,тексеріп көрсек:
Сандар өсіне осы екі жағдайды
салып,тексеріп көрсек:
1.егер 
2.егер -1-(- Шешімі:
-1<x<-
Шешімі:
-1<x<-
1.D= болса,яғни
болса,яғни  болса,теңсіздіктің шешімі кез
келген
болса,теңсіздіктің шешімі кез
келген  себебі
:
себебі
:

2.егер D= болса,
болса,  , 0<a<1 және a>1 болуы
мүмкін.
, 0<a<1 және a>1 болуы
мүмкін.
А) 0<a<1
,яғни  болғанда ,онда x>-1,x<-
болғанда ,онда x>-1,x<-
б) егер a>1
болса,x>- онда
-
онда
- .
.
Егер ,-1-(-
Жауабы: 1)  болса, -1<x<-
болса, -1<x<-
2) a=0 болса,
3) болса,
болса, , x<-
, x<-
4) болса,х- кез келген,бірақ
болса,х- кез келген,бірақ

5) a>1 болса, x>-
5. теңсіздігі кез келген х мәнінде
орындалуы үшін
теңсіздігі кез келген х мәнінде
орындалуы үшін  шарты орындалуы қажет.
шарты орындалуы қажет.


Егер  болса,сызықтық теңсіздікке
айналады,мұнда a=1 болса, 1>0 ақиқат, теңсіздік кез келген х
үшін орындалады, a=-1 болса,-2x+1>0
болса,сызықтық теңсіздікке
айналады,мұнда a=1 болса, 1>0 ақиқат, теңсіздік кез келген х
үшін орындалады, a=-1 болса,-2x+1>0 есеп шарты орындалмайды.
есеп шарты орындалмайды.
 және
және  болса, теңсіздік кез келген х үшін
орындалмайды. Жауабы:
болса, теңсіздік кез келген х үшін
орындалмайды. Жауабы:
6.
f(x)= үшмүшелігі 1<x<2 аралығында
теріс болуы қажет және жеткілікті.Ол үшін (1:2) аралығы түгілімен
үшмүшеліктің түбірлерінің арасында орналауы қажет.
Сондықтан
үшмүшелігі 1<x<2 аралығында
теріс болуы қажет және жеткілікті.Ол үшін (1:2) аралығы түгілімен
үшмүшеліктің түбірлерінің арасында орналауы қажет.
Сондықтан
 Жауабы:
Жауабы: 
Берілетін тапсырмалар:
1. теңсіздігі кез келген үшін
орындалатындай барлық мәндерін тап.
теңсіздігі кез келген үшін
орындалатындай барлық мәндерін тап.
Ж: m>1
1.а параметрінің қандай мәнінде  теңсіздігі
теңсіздігі
а) барлық x<1үшін орындалады?
Б) x<1
ең болмағанда бір мәнінде орындалады? Ж: 1)
ондай а мәні табылмайды 2)a>
1.Қандай а мәндерінде  теңсіздігін қанағаттандыратын х-тің
кез келген мәнінің модулі 2-ден артық емес? Ж: -2
теңсіздігін қанағаттандыратын х-тің
кез келген мәнінің модулі 2-ден артық емес? Ж: -2
1.a теңсіздігінен 0<x<1
теңсіздігі шығатындай барлық а мәндерін тап.
теңсіздігінен 0<x<1
теңсіздігі шығатындай барлық а мәндерін тап.
Ж: 
1.қандай нақты m мәндерінде  теңсіздігі барлық x>1 үшін
орындалады?
теңсіздігі барлық x>1 үшін
орындалады?
Ж: m
Параметрі бар сықықтық , квадрат теңдеулер мен теңсіздіктерді шешуге практикалық сабақ
1.Қандай бүтін а мәндері үшін (a-5)x+a=3 теңдеуінің түбірі [0;5] кесіндісінде жатады? Ж:а=3;a=4
2.Теңдеуін шеш:  Ж: егер
Ж: егер  болса,x=
болса,x=
егер m=1 болса,x- кез келген , егер m=0 болса, шешімі жоқ
3.(a-3)x>5 теңсіздігінің шешімдері ax>2
теңсіздігінің де шешімдері болатындай а параметрінің барлық
мәндерін тап. Ж: 
4.Теңдеулерді шеш: 1.  2.
2. 3.
3.
5. 
Ж: 1.a болса, онда x=a,егер a=1
болса,онда x
болса, онда x=a,егер a=1
болса,онда x
2.егер a=-3,a=
3.  болса,онда
x=
болса,онда
x= егер a=2 немесе a=3 болса,онда x
егер a=2 немесе a=3 болса,онда x егер a=-2 болса,онда
егер a=-2 болса,онда 
4. болса,онда x=
болса,онда x= егер
егер  онда x
онда x
1. теңсіздігі
теңсіздігі  орындалатындай а параметрінің
барлық мәндерін тап
орындалатындай а параметрінің
барлық мәндерін тап
Ж: 
2. kвадрат
теңдеуінің қандай m мәндері үшін шешімдері бар болады?Түбірлерінің
таңбасын анықта ? Ж: m<-5 болса,екі
оң түбірі бар; -5<m<1 болса, түбірлерінің таңбалары әртүрлі;
m=-5 болса, түбірдің бірі 0-ге тең; m>1 болса нақты түбірлері
жоқ.
kвадрат
теңдеуінің қандай m мәндері үшін шешімдері бар болады?Түбірлерінің
таңбасын анықта ? Ж: m<-5 болса,екі
оң түбірі бар; -5<m<1 болса, түбірлерінің таңбалары әртүрлі;
m=-5 болса, түбірдің бірі 0-ге тең; m>1 болса нақты түбірлері
жоқ.
3.  теңсіздігінен (
теңсіздігінен ( теңсіздігі шығатындай а
параметрінің барлық мәндерін тап? Ж:
теңсіздігі шығатындай а
параметрінің барлық мәндерін тап? Ж: 
4.Қандай нақты m мәндерінде  теңсіздігінен x>1 теңсіздігі
шығады?Ж:ондай сан
табылмайды.
теңсіздігінен x>1 теңсіздігі
шығады?Ж:ондай сан
табылмайды.
5. теңдеуінің
қандай m үшін нақты түбірлері бар болады? Түбірлерінің таңбасын
зертте? Ж: 1) m
теңдеуінің
қандай m үшін нақты түбірлері бар болады? Түбірлерінің таңбасын
зертте? Ж: 1) m болса,нақты түбірлері бар.
2)
болса,нақты түбірлері бар.
2) болса,екі
түбірі теріс 3)
болса,екі
түбірі теріс 3) болса,түбірлерінің таңбалары
әртүрлі 4)
болса,түбірлерінің таңбалары
әртүрлі 4) болса,екі түбірі де оң 5)m=-5
болса,бір түбірі 0-ге тең.
болса,екі түбірі де оң 5)m=-5
болса,бір түбірі 0-ге тең.
6.(a-1) теңдеуінің қандай а үшін нақты
түбірлері бар болады? Түбірлерінің таңбасын зертте.
Ж: 1) 1
теңдеуінің қандай а үшін нақты
түбірлері бар болады? Түбірлерінің таңбасын зертте.
Ж: 1) 1 болса,нақты түбірлері бар.
2)
болса,нақты түбірлері бар.
2) болса,екі
түбірі теріс 3)
болса,екі
түбірі теріс 3) болса,түбірі де оң
4)
болса,түбірі де оң
4) болса,
түбірлерінің таңбалары әртүрлі 5) a=2 болса, x=
болса,
түбірлерінің таңбалары әртүрлі 5) a=2 болса, x= 6) a=
6) a= болса,бір түбірі 0-ге
тең
болса,бір түбірі 0-ге
тең
7. теңдеуінің
бір түбірі (1;2) аралығында,екінші түбірі одан сырт жататындай а
параметрінің барлық мәндерін тап.Жауабына осы шартты
қанағаттандыратын параметрдің бүтін мәндерінің санын
жаз.
теңдеуінің
бір түбірі (1;2) аралығында,екінші түбірі одан сырт жататындай а
параметрінің барлық мәндерін тап.Жауабына осы шартты
қанағаттандыратын параметрдің бүтін мәндерінің санын
жаз.
Ж:

8. теңсіздігінен 0<x<1 теңсіздігі шығатын а параметрінің
барлық мәнін тап
теңсіздігінен 0<x<1 теңсіздігі шығатын а параметрінің
барлық мәнін тап 
9.a теңсіздігінен x>1 теңсіздігі шығатындай а параметрінің
барлық мәнін тап Ж:
теңсіздігінен x>1 теңсіздігі шығатындай а параметрінің
барлық мәнін тап Ж:
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Параметрлі теңдеулер мен теңсіздіктерді шешу
Параметрлі теңдеулер мен теңсіздіктерді шешу
К.К.Есмуханова –БҚО,Ақжайық ауданы,Тайпақ орта жалпы білім беретін мектебі,жоғарғы санатты математика пәні мұғалімі
«Параметрлі теңдеулер мен теңсіздіктерді шешу»
Бұл қолданбалы курстың бағдарламасы жаратылыстану-математика бағытында оқитын оқушыларға және мұғалімдерге арналған.
Бағдарламада математиканың маңызды тақырыптарының бірі параметрлі теңдеулер мен теңсіздіктерді шешу әдіс-тәсілдері қарастырылған.
Бағыты: Жаратылыстану-математика
Өзектілігі: «Параметрлі теңдеулер мен теңсіздіктерді шешу» қолданбалы бағдарлы оқыту курсының бағдарламасы оқушылардың теориялық білімін нығайтып, математикалық заңдылықтарды терең біліп, дәлелдей алуға ,өздігінен іздендіру арқылы шығармашылық дамуын шыңдау мақсатында құрылған.
Курс бағдарламасы бойынша оқушылар параметрі бар сызықтық теңдеулер мен теңсіздіктерді, бүтін теңдеулер мен теңсіздіктерді , квадрат теңдеулер мен теңсіздіктерді, бөлшек-рационал теңдеулер мен теңсіздіктерді, рационал теңдеулер мен теңсіздіктерді, иррационал теңдеулер мен теңсіздіктерді, жоғары дәрежелі теңдеулер мен теңсіздіктерді,трансценденттік теңдеулер,яғни ,параметрі бар тригонометриялық теңдеулер мен теңсіздіктерді, көрсеткіштік теңдеулер мен теңсіздіктерді, логарифмдік теңдеулер мен теңсіздіктерді шешу арқылы математикадан терең білім алуға мүмкіндігі мол.
Бағдарлама : 11- сынып оқушыларына және мұғалімдерге арналған.
Қажеттілігі: Математика пәні жалпы білім берудің негізгі компоненті болып табылады. Оның оқушыға қатысты басты мақсаты –оқушылардың математикалық сауаттылығын арттыру ,олардың білімдерінің тиянақты болуын қамтамасыз ету болып саналады. Математикалық білім- оқушының жоғары деңгейде дамуы мен шығармашылық іс-әрекет тәжірибесімен қаруланған , бүгінгі жағдайда бағдарлама алуға дайын тұлға ретінде қалыптасуы үшін қажет. Оқушының ойлау қабілетін дамытуға, олардың математиканы оқуға деген ынта –талабын арттыруға жәрдем етеді.
Түсінік хат
Математиканы оқыту процесінің мақсаты–жеке оқушының есеп шығару қабілетін дамыту және математикалық ойлау қабілетін дамыту үшін жаратылыстану –математикалық бағыттағы оқытуға сәйкес мектептегі білім сапасын арттыру болып табылады.
Қазіргі заман математика ғылымының өте кең тараған кезеңі . Ал талапқа сай математикалық білім берудің басты шарты математикалық мәдениеттің деңгейін көтеру болып табылады.
Математикалық есептерді шешу , теоремаларды дәлелдеу оқушылардың ойын оятып , ойлау, есте сақ-тау қабілеттерін дамытуда , батыл қимылдар жасауға , шығармашылық ізденіске тәрбиелейді.
Ендеше оқушылардың математикаға дайындығын жан-жақты жетілдіру қазіргі аса маңызды міндеттердің бірі.
11- сыныптағы жаратылыстану–математикалық бағыттағы математика курсында қосымша түрде қолданбалы курс қарастырылады.
Бейіндік оқытудың мақсаты – математика пәні мазмұны ғылыми жетістігіне сай болып, оны түсініп қолдануға және әрі қарай дамытуға жағдай жасай-тындай болуға және де жаңа ғылымдарды жай ғана меңгеру емес, жеке тұлғаның интеллектуалдық қорын ұлғайту. Математиканың ерекше орны басқа ғылымдарды меңгеруде негіз болатын ойлаудың сапалық та, сандық та дамытуына әсер етуінен көрінеді.
Есеп шығара білу – математикадан алған білім деңгейінің , оқу материалын қаншалықты терең меңгергенінің көрсеткіші.
Сондықтан кез келген емтихан мен білімді тексеру математика курсында теңдеулер мен теңсіздіктерді, олардың жүйелерін шешу, есептерді теңдеу құру арқылы шығару оқушы меңгеруге тиісті материалдың бірі болып табылады.
Бұл қолданбалы курста 11- сынып оқушыларына сабақта алған білімдеріне қосымша білім беруге, оқыған материалдарын тереңдетуге және мектеп курсында көп мағлұмат берілмейтін мынадай: «Параметрлі теңдеулер мен теңсіздіктер» тақырыптарын меңгеруге бағытталған.
Есептердің шығарылу жолдары алдымен әртүрлі тәсілдермен көрсетіліп, ал қалған есептерді оқушылардың өздерінің тиімді тәсілді таңдап алуына баса назар аударылады. Шешімдерді іздеудің математикалық методтарын, логикалық пайымдаулардың , математикалық модельдердің , адекваттылық мәселелерін оқушылар меңгеріп алуларына зор көңіл бөлінеді. Бұл курс орта мектептері түлектеріне теңдеу шешуге қажетті және жеткілікті білім жинақтауға мүмкіндік бере отырып, математика негізгі пән болып келетін ҰБТ есептерін шығаруға дайындық болып табылады.
Мақсаттары:
-
Жалпы теңдеулер мен теңсіздіктерді және оларды шешу әдістері туралы толық мағлұмат алу, алған білімдерін тереңдету;
-
Жалпы мәдениеттің ішінде ойлау мәдениетінің логикалық және әдістемелік тұрғыдан дамуы;
-
Жалпы логикалық ойлау мәдениетін дамыта отырып , оқушының
математикаға қызығушылығын арттыру;
-
Орта мектепті бітіруші түлектердің жоғары оқу орындарында білімдерін жалғастыру үшін математикалық білімдерін
жүйелеу,тереңдету, тұжырымдау және нақтылау;
-
Жоғары математика мен элементар математиканың арасындағы байланысты түсіне білу, арифметика, алгебра, математикалық анализдің, жалпы математиканың бірлігі туралы білу;
-
Оқушылардың математика және оның салалары бойынша мамандық таңдауға көмектесу
Оқушылардың дайындығына қойылатын талаптар:
-
Теңдеулер мен теңсіздіктерді шеше білу;
-
Алгебралық теңдеулер мен теңсіздіктер жүйелерінің шешімдерін анықтай білу;
-
Трансценденттік параметрлі теңдеулер мен теңсіздіктерді шеше білу;
-
Тереңірек білім беру;
-
Ойлау , есте сақтау қабілеттерін дамыту;
-
Игерген білімдерін болашақта қолдана білу, жетілдіру;
-
Әртүрлі ақпарат көздерімен жұмыс жасауға; қорытынды ой жасау және нәтижені сараптауды,пікірталасқа қатысу , өз қызметінің нәтижесін көре білу , параметрлері берілген теңдеулер мен теңсіздіктерді әртүрлі әдістермен шешу;
-
есеп шығарудың ұтымды жолын таңдау.
Курсты жүргізудегі негізгі принциптер:
-
Жүйелілік (негізгі жұмысты оқушы үйде өз бетімен орындауы керек);
-
Ілгерілемелі күрделілік (үйде орындауға аптасына 5-10 есептер беріледі, мұндағы, 3-5 есептер барлығы шығара алатындай, 1-3 есеп оқушылардың кейбірі шығара алатындай және 1-2 есеп ешкім шығара алмайтындай );
-
Вариативтік (бір теңдеудің немесе есептің бірнеше тәсілмен алынған шешімдерін салыстыру);
-
Басымдылықтың ауысымы (қиындау есептерді шешкенде ойлау идеясына басымдылық берілсе, оңай , стандартты есептердің тек дұрыс жауптарына басымдылық беріледі).
Күтілетін нәтиже:
-оқушылардың мектеп курсындағы сызықтық, квадрат және рационал теңдеулер мен теңсіздіктерді әртүрлі, тиімді тәсілдермен шеше алулары;
- параметрлі сызықтық, квадрат және рационал теңдеулер мен теңсіздіктерді шеше алулары;
- тригонометриялық теңдеулерді шеше алулары, бірлік шеңберді тригонометриялық теңсіздіктерді шешуде қолдана алулары;
- мәтінмен берілген есептерге теңдеу құрып, оны шеше алулары;
-оқушылардың математикалық білімінің жоғарылауы;
-қиындығы жоғары есептер шығару арқылы
шығармашылық жұмыстану деңгейінің жоғарылауы;
- білімдерін ұшқырлау арқылы ҰБТ –дан жоғарғы
нәтижеге жету.
Пәнаралық кіріктіру:
Алгебра, физика, сызу, информатика
Кәсіпке бағдарлау:
Математика, информатика, инженер, экономист, бухгалтер, менеджер т.б. мамандықтарын таңдайтын оқушылардың білімдерінің терең де мазмұнды болуына ықпалын тигізеді.
Оқу уақытының көлемі, сабақтың мерзімділігі:
Сағат саны-34, аптасына 1 рет.
Оқу материалының мазмұны мен құрылымы:
-
Алгебралық теңдеулер мен теңсіздіктер-25 сағат(теорияға-14 сағат, практикаға-11 сағат)
-
Параметрі бар сызықтық теңдеулер мен теңсіздіктерді шешу-1 сағат
-
Параметрі бар бүтін теңдеулер мен теңсіздіктерді шешу-1 сағат
-
Квадрат үшмүшені зерттеу. Параметрі бар квадрат теңдеулер мен теңсіздіктерді шешу-2 сағат
-
Параметрі бар бөлшек-рационал теңдеулер мен теңсіздіктерді шешу-2 сағат
-
Параметрі бар рационал теңдеулер мен теңсіздіктерді шешу-2 сағат
-
Параметрі бар иррационал теңдеулер мен теңсіздіктерді шешу-2 сағат
-
Параметрі бар жоғары дәрежелі теңдеулер мен теңсіздіктерді шешу-2 сағат
Трансценденттік теңдеулер-9 сағат(теорияға 3 сағат,практикаға-3 сағат,қорытындығы-3 сағат)
-
Параметрі бар тригонометриялық теңдеулер мен теңсіздіктерді шешу-2 сағат
-
Параметрі бар көрсеткіштік теңдеулер мен теңсіздіктерді шешу-2сағат
-
Параметрі бар логарифмдік теңдеулер мен теңсіздіктерді шешу-2 сағат
|
№ |
сабақ № |
Сабақтың тақырыбы |
сағат саны |
||
|
барлығы |
теориялық бөлім |
практикалық бөлім |
|||
|
Алгебралық теңдеулер мен теңсіздіктер -25 сағат |
|||||
|
1 |
1 |
Параметрі бар сызықтық теңдеулерді шешу |
1 |
1 |
|
|
2 |
2 |
Параметрі бар бүтін теңдеулерді шешу |
1 |
1 |
|
|
3 |
3,4 |
Квадрат үшмүшені зерттеу. Параметрі бар квадрат теңдеулерді шешу |
2 |
1 |
1 |
|
3 |
5,6 |
Параметрі бар бөлшек-рационал теңдеулерді шешу |
2 |
1 |
1 |
|
5 |
7,8 |
Параметрі бар рационал теңдеулерді шешу |
2 |
1 |
1 |
|
6 |
9,10,11 |
Параметрі бар иррационал теңдеулерді шешу |
3 |
1 |
2 |
|
7 |
12,13 |
Параметрі бар жоғары дәрежелі теңдеулерді шешу |
2 |
1 |
1 |
|
8 |
14 |
Параметрі бар сызықтық теңсіздіктерді шешу |
1 |
1 |
|
|
9 |
15 |
Параметрі бар бүтін теңсіздіктерді шешу |
1 |
1 |
|
|
10 |
16,17 |
Параметрі бар квадрат теңсіздіктерді шешу |
2 |
1 |
1 |
|
11 |
18,19 |
Параметрі бар бөлшек-рационал теңсіздіктерді шешу |
2 |
1 |
1 |
|
12 |
20,21 |
Параметрі бар рационал теңсіздіктерді шешу |
2 |
1 |
1 |
|
13 |
22,23 |
Параметрі бар иррационал теңсіздіктерді шешу |
2 |
1 |
1 |
|
14 |
24,25 |
Параметрі бар жоғары дәрежелі теңсіздіктерді шешу |
2 |
1 |
1 |
|
Трансценденттік теңдеулер мен теңсіздіктер -9 сағат |
|||||
|
15 |
26,27 |
Параметрі бар тригонометриялық теңдеулер мен теңсіздіктерді шешу |
2 |
1 |
1 |
|
16 |
28,29 |
Параметрі бар көрсеткіштік теңдеулер мен теңсіздіктерді шешу |
2 |
1 |
1 |
|
17 |
30,31 |
Параметрі бар логарифмдік теңдеулер мен теңсіздіктерді шешу |
2 |
1 |
1 |
|
18 |
32, 33,34 |
Қорытынды сабақ |
3 |
1 |
2 |
|
барлығы |
34 |
18 |
16 |
||
Курсты ұйымдастыру формасын анықтау:
-интерактивті әдіс;
-топтық жұмыстар;
-жеке жұмыстар;
-практикум;
Курсты оқытуды аяқтау формасы:
-қорытынды аттестаттау;
Оқушылардың оқу жетістіктерін бағалау жүйесі:
-сынақ
Параметрлі сызықтық бөлшек-рационал теңдеулер мен теңсіздіктерді шешу
1. жүйеде а-ның қандай мәндерінде
тек бір ғана шешім болады?
жүйеде а-ның қандай мәндерінде
тек бір ғана шешім болады?
 Жауабы:
Жауабы: 
2.  жүйеде а-ның қандай мәндерінде
тек бір ғана шешім болады?
жүйеде а-ның қандай мәндерінде
тек бір ғана шешім болады?
Шешуі: 

Жауабы: 
Өз беттерімен шығаруға:
 жүйеде а-ның қандай мәндерінде
тек бір ғана шешім болады?
жүйеде а-ның қандай мәндерінде
тек бір ғана шешім болады?
Шешуі: 

Жауабы: 
4.  теңдеулер жүйесінің m-нің қандай
мәнінде а)бір шешімі ә)екі шешімі болады?
теңдеулер жүйесінің m-нің қандай
мәнінде а)бір шешімі ә)екі шешімі болады?
5. а параметрінің әрбір мәні үшін теңдеуді
шеш: 
1)a=-2 болса,онда берілген теңдеу 0*x=0 түріне көшеді.Бұл теңдеуді x-тің кез келген нақты мәні қанағаттандырады
2) болса,онда
берілген теңдеу бір ғана x=a-2 түріндегі шешімі бар сызықтық
теңдеуді береді
болса,онда
берілген теңдеу бір ғана x=a-2 түріндегі шешімі бар сызықтық
теңдеуді береді
Жауабы: a=-2 болғанда теңдеудің түбірі кез келген сан
 болғанда теңдеудің түбірі
x=a-2
болғанда теңдеудің түбірі
x=a-2
6. Теңдеуді шеш: 
 жағдайларын қарастырамыз ,егер a=0
болса,теңдеу 0*x=-2 болады,яғни шешімі жоқ
жағдайларын қарастырамыз ,егер a=0
болса,теңдеу 0*x=-2 болады,яғни шешімі жоқ
2. a=2 болса, теңдеу 0*x=0 болады,шешімі кез келген сан
3. 
Жауабы: a=0 болса,шешімі жоқ, a=2 болса, шешімі кез
келген сан,
7. Анықталу облысы: (m-1)(x+3)
Анықталу облысы: (m-1)(x+3)
3mx-5+(3m-11)(x+3)=(2x+7)(m-1);(4m-9)x=31-2m;
Ж:1)x=-3 -0,4 болғанда теңдеудің
бір ғана шешімі бар. m=2,25 және m=-0,4 болғанда
шешуі жоқ,m-1
болғанда теңдеудің мағынасы
болмайды.
-0,4 болғанда теңдеудің
бір ғана шешімі бар. m=2,25 және m=-0,4 болғанда
шешуі жоқ,m-1
болғанда теңдеудің мағынасы
болмайды.
8.
теңдеудің мағынасы бойынша

a=b болғанда 0*x=0;x= x-тің кез келген нақты мәнін
қанағаттандырады.
x-тің кез келген нақты мәнін
қанағаттандырады.  болғанда x=
болғанда x= Енді
Енді  болатын а мен в –ның мәндерін
табамыз.
болатын а мен в –ның мәндерін
табамыз.
1)  яғни
a=
яғни
a=
2)  яғни
a=
яғни
a=
Жауабы:1)  a
a ,a
,a болғанда x=
болғанда x=
2) a=b болғанда  –тан басқа
x –кез
келген сан.
–тан басқа
x –кез
келген сан.
3)
a= болғанда шешуі
жоқ
болғанда шешуі
жоқ
Өз бетімен орындауға берілетін тапсырмалар:
1. в-ның қандай мәндерінде (2-b)(b+x)=15-7b теңдеуінің түбірі 3-тен артық немесе тең? Жауапта осы мәндердің ең үлкенін көрсет
2. а-ның қандай мәндерінде (x-1)( теңдеуінің түбірі 0-ден артық
немесе тең? Жауапта осы мәндердің ең үлкенін көрсет
теңдеуінің түбірі 0-ден артық
немесе тең? Жауапта осы мәндердің ең үлкенін көрсет
3. k коэффициентінің қандай мәндерінде  теңдеудің түбірі
болмайды?
теңдеудің түбірі
болмайды?
4. p коэффициентінің қандай мәндерінде  теңдеудің 2 түбірі
болады?
теңдеудің 2 түбірі
болады?
5.  теңдеуінің
түбірлерінің бірі 3-ке тең болатындай а-ның мәнін тап?
теңдеуінің
түбірлерінің бірі 3-ке тең болатындай а-ның мәнін тап?
6. k -ның қандай мәнінде  теңдеуінің
теңдеуінің  –ге тең түбірі болады?
–ге тең түбірі болады?
7.  k-ның қандай
мәндерінде теңдеуінің түбірлерінің кубтарының қосындысы 7-ге тең
болады?
k-ның қандай
мәндерінде теңдеуінің түбірлерінің кубтарының қосындысы 7-ге тең
болады?
8. k , k-ның
қандай мәндерінде теңдеуінің түбірлерінің кубтарының қосындысы
72-ге тең болады?
, k-ның
қандай мәндерінде теңдеуінің түбірлерінің кубтарының қосындысы
72-ге тең болады?
9. а параметрінің қандай мәнінде теңсіздігінің шешімдері болмайды?
1.ax>9x+6
2. ax<8x-7
10. а параметрінің қандай мәнінде теңсіздігінің шешімі кез келген нақты сан?
1.ax>4x-5
2.ax<3x+6
11. а параметрінің әрбір мәнінде теңсіздігін шешіңдер ?
1.ax+5a<4-6x
2.ax-6a<5x+3
7.  а-ның қандай мәндерінде теңсіздігі
кез келген х үшін орындалады?
а-ның қандай мәндерінде теңсіздігі
кез келген х үшін орындалады?
Берілген теңсіздіктің сол жағындағы өрнекті
түрлендірейік: емесе
емесе

Кез келген х үшін  себебі квадрат үшмүшеліктің
дискриминанты 0-ден кіші.
себебі квадрат үшмүшеліктің
дискриминанты 0-ден кіші.
 теңсіздігін шешейік. Квадрат
үшмүшеліктің таңбасы
теңсіздігін шешейік. Квадрат
үшмүшеліктің таңбасы  –тың коэффицентінің таңбасымен
бірдей болады,егер оның дискриминанты 0-ден кіші болса,яғни
–тың коэффицентінің таңбасымен
бірдей болады,егер оның дискриминанты 0-ден кіші болса,яғни
 Демек,-6<a<2
Демек,-6<a<2
8. Теңдеуді шеш: 
1. a
2.а
9.  жауабы: (a;3]
жауабы: (a;3]
Квадрат үшмүшеліктерді зерттеу. Параметрі бар квадрат теңдеулерді шешу
 вадрат үшмүшелігіне сәйкес
функцияның графигі парабола ,оның тармақтары а коэффициентінің
таңбасына байланысты.
вадрат үшмүшелігіне сәйкес
функцияның графигі парабола ,оның тармақтары а коэффициентінің
таңбасына байланысты.
а) a>0 болса,парабола тармағы жоғары, a<0 болса парабола тармағы төмен қарайды.
2. D = дискриминантына байланысты
параболаның абсцисса өсін қиятыны не қимайтыны белгілі
болады. f(x)=
дискриминантына байланысты
параболаның абсцисса өсін қиятыны не қимайтыны белгілі
болады. f(x)= -
-

3. y= үшмүшелігінің
түбірлері мен графигіне сәйкес келесі кестені қолданған
тиімді:
үшмүшелігінің
түбірлері мен графигіне сәйкес келесі кестені қолданған
тиімді:

 вадрат үшмүшелігінің түбірлері мен
коэффициенттерінің арасындағы тәуелділікті Виет теоремасы
/келтірілген квадрат үшмүше үшін / кез келген үшмүше үшін
береді:
вадрат үшмүшелігінің түбірлері мен
коэффициенттерінің арасындағы тәуелділікті Виет теоремасы
/келтірілген квадрат үшмүше үшін / кез келген үшмүше үшін
береді:

Салдар1:  квадрат үшмүшеліктің әртүрлі екі
нақты түбірлері бар болып және олардың таңбалары бірдей болуы
үшін
квадрат үшмүшеліктің әртүрлі екі
нақты түбірлері бар болып және олардың таңбалары бірдей болуы
үшін  және
және яғни
яғни
 шарттарының орындалуы қажет
және жеткілікті
шарттарының орындалуы қажет
және жеткілікті
Салдар 2:  болуы үшін ,
болуы үшін ,


 шарттарының орындалуы қажет және жеткілікті .
шарттарының орындалуы қажет және жеткілікті .
Ал әртүрлі теріс екі түбірі бар болуы үшін
 шарттарының орындалуы қажет және
жеткілікті.
шарттарының орындалуы қажет және
жеткілікті.
Салдар 3: квадрат теңдеуінің әртүрлі нақты
екі түбірі бар болып және олардың таңбалары әртүрлі болуы
үшін
квадрат теңдеуінің әртүрлі нақты
екі түбірі бар болып және олардың таңбалары әртүрлі болуы
үшін  ,
,
яғни  теңсіздіктержүйесі орындалуы қажет және жеткілікті ,
теңсіздіктержүйесі орындалуы қажет және жеткілікті ,
 болса,
болса,
 болса, теріс түбірдің модулі үлкен
болады.
болса, теріс түбірдің модулі үлкен
болады.
Сабақта берілетін денгейлік тапсырмалар:
1.m параметрінің қандай мәнінде  теңдеуінің түбірлерінің
таңбалары әртүрлі болады? Қандай таңбадағы түбірдің абсолют шамасы
ең үлкен?
теңдеуінің түбірлерінің
таңбалары әртүрлі болады? Қандай таңбадағы түбірдің абсолют шамасы
ең үлкен?
Шешуі:  үшмүшелігі үшін 3-салдарды
пайдалансақ, түбірлердің таңбалары әртүрлі болу үшін
үшмүшелігі үшін 3-салдарды
пайдалансақ, түбірлердің таңбалары әртүрлі болу үшін
 шарттары бойынша
шарттары бойынша
 болады.
болады.
Ал a*b<0 ,яғни -5<0 болғандықтан оң таңбадағы түбірдің модулі үлкен.
Жауабы: m<0,оң түбірдікі
 теңдеуінің әртүрлі нақты екі оң
түбірі бар болатындай а параметрінің мәнін тап
теңдеуінің әртүрлі нақты екі оң
түбірі бар болатындай а параметрінің мәнін тап
 2-салдар бойынша (екі оң түбірі бар
болуы үшін)
2-салдар бойынша (екі оң түбірі бар
болуы үшін)  шарттарынан
шарттарынан 


Ескерту: бұл есепті графиктік-аналитикалық тәсілмен шығаруға болады /оқушыларға жеке жұмыстануға/
3.Қандай b үшін  теңдеуінің а) теріс екі түбірі
болады? б)оң екі түбірі болады? в) әртүрлі таңбадағы екі түбірі бар
болады?
теңдеуінің а) теріс екі түбірі
болады? б)оң екі түбірі болады? в) әртүрлі таңбадағы екі түбірі бар
болады?
Шешуі: 1-3 салдарларды пайдалансақ:
а) 
б) 
 болса,
болса,
b)
Жауабы: 
Ескерту: бұл есепті графиктік-аналитикалық тәсілмен шығаруға болады /оқушыларға жеке жұмыстануға/
4.f(x)=(2a-3) үшмүшелігінің түбірлері теріс
болатындай барлық а мәндерін табыңдар.
үшмүшелігінің түбірлері теріс
болатындай барлық а мәндерін табыңдар.
Шешуі: 1) 2a-3=0
2) a 2-салдарды
пайдаланып,теңсіздіктер жүйесін құрамыз.
2-салдарды
пайдаланып,теңсіздіктер жүйесін құрамыз. 
Жауабы:a
5.y=a үшмүшелігінің графигі ОХ өсімен
ортақ екі оң нүктесі бар болатындай а параметрінің мәндерінің
жиынын тап
үшмүшелігінің графигі ОХ өсімен
ортақ екі оң нүктесі бар болатындай а параметрінің мәндерінің
жиынын тап
Шешуі: 1)егер a=0 болса,сызықтық теңдеу шығады,ОХ өсі бір ғана нүктеде қиылады, есеп шарты орындалмайды.
2)үшмүшеліктің  алдындағы коэффициенттер оң немесе
теріс болуы мүмкін.
алдындағы коэффициенттер оң немесе
теріс болуы мүмкін.
а) a>0 болсын. Тармағы жоғары қарайды, ( төбесі ІУ ширекте ,яғни
төбесі ІУ ширекте ,яғни
 ал f(0)>0 болуы
керек.
ал f(0)>0 болуы
керек.
Жүйе құрсақ:
б) a<0 болсын. Тармағы төмен қарайды, ( өбесі І ширекте ,яғни
өбесі І ширекте ,яғни
 ал f(0) <0 болуы
керек.
ал f(0) <0 болуы
керек. Шешімі:
Шешімі:
 Жауабы: a
Жауабы: a
6.  теңдеуінің бір түбірі -3 тен
кіші,екіншісі 2-ден артық болатындай р параметрінің бүтін
мәндерінің қосындысын тап
теңдеуінің бір түбірі -3 тен
кіші,екіншісі 2-ден артық болатындай р параметрінің бүтін
мәндерінің қосындысын тап
Шешуі:  үшмүшелігінің графигі тармақтары
жоғары қараған парабола ,
үшмүшелігінің графигі тармақтары
жоғары қараған парабола , оның түбірлері болсын,және
оның түбірлері болсын,және
 болғандықтан
[
болғандықтан
[ кесіндісі
[
кесіндісі
[ кесіндісін
қамтиды. Сондықтан тармағы жоғары параболаның
кесіндісін
қамтиды. Сондықтан тармағы жоғары параболаның
f(-3) . Сәйкес
жүйе құрайық:
. Сәйкес
жүйе құрайық:


Жауабы:-3
7. теңдеуінің түбірлерінің
таңбалары әртүрлі ,және оң түбірі теріс түбірдің модулінен үлкен
болатындай a
мәнін тап.
теңдеуінің түбірлерінің
таңбалары әртүрлі ,және оң түбірі теріс түбірдің модулінен үлкен
болатындай a
мәнін тап.
Шешуі: 3-салдар көмегімен шығарамыз:  Жауабы: a
Жауабы: a
І І-тәсіл:
І-тәсіл:  үшмүшелігінің графигі тармағы жоғары қараған парабола,
төбесі
үшмүшелігінің графигі тармағы жоғары қараған парабола,
төбесі  және
және
 болады. Жүйе
құрсақ:
болады. Жүйе
құрсақ:
 Жауабы: a
Жауабы: a
 -ден үлкен
-ден үлкен
болатындай а мәнін тап.
Шешуі: графиктік –аналитикалық тәсілмен шығарсақ:
1) болса, квадрат
теңдеу сызықтық теңдеуге айналады,ендеше
болса, квадрат
теңдеу сызықтық теңдеуге айналады,ендеше 
2) 2-a>0 болсын,тармағы жоғары қараған парабола
 теңсіздіктер жүйесі есептің
барлық шарттарын қанағаттандырады.
теңсіздіктер жүйесі есептің
барлық шарттарын қанағаттандырады.  Шешімі:
Шешімі:
3) 2-a<0 парабола тармақтары төмен қарайды
 шешімі:
шешімі: Жауабы:
Жауабы: 
9. 8 саны  теңдеуінің екі түбірінің
арасында болатындай а параметрінің мәнін тап.
теңдеуінің екі түбірінің
арасында болатындай а параметрінің мәнін тап.
Шешуі: 1) a=0 болса,сызықтық теңдеу шығады,оның түбірі
біреу ғана,есеп шартын қанағаттандырмайды. Ендеше ,
a
2) a>0 болсын, онда f(8) <0
болса,жеткілікті. f(8)
=64a-24a-24-2<0 ,20a<13, 0<a<
Шешімі: 0<a<
3) a<0 болcын .f(8)>0  . Жауабы: 0<a<
. Жауабы: 0<a<
11. теңдеуінің дәл бір түбірі
теңсіздігін қанағаттандыратын параметрінің барлық мәнін
тап.
теңдеуінің дәл бір түбірі
теңсіздігін қанағаттандыратын параметрінің барлық мәнін
тап.
Шешуі: берілген  үшмүшелігінің екі түбірінің дәл
бірі x<-1 теңсіздігін қанағаттандыру үшін D
үшмүшелігінің екі түбірінің дәл
бірі x<-1 теңсіздігін қанағаттандыру үшін D орындалуы қажет,яғни
D
орындалуы қажет,яғни
D
а)r=0 болса,онда  Ол x<-1 шартын
қанағаттандырмайды.
Ол x<-1 шартын
қанағаттандырмайды.
Б) r=5 болса,
 шартын қанағаттандырады.
шартын қанағаттандырады.
В)  болса, D>0. Бұл жағдайда дәл бір түбірі x<-1 орындалуы үшін
f(-1)<0,яғни
болса, D>0. Бұл жағдайда дәл бір түбірі x<-1 орындалуы үшін
f(-1)<0,яғни
1-2r+2+3r+1=r+4<0 болуы қажет немесе үлкен
түбірі
болуы қажет немесе үлкен
түбірі  болуы мүмкін
,яғни
болуы мүмкін
,яғни
1-2r+2+3r+1=r+4=0 болуы мүмкін .Берілген теңдеуге
r=-4 қоямыз:
болуы мүмкін .Берілген теңдеуге
r=-4 қоямыз:  Бірақ,
Бірақ, және бұл x<-1 шартын
қанағаттандырмайды. Жауабы: r<-4;r=5
және бұл x<-1 шартын
қанағаттандырмайды. Жауабы: r<-4;r=5
Параметрі бар екінші дәрежелі теңдеулерді шешу
Сабақта берілетін теориялық білім:
Егер  болса,
0*
болса,
0* теңдігі кез
келген х үшін орындалады.
теңдігі кез
келген х үшін орындалады.
Шешімі 
 болса, 0*
болса, 0* теңдігі ақиқат емес. Шешімі
жоқ
теңдігі ақиқат емес. Шешімі
жоқ
 болса, квадрат теңдеу сызықтық
теңдеуге айналады, bx+c=0
болса, квадрат теңдеу сызықтық
теңдеуге айналады, bx+c=0  түбірі біреу:
түбірі біреу:
егер  болса,
a*
болса,
a* ,екі түбірі
бар.
,екі түбірі
бар.
егер  болса,
болса, екі түбірі бар,біреуі 0-ге
тең
екі түбірі бар,біреуі 0-ге
тең
егер  болса
,
болса
, формуласымен
табылады,мұндағы D- дискриминант
формуласымен
табылады,мұндағы D- дискриминант
Сабақты бекітуге берілетін денгейлік тапсырмалар:
1.қандай а мәнінде  теңдеуінің түбірлері шексіз көп
болады?
теңдеуінің түбірлері шексіз көп
болады?
Шешуі: Теңдеу
0* түріне келсе кез
келген х үшін теңдік орындалады.
түріне келсе кез
келген х үшін теңдік орындалады.
Мұнда ,а =1 болса,x
Жауабы:a=1
2. теңдеуінің а параметрінің қандай
мәндерінде түбірлері екіден көп болады?
теңдеуінің а параметрінің қандай
мәндерінде түбірлері екіден көп болады?
Шешуі: Егер теңдеу
 түріне келсе,теңдеудің шексіз
көп шешімі болады, ендеше оның түбірлерінің саны 2-ден көп.
Коэффициенттерін көбейткіштерге жіктейік.
түріне келсе,теңдеудің шексіз
көп шешімі болады, ендеше оның түбірлерінің саны 2-ден көп.
Коэффициенттерін көбейткіштерге жіктейік.


10-3a-
Берілген теңдеу келесі түрге келеді: 
Егер a=2 болса,теңдеу 0* түріне келеді. Жауабы:
a=2
түріне келеді. Жауабы:
a=2
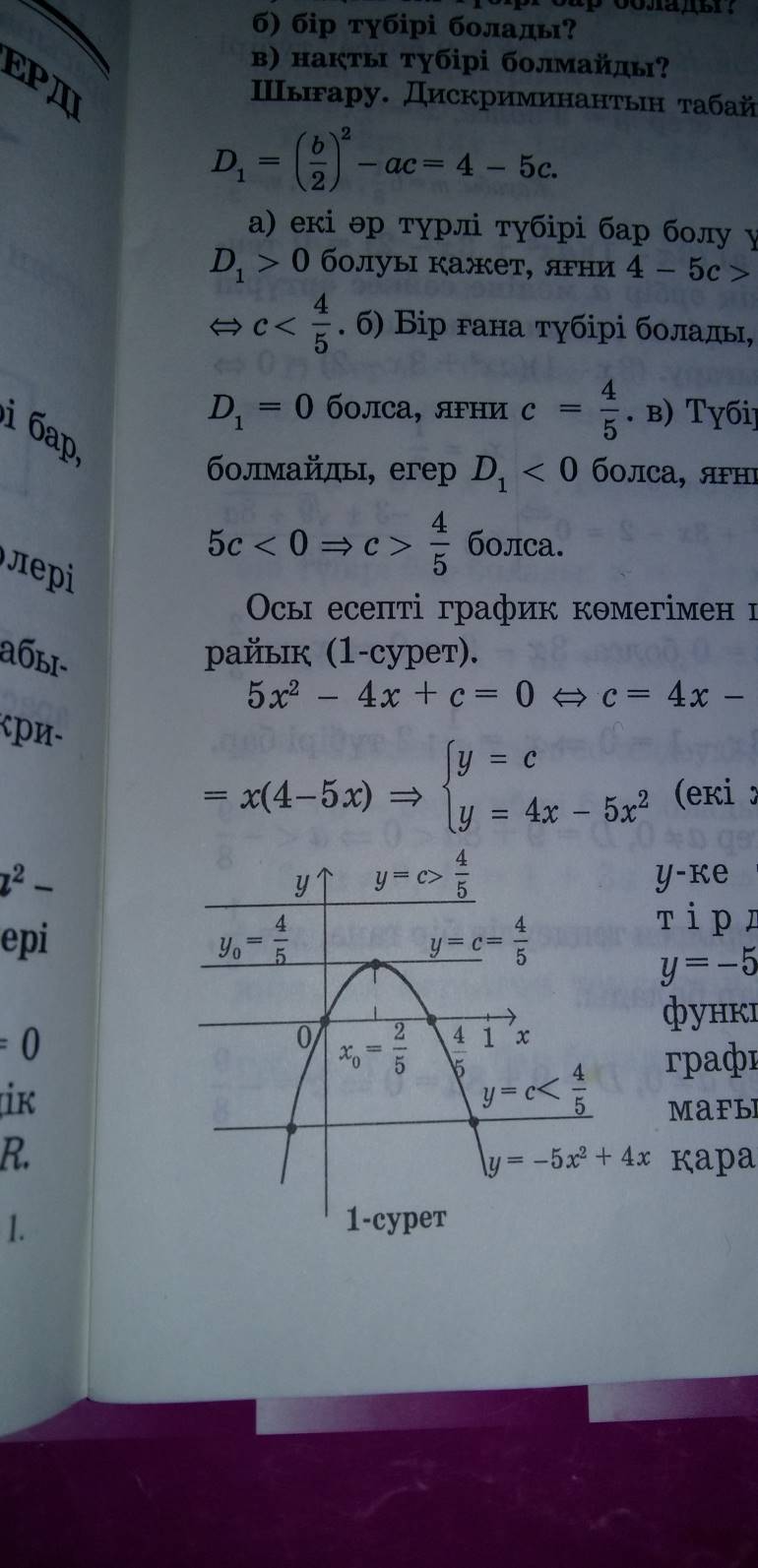 с параметрінің қандай мәнінде
с параметрінің қандай мәнінде  теңдеуінің
теңдеуінің
а)нақты екі түбірі бар болады?
б)бір түбірі болады?
в)нақты түбірі болмайды?
Шешуі:Дискриминантын
табайық:D=
а)екі әр түрлі түбірі бар болу үшін  болуы қажет,яғни
4-5c
болуы қажет,яғни
4-5c
б)бір ғана түбірі болады,егер  болса,яғни c=
болса,яғни c=
в) түбірлері болмайды,егер  болса,яғни 4-5c<0
болса,яғни 4-5c<0 болса.
болса.
Осы есепті графиктік тәсілмен шығарайық:
 4x-5
4x-5
 функциясының графигі тармағы төмен
қараған парабола, төбесінің координаттары:
функциясының графигі тармағы төмен
қараған парабола, төбесінің координаттары: 
 қиылыспайды,егер
c>
қиылыспайды,егер
c> болса.
болса.
б) түзу мен парабола 1 нүктеде қиылысады,егер
c= болса
болса
в)түзу және парабола 2 нүктеде қиылысады,егер с болса.
болса.
Жауабы: 1)c болса,шешімі жоқ
2)c=
болса,шешімі жоқ
2)c= болса,1 шешім
3)
болса,1 шешім
3)  болса,2
шешім
болса,2
шешім
3.Қандай а мәнінде  теңдеуінің түбірі біреу ғана
болады?
теңдеуінің түбірі біреу ғана
болады?
Шешеуі: 1)a=0 болса,берілген квадрат теңдеу сызықтық
теңдеуге айналады: -x-1=0
2)D=0 болса,1 шешім болады:D=
4.  теңдеуінің түбірі біреу ғана
болатындай а параметрінің барлық мәнін
табыңыз.
теңдеуінің түбірі біреу ғана
болатындай а параметрінің барлық мәнін
табыңыз.
Шешуі: 1)  болса,берілген теңдеу сызықтық
теңдеуге айналады:-1,5x+0,5
=0,x=
болса,берілген теңдеу сызықтық
теңдеуге айналады:-1,5x+0,5
=0,x= жалғыз шешімі болады
жалғыз шешімі болады
2) болсын,берілген квадрат теңдеудің жалғыз түбірі болады,егер
оның дискриминанты 0-ге тең болса: D=9
болсын,берілген квадрат теңдеудің жалғыз түбірі болады,егер
оның дискриминанты 0-ге тең болса: D=9 егер,
егер,  немесе
немесе  Есеп шартын а параметрінің үш мәні
қанағаттандырады.
Есеп шартын а параметрінің үш мәні
қанағаттандырады.
Жауабы:-5;-1;-0,5
9. ,егер
,егер  болса,а-ны
табыңдар
болса,а-ны
табыңдар
Виет теоремасы бойынша  ,
,
5 =
=

а-ның қандай мәндерінде теңдеудің нақты түбірлері болмайды?
1) 
7. Теңдеуді шеш:  +2(2a+1)x+(4a+3)=0
+2(2a+1)x+(4a+3)=0
1.егер a=1 онда теңдеу 6x+7=0 болады, x=-
2. 
a

Жауабы: a=1
болса, x=- ,
,  ,
,  б
б
Параметрі бар екінші дәрежелі теңсіздіктерді шешу
Әрбір нақты а мәні үшін келесі теңсіздіктерді шешеміз:
1.
2.
3.
4.
5.
6.Қандай нақты m мәндері үшін  үшін орындалады?
үшін орындалады?
1. y=


2) егер
a=
3)егер
a> D<0 ,
D<0 , себебі парабола ОХ өсін қимайды,әр
уақытта функция оң.
себебі парабола ОХ өсін қимайды,әр
уақытта функция оң.
Жауабы:
2.y= үшмүшелігінің графигі тармағы
.Төбесінің координаттары
үшмүшелігінің графигі тармағы
.Төбесінің координаттары 
 болса,ОХ
өсімен
болса,ОХ
өсімен  екі нүктеде
қияды.
екі нүктеде
қияды.  >0
теңсіздігінің шешімі:
>0
теңсіздігінің шешімі: 
Егер  болса,
болса, шешімі
шешімі  .Егер
.Егер  болса,парабола ОХ өсін
қимайды,
болса,парабола ОХ өсін
қимайды,  >0
теңсіздігі
>0
теңсіздігі  яғни кез
келген х үшін орындалады. Жауабы: егер |a|
яғни кез
келген х үшін орындалады. Жауабы: егер |a| ,егер a|<2 болса,x-кез келген
сан.
,егер a|<2 болса,x-кез келген
сан.
1) егер a=0 болса, x+1>0
2) егер  болса,тармағы төмен қараған
парабола ОХ өсін
болса,тармағы төмен қараған
парабола ОХ өсін  екі нүктеде қияды, мұнда
екі нүктеде қияды, мұнда
 ; шешімі:
; шешімі: 
 егер
егер  болса, яғни
болса, яғни  болса,яғни
0<a<
болса,яғни
0<a< болса,
болса,
 егер
егер  болса,
болса, болғанда ,парабола ОХ өсін
қимайды,ендеше
болғанда ,парабола ОХ өсін
қимайды,ендеше 

 болса,
болса,

 болса,
болса, x<-2,x>-2
x<-2,x>-2
 ал егер
ал егер  болса,
болса, шешімі жоқ
шешімі жоқ
Жауабы: 1) болса,
болса, 2)
2) болса, x<-2,x>-2
болса, x<-2,x>-2
 0<a<
0<a< болса,
болса,
 a=0 болса,x>-1
a=0 болса,x>-1

 a<0 болса,
a<0 болса,
4.
a=0 болса, x+1>0  .Егер
.Егер  болса,D=
болса,D= кез келген
кез келген  үшін түбірлері
үшін түбірлері 
1.a<0 болса,  және
және түбірлерінің өзара орналасуының екі
жағдайы болуы мүмкін:
түбірлерінің өзара орналасуының екі
жағдайы болуы мүмкін:  <
< немесе
немесе  яғни
яғни  немесе -1-(-
немесе -1-(- Сандар өсіне осы екі жағдайды
салып,тексеріп көрсек:
Сандар өсіне осы екі жағдайды
салып,тексеріп көрсек:
1.егер 
2.егер -1-(- Шешімі:
-1<x<-
Шешімі:
-1<x<-
1.D= болса,яғни
болса,яғни  болса,теңсіздіктің шешімі кез
келген
болса,теңсіздіктің шешімі кез
келген  себебі
:
себебі
:

2.егер D= болса,
болса,  , 0<a<1 және a>1 болуы
мүмкін.
, 0<a<1 және a>1 болуы
мүмкін.
А) 0<a<1
,яғни  болғанда ,онда x>-1,x<-
болғанда ,онда x>-1,x<-
б) егер a>1
болса,x>- онда
-
онда
- .
.
Егер ,-1-(-
Жауабы: 1)  болса, -1<x<-
болса, -1<x<-
2) a=0 болса,
3) болса,
болса, , x<-
, x<-
4) болса,х- кез келген,бірақ
болса,х- кез келген,бірақ

5) a>1 болса, x>-
5. теңсіздігі кез келген х мәнінде
орындалуы үшін
теңсіздігі кез келген х мәнінде
орындалуы үшін  шарты орындалуы қажет.
шарты орындалуы қажет.


Егер  болса,сызықтық теңсіздікке
айналады,мұнда a=1 болса, 1>0 ақиқат, теңсіздік кез келген х
үшін орындалады, a=-1 болса,-2x+1>0
болса,сызықтық теңсіздікке
айналады,мұнда a=1 болса, 1>0 ақиқат, теңсіздік кез келген х
үшін орындалады, a=-1 болса,-2x+1>0 есеп шарты орындалмайды.
есеп шарты орындалмайды.
 және
және  болса, теңсіздік кез келген х үшін
орындалмайды. Жауабы:
болса, теңсіздік кез келген х үшін
орындалмайды. Жауабы:
6.
f(x)= үшмүшелігі 1<x<2 аралығында
теріс болуы қажет және жеткілікті.Ол үшін (1:2) аралығы түгілімен
үшмүшеліктің түбірлерінің арасында орналауы қажет.
Сондықтан
үшмүшелігі 1<x<2 аралығында
теріс болуы қажет және жеткілікті.Ол үшін (1:2) аралығы түгілімен
үшмүшеліктің түбірлерінің арасында орналауы қажет.
Сондықтан
 Жауабы:
Жауабы: 
Берілетін тапсырмалар:
1. теңсіздігі кез келген үшін
орындалатындай барлық мәндерін тап.
теңсіздігі кез келген үшін
орындалатындай барлық мәндерін тап.
Ж: m>1
1.а параметрінің қандай мәнінде  теңсіздігі
теңсіздігі
а) барлық x<1үшін орындалады?
Б) x<1
ең болмағанда бір мәнінде орындалады? Ж: 1)
ондай а мәні табылмайды 2)a>
1.Қандай а мәндерінде  теңсіздігін қанағаттандыратын х-тің
кез келген мәнінің модулі 2-ден артық емес? Ж: -2
теңсіздігін қанағаттандыратын х-тің
кез келген мәнінің модулі 2-ден артық емес? Ж: -2
1.a теңсіздігінен 0<x<1
теңсіздігі шығатындай барлық а мәндерін тап.
теңсіздігінен 0<x<1
теңсіздігі шығатындай барлық а мәндерін тап.
Ж: 
1.қандай нақты m мәндерінде  теңсіздігі барлық x>1 үшін
орындалады?
теңсіздігі барлық x>1 үшін
орындалады?
Ж: m
Параметрі бар сықықтық , квадрат теңдеулер мен теңсіздіктерді шешуге практикалық сабақ
1.Қандай бүтін а мәндері үшін (a-5)x+a=3 теңдеуінің түбірі [0;5] кесіндісінде жатады? Ж:а=3;a=4
2.Теңдеуін шеш:  Ж: егер
Ж: егер  болса,x=
болса,x=
егер m=1 болса,x- кез келген , егер m=0 болса, шешімі жоқ
3.(a-3)x>5 теңсіздігінің шешімдері ax>2
теңсіздігінің де шешімдері болатындай а параметрінің барлық
мәндерін тап. Ж: 
4.Теңдеулерді шеш: 1.  2.
2. 3.
3.
5. 
Ж: 1.a болса, онда x=a,егер a=1
болса,онда x
болса, онда x=a,егер a=1
болса,онда x
2.егер a=-3,a=
3.  болса,онда
x=
болса,онда
x= егер a=2 немесе a=3 болса,онда x
егер a=2 немесе a=3 болса,онда x егер a=-2 болса,онда
егер a=-2 болса,онда 
4. болса,онда x=
болса,онда x= егер
егер  онда x
онда x
1. теңсіздігі
теңсіздігі  орындалатындай а параметрінің
барлық мәндерін тап
орындалатындай а параметрінің
барлық мәндерін тап
Ж: 
2. kвадрат
теңдеуінің қандай m мәндері үшін шешімдері бар болады?Түбірлерінің
таңбасын анықта ? Ж: m<-5 болса,екі
оң түбірі бар; -5<m<1 болса, түбірлерінің таңбалары әртүрлі;
m=-5 болса, түбірдің бірі 0-ге тең; m>1 болса нақты түбірлері
жоқ.
kвадрат
теңдеуінің қандай m мәндері үшін шешімдері бар болады?Түбірлерінің
таңбасын анықта ? Ж: m<-5 болса,екі
оң түбірі бар; -5<m<1 болса, түбірлерінің таңбалары әртүрлі;
m=-5 болса, түбірдің бірі 0-ге тең; m>1 болса нақты түбірлері
жоқ.
3.  теңсіздігінен (
теңсіздігінен ( теңсіздігі шығатындай а
параметрінің барлық мәндерін тап? Ж:
теңсіздігі шығатындай а
параметрінің барлық мәндерін тап? Ж: 
4.Қандай нақты m мәндерінде  теңсіздігінен x>1 теңсіздігі
шығады?Ж:ондай сан
табылмайды.
теңсіздігінен x>1 теңсіздігі
шығады?Ж:ондай сан
табылмайды.
5. теңдеуінің
қандай m үшін нақты түбірлері бар болады? Түбірлерінің таңбасын
зертте? Ж: 1) m
теңдеуінің
қандай m үшін нақты түбірлері бар болады? Түбірлерінің таңбасын
зертте? Ж: 1) m болса,нақты түбірлері бар.
2)
болса,нақты түбірлері бар.
2) болса,екі
түбірі теріс 3)
болса,екі
түбірі теріс 3) болса,түбірлерінің таңбалары
әртүрлі 4)
болса,түбірлерінің таңбалары
әртүрлі 4) болса,екі түбірі де оң 5)m=-5
болса,бір түбірі 0-ге тең.
болса,екі түбірі де оң 5)m=-5
болса,бір түбірі 0-ге тең.
6.(a-1) теңдеуінің қандай а үшін нақты
түбірлері бар болады? Түбірлерінің таңбасын зертте.
Ж: 1) 1
теңдеуінің қандай а үшін нақты
түбірлері бар болады? Түбірлерінің таңбасын зертте.
Ж: 1) 1 болса,нақты түбірлері бар.
2)
болса,нақты түбірлері бар.
2) болса,екі
түбірі теріс 3)
болса,екі
түбірі теріс 3) болса,түбірі де оң
4)
болса,түбірі де оң
4) болса,
түбірлерінің таңбалары әртүрлі 5) a=2 болса, x=
болса,
түбірлерінің таңбалары әртүрлі 5) a=2 болса, x= 6) a=
6) a= болса,бір түбірі 0-ге
тең
болса,бір түбірі 0-ге
тең
7. теңдеуінің
бір түбірі (1;2) аралығында,екінші түбірі одан сырт жататындай а
параметрінің барлық мәндерін тап.Жауабына осы шартты
қанағаттандыратын параметрдің бүтін мәндерінің санын
жаз.
теңдеуінің
бір түбірі (1;2) аралығында,екінші түбірі одан сырт жататындай а
параметрінің барлық мәндерін тап.Жауабына осы шартты
қанағаттандыратын параметрдің бүтін мәндерінің санын
жаз.
Ж:

8. теңсіздігінен 0<x<1 теңсіздігі шығатын а параметрінің
барлық мәнін тап
теңсіздігінен 0<x<1 теңсіздігі шығатын а параметрінің
барлық мәнін тап 
9.a теңсіздігінен x>1 теңсіздігі шығатындай а параметрінің
барлық мәнін тап Ж:
теңсіздігінен x>1 теңсіздігі шығатындай а параметрінің
барлық мәнін тап Ж:

шағым қалдыра аласыз















