
Параметрлі теңдеулер.
Математика пәнінің мұғалімі, педагог-зерттеуші Спабекова Бибигуль Ахметжановна.
Жоғары сыныптарда кездесетін параметрлі теңдеулерді шешу әдістемесін жас мамандарға немесе математикаға қызығушылығы жоғары оқушыларға пайдалы болар деген оймен ұсынып отырмын. Біліктілікті арттыру курсында жеке орындаған жұмысым болатын.
Параметрлі теңдеулерді шешуде оқушыларға Геогебра бағдарламасын қолданып түсіндіру тиімді болады.
Мысалы:
-
Теңдеуді шешіңіз: а)
 -a=0
-a=0
Шешуі:
-
y=
 2)
y=a
2)
y=a
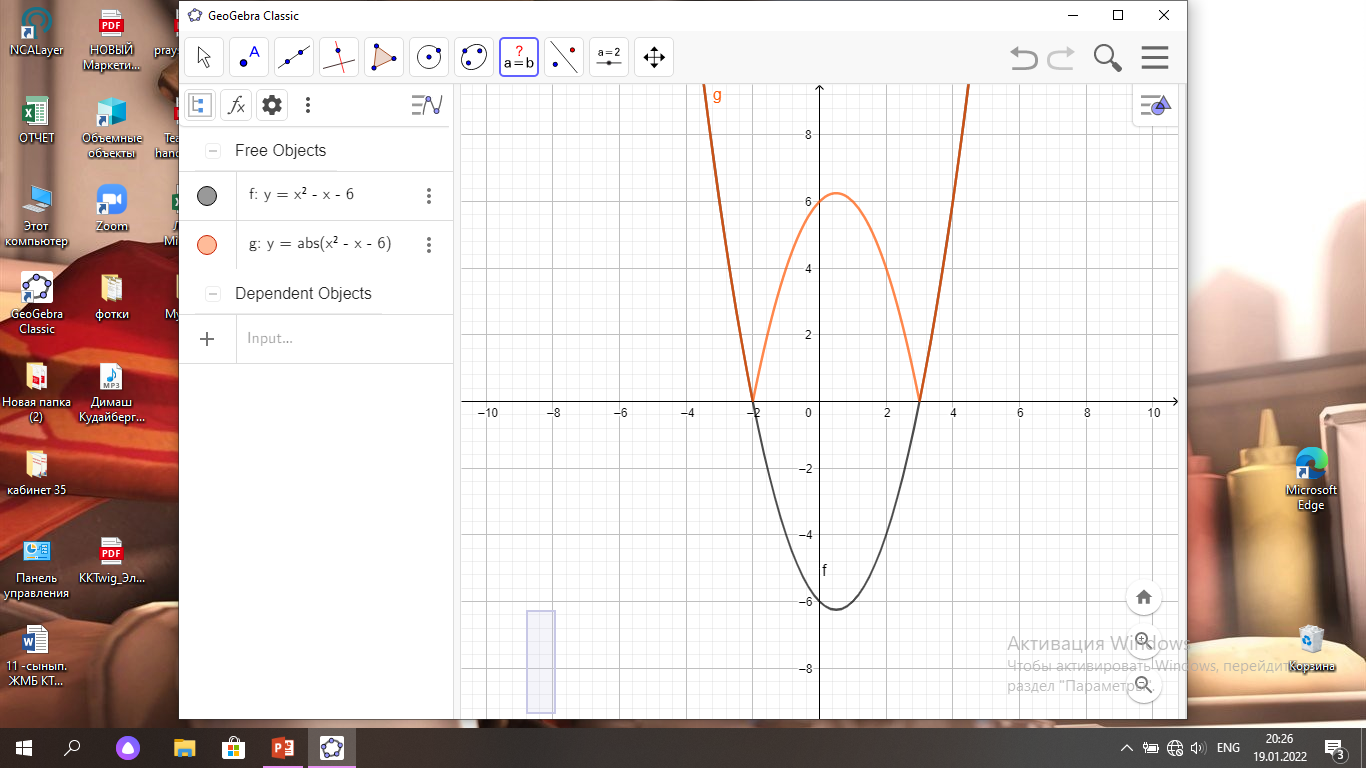
y= x2 –x-6 графигін салу керек:
параболаның төбесінің координаталарын табамыз: О(0,5; -6,25)
Ох осімен қиылысу нүктелері: (-2; 0), (3; 0)
y=
 функциясының
графигін саламыз;
функциясының
графигін саламыз;
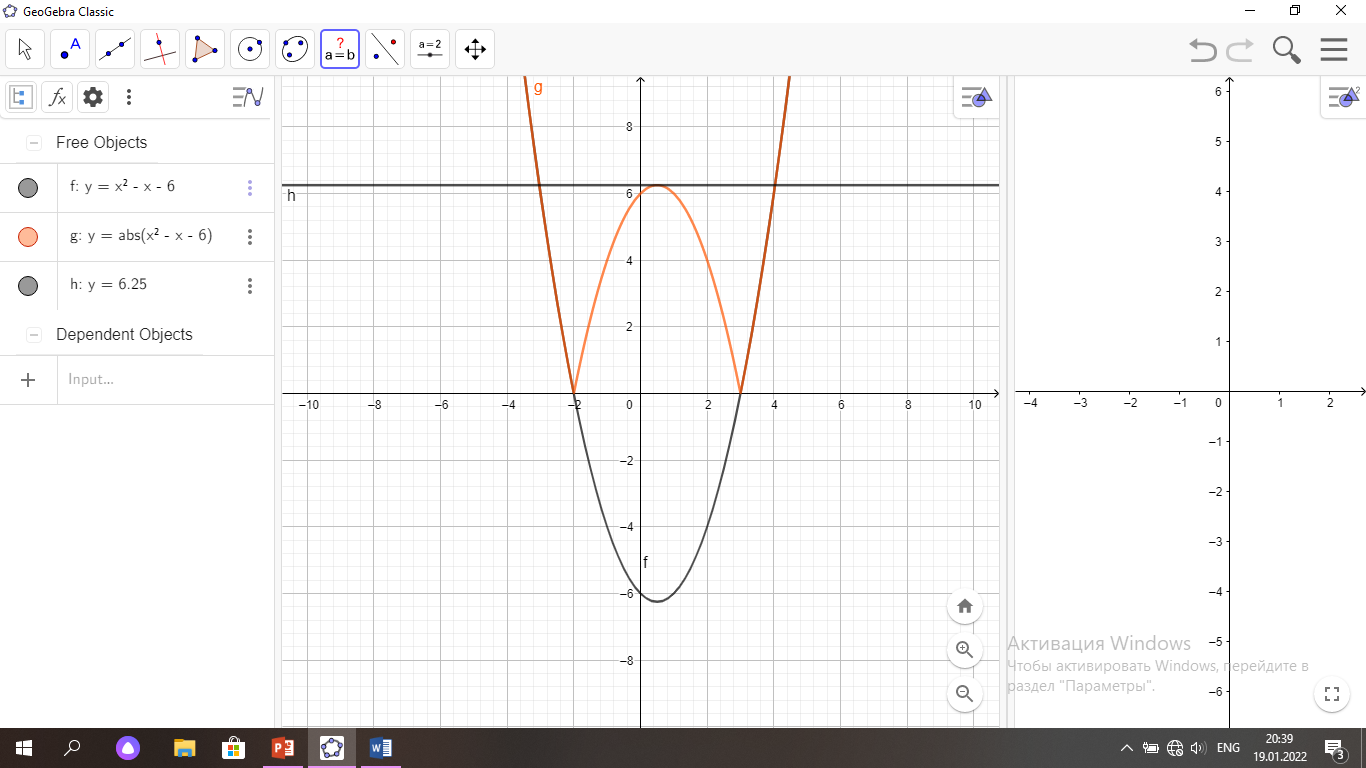
Үш түрлі түбірі болу үшін екі функцияның графигі үш нүктеде қиылысуы керек. Яғни, Ох осіне параллель у= 6, 25 түзу сызығын жүргізу керек.
Жауабы: а= 6,25 болғанда үш түбірі болады.
![]()
![]()
![]()
b)
 -a=0
-a=0
Шешуі:
-
y=
 2)
y=a
2)
y=a
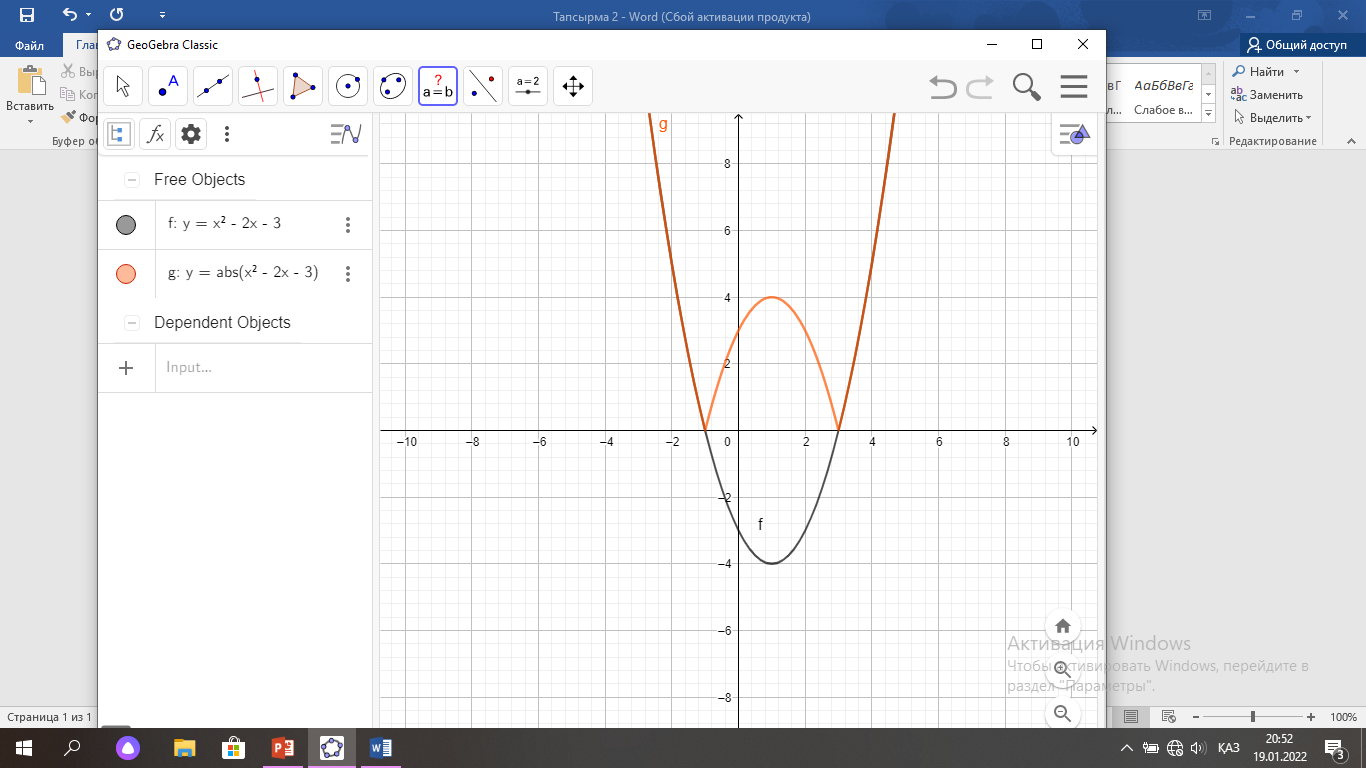
y= x2 –2x-3 графигін салу керек:
параболаның төбесінің координаталарын табамыз: О(1; -4)
Ох өсімен қиылысу нүктелері: (-1; 0), (3; 0)
y=  функциясының графигін
саламыз;
функциясының графигін
саламыз;
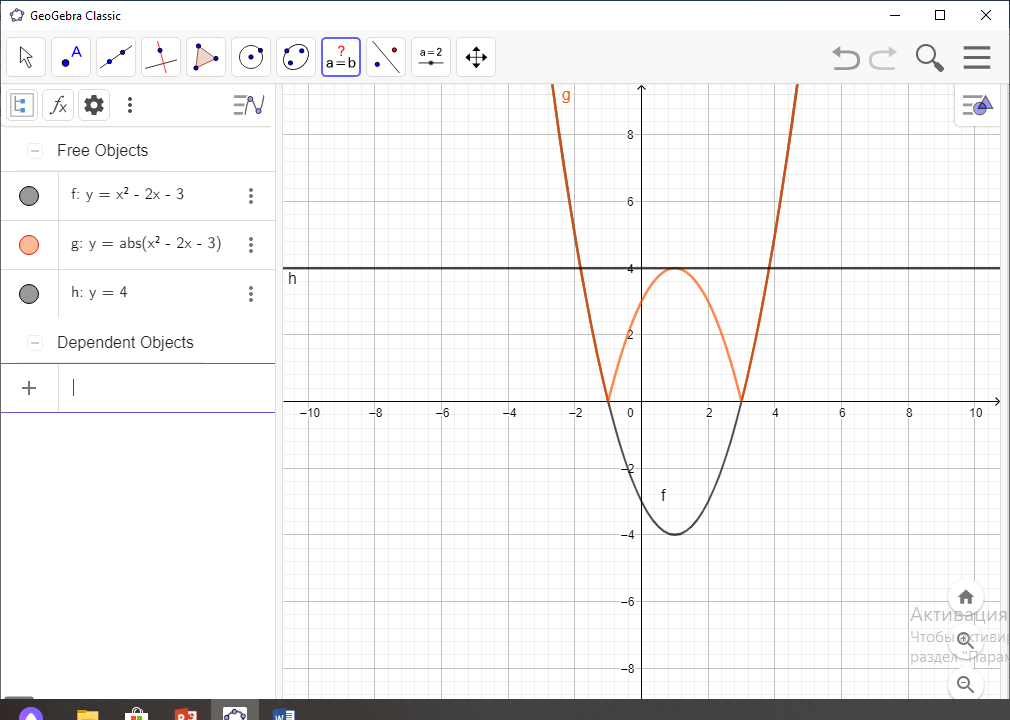
Үш түрлі түбірі болу үшін екі функцияның графигі үш нүктеде қиылысуы керек. Яғни, Ох осіне параллель у= 4 түзу сызығын жүргізу керек.
Жауабы: а= 4 болғанда үш түбірі болады.
![]()
![]()
![]()
-
a)
 =x2
-6x+1
=x2
-6x+1
Шешуі:
1) y=
 2) y=
x2
-6x+1
2) y=
x2
-6x+1
y=x-3 функциясының графигін салу керек; O(3; -8) –параболаның төбесі
y= функциясының графигін
салу керек;
функциясының графигін
салу керек;
y= 
Жауабы: бір түбірі болатындай а-ның мәні болмайды
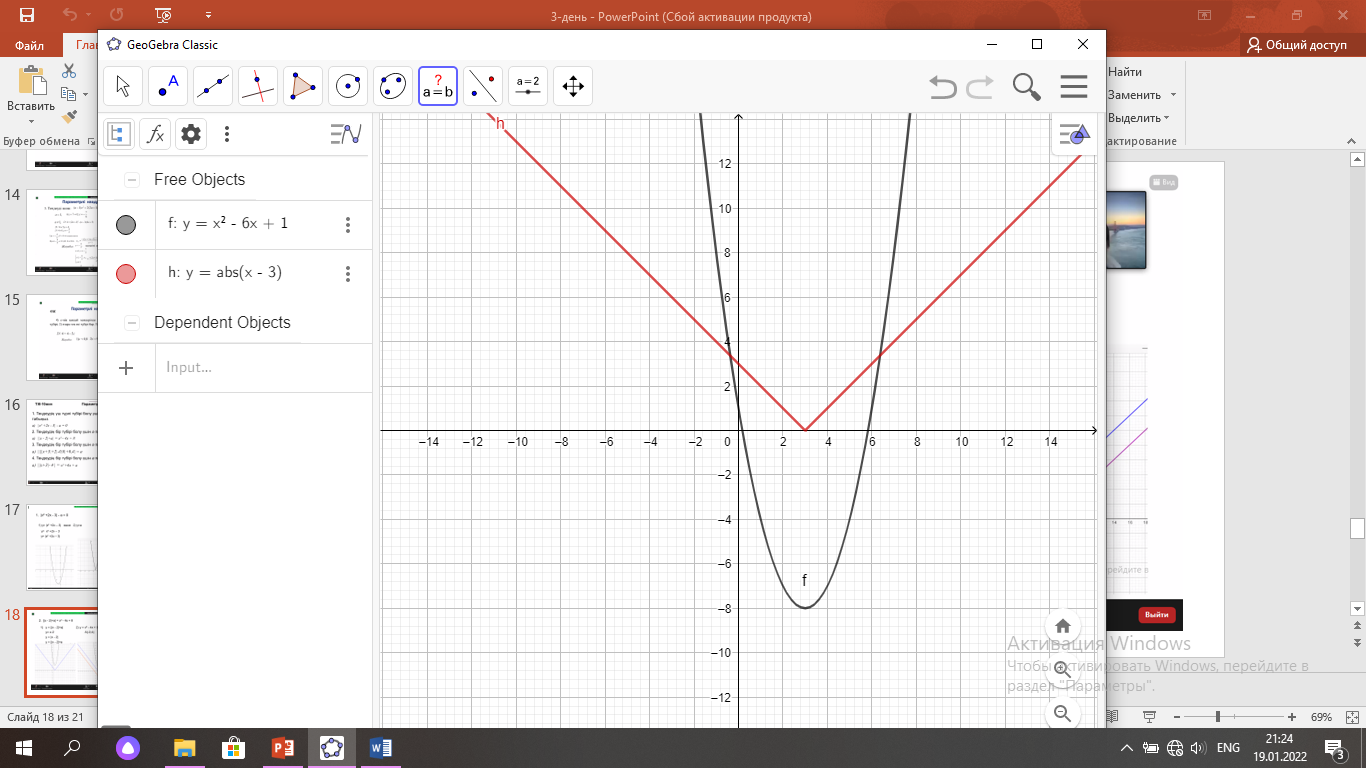
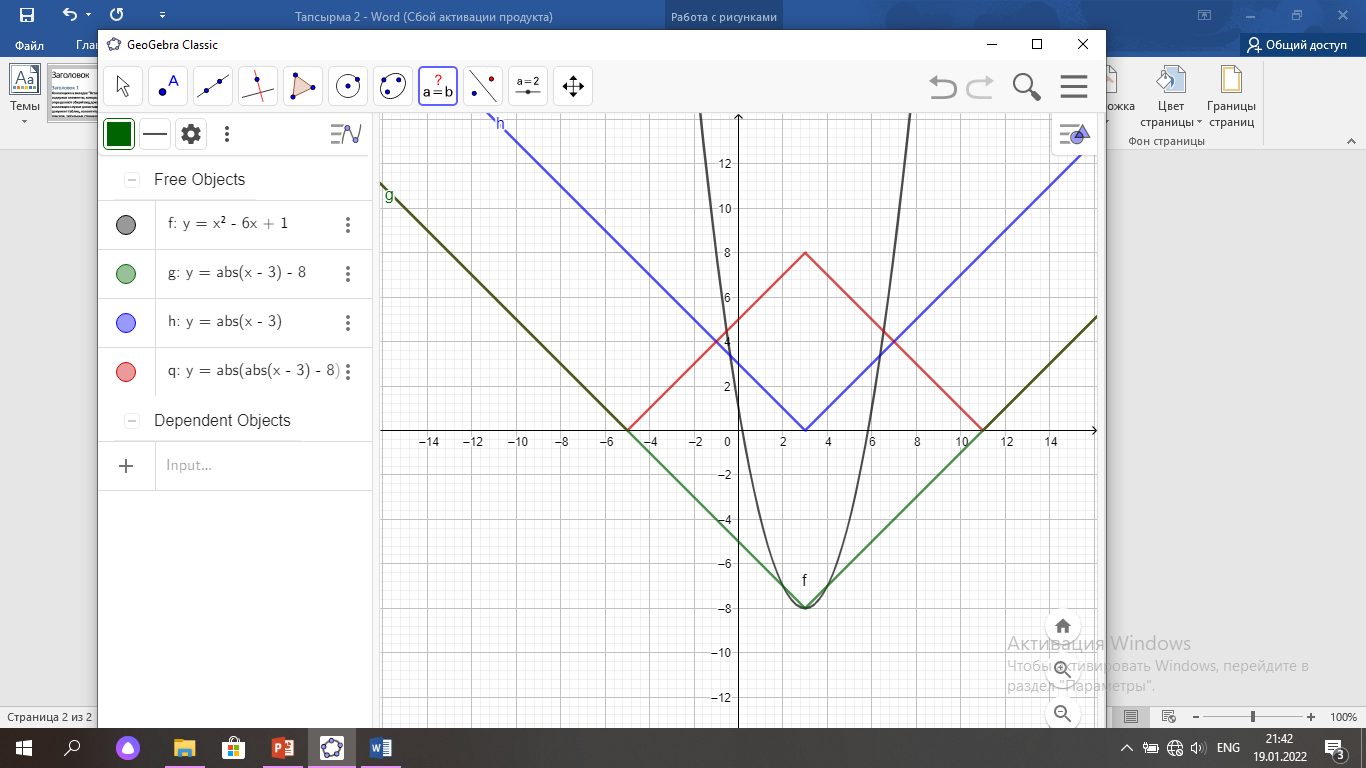
b)  =x2 +6x+12
=x2 +6x+12
Шешуі:
1) y=  2) y= x2 +6x+12
2) y= x2 +6x+12
y=x+3 O(-3; 3) –параболаның төбесі
y=
y=

Жауабы: а= 3 болғанда бір түбірі болады
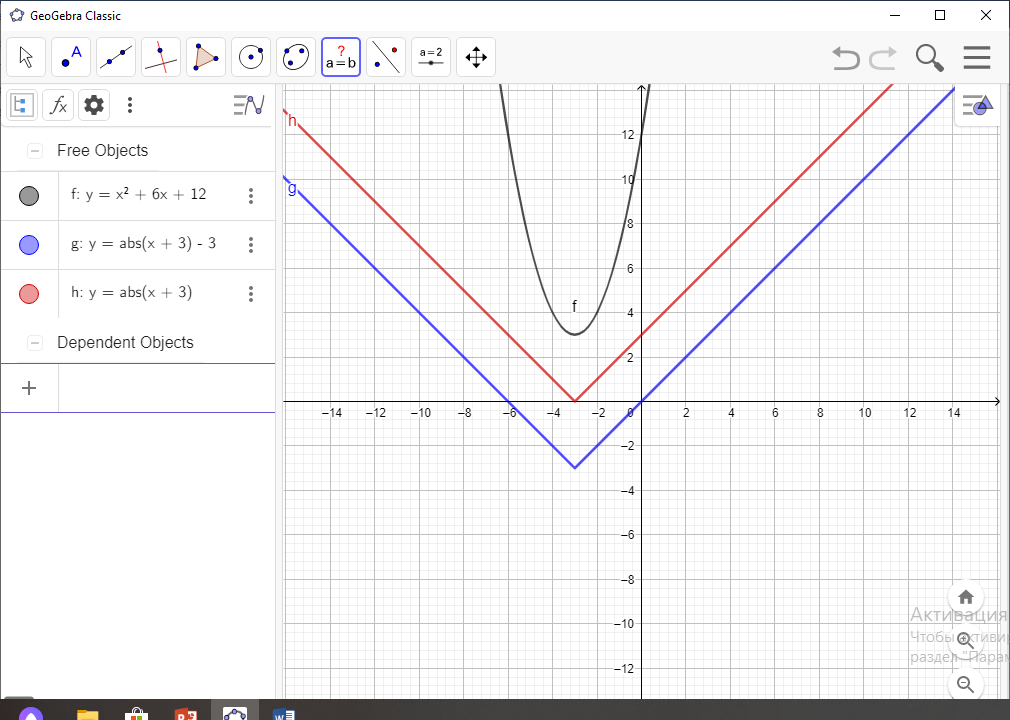
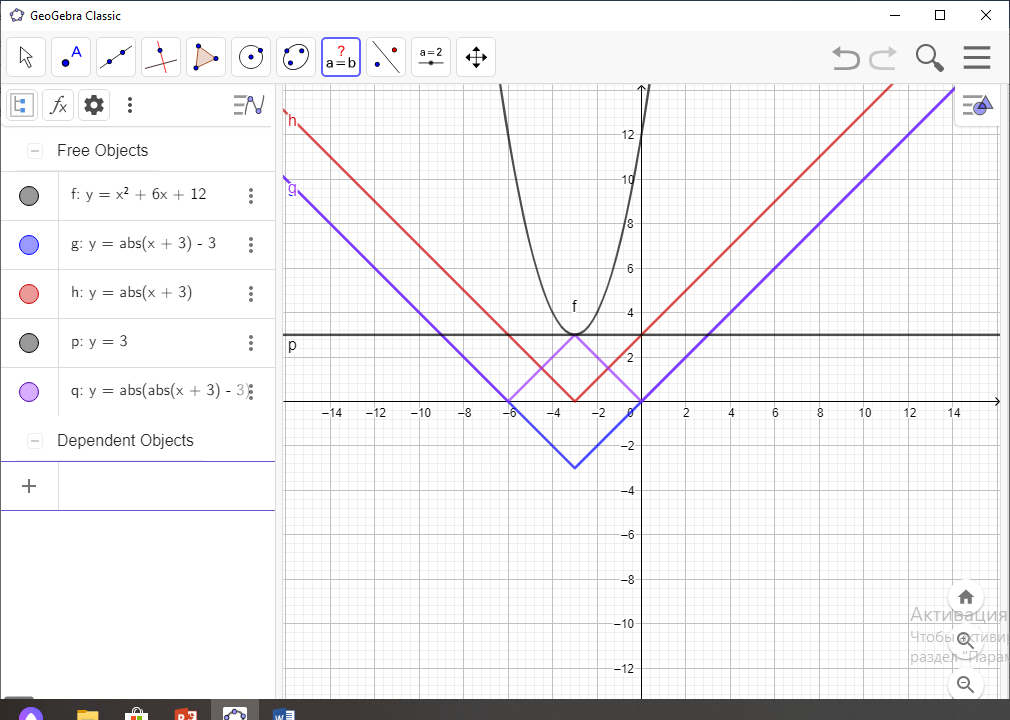
-
а)

Шешуі:




 =0 болса,
онда a-4,1=0
, бұдан
a=4,1
екені
шығады.
=0 болса,
онда a-4,1=0
, бұдан
a=4,1
екені
шығады.
 болғанда бір
түбірі болады.
болғанда бір
түбірі болады.
b)

Шешуі:




 =0 болса,
онда a-2,5=0
, бұдан
a=2,5
екені
шығады.
=0 болса,
онда a-2,5=0
, бұдан
a=2,5
екені
шығады.
 болғанда бір
түбірі болады
болғанда бір
түбірі болады
-
a)
 x2
-4x
-2a
x2
-4x
-2a
-
y=
 2) y=
x2
-4x
-2a
2) y=
x2
-4x
-2a
1-қадам: y= x-2 x0. = 2, y0 = 4-8-2a= -4-2a
2-қадам:
y=  O(2;
4) –парабола
төбесі
O(2;
4) –парабола
төбесі
3-қадам:
y=
 -4-2a=4
-4-2a=4
4-қадам:
y=
 a= -
4
a= -
4
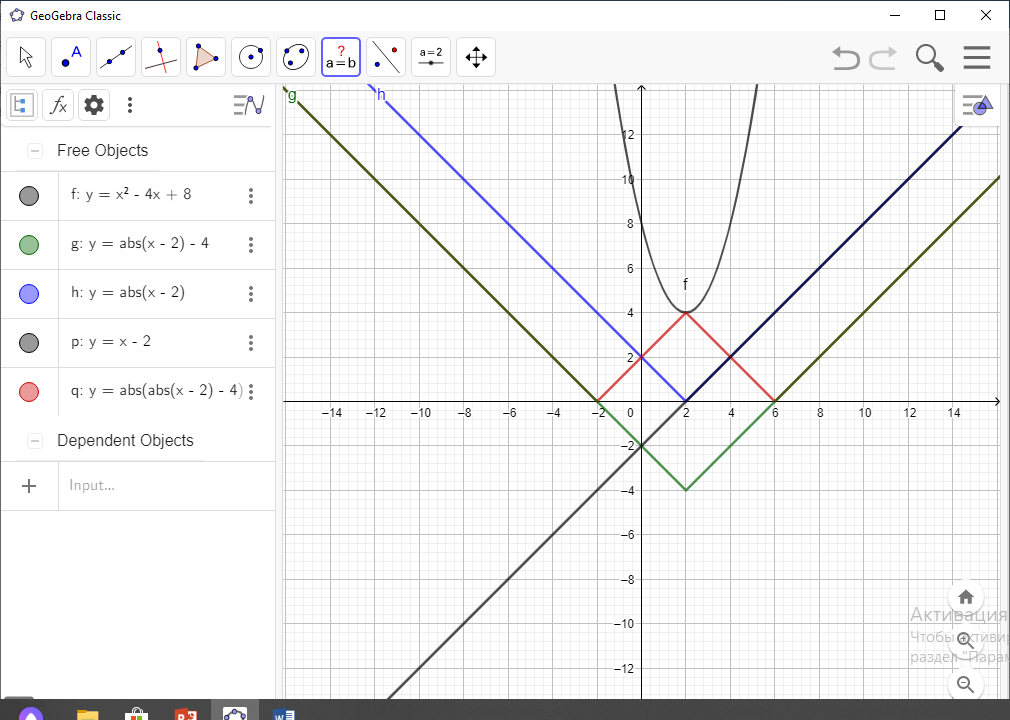
b)
 x2
-6x
+a
x2
-6x
+a
-
y=
 2) y=
x2
-6x
+a
2) y=
x2
-6x
+a
1-қадам: y= x-3 x0. = 3, y0 = 9-18+a= -9+a
2-қадам:
y=  O(3;
2)-парабола
төбесі
O(3;
2)-парабола
төбесі
3-қадам:
y=
 -9+a=
2
-9+a=
2
4-қадам:
y=
 a=11
a=11
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Параметрлі теңдеулерді шешу
Параметрлі теңдеулерді шешу
Параметрлі теңдеулер.
Математика пәнінің мұғалімі, педагог-зерттеуші Спабекова Бибигуль Ахметжановна.
Жоғары сыныптарда кездесетін параметрлі теңдеулерді шешу әдістемесін жас мамандарға немесе математикаға қызығушылығы жоғары оқушыларға пайдалы болар деген оймен ұсынып отырмын. Біліктілікті арттыру курсында жеке орындаған жұмысым болатын.
Параметрлі теңдеулерді шешуде оқушыларға Геогебра бағдарламасын қолданып түсіндіру тиімді болады.
Мысалы:
-
Теңдеуді шешіңіз: а)
 -a=0
-a=0
Шешуі:
-
y=
 2)
y=a
2)
y=a
y= x2 –x-6 графигін салу керек:
параболаның төбесінің координаталарын табамыз: О(0,5; -6,25)
Ох осімен қиылысу нүктелері: (-2; 0), (3; 0)
y=
 функциясының
графигін саламыз;
функциясының
графигін саламыз;
Үш түрлі түбірі болу үшін екі функцияның графигі үш нүктеде қиылысуы керек. Яғни, Ох осіне параллель у= 6, 25 түзу сызығын жүргізу керек.
Жауабы: а= 6,25 болғанда үш түбірі болады.

![]()
![]()
![]()

b)
 -a=0
-a=0
Шешуі:
-
y=
 2)
y=a
2)
y=a
y= x2 –2x-3 графигін салу керек:
параболаның төбесінің координаталарын табамыз: О(1; -4)
Ох өсімен қиылысу нүктелері: (-1; 0), (3; 0)
y=  функциясының графигін
саламыз;
функциясының графигін
саламыз;
Үш түрлі түбірі болу үшін екі функцияның графигі үш нүктеде қиылысуы керек. Яғни, Ох осіне параллель у= 4 түзу сызығын жүргізу керек.
Жауабы: а= 4 болғанда үш түбірі болады.

![]()
![]()
![]()

-
a)
 =x2
-6x+1
=x2
-6x+1
Шешуі:
1) y=
 2) y=
x2
-6x+1
2) y=
x2
-6x+1
y=x-3 функциясының графигін салу керек; O(3; -8) –параболаның төбесі
y= функциясының графигін
салу керек;
функциясының графигін
салу керек;
y= 
Жауабы: бір түбірі болатындай а-ның мәні болмайды


b)  =x2 +6x+12
=x2 +6x+12
Шешуі:
1) y=  2) y= x2 +6x+12
2) y= x2 +6x+12
y=x+3 O(-3; 3) –параболаның төбесі
y=
y=

Жауабы: а= 3 болғанда бір түбірі болады


-
а)

Шешуі:




 =0 болса,
онда a-4,1=0
, бұдан
a=4,1
екені
шығады.
=0 болса,
онда a-4,1=0
, бұдан
a=4,1
екені
шығады.
 болғанда бір
түбірі болады.
болғанда бір
түбірі болады.
b)

Шешуі:




 =0 болса,
онда a-2,5=0
, бұдан
a=2,5
екені
шығады.
=0 болса,
онда a-2,5=0
, бұдан
a=2,5
екені
шығады.
 болғанда бір
түбірі болады
болғанда бір
түбірі болады
-
a)
 x2
-4x
-2a
x2
-4x
-2a
-
y=
 2) y=
x2
-4x
-2a
2) y=
x2
-4x
-2a
1-қадам: y= x-2 x0. = 2, y0 = 4-8-2a= -4-2a
2-қадам:
y=  O(2;
4) –парабола
төбесі
O(2;
4) –парабола
төбесі
3-қадам:
y=
 -4-2a=4
-4-2a=4
4-қадам:
y=
 a= -
4
a= -
4

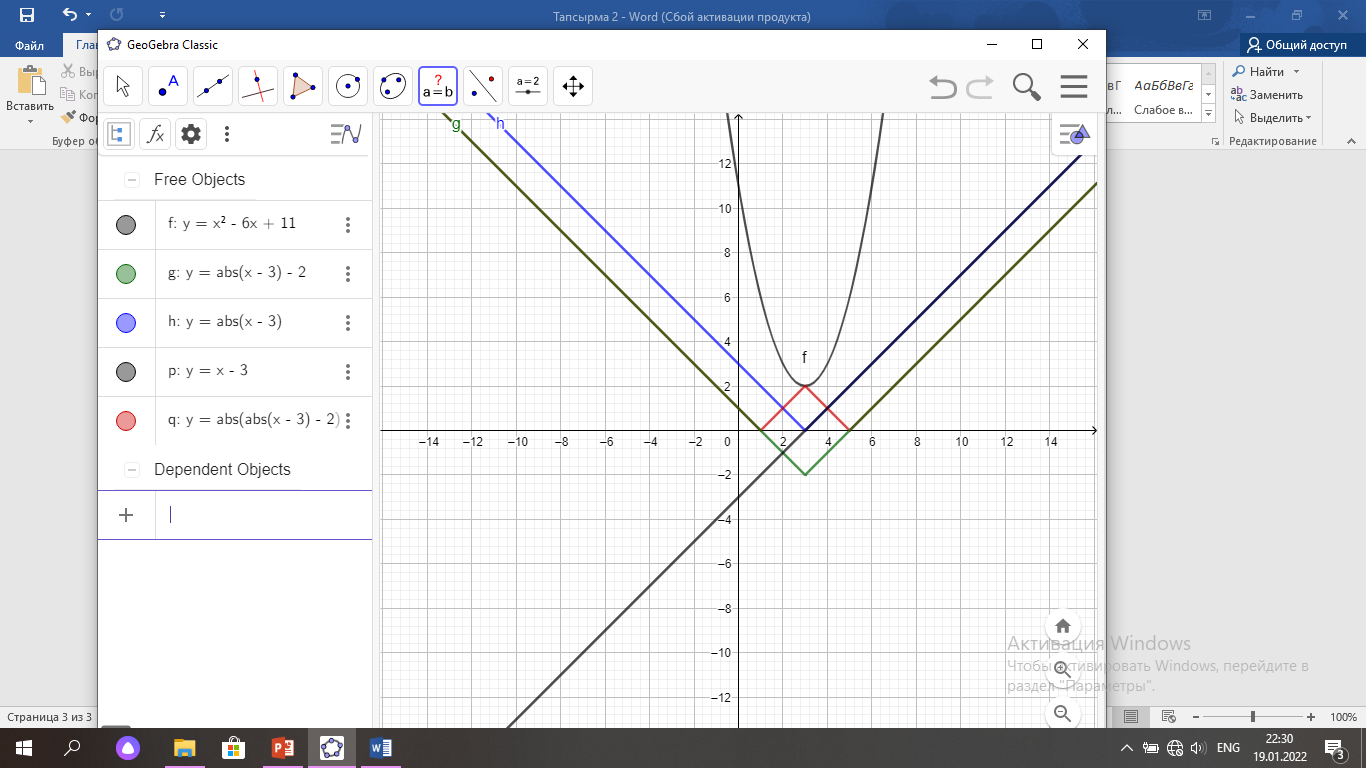
b)
 x2
-6x
+a
x2
-6x
+a
-
y=
 2) y=
x2
-6x
+a
2) y=
x2
-6x
+a
1-қадам: y= x-3 x0. = 3, y0 = 9-18+a= -9+a
2-қадам:
y=  O(3;
2)-парабола
төбесі
O(3;
2)-парабола
төбесі
3-қадам:
y=
 -9+a=
2
-9+a=
2
4-қадам:
y=
 a=11
a=11


шағым қалдыра аласыз















