
ПАРАМЕТРЛІ ТЕҢДЕУЛЕРДІ ШЕШУ
“Абай атындағы мектеп-гимназиясы» КММ, математика пәнінің мұғалімі Спабекова Бибигуль Ахметжановна
Параметрлі теңдеулерді «Геогебра» бағдарламасы көмегімен шешуге бірнеше есептерді ұсынып отырмын. Бұл мақала жас мамандарға және математикаға қызығушылығы бар жоғары сынып оқушыларына қосымша көмек ретінде немесе факультатив сабақтарында қосымша материал ретінде пайдалануға болады.
«Геогебра» – тегін таратылатын математикалық, (www.geogebra.org) геометрия және алгебраны байланыстыратын компьютерлік интерактивті бағдарлама. Бағдарлама тегін болғандықтан оны кез-келген компьютерге орнатып, қолдануға болады.
Қарастырылатын параметрлі теңдеулер:
-
а)
 -a=0 теңдеуінің
а-ның қандай мәнінде әр түрлі үш түбірі болатынын
анықтаңыз.
-a=0 теңдеуінің
а-ның қандай мәнінде әр түрлі үш түбірі болатынын
анықтаңыз.
Шешуі: Екі функция түрінде қарастырамыз:
1) y=
 2)
y=a
2)
y=a
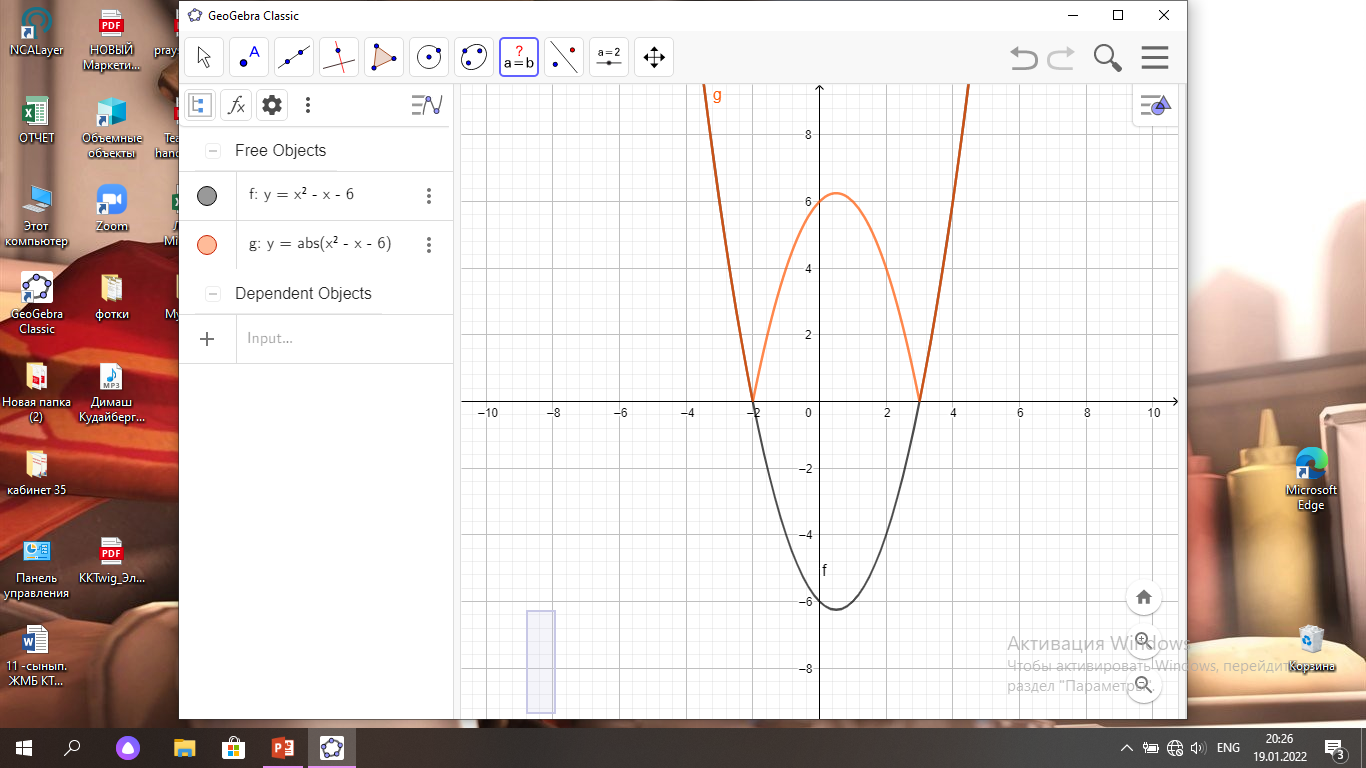
Алдымен y= x2 –x-6 функциясының графигін салу керек.
Ол үшін параболаның төбесінің координаталарын табамыз: O(m;n)
 формуласы бойынша бірінші
координатасын, шыққан мәнді х-тің орнына қойып, екінші
координатасын табамыз: n=m2
–m-6.
формуласы бойынша бірінші
координатасын, шыққан мәнді х-тің орнына қойып, екінші
координатасын табамыз: n=m2
–m-6.
Сонымен парабола төбесі- О(0,5; -6,25) нүктесі.
Ох осімен қиылысу нүктелерін анықтаймыз:
x2 –x-6=0 квадрат теңдеуінің түбірлері: -2 және 3 болғандықтан Ох осімен қиылысу нүктелері: (-2; 0), (3; 0)
y=
 функциясының
графигін саламыз(1-сурет);
функциясының
графигін саламыз(1-сурет);
Үш түрлі түбірі болу үшін екі функцияның графигі үш нүктеде қиылысуы керек. Ох осіне параллель у= 6, 25 түзу сызығын жүргізу керек(2-сурет).
Жауабы: а= 6,25 болғанда үш түбірі болады.
![]()
![]()
![]()
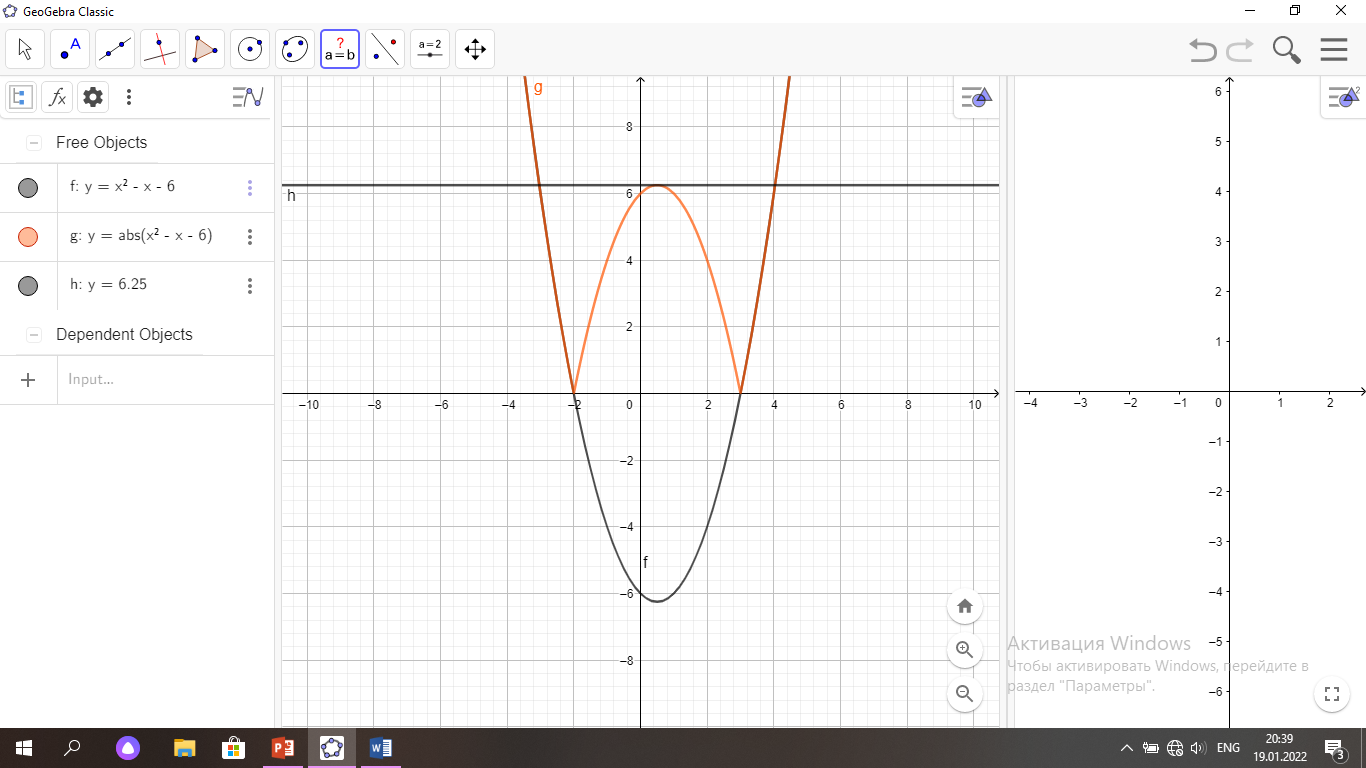
1-сурет 2-сурет
b)
 -a=0 теңдеуінің
а-ның қандай мәнінде әр түрлі үш түбірі болатынын
анықтаңыз.
-a=0 теңдеуінің
а-ның қандай мәнінде әр түрлі үш түбірі болатынын
анықтаңыз.
Шешуі: 1) y=
 2)
y=a
2)
y=a
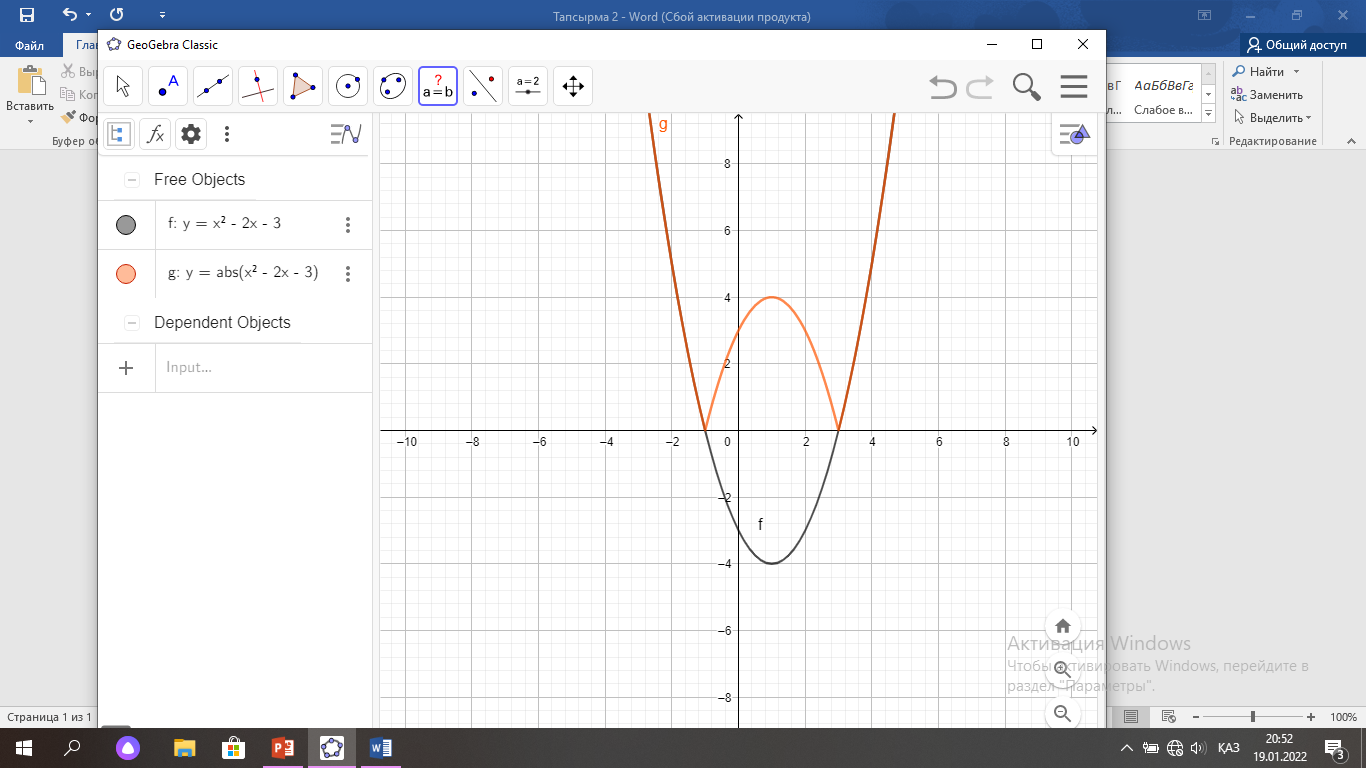
y= x2 –2x-3 графигін салу керек:
Параболаның төбесінің координаталарын табамыз: О(1; -4)
Ох өсімен қиылысу нүктелерін табамыз: (-1; 0), (3; 0)
y=
 функциясының
графигін саламыз(3-сурет);
функциясының
графигін саламыз(3-сурет);
Үш түрлі түбірі болу үшін екі функцияның графигі үш нүктеде қиылысуы керек. Яғни, Ох осіне параллель у= 4 түзу сызығын жүргізу керек(4-сурет).
Жауабы: а= 4 болғанда үш түбірі болады.
![]()
![]()
![]()
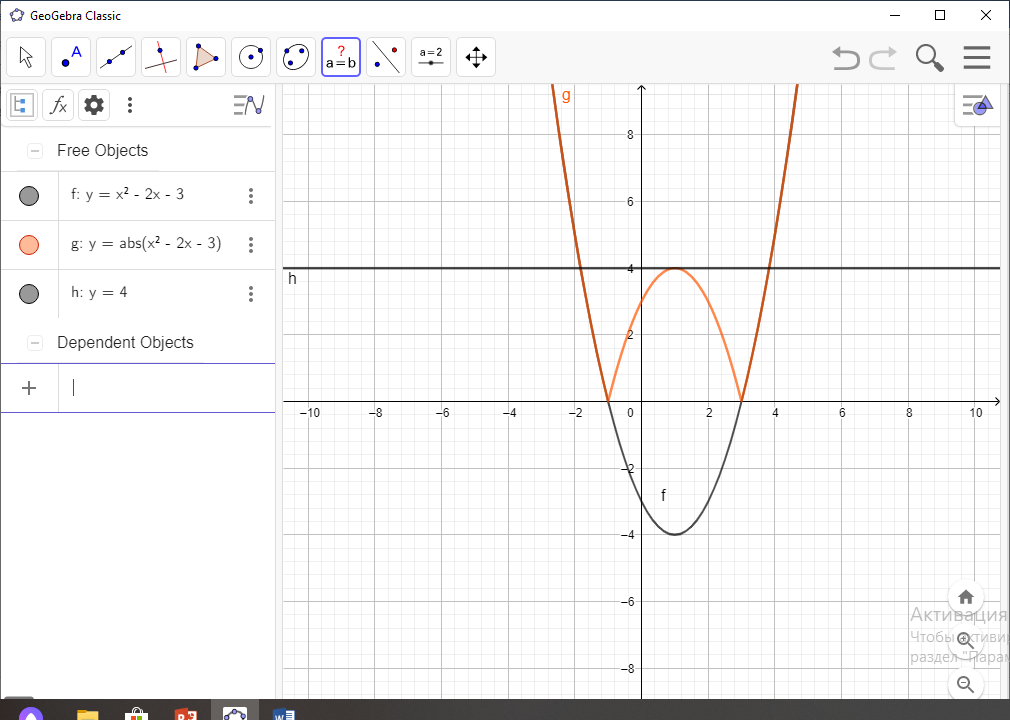
3-сурет 4-сурет
2.
a)  =x2 -6x+1 теңдеуінің бір түбірі
болатындай а-ның мәнін табылады ма?
=x2 -6x+1 теңдеуінің бір түбірі
болатындай а-ның мәнін табылады ма?
Шешуі: 1)
y= 2) y=
x2
-6x+1
2) y=
x2
-6x+1
y=x-3 функциясының графигін салу керек; y= x2 -6x+1 функциясының графигін салу керек: O(3; -8) –параболаның төбесі.
y= функциясының графигін
салу керек(5-сурет);
функциясының графигін
салу керек(5-сурет);
y=

Жауабы: бір түбірі болатындай а-ның мәні болмайды(6-сурет)
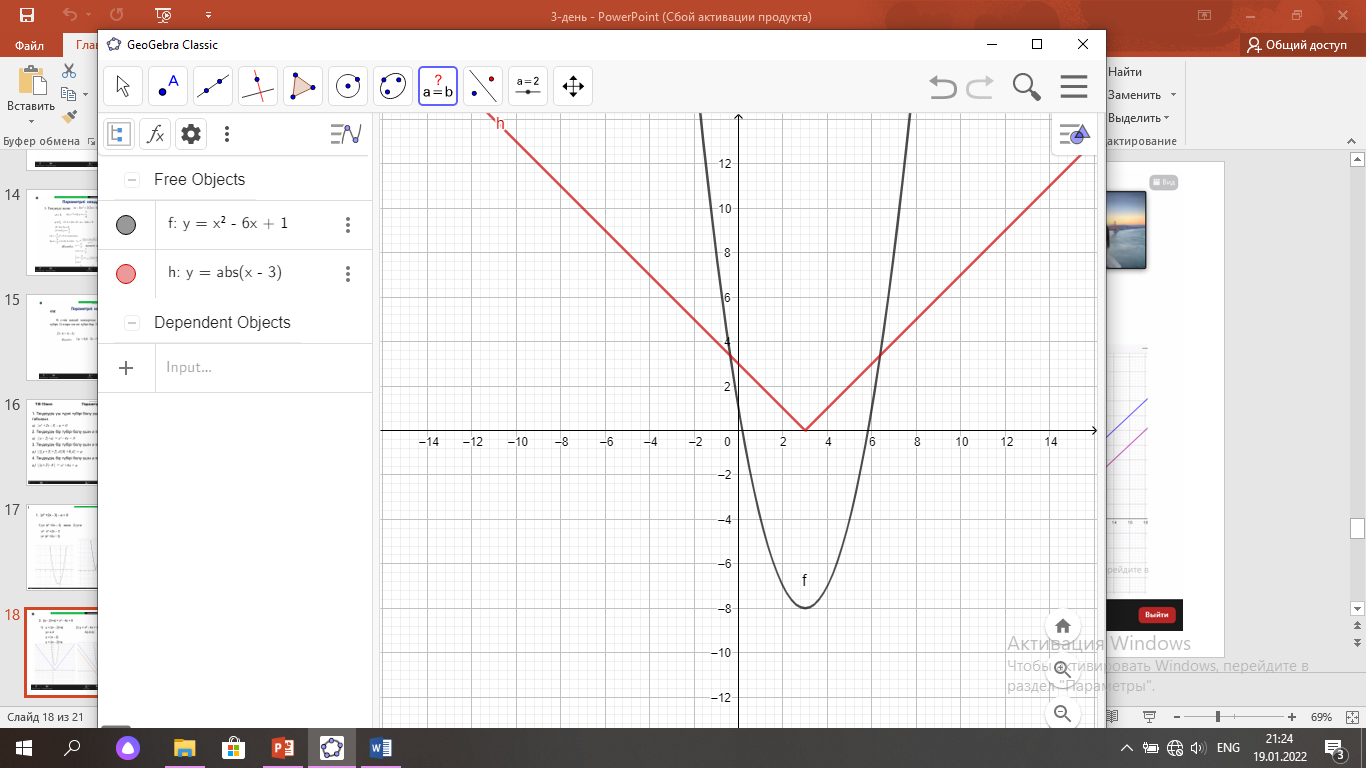
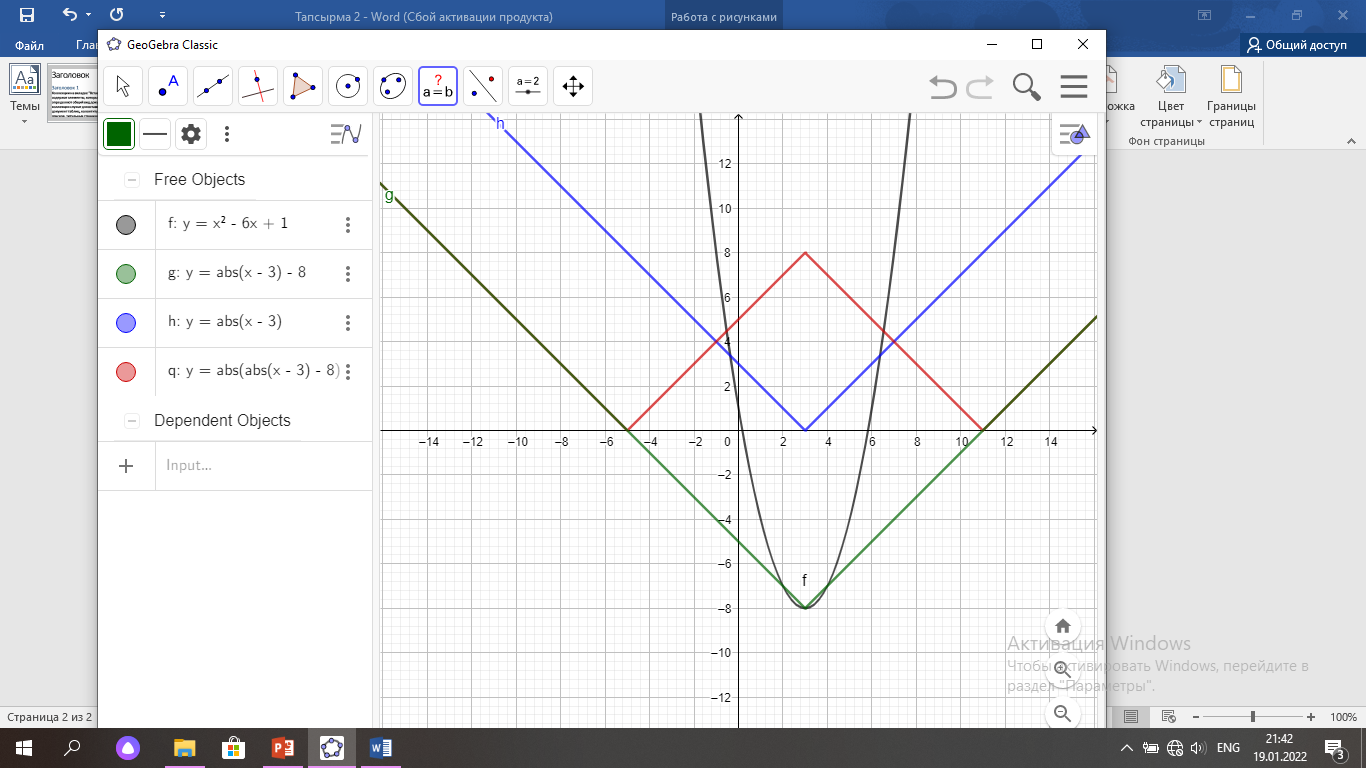
5-сурет 6-сурет
b)
 =x2 +6x+12 теңдеуінің бір
түбірі болатындай а-ның мәнін табыңыз.
=x2 +6x+12 теңдеуінің бір
түбірі болатындай а-ның мәнін табыңыз.
Шешуі: 1)
y= 2) y=
x2
+6x+12
2) y=
x2
+6x+12
y=x+3 графигін салу; O(-3; 3) –параболаның төбесі
y= графигін
салу(7-сурет);
графигін
салу(7-сурет);
y=

Жауабы: а= 3 болғанда бір түбірі болады(8-сурет)
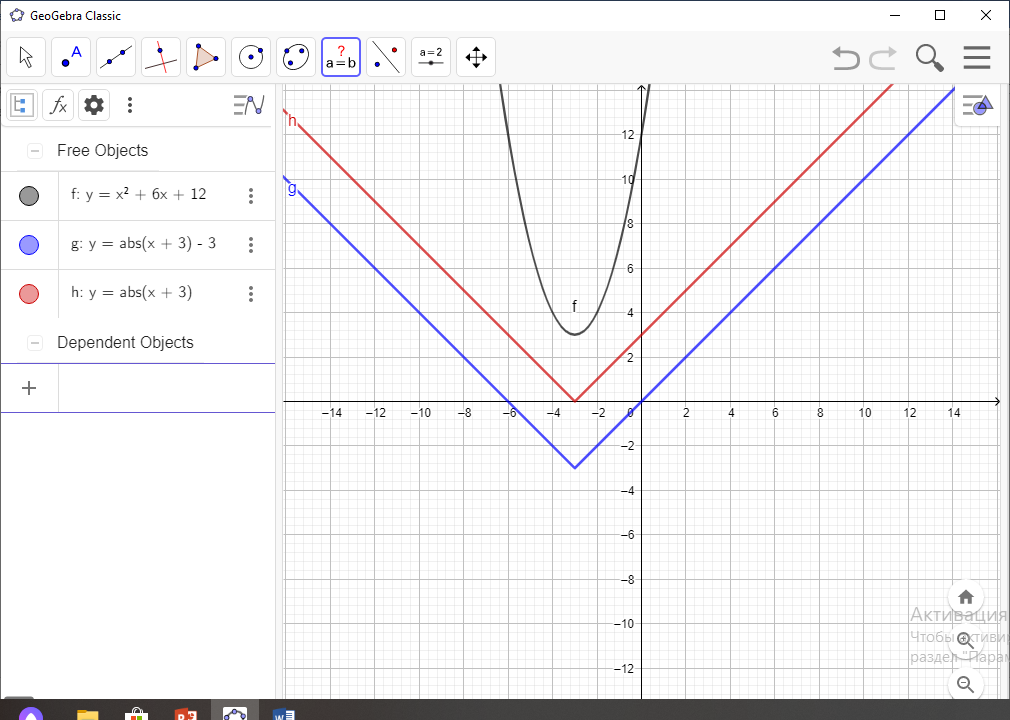
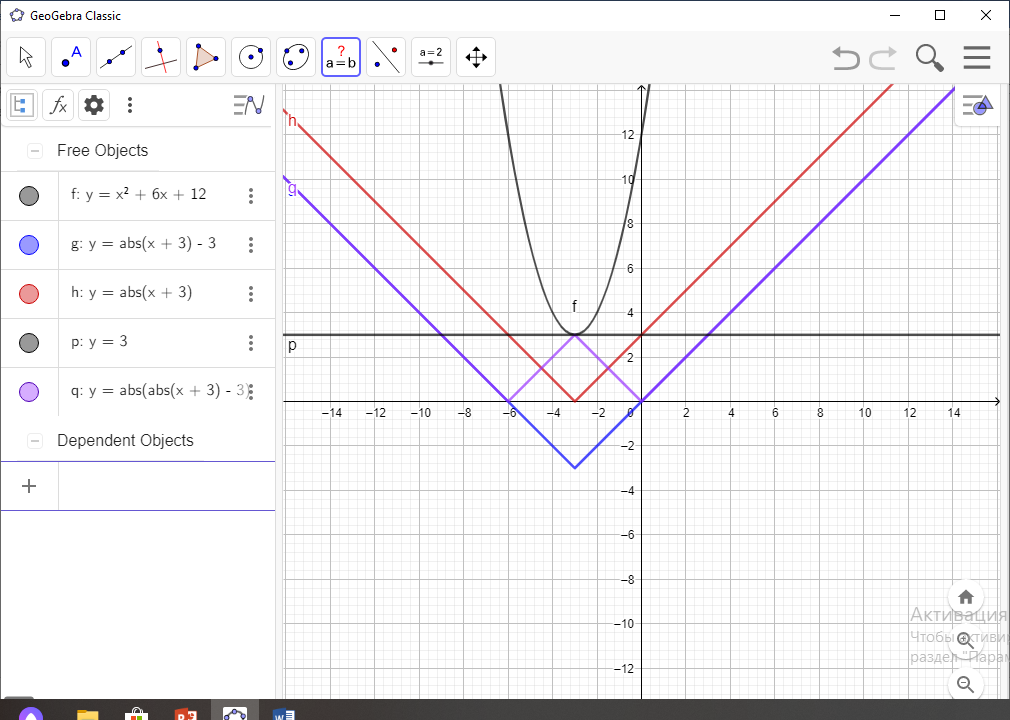
7-сурет 8-сурет
3.
а)  теңдеуінің бір түбірі
болатындай а-ның мәнін табыңыз.
теңдеуінің бір түбірі
болатындай а-ның мәнін табыңыз.
Шешуі: 



 =0 болса,
онда a-4,1=0
, бұдан
a=4,1
екені
шығады.
=0 болса,
онда a-4,1=0
, бұдан
a=4,1
екені
шығады.
 болғанда бір
түбірі болады.
болғанда бір
түбірі болады.
b)
 теңдеуінің бір
түбірі болатындай а-ның мәнін табыңыз.
теңдеуінің бір
түбірі болатындай а-ның мәнін табыңыз.
Шешуі:




 =0 болса,
онда a-2,5=0
, бұдан
a=2,5
екені
шығады.
=0 болса,
онда a-2,5=0
, бұдан
a=2,5
екені
шығады.
 болғанда бір
түбірі болады
болғанда бір
түбірі болады
-
a)
 x2 -4x -2a. а-ның қандай
мәнінде бір түбірі болады?
x2 -4x -2a. а-ның қандай
мәнінде бір түбірі болады?
Шешуі:
-
y=
 2) y=
x2
-4x
-2a
2) y=
x2
-4x
-2a
1-қадам: y= x-2 x0. = 2, y0 = 4-8-2a= -4-2a
2-қадам:
y=  O(2;
4) –парабола
төбесі
O(2;
4) –парабола
төбесі
3-қадам:
y=
 -4-2a=4
-4-2a=4
4-қадам:
y=
 a= -
4
a= -
4
Жауабы: a= - 4 болғанда бір түбірі болады(9-сурет)
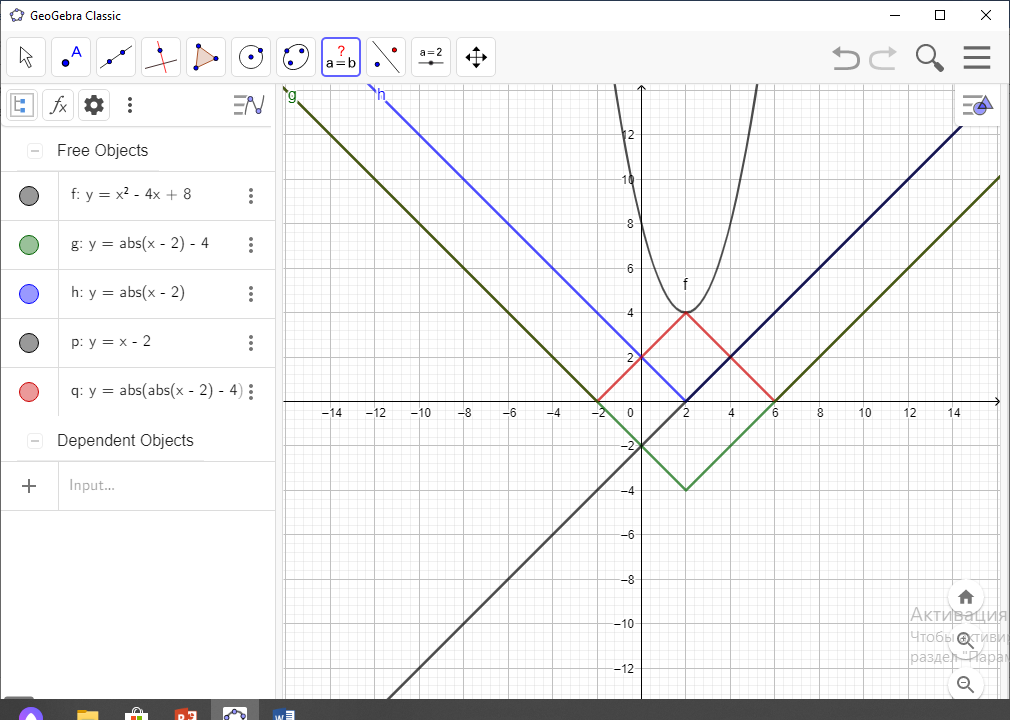
9-сурет
b)
 x2 -6x +a. а-ның қандай
мәнінде бір түбірі болады?
x2 -6x +a. а-ның қандай
мәнінде бір түбірі болады?
Шешуі:
-
y=
 2) y=
x2
-6x
+a
2) y=
x2
-6x
+a
1-қадам: y= x-3 x0. = 3, y0 = 9-18+a= -9+a
2-қадам:
y=  O(3;
2)-парабола
төбесі
O(3;
2)-парабола
төбесі
3-қадам:
y=
 -9+a=
2
-9+a=
2
4-қадам:
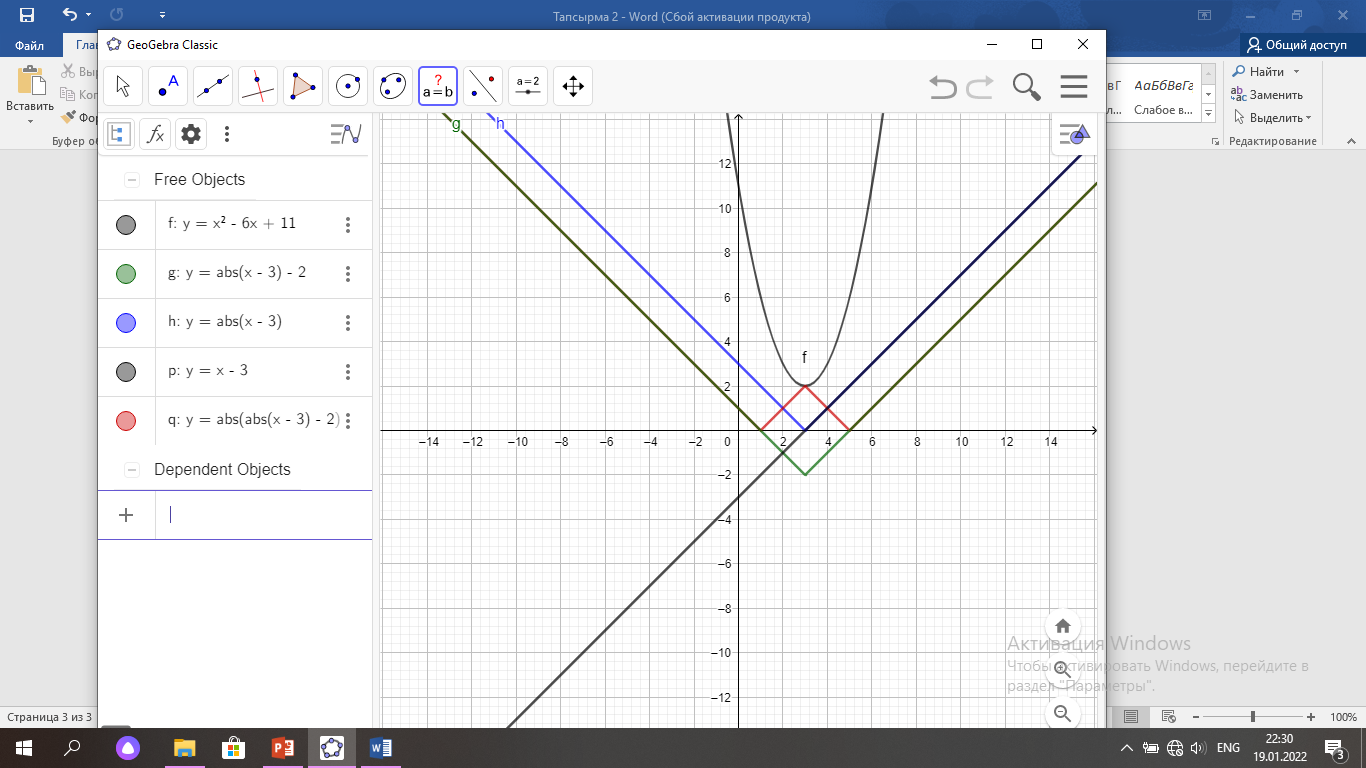
y=  Жауабы: a=11 болғанда (10-сурет)
Жауабы: a=11 болғанда (10-сурет)
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Параметрлі теңдеулерді шешу
Параметрлі теңдеулерді шешу
ПАРАМЕТРЛІ ТЕҢДЕУЛЕРДІ ШЕШУ
“Абай атындағы мектеп-гимназиясы» КММ, математика пәнінің мұғалімі Спабекова Бибигуль Ахметжановна
Параметрлі теңдеулерді «Геогебра» бағдарламасы көмегімен шешуге бірнеше есептерді ұсынып отырмын. Бұл мақала жас мамандарға және математикаға қызығушылығы бар жоғары сынып оқушыларына қосымша көмек ретінде немесе факультатив сабақтарында қосымша материал ретінде пайдалануға болады.
«Геогебра» – тегін таратылатын математикалық, (www.geogebra.org) геометрия және алгебраны байланыстыратын компьютерлік интерактивті бағдарлама. Бағдарлама тегін болғандықтан оны кез-келген компьютерге орнатып, қолдануға болады.
Қарастырылатын параметрлі теңдеулер:
-
а)
 -a=0 теңдеуінің
а-ның қандай мәнінде әр түрлі үш түбірі болатынын
анықтаңыз.
-a=0 теңдеуінің
а-ның қандай мәнінде әр түрлі үш түбірі болатынын
анықтаңыз.
Шешуі: Екі функция түрінде қарастырамыз:
1) y=
 2)
y=a
2)
y=a
Алдымен y= x2 –x-6 функциясының графигін салу керек.
Ол үшін параболаның төбесінің координаталарын табамыз: O(m;n)
 формуласы бойынша бірінші
координатасын, шыққан мәнді х-тің орнына қойып, екінші
координатасын табамыз: n=m2
–m-6.
формуласы бойынша бірінші
координатасын, шыққан мәнді х-тің орнына қойып, екінші
координатасын табамыз: n=m2
–m-6.
Сонымен парабола төбесі- О(0,5; -6,25) нүктесі.
Ох осімен қиылысу нүктелерін анықтаймыз:
x2 –x-6=0 квадрат теңдеуінің түбірлері: -2 және 3 болғандықтан Ох осімен қиылысу нүктелері: (-2; 0), (3; 0)
y=
 функциясының
графигін саламыз(1-сурет);
функциясының
графигін саламыз(1-сурет);
Үш түрлі түбірі болу үшін екі функцияның графигі үш нүктеде қиылысуы керек. Ох осіне параллель у= 6, 25 түзу сызығын жүргізу керек(2-сурет).
Жауабы: а= 6,25 болғанда үш түбірі болады.

![]()
![]()
![]()

1-сурет 2-сурет
b)
 -a=0 теңдеуінің
а-ның қандай мәнінде әр түрлі үш түбірі болатынын
анықтаңыз.
-a=0 теңдеуінің
а-ның қандай мәнінде әр түрлі үш түбірі болатынын
анықтаңыз.
Шешуі: 1) y=
 2)
y=a
2)
y=a
y= x2 –2x-3 графигін салу керек:
Параболаның төбесінің координаталарын табамыз: О(1; -4)
Ох өсімен қиылысу нүктелерін табамыз: (-1; 0), (3; 0)
y=
 функциясының
графигін саламыз(3-сурет);
функциясының
графигін саламыз(3-сурет);
Үш түрлі түбірі болу үшін екі функцияның графигі үш нүктеде қиылысуы керек. Яғни, Ох осіне параллель у= 4 түзу сызығын жүргізу керек(4-сурет).
Жауабы: а= 4 болғанда үш түбірі болады.

![]()
![]()
![]()

3-сурет 4-сурет
2.
a)  =x2 -6x+1 теңдеуінің бір түбірі
болатындай а-ның мәнін табылады ма?
=x2 -6x+1 теңдеуінің бір түбірі
болатындай а-ның мәнін табылады ма?
Шешуі: 1)
y= 2) y=
x2
-6x+1
2) y=
x2
-6x+1
y=x-3 функциясының графигін салу керек; y= x2 -6x+1 функциясының графигін салу керек: O(3; -8) –параболаның төбесі.
y= функциясының графигін
салу керек(5-сурет);
функциясының графигін
салу керек(5-сурет);
y=

Жауабы: бір түбірі болатындай а-ның мәні болмайды(6-сурет)


5-сурет 6-сурет
b)
 =x2 +6x+12 теңдеуінің бір
түбірі болатындай а-ның мәнін табыңыз.
=x2 +6x+12 теңдеуінің бір
түбірі болатындай а-ның мәнін табыңыз.
Шешуі: 1)
y= 2) y=
x2
+6x+12
2) y=
x2
+6x+12
y=x+3 графигін салу; O(-3; 3) –параболаның төбесі
y= графигін
салу(7-сурет);
графигін
салу(7-сурет);
y=

Жауабы: а= 3 болғанда бір түбірі болады(8-сурет)


7-сурет 8-сурет
3.
а)  теңдеуінің бір түбірі
болатындай а-ның мәнін табыңыз.
теңдеуінің бір түбірі
болатындай а-ның мәнін табыңыз.
Шешуі: 



 =0 болса,
онда a-4,1=0
, бұдан
a=4,1
екені
шығады.
=0 болса,
онда a-4,1=0
, бұдан
a=4,1
екені
шығады.
 болғанда бір
түбірі болады.
болғанда бір
түбірі болады.
b)
 теңдеуінің бір
түбірі болатындай а-ның мәнін табыңыз.
теңдеуінің бір
түбірі болатындай а-ның мәнін табыңыз.
Шешуі:




 =0 болса,
онда a-2,5=0
, бұдан
a=2,5
екені
шығады.
=0 болса,
онда a-2,5=0
, бұдан
a=2,5
екені
шығады.
 болғанда бір
түбірі болады
болғанда бір
түбірі болады
-
a)
 x2 -4x -2a. а-ның қандай
мәнінде бір түбірі болады?
x2 -4x -2a. а-ның қандай
мәнінде бір түбірі болады?
Шешуі:
-
y=
 2) y=
x2
-4x
-2a
2) y=
x2
-4x
-2a
1-қадам: y= x-2 x0. = 2, y0 = 4-8-2a= -4-2a
2-қадам:
y=  O(2;
4) –парабола
төбесі
O(2;
4) –парабола
төбесі
3-қадам:
y=
 -4-2a=4
-4-2a=4
4-қадам:
y=
 a= -
4
a= -
4
Жауабы: a= - 4 болғанда бір түбірі болады(9-сурет)

9-сурет
b)
 x2 -6x +a. а-ның қандай
мәнінде бір түбірі болады?
x2 -6x +a. а-ның қандай
мәнінде бір түбірі болады?
Шешуі:
-
y=
 2) y=
x2
-6x
+a
2) y=
x2
-6x
+a
1-қадам: y= x-3 x0. = 3, y0 = 9-18+a= -9+a
2-қадам:
y=  O(3;
2)-парабола
төбесі
O(3;
2)-парабола
төбесі
3-қадам:
y=
 -9+a=
2
-9+a=
2
4-қадам:
y=  Жауабы: a=11 болғанда (10-сурет)
Жауабы: a=11 болғанда (10-сурет)


шағым қалдыра аласыз















