
Параметрмен берілген тригонометриялық теңдеулерді шешу
1.1 Қарапайым тригонометриялық теңдеулерді шешу
Кей жағдайларда құрамында параметрі бар болатын көрсеткіштік, логарифмдік және тригонометриялық теңдеулер мен теңсіздіктерді шешу керек болады. Мұндай теңдеулер мен теңсіздіктерді жалпы жағдайда транценденттік деп атайды. Параметрдің мәндеріне байланысты теңдеулер мен теңсіздіктердің түбірлері бірнешеу болуы немесе болмауы мүмкін, кей жағдайларда белгілі бір аралықтарда жататын түбірлері табылуы мүмкін.
Тригонометриялық теңдеу–белгісіз аргументтің
тригонометриялық функциясына қатысты алгебралық теңдеу.
Тригонометриялық теңдеуді шешу үшін тригонометриялық функциялардың
арасындағы әр түрлі қатынастарды пайдалана отырып, тригонометриялық
теңдеулерді ізделініп отырған аргументтің тригонометриялық
функциялары біреуінің мәнін анықтауға болатындай түрге келтіру
керек.  ,
,  ,
,  ,
,  түрінде берілген теңдеу қарапайым
тригонометриялық теңдеу деп аталады. Кез
келген тригонометриялық теңдеуді шешу қарапайым тригонометриялық
теңдеуді шешуге арқылы шығады, ал қарапайым тригонометриялық
теңдеулер келесі формулалар арқылы есептеледі:
түрінде берілген теңдеу қарапайым
тригонометриялық теңдеу деп аталады. Кез
келген тригонометриялық теңдеуді шешу қарапайым тригонометриялық
теңдеуді шешуге арқылы шығады, ал қарапайым тригонометриялық
теңдеулер келесі формулалар арқылы есептеледі:
-
Егер
 болса, онда
болса, онда  теңдеуінің шешімі
теңдеуінің шешімі  формуласымен анықталады.
формуласымен анықталады.
Дербес
жағдайлары: 
2. Егер
 болса, онда
болса, онда теңдеуінің шешімі
теңдеуінің шешімі  формуласымен анықталады.
формуласымен анықталады.
Дербес
жағдайлары: 
3.  теңдеуінің
шешімі
теңдеуінің
шешімі  формуласымен
анықталады.
формуласымен
анықталады.
Дербес
жағдайлары: 
4.  теңдеуінің
шешімі
теңдеуінің
шешімі  формуласымен
анықталады.
формуласымен
анықталады.
Дербес
жағдайлары: 
Тригонометриялық теңдеулерді шешу әдістері
-
Көбейткіштерге жіктеу
Бұл
тәсілде  теңдеуінің
шешімі
теңдеуінің
шешімі  теңдеулерінің
шешімімен тең екендігі негізге алынып шығарылады.
теңдеулерінің
шешімімен тең екендігі негізге алынып шығарылады.
1- мысал .
 .
.
Шешуі: 

-
Жаңа айнымалы енгізу
Егер теңдеу бір ғана тригонометиялық функциялардан құралған болса, теңдеу алгебралық әдіс арқылы шығады.
2-
мысал. 
Шешуі:  формуласын қолдана отырып, келесі
теңдеуді аламыз:
формуласын қолдана отырып, келесі
теңдеуді аламыз: 
-
 түріндегі
тригонометриялық теңдеулерді шешу.
түріндегі
тригонометриялық теңдеулерді шешу.
Бұл
түрдегі теңдеулерді шығару үшін теңдеудің екі жағында
 және
және  - ге бөлу керек.
- ге бөлу керек.

теңдеуін
аламыз.  айнымалысын
енгізу арқылы теңдеуді шығарамыз.
айнымалысын
енгізу арқылы теңдеуді шығарамыз.
3- мысал.
 теңдеуін шешіңдер.
теңдеуін шешіңдер.
Шешуі:
теңдеуді  ке бөлу
арқылы
ке бөлу
арқылы  теңдеуін аламыз. Бұл
теңдеудің шешімі:
теңдеуін аламыз. Бұл
теңдеудің шешімі:  .
.
-
 түріндегі
тригонометриялық теңделерді шешу. Бұл түрдегі теңдеулерді шешудің
бірнеше әдістері бар.
түріндегі
тригонометриялық теңделерді шешу. Бұл түрдегі теңдеулерді шешудің
бірнеше әдістері бар.
4.1
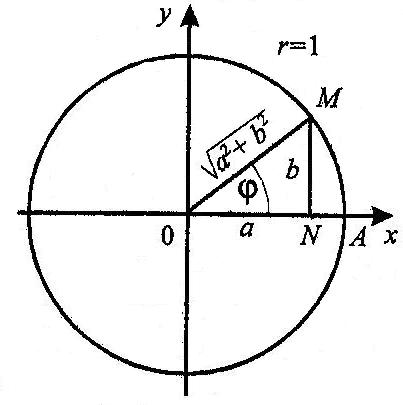
Көмекші аргумент енгізу. Бұл
кезде  өрнегінің
орнына
өрнегінің
орнына  өрнегін
жазамыз.
өрнегін
жазамыз.  .
.
 - бұрышы көмекші аргумент деп
аталады.
- бұрышы көмекші аргумент деп
аталады.
4- мысал.
 теңдеуін шешіңдер.
теңдеуін шешіңдер.
Шешуі:  болатындығынан,
болатындығынан,  -нің қандай да бір мәнінде
-нің қандай да бір мәнінде
 және
және  болады. Олай болса,
болады. Олай болса,  немесе
немесе  .
.  . Ал теңдеуіміздің жауабы:
. Ал теңдеуіміздің жауабы:
 .
.
4.2
Универсал алмастыру. Бұл кезде
 және
және  функцияларын
функцияларын  формуласымен ауыстырамыз.
формуласымен ауыстырамыз.
5- мысал.
 теңдеуін шешіңдер.
теңдеуін шешіңдер.
Шешуі:  -ті
-ті  мен ауыстырамыз, ал
мен ауыстырамыз, ал  белгілейміз.
белгілейміз. 
5.  түріндегі
тригонометриялық теңдеулерді шешу.
түріндегі
тригонометриялық теңдеулерді шешу.
Теңдеу  немесе
немесе  түріне келтіріп шығарылады. Теңдеуді
шешу үшін
түріне келтіріп шығарылады. Теңдеуді
шешу үшін  бөліп,
бөліп,
 теңдеуін аламыз. Бұл теңдеуді
шығарсақ,
теңдеуін аламыз. Бұл теңдеуді
шығарсақ,  . Осылайша,
берілген теңдеудің шешімі:
. Осылайша,
берілген теңдеудің шешімі:  [15].
[15].
Тригонометриялық теңдеулерді шығарылу жолына байланысты 6
топқа бөлуге болады:
1. Тригонометриялық функциясының бір ғана түрлерімен берілген,
алгебралық теңдеулерге келтірілетін тригонометриялық теңдеулер;
2. Тригонометриялық формулаларды түрлендіру жолымен шешілетін
тригонометриялық теңдеулер;
3. Функциялардың дәрежесін төмендету арқылы шешілетін
тригонометриялық теңдеулер;
4. Біртектес тригонометриялық теңдеулерді шешу;
5. Қосымша аргумент енгізу арқылы шығарылатын тригонометриялық
теңдеулер;
6. Тригонометриялық теңдеулер жүйесін шешу[17].
Жіктеу арқылы шешілетін тригонометриялық теңдеулер.
Яғни  түріне
келтіретін теңдеулер. Сол белгілі бір бірнеше көбейтінділерден
тұрады. Оң бөлігі нөл, сондықтан ең болмағанда бір көбейткіш нөлге
тең болса ғана көбейтінді нөлге тең болады.
түріне
келтіретін теңдеулер. Сол белгілі бір бірнеше көбейтінділерден
тұрады. Оң бөлігі нөл, сондықтан ең болмағанда бір көбейткіш нөлге
тең болса ғана көбейтінді нөлге тең болады.
6- мысал.
 теңдеуді шешіңдер. (ММЖ) – мүмкін мәндер
жиыны.
теңдеуді шешіңдер. (ММЖ) – мүмкін мәндер
жиыны.
Шешуі:
(ММЖ) тапсақ  немесе
немесе

1)  бұдан
бұдан
 яғни
яғни
2)  бұдан
бұдан
 ММЖ-ға жатпайтынын көрсетейік.
ММЖ-ға жатпайтынын көрсетейік.


 -ның қандай мәнінде
тақ емес, ММЖ жатпайды.
-ның қандай мәнінде
тақ емес, ММЖ жатпайды.
7- мысал.
 теңдеуін шешіңдер.
теңдеуін шешіңдер.
Шешуі:
ММЖ 

1) бұдан
бұдан

2)  шешімі болмайды,
себебі сол бөлігі әруақытта оң сан. Теңдеудің түбірі
шешімі болмайды,
себебі сол бөлігі әруақытта оң сан. Теңдеудің түбірі
 .
.
Қосу формулаларын пайдаланып шешілетін теңдеулер.
8- мысал.
 теңдеуін шешіңдер.
теңдеуін шешіңдер.
Шешуі:  -ті
-ті  түріне келтіріп аламыз:
түріне келтіріп аламыз:

1)  яғни
яғни

2)  яғни
яғни

9- мысал.
 теңдеуін шешіңдер.
теңдеуін шешіңдер.
Шешуі:  немесе
немесе 

 мұндағы
мұндағы 
 мұндағы
мұндағы  .
.
Жауабы:  мұндағы
мұндағы 
 мұндағы
мұндағы  .
.
10- мысал.
 теңдеуді шешіңдер.
теңдеуді шешіңдер.
Шешуі:  формуласын пайдалансақ
формуласын пайдалансақ
 немесе
немесе 
1)  яғни
яғни

2) 
 .
.

 түріндегі
теңдеулер. Бұл теңдеулерді
түріндегі
теңдеулер. Бұл теңдеулерді
 және
және  -ге қарағанда біртекті теңдеулерге
келтіруге болады. Немесе
-ге қарағанда біртекті теңдеулерге
келтіруге болады. Немесе  формуласын пайдаланып шешуге болады,
мұндағы
формуласын пайдаланып шешуге болады,
мұндағы  .
.
11- мысал.
 теңдеуді шешу керек. Жарты аргумент
функцияларға көшсек,
теңдеуді шешу керек. Жарты аргумент
функцияларға көшсек, 
 Немесе
Немесе  бұл біртекті теңдеу,
бұл біртекті теңдеу,  -ге
-ге
бөлгенде  бұдан табатынымыз:
бұдан табатынымыз: 
 теңдеуінде
теңдеуінде  және
және  -кез келген нақты сандар.
-кез келген нақты сандар.
Егер 
 және
және  -ке қарағанда біртекті
теңдеулер.
-ке қарағанда біртекті
теңдеулер.
 теңдеуі бірінші дәрежелі біртекті
теңдеу деп аталады. Бұл теңдеудің екі бөлігін де
теңдеуі бірінші дәрежелі біртекті
теңдеу деп аталады. Бұл теңдеудің екі бөлігін де  деп бөлсек,
деп бөлсек,  осы теңдеудің түбірін
табамыз.
осы теңдеудің түбірін
табамыз.
12- мысал.
 теңдеуін шешу керек.
теңдеуін шешу керек.  теңдеуімен мәндес.
теңдеуімен мәндес.  немесе
немесе  .
.
 теңдеуін қос бұрыш енгізу әдісі арқылы
шешу.
теңдеуін қос бұрыш енгізу әдісі арқылы
шешу.
Біз
білеміз, егер  болса,
болса,  бұрышы болады,
бұрышы болады,  немесе керісінше.
немесе керісінше.  теңдеуін шешу үшін
теңдеуін шешу үшін  көбейткішін жақша сыртына шығарамыз.
Сонда
көбейткішін жақша сыртына шығарамыз.
Сонда  теңдеуін
аламыз.
теңдеуін
аламыз.  болғандықтан,
бірінші
болғандықтан,
бірінші  санды
кейбір
санды
кейбір
 бұрышының косинусы деп қабылдап, ал
екінші
бұрышының косинусы деп қабылдап, ал
екінші  сол
сол
 бұрышының синусымен алмастырып
жазамыз, яғни
бұрышының синусымен алмастырып
жазамыз, яғни  ,
,  . Мұндай жағдайда теңдеу
. Мұндай жағдайда теңдеу
 немесе
немесе  түріне келеді, бұдан
түріне келеді, бұдан  . Бұл теңдеудің шешімі болады,
егер
. Бұл теңдеудің шешімі болады,
егер  , сонда
, сонда
 ,
,
 .
.
 бұрышы
бұрышы  теңдігінен табылады,
теңдігінен табылады,  .
.
Жауабы:  .
.
 – теңдеуін рационалдау әдісімен
шешу.
– теңдеуін рационалдау әдісімен
шешу.
Белгілі,
егер  , онда
, онда
 ,
,  және
және  ,
,  арқылы рационалды өрнектеледі,
яғни
арқылы рационалды өрнектеледі,
яғни  ,
,  және
және  . Рационалдау әдісі мыналардан
қорытылады: алмастырудан кейін рационалды теңдеу белгісіз
көмекшімен салыстыруға болатын, белгісіз көмекші ендіреміз.
. Рационалдау әдісі мыналардан
қорытылады: алмастырудан кейін рационалды теңдеу белгісіз
көмекшімен салыстыруға болатын, белгісіз көмекші ендіреміз.
 теңдеуін қарастырамыз,
бұдан
теңдеуін қарастырамыз,
бұдан  теңдеуін
аламыз.
теңдеуін
аламыз.  деп алсақ,
онда
деп алсақ,
онда  аламыз. Бұл теңдеу-
рационалды салыстырмалы
аламыз. Бұл теңдеу-
рационалды салыстырмалы  .
.
Теңдеудің екі бөлігін  көбейтеміз, сонда
көбейтеміз, сонда 
 болады.
болады.
 немесе
немесе  деп көрсек,
деп көрсек,  болады.
болады.  мәні –нақты, егер
мәні –нақты, егер  . Егер
. Егер  теңдеуінде
теңдеуінде  деп алсақ, ендеше ол бірінші дәрежелі
теңдеуге айналады:
деп алсақ, ендеше ол бірінші дәрежелі
теңдеуге айналады:  яғни
яғни  ,
,  .
.  болғанда,
болғанда,  өрнегі көмекші белгісізге мәнін
жоғалтады, яғни
өрнегі көмекші белгісізге мәнін
жоғалтады, яғни  .
.  теңдеудің шешімі
теңдеудің шешімі  жоғалуы мүмкін.
жоғалуы мүмкін.  теңдеуді
теңдеуді  алмастыру арқылы:
алмастыру арқылы: 
 ;
;  .
.
Мұндай
жағдайда  теңдеу
теңдеу
 түріндегі шешімдер жиыны көп
болады.
түріндегі шешімдер жиыны көп
болады.
-
Егер
 болса,
онда
болса,
онда  теңдеудің шешімі
болмайды,
теңдеудің шешімі
болмайды,  теңдеудің нақты
түбірлері болмағандықтан.
теңдеудің нақты
түбірлері болмағандықтан. -
Егер
 және
және
 болса, онда
болса, онда  теңдеуден
теңдеуден  табамыз.
табамыз. -
Егер
 , онда
, онда
 теңдеудің 2 шешімі бар:
теңдеудің 2 шешімі бар:
 және
және  .
.
Теңбе-тең түрлендірулер арқылы қарапайым түрге келтірілетін тригонометриялық теңдеулер.
Тигонометриялық теңдеудің сипаты оның құрамындағы тригонометриялық өрнектің қабылдайтын мәндеріне немесе анықталу облысына байланысты. Алгебралық өрнектер сияқты тригонометриялық теңбе-теңдікті құрайтын өрнектерде түрлендіру есептер шешуде аса маңызды роль атқарады. Әсіресе теңдеулер шешуде тригонометриялық теңбе-теңдіктер аклғашқы немесе негізгі ұғым болып саналады. Теңдеулер шешуге өте көп теңбе-теңдіктерден ең қажеттісін таңдап алу–есептің тиімді тәсілдер көмегімен оңай шешілуіне мүмкіндік береді.
13- мысал.
Теңдеуді
шешіңдер. 
Теңдеуді  түрінде жазалық. Қосындыға
түрлендіріп,
түрінде жазалық. Қосындыға
түрлендіріп,  өрнегін қос
бұрыштың формуласы бойынша жазсақ, теңдеуді
өрнегін қос
бұрыштың формуласы бойынша жазсақ, теңдеуді  деп жазуға болады. Бұдан
деп жазуға болады. Бұдан
 қарапайым теңдеулерге келеді.
Бұл арада
қарапайым теңдеулерге келеді.
Бұл арада

Түбірлерді салыстыра келіп,  түбірлерінің жалпы түбір екенін
байқаймыз.
түбірлерінің жалпы түбір екенін
байқаймыз.
Жауабы:  .
.
Біртектес тригонометриялық теңдеулер.

түріндегі теңдеуді біртектес теңдеу деп атайды.
 жағдайында
жағдайында  теңдеудің екі бөлігінде
теңдеудің екі бөлігінде
 өрнегіне көбейтіп
өрнегіне көбейтіп
 теңдеуді аламыз, егер болса,
онда соңғы теңдеудің мәні болмайды.
теңдеуді аламыз, егер болса,
онда соңғы теңдеудің мәні болмайды.
14- мысал.
 теңдеуді шешейік.
теңдеуді шешейік.
Шешуі:
Теңдеудің екі жағын  өрнегіне көбейтіп,
өрнегіне көбейтіп, 
 немесе
немесе
 Бұл арадан
Бұл арадан 
 .
.
Жауабы: 
1.2 Параметрі бар тригонометриялық теңдеулерді шешу әдістері
Параметрі бар тригонометриялық теңдеулерді шешу барысында параметрдің бақыланатын мәндеріне нүктелеріне ерекше назар аудару керек.
15- мысал.
Теңдеудің шешімін тап: .
.
Шешуі:
Берілген теңдеуде  мәні бірінші бақылау мәні. Егер
мәні бірінші бақылау мәні. Егер
 болса, онда теңдеудің шешімі
болмайды. Егер
болса, онда теңдеудің шешімі
болмайды. Егер  болса, онда
болса, онда
 (2.1.1)
(2.1.1)
теңдеуін
аламыз. Бұл теңдеудің шешімінің барлығы  теңсіздінің шешіміне байланысты
болады. Олай болса,
теңсіздінің шешіміне байланысты
болады. Олай болса,  мәндері екінші бақылау мәндері болады.
Сонда
мәндері екінші бақылау мәндері болады.
Сонда

мәндері үшін (2.1.1) теңдеуінің шешімі

түрінде анықталады. Ал

мәндері
үшін (2.1.1) теңдеудің шешімдері болмайды. Себебі  теңсіздігі орындалады.
теңсіздігі орындалады.
Жауабы:
Егер  болса, онда
берілген теңдеудің шешімі болмайды.
болса, онда
берілген теңдеудің шешімі болмайды.
Егер  болса,
онда
болса,
онда [25]
.
[25]
.
16- мысал.
Теңдеудің шешімін тап: .
.
Шешуі:
Егер  болса, онда
теңдеудің шексіз көп шешімі болады. Себебі
болса, онда
теңдеудің шексіз көп шешімі болады. Себебі кез келген мәнінде
кез келген мәнінде  теңбе теңдігін аламыз.
теңбе теңдігін аламыз.
 болған жағдайда
болған жағдайда  ~
~  шешімін аламыз.
шешімін аламыз.
Жауабы:
Егер  болса,
онда
болса,
онда ал
ал  болса, онда
болса, онда берілген теңдеудің шешімдері
болады.
берілген теңдеудің шешімдері
болады.
17- мысал.
Теңдеудің шешімін тап:  .
.
Шешуі:
Егер  болса, онда
теңдеудің шексіз көп шешімі болады. Себебі
болса, онда
теңдеудің шексіз көп шешімі болады. Себебі  кез келген мәнінде
кез келген мәнінде  теңбе теңдігін аламыз.
теңбе теңдігін аламыз.
 болған жағдайда
болған жағдайда

шешімін табамыз.
Жауабы:
Егер  болса,
онда
болса,
онда
Егер  болса,
онда
болса,
онда

 теңдеуінің шешімі
теңдеуінің шешімі  формуласымен анықталады.
формуласымен анықталады.
18- мысал.
Теңдеудің шешімін тап: 
Шешуі: Берілген теңдеу белгілі формулаларды пайдалану арқылы
 (2.1.2)
(2.1.2)
Егер  ,
онда
,
онда . Олай болса (2.1.2)
теңдеудің шешімдері болмайды. Егер
. Олай болса (2.1.2)
теңдеудің шешімдері болмайды. Егер  онда
онда Соңғы теңдеудің шешімі болуы
үшін
Соңғы теңдеудің шешімі болуы
үшін  ~
~  шартының орындалуы керек.
Сонда
шартының орындалуы керек.
Сонда шешімін
аламыз.
шешімін
аламыз.
Жауабы:
Егер  болса,
онда
болса,
онда ,
,
Егер  болса, онда
теңдеудің шешімі болмайды.
болса, онда
теңдеудің шешімі болмайды.
19- мысал.
Теңдеудің шешімін тап: 
Шешуі: Берілген теңдеуде бірден бақылау мәндерін көру қиындық келтіреді. Сондықтан берілген теңдеуді теңбе-тең түрлендірелік:
 ~
~  ~
~  ~
~
~
 ~
~  . Бұдан
. Бұдан  бақылау мәндерін табамыз. Сонымен,
егер
бақылау мәндерін табамыз. Сонымен,
егер  болса,
онда
болса,
онда

шешімін
аламыз. Ал,  болса, онда
теңдеудің шешімі болмайды.
болса, онда
теңдеудің шешімі болмайды.
Жауабы:
 болса, онда
болса, онда ;
;
 болса, онда теңдеудің шешімі
болмайды.
болса, онда теңдеудің шешімі
болмайды.
20- мысал.
Теңдеудің шешімін тап: 
Шешуі: Берілген теңдеуде қосымша бұрыш енгізу үшін, оның екі жағын да

өрнегіне бөлелік. Мұнда

болғандықтан, қандай да бір  бұрышы табылып
бұрышы табылып

 (2.1.3)
(2.1.3)
теңдіктері орындалатын болады. Онда
 ~
~  (2.1.4)
(2.1.4)
теңдеуіне келеміз. Бұл теңдеудің нақты шешімдері болуы
үшін  теңсіздігі орындалуы
керек. Онда қандай да бір
теңсіздігі орындалуы
керек. Онда қандай да бір  бұрышы табылып
бұрышы табылып
 (2.1.5)
(2.1.5)
теңдігі орындалатын болады және (2.1.4) теңдеуі

түріне келеді. Бұл теңдеудің шешімдері
 ~
~ 
немесе
 ~
~ 
болады. Сонда, (2.1.3) және (2.1.5) пайдалана отырып бірінші шешімді
 ,
,
екінші шешімді

түрінде анықтаймыз.
Жауабы:
 болса, онда
болса, онда
 ,
,

 болса, онда теңдеудің шешімі
болмайды.
болса, онда теңдеудің шешімі
болмайды.
21- мысал.
Теңдеудің шешімін тап: 
Шешуі: Берілген теңдеуді теңбе-тең түрлендірелік. Теңдеудің сол жағын толық квадратқакелтіру арқылы түрлендірелік.
 ~
~
 ~
~  ~
~  ~
~

 ~
~  .
.
Соңғы
теңдеудің  ~
~
 шарты орындалғанда ғана шешімі
болады. Сонымен, егер
шарты орындалғанда ғана шешімі
болады. Сонымен, егер  орындалатын болса, онда
орындалатын болса, онда

шешімін табамыз.
Жауабы:
 болса, онда
болса, онда ;
;
 болса, онда теңдеудің шешімі
болмайды [28].
болса, онда теңдеудің шешімі
болмайды [28].
22- мысал.
Теңдеудің шешімін тап: 
Шешуі:
Берілген теңдеудің анықталу облысы  теңсіздігімен беріледі. Берілген
теңдеуді теңбе-тең түрлендірелік:
теңсіздігімен беріледі. Берілген
теңдеуді теңбе-тең түрлендірелік:
 ~
~  ~
~
~  .
.
Бұл
теңдеуден  теңдеуін, оның
шешімі
теңдеуін, оның
шешімі  аламыз. Бұл
шешім
аламыз. Бұл
шешім  параметрінен
тәуелсіз, яғни
параметрінен
тәуелсіз, яғни  Ал
Ал  биквадрат теңдеуінің шешімі болуы
үшін, оның дискриминанты теріс болмауы керек:
биквадрат теңдеуінің шешімі болуы
үшін, оның дискриминанты теріс болмауы керек:  Бұл жағдайда
Бұл жағдайда бірақ
бірақ  Соңғы теңсіздіктің орындалуын
тексерелік:
Соңғы теңсіздіктің орындалуын
тексерелік:
1)  ~
~
 ~
~  ~
~ ~
~  ~
~  ~
~ 
Соңғы теңсіздік орындалған жағдайда
 ,
,  шешімін аламыз.
шешімін аламыз.
2)  ~
~
 ~
~  ~
~  ~
~  ~
~ 
Соңғы теңсіздік орындалған жағдайда
 ,
,  шешімін аламыз.
шешімін аламыз.
Жауабы:
 болса, онда,
болса, онда,  .
.
 болса, онда:
болса, онда:
 ;
;
 ;
;
 .
.
 болса, онда:
болса, онда:
 ;
;  .
.
23- мысал.
Теңдеудің шешімін тап: 
Шешуі:
Берілген теңдеудің екі жағын  көбейтесек
көбейтесек теңдеуін аламыз. Бұл теңдеудің сол
жағындағы көбейтіндіні қосындыға түрлендірелік, сонда
теңдеуін аламыз. Бұл теңдеудің сол
жағындағы көбейтіндіні қосындыға түрлендірелік, сонда
 ~
~  .
.
Соңғы теңдеуде косинустардың тең болу шартын пайдалансақ
 ~
~ 
Тексеру.
Жоғарыда берілген теңдеудің екі жағын  көбейту барысында берілген теңдеудің
анықталу облысын кеңейттік. Олай болса бөгде түбірлердің пайда
болуы мүмкін. Сондықтан табылған шешімдер жиынтығынан берілген
теңдеудің шешімі болатындай шешімдер жиынтығын бөліп алалық. Ол
үшін табылған шешімдер жиынтығынан
көбейту барысында берілген теңдеудің
анықталу облысын кеңейттік. Олай болса бөгде түбірлердің пайда
болуы мүмкін. Сондықтан табылған шешімдер жиынтығынан берілген
теңдеудің шешімі болатындай шешімдер жиынтығын бөліп алалық. Ол
үшін табылған шешімдер жиынтығынан  теңдеуін қанағаттандыратын
теңдеуін қанағаттандыратын
 -тің
-тің  мәндерін шығарып тасталық. Табылған
шешімдер жиынтығындағы
мәндерін шығарып тасталық. Табылған
шешімдер жиынтығындағы  мәндер
мәндер  мәндерімен қиылыспайды. Онда
мәндерімен қиылыспайды. Онда
 берілген теңдеудің шешімі
болады. Шешімдер жиынтығындағы екінші топ шешімдері үшін
берілген теңдеудің шешімі
болады. Шешімдер жиынтығындағы екінші топ шешімдері үшін
 ~
~ 
теңдігін
жазуға болады. Сонымен  жиынтығы шешім болуы үшін
жиынтығы шешім болуы үшін
 шарты орындалуы
керек.
шарты орындалуы
керек.
Жауабы:
 болса, онда,
болса, онда,  .
.
 болса, онда
болса, онда
24- мысал.
 теңдеуінде,
теңдеуінде,  параметрінің барлық мәнін табу
керек.
параметрінің барлық мәнін табу
керек.
Бірінші қосылғышты мына

түрге
келтіріп, ал екінші қосылғышты  ,
,  айнымалысын енгізіп теңдеуді мына
түрде жазып аламыз
айнымалысын енгізіп теңдеуді мына
түрде жазып аламыз

Оның
түбірі болады, егер 
Солайша  -ның кез келген мәнінде
-ның кез келген мәнінде
 екі түбірі (
екі түбірі ( ) болады.
) болады.  болғандықтан, егер
болғандықтан, егер  түбірлерінің тым болмаса біреуі
түбірлерінің тым болмаса біреуі
 аралыққа кірсе, бастапқы
теңдеудің мәні болады,
аралыққа кірсе, бастапқы
теңдеудің мәні болады,
А. Екі
түбірді де осы аралықта жатады деп алайық, яғни . Онда
. Онда  функциясының минимум нүктесінің
абциссасы мына аралықта жатады:
функциясының минимум нүктесінің
абциссасы мына аралықта жатады: 
функцияның минимал мәні теріс:  а-ның кез келген мәнінде орындалады;
функцияның мәні аралықтың соңында теріс емес:
а-ның кез келген мәнінде орындалады;
функцияның мәні аралықтың соңында теріс емес: 
 . Қарастырылған
шарттардың жүйесі
. Қарастырылған
шарттардың жүйесі  үйлеспегендіктен,
үйлеспегендіктен,  аралықтарда
аралықтарда  екі шешімі болуы мүмкін
емес.
екі шешімі болуы мүмкін
емес.
В.  аралыққа
аралыққа
 түбірлерінің біреуі жатады деп
алайық. Онда
түбірлерінің біреуі жатады деп
алайық. Онда  аралықтың
соңында әр түрлі таңбалы екі мән қабылдайды, оның біреуі нөлдік
болуы мүмкін, яғни
аралықтың
соңында әр түрлі таңбалы екі мән қабылдайды, оның біреуі нөлдік
болуы мүмкін, яғни  шарты орындалады, бұдан интервалдар
әдісімен
шарты орындалады, бұдан интервалдар
әдісімен  аламыз.
аламыз.
Жауабы:  .
.
25- мысал.

Шешуі.
Теңдеудің сол жақ бөлігін кубтардың қосындысы бойынша
 теңдеуін аламыз немесе
теңдеуін аламыз немесе
 яғни
яғни 
 мәні
болады.
мәні
болады.
Соңғы
теңсіздік  береді. Ерекше
жағдай
береді. Ерекше
жағдай  . Онда теңдеу мына
түрге келеді
. Онда теңдеу мына
түрге келеді  , шешімі
жоқ.
, шешімі
жоқ.
Жауабы:  болғанда,
болғанда, 
 және
және  болғанда, шешімі болмайды.
болғанда, шешімі болмайды.
26- мысал.
 - теңдеуін шешу.
- теңдеуін шешу.

а)  Бір мезгілде
мына теңсіздіктер орындалуы тиіс:
Бір мезгілде
мына теңсіздіктер орындалуы тиіс:
 бұдан
бұдан 
Осы
шарт бойынша 
б)  Бір мезгілде
мына теңсіздіктер орындалуы тиіс:
Бір мезгілде
мына теңсіздіктер орындалуы тиіс:
 бұдан
бұдан  .
.
Осы шарт
бойынша 
Жауабы:  болғанда,
болғанда, 

 болғанда,
болғанда, 

 болғанда,
болғанда, 
Параметрі бар теңдеулерді шешу үшін төмендегі әдістерді қолдану көптеген күрделі есептерді шешуді айтарлықтай жеңілдетеді. Әрбір әдіс үлгісін қолдану арқылы студент оған оңайсәйкес әдісті таниды және қолданаалады. Берілген мысалдар факультативті сабақтарда қолданылуы мүмкін. Бұл студенттерге осы түрдегі мәселелерді шешуде тәжірибе жинақтауға көмектеседі [29].
А) Жаңа айнымалыларды енгізу.
Жаңа айнымалы мәндерді енгізу сізге тапсырманы түсінуді жеңілдетуге және тапсырманы жеңілдетуге мүмкіндік береді. Мұндай тәсіл мынадай жағдайларда қолданылуы мүмкін.
-
төмендегі түрде берілген тригонометриялық теңдеулерде

Жаңа
айнымалы енгізу арқылы келесі теңдіктерді
қолданамыз
арқылы келесі теңдіктерді
қолданамыз

Төмендегі түрде берілген теңдеуге

Жаңа
айнымалы енгізуге болады және келесі түрлендірулер
енгіземіз
және келесі түрлендірулер
енгіземіз

Төмендегі түрде берілген теңдеуге

Жаңа
айнымалы енгізуге болады және келесі түрлендірулер
енгіземіз
және келесі түрлендірулер
енгіземіз

1.4. Төмендегі түрде берілген теңдеуге

Жаңа
айнымалы енгізуге болады  , где
, где

және
келесі түрлендірулер енгіземіз .
.
Жоғарыда айтылған әдістерге байланысты бірнеше мысал қарастырайық.
27- мысал.
 параметрінің қандай мәнінде
теңдеу
параметрінің қандай мәнінде
теңдеу


аралықта бірден көп шешімі болады.
Шешуі:  деп аламыз, сонда
деп аламыз, сонда










 және
және  .
.
Бізге (0,1) аралықта теңдеудің бірден көп түбірі керек , сол себепті


Жауабы
:  .
.
B) Айнымалылар мен параметрлердің мүмкінмәндерінің облысының бөлінуі
Айнымалылардың немесе параметрлердің мүмкін мәндерінің облысы немесе кейбір өрнектер бөлінбеген жиынтықтарға бөлінеді. Бұл тапсырманы жеңілдетуге немесе тапсырманы жаңа пішінге аударуға мүмкіндік береді.
28- мысал.
 параметріне байланысты теңдеуді
шешу
параметріне байланысты теңдеуді
шешу .
.
Шешуі
: бірден белгілі,  әркезде дұрыс жауабы
болатыны.
әркезде дұрыс жауабы
болатыны.
Егер  деп алсақ,
онда
деп алсақ,
онда  теңдеуін аламыз.
Егер
теңдеуін аламыз.
Егер , онда есептің
жауабы болмайды, егер
, онда есептің
жауабы болмайды, егер  , онда
, онда . Біз
. Біз  екенін ескере отырып:
екенін ескере отырып: болған жағдайда
болған жағдайда және
және ,
,  .
.
Енді  болған
жағдайда, онда
болған
жағдайда, онда . Егер
. Егер , онда жауабы болмайды,
егер
, онда жауабы болмайды,
егер  ,
онда
,
онда . Егер
. Егер
 ескерсек:
ескерсек:
 және
және 
 .
.
Енді жауабын жазсақ болады.
Жауабы
: болған
жағдайда
болған
жағдайда  ,
,
 ,
, ,
,  ,
,
 ,
, ,
,  .
.
C) Көмекші түрлендірулер
Көмекші түрлендірулерді қолдану арқылы теңдеудегі өрнектерді жеңілдетуге болады немесе 1 және 2 тәсілдерін қолдануға мүмкіндік береді.
29- мысал.
Теңдеудің кем дегенде бір шешімі болатын табу
табу

Шешуі: Бұл теңдеуді түрлендіру үшін қысқаша көбейту формулаларын және негізгі тригонометриялық сәйкестіктерді пайдаланамыз:

Теңдеудің екі бөлігін де 4 ке бөлеміз:


Теңдеудің сол жақ бөлігіндегі  ортақ көбейткіштерді жақшаның сыртына
шығарып төмендегі өрнекті аламыз:
ортақ көбейткіштерді жақшаның сыртына
шығарып төмендегі өрнекті аламыз:

 .
.
 болса,
болса, , теңдеудің жауабы
болмайды.
, теңдеудің жауабы
болмайды.
Енді  болғанда
болғанда аламыз.
аламыз.
 аралығында жататынын білеміз, сол
себепті
аралығында жататынын білеміз, сол
себепті ,
демек
,
демек


 .
.
Соңғы жүйеден жауабын аламыз.
Жауабы
:
D) Дәстүрлі формулаларды қолдану
Классикалық сәйкестіктерді, теңсіздікті, қасиеттерері мен теоремалары пайдалану арқылы көптеген теңдеулердің шешімін жеңілдетуге болады. Осындай теңдеулерге мысал келтірейік.
30- мысал.
Функцияның ең үлкен мәнін табыңыз
 егер
егер  .
.
Шешуі : Осы функцияның квадратының ең үлкен мәнін табыңыз
 .
.
 болатынын ескере
отырып,
болатынын ескере
отырып, функциясын
аламыз.
функциясын
аламыз.
Ең үлкен мән радикал болғанда, өрнек ең үлкен мәнді қабылдайды.
 теңдеуін аламыз.
теңдеуін аламыз.
Егер екі оң айнымалының мәні тұрақты болса, екі көбейтінді бір мәнге ие болғанда, онда осы айнымалылардың шешімі ең үлкен мәнге ие болады.

 .
.
Егер  , онда
, онда .
.
Бұл
жағдайда оның әрқайсысы бағынатын өрнектерге тең және
және
 .
.
Егер , онда
функцияның мәні 2-ге тең.
, онда
функцияның мәні 2-ге тең.
Жауабы
:  .
.
Осы әдістерді пайдаланып есептер шығарып көрейік
31- мысал.
Теңдеуді
шешейік  .
.
 болған жағдайда теңдеудің мағынасы
болады.
болған жағдайда теңдеудің мағынасы
болады.  мәні
мәні , осы жағдайды
қанағаттандыру қажет.
, осы жағдайды
қанағаттандыру қажет.

Егер  .
.
Қарапайым түрлендірулер мына теңдеуге алып келеді

және осы теңдеудің екі түбірі болады:
 ,
,  . Жоғарыда айтылып кеткендей
. Жоғарыда айтылып кеткендей
 мәні мына жағдайды
мәні мына жағдайды
 қанағаттандыру қажет.
қанағаттандыру қажет.
Демек,  немесе
немесе  (немесе екі сан) тең болатын m
мәндерін алып тастау қажет.
(немесе екі сан) тең болатын m
мәндерін алып тастау қажет.
 егер
егер болса онда
болса онда .
.
 егер
егер болса онда
болса онда
егер 
 ;
;
егер 
 ;
;
егер ,
,
 , m ≠ 0 теңдеудің екі түбірі бар
болады:
, m ≠ 0 теңдеудің екі түбірі бар
болады:
 ,
,  ,
,
k, n, s – бір-біріне тәуелсіз, барлық бүтін сандардың мәндерін қабылдайды.
32- мысал.
Параметрдің  теңдеуі бар параметрдің ең үлкен бүтін
мәнін табыңыз.
теңдеуі бар параметрдің ең үлкен бүтін
мәнін табыңыз.
Шешім:
осы теңдеуді түрлендіру:  ;
; 
 ;
;  ;
;
 .
.
Теңдеудің шешімі береді:
береді:
 ; х бос жиынға жатады.
; х бос жиынға жатады.
 ;
;
 егер
егер .
.
Теңсіздіктің шешімі
шешімі болады және бұл жерден
аңғаратынымыз,оның ең үлкен мәні 6-ға тең.
болады және бұл жерден
аңғаратынымыз,оның ең үлкен мәні 6-ға тең.
Жауабы: 6.
33- мысал.

Шешуі:  Теңдеуді мына түрде жазып
алайық
Теңдеуді мына түрде жазып
алайық  . Қосындыны
түрлендіріп мынаны аламыз:
. Қосындыны
түрлендіріп мынаны аламыз:  немесе
немесе

а) 

б) 


34- мысал.

Шешуі: Теңдеу мына функцияға қатысты квадраттық теңдеуге айналады
 , осыдан
, осыдан

а)  әрқашан, сонымен қатар
әрқашан, сонымен қатар
 болуы тиіс. Теңсіздікті шеше
отырып, а- кез келген нақты сан екенін аламыз.
болуы тиіс. Теңсіздікті шеше
отырып, а- кез келген нақты сан екенін аламыз.
б)  .
.  теңсіздігі а-ның ешқандай мәнінде
орындалмайды.
теңсіздігі а-ның ешқандай мәнінде
орындалмайды.
 болғандағы ерекше жағдай! Тендеу
келесі түрге келеді:
болғандағы ерекше жағдай! Тендеу
келесі түрге келеді: 
Жауабы: 


35- мысал.

Шешуі: . Тендеу мына түрге
түрленеді:
. Тендеу мына түрге
түрленеді:
 яғни
яғни 
Егер

 , онда соңғы теңдеу мынандай шешімін
табады
, онда соңғы теңдеу мынандай шешімін
табады 

Жауабы: 

 .
.
Жаттығулар:


 теңдеуін шеш;
теңдеуін шеш;
 теңдеуін шеш;
теңдеуін шеш;
 теңдеуін шеш;
теңдеуін шеш;
 теңдеуін шеш;
теңдеуін шеш;
 теңдеуін шеш;
теңдеуін шеш;
 теңдеуін шеш;
теңдеуін шеш;
 теңдеуін шеш және
теңдеуін шеш және  аралығында неше шешімі болатынын
анықта;
аралығында неше шешімі болатынын
анықта;
 теңдеуін шешіңіз.
теңдеуін шешіңіз.




жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Параметрмен берілген тригонометриялық теңдеулерді шешу
Параметрмен берілген тригонометриялық теңдеулерді шешу
Параметрмен берілген тригонометриялық теңдеулерді шешу
1.1 Қарапайым тригонометриялық теңдеулерді шешу
Кей жағдайларда құрамында параметрі бар болатын көрсеткіштік, логарифмдік және тригонометриялық теңдеулер мен теңсіздіктерді шешу керек болады. Мұндай теңдеулер мен теңсіздіктерді жалпы жағдайда транценденттік деп атайды. Параметрдің мәндеріне байланысты теңдеулер мен теңсіздіктердің түбірлері бірнешеу болуы немесе болмауы мүмкін, кей жағдайларда белгілі бір аралықтарда жататын түбірлері табылуы мүмкін.
Тригонометриялық теңдеу–белгісіз аргументтің
тригонометриялық функциясына қатысты алгебралық теңдеу.
Тригонометриялық теңдеуді шешу үшін тригонометриялық функциялардың
арасындағы әр түрлі қатынастарды пайдалана отырып, тригонометриялық
теңдеулерді ізделініп отырған аргументтің тригонометриялық
функциялары біреуінің мәнін анықтауға болатындай түрге келтіру
керек.  ,
,  ,
,  ,
,  түрінде берілген теңдеу қарапайым
тригонометриялық теңдеу деп аталады. Кез
келген тригонометриялық теңдеуді шешу қарапайым тригонометриялық
теңдеуді шешуге арқылы шығады, ал қарапайым тригонометриялық
теңдеулер келесі формулалар арқылы есептеледі:
түрінде берілген теңдеу қарапайым
тригонометриялық теңдеу деп аталады. Кез
келген тригонометриялық теңдеуді шешу қарапайым тригонометриялық
теңдеуді шешуге арқылы шығады, ал қарапайым тригонометриялық
теңдеулер келесі формулалар арқылы есептеледі:
-
Егер
 болса, онда
болса, онда  теңдеуінің шешімі
теңдеуінің шешімі  формуласымен анықталады.
формуласымен анықталады.
Дербес
жағдайлары: 
2. Егер
 болса, онда
болса, онда теңдеуінің шешімі
теңдеуінің шешімі  формуласымен анықталады.
формуласымен анықталады.
Дербес
жағдайлары: 
3.  теңдеуінің
шешімі
теңдеуінің
шешімі  формуласымен
анықталады.
формуласымен
анықталады.
Дербес
жағдайлары: 
4.  теңдеуінің
шешімі
теңдеуінің
шешімі  формуласымен
анықталады.
формуласымен
анықталады.
Дербес
жағдайлары: 
Тригонометриялық теңдеулерді шешу әдістері
-
Көбейткіштерге жіктеу
Бұл
тәсілде  теңдеуінің
шешімі
теңдеуінің
шешімі  теңдеулерінің
шешімімен тең екендігі негізге алынып шығарылады.
теңдеулерінің
шешімімен тең екендігі негізге алынып шығарылады.
1- мысал .
 .
.
Шешуі: 

-
Жаңа айнымалы енгізу
Егер теңдеу бір ғана тригонометиялық функциялардан құралған болса, теңдеу алгебралық әдіс арқылы шығады.
2-
мысал. 
Шешуі:  формуласын қолдана отырып, келесі
теңдеуді аламыз:
формуласын қолдана отырып, келесі
теңдеуді аламыз: 
-
 түріндегі
тригонометриялық теңдеулерді шешу.
түріндегі
тригонометриялық теңдеулерді шешу.
Бұл
түрдегі теңдеулерді шығару үшін теңдеудің екі жағында
 және
және  - ге бөлу керек.
- ге бөлу керек.

теңдеуін
аламыз.  айнымалысын
енгізу арқылы теңдеуді шығарамыз.
айнымалысын
енгізу арқылы теңдеуді шығарамыз.
3- мысал.
 теңдеуін шешіңдер.
теңдеуін шешіңдер.
Шешуі:
теңдеуді  ке бөлу
арқылы
ке бөлу
арқылы  теңдеуін аламыз. Бұл
теңдеудің шешімі:
теңдеуін аламыз. Бұл
теңдеудің шешімі:  .
.
-
 түріндегі
тригонометриялық теңделерді шешу. Бұл түрдегі теңдеулерді шешудің
бірнеше әдістері бар.
түріндегі
тригонометриялық теңделерді шешу. Бұл түрдегі теңдеулерді шешудің
бірнеше әдістері бар.
4.1
Көмекші аргумент енгізу. Бұл
кезде  өрнегінің
орнына
өрнегінің
орнына  өрнегін
жазамыз.
өрнегін
жазамыз.  .
.
 - бұрышы көмекші аргумент деп
аталады.
- бұрышы көмекші аргумент деп
аталады.
4- мысал.
 теңдеуін шешіңдер.
теңдеуін шешіңдер.
Шешуі:  болатындығынан,
болатындығынан,  -нің қандай да бір мәнінде
-нің қандай да бір мәнінде
 және
және  болады. Олай болса,
болады. Олай болса,  немесе
немесе  .
.  . Ал теңдеуіміздің жауабы:
. Ал теңдеуіміздің жауабы:
 .
.
4.2
Универсал алмастыру. Бұл кезде
 және
және  функцияларын
функцияларын  формуласымен ауыстырамыз.
формуласымен ауыстырамыз.
5- мысал.
 теңдеуін шешіңдер.
теңдеуін шешіңдер.
Шешуі:  -ті
-ті  мен ауыстырамыз, ал
мен ауыстырамыз, ал  белгілейміз.
белгілейміз. 
5.  түріндегі
тригонометриялық теңдеулерді шешу.
түріндегі
тригонометриялық теңдеулерді шешу.
Теңдеу  немесе
немесе  түріне келтіріп шығарылады. Теңдеуді
шешу үшін
түріне келтіріп шығарылады. Теңдеуді
шешу үшін  бөліп,
бөліп,
 теңдеуін аламыз. Бұл теңдеуді
шығарсақ,
теңдеуін аламыз. Бұл теңдеуді
шығарсақ,  . Осылайша,
берілген теңдеудің шешімі:
. Осылайша,
берілген теңдеудің шешімі:  [15].
[15].
Тригонометриялық теңдеулерді шығарылу жолына байланысты 6
топқа бөлуге болады:
1. Тригонометриялық функциясының бір ғана түрлерімен берілген,
алгебралық теңдеулерге келтірілетін тригонометриялық теңдеулер;
2. Тригонометриялық формулаларды түрлендіру жолымен шешілетін
тригонометриялық теңдеулер;
3. Функциялардың дәрежесін төмендету арқылы шешілетін
тригонометриялық теңдеулер;
4. Біртектес тригонометриялық теңдеулерді шешу;
5. Қосымша аргумент енгізу арқылы шығарылатын тригонометриялық
теңдеулер;
6. Тригонометриялық теңдеулер жүйесін шешу[17].
Жіктеу арқылы шешілетін тригонометриялық теңдеулер.
Яғни  түріне
келтіретін теңдеулер. Сол белгілі бір бірнеше көбейтінділерден
тұрады. Оң бөлігі нөл, сондықтан ең болмағанда бір көбейткіш нөлге
тең болса ғана көбейтінді нөлге тең болады.
түріне
келтіретін теңдеулер. Сол белгілі бір бірнеше көбейтінділерден
тұрады. Оң бөлігі нөл, сондықтан ең болмағанда бір көбейткіш нөлге
тең болса ғана көбейтінді нөлге тең болады.
6- мысал.
 теңдеуді шешіңдер. (ММЖ) – мүмкін мәндер
жиыны.
теңдеуді шешіңдер. (ММЖ) – мүмкін мәндер
жиыны.
Шешуі:
(ММЖ) тапсақ  немесе
немесе

1)  бұдан
бұдан
 яғни
яғни
2)  бұдан
бұдан
 ММЖ-ға жатпайтынын көрсетейік.
ММЖ-ға жатпайтынын көрсетейік.


 -ның қандай мәнінде
тақ емес, ММЖ жатпайды.
-ның қандай мәнінде
тақ емес, ММЖ жатпайды.
7- мысал.
 теңдеуін шешіңдер.
теңдеуін шешіңдер.
Шешуі:
ММЖ 

1) бұдан
бұдан

2)  шешімі болмайды,
себебі сол бөлігі әруақытта оң сан. Теңдеудің түбірі
шешімі болмайды,
себебі сол бөлігі әруақытта оң сан. Теңдеудің түбірі
 .
.
Қосу формулаларын пайдаланып шешілетін теңдеулер.
8- мысал.
 теңдеуін шешіңдер.
теңдеуін шешіңдер.
Шешуі:  -ті
-ті  түріне келтіріп аламыз:
түріне келтіріп аламыз:

1)  яғни
яғни

2)  яғни
яғни

9- мысал.
 теңдеуін шешіңдер.
теңдеуін шешіңдер.
Шешуі:  немесе
немесе 

 мұндағы
мұндағы 
 мұндағы
мұндағы  .
.
Жауабы:  мұндағы
мұндағы 
 мұндағы
мұндағы  .
.
10- мысал.
 теңдеуді шешіңдер.
теңдеуді шешіңдер.
Шешуі:  формуласын пайдалансақ
формуласын пайдалансақ
 немесе
немесе 
1)  яғни
яғни

2) 
 .
.

 түріндегі
теңдеулер. Бұл теңдеулерді
түріндегі
теңдеулер. Бұл теңдеулерді
 және
және  -ге қарағанда біртекті теңдеулерге
келтіруге болады. Немесе
-ге қарағанда біртекті теңдеулерге
келтіруге болады. Немесе  формуласын пайдаланып шешуге болады,
мұндағы
формуласын пайдаланып шешуге болады,
мұндағы  .
.
11- мысал.
 теңдеуді шешу керек. Жарты аргумент
функцияларға көшсек,
теңдеуді шешу керек. Жарты аргумент
функцияларға көшсек, 
 Немесе
Немесе  бұл біртекті теңдеу,
бұл біртекті теңдеу,  -ге
-ге
бөлгенде  бұдан табатынымыз:
бұдан табатынымыз: 
 теңдеуінде
теңдеуінде  және
және  -кез келген нақты сандар.
-кез келген нақты сандар.
Егер 
 және
және  -ке қарағанда біртекті
теңдеулер.
-ке қарағанда біртекті
теңдеулер.
 теңдеуі бірінші дәрежелі біртекті
теңдеу деп аталады. Бұл теңдеудің екі бөлігін де
теңдеуі бірінші дәрежелі біртекті
теңдеу деп аталады. Бұл теңдеудің екі бөлігін де  деп бөлсек,
деп бөлсек,  осы теңдеудің түбірін
табамыз.
осы теңдеудің түбірін
табамыз.
12- мысал.
 теңдеуін шешу керек.
теңдеуін шешу керек.  теңдеуімен мәндес.
теңдеуімен мәндес.  немесе
немесе  .
.
 теңдеуін қос бұрыш енгізу әдісі арқылы
шешу.
теңдеуін қос бұрыш енгізу әдісі арқылы
шешу.
Біз
білеміз, егер  болса,
болса,  бұрышы болады,
бұрышы болады,  немесе керісінше.
немесе керісінше.  теңдеуін шешу үшін
теңдеуін шешу үшін  көбейткішін жақша сыртына шығарамыз.
Сонда
көбейткішін жақша сыртына шығарамыз.
Сонда  теңдеуін
аламыз.
теңдеуін
аламыз.  болғандықтан,
бірінші
болғандықтан,
бірінші  санды
кейбір
санды
кейбір
 бұрышының косинусы деп қабылдап, ал
екінші
бұрышының косинусы деп қабылдап, ал
екінші  сол
сол
 бұрышының синусымен алмастырып
жазамыз, яғни
бұрышының синусымен алмастырып
жазамыз, яғни  ,
,  . Мұндай жағдайда теңдеу
. Мұндай жағдайда теңдеу
 немесе
немесе  түріне келеді, бұдан
түріне келеді, бұдан  . Бұл теңдеудің шешімі болады,
егер
. Бұл теңдеудің шешімі болады,
егер  , сонда
, сонда
 ,
,
 .
.
 бұрышы
бұрышы  теңдігінен табылады,
теңдігінен табылады,  .
.
Жауабы:  .
.
 – теңдеуін рационалдау әдісімен
шешу.
– теңдеуін рационалдау әдісімен
шешу.
Белгілі,
егер  , онда
, онда
 ,
,  және
және  ,
,  арқылы рационалды өрнектеледі,
яғни
арқылы рационалды өрнектеледі,
яғни  ,
,  және
және  . Рационалдау әдісі мыналардан
қорытылады: алмастырудан кейін рационалды теңдеу белгісіз
көмекшімен салыстыруға болатын, белгісіз көмекші ендіреміз.
. Рационалдау әдісі мыналардан
қорытылады: алмастырудан кейін рационалды теңдеу белгісіз
көмекшімен салыстыруға болатын, белгісіз көмекші ендіреміз.
 теңдеуін қарастырамыз,
бұдан
теңдеуін қарастырамыз,
бұдан  теңдеуін
аламыз.
теңдеуін
аламыз.  деп алсақ,
онда
деп алсақ,
онда  аламыз. Бұл теңдеу-
рационалды салыстырмалы
аламыз. Бұл теңдеу-
рационалды салыстырмалы  .
.
Теңдеудің екі бөлігін  көбейтеміз, сонда
көбейтеміз, сонда 
 болады.
болады.
 немесе
немесе  деп көрсек,
деп көрсек,  болады.
болады.  мәні –нақты, егер
мәні –нақты, егер  . Егер
. Егер  теңдеуінде
теңдеуінде  деп алсақ, ендеше ол бірінші дәрежелі
теңдеуге айналады:
деп алсақ, ендеше ол бірінші дәрежелі
теңдеуге айналады:  яғни
яғни  ,
,  .
.  болғанда,
болғанда,  өрнегі көмекші белгісізге мәнін
жоғалтады, яғни
өрнегі көмекші белгісізге мәнін
жоғалтады, яғни  .
.  теңдеудің шешімі
теңдеудің шешімі  жоғалуы мүмкін.
жоғалуы мүмкін.  теңдеуді
теңдеуді  алмастыру арқылы:
алмастыру арқылы: 
 ;
;  .
.
Мұндай
жағдайда  теңдеу
теңдеу
 түріндегі шешімдер жиыны көп
болады.
түріндегі шешімдер жиыны көп
болады.
-
Егер
 болса,
онда
болса,
онда  теңдеудің шешімі
болмайды,
теңдеудің шешімі
болмайды,  теңдеудің нақты
түбірлері болмағандықтан.
теңдеудің нақты
түбірлері болмағандықтан. -
Егер
 және
және
 болса, онда
болса, онда  теңдеуден
теңдеуден  табамыз.
табамыз. -
Егер
 , онда
, онда
 теңдеудің 2 шешімі бар:
теңдеудің 2 шешімі бар:
 және
және  .
.
Теңбе-тең түрлендірулер арқылы қарапайым түрге келтірілетін тригонометриялық теңдеулер.
Тигонометриялық теңдеудің сипаты оның құрамындағы тригонометриялық өрнектің қабылдайтын мәндеріне немесе анықталу облысына байланысты. Алгебралық өрнектер сияқты тригонометриялық теңбе-теңдікті құрайтын өрнектерде түрлендіру есептер шешуде аса маңызды роль атқарады. Әсіресе теңдеулер шешуде тригонометриялық теңбе-теңдіктер аклғашқы немесе негізгі ұғым болып саналады. Теңдеулер шешуге өте көп теңбе-теңдіктерден ең қажеттісін таңдап алу–есептің тиімді тәсілдер көмегімен оңай шешілуіне мүмкіндік береді.
13- мысал.
Теңдеуді
шешіңдер. 
Теңдеуді  түрінде жазалық. Қосындыға
түрлендіріп,
түрінде жазалық. Қосындыға
түрлендіріп,  өрнегін қос
бұрыштың формуласы бойынша жазсақ, теңдеуді
өрнегін қос
бұрыштың формуласы бойынша жазсақ, теңдеуді  деп жазуға болады. Бұдан
деп жазуға болады. Бұдан
 қарапайым теңдеулерге келеді.
Бұл арада
қарапайым теңдеулерге келеді.
Бұл арада

Түбірлерді салыстыра келіп,  түбірлерінің жалпы түбір екенін
байқаймыз.
түбірлерінің жалпы түбір екенін
байқаймыз.
Жауабы:  .
.
Біртектес тригонометриялық теңдеулер.

түріндегі теңдеуді біртектес теңдеу деп атайды.
 жағдайында
жағдайында  теңдеудің екі бөлігінде
теңдеудің екі бөлігінде
 өрнегіне көбейтіп
өрнегіне көбейтіп
 теңдеуді аламыз, егер болса,
онда соңғы теңдеудің мәні болмайды.
теңдеуді аламыз, егер болса,
онда соңғы теңдеудің мәні болмайды.
14- мысал.
 теңдеуді шешейік.
теңдеуді шешейік.
Шешуі:
Теңдеудің екі жағын  өрнегіне көбейтіп,
өрнегіне көбейтіп, 
 немесе
немесе
 Бұл арадан
Бұл арадан 
 .
.
Жауабы: 
1.2 Параметрі бар тригонометриялық теңдеулерді шешу әдістері
Параметрі бар тригонометриялық теңдеулерді шешу барысында параметрдің бақыланатын мәндеріне нүктелеріне ерекше назар аудару керек.
15- мысал.
Теңдеудің шешімін тап: .
.
Шешуі:
Берілген теңдеуде  мәні бірінші бақылау мәні. Егер
мәні бірінші бақылау мәні. Егер
 болса, онда теңдеудің шешімі
болмайды. Егер
болса, онда теңдеудің шешімі
болмайды. Егер  болса, онда
болса, онда
 (2.1.1)
(2.1.1)
теңдеуін
аламыз. Бұл теңдеудің шешімінің барлығы  теңсіздінің шешіміне байланысты
болады. Олай болса,
теңсіздінің шешіміне байланысты
болады. Олай болса,  мәндері екінші бақылау мәндері болады.
Сонда
мәндері екінші бақылау мәндері болады.
Сонда

мәндері үшін (2.1.1) теңдеуінің шешімі

түрінде анықталады. Ал

мәндері
үшін (2.1.1) теңдеудің шешімдері болмайды. Себебі  теңсіздігі орындалады.
теңсіздігі орындалады.
Жауабы:
Егер  болса, онда
берілген теңдеудің шешімі болмайды.
болса, онда
берілген теңдеудің шешімі болмайды.
Егер  болса,
онда
болса,
онда [25]
.
[25]
.
16- мысал.
Теңдеудің шешімін тап: .
.
Шешуі:
Егер  болса, онда
теңдеудің шексіз көп шешімі болады. Себебі
болса, онда
теңдеудің шексіз көп шешімі болады. Себебі кез келген мәнінде
кез келген мәнінде  теңбе теңдігін аламыз.
теңбе теңдігін аламыз.
 болған жағдайда
болған жағдайда  ~
~  шешімін аламыз.
шешімін аламыз.
Жауабы:
Егер  болса,
онда
болса,
онда ал
ал  болса, онда
болса, онда берілген теңдеудің шешімдері
болады.
берілген теңдеудің шешімдері
болады.
17- мысал.
Теңдеудің шешімін тап:  .
.
Шешуі:
Егер  болса, онда
теңдеудің шексіз көп шешімі болады. Себебі
болса, онда
теңдеудің шексіз көп шешімі болады. Себебі  кез келген мәнінде
кез келген мәнінде  теңбе теңдігін аламыз.
теңбе теңдігін аламыз.
 болған жағдайда
болған жағдайда

шешімін табамыз.
Жауабы:
Егер  болса,
онда
болса,
онда
Егер  болса,
онда
болса,
онда

 теңдеуінің шешімі
теңдеуінің шешімі  формуласымен анықталады.
формуласымен анықталады.
18- мысал.
Теңдеудің шешімін тап: 
Шешуі: Берілген теңдеу белгілі формулаларды пайдалану арқылы
 (2.1.2)
(2.1.2)
Егер  ,
онда
,
онда . Олай болса (2.1.2)
теңдеудің шешімдері болмайды. Егер
. Олай болса (2.1.2)
теңдеудің шешімдері болмайды. Егер  онда
онда Соңғы теңдеудің шешімі болуы
үшін
Соңғы теңдеудің шешімі болуы
үшін  ~
~  шартының орындалуы керек.
Сонда
шартының орындалуы керек.
Сонда шешімін
аламыз.
шешімін
аламыз.
Жауабы:
Егер  болса,
онда
болса,
онда ,
,
Егер  болса, онда
теңдеудің шешімі болмайды.
болса, онда
теңдеудің шешімі болмайды.
19- мысал.
Теңдеудің шешімін тап: 
Шешуі: Берілген теңдеуде бірден бақылау мәндерін көру қиындық келтіреді. Сондықтан берілген теңдеуді теңбе-тең түрлендірелік:
 ~
~  ~
~  ~
~
~
 ~
~  . Бұдан
. Бұдан  бақылау мәндерін табамыз. Сонымен,
егер
бақылау мәндерін табамыз. Сонымен,
егер  болса,
онда
болса,
онда

шешімін
аламыз. Ал,  болса, онда
теңдеудің шешімі болмайды.
болса, онда
теңдеудің шешімі болмайды.
Жауабы:
 болса, онда
болса, онда ;
;
 болса, онда теңдеудің шешімі
болмайды.
болса, онда теңдеудің шешімі
болмайды.
20- мысал.
Теңдеудің шешімін тап: 
Шешуі: Берілген теңдеуде қосымша бұрыш енгізу үшін, оның екі жағын да

өрнегіне бөлелік. Мұнда

болғандықтан, қандай да бір  бұрышы табылып
бұрышы табылып

 (2.1.3)
(2.1.3)
теңдіктері орындалатын болады. Онда
 ~
~  (2.1.4)
(2.1.4)
теңдеуіне келеміз. Бұл теңдеудің нақты шешімдері болуы
үшін  теңсіздігі орындалуы
керек. Онда қандай да бір
теңсіздігі орындалуы
керек. Онда қандай да бір  бұрышы табылып
бұрышы табылып
 (2.1.5)
(2.1.5)
теңдігі орындалатын болады және (2.1.4) теңдеуі

түріне келеді. Бұл теңдеудің шешімдері
 ~
~ 
немесе
 ~
~ 
болады. Сонда, (2.1.3) және (2.1.5) пайдалана отырып бірінші шешімді
 ,
,
екінші шешімді

түрінде анықтаймыз.
Жауабы:
 болса, онда
болса, онда
 ,
,

 болса, онда теңдеудің шешімі
болмайды.
болса, онда теңдеудің шешімі
болмайды.
21- мысал.
Теңдеудің шешімін тап: 
Шешуі: Берілген теңдеуді теңбе-тең түрлендірелік. Теңдеудің сол жағын толық квадратқакелтіру арқылы түрлендірелік.
 ~
~
 ~
~  ~
~  ~
~

 ~
~  .
.
Соңғы
теңдеудің  ~
~
 шарты орындалғанда ғана шешімі
болады. Сонымен, егер
шарты орындалғанда ғана шешімі
болады. Сонымен, егер  орындалатын болса, онда
орындалатын болса, онда

шешімін табамыз.
Жауабы:
 болса, онда
болса, онда ;
;
 болса, онда теңдеудің шешімі
болмайды [28].
болса, онда теңдеудің шешімі
болмайды [28].
22- мысал.
Теңдеудің шешімін тап: 
Шешуі:
Берілген теңдеудің анықталу облысы  теңсіздігімен беріледі. Берілген
теңдеуді теңбе-тең түрлендірелік:
теңсіздігімен беріледі. Берілген
теңдеуді теңбе-тең түрлендірелік:
 ~
~  ~
~
~  .
.
Бұл
теңдеуден  теңдеуін, оның
шешімі
теңдеуін, оның
шешімі  аламыз. Бұл
шешім
аламыз. Бұл
шешім  параметрінен
тәуелсіз, яғни
параметрінен
тәуелсіз, яғни  Ал
Ал  биквадрат теңдеуінің шешімі болуы
үшін, оның дискриминанты теріс болмауы керек:
биквадрат теңдеуінің шешімі болуы
үшін, оның дискриминанты теріс болмауы керек:  Бұл жағдайда
Бұл жағдайда бірақ
бірақ  Соңғы теңсіздіктің орындалуын
тексерелік:
Соңғы теңсіздіктің орындалуын
тексерелік:
1)  ~
~
 ~
~  ~
~ ~
~  ~
~  ~
~ 
Соңғы теңсіздік орындалған жағдайда
 ,
,  шешімін аламыз.
шешімін аламыз.
2)  ~
~
 ~
~  ~
~  ~
~  ~
~ 
Соңғы теңсіздік орындалған жағдайда
 ,
,  шешімін аламыз.
шешімін аламыз.
Жауабы:
 болса, онда,
болса, онда,  .
.
 болса, онда:
болса, онда:
 ;
;
 ;
;
 .
.
 болса, онда:
болса, онда:
 ;
;  .
.
23- мысал.
Теңдеудің шешімін тап: 
Шешуі:
Берілген теңдеудің екі жағын  көбейтесек
көбейтесек теңдеуін аламыз. Бұл теңдеудің сол
жағындағы көбейтіндіні қосындыға түрлендірелік, сонда
теңдеуін аламыз. Бұл теңдеудің сол
жағындағы көбейтіндіні қосындыға түрлендірелік, сонда
 ~
~  .
.
Соңғы теңдеуде косинустардың тең болу шартын пайдалансақ
 ~
~ 
Тексеру.
Жоғарыда берілген теңдеудің екі жағын  көбейту барысында берілген теңдеудің
анықталу облысын кеңейттік. Олай болса бөгде түбірлердің пайда
болуы мүмкін. Сондықтан табылған шешімдер жиынтығынан берілген
теңдеудің шешімі болатындай шешімдер жиынтығын бөліп алалық. Ол
үшін табылған шешімдер жиынтығынан
көбейту барысында берілген теңдеудің
анықталу облысын кеңейттік. Олай болса бөгде түбірлердің пайда
болуы мүмкін. Сондықтан табылған шешімдер жиынтығынан берілген
теңдеудің шешімі болатындай шешімдер жиынтығын бөліп алалық. Ол
үшін табылған шешімдер жиынтығынан  теңдеуін қанағаттандыратын
теңдеуін қанағаттандыратын
 -тің
-тің  мәндерін шығарып тасталық. Табылған
шешімдер жиынтығындағы
мәндерін шығарып тасталық. Табылған
шешімдер жиынтығындағы  мәндер
мәндер  мәндерімен қиылыспайды. Онда
мәндерімен қиылыспайды. Онда
 берілген теңдеудің шешімі
болады. Шешімдер жиынтығындағы екінші топ шешімдері үшін
берілген теңдеудің шешімі
болады. Шешімдер жиынтығындағы екінші топ шешімдері үшін
 ~
~ 
теңдігін
жазуға болады. Сонымен  жиынтығы шешім болуы үшін
жиынтығы шешім болуы үшін
 шарты орындалуы
керек.
шарты орындалуы
керек.
Жауабы:
 болса, онда,
болса, онда,  .
.
 болса, онда
болса, онда
24- мысал.
 теңдеуінде,
теңдеуінде,  параметрінің барлық мәнін табу
керек.
параметрінің барлық мәнін табу
керек.
Бірінші қосылғышты мына

түрге
келтіріп, ал екінші қосылғышты  ,
,  айнымалысын енгізіп теңдеуді мына
түрде жазып аламыз
айнымалысын енгізіп теңдеуді мына
түрде жазып аламыз

Оның
түбірі болады, егер 
Солайша  -ның кез келген мәнінде
-ның кез келген мәнінде
 екі түбірі (
екі түбірі ( ) болады.
) болады.  болғандықтан, егер
болғандықтан, егер  түбірлерінің тым болмаса біреуі
түбірлерінің тым болмаса біреуі
 аралыққа кірсе, бастапқы
теңдеудің мәні болады,
аралыққа кірсе, бастапқы
теңдеудің мәні болады,
А. Екі
түбірді де осы аралықта жатады деп алайық, яғни . Онда
. Онда  функциясының минимум нүктесінің
абциссасы мына аралықта жатады:
функциясының минимум нүктесінің
абциссасы мына аралықта жатады: 
функцияның минимал мәні теріс:  а-ның кез келген мәнінде орындалады;
функцияның мәні аралықтың соңында теріс емес:
а-ның кез келген мәнінде орындалады;
функцияның мәні аралықтың соңында теріс емес: 
 . Қарастырылған
шарттардың жүйесі
. Қарастырылған
шарттардың жүйесі  үйлеспегендіктен,
үйлеспегендіктен,  аралықтарда
аралықтарда  екі шешімі болуы мүмкін
емес.
екі шешімі болуы мүмкін
емес.
В.  аралыққа
аралыққа
 түбірлерінің біреуі жатады деп
алайық. Онда
түбірлерінің біреуі жатады деп
алайық. Онда  аралықтың
соңында әр түрлі таңбалы екі мән қабылдайды, оның біреуі нөлдік
болуы мүмкін, яғни
аралықтың
соңында әр түрлі таңбалы екі мән қабылдайды, оның біреуі нөлдік
болуы мүмкін, яғни  шарты орындалады, бұдан интервалдар
әдісімен
шарты орындалады, бұдан интервалдар
әдісімен  аламыз.
аламыз.
Жауабы:  .
.
25- мысал.

Шешуі.
Теңдеудің сол жақ бөлігін кубтардың қосындысы бойынша
 теңдеуін аламыз немесе
теңдеуін аламыз немесе
 яғни
яғни 
 мәні
болады.
мәні
болады.
Соңғы
теңсіздік  береді. Ерекше
жағдай
береді. Ерекше
жағдай  . Онда теңдеу мына
түрге келеді
. Онда теңдеу мына
түрге келеді  , шешімі
жоқ.
, шешімі
жоқ.
Жауабы:  болғанда,
болғанда, 
 және
және  болғанда, шешімі болмайды.
болғанда, шешімі болмайды.
26- мысал.
 - теңдеуін шешу.
- теңдеуін шешу.

а)  Бір мезгілде
мына теңсіздіктер орындалуы тиіс:
Бір мезгілде
мына теңсіздіктер орындалуы тиіс:
 бұдан
бұдан 
Осы
шарт бойынша 
б)  Бір мезгілде
мына теңсіздіктер орындалуы тиіс:
Бір мезгілде
мына теңсіздіктер орындалуы тиіс:
 бұдан
бұдан  .
.
Осы шарт
бойынша 
Жауабы:  болғанда,
болғанда, 

 болғанда,
болғанда, 

 болғанда,
болғанда, 
Параметрі бар теңдеулерді шешу үшін төмендегі әдістерді қолдану көптеген күрделі есептерді шешуді айтарлықтай жеңілдетеді. Әрбір әдіс үлгісін қолдану арқылы студент оған оңайсәйкес әдісті таниды және қолданаалады. Берілген мысалдар факультативті сабақтарда қолданылуы мүмкін. Бұл студенттерге осы түрдегі мәселелерді шешуде тәжірибе жинақтауға көмектеседі [29].
А) Жаңа айнымалыларды енгізу.
Жаңа айнымалы мәндерді енгізу сізге тапсырманы түсінуді жеңілдетуге және тапсырманы жеңілдетуге мүмкіндік береді. Мұндай тәсіл мынадай жағдайларда қолданылуы мүмкін.
-
төмендегі түрде берілген тригонометриялық теңдеулерде

Жаңа
айнымалы енгізу арқылы келесі теңдіктерді
қолданамыз
арқылы келесі теңдіктерді
қолданамыз

Төмендегі түрде берілген теңдеуге

Жаңа
айнымалы енгізуге болады және келесі түрлендірулер
енгіземіз
және келесі түрлендірулер
енгіземіз

Төмендегі түрде берілген теңдеуге

Жаңа
айнымалы енгізуге болады және келесі түрлендірулер
енгіземіз
және келесі түрлендірулер
енгіземіз

1.4. Төмендегі түрде берілген теңдеуге

Жаңа
айнымалы енгізуге болады  , где
, где

және
келесі түрлендірулер енгіземіз .
.
Жоғарыда айтылған әдістерге байланысты бірнеше мысал қарастырайық.
27- мысал.
 параметрінің қандай мәнінде
теңдеу
параметрінің қандай мәнінде
теңдеу


аралықта бірден көп шешімі болады.
Шешуі:  деп аламыз, сонда
деп аламыз, сонда










 және
және  .
.
Бізге (0,1) аралықта теңдеудің бірден көп түбірі керек , сол себепті


Жауабы
:  .
.
B) Айнымалылар мен параметрлердің мүмкінмәндерінің облысының бөлінуі
Айнымалылардың немесе параметрлердің мүмкін мәндерінің облысы немесе кейбір өрнектер бөлінбеген жиынтықтарға бөлінеді. Бұл тапсырманы жеңілдетуге немесе тапсырманы жаңа пішінге аударуға мүмкіндік береді.
28- мысал.
 параметріне байланысты теңдеуді
шешу
параметріне байланысты теңдеуді
шешу .
.
Шешуі
: бірден белгілі,  әркезде дұрыс жауабы
болатыны.
әркезде дұрыс жауабы
болатыны.
Егер  деп алсақ,
онда
деп алсақ,
онда  теңдеуін аламыз.
Егер
теңдеуін аламыз.
Егер , онда есептің
жауабы болмайды, егер
, онда есептің
жауабы болмайды, егер  , онда
, онда . Біз
. Біз  екенін ескере отырып:
екенін ескере отырып: болған жағдайда
болған жағдайда және
және ,
,  .
.
Енді  болған
жағдайда, онда
болған
жағдайда, онда . Егер
. Егер , онда жауабы болмайды,
егер
, онда жауабы болмайды,
егер  ,
онда
,
онда . Егер
. Егер
 ескерсек:
ескерсек:
 және
және 
 .
.
Енді жауабын жазсақ болады.
Жауабы
: болған
жағдайда
болған
жағдайда  ,
,
 ,
, ,
,  ,
,
 ,
, ,
,  .
.
C) Көмекші түрлендірулер
Көмекші түрлендірулерді қолдану арқылы теңдеудегі өрнектерді жеңілдетуге болады немесе 1 және 2 тәсілдерін қолдануға мүмкіндік береді.
29- мысал.
Теңдеудің кем дегенде бір шешімі болатын табу
табу

Шешуі: Бұл теңдеуді түрлендіру үшін қысқаша көбейту формулаларын және негізгі тригонометриялық сәйкестіктерді пайдаланамыз:

Теңдеудің екі бөлігін де 4 ке бөлеміз:


Теңдеудің сол жақ бөлігіндегі  ортақ көбейткіштерді жақшаның сыртына
шығарып төмендегі өрнекті аламыз:
ортақ көбейткіштерді жақшаның сыртына
шығарып төмендегі өрнекті аламыз:

 .
.
 болса,
болса, , теңдеудің жауабы
болмайды.
, теңдеудің жауабы
болмайды.
Енді  болғанда
болғанда аламыз.
аламыз.
 аралығында жататынын білеміз, сол
себепті
аралығында жататынын білеміз, сол
себепті ,
демек
,
демек


 .
.
Соңғы жүйеден жауабын аламыз.
Жауабы
:
D) Дәстүрлі формулаларды қолдану
Классикалық сәйкестіктерді, теңсіздікті, қасиеттерері мен теоремалары пайдалану арқылы көптеген теңдеулердің шешімін жеңілдетуге болады. Осындай теңдеулерге мысал келтірейік.
30- мысал.
Функцияның ең үлкен мәнін табыңыз
 егер
егер  .
.
Шешуі : Осы функцияның квадратының ең үлкен мәнін табыңыз
 .
.
 болатынын ескере
отырып,
болатынын ескере
отырып, функциясын
аламыз.
функциясын
аламыз.
Ең үлкен мән радикал болғанда, өрнек ең үлкен мәнді қабылдайды.
 теңдеуін аламыз.
теңдеуін аламыз.
Егер екі оң айнымалының мәні тұрақты болса, екі көбейтінді бір мәнге ие болғанда, онда осы айнымалылардың шешімі ең үлкен мәнге ие болады.

 .
.
Егер  , онда
, онда .
.
Бұл
жағдайда оның әрқайсысы бағынатын өрнектерге тең және
және
 .
.
Егер , онда
функцияның мәні 2-ге тең.
, онда
функцияның мәні 2-ге тең.
Жауабы
:  .
.
Осы әдістерді пайдаланып есептер шығарып көрейік
31- мысал.
Теңдеуді
шешейік  .
.
 болған жағдайда теңдеудің мағынасы
болады.
болған жағдайда теңдеудің мағынасы
болады.  мәні
мәні , осы жағдайды
қанағаттандыру қажет.
, осы жағдайды
қанағаттандыру қажет.

Егер  .
.
Қарапайым түрлендірулер мына теңдеуге алып келеді

және осы теңдеудің екі түбірі болады:
 ,
,  . Жоғарыда айтылып кеткендей
. Жоғарыда айтылып кеткендей
 мәні мына жағдайды
мәні мына жағдайды
 қанағаттандыру қажет.
қанағаттандыру қажет.
Демек,  немесе
немесе  (немесе екі сан) тең болатын m
мәндерін алып тастау қажет.
(немесе екі сан) тең болатын m
мәндерін алып тастау қажет.
 егер
егер болса онда
болса онда .
.
 егер
егер болса онда
болса онда
егер 
 ;
;
егер 
 ;
;
егер ,
,
 , m ≠ 0 теңдеудің екі түбірі бар
болады:
, m ≠ 0 теңдеудің екі түбірі бар
болады:
 ,
,  ,
,
k, n, s – бір-біріне тәуелсіз, барлық бүтін сандардың мәндерін қабылдайды.
32- мысал.
Параметрдің  теңдеуі бар параметрдің ең үлкен бүтін
мәнін табыңыз.
теңдеуі бар параметрдің ең үлкен бүтін
мәнін табыңыз.
Шешім:
осы теңдеуді түрлендіру:  ;
; 
 ;
;  ;
;
 .
.
Теңдеудің шешімі береді:
береді:
 ; х бос жиынға жатады.
; х бос жиынға жатады.
 ;
;
 егер
егер .
.
Теңсіздіктің шешімі
шешімі болады және бұл жерден
аңғаратынымыз,оның ең үлкен мәні 6-ға тең.
болады және бұл жерден
аңғаратынымыз,оның ең үлкен мәні 6-ға тең.
Жауабы: 6.
33- мысал.

Шешуі:  Теңдеуді мына түрде жазып
алайық
Теңдеуді мына түрде жазып
алайық  . Қосындыны
түрлендіріп мынаны аламыз:
. Қосындыны
түрлендіріп мынаны аламыз:  немесе
немесе

а) 

б) 


34- мысал.

Шешуі: Теңдеу мына функцияға қатысты квадраттық теңдеуге айналады
 , осыдан
, осыдан

а)  әрқашан, сонымен қатар
әрқашан, сонымен қатар
 болуы тиіс. Теңсіздікті шеше
отырып, а- кез келген нақты сан екенін аламыз.
болуы тиіс. Теңсіздікті шеше
отырып, а- кез келген нақты сан екенін аламыз.
б)  .
.  теңсіздігі а-ның ешқандай мәнінде
орындалмайды.
теңсіздігі а-ның ешқандай мәнінде
орындалмайды.
 болғандағы ерекше жағдай! Тендеу
келесі түрге келеді:
болғандағы ерекше жағдай! Тендеу
келесі түрге келеді: 
Жауабы: 


35- мысал.

Шешуі: . Тендеу мына түрге
түрленеді:
. Тендеу мына түрге
түрленеді:
 яғни
яғни 
Егер

 , онда соңғы теңдеу мынандай шешімін
табады
, онда соңғы теңдеу мынандай шешімін
табады 

Жауабы: 

 .
.
Жаттығулар:


 теңдеуін шеш;
теңдеуін шеш;
 теңдеуін шеш;
теңдеуін шеш;
 теңдеуін шеш;
теңдеуін шеш;
 теңдеуін шеш;
теңдеуін шеш;
 теңдеуін шеш;
теңдеуін шеш;
 теңдеуін шеш;
теңдеуін шеш;
 теңдеуін шеш және
теңдеуін шеш және  аралығында неше шешімі болатынын
анықта;
аралығында неше шешімі болатынын
анықта;
 теңдеуін шешіңіз.
теңдеуін шешіңіз.





шағым қалдыра аласыз















