
30
"ПAPКЕТ САЛУДАҒЫ ГЕОМЕТРИЯНЫҢ РӨЛІ"
МАЗМҰНЫ
Кіріспе
I тарау фигуралардың теңдігі
II тарау симметрия түрлері
III тарау жазықтықтағы фигуралардың қозғалысы
IV тарау ою-өрнек
4.1. Ою-өрнектің жалпы түсінігі.
4.2. Ою-өрнек түрлері.
V тарау тұрақты көпбұрыштардан жасалған Пapкет
5.1. Пapкет ұғымы ою-өрнек ретінде.
5.2. Нүктенің айналасын бір типтегі тұрақты көпбұрыштармен төсеу.
5.3. Нүктенің айналасын төсеу үшін қажет тұрақты көпбұрыштардың ең аз және көп санын бағалау.
5.4. Нүктенің айналасын үш тұрақты көпбұрышпен төсеу.
5.5. Нүктенің айналасын төрт тұрақты көпбұрышпен төсеу.
5.6. Нүктенің айналасын бес және алты тұрақты көпбұрыштармен төсеу.
VI тарау тұрақты көпбұрыштардан басқа фигуралардан пapкет салу
Қорытынды
Әдебиет
Қосымша
КІРІСПЕ
Тақырыптың өзектілігі: бұл жоба жазықтықтағы фигураның қозғалысы сияқты геометрия ұғымына арналған. Геометрияда қозғалыс-бұл нүктелер арасындағы қашықтық сақталатын фигураларды түрлендіру. Ою-өрнектердің құрылысы фигураның жазықтықтағы қозғалысына толығымен негізделген. Ою-өрнектермен адам күн сайын кездеседі. Бір мысал-қабырғаға жабыстырылған тұсқағаз. Сондай – ақ, әр ұлттық мәдениет ою-өрнектің өзіндік жүйесін-мотивтерді, пішіндерді, әшекейленген бетке орналастыруды жасаған халық шығармашылығы мысал бола алады. Ою-өрнек ыдыс-аяқтарды, жиһаздарды, тоқыма бұйымдарын, сондай-ақ сәулет құрылыстарын безендіруге арналған. Көптеген ою-өрнектердің арасында пapкет ерекшеленеді. Пәтерлерге еден төселген пapкет ою-өрнек деп кім ойлаған? Ою-өрнек өнері ежелгі дәуірден бері қолданылып келеді. Біз оны ежелгі Египеттің, Ежелгі Грецияның және ортағасырлық Ресейдің сәулетінде кездестіре аламыз. Бүгінгі таңда өнердің бұл түрі өзектілігін жоғалтпайды, керісінше дамып келеді.
Біздің зерттеуіміздің тақырыбы - "пapкет салудағы геометрияның рөлі". "Геометрия: Сұлулық және үйлесімділік", Александров А. Д., Нецветаев Н.Ю. "Геометрия", Погорелов А. В. "Геометрия", Шарыгин и. Ф., Ерганжиева Л. Н. "көрнекі геометрия".
Мақсаты:
1. пapкет қандай фигуралардан жасалуы мүмкін екенін зерттеңіз;
2. көпбұрыштардан пapкет салу заңдылықтарын анықтаңыз;
3. анықталған заңдылықтардан кейін пapкет эскиздерін сызыңыз;
4. пapкетті ою-өрнектің бір түрі ретінде зерттеп, пapкет дизайнын жасаңыз.
Міндеттері:
1. осы тақырып бойынша теориялық материалды зерттеу;
2. жазықтықтағы фигуралардың қозғалысын қарастырыңыз;
3. дұрыс көпбұрыштарды зерттеу және тұрақты көпбұрыштардан пapкет салу мүмкіндігін анықтау;
4. басқа фигуралардан пapкет салу мүмкіндігі;
5. қорытынды жасау және жасалған жұмысқа баға беру;
Зерттеу нысаны: жазықтықтағы геометрия.
Зерттеу пәні: фигураның жазықтықтағы қозғалысы, пapкет.
Гипотеза:
1. Егер пapкет тұрақты көпбұрыштардан алынуы мүмкін болса, онда тек мысалы: шаршы, үшбұрыш және алтыбұрыш.
2. Тұрақты көпбұрыштардан басқа фигуралардан пapкет салудың кез-келген үлгісі болуы мүмкін.
Әдісі:
1. анықтамалық әдебиеттерді талдау (Сагателова л. с., Студенецкая В. Н. "Геометрия: Сұлулық және үйлесімділік", Александров А. Д., Нецветаев Н. Ю. "Геометрия", Погорелов А. В. "Геометрия", Шарыгин и. Ф., Ерганжиева Л. Н. "көрнекі геометрия");
2. тұрақты көпбұрыштардан пapкет құрылысын зерттеу;
3. тұрақты көпбұрыштардан басқа фигуралардан жасалған пapкеттерді зерттеу;
4. алынған нәтижелерді синтездеу.
I ТАРАУ САНДАРДЫҢ ТЕҢДІГІ
Егер екі фигура қозғалыс арқылы бір-бірімен дәл сәйкес келсе, онда бұл сандар бірдей, тең. Бұл дегеніміз, егер екі үшбұрыштың сәйкес жақтары тең болса және сәйкес бұрыштары тең болса, онда бұл үшбұрыштар қозғалыспен біріктіріледі. Және керісінше: егер екі үшбұрыш қозғалыспен біріктірілсе, онда олардың тиісті жақтары тең және сәйкес бұрыштары тең болады. Осы екі мәлімдемені де дәлелдейік.
АВС үшбұрышы қозғалысты үшбұрышпен біріктірсін А1В1С1 сонымен қатар, А шыңы шыңға өтеді А1, В - В1 және С - С1. Қозғалыс кезінде қашықтықтар мен бұрыштар сақталатындықтан, біздің үшбұрыштарымыз үшін АВ = А1В1, ВС = В1С1 ,АС = А1С1 , ∟А = А1, ∟В = В1, ∟С = С1.
Енді үшбұрыштарда болсын АВС және А1В1С АВ = А1В1, ВС = В1С1 ,АС = А1С1 , ∟А = А1, ∟В = В1, ∟С = С1. Біз олардың қозғалыспен үйлесетінін дәлелдейміз, ал А шыңы шыңға өтеді А1, В - В1, С - С1. АВС үшбұрышын кесіндіге перпендикуляр а сызығына қатысты симметрияны түрлендіруге ұшыратамыз АА1 және оның ортасынан өтеді (сурет. 1). Үшбұрыш алыңыз А1В2С2. Егер нүктелер В және В2 әр түрлі, біз оны нүкте арқылы өтетін B сызығына қатысты симметрияға ұшыратамыз А1 және түзу сызыққа перпендикуляр В1В2. Үшбұрыш Алыңыз A1B1C3.
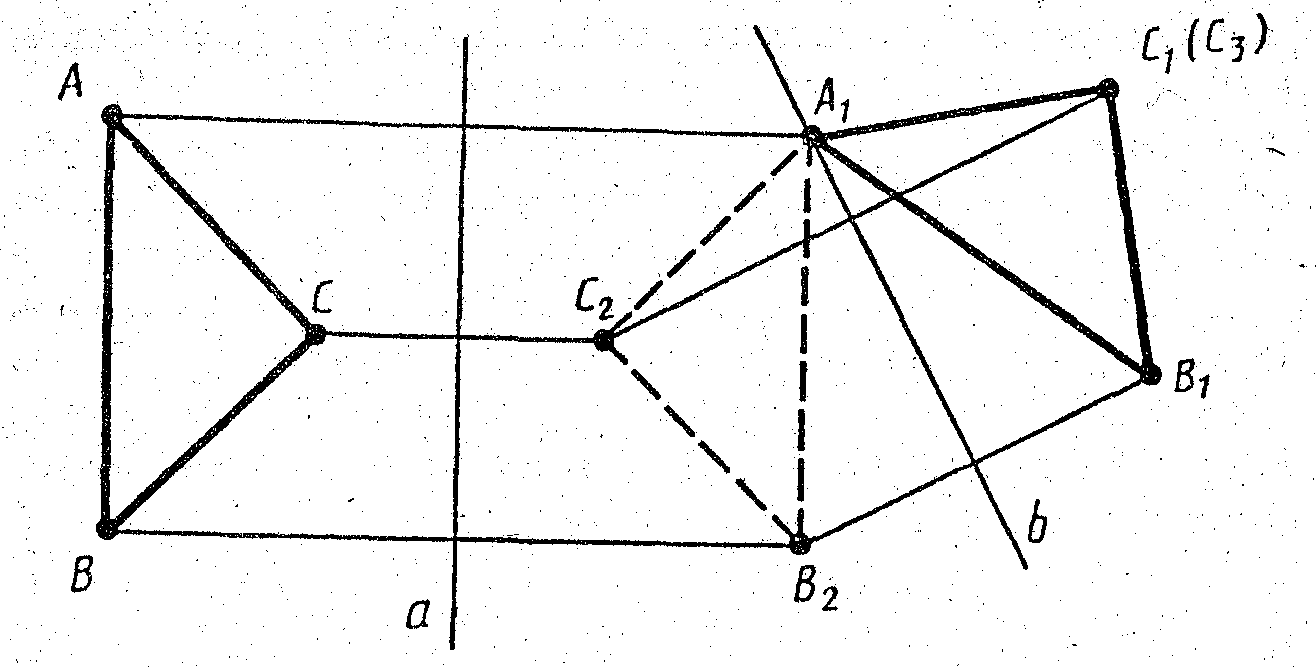
Рис.1
Егер нүктелер С1 және С3 түзу сызықтың бір жағында жатыр А1В1, олар шынымен сәйкес келеді, өйткені бұрыштар В1А1С1 және В1А1C3 тең, содан кейін сәулелер А1С1 және А1C3 сәйкес келеді, өйткені сегменттер А1С1 және А1C3 тең, содан кейін сәйкес нүктелер С1 және С3. Осылайша, АВС үшбұрышы қозғалыс арқылы үшбұрышқа аударылады А1В1С1.
Егер нүктелер С1 және С3 түзу сызықтың әртүрлі жағында жатыр А1В1, содан кейін дәлелдеу үшін тікелей қатысты симметрияны қолдану қажет А1В1.
II ТАРАУ СИММЕТРИЯ ТҮРЛЕРІ
Фигураның симметриясы-бұл фигураның қасиеті,оның өзіне қабаттасуы бар. Басқаша айтқанда, симметрия дегеніміз-қандай да бір түрде өзгертуге болатын, нәтижесінде олар басталған объектіні алу. Кеңістіктік фигуралардың симметриясының мысалдары дұрыс призмалар мен пирамидаларды береді: олар өздері, мысалы, базаның жазықтығына перпендикуляр және оның ортасынан өтетін осьтің айналуымен біріктіріледі. Жазық фигуралардың симметриясына мысалдар тұрақты көпбұрыштарды береді.
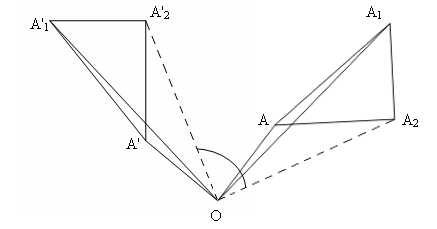
Симметрияның бірнеше түрі бар. Жазықтықта-осьтік симметрия (түзу сызықтан шағылысу).2, нүктенің айналуы (ішінара жағдай – Орталық симметрия) сурет.3, параллель беру (сурет.4) және жылжымалы симметрия (сурет.5). Ғарышта жоғарыда аталған симметрия түрлеріне айна симметриясы қосылады (сурет.6)
.
α
Рис.3
Рис.2



Рис.4
А'
Рис.5
Рис.6
III ТАРАУ ФИГУРАЛАРДЫҢ ЖАЗЫҚТЫҚТАҒЫ ҚОЗҒАЛЫСЫ
Ұшақтың қозғалысын келесідей елестетуге болады. Жазықтықта кейбір нүктелер мен фигуралар берілген деп елестетеміз. Біз оған қағаз парағын қойып, сол нүктелер мен фигураларды дөңгелектейміз. Содан кейін біз бақылау қағазын алып, оны қайтадан ұшаққа қайтарамыз, бірақ жаңа күйде. Бақылау қағазы мөлдір болғандықтан, жазықтықтағы бастапқы нүктелер мен фигуралар да, олардың кескіндері де қағаз парағының (суреттердің) офсеттік парағында көрінеді. Жазықтықтың әр нүктесі жаңа позицияға (кескінге) өтеді. Бұл қозғалыс деп аталатын геометриялық түрлендіру.
Жазықтықтағы кез-келген екі фигураны, егер олар тең болса, қозғалыспен біріктіруге болады, яғни.фигураны оның тең фигурасына салыңыз.
Бұрылу-бұл қозғалыс, өйткені бұрылғаннан кейін нүктелер арасындағы қашықтық өзгермейді. Қозғалысты геометриялық тұрғыдан түсіну кезінде олар қозғалатын нүктенің бастапқы және соңғы жағдайына (кескініне) назар аударады, оның аралық позицияларынан, жылдамдығынан және т.б. бұл қозғалысқа геометриялық көзқарас физикалықтан өзгеше.
Жазықтықтың барлық нүктелері бір бағытта бірдей қашықтыққа ауысқанда параллель беру де қозғалыс болып табылады. Бір векторға параллель беру кезінде нүкте мен оның кескінін байланыстыратын Вектор .
Қозғалыстың тағы бір мысалы – осьтік симметрия. Жазықтықта l сызығы (симметрия осі), сондай-ақ кейбір фигуралар мен нүктелер сызылсын. Жазықтыққа бақылау қағазының парағын қойып, оған l түзуін, сондай-ақ фигуралар мен нүктелерді аударамыз. Содан кейін бақылау қағазын төңкеріп, оны l түзуінің әр нүктесі өзімен үйлесетін етіп артқы жағымен жазықтыққа салыңыз. Содан кейін кез-келген нүкте мен кез-келген фигура l сызығына қатысты түпнұсқаға симметриялы позицияға түседі.
IV ТАРАУ ОЮ-ӨРНЕК
4.1. Ою-өрнектің жалпы түсінігі.
Симметрия принципі ою-өрнек салуда қолданылады. Ою-өрнек (лат. ornamentum-әшекейлер) - қайталанатын, ырғақты реттелген элементтерден тұратын өрнек. Ою-өрнек әртүрлі заттарды (ыдыс-аяқ, жиһаз, тоқыма бұйымдары, қару-жарақ) және сәулет құрылыстарын безендіруге арналған.
Ою-өрнектердің симметриялық құрылысының түрлерін қарастырыңыз (I қосымша).
1.Айна симметриясы, онда фигура және оның симметрия жазықтығындағы көрінісі бір-біріне қолданылған кезде біріктіріледі.
2.Динамикалық Симметрияның күрделі түрлері әртүрлі симметриялық қайталанулармен, бұрылыстармен, берілістермен, бастапқы фигураның шағылысуымен алынады.
3.Жиек-қайталанатын фигуралар бір түзу немесе қисық сызық бойымен қозғалатын ою-өрнек (ленталар, жолақтар, фриздер, тартқыштар, панельдер, пилястрлар және т.б.).
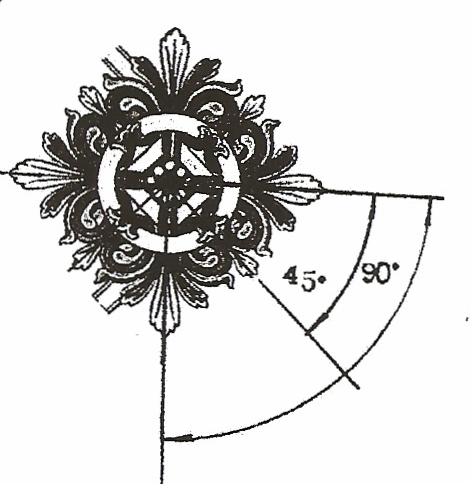
4.Нүктелік (сәулелік, орталық) симметрияда фигураның симметрия осінің айналасында белгілі бір бұрышқа (розеткалар, жұлдыздар) қайталанған кезде өрнектің пайда болуы жүреді.
5.Торлы (фондық) ою-өрнектің фигуралары тасымалдың екі осі бойынша жасалады, әртүрлі түйіндер жүйесі бар бес тордан орналасуы мүмкін.
Композицияның сипаты мен безендірілген бетке орналасуы бойынша ою-өрнектің бірнеше түрі болуы мүмкін: лента (ол шекара деп те аталады), торлы және розетка. Торлы ою-өрнектердің симметриясының 17 мүмкін түрі бар. Мұнда Симметрияның мұндай түрлері әртүрлі комбинацияларда жүзеге асырылуы мүмкін: бұрылыс – екінші, үшінші, төртінші және алтыншы ретті, айна және жылжымалы шағылысу. Әр жағдайда мүмкін болатын көріністер мен бұрылыстардың белгілі бір жиынтығы үлгінің ырғағына әсер етеді, өзінің тепе-теңдігі мен қозғалғыштығын, ою-өрнек көрерменнің көзқарасын басқаратын өз бағыттарын жасайды (II қосымша).
4.2. Ою-өрнек түрлері.
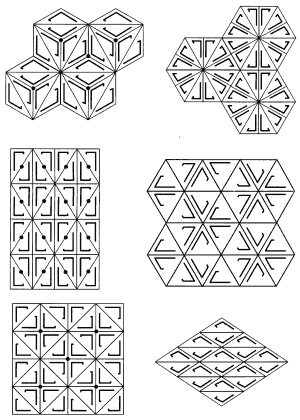
Ою-өрнектер түрлерге бөлінеді (III қосымша):
1.Геометриялық ою. Геометриялық ою-өрнекте ритмикалық және олардың түс комбинацияларының қатаң ауысуына, кейде табиғаттың жеке мотивтерінің белсенді стилизациясына баса назар аударылады.
2.Өсімдік ою-өрнегі. Бұл геометриялық өрнектен кейінгі ең көп таралған ою-өрнек, ол өзінің сүйікті мотивтерімен және әртүрлі елдерде, әр түрлі уақытта сипатталады. Гүлді ою-өрнек қолданылатын мотивтердің, орындау әдістерінің алуан түрлілігінде үлкен мүмкіндіктерге ие.
3.Каллиграфиялық ою-өрнек. Ол жеке әріптерден немесе мәтін элементтерінен тұрады, олардың пластикалық үлгісі мен ырғағы бойынша мәнерлі.
4.Фантастикалық ою-өрнек. Ою-өрнек көбінесе символдық және мифологиялық мазмұндағы ойдан шығарылған суреттерге негізделген.
5.Символдық ою. Ою-өрнек көбінесе қандай да бір ерекше маңызы бар символдар немесе символдар жүйесі (елтаңбалар, орден белгілері, әскери, музыкалық, театр өнерінің заттары) болып табылады.
6.Бейнелі (адамдық) ою-өрнек. Ол адам денелерінен, геометриялық және өсімдік мотивтерінен тұрады, әскери өмір, өмір, мифтік және библиялық тақырыптармен қоршалған адамдардың әрекеттерін бейнелейді.
7.Пейзаждық ою-өрнек. Әсіресе Жапония мен Қытай шығарған тоқыма бұйымдарында жиі қолданылады және қолданылады.
8.Астралдық ою. Аспанға табынуды бекітеді. Негізгі элементтер аспан, күн, бұлттар, жұлдыздар бейнелері болды.
9.Жануарлардың ою-өрнегі (Жануарлар). Құстардың, жануарлардың, жануарлардың (арыстандар, пантерлер, жылқылар, бүркіттер, үйректер және т.б.) шынайы, шартты, стильдендірілген бейнелері.
10.Аралас ою (күрделі). Әр түрлі элементтерден жиналған, мысалы: геометриялық және өсімдік, өсімдік және жануар, лента, қару-жарақ қалқандары, аң аулау атрибуттары, құралдар және т. б.
V ТАРАУ ТҰРАҚТЫ КӨПБҰРЫШТАРДАН ЖАСАЛҒАН ПAPКЕТ
5.1. Пapкет ұғымы ою-өрнек ретінде.
Көптеген ою-өрнектердің арасында "пapкет" (Мозаика) ерекшеленеді. Пapкет жазықтықты бір-бірімен қабаттаспайтын және жазықтықта бос орын қалдырмайтын бірдей фигуралармен толтыру деп аталады (кейде пapкет бүкіл жазықтықты жабатын, бір-біріне жақын орналасқан тең көпбұрыштар жүйесі деп аталады). Пapкет (немесе мозаика) - бұл жазықтықты саңылаусыз және қос жабынсыз жабатын шексіз көпбұрыштар тобы. Біз тек бірдей көпбұрыштардан-пapкет тақталарынан тұратын пapкет едендерін қарастырамыз. Сонымен қатар, егер пapкет дөңес көпбұрыштың көшірмелерінен тұрса, онда әр екі көшірменің ортақ нүктелері жоқ немесе ортақ жағы (пapкет шеті деп те аталады) немесе ортақ шыңы (пapкет шыңы деп аталады) болады деп болжанады.
Бұл біздің пәтерлердегідей пapкет, линолеум әшекейлері, тұсқағаздағы суреттер сияқты (IV қосымша).
Пapкет өмірде жиі кездесетіні соншалық, біз оларды байқамаймыз. Ұяшықтағы ноутбук парағы-қарапайым пapкет мысалы (V қосымшасы, сурет. 7, а). Мұндағы пapкет элементі-шаршы. Бұл торда сіз басқа пapкет жасай аласыз (оларды тор деп атауға болады) [V қосымшасы, сурет. 7, б].
5.2. Нүктенің айналасын бір типтегі тұрақты көпбұрыштармен төсеу.
Сонымен, ұшақты қандай көпбұрыштармен салуға болады? 9-сыныптың мектеп курсының бөлігі "дұрыс көпбұрыштар"тақырыбына арналған. Барлық жақтары тең және барлық бұрыштары тең болатын көпбұрыш дұрыс деп аталады. Суретте (VI қосымша) тұрақты үшбұрыш, төртбұрыш, бесбұрыш және алтыбұрыш көрсетілген.
Біз нүктенің айналасын бір типтегі тұрақты көпбұрыштармен жабуды қарастырып, бізді қызықтыратын сұрақтың жауабын табамыз. Нүктенің айналасын бірдей тұрақты көпбұрыштармен жабыңыз (мысалы, тек 3-квадраттар немесе тек 4-квадраттар,..., тек n-квадраттар). Мұндай төсеу қандай N мәндері үшін мүмкін екенін білеміз.
Б![]() елгілі болғандай, дұрыс
N-шаршы бұрышының шамасы мына формула бойынша
анықталады:
елгілі болғандай, дұрыс
N-шаршы бұрышының шамасы мына формула бойынша
анықталады:
![]()
, қайда .
Осы формуланы қолдана отырып, әр түрлі N мәндері үшін тұрақты N-квадраттардың бұрыштарының келесі мәндерін аламыз:
-
n
3
4
5
6
7
8
9
10
11
12

60o
90o
108o
120o

135o
140o
144o

150o
Пapкет алу үшін бұрыштардың
қосындысын теру керек 360о. Егер пapкет N-квадраттардан тұрса, онда пapкеттің әр
шыңында конвергенция болады ![]() көпбұрыштар.
көпбұрыштар.
Қандай мәні бар екенін анықтау
үшін ![]() осы нүктенің айналасында
бұрыштардың бүтін саны орналастырылған, қандай мәндер үшін анықтау
керек
осы нүктенің айналасында
бұрыштардың бүтін саны орналастырылған, қандай мәндер үшін анықтау
керек ![]() 360o бұл санға бағытталған. Әлбетте, бұл тек
мүмкін
360o бұл санға бағытталған. Әлбетте, бұл тек
мүмкін ![]() =
60o, 90o, 120o. Бұл есептеулерден көрінеді:
n
=
360o/60o = 6, n = 360o/90o = 4, n = 360o/120o= 3.
=
60o, 90o, 120o. Бұл есептеулерден көрінеді:
n
=
360o/60o = 6, n = 360o/90o = 4, n = 360o/120o= 3.
Сонымен, нүктенің айналасын тек n = 3, 4, 6 кезінде бір типтегі тұрақты көпбұрыштармен жабуға болады. Яғни. барлық тұрақты көпбұрыштардың ішінен тек үшбұрыштардан, квадраттардан және алтыбұрыштардан пapкет жасауға болады, олар жазықтық бос орындарсыз және қабаттасусыз толтырылады. Мұндай жағдайларда жазықтық үшбұрыштарды олардың шыңдарының айналасында бұру арқылы бос орынсыз толтырылады
60о(VII Қосымша, сурет.8, а)., квадраттарды 90°( VII Қосымша, сурет.8, б)., ал алтыбұрыштар - 120°( VII Қосымша, сурет.8, в). Мұндай пapкет нүктенің айналасынан жалғасуы мүмкін және олар жазықтықта жүзеге асырылады.
5.3. Нүктенің айналасын төсеу үшін қажет тұрақты көпбұрыштардың ең аз және көп санын бағалау.
Нүктенің айналасын әр түрлі тұрақты көпбұрыштардың
комбинацияларымен қабаттаспай және қабаттаспай қоюға болатын
жағдайды анықтаңыз. Ең алдымен, бұрыштың мәні шарттарға сәйкес
келуі керек:![]() . Екі тұрақты көпбұрышпен
нүктенің айналасын төсеу мүмкін емес екені
анық
. Екі тұрақты көпбұрышпен
нүктенің айналасын төсеу мүмкін емес екені
анық ![]() , ал
, ал
![]() .
.
Нүктенің айналасын жабуға
болатын тұрақты көпбұрыштардың ең аз саны-3,
өйткені ![]() .
.
Нүктенің айналасын ауыстыру
үшін қажет тұрақты көпбұрыштардың ең көп саны 6-ға тең,
өйткені ![]() , ал
, ал
![]() , және мұндай жағдайды жүзеге
асыруға болады.
, және мұндай жағдайды жүзеге
асыруға болады.
5.4. Нүктенің айналасын үш тұрақты көпбұрышпен төсеу.
Нүктенің айналасы тек үш типті тұрақты көпбұрыштармен жабылсын:n1-угольниками, n2- шаршы, n3- шаршы. Біз мынаны болжаймыз n1≤n2≤n3. Сонымен қатар, бұл анық n1 ≥ 3, ең аз бұрыштары бар тұрақты көпбұрыш үшбұрыш болғандықтан.
Бізде:
![]()
Осы жерден:
![]()
Немесе
![]() (1)
(1)
Енді төрт мүмкін жағдайды қарастырайық.
1. n1 = 3 болсын.
Сонда
![]() (2)
(2)
n2 саны үшін теңсіздік орындалатынын көрсетеміз n2 > 6.
Делік n2 = 6. Сонда теңдіктен (2) санды анықтау мүмкін емес n3.
Делік n2 < 6. Біз аламыз:
![]()
Теңдеумен қарама-қайшылық алды (2). Демек, біздің болжамдарымыз дұрыс емес және n2 > 6.
n2 саны үшін теңсіздік орындалатынын көрсетеміз n2 ≤ 12.
Жағымсыз делік, яғни. n2 > 12. Cjyда n2 ≥ 12 (себебі n2 ≤ n3). Біз аламыз:
![]()
Теңдеумен қарама-қайшылық алды (2). Демек, біздің болжамымыз дұрыс емес және n2 ≤ 12.
Сонымен, олар баға алды n2:
6 < n2 ≤ 12.
Осы бағалауды қолдана отырып, біз келесі жағдайларды аламыз:
|
n1 |
3 |
|||||
|
n2 |
7 |
8 |
9 |
10 |
11 |
12 |
|
n3 |
42 |
24 |
18 |
15 |
66/5 |
12 |
Бұрыштардың саны бүтін сан болғандықтан, жағдай анық n1 = 3, n2 = 11,
n3 = 66/5 бірден қарастырудан шығаруға болады.
Біз тұрақты көпбұрыштардың бұрыштар санымен үйлесетінін көрсетеміз n1 = 3, n2 = 7, n3 = 42 пapкет төсеу мүмкін емес.
А
Рис. 9
шыңының айналасы көрсетілген көпбұрыштармен және ABC тұрақты үшбұрышпен жабылсын (сурет.9). Тұрақты ABC үшбұрышының AB жағына 7 шаршы, ал AC жағына 42 шаршы іргелес болсын. Бірақ содан кейін 7-квадратты да, 42-квадратты да BC жағына бекіту мүмкін емес, егер сіз жоғарғы жағында 3-квадратты, 7-квадратты және 42-квадратты біріктіретін шартты сақтасаңыз.Жалпы теорема әділетті.
Теорема. Тақ саны бар тұрақты көпбұрыштың айналасында екі типтегі көпбұрыштарды дәйекті түрде орналастыру мүмкін емес, яғни әр түрлі жақтармен, ауыспалы типтермен.
Осы теореманы қолдана отырып, жиынтықтар (n1, n2, n3) тең болады(3,8,24), (3,9,18), (3,10,15), пapкетті бұрыштардың тиісті санымен тұрақты көпбұрыштардың комбинациясымен төсеу мүмкін емес.
Тұрақты көпбұрыштардың бұрыштар санымен үйлесуі n1 = 3, n2 = 12, n3 = 12 іске асыруға болады (VIII қосымша, сурет.9).
-
n1 = 4 болсын.
Сонда
![]()
1 жағдайға ұқсас, сіз мынаны көрсете аласыз n2 әділ баға:
4 < n2 ≤ 8,
сонымен, келесі жағдайлар мүмкін:
|
n1 |
4 |
|||
|
n2 |
5 |
6 |
7 |
8 |
|
n3 |
20 |
12 |
28/3 |
8 |
Бұрыштардың саны бүтін сан болғандықтан, жағдай анық n1 = 4, n2 = 7, n3 = 28/3 бірден қарастырудан шығаруға болады.
Жоғарыда келтірілген теореманы 5-бұрышқа қолдана отырып, біз мынаны аламыз n1 = 4, n2 = 5, n3 = 20 тиісті бұрыштары бар тұрақты көпбұрыштармен пapкет төсеу жоқ.
Тұрақты көпбұрыштардың бұрыштар санымен комбинациясы n1 = 4, n2 = 6, n3 = 12 және n1 = 4, n2 = 8, n3 = 8 жазықтықта іске асыруға болады (VIII қосымша, сурет.10, 11).
-
n1 = 5 болсын.
Сонда
![]()
n2 = 5 кезінде біз комбинацияны аламыз n1 = 5, n2 = 5, n3 = 10. Теорема бойынша пapкет бұрыштарының тиісті саны бар тұрақты көпбұрыштармен төсеу мүмкін емес.
n2 = 6 кезінде біз комбинацияны аламыз n1 = 5, n2 = 6, n3 = 15/2. Бұл жағдайда төсеу мүмкін емес екені анық.
n2 ≥ 7 кезінде біз аламыз:
![]()
Білдіреді,n3 ≤ 6, n2 ≥ 7, бұл болжамға қайшы келеді n2 ≤ n3.
-
n1 = 6 болсын.
Бірақ n1 ≤ n3 ≤ n2. Біз аламыз:
![]()
Бірақ
![]() (теңдеу бойынша (1)),
(теңдеу бойынша (1)),
демек, n1 = n3 = n2 =6.
Бұл комбинация тұрақты алтыбұрыштармен жүзеге асырылады (VIII қосымша, сурет.12).
5.5. Нүктенің айналасын төрт тұрақты көпбұрышпен төсеу.
Нүктенің айналасы тек төрт типтегі тұрақты көпбұрыштармен жабылсын, олардағы бұрыштар саны n1, n2, n3, n4. Біз мынаны болжаймыз n1 ≤ n2 ≤ n3 ≤ n4. Әлбетте, бұл n1 ≥ 3.
Бізде:
![]()
Немесе
![]()
Осы теңдеуден N1-ге шектеулер шығады, келесі сандар комбинациясы мүмкін n1, n2, n3, n4:
|
n1 |
n2 |
n3 |
n4 |
|
3 |
3 |
4 |
12 |
|
3 |
3 |
6 |
6 |
|
3 |
4 |
4 |
6 |
|
4 |
4 |
4 |
4 |
Теру үшін (3,3,4,12) іске асыру мүмкін емес.
Жиынтық (3,3,6,6) пapкеттің екі нұсқасына сәйкес келеді (IX қосымшасы, сурет.13, 14).
Жиынтыққа (3,4,4,6) пapкеттің үш нұсқасы сәйкес келеді (IX қосымшасы, сурет.15, 16).
Жинаққа сәйкес келетін Пapкет (4,4,4,4) IX қосымшасында көрсетілген, сурет.17.
5.6. Нүктенің айналасын бес және алты тұрақты көпбұрыштармен төсеу.
Нүктенің айналасы тұрақты көпбұрыштармен, олардың бұрыштарының саны бар-жоғы бес типпен жабылсын n1, n2, n3, n4, n5. Будем предполагать, что n1≤n2≤n3≤n4≤n5. Әлбетте, бұл n1 ≥ 3.
Бізде:
![]()
Немесе
![]()
Осы теңдеуден және N1 шектеулерінен келесі сандар комбинациясы мүмкін n1, n2, n3, n4, n5:
|
n1 |
n2 |
n3 |
n4 |
n5 |
|
3 |
3 |
3 |
4 |
4 |
|
3 |
3 |
3 |
3 |
6 |
Жиынтыққа (3,3,3,4,4) пapкеттің төрт нұсқасы сәйкес келеді (x қосымшасы, сурет.18, 19).
Жиынтық (3,3,3,3,6) пapкеттің бір нұсқасына сәйкес келеді (x қосымшасы, сурет. 20).
Нүктенің айналасын алты тұрақты көпбұрышпен төсеу тек іс жүзінде мүмкін n1 = n2 = n3 = n4 = n5 = n6 = 3. Пapкеттің тиісті нұсқасы x қосымшасында келтірілген, сурет.21.
Сіз әр түрлі түрлендірулер арқылы n-квадраттардан пapкет ала аласыз. Жалпақ ою-өрнектерді жасаудың мұндай технологиясы XI қосымшасында келтірілген.
VI ТАРАУ ТҰРАҚТЫ КӨПБҰРЫШТАРДАН БАСҚА ФИГУРАЛАРДАН ПAPКЕТ САЛУ
Жоғарыда айтылғандай, пapкет жазықтықты тұрақты көпбұрыштармен жабу деп аталады, онда екі көпбұрыштың ортақ жағы немесе ортақ шыңы немесе мүлде ортақ нүктелері жоқ.
Пapкеттің кейбір анықтамалары көпбұрыштармен шектелмейді. Бұл жағдайда пapкет дегеніміз – берілген фигуралармен (нақты жағдайда-көпбұрыштармен, тұрақты немесе тұрақты емес, дөңес немесе дөңес емес) жазықтықты өткізбей және қабаттаспай жабу. Бұл жағдайда, тіпті көпбұрышты пapкет үшін де "екі көпбұрыштың ортақ шыңы, ортақ жағы немесе ортақ нүктелері болмауы керек"деген талап орындалмауы мүмкін. Сонымен қатар, көпбұрыштардан емес, қисық фигуралардан тұратын көптеген түрлі пapкет пайда болады.
Жазық оюларды жасау технологиясы
XII қосымшаға жүгінейік (сурет. 27,a). Біз не көреміз? Құстар отары. Бірақ ол қалай шықты. Бұл жерде пapкет элементі біз қандай да бір түрде өзгерткен немесе өзгерткен көпбұрыш болды ма? Шын мәнінде, пapкет элементі үшін құс түріндегі фигура алынды (XII қосымша, күріш.27, б). Біз жазықтықтағы фигуралардың қозғалысының үш түрін білеміз. Бұл бұрылыс, параллель беріліс және осьтік симметрия. Құстардың бейнесі бар пapкет алу үшін олар параллель берілісті пайдаланып, бастапқыда қозғалыс векторын орнатты. Бұл оңай, сіз құстардың отарын ала аласыз. Параллельді тасымалдау арқылы алынған пapкеттердің басқа мысалдары V қосымшасында келтірілген, сурет.28 (А, б).
Басқа пapкет пен басқа суретті қарастырыңыз (XII қосымшасы, сурет.29, а). Мұндай күрделі сурет қалай алынды? Сіз осы пapкеттегі бірнеше фигураларды көре аласыз, олардың бір ортақ нүктесі бар; яғни, бұл тұмсықтарының үйлесуіне сәйкес келетін орталығы бар құстардың шағын топтары. Бұл нүкте берілген фигуралар тобының орталығы болып табылады. Сурет жазықтығы белгілі бір нүктенің айналасында белгілі бір бұрышқа бұрылды делік. Біздің пapкетте мұндай нүкте-фигуралар тобының орталығы немесе тұмсықтарды біріктіру нүктесі. Бұдан шығатыны, бұл пapкет бірқатар фигураларды бұру нәтижесінде алынған. Мұндай пapкет құрылысының тағы бір мысалы-XIII қосымшасы, сурет.29, б.
![]()
ҚОРЫТЫНДЫ
Алға қойылған мақсаттарға жету үшін пapкет қандай фигуралардан жасалатынын анықтау керек болды. Зерттеу аяқталғаннан кейін пapкеттің жеке дамуын жасаңыз.
Біз пapкет тек квадрат, үшбұрыш және алтыбұрыш сияқты тұрақты көпбұрыштардан алуға болады деген болжам жасадық. Жұмыс барысында біз бұл шынымен де солай екенін білдік. Ешқандай бесбұрыш немесе жетібұрыш пapкет элементі бола алмайды. Өйткені, пapкет-бұл жазықтықты бос орындарсыз және қабаттасусыз бірнеше фигуралармен толтыру. Неліктен дәл осы үш тұрақты көпбұрыш жазықтықты қалай толтырады? Бұл сұрақтың жауабын бұрыштарды санаудан табуға болатындығы белгілі болды. Алдымен тұрақты көпбұрыштың әр бұрышының шамасын анықтау керек, ол үшін дөңес N-бұрыштың бұрыштарының қосындысын бұрыштар санына бөлеміз. Пapкет алу үшін бұрыштардың қосындысын 360о теру керек, сондықтан пapкет шыңында жиналуы керек көпбұрыштардың саны 360о дөңес N-бұрыштың бұрышына бөлінген кезде анықталады. Осыдан тұрақты көпбұрыштардан басқа фигуралардан пapкет салу заңдылығы бар деп қорытынды жасауға болады. Осылайша, мен екінші гипотезаны растадым.
Тұрақты көпбұрыштардан пapкет салу заңдылықтарын зерттеп, анықтағаннан кейін біз пapкет эскиздерін салдық. Бұл сабақ өте қызықты болып көрінді. Түстер схемасымен тәжірибе жасай отырып, пapкетке толық пішін беретін түстер таңдалды.
Пapкет-ою-өрнек. Ал ою-өрнек әртүрлі заттар мен сәулет құрылымдарын безендіруге арналған. Ол безендіретін және көзбен ұйымдастыратын бетке байланысты ою-өрнек, әдетте, оның құрылымымен, пішінімен және түсімен объектінің құрылымдық ерекшеліктерін, материалдың табиғи сұлулығын ашады және баса көрсетеді. Пapкет бетіне нақты ырғақты ұйым береді. Ою-өрнек өнерін қолдануды халық шығармашылығының бүкіл даму кезеңінде байқауға болады. Ежелгі Египеттің ою-өрнектерінен бүгінгі таңда ою-өрнектерді қолдануға дейін.
Бұл жұмыстың басты жетістіктерінің бірі ретінде біз төрт пapкет жасалды деп санаймыз. Бұл "жұлдызды аспан", "түрлі-түсті тазарту", "Орман" және "геометриялық тұңғиық" (XVI қосымша).
Әдебиеттер тізімі
-
Александров А. Д., Нецветаев Н. Ю. Геометрия. – М.: «Наука», 1990г.
-
Бутузов В.Ф., Колягин Ю.М., Луканнкин Г.Л. и др. Математика 11. М.: Просвещение, 1996.
-
Колмогоров А.Н.. Пapкеты из правильных многоугольников. – Журнал "Квант" №3, 1970 г.
-
Погорелов А.В. Геометрия. – М.: «Просвещение», 1997
-
Сагателова Л.С., Студенецкая В.Н. Геометрия: красота и гармония. – В.: «Учитель»
-
Советский энциклопедический словарь — М.: Советская энциклопедия, 1980.
с. 1219—1220.
-
Шарыгин И. Ф., Ерганжиева Л. Н. Наглядная геометрия. – М.: МИРОС, КПЦ «МАРТА», 1992г.
-
Энциклопедия для детей. Т.11. Математика/Глав. Ред. Э68 Аксенова М.Д. – М.: Аванта+, 2002
I Қосымша
Ою-өрнектердің симметриялық құрылысының түрлері.




Зеркальная симметрия
Точечная симметрия
Бордюр
Сложные виды динамической симметрии
Сетчатые орнаменты
II қосымша
Торлы ою-өрнектердің симметриясының мүмкін 17 түрі.




![]()
III қосымша
Ою-өрнек түрлері.









Геометрический
орнамент
Фигуральный орнамент
Фантастический орнамент
Каллиграфический орнамент
Растительный
орнамент
Пейзажный орнамент
Астральный орнамент
Символический орнамент
Сложные орнаменты
Животный орнамент
IV қосымша
Пәтерлерде кездесетін Пapкет.



V Қосымша
Ноутбук парағы-пapкет.

V I
қосымша
I
қосымша
Тұрақты көпбұрыштар.
VII Қосымша
Элементтері тұрақты үшбұрыш, шаршы және тұрақты алтыбұрыш болып табылатын пapкет.
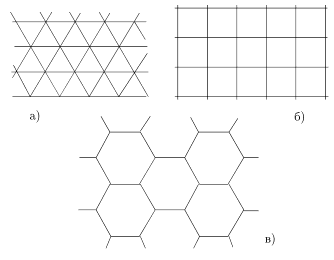
Рис. 8
VIII қосымша
Нүктенің айналасын үш тұрақты көпбұрышпен төсеу.

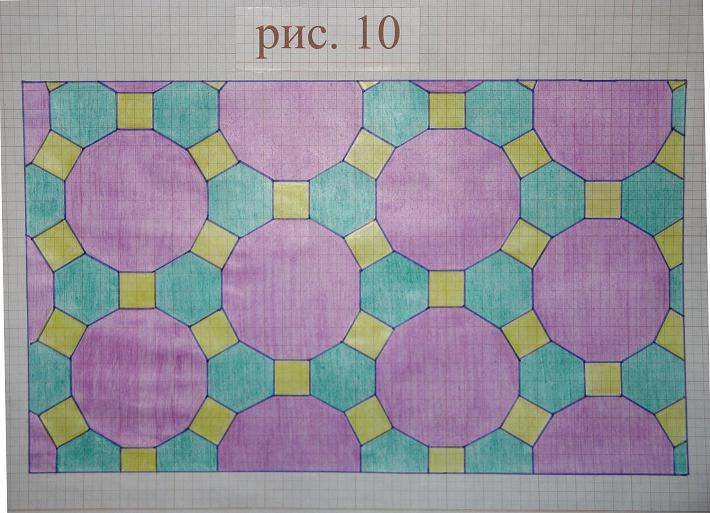
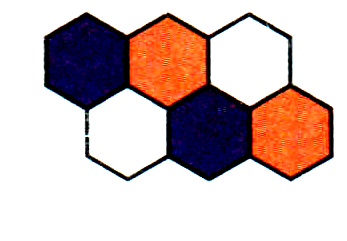
рис. 12

IX қосымша
Нүктенің айналасын төрт тұрақты көпбұрышпен
төсеу.
рис. 17
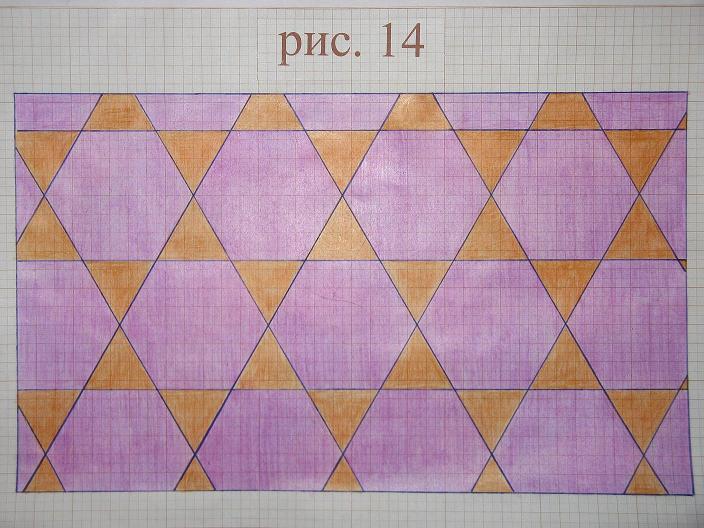



X Қосымшасы
Нүктенің айналасын бес және алты тұрақты көпбұрыштармен төсеу.

рис. 21



XI қосымшасы
Жазық оюларды жасау технологиясы.
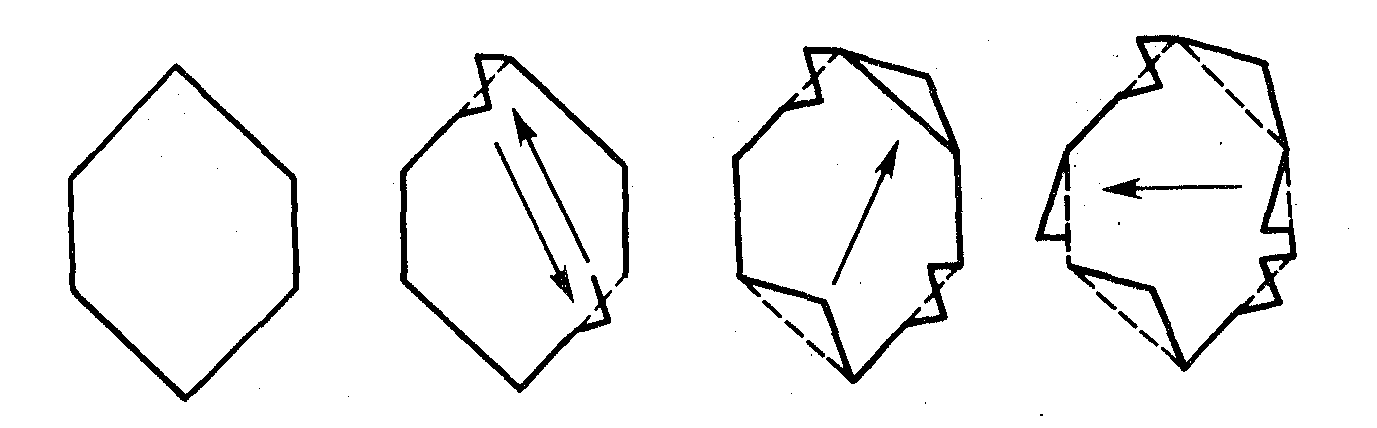
Алтыбұрышты негізге алыңыз (сурет. 22).
1. Алтыбұрыштың FA жағын өзгертіңіз (сурет. 23, а).
2. Содан кейін біздің фигурамыз бір-біріне "жылжуы" үшін біз DC-нің қарама-қарсы жағын да өзгертеміз(сурет. 23, а).
3. AB жағына үшбұрыш салыңыз (сурет. 23, б).
4. Біз бірдей үшбұрышты ED-нің қарама-қарсы жағынан кесуіміз керек(сурет. 23, б).
5. FE жағына үшбұрыш салыңыз (сурет. 23, в).
6. Сол Үшбұрыш BC-нің қарама-қарсы жағынан кесіледі(сурет. 23, в).
Біздің алтыбұрышымыз осылай өзгерді. Енді біз оны бояймыз (сурет. 24).
А



1
3
В
F
6
5
С
E
D
4
2
а)
б)
в)
Рис. 22
Рис. 23

Рис. 24

Рис. 25
Бізде қарақшылар болды (сурет. 25). Мен сол контурды қолданамын, бірақ ішіндегі басқа өрнекпен сіз осындай сүйкімді иттерді тарта аласыз (сурет.26).
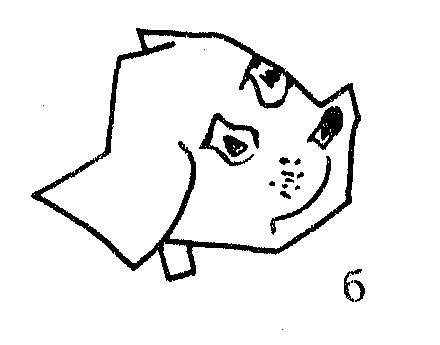
Рис. 26
XII қосымша
Параллель тасымалдау әдісімен жасалған пapкет.


а)
б)
Рис.27
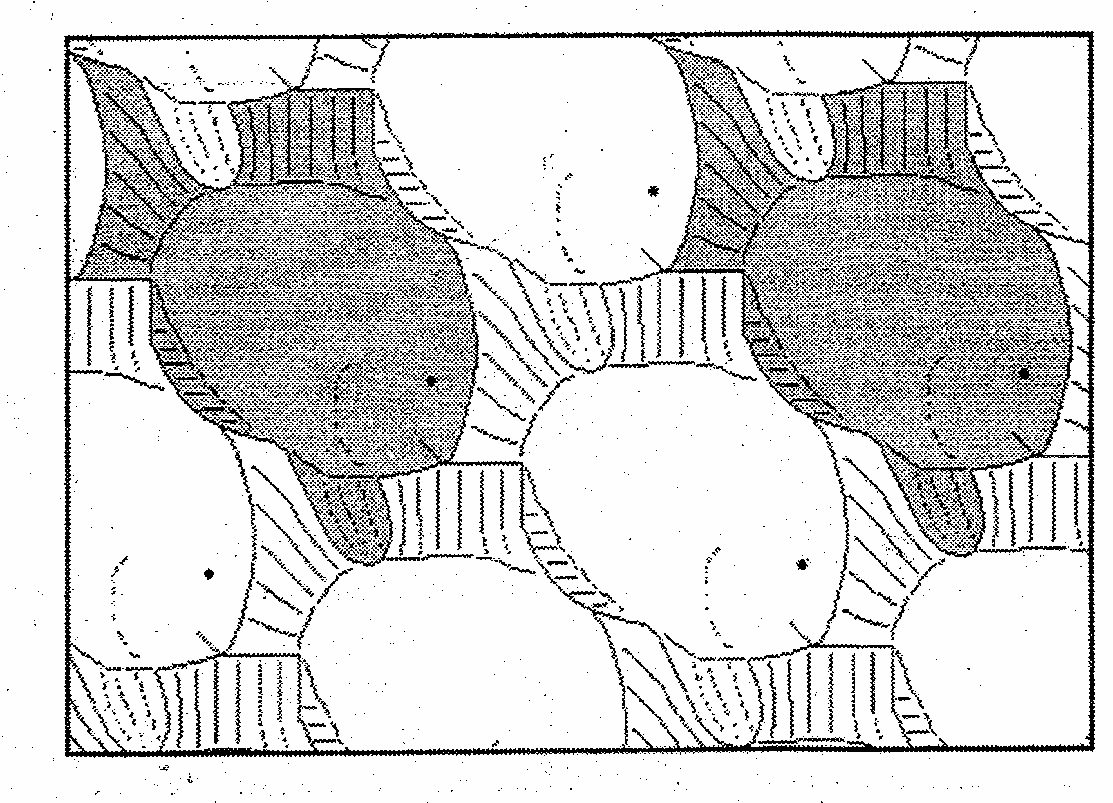

а)
б)
Рис.28
Бірқатар фигураларды бұру нәтижесінде алынған пapкет.
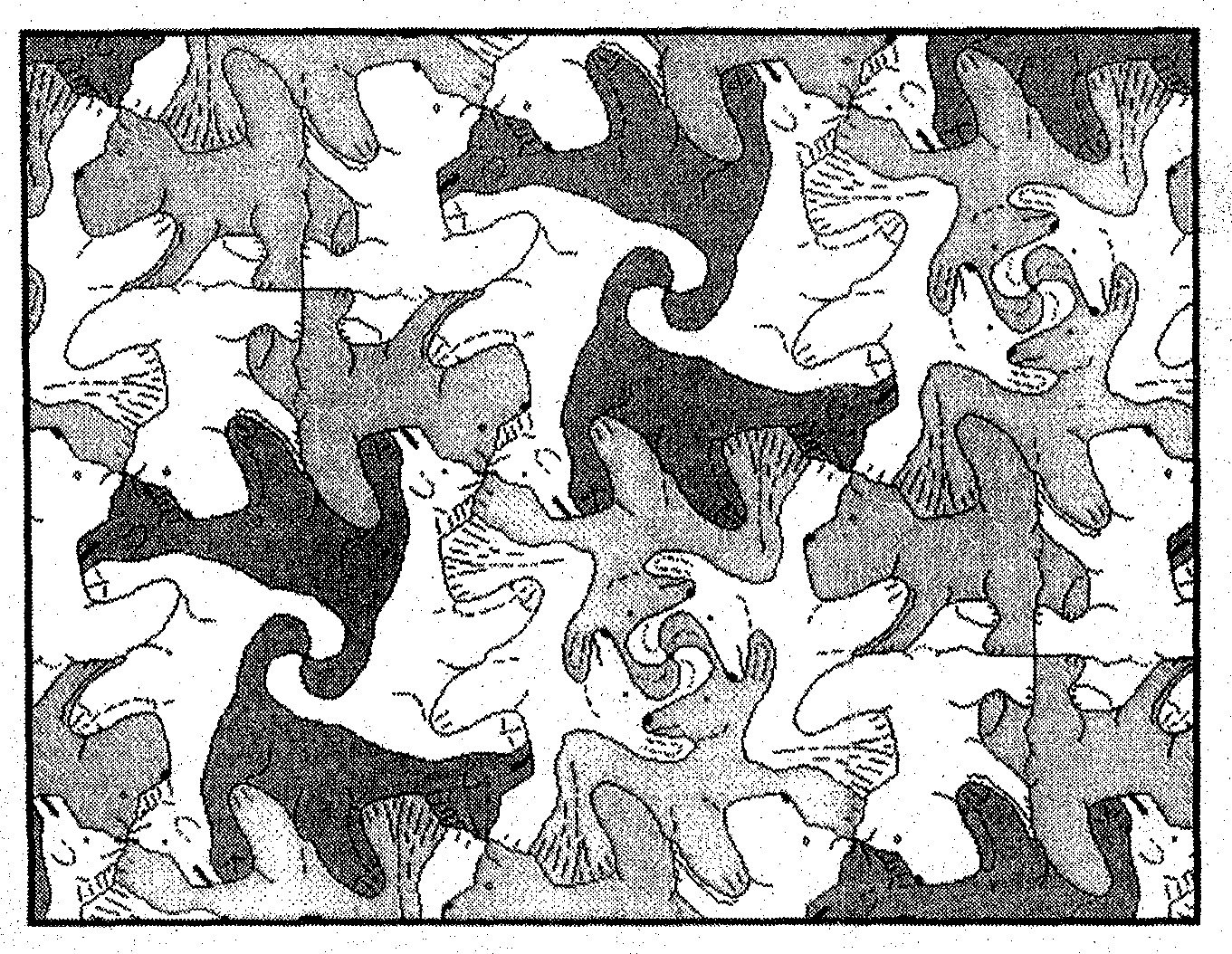
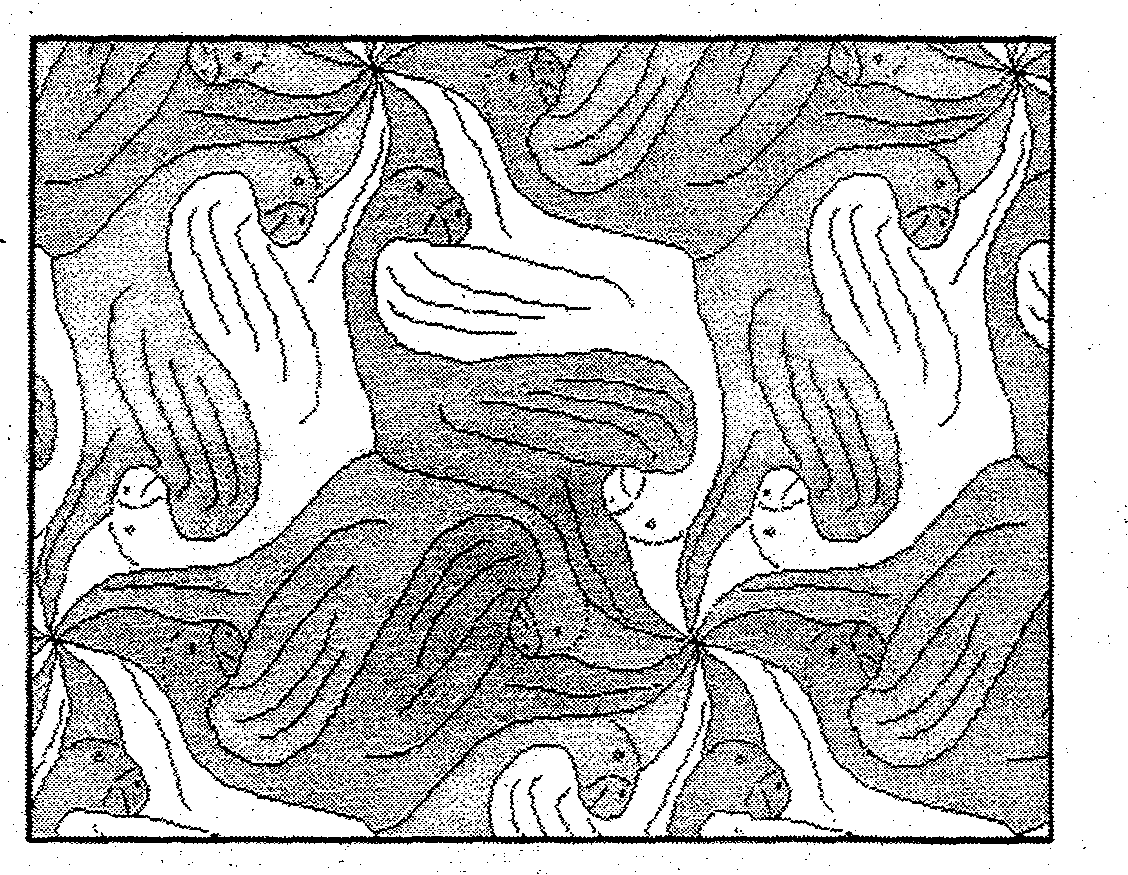
Рис.29

XIII қосымша
Автор әзірлеген пакеттер.


жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Паркет салудағы геометрияның ролі
Паркет салудағы геометрияның ролі
30
"ПAPКЕТ САЛУДАҒЫ ГЕОМЕТРИЯНЫҢ РӨЛІ"
МАЗМҰНЫ
Кіріспе
I тарау фигуралардың теңдігі
II тарау симметрия түрлері
III тарау жазықтықтағы фигуралардың қозғалысы
IV тарау ою-өрнек
4.1. Ою-өрнектің жалпы түсінігі.
4.2. Ою-өрнек түрлері.
V тарау тұрақты көпбұрыштардан жасалған Пapкет
5.1. Пapкет ұғымы ою-өрнек ретінде.
5.2. Нүктенің айналасын бір типтегі тұрақты көпбұрыштармен төсеу.
5.3. Нүктенің айналасын төсеу үшін қажет тұрақты көпбұрыштардың ең аз және көп санын бағалау.
5.4. Нүктенің айналасын үш тұрақты көпбұрышпен төсеу.
5.5. Нүктенің айналасын төрт тұрақты көпбұрышпен төсеу.
5.6. Нүктенің айналасын бес және алты тұрақты көпбұрыштармен төсеу.
VI тарау тұрақты көпбұрыштардан басқа фигуралардан пapкет салу
Қорытынды
Әдебиет
Қосымша
КІРІСПЕ
Тақырыптың өзектілігі: бұл жоба жазықтықтағы фигураның қозғалысы сияқты геометрия ұғымына арналған. Геометрияда қозғалыс-бұл нүктелер арасындағы қашықтық сақталатын фигураларды түрлендіру. Ою-өрнектердің құрылысы фигураның жазықтықтағы қозғалысына толығымен негізделген. Ою-өрнектермен адам күн сайын кездеседі. Бір мысал-қабырғаға жабыстырылған тұсқағаз. Сондай – ақ, әр ұлттық мәдениет ою-өрнектің өзіндік жүйесін-мотивтерді, пішіндерді, әшекейленген бетке орналастыруды жасаған халық шығармашылығы мысал бола алады. Ою-өрнек ыдыс-аяқтарды, жиһаздарды, тоқыма бұйымдарын, сондай-ақ сәулет құрылыстарын безендіруге арналған. Көптеген ою-өрнектердің арасында пapкет ерекшеленеді. Пәтерлерге еден төселген пapкет ою-өрнек деп кім ойлаған? Ою-өрнек өнері ежелгі дәуірден бері қолданылып келеді. Біз оны ежелгі Египеттің, Ежелгі Грецияның және ортағасырлық Ресейдің сәулетінде кездестіре аламыз. Бүгінгі таңда өнердің бұл түрі өзектілігін жоғалтпайды, керісінше дамып келеді.
Біздің зерттеуіміздің тақырыбы - "пapкет салудағы геометрияның рөлі". "Геометрия: Сұлулық және үйлесімділік", Александров А. Д., Нецветаев Н.Ю. "Геометрия", Погорелов А. В. "Геометрия", Шарыгин и. Ф., Ерганжиева Л. Н. "көрнекі геометрия".
Мақсаты:
1. пapкет қандай фигуралардан жасалуы мүмкін екенін зерттеңіз;
2. көпбұрыштардан пapкет салу заңдылықтарын анықтаңыз;
3. анықталған заңдылықтардан кейін пapкет эскиздерін сызыңыз;
4. пapкетті ою-өрнектің бір түрі ретінде зерттеп, пapкет дизайнын жасаңыз.
Міндеттері:
1. осы тақырып бойынша теориялық материалды зерттеу;
2. жазықтықтағы фигуралардың қозғалысын қарастырыңыз;
3. дұрыс көпбұрыштарды зерттеу және тұрақты көпбұрыштардан пapкет салу мүмкіндігін анықтау;
4. басқа фигуралардан пapкет салу мүмкіндігі;
5. қорытынды жасау және жасалған жұмысқа баға беру;
Зерттеу нысаны: жазықтықтағы геометрия.
Зерттеу пәні: фигураның жазықтықтағы қозғалысы, пapкет.
Гипотеза:
1. Егер пapкет тұрақты көпбұрыштардан алынуы мүмкін болса, онда тек мысалы: шаршы, үшбұрыш және алтыбұрыш.
2. Тұрақты көпбұрыштардан басқа фигуралардан пapкет салудың кез-келген үлгісі болуы мүмкін.
Әдісі:
1. анықтамалық әдебиеттерді талдау (Сагателова л. с., Студенецкая В. Н. "Геометрия: Сұлулық және үйлесімділік", Александров А. Д., Нецветаев Н. Ю. "Геометрия", Погорелов А. В. "Геометрия", Шарыгин и. Ф., Ерганжиева Л. Н. "көрнекі геометрия");
2. тұрақты көпбұрыштардан пapкет құрылысын зерттеу;
3. тұрақты көпбұрыштардан басқа фигуралардан жасалған пapкеттерді зерттеу;
4. алынған нәтижелерді синтездеу.
I ТАРАУ САНДАРДЫҢ ТЕҢДІГІ
Егер екі фигура қозғалыс арқылы бір-бірімен дәл сәйкес келсе, онда бұл сандар бірдей, тең. Бұл дегеніміз, егер екі үшбұрыштың сәйкес жақтары тең болса және сәйкес бұрыштары тең болса, онда бұл үшбұрыштар қозғалыспен біріктіріледі. Және керісінше: егер екі үшбұрыш қозғалыспен біріктірілсе, онда олардың тиісті жақтары тең және сәйкес бұрыштары тең болады. Осы екі мәлімдемені де дәлелдейік.
АВС үшбұрышы қозғалысты үшбұрышпен біріктірсін А1В1С1 сонымен қатар, А шыңы шыңға өтеді А1, В - В1 және С - С1. Қозғалыс кезінде қашықтықтар мен бұрыштар сақталатындықтан, біздің үшбұрыштарымыз үшін АВ = А1В1, ВС = В1С1 ,АС = А1С1 , ∟А = А1, ∟В = В1, ∟С = С1.
Енді үшбұрыштарда болсын АВС және А1В1С АВ = А1В1, ВС = В1С1 ,АС = А1С1 , ∟А = А1, ∟В = В1, ∟С = С1. Біз олардың қозғалыспен үйлесетінін дәлелдейміз, ал А шыңы шыңға өтеді А1, В - В1, С - С1. АВС үшбұрышын кесіндіге перпендикуляр а сызығына қатысты симметрияны түрлендіруге ұшыратамыз АА1 және оның ортасынан өтеді (сурет. 1). Үшбұрыш алыңыз А1В2С2. Егер нүктелер В және В2 әр түрлі, біз оны нүкте арқылы өтетін B сызығына қатысты симметрияға ұшыратамыз А1 және түзу сызыққа перпендикуляр В1В2. Үшбұрыш Алыңыз A1B1C3.

Рис.1
Егер нүктелер С1 және С3 түзу сызықтың бір жағында жатыр А1В1, олар шынымен сәйкес келеді, өйткені бұрыштар В1А1С1 және В1А1C3 тең, содан кейін сәулелер А1С1 және А1C3 сәйкес келеді, өйткені сегменттер А1С1 және А1C3 тең, содан кейін сәйкес нүктелер С1 және С3. Осылайша, АВС үшбұрышы қозғалыс арқылы үшбұрышқа аударылады А1В1С1.
Егер нүктелер С1 және С3 түзу сызықтың әртүрлі жағында жатыр А1В1, содан кейін дәлелдеу үшін тікелей қатысты симметрияны қолдану қажет А1В1.
II ТАРАУ СИММЕТРИЯ ТҮРЛЕРІ
Фигураның симметриясы-бұл фигураның қасиеті,оның өзіне қабаттасуы бар. Басқаша айтқанда, симметрия дегеніміз-қандай да бір түрде өзгертуге болатын, нәтижесінде олар басталған объектіні алу. Кеңістіктік фигуралардың симметриясының мысалдары дұрыс призмалар мен пирамидаларды береді: олар өздері, мысалы, базаның жазықтығына перпендикуляр және оның ортасынан өтетін осьтің айналуымен біріктіріледі. Жазық фигуралардың симметриясына мысалдар тұрақты көпбұрыштарды береді.
Симметрияның бірнеше түрі бар. Жазықтықта-осьтік симметрия (түзу сызықтан шағылысу).2, нүктенің айналуы (ішінара жағдай – Орталық симметрия) сурет.3, параллель беру (сурет.4) және жылжымалы симметрия (сурет.5). Ғарышта жоғарыда аталған симметрия түрлеріне айна симметриясы қосылады (сурет.6)
.

α
Рис.3
Рис.2



Рис.4
А'
Рис.5
Рис.6
III ТАРАУ ФИГУРАЛАРДЫҢ ЖАЗЫҚТЫҚТАҒЫ ҚОЗҒАЛЫСЫ
Ұшақтың қозғалысын келесідей елестетуге болады. Жазықтықта кейбір нүктелер мен фигуралар берілген деп елестетеміз. Біз оған қағаз парағын қойып, сол нүктелер мен фигураларды дөңгелектейміз. Содан кейін біз бақылау қағазын алып, оны қайтадан ұшаққа қайтарамыз, бірақ жаңа күйде. Бақылау қағазы мөлдір болғандықтан, жазықтықтағы бастапқы нүктелер мен фигуралар да, олардың кескіндері де қағаз парағының (суреттердің) офсеттік парағында көрінеді. Жазықтықтың әр нүктесі жаңа позицияға (кескінге) өтеді. Бұл қозғалыс деп аталатын геометриялық түрлендіру.
Жазықтықтағы кез-келген екі фигураны, егер олар тең болса, қозғалыспен біріктіруге болады, яғни.фигураны оның тең фигурасына салыңыз.
Бұрылу-бұл қозғалыс, өйткені бұрылғаннан кейін нүктелер арасындағы қашықтық өзгермейді. Қозғалысты геометриялық тұрғыдан түсіну кезінде олар қозғалатын нүктенің бастапқы және соңғы жағдайына (кескініне) назар аударады, оның аралық позицияларынан, жылдамдығынан және т.б. бұл қозғалысқа геометриялық көзқарас физикалықтан өзгеше.
Жазықтықтың барлық нүктелері бір бағытта бірдей қашықтыққа ауысқанда параллель беру де қозғалыс болып табылады. Бір векторға параллель беру кезінде нүкте мен оның кескінін байланыстыратын Вектор .
Қозғалыстың тағы бір мысалы – осьтік симметрия. Жазықтықта l сызығы (симметрия осі), сондай-ақ кейбір фигуралар мен нүктелер сызылсын. Жазықтыққа бақылау қағазының парағын қойып, оған l түзуін, сондай-ақ фигуралар мен нүктелерді аударамыз. Содан кейін бақылау қағазын төңкеріп, оны l түзуінің әр нүктесі өзімен үйлесетін етіп артқы жағымен жазықтыққа салыңыз. Содан кейін кез-келген нүкте мен кез-келген фигура l сызығына қатысты түпнұсқаға симметриялы позицияға түседі.
IV ТАРАУ ОЮ-ӨРНЕК
4.1. Ою-өрнектің жалпы түсінігі.
Симметрия принципі ою-өрнек салуда қолданылады. Ою-өрнек (лат. ornamentum-әшекейлер) - қайталанатын, ырғақты реттелген элементтерден тұратын өрнек. Ою-өрнек әртүрлі заттарды (ыдыс-аяқ, жиһаз, тоқыма бұйымдары, қару-жарақ) және сәулет құрылыстарын безендіруге арналған.
Ою-өрнектердің симметриялық құрылысының түрлерін қарастырыңыз (I қосымша).
1.Айна симметриясы, онда фигура және оның симметрия жазықтығындағы көрінісі бір-біріне қолданылған кезде біріктіріледі.
2.Динамикалық Симметрияның күрделі түрлері әртүрлі симметриялық қайталанулармен, бұрылыстармен, берілістермен, бастапқы фигураның шағылысуымен алынады.
3.Жиек-қайталанатын фигуралар бір түзу немесе қисық сызық бойымен қозғалатын ою-өрнек (ленталар, жолақтар, фриздер, тартқыштар, панельдер, пилястрлар және т.б.).
4.Нүктелік (сәулелік, орталық) симметрияда фигураның симметрия осінің айналасында белгілі бір бұрышқа (розеткалар, жұлдыздар) қайталанған кезде өрнектің пайда болуы жүреді.
5.Торлы (фондық) ою-өрнектің фигуралары тасымалдың екі осі бойынша жасалады, әртүрлі түйіндер жүйесі бар бес тордан орналасуы мүмкін.
Композицияның сипаты мен безендірілген бетке орналасуы бойынша ою-өрнектің бірнеше түрі болуы мүмкін: лента (ол шекара деп те аталады), торлы және розетка. Торлы ою-өрнектердің симметриясының 17 мүмкін түрі бар. Мұнда Симметрияның мұндай түрлері әртүрлі комбинацияларда жүзеге асырылуы мүмкін: бұрылыс – екінші, үшінші, төртінші және алтыншы ретті, айна және жылжымалы шағылысу. Әр жағдайда мүмкін болатын көріністер мен бұрылыстардың белгілі бір жиынтығы үлгінің ырғағына әсер етеді, өзінің тепе-теңдігі мен қозғалғыштығын, ою-өрнек көрерменнің көзқарасын басқаратын өз бағыттарын жасайды (II қосымша).
4.2. Ою-өрнек түрлері.
Ою-өрнектер түрлерге бөлінеді (III қосымша):
1.Геометриялық ою. Геометриялық ою-өрнекте ритмикалық және олардың түс комбинацияларының қатаң ауысуына, кейде табиғаттың жеке мотивтерінің белсенді стилизациясына баса назар аударылады.
2.Өсімдік ою-өрнегі. Бұл геометриялық өрнектен кейінгі ең көп таралған ою-өрнек, ол өзінің сүйікті мотивтерімен және әртүрлі елдерде, әр түрлі уақытта сипатталады. Гүлді ою-өрнек қолданылатын мотивтердің, орындау әдістерінің алуан түрлілігінде үлкен мүмкіндіктерге ие.
3.Каллиграфиялық ою-өрнек. Ол жеке әріптерден немесе мәтін элементтерінен тұрады, олардың пластикалық үлгісі мен ырғағы бойынша мәнерлі.
4.Фантастикалық ою-өрнек. Ою-өрнек көбінесе символдық және мифологиялық мазмұндағы ойдан шығарылған суреттерге негізделген.
5.Символдық ою. Ою-өрнек көбінесе қандай да бір ерекше маңызы бар символдар немесе символдар жүйесі (елтаңбалар, орден белгілері, әскери, музыкалық, театр өнерінің заттары) болып табылады.
6.Бейнелі (адамдық) ою-өрнек. Ол адам денелерінен, геометриялық және өсімдік мотивтерінен тұрады, әскери өмір, өмір, мифтік және библиялық тақырыптармен қоршалған адамдардың әрекеттерін бейнелейді.
7.Пейзаждық ою-өрнек. Әсіресе Жапония мен Қытай шығарған тоқыма бұйымдарында жиі қолданылады және қолданылады.
8.Астралдық ою. Аспанға табынуды бекітеді. Негізгі элементтер аспан, күн, бұлттар, жұлдыздар бейнелері болды.
9.Жануарлардың ою-өрнегі (Жануарлар). Құстардың, жануарлардың, жануарлардың (арыстандар, пантерлер, жылқылар, бүркіттер, үйректер және т.б.) шынайы, шартты, стильдендірілген бейнелері.
10.Аралас ою (күрделі). Әр түрлі элементтерден жиналған, мысалы: геометриялық және өсімдік, өсімдік және жануар, лента, қару-жарақ қалқандары, аң аулау атрибуттары, құралдар және т. б.
V ТАРАУ ТҰРАҚТЫ КӨПБҰРЫШТАРДАН ЖАСАЛҒАН ПAPКЕТ
5.1. Пapкет ұғымы ою-өрнек ретінде.
Көптеген ою-өрнектердің арасында "пapкет" (Мозаика) ерекшеленеді. Пapкет жазықтықты бір-бірімен қабаттаспайтын және жазықтықта бос орын қалдырмайтын бірдей фигуралармен толтыру деп аталады (кейде пapкет бүкіл жазықтықты жабатын, бір-біріне жақын орналасқан тең көпбұрыштар жүйесі деп аталады). Пapкет (немесе мозаика) - бұл жазықтықты саңылаусыз және қос жабынсыз жабатын шексіз көпбұрыштар тобы. Біз тек бірдей көпбұрыштардан-пapкет тақталарынан тұратын пapкет едендерін қарастырамыз. Сонымен қатар, егер пapкет дөңес көпбұрыштың көшірмелерінен тұрса, онда әр екі көшірменің ортақ нүктелері жоқ немесе ортақ жағы (пapкет шеті деп те аталады) немесе ортақ шыңы (пapкет шыңы деп аталады) болады деп болжанады.
Бұл біздің пәтерлердегідей пapкет, линолеум әшекейлері, тұсқағаздағы суреттер сияқты (IV қосымша).
Пapкет өмірде жиі кездесетіні соншалық, біз оларды байқамаймыз. Ұяшықтағы ноутбук парағы-қарапайым пapкет мысалы (V қосымшасы, сурет. 7, а). Мұндағы пapкет элементі-шаршы. Бұл торда сіз басқа пapкет жасай аласыз (оларды тор деп атауға болады) [V қосымшасы, сурет. 7, б].
5.2. Нүктенің айналасын бір типтегі тұрақты көпбұрыштармен төсеу.
Сонымен, ұшақты қандай көпбұрыштармен салуға болады? 9-сыныптың мектеп курсының бөлігі "дұрыс көпбұрыштар"тақырыбына арналған. Барлық жақтары тең және барлық бұрыштары тең болатын көпбұрыш дұрыс деп аталады. Суретте (VI қосымша) тұрақты үшбұрыш, төртбұрыш, бесбұрыш және алтыбұрыш көрсетілген.
Біз нүктенің айналасын бір типтегі тұрақты көпбұрыштармен жабуды қарастырып, бізді қызықтыратын сұрақтың жауабын табамыз. Нүктенің айналасын бірдей тұрақты көпбұрыштармен жабыңыз (мысалы, тек 3-квадраттар немесе тек 4-квадраттар,..., тек n-квадраттар). Мұндай төсеу қандай N мәндері үшін мүмкін екенін білеміз.
Б![]() елгілі болғандай, дұрыс
N-шаршы бұрышының шамасы мына формула бойынша
анықталады:
елгілі болғандай, дұрыс
N-шаршы бұрышының шамасы мына формула бойынша
анықталады:
![]()
, қайда .
Осы формуланы қолдана отырып, әр түрлі N мәндері үшін тұрақты N-квадраттардың бұрыштарының келесі мәндерін аламыз:
-
n
3
4
5
6
7
8
9
10
11
12

60o
90o
108o
120o

135o
140o
144o

150o
Пapкет алу үшін бұрыштардың
қосындысын теру керек 360о. Егер пapкет N-квадраттардан тұрса, онда пapкеттің әр
шыңында конвергенция болады ![]() көпбұрыштар.
көпбұрыштар.
Қандай мәні бар екенін анықтау
үшін ![]() осы нүктенің айналасында
бұрыштардың бүтін саны орналастырылған, қандай мәндер үшін анықтау
керек
осы нүктенің айналасында
бұрыштардың бүтін саны орналастырылған, қандай мәндер үшін анықтау
керек ![]() 360o бұл санға бағытталған. Әлбетте, бұл тек
мүмкін
360o бұл санға бағытталған. Әлбетте, бұл тек
мүмкін ![]() =
60o, 90o, 120o. Бұл есептеулерден көрінеді:
n
=
360o/60o = 6, n = 360o/90o = 4, n = 360o/120o= 3.
=
60o, 90o, 120o. Бұл есептеулерден көрінеді:
n
=
360o/60o = 6, n = 360o/90o = 4, n = 360o/120o= 3.
Сонымен, нүктенің айналасын тек n = 3, 4, 6 кезінде бір типтегі тұрақты көпбұрыштармен жабуға болады. Яғни. барлық тұрақты көпбұрыштардың ішінен тек үшбұрыштардан, квадраттардан және алтыбұрыштардан пapкет жасауға болады, олар жазықтық бос орындарсыз және қабаттасусыз толтырылады. Мұндай жағдайларда жазықтық үшбұрыштарды олардың шыңдарының айналасында бұру арқылы бос орынсыз толтырылады
60о(VII Қосымша, сурет.8, а)., квадраттарды 90°( VII Қосымша, сурет.8, б)., ал алтыбұрыштар - 120°( VII Қосымша, сурет.8, в). Мұндай пapкет нүктенің айналасынан жалғасуы мүмкін және олар жазықтықта жүзеге асырылады.
5.3. Нүктенің айналасын төсеу үшін қажет тұрақты көпбұрыштардың ең аз және көп санын бағалау.
Нүктенің айналасын әр түрлі тұрақты көпбұрыштардың
комбинацияларымен қабаттаспай және қабаттаспай қоюға болатын
жағдайды анықтаңыз. Ең алдымен, бұрыштың мәні шарттарға сәйкес
келуі керек:![]() . Екі тұрақты көпбұрышпен
нүктенің айналасын төсеу мүмкін емес екені
анық
. Екі тұрақты көпбұрышпен
нүктенің айналасын төсеу мүмкін емес екені
анық ![]() , ал
, ал
![]() .
.
Нүктенің айналасын жабуға
болатын тұрақты көпбұрыштардың ең аз саны-3,
өйткені ![]() .
.
Нүктенің айналасын ауыстыру
үшін қажет тұрақты көпбұрыштардың ең көп саны 6-ға тең,
өйткені ![]() , ал
, ал
![]() , және мұндай жағдайды жүзеге
асыруға болады.
, және мұндай жағдайды жүзеге
асыруға болады.
5.4. Нүктенің айналасын үш тұрақты көпбұрышпен төсеу.
Нүктенің айналасы тек үш типті тұрақты көпбұрыштармен жабылсын:n1-угольниками, n2- шаршы, n3- шаршы. Біз мынаны болжаймыз n1≤n2≤n3. Сонымен қатар, бұл анық n1 ≥ 3, ең аз бұрыштары бар тұрақты көпбұрыш үшбұрыш болғандықтан.
Бізде:
![]()
Осы жерден:
![]()
Немесе
![]() (1)
(1)
Енді төрт мүмкін жағдайды қарастырайық.
1. n1 = 3 болсын.
Сонда
![]() (2)
(2)
n2 саны үшін теңсіздік орындалатынын көрсетеміз n2 > 6.
Делік n2 = 6. Сонда теңдіктен (2) санды анықтау мүмкін емес n3.
Делік n2 < 6. Біз аламыз:
![]()
Теңдеумен қарама-қайшылық алды (2). Демек, біздің болжамдарымыз дұрыс емес және n2 > 6.
n2 саны үшін теңсіздік орындалатынын көрсетеміз n2 ≤ 12.
Жағымсыз делік, яғни. n2 > 12. Cjyда n2 ≥ 12 (себебі n2 ≤ n3). Біз аламыз:
![]()
Теңдеумен қарама-қайшылық алды (2). Демек, біздің болжамымыз дұрыс емес және n2 ≤ 12.
Сонымен, олар баға алды n2:
6 < n2 ≤ 12.
Осы бағалауды қолдана отырып, біз келесі жағдайларды аламыз:
|
n1 |
3 |
|||||
|
n2 |
7 |
8 |
9 |
10 |
11 |
12 |
|
n3 |
42 |
24 |
18 |
15 |
66/5 |
12 |
Бұрыштардың саны бүтін сан болғандықтан, жағдай анық n1 = 3, n2 = 11,
n3 = 66/5 бірден қарастырудан шығаруға болады.
Біз тұрақты көпбұрыштардың бұрыштар санымен үйлесетінін көрсетеміз n1 = 3, n2 = 7, n3 = 42 пapкет төсеу мүмкін емес.
А
Рис. 9
шыңының айналасы көрсетілген көпбұрыштармен және ABC тұрақты үшбұрышпен жабылсын (сурет.9). Тұрақты ABC үшбұрышының AB жағына 7 шаршы, ал AC жағына 42 шаршы іргелес болсын. Бірақ содан кейін 7-квадратты да, 42-квадратты да BC жағына бекіту мүмкін емес, егер сіз жоғарғы жағында 3-квадратты, 7-квадратты және 42-квадратты біріктіретін шартты сақтасаңыз.Жалпы теорема әділетті.
Теорема. Тақ саны бар тұрақты көпбұрыштың айналасында екі типтегі көпбұрыштарды дәйекті түрде орналастыру мүмкін емес, яғни әр түрлі жақтармен, ауыспалы типтермен.
Осы теореманы қолдана отырып, жиынтықтар (n1, n2, n3) тең болады(3,8,24), (3,9,18), (3,10,15), пapкетті бұрыштардың тиісті санымен тұрақты көпбұрыштардың комбинациясымен төсеу мүмкін емес.
Тұрақты көпбұрыштардың бұрыштар санымен үйлесуі n1 = 3, n2 = 12, n3 = 12 іске асыруға болады (VIII қосымша, сурет.9).
-
n1 = 4 болсын.
Сонда
![]()
1 жағдайға ұқсас, сіз мынаны көрсете аласыз n2 әділ баға:
4 < n2 ≤ 8,
сонымен, келесі жағдайлар мүмкін:
|
n1 |
4 |
|||
|
n2 |
5 |
6 |
7 |
8 |
|
n3 |
20 |
12 |
28/3 |
8 |
Бұрыштардың саны бүтін сан болғандықтан, жағдай анық n1 = 4, n2 = 7, n3 = 28/3 бірден қарастырудан шығаруға болады.
Жоғарыда келтірілген теореманы 5-бұрышқа қолдана отырып, біз мынаны аламыз n1 = 4, n2 = 5, n3 = 20 тиісті бұрыштары бар тұрақты көпбұрыштармен пapкет төсеу жоқ.
Тұрақты көпбұрыштардың бұрыштар санымен комбинациясы n1 = 4, n2 = 6, n3 = 12 және n1 = 4, n2 = 8, n3 = 8 жазықтықта іске асыруға болады (VIII қосымша, сурет.10, 11).
-
n1 = 5 болсын.
Сонда
![]()
n2 = 5 кезінде біз комбинацияны аламыз n1 = 5, n2 = 5, n3 = 10. Теорема бойынша пapкет бұрыштарының тиісті саны бар тұрақты көпбұрыштармен төсеу мүмкін емес.
n2 = 6 кезінде біз комбинацияны аламыз n1 = 5, n2 = 6, n3 = 15/2. Бұл жағдайда төсеу мүмкін емес екені анық.
n2 ≥ 7 кезінде біз аламыз:
![]()
Білдіреді,n3 ≤ 6, n2 ≥ 7, бұл болжамға қайшы келеді n2 ≤ n3.
-
n1 = 6 болсын.
Бірақ n1 ≤ n3 ≤ n2. Біз аламыз:
![]()
Бірақ
![]() (теңдеу бойынша (1)),
(теңдеу бойынша (1)),
демек, n1 = n3 = n2 =6.
Бұл комбинация тұрақты алтыбұрыштармен жүзеге асырылады (VIII қосымша, сурет.12).
5.5. Нүктенің айналасын төрт тұрақты көпбұрышпен төсеу.
Нүктенің айналасы тек төрт типтегі тұрақты көпбұрыштармен жабылсын, олардағы бұрыштар саны n1, n2, n3, n4. Біз мынаны болжаймыз n1 ≤ n2 ≤ n3 ≤ n4. Әлбетте, бұл n1 ≥ 3.
Бізде:
![]()
Немесе
![]()
Осы теңдеуден N1-ге шектеулер шығады, келесі сандар комбинациясы мүмкін n1, n2, n3, n4:
|
n1 |
n2 |
n3 |
n4 |
|
3 |
3 |
4 |
12 |
|
3 |
3 |
6 |
6 |
|
3 |
4 |
4 |
6 |
|
4 |
4 |
4 |
4 |
Теру үшін (3,3,4,12) іске асыру мүмкін емес.
Жиынтық (3,3,6,6) пapкеттің екі нұсқасына сәйкес келеді (IX қосымшасы, сурет.13, 14).
Жиынтыққа (3,4,4,6) пapкеттің үш нұсқасы сәйкес келеді (IX қосымшасы, сурет.15, 16).
Жинаққа сәйкес келетін Пapкет (4,4,4,4) IX қосымшасында көрсетілген, сурет.17.
5.6. Нүктенің айналасын бес және алты тұрақты көпбұрыштармен төсеу.
Нүктенің айналасы тұрақты көпбұрыштармен, олардың бұрыштарының саны бар-жоғы бес типпен жабылсын n1, n2, n3, n4, n5. Будем предполагать, что n1≤n2≤n3≤n4≤n5. Әлбетте, бұл n1 ≥ 3.
Бізде:
![]()
Немесе
![]()
Осы теңдеуден және N1 шектеулерінен келесі сандар комбинациясы мүмкін n1, n2, n3, n4, n5:
|
n1 |
n2 |
n3 |
n4 |
n5 |
|
3 |
3 |
3 |
4 |
4 |
|
3 |
3 |
3 |
3 |
6 |
Жиынтыққа (3,3,3,4,4) пapкеттің төрт нұсқасы сәйкес келеді (x қосымшасы, сурет.18, 19).
Жиынтық (3,3,3,3,6) пapкеттің бір нұсқасына сәйкес келеді (x қосымшасы, сурет. 20).
Нүктенің айналасын алты тұрақты көпбұрышпен төсеу тек іс жүзінде мүмкін n1 = n2 = n3 = n4 = n5 = n6 = 3. Пapкеттің тиісті нұсқасы x қосымшасында келтірілген, сурет.21.
Сіз әр түрлі түрлендірулер арқылы n-квадраттардан пapкет ала аласыз. Жалпақ ою-өрнектерді жасаудың мұндай технологиясы XI қосымшасында келтірілген.
VI ТАРАУ ТҰРАҚТЫ КӨПБҰРЫШТАРДАН БАСҚА ФИГУРАЛАРДАН ПAPКЕТ САЛУ
Жоғарыда айтылғандай, пapкет жазықтықты тұрақты көпбұрыштармен жабу деп аталады, онда екі көпбұрыштың ортақ жағы немесе ортақ шыңы немесе мүлде ортақ нүктелері жоқ.
Пapкеттің кейбір анықтамалары көпбұрыштармен шектелмейді. Бұл жағдайда пapкет дегеніміз – берілген фигуралармен (нақты жағдайда-көпбұрыштармен, тұрақты немесе тұрақты емес, дөңес немесе дөңес емес) жазықтықты өткізбей және қабаттаспай жабу. Бұл жағдайда, тіпті көпбұрышты пapкет үшін де "екі көпбұрыштың ортақ шыңы, ортақ жағы немесе ортақ нүктелері болмауы керек"деген талап орындалмауы мүмкін. Сонымен қатар, көпбұрыштардан емес, қисық фигуралардан тұратын көптеген түрлі пapкет пайда болады.
Жазық оюларды жасау технологиясы
XII қосымшаға жүгінейік (сурет. 27,a). Біз не көреміз? Құстар отары. Бірақ ол қалай шықты. Бұл жерде пapкет элементі біз қандай да бір түрде өзгерткен немесе өзгерткен көпбұрыш болды ма? Шын мәнінде, пapкет элементі үшін құс түріндегі фигура алынды (XII қосымша, күріш.27, б). Біз жазықтықтағы фигуралардың қозғалысының үш түрін білеміз. Бұл бұрылыс, параллель беріліс және осьтік симметрия. Құстардың бейнесі бар пapкет алу үшін олар параллель берілісті пайдаланып, бастапқыда қозғалыс векторын орнатты. Бұл оңай, сіз құстардың отарын ала аласыз. Параллельді тасымалдау арқылы алынған пapкеттердің басқа мысалдары V қосымшасында келтірілген, сурет.28 (А, б).
Басқа пapкет пен басқа суретті қарастырыңыз (XII қосымшасы, сурет.29, а). Мұндай күрделі сурет қалай алынды? Сіз осы пapкеттегі бірнеше фигураларды көре аласыз, олардың бір ортақ нүктесі бар; яғни, бұл тұмсықтарының үйлесуіне сәйкес келетін орталығы бар құстардың шағын топтары. Бұл нүкте берілген фигуралар тобының орталығы болып табылады. Сурет жазықтығы белгілі бір нүктенің айналасында белгілі бір бұрышқа бұрылды делік. Біздің пapкетте мұндай нүкте-фигуралар тобының орталығы немесе тұмсықтарды біріктіру нүктесі. Бұдан шығатыны, бұл пapкет бірқатар фигураларды бұру нәтижесінде алынған. Мұндай пapкет құрылысының тағы бір мысалы-XIII қосымшасы, сурет.29, б.
![]()
ҚОРЫТЫНДЫ
Алға қойылған мақсаттарға жету үшін пapкет қандай фигуралардан жасалатынын анықтау керек болды. Зерттеу аяқталғаннан кейін пapкеттің жеке дамуын жасаңыз.
Біз пapкет тек квадрат, үшбұрыш және алтыбұрыш сияқты тұрақты көпбұрыштардан алуға болады деген болжам жасадық. Жұмыс барысында біз бұл шынымен де солай екенін білдік. Ешқандай бесбұрыш немесе жетібұрыш пapкет элементі бола алмайды. Өйткені, пapкет-бұл жазықтықты бос орындарсыз және қабаттасусыз бірнеше фигуралармен толтыру. Неліктен дәл осы үш тұрақты көпбұрыш жазықтықты қалай толтырады? Бұл сұрақтың жауабын бұрыштарды санаудан табуға болатындығы белгілі болды. Алдымен тұрақты көпбұрыштың әр бұрышының шамасын анықтау керек, ол үшін дөңес N-бұрыштың бұрыштарының қосындысын бұрыштар санына бөлеміз. Пapкет алу үшін бұрыштардың қосындысын 360о теру керек, сондықтан пapкет шыңында жиналуы керек көпбұрыштардың саны 360о дөңес N-бұрыштың бұрышына бөлінген кезде анықталады. Осыдан тұрақты көпбұрыштардан басқа фигуралардан пapкет салу заңдылығы бар деп қорытынды жасауға болады. Осылайша, мен екінші гипотезаны растадым.
Тұрақты көпбұрыштардан пapкет салу заңдылықтарын зерттеп, анықтағаннан кейін біз пapкет эскиздерін салдық. Бұл сабақ өте қызықты болып көрінді. Түстер схемасымен тәжірибе жасай отырып, пapкетке толық пішін беретін түстер таңдалды.
Пapкет-ою-өрнек. Ал ою-өрнек әртүрлі заттар мен сәулет құрылымдарын безендіруге арналған. Ол безендіретін және көзбен ұйымдастыратын бетке байланысты ою-өрнек, әдетте, оның құрылымымен, пішінімен және түсімен объектінің құрылымдық ерекшеліктерін, материалдың табиғи сұлулығын ашады және баса көрсетеді. Пapкет бетіне нақты ырғақты ұйым береді. Ою-өрнек өнерін қолдануды халық шығармашылығының бүкіл даму кезеңінде байқауға болады. Ежелгі Египеттің ою-өрнектерінен бүгінгі таңда ою-өрнектерді қолдануға дейін.
Бұл жұмыстың басты жетістіктерінің бірі ретінде біз төрт пapкет жасалды деп санаймыз. Бұл "жұлдызды аспан", "түрлі-түсті тазарту", "Орман" және "геометриялық тұңғиық" (XVI қосымша).
Әдебиеттер тізімі
-
Александров А. Д., Нецветаев Н. Ю. Геометрия. – М.: «Наука», 1990г.
-
Бутузов В.Ф., Колягин Ю.М., Луканнкин Г.Л. и др. Математика 11. М.: Просвещение, 1996.
-
Колмогоров А.Н.. Пapкеты из правильных многоугольников. – Журнал "Квант" №3, 1970 г.
-
Погорелов А.В. Геометрия. – М.: «Просвещение», 1997
-
Сагателова Л.С., Студенецкая В.Н. Геометрия: красота и гармония. – В.: «Учитель»
-
Советский энциклопедический словарь — М.: Советская энциклопедия, 1980.
с. 1219—1220.
-
Шарыгин И. Ф., Ерганжиева Л. Н. Наглядная геометрия. – М.: МИРОС, КПЦ «МАРТА», 1992г.
-
Энциклопедия для детей. Т.11. Математика/Глав. Ред. Э68 Аксенова М.Д. – М.: Аванта+, 2002
I Қосымша
Ою-өрнектердің симметриялық құрылысының түрлері.





Зеркальная симметрия
Точечная симметрия
Бордюр
Сложные виды динамической симметрии
Сетчатые орнаменты
II қосымша
Торлы ою-өрнектердің симметриясының мүмкін 17 түрі.





![]()
III қосымша
Ою-өрнек түрлері.









Геометрический
орнамент
Фигуральный орнамент
Фантастический орнамент
Каллиграфический орнамент
Растительный
орнамент
Пейзажный орнамент
Астральный орнамент
Символический орнамент
Сложные орнаменты
Животный орнамент
IV қосымша
Пәтерлерде кездесетін Пapкет.



V Қосымша
Ноутбук парағы-пapкет.

V I
қосымша
I
қосымша
Тұрақты көпбұрыштар.
VII Қосымша
Элементтері тұрақты үшбұрыш, шаршы және тұрақты алтыбұрыш болып табылатын пapкет.

Рис. 8
VIII қосымша
Нүктенің айналасын үш тұрақты көпбұрышпен төсеу.



рис. 12

IX қосымша
Нүктенің айналасын төрт тұрақты көпбұрышпен
төсеу.
рис. 17




X Қосымшасы
Нүктенің айналасын бес және алты тұрақты көпбұрыштармен төсеу.

рис. 21



XI қосымшасы
Жазық оюларды жасау технологиясы.
Алтыбұрышты негізге алыңыз (сурет. 22).
1. Алтыбұрыштың FA жағын өзгертіңіз (сурет. 23, а).
2. Содан кейін біздің фигурамыз бір-біріне "жылжуы" үшін біз DC-нің қарама-қарсы жағын да өзгертеміз(сурет. 23, а).
3. AB жағына үшбұрыш салыңыз (сурет. 23, б).
4. Біз бірдей үшбұрышты ED-нің қарама-қарсы жағынан кесуіміз керек(сурет. 23, б).
5. FE жағына үшбұрыш салыңыз (сурет. 23, в).
6. Сол Үшбұрыш BC-нің қарама-қарсы жағынан кесіледі(сурет. 23, в).
Біздің алтыбұрышымыз осылай өзгерді. Енді біз оны бояймыз (сурет. 24).
А




1
3
В
F
6
5
С
E
D
4
2
а)
б)
в)
Рис. 22
Рис. 23

Рис. 24

Рис. 25
Бізде қарақшылар болды (сурет. 25). Мен сол контурды қолданамын, бірақ ішіндегі басқа өрнекпен сіз осындай сүйкімді иттерді тарта аласыз (сурет.26).

Рис. 26
XII қосымша
Параллель тасымалдау әдісімен жасалған пapкет.


а)
б)
Рис.27


а)
б)
Рис.28
Бірқатар фигураларды бұру нәтижесінде алынған пapкет.


Рис.29

XIII қосымша
Автор әзірлеген пакеттер.



шағым қалдыра аласыз















