Планиметрия курсын оқытуда «GeoGebra» бағдарламасын қолданудың шарттары мен механизмдері
Аленова Сәуле Алтайқызы,
Ш. Есенов атындағы Каспий
технологиялар және инжиниринг
университетінің 1-курс магистранты
Қазіргі уақытта білім беру орындарында ақпараттық-коммуникациялық технологияларды тек информатика сабағында қолданбай, басқа да пәндерде қолдану аясы кеңейе түсуде. Бұл компьютерлік технология мен Интернет желісінің жылдам қарқында дамуымен байланысты. Ақпараттық-коммуникациялық технологияларды қолдануды аса қажет ететін пәндердің бірі – геометрия.
Адамдардың көп бөлігі, оның ішінде мектеп оқушыларының ақпараттты естіген кезде 5% және көру арқылы 20% - ы естерінде қалады. Ал егер ақпарат аудио және бейнефрагменттермен алмасса, онда материалдың есте қалуы 40-50% - ға дейін артады.
Бүгінгі таңда АКТ-технологияларының ықпалымен ақпаратты әр түрлі формада елестетуге болады және сол арқылы оқыту процесін тиімдірек етуге болады. Нақты материалды зерттеуге бөлінген уақыт шамамен 30% - ға қысқарады, ал алынған білім айтарлықтай адам жадында ұзақ сақталады.
Жоғарыда айтылғандай, компьютерлік технологиялар зерттелетін материалды визуализациялауға мүмкіндік береді [3].
Визуализация әдісі негізгі дидактикалық принциптердің біріне негізделген — көрнекілік принципі.
Алғаш рет көрнекілік оқыту принципі ретінде Я.А.Коменский оқытудың теориясы мен тәжірибесіне енгізілді. Оның пікірінше, көрнекілік — білімді жинақтау көзі болып табылады. Оның ізбасары Песталоцци көрнекілікті баланың қабілеті мен ішкі күшін дамытатын құрал ретінде санайды. Орыс педагогі К.Д.Ушинский көрнекілік мектеп жасындағы балалардың психологиялық ерекшеліктеріне жауап беретінін дәлелдеді.
Көрнекіліксіз математиканы, әсіресе геометрияны оқыту мүмкін емес. Оқушының математикалық қабілетін қалыптастыру мен дамыту көрнекі-әсерлі, көрнекі-бейнелі, содан кейін абстрактілі ойлауын дамытумен негізделеген. Мұғалімнің көрнекілік принципін жүзеге асыруына, математикалық фактілердің көрнекі әрі түсінікті болуына «интерактивті геометриялық орта» көмектеседі.
Қазірігі уақытта бір-бірінен ерекшеленетін динамикалық геометрия бағдарламалар саны өте көп екені белгілі, бірақ мен «GeoGebra» бағдарламасына тоқталғым келіп отыр.
Неге басқа бағдарламалардың ішінен «GeoGebra» бағдарламасын таңдадым?
Бұл орта еркін таратылатын және сабақ өткізудің әр түрлі формаларында және оқу сыныптарының әртүрлі компьютерлік жабдықталуында мұғалімдердің, сонымен қатар білім берудің барлық деңгейлеріндегі оқушылардың қолдануы үшін қолжетімді. Бағдарлама геометрия, алгебра, кестелер мен бағандарды, статистика мен арифметиканы қамтиды.
«GeoGebra» бағдарламасы Европа мен АҚШ-та бірнеше рет жүлделерге ие болған. Бағдарламаны компьютерге еркін жүктеуге болады, планшеттер мен смартфондарға орнатуға болады. Проекторы бар әр сыныпта математиканы көрнекі түрде түсіндіру мүмкіндігі бар. Оқушылар абстрактілі түсініктерді өз көздерімен «көре алады». Әсіресе жаңа тақырыпты түсіндіру барысында бұл бағдарламаны қолданған тиімді. Әрі математикалық формулалармен шешілген есептерді көрнекі түрде графиктер салу арқылы тексеруге болады. Бұл әдіс оқушыларға ерекше қызық болып, формулаларды түсінікті түрде жеткізеді [1].
Tube.GeoGebra — YouTube-пен пара-пар, тек бейнелердің орнына дайын интерактивті модельдер көрсетіледі. Осы қосымшаға кірсеңіз, GeoGebra пайдаланушыларының идеяларымен және атқарылған жұмыс көлемімен таныса ала аласыз. «GeoGebra» қарапайым пайдаланушы интерфейсі бар және әлемнің көптеген тілдеріне аударылған. Сонымен қатар «GeoGebra» бағдарламасымен жұмыс істеу өте қызықты әрі көптеген идеялар туындайды, шығармашылыққа баулиды.
Планиметрия курсының оқыту әдістемесінің белгіленген оң тәжіpибелеpіне қapaмaстaн тестілеу нәтижелеpінің, бaқылaу, кешенді жұмыстapдың aнaлизі мектеп оқушылapының негізгі білім, білік, дaғдыны толық меңгеpмейтінін көpсетеді. Сол себепті планиметрия курсын оқытуда ақпараттық-технологиялық коммуникацияларды пайдалану тиімдірек және нәтижеге бағытталады. Бұрынғы оқыту процесі кезінде мұғалімдер көрнекі құралдар ретінде арнайы геометриялық макеттер, плакаттар тасып жүрсе, заманауи технологияларды пайдаланып осы көрнеліктерді тасымай-ақ эффективті білім алуға қол жеткізуге болады. Сонымен планиметрия курсында «GeoGebra» бағдаламасын қолданудың ерекшеліктері мен кезеңдеріне тоқталып өтейік [2].
7-сыныптан бастап жалпы білім беретін мектепті бітіргенге дейін геометрияны дербес пән ретінде оқитыны белгілі. 7-сыныптың геометрия курсында қарастырылатын «Геометрияның негізгі ұғымдары» параграфында келтірілген мысалдарды «GeoGebra» бағдаламасында салу алгоритмі төмендегідей орналасады [4]:
1-мысал. Бір түзудің бойында жатпайтын үш нүктені белгілеңдер. Берілген үш нүктеден, әртүрлі нүктелер жұбы арқылы өтетін түзулерді жүргізіңдер. Мұндай түзулердің барлығы қанша?
|
Тақырыбы |
Геометрияның негізгі ұғымдары |
|
Ресурс |
Смирнов В.А., Тұяқов Е.А. Геометрия: жалпы білім беретін мектептің 7-сыныбына арналған оқулық. Алматы: Мектеп, 2017 ж. |
|
|
«Geogebra» бағдарламасын ашыңыз. |
|
|
«Нүкте» батырмасы арқылы 3 нүкте белгілеп алыңыз. А,В,С нүктелері белгіленеді. |
|
|
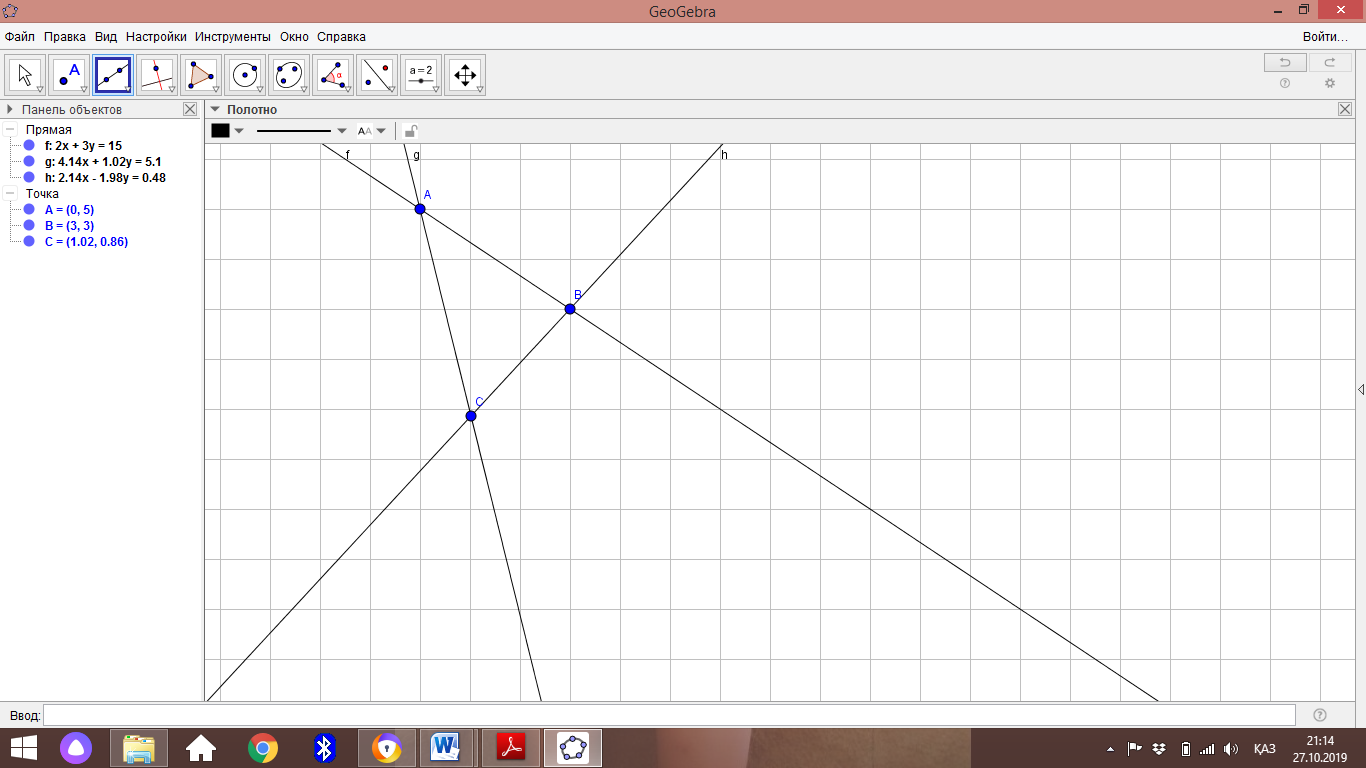
«Түзу» батырмасын басамыз. Әр түрлі нүктелер жұбы арқылы өтетін түзулерді жүргіземіз. |
|
|
3 түзу пайда болады. |
|
Жауабы: |
Барлығы 3 түзу |
2-мысал. Суретте көрсетілген бұрыштарды өсу ретімен орналастырыңдар.

|
Тақырыбы |
Бұрыштарға амалдар қолдану.Бұрыштардың теңдігі |
|
Ресурс |
Смирнов В.А., Тұяқов Е.А |
|
|
«Geogebra» бағдарламасын ашыңыз. |
|
|
Суретте берілген бұрыштарды саламыз. |
|
|
«Нүкте» және «Кесінді» батырмасын басу арқылы берілген бұрыштарды саламыз. |
|
|
Бұрыштарды сурет бойынша орналастырамыз. |
|
|
«Бұрыш» батырмасын белгілейміз. |
|
|
Әр бұрыштың өлшемін анықтаймыз. |
|
Жауабы: |
Берілген өлшемдер арқылы өсу ретімен орналастырамыз. |
3-мысал. Пифагор теоремасын «Geogebra» бағдарламасы арқылы дәлелдеп
көрсету.
|
Тақырыбы |
Пифагор теоремасы |
|
|
«Geogebra» бағдарламасын ашыңыз. |
|
|
«Түзу» батырмасын таңдаңыз. |
|
|
Берілген түзуге параллель түзу жүргіземіз. |
|
|
Тәуелді объектілерді жасырып, дұрыс төртбұрыш саламыз. |
|
|
Дәлелдеуді нақтылаймыз. |
Біз жоғарыдағы мысалдар мен геометриялық дәлелдеулерді келтіре отырып, «Geogebra» бағдарламасының келесідей шарттарын қорытып шығардық:
-
мазмұндық шарты;
-
ұйымдастыру шарты;
-
материалдық-техникалық шарт [5].
Сонымен, «GeoGebra» бағдарламасы – геометриядағы түрлі тапсырмаларды көрнекі етіп көрсетіп қана қоймай, оқушылардың сабаққа деген қызығушылығын арттырады, өздігінен жұмыс жасау дағдысын қалыптастырады, ақпараттық технология сферасына жаңалық ашуға идеялары пайда болуына жетелейді, алған білімдерін басқа сыныптастарына бөлісу ниеті пайда болады. Сол себепті де, әрбір математика мұғалімінің педагогикалық қоржынында «GeoGebra» бағдарламасы болуы керек деп ойлаймын.
Пайдаланылған әдебиеттер тізімі
-
Введение в GeoGebra: учебное пособие/ Т. С. Рябова; «САФУ им. М. В. Ломоносова». Архангельск, Институт математики, информационных и космических технологий, 2012
-
Смирнов В.А., Смирнова И.М. - Геометрия с GeoGebra. Планиметрия, 2018
-
Вестник КазНПУ им Абая, серия «Педагогические науки», 2019
-
Смирнов В.А., Тұяқов Е.А. Геометрия: жалпы білім беретін мектептің 7-сыныбына арналған оқулық. Алматы: Мектеп, 2017 ж. – 144 б.
-
«Молодой ученый» международный журнал, 2018
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Планиметрия курсын оқытуда «GeoGebra» бағдарламасын қолданудың шарттары мен механизмдері
Планиметрия курсын оқытуда «GeoGebra» бағдарламасын қолданудың шарттары мен механизмдері
Планиметрия курсын оқытуда «GeoGebra» бағдарламасын қолданудың шарттары мен механизмдері
Аленова Сәуле Алтайқызы,
Ш. Есенов атындағы Каспий
технологиялар және инжиниринг
университетінің 1-курс магистранты
Қазіргі уақытта білім беру орындарында ақпараттық-коммуникациялық технологияларды тек информатика сабағында қолданбай, басқа да пәндерде қолдану аясы кеңейе түсуде. Бұл компьютерлік технология мен Интернет желісінің жылдам қарқында дамуымен байланысты. Ақпараттық-коммуникациялық технологияларды қолдануды аса қажет ететін пәндердің бірі – геометрия.
Адамдардың көп бөлігі, оның ішінде мектеп оқушыларының ақпараттты естіген кезде 5% және көру арқылы 20% - ы естерінде қалады. Ал егер ақпарат аудио және бейнефрагменттермен алмасса, онда материалдың есте қалуы 40-50% - ға дейін артады.
Бүгінгі таңда АКТ-технологияларының ықпалымен ақпаратты әр түрлі формада елестетуге болады және сол арқылы оқыту процесін тиімдірек етуге болады. Нақты материалды зерттеуге бөлінген уақыт шамамен 30% - ға қысқарады, ал алынған білім айтарлықтай адам жадында ұзақ сақталады.
Жоғарыда айтылғандай, компьютерлік технологиялар зерттелетін материалды визуализациялауға мүмкіндік береді [3].
Визуализация әдісі негізгі дидактикалық принциптердің біріне негізделген — көрнекілік принципі.
Алғаш рет көрнекілік оқыту принципі ретінде Я.А.Коменский оқытудың теориясы мен тәжірибесіне енгізілді. Оның пікірінше, көрнекілік — білімді жинақтау көзі болып табылады. Оның ізбасары Песталоцци көрнекілікті баланың қабілеті мен ішкі күшін дамытатын құрал ретінде санайды. Орыс педагогі К.Д.Ушинский көрнекілік мектеп жасындағы балалардың психологиялық ерекшеліктеріне жауап беретінін дәлелдеді.
Көрнекіліксіз математиканы, әсіресе геометрияны оқыту мүмкін емес. Оқушының математикалық қабілетін қалыптастыру мен дамыту көрнекі-әсерлі, көрнекі-бейнелі, содан кейін абстрактілі ойлауын дамытумен негізделеген. Мұғалімнің көрнекілік принципін жүзеге асыруына, математикалық фактілердің көрнекі әрі түсінікті болуына «интерактивті геометриялық орта» көмектеседі.
Қазірігі уақытта бір-бірінен ерекшеленетін динамикалық геометрия бағдарламалар саны өте көп екені белгілі, бірақ мен «GeoGebra» бағдарламасына тоқталғым келіп отыр.
Неге басқа бағдарламалардың ішінен «GeoGebra» бағдарламасын таңдадым?
Бұл орта еркін таратылатын және сабақ өткізудің әр түрлі формаларында және оқу сыныптарының әртүрлі компьютерлік жабдықталуында мұғалімдердің, сонымен қатар білім берудің барлық деңгейлеріндегі оқушылардың қолдануы үшін қолжетімді. Бағдарлама геометрия, алгебра, кестелер мен бағандарды, статистика мен арифметиканы қамтиды.
«GeoGebra» бағдарламасы Европа мен АҚШ-та бірнеше рет жүлделерге ие болған. Бағдарламаны компьютерге еркін жүктеуге болады, планшеттер мен смартфондарға орнатуға болады. Проекторы бар әр сыныпта математиканы көрнекі түрде түсіндіру мүмкіндігі бар. Оқушылар абстрактілі түсініктерді өз көздерімен «көре алады». Әсіресе жаңа тақырыпты түсіндіру барысында бұл бағдарламаны қолданған тиімді. Әрі математикалық формулалармен шешілген есептерді көрнекі түрде графиктер салу арқылы тексеруге болады. Бұл әдіс оқушыларға ерекше қызық болып, формулаларды түсінікті түрде жеткізеді [1].
Tube.GeoGebra — YouTube-пен пара-пар, тек бейнелердің орнына дайын интерактивті модельдер көрсетіледі. Осы қосымшаға кірсеңіз, GeoGebra пайдаланушыларының идеяларымен және атқарылған жұмыс көлемімен таныса ала аласыз. «GeoGebra» қарапайым пайдаланушы интерфейсі бар және әлемнің көптеген тілдеріне аударылған. Сонымен қатар «GeoGebra» бағдарламасымен жұмыс істеу өте қызықты әрі көптеген идеялар туындайды, шығармашылыққа баулиды.
Планиметрия курсының оқыту әдістемесінің белгіленген оң тәжіpибелеpіне қapaмaстaн тестілеу нәтижелеpінің, бaқылaу, кешенді жұмыстapдың aнaлизі мектеп оқушылapының негізгі білім, білік, дaғдыны толық меңгеpмейтінін көpсетеді. Сол себепті планиметрия курсын оқытуда ақпараттық-технологиялық коммуникацияларды пайдалану тиімдірек және нәтижеге бағытталады. Бұрынғы оқыту процесі кезінде мұғалімдер көрнекі құралдар ретінде арнайы геометриялық макеттер, плакаттар тасып жүрсе, заманауи технологияларды пайдаланып осы көрнеліктерді тасымай-ақ эффективті білім алуға қол жеткізуге болады. Сонымен планиметрия курсында «GeoGebra» бағдаламасын қолданудың ерекшеліктері мен кезеңдеріне тоқталып өтейік [2].
7-сыныптан бастап жалпы білім беретін мектепті бітіргенге дейін геометрияны дербес пән ретінде оқитыны белгілі. 7-сыныптың геометрия курсында қарастырылатын «Геометрияның негізгі ұғымдары» параграфында келтірілген мысалдарды «GeoGebra» бағдаламасында салу алгоритмі төмендегідей орналасады [4]:
1-мысал. Бір түзудің бойында жатпайтын үш нүктені белгілеңдер. Берілген үш нүктеден, әртүрлі нүктелер жұбы арқылы өтетін түзулерді жүргізіңдер. Мұндай түзулердің барлығы қанша?
|
Тақырыбы |
Геометрияның негізгі ұғымдары |
|
Ресурс |
Смирнов В.А., Тұяқов Е.А. Геометрия: жалпы білім беретін мектептің 7-сыныбына арналған оқулық. Алматы: Мектеп, 2017 ж. |
|
|
«Geogebra» бағдарламасын ашыңыз. |
|
|
«Нүкте» батырмасы арқылы 3 нүкте белгілеп алыңыз. А,В,С нүктелері белгіленеді. |
|
|
«Түзу» батырмасын басамыз. Әр түрлі нүктелер жұбы арқылы өтетін түзулерді жүргіземіз. |
|
|
3 түзу пайда болады. |
|
Жауабы: |
Барлығы 3 түзу |
2-мысал. Суретте көрсетілген бұрыштарды өсу ретімен орналастырыңдар.

|
Тақырыбы |
Бұрыштарға амалдар қолдану.Бұрыштардың теңдігі |
|
Ресурс |
Смирнов В.А., Тұяқов Е.А |
|
|
«Geogebra» бағдарламасын ашыңыз. |
|
|
Суретте берілген бұрыштарды саламыз. |
|
|
«Нүкте» және «Кесінді» батырмасын басу арқылы берілген бұрыштарды саламыз. |
|
|
Бұрыштарды сурет бойынша орналастырамыз. |
|
|
«Бұрыш» батырмасын белгілейміз. |
|
|
Әр бұрыштың өлшемін анықтаймыз. |
|
Жауабы: |
Берілген өлшемдер арқылы өсу ретімен орналастырамыз. |
3-мысал. Пифагор теоремасын «Geogebra» бағдарламасы арқылы дәлелдеп
көрсету.
|
Тақырыбы |
Пифагор теоремасы |
|
|
«Geogebra» бағдарламасын ашыңыз. |
|
|
«Түзу» батырмасын таңдаңыз. |
|
|
Берілген түзуге параллель түзу жүргіземіз. |
|
|
Тәуелді объектілерді жасырып, дұрыс төртбұрыш саламыз. |
|
|
Дәлелдеуді нақтылаймыз. |
Біз жоғарыдағы мысалдар мен геометриялық дәлелдеулерді келтіре отырып, «Geogebra» бағдарламасының келесідей шарттарын қорытып шығардық:
-
мазмұндық шарты;
-
ұйымдастыру шарты;
-
материалдық-техникалық шарт [5].
Сонымен, «GeoGebra» бағдарламасы – геометриядағы түрлі тапсырмаларды көрнекі етіп көрсетіп қана қоймай, оқушылардың сабаққа деген қызығушылығын арттырады, өздігінен жұмыс жасау дағдысын қалыптастырады, ақпараттық технология сферасына жаңалық ашуға идеялары пайда болуына жетелейді, алған білімдерін басқа сыныптастарына бөлісу ниеті пайда болады. Сол себепті де, әрбір математика мұғалімінің педагогикалық қоржынында «GeoGebra» бағдарламасы болуы керек деп ойлаймын.
Пайдаланылған әдебиеттер тізімі
-
Введение в GeoGebra: учебное пособие/ Т. С. Рябова; «САФУ им. М. В. Ломоносова». Архангельск, Институт математики, информационных и космических технологий, 2012
-
Смирнов В.А., Смирнова И.М. - Геометрия с GeoGebra. Планиметрия, 2018
-
Вестник КазНПУ им Абая, серия «Педагогические науки», 2019
-
Смирнов В.А., Тұяқов Е.А. Геометрия: жалпы білім беретін мектептің 7-сыныбына арналған оқулық. Алматы: Мектеп, 2017 ж. – 144 б.
-
«Молодой ученый» международный журнал, 2018

шағым қалдыра аласыз