
|
Тема урока |
Построение графиков тригонометрических функций с помощью простейших преобразований. |
|
Цель урока |
- знать основные пукты исследования функции; - строить график тригонометрических функций с помощью простейших преобразований; - самостоятельно составлять тригонометрические функции и исследовать. |
Ход урока
|
Запланированные этапы урока |
Виды упражнений, запланированных на урок: |
Ресурсы |
|
|
Начало урока |
Учитель приветствует учащихся, эмоциональный настрой «Снежный ком», проверяет их готовность к уроку, по теме «Исследование функции» - У каждого из вас на столах лежат листы оценивания. Подпишите листы оценивания. В течение урока мы с вами будем выполнять различные задания. По окончанию решения каждого задания, вы должны оценить свою работу или вашу работу оценят одноклассники (Приложение 1) «+» – справился без затруднений, «±» – справился, но возникали сложности, «-« – не справился с заданием. Прием «Да, нет» На доске изображен график функции у= х^3+1. Учащиеся работают индивидуально. Исследуют решение функции записывая ответ – если утверждение верно, то пишут ˄, если нет – . Схема исследования функции. 1.Область определения функции- множество всех действительных чисел; 2.функция четная; 3. Функция не периодическая; 4.Координаты точек пересечения графика с осями координат: А) х=0, у= 0^3+1=1. Значит, график функции рересекаются с осью Оу в точке N(-1;0); Б) у=0, х^3+1=0, х^3=-1, х=1. Значит, график фукции пересекаются с осью Ох в точке N(-1;0); 5.Промежутки возрастания, убывания функции. График функции пересекается с осью абсцисс в точке N(-1;0). Тогда на промежутке (-∞; -1) функция f(x)<0, на промежутке (-1;+∞) функция f(x)>0 6.Для любых х1, х2 из области определения при х1<x2 выполняется у(х1) <у(х2), поэтому функция убывает. |
Ответ в виде «кардиограммы» на доске (образец) ˄_˄_˄˄_ |
|
|
Критерии успеха |
Учащиеся, сравнивая свою «кардиограмму» с образцом, оценивают себя в оценочном листе |
|
|
|
Середина урока |
Деление на группы равноуровневые (по карточкам) Используя метод "ДЖИГСО" учащиеся рассматривают примеры на построение тригонометрических функций с помощью простейших преобразований. Каждая группа должна исследовать функцию, построить график и оформить кластер. І группа: у=1+2sinx ІІ группа): y=2+cos 3x ІІІ группа: y=3tg x/2 ІҮ группа: y=2ctg x/3 Оценивание с помощью стратегии "Уточняющие вопросы» |
|
|
|
Конец урока |
Тесты по дифференциации «Темп» взаимопроверка с ключами. Приложение 1. Рефлексия «Похвальный бутерброд» по листам ответов |
|
|
Вариант 1
1.График, какой функции, изображен на рисунке?
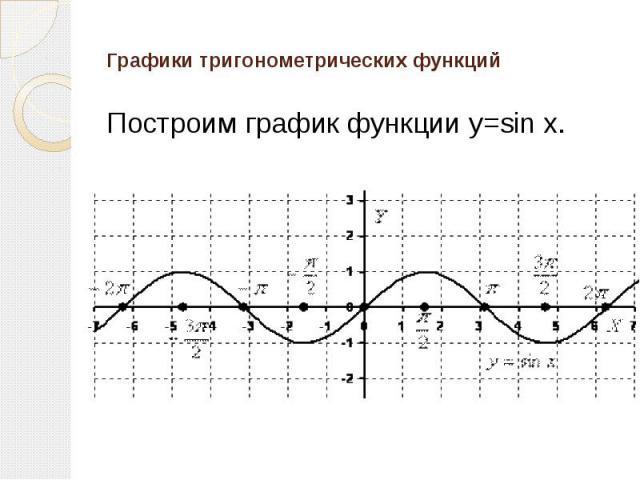
а)у=cosx b)y=sinx c) y=tgx d)y=ctgx
2. Какое наибольшее значение принимает функция?
Ответ_____________
3.Какие точки являются нулями функции данного графика?
а)(0;0) b)( ;0)
c)
(π;0) d)
;0)
c)
(π;0) d) ;0)
;0)
4.Сколько нулей функции, изображено на графике?
а)1 b)5 c) 3 d)0
5.Сколько полных волн изображено на графике?
. Ответ_____________
6. Функция y=tgx является:
а)четной b)нечетной с)функцией общего вида
7.Изображеная на рисунке функция :
а)симметрична, относительно начала координат
b) симметрична, относительно оси ординат
с) симметрична, относительно оси абсцисс
8.Период функции y=сtgx
а)π b)2π c) не периодическая
9.
Функция, изображенная на рисунке функция на
промежутке (-  ;0)
;0)
а)возрастает b)убывает
10. На рисунке изображена функция. При каких х , не существует данной функции
. 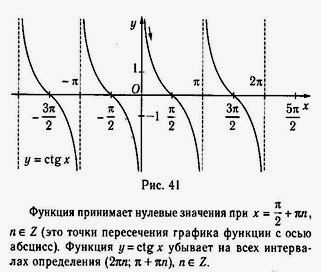
а)0 b) ;
c)
(π
d)
;
c)
(π
d) ;
;
Вариант 2.
1.График, какой функции, изображен на
рисунке? 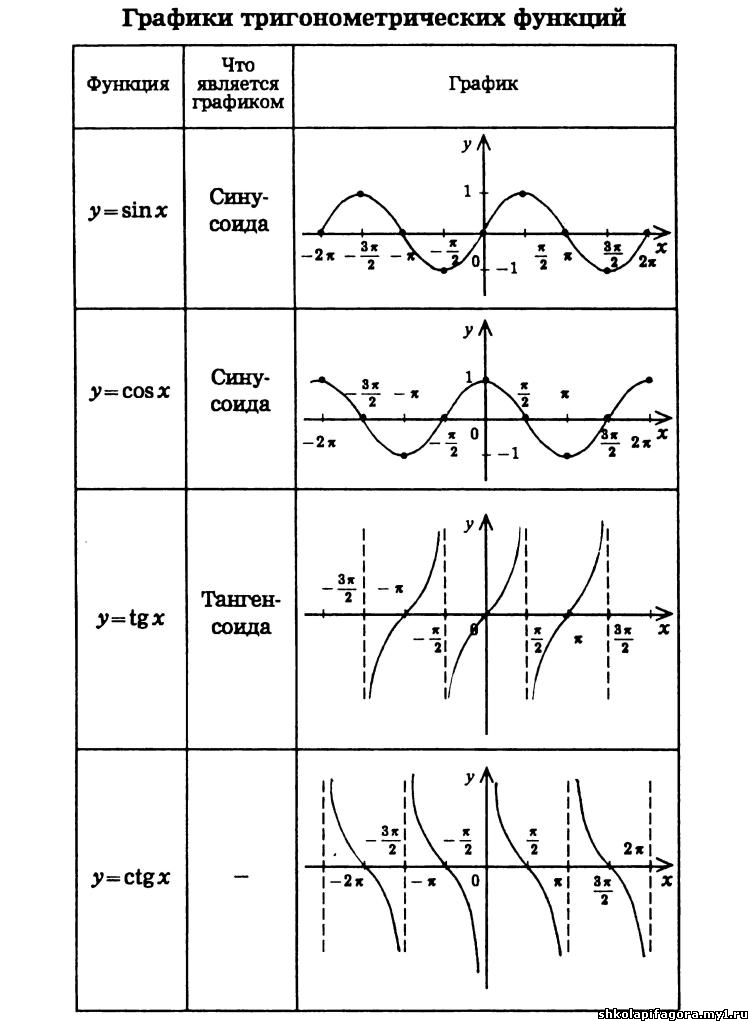
а)у=cosx b)y=sinx c) y=tgx d)y=ctgx
2. Какое наибольшее значение принимает функция?
Ответ_____________
3.Какие точки являются нулями функции данного графика?
а)(0;0) b)( ;0)
c)
(π;0) d)
;0)
c)
(π;0) d) ;0)
;0)
4.Сколько нулей функции, изображено на графике?
а)1 b)5 c) 4 d)0
5.Сколько полных волн изображено на графике?
. Ответ_____________
6. Функция y=сtgx является:
а)четной b)нечетной с)функцией общего вида
7.Изображеная на рисунке функция :
а)симметрична, относительно начала координат
b) симметрична, относительно оси ординат
с) симметрична, относительно оси абсцисс
8.Период функции y=tgx
а)π b)2π c) не периодическая
9.
Функция, изображенная на рисунке функция на
промежутке (0;  )
)
а)возрастает b)убывает
10. На рисунке изображена функция. При каких х , не существует данной функции
. 
а)0 b) ;
c)
(π
d)
;
c)
(π
d) ;
;
Дескрипторы
І группа: у=1+2sinx
1)Строит график функции у=sinx;
2) Растягивает график растягивает в 2 раза вдоль оси Оу, получает график функции у=2sinx;
3) Переносит график параллельно вдоль оси Оу на одну единицу вверх;
4) Получает график искомой фукции.
ІІ группа): y=2+cos 3x
1)Строит график функции у= cos x
2) Сжимает график в 3 раза вдоль оси Ох, получает график функции у= cos 3x
3) Переносит график параллельно вдоль оси Оу на две единицы вверх;
4) Получает график искомой фукции.
ІІІ группа: y=3tg x/2
1)Строит график функции у= tg x
2) Растягивает график растягивает в 3 раза вдоль оси Оy, получает график функции у= 3tgx
3) Сжимает график функции в 2 раза вдоль оси Ох, получает график функции y=3tg x/2;
4) Получает график искомой фукции.
ІҮ группа: y=2ctg x/3
1)Строит график функции у= сtg x
2) Растягивает график растягивает в 2 раза вдоль оси Оy, получает график функции у= 2сtgx
3) Сжимает график функции в 3 раза вдоль оси Ох, получает график функции y=2tg x/3;
4) Получает график искомой фукции.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
построение графика тригонометрических функций с помощью простейших преобразований, 10 класс
построение графика тригонометрических функций с помощью простейших преобразований, 10 класс
|
Тема урока |
Построение графиков тригонометрических функций с помощью простейших преобразований. |
|
Цель урока |
- знать основные пукты исследования функции; - строить график тригонометрических функций с помощью простейших преобразований; - самостоятельно составлять тригонометрические функции и исследовать. |
Ход урока
|
Запланированные этапы урока |
Виды упражнений, запланированных на урок: |
Ресурсы |
|
|
Начало урока |
Учитель приветствует учащихся, эмоциональный настрой «Снежный ком», проверяет их готовность к уроку, по теме «Исследование функции» - У каждого из вас на столах лежат листы оценивания. Подпишите листы оценивания. В течение урока мы с вами будем выполнять различные задания. По окончанию решения каждого задания, вы должны оценить свою работу или вашу работу оценят одноклассники (Приложение 1) «+» – справился без затруднений, «±» – справился, но возникали сложности, «-« – не справился с заданием. Прием «Да, нет» На доске изображен график функции у= х^3+1. Учащиеся работают индивидуально. Исследуют решение функции записывая ответ – если утверждение верно, то пишут ˄, если нет – . Схема исследования функции. 1.Область определения функции- множество всех действительных чисел; 2.функция четная; 3. Функция не периодическая; 4.Координаты точек пересечения графика с осями координат: А) х=0, у= 0^3+1=1. Значит, график функции рересекаются с осью Оу в точке N(-1;0); Б) у=0, х^3+1=0, х^3=-1, х=1. Значит, график фукции пересекаются с осью Ох в точке N(-1;0); 5.Промежутки возрастания, убывания функции. График функции пересекается с осью абсцисс в точке N(-1;0). Тогда на промежутке (-∞; -1) функция f(x)<0, на промежутке (-1;+∞) функция f(x)>0 6.Для любых х1, х2 из области определения при х1<x2 выполняется у(х1) <у(х2), поэтому функция убывает. |
Ответ в виде «кардиограммы» на доске (образец) ˄_˄_˄˄_ |
|
|
Критерии успеха |
Учащиеся, сравнивая свою «кардиограмму» с образцом, оценивают себя в оценочном листе |
|
|
|
Середина урока |
Деление на группы равноуровневые (по карточкам) Используя метод "ДЖИГСО" учащиеся рассматривают примеры на построение тригонометрических функций с помощью простейших преобразований. Каждая группа должна исследовать функцию, построить график и оформить кластер. І группа: у=1+2sinx ІІ группа): y=2+cos 3x ІІІ группа: y=3tg x/2 ІҮ группа: y=2ctg x/3 Оценивание с помощью стратегии "Уточняющие вопросы» |
|
|
|
Конец урока |
Тесты по дифференциации «Темп» взаимопроверка с ключами. Приложение 1. Рефлексия «Похвальный бутерброд» по листам ответов |
|
|
Вариант 1
1.График, какой функции, изображен на рисунке?

а)у=cosx b)y=sinx c) y=tgx d)y=ctgx
2. Какое наибольшее значение принимает функция?
Ответ_____________
3.Какие точки являются нулями функции данного графика?
а)(0;0) b)( ;0)
c)
(π;0) d)
;0)
c)
(π;0) d) ;0)
;0)
4.Сколько нулей функции, изображено на графике?
а)1 b)5 c) 3 d)0
5.Сколько полных волн изображено на графике?
. Ответ_____________
6. Функция y=tgx является:
а)четной b)нечетной с)функцией общего вида
7.Изображеная на рисунке функция :
а)симметрична, относительно начала координат
b) симметрична, относительно оси ординат
с) симметрична, относительно оси абсцисс
8.Период функции y=сtgx
а)π b)2π c) не периодическая
9.
Функция, изображенная на рисунке функция на
промежутке (-  ;0)
;0)
а)возрастает b)убывает
10. На рисунке изображена функция. При каких х , не существует данной функции
. 
а)0 b) ;
c)
(π
d)
;
c)
(π
d) ;
;
Вариант 2.
1.График, какой функции, изображен на
рисунке? 
а)у=cosx b)y=sinx c) y=tgx d)y=ctgx
2. Какое наибольшее значение принимает функция?
Ответ_____________
3.Какие точки являются нулями функции данного графика?
а)(0;0) b)( ;0)
c)
(π;0) d)
;0)
c)
(π;0) d) ;0)
;0)
4.Сколько нулей функции, изображено на графике?
а)1 b)5 c) 4 d)0
5.Сколько полных волн изображено на графике?
. Ответ_____________
6. Функция y=сtgx является:
а)четной b)нечетной с)функцией общего вида
7.Изображеная на рисунке функция :
а)симметрична, относительно начала координат
b) симметрична, относительно оси ординат
с) симметрична, относительно оси абсцисс
8.Период функции y=tgx
а)π b)2π c) не периодическая
9.
Функция, изображенная на рисунке функция на
промежутке (0;  )
)
а)возрастает b)убывает
10. На рисунке изображена функция. При каких х , не существует данной функции
. 
а)0 b) ;
c)
(π
d)
;
c)
(π
d) ;
;
Дескрипторы
І группа: у=1+2sinx
1)Строит график функции у=sinx;
2) Растягивает график растягивает в 2 раза вдоль оси Оу, получает график функции у=2sinx;
3) Переносит график параллельно вдоль оси Оу на одну единицу вверх;
4) Получает график искомой фукции.
ІІ группа): y=2+cos 3x
1)Строит график функции у= cos x
2) Сжимает график в 3 раза вдоль оси Ох, получает график функции у= cos 3x
3) Переносит график параллельно вдоль оси Оу на две единицы вверх;
4) Получает график искомой фукции.
ІІІ группа: y=3tg x/2
1)Строит график функции у= tg x
2) Растягивает график растягивает в 3 раза вдоль оси Оy, получает график функции у= 3tgx
3) Сжимает график функции в 2 раза вдоль оси Ох, получает график функции y=3tg x/2;
4) Получает график искомой фукции.
ІҮ группа: y=2ctg x/3
1)Строит график функции у= сtg x
2) Растягивает график растягивает в 2 раза вдоль оси Оy, получает график функции у= 2сtgx
3) Сжимает график функции в 3 раза вдоль оси Ох, получает график функции y=2tg x/3;
4) Получает график искомой фукции.

шағым қалдыра аласыз















