

КГУ «Общеобразовательная школа села Ишимское
отдела образования по Жаксынскому району
управления образования Акмолинской области»
Шумкова Наталья Александровна – учитель начальных классов
Рабочая программа
учебного предмета
«Практикум по
математике»
4 класс
2025 г.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Учебная программа разработана всоответствии с Государственным общеобязательным стандартом среднего образования (начального, основного среднего, общего среднего образования), утвержденным постановлением Правительства Республики Казахстан.
Методологическую основу организации дополнительных занятий «Практикум по математике» обеспечивает личностно-деятельностный подход, который признаёт центром внимания личность учащегося с его интересами, способностями, потребностями. С точки зрения этого подхода ученик рассматривается как субъект деятельности, что предполагает сотрудничество и взаимодействие обучающего и обучаемого, создание и поддержание положительной мотивации к процессу получения новых знаний и саморазвития. В ходе обучения предполагается учёт индивидуальных и возрастных особенностей учащихся. В программе предлагается определённая последовательность изучения разделов и тем, однако по усмотрению учителя возможна их перестановка, некоторые из тем могут не рассматриваться или рассматриваться частично.
Цель рабочей программы: Формирование предметных, метапредметных и личностных компетенций обучающегося в контексте его возрастных особенностей, математическое развитие младших школьников, формирование системы начальных математических знаний, воспитание интереса к математике, к умственной деятельности.
Основные задачи рабочей программы:
1) осознание ребёнком ценности образования и понимание возможностей для образования, как в традиционной классно-урочной системе, так и в условиях дистанционного и самостоятельного изучения предмета;
2) формирование системы начальных математических знаний и умений их применять для решения учебно-познавательных и практических задач;
3) развитие основ логического, знаково-символического и алгоритмического мышления;
4) развитие пространственного воображения и математической речи;
5) развитие познавательных способностей;
6) воспитание стремления к расширению математических знаний. Курс позволяет учителю использовать его как в условиях традиционной классно-урочной системы, так и для дистанционных форм и самостоятельного изучения предмета обучающимися разных учебных возможностей, находящихся в разных жизненных ситуациях при наличии необходимых технических средств.
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ С ОПРЕДЕЛЕНИЕМ ОСНОВНЫХ ВИДОВ УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ
Предмет «Практикум по математике». 4 класс
|
№ |
Содержание |
Кол-во часов |
|
1 |
Урок 1. Нумерация. Счёт предметов. Разряды |
1 |
|
2 |
Урок 2. Числовые выражения. Порядок выполнения действий. Сложение нескольких слагаемых |
1 |
|
3 |
Урок 3. Вычитание вида 903 – 574 |
1 |
|
4 |
Урок 4. Умножение |
1 |
|
5 |
Урок 5. Деление |
1 |
|
6 |
Урок 6. Диаграммы |
1 |
|
7 |
Урок 7. Новые счётные единицы. Класс единиц и класс тысяч |
1 |
|
8 |
Урок 8. Чтение и запись многозначных чисел |
1 |
|
9 |
Урок 9. Разрядные слагаемые. Сравнение многозначных чисел |
1 |
|
10 |
Урок 10. Увеличение и уменьшение числа в 10, 100, 1000 раз. Выделение в числе общего количества единиц любого разряда |
1 |
|
11 |
Урок 11. Класс миллионов. Класс миллиардов. Повторение пройденного материала |
1 |
|
12 |
Урок 12. Единица длины — километр. Таблица единиц длины |
1 |
|
13 |
Урок 13. Единицы площади — квадратный километр, квадратный миллиметр. Таблица единиц площади |
1 |
|
14 |
Урок 14. Измерение площади фигуры с помощью палетки |
1 |
|
15 |
Урок 15. Единицы массы — центнер, тонна. Таблица единиц массы |
1 |
|
16 |
Урок 16. Единицы времени. Сутки. Задачи на нахождение начала, продолжительности и конца события |
1 |
|
17 |
Урок 17. Единицы времени — секунда, век. Таблица единиц времени |
1 |
|
18 |
Урок 18. Повторение пройденного по теме «Величины» |
1 |
|
19 |
Урок 19. Устные и письменные приёмы вычислений |
1 |
|
20 |
Урок 20. Вычитание с переходом через несколько разрядов вида 30 007 – 648 |
1 |
|
21 |
Урок 21. Решение уравнений |
1 |
|
22 |
Урок 22. Нахождение нескольких долей целого. Задачи разных видов |
1 |
|
23 |
Урок 23. Сложение и вычитание значений величин |
1 |
|
24 |
Урок 24. Задачи на увеличение (уменьшение) числа на несколько единиц, выраженных в косвенной форме |
1 |
|
25 |
Урок 25. Письменные приёмы умножения |
1 |
|
26 |
Урок 26. Умножение чисел, оканчивающихся нулями |
1 |
|
27 |
Урок 27. Решение уравнений вида: х ∙ 8 = 26 + 70, х : 6 = 18 ∙ 5, 80 : х = 46 – 30 |
1 |
|
28 |
Урок 28. Деление |
1 |
|
29 |
Урок 29. Деление многозначного числа на однозначное |
1 |
|
30 |
Урок 30. Задачи на увеличение (уменьшение) числа в несколько раз, выраженные в косвенной форме |
1 |
|
31 |
Урок 31. Деление многозначного числа на однозначное число с записью в частном нулей |
1 |
|
32 |
Урок 32. Задачи на пропорциональное деление. Закрепление изученного материала |
1 |
|
33 |
Урок 33. Повторение пройденного материала по теме «Алгоритмы письменного умножения и деления» |
1 |
|
34 |
Урок 34. Решение текстовых задач на пропорциональное деление |
1 |

Урок 1. Нумерация. Счёт предметов. Разряды
Цель: повторить способ образования трёхзначных чисел.
Задачи: закрепить знания о трёхзначных числах, навыки их чтения и определения разрядного состава.
Узнаем, научимся, сможем
На уроке мы узнаем: как образуются трёхзначные числа;
мы научимся: определять последующее и предыдущее число;
мы сможем: сравнивать многозначные числа.
Теоретический материал для самостоятельного изучения
Числа, которые используются при счете предметов, называются натуральными. Если записать числа в том порядке, в котором они называются при счёте, получим натуральный ряд чисел: 1, 2, 3, … Каждое следующее число на единицу больше предыдущего. Самое маленькое число – единица. Натуральный ряд бесконечен.
Если запись натурального числа состоит из одного знака, то его называют однозначным. Например 1, 5, 8, 9 –однозначны, 14, 33, 67 – двухзначные. Числа 578, 601, 999 – трехзначные. Двухзначные, трехзначные и т.д. числа называются многозначными.
Для счета предметов применяют натуральные числа. Любое натуральное число можно записать с помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Цифра – это знак, участвующий в записи числа. Цифры – это единицы счета от 0 до 9.
Число – это величина, при помощи которого производится счет. Такую запись называют десятичной.
Многозначное число – это целые числа, при записи которых нужно использовать несколько цифр (знаков).
При чтении трехзначных чисел сначала читается разряд сотен, затем разряд десятков, затем единиц, например число триста сорок два состоит из трёх сотен, четырех десятков и двух единиц. Каждое числоможно представить в виде суммы разрядных слагаемых. Например число 523 содержит 5 сотен, 2 десятка, 3 единицы. Его можно записать в виде суммы: 523=500+20+3. Каждое слагаемое суммы называется разрядным слагаемым, число 523 представлено в виде суммы разрядных слагаемых.
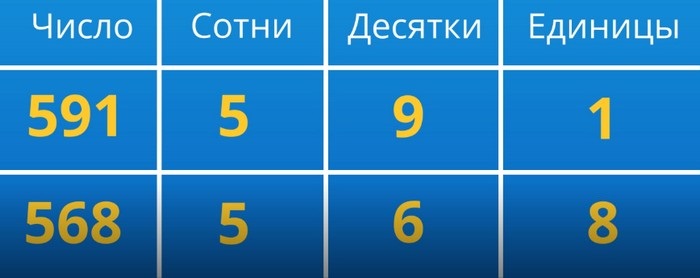
Многозначные числа можно сравнивать, используя способ поразрядного сравнения.
Например: 591 больше числа 568, так как сотен в них поровну, а десятков в числе 591 больше чем в числе 568
Задания тренировочного модуля:
1. Полина задумала несколько чисел, среди них есть трехзначные. Какие это числа?
-
4 дес. 6 ед.
-
1 сот. 5 дес. 3 ед.
-
5 сот. 5 ед.
-
6 дес. 2 ед.
-
0 сот.3 дес. 9 ед.
Правильный ответ:
1 сот. 5 дес. 3 ед.= 153
5 сот. 5 ед.= 505
2. Вставьте пропущенные слова.
Числа при записи которых используют несколько цифр называются ____________. В записи трехзначного числа есть ____________, десятки и _________. Класс единиц образует первые три ____________.
Правильный ответ:
Числа при записи которых используют несколько цифр называются многозначными . В записи трехзначного числа есть сотни, десятки и единицы. Класс единиц образует первые три разряда.
Необходимо запомнить
ВАЖНО!
Многозначные числа – это такие целые числа, при записи которых нужно использовать несколько цифр (знаков). Числа, для записи которых необходимо использовать 2 цифры – двузначные. Числа, в записи которых 3 цифры – трёхзначные, и так далее. В записи числа разряды, начиная справа, группируются в классы по три разряда в каждом. Читаются многозначные числа слева направо (поразрядно).
Интересные факты
Известный факт, что в записи числа 679 цифры образуют разряды: единицы, десятки, сотни. Разрядов всего три, и вместе они называются классом единиц.
Число 986 754 называется шестизначным. Первые три цифры справа образуют класс единиц, а следующие три – класс тысяч.
Число 123 643 671 – девятизначное. Первые три цифры справа образуют класс единиц, следующие три цифры – класс тысяч, последние три – класс миллионов.
Такая запись чисел называется десятичная. В математике существует еще римская система записи чисел, и она часто встречается в жизни, например, в часах (циферблате), при записи номера века или главы книги.
Вычисления
Помогите Полине пройти лабиринт к правильному ответу, решив выражение: 900 – 80 – 100 + 8.

Урок 2. Числовые выражения. Порядок выполнения действий. Сложение нескольких слагаемых
Цель: повторить порядок выполнения действий в выражениях.
Задачи: повторить правила выполнения действий в пределах 1000;
познакомиться с понятием выражения со скобками.
На уроке
мы узнаем:
правила о порядке выполнения действий в выражениях со скобками и без них;
мы научимся:
применять правила о порядке выполнения действий в выражениях;
мы сможем:
вычислять значения числовых выражений в два-три действия со скобками и без скобок.
Теоретический материал для самостоятельного изучения
Существуют следующие правила порядка действий в числовых выражениях.
Правило 1. Если числовое выражение содержит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку.
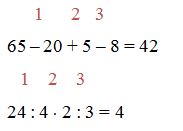
Правило 2. Если числовое выражение содержит не только сложение и вычитание, но и умножение и деление, то сначала выполняются по порядку (слева направо) действия умножение и деление, а потом – сложение и вычитание (слева направо).

П равило 3.
Если числовое выражение содержит одну пару или несколько пар
скобок, то сначала находят значение выражения в скобках, а затем
выполняют действия по правилам 1 и
2.
равило 3.
Если числовое выражение содержит одну пару или несколько пар
скобок, то сначала находят значение выражения в скобках, а затем
выполняют действия по правилам 1 и
2.
Задания тренировочного модуля:
1. Найдите правильное значение выражения:
15 ∙ 10 + (30 - 20) ∙ 5
-
200
-
230
-
20
-
250
Правильный ответ:
200
2. Заполните таблицу:
-
-
слагаемое
170
90
80
слагаемое
230
40
37
сумма
330
160
80
37
-
Правильный ответ:
-
-
слагаемое
170
290
90
80
74
слагаемое
230
40
70
0
37
сумма
400
330
160
80
37
-
3. Расставьте порядок действий:
80 - (42 : 7 ∙ 15 - 29)
Правильный вариант:

Необходимо запомнить
ВАЖНО!
Порядок действий в выражениях со скобками и без скобок такой:
если выражение содержит только сложение и вычитание или умножение и деление, то действия выполняются по порядку; если выражение содержит умножение и деление, то сначала выполняются эти действия;
если выражение содержит одну пару или несколько пар скобок, то сначала находят значение выражения в скобках, а затем за скобками по первому правилу.
Интересные факты
Возникновение знаков «+» и «−» уходит своими корнями в древность. Известно, что в давние времена виноторговцы черточкой отмечали, сколько продано мер вина. Знаком «−» (минус) отмечали уменьшение количества вина, соответственно «+» (плюс) — увеличение, когда в бочку с вином доливали содержимое.
Числовые выражения
Вставьте пропущенные слова.
Подсказка
Внимательно прочтите словарик.
Числа, соединённые знаками арифметических
действий, называются ![]() выражениями.
Действие вычитания обозначается знаком
выражениями.
Действие вычитания обозначается знаком ![]() . Действие
сложения − знаком
. Действие
сложения − знаком ![]() .
Результатом действия сложения является
.
Результатом действия сложения является ![]() двух или
более чисел.
двух или
более чисел.
Числовые выражения. Порядок выполнения действий. Сложение нескольких слагаемых
Распределите равенства и неравенства на верные и неверные.
|
Верно |
Неверно |
|
|
|
807 < 870 909 + 90 + 1 = 1000 590 - 400 - 90 = 180 35 ∙ 2 - (25 - 20) = 75

Урок 3. Вычитание вида 903 – 574
Цель: познакомиться с письменным приёмом вычитания вида 607 - 463, 903 - 574.
Задача: познакомиться с новым приёмом вычитания.
Глоссарий по теме:
Трёхзначные числа - это числа в записи, которых используется три цифры.
Алгоритм - последовательность действия (шагов).
Вычитание -математическая операция по вычитанию из целого части. На письме обычно обозначается с помощью знака «минус».
Задания тренировочного модуля:
1. Выбери правильный ответ
903 - 574
1.207
2. 329
3. 457
Правильный ответ:
329
2. Выполни вычисления:
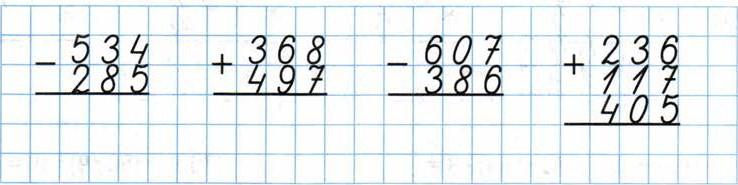
Правильный ответ:
1. 249
2. 865
3.222
4. 857
Необходимо запомнить
ВАЖНО!
Итак, чтобы вычесть из трёхзначного числа трехзначное вида 607 - 463 и 903 - 574, надо освоить алгоритм письменного вычитания чисел, в котором важно верно записать выражение в столбик. При вычислениях занимать нужное количество единиц у разряда, в котором присутствуют единицы.
Интересные факты
Первобытные люди не умели считать, и научить их было некому. Поэтому они вели наблюдения за природой и выделяли из многих объектов отдельные предметы. Например, из стаи птиц – самого крупного, из стада оленей – вожака, из грозди винограда – ягоду самого тёмного цвета. Определяли соотношение между предметами как «один» и «много». Наблюдения за парными предметами (рога, руки, глаза, уши и т.д.) привели их к пониманию чисел.
Вычитание вида 903 - 574
Найдите и выделите цветом по вертикали и горизонтали слова по теме урока.
1) разность; 2) выражение; 3) значение; 4) алгоритм.
|
д |
ж |
з |
л |
щ |
л |
к |
х |
з |
х |
ч |
е |
щ |
ф |
м |
|
ц |
ё |
у |
в |
р |
з |
c |
ч |
з |
о |
е |
д |
ю |
п |
в |
|
х |
ё |
р |
ы |
а |
н |
з |
т |
в |
и |
л |
д |
ч |
ж |
м |
|
ы |
ж |
щ |
р |
з |
а |
е |
т |
ы |
г |
и |
в |
ц |
д |
ё |
|
т |
ч |
г |
а |
н |
ч |
ч |
м |
к |
б |
ё |
г |
и |
ф |
т |
|
и |
в |
щ |
ж |
о |
е |
п |
м |
ю |
з |
ы |
д |
т |
д |
э |
|
э |
и |
ю |
е |
с |
н |
й |
х |
з |
ж |
о |
ш |
е |
ч |
з |
|
ю |
я |
э |
н |
т |
и |
ф |
э |
т |
р |
ф |
э |
я |
у |
г |
|
х |
з |
ю |
и |
ь |
е |
м |
ц |
е |
c |
у |
ё |
р |
ц |
ы |
|
ю |
у |
c |
е |
у |
у |
п |
ы |
я |
c |
м |
ш |
ц |
ж |
к |
|
з |
а |
л |
г |
о |
р |
и |
т |
м |
й |
ы |
и |
c |
о |
ф |
|
э |
ч |
б |
д |
ж |
й |
л |
ё |
л |
х |
ч |
д |
в |
ю |
ё |
|
у |
о |
з |
м |
з |
у |
в |
э |
ё |
ш |
э |
щ |
ш |
х |
з |
|
у |
ж |
м |
п |
б |
c |
к |
ч |
и |
р |
д |
т |
й |
ы |
д |
|
c |
з |
л |
у |
щ |
т |
ш |
т |
г |
з |
ы |
а |
т |
и |
в |

Урок 4. Умножение
Цель:
познакомиться с приёмом умножения трёхзначного числа на однозначное.
Задачи:
повторить запись выражения в столбик;
познакомиться с новым приёмом умножения.
Теоретический материал для самостоятельного изучения
Рассмотрим письменный прием умножения трёхзначного числа на однозначное. Решим выражение 216 ∙ 3.
Правило записи умножения трехзначного числа на однозначное: записываем числа друг под другом, единицы под единицами.
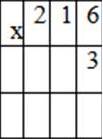
Алгоритм умножения трехзначного числа на однозначное:
1. Умножаем единицы.
6 умножим на 3, получится 18.
18 это 1 десяток и 8 единиц
8 единиц пишем под единицами.
1 десяток запоминаем, его позже прибавим к десяткам.

2. Умножаем десятки.
1 умножить на 3 равно 3, и прибавляем 1 десяток, который получился при умножении десятков, получится 4.
Записываем десятки под десятками
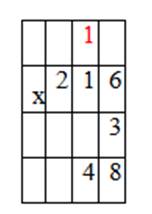
3. Умножаем сотни.
2 умножить на 3 равно 6.
6 подписываем сотни под сотнями
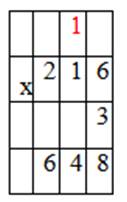
Ответ: 648.
Задания тренировочного модуля:
1. Выполните вычисления

Правильный ответ:
828
708
2. Вставьте пропущенные знаки вместо * (>< =)
125 ∙ 4 - 250 * 125 ∙ 4 ∙ 1
Правильный ответ:
125 ∙ 4 - 250 < 125 ∙ 4 ∙ 1
ВАЖНО!
Чтобы умножить трёхзначное число на однозначное, надо верно записать выражение в столбик (единицы под единицами) и умножить поочередно единицы, десятки, сотни.
При выполнении умножения каждого разряда записываются единицы полученного числа, а десятки запоминаются.
При вычислении следующего разряда к полученному числу прибавляются оставшиеся единицы.
Интересные факты
Известно, что у древних египтян не было правил и таблиц. Но они умели умножать путем разложения в двоичный ряд чисел.
Например, нужно умножить 22 на 35. Записываем 22 и 35. Теперь делим левое число на 2, а правое умножаем на 2.
Так продолжается, пока в левом столбце не появится единица.
Нечётные числа при делении на 2 округляем в меньшую сторону. И подчеркиваем.
В левом столбце нечётное число отмечается знаком плюс. А затем складываются 70 + 140 + 560 = 770.
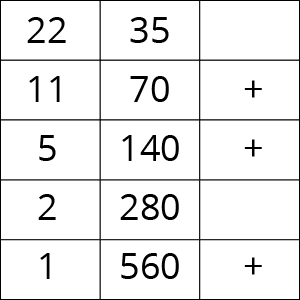
Составление последовательности
Укажите последовательность чисел по правилу: каждое последующее число в 2 раза больше, начиная с 24. Последнее число не должно превышать 1000.
24 ![]()
![]()
![]()
![]()
![]()
Приёмы умножения
Заполните пропуски в таблице.
|
a |
6 |
247 |
71 |
5 |
|
b |
7 |
4 |
|
|
|
a • b |
|
|
71 |
0 |
988 1 0 42
Спрятанные слова
Найдите и выделите цветом слова по теме урока.
Подсказка
В филворде спрятаны 3 слова, связанные с умножением.
|
c |
т |
ф |
я |
а |
ё |
у |
з |
ы |
р |
в |
п |
в |
и |
б |
|
з |
б |
у |
м |
н |
о |
ж |
е |
н |
и |
е |
п |
ж |
а |
п |
|
д |
м |
ж |
н |
м |
е |
ю |
ш |
б |
т |
ш |
р |
з |
а |
т |
|
а |
в |
в |
о |
п |
у |
к |
д |
п |
к |
д |
о |
г |
щ |
и |
|
з |
е |
л |
ж |
а |
х |
о |
х |
э |
е |
э |
и |
к |
щ |
ж |
|
ю |
к |
м |
и |
о |
к |
п |
м |
р |
г |
ю |
з |
ж |
ё |
п |
|
ф |
щ |
ё |
т |
й |
э |
к |
к |
д |
c |
ц |
в |
э |
ю |
к |
|
л |
п |
к |
е |
е |
в |
в |
а |
ф |
е |
c |
е |
х |
ц |
ё |
|
ц |
у |
д |
л |
о |
у |
м |
э |
т |
ю |
т |
д |
ф |
ч |
е |
|
ф |
ё |
х |
ь |
р |
т |
л |
c |
в |
й |
ё |
е |
у |
c |
м |
|
ф |
ё |
л |
у |
к |
ф |
у |
д |
ч |
л |
з |
н |
б |
в |
з |
|
ж |
у |
ч |
щ |
и |
ё |
е |
ч |
ю |
т |
я |
и |
г |
ю |
ю |
|
в |
е |
щ |
т |
ц |
е |
р |
ж |
т |
т |
х |
е |
э |
ю |
г |
|
й |
п |
ш |
р |
з |
е |
ю |
в |
е |
й |
к |
й |
э |
а |
е |
|
в |
у |
р |
ф |
т |
д |
б |
п |
о |
б |
э |
ц |
щ |
т |
д |

Урок 5. Деление
Цель:
познакомиться с письменным приёмом деления трёхзначного числа на однозначное.
Задачи:
познакомиться с новым приёмом деления;
повторить запись математического выражения.
Теоретический материал для самостоятельного изучения
Рассмотрим письменный прием деления трёхзначного числа на однозначное. Решим выражение 876:3.
При письменном делении запись ведется в столбик.
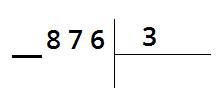
Алгоритм деления трехзначного чиста на однозначное.
1. Делю сотни.
Разделим 8 на 3, в частном будет 2 сот.
Умножу 3 на 2 равно 6, это значит, что разделили 6 сотен.
Из 8 вычесть 6 получится 2. Осталось разделить 2 сотни.
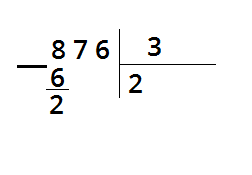
2. Делю десятки.
2 сотни и 7 десяток - это 27 десяток. Разделю 27 на 3. В частном будет 9 десятков.
Умножу 9 на 3 равно 27, это значит, что разделили 27 десятков.
Вычту из 27 27 равно 0, десятки разделили.

3. Делю единицы.
Разделим 6 на 3 равно 2.
Умножим 2 на 3 получится 6.
Из 6 вычесть 6 равно 0.
Деление закончили. Читаем ответ: 292.
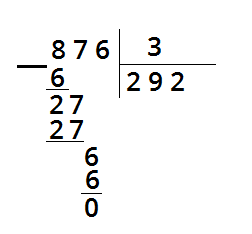
Задания тренировочного модуля:
1. Выберите правильный ответ, выполнив вычисления.
782 : 2
1. 207
2. 374
3. 457
Правильный ответ:
374
2. Решите задачу, используя прием деления трехзначного числа на однозначное:
В первый день бригада сборщиков собрала 435 кг яблок, во второй день пошел дождь, и бригада собрала в 3 раза меньше чем в первый день. В третий день собрали яблок на 200 кг больше, чем во второй. Сколько яблок собрали в третий день?
Правильный ответ:
Решение:
1. 435 : 3 = 145 (яб.) – собрали во второй день.
2. 145 + 200 = 345 (яб.) – собрали в третий день
Ответ: 345 кг яблок.
Необходимо запомнить
ВАЖНО!
Чтобы выполнить деление трёхзначного числа на однозначное, необходимо верно записать выражение в столбик.Деление выполняется по алгоритму, в котором сначала делятся сотни на делитель, в частном записывается число, полученное при делении, затем его умножают на делитель, и полученное при умножении число вычитается из сотен. Затем, по аналогии, выполняется деление десятков и единиц.
Интересные факты
Известно, что некоторые животные умеют считать.Например, муравьи выполняют простейшие арифметические действия.Доказано, что муравей-разведчик находит пищу в лабиринте и сообщает своим сородичам путь – сколько ответвлений нужно пройти, отнимая или прибавляя нужное число.
Заполните таблицу.
|
|
|
|
|
|
b |
180 |
720 |
3 |
|
b : 3 |
|
|
|
1 60 240

Урок 6. Диаграммы
Цель:
познакомиться с понятием «столбчатые диаграммы».
Задачи:
уметь извлекать информацию из различных источников;
научиться читать и составлять диаграммы.
Теоретический материал для самостоятельного изучения
Маша – 10 мин.
Оля – 12 мин.
Костя – 25 мин.
Илья – 7 мин.
Учительница детям задала задание: проследить и зафиксировать время, которые они тратят на дорогу в школу. И у детей получилась такая запись:
Никита – 19 мин.
Для наглядности дети записали результаты в таблицу
|
Имя ученика |
Время на дорогу в школу |
|
Маша |
10 |
|
Оля |
12 |
|
Костя |
25 |
|
Илья |
7 |
|
Никита |
19 |
Учительница на основании информации в таблице составила рисунок, который называется – диаграмма.

Слово "диаграмма" пришло к нам из греческого языка и переводиться как «чертеж». В энциклопедии написано, что оно обозначает графическое изображение информации.
На изображении выше мы видим столбчатую диаграмму, т к . данные времени, которые дети тратят на дорогу изображены в виде столбиков.
С левой стороны диаграммы отмечено время, одно деление равно одной минуте. Внизу по горизонтальной линии имена детей.
По диаграмме мы сможем увидеть следующие данные:
У Кости дорога от дома до школы самая длинная.
Самая короткая - у Ильи.
На сколько один ученик тратит время на дорогу больше или меньше другого. Например: Никита дольше, чем Маша и т.д.
Таким образом, «читается информация», которая записана на диаграмме.
Диаграмму можно построить.
Для этого:
Рисуется прямой угол.
Определим, какие величины будем располагаться на вертикальной и горизонтальной стороне угла.
На вертикальной стороне угла откладываются единичные отрезки, чаще всего одна клетка в тетради – один отрезок.
На горизонтальной стороне угла точки, которые обозначают то, что и о ком идет представление в диаграмме.
При помощи линейки прорисовываются столбики с нужным количеством единичных отрезков или клеток.
В диаграмме подписываются все данные.
Задания тренировочного модуля:
1. Прочитайте диаграмму, выберите, сколько стоит книга и сколько стоит альбом.
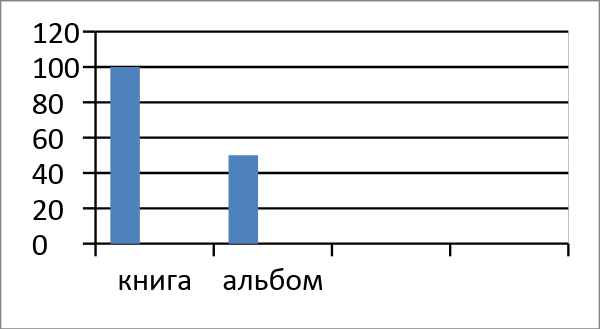
Варианты ответа:
Книга: 50 руб., 20 руб., 100 руб., 150 руб.
Альбом: 50 руб., 20 руб., 100 руб., 150 руб.
Правильный ответ:
Книга стоит 100 руб.
Альбом стоит 50 руб.
2. Учительница дала Диме таблицу и попросила его указать диаграмму, на которой правильно изображены данные, представленные в этой таблице.
Определи диаграмму, которую ему надо выбрать?
|
Имя |
Сбережения |
|
Сара |
22 зеда |
|
Пётр |
15 зедов |
|
Полина |
17 зедов |
|
Кристина |
10 зедов |
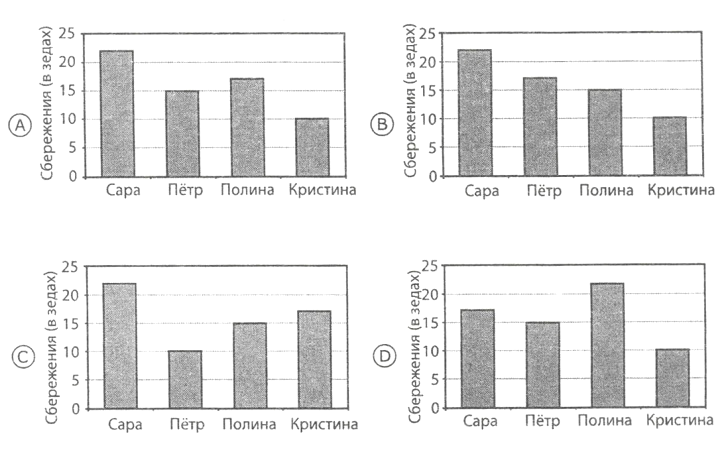
Правильный ответ:
Вариант А.
Необходимо запомнить
ВАЖНО!
Информацию можно отображать в тексте, таблице, рисунке и диаграмме. Диаграмма - это графическое изображение информации. Если на изображении диаграммы используют столбцы, то она называется столбчатой. При чтении диаграммы можно увидеть количественный показатель данных, сравнить их, найти разность в представленных данных. Диаграмму можно построить в виде прямого угла, внутри которого размещаются данные в виде столбцов.
Интересные факты
Слово «диаграмма» переводится с греческого языка как «чертёж». И правда, диаграмма – это рисунок или чертёж, на котором изображены данные в виде отрезков, столбцов, частей круга, точек. В истории математики известно, что первым стал использовать диаграммы Уильям Плейфер, английский экономист (1786 год).
Чтение диаграмм
Выберите, сколько стоит книга, сколько стоит альбом.
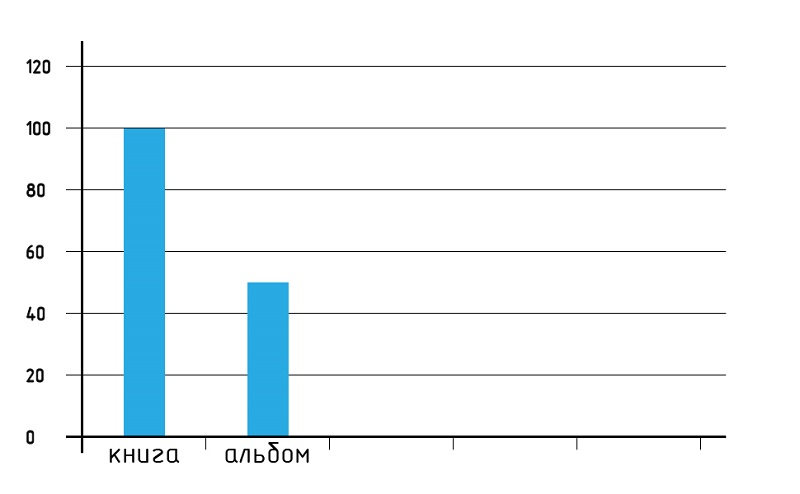
Книга:
![]()
Альбом:
![]()
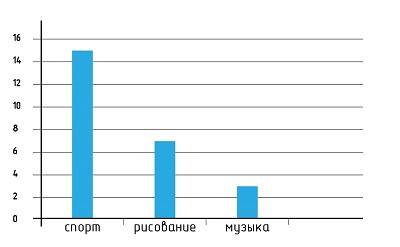
Чтение столбчатых диаграмм
Рассмотрите диаграмму и заполните таблицу.
|
Увлечение учеников 4-А класса |
Количество человек |
|
Спорт |
|
|
Рисование |
|
|
Музыка |
|
3 15 7

Урок 7. Новые счётные единицы. Класс единиц и класс тысяч
Цель: познакомиться с многозначными числами больше 1000.
Задачи: познакомиться с понятиями класс сотен, класс единиц;
научиться считать тысячами.
Теоретический материал для самостоятельного изучения
Если предметов много, то при счете используют не только знакомые единицы счета - единицы, десятки, сотни, но и более крупные, например тысячи.
Тысячи считают так же, как и простые единицы:
Десять тысяч – это один десяток тысяч.
Десять десятков тысяч – это одна сотня тысяч.
Десять сотен тысяч – это тысяча тысяч, или миллион.
10 тысяч - 1 десяток тысяч
10 десятков тысяч - 1 сотня тысяч
10 сотен тысяч - 1 тысяча тысяч или 1 миллион
Единицы, десятки, сотни составляют класс единиц, или первый класс.
Единицы тысяч, десятки тысяч и сотни тысяч составляют класс тысяч, или второй класс.
|
II класс - Класс тысяч |
I класс - Класс единиц |
||||
|
Сотни тысяч |
Десятки тысяч |
Единицы тысяч |
Сотни |
Десятки |
Единицы |
Посмотрите на таблицу: в каждом классе три разряда.
Разряды первого класса: единицы, десятки, сотни.
Разряды второго класса: единицы тысяч, десятки тысяч и сотни тысяч.
Чтобы прочитать многозначное число, его разбивают на классы, отсчитывая справа по три цифры, затем считают, сколько единиц каждого класса, начиная с высшего.
Например: 123 456
Читается три цифры справа класс тысяч - "сто двадцать три тысячи".
Затем класс единиц - "четыреста пятьдесят шесть".
В числе 372 000 три нуля в записи показывают отсутствие единиц первого класса. Название класса единиц не произносится. Читаем число с высшего класса: «триста семьдесят две тысячи».
Прочитаем число, в котором 145 единиц второго класса и 312 единиц первого класса. Читаем число с высшего класса: «сто сорок пять тысяч триста двенадцать».
Научимся записывать числа больше 1000.
1. В таблице записано число, в котором содержится только 69 единиц класса тысяч, в классе единиц записываем нули или 6 единиц в разряде десятков тысяч и 9 единиц в разряде единиц тысяч.
|
II класс - Класс тысяч |
I класс - Класс единиц |
||||
|
Сотни тысяч |
Десятки тысяч |
Единицы тысяч |
Сотни |
Десятки |
Единицы |
|
|
6 |
9 |
0 |
0 |
0 |
Записывается это число, начиная с класса тысяч, а затем цифры в классе единиц
69 000
2. Запишем следующее число, в котором содержится 307 единиц класса тысяч, а в классе единиц число 1. Нули показывают отсутствие единиц в разрядах десятков тысяч, сотен и десятков.
|
II класс - Класс тысяч |
I класс - Класс единиц |
||||
|
Сотни тысяч |
Десятки тысяч |
Единицы тысяч |
Сотни |
Десятки |
Единицы |
|
3 |
0 |
7 |
0 |
0 |
1 |
Записывается это число, начиная с класса тысяч, а затем цифры в классе единиц
307 001
Таким образом, все числа больше 1000 читаются с класса тысяч (слева направо). Также производиться запись. В случае отсутствия единиц в разрядах записывается нуль.
Задания тренировочного модуля:
1.Укажите, сколько единиц тысяч в числах:
23 769 125 603
Правильный ответ:
1. 3 ед. 2. 5 ед.
2 .Установите соответствие между записью числа и его чтением
-
-
Пятьсот тысяч сто семь
500 107
Тридцать семь тысяч
190 003
Сто девяносто тысяч три
37 000
Двести шестьдесят восемь тысяч двести шестьдесят восемь
999 117
Девятьсот девяносто девять тысяч сто семнадцать
268 268
-
Правильный ответ:
-
-
Пятьсот тысяч сто семь
500 107
Тридцать семь тысяч
37 000
Сто девяносто тысяч три
190 003
Двести шестьдесят восемь тысяч двести шестьдесят восемь
268 268
Девятьсот девяносто девять тысяч сто семнадцать
999 117
-
Необходимо запомнить
ВАЖНО!
Единицы, десятки, сотни составляют класс единиц (первый). Единицы тысяч, десятки тысяч и сотни тысяч составляют класс тысяч (второй). Чтобы прочитать многозначное число, его разбивают на классы, отсчитывая справа по три цифры; считают, сколько единиц каждого класса, начиная с высшего. Записывают многозначные числа, начиная с разрядов класса тысяч, затем разряды класса единиц.
Интересные факты
В древние времена счёт был до нескольких тысяч, так как не было необходимости в больших числах.
Если речь заводилась о множестве предметов, то говорили такую фразу: «Больше, чем звёзд на небе!».
Известно, что число «миллион» появилось в средние века и обозначало «большая тысяча» или «тысяча раз тысяча».
Многозначные числа
Заполните пропуски в тексте.
Наибольшее четырехзначное число
– ![]() .
.
Наименьшее четырехзначное число
– ![]() .
.
Наибольшее шестизначное число
– ![]() .
.
Наименьшее семизначное число
– ![]() .
.

Урок 8. Чтение и запись многозначных чисел
Цель:
закрепить умение считать и записывать многозначные числа.
Задачи:
читать, записывать, сравнивать многозначные числа.
Теоретический материал для самостоятельного изучения
Вы помните правило чтения многозначных чисел. Оно звучит так «Чтобы прочитать многозначное число, его разбивают на классы, отсчитывая справа по три цифры, затем считают, сколько единиц каждого класса, начиная с высшего».
Повторим это правило.
Например: записано число 253 400. В нем 253 единицы класса тысяч и 400 единиц класса единиц. Читается оно так: «двести пятьдесят три тысячи четыреста».
Пробуем ещё раз: в числе содержится 69 единиц класса тысяч, класс единиц отсутствует. Читается оно так «шестьдесят девять тысяч». Записать данное число надо так 69 000.
В числе содержится 307 единиц класса тысяч и 1 единица. Данное число прочитаем слева направо " триста семь тысяч один". Записываем его тоже слева направо, сначала класс тысяч, затем класс единиц, учитывая, что разряде сотен и десятков будет цифра нуль. Получается 307 001.
Задания тренировочного модуля:
Выберите правильный ответ записи числа:
1.145 ед. 2 класса и 326 ед. 1 класса
-
145 000
-
326 145
-
145 326
Правильный ответ:
3.145 326
2. Найдите и закрасьте числа:
1. 7 ед. 2 класса и 5 ед. 1 класса.
2. 367 ед. 2 класса и единицы 1 класса отсутствуют
3. 4 сот. тысяч 45 ед.
4. пятьсот шестьдесят две тысячи тридцать два
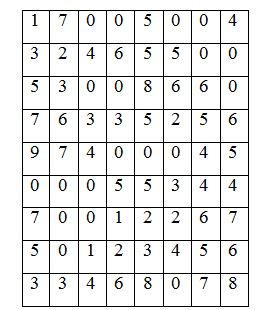
Правильный ответ:
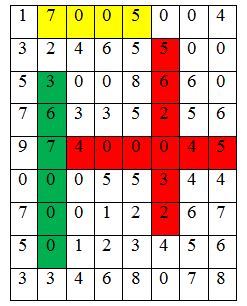
Запишите:
наибольшее шестизначное число___
наименьшее пятизначное число ____
наименьшее шестизначное число ___
Ответ:
наибольшее шестизначное число: 999999
наименьшее пятизначное число 10000
наименьшее шестизначное число 100000.
Необходимо запомнить
ВАЖНО!
Чтобы прочитать многозначное число, его разбивают на классы, отсчитывая справа по три цифры, затем считают, сколько единиц каждого класса, начиная с высшего. Записывают многозначные числа начиная с разрядов класса тысяч, затем разряды класса единиц.
Интересные факты
А вы знаете, что получится, если сложить все числа от 1 до 10? Число 55! Если сложить числа от 1 до 100, то получится 5050. Интересные арифметические задачки подобного рода можно решать при помощи калькулятора.
Например, ввести первые 3 цифры своего номера телефона (без оператора), умножить их на 80, прибавить 1, и всё это умножить на 250. Затем прибавить последние 4 цифры своего номера два раза, отнять 250, разделить на 2.
Какой ответ вы получили?
Спрятанные числа
Найдите и выделите цветом числа:
1) 7 ед. 2 класса и 5 ед. 1 класса;
2) 367 ед. 2 класса и единицы 1 класса отсутствуют;
3) 4 сот. тысяч 45 ед.;
4) пятьсот шестьдесят две тысячи тридцать два.
Подсказка
Наведите курсор на первое число и тяните, не отпуская, до последнего числа. Ответ выделится пунктиром.
|
1 |
7 |
0 |
0 |
5 |
5 |
2 |
2 |
1 |
5 |
|
2 |
1 |
3 |
1 |
4 |
5 |
7 |
4 |
7 |
9 |
|
5 |
3 |
4 |
1 |
6 |
6 |
1 |
4 |
3 |
5 |
|
4 |
6 |
7 |
4 |
7 |
2 |
6 |
2 |
6 |
1 |
|
1 |
7 |
4 |
0 |
0 |
0 |
4 |
5 |
9 |
2 |
|
7 |
0 |
3 |
0 |
0 |
3 |
6 |
2 |
4 |
0 |
|
2 |
0 |
2 |
1 |
2 |
2 |
4 |
3 |
0 |
3 |
|
6 |
0 |
8 |
8 |
3 |
5 |
4 |
1 |
2 |
1 |
|
1 |
8 |
3 |
1 |
2 |
3 |
8 |
3 |
4 |
6 |
|
5 |
2 |
4 |
1 |
6 |
0 |
2 |
0 |
9 |
5 |

Урок 9. Разрядные слагаемые. Сравнение многозначных чисел
Цель: научиться записывать многозначные числа в виде суммы разрядных слагаемых.
Задачи: записывать и сравнивать многозначные числа.
Теоретический материал для самостоятельного изучения
Рассмотрим шестизначное число 721 948. Оно содержит 7 сотен тысяч 2 десятка тысяч 1 тысячу 9 сотен 4 десятка и 8 единиц.
Запись данного числа в таблице разрядов выглядит так:
|
II класс - Класс тысяч |
I класс -Класс единиц |
||||
|
Сотни тысяч |
Десятки тысяч |
Единицы тысяч |
Сотни |
Десятки |
Единицы |
|
7 |
2 |
1 |
9 |
4 |
8 |
Из неё можем выяснить, сколько единиц содержится в каждом разряде данного числа. Итак:
7 сотен тысяч это 700 000 единиц,
2 десятка тысяч это 20 000единиц,
1 тысяча это 1000 единиц.
9 сотен это 900 единиц,
4 десятка это 40единиц и 8 единиц.
Число 721 948 можно заменить суммой
700 000 + 20 000 + 1000 + 900 + 40 + 8
Верной будет такая запись 721 948 = 700 000 + 20 000 +1000+900+40+8
Рассмотрим еще пример записи многозначного числа в виде суммы разрядных слагаемых.
Прочитаем число 580 302.
В этом числе:
5 сотен тысяч это 500 000 единиц,
8 десятков тысяч это 80 000 единиц,
Разряд единиц тысяч отсутствует.
3 сотни это 300 единиц,
Разряд десятков отсутствует и 2 единицы.
580 302 = 500 000+80 000+300+2
Теперь рассмотрим способ сравнения чисел до миллиона.
При сравнении чисел до миллиона работает принцип поразрядного сравнения.
Рассмотрим сравнение чисел 5489 и 5367. В обоих числах по 5 тысяч. Сравниваем сотни:4 сотни > 3 сотен.
Сравниваем десятки:8 десятков больше чем6 десятков.
Сравниваем единицы: 9 единиц больше чем 5 единиц.Значит, 5489 > 5365
Задания тренировочного модуля:
1. Заполните таблицу
|
Число |
Всего тысяч |
Всего сотен |
Всего десятков |
Всего единиц |
|
5 009 |
|
|
|
|
|
26 320 |
|
|
|
|
|
216 746 |
|
|
|
|
|
999999 |
|
|
|
|
Правильный ответ:
|
Число |
Всего тысяч |
Всего сотен |
Всего десятков |
Всего единиц |
|
5 009 |
5 |
0 |
0 |
9 |
|
26 320 |
26 |
3 |
2 |
0 |
|
216 746 |
216 |
7 |
4 |
6 |
|
999999 |
999 |
9 |
9 |
9 |
2. Вставьте пропущенные знаки (><)
70000+2000+600+20+7* 700000+20000+600+20+7
10000+3000+60+2 * 10000+300+60+2
300000+1000000+7000+2 * 100000+30000+7000+2
Правильны ответ:
70000+2000+600+20+7< 700000+20000+600+20+7
10000+3000+60+2 >10000+300+60+2
300000+1000000+7000+2 > 100000+30000+7000+2
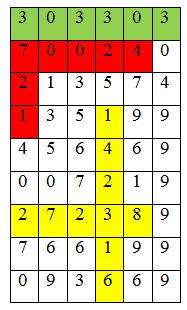
3. Найдите и закрасьте числа:
1. 3000+700+20+1
2. 100000+40 000+2000+300+10+6
3. 20000+7000+200+30+8
4. 300000+3000+300+3
5. 900000+90000+9000+900+9
6. 70000+20+4
 Правильный ответ:
Правильный ответ:
Необходимо запомнить
ВАЖНО!
Чтобы записать многозначное число в виде суммы разрядных слагаемых, надо определить количество единиц любого разряда, содержащихся в числе, и сложить их.
Например, 65 458 = 60 000 + 5 000 + 400 + 50 + 8
Сравнение многозначных чисел производится по классам и разрядам.
Интересные факты
В истории известно много сказаний, как человек расплачивался за услугу. Одно из самых интересных – с использованием шахматной доски. Предлагается на первую клетку положить одно зернышко, на вторую – два, на третью – три и так далее. Когда дело доходило до последней клетки, общий вес зерна составлял 460 миллиардов тонн.
Классы и разряды
Многозначные числа
Найдите и выделите цветом числа:
1) 3000 + 700 + 20 + 1
2) 100000 + 40000 + 2000 + 300 + 10 + 6
3) 20000 + 7000 + 200 + 30 + 8
4) 300000 + 3000 + 300 + 3
5) 900000 + 90000 + 9000 + 900 + 90 + 9
6) 70000 + 20 + 4
Разрядные слагаемые
Подчеркните равенства, в которых число правильно записано в виде суммы разрядных слагаемых.
1) 40009 = 40000 + 9
2) 302050 = 302 + 50
3) 145906 = 100000 + 40000 + 5000 + 900 + 6
4) 750345 = 700000 + 50000 + 300 + 45

Урок 10. Увеличение и уменьшение числа в 10, 100, 1000 раз. Выделение в числе общего количества единиц любого разряда
Цель: научиться увеличивать и уменьшать числа в 10, 100, 1000 раз.
Задача: определять общее количество единиц любого разряда в числе.
Теоретический материал для самостоятельного изучения
Они похожи тем, что в записи у всех присутствует цифра 7. А отличаются они наличием и количеством нулей в записи.
Цифра 7 в записи этих чисел обозначает разряд: 7 это 7 единиц, 70 это 7 десятков, 700 это 7 сотен, 7000 это 7 тысяч.
Понаблюдайте, в записи каждого следующего числа цифра 7 перемещается влево, а на ее место ставиться цифра нуль. При этом значение числа увеличивается в 10 раз. Можно сделать вывод, что каждое следующее число в 10 раз больше предыдущего.
Из наших наблюдений можно вывести правило увеличения числа в 10 раз.
Для увеличения числа в 10 раз
надо приписать цифру 0 справа
Соответственно, для увеличения числа в 100 раз нужно приписать справа два нуля. В тысячу раз три нуля.
7→700
7 →7000
Правило уменьшения числа в 10 раз работает наоборот.
Чтобы уменьшить число в 10 раз
надо в записи числа убрать справа один нуль
При уменьшении числа в 100 раз надо в записи числа справа убрать два нуля 700→7
7000→70
При уменьшении числа в 1000 раз надо в записи числа справа убрать три нуля
7000→7
70000→70
Следует заметить, что правило уменьшения числа в 10, 100 и 1000 раз работает только тогда, когда в записи числа справа находится достаточное количество нулей.
Теперь рассмотрим, как можно определять общее количество единиц любого разряда в многозначном числе. Возьмем число 3543. В нем 3 тысячи 5 сотен 4 десятка и 3 единицы.
Выдели общее число тысяч - это 3. 3543 → 3 тыс.
Теперь выделим общее число сотен, подчеркнем слева направо все цифры, включая разряд сотен 3543 → 35 сот. Получилось 35 сотен всего в 3543.
Найдем общее число десятков, подчеркнем слева направо все цифры, включая разряд десятков. 3543 → 354 дес. Это число 354. Значит в числе 3543 всего 354 десятка.
Соответственно общее количество единиц в числе 3543 составляет 3543.
Задания тренировочного модуля:
1. Заполните таблицу
|
множитель |
450 |
25 |
|
1000 |
|
|
множитель |
|
1000 |
1000 |
|
10 |
|
произведение |
45000 |
|
457000 |
1000000 |
1090000 |
Правильный ответ:
|
множитель |
450 |
25 |
457 |
1000 |
109 000 |
|
множитель |
100 |
1000 |
1000 |
1000 |
10 |
|
произведение |
45000 |
25000 |
457000 |
1000000 |
1090000 |
2 . Распределите по группам числа, которые можно разделить на 100 и 1000 и нельзя.
100, 12, 34890, 40000, 1900000, 204040, 202, 4500
Правильный ответ:
Можно разделить: 100, 40000, 1900000, 4500
Нельзя разделить: 12, 34890, 204040, 202
3. Общее количество какого разряда выделено в числах? Подпишите ответ.

Правильный ответ:

Деление на 100 и 1000
Распределите по группам числа, которые можно разделить без остатка на 100 или 1000, и нельзя.
|
Можно разделить: |
Нельзя разделить: |
|
|
|
100 40000 1900000 4500
12 34890 204040 202

Урок 11. Класс миллионов. Класс миллиардов. Повторение пройденного материала
Цель: познакомиться с числами в пределах двенадцати разрядов.
Задачи: научиться читать и записывать многозначные числа более миллиона.
Теоретический материал для самостоятельного изучения
Сколько разрядов в каждом классе? Верно, в каждом классе три разряда.
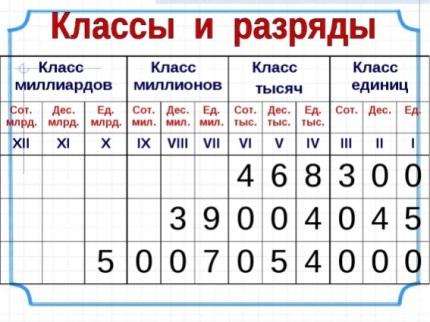
Единицы, десятки, сотни образуют I класс – класс единиц.
Единицы тысяч, десятки тысяч и сотни тысяч образуют II класс – класс тысяч.
Единицы миллионов, десятки миллионов, сотни миллионов образуют III класс – класс миллионов.
Единицы миллиардов, десятки миллиардов, сотни миллиардов образуют IV класс – класс миллиардов.
При чтении числа, записанного вне таблицы, удобнее сначала выделить все классы: для этого необходимо разбить число на группы по три цифры справа налево, а затем прочитать слева направо группы из трех цифр добавив название класса.
Например:
9 876 543![]()
![]()
![]()
В записи числа справа налево выделяем по три цифры, а затем читаем слева направо, называя классы.
Девять миллионов восемьсот семьдесят шесть тысяч пятьсот сорок три.
9
876 543 210![]()
![]()
![]()
![]()
Девять миллиардов восемьсот семьдесят шесть миллионов пятьсот сорок три тысячи двести десять
На письме при записи многозначного числа принято делать разрядку (промежуток) между классами.
Правило записи многозначных чисел: многозначные числа записывают по классам, начиная с высших. Чтобы записать цифрами число, например, двенадцать миллионов четыреста пятьдесят одна тысяча семьсот сорок два, поступают так: записывают группами единицы каждого названного класса, отделяя один класс от другого небольшим промежутком (разрядкой): 12 451 742.
Если отсутствуют разряды в записи натурального числа, то вместо них записываем нули.
Любое натуральное многозначное число можно представить в виде суммы разрядных слагаемых.
Число 98 523 (девяносто восемь тысяч пятьсот двадцать три) содержит девять десятков тысяч, восемь единиц тысяч, пять сотен, два десятка, три единицы. Его можно записать в виде суммы:98 523 = 90 000 + 8 000 + 500 + 20 +3.
Выполним несколько тренировочных заданий
1. Какое число читается так: «Семь миллионов пять тысяч восемьсот один»?
-
7581
-
7005801
-
7500801
-
7000005801
Правильный вариант/варианты: 2
2. Впиши результат
вычисления![]()
7000 000 + 800 000 + 1 000 + 9 =
30
000 000 + 300 000 + 300 =![]()
Правильный вариант/варианты:
7 801 009 30 300 300
Необходимо запомнить
ВАЖНО!
10 сотен тысяч составляет 1 тысячу тысяч, или 1 МИЛЛИОН. Миллион записывают так: 1 000 000. Миллион - это единица третьего класса. В классе миллионов три разряда: единицы миллионов, десятки миллионов, сотни миллионов.
10 сотен миллионов составляет 1 тысячу миллионов, или 1 МИЛЛИАРД. Миллиард – единица четвертого класса. В классе миллиардов тоже три разряда.
Гугол и математика
Действительность с многозначными числами касается и современных технологий. Например, Google – одна из известных поисковых систем. Её придумали Сергей Брин и Ларри Пейдж. Название данной поисковой системы было выбрано не случайно. Её разработчики захотели показать то количество информации, которое система может обработать. В математике число, которое состоит из единицы и ста нулей, называется «гуго́л».
Вставьте пропущенные слова.
Число, в записи которого используют единицу с
шестью нулями, называется ![]() .
.
Класс тысяч образуют ![]() ,
, ![]() ,
, ![]() .
.
Числовой ряд
Расставьте числа в порядке возрастания.
32 008
1 258 067
230 250
4 006
204 500

Урок 12. Единица длины — километр. Таблица единиц длины
Цель:
узнать единицу измерения - километр.
Задача:
получить представление об использовании новой единицы измерения на практике.
Теоретический материал для самостоятельного изучения
Какие известны вам единицы измерения длины удобно использовать при измерении толщины спички?
 - миллиметр
- миллиметр
Какие единицы измерения длины удобно использовать при измерении длины карандаша?
 - сантиметр
- сантиметр
А при измерении ширины окна?
 - дециметр
- дециметр
А если нужно измерить длину коридора? Какие единицы длины вы будете использовать?
 - метр
- метр
Какими единицами измерения удобнее пользоваться для определения расстояния между городами?
 -
- 
Для измерения больших расстояний используют более крупную, чем метр, единицу длины – километр. Первая часть слова «кило» - обозначает «тысяча». Километр – мера длины, равная 1000 м. Слово «километр» сокращённо записывают двумя буквами «ка», «эм». Точка после буквы «эм» не ставится. Теперь вы знаете, что в 1километре тысяча метров, в 1 метре 10 дециметров, в 1дециметре 10 сантиметров, в 1сантиметрн 10 миллиметров.
Таблица единиц длины
1 км = 1000 м
1 м = 10 дм
1 дм = 10 см
1 см = 10 мм
Задания тренировочного модуля:
1.Что не является единицей длины? Выберите правильный ответ.
миллиметр килограмм
километр сантиметр
Правильный ответ:
килограмм
2. Установите правильные соотношения:
1 км 10 дм
1 м 10 см
1 см 10 мм
1 дм 1000 м
Правильный ответ:
1 км 10 дм
1 м 10 см
1 см 10 мм
1 дм 1000 м
Необходимо запомнить
ВАЖНО!
Километр – это единица измерения длины. Этой единицей длины измеряют большие расстояния.
Километр – мера длины, равная 1000 м.
Историческая справка
Локоть и сажень – старые меры длины.
Локоть – длина от кончиков пальцев до локтя (от 38 см до 47 см).
Название "сажень" означает дотягиваться рукой. "Маховая сажень" – расстояние между раскинутыми в стороны руками мужчины (176 см).
Вёрстами измеряли большие расстояния. В разных частях России версту считали по-разному – от 500 до 750 сажен (1 км 67 м).
Спрятанные слова
Найдите и выделите цветом по вертикали или горизонтали слова по теме изучения:
1) километр;
2) длина;
3) расстояние.
|
л |
ч |
ж |
л |
е |
к |
м |
р |
х |
и |
л |
ё |
ж |
э |
ч |
|
в |
ю |
д |
т |
т |
и |
у |
а |
н |
и |
л |
д |
ш |
а |
ж |
|
х |
ж |
c |
ш |
з |
л |
э |
с |
щ |
ш |
б |
ы |
ю |
к |
т |
|
з |
ш |
ю |
ц |
я |
о |
л |
с |
ф |
м |
д |
э |
л |
к |
щ |
|
п |
ю |
ф |
б |
т |
м |
c |
т |
а |
ц |
л |
c |
в |
д |
ф |
|
р |
щ |
щ |
ж |
щ |
е |
c |
о |
д |
к |
и |
ю |
к |
й |
ю |
|
б |
а |
а |
ё |
ю |
т |
ц |
я |
р |
к |
н |
г |
л |
е |
г |
|
к |
п |
д |
й |
я |
р |
б |
н |
е |
з |
а |
т |
б |
ч |
в |
|
у |
ц |
ц |
c |
т |
е |
ё |
и |
ш |
щ |
о |
в |
й |
ф |
х |
|
р |
в |
й |
к |
м |
х |
c |
е |
э |
т |
о |
х |
т |
о |
г |
|
у |
ч |
а |
к |
л |
ё |
б |
и |
т |
у |
c |
д |
ю |
э |
щ |
|
й |
м |
е |
ш |
й |
в |
п |
и |
п |
ф |
ц |
т |
я |
э |
л |
|
р |
е |
я |
д |
ж |
ё |
м |
ф |
ё |
б |
з |
д |
т |
й |
х |
|
й |
ф |
р |
з |
о |
ю |
й |
е |
ч |
ч |
й |
й |
ц |
о |
е |
|
ю |
ё |
ц |
х |
ф |
и |
ж |
ш |
д |
и |
й |
ф |
а |
х |
х |
Перевод величин
Заполните пропуски.
2 км 5 м = ![]() м
м
106 000 м = ![]() км
км

Урок 13. Единицы площади — квадратный километр, квадратный миллиметр. Таблица единиц площади
Цель:
познакомиться с новыми единицами площади.
Задачи:
получить представление об использовании новой единицы измерения на практике;
научиться сравнивать значения площадей разных фигур.
Теоретический материал для самостоятельного изучения
Сегодня мы будем говорить о единицах измерения площади.
За единицу измерения площади принимается квадрат со стороной, равной единице измерения длины

Вы уже знакомы с такими единицами площади, как квадратный сантиметр, квадратный дециметр и квадратный метр. Квадратными сантиметрами мы измеряем площадь небольших предметов, таких, как тетрадь. Квадратными дециметрами можно измерить площадь парты. Квадратными метрами измеряют площадь помещений – комнат, коридоров, залов.



см2 дм2 м2
А если надо будет вычислить площадь какой-нибудь страны.
Например, вычислить площадь России.
Ведь наша страна очень большая, и если измерять её в квадратных метрах, получится число гораздо больше миллиона. А это очень неудобно.
Для измерения больших площадей используют квадратный километр. Это площадь квадрата, сторона которого равна 1 км. Слова «квадратный километр» при числе сокращенно записывают так:1 км2
В квадратных километрах измеряют площади государств; так Россия занимает площадь более 17000000 км2, а Франция - 551000 км2
Но иногда надо измерить площади очень маленьких предметов. Единица измерения маленьких площадей – это квадратный миллиметр. Квадратный миллиметр - это площадь квадрата, сторона которого 1 мм.
Обозначается он так: 1 мм2.
Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.

Для измерения площади земельных участков оказалось удобным ввести промежуточные единицы 1 ар и 1 гектар.
 1 ар - это квадрат со стороной 10 м, значит его
площадь равна
1 ар - это квадрат со стороной 10 м, значит его
площадь равна
1 а = 10 м ∙ 10 м = 100 м2.
Поскольку 1 ар равен 100 квадратным метрам, то эту единицу площади часто называют соткой.
1 гектар - это квадрат со стороной 100 м ,значит его площадь равна
1 га = 100м ∙ 100м = 10000м2
Вот теперь вы можете составить таблицу единиц площади. А помогут вам знание таблицы единиц длины и умение находить площадь квадрата.
1 см2 = 100 мм2
1 см2 = 10 мм2 ∙ 10 мм2 = 100 мм2
1 дм2 = 100 см2
1 дм2 = 10 см2 ∙ 10 см2 = 100 см2
1 м2 = 100 дм2
1 м2 = 10дм2 ∙ 10 дм2 = 100 дм2
1 дм2 = 10000 мм2
1 дм2 = 100 мм2 ∙ 100 мм2 = 10000 мм2
1 м2 = 10000 см2
1 м2 = 100см2 ∙ 100 см2 = 10000 дм2
Теперь внимательно рассмотрите таблицу и постарайтесь ее запомнить.
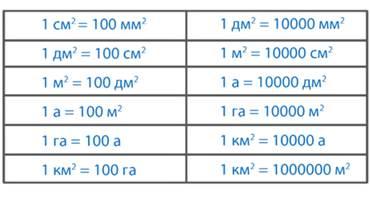
Задания тренировочного модуля:
1. Установите правильные соотношения
1 см2 100 дм2
1 м2 100 см2
1 дм2 1000000 м2
1 км2 100 мм2
Правильный ответ.
1 см2 100 дм2
1 м2 100 см2
1 дм2 1000000 м2
1 км2 100 мм2
2. Укажите какими единицами площади, ты будешь измерять
1. Площадь Евразии - квадратный__________________
2. Площадь цветка незабудки - квадратный___________
3. Площадь тетради – квадратный __________________
Правильный ответ.
1. Площадь Евразии - квадратный километр
2. Площадь цветка незабудки - квадратный миллиметр
3. Площадь тетради – квадратный сантиметр
Подчеркните запись, в которой допущена ошибка.
1. 30 дм2 = 3000 см2
2. 16 м2 = 1600 дм2
3. 5 км2 = 500000 м2
4. 60 см2 = 6000 мм2
Единицы площади
Укажите, какими единицами площади вы будете измерять:
1. Площадь Евразии –
квадратный ![]() .
.
2. Площадь цветка незабудки –
квадратный ![]() .
.
3. Площадь тетради –
квадратный ![]() .
.

Урок 14. Измерение площади фигуры с помощью палетки
Цель:
научиться определять площадь с помощью палетки.
Задача:
научиться определять площади фигур произвольной формы, используя палетку.
Теоретический материал для самостоятельного изучения
Вычислите площадь прямоугольника, если известно, что его длина равна 8см, а ширина 5см.
Вы уже знаете, чтобы найти площадь прямоугольника, нужно длину умножить на ширину. S= 8 ∙ 5 = 40 см2
А теперь попробуйте вычислить площадь данной фигуры:
 -?
-?
Сегодня мы узнаем, что для нахождения площади фигур можно использовать палетку. Палетка – это прозрачная плёнка, которая может быть разбита на квадратные дециметры, квадратные сантиметры, квадратные миллиметры. Простейшая палетка - лист кальки, разделенный на квадратные сантиметры. Палетку используют для измерения площади фигур, ограниченных кривой линией.
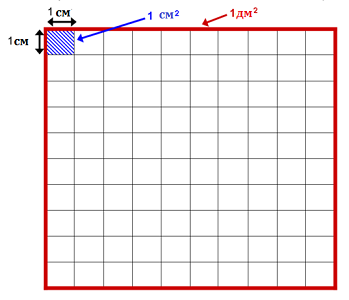
Чтобы найти площадь данной фигуры, нужно:
1) На данную фигуру наложить палетку. Не сдвигать!
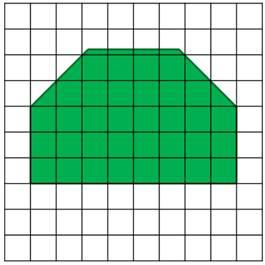
2)Сосчитать, сколько целых клеток- квадратных единиц - содержится в фигуре.
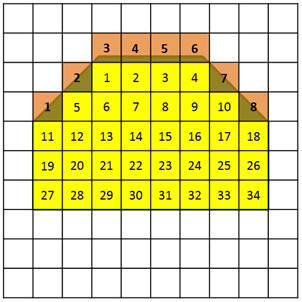
Целых 34 клетки.
3) Сосчитать, сколько нецелых квадратных единиц содержится в фигуре.
Неполных 8 клеток.
4) Количество нецелых квадратных единиц разделить на 2, примерно столько целых квадратных единиц они образуют.
8 : 2 = 4
5) Сложить числа, полученные в пунктах 2 и 4.
6) В ответе записать, что площадь фигуры приблизительно равна найденной сумме.
S = 34 + (8 : 2) = 38 см2
Ответ: S = 38 см2
Задания тренировочного модуля:
1. Определите, какая фигура имеет большую площадь, а какая - меньшую, и решите ребус соответствия.
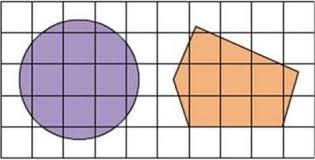
Правильный ответ: Прямоугольник – большую, круг – меньшую.
Сторона клетки фигуры на рисунке равна 1 см. Найдите её площадь и периметр.

Правильный ответ:
Площадь 7 см2
Периметр 12 см
Измерение площади фигуры
.Сторона клетки фигуры на рисунке равна 1 см. Найдите её площадь и периметр.

Площадь ![]() см2.
см2.
Периметр ![]() см.
см.

Урок 15. Единицы массы — центнер, тонна. Таблица единиц массы
Цель:
познакомиться с единицами массы: тонной, центнером.
Задачи:
получить представление об использовании новой единицы измерения на практике;
научиться переводить одни единицы массы в другие, используя соотношения между ними.
Теоретический материал для самостоятельного изучения
Когда мы берем в руки какой-либо предмет, то ощущаем его тяжесть. Величина, которая характеризует вес предмета ,называется массой.
Если нужно узнать массу одного зернышка, какой единицей массы вы воспользуетесь?

- грамм
А если нужно узнать массу мешка с зерном ?
 - килограмм
- килограмм
Ну, а если нужно узнать массу целой машины с зерном?

Для измерения массы больших грузов используют более крупные, чем килограмм, единицы массы- центнер и тонну.Слово тонна в переводе с греческого языка обозначает «бочка», а слово центнер-«весящий 100»
Слово центнер сокращенно записывают буквой «цэ», слово-тонна буквой «тэ» Точка при сокращении слова не ставится.
Если 1 грамм умножить на 1000, то получим кг. Поэтому 1кг = 1000г
Если 1кг умножить на 100, то получим 1 центнер. Поэтому 1ц =100кг.
Если 1ц умножить на 10, то получим 1 тонну. Поэтому 1т =10ц.
Если 1кг умножить на 1000, то получим 1тонну. Поэтому 1т-1000кг.
Таблица единиц массы:
-
-
1 кг = 1000 г
1 ц = 100 кг
1 т = 1000 кг
1 т = 10 ц
-
Задания тренировочного модуля:
1. Распределите рисунки по группам «Измерение массы в тоннах» и «Измерение массы в килограммах».






Правильный ответ:
-
-
Измерение массы в тоннах
Измерение массы в килограммах






-
2. Допишите пропущенные числа
2т 5ц = ______ кг
800 кг = ______ ц
4 кг 250 г = ______ г
3 ц 50 кг = ______ кг
Правильный ответ:
2 т 5 ц = 2500 кг
800 кг = 8 ц
4 кг 250 г = 4250 г
3 ц 50 кг = 350 кг
Перевод единиц массы
Допишите пропущенные числа.
2 т 5 ц = ![]() кг
кг
800 кг = ![]() ц
ц
4 кг 250 г = ![]() г
г
3 ц 50 кг = ![]() кг
кг

Урок 16. Единицы времени. Сутки. Задачи на нахождение начала, продолжительности и конца события
Цель:узнать единицу времени – сутки.
Задачи: повторить изученные единицы времени;
составить таблицу единиц времени.
Теоретический материал для самостоятельного изучения
Отгадайте ребус и вы узнаете тему урока.
С

 - сутки
- сутки
Вы уже знаете некоторые единицы времени. Например, год. В году 12 месяцев. Это 365 дней в обычном, или 366 в високосном году. Более крупная единица времени, чем год - век. Век равен 100 годам.

Более мелкой единицей времени служит месяц - промежуток времени, близкий к периоду обращения Луны вокруг Земли.
Один месяц - это 30 или 31 сутки (в феврале 28 или 29 суток).

А что же такое сутки?
Су́тки — единица измерения времени, приблизительно равная периоду обращения Земли вокруг своей оси. Сутки делятся на 24 часа и условно делятся на четыре характерных интервала — утро, день, вечер и ночь.
Сутки – это день и ночь. Говорят, что сутки прошли, если прошли день и ночь. Но отсчитывать время днём и ночью можно только в жизненных ситуациях, а если речь идёт о математической точности, то здесь нужен специальный прибор, который измеряет время. Этим прибором являются часы.

Вы знаете, что в сутках 24 часа. Но на циферблате часов стоят числа от 1 до 12. Поэтому иногда нужно уточнять, 3 часа дня или 3 часа ночи.
Начало суток - 0 часов. От 0 часов до 12 часов проходит первая половина суток, через час после 12 часов дня буде 13 часов (или 1 час дня).
Век, год, месяц, неделя, сутки, час, минута, секунда - всё это единицы измерения времени.
Год, месяц и сутки были взяты из природы, а час, минута, секунда - придуманы человеком.
Для решения задач на определение начала, продолжительности и конца событий, необходимо помнить некоторые правила:
1) Чтобы найти длительность события, надо из конца вычесть его начало.
2) Чтобы найти начало события. Нужно из конца вычесть его длительность.
3) Чтобы найти длительность события, надо к началу прибавить его длительность.
Задания тренировочного модуля:
1. Решите задачи, пользуясь правилом.
А) Экскурсия в музее началась в 11 ч. и продолжалась 1 ч. 40 мин. Когда экскурсия закончилась?
Решение:__________
Ответ: экскурсия закончилась________
Б) Фильм начался в 12 ч., а закончился в 13 ч. 30 мин. Сколько длился фильм?
Решение:_____________
Ответ: фильм длился________
В) Урок длился 45 мин. и закончился в 11 ч. 20 мин. В котором часу начался урок?
Решение:________
Ответ: урок начался______
Правильный ответ:
А) Решение:11 ч. + 1 ч. 40 мин. = 12 ч. 40 мин.
Ответ: экскурсия закончилась в 12 ч. 40 мин.
Б) Решение: 13 ч. 30 мин. - 12 ч. = 1 ч. 30 мин.
Ответ: фильм длился 1 ч. 30 мин.
В) Решение: 11 ч. 20 мин. – 45 мин. = 10 ч. 35 мин.
Ответ: урок начался 10 ч. 35 мин.
2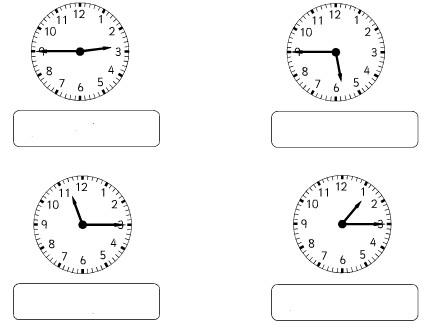 . Какое
время показывают часы? Заполните окошки. Напишите два варианта – до
полудня и после полудня.
. Какое
время показывают часы? Заполните окошки. Напишите два варианта – до
полудня и после полудня.

Правильный ответ:
1) 2:45 или 14:45 2) 5:45 или 17:45
3) 11:15 или 23:15 4) 1:15 или13:15
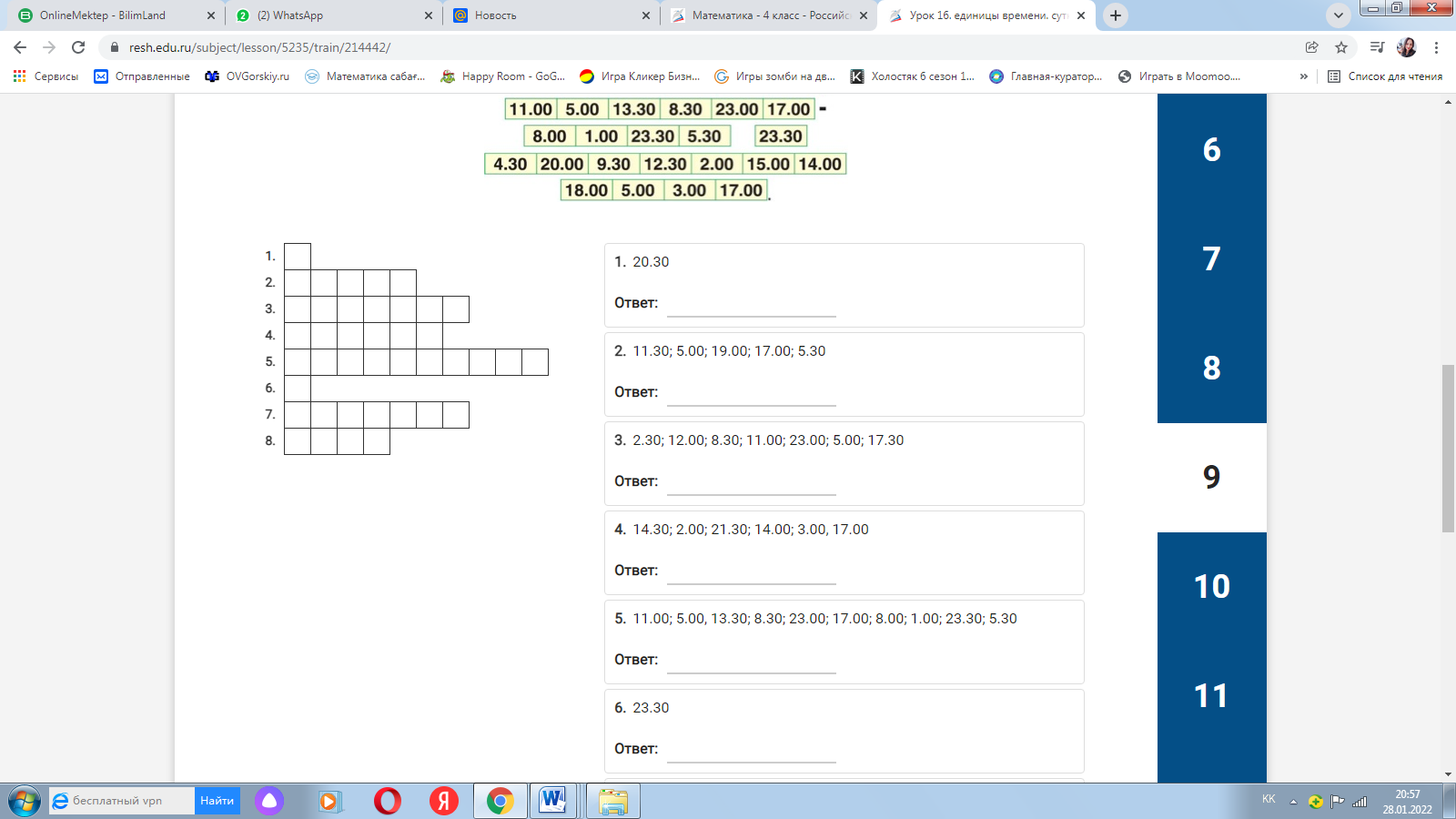
Определение времени по часам
Расшифруйте: какому значению времени соответствуют буквы и прочитайте крылатую фразу.


Урок 17. Единицы времени — секунда, век. Таблица единиц времени
Цель:
изучить новые единицы времени.
Задачи:
применять соотношения единиц времени в вычислениях;
сравнивать продолжительность событий.
Теоретический материал для самостоятельного изучения
Назовём:
Единицу времени больше часа: год, месяц, неделя, сутки.
Единицу времени меньше часа: минута.
Минута составляет 1/60 часа.
Выразим
2 часа=120 минут;
1 час 40 мин=100минут;
2 часа 30 мин=150 мин;
½ ч = 30 мин;
¼ ч = 15 мин;
1/3 ч = 20 мин
Как называется 1/60 минуты?
С помощью какого прибора измеряют время в этих единицах?
Есть единица времени, которая меньше минуты. Это секунда. На некоторых часах, кроме часовой и минутной стрелки, есть и маленькая стрелка, которая движется по своему маленькому циферблату. Эта стрелка отсчитывает секунды.
Секунда – это единица времени, равная одной шестидесятой минуты.
1/60 мин = 1 с
Сейчас на часах 12 часов 47 минут. За одну минуту секундная стрелка сделает полный оборот, т. е. отсчитает 60 секунд. Часы покажут 12 часов 48 минут.

За 1 секунду можно сделать 1-2 шага. Примерно с периодом 1 секунда бьётся пульс человека.
В математике существует соотношение величин времени, которое показывает их количественную взаимосвязь. Необходимо запомнить:
1 мин = 60 с
1 ч = 60 мин = 3 600 с
Обозначается секунда буквой «эс» без точки.
Например: 1 с, 30 с, 9 мин 45 с, 600 с.
Прибор для измерения самой маленькой единицы времени называют секундомер.

С помощью него учитель проверяет у вас технику чтения. На физкультуре при помощи этого прибора у вас определяют время пробега на дистанциях.
Мы с вами познакомились с самой маленькой единицей времени, а теперь поговорим, о самой большой единице времени.
Это – век, или столетие.1 век равен ста годам. Необходимо запомнить:
1 в = 100 г
Много веков назад люди договорились об условной точке отсчёта времени.

Обозначим её красной вертикальной линией. (Её наличие не говорит о том, что до этого момента ничего не происходило). Мы говорили о годах нашей эры и годах до нашей эры. Годы принято обозначать арабскими цифрами. Века – римскими цифрами.
Первый век продолжался с первого по сотый год. В сто первом году начался и в двухсотом закончился второй век. И так далее.
Теперь давайте покажем часть луча, который охватывает ближайшие к нам века.

31 декабря в тысяча девятисотом году закончился девятнадцатый век.
А 31 декабря в двухтысячном году закончился двадцатый век.
1 января две тысячи первого года и продолжается сегодня двадцать первый век.
Да, ребята! Мы живем в двадцать первом веке.
Веками измеряются длительные периоды в истории городов, стран, жизнь некоторых деревьев и животных.
Выразим в секундах:
1 мин 30 с = 90 с
1 мин 5 с = 65 с
½ мин = 30 с
¼ мин =15 с
2 ч – 7200 с
Определим век по году:
В 1147 году по приказу князя Юрия Долгорукова была основана Москва. Какой это был век? (Одна тысяча сто сорок седьмой год относится к двенадцатому веку)
Московский университет открылся в 1755 году, определите век. (Одна тысяча семьсот пятьдесят пятый год - это восемнадцатый век)
Победа в Великой Отечественной войне произошла в 1945 году, назовите век. (Одна тысяча сорок пятый год – это двадцатый век)
Сколько веков существует столица нашей Родины? (Сейчас идет двадцать первый век, Москва основана в двенадцатом веке, значит, столица существует уже девять веков)
Решим задачу:
Мальчик добежал от дома до станции за 20 мин. Обратно он шёл медленно, и на тот путь ему потребовалось 1 800 с. На сколько больше минут мальчик затратил на обратный путь?
Сразу ответить на вопрос задачи нельзя, нужно секунды перевести в минуты, т.е. сравнивать одинаковые единицы измерения.
1800 с = 1800 : 60 = 30 мин
30 мин > 20 мин
30 – 20 = 10 мин
Ответ: на 10 мин больше мальчик затратил на обратный путь
Вывод:
Ответим на вопросы, поставленные в начале урока.
Секунда – это единица времени, равная одной шестидесятой минуты.
1/60 мин = 1 с
1 мин = 60 с
1 ч = 60 мин = 3 600 с
Прибор для измерения самой маленькой единицы времени называют секундомер.
Век (столетие) – единица времени, равная 100 годам.
Выполним несколько тренировочных заданий.
1. Сколько секунд составляют 2 мин 30 с? Подчеркни верный ответ
-
-
□ 230 с
□ 120 с
□ 150 с
-
Решение:
-
-
□ 230 с
□ 120 с
□ 150 с
-
2.Укажи верную запись.
-
□ 4 мин 50 с = 450 с
-
□ З ч < 200 мин
Решение:
-
□ 4 мин 50 с = 450 с
-
⊗ З ч < 200 мин
3.Решим задачу
Громозека прочитал страницу книги за 1 мин 15 с, а Алиса за 45 с. Кто дольше читал эту страницу и на сколько?
Сразу ответить на вопрос задачи нельзя, нужно минуты перевести в секунды, т.е. сравнивать одинаковые единицы измерения.
1мин 15 с = 75 с
75 с >45 с
75-45=30(с)
Ответ: Громозека читал эту страницу на 30 секунд дольше.
Единицы времени
Вставьте слова в пословицы и поговорки, заменяя выделенные числа на единицы времени.
100 лет живи, 100 лет учись.
![]() живи,
живи, ![]() учись.
учись.
Обещанного 36 месяцев ждут.
Обещанного ![]() ждут.
ждут.
Делу время, а потехе 60 минут.
Делу
время, а потехе ![]() .
.
7 дней 12 месяцев кормит.
![]()
![]() кормит.
кормит.
Действия с единицами времени
Выполните вычисления и заполните пропуски верными значениями величин.
2 ч - 30 мин = ![]()
2 сут - 20 ч = ![]()
3 мин - 54 с = ![]()
1 век - 32 года = ![]()

Урок 18. Повторение пройденного по теме «Величины»
Цель: повторение знаний, умений и навыков о величинах.
Задачи: закрепить представления о величинах;
применять знания о величинах при вычислениях.
Теоретический материал для самостоятельного изучения
Назовём известные величины: длина, площадь, масса, время.
Называют их величинами, потому, что их можно измерить, сравнить и результат выразить числом.
Выполним задание:
Разбейте числа на две группы по определённому признаку.
43, 5 м 6 дм, 1001, 4 кг, 5 мин, 890, 10 с, 12, 6 кг, 2 т, 7 сут., 98, 120 г, 8 дм², 5 км, 1 ч 20 мин, 8 м², 1000 см², 555
Мы видим, что в этом ряду есть натуральные числа, которые являются результатом вычислений или счёта. И есть именованные числа, которые получают в результате измерения величин и сопровождающих названием единиц измерения.
Группу именованные числа можно разбить на несколько групп по признаку разных величин. Единицы измерения нам укажут на величину, о которой идёт речь. Для этого нужно вспомнить единицы измерения величин.
Единицы измерения длины: км, м, дм, см, мм.
Единицы измерения времени: сутки, час, мин, сек.
Единицы измерения массы: т, ц, кг, г.
Единицы измерения площади: м2, дм2, см2.
Для измерения величин используют различные инструменты и приборы.
-
Величины
Длина
Площадь
Масса
Время
Измерительные приборы

 формулы
формулы

Единицы измерения
мм, см, дм, м, км
мм², см², дм², м²
г, кг, ц, т
с, мин, ч
Надо всегда помнить одно правило – сравнивать, складывать и вычитать можно только именованные числа с одинаковыми единицами (мерами). Для этого нужно помнить соотношения единиц измерения величин.

Сравним:
555м * 5 км
Для того, чтобы сравнить длину, нужно выразить в одни и те же единицы.
5км = 5000 м
555м < 5 км
8 м² * 80 дм², переведём 8 м² = 800 дм²
8 м²> 80 дм²
4 кг30 г * 5100 г, переведем 4 кг30 г = 4030 г
4 кг30 г < 5100 г
100 мин * 1 ч 40 мин, переведём 1 ч 40 мин = 100 мин
100 мин = 1 ч 40 мин
Решим задачу:
Длина тела кита 26 м, а тюленя – 20 дм. Во сколько раз тюлень короче кита?
26 м = 260 дм
260 : 20 = 13 раз
Ответ: в 13 раз длина тюленя короче длины кита.
Вывод:
Таким образом, длина, площадь, масса и время – это величины.
Величину можно измерить, сравнить и результат представить в виде числа.
Единица измерения – это величина, в которой выражаются другие, однородные с ней величины. При письменных вычислениях значения величин выражают в одних и тех же единицах измерения и выполняют действия с ними так же, как с числами.
Выполним несколько тренировочных заданий.
1. Выберите и отметьте столбик, где написаны только единицы измерения длины:
а) миллиметр б) дециметр в) минута
грамм сантиметр тонна
километр миллиметр дециметр
сутки километр секунда
дециметр метр километр
Ответ: б
2. Выберите вариант, где единицы массы расположены в порядке возрастания:
а) 3000 г, 30ц, 300 кг, 30 т, 3кг 3г.
б) 30т, 30 ц, 3кг 3г, 300кг, 3000 г.
в) 3000г, 3 кг 3г, 300кг, 30ц, 30т.
Ответ: в
3. Выберите ошибочный ответ:
а) Кирпич массой 5 граммов
б) В пакете 5 килограммов конфет
в) На уроке физкультуры мы пробежали 100 метров
Ответ : а
4. Найдите ошибку при переводе величин:
5. а) 2м 3дм = 230 см б) 2м 3дм = 23 дм в) 2м 3дм = 203см
6. а) 8000кг = 8т б) 8000 кг = 800000г в) 8000 кг = 80ц
7. а) 2 ч = 120 мин б) 2ч = 200 мин в) 2ч = 7200с
Ответ: в) 2м 3дм = 203см
Действия с величинами
Преобразуйте величины.
1. 4 км 125 м + 46
км 85 м = ![]() км
км ![]() м
м
2. 7 т 2 ц 66 кг – 5
ц 93 кг = ![]() т
т ![]() ц
ц ![]() кг
кг
3. 2 мин 20 с – 1
мин 30 с = ![]() мин
мин ![]() с
с

Урок 19. Устные и письменные приёмы вычислений
Цель:
изучение вычислительных приёмов с многозначными числами.
Задача:
научиться применять алгоритм вычислений.
Теоретический материал для самостоятельного изучения
Рассмотрим выражение
164 + 45 + 36 + 355
Для быстрого вычисления нужно вспомнить свойства сложения переместительное и сочетательное.
Переместительное свойство подсказывает, что от перестановки слагаемых сумма не изменяется.
А в сочетательном свойстве говорится, что два соседних слагаемых можно заменить их суммой.
Воспользуемся этими свойствами.
164 + 45 + 36 + 355 = (164 + 36) + (355 + 45) = 200 + 400 = 600
Если уметь применять свойства сложения, то значение выражений можно считать устно.
Но, конечно, не всегда удаётся устно выполнить вычисления. Ведь иногда надо выполнять их с многозначными числами. И тогда приходится пользоваться письменным приёмом вычисления. Вспомним алгоритм письменного сложения и вычитания трёхзначных чисел. Допустим, надо сложить числа четыреста шестьдесят пять и двести восемьдесят девять.
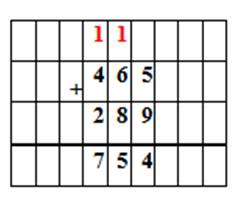
Числа записаны одно под другим, одинаковые разряды стоят строго друг под другом: единицы под единицами, десятки под десятками, сотни под сотнями. Выполняем вычисления с наименьшего разряда. Складываем единицы. Пять плюс девять – четырнадцать. Четыре пишем под единицами, а один десяток добавляем к десяткам.
Складываем шесть десятков и восемь десятков – четырнадцать. Да ещё десяток – пятнадцать десятков. Это пять десятков и одна сотня, которую добавляем к сотням.
Складываем четыре и две сотни, да ещё одну сотню. Всего семь сотен. Ответ: семьсот пятьдесят четыре.
Ну а если бы надо было складывать не трёхзначные числа, а, например, пяти- или шестизначные?
Письменное сложение и вычитание любых многозначных чисел выполняется так же, как сложение и вычитание трёхзначных чисел.
Допишем в наших слагаемых цифры в классе тысяч.
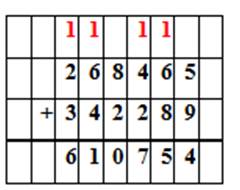
Теперь надо сложить шестизначные числа. Действие сложения с классом единиц в них уже выполнено. Продолжаем. Складываем единицы тысяч. Восемь и два – десять. Нуль пишем под единицами тысяч, единицу добавляем к десяткам тысяч. Складываем их. Шесть, четыре и один – одиннадцать десятков тысяч. Это одна сотня и один десяток тысяч. Один десяток тысяч пишем под десятками тысяч и одну сотню тысяч добавляем к сотням тысяч. Складываем их. Шесть. Читаю ответ: шестьсот десять тысяч семьсот пятьдесят четыре.
Ну что ж, надо проверить сложение. А проверяем сложение, естественно, вычитанием.
Из шестисот десяти тысяч семисот пятидесяти четырёх вычитаем триста сорок две тысячи двести восемьдесят девять.
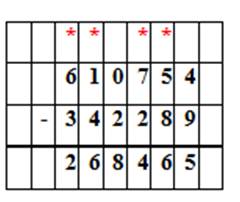
Так же, как при вычитании трёхзначных чисел, начинаем с наименьшего разряда – единиц. Четыре минус девять. Надо занять один десяток. Четырнадцать минус девять – пять.
Вычитаем десятки. Мы заняли один десяток. Их осталось четыре. Из четырёх восемь вычесть не можем. Занимаем одну сотню. Четырнадцать минус восемь – шесть. Вычитаем сотни. Точка подсказывает, что их на одну меньше. Шесть минус два – четыре.
Вычитаем единицы тысяч. Из нуля вычитать нельзя. Занимаем десяток тысяч и вычитаем из десяти. Десять минус два – восемь.
Вычитаем десятки тысяч. У нас был один десяток тысяч, но его заняли. Остался нуль. Занимаем сотню тысяч. Это десять десятков тысяч. Из них вычитаем четыре, получается шесть.
Вычитаем сотни тысяч. Точка подсказывает, что их осталось пять. Пять минус три равно два. Читаю ответ: двести шестьдесят восемь тысяч четыреста шестьдесят пять.
Разность такая же, как первое слагаемое примера на сложение. Значит, всё выполнено верно.
Необходимо запомнить: письменное сложение и вычитание любых многозначных чисел выполняется так же, как сложение и вычитание трёхзначных чисел.
Решим задачу:
Гуляя после уроков, мальчики и девочки произносят каждый день 11875 слов по делу, 5316 – со смыслом, 27981 – не задумываясь, а 379 слов лучше было бы вообще не произносить. Сколько всего слов в день говорят мальчики и девочки, гуляя после уроков?
Р ешение:
ешение:
11875 + 5316 + 27981 + 379 = 45551 (с.)
Ответ: 45551 слово всего говорят в день дети.
Вывод:
Если надо что-нибудь посчитать устно, то иногда это можно сделать быстрее и легче, пользуясь переместительным и сочетательным свойствами сложения.
При сложении и вычитании многозначных чисел числа записывают одно под другим, одинаковые разряды стоят строго друг под другом: единицы под единицами, десятки под десятками, сотни под сотнями. Выполняем вычисления с наименьшего разряда.
Письменное сложение и вычитание любых многозначных чисел выполняется так же, как сложение и вычитание трёхзначных чисел.
Проверяем сложение вычитанием, а вычитание сложением.
Выполним тренировочное задание.
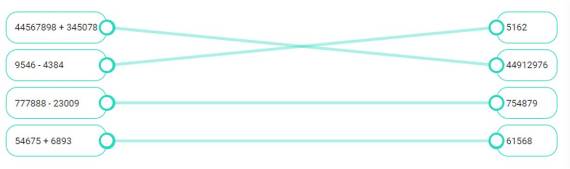
Проверка сложения вычитанием
Выполните вычисления и сделайте проверку. Ответы впишите в пропуски.
1) 39758 + 71396
= ![]()
проверка: ![]() - 39758 =
- 39758 = ![]()
2) 90859 + 81738
= ![]()
проверка: ![]() - 81738 =
- 81738 = ![]()

Урок 20. Вычитание с переходом через несколько разрядов вида 30 007 – 648
Цель:
познакомиться с приёмом вычитания, когда отсутствуют цифры в разрядах уменьшаемого.
Задачи:вычитать числа в пределах миллиона.
Теоретический материал для самостоятельного изучения
Вспомним десятичную систему счисления:
1 тыс. = 10 сот.
1 сот. = 10 дес.
1 дес. = 10 ед.
1 млн. = 10 сот. тыс.
1 сот. тыс. = 10 дес. тыс.
1 дес. тыс. = 10 ед. тыс.
1 дес. – 1 (Чтобы из 1 дес. вычесть единицу, заменим 1 дес. десятью единицами и вычтем 1из 10, получится 9)
1 сот. – 1 дес. ( изз 1 сот. вычесть 1 дес., заменим 1 сот 10 дес. и вычтем 1 дес. из 10, останется 9 дес., или 90)
1 тыс. – 1 сот. ( из 1 тыс. вычитаем 1 сотню, заменим 1 тыс. 10 сотнями и вычтем 1 сотню из 10, останется 9 сотен или 900)
Рассмотрим приём письменного вычисления (в столбик), из круглых чисел, используя занимание единицы через несколько разрядов. Запишите единицы под единицами, десятки под десятками.

Вычисляем десятки. Мы добавили к десяткам одну сотню, то есть десять десятков, но при этом заняли десяток, осталось 9 дес. Чтобы не забыть запишем наверху в разряде десятков цифру 9. 9 – 2 = 7
 Вычисляем сотни. Мы заняли одну сотню из шести,
поэтому записываем пять сотен. Итого результат вычисления равнее
574.
Вычисляем сотни. Мы заняли одну сотню из шести,
поэтому записываем пять сотен. Итого результат вычисления равнее
574.
 А
теперь попробуем рассмотреть особый случай вычитания: когда в
записи уменьшаемого есть несколько нулей. Обнаружилась проблема,
предыдущего алгоритма вычисления не хватает, т. к. приходится
занимать единицу через несколько разрядов и выполнять раздробление
в единицы низших разрядов не один раз. Запишем единицы под
единицами, десятки под десятками, сотни под
сотнями.
А
теперь попробуем рассмотреть особый случай вычитания: когда в
записи уменьшаемого есть несколько нулей. Обнаружилась проблема,
предыдущего алгоритма вычисления не хватает, т. к. приходится
занимать единицу через несколько разрядов и выполнять раздробление
в единицы низших разрядов не один раз. Запишем единицы под
единицами, десятки под десятками, сотни под
сотнями.
Из семи вычесть восемь нельзя, потому занимаем один десяток. Но единицы в разряде десятков отсутствуют, потому занимаем сотню. Отсутствуют сотни и отсутствуют единицы тысяч, потому занимаем один десяток тысяч.
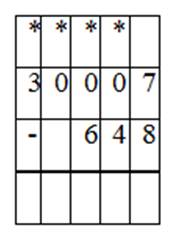
Один десяток тысяч – это десять единиц тысяч, можем занять одну тысячу. Одна тысяча – это 10 сотен, можем занять из сотен. Одна сотня – это десять десятков, теперь занимаем один десяток. Один десяток – это десять единиц да ещё 7. 17 – 8 = 9.
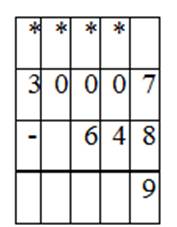
Вычисляем десятки. Мы добавили 10 десятков, но один заняли, чтобы не забыть, запишем наверху в разряде десятков цифру 9. 9 – 4 = 5 десятков.
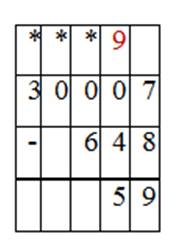
Вычисляем сотни. Мы добавили 10 сотен, но одну заняли, осталось 9. Чтобы не забыть, запишем наверху в разряде сотен цифру 9. 9 – 6 = 3 сотни.

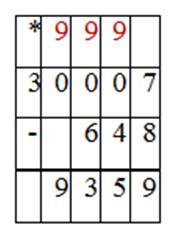
В ычисляем
единицы тысяч. Мы добавили 10 единиц тысяч, но одну заняли,
осталось 9 единиц тысяч. Чтобы не забыть, запишем наверху в разряде
единиц тысяч цифру 9. Переписываем 9, так как единицы тысяч в
вычитаемом отсутствуют.
ычисляем
единицы тысяч. Мы добавили 10 единиц тысяч, но одну заняли,
осталось 9 единиц тысяч. Чтобы не забыть, запишем наверху в разряде
единиц тысяч цифру 9. Переписываем 9, так как единицы тысяч в
вычитаемом отсутствуют.
Осталось два десятка тысяч, их переписываем. Итого результат вычисления равен 29 359.
Вывод: Ответим на вопросы, поставленные в начале урока. Десятичная система счисления – позиционная система счисления по основанию 10. Вычитание многозначных чисел с переходом через несколько разрядов надо выполнять поразрядно: из единиц – единицы, из десятков – десятки, из сотен – сотни, из тысяч – тысячи. При записи вычитания в столбик для памяти ставим точки над теми разрядами, которые подвергались дроблению (замена 1 единицы высшего разряда 10 единицами низшего соседнего разряда.).
Выполним несколько тренировочных заданий.
1. К каждой позиции первого столбика подберите соответствующую позицию второго:
Варианты ответов:
-
-
300 025 – 147 328
424 399
268 765 + 183 426
152 697
507 425 – 83 026
127 507
506 021 – 378 514
452 191
-
Правильный вариант/варианты:
-
-
300 025 – 147 328
152 697
268 765 + 183 426
452 191
507 425 – 83 026
424 399
506 021 – 378 514
7
-
Выполните вычисления:

Правильный вариант:
-
7 258 – 3 028 = 4 230
-
20 456 + 5703 = 26 159
-
93 698 – 542 = 93 156
-
121 212 + 434 343 = 555 555
Сложение и вычитание
Выполните вычисления:
7258 - 3028 = ![]()
20456 + 5703 = ![]()
93698 - 542 = ![]()
121212 + 434343 = ![]()
Восстановление последовательности чисел
Впишите пропущенное число:
740 000, 740 200, 740
400, ![]() ,
740 800, 741 000.
,
740 800, 741 000.

Урок 21. Решение уравнений
Цель: совершенствование умения решать составные уравнения.
Задачи:
решать уравнения новых видов;
объяснять выполнение действий при решении уравнений.
Теоретический материал для самостоятельного изучения:
Рассмотрите записи:
376 + 282; (х - у) : 3
Являются ли эти записи уравнениями?
Это не уравнения, так как в уравнении должен быть знак «=». Это выражения.
Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают латинской буквой.
Рассмотрите другие записи:
24 + х = 49; 24 + х = 79 - 30
Это уравнения, так как это равенства, содержащие переменную.
Попробуем их решить.
Что значит решить уравнение?
Решить уравнение – это значит найти значение неизвестного, при котором равенство будет верным.
Вспомните алгоритм решения уравнений.
Алгоритм:
-
Вспомнить компоненты действия данного уравнения.
-
Определить неизвестный компонент.
-
Вспомнить правило нахождения неизвестного компонента.
-
Применить правило и найти неизвестный компонент.
-
Записать ответ.
-
Сделать проверку
Используя алгоритм, решите первое уравнение
24 + х = 49
х = 49 - 24
х = 25
Значение неизвестного х = 25. Это корень уравнения.
Корень уравнения – это значение неизвестного, обозначенного латинской буквой в уравнении. В данном случае – это х.
Можно ли решить второе уравнение, используя этот же алгоритм?
Нет.
Такие уравнения не рассматривались. Какова же цель нашего урока?
Цель урока: научиться решать уравнения, в которых в ответе не число, а числовое выражение.
Такие уравнения мы будем называть составные. Поэтому тема урока: «Решение составных уравнений»
Чтобы решить это уравнение, нужно упростить правую часть.
24 + х = 79 - 30, после чего получаем уравнение известного вам вида
24 + х = 49
х = 49 - 24
х = 25
Проверка:
24 + 25 = 79 - 30
49 = 49
Ответ: корень уравнения 25
Составим алгоритм решения составных уравнений.
Алгоритм решения составных уравнений
1. Найти значение числового выражения.
2. Вспомнить компоненты действия данного уравнения.
3. Определить неизвестный компонент.
4. Вспомнить правило нахождения неизвестного компонента.
5. Применить правило и найти неизвестный компонент.
6. Записать ответ.
7. Сделать проверку.
Решим еще одно уравнение:
75 - х = 9 ∙ 7
Применяем алгоритм решения составных уравнений:
-
Найти значение числового выражения: 75 - х = 9 ∙ 7
75 - х = 63
-
Вспомнить компоненты действия данного уравнения: 75 - х = 63


3. Определить неизвестный компонент.
Неизвестно – вычитаемое.
4. Вспомнить правило нахождения неизвестного компонента.
5. Применить правило и найти неизвестный компонент.
х = 75 - 63
6. Записать ответ.
х = 12
7. Сделать проверку.
75 - 12 = 9 ∙ 7
63 = 63
Ответ: корень уравнения 12
Вывод: чтобы решить составное уравнение, в которых в ответе не число, а числовое выражение, необходимо упростить правую часть ( т.е решить выражение), после чего получаем уравнение известного вам вида и решаем его, используя алгоритм решения уравнений.
Решим задачу, составив уравнение:
Сумма неизвестного числа и числа 390 равна произведению чисел 70 и 6. Найди это число.
1. Сумма неизвестного числа и числа 390 – обозначим неизвестное число переменной х, тогда получим х + 390
2. Произведение чисел 70 и 6: 70 ∙ 6
3. Получаем уравнение: х + 390 = 70 ∙ 6
Применяя алгоритм решения составных уравнений, решим его:
х + 390 = 70 ∙ 6
х + 390 = 420
х = 420 - 390
х = 30
Проверка:
30 + 390 = 70 ∙ 6
420 = 420
Ответ: неизвестное число - 30
Компоненты сложения
Заполните пропуски в таблице:
|
слагаемое |
3 |
62 |
|
|
|
1017 |
|
слагаемое |
|
|
24 |
179 |
75 |
|
|
сумма |
7 |
82 |
76 |
964 |
523 |
8192 |
20/7175/785/448/4/52

Урок 22. Нахождение нескольких долей целого. Задачи разных видов
Цель: научиться находить несколько долей целого.
Задачи:
изучить и применять алгоритм нахождения нескольких долей целого.
Теоретический материал для самостоятельного изучения
Начертим в тетради отрезок длиной 12 см.
Нам
надо узнать, сколько см в ![]() отрезка. Сначала разделим отрезок на
4
отрезка. Сначала разделим отрезок на
4
равные части. Как назвать каждую часть? (Одна четвертая часть.)
Сколько см в ![]() отрезка? (3 см)
отрезка? (3 см)
Как узнали? (12 : 4 = 3)
Покажите на
чертеже ![]() отрезка. Проводят сверху дугу и
подписывают
отрезка. Проводят сверху дугу и
подписывают ![]() .
.
Покажем ![]() отрезка.
отрезка.
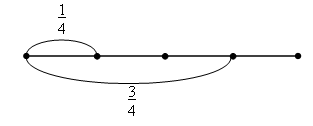
Как
узнать, сколько см в ![]() отрезка? (3 · 3 = 9
(см))
отрезка? (3 · 3 = 9
(см))
1)
12 : 4 = 3 (см) – ![]() отрезка
отрезка
2) 3 · 3 = 9 (см)
Решение можно записать выражением: 12 : 4 ∙ 3=9(см)
О т
в е т: 9 см в ![]() отрезка.
отрезка.
Решим задачу №291. Выполним чертеж,
покажем ![]() отрезка. Объясняем, как
получили
отрезка. Объясняем, как
получили ![]() отрезка. Как узнать, сколько мм
в
отрезка. Как узнать, сколько мм
в ![]() отрезка?
отрезка?
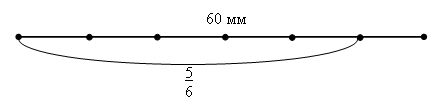
1)
60 : 6 = 10 (мм) – ![]() отрезка
отрезка
2) 10 ·5 = 50 (мм)
3) 60 : 6 ∙ 5= 50(мм)
О т
в е т: 50 мм в ![]() отрезка.
отрезка.
Вывод.
- Как же решать задачи на нахождение нескольких долей целого?
Надо найти величину одной доли целого и умножить на количество долей.
Составим алгоритм.
1. Разделить целое на равные части.
2. Умножить на количество, которое берём.
Выполним несколько тренировочных заданий
1. Найти числа 15 (9)
![]() числа 200 (90)
числа 200 (90)
![]() числа 18 (12)
числа 18 (12)
![]() от
числа 800 (560)
от
числа 800 (560)
![]() числа 50 (40)
числа 50 (40)
![]() от
числа 66 (44)
от
числа 66 (44)
![]() от
числа 300 (160)
от
числа 300 (160)
2. В четвёртых классах 75 учащихся. Из
них![]() – хорошисты. Сколько учащихся 4-х классов учатся
на 4 и 5?
– хорошисты. Сколько учащихся 4-х классов учатся
на 4 и 5?
75 : 5 ∙ 3 = 45 (уч.)
Ответ: 45 учащихся.
Задача № 293

1) 21 : 7 = 3 (кг) – за 1 день
2) 36 : 3 = 12 (д.) – хватит 36 кг
3) 3 + 1 = 4 (кг) – стали расходовать за 1 день
4) 36 : 4 = 9 (д.)
О т в е т: 12 дней, 9 дней
Доли величин
Выделите цветом правильные ответы.
2/3 от 60 - это: 40; 20; 10
3/4 суток - это: 12 часов; 18 часов; 10 часов.

Урок 23. Сложение и вычитание значений величин
Цель:познакомиться со способами сложения и вычитания величин.
Задачи:
выполнять преобразования и другие действия с величинами.
Теоретический материал для самостоятельного изучения
Рассмотрите выражения и найдите лишнее
5400 - 2300
6 см 8 мм + 40 см
524м 95см +29м 85см
- Лишняя запись: 5400 - 2300
- Почему? (Выражение не содержит величин.)
Какие действия с величинами мы уже умеем выполнять? (Сравниваем, преобразуем, вычитаем, складываем)
- Выполним вычисления.
С первым выражением мы легко справляемся, а вот второе вызвало затруднение. Почему? Первое мы посчитали устно, а второе в уме выполнить трудно.
- Какова же цель нашего урока? (Научиться складывать и вычитать величины, выраженные разными единицами)
Попробуем выполнить сложение письменно. Что для этого нужно сделать? ( Привести к одинаковым единицам)
524 м 95 см = 52 495 см
29 м 85 см = 2 985 м, запишем выражение в столбик и выполним сложение
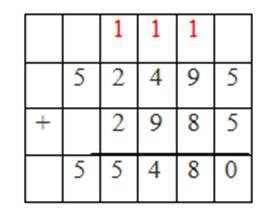
Получаем 55 480 см. Выразим результат в более крупных единицах 55480 см = 554 м 80 см, значит:
524 м 95 см +29 м 85 см = 554 м 80 см
Выполним вычитание
25 т 204 кг – 9 т 975 кг
Переведём величины в одинаковые единицы
25 т 204 кг = 25 204 кг
9 т 975 кг = 9 975 кг
Запишем выражение столбиком
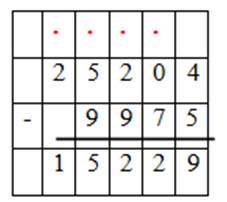
Получилось 15 229 кг. Переведём в более крупные единицы 15 229 кг = 15 т 229 кг, значит:
25 т 204 кг – 9 т 975 кг = 15 т 229 кг.
Составим алгоритм письменного сложения и вычитания величин:
-
Сначала надо привести величины к одной единице;
-
Сложить или вычесть столбиком, как обычные многозначные числа.
-
Перевести полученный результат в более крупные единицы.
Вывод 1: Величины с разными единицами складываются и вычитаются как обычные числа.
Попробуем решить ещё один пример:
5ч 23 мин + 12 кг 300 г
Этот пример не имеет решения, так как нужно сложить разные величины
Вывод 2: Выполнять действия можно только с однородными величинами.
Выполним несколько тренировочных заданий:
Решим задачу:
Расстояние между городами А и В - 368км 576м. За два часа автомобиль проехал 214 км 865м. Какое расстояние ему ещё нужно проехать, чтобы добраться до места назначения? Нарисуйте схему к задаче.
Решение: 368 км 576 м
А____________________________В
214км 865м – ?
368 км 576 м – 214 км 865 м = 368 576 – 214 865 = 153 711 (м)
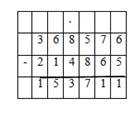
Ответ: осталось проехать 153 км 711 м
Запишите вычисления столбиком
12 м 86 см + 3 м 45 см = 16 м 31см
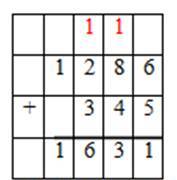
5 ч 48 мин + 35 мин = 383 мин = 6 ч 23 мин
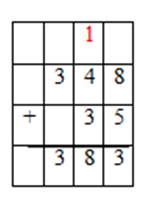
45 т 275кг – 18 т 130 кг = 27 т 145 кг

26 кг 350 г – 24 кг 002 г = 2 кг 348 г

Однородные величины
В каждом ряду подчеркните лишние величины.
1. 600 дм, 3 м 15 см, 1 см 5 мм, 1кг 200г, 12дм
2. 3 ч 15 мин, 2 сут 12 ч, 3 га, 24 мин 15 с, 1 нед
3
Урок 24. Задачи на увеличение (уменьшение) числа на несколько единиц, выраженных в косвенной форме
. 5 кг 120 г, 4 т 500 кг, 3 ц 25 кг, 6 км 125 м, 235 г
Цель:формирование умения решать задачи в косвенной форме.
Задача:
научиться распознавать задачи нового вида среди других задач.
Теоретический материал для самостоятельного изучения
Рассмотрим рисунок 1:
-
-







 На 5 >
На 5 >?
-
Рис. 1. Иллюстрация к задаче
В первом ряду – 8 квадратов. Это на 5 больше, чем во втором ряду. Сколько квадратов во втором ряду – больше или меньше, чем 8?
Решение
Если в первом ряду больше на 5, то во втором ряду меньше на 5, а значит:
8 – 5 = 3 квадрата (рис. 2)
-
-







 На 5 >
На 5 >

 На 5 <
На 5 <
-
8 - 5 = 3
(Рис. 2. Иллюстрация к задаче)
Ответ: во втором ряду – 3 квадрата.
Рассмотрим новую задачу
В первом ряду – 5 треугольников. Это на 7 треугольников меньше, чем во втором ряду. Сколько треугольников во втором ряду – больше или меньше, чем 5?
Решение
Если в первом ряду треугольников меньше на 7, то
во втором – на 7 больше, а значит:
5 + 7 = 12 треугольников (рис. 3).
Ответ: 12 треугольников во втором ряду.
При решении следующих задач будет использован точно такой же ход рассуждений. Важно обращать внимание – большее или меньшее число требуется найти.
Задание
В спортивном отряде 16 девочек. Их на 7 больше, чем мальчиков. Сколько мальчиков в спортивном отряде?
Решение:
Слово «их» указывает на девочек. Если девочек на 7 больше, чем мальчиков, значит мальчиков – на 7 меньше, чем девочек. То есть, надо найти меньшее число:
16 – 7 = 9 (м.)
Ответ: в спортивном отряде 9 мальчиков.
Две задачи на сравнение
Задача 1.
У Пети есть марки с автомобилями и самолетами. Марок с автомобилями – 12. Марок с самолетами – на 4 больше, чем марок с автомобилями. Сколько марок с самолетами у Пети?
Задача 2.
У Пети есть марки с автомобилями и самолетами. Марок с автомобилями – 12. Их на 4 больше, чем марок с самолетами. Сколько марок с самолетами у Пети?
Эти задачи отличаются лишь одним предложением: в первой задаче сказано, что марок с самолетами на 4 больше, чем марок с автомобилями; во второй задаче – их на 4 больше, чем марок с самолетами.
Составим краткую запись.
Обозначим марки с автомобилями буквой А. Марки с самолетами - буквой С.
Задача 1
А. – 12 марок
С. –
? на 4 марки больше, чем А.
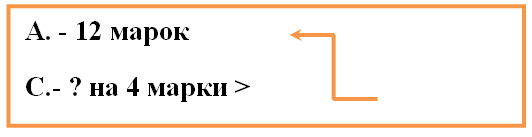
Найти надо большее число.
Решение:
12 + 4 = 16 (м.)
Ответ: у Пети16 марок с самолетами.
Задача 2
А. – 12 марок, на 4 марки больше, чем С.
С. – ?
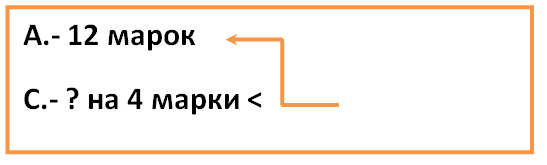
Значит, надо найти меньшее число.
Решение:
12 - 4 = 8 (м.)
Ответ: у Пети 8 марок с самолетами.
Вывод: Отличие второй задачи – в её решении, и оно вызвано тем, что слово «больше» относится к известному числу, а значит неизвестное число – меньшее.
Задание
Прочитайте задачу (№319 стр. 68) и назовите, большее или меньшее число надо найти, затем решите задачу.
Задание 2
В соседнем доме 12 этажей. В нем на три этажа больше, чем в нашем. Сколько этажей в нашем доме?
Решение
Слово «в нем» указывает на соседний дом. В нем на 3 этажа больше, а значит в нашем на 3 этажа меньше, чем в соседнем. То есть, надо найти меньшее число.
12-3=9 этажей
Ответ: 9 этажей в нашем доме.
Вывод
На уроке мы познакомились с решением задач на увеличение (уменьшение) чисел, выраженных в косвенной форме. Чтобы не ошибиться в выборе действия при решении задач, необходимо обращать внимание – большее или меньшее число нужно найти.Слова «это», «в нем», «их» – слова-помощники. Они помогают определить большее или меньшее число в задаче нужно найти.
Выполним несколько тренировочных заданий.
-
Решите задачу:
Брату 17 лет. Он младше сестры на три года. Сколько лет сестре?
Рассуждайте так: если брат младше, значит сестра старше. Старше –находим большее число.
Проверьте себя: 17 + 3 = 20 лет сестре
-
Папе 35 лет. Он старше мамы на 3 года. Сколько лет маме?
Рассуждайте так: если папа старше. Значит, мама младше. Младше – находим меньшее число.
Проверьте себя: 35 - 3 = 32 года маме.
Выбор выражения для решения задачи
Масса лошади 350 кг, а масса телёнка 100 кг. Масса овцы в 9 раз меньше, чем масса лошади и телёнка вместе. С помощью какого выражения можно узнать ответ? Подчеркните верное.
3
Урок 25. Письменные приёмы умножения
50 + 100 - 9; ( 350 + 100 ) : 9; 350 + 100 +9
Цель:познакомиться с письменным приёмом умножения многозначного числа на однозначное.
Задача: научиться применять алгоритм умножения.
Теоретический материал для самостоятельного изучения
В предыдущих уроках было изучено умножение трёхзначных чисел на однозначное «столбиком». Вспомним письменный приём умножения трёхзначного числа на однозначное, 327 умножить на 2.
Записываем числа друг под другом, единицы под единицами.
-
-
3
2
7
х
2
-
Умножаем единицы 7 ∙ 2 = 14 это 1 дес. и 4 ед., 4 ед. пишем под единицами, 1 дес. запоминаем, его позже прибавим к десяткам.
-
-
1
3
2
7
х
2
4
-
Умножаем десятки 2 ∙ 2 = 4 дес. и прибавляем 1 дес., который получился при умножении десятков, получится 5. Записываем десятки под десятками.
-
-
1
3
2
7
х
2
5
4
-
Умножаем сотни 3 ∙ 2 = 6 сот. Подписываем сотни под сотнями. Получилось 654.
-
-
1
3
2
7
х
2
6
5
4
-
А теперь попробуем умножить четырёхзначное число на однозначное: 6 427 ∙ 3. Обнаружилась проблема, предыдущего алгоритма не хватает, т. к. первый множитель – многозначное число. Вывод: составить алгоритм письменного умножения многозначного числа на однозначное.
Записываем 3 под разрядом единиц многозначного числа.
-
-
6
4
2
7
х
3
-
Умножаем единицы 7 ∙ 3 = 21, записываем 1 под единицами, а 2 дес. запоминаем.
-
-
2
6
4
2
7
х
3
1
-
Умножаем десятки 2 ∙ 3 = 6 дес. плюс 2 дес. получится 8 дес., записываем под десятками.
-
-
2
6
4
2
7
х
3
8
1
-
Умножаем сотни 4 ∙ 3 = 12 сот., 2 записываю под сотнями, 1 запоминаю, пишем над единицами тысяч.
-
-
1
2
6
4
2
7
х
3
2
8
1
-
Умножаем единицы тысяч 6 ∙ 3 = 18, плюс 1, получится 19 ед. тыс. Записываем 9 под единицами тысяч, а 1 – под десятками тысяч. Получилось 19 281.
-
-
1
2
6
4
2
7
х
3
1
9
2
8
1
-
Познакомимся с приёмом письменного умножения, когда в записи первого множителя есть нули: 4 ∙ 21 803.
По переместительному свойству, при перемене мест множителей значение умножения не меняется, поэтому четыре умножить на двадцать одну тысячу восемьсот три равно двадцать одна тысяча восемьсот три умножить на четыре.
4 ∙21 803= 21 803 ∙ 4
Записываем 4 под разрядом единиц многозначного числа.
-
-
2
1
8
0
3
х
4
-
Умножаем единицы 3 ∙ 4 = 12, записываем 2 под единицами, а один десяток запоминаем.
-
-
1
2
1
8
0
3
х
4
2
-
Умножаем десятки 0 ∙ 4 = 0 дес. плюс 1 дес., получится 1 дес., записываю 1 дес. под десятками.
-
-
1
2
1
8
0
3
х
4
1
2
-
Умножаем сотни 8 ∙ 4 = 32 сот., 2 сот. записываем под сотнями, 3 запоминаем.
-
-
3
1
2
1
8
0
3
х
4
2
1
2
-
Умножаем единицы тысяч 1 ∙ 4 = 4 ед. тыс., плюс 3, получится 7 ед. тыс., пишем под единицами тысяч.
-
-
3
1
2
1
8
0
3
х
4
7
2
1
2
-
Умножаем десятки тысяч 2 ∙ 4 = 8 дес. тыс.Записываем 8 под десятками тысяч.
-
-
3
1
2
1
8
0
3
х
4
8
7
2
1
2
-
Получилось 87 212.
Рассмотрим использование приёмов при умножении величин: 2 км 175 м ∙ 6
В вычислениях значения величин принято выражать в одних единицах измерения, поэтому 2 км 175 м переводим в метры, получится 2 175 м.
Далее выполняем вычисления также, как умножение многозначного числа на однозначное:
-
-
1
4
3
2
1
7
5
х
6
1
3
0
5
0
-
Ответ: 13 050 м или 13 км 050 м.
Вывод: Таким образом, надо записать однозначное число под разрядом единиц многозначного числа. Потом умножить единицы и записать единицы под единицами, а десятки (если они есть) запомнить. Затем умножить десятки и прибавить количество десятков, которые запоминали. Записать десятки под десятками, а сотни (если они есть) запомнить. Аналогично умножить все разряды многозначного числа. Назвать число.
Выполним несколько тренировочных заданий:
-
Выберите правильный вариант вычисления:
Варианты ответов:
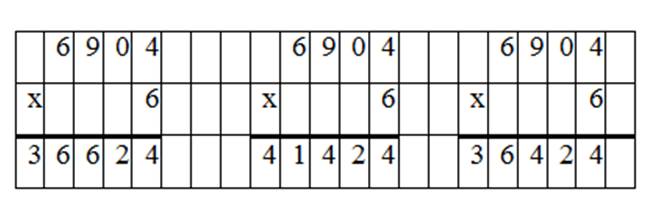
Правильный ответ:
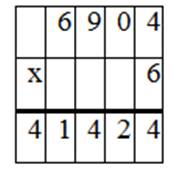
Заполните пропуски в таблице:
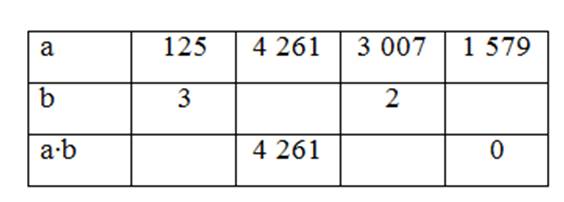
Правильный ответ:
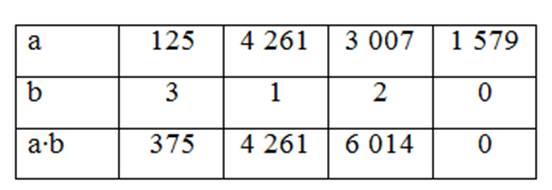
Решение примеров на умножение
Выполните вычисления, вставьте ответ.
8023 ∙ 4 = ![]()
34216 ∙ 2 = ![]()

Урок 26. Умножение чисел, оканчивающихся нулями
Цель: познакомиться с письменным приёмом умножения чисел, оканчивающихся нулями.
Задачи: применять алгоритм письменного умножения.
Теоретический материал для самостоятельного изучения
Рассмотрим выражение: 800 ∙ 7
Воспользуемся правилом умножения числа на произведение чисел, для этого заменим число 800 произведением чисел 8 и 100:
800 ∙ 7 = (8 ∙ 100) ∙ 7
При умножении произведения на число, сначала первый множитель умножаем на число(8 ∙ 7), а затем получившийся результат умножаем на второй множитель 100, ведь второй множитель - круглое число. Получим ответ 5 600.
800 ∙ 7 = (8 ∙ 100) ∙ 7 = (8 ∙ 7) ∙ 100 = 56 ∙ 100 = 5 600
Усложним задачу, решим следующее математическое выражение:
380 ∙ 9
Как и в предыдущем выражении, воспользуемся правилом умножения числа на произведение чисел, для этого заменим число 380 на произведение чисел 38 и 9:
380 ∙ 9 = (38 ∙ 10) ∙ 9
При умножении произведения на число, сначала умножаем на число первый множитель (38 ∙ 9), а затем получившийся результат умножим на второй множитель 10, ведь второй множитель – круглое число.
380 ∙ 9 = (38 ∙ 10) ∙ 9 = (38 ∙ 9) ∙ 10
Возникла проблема: надо умножить двузначное число на однозначное, подобного рода выражения в уме решить сложнее, т. к. увеличивается количество действий.
Сначала надо умножить единицы 8 ∙ 9 = 72. Затем десятки 30 ∙ 9 = 270, сложить полученные результаты и полученный результат умножить на десять 342 ∙ 10. Получили 3 420.
380 ∙ 9 = (38 ∙10) ∙ 9 = (38 ∙ 9) ∙ 10 = (8 ∙ 9 + 30 ∙ 9) ∙ 10 = 342 ∙ 10 = 3 420
Вывод: устно такие вычисления выполнять неудобно.
Рассмотрим письменный случай умножения, когда первый множитель заканчивается нулями: 8 400 ∙ 7 . Пишем однозначный множитель 7 под значимыми цифрами первого множителя.
-
-
8
4
0
0
х
7
-
Умножаем, не глядя на нули: 4 ∙ 7 = 28. Записываем 8 под цифрой 7, а 2 тыс. запоминаем.
-
-
2
8
4
0
0
х
7
8
-
Умножаем тысячи: 8 ∙ 7 = 56, и прибавим тысячи, которые запоминали: 56 + 2 = 58. Записываем 58 перед цифрой 8.
-
-
2
8
4
0
0
х
7
5
8
8
-
Приписываем столько нулей, столько в обоих множителях вместе. Ответ: 58 800.
-
-
2
8
4
0
0
х
7
5
8
8
0
0
-
Рассмотрим ещё один пример умножения, когда первый множитель заканчивается нулями: 30 800 ∙ 5.
Пишем однозначный множитель 5 под значимыми цифрами первого множителя.
-
-
3
0
8
0
0
х
5
-
Умножаем, не глядя на нули: 8 ∙ 5 = 40. Записываем 0 под цифрой 5, а 4 тыс. запоминаем.
-
-
4
3
0
8
0
0
х
5
0
-
Умножаем единицы тысяч: 0 ∙ 5 = 0 и прибавим тысячи, которые запоминали: 0 + 4 =4. Записываем 4 перед цифрой 0.
-
-
4
3
0
8
0
0
х
5
4
0
-
Умножаем десятки тысяч: 3 ∙ 5 = 15, записываем 15 перед цифрой 4.
-
-
4
3
0
8
0
0
х
5
1
5
4
0
-
Приписываем столько нулей, сколько нулей в первом множителе.
-
-
4
3
0
8
0
0
х
5
1
5
4
0
0
0
-
Ответ: 154 000
Вывод: Итак, чтобы умножить многозначные числа, оканчивающиеся нулём, на однозначные, надо записать второй множитель так, чтобы нули остались в стороне. Умножить многозначное число на однозначное, не обращая внимание на нули. К полученному результату приписать столько нулей, сколько их было в первом множителе, прочитать ответ.
Выполним несколько тренировочных заданий:
Выполнить вычисления, вставить ответ:
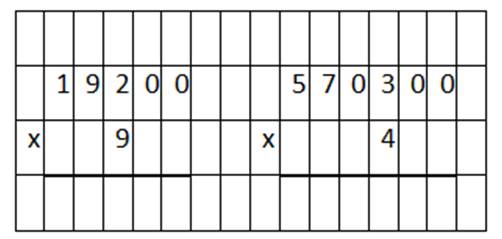
Правильный ответ:
19 200 · 9 = 172 800
570 300 ·4 = 2 281 200
Какое число нужно увеличить в 7 раз, чтобы получить 8 400? Выделите цветом правильный ответ:
Варианты ответов:
58 800
8 407
8 393
1 200
Правильный ответ:
1 200
К каждой позиции первого столбца подберите соответствующую позицию второго:
Варианты ответов: Правильный ответ:
-
-
6 700 ∙ 7
194 400
24 300 ∙ 8
254 800
53 780 ∙ 6
46 900
63 700 ∙ 4
322 680
-
|
6 700 ∙ 7 |
46 900 |
|
24 300 ∙ 8 |
194 400 |
|
53 780 ∙ 6 |
322 680 |
|
63 700 ∙ 4 |
254 800 |
Умножение чисел, оканчивающихся нулями
Выполните вычисления, вставьте ответы в пропуски:
19200 ∙ 9 = ![]()
570300 ∙ 4 = ![]()

Урок 27. Решение уравнений вида: х ∙ 8 = 26 + 70, х : 6 = 18 ∙ 5, 80 : х = 46 – 30
Цель: познакомиться с решением сложных уравнений.
Задачи:
повторить компоненты умножения и деления;
научиться решать уравнения нового вида.
Теоретический материал для самостоятельного изучения
Вспомните, как связаны между собой числа при умножении.
Посмотрите, множитель 20, множитель 3, произведение 60.
Если 60 разделить на 20, получится 3.
Если 60 разделить на 3, получится 20.
Значит, если произведение разделить на один из множителей, то получится другой множитель. Это правило потребуется при решении уравнений, в которых неизвестен один из множителей.
20 ∙ 3 = 60
60 : 20 = 3
60 : 3 = 20
Решим уравнение:
произведение неизвестного числа и числа 7 равно числу 91. В нем неизвестен первый множитель. Как его найти? Для нахождения неизвестного первого множителя надо произведение 91 разделить на известный множитель 7. Делим 91 на 7 - получаем 13. Выполним проверку. Подставим в уравнение вместо икс число 13.
13 умножить на 7 получим 91. Получили верное равенство:
91 равно девяносто одному. Значит, решили правильно.
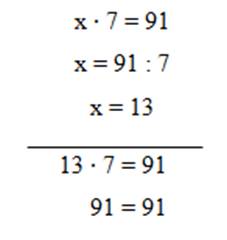
А теперь догадайтесь, как решить уравнение: произведение неизвестного числа и числа 7 равно сумме чисел восьмидесяти и одиннадцати. Найдем значение выражения в правой части уравнения: 80 плюс 11 равно 91. Тем самым мы получили уравнение, которое уже умеем решать. Посмотрите, как записывается решение этого уравнения и его проверка.
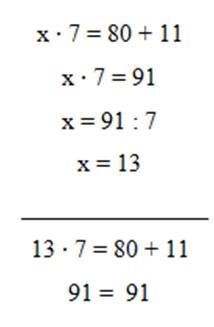
Вспомним, как связаны между собой числа при делении.
Посмотрите: делимое 15, делитель 3, частное равно пяти.
Если делитель 3 умножить на частное 5, получим делимое 15.
Если делимое 15 разделить на частное 5, получим делитель 3.
15 : 3 = 5
3 ∙ 5 = 15
15 : 5 = 3
Знание связей между делимым, делителем и частным потребуется для решения уравнений, в которых неизвестен один из компонентов: делимое или делитель. Посмотрите, как решаются такие уравнения. В первом уравнении неизвестно делимое. Чтобы его найти, нужно делитель 3 умножить на частное 9.
Во втором уравнении неизвестен делитель. Чтобы его найти, нужно делимое 45 разделить на частное 3.
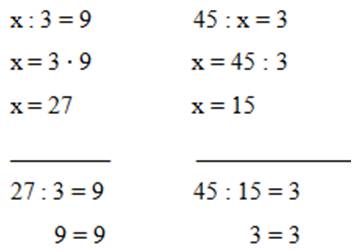
А как решить такое уравнение? Вычислим произведение в правой части: 18 умножить на 5 получим 90. Получается уравнение, в котором неизвестно делимое. Вы уже знаете, как его решать. Выполним проверку решения уравнения. Подставим число 540 вместо икс, вычислим левую часть и правую часть выражения: 90 равно 90. Значит уравнение решили верно.
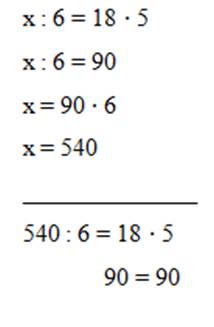
Задания тренировочного модуля:
1.К каждой позиции первого столбца подберите соответствующую позицию второго.
|
91 : х = 13 |
x = 20 |
|
х : 21=4 |
x = 7 |
|
24 ∙x = 96 |
x = 84 |
|
x∙ 3 = 60 |
x = 4 |
Правильный ответ:
-
-
91 : х = 13
x = 7
х : 21= 4
x = 84
24 ∙x = 96
x = 4
x∙3 = 60
x = 20
-
2. Выполните вычисления и выделите верный ответ:
7 ∙x = 140 : 2
Варианты ответов: 10, 400, 2
Правильный вариант:
10
3.Решите уравнение, подчеркните правильный ответ:
(80 : у) ∙ 700 = 2800
Варианты ответов:
2, 4, 20
Правильные варианты: 20
Математические термины
Найдите и выделите цветом слова по теме изучения.
Подсказка
Среди букв спрятались 4 слова.
|
о |
а |
ю |
л |
р |
у |
c |
к |
ы |
о |
|
о |
л |
щ |
й |
е |
ы |
х |
о |
щ |
ж |
|
ц |
г |
й |
c |
ш |
щ |
г |
р |
м |
б |
|
у |
о |
у |
о |
е |
ы |
й |
е |
о |
х |
|
п |
р |
э |
о |
н |
р |
у |
н |
а |
п |
|
е |
и |
б |
ё |
и |
е |
ц |
ь |
ю |
ц |
|
ы |
т |
c |
ю |
е |
у |
я |
ю |
у |
и |
|
э |
м |
ы |
б |
у |
к |
ф |
ц |
ц |
ю |
|
з |
е |
г |
к |
c |
р |
л |
п |
п |
р |
|
у |
р |
а |
в |
н |
е |
н |
и |
е |
о |

Урок 28. Деление
Цель: вспомнить письменное деление.
Задачи:
повторить действия с многозначными числами;
научить делению трёхзначного числа на однозначное.
Теоретический материал для самостоятельного изучения:
Вы уже умеете делить числа в столбик. Рассмотрим теперь более сложный случай.
Фермер Василий собрал в своем саду 372 кг вишни. Он и его 3 сына поделили ягоды поровну между собой и отправились на рынок. Сколько килограммов вишни должен продать каждый член семьи?


Начинаем деление с сотен. Сотен 3, но 3 сотни нельзя разделить на 4 так, чтобы в частном получились сотни. Делим десятки. Три сотни и 7 десятков – это 37 десятков. Делим 37 десятков на 4. В частном будет 9. Умножаем 9 на 4, чтобы узнать сколько десятков разделили. Получается, что разделили 36 десятков. Вычитаем из тридцати семи 36, получается 1. Значит, осталось разделить еще 1 десяток.
Переходим к делению единиц. Записываем две единицы рядом с остатком от деления десятков. 1десяток и 2 единицы – это 12 единиц. Делим 12 на 4, в частном 3. Умножаем 3 на 4, получаем 12. Вычитаем 12 из двенадцати. Осталось 0. Читаем ответ: 93.

Итак, важно запомнить: деление трехзначных чисел в столбик происходит поразрядно и начинается с высшего разряда. При нахождении каждой цифры частного, надо вспомнить три операции: деление, умножение и вычитание.
Рассмотрим еще один случай деления.
 Слив фермер собрал 621 кг. Поделил их между тремя
сыновьями и отправил их на рынок. Сколько килограммов слив должен
продать каждый сын?
Слив фермер собрал 621 кг. Поделил их между тремя
сыновьями и отправил их на рынок. Сколько килограммов слив должен
продать каждый сын?

Разделим 621 на 3. Начнем деление с сотен. Делим 6 сотен на 3, в частном будет 2 сотни. Умножаем 2 на 3, чтобы узнать, сколько сотен разделили. Получается, разделили 6 сотен. Вычитаем 6 из шести, получаем 0. Значит, все сотни разделили. Ноль не пишем. Приступаем к делению десятков. Записываем 2 десятка ниже. При делении числа 2 на 3 получается 0. Умножаем 0 на 3, чтобы узнать сколько десятков разделили. Получается, что разделили 0 десятков. Вычитаем из двух ноль. Получается 2. Нам по-прежнему осталось разделить 2 десятка. Переходим к делению единиц. Записываем единицу ниже рядом с остатком 2. Два десятка и одна единица – это 21 единица. 21 делим на 3. В частном получаем 7 единиц. Умножаем 7 на 3, чтобы узнать сколько разделили единиц. Вычитаем 21 из двадцати одного, чтобы узнать остаток от деления единиц. Остаток равен 0. Читаем ответ: двести семь.
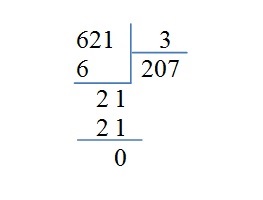
Задания тренировочного модуля:
1. Найдите значения выражения, считая устно или письменно:
268 : 2
Варианты ответов:
134
143
434
Правильный вариант:
134
2. Вставьте пропущенные знаки (> < =)
356 : 2 ∙ 972 : 4
Варианты ответов:
356 : 2 < 972 : 4
356 : 2 > 972 : 4
356 : 2 = 972 : 4
Правильный вариант:
356 : 2 < 972 : 4
Деление с остатком
Выполните вычисления.
Подсказка
Обратите внимание на точки и пробелы.
Пример: 10 : 9 = 1 (ост. 1)
56
: 15 = ![]()
92
: 30 = ![]()
399
: 9 = ![]()

Урок 29. Деление многозначного числа на однозначное
Цель: познакомить с делением многозначного числа на однозначное.
Задачи:
повторить арифметические действия;
научить делению чисел.
Теоретический материал для самостоятельного изучения:
Посмотрите на выражения. Что их объединяет? Это числовые выражения на действие деление, делитель – однозначное число. Как вы думаете, какое лишнее? Да, вы правы: второе выражение лишнее, потому что делимое – многозначное число. Мы еще не умеем решать такие выражения. Этому и предстоит нам научиться.
852 : 3, 7854 : 7, 768 : 8, 915 : 3
Давайте вспомним, как делить трехзначное число на однозначное. Разделим 852 на 3 столбиком. Начинаем деление с сотен – это первое неполное делимое: в частном будет три цифры. Делим 8 на 3, в частном будет 2 сотни. Умножаем 2 на 3, чтобы узнать сколько сотен разделили. Получается 6 сотен разделили. Вычитаем 6 из восьми, получаем 2. Столько сотен осталось. Сравниваем остаток 2 с делителем : 2 меньше трех, значит цифра в частном побрана верно. Сносим 5 десятков. Две сотни и пять десятков – это 25 десятков. Делим десятки на 3. В частном пишем цифру 8. Умножаем 8 на 3, получаем 24. Столько десятков разделили. Вычитаем 24 из двадцати пяти, остаток 1. Один меньше трех. Сносим единицы. Один десяток и две единицы – это 12 единиц. Делим на 3, берем по 4. Четыре умножаем на 3, получаем 12. Двенадцать вычитаем из двенадцати. Остаток 0. Деление завершили. Читаем результат: 284.
 Рассмотрим деление числа пяти тысяч пятьсот
сорока четырех на 6. Деление начинать надо с высшего разряда тысяч.
Но 5000 нельзя разделить на 6, чтобы в частном были тысячи. Поэтому
будем делить сотни.
Рассмотрим деление числа пяти тысяч пятьсот
сорока четырех на 6. Деление начинать надо с высшего разряда тысяч.
Но 5000 нельзя разделить на 6, чтобы в частном были тысячи. Поэтому
будем делить сотни.
55 сотен мы сможем разделить на 6 так, чтобы в частном получились сотни. В этом случае говорят 55 – это первое неполное делимое числа 5544. Посмотри, как можно его выделить. Теперь определим количество цифр в частном. Так как деление мы начали с сотен, в частном получим три цифры. Обозначим тремя точками места, где будем записывать цифры частного. Теперь находим первую цифру частного: для этого 55 делим на 6, получаем 9. Пишем 9 на месте сотен в частном. Умножаем 9 на 6, получаем 54. Столько сотен разделили. Записываем 54 под неполным делителем 55. Находим остаток, для этого вычитаем 54 из пятидесяти пяти. Получим 1. Столько сотен разделили. Теперь надо сравнить остаток с делителем: 1 меньше 6, значит цифра 9 в частном подобрана верно. Деление еще не закончено, так как можно образовать следующее неполное делимое из десятков. При делении сотен осталась 1 сотня, добавим еще 4 десятка. Всего 14 десятков. И повторяем все действия пункта по плану. Первые два пункта повторять не надо.
 Делим 14 на 6, получаем 2. Столько десятков будет
в частном. Умножим 2 на 6. Получаем 12. Столько десятков разделили.
Вычитаем 12 из четырнадцати, получаем 2. Столько десятков осталось
разделить. Сравниваем остаток с делителем: 2 меньше шести, значит
цифра 2 в частном побрана верно.
Делим 14 на 6, получаем 2. Столько десятков будет
в частном. Умножим 2 на 6. Получаем 12. Столько десятков разделили.
Вычитаем 12 из четырнадцати, получаем 2. Столько десятков осталось
разделить. Сравниваем остаток с делителем: 2 меньше шести, значит
цифра 2 в частном побрана верно.
Деление еще не закончено. Образуем следующее неполное делимое из единиц. При делении десятков осталось 2 десятка. Добавим 4 единицы, получаем 24 единицы. Делим 24 на 6, получаем 4 – столько единиц мы разделили. Запишем цифру 4 на месте единиц в частном. Умножаем 4на 6 , получаем 24. Столько единиц разделили. Вычитаем 24 из двадцати четырех. Осталось 0, он меньше делителя. Значит число единиц подобрано верно. Больше неполных делимых образовать нельзя. Значит деление завершено. Получили 924.
Задания тренировочного модуля:
1.Найдите значения выражения, считая устно или письменно:
6524 : 7
Варианты ответов:
1.842
2.934
3.932
Правильный вариант:
932
2. Выполните вычисления:
(17437 – 10297) : 7
Правильный вариант:
1020
3. Допишите предложения:
Чтобы найти неизвестный множитель, нужно…
Чтобы найти неизвестный делитель, нужно...
Правильные варианты:
1) произведение разделить на другой множитель
2) делимое разделить на частное
Порядок действий в числовых выражениях

Урок 30. Задачи на увеличение (уменьшение) числа в несколько раз, выраженные в косвенной форме
Цель: научить решать задачи на увеличение (уменьшение) в несколько раз в косвенной форме.
Задачи: познакомить учащихся с решением задач нового вида.
Теоретический материал для самостоятельного изучения
Решите задачу:
В 4 «а» классе 25 учеников, это на 1 ученика больше, чем в
4 «б» классе. Сколько учеников в 4 «б» классе?
Вспомнили, к какому типу относится эта задача? Верно: уменьшение числа на несколько единиц в косвенной форме. Давайте составим задачу с этими данными в прямой форме.
В 4 «а» классе 25 учеников, а в 4 «б» классе на 1 ученика меньше. Сколько учеников в 4 «б» классе?
Сегодня мы продолжим учиться различать задачи с формулировками в прямой и косвенной форме.
Перед вами условие задачи:
Масса тыквы 8кг. Кабачок в 2 раза легче тыквы. Какова масса кабачка?

По условию задачи кабачок меньше тыквы в 2 раза.
Посмотрите, какой схематический рисунок можно сделать к задаче:
на нем кружком обозначена масса тыквы, овалом – масса кабачка Стрелочкой показано, как связаны масса тыквы и масса кабачка. Такие задачи вы уже умеете решать.
8 кг в 2 раза меньше ?
Поэтому для ответа на вопрос задачи надо массу тыквы разделить на два.
8 : 2 = 4 (кг)
Но если кабачок меньше тыквы, о тыкве можно сказать: она тяжелее кабачка и ее масса в два раза больше, чем масса кабачка. Поэтому условие нашей задачи можно сформулировать по-другому:
Тыква, масса которой 8 кг, в 2 раза тяжелее кабачка. Какова масса кабачка?
Посмотрите, что изменилось на схематическом рисунке к этой задаче. На этом рисунке стрелка направлена в противоположную сторону. Теперь она показывает, как связана масса тыквы с массой кабачка.
8 кг в 2 раза тяжелее ?
Обратите внимание, что решение задачи не изменилось, хотя в условии вместо слова легче используется слово тяжелее.
8 : 2 = 4 (кг)
Поэтому в решении задач, в которых речь идет об увеличении или уменьшении величин в несколько раз, сначала сравни неизвестную величину с той, которая дана в задаче. Это поможет вам правильно определить каким действием (делением или умножением) решается задача. В нашей задаче масса кабачка меньше, поэтому задача решается делением.
Давайте решим еще одну задачу:
Маша прочитала 12 страниц, это в 3 раза меньше, чем прочитал Юра. Сколько страниц прочитал Юра?
К этой задаче можно сделать такой схематический рисунок. На нем количество страниц, прочитанных Машей, обозначено квадратом, а количество страниц, прочитанных Юрой – прямоугольником. Для решения задачи нам важно понять, Юра прочитал больше Маши или меньше. Если Маша прочитала в 3 раза меньше, чем Юра, значит Юра прочитал больше в 3 раза. Поэтому задача решается действием умножения: 12 умножить на 3 получаем 36.
12 в 3 раза меньше ?
в 3 раза больше
12 ∙ 3 = 36 (стр.)
Ответ: 36 страниц
Задания тренировочного модуля:
Решите задачу, выберите верный ответ:
В первом аквариуме 9 рыбок, это на 3 рыбки больше, чем во втором аквариуме. Сколько рыбок во втором аквариуме?
Варианты ответа:
1. 27;
2. 3;
4. 12;
5. 6.
Правильный вариант: 6
2. Подберите к задаче верное решение:
Белка принесла в дупло утром 24 ореха, что в 4 раза больше, чем вечером. Сколько орехов принесла белка вечером?
24 ∙ 4 24 : 4
Правильный вариант: 24 : 4 = 6
3. Сравните неизвестную величину с данной в задаче. Выберите действие, которым решается задача, и укажите правильный ответ.
У фермера 8 коров. Это в 16 раз меньше, чем овец. Сколько овец у фермера?
У фермера ○ овец больше, чем коров
У фермера ○ овец меньше, чем коров
Задача решается:
○ умножением ○ делением ○ сложением ○ вычитанием
Ответ:
○ 2 овцы ○ 128 овец ○ 24 овцы ○ 8 овец
Задачи на увеличение (уменьшение) числа в несколько раз, выраженные в косвенной форме
Для школы купили 4 компьютера по с р. каждый и телевизор. За всю покупку заплатили k р.
Объясните, что обозначают выражения:
с * 4, k – с * 4. Найдите значения выражений при с = 10000, k = 45000
![]()
![]()

Урок 31. Деление многозначного числа на однозначное число с записью в частном нулей
Цель: научить делить многозначные числа на однозначные, когда в записи частного есть нули.
Задача:
научить делить многозначные числа на однозначные.
Теоретический материал для самостоятельного изучения
Вспомните алгоритм деления многозначного числа на однозначное число.
Алгоритм деления
1. Выделяем первое неполное делимое.
2. Определяем, сколько цифр будет в частном.
3. Делим неполное делимое на делитель.
4. Умножаем делитель на полученное число.
5. Находим остаток от деления вычитанием.
6. Сравниваем остаток с делителем.
7. Есть следующее неполное делимое?
Рассмотрим деление 1560 на 6. Выделяем первое неполное делимое числа 1560. Одну тысячу нельзя разделить на 6 так, чтобы в частном были тысячи. Поэтому будем делить сотни. 15 сотен мы уже сможем разделить так, чтобы в частном были сотни. Значит 15 -это первое неполное делимое числа одна 1560. Теперь определим количество цифр в частном. Так как деление мы начинаем с сотен, значит, в частном будет три цифры. Находим первую цифру частного: для этого 15 делим на 6. Получается 2, пишем цифру 2 на месте сотен в частном. Умножим 6 на 2, получим 12. Столько сотен разделили. Записываем число 12 под неполным делимым 15. Находим остаток от деления: для этого вычитаем 12 из пятнадцати. Получится 3 – столько сотен осталось разделить. Теперь надо сравнить остаток с делителем: 3 меньше 6 – значит, цифру частного подобрали верно. Деление еще не закончено. Образуем следующее неполное делимое из десятков. При делении сотен осталось три сотни, добавим шесть десятков – получаем второе неполное делимое 36 десятков. Делим 36 на 6, получим 6. Столько десятков будет в частном. Умножим 6 на 6, получим 36 – столько десятков разделили. Вычтем 36 из тридцати шести, получим 0. Значит, разделили все десятки. Но деление еще не закончилось, так как мы не делили единицы. У нас должно быть еще одно неполное делимое. Поэтому чтобы следующее неполное делимое не началось с нуля, не будем записывать ноль как разность чисел тридцати шести и тридцати шести. Остаток 0 меньше 6, значит, цифра частного подобрана верно. Образуем следующее неполное делимое: это 0 единиц. Делим 0 на 6, получим 0. Записываем число 0 на месте единиц в частном. Умножаем 0 на 6, получаем 0. Вычтем 0 из 0, получим 0. Остаток меньше делителя, значит, число единиц в частном подобрано верно. Мы разделили единицы, больше неполных делимых образовать нельзя, значит, деление числа 1560 на 6 завершено. Получили в частном число 260.
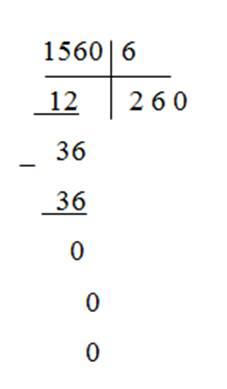
А теперь рассмотрите более краткую запись этого же примера.
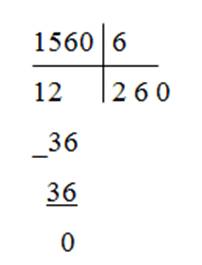
Задания тренировочного модуля:
1. Объясните, какой из учеников прав? При делении числа 32056 на 8 первый ученик получил в частном 407, второй – 4007, а третий – 47.
Правильный ответ: 4007
2. Найдите значение числового выражения.
5 ∙ 23417 – 10305 : 5
Варианты ответов:
1.11524
2.115240
3.115024
Правильный вариант:
115 024
Ряд чисел
Вставьте пропущенное число.
630, 560, 490, ![]() ,
350
,
350
Решение задач
Статистики подсчитали, в среднем за день человек делает 20000 шагов. А сколько шагов он делает за год? Пройдите лабиринт к правильному ответу.
1) 7 300 000 шагов
2) 730 000 шагов
3) 73 000 шагов
Ряд чисел
Догадайтесь, каким должно быть следующее число в ряду. Запишите еще три числа.
112 223 445 556

Урок 32. Задачи на пропорциональное деление. Закрепление изученного материала
Цель: закрепить умение решать задачи на пропорциональное деление.
Задачи:
научиться составлять план решения;
научиться решать задачи на пропорциональное деление арифметическим способом.
Теоретический материал для самостоятельного изучения
Задачи на пропорциональное деление получили свое название по способу их решения. Чтобы дать ответ на вопрос задачи необходимо составить некоторую пропорцию и рассчитать, как соотносятся между собой искомые величины.
Рассмотрим решение задачи на пропорциональное деление на примере:
Задача: Двое рабочих заработали 9000 рублей. Один работал 2 недели, а другой 8 недель. Сколько денег заработал каждый?
Решение: Исходя из условия задачи, можно найти, как оплачивается одна неделя такой работы:
9000 : (8 + 2) = 900 рублей за неделю.
Теперь можно рассчитать, сколько заработал каждый рабочий пропорционально времени потраченному каждым из них на работу:
900 · 2 = 1800 рублей - один рабочий;
900 · 8 = 7200 рублей - другой рабочий.
Ответ: 1800 и 7200 рублей
Прочитайте задачу.
Два куска одинаковой ткани стоят 360 рублей. В одном из них 5м, а в другом – 4м. Сколько стоит каждый кусок ткани?
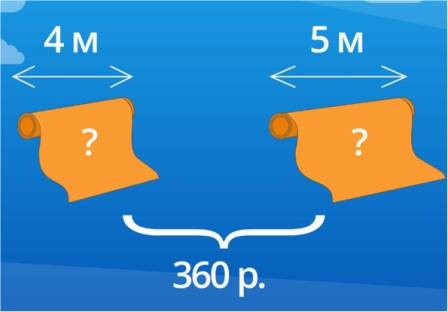
Повторите алгоритм решения задачи.
- Определить, что известно.
- Что нужно найти.
- Выполнить краткую запись.
- Записать решение.
Выполните краткую запись в виде таблицы:
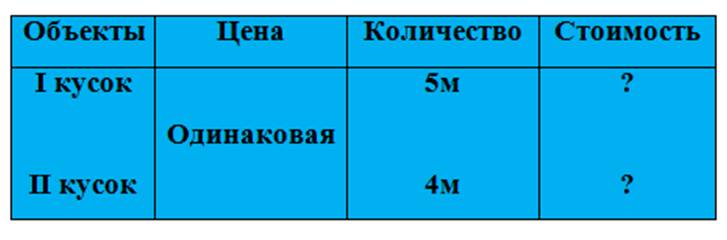
Узнаем, сколько всего купили ткани.
5 + 4 = 9 (м)
Найдем цену ткани.
360 : 9 = 40 (р.)
Посчитаем, сколько стоит первый кусок ткани.
40 ∙ 5 = 200 (р.)
Посчитаем, сколько стоит второй кусок ткани.
40 ∙ 4 = 160 (р.)
Ответ: за первый кусок ткани заплатили 200 рублей, за второй – 160 рублей.
Проверьте правильность решения: сложите стоимость двух кусков ткани.
200 + 160 = 360 (р.)
Задания тренировочного модуля:
Прочитай задачу:
В одном мешке было 56 кг муки, а в другом – 24 кг. Эту муку расфасовали в 40 пакетов поровну. Сколько потребовалось пакетов для расфасовки муки из каждого мешка?
Расставь порядок действий и запиши пояснения.
1. 80 : 40 = 2 (кг)
2. 56 + 24 = 80 (кг)
3. 24 : 2 = 12 (п.)
4. 56 : 2 = 28 (п.)
Правильный вариант:
2. В одном пакете
1. Всего было муки
4. Для муки из второго мешка
3. Для муки из первого мешка
2. Прочитай задачу и выбери те вопросы, на которые можно ответить, пользуясь условием.
Двое рабочих заработали 840 р. Первый работал 5
недель, а второй — 7 недель. Сколько денег заработал каждый
рабочий?
Варианты ответов:
-
Сколько денег заработал первый рабочий?
-
Сколько всего рабочих работало на заводе?
-
Сколько недель рабочие работали вместе?
-
Сколько денег они заработали?
-
Какую работу выполняли рабочие?
-
Сколько они зарабатывали за неделю?
-
Сколько денег заработал второй рабочий?
Правильный вариант:
-
Сколько денег заработал первый рабочий?
-
Сколько недель рабочие работали вместе?
-
Сколько денег они заработали?
-
Сколько они зарабатывали за неделю?
-
Сколько денег заработал второй рабочий?

Урок 33. Повторение пройденного материала по теме «Алгоритмы письменного умножения и деления»
Цель: систематизировать знания по теме «Числа, которые больше 1000».
Задачи:
совершенствовать вычислительные навыки;
решать задачи и уравнения.
Теоретический материал для самостоятельного изучения
На уроке мы вспомним:
Алгоритмы письменного умножения и деления многозначного числа на однозначное.
Сможем:
Совершенствовать вычислительные навыки в процессе решения задач, выражений, уравнений.
Повторим: алгоритм умножения многозначного числа на однозначное.

Повторим алгоритм деления многозначного числа на однозначное

Повторим письменный прием умножения многозначного числа на однозначное, умножим 15 719 ∙ 5
Записываем числа друг под другом: единицы под единицами

Умножаем единицы 9 на 5, получится 45.
45 – это 4 десятка и 5 единиц
5 единиц пишем под единицами
4 десятка запоминаем,
его позже прибавим к десяткам
Умножаем десятки 1 ∙ 5 = 5 и прибавляем 4 десятка, который получился при умножении десятков, получится 9
Записываем десятки под десятками
Умножаем сотни 7 ∙ 5 = 35.
35 – это 5сотен и 3 тысячи.
Записываем 5 сотен под сотнями, 3 тысячи запоминаем. Их позже прибавим к тысячам.
Умножаем тысячи: 5 ∙ 5=25 и прибавляем 3 тысячи, которые получились при умножении сотен. Получается 28.
8 тысяч записываем под тысячами, а 2десятка тысяч запоминаем. Их позже прибавим к десяткам тысяч.
Умножаем десятки тысяч: 1 ∙ 5 = 5 и прибавляем 2 десятка тысяч, которые получились при умножении тысяч. Получается 7. Записываем под десятками тысяч.
Получилось 78595.
Повторим письменный прием деления многозначного числа на однозначное
83 216 : 4
Помним, что при письменном делении запись ведется в столбик
Делим десятки тысяч.
Разделим: 8 : 4, в частном будет 2 десятка тысяч.

Умножим 4 на 2 = 8, это значит, что разделили 8десятков тысяч.
Вычтем из 8 -8=0.
Делим тысячи:
3:4. В частном будет 0 тысяч
Сносим 2 сотни. 32 сотни делим на 4, получается 8.
8 ∙ 4 = 32. Вычтем 32 – 32 = 0
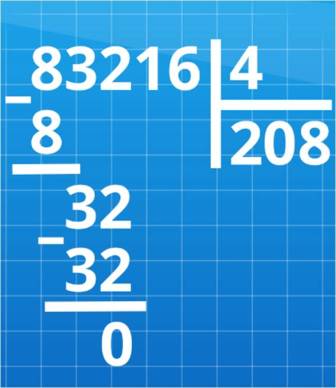
Делим десятки: 1 : 4 = 0. Остаток 1. Сносим 6 единиц. 16:4 = 4.
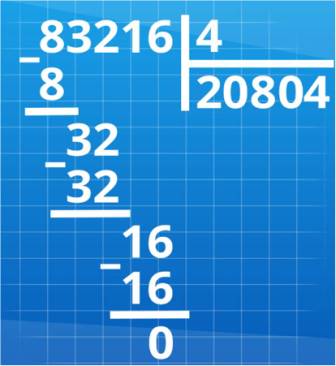
Умножаем 4 на 4, получается 16.
16 – 16 = 0.
Деление закончили.
Читаем ответ: 20 804.
Задания тренировочного модуля:
1. Найдите значение выражений:

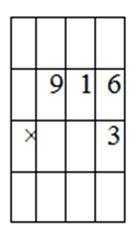
Правильный вариант:
824 · 9 = 7416
916 · 3 = 2748
2. Найдите значение выражений:
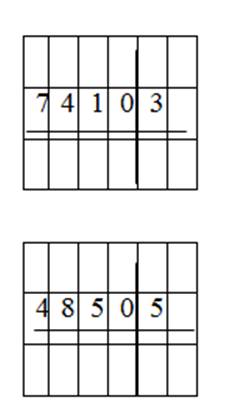
Правильный вариант:
7410 : 3 = 2470
4850 : 5 = 970
Деление с остатком
Выполните деление и запишите неполное частное и остаток.
33 : 8
= ![]() ост.
ост. ![]()
244 : 7
= ![]() ост.
ост. ![]()
6 539 : 5
= ![]() ост.
ост. ![]()
130 : 400
= ![]() ост.
ост. ![]()

Урок 34. Решение текстовых задач на пропорциональное деление
Цель: закрепить умение решать задачи на пропорциональное деление.
Задачи:
научиться составлять план решения;
научиться решать задачи на пропорциональное деление арифметическим способом.
Теоретический материал для самостоятельного изучения
Прочитаем задачу.
Для подготовки к новогоднему празднику в первый день купили 5 гирлянд, а во второй – ещё 3 гирлянды по той же цене. Всего заплатили 640 рублей. Сколько денег заплатили в первый день и сколько во второй?
Запишем условие задачи в таблицу.
В первый день купили пять гирлянд.
Во второй – еще три гирлянды.
Всего заплатили шестьсот сорок рублей. Это общая стоимость покупки.
Что можно сказать о цене гирлянды? У всех гирлянд она одинаковая.
В задаче нужно узнать, сколько заплатили в первый день, а сколько – во второй.
Как вы думаете, одинаковую ли сумму денег заплатили в первый и во второй дни? Конечно же, нет. Ведь в первый день купили больше гирлянд, чем во второй. Поэтому денег в первый день потратили больше, чем во второй.
-
-
Цена
Количество
Стоимость
1 день
Одинаковая
5г.
2 день
3г.
Всего
640руб.
-
Нам известна стоимость покупок, сделанных в 1 и 2 дни. Чтобы узнать стоимость покупки, надо знать цену товара и его количество. Количество нам дано, а вот цена неизвестна. Как ее найти? Посмотрите в таблицу. В ней указана еще одна величина, данная в задаче. Это общая стоимость гирлянд, купленных за два дня. Если мы узнаем общее количество купленных гирлянд, значит, сможем найти и цену одной гирлянды, поскольку все гирлянды куплены по одной цене.
Таким образом, план решения этой задачи будет таким:
-
Найдем количество купленных гирлянд.
-
Узнаем цену одной гирлянды.
-
Найдем стоимость гирлянд, купленных в первый и во второй дни.
Запишем решение.
Пять плюс три равно восемь гирлянд – это общее количество купленных гирлянд за два дня.
5+3=8 (г.)
Разделим общую стоимость покупок шестьсот сорок рублей на общее количество гирлянд, получим цену одной гирлянды. Это восемьдесят рублей.
640:8=80 (р.)
Узнаем, сколько денег заплатили в первый день. Восемьдесят умножим на пять, получим четыреста рублей.
80∙5=400 (р.)
Узнаем, сколько денег заплатили во второй день. Восемьдесят умножим на три, получается двести сорок рублей.
80∙3=240 (р.)
А теперь проверим правильность решения задачи. В первый день потратили четыреста рублей, во второй день – двести сорок рублей. Всего – шестьсот сорок рублей. Получилась та величина, которая дана в условии. Можем записать ответ.
400+240 = 640 (р.)
Ответ: 400 рублей – в первый день,
240 рублей – во второй день.
Задания тренировочного модуля:
Прочитайте задачу, вычислите значения выражений и укажите, что оно обозначает.
На обед в школьную столовую пришли ученики 4А и 4Б классов, всего 52 человека. Ученики 4А класса заняли 6 столов, а ученики 4Б класса 7 таких же столов. За каждым столом оказалось одинаковое количество человек.
-
6 + 7=
-
52 : (6 + 7) =
-
52 : (6 + 7) ∙ 6 =
-
52 : ( 6 + 7) ∙ 7 =
Варианты ответов:
На экране поместить таблички с числами от 1 до 30 для выбора ответа.
Выпадающий список:
Количество человек из 4Б класса.
Количество человек за одним столом.
Количество столов, занятых учениками 4А и 4Б классов.
Количество человек из 4А класса
Правильный вариант/варианты (или правильные комбинации вариантов):
-
6 + 7 = 13 – Количество столов, занятых учениками 4А и 4Б классов.
-
52 : (6 + 7) = 4 – Количество человек за одним столом.
-
52 : (6 + 7) ∙ 6 = 24 – Количество человек из 4А класса
-
52 : (6 + 7) ∙ 7 = 28 – Количество человек из 4Б класса
Прочитайте задачу и заполните таблицу.
В двух домах всего 336 квартир. Число квартир на каждом этаже в обоих домах одинаково. Но в первом доме 12 этажей, а во втором 16. Сколько квартир в каждом доме?
-
-
Число квартир на одном этаже
Количество этажей
Всего квартир
1 дом
2 дом
Всего
-
Правильный вариант:
-
-
Число квартир на одном этаже
Количество этажей
Всего квартир
1 дом
Одинаковое
12
2 дом
16
Всего
336
-
Список литературы:
-
Моро М. И. и др. Математика. Рабочие программы. 1–4 классы.
-
Моро М. И. и др. Учебник. 4 кл. В 2 ч. Ч. 1
-
Моро М. И., Волкова С. И. Математика. Рабочая тетрадь. 4 кл. В 2 ч. Ч. 1.
-
Моро М. И., Волкова С. И. Математика. Рабочая тетрадь. 4 кл. В 2 ч. Ч. 2.
-
Волкова С. И. Математика. Проверочные работы. 4 класс.
-
Бантова М. А., Бельтюкова Г. В., Волкова С. И. и др. Математика. Методические рекомендации. 4 класс.
-
Волкова С. И. Математика и конструирование. 4 класс.
-
Моро М. И., Волкова С. И. Для тех, кто любит математику. 4 класс.
-
Электронное приложение к учебнику «Математика», 4 класс, автор В. Л. Соколов.
-
Смолеусова Т.В. Наглядные таблицы по математике для начальных классов М.:Просвещение.
-
Смолеусова Т.В. Математика в схемах и таблицах: справочник для учителей
начальных классов Самара: Федоров: Учебная лит.
-
Издательства «Просвещение» www.prosv.ru (раздел «Школа России www.schoolrussia.ru)
-
Федерация Интернет-образования, сетевое объединение методистов www.som.fio.ru
-
Российская версия международного проекта Сеть творческих учителей it-n.ru
-
Российский общеобразовательный Портал www.school.edu.ru
-
Интернет ресурсы.


75
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Практикум по математике. 4 класс
Практикум по математике. 4 класс

КГУ «Общеобразовательная школа села Ишимское
отдела образования по Жаксынскому району
управления образования Акмолинской области»
Шумкова Наталья Александровна – учитель начальных классов
Рабочая программа
учебного предмета
«Практикум по
математике»
4 класс
2025 г.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Учебная программа разработана всоответствии с Государственным общеобязательным стандартом среднего образования (начального, основного среднего, общего среднего образования), утвержденным постановлением Правительства Республики Казахстан.
Методологическую основу организации дополнительных занятий «Практикум по математике» обеспечивает личностно-деятельностный подход, который признаёт центром внимания личность учащегося с его интересами, способностями, потребностями. С точки зрения этого подхода ученик рассматривается как субъект деятельности, что предполагает сотрудничество и взаимодействие обучающего и обучаемого, создание и поддержание положительной мотивации к процессу получения новых знаний и саморазвития. В ходе обучения предполагается учёт индивидуальных и возрастных особенностей учащихся. В программе предлагается определённая последовательность изучения разделов и тем, однако по усмотрению учителя возможна их перестановка, некоторые из тем могут не рассматриваться или рассматриваться частично.
Цель рабочей программы: Формирование предметных, метапредметных и личностных компетенций обучающегося в контексте его возрастных особенностей, математическое развитие младших школьников, формирование системы начальных математических знаний, воспитание интереса к математике, к умственной деятельности.
Основные задачи рабочей программы:
1) осознание ребёнком ценности образования и понимание возможностей для образования, как в традиционной классно-урочной системе, так и в условиях дистанционного и самостоятельного изучения предмета;
2) формирование системы начальных математических знаний и умений их применять для решения учебно-познавательных и практических задач;
3) развитие основ логического, знаково-символического и алгоритмического мышления;
4) развитие пространственного воображения и математической речи;
5) развитие познавательных способностей;
6) воспитание стремления к расширению математических знаний. Курс позволяет учителю использовать его как в условиях традиционной классно-урочной системы, так и для дистанционных форм и самостоятельного изучения предмета обучающимися разных учебных возможностей, находящихся в разных жизненных ситуациях при наличии необходимых технических средств.
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ С ОПРЕДЕЛЕНИЕМ ОСНОВНЫХ ВИДОВ УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ
Предмет «Практикум по математике». 4 класс
|
№ |
Содержание |
Кол-во часов |
|
1 |
Урок 1. Нумерация. Счёт предметов. Разряды |
1 |
|
2 |
Урок 2. Числовые выражения. Порядок выполнения действий. Сложение нескольких слагаемых |
1 |
|
3 |
Урок 3. Вычитание вида 903 – 574 |
1 |
|
4 |
Урок 4. Умножение |
1 |
|
5 |
Урок 5. Деление |
1 |
|
6 |
Урок 6. Диаграммы |
1 |
|
7 |
Урок 7. Новые счётные единицы. Класс единиц и класс тысяч |
1 |
|
8 |
Урок 8. Чтение и запись многозначных чисел |
1 |
|
9 |
Урок 9. Разрядные слагаемые. Сравнение многозначных чисел |
1 |
|
10 |
Урок 10. Увеличение и уменьшение числа в 10, 100, 1000 раз. Выделение в числе общего количества единиц любого разряда |
1 |
|
11 |
Урок 11. Класс миллионов. Класс миллиардов. Повторение пройденного материала |
1 |
|
12 |
Урок 12. Единица длины — километр. Таблица единиц длины |
1 |
|
13 |
Урок 13. Единицы площади — квадратный километр, квадратный миллиметр. Таблица единиц площади |
1 |
|
14 |
Урок 14. Измерение площади фигуры с помощью палетки |
1 |
|
15 |
Урок 15. Единицы массы — центнер, тонна. Таблица единиц массы |
1 |
|
16 |
Урок 16. Единицы времени. Сутки. Задачи на нахождение начала, продолжительности и конца события |
1 |
|
17 |
Урок 17. Единицы времени — секунда, век. Таблица единиц времени |
1 |
|
18 |
Урок 18. Повторение пройденного по теме «Величины» |
1 |
|
19 |
Урок 19. Устные и письменные приёмы вычислений |
1 |
|
20 |
Урок 20. Вычитание с переходом через несколько разрядов вида 30 007 – 648 |
1 |
|
21 |
Урок 21. Решение уравнений |
1 |
|
22 |
Урок 22. Нахождение нескольких долей целого. Задачи разных видов |
1 |
|
23 |
Урок 23. Сложение и вычитание значений величин |
1 |
|
24 |
Урок 24. Задачи на увеличение (уменьшение) числа на несколько единиц, выраженных в косвенной форме |
1 |
|
25 |
Урок 25. Письменные приёмы умножения |
1 |
|
26 |
Урок 26. Умножение чисел, оканчивающихся нулями |
1 |
|
27 |
Урок 27. Решение уравнений вида: х ∙ 8 = 26 + 70, х : 6 = 18 ∙ 5, 80 : х = 46 – 30 |
1 |
|
28 |
Урок 28. Деление |
1 |
|
29 |
Урок 29. Деление многозначного числа на однозначное |
1 |
|
30 |
Урок 30. Задачи на увеличение (уменьшение) числа в несколько раз, выраженные в косвенной форме |
1 |
|
31 |
Урок 31. Деление многозначного числа на однозначное число с записью в частном нулей |
1 |
|
32 |
Урок 32. Задачи на пропорциональное деление. Закрепление изученного материала |
1 |
|
33 |
Урок 33. Повторение пройденного материала по теме «Алгоритмы письменного умножения и деления» |
1 |
|
34 |
Урок 34. Решение текстовых задач на пропорциональное деление |
1 |

Урок 1. Нумерация. Счёт предметов. Разряды
Цель: повторить способ образования трёхзначных чисел.
Задачи: закрепить знания о трёхзначных числах, навыки их чтения и определения разрядного состава.
Узнаем, научимся, сможем
На уроке мы узнаем: как образуются трёхзначные числа;
мы научимся: определять последующее и предыдущее число;
мы сможем: сравнивать многозначные числа.
Теоретический материал для самостоятельного изучения
Числа, которые используются при счете предметов, называются натуральными. Если записать числа в том порядке, в котором они называются при счёте, получим натуральный ряд чисел: 1, 2, 3, … Каждое следующее число на единицу больше предыдущего. Самое маленькое число – единица. Натуральный ряд бесконечен.
Если запись натурального числа состоит из одного знака, то его называют однозначным. Например 1, 5, 8, 9 –однозначны, 14, 33, 67 – двухзначные. Числа 578, 601, 999 – трехзначные. Двухзначные, трехзначные и т.д. числа называются многозначными.
Для счета предметов применяют натуральные числа. Любое натуральное число можно записать с помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Цифра – это знак, участвующий в записи числа. Цифры – это единицы счета от 0 до 9.
Число – это величина, при помощи которого производится счет. Такую запись называют десятичной.
Многозначное число – это целые числа, при записи которых нужно использовать несколько цифр (знаков).
При чтении трехзначных чисел сначала читается разряд сотен, затем разряд десятков, затем единиц, например число триста сорок два состоит из трёх сотен, четырех десятков и двух единиц. Каждое числоможно представить в виде суммы разрядных слагаемых. Например число 523 содержит 5 сотен, 2 десятка, 3 единицы. Его можно записать в виде суммы: 523=500+20+3. Каждое слагаемое суммы называется разрядным слагаемым, число 523 представлено в виде суммы разрядных слагаемых.
Многозначные числа можно сравнивать, используя способ поразрядного сравнения.
Например: 591 больше числа 568, так как сотен в них поровну, а десятков в числе 591 больше чем в числе 568
Задания тренировочного модуля:
1. Полина задумала несколько чисел, среди них есть трехзначные. Какие это числа?
-
4 дес. 6 ед.
-
1 сот. 5 дес. 3 ед.
-
5 сот. 5 ед.
-
6 дес. 2 ед.
-
0 сот.3 дес. 9 ед.
Правильный ответ:
1 сот. 5 дес. 3 ед.= 153
5 сот. 5 ед.= 505
2. Вставьте пропущенные слова.
Числа при записи которых используют несколько цифр называются ____________. В записи трехзначного числа есть ____________, десятки и _________. Класс единиц образует первые три ____________.
Правильный ответ:
Числа при записи которых используют несколько цифр называются многозначными . В записи трехзначного числа есть сотни, десятки и единицы. Класс единиц образует первые три разряда.
Необходимо запомнить
ВАЖНО!
Многозначные числа – это такие целые числа, при записи которых нужно использовать несколько цифр (знаков). Числа, для записи которых необходимо использовать 2 цифры – двузначные. Числа, в записи которых 3 цифры – трёхзначные, и так далее. В записи числа разряды, начиная справа, группируются в классы по три разряда в каждом. Читаются многозначные числа слева направо (поразрядно).

Интересные факты
Известный факт, что в записи числа 679 цифры образуют разряды: единицы, десятки, сотни. Разрядов всего три, и вместе они называются классом единиц.
Число 986 754 называется шестизначным. Первые три цифры справа образуют класс единиц, а следующие три – класс тысяч.
Число 123 643 671 – девятизначное. Первые три цифры справа образуют класс единиц, следующие три цифры – класс тысяч, последние три – класс миллионов.
Такая запись чисел называется десятичная. В математике существует еще римская система записи чисел, и она часто встречается в жизни, например, в часах (циферблате), при записи номера века или главы книги.
Вычисления
Помогите Полине пройти лабиринт к правильному ответу, решив выражение: 900 – 80 – 100 + 8.

Урок 2. Числовые выражения. Порядок выполнения действий. Сложение нескольких слагаемых
Цель: повторить порядок выполнения действий в выражениях.
Задачи: повторить правила выполнения действий в пределах 1000;
познакомиться с понятием выражения со скобками.
На уроке
мы узнаем:
правила о порядке выполнения действий в выражениях со скобками и без них;
мы научимся:
применять правила о порядке выполнения действий в выражениях;
мы сможем:
вычислять значения числовых выражений в два-три действия со скобками и без скобок.
Теоретический материал для самостоятельного изучения
Существуют следующие правила порядка действий в числовых выражениях.
Правило 1. Если числовое выражение содержит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку.
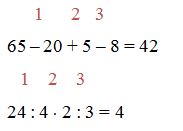
Правило 2. Если числовое выражение содержит не только сложение и вычитание, но и умножение и деление, то сначала выполняются по порядку (слева направо) действия умножение и деление, а потом – сложение и вычитание (слева направо).

П равило 3.
Если числовое выражение содержит одну пару или несколько пар
скобок, то сначала находят значение выражения в скобках, а затем
выполняют действия по правилам 1 и
2.
равило 3.
Если числовое выражение содержит одну пару или несколько пар
скобок, то сначала находят значение выражения в скобках, а затем
выполняют действия по правилам 1 и
2.
Задания тренировочного модуля:
1. Найдите правильное значение выражения:
15 ∙ 10 + (30 - 20) ∙ 5
-
200
-
230
-
20
-
250
Правильный ответ:
200
2. Заполните таблицу:
-
-
слагаемое
170
90
80
слагаемое
230
40
37
сумма
330
160
80
37
-
Правильный ответ:
-
-
слагаемое
170
290
90
80
74
слагаемое
230
40
70
0
37
сумма
400
330
160
80
37
-
3. Расставьте порядок действий:
80 - (42 : 7 ∙ 15 - 29)
Правильный вариант:

Необходимо запомнить
ВАЖНО!
Порядок действий в выражениях со скобками и без скобок такой:
если выражение содержит только сложение и вычитание или умножение и деление, то действия выполняются по порядку; если выражение содержит умножение и деление, то сначала выполняются эти действия;
если выражение содержит одну пару или несколько пар скобок, то сначала находят значение выражения в скобках, а затем за скобками по первому правилу.
Интересные факты
Возникновение знаков «+» и «−» уходит своими корнями в древность. Известно, что в давние времена виноторговцы черточкой отмечали, сколько продано мер вина. Знаком «−» (минус) отмечали уменьшение количества вина, соответственно «+» (плюс) — увеличение, когда в бочку с вином доливали содержимое.
Числовые выражения
Вставьте пропущенные слова.
Подсказка
Внимательно прочтите словарик.
Числа, соединённые знаками арифметических
действий, называются ![]() выражениями.
Действие вычитания обозначается знаком
выражениями.
Действие вычитания обозначается знаком ![]() . Действие
сложения − знаком
. Действие
сложения − знаком ![]() .
Результатом действия сложения является
.
Результатом действия сложения является ![]() двух или
более чисел.
двух или
более чисел.
Числовые выражения. Порядок выполнения действий. Сложение нескольких слагаемых
Распределите равенства и неравенства на верные и неверные.
|
Верно |
Неверно |
|
|
|
807 < 870 909 + 90 + 1 = 1000 590 - 400 - 90 = 180 35 ∙ 2 - (25 - 20) = 75

Урок 3. Вычитание вида 903 – 574
Цель: познакомиться с письменным приёмом вычитания вида 607 - 463, 903 - 574.
Задача: познакомиться с новым приёмом вычитания.
Глоссарий по теме:
Трёхзначные числа - это числа в записи, которых используется три цифры.
Алгоритм - последовательность действия (шагов).
Вычитание -математическая операция по вычитанию из целого части. На письме обычно обозначается с помощью знака «минус».
Задания тренировочного модуля:
1. Выбери правильный ответ
903 - 574
1.207
2. 329
3. 457
Правильный ответ:
329
2. Выполни вычисления:

Правильный ответ:
1. 249
2. 865
3.222
4. 857
Необходимо запомнить
ВАЖНО!
Итак, чтобы вычесть из трёхзначного числа трехзначное вида 607 - 463 и 903 - 574, надо освоить алгоритм письменного вычитания чисел, в котором важно верно записать выражение в столбик. При вычислениях занимать нужное количество единиц у разряда, в котором присутствуют единицы.
Интересные факты
Первобытные люди не умели считать, и научить их было некому. Поэтому они вели наблюдения за природой и выделяли из многих объектов отдельные предметы. Например, из стаи птиц – самого крупного, из стада оленей – вожака, из грозди винограда – ягоду самого тёмного цвета. Определяли соотношение между предметами как «один» и «много». Наблюдения за парными предметами (рога, руки, глаза, уши и т.д.) привели их к пониманию чисел.
Вычитание вида 903 - 574
Найдите и выделите цветом по вертикали и горизонтали слова по теме урока.
1) разность; 2) выражение; 3) значение; 4) алгоритм.
|
д |
ж |
з |
л |
щ |
л |
к |
х |
з |
х |
ч |
е |
щ |
ф |
м |
|
ц |
ё |
у |
в |
р |
з |
c |
ч |
з |
о |
е |
д |
ю |
п |
в |
|
х |
ё |
р |
ы |
а |
н |
з |
т |
в |
и |
л |
д |
ч |
ж |
м |
|
ы |
ж |
щ |
р |
з |
а |
е |
т |
ы |
г |
и |
в |
ц |
д |
ё |
|
т |
ч |
г |
а |
н |
ч |
ч |
м |
к |
б |
ё |
г |
и |
ф |
т |
|
и |
в |
щ |
ж |
о |
е |
п |
м |
ю |
з |
ы |
д |
т |
д |
э |
|
э |
и |
ю |
е |
с |
н |
й |
х |
з |
ж |
о |
ш |
е |
ч |
з |
|
ю |
я |
э |
н |
т |
и |
ф |
э |
т |
р |
ф |
э |
я |
у |
г |
|
х |
з |
ю |
и |
ь |
е |
м |
ц |
е |
c |
у |
ё |
р |
ц |
ы |
|
ю |
у |
c |
е |
у |
у |
п |
ы |
я |
c |
м |
ш |
ц |
ж |
к |
|
з |
а |
л |
г |
о |
р |
и |
т |
м |
й |
ы |
и |
c |
о |
ф |
|
э |
ч |
б |
д |
ж |
й |
л |
ё |
л |
х |
ч |
д |
в |
ю |
ё |
|
у |
о |
з |
м |
з |
у |
в |
э |
ё |
ш |
э |
щ |
ш |
х |
з |
|
у |
ж |
м |
п |
б |
c |
к |
ч |
и |
р |
д |
т |
й |
ы |
д |
|
c |
з |
л |
у |
щ |
т |
ш |
т |
г |
з |
ы |
а |
т |
и |
в |

Урок 4. Умножение
Цель:
познакомиться с приёмом умножения трёхзначного числа на однозначное.
Задачи:
повторить запись выражения в столбик;
познакомиться с новым приёмом умножения.
Теоретический материал для самостоятельного изучения
Рассмотрим письменный прием умножения трёхзначного числа на однозначное. Решим выражение 216 ∙ 3.
Правило записи умножения трехзначного числа на однозначное: записываем числа друг под другом, единицы под единицами.

Алгоритм умножения трехзначного числа на однозначное:
1. Умножаем единицы.
6 умножим на 3, получится 18.
18 это 1 десяток и 8 единиц
8 единиц пишем под единицами.
1 десяток запоминаем, его позже прибавим к десяткам.

2. Умножаем десятки.
1 умножить на 3 равно 3, и прибавляем 1 десяток, который получился при умножении десятков, получится 4.
Записываем десятки под десятками

3. Умножаем сотни.
2 умножить на 3 равно 6.
6 подписываем сотни под сотнями

Ответ: 648.
Задания тренировочного модуля:
1. Выполните вычисления

Правильный ответ:
828
708
2. Вставьте пропущенные знаки вместо * (>< =)
125 ∙ 4 - 250 * 125 ∙ 4 ∙ 1
Правильный ответ:
125 ∙ 4 - 250 < 125 ∙ 4 ∙ 1
ВАЖНО!
Чтобы умножить трёхзначное число на однозначное, надо верно записать выражение в столбик (единицы под единицами) и умножить поочередно единицы, десятки, сотни.
При выполнении умножения каждого разряда записываются единицы полученного числа, а десятки запоминаются.
При вычислении следующего разряда к полученному числу прибавляются оставшиеся единицы.
Интересные факты
Известно, что у древних египтян не было правил и таблиц. Но они умели умножать путем разложения в двоичный ряд чисел.
Например, нужно умножить 22 на 35. Записываем 22 и 35. Теперь делим левое число на 2, а правое умножаем на 2.
Так продолжается, пока в левом столбце не появится единица.
Нечётные числа при делении на 2 округляем в меньшую сторону. И подчеркиваем.
В левом столбце нечётное число отмечается знаком плюс. А затем складываются 70 + 140 + 560 = 770.

Составление последовательности
Укажите последовательность чисел по правилу: каждое последующее число в 2 раза больше, начиная с 24. Последнее число не должно превышать 1000.
24 ![]()
![]()
![]()
![]()
![]()
Приёмы умножения
Заполните пропуски в таблице.
|
a |
6 |
247 |
71 |
5 |
|
b |
7 |
4 |
|
|
|
a • b |
|
|
71 |
0 |
988 1 0 42
Спрятанные слова
Найдите и выделите цветом слова по теме урока.
Подсказка
В филворде спрятаны 3 слова, связанные с умножением.
|
c |
т |
ф |
я |
а |
ё |
у |
з |
ы |
р |
в |
п |
в |
и |
б |
|
з |
б |
у |
м |
н |
о |
ж |
е |
н |
и |
е |
п |
ж |
а |
п |
|
д |
м |
ж |
н |
м |
е |
ю |
ш |
б |
т |
ш |
р |
з |
а |
т |
|
а |
в |
в |
о |
п |
у |
к |
д |
п |
к |
д |
о |
г |
щ |
и |
|
з |
е |
л |
ж |
а |
х |
о |
х |
э |
е |
э |
и |
к |
щ |
ж |
|
ю |
к |
м |
и |
о |
к |
п |
м |
р |
г |
ю |
з |
ж |
ё |
п |
|
ф |
щ |
ё |
т |
й |
э |
к |
к |
д |
c |
ц |
в |
э |
ю |
к |
|
л |
п |
к |
е |
е |
в |
в |
а |
ф |
е |
c |
е |
х |
ц |
ё |
|
ц |
у |
д |
л |
о |
у |
м |
э |
т |
ю |
т |
д |
ф |
ч |
е |
|
ф |
ё |
х |
ь |
р |
т |
л |
c |
в |
й |
ё |
е |
у |
c |
м |
|
ф |
ё |
л |
у |
к |
ф |
у |
д |
ч |
л |
з |
н |
б |
в |
з |
|
ж |
у |
ч |
щ |
и |
ё |
е |
ч |
ю |
т |
я |
и |
г |
ю |
ю |
|
в |
е |
щ |
т |
ц |
е |
р |
ж |
т |
т |
х |
е |
э |
ю |
г |
|
й |
п |
ш |
р |
з |
е |
ю |
в |
е |
й |
к |
й |
э |
а |
е |
|
в |
у |
р |
ф |
т |
д |
б |
п |
о |
б |
э |
ц |
щ |
т |
д |

Урок 5. Деление
Цель:
познакомиться с письменным приёмом деления трёхзначного числа на однозначное.
Задачи:
познакомиться с новым приёмом деления;
повторить запись математического выражения.
Теоретический материал для самостоятельного изучения
Рассмотрим письменный прием деления трёхзначного числа на однозначное. Решим выражение 876:3.
При письменном делении запись ведется в столбик.
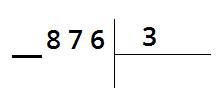
Алгоритм деления трехзначного чиста на однозначное.
1. Делю сотни.
Разделим 8 на 3, в частном будет 2 сот.
Умножу 3 на 2 равно 6, это значит, что разделили 6 сотен.
Из 8 вычесть 6 получится 2. Осталось разделить 2 сотни.
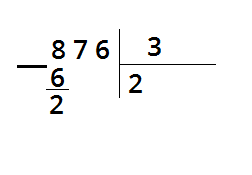
2. Делю десятки.
2 сотни и 7 десяток - это 27 десяток. Разделю 27 на 3. В частном будет 9 десятков.
Умножу 9 на 3 равно 27, это значит, что разделили 27 десятков.
Вычту из 27 27 равно 0, десятки разделили.

3. Делю единицы.
Разделим 6 на 3 равно 2.
Умножим 2 на 3 получится 6.
Из 6 вычесть 6 равно 0.
Деление закончили. Читаем ответ: 292.
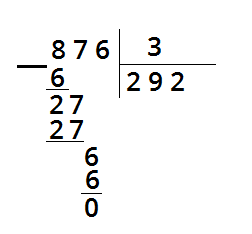
Задания тренировочного модуля:
1. Выберите правильный ответ, выполнив вычисления.
782 : 2
1. 207
2. 374
3. 457
Правильный ответ:
374
2. Решите задачу, используя прием деления трехзначного числа на однозначное:
В первый день бригада сборщиков собрала 435 кг яблок, во второй день пошел дождь, и бригада собрала в 3 раза меньше чем в первый день. В третий день собрали яблок на 200 кг больше, чем во второй. Сколько яблок собрали в третий день?
Правильный ответ:
Решение:
1. 435 : 3 = 145 (яб.) – собрали во второй день.
2. 145 + 200 = 345 (яб.) – собрали в третий день
Ответ: 345 кг яблок.
Необходимо запомнить
ВАЖНО!
Чтобы выполнить деление трёхзначного числа на однозначное, необходимо верно записать выражение в столбик.Деление выполняется по алгоритму, в котором сначала делятся сотни на делитель, в частном записывается число, полученное при делении, затем его умножают на делитель, и полученное при умножении число вычитается из сотен. Затем, по аналогии, выполняется деление десятков и единиц.
Интересные факты
Известно, что некоторые животные умеют считать.Например, муравьи выполняют простейшие арифметические действия.Доказано, что муравей-разведчик находит пищу в лабиринте и сообщает своим сородичам путь – сколько ответвлений нужно пройти, отнимая или прибавляя нужное число.
Заполните таблицу.
|
|
|
|
|
|
b |
180 |
720 |
3 |
|
b : 3 |
|
|
|

1 60 240

Урок 6. Диаграммы
Цель:
познакомиться с понятием «столбчатые диаграммы».
Задачи:
уметь извлекать информацию из различных источников;
научиться читать и составлять диаграммы.
Теоретический материал для самостоятельного изучения
Маша – 10 мин.
Оля – 12 мин.
Костя – 25 мин.
Илья – 7 мин.
Учительница детям задала задание: проследить и зафиксировать время, которые они тратят на дорогу в школу. И у детей получилась такая запись:
Никита – 19 мин.
Для наглядности дети записали результаты в таблицу
|
Имя ученика |
Время на дорогу в школу |
|
Маша |
10 |
|
Оля |
12 |
|
Костя |
25 |
|
Илья |
7 |
|
Никита |
19 |
Учительница на основании информации в таблице составила рисунок, который называется – диаграмма.

Слово "диаграмма" пришло к нам из греческого языка и переводиться как «чертеж». В энциклопедии написано, что оно обозначает графическое изображение информации.
На изображении выше мы видим столбчатую диаграмму, т к . данные времени, которые дети тратят на дорогу изображены в виде столбиков.
С левой стороны диаграммы отмечено время, одно деление равно одной минуте. Внизу по горизонтальной линии имена детей.
По диаграмме мы сможем увидеть следующие данные:
У Кости дорога от дома до школы самая длинная.
Самая короткая - у Ильи.
На сколько один ученик тратит время на дорогу больше или меньше другого. Например: Никита дольше, чем Маша и т.д.
Таким образом, «читается информация», которая записана на диаграмме.
Диаграмму можно построить.
Для этого:
Рисуется прямой угол.
Определим, какие величины будем располагаться на вертикальной и горизонтальной стороне угла.
На вертикальной стороне угла откладываются единичные отрезки, чаще всего одна клетка в тетради – один отрезок.
На горизонтальной стороне угла точки, которые обозначают то, что и о ком идет представление в диаграмме.
При помощи линейки прорисовываются столбики с нужным количеством единичных отрезков или клеток.
В диаграмме подписываются все данные.
Задания тренировочного модуля:
1. Прочитайте диаграмму, выберите, сколько стоит книга и сколько стоит альбом.

Варианты ответа:
Книга: 50 руб., 20 руб., 100 руб., 150 руб.
Альбом: 50 руб., 20 руб., 100 руб., 150 руб.
Правильный ответ:
Книга стоит 100 руб.
Альбом стоит 50 руб.
2. Учительница дала Диме таблицу и попросила его указать диаграмму, на которой правильно изображены данные, представленные в этой таблице.
Определи диаграмму, которую ему надо выбрать?
|
Имя |
Сбережения |
|
Сара |
22 зеда |
|
Пётр |
15 зедов |
|
Полина |
17 зедов |
|
Кристина |
10 зедов |

Правильный ответ:
Вариант А.
Необходимо запомнить
ВАЖНО!
Информацию можно отображать в тексте, таблице, рисунке и диаграмме. Диаграмма - это графическое изображение информации. Если на изображении диаграммы используют столбцы, то она называется столбчатой. При чтении диаграммы можно увидеть количественный показатель данных, сравнить их, найти разность в представленных данных. Диаграмму можно построить в виде прямого угла, внутри которого размещаются данные в виде столбцов.
Интересные факты
Слово «диаграмма» переводится с греческого языка как «чертёж». И правда, диаграмма – это рисунок или чертёж, на котором изображены данные в виде отрезков, столбцов, частей круга, точек. В истории математики известно, что первым стал использовать диаграммы Уильям Плейфер, английский экономист (1786 год).
Чтение диаграмм
Выберите, сколько стоит книга, сколько стоит альбом.

Книга:
![]()
Альбом:
![]()
Чтение столбчатых диаграмм
Рассмотрите диаграмму и заполните таблицу.

|
Увлечение учеников 4-А класса |
Количество человек |
|
Спорт |
|
|
Рисование |
|
|
Музыка |
|
3 15 7

Урок 7. Новые счётные единицы. Класс единиц и класс тысяч
Цель: познакомиться с многозначными числами больше 1000.
Задачи: познакомиться с понятиями класс сотен, класс единиц;
научиться считать тысячами.
Теоретический материал для самостоятельного изучения
Если предметов много, то при счете используют не только знакомые единицы счета - единицы, десятки, сотни, но и более крупные, например тысячи.
Тысячи считают так же, как и простые единицы:
Десять тысяч – это один десяток тысяч.
Десять десятков тысяч – это одна сотня тысяч.
Десять сотен тысяч – это тысяча тысяч, или миллион.
10 тысяч - 1 десяток тысяч
10 десятков тысяч - 1 сотня тысяч
10 сотен тысяч - 1 тысяча тысяч или 1 миллион
Единицы, десятки, сотни составляют класс единиц, или первый класс.
Единицы тысяч, десятки тысяч и сотни тысяч составляют класс тысяч, или второй класс.
|
II класс - Класс тысяч |
I класс - Класс единиц |
||||
|
Сотни тысяч |
Десятки тысяч |
Единицы тысяч |
Сотни |
Десятки |
Единицы |
Посмотрите на таблицу: в каждом классе три разряда.
Разряды первого класса: единицы, десятки, сотни.
Разряды второго класса: единицы тысяч, десятки тысяч и сотни тысяч.
Чтобы прочитать многозначное число, его разбивают на классы, отсчитывая справа по три цифры, затем считают, сколько единиц каждого класса, начиная с высшего.
Например: 123 456
Читается три цифры справа класс тысяч - "сто двадцать три тысячи".
Затем класс единиц - "четыреста пятьдесят шесть".
В числе 372 000 три нуля в записи показывают отсутствие единиц первого класса. Название класса единиц не произносится. Читаем число с высшего класса: «триста семьдесят две тысячи».
Прочитаем число, в котором 145 единиц второго класса и 312 единиц первого класса. Читаем число с высшего класса: «сто сорок пять тысяч триста двенадцать».
Научимся записывать числа больше 1000.
1. В таблице записано число, в котором содержится только 69 единиц класса тысяч, в классе единиц записываем нули или 6 единиц в разряде десятков тысяч и 9 единиц в разряде единиц тысяч.
|
II класс - Класс тысяч |
I класс - Класс единиц |
||||
|
Сотни тысяч |
Десятки тысяч |
Единицы тысяч |
Сотни |
Десятки |
Единицы |
|
|
6 |
9 |
0 |
0 |
0 |
Записывается это число, начиная с класса тысяч, а затем цифры в классе единиц
69 000
2. Запишем следующее число, в котором содержится 307 единиц класса тысяч, а в классе единиц число 1. Нули показывают отсутствие единиц в разрядах десятков тысяч, сотен и десятков.
|
II класс - Класс тысяч |
I класс - Класс единиц |
||||
|
Сотни тысяч |
Десятки тысяч |
Единицы тысяч |
Сотни |
Десятки |
Единицы |
|
3 |
0 |
7 |
0 |
0 |
1 |
Записывается это число, начиная с класса тысяч, а затем цифры в классе единиц
307 001
Таким образом, все числа больше 1000 читаются с класса тысяч (слева направо). Также производиться запись. В случае отсутствия единиц в разрядах записывается нуль.
Задания тренировочного модуля:
1.Укажите, сколько единиц тысяч в числах:
23 769 125 603
Правильный ответ:
1. 3 ед. 2. 5 ед.
2 .Установите соответствие между записью числа и его чтением
-
-
Пятьсот тысяч сто семь
500 107
Тридцать семь тысяч
190 003
Сто девяносто тысяч три
37 000
Двести шестьдесят восемь тысяч двести шестьдесят восемь
999 117
Девятьсот девяносто девять тысяч сто семнадцать
268 268
-
Правильный ответ:
-
-
Пятьсот тысяч сто семь
500 107
Тридцать семь тысяч
37 000
Сто девяносто тысяч три
190 003
Двести шестьдесят восемь тысяч двести шестьдесят восемь
268 268
Девятьсот девяносто девять тысяч сто семнадцать
999 117
-
Необходимо запомнить
ВАЖНО!
Единицы, десятки, сотни составляют класс единиц (первый). Единицы тысяч, десятки тысяч и сотни тысяч составляют класс тысяч (второй). Чтобы прочитать многозначное число, его разбивают на классы, отсчитывая справа по три цифры; считают, сколько единиц каждого класса, начиная с высшего. Записывают многозначные числа, начиная с разрядов класса тысяч, затем разряды класса единиц.
Интересные факты
В древние времена счёт был до нескольких тысяч, так как не было необходимости в больших числах.
Если речь заводилась о множестве предметов, то говорили такую фразу: «Больше, чем звёзд на небе!».
Известно, что число «миллион» появилось в средние века и обозначало «большая тысяча» или «тысяча раз тысяча».
Многозначные числа
Заполните пропуски в тексте.
Наибольшее четырехзначное число
– ![]() .
.
Наименьшее четырехзначное число
– ![]() .
.
Наибольшее шестизначное число
– ![]() .
.
Наименьшее семизначное число
– ![]() .
.

Урок 8. Чтение и запись многозначных чисел
Цель:
закрепить умение считать и записывать многозначные числа.
Задачи:
читать, записывать, сравнивать многозначные числа.
Теоретический материал для самостоятельного изучения
Вы помните правило чтения многозначных чисел. Оно звучит так «Чтобы прочитать многозначное число, его разбивают на классы, отсчитывая справа по три цифры, затем считают, сколько единиц каждого класса, начиная с высшего».
Повторим это правило.
Например: записано число 253 400. В нем 253 единицы класса тысяч и 400 единиц класса единиц. Читается оно так: «двести пятьдесят три тысячи четыреста».
Пробуем ещё раз: в числе содержится 69 единиц класса тысяч, класс единиц отсутствует. Читается оно так «шестьдесят девять тысяч». Записать данное число надо так 69 000.
В числе содержится 307 единиц класса тысяч и 1 единица. Данное число прочитаем слева направо " триста семь тысяч один". Записываем его тоже слева направо, сначала класс тысяч, затем класс единиц, учитывая, что разряде сотен и десятков будет цифра нуль. Получается 307 001.
Задания тренировочного модуля:
Выберите правильный ответ записи числа:
1.145 ед. 2 класса и 326 ед. 1 класса
-
145 000
-
326 145
-
145 326
Правильный ответ:
3.145 326
2. Найдите и закрасьте числа:
1. 7 ед. 2 класса и 5 ед. 1 класса.
2. 367 ед. 2 класса и единицы 1 класса отсутствуют
3. 4 сот. тысяч 45 ед.
4. пятьсот шестьдесят две тысячи тридцать два

Правильный ответ:

Запишите:
наибольшее шестизначное число___
наименьшее пятизначное число ____
наименьшее шестизначное число ___
Ответ:
наибольшее шестизначное число: 999999
наименьшее пятизначное число 10000
наименьшее шестизначное число 100000.
Необходимо запомнить
ВАЖНО!
Чтобы прочитать многозначное число, его разбивают на классы, отсчитывая справа по три цифры, затем считают, сколько единиц каждого класса, начиная с высшего. Записывают многозначные числа начиная с разрядов класса тысяч, затем разряды класса единиц.
Интересные факты
А вы знаете, что получится, если сложить все числа от 1 до 10? Число 55! Если сложить числа от 1 до 100, то получится 5050. Интересные арифметические задачки подобного рода можно решать при помощи калькулятора.
Например, ввести первые 3 цифры своего номера телефона (без оператора), умножить их на 80, прибавить 1, и всё это умножить на 250. Затем прибавить последние 4 цифры своего номера два раза, отнять 250, разделить на 2.
Какой ответ вы получили?
Спрятанные числа
Найдите и выделите цветом числа:
1) 7 ед. 2 класса и 5 ед. 1 класса;
2) 367 ед. 2 класса и единицы 1 класса отсутствуют;
3) 4 сот. тысяч 45 ед.;
4) пятьсот шестьдесят две тысячи тридцать два.
Подсказка
Наведите курсор на первое число и тяните, не отпуская, до последнего числа. Ответ выделится пунктиром.
|
1 |
7 |
0 |
0 |
5 |
5 |
2 |
2 |
1 |
5 |
|
2 |
1 |
3 |
1 |
4 |
5 |
7 |
4 |
7 |
9 |
|
5 |
3 |
4 |
1 |
6 |
6 |
1 |
4 |
3 |
5 |
|
4 |
6 |
7 |
4 |
7 |
2 |
6 |
2 |
6 |
1 |
|
1 |
7 |
4 |
0 |
0 |
0 |
4 |
5 |
9 |
2 |
|
7 |
0 |
3 |
0 |
0 |
3 |
6 |
2 |
4 |
0 |
|
2 |
0 |
2 |
1 |
2 |
2 |
4 |
3 |
0 |
3 |
|
6 |
0 |
8 |
8 |
3 |
5 |
4 |
1 |
2 |
1 |
|
1 |
8 |
3 |
1 |
2 |
3 |
8 |
3 |
4 |
6 |
|
5 |
2 |
4 |
1 |
6 |
0 |
2 |
0 |
9 |
5 |

Урок 9. Разрядные слагаемые. Сравнение многозначных чисел
Цель: научиться записывать многозначные числа в виде суммы разрядных слагаемых.
Задачи: записывать и сравнивать многозначные числа.
Теоретический материал для самостоятельного изучения
Рассмотрим шестизначное число 721 948. Оно содержит 7 сотен тысяч 2 десятка тысяч 1 тысячу 9 сотен 4 десятка и 8 единиц.
Запись данного числа в таблице разрядов выглядит так:
|
II класс - Класс тысяч |
I класс -Класс единиц |
||||
|
Сотни тысяч |
Десятки тысяч |
Единицы тысяч |
Сотни |
Десятки |
Единицы |
|
7 |
2 |
1 |
9 |
4 |
8 |
Из неё можем выяснить, сколько единиц содержится в каждом разряде данного числа. Итак:
7 сотен тысяч это 700 000 единиц,
2 десятка тысяч это 20 000единиц,
1 тысяча это 1000 единиц.
9 сотен это 900 единиц,
4 десятка это 40единиц и 8 единиц.
Число 721 948 можно заменить суммой
700 000 + 20 000 + 1000 + 900 + 40 + 8
Верной будет такая запись 721 948 = 700 000 + 20 000 +1000+900+40+8
Рассмотрим еще пример записи многозначного числа в виде суммы разрядных слагаемых.
Прочитаем число 580 302.
В этом числе:
5 сотен тысяч это 500 000 единиц,
8 десятков тысяч это 80 000 единиц,
Разряд единиц тысяч отсутствует.
3 сотни это 300 единиц,
Разряд десятков отсутствует и 2 единицы.
580 302 = 500 000+80 000+300+2
Теперь рассмотрим способ сравнения чисел до миллиона.
При сравнении чисел до миллиона работает принцип поразрядного сравнения.
Рассмотрим сравнение чисел 5489 и 5367. В обоих числах по 5 тысяч. Сравниваем сотни:4 сотни > 3 сотен.
Сравниваем десятки:8 десятков больше чем6 десятков.
Сравниваем единицы: 9 единиц больше чем 5 единиц.Значит, 5489 > 5365
Задания тренировочного модуля:
1. Заполните таблицу
|
Число |
Всего тысяч |
Всего сотен |
Всего десятков |
Всего единиц |
|
5 009 |
|
|
|
|
|
26 320 |
|
|
|
|
|
216 746 |
|
|
|
|
|
999999 |
|
|
|
|
Правильный ответ:
|
Число |
Всего тысяч |
Всего сотен |
Всего десятков |
Всего единиц |
|
5 009 |
5 |
0 |
0 |
9 |
|
26 320 |
26 |
3 |
2 |
0 |
|
216 746 |
216 |
7 |
4 |
6 |
|
999999 |
999 |
9 |
9 |
9 |
2. Вставьте пропущенные знаки (><)
70000+2000+600+20+7* 700000+20000+600+20+7
10000+3000+60+2 * 10000+300+60+2
300000+1000000+7000+2 * 100000+30000+7000+2
Правильны ответ:
70000+2000+600+20+7< 700000+20000+600+20+7
10000+3000+60+2 >10000+300+60+2
300000+1000000+7000+2 > 100000+30000+7000+2
3. Найдите и закрасьте числа:
1. 3000+700+20+1
2. 100000+40 000+2000+300+10+6
3. 20000+7000+200+30+8
4. 300000+3000+300+3
5. 900000+90000+9000+900+9
6. 70000+20+4
 Правильный ответ:
Правильный ответ:

Необходимо запомнить
ВАЖНО!
Чтобы записать многозначное число в виде суммы разрядных слагаемых, надо определить количество единиц любого разряда, содержащихся в числе, и сложить их.
Например, 65 458 = 60 000 + 5 000 + 400 + 50 + 8
Сравнение многозначных чисел производится по классам и разрядам.
Интересные факты
В истории известно много сказаний, как человек расплачивался за услугу. Одно из самых интересных – с использованием шахматной доски. Предлагается на первую клетку положить одно зернышко, на вторую – два, на третью – три и так далее. Когда дело доходило до последней клетки, общий вес зерна составлял 460 миллиардов тонн.
Классы и разряды
Многозначные числа
Найдите и выделите цветом числа:
1) 3000 + 700 + 20 + 1
2) 100000 + 40000 + 2000 + 300 + 10 + 6
3) 20000 + 7000 + 200 + 30 + 8
4) 300000 + 3000 + 300 + 3
5) 900000 + 90000 + 9000 + 900 + 90 + 9
6) 70000 + 20 + 4
Разрядные слагаемые
Подчеркните равенства, в которых число правильно записано в виде суммы разрядных слагаемых.
1) 40009 = 40000 + 9
2) 302050 = 302 + 50
3) 145906 = 100000 + 40000 + 5000 + 900 + 6
4) 750345 = 700000 + 50000 + 300 + 45

Урок 10. Увеличение и уменьшение числа в 10, 100, 1000 раз. Выделение в числе общего количества единиц любого разряда
Цель: научиться увеличивать и уменьшать числа в 10, 100, 1000 раз.
Задача: определять общее количество единиц любого разряда в числе.
Теоретический материал для самостоятельного изучения
Они похожи тем, что в записи у всех присутствует цифра 7. А отличаются они наличием и количеством нулей в записи.
Цифра 7 в записи этих чисел обозначает разряд: 7 это 7 единиц, 70 это 7 десятков, 700 это 7 сотен, 7000 это 7 тысяч.
Понаблюдайте, в записи каждого следующего числа цифра 7 перемещается влево, а на ее место ставиться цифра нуль. При этом значение числа увеличивается в 10 раз. Можно сделать вывод, что каждое следующее число в 10 раз больше предыдущего.
Из наших наблюдений можно вывести правило увеличения числа в 10 раз.
Для увеличения числа в 10 раз
надо приписать цифру 0 справа
Соответственно, для увеличения числа в 100 раз нужно приписать справа два нуля. В тысячу раз три нуля.
7→700
7 →7000
Правило уменьшения числа в 10 раз работает наоборот.
Чтобы уменьшить число в 10 раз
надо в записи числа убрать справа один нуль
При уменьшении числа в 100 раз надо в записи числа справа убрать два нуля 700→7
7000→70
При уменьшении числа в 1000 раз надо в записи числа справа убрать три нуля
7000→7
70000→70
Следует заметить, что правило уменьшения числа в 10, 100 и 1000 раз работает только тогда, когда в записи числа справа находится достаточное количество нулей.
Теперь рассмотрим, как можно определять общее количество единиц любого разряда в многозначном числе. Возьмем число 3543. В нем 3 тысячи 5 сотен 4 десятка и 3 единицы.
Выдели общее число тысяч - это 3. 3543 → 3 тыс.
Теперь выделим общее число сотен, подчеркнем слева направо все цифры, включая разряд сотен 3543 → 35 сот. Получилось 35 сотен всего в 3543.
Найдем общее число десятков, подчеркнем слева направо все цифры, включая разряд десятков. 3543 → 354 дес. Это число 354. Значит в числе 3543 всего 354 десятка.
Соответственно общее количество единиц в числе 3543 составляет 3543.
Задания тренировочного модуля:
1. Заполните таблицу
|
множитель |
450 |
25 |
|
1000 |
|
|
множитель |
|
1000 |
1000 |
|
10 |
|
произведение |
45000 |
|
457000 |
1000000 |
1090000 |
Правильный ответ:
|
множитель |
450 |
25 |
457 |
1000 |
109 000 |
|
множитель |
100 |
1000 |
1000 |
1000 |
10 |
|
произведение |
45000 |
25000 |
457000 |
1000000 |
1090000 |
2 . Распределите по группам числа, которые можно разделить на 100 и 1000 и нельзя.
100, 12, 34890, 40000, 1900000, 204040, 202, 4500
Правильный ответ:
Можно разделить: 100, 40000, 1900000, 4500
Нельзя разделить: 12, 34890, 204040, 202
3. Общее количество какого разряда выделено в числах? Подпишите ответ.

Правильный ответ:

Деление на 100 и 1000
Распределите по группам числа, которые можно разделить без остатка на 100 или 1000, и нельзя.
|
Можно разделить: |
Нельзя разделить: |
|
|
|
100 40000 1900000 4500
12 34890 204040 202

Урок 11. Класс миллионов. Класс миллиардов. Повторение пройденного материала
Цель: познакомиться с числами в пределах двенадцати разрядов.
Задачи: научиться читать и записывать многозначные числа более миллиона.
Теоретический материал для самостоятельного изучения
Сколько разрядов в каждом классе? Верно, в каждом классе три разряда.

Единицы, десятки, сотни образуют I класс – класс единиц.
Единицы тысяч, десятки тысяч и сотни тысяч образуют II класс – класс тысяч.
Единицы миллионов, десятки миллионов, сотни миллионов образуют III класс – класс миллионов.
Единицы миллиардов, десятки миллиардов, сотни миллиардов образуют IV класс – класс миллиардов.
При чтении числа, записанного вне таблицы, удобнее сначала выделить все классы: для этого необходимо разбить число на группы по три цифры справа налево, а затем прочитать слева направо группы из трех цифр добавив название класса.
Например:
9 876 543![]()
![]()
![]()
В записи числа справа налево выделяем по три цифры, а затем читаем слева направо, называя классы.
Девять миллионов восемьсот семьдесят шесть тысяч пятьсот сорок три.
9
876 543 210![]()
![]()
![]()
![]()
Девять миллиардов восемьсот семьдесят шесть миллионов пятьсот сорок три тысячи двести десять
На письме при записи многозначного числа принято делать разрядку (промежуток) между классами.
Правило записи многозначных чисел: многозначные числа записывают по классам, начиная с высших. Чтобы записать цифрами число, например, двенадцать миллионов четыреста пятьдесят одна тысяча семьсот сорок два, поступают так: записывают группами единицы каждого названного класса, отделяя один класс от другого небольшим промежутком (разрядкой): 12 451 742.
Если отсутствуют разряды в записи натурального числа, то вместо них записываем нули.
Любое натуральное многозначное число можно представить в виде суммы разрядных слагаемых.
Число 98 523 (девяносто восемь тысяч пятьсот двадцать три) содержит девять десятков тысяч, восемь единиц тысяч, пять сотен, два десятка, три единицы. Его можно записать в виде суммы:98 523 = 90 000 + 8 000 + 500 + 20 +3.
Выполним несколько тренировочных заданий
1. Какое число читается так: «Семь миллионов пять тысяч восемьсот один»?
-
7581
-
7005801
-
7500801
-
7000005801
Правильный вариант/варианты: 2
2. Впиши результат
вычисления![]()
7000 000 + 800 000 + 1 000 + 9 =
30
000 000 + 300 000 + 300 =![]()
Правильный вариант/варианты:
7 801 009 30 300 300
Необходимо запомнить
ВАЖНО!
10 сотен тысяч составляет 1 тысячу тысяч, или 1 МИЛЛИОН. Миллион записывают так: 1 000 000. Миллион - это единица третьего класса. В классе миллионов три разряда: единицы миллионов, десятки миллионов, сотни миллионов.
10 сотен миллионов составляет 1 тысячу миллионов, или 1 МИЛЛИАРД. Миллиард – единица четвертого класса. В классе миллиардов тоже три разряда.
Гугол и математика
Действительность с многозначными числами касается и современных технологий. Например, Google – одна из известных поисковых систем. Её придумали Сергей Брин и Ларри Пейдж. Название данной поисковой системы было выбрано не случайно. Её разработчики захотели показать то количество информации, которое система может обработать. В математике число, которое состоит из единицы и ста нулей, называется «гуго́л».
Вставьте пропущенные слова.
Число, в записи которого используют единицу с
шестью нулями, называется ![]() .
.
Класс тысяч образуют ![]() ,
, ![]() ,
, ![]() .
.
Числовой ряд
Расставьте числа в порядке возрастания.
32 008
1 258 067
230 250
4 006
204 500

Урок 12. Единица длины — километр. Таблица единиц длины
Цель:
узнать единицу измерения - километр.
Задача:
получить представление об использовании новой единицы измерения на практике.
Теоретический материал для самостоятельного изучения
Какие известны вам единицы измерения длины удобно использовать при измерении толщины спички?
 - миллиметр
- миллиметр
Какие единицы измерения длины удобно использовать при измерении длины карандаша?
 - сантиметр
- сантиметр
А при измерении ширины окна?
 - дециметр
- дециметр
А если нужно измерить длину коридора? Какие единицы длины вы будете использовать?
 - метр
- метр
Какими единицами измерения удобнее пользоваться для определения расстояния между городами?
 -
- 
Для измерения больших расстояний используют более крупную, чем метр, единицу длины – километр. Первая часть слова «кило» - обозначает «тысяча». Километр – мера длины, равная 1000 м. Слово «километр» сокращённо записывают двумя буквами «ка», «эм». Точка после буквы «эм» не ставится. Теперь вы знаете, что в 1километре тысяча метров, в 1 метре 10 дециметров, в 1дециметре 10 сантиметров, в 1сантиметрн 10 миллиметров.
Таблица единиц длины
1 км = 1000 м
1 м = 10 дм
1 дм = 10 см
1 см = 10 мм
Задания тренировочного модуля:
1.Что не является единицей длины? Выберите правильный ответ.
миллиметр килограмм
километр сантиметр
Правильный ответ:
килограмм
2. Установите правильные соотношения:
1 км 10 дм
1 м 10 см
1 см 10 мм
1 дм 1000 м
Правильный ответ:
1 км 10 дм
1 м 10 см
1 см 10 мм
1 дм 1000 м
Необходимо запомнить
ВАЖНО!
Километр – это единица измерения длины. Этой единицей длины измеряют большие расстояния.
Километр – мера длины, равная 1000 м.
Историческая справка
Локоть и сажень – старые меры длины.
Локоть – длина от кончиков пальцев до локтя (от 38 см до 47 см).
Название "сажень" означает дотягиваться рукой. "Маховая сажень" – расстояние между раскинутыми в стороны руками мужчины (176 см).
Вёрстами измеряли большие расстояния. В разных частях России версту считали по-разному – от 500 до 750 сажен (1 км 67 м).
Спрятанные слова
Найдите и выделите цветом по вертикали или горизонтали слова по теме изучения:
1) километр;
2) длина;
3) расстояние.
|
л |
ч |
ж |
л |
е |
к |
м |
р |
х |
и |
л |
ё |
ж |
э |
ч |
|
в |
ю |
д |
т |
т |
и |
у |
а |
н |
и |
л |
д |
ш |
а |
ж |
|
х |
ж |
c |
ш |
з |
л |
э |
с |
щ |
ш |
б |
ы |
ю |
к |
т |
|
з |
ш |
ю |
ц |
я |
о |
л |
с |
ф |
м |
д |
э |
л |
к |
щ |
|
п |
ю |
ф |
б |
т |
м |
c |
т |
а |
ц |
л |
c |
в |
д |
ф |
|
р |
щ |
щ |
ж |
щ |
е |
c |
о |
д |
к |
и |
ю |
к |
й |
ю |
|
б |
а |
а |
ё |
ю |
т |
ц |
я |
р |
к |
н |
г |
л |
е |
г |
|
к |
п |
д |
й |
я |
р |
б |
н |
е |
з |
а |
т |
б |
ч |
в |
|
у |
ц |
ц |
c |
т |
е |
ё |
и |
ш |
щ |
о |
в |
й |
ф |
х |
|
р |
в |
й |
к |
м |
х |
c |
е |
э |
т |
о |
х |
т |
о |
г |
|
у |
ч |
а |
к |
л |
ё |
б |
и |
т |
у |
c |
д |
ю |
э |
щ |
|
й |
м |
е |
ш |
й |
в |
п |
и |
п |
ф |
ц |
т |
я |
э |
л |
|
р |
е |
я |
д |
ж |
ё |
м |
ф |
ё |
б |
з |
д |
т |
й |
х |
|
й |
ф |
р |
з |
о |
ю |
й |
е |
ч |
ч |
й |
й |
ц |
о |
е |
|
ю |
ё |
ц |
х |
ф |
и |
ж |
ш |
д |
и |
й |
ф |
а |
х |
х |
Перевод величин
Заполните пропуски.
2 км 5 м = ![]() м
м
106 000 м = ![]() км
км

Урок 13. Единицы площади — квадратный километр, квадратный миллиметр. Таблица единиц площади
Цель:
познакомиться с новыми единицами площади.
Задачи:
получить представление об использовании новой единицы измерения на практике;
научиться сравнивать значения площадей разных фигур.
Теоретический материал для самостоятельного изучения
Сегодня мы будем говорить о единицах измерения площади.
За единицу измерения площади принимается квадрат со стороной, равной единице измерения длины

Вы уже знакомы с такими единицами площади, как квадратный сантиметр, квадратный дециметр и квадратный метр. Квадратными сантиметрами мы измеряем площадь небольших предметов, таких, как тетрадь. Квадратными дециметрами можно измерить площадь парты. Квадратными метрами измеряют площадь помещений – комнат, коридоров, залов.



см2 дм2 м2
А если надо будет вычислить площадь какой-нибудь страны.
Например, вычислить площадь России.
Ведь наша страна очень большая, и если измерять её в квадратных метрах, получится число гораздо больше миллиона. А это очень неудобно.
Для измерения больших площадей используют квадратный километр. Это площадь квадрата, сторона которого равна 1 км. Слова «квадратный километр» при числе сокращенно записывают так:1 км2
В квадратных километрах измеряют площади государств; так Россия занимает площадь более 17000000 км2, а Франция - 551000 км2
Но иногда надо измерить площади очень маленьких предметов. Единица измерения маленьких площадей – это квадратный миллиметр. Квадратный миллиметр - это площадь квадрата, сторона которого 1 мм.
Обозначается он так: 1 мм2.
Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.

Для измерения площади земельных участков оказалось удобным ввести промежуточные единицы 1 ар и 1 гектар.
 1 ар - это квадрат со стороной 10 м, значит его
площадь равна
1 ар - это квадрат со стороной 10 м, значит его
площадь равна
1 а = 10 м ∙ 10 м = 100 м2.
Поскольку 1 ар равен 100 квадратным метрам, то эту единицу площади часто называют соткой.
1 гектар - это квадрат со стороной 100 м ,значит его площадь равна
1 га = 100м ∙ 100м = 10000м2
Вот теперь вы можете составить таблицу единиц площади. А помогут вам знание таблицы единиц длины и умение находить площадь квадрата.
1 см2 = 100 мм2
1 см2 = 10 мм2 ∙ 10 мм2 = 100 мм2
1 дм2 = 100 см2
1 дм2 = 10 см2 ∙ 10 см2 = 100 см2
1 м2 = 100 дм2
1 м2 = 10дм2 ∙ 10 дм2 = 100 дм2
1 дм2 = 10000 мм2
1 дм2 = 100 мм2 ∙ 100 мм2 = 10000 мм2
1 м2 = 10000 см2
1 м2 = 100см2 ∙ 100 см2 = 10000 дм2
Теперь внимательно рассмотрите таблицу и постарайтесь ее запомнить.

Задания тренировочного модуля:
1. Установите правильные соотношения
1 см2 100 дм2
1 м2 100 см2
1 дм2 1000000 м2
1 км2 100 мм2
Правильный ответ.
1 см2 100 дм2
1 м2 100 см2
1 дм2 1000000 м2
1 км2 100 мм2
2. Укажите какими единицами площади, ты будешь измерять
1. Площадь Евразии - квадратный__________________
2. Площадь цветка незабудки - квадратный___________
3. Площадь тетради – квадратный __________________
Правильный ответ.
1. Площадь Евразии - квадратный километр
2. Площадь цветка незабудки - квадратный миллиметр
3. Площадь тетради – квадратный сантиметр
Подчеркните запись, в которой допущена ошибка.
1. 30 дм2 = 3000 см2
2. 16 м2 = 1600 дм2
3. 5 км2 = 500000 м2
4. 60 см2 = 6000 мм2
Единицы площади
Укажите, какими единицами площади вы будете измерять:
1. Площадь Евразии –
квадратный ![]() .
.
2. Площадь цветка незабудки –
квадратный ![]() .
.
3. Площадь тетради –
квадратный ![]() .
.

Урок 14. Измерение площади фигуры с помощью палетки
Цель:
научиться определять площадь с помощью палетки.
Задача:
научиться определять площади фигур произвольной формы, используя палетку.
Теоретический материал для самостоятельного изучения
Вычислите площадь прямоугольника, если известно, что его длина равна 8см, а ширина 5см.
Вы уже знаете, чтобы найти площадь прямоугольника, нужно длину умножить на ширину. S= 8 ∙ 5 = 40 см2
А теперь попробуйте вычислить площадь данной фигуры:
 -?
-?
Сегодня мы узнаем, что для нахождения площади фигур можно использовать палетку. Палетка – это прозрачная плёнка, которая может быть разбита на квадратные дециметры, квадратные сантиметры, квадратные миллиметры. Простейшая палетка - лист кальки, разделенный на квадратные сантиметры. Палетку используют для измерения площади фигур, ограниченных кривой линией.

Чтобы найти площадь данной фигуры, нужно:
1) На данную фигуру наложить палетку. Не сдвигать!

2)Сосчитать, сколько целых клеток- квадратных единиц - содержится в фигуре.

Целых 34 клетки.
3) Сосчитать, сколько нецелых квадратных единиц содержится в фигуре.
Неполных 8 клеток.
4) Количество нецелых квадратных единиц разделить на 2, примерно столько целых квадратных единиц они образуют.
8 : 2 = 4
5) Сложить числа, полученные в пунктах 2 и 4.
6) В ответе записать, что площадь фигуры приблизительно равна найденной сумме.
S = 34 + (8 : 2) = 38 см2
Ответ: S = 38 см2
Задания тренировочного модуля:
1. Определите, какая фигура имеет большую площадь, а какая - меньшую, и решите ребус соответствия.

Правильный ответ: Прямоугольник – большую, круг – меньшую.
Сторона клетки фигуры на рисунке равна 1 см. Найдите её площадь и периметр.

Правильный ответ:
Площадь 7 см2
Периметр 12 см
Измерение площади фигуры
.Сторона клетки фигуры на рисунке равна 1 см. Найдите её площадь и периметр.

Площадь ![]() см2.
см2.
Периметр ![]() см.
см.

Урок 15. Единицы массы — центнер, тонна. Таблица единиц массы
Цель:
познакомиться с единицами массы: тонной, центнером.
Задачи:
получить представление об использовании новой единицы измерения на практике;
научиться переводить одни единицы массы в другие, используя соотношения между ними.
Теоретический материал для самостоятельного изучения
Когда мы берем в руки какой-либо предмет, то ощущаем его тяжесть. Величина, которая характеризует вес предмета ,называется массой.
Если нужно узнать массу одного зернышка, какой единицей массы вы воспользуетесь?

- грамм
А если нужно узнать массу мешка с зерном ?
 - килограмм
- килограмм
Ну, а если нужно узнать массу целой машины с зерном?

Для измерения массы больших грузов используют более крупные, чем килограмм, единицы массы- центнер и тонну.Слово тонна в переводе с греческого языка обозначает «бочка», а слово центнер-«весящий 100»
Слово центнер сокращенно записывают буквой «цэ», слово-тонна буквой «тэ» Точка при сокращении слова не ставится.
Если 1 грамм умножить на 1000, то получим кг. Поэтому 1кг = 1000г
Если 1кг умножить на 100, то получим 1 центнер. Поэтому 1ц =100кг.
Если 1ц умножить на 10, то получим 1 тонну. Поэтому 1т =10ц.
Если 1кг умножить на 1000, то получим 1тонну. Поэтому 1т-1000кг.
Таблица единиц массы:
-
-
1 кг = 1000 г
1 ц = 100 кг
1 т = 1000 кг
1 т = 10 ц
-
Задания тренировочного модуля:
1. Распределите рисунки по группам «Измерение массы в тоннах» и «Измерение массы в килограммах».






Правильный ответ:
-
-
Измерение массы в тоннах
Измерение массы в килограммах






-
2. Допишите пропущенные числа
2т 5ц = ______ кг
800 кг = ______ ц
4 кг 250 г = ______ г
3 ц 50 кг = ______ кг
Правильный ответ:
2 т 5 ц = 2500 кг
800 кг = 8 ц
4 кг 250 г = 4250 г
3 ц 50 кг = 350 кг
Перевод единиц массы
Допишите пропущенные числа.
2 т 5 ц = ![]() кг
кг
800 кг = ![]() ц
ц
4 кг 250 г = ![]() г
г
3 ц 50 кг = ![]() кг
кг

Урок 16. Единицы времени. Сутки. Задачи на нахождение начала, продолжительности и конца события
Цель:узнать единицу времени – сутки.
Задачи: повторить изученные единицы времени;
составить таблицу единиц времени.
Теоретический материал для самостоятельного изучения
Отгадайте ребус и вы узнаете тему урока.
С

 - сутки
- сутки
Вы уже знаете некоторые единицы времени. Например, год. В году 12 месяцев. Это 365 дней в обычном, или 366 в високосном году. Более крупная единица времени, чем год - век. Век равен 100 годам.

Более мелкой единицей времени служит месяц - промежуток времени, близкий к периоду обращения Луны вокруг Земли.
Один месяц - это 30 или 31 сутки (в феврале 28 или 29 суток).

А что же такое сутки?
Су́тки — единица измерения времени, приблизительно равная периоду обращения Земли вокруг своей оси. Сутки делятся на 24 часа и условно делятся на четыре характерных интервала — утро, день, вечер и ночь.

Сутки – это день и ночь. Говорят, что сутки прошли, если прошли день и ночь. Но отсчитывать время днём и ночью можно только в жизненных ситуациях, а если речь идёт о математической точности, то здесь нужен специальный прибор, который измеряет время. Этим прибором являются часы.

Вы знаете, что в сутках 24 часа. Но на циферблате часов стоят числа от 1 до 12. Поэтому иногда нужно уточнять, 3 часа дня или 3 часа ночи.
Начало суток - 0 часов. От 0 часов до 12 часов проходит первая половина суток, через час после 12 часов дня буде 13 часов (или 1 час дня).
Век, год, месяц, неделя, сутки, час, минута, секунда - всё это единицы измерения времени.
Год, месяц и сутки были взяты из природы, а час, минута, секунда - придуманы человеком.

Для решения задач на определение начала, продолжительности и конца событий, необходимо помнить некоторые правила:
1) Чтобы найти длительность события, надо из конца вычесть его начало.
2) Чтобы найти начало события. Нужно из конца вычесть его длительность.
3) Чтобы найти длительность события, надо к началу прибавить его длительность.
Задания тренировочного модуля:
1. Решите задачи, пользуясь правилом.
А) Экскурсия в музее началась в 11 ч. и продолжалась 1 ч. 40 мин. Когда экскурсия закончилась?
Решение:__________
Ответ: экскурсия закончилась________
Б) Фильм начался в 12 ч., а закончился в 13 ч. 30 мин. Сколько длился фильм?
Решение:_____________
Ответ: фильм длился________
В) Урок длился 45 мин. и закончился в 11 ч. 20 мин. В котором часу начался урок?
Решение:________
Ответ: урок начался______
Правильный ответ:
А) Решение:11 ч. + 1 ч. 40 мин. = 12 ч. 40 мин.
Ответ: экскурсия закончилась в 12 ч. 40 мин.
Б) Решение: 13 ч. 30 мин. - 12 ч. = 1 ч. 30 мин.
Ответ: фильм длился 1 ч. 30 мин.
В) Решение: 11 ч. 20 мин. – 45 мин. = 10 ч. 35 мин.
Ответ: урок начался 10 ч. 35 мин.
2 . Какое
время показывают часы? Заполните окошки. Напишите два варианта – до
полудня и после полудня.
. Какое
время показывают часы? Заполните окошки. Напишите два варианта – до
полудня и после полудня.

Правильный ответ:
1) 2:45 или 14:45 2) 5:45 или 17:45
3) 11:15 или 23:15 4) 1:15 или13:15
Определение времени по часам
Расшифруйте: какому значению времени соответствуют буквы и прочитайте крылатую фразу.



Урок 17. Единицы времени — секунда, век. Таблица единиц времени
Цель:
изучить новые единицы времени.
Задачи:
применять соотношения единиц времени в вычислениях;
сравнивать продолжительность событий.
Теоретический материал для самостоятельного изучения
Назовём:
Единицу времени больше часа: год, месяц, неделя, сутки.
Единицу времени меньше часа: минута.
Минута составляет 1/60 часа.
Выразим
2 часа=120 минут;
1 час 40 мин=100минут;
2 часа 30 мин=150 мин;
½ ч = 30 мин;
¼ ч = 15 мин;
1/3 ч = 20 мин
Как называется 1/60 минуты?
С помощью какого прибора измеряют время в этих единицах?
Есть единица времени, которая меньше минуты. Это секунда. На некоторых часах, кроме часовой и минутной стрелки, есть и маленькая стрелка, которая движется по своему маленькому циферблату. Эта стрелка отсчитывает секунды.
Секунда – это единица времени, равная одной шестидесятой минуты.
1/60 мин = 1 с
Сейчас на часах 12 часов 47 минут. За одну минуту секундная стрелка сделает полный оборот, т. е. отсчитает 60 секунд. Часы покажут 12 часов 48 минут.

За 1 секунду можно сделать 1-2 шага. Примерно с периодом 1 секунда бьётся пульс человека.
В математике существует соотношение величин времени, которое показывает их количественную взаимосвязь. Необходимо запомнить:
1 мин = 60 с
1 ч = 60 мин = 3 600 с
Обозначается секунда буквой «эс» без точки.
Например: 1 с, 30 с, 9 мин 45 с, 600 с.
Прибор для измерения самой маленькой единицы времени называют секундомер.

С помощью него учитель проверяет у вас технику чтения. На физкультуре при помощи этого прибора у вас определяют время пробега на дистанциях.
Мы с вами познакомились с самой маленькой единицей времени, а теперь поговорим, о самой большой единице времени.
Это – век, или столетие.1 век равен ста годам. Необходимо запомнить:
1 в = 100 г
Много веков назад люди договорились об условной точке отсчёта времени.

Обозначим её красной вертикальной линией. (Её наличие не говорит о том, что до этого момента ничего не происходило). Мы говорили о годах нашей эры и годах до нашей эры. Годы принято обозначать арабскими цифрами. Века – римскими цифрами.
Первый век продолжался с первого по сотый год. В сто первом году начался и в двухсотом закончился второй век. И так далее.
Теперь давайте покажем часть луча, который охватывает ближайшие к нам века.

31 декабря в тысяча девятисотом году закончился девятнадцатый век.
А 31 декабря в двухтысячном году закончился двадцатый век.
1 января две тысячи первого года и продолжается сегодня двадцать первый век.
Да, ребята! Мы живем в двадцать первом веке.
Веками измеряются длительные периоды в истории городов, стран, жизнь некоторых деревьев и животных.
Выразим в секундах:
1 мин 30 с = 90 с
1 мин 5 с = 65 с
½ мин = 30 с
¼ мин =15 с
2 ч – 7200 с
Определим век по году:
В 1147 году по приказу князя Юрия Долгорукова была основана Москва. Какой это был век? (Одна тысяча сто сорок седьмой год относится к двенадцатому веку)
Московский университет открылся в 1755 году, определите век. (Одна тысяча семьсот пятьдесят пятый год - это восемнадцатый век)
Победа в Великой Отечественной войне произошла в 1945 году, назовите век. (Одна тысяча сорок пятый год – это двадцатый век)
Сколько веков существует столица нашей Родины? (Сейчас идет двадцать первый век, Москва основана в двенадцатом веке, значит, столица существует уже девять веков)
Решим задачу:
Мальчик добежал от дома до станции за 20 мин. Обратно он шёл медленно, и на тот путь ему потребовалось 1 800 с. На сколько больше минут мальчик затратил на обратный путь?
Сразу ответить на вопрос задачи нельзя, нужно секунды перевести в минуты, т.е. сравнивать одинаковые единицы измерения.
1800 с = 1800 : 60 = 30 мин
30 мин > 20 мин
30 – 20 = 10 мин
Ответ: на 10 мин больше мальчик затратил на обратный путь
Вывод:
Ответим на вопросы, поставленные в начале урока.
Секунда – это единица времени, равная одной шестидесятой минуты.
1/60 мин = 1 с
1 мин = 60 с
1 ч = 60 мин = 3 600 с
Прибор для измерения самой маленькой единицы времени называют секундомер.
Век (столетие) – единица времени, равная 100 годам.
Выполним несколько тренировочных заданий.
1. Сколько секунд составляют 2 мин 30 с? Подчеркни верный ответ
-
-
□ 230 с
□ 120 с
□ 150 с
-
Решение:
-
-
□ 230 с
□ 120 с
□ 150 с
-
2.Укажи верную запись.
-
□ 4 мин 50 с = 450 с
-
□ З ч < 200 мин
Решение:
-
□ 4 мин 50 с = 450 с
-
⊗ З ч < 200 мин
3.Решим задачу
Громозека прочитал страницу книги за 1 мин 15 с, а Алиса за 45 с. Кто дольше читал эту страницу и на сколько?
Сразу ответить на вопрос задачи нельзя, нужно минуты перевести в секунды, т.е. сравнивать одинаковые единицы измерения.
1мин 15 с = 75 с
75 с >45 с
75-45=30(с)
Ответ: Громозека читал эту страницу на 30 секунд дольше.
Единицы времени
Вставьте слова в пословицы и поговорки, заменяя выделенные числа на единицы времени.
100 лет живи, 100 лет учись.
![]() живи,
живи, ![]() учись.
учись.
Обещанного 36 месяцев ждут.
Обещанного ![]() ждут.
ждут.
Делу время, а потехе 60 минут.
Делу
время, а потехе ![]() .
.
7 дней 12 месяцев кормит.
![]()
![]() кормит.
кормит.
Действия с единицами времени
Выполните вычисления и заполните пропуски верными значениями величин.
2 ч - 30 мин = ![]()
2 сут - 20 ч = ![]()
3 мин - 54 с = ![]()
1 век - 32 года = ![]()

Урок 18. Повторение пройденного по теме «Величины»
Цель: повторение знаний, умений и навыков о величинах.
Задачи: закрепить представления о величинах;
применять знания о величинах при вычислениях.
Теоретический материал для самостоятельного изучения
Назовём известные величины: длина, площадь, масса, время.
Называют их величинами, потому, что их можно измерить, сравнить и результат выразить числом.
Выполним задание:
Разбейте числа на две группы по определённому признаку.
43, 5 м 6 дм, 1001, 4 кг, 5 мин, 890, 10 с, 12, 6 кг, 2 т, 7 сут., 98, 120 г, 8 дм², 5 км, 1 ч 20 мин, 8 м², 1000 см², 555
Мы видим, что в этом ряду есть натуральные числа, которые являются результатом вычислений или счёта. И есть именованные числа, которые получают в результате измерения величин и сопровождающих названием единиц измерения.
Группу именованные числа можно разбить на несколько групп по признаку разных величин. Единицы измерения нам укажут на величину, о которой идёт речь. Для этого нужно вспомнить единицы измерения величин.
Единицы измерения длины: км, м, дм, см, мм.
Единицы измерения времени: сутки, час, мин, сек.
Единицы измерения массы: т, ц, кг, г.
Единицы измерения площади: м2, дм2, см2.
Для измерения величин используют различные инструменты и приборы.
-
Величины
Длина
Площадь
Масса
Время
Измерительные приборы

 формулы
формулы

Единицы измерения
мм, см, дм, м, км
мм², см², дм², м²
г, кг, ц, т
с, мин, ч
Надо всегда помнить одно правило – сравнивать, складывать и вычитать можно только именованные числа с одинаковыми единицами (мерами). Для этого нужно помнить соотношения единиц измерения величин.

Сравним:
555м * 5 км
Для того, чтобы сравнить длину, нужно выразить в одни и те же единицы.
5км = 5000 м
555м < 5 км
8 м² * 80 дм², переведём 8 м² = 800 дм²
8 м²> 80 дм²
4 кг30 г * 5100 г, переведем 4 кг30 г = 4030 г
4 кг30 г < 5100 г
100 мин * 1 ч 40 мин, переведём 1 ч 40 мин = 100 мин
100 мин = 1 ч 40 мин
Решим задачу:
Длина тела кита 26 м, а тюленя – 20 дм. Во сколько раз тюлень короче кита?
26 м = 260 дм
260 : 20 = 13 раз
Ответ: в 13 раз длина тюленя короче длины кита.
Вывод:
Таким образом, длина, площадь, масса и время – это величины.
Величину можно измерить, сравнить и результат представить в виде числа.
Единица измерения – это величина, в которой выражаются другие, однородные с ней величины. При письменных вычислениях значения величин выражают в одних и тех же единицах измерения и выполняют действия с ними так же, как с числами.
Выполним несколько тренировочных заданий.
1. Выберите и отметьте столбик, где написаны только единицы измерения длины:
а) миллиметр б) дециметр в) минута
грамм сантиметр тонна
километр миллиметр дециметр
сутки километр секунда
дециметр метр километр
Ответ: б
2. Выберите вариант, где единицы массы расположены в порядке возрастания:
а) 3000 г, 30ц, 300 кг, 30 т, 3кг 3г.
б) 30т, 30 ц, 3кг 3г, 300кг, 3000 г.
в) 3000г, 3 кг 3г, 300кг, 30ц, 30т.
Ответ: в
3. Выберите ошибочный ответ:
а) Кирпич массой 5 граммов
б) В пакете 5 килограммов конфет
в) На уроке физкультуры мы пробежали 100 метров
Ответ : а
4. Найдите ошибку при переводе величин:
5. а) 2м 3дм = 230 см б) 2м 3дм = 23 дм в) 2м 3дм = 203см
6. а) 8000кг = 8т б) 8000 кг = 800000г в) 8000 кг = 80ц
7. а) 2 ч = 120 мин б) 2ч = 200 мин в) 2ч = 7200с
Ответ: в) 2м 3дм = 203см
Действия с величинами
Преобразуйте величины.
1. 4 км 125 м + 46
км 85 м = ![]() км
км ![]() м
м
2. 7 т 2 ц 66 кг – 5
ц 93 кг = ![]() т
т ![]() ц
ц ![]() кг
кг
3. 2 мин 20 с – 1
мин 30 с = ![]() мин
мин ![]() с
с

Урок 19. Устные и письменные приёмы вычислений
Цель:
изучение вычислительных приёмов с многозначными числами.
Задача:
научиться применять алгоритм вычислений.
Теоретический материал для самостоятельного изучения
Рассмотрим выражение
164 + 45 + 36 + 355
Для быстрого вычисления нужно вспомнить свойства сложения переместительное и сочетательное.
Переместительное свойство подсказывает, что от перестановки слагаемых сумма не изменяется.
А в сочетательном свойстве говорится, что два соседних слагаемых можно заменить их суммой.
Воспользуемся этими свойствами.
164 + 45 + 36 + 355 = (164 + 36) + (355 + 45) = 200 + 400 = 600
Если уметь применять свойства сложения, то значение выражений можно считать устно.
Но, конечно, не всегда удаётся устно выполнить вычисления. Ведь иногда надо выполнять их с многозначными числами. И тогда приходится пользоваться письменным приёмом вычисления. Вспомним алгоритм письменного сложения и вычитания трёхзначных чисел. Допустим, надо сложить числа четыреста шестьдесят пять и двести восемьдесят девять.

Числа записаны одно под другим, одинаковые разряды стоят строго друг под другом: единицы под единицами, десятки под десятками, сотни под сотнями. Выполняем вычисления с наименьшего разряда. Складываем единицы. Пять плюс девять – четырнадцать. Четыре пишем под единицами, а один десяток добавляем к десяткам.
Складываем шесть десятков и восемь десятков – четырнадцать. Да ещё десяток – пятнадцать десятков. Это пять десятков и одна сотня, которую добавляем к сотням.
Складываем четыре и две сотни, да ещё одну сотню. Всего семь сотен. Ответ: семьсот пятьдесят четыре.
Ну а если бы надо было складывать не трёхзначные числа, а, например, пяти- или шестизначные?
Письменное сложение и вычитание любых многозначных чисел выполняется так же, как сложение и вычитание трёхзначных чисел.
Допишем в наших слагаемых цифры в классе тысяч.

Теперь надо сложить шестизначные числа. Действие сложения с классом единиц в них уже выполнено. Продолжаем. Складываем единицы тысяч. Восемь и два – десять. Нуль пишем под единицами тысяч, единицу добавляем к десяткам тысяч. Складываем их. Шесть, четыре и один – одиннадцать десятков тысяч. Это одна сотня и один десяток тысяч. Один десяток тысяч пишем под десятками тысяч и одну сотню тысяч добавляем к сотням тысяч. Складываем их. Шесть. Читаю ответ: шестьсот десять тысяч семьсот пятьдесят четыре.
Ну что ж, надо проверить сложение. А проверяем сложение, естественно, вычитанием.
Из шестисот десяти тысяч семисот пятидесяти четырёх вычитаем триста сорок две тысячи двести восемьдесят девять.

Так же, как при вычитании трёхзначных чисел, начинаем с наименьшего разряда – единиц. Четыре минус девять. Надо занять один десяток. Четырнадцать минус девять – пять.
Вычитаем десятки. Мы заняли один десяток. Их осталось четыре. Из четырёх восемь вычесть не можем. Занимаем одну сотню. Четырнадцать минус восемь – шесть. Вычитаем сотни. Точка подсказывает, что их на одну меньше. Шесть минус два – четыре.
Вычитаем единицы тысяч. Из нуля вычитать нельзя. Занимаем десяток тысяч и вычитаем из десяти. Десять минус два – восемь.
Вычитаем десятки тысяч. У нас был один десяток тысяч, но его заняли. Остался нуль. Занимаем сотню тысяч. Это десять десятков тысяч. Из них вычитаем четыре, получается шесть.
Вычитаем сотни тысяч. Точка подсказывает, что их осталось пять. Пять минус три равно два. Читаю ответ: двести шестьдесят восемь тысяч четыреста шестьдесят пять.
Разность такая же, как первое слагаемое примера на сложение. Значит, всё выполнено верно.
Необходимо запомнить: письменное сложение и вычитание любых многозначных чисел выполняется так же, как сложение и вычитание трёхзначных чисел.
Решим задачу:
Гуляя после уроков, мальчики и девочки произносят каждый день 11875 слов по делу, 5316 – со смыслом, 27981 – не задумываясь, а 379 слов лучше было бы вообще не произносить. Сколько всего слов в день говорят мальчики и девочки, гуляя после уроков?
Р ешение:
ешение:
11875 + 5316 + 27981 + 379 = 45551 (с.)
Ответ: 45551 слово всего говорят в день дети.
Вывод:
Если надо что-нибудь посчитать устно, то иногда это можно сделать быстрее и легче, пользуясь переместительным и сочетательным свойствами сложения.
При сложении и вычитании многозначных чисел числа записывают одно под другим, одинаковые разряды стоят строго друг под другом: единицы под единицами, десятки под десятками, сотни под сотнями. Выполняем вычисления с наименьшего разряда.
Письменное сложение и вычитание любых многозначных чисел выполняется так же, как сложение и вычитание трёхзначных чисел.
Проверяем сложение вычитанием, а вычитание сложением.
Выполним тренировочное задание.

Проверка сложения вычитанием
Выполните вычисления и сделайте проверку. Ответы впишите в пропуски.
1) 39758 + 71396
= ![]()
проверка: ![]() - 39758 =
- 39758 = ![]()
2) 90859 + 81738
= ![]()
проверка: ![]() - 81738 =
- 81738 = ![]()

Урок 20. Вычитание с переходом через несколько разрядов вида 30 007 – 648
Цель:
познакомиться с приёмом вычитания, когда отсутствуют цифры в разрядах уменьшаемого.
Задачи:вычитать числа в пределах миллиона.
Теоретический материал для самостоятельного изучения
Вспомним десятичную систему счисления:
1 тыс. = 10 сот.
1 сот. = 10 дес.
1 дес. = 10 ед.
1 млн. = 10 сот. тыс.
1 сот. тыс. = 10 дес. тыс.
1 дес. тыс. = 10 ед. тыс.
1 дес. – 1 (Чтобы из 1 дес. вычесть единицу, заменим 1 дес. десятью единицами и вычтем 1из 10, получится 9)
1 сот. – 1 дес. ( изз 1 сот. вычесть 1 дес., заменим 1 сот 10 дес. и вычтем 1 дес. из 10, останется 9 дес., или 90)
1 тыс. – 1 сот. ( из 1 тыс. вычитаем 1 сотню, заменим 1 тыс. 10 сотнями и вычтем 1 сотню из 10, останется 9 сотен или 900)
Рассмотрим приём письменного вычисления (в столбик), из круглых чисел, используя занимание единицы через несколько разрядов. Запишите единицы под единицами, десятки под десятками.

Вычисляем десятки. Мы добавили к десяткам одну сотню, то есть десять десятков, но при этом заняли десяток, осталось 9 дес. Чтобы не забыть запишем наверху в разряде десятков цифру 9. 9 – 2 = 7
 Вычисляем сотни. Мы заняли одну сотню из шести,
поэтому записываем пять сотен. Итого результат вычисления равнее
574.
Вычисляем сотни. Мы заняли одну сотню из шести,
поэтому записываем пять сотен. Итого результат вычисления равнее
574.
 А
теперь попробуем рассмотреть особый случай вычитания: когда в
записи уменьшаемого есть несколько нулей. Обнаружилась проблема,
предыдущего алгоритма вычисления не хватает, т. к. приходится
занимать единицу через несколько разрядов и выполнять раздробление
в единицы низших разрядов не один раз. Запишем единицы под
единицами, десятки под десятками, сотни под
сотнями.
А
теперь попробуем рассмотреть особый случай вычитания: когда в
записи уменьшаемого есть несколько нулей. Обнаружилась проблема,
предыдущего алгоритма вычисления не хватает, т. к. приходится
занимать единицу через несколько разрядов и выполнять раздробление
в единицы низших разрядов не один раз. Запишем единицы под
единицами, десятки под десятками, сотни под
сотнями.
Из семи вычесть восемь нельзя, потому занимаем один десяток. Но единицы в разряде десятков отсутствуют, потому занимаем сотню. Отсутствуют сотни и отсутствуют единицы тысяч, потому занимаем один десяток тысяч.

Один десяток тысяч – это десять единиц тысяч, можем занять одну тысячу. Одна тысяча – это 10 сотен, можем занять из сотен. Одна сотня – это десять десятков, теперь занимаем один десяток. Один десяток – это десять единиц да ещё 7. 17 – 8 = 9.

Вычисляем десятки. Мы добавили 10 десятков, но один заняли, чтобы не забыть, запишем наверху в разряде десятков цифру 9. 9 – 4 = 5 десятков.

Вычисляем сотни. Мы добавили 10 сотен, но одну заняли, осталось 9. Чтобы не забыть, запишем наверху в разряде сотен цифру 9. 9 – 6 = 3 сотни.


В ычисляем
единицы тысяч. Мы добавили 10 единиц тысяч, но одну заняли,
осталось 9 единиц тысяч. Чтобы не забыть, запишем наверху в разряде
единиц тысяч цифру 9. Переписываем 9, так как единицы тысяч в
вычитаемом отсутствуют.
ычисляем
единицы тысяч. Мы добавили 10 единиц тысяч, но одну заняли,
осталось 9 единиц тысяч. Чтобы не забыть, запишем наверху в разряде
единиц тысяч цифру 9. Переписываем 9, так как единицы тысяч в
вычитаемом отсутствуют.
Осталось два десятка тысяч, их переписываем. Итого результат вычисления равен 29 359.
Вывод: Ответим на вопросы, поставленные в начале урока. Десятичная система счисления – позиционная система счисления по основанию 10. Вычитание многозначных чисел с переходом через несколько разрядов надо выполнять поразрядно: из единиц – единицы, из десятков – десятки, из сотен – сотни, из тысяч – тысячи. При записи вычитания в столбик для памяти ставим точки над теми разрядами, которые подвергались дроблению (замена 1 единицы высшего разряда 10 единицами низшего соседнего разряда.).
Выполним несколько тренировочных заданий.
1. К каждой позиции первого столбика подберите соответствующую позицию второго:
Варианты ответов:
-
-
300 025 – 147 328
424 399
268 765 + 183 426
152 697
507 425 – 83 026
127 507
506 021 – 378 514
452 191
-
Правильный вариант/варианты:
-
-
300 025 – 147 328
152 697
268 765 + 183 426
452 191
507 425 – 83 026
424 399
506 021 – 378 514
7
-
Выполните вычисления:

Правильный вариант:
-
7 258 – 3 028 = 4 230
-
20 456 + 5703 = 26 159
-
93 698 – 542 = 93 156
-
121 212 + 434 343 = 555 555
Сложение и вычитание
Выполните вычисления:
7258 - 3028 = ![]()
20456 + 5703 = ![]()
93698 - 542 = ![]()
121212 + 434343 = ![]()
Восстановление последовательности чисел
Впишите пропущенное число:
740 000, 740 200, 740
400, ![]() ,
740 800, 741 000.
,
740 800, 741 000.

Урок 21. Решение уравнений
Цель: совершенствование умения решать составные уравнения.
Задачи:
решать уравнения новых видов;
объяснять выполнение действий при решении уравнений.
Теоретический материал для самостоятельного изучения:
Рассмотрите записи:
376 + 282; (х - у) : 3
Являются ли эти записи уравнениями?
Это не уравнения, так как в уравнении должен быть знак «=». Это выражения.
Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают латинской буквой.
Рассмотрите другие записи:
24 + х = 49; 24 + х = 79 - 30
Это уравнения, так как это равенства, содержащие переменную.
Попробуем их решить.
Что значит решить уравнение?
Решить уравнение – это значит найти значение неизвестного, при котором равенство будет верным.
Вспомните алгоритм решения уравнений.
Алгоритм:
-
Вспомнить компоненты действия данного уравнения.
-
Определить неизвестный компонент.
-
Вспомнить правило нахождения неизвестного компонента.
-
Применить правило и найти неизвестный компонент.
-
Записать ответ.
-
Сделать проверку
Используя алгоритм, решите первое уравнение
24 + х = 49
х = 49 - 24
х = 25
Значение неизвестного х = 25. Это корень уравнения.
Корень уравнения – это значение неизвестного, обозначенного латинской буквой в уравнении. В данном случае – это х.
Можно ли решить второе уравнение, используя этот же алгоритм?
Нет.
Такие уравнения не рассматривались. Какова же цель нашего урока?
Цель урока: научиться решать уравнения, в которых в ответе не число, а числовое выражение.
Такие уравнения мы будем называть составные. Поэтому тема урока: «Решение составных уравнений»
Чтобы решить это уравнение, нужно упростить правую часть.
24 + х = 79 - 30, после чего получаем уравнение известного вам вида
24 + х = 49
х = 49 - 24
х = 25
Проверка:
24 + 25 = 79 - 30
49 = 49
Ответ: корень уравнения 25
Составим алгоритм решения составных уравнений.
Алгоритм решения составных уравнений
1. Найти значение числового выражения.
2. Вспомнить компоненты действия данного уравнения.
3. Определить неизвестный компонент.
4. Вспомнить правило нахождения неизвестного компонента.
5. Применить правило и найти неизвестный компонент.
6. Записать ответ.
7. Сделать проверку.
Решим еще одно уравнение:
75 - х = 9 ∙ 7
Применяем алгоритм решения составных уравнений:
-
Найти значение числового выражения: 75 - х = 9 ∙ 7
75 - х = 63
-
Вспомнить компоненты действия данного уравнения: 75 - х = 63


3. Определить неизвестный компонент.
Неизвестно – вычитаемое.
4. Вспомнить правило нахождения неизвестного компонента.
5. Применить правило и найти неизвестный компонент.
х = 75 - 63
6. Записать ответ.
х = 12
7. Сделать проверку.
75 - 12 = 9 ∙ 7
63 = 63
Ответ: корень уравнения 12
Вывод: чтобы решить составное уравнение, в которых в ответе не число, а числовое выражение, необходимо упростить правую часть ( т.е решить выражение), после чего получаем уравнение известного вам вида и решаем его, используя алгоритм решения уравнений.
Решим задачу, составив уравнение:
Сумма неизвестного числа и числа 390 равна произведению чисел 70 и 6. Найди это число.
1. Сумма неизвестного числа и числа 390 – обозначим неизвестное число переменной х, тогда получим х + 390
2. Произведение чисел 70 и 6: 70 ∙ 6
3. Получаем уравнение: х + 390 = 70 ∙ 6
Применяя алгоритм решения составных уравнений, решим его:
х + 390 = 70 ∙ 6
х + 390 = 420
х = 420 - 390
х = 30
Проверка:
30 + 390 = 70 ∙ 6
420 = 420
Ответ: неизвестное число - 30
Компоненты сложения
Заполните пропуски в таблице:
|
слагаемое |
3 |
62 |
|
|
|
1017 |
|
слагаемое |
|
|
24 |
179 |
75 |
|
|
сумма |
7 |
82 |
76 |
964 |
523 |
8192 |
20/7175/785/448/4/52

Урок 22. Нахождение нескольких долей целого. Задачи разных видов
Цель: научиться находить несколько долей целого.
Задачи:
изучить и применять алгоритм нахождения нескольких долей целого.
Теоретический материал для самостоятельного изучения
Начертим в тетради отрезок длиной 12 см.
Нам
надо узнать, сколько см в ![]() отрезка. Сначала разделим отрезок на
4
отрезка. Сначала разделим отрезок на
4
равные части. Как назвать каждую часть? (Одна четвертая часть.)
Сколько см в ![]() отрезка? (3 см)
отрезка? (3 см)
Как узнали? (12 : 4 = 3)
Покажите на
чертеже ![]() отрезка. Проводят сверху дугу и
подписывают
отрезка. Проводят сверху дугу и
подписывают ![]() .
.
Покажем ![]() отрезка.
отрезка.

Как
узнать, сколько см в ![]() отрезка? (3 · 3 = 9
(см))
отрезка? (3 · 3 = 9
(см))
1)
12 : 4 = 3 (см) – ![]() отрезка
отрезка
2) 3 · 3 = 9 (см)
Решение можно записать выражением: 12 : 4 ∙ 3=9(см)
О т
в е т: 9 см в ![]() отрезка.
отрезка.
Решим задачу №291. Выполним чертеж,
покажем ![]() отрезка. Объясняем, как
получили
отрезка. Объясняем, как
получили ![]() отрезка. Как узнать, сколько мм
в
отрезка. Как узнать, сколько мм
в ![]() отрезка?
отрезка?

1)
60 : 6 = 10 (мм) – ![]() отрезка
отрезка
2) 10 ·5 = 50 (мм)
3) 60 : 6 ∙ 5= 50(мм)
О т
в е т: 50 мм в ![]() отрезка.
отрезка.
Вывод.
- Как же решать задачи на нахождение нескольких долей целого?
Надо найти величину одной доли целого и умножить на количество долей.
Составим алгоритм.
1. Разделить целое на равные части.
2. Умножить на количество, которое берём.
Выполним несколько тренировочных заданий
1. Найти числа 15 (9)
![]() числа 200 (90)
числа 200 (90)
![]() числа 18 (12)
числа 18 (12)
![]() от
числа 800 (560)
от
числа 800 (560)
![]() числа 50 (40)
числа 50 (40)
![]() от
числа 66 (44)
от
числа 66 (44)
![]() от
числа 300 (160)
от
числа 300 (160)
2. В четвёртых классах 75 учащихся. Из
них![]() – хорошисты. Сколько учащихся 4-х классов учатся
на 4 и 5?
– хорошисты. Сколько учащихся 4-х классов учатся
на 4 и 5?
75 : 5 ∙ 3 = 45 (уч.)
Ответ: 45 учащихся.
Задача № 293

1) 21 : 7 = 3 (кг) – за 1 день
2) 36 : 3 = 12 (д.) – хватит 36 кг
3) 3 + 1 = 4 (кг) – стали расходовать за 1 день
4) 36 : 4 = 9 (д.)
О т в е т: 12 дней, 9 дней
Доли величин
Выделите цветом правильные ответы.
2/3 от 60 - это: 40; 20; 10
3/4 суток - это: 12 часов; 18 часов; 10 часов.

Урок 23. Сложение и вычитание значений величин
Цель:познакомиться со способами сложения и вычитания величин.
Задачи:
выполнять преобразования и другие действия с величинами.
Теоретический материал для самостоятельного изучения
Рассмотрите выражения и найдите лишнее
5400 - 2300
6 см 8 мм + 40 см
524м 95см +29м 85см
- Лишняя запись: 5400 - 2300
- Почему? (Выражение не содержит величин.)
Какие действия с величинами мы уже умеем выполнять? (Сравниваем, преобразуем, вычитаем, складываем)
- Выполним вычисления.
С первым выражением мы легко справляемся, а вот второе вызвало затруднение. Почему? Первое мы посчитали устно, а второе в уме выполнить трудно.
- Какова же цель нашего урока? (Научиться складывать и вычитать величины, выраженные разными единицами)
Попробуем выполнить сложение письменно. Что для этого нужно сделать? ( Привести к одинаковым единицам)
524 м 95 см = 52 495 см
29 м 85 см = 2 985 м, запишем выражение в столбик и выполним сложение

Получаем 55 480 см. Выразим результат в более крупных единицах 55480 см = 554 м 80 см, значит:
524 м 95 см +29 м 85 см = 554 м 80 см
Выполним вычитание
25 т 204 кг – 9 т 975 кг
Переведём величины в одинаковые единицы
25 т 204 кг = 25 204 кг
9 т 975 кг = 9 975 кг
Запишем выражение столбиком

Получилось 15 229 кг. Переведём в более крупные единицы 15 229 кг = 15 т 229 кг, значит:
25 т 204 кг – 9 т 975 кг = 15 т 229 кг.
Составим алгоритм письменного сложения и вычитания величин:
-
Сначала надо привести величины к одной единице;
-
Сложить или вычесть столбиком, как обычные многозначные числа.
-
Перевести полученный результат в более крупные единицы.
Вывод 1: Величины с разными единицами складываются и вычитаются как обычные числа.
Попробуем решить ещё один пример:
5ч 23 мин + 12 кг 300 г
Этот пример не имеет решения, так как нужно сложить разные величины
Вывод 2: Выполнять действия можно только с однородными величинами.
Выполним несколько тренировочных заданий:
Решим задачу:
Расстояние между городами А и В - 368км 576м. За два часа автомобиль проехал 214 км 865м. Какое расстояние ему ещё нужно проехать, чтобы добраться до места назначения? Нарисуйте схему к задаче.
Решение: 368 км 576 м
А____________________________В
214км 865м – ?
368 км 576 м – 214 км 865 м = 368 576 – 214 865 = 153 711 (м)

Ответ: осталось проехать 153 км 711 м
Запишите вычисления столбиком
12 м 86 см + 3 м 45 см = 16 м 31см

5 ч 48 мин + 35 мин = 383 мин = 6 ч 23 мин

45 т 275кг – 18 т 130 кг = 27 т 145 кг

26 кг 350 г – 24 кг 002 г = 2 кг 348 г

Однородные величины
В каждом ряду подчеркните лишние величины.
1. 600 дм, 3 м 15 см, 1 см 5 мм, 1кг 200г, 12дм
2. 3 ч 15 мин, 2 сут 12 ч, 3 га, 24 мин 15 с, 1 нед
3
Урок 24. Задачи на увеличение (уменьшение) числа на несколько единиц, выраженных в косвенной форме
. 5 кг 120 г, 4 т 500 кг, 3 ц 25 кг, 6 км 125 м, 235 г
Цель:формирование умения решать задачи в косвенной форме.
Задача:
научиться распознавать задачи нового вида среди других задач.
Теоретический материал для самостоятельного изучения
Рассмотрим рисунок 1:
-
-







 На 5 >
На 5 >?
-
Рис. 1. Иллюстрация к задаче
В первом ряду – 8 квадратов. Это на 5 больше, чем во втором ряду. Сколько квадратов во втором ряду – больше или меньше, чем 8?
Решение
Если в первом ряду больше на 5, то во втором ряду меньше на 5, а значит:
8 – 5 = 3 квадрата (рис. 2)
-
-







 На 5 >
На 5 >

 На 5 <
На 5 <
-
8 - 5 = 3
(Рис. 2. Иллюстрация к задаче)
Ответ: во втором ряду – 3 квадрата.
Рассмотрим новую задачу
В первом ряду – 5 треугольников. Это на 7 треугольников меньше, чем во втором ряду. Сколько треугольников во втором ряду – больше или меньше, чем 5?
Решение
Если в первом ряду треугольников меньше на 7, то
во втором – на 7 больше, а значит:
5 + 7 = 12 треугольников (рис. 3).
Ответ: 12 треугольников во втором ряду.
При решении следующих задач будет использован точно такой же ход рассуждений. Важно обращать внимание – большее или меньшее число требуется найти.
Задание
В спортивном отряде 16 девочек. Их на 7 больше, чем мальчиков. Сколько мальчиков в спортивном отряде?
Решение:
Слово «их» указывает на девочек. Если девочек на 7 больше, чем мальчиков, значит мальчиков – на 7 меньше, чем девочек. То есть, надо найти меньшее число:
16 – 7 = 9 (м.)
Ответ: в спортивном отряде 9 мальчиков.
Две задачи на сравнение
Задача 1.
У Пети есть марки с автомобилями и самолетами. Марок с автомобилями – 12. Марок с самолетами – на 4 больше, чем марок с автомобилями. Сколько марок с самолетами у Пети?
Задача 2.
У Пети есть марки с автомобилями и самолетами. Марок с автомобилями – 12. Их на 4 больше, чем марок с самолетами. Сколько марок с самолетами у Пети?
Эти задачи отличаются лишь одним предложением: в первой задаче сказано, что марок с самолетами на 4 больше, чем марок с автомобилями; во второй задаче – их на 4 больше, чем марок с самолетами.
Составим краткую запись.
Обозначим марки с автомобилями буквой А. Марки с самолетами - буквой С.
Задача 1
А. – 12 марок
С. –
? на 4 марки больше, чем А.

Найти надо большее число.
Решение:
12 + 4 = 16 (м.)
Ответ: у Пети16 марок с самолетами.
Задача 2
А. – 12 марок, на 4 марки больше, чем С.
С. – ?

Значит, надо найти меньшее число.
Решение:
12 - 4 = 8 (м.)
Ответ: у Пети 8 марок с самолетами.
Вывод: Отличие второй задачи – в её решении, и оно вызвано тем, что слово «больше» относится к известному числу, а значит неизвестное число – меньшее.
Задание
Прочитайте задачу (№319 стр. 68) и назовите, большее или меньшее число надо найти, затем решите задачу.
Задание 2
В соседнем доме 12 этажей. В нем на три этажа больше, чем в нашем. Сколько этажей в нашем доме?
Решение
Слово «в нем» указывает на соседний дом. В нем на 3 этажа больше, а значит в нашем на 3 этажа меньше, чем в соседнем. То есть, надо найти меньшее число.
12-3=9 этажей
Ответ: 9 этажей в нашем доме.
Вывод
На уроке мы познакомились с решением задач на увеличение (уменьшение) чисел, выраженных в косвенной форме. Чтобы не ошибиться в выборе действия при решении задач, необходимо обращать внимание – большее или меньшее число нужно найти.Слова «это», «в нем», «их» – слова-помощники. Они помогают определить большее или меньшее число в задаче нужно найти.
Выполним несколько тренировочных заданий.
-
Решите задачу:
Брату 17 лет. Он младше сестры на три года. Сколько лет сестре?
Рассуждайте так: если брат младше, значит сестра старше. Старше –находим большее число.
Проверьте себя: 17 + 3 = 20 лет сестре
-
Папе 35 лет. Он старше мамы на 3 года. Сколько лет маме?
Рассуждайте так: если папа старше. Значит, мама младше. Младше – находим меньшее число.
Проверьте себя: 35 - 3 = 32 года маме.
Выбор выражения для решения задачи
Масса лошади 350 кг, а масса телёнка 100 кг. Масса овцы в 9 раз меньше, чем масса лошади и телёнка вместе. С помощью какого выражения можно узнать ответ? Подчеркните верное.
3
Урок 25. Письменные приёмы умножения
50 + 100 - 9; ( 350 + 100 ) : 9; 350 + 100 +9
Цель:познакомиться с письменным приёмом умножения многозначного числа на однозначное.
Задача: научиться применять алгоритм умножения.
Теоретический материал для самостоятельного изучения
В предыдущих уроках было изучено умножение трёхзначных чисел на однозначное «столбиком». Вспомним письменный приём умножения трёхзначного числа на однозначное, 327 умножить на 2.
Записываем числа друг под другом, единицы под единицами.
-
-
3
2
7
х
2
-
Умножаем единицы 7 ∙ 2 = 14 это 1 дес. и 4 ед., 4 ед. пишем под единицами, 1 дес. запоминаем, его позже прибавим к десяткам.
-
-
1
3
2
7
х
2
4
-
Умножаем десятки 2 ∙ 2 = 4 дес. и прибавляем 1 дес., который получился при умножении десятков, получится 5. Записываем десятки под десятками.
-
-
1
3
2
7
х
2
5
4
-
Умножаем сотни 3 ∙ 2 = 6 сот. Подписываем сотни под сотнями. Получилось 654.
-
-
1
3
2
7
х
2
6
5
4
-
А теперь попробуем умножить четырёхзначное число на однозначное: 6 427 ∙ 3. Обнаружилась проблема, предыдущего алгоритма не хватает, т. к. первый множитель – многозначное число. Вывод: составить алгоритм письменного умножения многозначного числа на однозначное.
Записываем 3 под разрядом единиц многозначного числа.
-
-
6
4
2
7
х
3
-
Умножаем единицы 7 ∙ 3 = 21, записываем 1 под единицами, а 2 дес. запоминаем.
-
-
2
6
4
2
7
х
3
1
-
Умножаем десятки 2 ∙ 3 = 6 дес. плюс 2 дес. получится 8 дес., записываем под десятками.
-
-
2
6
4
2
7
х
3
8
1
-
Умножаем сотни 4 ∙ 3 = 12 сот., 2 записываю под сотнями, 1 запоминаю, пишем над единицами тысяч.
-
-
1
2
6
4
2
7
х
3
2
8
1
-
Умножаем единицы тысяч 6 ∙ 3 = 18, плюс 1, получится 19 ед. тыс. Записываем 9 под единицами тысяч, а 1 – под десятками тысяч. Получилось 19 281.
-
-
1
2
6
4
2
7
х
3
1
9
2
8
1
-
Познакомимся с приёмом письменного умножения, когда в записи первого множителя есть нули: 4 ∙ 21 803.
По переместительному свойству, при перемене мест множителей значение умножения не меняется, поэтому четыре умножить на двадцать одну тысячу восемьсот три равно двадцать одна тысяча восемьсот три умножить на четыре.
4 ∙21 803= 21 803 ∙ 4
Записываем 4 под разрядом единиц многозначного числа.
-
-
2
1
8
0
3
х
4
-
Умножаем единицы 3 ∙ 4 = 12, записываем 2 под единицами, а один десяток запоминаем.
-
-
1
2
1
8
0
3
х
4
2
-
Умножаем десятки 0 ∙ 4 = 0 дес. плюс 1 дес., получится 1 дес., записываю 1 дес. под десятками.
-
-
1
2
1
8
0
3
х
4
1
2
-
Умножаем сотни 8 ∙ 4 = 32 сот., 2 сот. записываем под сотнями, 3 запоминаем.
-
-
3
1
2
1
8
0
3
х
4
2
1
2
-
Умножаем единицы тысяч 1 ∙ 4 = 4 ед. тыс., плюс 3, получится 7 ед. тыс., пишем под единицами тысяч.
-
-
3
1
2
1
8
0
3
х
4
7
2
1
2
-
Умножаем десятки тысяч 2 ∙ 4 = 8 дес. тыс.Записываем 8 под десятками тысяч.
-
-
3
1
2
1
8
0
3
х
4
8
7
2
1
2
-
Получилось 87 212.
Рассмотрим использование приёмов при умножении величин: 2 км 175 м ∙ 6
В вычислениях значения величин принято выражать в одних единицах измерения, поэтому 2 км 175 м переводим в метры, получится 2 175 м.
Далее выполняем вычисления также, как умножение многозначного числа на однозначное:
-
-
1
4
3
2
1
7
5
х
6
1
3
0
5
0
-
Ответ: 13 050 м или 13 км 050 м.
Вывод: Таким образом, надо записать однозначное число под разрядом единиц многозначного числа. Потом умножить единицы и записать единицы под единицами, а десятки (если они есть) запомнить. Затем умножить десятки и прибавить количество десятков, которые запоминали. Записать десятки под десятками, а сотни (если они есть) запомнить. Аналогично умножить все разряды многозначного числа. Назвать число.
Выполним несколько тренировочных заданий:
-
Выберите правильный вариант вычисления:
Варианты ответов:

Правильный ответ:

Заполните пропуски в таблице:

Правильный ответ:

Решение примеров на умножение
Выполните вычисления, вставьте ответ.
8023 ∙ 4 = ![]()
34216 ∙ 2 = ![]()

Урок 26. Умножение чисел, оканчивающихся нулями
Цель: познакомиться с письменным приёмом умножения чисел, оканчивающихся нулями.
Задачи: применять алгоритм письменного умножения.
Теоретический материал для самостоятельного изучения
Рассмотрим выражение: 800 ∙ 7
Воспользуемся правилом умножения числа на произведение чисел, для этого заменим число 800 произведением чисел 8 и 100:
800 ∙ 7 = (8 ∙ 100) ∙ 7
При умножении произведения на число, сначала первый множитель умножаем на число(8 ∙ 7), а затем получившийся результат умножаем на второй множитель 100, ведь второй множитель - круглое число. Получим ответ 5 600.
800 ∙ 7 = (8 ∙ 100) ∙ 7 = (8 ∙ 7) ∙ 100 = 56 ∙ 100 = 5 600
Усложним задачу, решим следующее математическое выражение:
380 ∙ 9
Как и в предыдущем выражении, воспользуемся правилом умножения числа на произведение чисел, для этого заменим число 380 на произведение чисел 38 и 9:
380 ∙ 9 = (38 ∙ 10) ∙ 9
При умножении произведения на число, сначала умножаем на число первый множитель (38 ∙ 9), а затем получившийся результат умножим на второй множитель 10, ведь второй множитель – круглое число.
380 ∙ 9 = (38 ∙ 10) ∙ 9 = (38 ∙ 9) ∙ 10
Возникла проблема: надо умножить двузначное число на однозначное, подобного рода выражения в уме решить сложнее, т. к. увеличивается количество действий.
Сначала надо умножить единицы 8 ∙ 9 = 72. Затем десятки 30 ∙ 9 = 270, сложить полученные результаты и полученный результат умножить на десять 342 ∙ 10. Получили 3 420.
380 ∙ 9 = (38 ∙10) ∙ 9 = (38 ∙ 9) ∙ 10 = (8 ∙ 9 + 30 ∙ 9) ∙ 10 = 342 ∙ 10 = 3 420
Вывод: устно такие вычисления выполнять неудобно.
Рассмотрим письменный случай умножения, когда первый множитель заканчивается нулями: 8 400 ∙ 7 . Пишем однозначный множитель 7 под значимыми цифрами первого множителя.
-
-
8
4
0
0
х
7
-
Умножаем, не глядя на нули: 4 ∙ 7 = 28. Записываем 8 под цифрой 7, а 2 тыс. запоминаем.
-
-
2
8
4
0
0
х
7
8
-
Умножаем тысячи: 8 ∙ 7 = 56, и прибавим тысячи, которые запоминали: 56 + 2 = 58. Записываем 58 перед цифрой 8.
-
-
2
8
4
0
0
х
7
5
8
8
-
Приписываем столько нулей, столько в обоих множителях вместе. Ответ: 58 800.
-
-
2
8
4
0
0
х
7
5
8
8
0
0
-
Рассмотрим ещё один пример умножения, когда первый множитель заканчивается нулями: 30 800 ∙ 5.
Пишем однозначный множитель 5 под значимыми цифрами первого множителя.
-
-
3
0
8
0
0
х
5
-
Умножаем, не глядя на нули: 8 ∙ 5 = 40. Записываем 0 под цифрой 5, а 4 тыс. запоминаем.
-
-
4
3
0
8
0
0
х
5
0
-
Умножаем единицы тысяч: 0 ∙ 5 = 0 и прибавим тысячи, которые запоминали: 0 + 4 =4. Записываем 4 перед цифрой 0.
-
-
4
3
0
8
0
0
х
5
4
0
-
Умножаем десятки тысяч: 3 ∙ 5 = 15, записываем 15 перед цифрой 4.
-
-
4
3
0
8
0
0
х
5
1
5
4
0
-
Приписываем столько нулей, сколько нулей в первом множителе.
-
-
4
3
0
8
0
0
х
5
1
5
4
0
0
0
-
Ответ: 154 000
Вывод: Итак, чтобы умножить многозначные числа, оканчивающиеся нулём, на однозначные, надо записать второй множитель так, чтобы нули остались в стороне. Умножить многозначное число на однозначное, не обращая внимание на нули. К полученному результату приписать столько нулей, сколько их было в первом множителе, прочитать ответ.
Выполним несколько тренировочных заданий:
Выполнить вычисления, вставить ответ:

Правильный ответ:
19 200 · 9 = 172 800
570 300 ·4 = 2 281 200
Какое число нужно увеличить в 7 раз, чтобы получить 8 400? Выделите цветом правильный ответ:
Варианты ответов:
58 800
8 407
8 393
1 200
Правильный ответ:
1 200
К каждой позиции первого столбца подберите соответствующую позицию второго:
Варианты ответов: Правильный ответ:
-
-
6 700 ∙ 7
194 400
24 300 ∙ 8
254 800
53 780 ∙ 6
46 900
63 700 ∙ 4
322 680
-
|
6 700 ∙ 7 |
46 900 |
|
24 300 ∙ 8 |
194 400 |
|
53 780 ∙ 6 |
322 680 |
|
63 700 ∙ 4 |
254 800 |
Умножение чисел, оканчивающихся нулями
Выполните вычисления, вставьте ответы в пропуски:
19200 ∙ 9 = ![]()
570300 ∙ 4 = ![]()

Урок 27. Решение уравнений вида: х ∙ 8 = 26 + 70, х : 6 = 18 ∙ 5, 80 : х = 46 – 30
Цель: познакомиться с решением сложных уравнений.
Задачи:
повторить компоненты умножения и деления;
научиться решать уравнения нового вида.
Теоретический материал для самостоятельного изучения
Вспомните, как связаны между собой числа при умножении.
Посмотрите, множитель 20, множитель 3, произведение 60.
Если 60 разделить на 20, получится 3.
Если 60 разделить на 3, получится 20.
Значит, если произведение разделить на один из множителей, то получится другой множитель. Это правило потребуется при решении уравнений, в которых неизвестен один из множителей.
20 ∙ 3 = 60
60 : 20 = 3
60 : 3 = 20
Решим уравнение:
произведение неизвестного числа и числа 7 равно числу 91. В нем неизвестен первый множитель. Как его найти? Для нахождения неизвестного первого множителя надо произведение 91 разделить на известный множитель 7. Делим 91 на 7 - получаем 13. Выполним проверку. Подставим в уравнение вместо икс число 13.
13 умножить на 7 получим 91. Получили верное равенство:
91 равно девяносто одному. Значит, решили правильно.
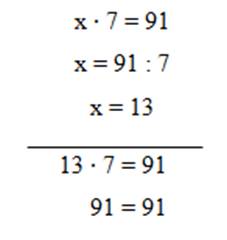
А теперь догадайтесь, как решить уравнение: произведение неизвестного числа и числа 7 равно сумме чисел восьмидесяти и одиннадцати. Найдем значение выражения в правой части уравнения: 80 плюс 11 равно 91. Тем самым мы получили уравнение, которое уже умеем решать. Посмотрите, как записывается решение этого уравнения и его проверка.
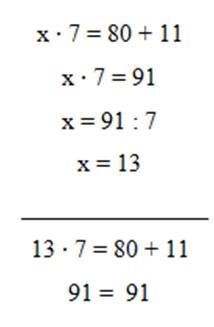
Вспомним, как связаны между собой числа при делении.
Посмотрите: делимое 15, делитель 3, частное равно пяти.
Если делитель 3 умножить на частное 5, получим делимое 15.
Если делимое 15 разделить на частное 5, получим делитель 3.
15 : 3 = 5
3 ∙ 5 = 15
15 : 5 = 3
Знание связей между делимым, делителем и частным потребуется для решения уравнений, в которых неизвестен один из компонентов: делимое или делитель. Посмотрите, как решаются такие уравнения. В первом уравнении неизвестно делимое. Чтобы его найти, нужно делитель 3 умножить на частное 9.
Во втором уравнении неизвестен делитель. Чтобы его найти, нужно делимое 45 разделить на частное 3.
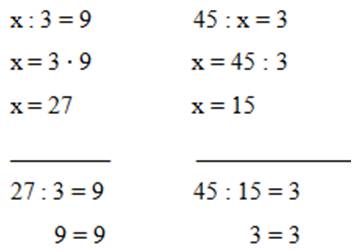
А как решить такое уравнение? Вычислим произведение в правой части: 18 умножить на 5 получим 90. Получается уравнение, в котором неизвестно делимое. Вы уже знаете, как его решать. Выполним проверку решения уравнения. Подставим число 540 вместо икс, вычислим левую часть и правую часть выражения: 90 равно 90. Значит уравнение решили верно.
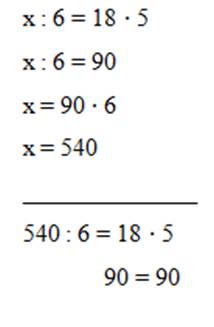
Задания тренировочного модуля:
1.К каждой позиции первого столбца подберите соответствующую позицию второго.
|
91 : х = 13 |
x = 20 |
|
х : 21=4 |
x = 7 |
|
24 ∙x = 96 |
x = 84 |
|
x∙ 3 = 60 |
x = 4 |
Правильный ответ:
-
-
91 : х = 13
x = 7
х : 21= 4
x = 84
24 ∙x = 96
x = 4
x∙3 = 60
x = 20
-
2. Выполните вычисления и выделите верный ответ:
7 ∙x = 140 : 2
Варианты ответов: 10, 400, 2
Правильный вариант:
10
3.Решите уравнение, подчеркните правильный ответ:
(80 : у) ∙ 700 = 2800
Варианты ответов:
2, 4, 20
Правильные варианты: 20
Математические термины
Найдите и выделите цветом слова по теме изучения.
Подсказка
Среди букв спрятались 4 слова.
|
о |
а |
ю |
л |
р |
у |
c |
к |
ы |
о |
|
о |
л |
щ |
й |
е |
ы |
х |
о |
щ |
ж |
|
ц |
г |
й |
c |
ш |
щ |
г |
р |
м |
б |
|
у |
о |
у |
о |
е |
ы |
й |
е |
о |
х |
|
п |
р |
э |
о |
н |
р |
у |
н |
а |
п |
|
е |
и |
б |
ё |
и |
е |
ц |
ь |
ю |
ц |
|
ы |
т |
c |
ю |
е |
у |
я |
ю |
у |
и |
|
э |
м |
ы |
б |
у |
к |
ф |
ц |
ц |
ю |
|
з |
е |
г |
к |
c |
р |
л |
п |
п |
р |
|
у |
р |
а |
в |
н |
е |
н |
и |
е |
о |

Урок 28. Деление
Цель: вспомнить письменное деление.
Задачи:
повторить действия с многозначными числами;
научить делению трёхзначного числа на однозначное.
Теоретический материал для самостоятельного изучения:
Вы уже умеете делить числа в столбик. Рассмотрим теперь более сложный случай.
Фермер Василий собрал в своем саду 372 кг вишни. Он и его 3 сына поделили ягоды поровну между собой и отправились на рынок. Сколько килограммов вишни должен продать каждый член семьи?


Начинаем деление с сотен. Сотен 3, но 3 сотни нельзя разделить на 4 так, чтобы в частном получились сотни. Делим десятки. Три сотни и 7 десятков – это 37 десятков. Делим 37 десятков на 4. В частном будет 9. Умножаем 9 на 4, чтобы узнать сколько десятков разделили. Получается, что разделили 36 десятков. Вычитаем из тридцати семи 36, получается 1. Значит, осталось разделить еще 1 десяток.
Переходим к делению единиц. Записываем две единицы рядом с остатком от деления десятков. 1десяток и 2 единицы – это 12 единиц. Делим 12 на 4, в частном 3. Умножаем 3 на 4, получаем 12. Вычитаем 12 из двенадцати. Осталось 0. Читаем ответ: 93.

Итак, важно запомнить: деление трехзначных чисел в столбик происходит поразрядно и начинается с высшего разряда. При нахождении каждой цифры частного, надо вспомнить три операции: деление, умножение и вычитание.
Рассмотрим еще один случай деления.
 Слив фермер собрал 621 кг. Поделил их между тремя
сыновьями и отправил их на рынок. Сколько килограммов слив должен
продать каждый сын?
Слив фермер собрал 621 кг. Поделил их между тремя
сыновьями и отправил их на рынок. Сколько килограммов слив должен
продать каждый сын?

Разделим 621 на 3. Начнем деление с сотен. Делим 6 сотен на 3, в частном будет 2 сотни. Умножаем 2 на 3, чтобы узнать, сколько сотен разделили. Получается, разделили 6 сотен. Вычитаем 6 из шести, получаем 0. Значит, все сотни разделили. Ноль не пишем. Приступаем к делению десятков. Записываем 2 десятка ниже. При делении числа 2 на 3 получается 0. Умножаем 0 на 3, чтобы узнать сколько десятков разделили. Получается, что разделили 0 десятков. Вычитаем из двух ноль. Получается 2. Нам по-прежнему осталось разделить 2 десятка. Переходим к делению единиц. Записываем единицу ниже рядом с остатком 2. Два десятка и одна единица – это 21 единица. 21 делим на 3. В частном получаем 7 единиц. Умножаем 7 на 3, чтобы узнать сколько разделили единиц. Вычитаем 21 из двадцати одного, чтобы узнать остаток от деления единиц. Остаток равен 0. Читаем ответ: двести семь.
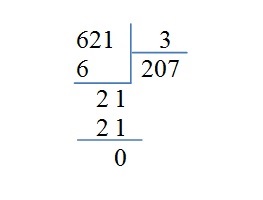
Задания тренировочного модуля:
1. Найдите значения выражения, считая устно или письменно:
268 : 2
Варианты ответов:
134
143
434
Правильный вариант:
134
2. Вставьте пропущенные знаки (> < =)
356 : 2 ∙ 972 : 4
Варианты ответов:
356 : 2 < 972 : 4
356 : 2 > 972 : 4
356 : 2 = 972 : 4
Правильный вариант:
356 : 2 < 972 : 4
Деление с остатком
Выполните вычисления.
Подсказка
Обратите внимание на точки и пробелы.
Пример: 10 : 9 = 1 (ост. 1)
56
: 15 = ![]()
92
: 30 = ![]()
399
: 9 = ![]()

Урок 29. Деление многозначного числа на однозначное
Цель: познакомить с делением многозначного числа на однозначное.
Задачи:
повторить арифметические действия;
научить делению чисел.
Теоретический материал для самостоятельного изучения:
Посмотрите на выражения. Что их объединяет? Это числовые выражения на действие деление, делитель – однозначное число. Как вы думаете, какое лишнее? Да, вы правы: второе выражение лишнее, потому что делимое – многозначное число. Мы еще не умеем решать такие выражения. Этому и предстоит нам научиться.
852 : 3, 7854 : 7, 768 : 8, 915 : 3
Давайте вспомним, как делить трехзначное число на однозначное. Разделим 852 на 3 столбиком. Начинаем деление с сотен – это первое неполное делимое: в частном будет три цифры. Делим 8 на 3, в частном будет 2 сотни. Умножаем 2 на 3, чтобы узнать сколько сотен разделили. Получается 6 сотен разделили. Вычитаем 6 из восьми, получаем 2. Столько сотен осталось. Сравниваем остаток 2 с делителем : 2 меньше трех, значит цифра в частном побрана верно. Сносим 5 десятков. Две сотни и пять десятков – это 25 десятков. Делим десятки на 3. В частном пишем цифру 8. Умножаем 8 на 3, получаем 24. Столько десятков разделили. Вычитаем 24 из двадцати пяти, остаток 1. Один меньше трех. Сносим единицы. Один десяток и две единицы – это 12 единиц. Делим на 3, берем по 4. Четыре умножаем на 3, получаем 12. Двенадцать вычитаем из двенадцати. Остаток 0. Деление завершили. Читаем результат: 284.
 Рассмотрим деление числа пяти тысяч пятьсот
сорока четырех на 6. Деление начинать надо с высшего разряда тысяч.
Но 5000 нельзя разделить на 6, чтобы в частном были тысячи. Поэтому
будем делить сотни.
Рассмотрим деление числа пяти тысяч пятьсот
сорока четырех на 6. Деление начинать надо с высшего разряда тысяч.
Но 5000 нельзя разделить на 6, чтобы в частном были тысячи. Поэтому
будем делить сотни.
55 сотен мы сможем разделить на 6 так, чтобы в частном получились сотни. В этом случае говорят 55 – это первое неполное делимое числа 5544. Посмотри, как можно его выделить. Теперь определим количество цифр в частном. Так как деление мы начали с сотен, в частном получим три цифры. Обозначим тремя точками места, где будем записывать цифры частного. Теперь находим первую цифру частного: для этого 55 делим на 6, получаем 9. Пишем 9 на месте сотен в частном. Умножаем 9 на 6, получаем 54. Столько сотен разделили. Записываем 54 под неполным делителем 55. Находим остаток, для этого вычитаем 54 из пятидесяти пяти. Получим 1. Столько сотен разделили. Теперь надо сравнить остаток с делителем: 1 меньше 6, значит цифра 9 в частном подобрана верно. Деление еще не закончено, так как можно образовать следующее неполное делимое из десятков. При делении сотен осталась 1 сотня, добавим еще 4 десятка. Всего 14 десятков. И повторяем все действия пункта по плану. Первые два пункта повторять не надо.
 Делим 14 на 6, получаем 2. Столько десятков будет
в частном. Умножим 2 на 6. Получаем 12. Столько десятков разделили.
Вычитаем 12 из четырнадцати, получаем 2. Столько десятков осталось
разделить. Сравниваем остаток с делителем: 2 меньше шести, значит
цифра 2 в частном побрана верно.
Делим 14 на 6, получаем 2. Столько десятков будет
в частном. Умножим 2 на 6. Получаем 12. Столько десятков разделили.
Вычитаем 12 из четырнадцати, получаем 2. Столько десятков осталось
разделить. Сравниваем остаток с делителем: 2 меньше шести, значит
цифра 2 в частном побрана верно.
Деление еще не закончено. Образуем следующее неполное делимое из единиц. При делении десятков осталось 2 десятка. Добавим 4 единицы, получаем 24 единицы. Делим 24 на 6, получаем 4 – столько единиц мы разделили. Запишем цифру 4 на месте единиц в частном. Умножаем 4на 6 , получаем 24. Столько единиц разделили. Вычитаем 24 из двадцати четырех. Осталось 0, он меньше делителя. Значит число единиц подобрано верно. Больше неполных делимых образовать нельзя. Значит деление завершено. Получили 924.
Задания тренировочного модуля:
1.Найдите значения выражения, считая устно или письменно:
6524 : 7
Варианты ответов:
1.842
2.934
3.932
Правильный вариант:
932
2. Выполните вычисления:
(17437 – 10297) : 7
Правильный вариант:
1020
3. Допишите предложения:
Чтобы найти неизвестный множитель, нужно…
Чтобы найти неизвестный делитель, нужно...
Правильные варианты:
1) произведение разделить на другой множитель
2) делимое разделить на частное
Порядок действий в числовых выражениях

Урок 30. Задачи на увеличение (уменьшение) числа в несколько раз, выраженные в косвенной форме
Цель: научить решать задачи на увеличение (уменьшение) в несколько раз в косвенной форме.
Задачи: познакомить учащихся с решением задач нового вида.
Теоретический материал для самостоятельного изучения
Решите задачу:
В 4 «а» классе 25 учеников, это на 1 ученика больше, чем в
4 «б» классе. Сколько учеников в 4 «б» классе?
Вспомнили, к какому типу относится эта задача? Верно: уменьшение числа на несколько единиц в косвенной форме. Давайте составим задачу с этими данными в прямой форме.
В 4 «а» классе 25 учеников, а в 4 «б» классе на 1 ученика меньше. Сколько учеников в 4 «б» классе?
Сегодня мы продолжим учиться различать задачи с формулировками в прямой и косвенной форме.
Перед вами условие задачи:
Масса тыквы 8кг. Кабачок в 2 раза легче тыквы. Какова масса кабачка?

По условию задачи кабачок меньше тыквы в 2 раза.
Посмотрите, какой схематический рисунок можно сделать к задаче:
на нем кружком обозначена масса тыквы, овалом – масса кабачка Стрелочкой показано, как связаны масса тыквы и масса кабачка. Такие задачи вы уже умеете решать.
8 кг в 2 раза меньше ?
Поэтому для ответа на вопрос задачи надо массу тыквы разделить на два.
8 : 2 = 4 (кг)
Но если кабачок меньше тыквы, о тыкве можно сказать: она тяжелее кабачка и ее масса в два раза больше, чем масса кабачка. Поэтому условие нашей задачи можно сформулировать по-другому:
Тыква, масса которой 8 кг, в 2 раза тяжелее кабачка. Какова масса кабачка?
Посмотрите, что изменилось на схематическом рисунке к этой задаче. На этом рисунке стрелка направлена в противоположную сторону. Теперь она показывает, как связана масса тыквы с массой кабачка.
8 кг в 2 раза тяжелее ?
Обратите внимание, что решение задачи не изменилось, хотя в условии вместо слова легче используется слово тяжелее.
8 : 2 = 4 (кг)
Поэтому в решении задач, в которых речь идет об увеличении или уменьшении величин в несколько раз, сначала сравни неизвестную величину с той, которая дана в задаче. Это поможет вам правильно определить каким действием (делением или умножением) решается задача. В нашей задаче масса кабачка меньше, поэтому задача решается делением.
Давайте решим еще одну задачу:
Маша прочитала 12 страниц, это в 3 раза меньше, чем прочитал Юра. Сколько страниц прочитал Юра?
К этой задаче можно сделать такой схематический рисунок. На нем количество страниц, прочитанных Машей, обозначено квадратом, а количество страниц, прочитанных Юрой – прямоугольником. Для решения задачи нам важно понять, Юра прочитал больше Маши или меньше. Если Маша прочитала в 3 раза меньше, чем Юра, значит Юра прочитал больше в 3 раза. Поэтому задача решается действием умножения: 12 умножить на 3 получаем 36.
12 в 3 раза меньше ?
в 3 раза больше
12 ∙ 3 = 36 (стр.)
Ответ: 36 страниц
Задания тренировочного модуля:
Решите задачу, выберите верный ответ:
В первом аквариуме 9 рыбок, это на 3 рыбки больше, чем во втором аквариуме. Сколько рыбок во втором аквариуме?
Варианты ответа:
1. 27;
2. 3;
4. 12;
5. 6.
Правильный вариант: 6
2. Подберите к задаче верное решение:
Белка принесла в дупло утром 24 ореха, что в 4 раза больше, чем вечером. Сколько орехов принесла белка вечером?
24 ∙ 4 24 : 4
Правильный вариант: 24 : 4 = 6
3. Сравните неизвестную величину с данной в задаче. Выберите действие, которым решается задача, и укажите правильный ответ.
У фермера 8 коров. Это в 16 раз меньше, чем овец. Сколько овец у фермера?
У фермера ○ овец больше, чем коров
У фермера ○ овец меньше, чем коров
Задача решается:
○ умножением ○ делением ○ сложением ○ вычитанием
Ответ:
○ 2 овцы ○ 128 овец ○ 24 овцы ○ 8 овец
Задачи на увеличение (уменьшение) числа в несколько раз, выраженные в косвенной форме
Для школы купили 4 компьютера по с р. каждый и телевизор. За всю покупку заплатили k р.
Объясните, что обозначают выражения:
с * 4, k – с * 4. Найдите значения выражений при с = 10000, k = 45000
![]()
![]()

Урок 31. Деление многозначного числа на однозначное число с записью в частном нулей
Цель: научить делить многозначные числа на однозначные, когда в записи частного есть нули.
Задача:
научить делить многозначные числа на однозначные.
Теоретический материал для самостоятельного изучения
Вспомните алгоритм деления многозначного числа на однозначное число.
Алгоритм деления
1. Выделяем первое неполное делимое.
2. Определяем, сколько цифр будет в частном.
3. Делим неполное делимое на делитель.
4. Умножаем делитель на полученное число.
5. Находим остаток от деления вычитанием.
6. Сравниваем остаток с делителем.
7. Есть следующее неполное делимое?
Рассмотрим деление 1560 на 6. Выделяем первое неполное делимое числа 1560. Одну тысячу нельзя разделить на 6 так, чтобы в частном были тысячи. Поэтому будем делить сотни. 15 сотен мы уже сможем разделить так, чтобы в частном были сотни. Значит 15 -это первое неполное делимое числа одна 1560. Теперь определим количество цифр в частном. Так как деление мы начинаем с сотен, значит, в частном будет три цифры. Находим первую цифру частного: для этого 15 делим на 6. Получается 2, пишем цифру 2 на месте сотен в частном. Умножим 6 на 2, получим 12. Столько сотен разделили. Записываем число 12 под неполным делимым 15. Находим остаток от деления: для этого вычитаем 12 из пятнадцати. Получится 3 – столько сотен осталось разделить. Теперь надо сравнить остаток с делителем: 3 меньше 6 – значит, цифру частного подобрали верно. Деление еще не закончено. Образуем следующее неполное делимое из десятков. При делении сотен осталось три сотни, добавим шесть десятков – получаем второе неполное делимое 36 десятков. Делим 36 на 6, получим 6. Столько десятков будет в частном. Умножим 6 на 6, получим 36 – столько десятков разделили. Вычтем 36 из тридцати шести, получим 0. Значит, разделили все десятки. Но деление еще не закончилось, так как мы не делили единицы. У нас должно быть еще одно неполное делимое. Поэтому чтобы следующее неполное делимое не началось с нуля, не будем записывать ноль как разность чисел тридцати шести и тридцати шести. Остаток 0 меньше 6, значит, цифра частного подобрана верно. Образуем следующее неполное делимое: это 0 единиц. Делим 0 на 6, получим 0. Записываем число 0 на месте единиц в частном. Умножаем 0 на 6, получаем 0. Вычтем 0 из 0, получим 0. Остаток меньше делителя, значит, число единиц в частном подобрано верно. Мы разделили единицы, больше неполных делимых образовать нельзя, значит, деление числа 1560 на 6 завершено. Получили в частном число 260.
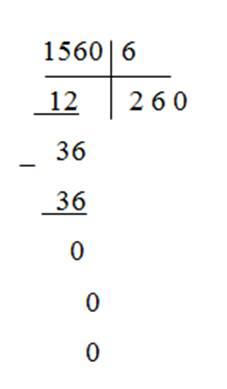
А теперь рассмотрите более краткую запись этого же примера.
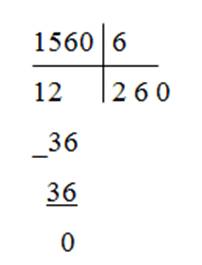
Задания тренировочного модуля:
1. Объясните, какой из учеников прав? При делении числа 32056 на 8 первый ученик получил в частном 407, второй – 4007, а третий – 47.
Правильный ответ: 4007
2. Найдите значение числового выражения.
5 ∙ 23417 – 10305 : 5
Варианты ответов:
1.11524
2.115240
3.115024
Правильный вариант:
115 024
Ряд чисел
Вставьте пропущенное число.
630, 560, 490, ![]() ,
350
,
350
Решение задач
Статистики подсчитали, в среднем за день человек делает 20000 шагов. А сколько шагов он делает за год? Пройдите лабиринт к правильному ответу.
1) 7 300 000 шагов
2) 730 000 шагов
3) 73 000 шагов
Ряд чисел
Догадайтесь, каким должно быть следующее число в ряду. Запишите еще три числа.
112 223 445 556

Урок 32. Задачи на пропорциональное деление. Закрепление изученного материала
Цель: закрепить умение решать задачи на пропорциональное деление.
Задачи:
научиться составлять план решения;
научиться решать задачи на пропорциональное деление арифметическим способом.
Теоретический материал для самостоятельного изучения
Задачи на пропорциональное деление получили свое название по способу их решения. Чтобы дать ответ на вопрос задачи необходимо составить некоторую пропорцию и рассчитать, как соотносятся между собой искомые величины.
Рассмотрим решение задачи на пропорциональное деление на примере:
Задача: Двое рабочих заработали 9000 рублей. Один работал 2 недели, а другой 8 недель. Сколько денег заработал каждый?
Решение: Исходя из условия задачи, можно найти, как оплачивается одна неделя такой работы:
9000 : (8 + 2) = 900 рублей за неделю.
Теперь можно рассчитать, сколько заработал каждый рабочий пропорционально времени потраченному каждым из них на работу:
900 · 2 = 1800 рублей - один рабочий;
900 · 8 = 7200 рублей - другой рабочий.
Ответ: 1800 и 7200 рублей
Прочитайте задачу.
Два куска одинаковой ткани стоят 360 рублей. В одном из них 5м, а в другом – 4м. Сколько стоит каждый кусок ткани?

Повторите алгоритм решения задачи.
- Определить, что известно.
- Что нужно найти.
- Выполнить краткую запись.
- Записать решение.
Выполните краткую запись в виде таблицы:

Узнаем, сколько всего купили ткани.
5 + 4 = 9 (м)
Найдем цену ткани.
360 : 9 = 40 (р.)
Посчитаем, сколько стоит первый кусок ткани.
40 ∙ 5 = 200 (р.)
Посчитаем, сколько стоит второй кусок ткани.
40 ∙ 4 = 160 (р.)
Ответ: за первый кусок ткани заплатили 200 рублей, за второй – 160 рублей.
Проверьте правильность решения: сложите стоимость двух кусков ткани.
200 + 160 = 360 (р.)
Задания тренировочного модуля:
Прочитай задачу:
В одном мешке было 56 кг муки, а в другом – 24 кг. Эту муку расфасовали в 40 пакетов поровну. Сколько потребовалось пакетов для расфасовки муки из каждого мешка?
Расставь порядок действий и запиши пояснения.
1. 80 : 40 = 2 (кг)
2. 56 + 24 = 80 (кг)
3. 24 : 2 = 12 (п.)
4. 56 : 2 = 28 (п.)
Правильный вариант:
2. В одном пакете
1. Всего было муки
4. Для муки из второго мешка
3. Для муки из первого мешка
2. Прочитай задачу и выбери те вопросы, на которые можно ответить, пользуясь условием.
Двое рабочих заработали 840 р. Первый работал 5
недель, а второй — 7 недель. Сколько денег заработал каждый
рабочий?
Варианты ответов:
-
Сколько денег заработал первый рабочий?
-
Сколько всего рабочих работало на заводе?
-
Сколько недель рабочие работали вместе?
-
Сколько денег они заработали?
-
Какую работу выполняли рабочие?
-
Сколько они зарабатывали за неделю?
-
Сколько денег заработал второй рабочий?
Правильный вариант:
-
Сколько денег заработал первый рабочий?
-
Сколько недель рабочие работали вместе?
-
Сколько денег они заработали?
-
Сколько они зарабатывали за неделю?
-
Сколько денег заработал второй рабочий?

Урок 33. Повторение пройденного материала по теме «Алгоритмы письменного умножения и деления»
Цель: систематизировать знания по теме «Числа, которые больше 1000».
Задачи:
совершенствовать вычислительные навыки;
решать задачи и уравнения.
Теоретический материал для самостоятельного изучения
На уроке мы вспомним:
Алгоритмы письменного умножения и деления многозначного числа на однозначное.
Сможем:
Совершенствовать вычислительные навыки в процессе решения задач, выражений, уравнений.
Повторим: алгоритм умножения многозначного числа на однозначное.

Повторим алгоритм деления многозначного числа на однозначное

Повторим письменный прием умножения многозначного числа на однозначное, умножим 15 719 ∙ 5
Записываем числа друг под другом: единицы под единицами

Умножаем единицы 9 на 5, получится 45.
45 – это 4 десятка и 5 единиц
5 единиц пишем под единицами
4 десятка запоминаем,
его позже прибавим к десяткам
Умножаем десятки 1 ∙ 5 = 5 и прибавляем 4 десятка, который получился при умножении десятков, получится 9
Записываем десятки под десятками
Умножаем сотни 7 ∙ 5 = 35.
35 – это 5сотен и 3 тысячи.
Записываем 5 сотен под сотнями, 3 тысячи запоминаем. Их позже прибавим к тысячам.
Умножаем тысячи: 5 ∙ 5=25 и прибавляем 3 тысячи, которые получились при умножении сотен. Получается 28.
8 тысяч записываем под тысячами, а 2десятка тысяч запоминаем. Их позже прибавим к десяткам тысяч.
Умножаем десятки тысяч: 1 ∙ 5 = 5 и прибавляем 2 десятка тысяч, которые получились при умножении тысяч. Получается 7. Записываем под десятками тысяч.
Получилось 78595.
Повторим письменный прием деления многозначного числа на однозначное
83 216 : 4
Помним, что при письменном делении запись ведется в столбик
Делим десятки тысяч.
Разделим: 8 : 4, в частном будет 2 десятка тысяч.

Умножим 4 на 2 = 8, это значит, что разделили 8десятков тысяч.
Вычтем из 8 -8=0.
Делим тысячи:
3:4. В частном будет 0 тысяч
Сносим 2 сотни. 32 сотни делим на 4, получается 8.
8 ∙ 4 = 32. Вычтем 32 – 32 = 0

Делим десятки: 1 : 4 = 0. Остаток 1. Сносим 6 единиц. 16:4 = 4.

Умножаем 4 на 4, получается 16.
16 – 16 = 0.
Деление закончили.
Читаем ответ: 20 804.
Задания тренировочного модуля:
1. Найдите значение выражений:


Правильный вариант:
824 · 9 = 7416
916 · 3 = 2748
2. Найдите значение выражений:

Правильный вариант:
7410 : 3 = 2470
4850 : 5 = 970
Деление с остатком
Выполните деление и запишите неполное частное и остаток.
33 : 8
= ![]() ост.
ост. ![]()
244 : 7
= ![]() ост.
ост. ![]()
6 539 : 5
= ![]() ост.
ост. ![]()
130 : 400
= ![]() ост.
ост. ![]()

Урок 34. Решение текстовых задач на пропорциональное деление
Цель: закрепить умение решать задачи на пропорциональное деление.
Задачи:
научиться составлять план решения;
научиться решать задачи на пропорциональное деление арифметическим способом.
Теоретический материал для самостоятельного изучения
Прочитаем задачу.
Для подготовки к новогоднему празднику в первый день купили 5 гирлянд, а во второй – ещё 3 гирлянды по той же цене. Всего заплатили 640 рублей. Сколько денег заплатили в первый день и сколько во второй?
Запишем условие задачи в таблицу.
В первый день купили пять гирлянд.
Во второй – еще три гирлянды.
Всего заплатили шестьсот сорок рублей. Это общая стоимость покупки.
Что можно сказать о цене гирлянды? У всех гирлянд она одинаковая.
В задаче нужно узнать, сколько заплатили в первый день, а сколько – во второй.
Как вы думаете, одинаковую ли сумму денег заплатили в первый и во второй дни? Конечно же, нет. Ведь в первый день купили больше гирлянд, чем во второй. Поэтому денег в первый день потратили больше, чем во второй.
-
-
Цена
Количество
Стоимость
1 день
Одинаковая
5г.
2 день
3г.
Всего
640руб.
-
Нам известна стоимость покупок, сделанных в 1 и 2 дни. Чтобы узнать стоимость покупки, надо знать цену товара и его количество. Количество нам дано, а вот цена неизвестна. Как ее найти? Посмотрите в таблицу. В ней указана еще одна величина, данная в задаче. Это общая стоимость гирлянд, купленных за два дня. Если мы узнаем общее количество купленных гирлянд, значит, сможем найти и цену одной гирлянды, поскольку все гирлянды куплены по одной цене.
Таким образом, план решения этой задачи будет таким:
-
Найдем количество купленных гирлянд.
-
Узнаем цену одной гирлянды.
-
Найдем стоимость гирлянд, купленных в первый и во второй дни.
Запишем решение.
Пять плюс три равно восемь гирлянд – это общее количество купленных гирлянд за два дня.
5+3=8 (г.)
Разделим общую стоимость покупок шестьсот сорок рублей на общее количество гирлянд, получим цену одной гирлянды. Это восемьдесят рублей.
640:8=80 (р.)
Узнаем, сколько денег заплатили в первый день. Восемьдесят умножим на пять, получим четыреста рублей.
80∙5=400 (р.)
Узнаем, сколько денег заплатили во второй день. Восемьдесят умножим на три, получается двести сорок рублей.
80∙3=240 (р.)
А теперь проверим правильность решения задачи. В первый день потратили четыреста рублей, во второй день – двести сорок рублей. Всего – шестьсот сорок рублей. Получилась та величина, которая дана в условии. Можем записать ответ.
400+240 = 640 (р.)
Ответ: 400 рублей – в первый день,
240 рублей – во второй день.
Задания тренировочного модуля:
Прочитайте задачу, вычислите значения выражений и укажите, что оно обозначает.
На обед в школьную столовую пришли ученики 4А и 4Б классов, всего 52 человека. Ученики 4А класса заняли 6 столов, а ученики 4Б класса 7 таких же столов. За каждым столом оказалось одинаковое количество человек.
-
6 + 7=
-
52 : (6 + 7) =
-
52 : (6 + 7) ∙ 6 =
-
52 : ( 6 + 7) ∙ 7 =
Варианты ответов:
На экране поместить таблички с числами от 1 до 30 для выбора ответа.
Выпадающий список:
Количество человек из 4Б класса.
Количество человек за одним столом.
Количество столов, занятых учениками 4А и 4Б классов.
Количество человек из 4А класса
Правильный вариант/варианты (или правильные комбинации вариантов):
-
6 + 7 = 13 – Количество столов, занятых учениками 4А и 4Б классов.
-
52 : (6 + 7) = 4 – Количество человек за одним столом.
-
52 : (6 + 7) ∙ 6 = 24 – Количество человек из 4А класса
-
52 : (6 + 7) ∙ 7 = 28 – Количество человек из 4Б класса
Прочитайте задачу и заполните таблицу.
В двух домах всего 336 квартир. Число квартир на каждом этаже в обоих домах одинаково. Но в первом доме 12 этажей, а во втором 16. Сколько квартир в каждом доме?
-
-
Число квартир на одном этаже
Количество этажей
Всего квартир
1 дом
2 дом
Всего
-
Правильный вариант:
-
-
Число квартир на одном этаже
Количество этажей
Всего квартир
1 дом
Одинаковое
12
2 дом
16
Всего
336
-
Список литературы:
-
Моро М. И. и др. Математика. Рабочие программы. 1–4 классы.
-
Моро М. И. и др. Учебник. 4 кл. В 2 ч. Ч. 1
-
Моро М. И., Волкова С. И. Математика. Рабочая тетрадь. 4 кл. В 2 ч. Ч. 1.
-
Моро М. И., Волкова С. И. Математика. Рабочая тетрадь. 4 кл. В 2 ч. Ч. 2.
-
Волкова С. И. Математика. Проверочные работы. 4 класс.
-
Бантова М. А., Бельтюкова Г. В., Волкова С. И. и др. Математика. Методические рекомендации. 4 класс.
-
Волкова С. И. Математика и конструирование. 4 класс.
-
Моро М. И., Волкова С. И. Для тех, кто любит математику. 4 класс.
-
Электронное приложение к учебнику «Математика», 4 класс, автор В. Л. Соколов.
-
Смолеусова Т.В. Наглядные таблицы по математике для начальных классов М.:Просвещение.
-
Смолеусова Т.В. Математика в схемах и таблицах: справочник для учителей
начальных классов Самара: Федоров: Учебная лит.
-
Издательства «Просвещение» www.prosv.ru (раздел «Школа России www.schoolrussia.ru)
-
Федерация Интернет-образования, сетевое объединение методистов www.som.fio.ru
-
Российская версия международного проекта Сеть творческих учителей it-n.ru
-
Российский общеобразовательный Портал www.school.edu.ru
-
Интернет ресурсы.


75

шағым қалдыра аласыз















