
Сабақтың тақырыбы: Проекциялаудың түрлері туралы мағлұмат. Тік бұрыштап (ортогональды) проекциялау. Нүктенің, түзудің, жазық фигураның және геометриялық денелердің жазықтық бетіндегі кешенді сызбасы. Проекциялау жазықтықтары және олардың белгіленуі.
|
Сабақтың мақсаты |
Білімділік – Оқушыларға проекция туралы жалпы мағлұмат беру. Тәрбиелік – Ұқыптылық, тазалық, өз ойын қағаз бетіне түсірудегі ұстамдылық пен шыдамдылыққа үйрету. Оқыту (дамытушылық) – Оқушылардың кеңістікте ойлауын дамыту, оларды шеберлікке баулу, танымдық қабылетін арттыру сонымен бірге өз бетінше әдебиеттермен анықтамалық оқу құралдарымен жұмыс істеуін арттыру. |
Әдебиеттер: НО-1 – Ж.М.Есмұханов «Сызу». Жалпы білім беретін орта мектепке арналған оқулық. Алматы, «Рауан», 1996 ж. ;
НО-2 - А.Д.Ботвинников «Сызу». Орта мектепке арналған оқулық. Алматы, «Рауан», 1980 ж. «Мектеп» (Аудармашы М. Бәйімбетов)
ҚО-1 – С.К.Боголюбов «Черчение». Учебник для ССУЗ-ов. Москва, «Машиностроитель», 1989 г.
ҚО-2 – «Бейнелеу өнері және сызу» Республикалық ғылыми-әдістемелік журналдар
Проекциялау
Проекциялау туралы жалпы малұматтар. Мемлекеттік стандарт ережесіне сәйкес келетін сызбалардағы нәрсе кескіндерін тік бұрыштап проекциялау тәсілі бойынша шығарып алады. Проекциялау дегеніміз нәрсенің проекциясын салу процесі.
«Проекция» - латын сөзі. Оны қазақтіліне аударғанда «алға қарай» (ілгері қарай) тастау» деген мағынаны береді.
К еңістіктегі кез келген А нүктесін және қандай болмасын
Н жазықтығын алайық. Н жазықтығын қайсібір а нүктесінде қиып
өтетіндей етіп А нүктесі арқылы түзу жүргізейік. Сонда а нүктесі А
нүктесінің проекциясы болады. Нәрсенің проекциясы түсетін жазықтық
проекциялар жазықтығы деп аталады. Аа түзуі проекциялаушы сәуле деп
аталады. Осы түзудің көмегімен А нүктесі Н жазықтығына
проекцияланады. Кез келген кеңістік фигурасының барлық нүктелерінің
проекцияларын осындай тәсілмен салады.
еңістіктегі кез келген А нүктесін және қандай болмасын
Н жазықтығын алайық. Н жазықтығын қайсібір а нүктесінде қиып
өтетіндей етіп А нүктесі арқылы түзу жүргізейік. Сонда а нүктесі А
нүктесінің проекциясы болады. Нәрсенің проекциясы түсетін жазықтық
проекциялар жазықтығы деп аталады. Аа түзуі проекциялаушы сәуле деп
аталады. Осы түзудің көмегімен А нүктесі Н жазықтығына
проекцияланады. Кез келген кеңістік фигурасының барлық нүктелерінің
проекцияларын осындай тәсілмен салады.
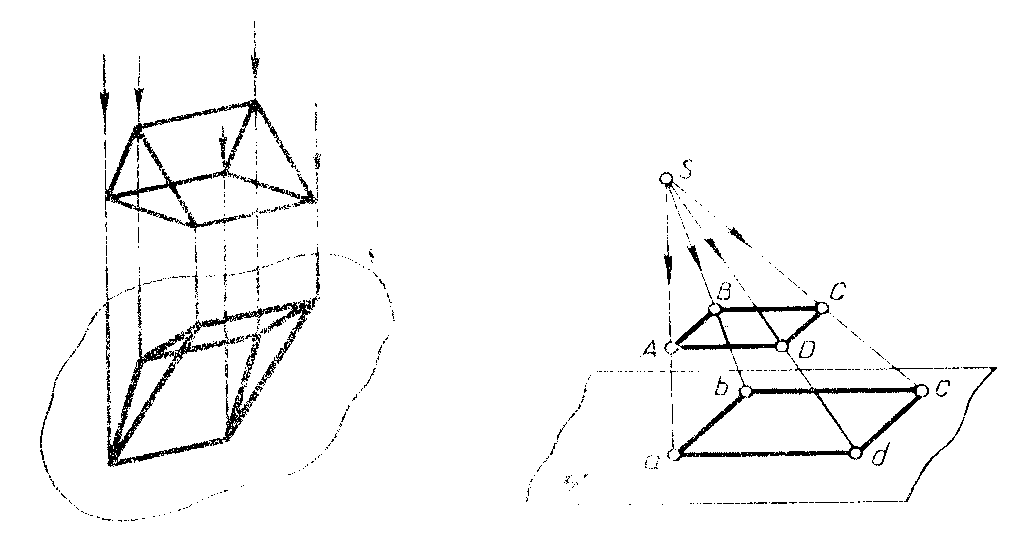
Д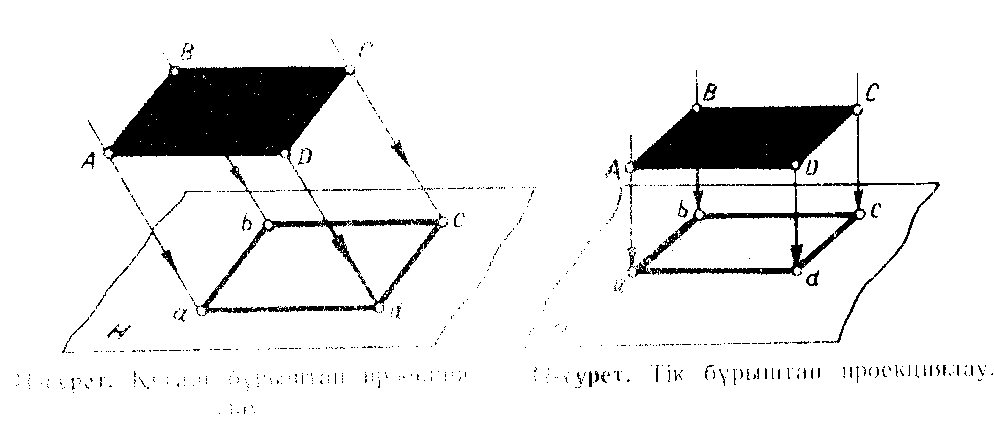 емек, қандай болмасын фигураның проекциясын жазықтыққа
салу үшін, осы фигура нүктесі арқылы жорамал проекциялаушы
сәулелерді жазықтықпен қиылысқанша жүргізу керек. Фигураның барлық
нүктелері проекцияларының жиыны берілген фигураның проекциясы
болады. Қандай болмасын геометриялық фигураның мысалы, үшбұрыштың
проекциясын шығарып алу жолын қарастырайық.
емек, қандай болмасын фигураның проекциясын жазықтыққа
салу үшін, осы фигура нүктесі арқылы жорамал проекциялаушы
сәулелерді жазықтықпен қиылысқанша жүргізу керек. Фигураның барлық
нүктелері проекцияларының жиыны берілген фигураның проекциясы
болады. Қандай болмасын геометриялық фигураның мысалы, үшбұрыштың
проекциясын шығарып алу жолын қарастырайық.
 Бұдан
былай нәрсенің өзіндегі нүктелерді бас әріптермен, ал олардың
проекцияларын кіші әріптермен белгілейміз. А нүктесінің берілген Н
жазықтығындағы проекциясы а нүктесі болады, бұл проекциялаушы Аа
сәулесінің проекциялар жазықтығымен қиылысу нәтижесінде шығады. В
және С нүктелерінің проекциялары в және с болады. Жазықтықтағы а,
б, және с нүктелерін түзу кесіндімен қосып, абс фигурасын шығарып
аламыз, бұл – берілген АВС фигурасының проекциясы
болады.
Бұдан
былай нәрсенің өзіндегі нүктелерді бас әріптермен, ал олардың
проекцияларын кіші әріптермен белгілейміз. А нүктесінің берілген Н
жазықтығындағы проекциясы а нүктесі болады, бұл проекциялаушы Аа
сәулесінің проекциялар жазықтығымен қиылысу нәтижесінде шығады. В
және С нүктелерінің проекциялары в және с болады. Жазықтықтағы а,
б, және с нүктелерін түзу кесіндімен қосып, абс фигурасын шығарып
аламыз, бұл – берілген АВС фигурасының проекциясы
болады.
Тік бұрыштап проекциялау.
Б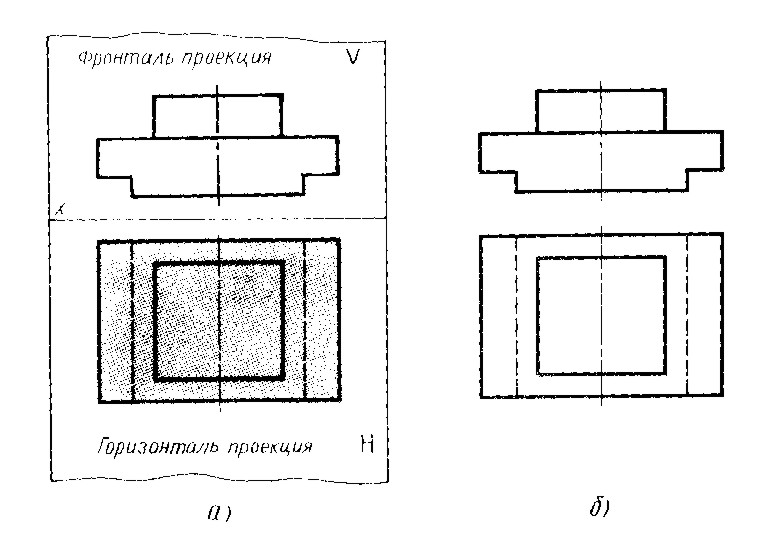 ір проекция жазықтығына проекциялау. Нәрсенің тік
бұрышты проекциясын салу қажет болсын. Прокциялардың вертикаль
жазықтығын таңдап аламыз (оны V әрпімен белгілейміз). Көрушінің
алдына орналасқан осындай жазықтықты фронталь жазықтық деп атайды.
Бұл француздың «фронталь», «беті көрушіге қараған» деген сөзінен
шыққан. Енді нәрсені алдыңғы жағынан қарай отырып, оның осы
жазықтықтағы проекциясын құрамыз. Ол үшін ойша бірнеше нүктелер
аламыз, мысалы нәрсенің төбелері және тесік нүктелері,
проекциялаушы сәулелер арқылы V проекция жазықтығына перпендикуляр
жүргіземіз. Олардың жазықтықпен қиылысу нүктелерін қисық сызықпен
қосамыз. Сөйтіп, нәрсенің жазықтықтағы проекциясын
аламыз.
ір проекция жазықтығына проекциялау. Нәрсенің тік
бұрышты проекциясын салу қажет болсын. Прокциялардың вертикаль
жазықтығын таңдап аламыз (оны V әрпімен белгілейміз). Көрушінің
алдына орналасқан осындай жазықтықты фронталь жазықтық деп атайды.
Бұл француздың «фронталь», «беті көрушіге қараған» деген сөзінен
шыққан. Енді нәрсені алдыңғы жағынан қарай отырып, оның осы
жазықтықтағы проекциясын құрамыз. Ол үшін ойша бірнеше нүктелер
аламыз, мысалы нәрсенің төбелері және тесік нүктелері,
проекциялаушы сәулелер арқылы V проекция жазықтығына перпендикуляр
жүргіземіз. Олардың жазықтықпен қиылысу нүктелерін қисық сызықпен
қосамыз. Сөйтіп, нәрсенің жазықтықтағы проекциясын
аламыз.
Бірнеше
проекция жазықтығына проекциялау. Бір проекция бойынша нәрсенің
геометриялық пішіні туралды әрқашан дәйекті пікір айтуға болады.
Мысалы 45, а-суреттер берілген бір проекция бойынша нәрсені 45, б
және в – суреттерде көрсетілгендей етіп түсінуге болады. Сондай-ақ
өз проекциясының кескіні 45, а-суреттер берілгендей болатын басқа
нәрселерді де таңдап алуға болады. Бұған қоса, мұндай кескінде
нәрсенің үшінші өлшемі бейнеленбеген.
Егер нәрсенің бір емес, екі проекциясын өзара перпендикуляр екі
жазықтықта: фронталь және горизонталь жазықтықта (оны Н әрпімен
белдгілейді) салсақ, онда мұндай кемшіліктің бәрін жоюға
болады.
Фронталь V жазықтықта проекция алу үшін нәрсені – алдыңғы жағынан, ал горизонталь Н жазықтықты үстіңгі жағынан қарастырамыз. Нәрсенің V жазықтықтағы проециясы – фронталь проекция, Н жазықтықтағы проекциясы горизонталь проекция деп аталады. Осы жазықтықтардың қиылысу сызықтарын проекциялар осі деп атайды.
О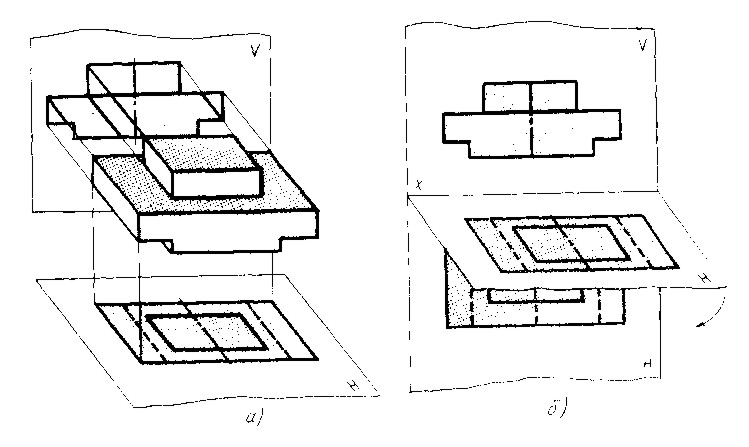 Сындай жолмен салынған проекциялар кеңістікте әр түрлі
жазықтарда орналасқан болып шығады. Нәрсенің кескінін бір парақ
қағазға, яғни бір жазықтыққа сызады. Сондықтан нәрсенің сызбасын
сызу үшін, екі жазықтықты да бір жазықтыққа келтіреді. Ол үшін
проекциялардың горизонталь жазықтығын, ол вертикаль жазықтықпен
беттесетіндей етіп х осінен төмен қарай 90º-қа бұрады. Сонда екі
проекция да бір жазықтықта орналасқандай болып
шығады.
Сындай жолмен салынған проекциялар кеңістікте әр түрлі
жазықтарда орналасқан болып шығады. Нәрсенің кескінін бір парақ
қағазға, яғни бір жазықтыққа сызады. Сондықтан нәрсенің сызбасын
сызу үшін, екі жазықтықты да бір жазықтыққа келтіреді. Ол үшін
проекциялардың горизонталь жазықтығын, ол вертикаль жазықтықпен
беттесетіндей етіп х осінен төмен қарай 90º-қа бұрады. Сонда екі
проекция да бір жазықтықта орналасқандай болып
шығады.
Проекциялар жазықтығының шекарасын сызбада көрсетпесе де болады. Егер қажет болмаса, проекциялаушы сәулелер мен проекциялар жазықтықтарының қиылысу сызығы, яғни проекциялар осі сызбаға түсірілмейді.
Беттестірілген жазықтықтарда нәрсенің фронталь және горизонталь проекцияларын проекциялық байланыста, яғни горизонталь проекцияны фронталь проекцияның дәл астына орналастырады.
Бірнеше тік бұрышты проекциялардан тұратын сызбаны тік бұрышты проекциялар жүйесіндегі сызбалар деп атайды. Нәрсенің сызбадағы геометриялық пішінінің күрделігігіне қарай, ол бір, екі және одан да көп проекциямен берілуі мүмкін.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Проекциялаудың түрлері туралы мағлұмат.
Проекциялаудың түрлері туралы мағлұмат.
Сабақтың тақырыбы: Проекциялаудың түрлері туралы мағлұмат. Тік бұрыштап (ортогональды) проекциялау. Нүктенің, түзудің, жазық фигураның және геометриялық денелердің жазықтық бетіндегі кешенді сызбасы. Проекциялау жазықтықтары және олардың белгіленуі.
|
Сабақтың мақсаты |
Білімділік – Оқушыларға проекция туралы жалпы мағлұмат беру. Тәрбиелік – Ұқыптылық, тазалық, өз ойын қағаз бетіне түсірудегі ұстамдылық пен шыдамдылыққа үйрету. Оқыту (дамытушылық) – Оқушылардың кеңістікте ойлауын дамыту, оларды шеберлікке баулу, танымдық қабылетін арттыру сонымен бірге өз бетінше әдебиеттермен анықтамалық оқу құралдарымен жұмыс істеуін арттыру. |
Әдебиеттер: НО-1 – Ж.М.Есмұханов «Сызу». Жалпы білім беретін орта мектепке арналған оқулық. Алматы, «Рауан», 1996 ж. ;
НО-2 - А.Д.Ботвинников «Сызу». Орта мектепке арналған оқулық. Алматы, «Рауан», 1980 ж. «Мектеп» (Аудармашы М. Бәйімбетов)
ҚО-1 – С.К.Боголюбов «Черчение». Учебник для ССУЗ-ов. Москва, «Машиностроитель», 1989 г.
ҚО-2 – «Бейнелеу өнері және сызу» Республикалық ғылыми-әдістемелік журналдар
Проекциялау
Проекциялау туралы жалпы малұматтар. Мемлекеттік стандарт ережесіне сәйкес келетін сызбалардағы нәрсе кескіндерін тік бұрыштап проекциялау тәсілі бойынша шығарып алады. Проекциялау дегеніміз нәрсенің проекциясын салу процесі.
«Проекция» - латын сөзі. Оны қазақтіліне аударғанда «алға қарай» (ілгері қарай) тастау» деген мағынаны береді.
К еңістіктегі кез келген А нүктесін және қандай болмасын
Н жазықтығын алайық. Н жазықтығын қайсібір а нүктесінде қиып
өтетіндей етіп А нүктесі арқылы түзу жүргізейік. Сонда а нүктесі А
нүктесінің проекциясы болады. Нәрсенің проекциясы түсетін жазықтық
проекциялар жазықтығы деп аталады. Аа түзуі проекциялаушы сәуле деп
аталады. Осы түзудің көмегімен А нүктесі Н жазықтығына
проекцияланады. Кез келген кеңістік фигурасының барлық нүктелерінің
проекцияларын осындай тәсілмен салады.
еңістіктегі кез келген А нүктесін және қандай болмасын
Н жазықтығын алайық. Н жазықтығын қайсібір а нүктесінде қиып
өтетіндей етіп А нүктесі арқылы түзу жүргізейік. Сонда а нүктесі А
нүктесінің проекциясы болады. Нәрсенің проекциясы түсетін жазықтық
проекциялар жазықтығы деп аталады. Аа түзуі проекциялаушы сәуле деп
аталады. Осы түзудің көмегімен А нүктесі Н жазықтығына
проекцияланады. Кез келген кеңістік фигурасының барлық нүктелерінің
проекцияларын осындай тәсілмен салады.
Д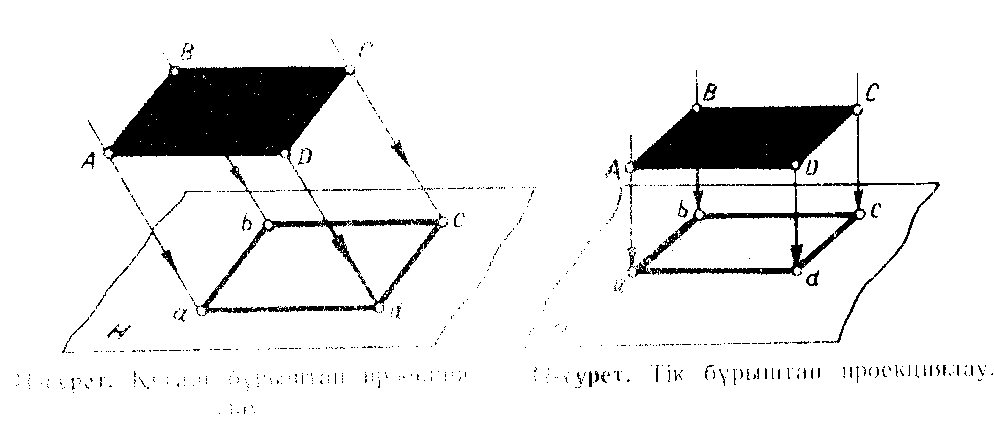 емек, қандай болмасын фигураның проекциясын жазықтыққа
салу үшін, осы фигура нүктесі арқылы жорамал проекциялаушы
сәулелерді жазықтықпен қиылысқанша жүргізу керек. Фигураның барлық
нүктелері проекцияларының жиыны берілген фигураның проекциясы
болады. Қандай болмасын геометриялық фигураның мысалы, үшбұрыштың
проекциясын шығарып алу жолын қарастырайық.
емек, қандай болмасын фигураның проекциясын жазықтыққа
салу үшін, осы фигура нүктесі арқылы жорамал проекциялаушы
сәулелерді жазықтықпен қиылысқанша жүргізу керек. Фигураның барлық
нүктелері проекцияларының жиыны берілген фигураның проекциясы
болады. Қандай болмасын геометриялық фигураның мысалы, үшбұрыштың
проекциясын шығарып алу жолын қарастырайық.
 Бұдан
былай нәрсенің өзіндегі нүктелерді бас әріптермен, ал олардың
проекцияларын кіші әріптермен белгілейміз. А нүктесінің берілген Н
жазықтығындағы проекциясы а нүктесі болады, бұл проекциялаушы Аа
сәулесінің проекциялар жазықтығымен қиылысу нәтижесінде шығады. В
және С нүктелерінің проекциялары в және с болады. Жазықтықтағы а,
б, және с нүктелерін түзу кесіндімен қосып, абс фигурасын шығарып
аламыз, бұл – берілген АВС фигурасының проекциясы
болады.
Бұдан
былай нәрсенің өзіндегі нүктелерді бас әріптермен, ал олардың
проекцияларын кіші әріптермен белгілейміз. А нүктесінің берілген Н
жазықтығындағы проекциясы а нүктесі болады, бұл проекциялаушы Аа
сәулесінің проекциялар жазықтығымен қиылысу нәтижесінде шығады. В
және С нүктелерінің проекциялары в және с болады. Жазықтықтағы а,
б, және с нүктелерін түзу кесіндімен қосып, абс фигурасын шығарып
аламыз, бұл – берілген АВС фигурасының проекциясы
болады.
Тік бұрыштап проекциялау.
Б ір проекция жазықтығына проекциялау. Нәрсенің тік
бұрышты проекциясын салу қажет болсын. Прокциялардың вертикаль
жазықтығын таңдап аламыз (оны V әрпімен белгілейміз). Көрушінің
алдына орналасқан осындай жазықтықты фронталь жазықтық деп атайды.
Бұл француздың «фронталь», «беті көрушіге қараған» деген сөзінен
шыққан. Енді нәрсені алдыңғы жағынан қарай отырып, оның осы
жазықтықтағы проекциясын құрамыз. Ол үшін ойша бірнеше нүктелер
аламыз, мысалы нәрсенің төбелері және тесік нүктелері,
проекциялаушы сәулелер арқылы V проекция жазықтығына перпендикуляр
жүргіземіз. Олардың жазықтықпен қиылысу нүктелерін қисық сызықпен
қосамыз. Сөйтіп, нәрсенің жазықтықтағы проекциясын
аламыз.
ір проекция жазықтығына проекциялау. Нәрсенің тік
бұрышты проекциясын салу қажет болсын. Прокциялардың вертикаль
жазықтығын таңдап аламыз (оны V әрпімен белгілейміз). Көрушінің
алдына орналасқан осындай жазықтықты фронталь жазықтық деп атайды.
Бұл француздың «фронталь», «беті көрушіге қараған» деген сөзінен
шыққан. Енді нәрсені алдыңғы жағынан қарай отырып, оның осы
жазықтықтағы проекциясын құрамыз. Ол үшін ойша бірнеше нүктелер
аламыз, мысалы нәрсенің төбелері және тесік нүктелері,
проекциялаушы сәулелер арқылы V проекция жазықтығына перпендикуляр
жүргіземіз. Олардың жазықтықпен қиылысу нүктелерін қисық сызықпен
қосамыз. Сөйтіп, нәрсенің жазықтықтағы проекциясын
аламыз.
Бірнеше
проекция жазықтығына проекциялау. Бір проекция бойынша нәрсенің
геометриялық пішіні туралды әрқашан дәйекті пікір айтуға болады.
Мысалы 45, а-суреттер берілген бір проекция бойынша нәрсені 45, б
және в – суреттерде көрсетілгендей етіп түсінуге болады. Сондай-ақ
өз проекциясының кескіні 45, а-суреттер берілгендей болатын басқа
нәрселерді де таңдап алуға болады. Бұған қоса, мұндай кескінде
нәрсенің үшінші өлшемі бейнеленбеген.
Егер нәрсенің бір емес, екі проекциясын өзара перпендикуляр екі
жазықтықта: фронталь және горизонталь жазықтықта (оны Н әрпімен
белдгілейді) салсақ, онда мұндай кемшіліктің бәрін жоюға
болады.
Фронталь V жазықтықта проекция алу үшін нәрсені – алдыңғы жағынан, ал горизонталь Н жазықтықты үстіңгі жағынан қарастырамыз. Нәрсенің V жазықтықтағы проециясы – фронталь проекция, Н жазықтықтағы проекциясы горизонталь проекция деп аталады. Осы жазықтықтардың қиылысу сызықтарын проекциялар осі деп атайды.
О Сындай жолмен салынған проекциялар кеңістікте әр түрлі
жазықтарда орналасқан болып шығады. Нәрсенің кескінін бір парақ
қағазға, яғни бір жазықтыққа сызады. Сондықтан нәрсенің сызбасын
сызу үшін, екі жазықтықты да бір жазықтыққа келтіреді. Ол үшін
проекциялардың горизонталь жазықтығын, ол вертикаль жазықтықпен
беттесетіндей етіп х осінен төмен қарай 90º-қа бұрады. Сонда екі
проекция да бір жазықтықта орналасқандай болып
шығады.
Сындай жолмен салынған проекциялар кеңістікте әр түрлі
жазықтарда орналасқан болып шығады. Нәрсенің кескінін бір парақ
қағазға, яғни бір жазықтыққа сызады. Сондықтан нәрсенің сызбасын
сызу үшін, екі жазықтықты да бір жазықтыққа келтіреді. Ол үшін
проекциялардың горизонталь жазықтығын, ол вертикаль жазықтықпен
беттесетіндей етіп х осінен төмен қарай 90º-қа бұрады. Сонда екі
проекция да бір жазықтықта орналасқандай болып
шығады.
Проекциялар жазықтығының шекарасын сызбада көрсетпесе де болады. Егер қажет болмаса, проекциялаушы сәулелер мен проекциялар жазықтықтарының қиылысу сызығы, яғни проекциялар осі сызбаға түсірілмейді.
Беттестірілген жазықтықтарда нәрсенің фронталь және горизонталь проекцияларын проекциялық байланыста, яғни горизонталь проекцияны фронталь проекцияның дәл астына орналастырады.
Бірнеше тік бұрышты проекциялардан тұратын сызбаны тік бұрышты проекциялар жүйесіндегі сызбалар деп атайды. Нәрсенің сызбадағы геометриялық пішінінің күрделігігіне қарай, ол бір, екі және одан да көп проекциямен берілуі мүмкін.

шағым қалдыра аласыз















