
Прогрессияға қатысты геометрия есептері
Долаев А.С. Алматы қаласындағы «Республикалық физика-математика мектебі» Коммерциялық емес Акционерлік Қоғамының филиалы
Орта мектепте 9 сыныпта геометрия пәнінде планиметрия курсы аяқталады, ал алгебрада тізбектер, арифметикалық және геометриялық прогрессиялары өтіледі. Мақалада қандай да бір элементтері прогрессия құрайтын геометрия есептері жинақталған. Бұл есептерді геометрия немесе алгебра сабақтарында сәйкес тақырыптарды өтіп жатқан кезде, немесе оқу жылы аяғында қайталау сабақтарында беруге болады.
1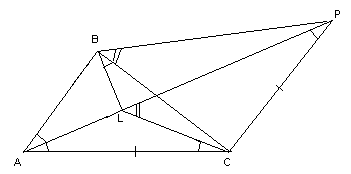 -есеп. АВС үшбұрышының
А бұрышының
биссектрисасының бойынан үшбұрыш ішінен
-есеп. АВС үшбұрышының
А бұрышының
биссектрисасының бойынан үшбұрыш ішінен ![]() =
=
![]() =
= ![]() теңдігі орындалатын L нүктесі табылды. Үшбұрыш
қабырғаларының ұзындықтары геометриялық прогрессия құрайтынын
дәлелдеңдер.
теңдігі орындалатын L нүктесі табылды. Үшбұрыш
қабырғаларының ұзындықтары геометриялық прогрессия құрайтынын
дәлелдеңдер.
Шешуі. АL
сәулесінің бойынан РС = СА болатындай
Р нүктесін
аламыз. АРС тең бүйірлі үшбұрыш болады. Сонда РС║АВ. Бұдан ![]() .
. ![]()
=![]() , яғни Р
және А
нүктелері СВ түзуінің екі жағында
жатады.
, яғни Р
және А
нүктелері СВ түзуінің екі жағында
жатады. ![]() болғандықтан СLBP төртбұрышына сырттай
шеңбер сызуға болады..
болғандықтан СLBP төртбұрышына сырттай
шеңбер сызуға болады.. ![]() . Олай
болса АВС және ВСР
үшбұрыштары ұқсас және
. Олай
болса АВС және ВСР
үшбұрыштары ұқсас және
СВ/АВ = СР/ВС = АС/СВ.
Бұдан ![]() және
және ![]() екендігі шығады.
екендігі шығады.
2-есеп. Қандай да бір үшбұрыштың қабырғаларының ұзындықтары және оған іштей сызылған шеңбердің диаметрі арифметикалық прогрессияның тізбектес төрт мүшесін құрайды. Осындай барлық үшбұрыштарды табыңдар.
Шешуі. Кез-келген
үшбұрышта ![]() , яғни шеңбер
диаметрі үшбұрыш қабырғаларынан кіші болады. 2r, а, b, с – арифметикалық прогрессия құрасын. (d >
0). Онда
, яғни шеңбер
диаметрі үшбұрыш қабырғаларынан кіші болады. 2r, а, b, с – арифметикалық прогрессия құрасын. (d >
0). Онда
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
. ![]() және
және
![]() теңдіктерінен
теңдіктерінен ![]() шығады.
шығады. ![]() екенін
ескерсек, теңдеуді шешіп
екенін
ескерсек, теңдеуді шешіп ![]() аламыз. Онда
үшбұрыш қабырғалары 3r, 4r, 5r болады. Есеп шартын
қабырғаларының ұзындықтары 3, 4, 5 сандарына пропорционал барлық
үшбұрыштар қанағаттандырады.
аламыз. Онда
үшбұрыш қабырғалары 3r, 4r, 5r болады. Есеп шартын
қабырғаларының ұзындықтары 3, 4, 5 сандарына пропорционал барлық
үшбұрыштар қанағаттандырады.
3-есеп. АВС үшбұрышының А бұрышының сыртқы бұрышы В бұрышынан үш есе артық, ал АВ, ВС, АС қабырғалары осы ретпен арифметикалық прогрессия құрайды. АВС үшбұрышының бұрыштарын табыңдар.
Шешуі. В
бұрышын х деп белгілеп алайық.
Онда ![]()
![]() .
Арифметикалық прогрессияның қасиеті бойынша АС
+АВ = 2∙ВС . Синустар теоремасы
бойынша
.
Арифметикалық прогрессияның қасиеті бойынша АС
+АВ = 2∙ВС . Синустар теоремасы
бойынша ![]() .
Бұдан
.
Бұдан ![]() теңдеуін аламыз немесе
теңдеуін аламыз немесе ![]() . Есептің
мағынасы бойынша
. Есептің
мағынасы бойынша ![]() , онда соңғы
теңдеуді
, онда соңғы
теңдеуді ![]() -қа қысқартып,
-қа қысқартып, ![]() теңдеуін
аламыз. Осы теңдеуден
теңдеуін
аламыз. Осы теңдеуден ![]() ескерсек
,
ескерсек
, ![]() шығады.
шығады. ![]() ,
,
![]() ,
, ![]()
4-есеп. Егер үшбұрыш қабырғалары арифметикалық прогрессия құрайтын болса, онда іштей сызылған шеңбердің центрі, ең үлкен және ең кіші қабырғалардың орталары және сол қабырғалармен құрылған бұрыштың төбесі бір шеңбердің бойында жататынын дәлелдеңдер.
Шешуі. АВС
үшбұрышының АВ, ВС және АС қабырғалары осы ретпен
арифметикалық прогрессия құрсын. АС = а, AB = a – d, BC = a + d болсын, мұндағы
d – прогрессия
айырымы. О1 және О2
–үшбұрышқа іштей және сырттай сызылған шеңберлер
центрлері. АЕ = х деп белгілейік. АЕ=АК және ВК + СЕ = ВL + LС = ВС немесе
a –
d – х + a + d – x = a.
Осыдан х
= a/2
= АЕ
= АК. ![]() ,
, ![]() . Бұдан ∆FKО1
= ∆ DEО1
. О1F
= О1D
. Егер АDО1
үшбұрышына сырттай шеңбер сызсақ, ол
шеңбер F нүктесінен өтеді. Себебі
. Бұдан ∆FKО1
= ∆ DEО1
. О1F
= О1D
. Егер АDО1
үшбұрышына сырттай шеңбер сызсақ, ол
шеңбер F нүктесінен өтеді. Себебі ![]() және О1F
пен О1D
тең хордалар болады. Олай болса
А,
D,
О1 және F нүктелері бір шеңбер
бойында жатады
және О1F
пен О1D
тең хордалар болады. Олай болса
А,
D,
О1 және F нүктелері бір шеңбер
бойында жатады
5-есеп. Үшбұрыштың
А, В және С
бұрыштары еселігі 2-ге тең геометриялық
прогрессия құрайды. Үшбұрыш қабырғалары
![]() қатынасын қанағаттандыратынын дәлелдеңдер.
қатынасын қанағаттандыратынын дәлелдеңдер.
Шешуі. Есеп
шартынан ![]() ,
, ![]() ,
,
![]() шығады. АВС
үшбұрышына сырттай шеңбер сызып және
ВАС бұрышына
тең ВАD бұрышын саламыз. Птолемей теорамасы бойынша
АВ·СD = ВС·АD + ВD·АС. (*)
шығады. АВС
үшбұрышына сырттай шеңбер сызып және
ВАС бұрышына
тең ВАD бұрышын саламыз. Птолемей теорамасы бойынша
АВ·СD = ВС·АD + ВD·АС. (*)
Бірақ СD
= АС, АD = АВ, ВD = ВС. Олай болса (*)
теңдігін АВ·АС = ВС·АВ + ВС·АС түрде жаза аламыз. Теңдіктің екі жағын АВ·АС·ВС өрнегіне бөліп,
![]() аламыз. Дәлелдеу керегі де осы.
аламыз. Дәлелдеу керегі де осы.
Есептер.
1. Егер үшбұрыш қабырғалары арифметикалық прогрессия құрайтын болса, онда медианалар қиылысатын нүкте мен іштей сызылған шеңбердің центрін қосатын кесінді үшбұрыштың ортаншы (ұзындығы бойынша) қабырғасына параллель болатынын дәлелдеңдер.
2. АВС үшбұрышының
қабырғалары арифметикалық прогрессия құрайды.
Онда ![]() ,
, ![]() ,
, ![]() сандары да
арифметикалық прогрессия құрайтынын дәлелдеңдер.
сандары да
арифметикалық прогрессия құрайтынын дәлелдеңдер.
3. Егер үшбұрыштың бір бұрышы 120º және оның қабырғалары арифметикалық прогрессия құрайтын болса, онда ол қабырғалар 3, 5, 7 сандарына пропорционал екенін дәлелдеңдер.
4. Егер үшбұрыш қабырғалары арифметикалық прогрессия құрайтын болса, онда іштей сызылған шеңбердің радиусы үшбұрыштың ортаншы қабырғасына түсірілген биіктіктің үштен біріне тең екенін дәлелдеңдер.
5. Егер үшбұрыш қабырғаларының квадраттары арифметикалық прогрессия құрайтын болса, онда осы үшбұрыштың медианаларынан құрылған үшбұрыш берілген үшбұрышқа ұқсас болатынын дәлелдеңдер.
6. Егер үшбұрыш қабырғалары геометриялық прогрессия құрайтын болса, онда ол үшбұрыш қабырғалары берілген үшбұрыштың биіктіктері болатын үшбұрышқа ұқсас болатынын дәлелдеңдер.
7. Егер үшбұрыш қабырғалары арифметикалық прогрессия құрайтын болса, онда ортаншы қабырғаға қарсы жатқан бұрыштың ішкі биссектрисасы үшбұрышқа іштей және сырттай сызылған шеңберлердің центрлері арқылы өтетін түзуге перпендикуляр болатынын дәлелдеңдер.
8. Егер үшбұрыш қабырғалары арифметикалық прогрессия құрайтын болса, онда ортаншы қабырғаға қарсы жатқан бұрыштың биссектрисасының бойында жатқан нүктелерден үшбұрыш қабырғаларына дейінгі қашықтықтардың қосындысы тұрақты екенін дәлелдеңдер.
9. Егер тікбұрышты үшбұрыштың қабырғалары арифметикалық прогрессия құрайтын болса, онда оның айырымы іштей сызылған шеңбердің радиусына тең екенін дәлелдеңдер.
10. Үшбұрыштың бір бұрышы 120º және оның қабырғалары айырымы 1-ге тең арифметикалық прогрессия құрайды. Үшбұрыштың қабырғаларын табыңдар.
11. Дөңес алтыбұрыштың ішкі бұрыштары айырымы 34º-қа тең арифметикалық прогрессия құрайды. Олардың ішіндегі ең кішісі тең:
A) 30º B) 35º C) 40º D) 45º E) 60º
12. Дөңес бесбұрыштың ішкі бұрыштары арифметикалық прогрессия құрайды. Прогрессияның үшінші мүшесі тең:
A) 108º B) 98º C) 120º D) 150º E) 54º
13. Дөңес төртбұрыштың ішкі бұрыштары еселігі 3-ке тең геометриялық прогрессия құрайды. Прогрессияның екінші мүшесі тең:
A) 39º B) 24º C) 27º D) 33º E) 21º
14. Үшбұрыштың бұрыштары геометриялық прогрессия құрайды. Егер кіші бұрышы 20º-қа тең болса, онда прогрессияның еселігі тең:
A)![]() B)
B) ![]() C)
C) ![]() D)
D) ![]() E)
E) ![]()
15. Тікбұрышты үшбұрыштың қабырғалары геометриялық прогрессия құрайды. Үшбұрыштың кіші бұрышының синусы тең:
A) ![]() B)
B) ![]() C)
C) ![]() D)
D) ![]() E)
E) ![]()
16. Дөңгелекке сырттай сүйір бұрышы α-ға тең теңбүйірлі трапеция сызылған. Трапеция табандары және дөңгелек диаметрі геометриялық прогрессия құрайды. Прогрессияның еселігі тең:
А) ![]() B)
B) ![]() C)
C)![]() D)
D) ![]() E)
E)
![]()
17. Ромбының кіші диагоналі, қабырғасы және оның үлкен диагоналі геометриялық прогрессияның тізбектес мүшелері болып табылады. Прогрессияның еселігі тең:
A) ![]() B)
B) ![]() C)
C)
![]() D)
D) ![]() E)
E) ![]()
18. Квадраттар тізбегі былай берілген: бірлік квадраттан бастап әрбір келесі квадраттың төбелері алдыңғысының қабырғаларын 3:1-ге қатынасындай бөліп отырады. Тізбектің барлық мүшелерінің аудандарының қосындысы тең:
А) ![]() B)
B) ![]() C)
C)
![]() D)
D) ![]() E)
E) ![]()
19. Бұрышқа әрбір келесісі алдыңғысын жанайтын және радиустары кемімелі шеңберлер іштей сызылған. Егер бірінші шеңбердің радиусы 10-ға, екінші шеңбермен шектелген дөңгелектің ауданы 64π –ге тең болса, онда барлық шеңберлер ұзындықтарының қосындысы тең:
A) 64π B) 75π C) 88π D) 96π E) 100π
Жауаптары
|
№ |
жауабы |
|
11 |
В |
|
12 |
А |
|
13 |
С |
|
14 |
А |
|
15 |
D |
|
16 |
А |
|
17 |
С |
|
18 |
В |
|
19 |
Е |
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Прогрессияға қатысты геометрия есептері
Прогрессияға қатысты геометрия есептері
Прогрессияға қатысты геометрия есептері
Долаев А.С. Алматы қаласындағы «Республикалық физика-математика мектебі» Коммерциялық емес Акционерлік Қоғамының филиалы
Орта мектепте 9 сыныпта геометрия пәнінде планиметрия курсы аяқталады, ал алгебрада тізбектер, арифметикалық және геометриялық прогрессиялары өтіледі. Мақалада қандай да бір элементтері прогрессия құрайтын геометрия есептері жинақталған. Бұл есептерді геометрия немесе алгебра сабақтарында сәйкес тақырыптарды өтіп жатқан кезде, немесе оқу жылы аяғында қайталау сабақтарында беруге болады.
1 -есеп. АВС үшбұрышының
А бұрышының
биссектрисасының бойынан үшбұрыш ішінен
-есеп. АВС үшбұрышының
А бұрышының
биссектрисасының бойынан үшбұрыш ішінен ![]() =
=
![]() =
= ![]() теңдігі орындалатын L нүктесі табылды. Үшбұрыш
қабырғаларының ұзындықтары геометриялық прогрессия құрайтынын
дәлелдеңдер.
теңдігі орындалатын L нүктесі табылды. Үшбұрыш
қабырғаларының ұзындықтары геометриялық прогрессия құрайтынын
дәлелдеңдер.
Шешуі. АL
сәулесінің бойынан РС = СА болатындай
Р нүктесін
аламыз. АРС тең бүйірлі үшбұрыш болады. Сонда РС║АВ. Бұдан ![]() .
. ![]()
=![]() , яғни Р
және А
нүктелері СВ түзуінің екі жағында
жатады.
, яғни Р
және А
нүктелері СВ түзуінің екі жағында
жатады. ![]() болғандықтан СLBP төртбұрышына сырттай
шеңбер сызуға болады..
болғандықтан СLBP төртбұрышына сырттай
шеңбер сызуға болады.. ![]() . Олай
болса АВС және ВСР
үшбұрыштары ұқсас және
. Олай
болса АВС және ВСР
үшбұрыштары ұқсас және
СВ/АВ = СР/ВС = АС/СВ.
Бұдан ![]() және
және ![]() екендігі шығады.
екендігі шығады.
2-есеп. Қандай да бір үшбұрыштың қабырғаларының ұзындықтары және оған іштей сызылған шеңбердің диаметрі арифметикалық прогрессияның тізбектес төрт мүшесін құрайды. Осындай барлық үшбұрыштарды табыңдар.
Шешуі. Кез-келген
үшбұрышта ![]() , яғни шеңбер
диаметрі үшбұрыш қабырғаларынан кіші болады. 2r, а, b, с – арифметикалық прогрессия құрасын. (d >
0). Онда
, яғни шеңбер
диаметрі үшбұрыш қабырғаларынан кіші болады. 2r, а, b, с – арифметикалық прогрессия құрасын. (d >
0). Онда
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
. ![]() және
және
![]() теңдіктерінен
теңдіктерінен ![]() шығады.
шығады. ![]() екенін
ескерсек, теңдеуді шешіп
екенін
ескерсек, теңдеуді шешіп ![]() аламыз. Онда
үшбұрыш қабырғалары 3r, 4r, 5r болады. Есеп шартын
қабырғаларының ұзындықтары 3, 4, 5 сандарына пропорционал барлық
үшбұрыштар қанағаттандырады.
аламыз. Онда
үшбұрыш қабырғалары 3r, 4r, 5r болады. Есеп шартын
қабырғаларының ұзындықтары 3, 4, 5 сандарына пропорционал барлық
үшбұрыштар қанағаттандырады.
3-есеп. АВС үшбұрышының А бұрышының сыртқы бұрышы В бұрышынан үш есе артық, ал АВ, ВС, АС қабырғалары осы ретпен арифметикалық прогрессия құрайды. АВС үшбұрышының бұрыштарын табыңдар.
Шешуі. В
бұрышын х деп белгілеп алайық.
Онда ![]()
![]() .
Арифметикалық прогрессияның қасиеті бойынша АС
+АВ = 2∙ВС . Синустар теоремасы
бойынша
.
Арифметикалық прогрессияның қасиеті бойынша АС
+АВ = 2∙ВС . Синустар теоремасы
бойынша ![]() .
Бұдан
.
Бұдан ![]() теңдеуін аламыз немесе
теңдеуін аламыз немесе ![]() . Есептің
мағынасы бойынша
. Есептің
мағынасы бойынша ![]() , онда соңғы
теңдеуді
, онда соңғы
теңдеуді ![]() -қа қысқартып,
-қа қысқартып, ![]() теңдеуін
аламыз. Осы теңдеуден
теңдеуін
аламыз. Осы теңдеуден ![]() ескерсек
,
ескерсек
, ![]() шығады.
шығады. ![]() ,
,
![]() ,
, ![]()
4-есеп. Егер үшбұрыш қабырғалары арифметикалық прогрессия құрайтын болса, онда іштей сызылған шеңбердің центрі, ең үлкен және ең кіші қабырғалардың орталары және сол қабырғалармен құрылған бұрыштың төбесі бір шеңбердің бойында жататынын дәлелдеңдер.
Шешуі. АВС
үшбұрышының АВ, ВС және АС қабырғалары осы ретпен
арифметикалық прогрессия құрсын. АС = а, AB = a – d, BC = a + d болсын, мұндағы
d – прогрессия
айырымы. О1 және О2
–үшбұрышқа іштей және сырттай сызылған шеңберлер
центрлері. АЕ = х деп белгілейік. АЕ=АК және ВК + СЕ = ВL + LС = ВС немесе
a –
d – х + a + d – x = a.
Осыдан х
= a/2
= АЕ
= АК. ![]() ,
, ![]() . Бұдан ∆FKО1
= ∆ DEО1
. О1F
= О1D
. Егер АDО1
үшбұрышына сырттай шеңбер сызсақ, ол
шеңбер F нүктесінен өтеді. Себебі
. Бұдан ∆FKО1
= ∆ DEО1
. О1F
= О1D
. Егер АDО1
үшбұрышына сырттай шеңбер сызсақ, ол
шеңбер F нүктесінен өтеді. Себебі ![]() және О1F
пен О1D
тең хордалар болады. Олай болса
А,
D,
О1 және F нүктелері бір шеңбер
бойында жатады
және О1F
пен О1D
тең хордалар болады. Олай болса
А,
D,
О1 және F нүктелері бір шеңбер
бойында жатады
5-есеп. Үшбұрыштың
А, В және С
бұрыштары еселігі 2-ге тең геометриялық
прогрессия құрайды. Үшбұрыш қабырғалары
![]() қатынасын қанағаттандыратынын дәлелдеңдер.
қатынасын қанағаттандыратынын дәлелдеңдер.
Шешуі. Есеп
шартынан ![]() ,
, ![]() ,
,
![]() шығады. АВС
үшбұрышына сырттай шеңбер сызып және
ВАС бұрышына
тең ВАD бұрышын саламыз. Птолемей теорамасы бойынша
АВ·СD = ВС·АD + ВD·АС. (*)
шығады. АВС
үшбұрышына сырттай шеңбер сызып және
ВАС бұрышына
тең ВАD бұрышын саламыз. Птолемей теорамасы бойынша
АВ·СD = ВС·АD + ВD·АС. (*)
Бірақ СD
= АС, АD = АВ, ВD = ВС. Олай болса (*)
теңдігін АВ·АС = ВС·АВ + ВС·АС түрде жаза аламыз. Теңдіктің екі жағын АВ·АС·ВС өрнегіне бөліп,
![]() аламыз. Дәлелдеу керегі де осы.
аламыз. Дәлелдеу керегі де осы.
Есептер.
1. Егер үшбұрыш қабырғалары арифметикалық прогрессия құрайтын болса, онда медианалар қиылысатын нүкте мен іштей сызылған шеңбердің центрін қосатын кесінді үшбұрыштың ортаншы (ұзындығы бойынша) қабырғасына параллель болатынын дәлелдеңдер.
2. АВС үшбұрышының
қабырғалары арифметикалық прогрессия құрайды.
Онда ![]() ,
, ![]() ,
, ![]() сандары да
арифметикалық прогрессия құрайтынын дәлелдеңдер.
сандары да
арифметикалық прогрессия құрайтынын дәлелдеңдер.
3. Егер үшбұрыштың бір бұрышы 120º және оның қабырғалары арифметикалық прогрессия құрайтын болса, онда ол қабырғалар 3, 5, 7 сандарына пропорционал екенін дәлелдеңдер.
4. Егер үшбұрыш қабырғалары арифметикалық прогрессия құрайтын болса, онда іштей сызылған шеңбердің радиусы үшбұрыштың ортаншы қабырғасына түсірілген биіктіктің үштен біріне тең екенін дәлелдеңдер.
5. Егер үшбұрыш қабырғаларының квадраттары арифметикалық прогрессия құрайтын болса, онда осы үшбұрыштың медианаларынан құрылған үшбұрыш берілген үшбұрышқа ұқсас болатынын дәлелдеңдер.
6. Егер үшбұрыш қабырғалары геометриялық прогрессия құрайтын болса, онда ол үшбұрыш қабырғалары берілген үшбұрыштың биіктіктері болатын үшбұрышқа ұқсас болатынын дәлелдеңдер.
7. Егер үшбұрыш қабырғалары арифметикалық прогрессия құрайтын болса, онда ортаншы қабырғаға қарсы жатқан бұрыштың ішкі биссектрисасы үшбұрышқа іштей және сырттай сызылған шеңберлердің центрлері арқылы өтетін түзуге перпендикуляр болатынын дәлелдеңдер.
8. Егер үшбұрыш қабырғалары арифметикалық прогрессия құрайтын болса, онда ортаншы қабырғаға қарсы жатқан бұрыштың биссектрисасының бойында жатқан нүктелерден үшбұрыш қабырғаларына дейінгі қашықтықтардың қосындысы тұрақты екенін дәлелдеңдер.
9. Егер тікбұрышты үшбұрыштың қабырғалары арифметикалық прогрессия құрайтын болса, онда оның айырымы іштей сызылған шеңбердің радиусына тең екенін дәлелдеңдер.
10. Үшбұрыштың бір бұрышы 120º және оның қабырғалары айырымы 1-ге тең арифметикалық прогрессия құрайды. Үшбұрыштың қабырғаларын табыңдар.
11. Дөңес алтыбұрыштың ішкі бұрыштары айырымы 34º-қа тең арифметикалық прогрессия құрайды. Олардың ішіндегі ең кішісі тең:
A) 30º B) 35º C) 40º D) 45º E) 60º
12. Дөңес бесбұрыштың ішкі бұрыштары арифметикалық прогрессия құрайды. Прогрессияның үшінші мүшесі тең:
A) 108º B) 98º C) 120º D) 150º E) 54º
13. Дөңес төртбұрыштың ішкі бұрыштары еселігі 3-ке тең геометриялық прогрессия құрайды. Прогрессияның екінші мүшесі тең:
A) 39º B) 24º C) 27º D) 33º E) 21º
14. Үшбұрыштың бұрыштары геометриялық прогрессия құрайды. Егер кіші бұрышы 20º-қа тең болса, онда прогрессияның еселігі тең:
A)![]() B)
B) ![]() C)
C) ![]() D)
D) ![]() E)
E) ![]()
15. Тікбұрышты үшбұрыштың қабырғалары геометриялық прогрессия құрайды. Үшбұрыштың кіші бұрышының синусы тең:
A) ![]() B)
B) ![]() C)
C) ![]() D)
D) ![]() E)
E) ![]()
16. Дөңгелекке сырттай сүйір бұрышы α-ға тең теңбүйірлі трапеция сызылған. Трапеция табандары және дөңгелек диаметрі геометриялық прогрессия құрайды. Прогрессияның еселігі тең:
А) ![]() B)
B) ![]() C)
C)![]() D)
D) ![]() E)
E)
![]()
17. Ромбының кіші диагоналі, қабырғасы және оның үлкен диагоналі геометриялық прогрессияның тізбектес мүшелері болып табылады. Прогрессияның еселігі тең:
A) ![]() B)
B) ![]() C)
C)
![]() D)
D) ![]() E)
E) ![]()
18. Квадраттар тізбегі былай берілген: бірлік квадраттан бастап әрбір келесі квадраттың төбелері алдыңғысының қабырғаларын 3:1-ге қатынасындай бөліп отырады. Тізбектің барлық мүшелерінің аудандарының қосындысы тең:
А) ![]() B)
B) ![]() C)
C)
![]() D)
D) ![]() E)
E) ![]()
19. Бұрышқа әрбір келесісі алдыңғысын жанайтын және радиустары кемімелі шеңберлер іштей сызылған. Егер бірінші шеңбердің радиусы 10-ға, екінші шеңбермен шектелген дөңгелектің ауданы 64π –ге тең болса, онда барлық шеңберлер ұзындықтарының қосындысы тең:
A) 64π B) 75π C) 88π D) 96π E) 100π
Жауаптары
|
№ |
жауабы |
|
11 |
В |
|
12 |
А |
|
13 |
С |
|
14 |
А |
|
15 |
D |
|
16 |
А |
|
17 |
С |
|
18 |
В |
|
19 |
Е |

шағым қалдыра аласыз















