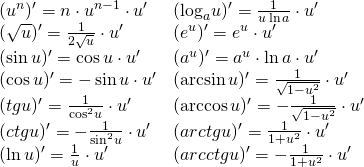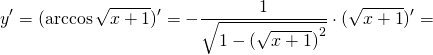ПЛАН- КОНСПЕКТ УРОКА 33 «Производная сложной функции»
|
Ход урока |
Время (минута) |
Действия преподавателя |
Действия обучающихся |
Учебные материалы и ресурсы |
|
1 |
2 |
3 |
4 |
5 |
|
3 мин |
Приветствовать обучающихся, отметить отсутствующих. Проверить подготовленность обучающихся к учебному занятию. |
Приветствовать. Подготовится к учебному занятию. |
|
|
7 мин |
Ответы на вопросы по домашнему заданию(решение примеров) Контроль усвоения материала. Фронтальный опрос: Производная степенной функции.
|
Ответить на вопросы Показать д-е задание. |
|
|
10 мин |
Цели урока: Обучающая: обобщить и систематизировать знания по теме «Производная сложной функции», умения применять полученные знания при решении задач,умение находить производных сложных функций, выявить и устранить пробелы в знаниях по данной теме; Развивающие: - содействовать развитию у учащихся мыслительных операций: умение анализировать, синтезировать, сравнивать; Воспитывающая: воспитание дисциплины и норм поведения, творческого отношения к изучаемому предмету; стимулировать активность учащихся, повышать мотивацию к изучению математики. Тип урока: комбинированный, включающий освоение новых знаний. Мобилизирующий момент: Вспомним о сложных функциях. Сложная функция — это функция от функции. Если u — функция от x, то есть u=u(x), а f — функция от u: f=f(u), то функция y=f(u) — сложная. А u в этом случае называют промежуточным аргументом. Еще часто f называют внешней функцией, а u — внутренней. Лучший способ понять, что такое сложная функция — рассмотреть примеры сложных функций. y=sin x — эта функция «простая». Синус зависит от x. Как только вместо x под знаком синуса появится выражение, зависящее от x, даже самое простое — такая функция называется сложной. То есть y=sin u — сложная функция, если u — некоторая функция от x. Примеры сложных функций с синусом: y=sin (x+1). Эта функция — сложная. Внутренняя функция u здесь равна x+1, а внешняя функция f — это синус. То есть u=x+1, f=sin u. y=sin (5x-2x³+3). Внутренняя функция u=5x-2x³+3, внешняя функция f=sin u.. Объявление темы урока Тема Производная сложной функции.
|
Подготовить тетради и ручки. Записывать важные информации. |
Алгебра и начала математического анализа. |
|
10 мин |
Консультация Мы уже рассмотрели понятие сложной функции. Следующий этап — нахождение производной. Легче всего понять, как находится производная сложной функции, рассматривая конкретные примеры. Если y=f(u), где u=u(x), то есть y — сложная функция, то производная сложной функции находится по следующему правилу: y’=f'(u)·u'(x), то есть производную внешней функции f надо умножить на производную внутренней функции u. На первых порах нам поможет разобраться, как находится производная сложной функции для каждой конкретной функции, следующая таблица:
Кроме того, полезно помнить следующие формулы:
Производная сложной функции.
Производная сложной функции равна производной
этой функции по промежуточному
аргументу
Теорема (О производной обратной функции)
Если функция Итак, найти производную сложной функции. Примеры. 1) y=sin(2x+3). Здесь внешняя функция синус: f=sinu, внутренняя — линейная: u=2x+3. Соответственно, производная данной сложной функции есть y’=cos(2x+3)·(2x+3)’=c0s(2x+3)·2=2c0s(2x+3). 2) y=cos(5-7x). Внешняя функция — косинус: f=cosu, внутренняя — линейная: u=5-7x. Поэтому y’=- sin(5-7x)·(5-7x)’=- sin(5-7x)·(-7)=7sin(5-7x).
|
Внимательно слушать консультацию. Записывать важные информации. |
Интернет. Википедия. Алгебра и начала математического анализа. |
|
5 мин |
Игра «Кто быстрее». На доске составляем кластер на тему «Производные» . |
Командная работа. |
|
|
15 мин |
Рассмотрим еще некоторые примеры нахождения производной сложной функции. Решение: Там, где возможно, перед дифференцированием примеры упрощаем: Данная функция — сложная. Внешняя функция f=u³, внутренняя — выражение, стоящее в скобках. Дифференцируем по правилу дифференцирования сложной функции: Имеем: 2) При нахождении производных логарифмов во многих случаях возможно предварительное преобразование выражений с использованием свойств логарифмов, что позволяет существенно облегчить дифференцирование: Здесь внешняя функция — ln u, внутренняя — выражение, стоящее под знаком логарифма. Внутренняя функция представляет собой дробь, поэтому для ее дифференцирования применяем правило нахождения производной частного: Сокращаем числитель и знаменатель на (х²+1) и 2: 3) Здесь внешняя функция — f=arccos u, u — выражение с квадратным корнем. Дифференцируем: 4) Первое слагаемое — сложная показательная функция 3 в степени u, u=cos x. Второе слагаемое дифференцируем по правилу нахождения производной произведения: |
Решить примеры вместе с преподавателем. Записывать важные информации. |
Алгебра и начала математического анализа. 10-11 Алимов Москва 2014 |
|
10 мин |
Учебник «Алгебра и начала математического анализа 10-11», Алимов
|
Работа на доске. |
|
|
5 мин |
А теперь посмотрите на картинку ниже, которая иллюстрирует решение задач на сложные производные по аналогии с простым примером из кулинарии - приготовлении запечёных яблок, фаршированных ягодами.
Итак, "яблоко" - это функция, аргументом которой является промежуточный аргумент, а промежуточный аргумент по независимой переменной x, в свою очередь, является "фаршем" (ягодами). Представим себе, что решая задачи на производные сложной функции, сначала помещаем яблоко с фаршем в особую (физико-математическую) духовку и устанавливаем режим 1. При таком режиме духовка воздействует только на "яблоко", поскольку нужно, допустим, больше пропечь яблоко, а фарш из ягод оставить более сочным, то есть обрабатывать в другом режиме. Итак, в при режиме 1 обрабатывается яблоко, а фарш остаётся незатронутым, или, ближе к нашим задачам, находим производную функции лишь от промежуточного аргумента, то есть, "яблока". Затем в духовке устанавливается режим 2, который воздействует только на фарш, иначе говоря, записываем производную функции, являющейся промежуточным аргументом по независимой переменной x. И, в конце концов, записываем произведение производной "яблока" и производной "фарша". Можно подавать! |
Коллективная работа. |
|
|
10 мин |
|
Индивидуальная работа. |
|
|
5 мин |
Метод «Вопрос - ответ»- обучающийся- преподаватель, обучающийся- обучающийся. |
Задавать вопросы. |
|
|
3 мин |
Задание на дом Учебник «Алгебра и начала математического анализа 10-11», Алимов §46, прочитать и конспектировать, № 824, 825 |
Записать домашнее задание |
Алгебра и начала анализа |
|
5 мин |
Дать качественную оценку работы всей группы и отдельных обучающихся. Рефлексия «Знал… Узнал… Хочу знать…» |
|
|
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
«Производная сложной функции»
«Производная сложной функции»
ПЛАН- КОНСПЕКТ УРОКА 33 «Производная сложной функции»
|
Ход урока |
Время (минута) |
Действия преподавателя |
Действия обучающихся |
Учебные материалы и ресурсы |
|
1 |
2 |
3 |
4 |
5 |
|
3 мин |
Приветствовать обучающихся, отметить отсутствующих. Проверить подготовленность обучающихся к учебному занятию. |
Приветствовать. Подготовится к учебному занятию. |
|
|
7 мин |
Ответы на вопросы по домашнему заданию(решение примеров) Контроль усвоения материала. Фронтальный опрос: Производная степенной функции.
|
Ответить на вопросы Показать д-е задание. |
|
|
10 мин |
Цели урока: Обучающая: обобщить и систематизировать знания по теме «Производная сложной функции», умения применять полученные знания при решении задач,умение находить производных сложных функций, выявить и устранить пробелы в знаниях по данной теме; Развивающие: - содействовать развитию у учащихся мыслительных операций: умение анализировать, синтезировать, сравнивать; Воспитывающая: воспитание дисциплины и норм поведения, творческого отношения к изучаемому предмету; стимулировать активность учащихся, повышать мотивацию к изучению математики. Тип урока: комбинированный, включающий освоение новых знаний. Мобилизирующий момент: Вспомним о сложных функциях. Сложная функция — это функция от функции. Если u — функция от x, то есть u=u(x), а f — функция от u: f=f(u), то функция y=f(u) — сложная. А u в этом случае называют промежуточным аргументом. Еще часто f называют внешней функцией, а u — внутренней. Лучший способ понять, что такое сложная функция — рассмотреть примеры сложных функций. y=sin x — эта функция «простая». Синус зависит от x. Как только вместо x под знаком синуса появится выражение, зависящее от x, даже самое простое — такая функция называется сложной. То есть y=sin u — сложная функция, если u — некоторая функция от x. Примеры сложных функций с синусом: y=sin (x+1). Эта функция — сложная. Внутренняя функция u здесь равна x+1, а внешняя функция f — это синус. То есть u=x+1, f=sin u. y=sin (5x-2x³+3). Внутренняя функция u=5x-2x³+3, внешняя функция f=sin u.. Объявление темы урока Тема Производная сложной функции.
|
Подготовить тетради и ручки. Записывать важные информации. |
Алгебра и начала математического анализа. |
|
10 мин |
Консультация Мы уже рассмотрели понятие сложной функции. Следующий этап — нахождение производной. Легче всего понять, как находится производная сложной функции, рассматривая конкретные примеры. Если y=f(u), где u=u(x), то есть y — сложная функция, то производная сложной функции находится по следующему правилу: y’=f'(u)·u'(x), то есть производную внешней функции f надо умножить на производную внутренней функции u. На первых порах нам поможет разобраться, как находится производная сложной функции для каждой конкретной функции, следующая таблица:
Кроме того, полезно помнить следующие формулы:
Производная сложной функции.
Производная сложной функции равна производной
этой функции по промежуточному
аргументу
Теорема (О производной обратной функции)
Если функция Итак, найти производную сложной функции. Примеры. 1) y=sin(2x+3). Здесь внешняя функция синус: f=sinu, внутренняя — линейная: u=2x+3. Соответственно, производная данной сложной функции есть y’=cos(2x+3)·(2x+3)’=c0s(2x+3)·2=2c0s(2x+3). 2) y=cos(5-7x). Внешняя функция — косинус: f=cosu, внутренняя — линейная: u=5-7x. Поэтому y’=- sin(5-7x)·(5-7x)’=- sin(5-7x)·(-7)=7sin(5-7x).
|
Внимательно слушать консультацию. Записывать важные информации. |
Интернет. Википедия. Алгебра и начала математического анализа. |
|
5 мин |
Игра «Кто быстрее». На доске составляем кластер на тему «Производные» . |
Командная работа. |
|
|
15 мин |
Рассмотрим еще некоторые примеры нахождения производной сложной функции. Решение: Там, где возможно, перед дифференцированием примеры упрощаем: Данная функция — сложная. Внешняя функция f=u³, внутренняя — выражение, стоящее в скобках. Дифференцируем по правилу дифференцирования сложной функции: Имеем: 2) При нахождении производных логарифмов во многих случаях возможно предварительное преобразование выражений с использованием свойств логарифмов, что позволяет существенно облегчить дифференцирование: Здесь внешняя функция — ln u, внутренняя — выражение, стоящее под знаком логарифма. Внутренняя функция представляет собой дробь, поэтому для ее дифференцирования применяем правило нахождения производной частного: Сокращаем числитель и знаменатель на (х²+1) и 2: 3) Здесь внешняя функция — f=arccos u, u — выражение с квадратным корнем. Дифференцируем: 4) Первое слагаемое — сложная показательная функция 3 в степени u, u=cos x. Второе слагаемое дифференцируем по правилу нахождения производной произведения: |
Решить примеры вместе с преподавателем. Записывать важные информации. |
Алгебра и начала математического анализа. 10-11 Алимов Москва 2014 |
|
10 мин |
Учебник «Алгебра и начала математического анализа 10-11», Алимов
|
Работа на доске. |
|
|
5 мин |
А теперь посмотрите на картинку ниже, которая иллюстрирует решение задач на сложные производные по аналогии с простым примером из кулинарии - приготовлении запечёных яблок, фаршированных ягодами.
Итак, "яблоко" - это функция, аргументом которой является промежуточный аргумент, а промежуточный аргумент по независимой переменной x, в свою очередь, является "фаршем" (ягодами). Представим себе, что решая задачи на производные сложной функции, сначала помещаем яблоко с фаршем в особую (физико-математическую) духовку и устанавливаем режим 1. При таком режиме духовка воздействует только на "яблоко", поскольку нужно, допустим, больше пропечь яблоко, а фарш из ягод оставить более сочным, то есть обрабатывать в другом режиме. Итак, в при режиме 1 обрабатывается яблоко, а фарш остаётся незатронутым, или, ближе к нашим задачам, находим производную функции лишь от промежуточного аргумента, то есть, "яблока". Затем в духовке устанавливается режим 2, который воздействует только на фарш, иначе говоря, записываем производную функции, являющейся промежуточным аргументом по независимой переменной x. И, в конце концов, записываем произведение производной "яблока" и производной "фарша". Можно подавать! |
Коллективная работа. |
|
|
10 мин |
|
Индивидуальная работа. |
|
|
5 мин |
Метод «Вопрос - ответ»- обучающийся- преподаватель, обучающийся- обучающийся. |
Задавать вопросы. |
|
|
3 мин |
Задание на дом Учебник «Алгебра и начала математического анализа 10-11», Алимов §46, прочитать и конспектировать, № 824, 825 |
Записать домашнее задание |
Алгебра и начала анализа |
|
5 мин |
Дать качественную оценку работы всей группы и отдельных обучающихся. Рефлексия «Знал… Узнал… Хочу знать…» |
|
|

шағым қалдыра аласыз