Қазақстан Республикасы
Білім және ғылым министрлігінің
2020 жылғы 6 сәуірдегі
№130 бұйрығына 35-қосымша
М.ТЫНЫШБАЕВ АТЫНДАҒЫ ҚАЗАҚ КӨЛІК ЖӘНЕ КОММУНИКАЦИЯЛАР АКАДЕМИЯСЫНЫҢ
ШЫМКЕНТ КӨЛІК КОЛЛЕДЖІ
2021-2022 оқу жылы
Сабақ жоспары №
|
Модуль/пән атауы |
Математика |
||||||||||
|
Сабақтың тақырыбы |
Қарапайым тригонометриялық теңдеулер |
||||||||||
|
Педагог |
Төлебаева Жанерке Мархабатқызы |
||||||||||
|
Курс |
1 |
||||||||||
|
Топ |
|
|
|
|
|
||||||
|
Сабақтың өткізілетін күні |
|
|
|
|
|
||||||
|
Сабақтың түрі |
Теориялық |
||||||||||
|
Сабақтың мақсаты немесе оқыту нәтижелері |
|
||||||||||
|
Бағалау критерийлері |
Тригонометриялық теңдеулерді шешеді, негізгі тригонометриялық формулалар, квадрат теңдеуге келтіру, бірінші және екінші дәрежелі біртекті теңдеулер, көбейткіштерге жіктеу әдістерін қолданады |
||||||||||
|
Оқу - әдістемелік құралдар, әдебиеттер |
Математика:Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 11-сыныбына арналған оқулық,1-2 бөлім, Алматы: «Мектеп», 2019ж. Деңгейлік саралау технологиясы |
||||||||||
|
Техникалық құралдар, материалдар |
Оқулықтар, үлестірме материалдар, стикерлер, плакаттар |
||||||||||
|
Сабақ барысы |
|||||||||||
|
Сабақ кезеңдері |
|
||||||||||
|
1.Ұйымдастыру кезеңі: (5 минут) |
а) сәлемдесу, оқушыларды түгендеу; б) сабақтың жүру жоспарын түсіндіру. |
||||||||||
|
2 Үй тапсырамасын тексеру кезеңі (20 минут) |
«Миға шабуыл» әдісі бойынша үйге берілген тапсырмаларды қайталап, еске түсіру. 11сыныптың алгебра және анализ бастамалары кітабының 88 бетіндегі 10.7 және 89 бетіндегі 10.14 және 10.15 есептерін шығару |
||||||||||
|
3. Жаңа материалды түсіндіруге дайындық кезеңі (жаңа тақырыпты болжау) / Практикалық, зертханалық жұмысқа дайындық кезеңі (5 минут) |
Функция, график, синусоида, синус, периодтылық, косинус, тангенс, котангенс |
||||||||||
|
4. Жаңа материалды түсіндіру кезеңі (Практикалық, зертханалық жұмысты орындау кезеңі) ( 35 минут) |
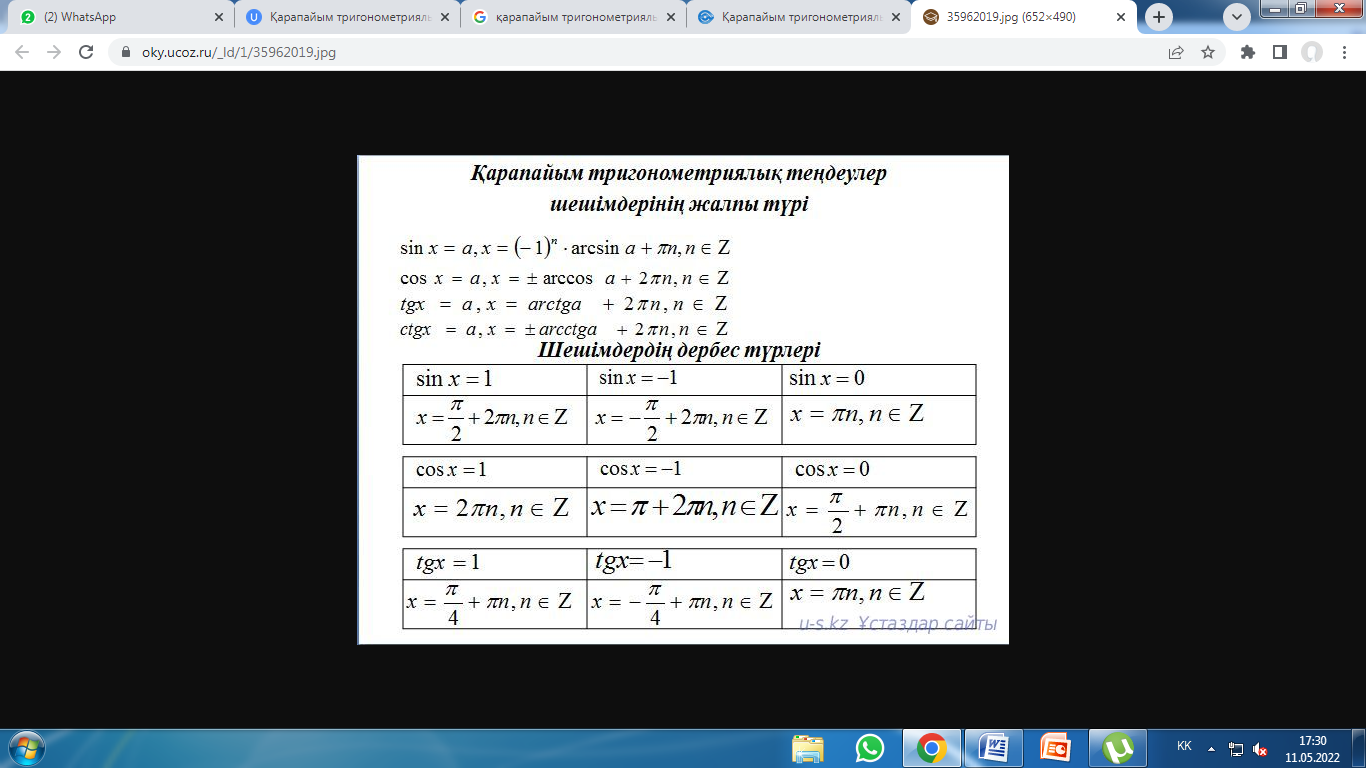
«Блум таксономиясы» әдісі арқылы жаңа сабақты түсіндіру. Айнымалысы тригонометриялық функция таңбасының ішінде болатын теңдеу тригонометриялық теңдеу деп аталады. sin x = а, , cos x= а , tg x= а, ctg x=a түрінде берілген теңдеу қарапайым тригонометриялық теңдеу деп аталады. Тригонометриялық теңдеуді шешу үшін тригонометриялық функциялардың арасындағы әр түрлі қатынастарды пайдалана отырып, тригонометриялық теңдеулерді ізделініп отырған аргументтің тригонометриялық функциялары біреуінің мәнін анықтауға болатындай түрге келтіру керек. Осыдан кейін тригонометриялық теңдеудің түбірлері кері тригонометриялық функциялардың көмегі арқылы табылады.Кез келген тригонометриялық теңдеуді тепе-тең түрлендіру арқылы қарапайым тригонометриялық теңдеуге келтіру керек.Енді қарапайым теңдеуді шешуді қарастырайық.
|
||||||||||
|
5. Жаңа материалды бекіту кезеңі. (Практикалық, зертханалық жұмысты тапсыру кезеңі) (15 минут) |
«Серпілген сауал» әдісі арқылы сабақты қорытындылау мақсатында студенттерге өтілген тақырып бойынша білімді меңгеруге арналған сұрақтар мен есептер беру.
|
||||||||||
|
6.Үй тапсырмасы туралы ақпараттандыру кезеңі (3 минут) |
Қарапайым тригонометриялық теңдеулер тақырыбы бойынша есептер: |
||||||||||
|
7.Сабақты қорытындылау және рефлексия (7 минут) |
Оқушыларды 100 балдық жүйе арқылы бағалау
|
||||||||||
Педагог: ___________________________________
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Қарапайым тригонометриялық теңдеулер
Қарапайым тригонометриялық теңдеулер
Қазақстан Республикасы
Білім және ғылым министрлігінің
2020 жылғы 6 сәуірдегі
№130 бұйрығына 35-қосымша
М.ТЫНЫШБАЕВ АТЫНДАҒЫ ҚАЗАҚ КӨЛІК ЖӘНЕ КОММУНИКАЦИЯЛАР АКАДЕМИЯСЫНЫҢ
ШЫМКЕНТ КӨЛІК КОЛЛЕДЖІ
2021-2022 оқу жылы
Сабақ жоспары №
|
Модуль/пән атауы |
Математика |
||||||||||
|
Сабақтың тақырыбы |
Қарапайым тригонометриялық теңдеулер |
||||||||||
|
Педагог |
Төлебаева Жанерке Мархабатқызы |
||||||||||
|
Курс |
1 |
||||||||||
|
Топ |
|
|
|
|
|
||||||
|
Сабақтың өткізілетін күні |
|
|
|
|
|
||||||
|
Сабақтың түрі |
Теориялық |
||||||||||
|
Сабақтың мақсаты немесе оқыту нәтижелері |
|
||||||||||
|
Бағалау критерийлері |
Тригонометриялық теңдеулерді шешеді, негізгі тригонометриялық формулалар, квадрат теңдеуге келтіру, бірінші және екінші дәрежелі біртекті теңдеулер, көбейткіштерге жіктеу әдістерін қолданады |
||||||||||
|
Оқу - әдістемелік құралдар, әдебиеттер |
Математика:Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 11-сыныбына арналған оқулық,1-2 бөлім, Алматы: «Мектеп», 2019ж. Деңгейлік саралау технологиясы |
||||||||||
|
Техникалық құралдар, материалдар |
Оқулықтар, үлестірме материалдар, стикерлер, плакаттар |
||||||||||
|
Сабақ барысы |
|||||||||||
|
Сабақ кезеңдері |
|
||||||||||
|
1.Ұйымдастыру кезеңі: (5 минут) |
а) сәлемдесу, оқушыларды түгендеу; б) сабақтың жүру жоспарын түсіндіру. |
||||||||||
|
2 Үй тапсырамасын тексеру кезеңі (20 минут) |
«Миға шабуыл» әдісі бойынша үйге берілген тапсырмаларды қайталап, еске түсіру. 11сыныптың алгебра және анализ бастамалары кітабының 88 бетіндегі 10.7 және 89 бетіндегі 10.14 және 10.15 есептерін шығару |
||||||||||
|
3. Жаңа материалды түсіндіруге дайындық кезеңі (жаңа тақырыпты болжау) / Практикалық, зертханалық жұмысқа дайындық кезеңі (5 минут) |
Функция, график, синусоида, синус, периодтылық, косинус, тангенс, котангенс |
||||||||||
|
4. Жаңа материалды түсіндіру кезеңі (Практикалық, зертханалық жұмысты орындау кезеңі) ( 35 минут) |
«Блум таксономиясы» әдісі арқылы жаңа сабақты түсіндіру. Айнымалысы тригонометриялық функция таңбасының ішінде болатын теңдеу тригонометриялық теңдеу деп аталады. sin x = а, , cos x= а , tg x= а, ctg x=a түрінде берілген теңдеу қарапайым тригонометриялық теңдеу деп аталады. Тригонометриялық теңдеуді шешу үшін тригонометриялық функциялардың арасындағы әр түрлі қатынастарды пайдалана отырып, тригонометриялық теңдеулерді ізделініп отырған аргументтің тригонометриялық функциялары біреуінің мәнін анықтауға болатындай түрге келтіру керек. Осыдан кейін тригонометриялық теңдеудің түбірлері кері тригонометриялық функциялардың көмегі арқылы табылады.Кез келген тригонометриялық теңдеуді тепе-тең түрлендіру арқылы қарапайым тригонометриялық теңдеуге келтіру керек.Енді қарапайым теңдеуді шешуді қарастырайық.
|
||||||||||
|
5. Жаңа материалды бекіту кезеңі. (Практикалық, зертханалық жұмысты тапсыру кезеңі) (15 минут) |
«Серпілген сауал» әдісі арқылы сабақты қорытындылау мақсатында студенттерге өтілген тақырып бойынша білімді меңгеруге арналған сұрақтар мен есептер беру.
|
||||||||||
|
6.Үй тапсырмасы туралы ақпараттандыру кезеңі (3 минут) |
Қарапайым тригонометриялық теңдеулер тақырыбы бойынша есептер: |
||||||||||
|
7.Сабақты қорытындылау және рефлексия (7 минут) |
Оқушыларды 100 балдық жүйе арқылы бағалау
|
||||||||||
Педагог: ___________________________________

шағым қалдыра аласыз