6.4В Шамалар арасындағы тәуелділіктер

Мектеп:

Педагогтің аты-жөні:

Күні:

Сыныбы: 6

Қатысушылар саны: Қатыспағандар саны:

Сабақтың тақырыбы:

Нақты процестердің графиктерін қолданып шамалар арасындағы тәуелділіктерді зерттеу

Оқу бағдарламасына сәйкес оқу мақсаты

6.5.2.10

шынайы процестердің графиктерін қолданып, шамалар арасындағы тәуелділіктерді табу және зерттеу;

Сабақтың мақсаты:

шынайы процестердің графиктерін қолданып, шамалар арасындағы тәуелділіктерді табу және зерттеу;

Сабақ кезеңі/Уақыты

I.Ұйымдастыру кезеңі.

Оқушының іс-әрекеті

Бағалау

Ресурстар

Сабақтың басы

I.Ұйымдастыру кезеңі.

Сәлемдесу, түгелдеу, сабаққа дайындықтарын тексеру.

Сабақты жағымды ахуалдан бастау. Үй тапсырмасын тексеру: Тақтада тапсырма дұрыс жауабымен көрсетіліп тұрады.

Шаттық шеңберін құрып «Өзіңе тілегенді,өзгеге тіле»! әдісі арқылы бір-біріне тілек айтып,жақсы көңіл күй сыйлайды.

Тиімділігі: Оқушыны бір-біріне тілек айту арқылы жақындастырады, көңіл -күйін көтереді, бауырмалдығын оятады.

«Мен саған, сен маған» арқылы оқушылар бір-бірінің үй тапсырмасын тексереді.

Мұғалім ұйымдастыру кезеңінде белсенділік танытқан оқушыларды «Мадақтау сөз» әдісіарқылы бағалайды: «Жарайсың! Жақсы! Өте жақсы! Талпын!»

Түрлі түсті қима қағаздар

Оқулық, оқу құрал жабдықтары, тақта, бор

Сабақтың ортасы

1-тапсырманы түсіндіреді. орындатады

1. Тапсырма.

№1. А және В қалалар арасындағы қашықтық 20км тең. Жылдамдықпен уақыттың тәуелділігін формула арқылы көрсетіңіз. Кестені толтырыңыз және графигін салыңыз.

Дескриптор:

-пойыздың жүрген

А нүктесінің координаталарын табады;

Уакыттың жылдамдыққа тәуелділігін корсетеді

Бағалаудың өзін-өзі бағалау түрі қолданылады

Оқулық, оқу құрал жабдықтары, тақта, бор

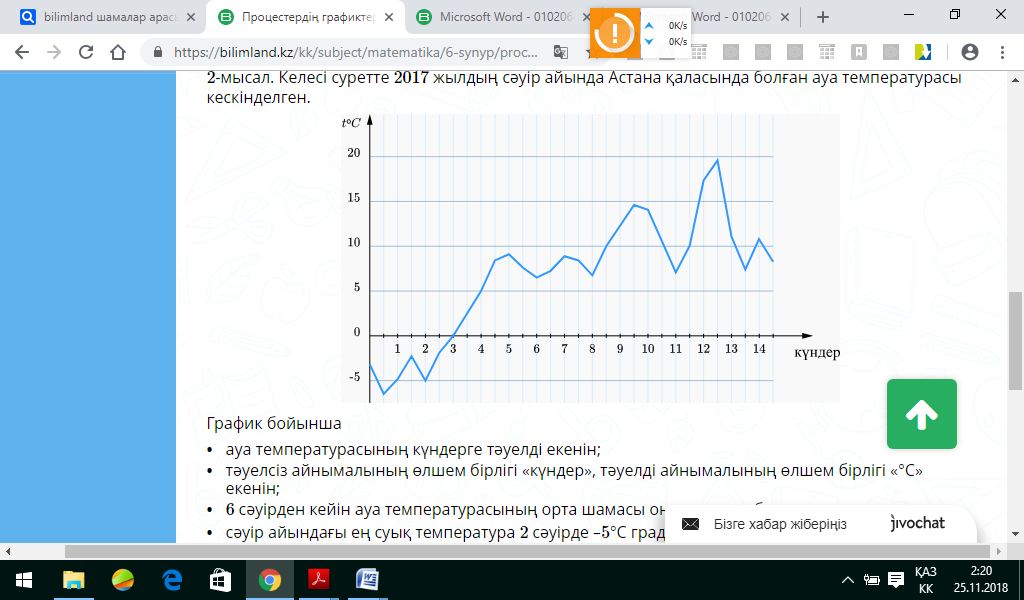
2-тапсырма. Келесі суретте 2020 жылдың сәуір айында Алматы қаласында болған ауа температурасы кескінделген.

График бойынша:

- ауа температурасының күндерге тәуелді екенін анықта;

- тәуелсіз айнымалының өлшем бірлігі «күндер», тәуелді айнымалының өлшем бірлігі ?

- 6 сәуірден кейін ауа температурасының орта шамасы кандай мәндер қабылдағанын тап;

- сәуір айындағы ең суық температура ,

- ең жылы температура

График бойынша:

- ауа температурасының күндерге тәуелді екенін;

- тәуелсіз айнымалының өлшем бірлігі «күндер», тәуелді айнымалының өлшем бірлігі «°С» екенін;

- 6 сәуірден кейін ауа температурасының орта шамасы оң мәндер қабылдағанын;

- сәуір айындағы ең суық температура 2 сәуірде –5°С градустан төмен болғанын, ең жылы температура 26сәуірде 20°С градустан жоғары болғанын көруге болады.

Графикті пайдаланып, 14 тәулік ішіндегі ең жоғарғы температура, ең төменгі температура, температуралардың оң мәндері мен теріс мәндері анықталды.

Оқулық, оқу құрал жабдықтары, тақта, бор

Кесте

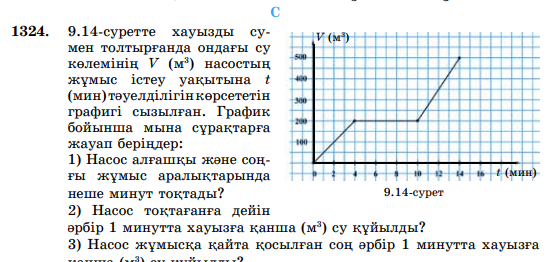
3-тапсырма

Дескриптор:

-график бойынша насостын жумыс жасамаган аралыгын табады;

-насос токтаганга дейін хауызга куйылган судын молшерін табады;

-насостын жумыс істеген кезедегі хауызга куйган су молшерін анықтайды

Бағалаудың өзін-өзі бағалау түрі қолданылады

Окулық

Даптер, калам

жабдықтары, тақта, бор

график

Кесте

Сабақтың аяғы

«Жетістік баспалдағы» кері байланыс парағы таратылады.

Мақсаты: Өз ойын айтып, сабақты бекіту, қорытындылау.

Тиімділігі:Оқушы алған білімін жинақтап, саралай білуге дағдыланады.

Саралау: Бұл тапсырмада саралаудың «Қорытынды» тәсілі көрініс табады.

Оқушылар бір-бірінің сабаққа қатысу белсенділігіне қарай «Мадақтау сөздері» әдісі арқылы бірін-бірі бағалайды. Жарайсың!, Керемет!, Жақсы!, Талпын!,.

6.4В Шамалар арасындағы тәуелділіктер

Мектеп:

Педагогтің аты-жөні:

Күні:

Сыныбы: 6

Қатысушылар саны: Қатыспағандар саны:

Сабақтың тақырыбы:

Тура пропорционалдық және оның графигі

Оқу бағдарламасына сәйкес оқу мақсаты

6.1.2.23

тура пропорционал тәуелділіктерді танып білу және мысалдар келтіру;

6.2.1.12

тура пропорционалдықтың формуласын білу және графигін салу;

6.5.2.11

тура пропорционал шамалардың арасындағы шынайы тәуелділік-тердің графиктеріне талдау беру;

6.5.2.12

сипаттамасы бойынша тура пропорционалдықтың формуласын жазу;

6.5.2.13

тура пропорционалдықтың графигін салу;

Сабақтың мақсаты:

тура пропорционал тәуелділіктерді танып білу және мысалдар келтіру;

тура пропорционалдықтың формуласын білу және графигін салу;

тура пропорционал шамалардың арасындағы шынайы тәуелділік-тердің графиктеріне талдау беру;

сипаттамасы бойынша тура пропорционалдықтың формуласын жазу;

тура пропорционалдықтың графигін салу;

Сабақ кезеңі/Уақыты

I.Ұйымдастыру кезеңі.

Оқушының іс-әрекеті

Бағалау

Ресурстар

Сабақтың басы

I.Ұйымдастыру кезеңі.

Сәлемдесу, түгелдеу, сабаққа дайындықтарын тексеру.

Үй тапсырмасын тексеру: Тақтада тапсырма дұрыс жауабымен көрсетіліп тұрады.

Шаттық шеңберін құрып «Өзіңе тілегенді,өзгеге тіле»! әдісі арқылы бір-біріне тілек айтып,жақсы көңіл күй сыйлайды.

Тиімділігі: Оқушыны бір-біріне тілек айту арқылы жақындастырады, көңіл -күйін көтереді, бауырмалдығын оятады.

«Мен саған, сен маған» арқылы оқушылар бір-бірінің үй тапсырмасын тексереді.

«Мадақтау сөз» әдісіарқылы бағалайды: «Жарайсың! Жақсы! Өте жақсы! Талпын!»

Түрлі түсті қима қағаздар

Оқулық, оқу құрал жабдықтары, тақта, бор

Кесте

Сабақтың ортасы

1. Тура пропорционалдық.

1-мысал. Екі балмұздақ 300 теңге тұрса, онда 5 балмұздақ қанша тұрады?

Шешуі: Есепте балмұздақтың бағасы белгісіз, алайда ол тұрақты. Балмұздақтың бағасын табу үшін 300-ді екіге бөлеміз. 300: 2 = 150 (т)

Заттың құны мен саны тура пропорционал болғандықтан К = 150·5 = 750 (т).

Егербірзаттыңмассасытұрақтыболса, ондабірдейзаттардыңжалпымассасы мен саны тура пропорционал болады. Ал жалпымассасытұрақтыболса, ондабірзаттыңмассасы мен заттардың саны керіпропорционалболады.

Мысалдардағы тура пропорционалдықты y=kx формуласымен беруге болады.

Мұндағы x- тәуелсіз айнымалы шама мәні (аргумент- қункцияның анықталу аймағы);

y- оған сәйкес тәуелді айнымалы шама (мәндер жиыны – функциянық мәндерінің аймағы);

k - нөлден өзге сан.

y=kx формуласымен берілетін x және y шамалары арасындағы тәуелділік тура пропорционалдық деп аталады. k – пропорционалдық коэффициенті, k

y=kx формуласындағы x –тің әрбір мәніне y – тің бір ғана мәні сәйкес келеді.

2. Тура пропорционалдықтың графигі.

3-мысал.  x және y шамалары арасындағы тура пропорционал тәуелділік кестемен берілген.

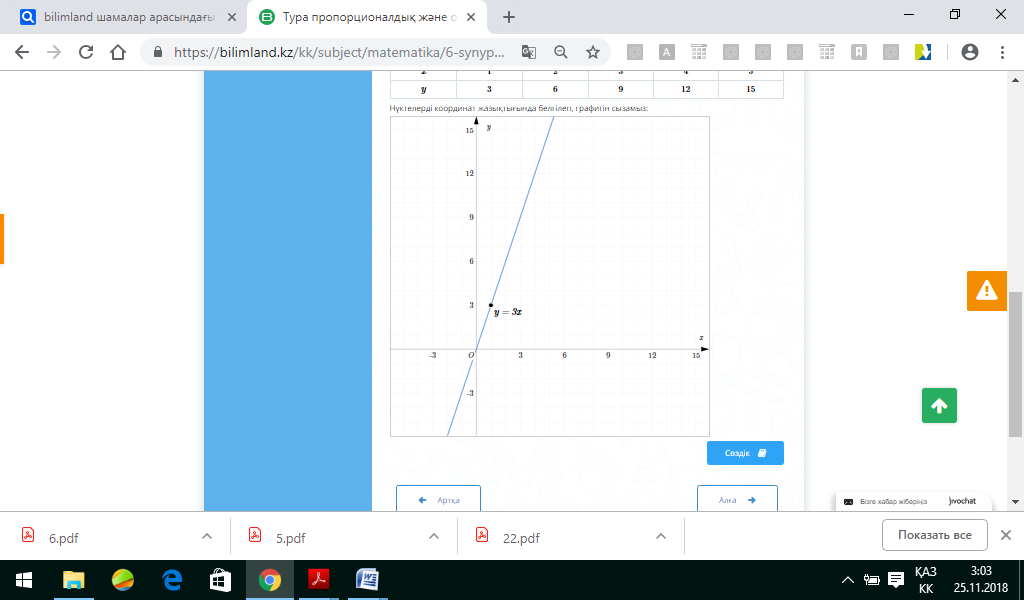
Тәуелділіктің формуласын,  x =1, x =3, x =4 және x =5 болғандағы y мәндерін тауып, графигін сызайық. Берілген тәуелділік тура пропорционал болғандықтан, оның формуласын y = kx түрінде құрастырамыз. Кестеде берілгені бойынша 6 = k ⋅ 2, осыдан пропорционалдық коэффициенті табылады: k =6 : 2 немесе k =3. Яғни тура пропорционал тәуелділіктің формуласы – y = 3x.

Формула бойынша ізделінді мәндерін табамыз:

x = 1,  y = 3 ⋅ 1 = 3;

x = 3 , y = 3 ⋅ 3 = 9;

x = 4 , y = 3 ⋅ 4 = 12;

x = 5,  y = 3 ⋅ 5 = 15.

Кестені толтырайық:

Нүктелерді координат жазықтығында белгілеп, графигін сызамыз:

«Мадақтау сөз» әдісі

Жүктеу

ЖИ арқылы жасау

ЖИ арқылы жасау

Бөлісу

1 - айлық

Материал тарифі

-96% жеңілдік

00

05

00

ҚМЖ

Ашық сабақ

Тәрбие сағаты

Презентация

БЖБ, ТЖБ тесттер

Көрнекіліктер

Балабақшаға арнарлған құжаттар

Мақала, Эссе

Дидактикалық ойындар

және тағы басқа 400 000 материал

Барлық 400 000 материалдарды шексіз
жүктеу мүмкіндігіне ие боласыз

1 990 ₸ 49 000₸

1 айға қосылу

Таңдау

Материалға шағымдану

Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз

Жариялаған:

Жалкашхан Майра

29 Наурыз 2023

2729

Шағым жылдам қаралу үшін барынша толық ақпарат жіберіңіз

Шағымды қалдыру

ҚМЖ 6 сынып 2023

Тақырып бойынша 31 материал табылды

ҚМЖ 6 сынып 2023

Материал туралы қысқаша түсінік

ҚМЖ 2023 жыл 6 сынып жаңа әдіс тәсілдер арқылы жасалған

Материалды жүктеу

Материалдың қысқаша нұсқасы

6.4В Шамалар арасындағы тәуелділіктер	Мектеп:
Педагогтің аты-жөні:
Күні:
Сыныбы: 6	Қатысушылар саны: Қатыспағандар саны:
Сабақтың тақырыбы:	Нақты процестердің графиктерін қолданып шамалар арасындағы тәуелділіктерді зерттеу
Оқу бағдарламасына сәйкес оқу мақсаты	6.5.2.10 шынайы процестердің графиктерін қолданып, шамалар арасындағы тәуелділіктерді табу және зерттеу;
Сабақтың мақсаты:	шынайы процестердің графиктерін қолданып, шамалар арасындағы тәуелділіктерді табу және зерттеу;

Сабақ кезеңі/Уақыты	I.Ұйымдастыру кезеңі.	Оқушының іс-әрекеті	Бағалау	Ресурстар
Сабақтың басы	I.Ұйымдастыру кезеңі. Сәлемдесу, түгелдеу, сабаққа дайындықтарын тексеру. Сабақты жағымды ахуалдан бастау. Үй тапсырмасын тексеру: Тақтада тапсырма дұрыс жауабымен көрсетіліп тұрады.	Шаттық шеңберін құрып «Өзіңе тілегенді,өзгеге тіле»! әдісі арқылы бір-біріне тілек айтып,жақсы көңіл күй сыйлайды. Тиімділігі: Оқушыны бір-біріне тілек айту арқылы жақындастырады, көңіл -күйін көтереді, бауырмалдығын оятады. «Мен саған, сен маған» арқылы оқушылар бір-бірінің үй тапсырмасын тексереді.	Мұғалім ұйымдастыру кезеңінде белсенділік танытқан оқушыларды «Мадақтау сөз» әдісіарқылы бағалайды: «Жарайсың! Жақсы! Өте жақсы! Талпын!»	Түрлі түсті қима қағаздар Оқулық, оқу құрал жабдықтары, тақта, бор
Сабақтың ортасы	1-тапсырманы түсіндіреді. орындатады	Тапсырма. №1. А және В қалалар арасындағы қашықтық 20км тең. Жылдамдықпен уақыттың тәуелділігін формула арқылы көрсетіңіз. Кестені толтырыңыз және графигін салыңыз. t(сағ) 1 2 2,5 3 4 4,5 6 9 18 v(км)	Дескриптор: -пойыздың жүрген А нүктесінің координаталарын табады; Уакыттың жылдамдыққа тәуелділігін корсетеді Бағалаудың өзін-өзі бағалау түрі қолданылады	Оқулық, оқу құрал жабдықтары, тақта, бор
	2-тапсырма. Келесі суретте 2020 жылдың сәуір айында Алматы қаласында болған ауа температурасы кескінделген. График бойынша: - ауа температурасының күндерге тәуелді екенін анықта; - тәуелсіз айнымалының өлшем бірлігі «күндер», тәуелді айнымалының өлшем бірлігі ? - 6 сәуірден кейін ауа температурасының орта шамасы кандай мәндер қабылдағанын тап; - сәуір айындағы ең суық температура , - ең жылы температура		График бойынша: - ауа температурасының күндерге тәуелді екенін; - тәуелсіз айнымалының өлшем бірлігі «күндер», тәуелді айнымалының өлшем бірлігі «°С» екенін; - 6 сәуірден кейін ауа температурасының орта шамасы оң мәндер қабылдағанын; - сәуір айындағы ең суық температура 2 сәуірде –5°С градустан төмен болғанын, ең жылы температура 26сәуірде 20°С градустан жоғары болғанын көруге болады. Графикті пайдаланып, 14 тәулік ішіндегі ең жоғарғы температура, ең төменгі температура, температуралардың оң мәндері мен теріс мәндері анықталды.	Оқулық, оқу құрал жабдықтары, тақта, бор Кесте
	3-тапсырма		Дескриптор: -график бойынша насостын жумыс жасамаган аралыгын табады; -насос токтаганга дейін хауызга куйылган судын молшерін табады; -насостын жумыс істеген кезедегі хауызга куйган су молшерін анықтайды Бағалаудың өзін-өзі бағалау түрі қолданылады	Окулық Даптер, калам
				жабдықтары, тақта, бор график Кесте
Сабақтың аяғы		«Жетістік баспалдағы» кері байланыс парағы таратылады. Мақсаты: Өз ойын айтып, сабақты бекіту, қорытындылау. Тиімділігі:Оқушы алған білімін жинақтап, саралай білуге дағдыланады. Саралау: Бұл тапсырмада саралаудың «Қорытынды» тәсілі көрініс табады.	Оқушылар бір-бірінің сабаққа қатысу белсенділігіне қарай «Мадақтау сөздері» әдісі арқылы бірін-бірі бағалайды. Жарайсың!, Керемет!, Жақсы!, Талпын!,.

6.4В Шамалар арасындағы тәуелділіктер	Мектеп:
Педагогтің аты-жөні:
Күні:
Сыныбы: 6	Қатысушылар саны: Қатыспағандар саны:
Сабақтың тақырыбы:	Тура пропорционалдық және оның графигі
Оқу бағдарламасына сәйкес оқу мақсаты	6.1.2.23 тура пропорционал тәуелділіктерді танып білу және мысалдар келтіру; 6.2.1.12 тура пропорционалдықтың формуласын білу және графигін салу; 6.5.2.11 тура пропорционал шамалардың арасындағы шынайы тәуелділік-тердің графиктеріне талдау беру; 6.5.2.12 сипаттамасы бойынша тура пропорционалдықтың формуласын жазу; 6.5.2.13 тура пропорционалдықтың графигін салу;
Сабақтың мақсаты:	тура пропорционал тәуелділіктерді танып білу және мысалдар келтіру; тура пропорционалдықтың формуласын білу және графигін салу; тура пропорционал шамалардың арасындағы шынайы тәуелділік-тердің графиктеріне талдау беру; сипаттамасы бойынша тура пропорционалдықтың формуласын жазу; тура пропорционалдықтың графигін салу;

Сабақ кезеңі/Уақыты	I.Ұйымдастыру кезеңі.	Оқушының іс-әрекеті	Бағалау	Ресурстар
Сабақтың басы	I.Ұйымдастыру кезеңі. Сәлемдесу, түгелдеу, сабаққа дайындықтарын тексеру. Үй тапсырмасын тексеру: Тақтада тапсырма дұрыс жауабымен көрсетіліп тұрады.	Шаттық шеңберін құрып «Өзіңе тілегенді,өзгеге тіле»! әдісі арқылы бір-біріне тілек айтып,жақсы көңіл күй сыйлайды. Тиімділігі: Оқушыны бір-біріне тілек айту арқылы жақындастырады, көңіл -күйін көтереді, бауырмалдығын оятады. «Мен саған, сен маған» арқылы оқушылар бір-бірінің үй тапсырмасын тексереді.	«Мадақтау сөз» әдісіарқылы бағалайды: «Жарайсың! Жақсы! Өте жақсы! Талпын!»	Түрлі түсті қима қағаздар Оқулық, оқу құрал жабдықтары, тақта, бор Кесте
Сабақтың ортасы	Тура пропорционалдық. 1-мысал. Екі балмұздақ 300 теңге тұрса, онда 5 балмұздақ қанша тұрады? Шешуі: Есепте балмұздақтың бағасы белгісіз, алайда ол тұрақты. Балмұздақтың бағасын табу үшін 300-ді екіге бөлеміз. 300: 2 = 150 (т) Заттың құны мен саны тура пропорционал болғандықтан К = 150·5 = 750 (т). Егербірзаттыңмассасытұрақтыболса, ондабірдейзаттардыңжалпымассасы мен саны тура пропорционал болады. Ал жалпымассасытұрақтыболса, ондабірзаттыңмассасы мен заттардың саны керіпропорционалболады. Мысалдардағы тура пропорционалдықты y=kx формуласымен беруге болады. Мұндағы x- тәуелсіз айнымалы шама мәні (аргумент- қункцияның анықталу аймағы); y- оған сәйкес тәуелді айнымалы шама (мәндер жиыны – функциянық мәндерінің аймағы); k - нөлден өзге сан. y=kx формуласымен берілетін x және y шамалары арасындағы тәуелділік тура пропорционалдық деп аталады. k – пропорционалдық коэффициенті, k y=kx формуласындағы x –тің әрбір мәніне y – тің бір ғана мәні сәйкес келеді. Тура пропорционалдықтың графигі. 3-мысал.  x және y шамалары арасындағы тура пропорционал тәуелділік кестемен берілген. x 2 y 6 Тәуелділіктің формуласын,  x =1, x =3, x =4 және x =5 болғандағы y мәндерін тауып, графигін сызайық. Берілген тәуелділік тура пропорционал болғандықтан, оның формуласын y = kx түрінде құрастырамыз. Кестеде берілгені бойынша 6 = k ⋅ 2, осыдан пропорционалдық коэффициенті табылады: k =6 : 2 немесе k =3. Яғни тура пропорционал тәуелділіктің формуласы – y = 3x. Формула бойынша ізделінді мәндерін табамыз: x = 1,  y = 3 ⋅ 1 = 3; x = 3 , y = 3 ⋅ 3 = 9; x = 4 , y = 3 ⋅ 4 = 12; x = 5,  y = 3 ⋅ 5 = 15. Кестені толтырайық: x 1 2 3 4 5 y 3 6 9 12 15 Нүктелерді координат жазықтығында белгілеп, графигін сызамыз:
			«Мадақтау сөз» әдісі Материалды жүктеу Жүктеу Сақтау Бөлісу ЖИ арқылы жасау Файл форматы: docx Математика Сабақ жоспары 6 сынып 29.03.2023 2729 Жүктеу Сақтау ЖИ арқылы жасау Жариялаған: Жалкашхан Майра Бұл материалды қолданушы жариялаған. Ustaz Tilegi ақпаратты жеткізуші ғана болып табылады. Жарияланған материалдың мазмұны мен авторлық құқық толықтай автордың жауапкершілігінде. Егер материал авторлық құқықты бұзады немесе сайттан алынуы тиіс деп есептесеңіз, шағым қалдыра аласыз Қазақстандағы ең үлкен материалдар базасынан іздеу Сіз үшін 400 000 ұстаздардың еңбегі мен тәжірибесін біріктіріп, ең үлкен материалдар базасын жасадық. Төменде керек материалды іздеп, жүктеп алып сабағыңызға қолдана аласыз Іздеу Материал жариялап, аттестацияға 100% жарамды сертификатты тегін алыңыз! Ustaz tilegi журналы министірліктің тізіміне енген. Qr коды мен тіркеу номері беріледі. Материал жариялаған соң сертификат тегін бірден беріледі. Толығырақ Оқу-ағарту министірлігінің ресми жауабы Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз! Қазақстан Республикасының білім беру жүйесін дамытуға қосқан жеке үлесі үшін және де Республика деңгейінде «Ustaz tilegi» Республикалық ғылыми – әдістемелік журналының желілік басылымына өз авторлық материалыңызбен бөлісіп, белсенді болғаныңыз үшін алғыс білдіреміз! Жариялау Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз! Тәуелсіз Қазақстанның білім беру жүйесін дамытуға және білім беру сапасын арттыру мақсатында Республика деңгейінде «Ustaz tilegi» Республикалық ғылыми – әдістемелік журналының желілік басылымына өз авторлық жұмысын жариялағаны үшін марапатталасыз! Жариялау Министірлікпен келісілген курстар тізімі Химия пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Тарих пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Биология пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Ағылшын тілі пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ География пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Информатика пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Мектепке дейінгі білім беру бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ «Қазақ тілі» жəне «Қазақ əдебиеті» бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Дене шынықтыру пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Білім алушылардың білім сапасын арттыру мақсатында сабақта цифрлық технологияларды қолдану 80/108 сағат Толығырақ Инклюзивті білім беру жүйесінде ерекше білім беру қажеттілігі бар білім алушыға психологиялық-педагогикалық қолдау көрсету бойынша педагогтердің кәсіби және пәндік құзыреттіліктерін дамыту 80/108 сағат Толығырақ