|
Бөлім: |
Функция. Функцияның графигі |
||||||
|
Педагогтің Тегі, Аты, Әкесінің аты (бар болса) |
Алимбек М |
||||||
|
Сынып: |
7 сынып. Қатысқандар саны: Қатыспағандар саны: |
||||||
|
Күні: |
25\11/2024 |
||||||
|
Сабақтың тақырыбы: |
Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу |
||||||
|
Оқу бағдарламасына сәйкес оқыту мақсаттары: |
7.4.2.4 екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу; |
||||||
|
Сабақтың мақсаттары: |
-Теңдеулер жүйесінің шешімдер саны неге тәуелді екендігін білу - Теңдеулер жүйесінің шешімдер санын анықтау. Әр түрлі шешімдер саны болатын теңдеулер жүйесінің мысалдарын келтіру. |
||||||
|
Сабақ барысы: |
|||||||
|
Уақыты |
Кезең дері |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
||
|
5 минут
|
Ұйым дастыру |
Сәлеметсіздерме! Бүгін, Сызықтық функциялардың графиктерінің өзара орналасуы тақырыбын қарастырамыз Бүгінгі сабақта меңгеретініңіз: -Теңдеулер жүйесінің шешімдер саны неге тәуелді екендігін білу - Теңдеулер жүйесінің шешімдер санын анықтау. Әр түрлі шешімдер саны болатын теңдеулер жүйесінің мысалдарын келтіру. |
|
|
|
||
|
10 мин |
Жаңа сабақ |
Жаңа сабақ ax + by = c түрінде берілген теңдеу екі айнымалысы бар сызықтық теңдеу деп аталады. Мұндағы x және y – айнымалылар, a , b және c – қандай да бір сандар. Екі айнымалысы бар теңдеудің шешімі деп осы теңдеуді дұрыс сандық теңдікке айналдыратын айнымалылардың мәндер жұбын айтады. Мысалы, x – y = 5 теңдеуі x = 8, y = 3 болғанда дұрыс теңдікке айналады: 8 – 3 = 5. Айнымалылардың x = 8, y = 3 мәндер жұбын осы теңдеудің шешімі деп айтады. Екі айнымалысы бар сызықтық теңдеудің шексіз көп шешімі бар. Сонымен қатар x = 15, y = 10; x = 86, y = 81 жұбы да x – y = 5 теңдеуінің шешімдері болатынын тексеру қиын емес. Кем дегенде бір айнымалысының коэффициенті нөлге тең емес екі айнымалысы бар сызықтық теңдеудің графигі түзу болады. Егер екі айнымалысы бар екі сызықтық теңдеу берілген болса және бір уақытта екі теңдеуді де қанағаттандыратын айнымалыларды мәндерін табу керек болса, онда осы теңдеулердің жүйесін шешу керек болады. Екі айнымалысы бар сызықтық теңдеулер жүйесінің шешімі деп жүйенің әр теңдеуін дұрыс теңдікке айналдыратын айнымалылар мәндерінің жұбын айтады. Теңдеулер жүйесін шешу дегеніміз – оның барлық шешімін табу немесе шешімдерінің жоқтығын дәлелдеу. Екі айнымалысы бар сызықтық теңдеулер жүйесін шешу үшін тек қосу тәсілін және алмастыру тәсілін ғана емес, теңдеулердің графиктерін де қолдануға болады. Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешуді қарастырып отырмыз. 1 жағдай. у=0,5х+2 у=-1,5х+6 жауабы (2; 3) егер теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер қиылысса, онда теңдеулер жүйесінің бір ғана шешімі болады. |
Сұрақтарға жауап береді
Тақырып бойынша ресурстарды қарап, танысады
|
Дескриптор: - сызықтық функцияның анықтама сын біледі және түсінеді; - сызықтық функцияның графигі түзу екенін біледі және түсінеді; |
ДК экраны 7-сынып оқулығы. Жұмыс дәптерлері. .
|
||
|
25 минут
|
Бекіту тапсырмасы |
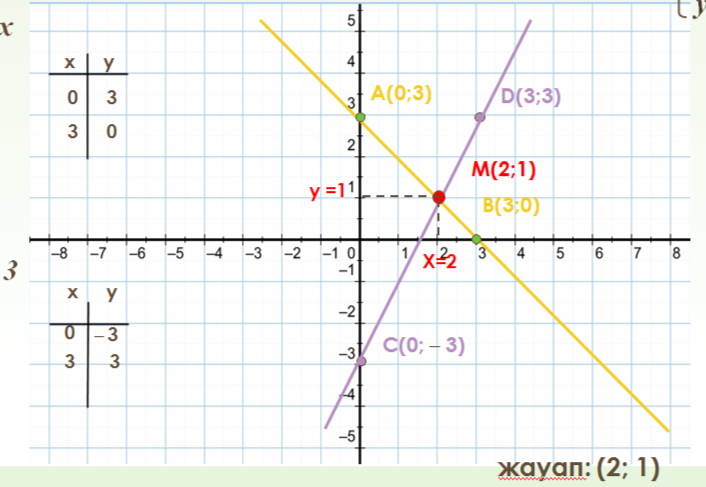
І- тапсырма. Жүйені шеш:
II-тапсырма. 3x+by=12 түзуі C(2;3) нүктесі арқылы өтеді. Бұл түзу: 1) A(0;6) 2) B(-4;6) нүктесі арқылы өте ме? – 6 3b=6 b=6:3 b=2 3x+2y=12
|
№1
Графиктер параллель болғандықтан жүйенің шешімі жоқ Оқушылар дескрипторға сәйкес тапсырмаларды орындайды. Дескриптор:
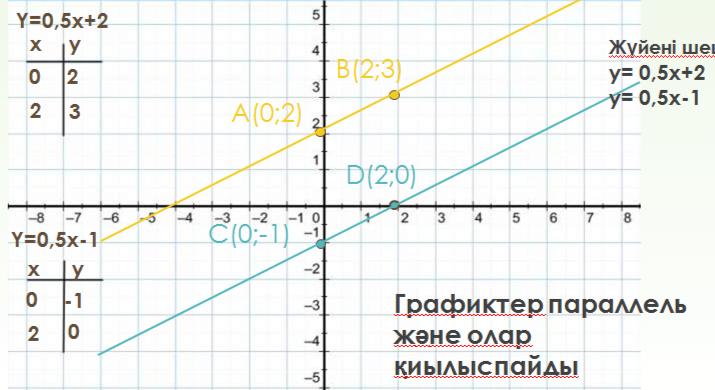
графиктер беттесті шексіз кқп шешімі болады Функциялардың берілген нүктелерге тиістілігін анықтайды. |
Дескриптор: Дескриптор: -y=kx+b түріне келтіреді -кесте құрады, мәнін есептейді -(х; у) нүктелерін координаталық жүйесінде белгілейді, графикті сызады -Түзулердің қиылысу нүктелерін белгілейді, жауабын жазады «Бағдаршам» арқылы қалыптастырушы бағалау
ҚБ:«Бас бармақ» әдісі
|
Жалпы білім беретін мектептің 7–сыныбына арналған оқулық.
ДК экраны 7-сынып оқулығы. Жұмыс дәптерлері.
|
||
|
|
|
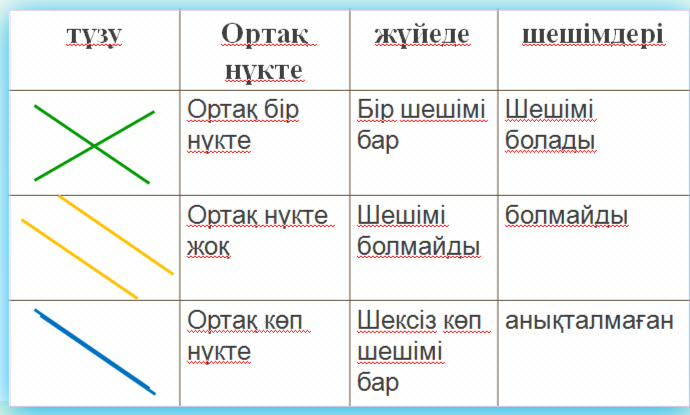
Қортынды. Жүйеде еі сызықтық теңдеудің графиктерінің түзулер орналасуы
|
|
|
7-сынып оқулығы. Жұмыс дәптерлері.
|
||
|
5 минут
|
|
Бүгінгі сабақта: -Теңдеулер жүйесінің шешімдер саны неге тәуелді екендігін білу - Теңдеулер жүйесінің шешімдер санын анықтау. Әр түрлі шешімдер саны болатын теңдеулер жүйесінің мысалдарын келтіру.
Үйге тапсырма.№3.94. |
Тақырыпты меңгергенін анықтау |
Кері байланыс |
7-сынып оқулығы. Жұмыс дәптерлері.
|
||
Бекітемін:
|
Бөлім: |
Функция. Функцияның графигі |
|||||||||||||||
|
Педагогтің Тегі, Аты, Әкесінің аты (бар болса) |
Алимбек М |
|||||||||||||||
|
Сынып: |
7 сынып. Қатысқандар саны: Қатыспағандар саны: |
|||||||||||||||
|
Күні: |
26\11/2024 |
|||||||||||||||
|
Сабақтың тақырыбы: |
Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу |
|||||||||||||||
|
Оқу бағдарламасына сәйкес оқыту мақсаттары: |
7.4.2.4 екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу; |
|||||||||||||||
|
Сабақтың мақсаттары: |
-Теңдеулер жүйесінің шешімдер саны неге тәуелді екендігін білу - Теңдеулер жүйесінің шешімдер санын анықтау. Әр түрлі шешімдер саны болатын теңдеулер жүйесінің мысалдарын келтіру. |
|||||||||||||||
|
Сабақ барысы: |
||||||||||||||||
|
Уақыты |
Кезең дері |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|||||||||||
|
5 минут
|
Ұйым дастыру |
Сәлеметсіздерме! Бүгін, Сызықтық функциялардың графиктерінің өзара орналасуы тақырыбын қарастырамыз Бүгінгі сабақта меңгеретініңіз: -Теңдеулер жүйесінің шешімдер саны неге тәуелді екендігін білу - Теңдеулер жүйесінің шешімдер санын анықтау. Әр түрлі шешімдер саны болатын теңдеулер жүйесінің мысалдарын келтіру. |
Сұрақтарға жауап береді
|
|
|
|||||||||||
|
8 мин |
Жаңа сабақ |
Жаңа сабақ. Видеотүсіндіру онлайн мектептен. ax + by = c түрінде берілген теңдеу екі айнымалысы бар сызықтық теңдеу деп аталады. Мұндағы x және y – айнымалылар, a , b және c – қандай да бір сандар. Екі айнымалысы бар теңдеудің шешімі деп осы теңдеуді дұрыс сандық теңдікке айналдыратын айнымалылардың мәндер жұбын айтады. Мысалы, x – y = 5 теңдеуі x = 8, y = 3 болғанда дұрыс теңдікке айналады: 8 – 3 = 5. Айнымалылардың x = 8, y = 3 мәндер жұбын осы теңдеудің шешімі деп айтады. Екі айнымалысы бар сызықтық теңдеудің шексіз көп шешімі бар. Сонымен қатар x = 15, y = 10; x = 86, y = 81 жұбы да x – y = 5 теңдеуінің шешімдері болатынын тексеру қиын емес. Кем дегенде бір айнымалысының коэффициенті нөлге тең емес екі айнымалысы бар сызықтық теңдеудің графигі түзу болады. Егер екі айнымалысы бар екі сызықтық теңдеу берілген болса және бір уақытта екі теңдеуді де қанағаттандыратын айнымалыларды мәндерін табу керек болса, онда осы теңдеулердің жүйесін шешу керек болады. Екі айнымалысы бар сызықтық теңдеулер жүйесінің шешімі деп жүйенің әр теңдеуін дұрыс теңдікке айналдыратын айнымалылар мәндерінің жұбын айтады. Теңдеулер жүйесін шешу дегеніміз – оның барлық шешімін табу немесе шешімдерінің жоқтығын дәлелдеу. Екі айнымалысы бар сызықтық теңдеулер жүйесін шешу үшін тек қосу тәсілін және алмастыру тәсілін ғана емес, теңдеулердің графиктерін де қолдануға болады. Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешуді қарастырып отырмыз. 1 жағдай. у=0,5х+2 у=-1,5х+6 жауабы (2; 3) егер теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер қиылысса, онда теңдеулер жүйесінің бір ғана шешімі болады. 2 |
Тақырып бойынша ресурстарды қарап, танысады
|
Дескриптор: - сызықтық функцияның анықтама сын біледі және түсінеді; - сызықтық функцияның графигі түзу екенін біледі және түсінеді; |
Презентация
Жалпы білім беретін мектептің 7–сыныбына арналған оқулық. Слайд
Тақта Бор
Кітап Дәптер
Бағалау парақтары
|
|||||||||||
|
17 минут
|
Бекіту тапсырмасы |
1.Теңдеулер жүйесін графиктік тәсілмен шешіңіз:
а)
Жүйенің шешімдер санын және салынған түзулердің өзара орналасуын жазыңыз.
Сәйкесін тап» әдісі. Тапсырма-2: Өтілген материалды бекіту, теңдеулер жүйесін графиктік тәсілмен шешу дағдысын қалыптастыру. Әрбір топқа жүйелерді графиктік тәсілмен шешуді ұсынамын, ал тез тексеру үшін алынған жауаптарды көрші бағандағы сандар жұбымен салыстырады.
Оқулықпен жұмыс. №3.88, №3.89 |
Функциялардың графиктерін координаталық жазықтыққа салады. Жауаптары: 1-К, 2-Е, 3-А, 4-С, 5-В. Дескриптор: -бірінші теңдеудің графигін салады -екінші теңдеудің графигін салады; -екі графиктің қиылысу нүктесін табады; Ол нүктенің координаталарын табады Жауабын жазады |
Дескриптор: -Екі айнымалы сы бар сызықтық теңдеулер жүйесін шешеді. -Кесте құрып, графигін салады.
ҚБ:«Бас бармақ» әдісі
|
Презентация Слайд ДК экраны 7-сынып оқулығы. Жұмыс дәптерлері. Слайд. Интернет ресурстары Жалпы білім беретін мектептің 7–сыныбына арналған оқулық |
|||||||||||
|
8 мин |
Жеке жұмыс |
Шешуі:
|
Тапсырманы орындайды Дескриптор: -бірінші теңдеудің графигін салады -екінші теңдеудің графигін салады; -екі графиктің қиылысу нүктесін табады; Ол нүктенің координаталарын табады Жауабын жазады |
Оқушылардың белсенділіген байланысты бағаланады.
ҚБ: Жұпта өзара бағалау «+», « - », қызықты |
ДК экраны 7-сынып оқулығы. Жұмыс дәптерлері. Слайд. |
|||||||||||
|
2 минут |
|
Бүгінгі сабақта: -Теңдеулер жүйесінің шешімдер саны неге тәуелді екендігін білу - Теңдеулер жүйесінің шешімдер санын анықтау. Әр түрлі шешімдер саны болатын теңдеулер жүйесінің мысалдарын келтіру.
Үйге тапсырма.№3.87. |
Тақырыпты меңгергенін анықтау |
Кері байланыс |
Презентация Слайд ДК экраны 7-сынып оқулығы. Жұмыс дәптерлері. |
|||||||||||
|
Бөлім: |
Функция. Функцияның графигі |
|||||
|
Педагогтің Тегі, Аты, Әкесінің аты (бар болса) |
Алимбек М |
|||||
|
Сынып: |
7 сынып. Қатысқандар саны: Қатыспағандар саны: |
|||||
|
Күні: |
27/11/2024 |
|||||
|
Сабақтың тақырыбы: |
Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешуБЖБ №3 |
|||||
|
Оқу бағдарламасына сәйкес оқыту мақсаттары: |
7.4.2.4 екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу; |
|||||
|
Сабақтың мақсаттары: |
-Теңдеулер жүйесінің шешімдер саны неге тәуелді екендігін білу - екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешуді үйрену |
|||||
|
Сабақ барысы: |
||||||
|
Уақыты |
Кезең дері |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
|
5 минут
|
Ұйым дастыру |
Сәлеметсіздерме! Бүгін, Сызықтық функциялардың графиктерінің өзара орналасуы тақырыбын қарастырамыз Бүгінгі сабақта меңгеретініңіз: -Теңдеулер жүйесінің шешімдер саны неге тәуелді екендігін білу - Теңдеулер жүйесінің шешімдер санын анықтау. Әр түрлі шешімдер саны болатын теңдеулер жүйесінің мысалдарын келтіру. Үй тапсырмасын қайталау.
|
Амандасады, сабаққа дайындалады.
Сұрақтарға жауап береді
|
|
Оқулық Тақта Оқу құралдары
|
|
|
10 мин |
Жаңа сабақ |
1.Екі айнымалысы бар сызықтық теңдеу дегеніміз не? 2.Екі айнымалысы бар сызықтық теңдеу дің қасиеттерін айтыңдар. 3.Екі айнымалысы бар сыз-қ теңд-ң графигі қалай салынады? Екі айнымалысы бар сызықтық теңдеулер жүйесіндегі теңдеулердің әрқайсысын тура теңдікке айналдыратын айнымалылардың мәндерінің жұбын сол теңдеулер жүйесінің шешімі деп атайды. Теңдеулер жүйесін шешу дегеніміз-оның барлық шешімдерін табу немесе оның шешімдерінің болмайтынын дәлелдеу.
Екі айнымалысы
бар сызықтық теңдеулер жүйесін шешудің
г Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешуді қарастырып отырмыз. 1 жағдай.
у-1,5х+6 жауабы (2; 3) егер теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер қиылысса, онда теңдеулер жүйесінің бір ғана шешімі болады. ІІ жағдай. Теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер өзара параллель
у у-0,5х-3 жауабы: шешімдері болмайды, Ø егер теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер өзара параллель болса, онда теңдеулер жүйесінің шешімі болмайды. ІІІ жағдай.
Ж 7х+2у12 35х+10у60 егер теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер беттесетін болса, онда теңдеулер жүйесінің шексіз көп шешімі болады. теңдеулер жүйесін графиктік тәсілмен шешу. Оқушылар тақтада орындайды.
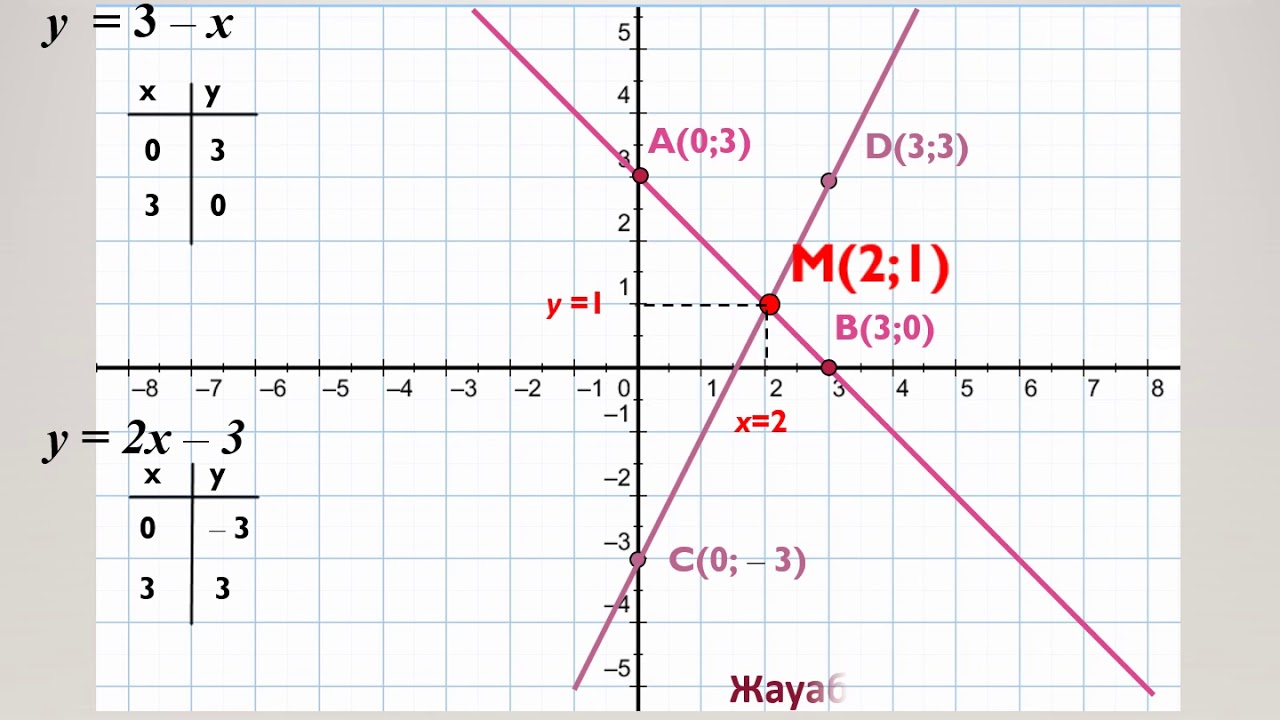
х-у3 ух-3 |
Тақырып бойынша ресурстарды қарап, танысады
|
Дескриптор: - сызықтық функцияның анықтама сын біледі және түсінеді; - сызықтық функцияның графигі түзу екенін біледі және түсінеді; |
7-сынып оқулығы. Жұмыс дәптерлері.
Жалпы білім беретін мектептің 7–сыныбына арналған оқулық.
|
|
|
25 минут
|
БЖБ |
Тапсырма қосымша парақта «ФУНКЦИЯ. ФУНКЦИЯНЫҢ ГРАФИГІ» бөлімі бойынша жиынтық бағалау Оқыту мақсаты: 7.4.1.8 сызықтық функция графиктерінің өзара орналасуы олардың коэффициенттеріне тәуелді болатынын негіздеу 7.4.1.5 y=kx+b түріндегі сызықтық функцияның анықтамасын білу, оның графигін салу және графиктің k және b коэффициенттеріне қатысты орналасуын анықтау 7.4.2.4 екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу Бағалау критерийі:Білім алушы:
Ойлау дағдыларының деңгейлері: Білу және түсіну. Қолдану Орындау уақыты: 20 минут |
Оқушылар дескрипторға сәйкес тапсырмаларды орындайды.
Теңдеулер жүйесін графиктік тәсілмен шешіп, оның бір ғана шешімі болатынын көрсетеді. |
Дескриптор: Дескриптор: -y=kx+b түріне келтіреді -кесте құрады, мәнін есептейді -(х; у) нүктелерін координаталық жүйесінде белгілейді, графикті сызады -Түзулердің қиылысу нүктелерін белгілейді, жауабын жазады «Бағдаршам» арқылы қалыптастырушы бағалау
ҚБ:«Бас бармақ» әдісі 5b |
7-сынып оқулығы. Жұмыс дәптерлері.
Жалпы білім беретін мектептің 7–сыныбына арналған оқулық.
|
|
|
2 минут
|
|
Бүгінгі сабақта: -Теңдеулер жүйесінің шешімдер саны неге тәуелді екендігін білу - Теңдеулер жүйесінің шешімдер санын анықтау. Әр түрлі шешімдер саны болатын теңдеулер жүйесінің мысалдарын келтіру.
Үйге тапсырма.№3.97. |
Тақырыпты меңгергенін анықтау |
Кері байланыс |
кітап дәптер
|
|
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Қысқа мерзімді сабақ жоспары
Қысқа мерзімді сабақ жоспары
|
Бөлім: |
Функция. Функцияның графигі |
||||||
|
Педагогтің Тегі, Аты, Әкесінің аты (бар болса) |
Алимбек М |
||||||
|
Сынып: |
7 сынып. Қатысқандар саны: Қатыспағандар саны: |
||||||
|
Күні: |
25\11/2024 |
||||||
|
Сабақтың тақырыбы: |
Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу |
||||||
|
Оқу бағдарламасына сәйкес оқыту мақсаттары: |
7.4.2.4 екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу; |
||||||
|
Сабақтың мақсаттары: |
-Теңдеулер жүйесінің шешімдер саны неге тәуелді екендігін білу - Теңдеулер жүйесінің шешімдер санын анықтау. Әр түрлі шешімдер саны болатын теңдеулер жүйесінің мысалдарын келтіру. |
||||||
|
Сабақ барысы: |
|||||||
|
Уақыты |
Кезең дері |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
||
|
5 минут
|
Ұйым дастыру |
Сәлеметсіздерме! Бүгін, Сызықтық функциялардың графиктерінің өзара орналасуы тақырыбын қарастырамыз Бүгінгі сабақта меңгеретініңіз: -Теңдеулер жүйесінің шешімдер саны неге тәуелді екендігін білу - Теңдеулер жүйесінің шешімдер санын анықтау. Әр түрлі шешімдер саны болатын теңдеулер жүйесінің мысалдарын келтіру. |
|
|
|
||
|
10 мин |
Жаңа сабақ |
Жаңа сабақ ax + by = c түрінде берілген теңдеу екі айнымалысы бар сызықтық теңдеу деп аталады. Мұндағы x және y – айнымалылар, a , b және c – қандай да бір сандар. Екі айнымалысы бар теңдеудің шешімі деп осы теңдеуді дұрыс сандық теңдікке айналдыратын айнымалылардың мәндер жұбын айтады. Мысалы, x – y = 5 теңдеуі x = 8, y = 3 болғанда дұрыс теңдікке айналады: 8 – 3 = 5. Айнымалылардың x = 8, y = 3 мәндер жұбын осы теңдеудің шешімі деп айтады. Екі айнымалысы бар сызықтық теңдеудің шексіз көп шешімі бар. Сонымен қатар x = 15, y = 10; x = 86, y = 81 жұбы да x – y = 5 теңдеуінің шешімдері болатынын тексеру қиын емес. Кем дегенде бір айнымалысының коэффициенті нөлге тең емес екі айнымалысы бар сызықтық теңдеудің графигі түзу болады. Егер екі айнымалысы бар екі сызықтық теңдеу берілген болса және бір уақытта екі теңдеуді де қанағаттандыратын айнымалыларды мәндерін табу керек болса, онда осы теңдеулердің жүйесін шешу керек болады. Екі айнымалысы бар сызықтық теңдеулер жүйесінің шешімі деп жүйенің әр теңдеуін дұрыс теңдікке айналдыратын айнымалылар мәндерінің жұбын айтады. Теңдеулер жүйесін шешу дегеніміз – оның барлық шешімін табу немесе шешімдерінің жоқтығын дәлелдеу. Екі айнымалысы бар сызықтық теңдеулер жүйесін шешу үшін тек қосу тәсілін және алмастыру тәсілін ғана емес, теңдеулердің графиктерін де қолдануға болады. Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешуді қарастырып отырмыз. 1 жағдай. у=0,5х+2 у=-1,5х+6 жауабы (2; 3) егер теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер қиылысса, онда теңдеулер жүйесінің бір ғана шешімі болады. |
Сұрақтарға жауап береді
Тақырып бойынша ресурстарды қарап, танысады
|
Дескриптор: - сызықтық функцияның анықтама сын біледі және түсінеді; - сызықтық функцияның графигі түзу екенін біледі және түсінеді; |
ДК экраны 7-сынып оқулығы. Жұмыс дәптерлері. .
|
||
|
25 минут
|
Бекіту тапсырмасы |
І- тапсырма. Жүйені шеш:
II-тапсырма. 3x+by=12 түзуі C(2;3) нүктесі арқылы өтеді. Бұл түзу: 1) A(0;6) 2) B(-4;6) нүктесі арқылы өте ме? – 6 3b=6 b=6:3 b=2 3x+2y=12
|
№1
Графиктер параллель болғандықтан жүйенің шешімі жоқ Оқушылар дескрипторға сәйкес тапсырмаларды орындайды. Дескриптор:
графиктер беттесті шексіз кқп шешімі болады Функциялардың берілген нүктелерге тиістілігін анықтайды. |
Дескриптор: Дескриптор: -y=kx+b түріне келтіреді -кесте құрады, мәнін есептейді -(х; у) нүктелерін координаталық жүйесінде белгілейді, графикті сызады -Түзулердің қиылысу нүктелерін белгілейді, жауабын жазады «Бағдаршам» арқылы қалыптастырушы бағалау
ҚБ:«Бас бармақ» әдісі
|
Жалпы білім беретін мектептің 7–сыныбына арналған оқулық.
ДК экраны 7-сынып оқулығы. Жұмыс дәптерлері.
|
||
|
|
|
Қортынды. Жүйеде еі сызықтық теңдеудің графиктерінің түзулер орналасуы
|
|
|
7-сынып оқулығы. Жұмыс дәптерлері.
|
||
|
5 минут
|
|
Бүгінгі сабақта: -Теңдеулер жүйесінің шешімдер саны неге тәуелді екендігін білу - Теңдеулер жүйесінің шешімдер санын анықтау. Әр түрлі шешімдер саны болатын теңдеулер жүйесінің мысалдарын келтіру.
Үйге тапсырма.№3.94. |
Тақырыпты меңгергенін анықтау |
Кері байланыс |
7-сынып оқулығы. Жұмыс дәптерлері.
|
||
Бекітемін:
|
Бөлім: |
Функция. Функцияның графигі |
|||||||||||||||
|
Педагогтің Тегі, Аты, Әкесінің аты (бар болса) |
Алимбек М |
|||||||||||||||
|
Сынып: |
7 сынып. Қатысқандар саны: Қатыспағандар саны: |
|||||||||||||||
|
Күні: |
26\11/2024 |
|||||||||||||||
|
Сабақтың тақырыбы: |
Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу |
|||||||||||||||
|
Оқу бағдарламасына сәйкес оқыту мақсаттары: |
7.4.2.4 екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу; |
|||||||||||||||
|
Сабақтың мақсаттары: |
-Теңдеулер жүйесінің шешімдер саны неге тәуелді екендігін білу - Теңдеулер жүйесінің шешімдер санын анықтау. Әр түрлі шешімдер саны болатын теңдеулер жүйесінің мысалдарын келтіру. |
|||||||||||||||
|
Сабақ барысы: |
||||||||||||||||
|
Уақыты |
Кезең дері |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|||||||||||
|
5 минут
|
Ұйым дастыру |
Сәлеметсіздерме! Бүгін, Сызықтық функциялардың графиктерінің өзара орналасуы тақырыбын қарастырамыз Бүгінгі сабақта меңгеретініңіз: -Теңдеулер жүйесінің шешімдер саны неге тәуелді екендігін білу - Теңдеулер жүйесінің шешімдер санын анықтау. Әр түрлі шешімдер саны болатын теңдеулер жүйесінің мысалдарын келтіру. |
Сұрақтарға жауап береді
|
|
|
|||||||||||
|
8 мин |
Жаңа сабақ |
Жаңа сабақ. Видеотүсіндіру онлайн мектептен. ax + by = c түрінде берілген теңдеу екі айнымалысы бар сызықтық теңдеу деп аталады. Мұндағы x және y – айнымалылар, a , b және c – қандай да бір сандар. Екі айнымалысы бар теңдеудің шешімі деп осы теңдеуді дұрыс сандық теңдікке айналдыратын айнымалылардың мәндер жұбын айтады. Мысалы, x – y = 5 теңдеуі x = 8, y = 3 болғанда дұрыс теңдікке айналады: 8 – 3 = 5. Айнымалылардың x = 8, y = 3 мәндер жұбын осы теңдеудің шешімі деп айтады. Екі айнымалысы бар сызықтық теңдеудің шексіз көп шешімі бар. Сонымен қатар x = 15, y = 10; x = 86, y = 81 жұбы да x – y = 5 теңдеуінің шешімдері болатынын тексеру қиын емес. Кем дегенде бір айнымалысының коэффициенті нөлге тең емес екі айнымалысы бар сызықтық теңдеудің графигі түзу болады. Егер екі айнымалысы бар екі сызықтық теңдеу берілген болса және бір уақытта екі теңдеуді де қанағаттандыратын айнымалыларды мәндерін табу керек болса, онда осы теңдеулердің жүйесін шешу керек болады. Екі айнымалысы бар сызықтық теңдеулер жүйесінің шешімі деп жүйенің әр теңдеуін дұрыс теңдікке айналдыратын айнымалылар мәндерінің жұбын айтады. Теңдеулер жүйесін шешу дегеніміз – оның барлық шешімін табу немесе шешімдерінің жоқтығын дәлелдеу. Екі айнымалысы бар сызықтық теңдеулер жүйесін шешу үшін тек қосу тәсілін және алмастыру тәсілін ғана емес, теңдеулердің графиктерін де қолдануға болады. Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешуді қарастырып отырмыз. 1 жағдай. у=0,5х+2 у=-1,5х+6 жауабы (2; 3) егер теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер қиылысса, онда теңдеулер жүйесінің бір ғана шешімі болады. 2 |
Тақырып бойынша ресурстарды қарап, танысады
|
Дескриптор: - сызықтық функцияның анықтама сын біледі және түсінеді; - сызықтық функцияның графигі түзу екенін біледі және түсінеді; |
Презентация
Жалпы білім беретін мектептің 7–сыныбына арналған оқулық. Слайд
Тақта Бор
Кітап Дәптер
Бағалау парақтары
|
|||||||||||
|
17 минут
|
Бекіту тапсырмасы |
1.Теңдеулер жүйесін графиктік тәсілмен шешіңіз:
а)
Жүйенің шешімдер санын және салынған түзулердің өзара орналасуын жазыңыз.
Сәйкесін тап» әдісі. Тапсырма-2: Өтілген материалды бекіту, теңдеулер жүйесін графиктік тәсілмен шешу дағдысын қалыптастыру. Әрбір топқа жүйелерді графиктік тәсілмен шешуді ұсынамын, ал тез тексеру үшін алынған жауаптарды көрші бағандағы сандар жұбымен салыстырады.
Оқулықпен жұмыс. №3.88, №3.89 |
Функциялардың графиктерін координаталық жазықтыққа салады. Жауаптары: 1-К, 2-Е, 3-А, 4-С, 5-В. Дескриптор: -бірінші теңдеудің графигін салады -екінші теңдеудің графигін салады; -екі графиктің қиылысу нүктесін табады; Ол нүктенің координаталарын табады Жауабын жазады |
Дескриптор: -Екі айнымалы сы бар сызықтық теңдеулер жүйесін шешеді. -Кесте құрып, графигін салады.
ҚБ:«Бас бармақ» әдісі
|
Презентация Слайд ДК экраны 7-сынып оқулығы. Жұмыс дәптерлері. Слайд. Интернет ресурстары Жалпы білім беретін мектептің 7–сыныбына арналған оқулық |
|||||||||||
|
8 мин |
Жеке жұмыс |
Шешуі:
|
Тапсырманы орындайды Дескриптор: -бірінші теңдеудің графигін салады -екінші теңдеудің графигін салады; -екі графиктің қиылысу нүктесін табады; Ол нүктенің координаталарын табады Жауабын жазады |
Оқушылардың белсенділіген байланысты бағаланады.
ҚБ: Жұпта өзара бағалау «+», « - », қызықты |
ДК экраны 7-сынып оқулығы. Жұмыс дәптерлері. Слайд. |
|||||||||||
|
2 минут |
|
Бүгінгі сабақта: -Теңдеулер жүйесінің шешімдер саны неге тәуелді екендігін білу - Теңдеулер жүйесінің шешімдер санын анықтау. Әр түрлі шешімдер саны болатын теңдеулер жүйесінің мысалдарын келтіру.
Үйге тапсырма.№3.87. |
Тақырыпты меңгергенін анықтау |
Кері байланыс |
Презентация Слайд ДК экраны 7-сынып оқулығы. Жұмыс дәптерлері. |
|||||||||||
|
Бөлім: |
Функция. Функцияның графигі |
|||||
|
Педагогтің Тегі, Аты, Әкесінің аты (бар болса) |
Алимбек М |
|||||
|
Сынып: |
7 сынып. Қатысқандар саны: Қатыспағандар саны: |
|||||
|
Күні: |
27/11/2024 |
|||||
|
Сабақтың тақырыбы: |
Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешуБЖБ №3 |
|||||
|
Оқу бағдарламасына сәйкес оқыту мақсаттары: |
7.4.2.4 екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу; |
|||||
|
Сабақтың мақсаттары: |
-Теңдеулер жүйесінің шешімдер саны неге тәуелді екендігін білу - екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешуді үйрену |
|||||
|
Сабақ барысы: |
||||||
|
Уақыты |
Кезең дері |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
|
5 минут
|
Ұйым дастыру |
Сәлеметсіздерме! Бүгін, Сызықтық функциялардың графиктерінің өзара орналасуы тақырыбын қарастырамыз Бүгінгі сабақта меңгеретініңіз: -Теңдеулер жүйесінің шешімдер саны неге тәуелді екендігін білу - Теңдеулер жүйесінің шешімдер санын анықтау. Әр түрлі шешімдер саны болатын теңдеулер жүйесінің мысалдарын келтіру. Үй тапсырмасын қайталау.
|
Амандасады, сабаққа дайындалады.
Сұрақтарға жауап береді
|
|
Оқулық Тақта Оқу құралдары
|
|
|
10 мин |
Жаңа сабақ |
1.Екі айнымалысы бар сызықтық теңдеу дегеніміз не? 2.Екі айнымалысы бар сызықтық теңдеу дің қасиеттерін айтыңдар. 3.Екі айнымалысы бар сыз-қ теңд-ң графигі қалай салынады? Екі айнымалысы бар сызықтық теңдеулер жүйесіндегі теңдеулердің әрқайсысын тура теңдікке айналдыратын айнымалылардың мәндерінің жұбын сол теңдеулер жүйесінің шешімі деп атайды. Теңдеулер жүйесін шешу дегеніміз-оның барлық шешімдерін табу немесе оның шешімдерінің болмайтынын дәлелдеу.
Екі айнымалысы
бар сызықтық теңдеулер жүйесін шешудің
г Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешуді қарастырып отырмыз. 1 жағдай.
у-1,5х+6 жауабы (2; 3) егер теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер қиылысса, онда теңдеулер жүйесінің бір ғана шешімі болады. ІІ жағдай. Теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер өзара параллель
у у-0,5х-3 жауабы: шешімдері болмайды, Ø егер теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер өзара параллель болса, онда теңдеулер жүйесінің шешімі болмайды. ІІІ жағдай.
Ж 7х+2у12 35х+10у60 егер теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер беттесетін болса, онда теңдеулер жүйесінің шексіз көп шешімі болады. теңдеулер жүйесін графиктік тәсілмен шешу. Оқушылар тақтада орындайды.
х-у3 ух-3 |
Тақырып бойынша ресурстарды қарап, танысады
|
Дескриптор: - сызықтық функцияның анықтама сын біледі және түсінеді; - сызықтық функцияның графигі түзу екенін біледі және түсінеді; |
7-сынып оқулығы. Жұмыс дәптерлері.
Жалпы білім беретін мектептің 7–сыныбына арналған оқулық.
|
|
|
25 минут
|
БЖБ |
Тапсырма қосымша парақта «ФУНКЦИЯ. ФУНКЦИЯНЫҢ ГРАФИГІ» бөлімі бойынша жиынтық бағалау Оқыту мақсаты: 7.4.1.8 сызықтық функция графиктерінің өзара орналасуы олардың коэффициенттеріне тәуелді болатынын негіздеу 7.4.1.5 y=kx+b түріндегі сызықтық функцияның анықтамасын білу, оның графигін салу және графиктің k және b коэффициенттеріне қатысты орналасуын анықтау 7.4.2.4 екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу Бағалау критерийі:Білім алушы:
Ойлау дағдыларының деңгейлері: Білу және түсіну. Қолдану Орындау уақыты: 20 минут |
Оқушылар дескрипторға сәйкес тапсырмаларды орындайды.
Теңдеулер жүйесін графиктік тәсілмен шешіп, оның бір ғана шешімі болатынын көрсетеді. |
Дескриптор: Дескриптор: -y=kx+b түріне келтіреді -кесте құрады, мәнін есептейді -(х; у) нүктелерін координаталық жүйесінде белгілейді, графикті сызады -Түзулердің қиылысу нүктелерін белгілейді, жауабын жазады «Бағдаршам» арқылы қалыптастырушы бағалау
ҚБ:«Бас бармақ» әдісі 5b |
7-сынып оқулығы. Жұмыс дәптерлері.
Жалпы білім беретін мектептің 7–сыныбына арналған оқулық.
|
|
|
2 минут
|
|
Бүгінгі сабақта: -Теңдеулер жүйесінің шешімдер саны неге тәуелді екендігін білу - Теңдеулер жүйесінің шешімдер санын анықтау. Әр түрлі шешімдер саны болатын теңдеулер жүйесінің мысалдарын келтіру.
Үйге тапсырма.№3.97. |
Тақырыпты меңгергенін анықтау |
Кері байланыс |
кітап дәптер
|
|

шағым қалдыра аласыз



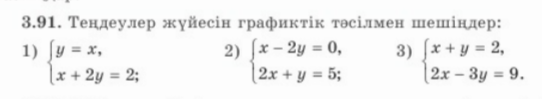

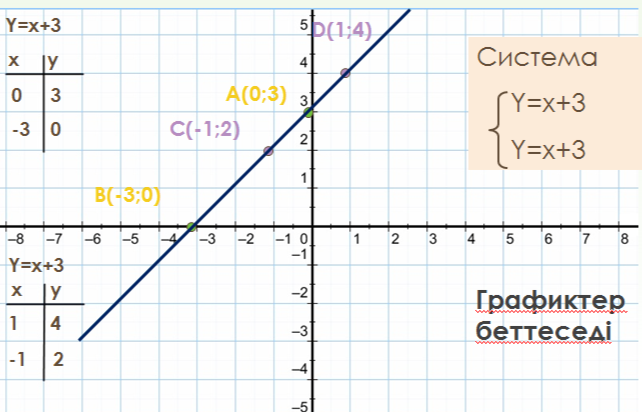
 -мысал
-мысал