
5 сынып математика ережелер
НАТУРАЛ САНДАР ЖӘНЕ 0 САНЫ.
Натурал сан- дегеніміз, күнделікті өмірде санауда қолданылатын сандар. Олар 1 ден басталып шексіздікке дейін жалғасады. Әр натурал саннан кейін одан 1-ге артық натурал сан бар. 0 саны натурал сан емес.
Координаталық сәуле – дегеніміз, сәуленің 0 басталу нүктесі санақ басы ретінде алынған, бірлік кесіндісі берілген, бағыты белгіленген сәулені айтамыз.
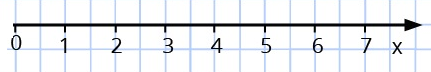
Натурал сандарды координаталық сәуледе салыстырғанда, сандардың кішісі сол жақта, ал үлкені оң жақта орналасады.
Кез келген бірдей натурал сандардың қосындысын көбейтінді түрінде жазуға болады. Мысалы: 2+2+2=2*3 (3 рет қосылғаны үшін)
Қосудың ауыстырылымдық қасиеті - қосылғыштардың орнын ауыстырғанда қосындының мәні өзгермейді. Мысалы: 5+16=16+5
Көбейтудің ауыстырылымдық қасиеті – көбейткіштердің орнын ауыстырғаннан көбейтіндінің мәні өзгермейді. Мысалы: 3*58=58*3
Көбейтудің үлестірімділік қасиеті – қосындыдағы ортақ көбейткішті жақша сыртына шығару тәсілін айтамыз. Мысалы 4*47+4*53=4(47+53)
Амалдарды ретімен орындау – дегеніміз, берілген есептегі арифметикалық (қосу, азайту, көбейту, бөлу) амалдарын орындалу ретін сақтау. Ең алдымен көбейту немесе бөлу орындалады. Сосын қосу немесе азайту амалдары. Егер жақша бар болса есепте жақша ішіндегі амалдарды бірінші орындаймыз. Мысалы: 3*4+(5-2)*8= есебінде 1) 5-2 орындалады, 2) бірінші амалдан шыққан мәнді 8 ге көбейтеміз 3) 3*4 орындаймыз 4) екінші және үшінші амал мәндерін қосамыз
Коэфициент – дегеніміз, ол әріпті өрнектегі әріп алдындағы көбейтіліп тұрған сан. Мысалы: 6а+5. Алты саны коэфициент болады.
Өрнектің коэфициенті – дегеніміз, әріпті өрнек ықшамдалып (қосылатындары қосылып, көбейтілетін сандар көбейтіліп) болған соң, әріп(тер)дің алдындағы әріпке көбейтіліп тұрған санды айтамыз. Мысалы: 2а+1,5а өрнегінің коэфициенті 3,5 ға тең себебі өрнектің мәні 3,5а болады. 5а*4b*0,1c өрнегінің коефициенті 2 болады, себебі өрнектің мәні 2abc - ға тең.
Сандық өрнек – дегеніміз сандармен, амалдармен таңбаларымен және жақшалармен жазылған өрнекті айтамыз: 3+4*5-8 немесе 5*(4,5+7)-1/5
Әріпті өрнек – дегеніміз құрамында әріптері бар өрнектерді айтамыз: а+4b немесе x-y
Өрнекті ықшамдау – дегеніміз өрнектің мәнін өзгертпей, бірақ амалдар саны алғашқыдан аз болатындай етіп түрлендіру. Мысалы: а+5+3а-2 өрнегі 4а+3 болып ықшамдалады.
Теңдеу – дегеніміз, құрамында әріппен белгіленген белгісіз саны бар бар теңдікті айтамыз. Мысалы: 5х+7=22
Теңдеу түбірі – дегеніміз әріптің теңдеуді тура теңдікке айналдыратын мәні. Мысалы 3х+1=7 теңдеуін шешсек х=2 болады. 2 теңдеудің түбірі
Квадрат – барлық қабырғалары тең тіктөртбұрыш
Периметр – жазықтықтағы геометриялық фигуралардың барлық қабырғалары ұзындықтарының қосындысы.
Формула – әріптері бар теңдік түрінде жазылған ереже. Формулада қандай да бір шама бір мәнінің өзге шамалардың мәндеріне тәуелділігі көрсетіледі.

НАТУРАЛ САНДАРДЫҢ БӨЛІНГІШТІГІ
Натурал санның бөлгіші – дегеніміз, сол санға қалдықсыз бөлінетін бөлінгіш сан. Мысалы: Б(12)={1,2,3,4,6,12} болады.
Натурал санның еселігі – дегеніміз, сол берілген натурал санға қалдықсыз бөлінетін сан. Кез келген натурал санның еселіктері шекстеусіз көп болады. Мысалы: Е(6)={6,12,18,24,30,…}
Жай сандар – тек 1-ге және өзіне ғана бөлінетін натурал сандар. Ең кіші жай сан: 2. Ал ең үлкен жай сан шектеусіз үлкен сан. Мысалы: 101, 2, 17, 29 т.с.с
Өзара жай сандар – берілген натурал сандардың ЕКОЕ-сі 1-ге тең болатын сандар. Мысалы: 25 және 16, 14 және 15
Құрама сандар – екіден көп бөлгіштері бар натурал сандар. Ең кіші құрама сан: 4. Мысалы: 4, 6, 8, 102
1 саны – жай сандарға да, құрама сандарға да жатпайды. Оның бір ғана бөлгіші бар.
Егер көбейткіштердің біреуі берілген санға бөлінсе, онда көбейтінді де сол санға бөлінеді. Мысалы: 24*19*7 көбейтіндісі 6 ға бөлінеді. Себебі 24 саны 6 ға бөлінеді.
Егер қосылғыштардың әрқайсысы жеке-жеке берілген санға бөлінсе, онда қосынды да сол санға бөлінеді. Мысалы: (84+28) қосындысы 14 ке бөлінеді, себебі 84 те, 28 де 14 ке қалдықсыз бөлінеді.
Егер азайғыш та, азайтқыш та берілген санға жеке-жеке бөлінсе, онда айырма да сол санға бөлінеді. Мысалы: (27-9) айырмасы 3 ке бөлінеді, себеі 27 де, 9 да 3 ке бөлінеді.
2-ге – жазылуы жұп цифрлармен аяқталған натурал сандар бөлінеді. Мысалы: 12, 100, 1882, 1134
4-ке – жазылуында соңғы екі цифрларынан құралған натурал сан 4 ке бөлінсе немесе екі нөлмен аяқталса, берілген санда 4-ке бөлінеді. Мысалы: 128, 1980, 112, 25436
8-ге – жазылуында соңғы үш цифрларынан құралған натурал сан 8-ге бөлінсе немесе үш нөлмен аяқталса, берілген сан 8-ге бөлінеді. Мысалы: 8120, 1880, 45120
3-ке – жазылуындағы цифрларының қосындысы 3-ке бөлінсе, берілген сол натурал сан 3-ке бөлінеді. Мысалы: 10245 ал 1+0+2+4+5=12 болады. Ал 12 саны 3-ке бөлінеді, демек 10245 саныда 3-ке бөлінеді.
6-ға – жазылуында соңғы цифры жұп болса және цифрлар қосындысы 3-ке бөлінсе, сол натурал сан 6-ға бөлінеді. Мысалы: 144810 саны жұп сан, және 1+4+4+8+1+0=18 болады. Содан 144810 саны 6-ға бөлінеді.
9-ға – жазылуындағы цифрлар қосындысы 9-ға бөлінсе, сол натурал сан 9-ға бөлінеді. Мысалы: 7893 саны 7+8+9+3=27 болады. Содан 7893 саны 9-ға бөлінеді.
5-ке – жазылуында соңғы цифры 0 немесе 5 цифрымен аяқталса,сол натурал сан 5-ке бөлінеді. Мысалы: 485, 770
10-ға – жазылуында соңғы цифры 0 мен аяқталса, сол натурал сан 10-ға бөлінеді. Мысалы: 1130, 190, 70
Дәреже – бірнеше бірдей
көбейткіштердің көбейтіндісін көрсететін өрнекті айтамыз. Мысалы:
2*2*2*2*2= деп жазуға
болады.
деп жазуға
болады.
Санның
квадраты – санның 2-ші дәрежесі.
Мысалы:  - он төрттің
квадраты.
- он төрттің
квадраты.
Санның
кубы – санның 3-ші
дәрежесі.  – бестің
кубы.
– бестің
кубы.
Құрама санды жай көбейткіштерге жіктеу – оны тек қана жай сандардың көбейтіндісі түрінде жазу. Оны вертикаль сызық арқылы баған түрінде бөліп табамыз. Мысалы: 420=2*2*3*5*7
Берілген натурал сандардың ЕҮОБ-і деп, сол сандардың әрқайсысы бөлінетін ең үлкен натурал сан. Мысалы ЕҮОБ(36,24)=12
Берілген натурал сандардың әрқайсысына еселік болатын ең кіші натурал санды сол сандардың ЕКОЕ-сі деп атаймыз. Мысалы: ЕКОЕ(4,6)=12
ЖАЙ БӨЛШЕКТЕР
Берілген шаманы өзара тең
бөліктерге бөліп, оның бір немесе бірнеше бөлігін кескіндейтін
сан жай
бөлшек түрінде жазуға болады.
Мысалы:  ,
,
 ,
, 
Бөлшектің
алымы – бөлшек сызығының төбесіндегі
сан. 
Бөлшектің
бөлімі – бөлшек сызығының астындағы
сан. 
Егер бөлшектің алымын да,
бөлімінде бірдей натурал санға көбейтсек немесе бөлсек, онда
оған тең
бөлшек алынады.
Мысалы: 
Бөлшектің алымын да, бөлімін
де 1-ден өзге ортақ бөлгішке бөлуді
бөлшекті
қысқарту деп атайды.
Мысалы: 
Бұрыс
бөлшек – алымы бөлімінен үлкен немесе
тең бөлшек. Кез келген бұрыс бөлшек 1-ден үлкен немесе тең.
Мысалы: 
Дұрыс
бөлшек – алымы бөлімінен кіші бөлшек.
Кез келген дұрыс бөлшек 1-ден кіші. Мысалы:

Аралас
сан – бүтін бөліктен және бөлшек
бөліктен тұратын сан аралас сан деп аталады.
Мысалы: 
Кез келген натурал
санды аралас сан түрінде
жазуға болады.
Мысалы: 
Кез
келген бұрыс бөлшекті аралас сан
түрінде жазуға болады.
Мысалы:  (13:3=4
(1қалдық))
(13:3=4
(1қалдық))
Кез
келген аралас санды бұрыс бөлшекке
айналдыруға болады.
Мысалы: 
Координаталық
сәуледе  дұрыс бөлшегін кескіндеу
үшін, бірлік кесіндіні өзара тең a бөлікке бөліп, санақ басынан
бастап b бөлігін алу керек.
Мысалы:
дұрыс бөлшегін кескіндеу
үшін, бірлік кесіндіні өзара тең a бөлікке бөліп, санақ басынан
бастап b бөлігін алу керек.
Мысалы: 
![]()
ЖАЙ БӨЛШЕКТЕРГЕ АМАЛДАР ҚОЛДАНУ
Берілген бөлшектердің
бөлімдерінің ең кіші ортақ еселігі сол
бөлшектердің ең кіші ортақ
бөлімі болады.
Мысалы:  бөлшектерінің
бөлімдерінің ең кіші ортақ еселігі 24 болады, себебі ЕКОЕ(8,6)=24.
Содан
бөлшектерінің
бөлімдерінің ең кіші ортақ еселігі 24 болады, себебі ЕКОЕ(8,6)=24.
Содан 
Жай бөлшектерді салыстыру:
-бөлімдері бірдей
бөлшектердің алымдары қайсысы үлкен сол
бөлшек үлкен болады. Мысалы:  ,
,

-алымдары бірдей
бөлшектердің бөлімі қайсысы үлкен
сол бөлшек кіші болады. Мысалы:  ,
,

-алымы да, бөліміде әр түрлі
бөлшектерді салыстыру үшін, оларды
көбелек тәсілімен тексеріп көреміз. Мысалы:
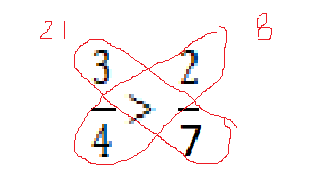
-аралас
cандарды салыстырғанда, алдымен бүтін
бөліктерін салыстырамыз. Егер бүтін бөліктері бірдей боглса, онда
бөлшек бөліктерін салыстырамыз. Мысалы:
 ,
, 
Бөлімдері
бірдей бөлшектерді қосқанда және
азайтқанда тек алымдарын есептейміз, ал
бөлімі өзгеріссіз қалады: 

Бөлімдері әр түрлі бөлшектерді қосқанда немесе азайтқанда, бөлшектерді бірдей ортақ бөлімдерге келтіріп, сосын есептейміз:


Аралас сандарды қосып
азайтқанда олардың алдымен бүтін
бөліктері, сосын бөлшек бөлімдері жеке-жеке қосылып азайтылады,
немесе бұрыс бөлшекке айналдырып есептелінеді.
Мысалы: 
Аликвоттық
бөлшек – алымы 1-ге тең дұрыс бөлшек.
Кез келген аликвоттық бөлшек 1-ден кіші. Ең үлкен аликвоттық
бөлшек  ге тең.
Мысалы:
ге тең.
Мысалы: 
Бөлшекті натурал санға көбейту үшін, оның алымын натурал санға көбейтіп, бөлімін өзін қалдыру керек:

Екі бөлшекті көбейту
үшін сол бөлшектердің алымдарын
өзара көбейту керек, және бөлімдерін өзара көбейтеміз.
Мысалы: 
Аралас сандарды көбейту
үшін оларды алдымен бұрыс
бөлшектерге айналдырып, сосын барып
көбейтеміз: 
Өзара кері
сандар – екі санның көбейтіндісі 1-ге
тең болатын сандарға айтамыз:  ,
,

Бөлшектерді бөлу
үшін бөлінгішті бөлгіштің кері
санына көбейту арқылы табамыз: 
МӘТІНДІ ЕСЕПТЕР
Санның бөлігін табу
үшін – санды осы бөлшекке көбейту
керек. Мыс: 18 км дің  бөлігін тап десе
18*
бөлігін тап десе
18* =2*2=4км,
=2*2=4км,  бөлігін тап
десе
бөлігін тап
десе

Бөлігі бойынша санды
табу үшін бөлікке сәйкес санды осы
бөлшекке бөлу керек. Мысалы: машина 145км жүрді. Бұл оның барлық
жүруге тиісті жолының  -індей. Машинаның барлық
жүруге тиісті жолын тап. 145:
-індей. Машинаның барлық
жүруге тиісті жолын тап. 145: =145*
=145*
Бірлесіп жұмыс
жасау формуласы:  мұндағы х-бұл бірінші
жұмысшының жалғыз өзі істесе сол жұмысты аяқтайтын уақыты, у-бұл
екінші жұмысшының уақыты, ал t-бұл екі жұмысшының бірлесе жасағанда
аяқтайтын уақыты.
мұндағы х-бұл бірінші
жұмысшының жалғыз өзі істесе сол жұмысты аяқтайтын уақыты, у-бұл
екінші жұмысшының уақыты, ал t-бұл екі жұмысшының бірлесе жасағанда
аяқтайтын уақыты.
ОНДЫҚ БӨЛШЕКТЕР ЖӘНЕ ОЛАРҒА АМАЛДАР ҚОЛДАНУ
Ондық
бөлшек деп - бірліктен де кіші
разрядтары бар ондық жүйеде жазылған санға айтылады. Мысалы: 3,724
ондық бөлшегінде 3 бірлік, 7 ондық үлес, 2 жүздік үлес, 4 мыңдық
үлес бар. 3 бүтін бөлігі, ал 724 бөлшек бөлігі. Және ол жай
бөлшекпен жазғанда оқылуы бойынша жазамыз және олар қысқарса
қысқартуға болады: 3,724= =
= 3
3
Жай бөлшекті ондық бөлшекке
айналдыру үшін бөлшектің бөлімін 10 ға еселі
санға айналдыру керек. Оның бөлімін жай көбейткіштерге жіктегенде
тек 2 немесе 5 немесе 10-ға еселі сандардан құралу
керек:  =
= =
=
Ондық бөлшекті
координаталық сәуледе кескіндеу
жай бөлшекті немесе аралас
санды кескіндеу сияқты орындалады: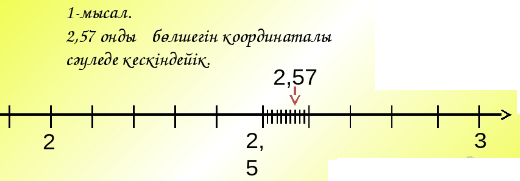
Ондық бөлшектерді салыстырғанда – алдымен олардың бүтін бөліктерін салыстырамыз, егер ол тең болған жағдайда бөлшек бөлігін үтірден кейінгі үлестері бойынша салыстырамыз: 6,78>6,762 , (мұнда бүтін бөліктері тең, 7 лері тең, бірақ 8>6) және координаталық сәуледе үлкен ондық бөлшек оң жақта, ал кіші ондық бөлшек сол жақта орналасады.
Ондық бөлшектерді қосқанда немесе азайтқанда олардың үтірден кейінгі үлестердегі цифрлар саны теңестіріледі баған түрінде жазылып есептелінеді, үтірлер бір қатарда тұру керек. Мысалы:
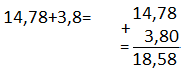
Ондық бөлшекті натурал санға көбейткенде үтірге назар аудармай көбейтеміз. Сосын көбейткіштің үтірінен кейін неше цифр болса, көбейтінді мәнінде сонша қалатындай етіп үтір қоямыз. Мысалы:
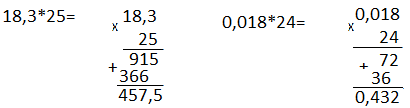
Ондық бөлшекті ондық бөлшекке көбейткенде, көбейткіштердің үтірлеріне назар аудармай көбейтеміз, шыққан мәніне көбейткіштердің үтірінен кейін неше цифр болса сонша цифр болатындай етіп үтір қоямыз:
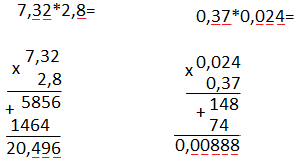
Ондық бөлшекті натурал санға бөлу натурал сандарды бөлудегідей орындалады. Ондық бөлшек
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Қысқа нұсқаулықтар мен ережелер жинағы. Математика. 5-сынып.
Қысқа нұсқаулықтар мен ережелер жинағы. Математика. 5-сынып.
5 сынып математика ережелер
НАТУРАЛ САНДАР ЖӘНЕ 0 САНЫ.
Натурал сан- дегеніміз, күнделікті өмірде санауда қолданылатын сандар. Олар 1 ден басталып шексіздікке дейін жалғасады. Әр натурал саннан кейін одан 1-ге артық натурал сан бар. 0 саны натурал сан емес.
Координаталық сәуле – дегеніміз, сәуленің 0 басталу нүктесі санақ басы ретінде алынған, бірлік кесіндісі берілген, бағыты белгіленген сәулені айтамыз.
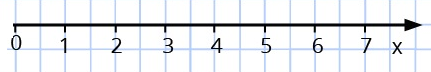
Натурал сандарды координаталық сәуледе салыстырғанда, сандардың кішісі сол жақта, ал үлкені оң жақта орналасады.
Кез келген бірдей натурал сандардың қосындысын көбейтінді түрінде жазуға болады. Мысалы: 2+2+2=2*3 (3 рет қосылғаны үшін)
Қосудың ауыстырылымдық қасиеті - қосылғыштардың орнын ауыстырғанда қосындының мәні өзгермейді. Мысалы: 5+16=16+5
Көбейтудің ауыстырылымдық қасиеті – көбейткіштердің орнын ауыстырғаннан көбейтіндінің мәні өзгермейді. Мысалы: 3*58=58*3
Көбейтудің үлестірімділік қасиеті – қосындыдағы ортақ көбейткішті жақша сыртына шығару тәсілін айтамыз. Мысалы 4*47+4*53=4(47+53)
Амалдарды ретімен орындау – дегеніміз, берілген есептегі арифметикалық (қосу, азайту, көбейту, бөлу) амалдарын орындалу ретін сақтау. Ең алдымен көбейту немесе бөлу орындалады. Сосын қосу немесе азайту амалдары. Егер жақша бар болса есепте жақша ішіндегі амалдарды бірінші орындаймыз. Мысалы: 3*4+(5-2)*8= есебінде 1) 5-2 орындалады, 2) бірінші амалдан шыққан мәнді 8 ге көбейтеміз 3) 3*4 орындаймыз 4) екінші және үшінші амал мәндерін қосамыз
Коэфициент – дегеніміз, ол әріпті өрнектегі әріп алдындағы көбейтіліп тұрған сан. Мысалы: 6а+5. Алты саны коэфициент болады.
Өрнектің коэфициенті – дегеніміз, әріпті өрнек ықшамдалып (қосылатындары қосылып, көбейтілетін сандар көбейтіліп) болған соң, әріп(тер)дің алдындағы әріпке көбейтіліп тұрған санды айтамыз. Мысалы: 2а+1,5а өрнегінің коэфициенті 3,5 ға тең себебі өрнектің мәні 3,5а болады. 5а*4b*0,1c өрнегінің коефициенті 2 болады, себебі өрнектің мәні 2abc - ға тең.
Сандық өрнек – дегеніміз сандармен, амалдармен таңбаларымен және жақшалармен жазылған өрнекті айтамыз: 3+4*5-8 немесе 5*(4,5+7)-1/5
Әріпті өрнек – дегеніміз құрамында әріптері бар өрнектерді айтамыз: а+4b немесе x-y
Өрнекті ықшамдау – дегеніміз өрнектің мәнін өзгертпей, бірақ амалдар саны алғашқыдан аз болатындай етіп түрлендіру. Мысалы: а+5+3а-2 өрнегі 4а+3 болып ықшамдалады.
Теңдеу – дегеніміз, құрамында әріппен белгіленген белгісіз саны бар бар теңдікті айтамыз. Мысалы: 5х+7=22
Теңдеу түбірі – дегеніміз әріптің теңдеуді тура теңдікке айналдыратын мәні. Мысалы 3х+1=7 теңдеуін шешсек х=2 болады. 2 теңдеудің түбірі
Квадрат – барлық қабырғалары тең тіктөртбұрыш
Периметр – жазықтықтағы геометриялық фигуралардың барлық қабырғалары ұзындықтарының қосындысы.
Формула – әріптері бар теңдік түрінде жазылған ереже. Формулада қандай да бір шама бір мәнінің өзге шамалардың мәндеріне тәуелділігі көрсетіледі.

НАТУРАЛ САНДАРДЫҢ БӨЛІНГІШТІГІ
Натурал санның бөлгіші – дегеніміз, сол санға қалдықсыз бөлінетін бөлінгіш сан. Мысалы: Б(12)={1,2,3,4,6,12} болады.
Натурал санның еселігі – дегеніміз, сол берілген натурал санға қалдықсыз бөлінетін сан. Кез келген натурал санның еселіктері шекстеусіз көп болады. Мысалы: Е(6)={6,12,18,24,30,…}
Жай сандар – тек 1-ге және өзіне ғана бөлінетін натурал сандар. Ең кіші жай сан: 2. Ал ең үлкен жай сан шектеусіз үлкен сан. Мысалы: 101, 2, 17, 29 т.с.с
Өзара жай сандар – берілген натурал сандардың ЕКОЕ-сі 1-ге тең болатын сандар. Мысалы: 25 және 16, 14 және 15
Құрама сандар – екіден көп бөлгіштері бар натурал сандар. Ең кіші құрама сан: 4. Мысалы: 4, 6, 8, 102
1 саны – жай сандарға да, құрама сандарға да жатпайды. Оның бір ғана бөлгіші бар.
Егер көбейткіштердің біреуі берілген санға бөлінсе, онда көбейтінді де сол санға бөлінеді. Мысалы: 24*19*7 көбейтіндісі 6 ға бөлінеді. Себебі 24 саны 6 ға бөлінеді.
Егер қосылғыштардың әрқайсысы жеке-жеке берілген санға бөлінсе, онда қосынды да сол санға бөлінеді. Мысалы: (84+28) қосындысы 14 ке бөлінеді, себебі 84 те, 28 де 14 ке қалдықсыз бөлінеді.
Егер азайғыш та, азайтқыш та берілген санға жеке-жеке бөлінсе, онда айырма да сол санға бөлінеді. Мысалы: (27-9) айырмасы 3 ке бөлінеді, себеі 27 де, 9 да 3 ке бөлінеді.
2-ге – жазылуы жұп цифрлармен аяқталған натурал сандар бөлінеді. Мысалы: 12, 100, 1882, 1134
4-ке – жазылуында соңғы екі цифрларынан құралған натурал сан 4 ке бөлінсе немесе екі нөлмен аяқталса, берілген санда 4-ке бөлінеді. Мысалы: 128, 1980, 112, 25436
8-ге – жазылуында соңғы үш цифрларынан құралған натурал сан 8-ге бөлінсе немесе үш нөлмен аяқталса, берілген сан 8-ге бөлінеді. Мысалы: 8120, 1880, 45120
3-ке – жазылуындағы цифрларының қосындысы 3-ке бөлінсе, берілген сол натурал сан 3-ке бөлінеді. Мысалы: 10245 ал 1+0+2+4+5=12 болады. Ал 12 саны 3-ке бөлінеді, демек 10245 саныда 3-ке бөлінеді.
6-ға – жазылуында соңғы цифры жұп болса және цифрлар қосындысы 3-ке бөлінсе, сол натурал сан 6-ға бөлінеді. Мысалы: 144810 саны жұп сан, және 1+4+4+8+1+0=18 болады. Содан 144810 саны 6-ға бөлінеді.
9-ға – жазылуындағы цифрлар қосындысы 9-ға бөлінсе, сол натурал сан 9-ға бөлінеді. Мысалы: 7893 саны 7+8+9+3=27 болады. Содан 7893 саны 9-ға бөлінеді.
5-ке – жазылуында соңғы цифры 0 немесе 5 цифрымен аяқталса,сол натурал сан 5-ке бөлінеді. Мысалы: 485, 770
10-ға – жазылуында соңғы цифры 0 мен аяқталса, сол натурал сан 10-ға бөлінеді. Мысалы: 1130, 190, 70
Дәреже – бірнеше бірдей
көбейткіштердің көбейтіндісін көрсететін өрнекті айтамыз. Мысалы:
2*2*2*2*2= деп жазуға
болады.
деп жазуға
болады.
Санның
квадраты – санның 2-ші дәрежесі.
Мысалы:  - он төрттің
квадраты.
- он төрттің
квадраты.
Санның
кубы – санның 3-ші
дәрежесі.  – бестің
кубы.
– бестің
кубы.
Құрама санды жай көбейткіштерге жіктеу – оны тек қана жай сандардың көбейтіндісі түрінде жазу. Оны вертикаль сызық арқылы баған түрінде бөліп табамыз. Мысалы: 420=2*2*3*5*7
Берілген натурал сандардың ЕҮОБ-і деп, сол сандардың әрқайсысы бөлінетін ең үлкен натурал сан. Мысалы ЕҮОБ(36,24)=12
Берілген натурал сандардың әрқайсысына еселік болатын ең кіші натурал санды сол сандардың ЕКОЕ-сі деп атаймыз. Мысалы: ЕКОЕ(4,6)=12
ЖАЙ БӨЛШЕКТЕР
Берілген шаманы өзара тең
бөліктерге бөліп, оның бір немесе бірнеше бөлігін кескіндейтін
сан жай
бөлшек түрінде жазуға болады.
Мысалы:  ,
,
 ,
, 
Бөлшектің
алымы – бөлшек сызығының төбесіндегі
сан. 
Бөлшектің
бөлімі – бөлшек сызығының астындағы
сан. 
Егер бөлшектің алымын да,
бөлімінде бірдей натурал санға көбейтсек немесе бөлсек, онда
оған тең
бөлшек алынады.
Мысалы: 
Бөлшектің алымын да, бөлімін
де 1-ден өзге ортақ бөлгішке бөлуді
бөлшекті
қысқарту деп атайды.
Мысалы: 
Бұрыс
бөлшек – алымы бөлімінен үлкен немесе
тең бөлшек. Кез келген бұрыс бөлшек 1-ден үлкен немесе тең.
Мысалы: 
Дұрыс
бөлшек – алымы бөлімінен кіші бөлшек.
Кез келген дұрыс бөлшек 1-ден кіші. Мысалы:

Аралас
сан – бүтін бөліктен және бөлшек
бөліктен тұратын сан аралас сан деп аталады.
Мысалы: 
Кез келген натурал
санды аралас сан түрінде
жазуға болады.
Мысалы: 
Кез
келген бұрыс бөлшекті аралас сан
түрінде жазуға болады.
Мысалы:  (13:3=4
(1қалдық))
(13:3=4
(1қалдық))
Кез
келген аралас санды бұрыс бөлшекке
айналдыруға болады.
Мысалы: 
Координаталық
сәуледе  дұрыс бөлшегін кескіндеу
үшін, бірлік кесіндіні өзара тең a бөлікке бөліп, санақ басынан
бастап b бөлігін алу керек.
Мысалы:
дұрыс бөлшегін кескіндеу
үшін, бірлік кесіндіні өзара тең a бөлікке бөліп, санақ басынан
бастап b бөлігін алу керек.
Мысалы: 
![]()
ЖАЙ БӨЛШЕКТЕРГЕ АМАЛДАР ҚОЛДАНУ
Берілген бөлшектердің
бөлімдерінің ең кіші ортақ еселігі сол
бөлшектердің ең кіші ортақ
бөлімі болады.
Мысалы:  бөлшектерінің
бөлімдерінің ең кіші ортақ еселігі 24 болады, себебі ЕКОЕ(8,6)=24.
Содан
бөлшектерінің
бөлімдерінің ең кіші ортақ еселігі 24 болады, себебі ЕКОЕ(8,6)=24.
Содан 
Жай бөлшектерді салыстыру:
-бөлімдері бірдей
бөлшектердің алымдары қайсысы үлкен сол
бөлшек үлкен болады. Мысалы:  ,
,

-алымдары бірдей
бөлшектердің бөлімі қайсысы үлкен
сол бөлшек кіші болады. Мысалы:  ,
,

-алымы да, бөліміде әр түрлі
бөлшектерді салыстыру үшін, оларды
көбелек тәсілімен тексеріп көреміз. Мысалы:

-аралас
cандарды салыстырғанда, алдымен бүтін
бөліктерін салыстырамыз. Егер бүтін бөліктері бірдей боглса, онда
бөлшек бөліктерін салыстырамыз. Мысалы:
 ,
, 
Бөлімдері
бірдей бөлшектерді қосқанда және
азайтқанда тек алымдарын есептейміз, ал
бөлімі өзгеріссіз қалады: 

Бөлімдері әр түрлі бөлшектерді қосқанда немесе азайтқанда, бөлшектерді бірдей ортақ бөлімдерге келтіріп, сосын есептейміз:


Аралас сандарды қосып
азайтқанда олардың алдымен бүтін
бөліктері, сосын бөлшек бөлімдері жеке-жеке қосылып азайтылады,
немесе бұрыс бөлшекке айналдырып есептелінеді.
Мысалы: 
Аликвоттық
бөлшек – алымы 1-ге тең дұрыс бөлшек.
Кез келген аликвоттық бөлшек 1-ден кіші. Ең үлкен аликвоттық
бөлшек  ге тең.
Мысалы:
ге тең.
Мысалы: 
Бөлшекті натурал санға көбейту үшін, оның алымын натурал санға көбейтіп, бөлімін өзін қалдыру керек:

Екі бөлшекті көбейту
үшін сол бөлшектердің алымдарын
өзара көбейту керек, және бөлімдерін өзара көбейтеміз.
Мысалы: 
Аралас сандарды көбейту
үшін оларды алдымен бұрыс
бөлшектерге айналдырып, сосын барып
көбейтеміз: 
Өзара кері
сандар – екі санның көбейтіндісі 1-ге
тең болатын сандарға айтамыз:  ,
,

Бөлшектерді бөлу
үшін бөлінгішті бөлгіштің кері
санына көбейту арқылы табамыз: 
МӘТІНДІ ЕСЕПТЕР
Санның бөлігін табу
үшін – санды осы бөлшекке көбейту
керек. Мыс: 18 км дің  бөлігін тап десе
18*
бөлігін тап десе
18* =2*2=4км,
=2*2=4км,  бөлігін тап
десе
бөлігін тап
десе

Бөлігі бойынша санды
табу үшін бөлікке сәйкес санды осы
бөлшекке бөлу керек. Мысалы: машина 145км жүрді. Бұл оның барлық
жүруге тиісті жолының  -індей. Машинаның барлық
жүруге тиісті жолын тап. 145:
-індей. Машинаның барлық
жүруге тиісті жолын тап. 145: =145*
=145*
Бірлесіп жұмыс
жасау формуласы:  мұндағы х-бұл бірінші
жұмысшының жалғыз өзі істесе сол жұмысты аяқтайтын уақыты, у-бұл
екінші жұмысшының уақыты, ал t-бұл екі жұмысшының бірлесе жасағанда
аяқтайтын уақыты.
мұндағы х-бұл бірінші
жұмысшының жалғыз өзі істесе сол жұмысты аяқтайтын уақыты, у-бұл
екінші жұмысшының уақыты, ал t-бұл екі жұмысшының бірлесе жасағанда
аяқтайтын уақыты.
ОНДЫҚ БӨЛШЕКТЕР ЖӘНЕ ОЛАРҒА АМАЛДАР ҚОЛДАНУ
Ондық
бөлшек деп - бірліктен де кіші
разрядтары бар ондық жүйеде жазылған санға айтылады. Мысалы: 3,724
ондық бөлшегінде 3 бірлік, 7 ондық үлес, 2 жүздік үлес, 4 мыңдық
үлес бар. 3 бүтін бөлігі, ал 724 бөлшек бөлігі. Және ол жай
бөлшекпен жазғанда оқылуы бойынша жазамыз және олар қысқарса
қысқартуға болады: 3,724= =
= 3
3
Жай бөлшекті ондық бөлшекке
айналдыру үшін бөлшектің бөлімін 10 ға еселі
санға айналдыру керек. Оның бөлімін жай көбейткіштерге жіктегенде
тек 2 немесе 5 немесе 10-ға еселі сандардан құралу
керек:  =
= =
=
Ондық бөлшекті
координаталық сәуледе кескіндеу
жай бөлшекті немесе аралас
санды кескіндеу сияқты орындалады:
Ондық бөлшектерді салыстырғанда – алдымен олардың бүтін бөліктерін салыстырамыз, егер ол тең болған жағдайда бөлшек бөлігін үтірден кейінгі үлестері бойынша салыстырамыз: 6,78>6,762 , (мұнда бүтін бөліктері тең, 7 лері тең, бірақ 8>6) және координаталық сәуледе үлкен ондық бөлшек оң жақта, ал кіші ондық бөлшек сол жақта орналасады.
Ондық бөлшектерді қосқанда немесе азайтқанда олардың үтірден кейінгі үлестердегі цифрлар саны теңестіріледі баған түрінде жазылып есептелінеді, үтірлер бір қатарда тұру керек. Мысалы:
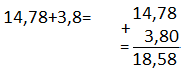
Ондық бөлшекті натурал санға көбейткенде үтірге назар аудармай көбейтеміз. Сосын көбейткіштің үтірінен кейін неше цифр болса, көбейтінді мәнінде сонша қалатындай етіп үтір қоямыз. Мысалы:
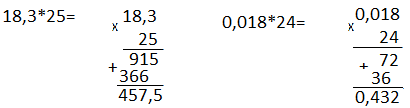
Ондық бөлшекті ондық бөлшекке көбейткенде, көбейткіштердің үтірлеріне назар аудармай көбейтеміз, шыққан мәніне көбейткіштердің үтірінен кейін неше цифр болса сонша цифр болатындай етіп үтір қоямыз:
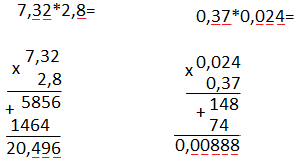
Ондық бөлшекті натурал санға бөлу натурал сандарды бөлудегідей орындалады. Ондық бөлшек

шағым қалдыра аласыз















