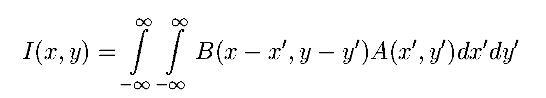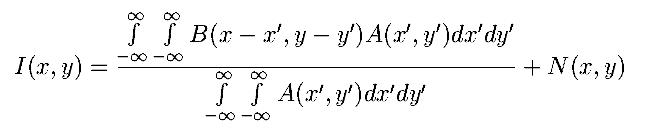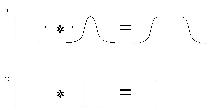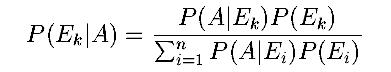Қазақстан Республикасы Білім
және ғылым министрлігі
Ы. Алтынсарин атындағы Арқалық
педагогикалық институты

Реферат
Тақырыбы: Радиоастрономиялық деректерді
талдаудың кейбір мәселелері
Орындаған: Пернебай
Асылай
Арқалық
2020ж.
|
№
|
Мазмұны
|
|
1.
|
Кіріспе
|
3
|
|
2.
|
Негізгі
бөлім
|
|
|
2.1
|
Эксперимент формуласы. Алгоритмдерді құру
|
3
|
|
2.2
|
Жіктеу параметрлері.
Жіктеулерді компьютерлік
модельдеу
|
5
|
|
2.3
|
Есептеу теоремасы.
Беріктік
|
10
|
|
2.4
|
Суреттерді қалпына келтіру
туралы. Максималды энтропия
әдісі
|
15
|
|
2.5
|
Көріністер. Көріністер
классификациясы. Көріністің статистикалық
сипаттамалары
|
18
|
|
2.6
|
Нысандар атаулары. МАС
ұсыныстары
|
22
|
|
2.7
|
Мұрағаттау мәселелері. FITS.
FITS кеңейтілімдері
|
24
|
|
2.8
|
Деректерді өңдеу жүйелері.
Linux және астрономиялық бағдарламалық
жасақтама
|
26
|
|
Қорытынды
|
33
|
|
Пайдаланылған әдебиеттер
тізімі
|
33
|
|
Қосымшалар
|
34
|
Кіріспе
Мүмкін, әрбір
астроном-бақылаушы, ең қызықты нысандарды зерттеуге алмас бұрын,
кейде: "Мұны істеу керек пе?''-деген сұрақ қояры анық. Бұл сұрақ
нақты адамның өмір сүру мәнімен ғана емес, оның техникалық және
ақпараттық жабдықталуымен байланысты.
Астрономиялық институттарға
келетін жастардың соңғы буынының тәжірибесі бірінші кезекте олар
алынған деректерді техникалық және бағдарламалық қамтамасыз етуге
және өңдеуге байланысты проблемалар кездесетінін көрсетеді. Жас
ғалымның жетістігі жиі осы міндеттерді жүзеге асыру деңгейіне
байланысты. Бағдарламалық қамтамасыз ету деңгейіндегі экспериментті
автоматтандырудың көптеген мәселелері қазір оңтайлы шешілген. Кейде
бірнеше апта болған нәрсе (мысалы, қажетті мақаланы іздеу) енді
бірнеше минут ішінде шешілуі
мүмкін.
Осы жұмысымда, аспанда не
болып жатқанын және соңғы нәтиже қалай болатынын түсіну үшін
маңызды болып табылатын бірнеше сәттерді атап көрсетуді мақсат
тұттым. Бұл жұмыс ақпараттың толықтығын талап етпейді, тек қана
радиоастрономдарға (және тек қана емес) кезігетін мәселелер
шеңберін бейнелейді. Бұл жұмысымда мен кең жолақты радиометрлерде
алынған құрлықтық деректерді өңдеу мәселелеріне
тоқталамын.
2.1. Эксперимент формуласы.
Алгоритмдерді құру
Эксперимент
формуласы
Аспанға қарапайым көзбен
немесе аспаптың көмегімен қарап, біз объектінің бейнесі туралы
келіп түскен ақпаратты іздедік. Біздің бақылауымыздың парадоксы біз
әрқашан шын мәнінде не екенін көре бермейміз. Әр түрлі адамдар
әртүрлі құбылыстарды байқайтыны бұрыннан белгілі (шектеулі
сезімталдығы бар кем дегенде түсті ажырата алмайтындарды
(дальтониктерді) еске түсіріңіз).
Оптикалық телескоп сияқты
радиоастрономияда радиотелескоп - зерттеу объектісін сипаттайтын
функцияға әсер ететін желілік оператордың рөлін атқарады.
Зерттелетін объект бойынша радиоқабылдағышты жіктеудегі әрбір нүкте
дифракциялық дақ немесе шашырау дақ түрінде радиотелескоп фокусында
бейнеленеді (Есепкинада сипатталған және т.б., 1974). Объектінің әр
түрлі нүктелерінен осы дақтардың суперпозициясы принципін пайдалана
отырып, антенна тегістеудің келесі іргелі теңдеуін жазуға
болады:
|
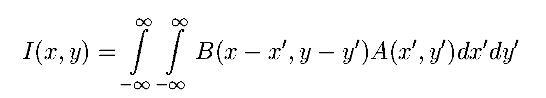
|
(1)
|
Мұндағы B(x,y) - объект бойынша
радиобіркілікті жіктеу, A(x',y') - радиотелескоптың бағытталу
диаграммасы, I(x,y) - сәулелену көзі жасайтын радиотелескоптың
фокальды жазықтығында қуаттың байқалатын
жіктелуі.
Толық дұрыс болу үшін
аппараттық функцияның астындағы интегралға нормалауды ескеру қажет
(жарықтық температура қоршаған антеннада кеңістікте тұрақты болған
жағдайда антенна мен орта арасындағы термодинамикалық тепе-теңдік
жағдайынан 1-ге тең). Сонымен қатар, "антенна-радиометр" жүйесінің
шығуында біз қабылдағыштың, антеннаның және жердің сәулеленуінің
тұрақсыздығынан туындаған N(x, y) кездейсоқ қуат тербелісін
байқаймыз. Сонда толық жарықтықты
жіктеу, біз осы түрде ұсына
аламыз:
|
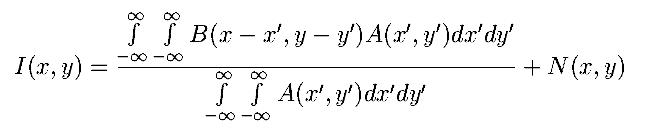
|
(2)
|
Жазуды жеңілдетіп, бақылау
процесін сипаттау үшін осындай формуланы аламыз (оны эксперимент
формуласы деп атаймыз):
I = B * A +
N
(3)
Мұнда I-бақылау нәтижесі,
B-объектінің жарықтығын нақты жіктеу, A - аппараттық функция: аспап
+ көз, N - көп компонентті шу N = Nsky * A + Nsys, мұнда Nsky -
сигналдың галактикалық газ және жер атмосферасы арқылы өтуіне
байланысты шу (аппараттық функциямен тегістеледі), Nsys-телескоп
жүйесінің шуы+қабылдағыш+көз. '*' (Жұлдызша) таңбасы орау әрекетін
білдіреді.
Интегралды көріністегі
функциялар қарама-қарсы белгілердің аргументтері бар, олардың
қиылысу аймағында интегралдау болады. Бұл интегралдың мәні осы
тегістеу қадамында ағымдағы ұю нүктесі бар. Бұл сурет
көрсетілген:
1. Аппараттық функцияның
астындағы интегралға нормалау сигналдың нақты амплитудасын сақтауға
мүмкіндік береді. –№1суретте орау функциясының түрленуін көрсететін
2 мысал келтірілген.
|
|
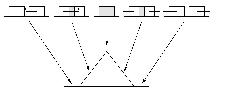
Сурет.1. Орау
процесін түсіндіретін схема. Екі бірдей тікбұрышты функциялардың
орамы үшбұрыш береді.
|
Бұл
коммутациялық операция, яғни функциялар орын ауыстырса, интеграл
өзгермейді:
B *
A = A * B,
(4)
бұл аддитивті операция, яғни A
функциясы бар екі функцияның санын орау, А функциясы бар әрбір
функцияның орамасын береді:
(B1 + B2) * A = B1 * A + B2 *
A.
(5)
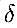 функциясымен орау функцияның
өзін өзгертпейді (сондай-ақ Сурет.2
қараңыз):
функциясымен орау функцияның
өзін өзгертпейді (сондай-ақ Сурет.2
қараңыз):
|
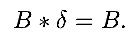
|
(6)
|
|
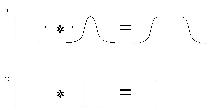
|
Сурет.2. Әртүрлі
функциялар: тіктөртбұрыш және гауссиана (1) және тіктөртбұрыш
және 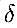 -функциялар, орамын
бейнелейтін схема. -функциялар, орамын
бейнелейтін схема.
|
Мүмкін, әзірге орам туралы
жеткілікті.
Осылайша, теңдеуді
шешкеннен(3) кейінгіобъектінің қалай көрінетінін түсінуге болады
(яғни B табу). Бірақ мәселе, түйіннен басқа, теңдеуде N шу бар. Шу
болмаса да, бұл мәселе дұрыс емес, яғни кіріс мәліметтерінің аз
өзгерістеріне кез-келген үлкен шешім өзгерістеріне сәйкес келуі
мүмкін. Жалпы айтқанда, бақылау астрофизикасының барлық міндеттері
дұрыс емес, өйткені, объектінің бақылау көріністері бойынша оның
тікелей өлшемдерге қол жетпейтін сипаттамаларын белгілеуді талап
етеді. Бірақ, кейбір тәсілдерді пайдалана отырып, біз көріп отырған
нәрселерді түсінуге жақындауға
болады.
Ал енді міндетті шешуге
көмектесуге қабілетті біздің құралдарымызға шолу
жүргізсек.
Біріншіден
бастайық.
Алгоритмдерді
құру
Алгоритмдер ұғымына есепті
шешудің жалпы әдісі, сондай-ақ теңдеулер немесе компьютерлік кодтар
түрінде әдісті нақты математикалық іске асыру кіреді. Біз екінші
жағдайды қарастырамыз.
Қазіргі кезде көптеген
қолданбалы астрономиялық міндеттер, атап айтқанда, бейнелерді
қалпына келтіру міндеттері (атап айтқанда, B теңдеуде (3) табу)
әртүрлі бағыттардағы әдістерді - геофизикадан медицинаға дейінгі
ғылымды дамытуға ықпал етеді.
Бірақ дұрыс емес есептерді
шешу мүмкіндігі туралы айтпас бұрын, өңдеу процедураларын түсіну
үшін математиканың бірнеше бөлімдері туралы айту қажет, олар одан
әрі өңдеу қадамдарын түсіндіру кезінде қажет болады. Бұл
Фурье-талдау статистикасының
негіздері.
2.2. Жіктеу параметрлері.
Жіктеулерді компьютерлік
модельдеу
Жіктеу
параметрлері
Алда пайдалы болуы мүмкін
ықтималдықтар теориясының кейбір анықтамалары еске
түсірейік.
Біріктіру (логикалық
сан) E1UE2U... (немесе E1+E2+...)
E1,
E2,..., оқиғалардың соңғы немесе
шексіз кезектілігі, E1,
E2,..., оқиғаларының кем дегенде
біреуін жүзеге асыруға арналған оқиға
бар.
Біріктіру (логикалық
туынды) E1,
E2 E1 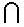 E2 (немесе E1 E2)
екі E1 және E2 ,
Е1 және
Е2 жүзеге асыруда болатын оқиға
бар.
E2 (немесе E1 E2)
екі E1 және E2 ,
Е1 және
Е2 жүзеге асыруда болатын оқиға
бар.
E1 және
E2 оқиғалары сәйкес емес деп
аталады, егер E1U
E2=0 болса, - логикалық туындыда
мүмкін емес оқиға бар (яғни
E1 және
E2 оқиғаларына
тиесілі Е класындағы бірде-бір оқиға
жүзеге асырылмайды).
Ықтималдықтың көптеген
анықтамалары бар. Классикалық анықтаманы
қарастыруды көрсете
отырып(қолайлы оқиғалар санының тең
мүмкіндіктерінің санына қатынасы ретінде), екуіне тоқталайық.
Бірінші анықтама ықтималдықтың мәнін көрсетеді, ал екіншісі оны
функция ретінде сипаттайды.
Оқиғаның ықтималдығы
(статистикалық мағынада) сынақтар (бақылаулар) санының шектелмеген
ұлғаюы кезінде оқиғаның салыстырмалы жиілігі ұмтылатын шек болып
табылады (Агекян, 1974).
P(E) оқиғаның ықтималдығы Е
оқиғалар класында анықталған Е үш шартты (Ықтималдықтар аксиомасы)
қанағаттандыратын бір мәнді нақты функция деп
аталады):
1) 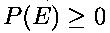 E
ішіндегі E кез келгеноқиға
үшін;
E
ішіндегі E кез келгеноқиға
үшін;
2) P(I) =
1 І нақты оқиға үшін;
3) P(E1UE1U...) =
P(E1) +
P(E2)+... кез келген (соңғы немесе
шексіз) бірізділік үшін екіге сәйкес емес оқиғалар E1, E2 (Корн &
Корн, 1984).
E1 оқиғасының
P(E|E1) шартты ықтималдығы
E1 оқиғаны жүзеге асыру шартымен
Р(E U E1) =
P(E1)
P(E|E1) (ықтималдықтарды көбейту
ережесі) аксиомамен анықталады.
Байес теоремасы
Ek оқиғаларының бірінің
E1 толық тобының шартты
ықтималдықтары үшін өрнек береді
E1...,
En (яғни үйлеспейтін оқиғалар
топтары, олардың бірі дұрыс болуы тиіс) А оқиғасы болған
жағдайда:
|
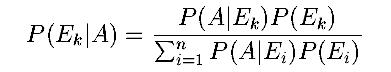
|
(7)
|
Немесе (Агекян,
1974)
|
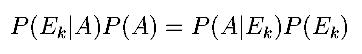
|
(8)
|